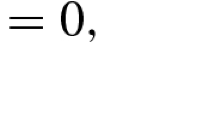On Stability and Instability of $C^{1,\alpha }$ Singular Solutions to the 3D Euler and 2D Boussinesq Equations

Abstract

Singularity formation of the 3D incompressible Euler equations is known to be extremely challenging (Majda and Bertozzi in Vorticity and incompressible flow, Cambridge University Press, Cambridge, vol 27, 2002; Gibbon in Physica D 237(14):1894–1904, 2008; Kiselev, in: Proceedings of the international congress of mathematicians, vol 3, 2018; Drivas and Elgindi in EMS Surv Math Sci 10(1):1–100, 2023; Constantin in Bull Am Math Soc 44(4):603–621, 2007). In Elgindi (Ann Math 194(3):647–727, 2021) (see also Elgindi et al. in Camb J Math 9(4), 2021), Elgindi proved that the 3D axisymmetric Euler equations with no swirl and $C^{1,\alpha }$ initial velocity develops a finite time singularity. Inspired by Elgindi’s work, we proved that the 3D axisymmetric Euler and 2D Boussinesq equations with $C^{1,\alpha }$ initial velocity and boundary develop a stable asymptotically self-similar (or approximately self-similar) finite time singularity (Chen and Hou in Commun Math Phys 383(3):1559–1667, 2021) in the same setting as the Hou-Luo blowup scenario (Luo and Hou in Proc Natl Acad Sci 111(36):12968–12973, 2014; Luo and Hou in SIAM Multiscale Model Simul 12(4):1722–1776, 2014). On the other hand, the authors of Vasseur and Vishik (Commun Math Phys 378(1):557–568, 2020) and Lafleche et al. (Journal de Mathématiques Pures et Appliquées 155:140–154, 2021) recently showed that blowup solutions to the 3D Euler equations are hydrodynamically unstable. The instability results obtained in Vasseur and Vishik (2020) and Lafleche et al. (2021) require some strong regularity assumption on the initial data, which is not satisfied by the $C^{1,\alpha }$ velocity field. In this paper, we generalize the analysis of Elgindi (Ann Math 194(3):647–727, 2021), Chen and Hou (Commun Math Phys 383(3):1559–1667, 2021), Vasseur and Vishik (2020) and Lafleche et al. (2021) to show that the blowup solutions of the 3D Euler and 2D Boussinesq equations with $C^{1,\alpha }$ velocity are unstable under the notion of stability introduced in Vasseur and Vishik (2020) and Lafleche et al. (2021). These two seemingly contradictory results reflect the difference of the two approaches in studying the stability of 3D Euler blowup solutions.

1 Introduction

Whether the 3D incompressible Euler equations can develop a finite time singularity from smooth initial data with finite energy is one of the most challenging open questions in nonlinear partial differential equations [20, 25, 37, 45, 51]. In [49, 50], the authors provided convincing numerical evidence that the 3D incompressible Euler equations with smooth initial data and boundary develop a finite time singularity. This work has inspired a number of subsequent theoretical studies,see e.g. [11, 15,16,17,18, 29, 31, 43, 44]. Inspired by Elgindi’s seminal work on singularity formation of the 3D axisymmetric Euler equations with no swirl and $C^{1,\alpha }$ velocity [26], we have proved rigorously that the axisymmetric Euler and the 2D Boussinesq equations with $C^{1,\alpha }$ initial velocity of finite energy and boundary develop a stable asymptotically self-similar (or approximately self-similar) finite time singularity [11]. There has been some important progress on singularity formation and small-scale creation in incompressible fluids. We refer to [25, 45] for excellent surveys. On the other hand, in two recent papers [46, 64], the authors showed that blow-up solutions to the 3D Euler equations are hydrodynamically unstable. The instability results obtained in [46, 64] require some strong regularity assumption on the initial data, which is not satisfied by the $C^{1,\alpha }$ velocity. In this paper, we generalize the analysis of [11, 26, 27, 46, 64] to prove that the $C^{1,\alpha }$ blowup solutions of the 3D Euler and the 2D Boussinesq equations [11, 26, 27] are unstable under the notion of stability introduced in [46, 64].

These two seemingly contradictory results reflect the difference of the two approaches in studying the stability of singular solutions to the 3D Euler equations. The stability analysis in [46, 64] is based on the linearized Euler equations around a blowup solution in the original physical variables. However, the perturbed solution of the linearized Euler equations is completely different from the perturbed solution of the original 3D Euler equations using a perturbed initial condition. To demonstrate this point, if the perturbed initial condition leads to a blowup time $T_*$ that is smaller than the blowup time T of the background blowup solution, i.e. $T_* < T$, the perturbed solution of the linearized Euler equations would not be able to capture this effect and will remain regular for $t \in [T_*,T)$. This seems to be one of the main sources of instability induced by the framework of studying stability of a singular solution to the 3D Euler equations using the linearized Euler equations. See more discussion on mechanisms of instability in Sect. 1.2. Note that the blowup time $T_*$ depends nonlinearly on the perturbed initial data [11, 27].

The nonlinear stability of the asymptotically self-similar (or approximately self-similar) blowup profile using the dynamic rescaling formulation [11, 13, 47, 54] is very different from the linear stability performed in [46, 64] and mentioned above. The method based on this formulation first involves a nonlinear transform of the physical equations by rescaling the solution dynamically in the spatial and the temporal variables, and then performs linearization around an approximate blowup profile and stability analysis in the reformulated equations. Since the linearization is performed after we make this nonlinear transform, the linear stability under this framework captures some nonlinear behaviors of the original physical equations. This approach allows us to incorporate the changes of the blowup time, the blowup profile and the blowup exponent (see $\beta$ below) by choosing suitable rescaling parameters that come from the scaling symmetry of (1.1) or (1.5). Note that the dynamic rescaling formulation is closely related to the modulation technique [42, 58], which has also been used to establish nonlinear stability of the blowup profile of 3D Euler [26, 27].

We remark that the authors of [46] also studied the profile instability of a self-similar blowup solution to the 3D Euler equations in [46]. More specifically, given a background self-similar blowup solution $u(x, t) = (T- t)^{\alpha } U( t, \frac{x}{ (T-t)^{\beta }} )$, the authors assumed that the perturbed solution of the linearized equation (1.2) takes the same form $v(x, t) = (T- t)^{\alpha } V( t, \frac{x}{ (T-t)^{\beta }} )$. Thus, the perturbed solution of the linearized equation does not capture the change in the blowup time and the dynamic changes of the rescaling rate of the perturbed profile and the blowup exponent $\beta$ of the original 3D Euler equations using a perturbed initial condition.

The 3D incompressible Euler equations read

$$\begin{aligned} {\textbf{u}}_{t} + {\textbf{u}}\cdot \nabla {\textbf{u}}= -\nabla p, \quad \nabla \cdot {\textbf{u}}= 0, \end{aligned}$$

(1.1)

where ${\textbf{u}}$ is the velocity field and p is the scalar pressure. In [64], the authors studied the stability of a singular solution ${\textbf{u}}(t)$ of the 3D Euler equations by analyzing the growth of the perturbation ${\textbf{v}}(t)$ using the following linearized Euler equations around ${\textbf{u}}(t)$:

$$\begin{aligned} {\textbf{v}}_t + {\textbf{u}}\cdot \nabla {\textbf{v}}+ {\textbf{v}}\cdot \nabla {\textbf{u}}+ \nabla q = 0, \quad \nabla \cdot {\textbf{v}}= 0. \end{aligned}$$

(1.2)

In a subsequent paper [46], the authors generalized their earlier results to the axisymmetric Euler equations. Recall that a vector field f(x) is axisymmetric [51] if it can be represented as

$$\begin{aligned} f(x) = f^r(r, z) e_r + f^{\vartheta }(r, z) e_{\vartheta } + f^z(r, z) e_z, \end{aligned}$$

(1.3)

where $(r,\vartheta , z)$ are the cylindrical coordinates with basis $e_r = ( \cos \vartheta , \sin \vartheta , 0 )$, $e_{\vartheta } = ( - \sin \vartheta , \cos \vartheta , 0)$, $e_z = (0, 0, 1)$. For a solution ${\textbf{u}}$ with axisymmetric initial data ${\textbf{u}}_0$, the axisymmetry property is preserved dynamically by the Euler equations (1.1).

1.1 Main results

We consider singular solutions ${\textbf{u}}$ to (1.1) in a domain D with the following symmetry in z

$$\begin{aligned} {\textbf{u}}= u^r e_r + u^{\vartheta } e_{\vartheta } + u^z e_z, \quad u^r, u^{\vartheta } \mathrm { \ are \ even \ in \ } z , \quad u^{z} \mathrm { \ is \ odd \ in \ } z. \end{aligned}$$

(Sym)

Denote by X the set of axisymmetric functions with symmetry given in (Sym), $H_X^1(D) = H^1( D) \cap X$. Let ${\textbf{v}}$ be the solution of the linearized Euler equations (1.2) with initial data ${\textbf{v}}_0$. Following [46], we define the growth factors $\lambda _{p, \sigma , D }(t)$ and $\lambda ^{sym}_{p, \sigma , D }(t)$ as follows:

$$\begin{aligned} \begin{aligned}&\lambda _{p, \sigma , D }(t) = \sup _{ {\textbf{v}}_0 \in H^1( D) \cap Y, {\textbf{v}}_0 \ne 0 } \frac{ || r^{-\sigma } {\textbf{v}}(t, \cdot ) ||_{L^{p}( D ) } }{ || r^{-\sigma } {\textbf{v}}_0 ||_{L^{p}(D ) } } , \\&\lambda ^{sym}_{p, \sigma , D }(t) = \sup _{ {\textbf{v}}_0 \in H_X^1( D) \cap Y, {\textbf{v}}_0 \ne 0 } \frac{ || r^{-\sigma } {\textbf{v}}(t, \cdot ) ||_{L^{p}( D ) } }{ || r^{-\sigma } {\textbf{v}}_0 ||_{L^{p}( D ) } } , \ Y = L^p, \ \\&\sigma \le \sigma _p , \ Y = H^1(D), \ \sigma > \sigma _p , \end{aligned} \end{aligned}$$

(1.4)

where $\sigma _p = - \frac{2(p-1)}{p}$. The functional spaces, e.g. the weight $r^{-\sigma }$ and $L^p$ norm, in the above definitions are the same as those in [46]. If $\sigma \le \sigma _p$, we further restrict the initial data to $v_0 \in L^p$ so that $r^{-\sigma } v(t, \cdot ) \in L^p(D)$ for a domain D with bounded r. See Remark 1.1 for more discussions about the spaces. We note that if one measures the growth in a norm X stronger than $L^p$, it is not difficult to prove instability. See Sect. 2.4 for more discussion. We also refer to [46, 64] for the motivations of the above definition of instability. Note that restricting $v_0$ to a smaller class of functions only makes the growth factor smaller. In particular, we have $\lambda ^{sym}_{p, \sigma }(t) \le \lambda _{p, \sigma }(t)$ since $H_X^1(D)$ is a subclass of axisymmetric functions in $H^1( D )$.

In the first main result, we consider (1.1) in a cylinder $D = \{ (r, z): r \le 1, z \in {\mathbb {T}}\}$ periodic in z (axial direction) with period 2, where r is the radial variable and ${\mathbb {T}}= {\mathbb {R}}/ (2 {\mathbb {Z}})$. This setting is the same as that in [11, 49, 50]. We prove that the blowup solution constructed in [11] is linearly unstable under the notion of stability introduced in [46], even in the symmetry class (Sym).

Theorem 1

There exists $\alpha _0 > 0$ such that for any $0< \alpha < \alpha _0$, the 3D axisymmetric Euler equations (1.1) in the cylinder $(r, z) \in [0, 1] \times {\mathbb {T}}$ develops a singularity at finite time $T_*$ from some $C^{1,\alpha }$ initial data ${\textbf{u}}_0$ with finite energy. Moreover, there exists $R_{2,\alpha } < \frac{1}{4}$, such that the solution ${\textbf{u}}$ (1.3) satisfies $u^r, u^z, u^{\vartheta } \in L^{\infty }( [0, T], C^{50}( \Sigma ) )$ for any compact domain $\Sigma \subset \{ (r, z): r \in (0, 1), z \ne 0 \} \cap B_{ (1,0)}( R_{2,\alpha })$ and $T < T_*$. For any $p \in [1, \infty )$ and $\sigma < \frac{2}{p}$, we have

$$\begin{aligned} \lim _{t \rightarrow T_*} \lambda ^{sym}_{p, \sigma , D}(t) = \infty . \end{aligned}$$

Note that the range of $\sigma$ is larger than that in [46]. We can prove this range of $\sigma$ since the singular solution [11] is supported near $(r, z) = (1, 0)$, which allows us to construct an unstable solution with fast growth near $(r, z) = (1, 0)$. In such a region, the weight $r^{-\sigma }$ in (1.4) is essentially equal to 1.

In the second main result, we consider the singular solution in ${\mathbb {R}}^3$ constructed by Elgindi [26] (see also [27]) and prove a similar instability result for a smaller range of parameter $\sigma < -1$.

Theorem 2

There exists $\alpha _0 > 0$ such that for any $0< \alpha < \alpha _0$, the 3D axisymmetric Euler equations (1.1) in ${\mathbb {R}}^3$ develops a singularity at finite time $T_*$ from some $C^{1,\alpha }$ initial data ${\textbf{u}}_0$ with finite energy and without swirl. Moreover, the solution ${\textbf{u}}$ (1.3) satisfies $u^{\vartheta } \equiv 0, u^r, u^z \in L^{\infty }( [0, T], C^{50}( \Sigma ) )$ for any compact domain $\Sigma \subset \{ (r, z): r >0, z \ne 0 \}$ and $T < T_*$. For any $p \in (2, \infty )$ and $\sigma \in ( - \frac{2 (p-1)}{ p}, -1 )$, we have

$$\begin{aligned} \lim _{t \rightarrow T_* } \lambda ^{sym}_{p, \sigma , {\mathbb {R}}^3}(t) = \infty . \end{aligned}$$

Note that for $p \in [1, 2]$, the interval $( - \frac{2 (p-1)}{ p}, -1 )$ is empty.

Remark 1.1

We remark that for general $\sigma , p$ and solution v to the linearized Euler equations (1.1) from smooth initial data $v_0$, v may not remain in the weighted space $r^{-\sigma } v \in L^p$ locally in time. For $\sigma \in (- \frac{2(p-1)}{p}, \frac{2}{p}), p \ge 1$, which covers the range of $(p, \sigma )$ in Theorem 2 and part of the range in Theorem 1, the existence and uniqueness of solution to (1.2) in the class $C^0([0, T), X ), X = \{ v \in H^1, v r^{-\sigma } \in L^p \}$ is established in Lemma 4.1 [46], where T is the blowup time of ${\textbf{u}}$. In the setting of Theorem 1 with $\sigma \le - \frac{2(p-1)}{p} \le 0$, since $r \le 1$ in the cylindrical domain, $v_0 \in L^p$ (1.4), and $|| v r^{-\sigma } ||_{L^p} \lesssim || v ||_{L^p} < +\infty$, v remains in $C^0([0, T), X \cap L^p )$. We assume $v_0 \in H^1$ in (1.4) to use the existence and uniqueness result to (1.2) [41, 46, 64]. Note that to solve the linearized equations (1.2), the regularity of the data $v_0 + {\textbf{u}}$ can be weaker than $H^s, s > \frac{3}{2}$ or $C^{1,\alpha },\alpha >0$, in which we have local well-posedness for 3D Euler (1.1).

Next, we generalize the instability results to the 2D Boussinesq equations in ${\mathbb {R}}_2^+$

$$\begin{aligned} \begin{aligned} \omega _t + {\textbf{u}}\cdot \nabla \omega&= \theta _{x}, \quad \theta _t + {\textbf{u}}\cdot \nabla \theta = 0 , \end{aligned} \end{aligned}$$

(1.5)

where the velocity field ${\textbf{u}}= (u, v)^T: {\mathbb {R}}_+^2 \times [0, T) \rightarrow {\mathbb {R}}^2_+$ is determined via the Biot-Savart law

$$\begin{aligned} - \Delta \psi = \omega , \quad u = - \psi _y , \quad v = \psi _x, \end{aligned}$$

(1.6)

with no flow boundary condition $v(x, 0) = 0$. Given a singular solution $(\theta , {\textbf{u}})$, the linearized equations of (1.5) in the velocity-density formulation around $(\theta , {\textbf{u}})$ read

$$\begin{aligned} \begin{aligned}&\partial _t \eta + {\textbf{u}}\cdot \nabla \eta + {\textbf{v}}\cdot \nabla \theta = 0, \\&\partial _t {\textbf{v}}+ {\textbf{u}}\cdot \nabla {\textbf{v}}+ {\textbf{v}}\cdot \nabla {\textbf{u}}+ \nabla q = - (0, \eta )^T, \quad \textrm{div} \ {\textbf{v}}= 0. \end{aligned} \end{aligned}$$

(1.7)

Denote $\textbf{w} = (\eta , {\textbf{v}})$ and define

$$\begin{aligned} \gamma ^{sym}_{p}(T) = \sup _{ || \textbf{w}_0||_{L^{p}} \le 1 } || \textbf{w} ||_{L^p}, \quad \textrm{ with } \ || \textbf{w} ||_{L^p} \sim || \eta ||_{L^p} + || {\textbf{v}}||_{L^p}, \end{aligned}$$

with the symmetry property that $v_1(x, y)$ is odd in x and $v_2(x, y), \eta _0$ are even in x.

Building on the instability result for Boussinesq equations in ${\mathbb {R}}^2$ [63], we have the following instability result for the singular solution constructed in [11].

Theorem 3

There exists $\alpha _0 > 0$ such that for $0< \alpha < \alpha _0$, the 2D Boussinesq equations (1.5) in $D = {\mathbb {R}}_2^+$ develops a singularity at finite time $T_*$ from some initial data $\omega _0 \in C_c^{\alpha }( {\mathbb {R}}^2_+), \theta _0 \in C_c^{1,\alpha }({\mathbb {R}}^2_+)$. The initial data satisfy that $\omega _0(x, y)$ is odd in x, $\theta _0(x, y)$ is even in x, and ${\textbf{u}}_0$ has finite energy $||{\textbf{u}}_0||_2 < +\infty$. Moreover, the solution satisfies $({\textbf{u}}, \theta ) \in L^{\infty }( [0, T], C^{50}( \Sigma ) )$ for any $T < T_*$ and any compact domain $\Sigma \subset \{ (x, y): x \ne 0, y > 0 \}$. For any $p \in (1, \infty )$, we have

$$\begin{aligned} \lim _{t \rightarrow T_*} \gamma ^{sym}_p(t) = \infty . \end{aligned}$$

For the same $C^{1,\alpha }$ blowup solution to these equations in Theorems 1–3 , stability of the asymptotically (or approximately) self-similar blowup profile has been established in [11, 26, 27] using the dynamic rescaling formulation [47, 54] or the modulation technique [42, 58]. In [11, 26, 27], a typical example of stability estimates is the following. There exist $B(\tau ) \rightarrow \infty , A(\tau ) \rightarrow \infty , t(\tau )$ increasing with $\lim _{\tau \rightarrow \infty } t(\tau ) < +\infty$ such that a rescaled version of the vorticity $\omega$ satisfies

$$\begin{aligned} \omega (x, t(\tau )) = A(\tau ) \Omega ( B(\tau ) x, \tau ), \quad || \Omega (\tau ) - {{\bar{\Omega }}}||_{X} \ll || {{\bar{\Omega }}} ||_{X}, \end{aligned}$$

for all $\tau > 0$ in some suitable norm X stronger than $L^{\infty }$. See Theorem 6 for a precise stability statement for a model problem.

Regularity of the singular solution. In [46, 64], instability results similar to Theorems 1, 2 are established for singular solutions ${\textbf{u}}$ satisfying

$$\begin{aligned} {\textbf{u}}\in C^0( [0, T), H^s(\Omega ) ) \cap C^1( [0, T), H^{s-1}(\Omega ) ) , \end{aligned}$$

(1.8)

with $s > \frac{7}{2}$, where $\Omega$ is the domain of the equation. See hypothesis (H1) and Theorem 1 in [46]. Using Sobolev embedding, one obtains that ${\textbf{u}}(t) \in C^0( [0, T), C^2(\Omega ) )$. See more discussions on this regularity assumption in Sect. 1.3. We remark that the singular solutions ${\textbf{u}}$ constructed in [11, 26, 27] and considered in Theorems 1, 2 do not satisfy the above assumption, and these results are not covered by the proof [46].

The estimates in [11, 26, 27] imply that for fixed $t < T$, the angular vorticity $\omega ^{\theta }(t, r, z)$ satisfies

$$\begin{aligned} \omega ^{\theta }( t) = {{\bar{\omega }}}^{\theta }(t) + {\tilde{\omega }}^{\theta }(t), \quad |\bar{\omega }^{\theta }(t, d + r_0, d ) | \asymp d^{\alpha }, \quad |{\tilde{\omega }}^{\theta }(t, s d + r_0, d ) | \lesssim d^{\alpha + \varepsilon }, \end{aligned}$$

for $0 < d \ll 1$ and $\varepsilon > 0$, where $(r_0, s) = (0, 1)$ in [26] or $(r_0, s) = (1, -1)$ in [11]. As a result, $\omega ^{\theta }$ is not in $C^{\beta }, \beta = \alpha + \min ( \frac{\varepsilon }{2}, \alpha ) < \frac{1}{2}$, and ${\textbf{u}}$ is not in $C^{1, \beta }$. For the same reason, the singular solution considered in Theorem 3 does not satisfy the regularity assumptions in [63].

1.2 Comparison of the stability and instability results

Given that the same blowup solution of the 3D Euler equations can be both linearly unstable under one definition and nonlinearly stable under a different definition, it is important to have a better understanding how we define stability and how to quantify instability. First of all, we would like to emphasize that the instability results in Theorems 1–3 measure the absolute instability, i.e. the growth of the perturbation relative to the initial perturbation. This rapid growth is not surprising since the background singular solution ${\textbf{u}}$ blows up and contributes to a singular forcing term ${\textbf{v}}\cdot \nabla {\textbf{u}}$ to the linearized equations (1.2), which is the driving force for instability. If one measures the growth in a norm X stronger than $L^{\infty }$, the instability result follows directly from the blowup criterion. See Sect. 2.4. This mechanism of instability can be captured by the following simple linear model with a unbounded coefficient

$$\begin{aligned} \partial _t u(t, x) = a(t, x) u(t, x), \quad \int _0^T a(s, x_0) d s = + \infty , \end{aligned}$$

for some $x_0$. Such instability is quite common in several nonlinear PDEs. In Sect. 2, we will use a nonlinear PDE of Riccati type and the inviscid Burgers’ equation to show that a similar forcing term generates linear instability for these equations.

The mechanism of instability considered in Theorems 1–3 is not due to the violation of or breaking certain symmetry conditions for the solutions. In fact, the perturbation in Theorems 1–3 satisfies the same symmetry as the blowup solution, e.g. (Sym). Moreover, it is not related to an unstable eigenfunction of certain linearized operator. The instability result in Sect. 2.4 further demonstrates these points. Note that the linearized operator ${{\mathcal {L}}}(t)$ in (1.2) is time-dependent with coefficients blowing up. For nonlinear 3D Euler equations (1.1), there are different mechanisms of instability due to the scaling symmetries and time-invariance of the equations. These instabilities can be modulated by performing suitable time-dependent rescaling. See discussions below Theorem 5.

We believe that it is more reasonable to study the relative stability or instability, which measures the relative growth of the perturbation compared with the growth of the background singular solution. More importantly, the nonlinear stability results presented in [11, 26, 27] quantify the relative stability: for a small initial perturbation to the blowup profile, some weighted norm X of the perturbation remains relatively small up to the blowup time. These estimates and the embedding inequalities imply that the growth of the perturbation of the vorticity $|| {\tilde{\omega }}||_{L^{\infty }}$ remains much smaller than the growth of the blowup solution $|| \omega ||_{L^{\infty }}$ up to the blowup time. Moreover, this stability result implies that for a small initial perturbation, the change of the blowup time $T_*$ is very small. Thus, one can perform reliable numerical computations to provide compelling evidence of finite time blowup [38,39,40, 49, 50].

Studying stability of the blowup based on the self-similar variables, dynamic rescaling formulation, or the modulation technique has been used in many other equations, such as the nonlinear heat equations [58], the Burgers’ equation [19, 60], the complex Ginzburg-Landau equation [53, 62], the nonlinear Schrödinger equation [55], the generalized KdV equation [52], compressible fluids [3, 4], and incompressible fluids [9, 11, 13, 26]. On the other hand, there are some instability results of the blowup based on these approaches. For example, the authors in [19, 60] proved that many blowup profiles of the 1D Burgers’ equation have a finite number of unstable directions. See also the blowup of the nonlinear Schrödinger equation [56], incompressible fluids [32], compressible fluids [57] with finitely many potential unstable directions, and further numerical investigation of the instability [2]. The (potential) instability in [19, 32, 57, 60] is due to unstable eigenfunctions of a linearized operator around the blowup profile in the equations of the self-similar variables. It is different from that in Theorems 1–3.

After the completion of this work, there has been substantial progress on singularity formation of 3D Euler equations. In [9, 13], we have established finite time blowup of 2D Boussinesq and 3D Euler equations with boundary from smooth initial data by proving the nonlinear stability of the blowup profile in the dynamic rescaling equations. This result also demonstrates that the concepts of stability based on self-similar variables and that in [46, 64] are different. In [32, 33], Elgindi-Pasqualotto established blowup of 2D Boussinesq and 3D Euler equations (with large swirl) with $C^{1,\alpha }$ velocity and without boundary. In [22], Cordoba-Martinez-Zoroa-Zheng developed a new method different from the above self-similar approach to establish blowup of Euler equations with ${\textbf{u}}(t) \in C^{\infty }({\mathbb {R}}^3 \backslash O) \cap C^{1,\alpha } \cap L^2$. In [8], the first author proved that such a blowup result can also be established by the self-similar approach. By adding an external force f uniformly bounded in $C^{1,1/2-}$ up to the blowup time, the authors of [21] established blowup of 3D Euler with smooth velocity.

1.3 Main ideas in the instability analysis

There are several main ideas in proving the main instability results stated in Theorems 1, 2. One of the main difficulties in proving Theorems 1, 2 is to relax the regularity assumptions in the arguments [46, 64] by using the properties of the singular solutions in [11, 26]. We then construct an axisymmetric approximate solution to (1.2) and follow the arguments in [46] to prove the main theorems.

For the 2D Boussinesq equations, we use ideas similar to the 3D Euler equations to relax the regularity assumption in [63] and then apply the argument in [63] to prove Theorem 3.

Relaxing the regularity assumption. In [46], the regularity assumption ${\textbf{u}}\in$$C^0( [0, T), H^s) \cap C^1( [0, T), H^{s-1})$ with $s > \frac{7}{2}$ (1.8) is to ensure

• (a) the solvability of the bicharacteristics-amplitude ODE system [35, 46, 64];

• (b) that the poloidal component of the vorticity $\omega _p = \omega ^r e_r + \omega ^z e_z$ satisfies $\frac{1}{r^a} \omega _p \in L^{\infty }$ for some $a > 0$, which is used in [46] to connect the blowup criteria with the instability.

To relax the regularity assumption for (a), we make an important observation that the singular solution ${\textbf{u}}$ constructed in [11, 26] is smooth away from the symmetry axis and the boundary. The $C^{1, \alpha }$ low regularity is used essentially near the singularity, the symmetry axis, and the boundary to weaken the advection. The higher-order interior regularity of the solution ${\textbf{u}}$ can be propagated by using careful higher-order weighted energy estimates and the elliptic estimates with weights degenerated near the symmetry axis and the boundary [11, 26]. In particular, in a compact interior domain, the weighted energy norms are comparable to the standard Sobolev norms, which allows us to establish higher-order interior regularity of the solution using the embedding inequalities. See Theorems 7–9.

Using the higher-order interior regularity, we can solve the bicharacteristics-amplitude ODE system, which is local in nature, in the interior of the domain and construct smooth solution to the modified bicharacteristics-amplitude ODE system. See Lemma 3.2 and Proposition 3.4 .

Remark 1.2

In [11], we proved blowup of the 3D axisymmetric Euler equations with initial data $(u_0^{\vartheta })^2, u_0^r, u_0^z \in C^{1,\alpha }, \omega _0^{\vartheta } \in C^{\alpha }$. Though the velocity $u^r, u^z$ in the axisymmetric setting is $C^{1,\alpha }$, our interpretation that the velocity is $C^{1,\alpha }$ is not correct since $u^{\vartheta }$ is not $C^{1,\alpha }$. This oversight can be fixed easily with minor changes in the construction of the approximate steady state and the truncation of the approximate steady state. These changes do not affect the nonlinear stability estimates of the 3D Euler equations, see [14] and the updated arXiv version of [11].

Blowup quantities. An important step in [46, 64] is to show that the growth factor $\lambda _{p, \sigma }$ (1.4) controls $|| \omega ||_{\infty }$, which blows up for a singular solution [1]. The singular solutions in [11, 26] are self-similar or approximately self-similar. There are several blowup quantities other than $|| \omega ||_{\infty }$. By comparing some blowup quantities and the growth factor $\lambda _{p, \sigma }$ (1.4), we can simplify the proof in [46] and further relax some constraints. For example, in the proof of Theorem 1, we use the property that $|| \omega _p||_{\infty }$ (the poloidal component) blows up and thus do not need the blowup criterion on $|| \omega _p / r^a||_{\infty }$ for some $a > 0$ established in [46]. This relaxes the condition (b).

The singularity considered in [26] develops near the axis $r = 0$ and has zero swirl $u^{\theta }\equiv 0$, which implies $\omega _p \equiv 0$. Thus we cannot follow the argument in [46] to prove Theorem 2. Instead, we use the bicharacteristics-amplitude ODE system and the flow structure near the singularity in [26] to show that the growth $\lambda _{\sigma , p}(t)$ controls another blowup quantity.

Axisymmetric velocity. Another important step in proving Theorems 1 and 2 is to construct an axisymmetric solution to (1.2). We remark that the initial data of (1.2) constructed in [46] is not axisymmetric under the canonical notion (1.3) [51], see Remark 3.5 for more discussions. We use the PDE (Eulerian) form of the bicharacteristics-amplitude ODE system to construct the amplitude b(t, x) and the phase S(t, x) in the WKB construction of the approximate solution to (1.2). The initial data $b(0, x), \xi (0, x)$ are axisymmetric flows in the whole domain, which are constructed by extending some constant initial data $b_0, \xi _0 = \nabla S_0 \in {\mathbb {R}}^3$ of the bicharacteristics-amplitude ODE system. The axisymmetry properties of $b(t, x), \xi (t, x)$ are preserved dynamically by the equations. We further show that b(t, x) controls the solution to the bicharacteristics-amplitude ODE system and captures the growth of the vorticity. Based on these functions, we construct the axisymmetric velocity using the formula in [46, 64].

Symmetry of the unstable solution. The singular solutions constructed in [11, 26] are symmetric with respect to some axis, e.g., (Sym), and the flow does not cross the symmetry axis or the symmetry plane. This allows us to first construct an unstable solution in the upper half domain following [46], and then extend it naturally to a symmetric solution to the linearized Euler equations using linear superposition. Therefore, we can further restrict the perturbation in (1.4) to the natural symmetry class.

The rest of the paper is organized as follows. In Sect. 2, we use several nonlinear PDEs to demonstrate the difference between the notion of stability introduced in [46, 64] and the stability based on dynamically rescaling formulation. Section 3 is devoted to proving the main theorems of this paper. Some important properties that we use in proving the main theorems will be established for the 2D Boussinesq equations in Sect. 4 and for the 3D Euler equations in Sects. 5, respectively. Some derivations and lemmas are deferred to the Appendix.

2 Comparison of Stability Versus Instability Through Several Nonlinear PDEs

In this section, we will use several examples to demonstrate that under the notion of stability introduced in [64], linear instability of a blowup solution is quite common in several nonlinear equations, even for those nonlinear equations whose blowup solutions can be shown to be nonlinearly stable using a suitable functional space and the dynamic rescaling formulation.

2.1 A nonlinear Riccati PDE and the inviscid Burgers’ equation

In the next two subsections, we first study the blowup solutions of the inviscid Burgers’ equation

$$\begin{aligned} \partial _t u + u u_x = 0 , \quad x \in {\mathbb {R}}\end{aligned}$$

(2.1)

and then a nonlinear PDE of Riccati type

$$\begin{aligned} \partial _t u (t, x) = u^2(t, x), \quad x \in {\mathbb {R}}. \end{aligned}$$

(2.2)

We will show that the blowup solutions to (2.1), (2.2) are unstable in Theorems 4, 5 under the notion of stability introduced in [64]. In Sect. 2.2, we will use (2.2) to illustrate the importance of studying the stability of the asymptotically (or approximate) self-similar blowup profile using suitable rescaling and renormalization rather than studying the stability of the blowup solution itself. Following [64], we define the growth factor

$$\begin{aligned} \lambda _p(t) = \sup _{ v_0 \ne 0, v_0 \in L^p } \frac{ || v(t)||_{L^p}}{ || v_0||_{ L^p}} \end{aligned}$$

(2.3)

for the solution v to the linearized equations of (2.1) or (2.2) around a singular solution.

It is well-known that the Burgers’ equation (2.1) blows up (develops a shock) in finite time $T_*$ for initial data $u_0 \in C_c^{\infty }$ satisfying $u_0(0) =0$ and that $\partial _x u_0$ is minimal at 0 with $\partial _x u_0(0) < 0$. Let v be a solution to the linearized equation of (2.1) around the blowup solution u

$$\begin{aligned} v_t + \partial _x( u v) = v_t + u v_x + u_x v = 0. \end{aligned}$$

(2.4)

It has been shown in [64] that the blowup is linearly stable in $L^1$ in the sense that $\lambda _p(t) \le 1$ (2.3) up to the blowup time. However, this stability result does not generalize to $L^p$ with $p> 1$. In particular, we have the following instability result.

Theorem 4

Suppose that the initial data $u_0 \in C^{1}$ of (2.1) satisfies that $u_0(0) = 0$, $\partial _x u_0$ is minimal at 0 with $\partial _x u_0(0) < 0$. Then the solution u blows up in finite time $T_* = - \frac{1}{ u_{0, x}(0)}$. Moreover, for any $p \in (1, \infty )$, we have

$$\begin{aligned} \lim _{t \rightarrow T_*} \lambda _p(t) \rightarrow \infty . \end{aligned}$$

Since $u_x$ in (2.4) blows up, it is not surprising that v(t) can blow up in some $L^p$ norm. Below, we localize v to the region where $-u_x$ blows up to show that v can grow rapidly. On the other hand, the stability of the blowup profile of (2.1) has been studied in details in [19] using the modulation technique.

Proof

Fix $T < T_* = - \frac{1}{u_{0,x}(0)} = \frac{1}{ |u_{0,x}(0)|}$. It is easy to obtain that $u(t, 0) = 0$ for any $t < T_*$. Note that $u_x(t, 0)$ satisfies the ODE

$$\begin{aligned} \partial _t u_x(t, 0) = - ( u_x(t, 0) )^2, \quad u_{0,x}( 0) < 0 , \quad u_x(t, 0) = \frac{ - |u_{0, x}(0)| }{ 1 - t |u_{0, x}(0)| } = - \frac{1}{T_*- t}, \end{aligned}$$

(2.5)

where we have used $T_* = | u_{0, x}(0)|^{-1}$ in the last equality. It follows from the blowup result and $u_x(t, 0) \le u_{0,x}( 0) < 0$. Since $u(t) \in C^0( [0, T], C^1)$, there exists $\delta >0$ such that

$$\begin{aligned} u_x(t, x) \ge - \frac{1}{2} u_x( t, 0 ) > 0 , \quad x \in [-\delta , \delta ], \end{aligned}$$

(2.6)

for any $t \le T$, which implies

$$\begin{aligned} u(t, x) \le 0 , \ x \in [0, \delta ] , \quad u(t, x) \ge 0, \ x \in [-\delta , 0], \end{aligned}$$

(2.7)

for any $t \le T$. Consider $v_0 \in C^{\infty }, v_0 \ne 0, \textrm{supp}(v_0) \subset [-\delta , \delta ]$. Due to (2.7), $\textrm{supp}( v(t))$ remains in $[-\delta , \delta ]$ for $t \le T$. Performing $L^p$ estimate on (2.4) and using integration by parts, we obtain

$$\begin{aligned} \frac{1}{p} \frac{d}{dt} || v||_{L^p}^p= & {} \int _{{\mathbb {R}}} - (u v)_x \cdot |v|^{p-2} v dx = \int _{{\mathbb {R}}} - u_x |v|^p - u v_x |v|^{p-2} v dx \\= & {} \int _{{\mathbb {R}}} - u_x |v|^p + \frac{1}{p} u_x |v|^p dx. \end{aligned}$$

Since $\textrm{supp}( v(t)) \subset [-\delta , \delta ]$, using (2.6), we further obtain

$$\begin{aligned} \frac{1}{p}\frac{d}{dt} || v||^p_{L^p}= & {} (1- \frac{1}{p}) \int _{[-\delta , \delta ]} - u_x |v|^p dx \ge (1 - \frac{1}{p}) \frac{ - u_x(t, 0)}{2} \int _{[-\delta , \delta ]} |v|^p dx \\= & {} (1 - \frac{1}{p}) \frac{ - u_x(t, 0)}{2} || v||_{L^p}^p. \end{aligned}$$

Solving the above ODE and using (2.5), we prove

$$\begin{aligned} \begin{aligned} || v(T)||_{L^p}&\ge || v_0||_{L^p} \exp \Big ( \frac{1}{2}(1 - \frac{1}{p})\int _0^T - u_x( t, 0) dt \Big )\\&= || v_0||_{L^p} \exp \Big ( - \frac{1}{2}(1 - \frac{1}{p}) \log (T_* - T) \Big ). \end{aligned} \end{aligned}$$

From the definition of $\lambda _p(t)$, we yield

$$\begin{aligned} \lambda _p(T) \ge \exp \Big ( - \frac{1}{2}(1 - \frac{1}{p}) \log (T_* - T) \Big ) =(T_* - T)^{ - \frac{1}{2}(1 - \frac{1}{p}) }. \end{aligned}$$

Since $p > 1$, taking $T \rightarrow T_*$, we obtain the desired result. $\square$

2.2 The Riccati-type PDE

It is easy to show that if the initial data $u_0$ of (2.2) satisfies $\max (u_0) > 0$, the PDE blows up at finite time $T(u_0) = \frac{1}{ \max (u_0)}$. Moreover, the equation can develop a self-similar blowup

$$\begin{aligned} {{\bar{u}}} (t, x) = \frac{1}{1 - t+ x^2} = \frac{1}{1-t} {{\bar{U}}}( \frac{ x}{ (1 -t)^{1/2} }), \quad {{\bar{U}}} = \frac{1}{1 + x^2}. \end{aligned}$$

(2.8)

The linearized equation around the blowup solution ${{\bar{u}}}$ (2.2) reads

$$\begin{aligned} \partial _t v = 2 {{\bar{u}}} v . \end{aligned}$$

(2.9)

Denote $P_{\varepsilon }$

$$\begin{aligned} P_{\varepsilon } \triangleq \{ u : u = C( {{\bar{U}}} + V_0 ), \ C> 0 , \ | V_0 | \le \varepsilon \min (1, |x|^3) \}. \end{aligned}$$

(2.10)

We will study the stability of the blowup solution of (2.2) for initial data in $P_{\varepsilon }$. Let us motivate the class $P_{\varepsilon }$. For initial data $u_0$ close to (2.8), we have $u_0(x) = u_0(0) u_1(x)$ with $u_1(0) = 1$ and $u_1$ being a perturbation of ${{\bar{U}}}$. Since the solution u first blows up at $\arg \max u_0$ and ${{\bar{U}}}(x) = 1 - x^2 + O(x^4)$ near $x=0$, we require that $V_0$ vanishes to higher order $O(|x|^3)$ near $x=0$ and $\varepsilon$ is small so that the maximum of $u_0$ does not shift.

To further study the instability of the blowup profile ${{\bar{U}}}$ (2.8) to (2.2), we consider the following ansatz of the linearized solution (2.9) and the rescaled growth factor $\Lambda _p(t)$ similar to that for the 3D Euler equations in [46]

$$\begin{aligned} v(t, x) = \frac{1}{1 - t} V( \frac{x}{ (1-t)^{\beta } }, t), \quad \beta = \frac{1}{2}, \quad \Lambda _p( v, t) = \frac{ || V(t)||_{L^p} }{ || V_0||_{L^p}}. \end{aligned}$$

(2.11)

Since the blowup exponent $\frac{1}{1-t}$ is factored out, $\Lambda _p$ can be seen as measuring the relative linear instability between V and the background profile ${{\bar{U}}}$ (2.8), while $\lambda _p$ (2.3) measures the absolute linear instability. We have the following instability results.

Theorem 5

For any $v_0 \in C_c^0$ with $v_0(0)> 0$ and any $p \in [1, \infty ]$, we have

$$\begin{aligned} || v(t) ||_{L^p} \gtrsim C(v_0, p) (1- t)^{-2 + \frac{1}{2p} }, \quad \lim _{ t \rightarrow 1} || v(t)||_p = \infty , \quad \lim _{t \rightarrow 1} \frac{ || v(t)||_{L^p}}{ || u(t) ||_{L^p} } = \infty . \end{aligned}$$

As a result, we have $\lambda _p(t) \rightarrow \infty , \Lambda _p(v, t) \rightarrow \infty$ as $t \rightarrow 1$.

In the above theorem, we can choose perturbation $v_0$ with $u_0 = {{\bar{u}}} + v_0 \in P_{\varepsilon }$ (2.10). On the other hand, we can prove stability of the blowup for $u_0 \in P_{\varepsilon }$ in Theorem 6.

The above instability results are not surprising since ${{\bar{u}}}$ in the forcing term ${{\bar{u}}} v$ (2.9) blows up. The problems of using the ansatz (2.11) to study the stability of the blowup profile ${{\bar{U}}}$ (2.8) are the following. For initial data $u_0$ perturbed from ${{\bar{u}}}$, we expect that the blowup time T changes and the blowup exponent $\beta$ in (2.11) can also change. For the nonlinear 3D Euler (1.1), if ${\textbf{u}}$ is a singular solution to (1.1) with $|| \omega ||_{L^p}, || \omega ||_{L^{\infty }}$ blowing up at $t = T$, where $\omega =\nabla \times {\textbf{u}}$, using the temporal and spatial symmetries of the Euler equations, we can construct the following three solutions

$$\begin{aligned}{} & {} {\textbf{u}}_1(x, t) \triangleq \lambda ^{-1} {\textbf{u}}(\lambda x, t), \quad {\textbf{u}}_2(x, t) \triangleq {\textbf{u}}(x, t - \varepsilon ), \quad {\textbf{u}}_3(x,t) \triangleq \lambda {\textbf{u}}( x, \lambda t), \\{} & {} \quad \quad \omega _i \triangleq \nabla \times {\textbf{u}}_i, \quad \omega = \nabla \times {\textbf{u}}, \end{aligned}$$

to (1.1). Choosing $0 < 1 - \lambda \ll 1, |\varepsilon | \ll 1$, ${\textbf{u}}_i( x, 0)$ can be arbitrary close to ${\textbf{u}}( x, 0)$. Yet, we get

$$\begin{aligned} \begin{aligned} || \omega _1(x, t) - \omega (x, t) ||_{L^{p}}&\ge | || \omega _1(t)||_{L^p} -|| \omega (t) ||_{L^p} |= |\lambda ^{-3/p} - 1| \cdot || \omega (t) ||_{L^p}, \\ || \omega _2(t) - \omega (t) ||_{L^{\infty }}&\ge || \omega (t)||_{L^{\infty }} - || \omega (t - \varepsilon ) ||_{L^{\infty }}, \\ || \omega _3(t) - \omega (t) ||_{L^{\infty }}&\ge (1 - \lambda ) || \omega (t)||_{L^{\infty }}, \end{aligned} \end{aligned}$$

which all blow up as $t \rightarrow T^-$. Thus, to observe certain stability of the blowup solution to the nonlinear Euler equations, we need to rescale the solution using a different rescaling rate in the spatial variable. For the model problem, these lead to the following ansatz of the singular solution u from initial data $u_0$ near ${{\bar{u}}}$

$$\begin{aligned} u(x, t) = \frac{1}{\tilde{T}- t} U\Big ( \mu \frac{x}{ (\tilde{T} - t)^{ {\tilde{\beta }} }}, t \Big ), \quad {\tilde{\beta }} \approx \frac{1}{2}, \quad \tilde{T} \approx 1, \quad \mu \approx 1 , \quad U \approx {{\bar{U}}}. \end{aligned}$$

(2.12)

However, in (2.11), the parameters $\tilde{T}, {\tilde{\beta }}, \mu$ are all fixed. Moreover, in (2.12), due to the composition, the parameters ${\tilde{\beta }}, \tilde{T}, \mu$ depend on the initial data and perturbation nonlinearly. Thus, they cannot be captured by the linearized equation (2.9) around $\bar{u}$. Without incorporating the perturbation of these parameters, it is not expected to observe the stability of the profile.

Using the dynamic rescaling formulation, we can obtain the stability of the blowup of (2.2).

Theorem 6

There exists an absolute constant $\varepsilon > 0$, such that for any $u_0 \in P_{\varepsilon } \cap L^{\infty }$, we have

$$\begin{aligned} u( x, t(\tau )) = \frac{1}{ T - t(\tau )} U\Big ( T^{1/2} \frac{ x}{ (T- t(\tau ))^{1/2} } , \tau \Big ) , T = \frac{1}{C} = \frac{1}{u_0(0)}, t(\tau ) = T( 1 - e^{-\tau }), \end{aligned}$$

(2.13)

for any $\tau \in [0, \infty )$. Moreover, we have the following stability estimate

$$\begin{aligned} || ( U(\cdot , \tau ) - {{\bar{U}}} ) ( |x|^{-3} + 1)||_{L^{\infty }} \le || ( U_0 - {{\bar{U}}} ) (|x|^{-3} + 1)||_{L^{\infty }} e^{- \frac{\tau }{4}} . \end{aligned}$$

(2.14)

The formula (2.13) and estimate (2.14) are consistent with the ansatz (2.12). For initial data u different from ${{\bar{u}}}$ (2.8), we have a different blowup time T and we need to adjust the rescaling rate $T^{1/2} (T-t)^{-1/2}$ in the spatial variable. To study the stability of the blowup profile, we rescale the spatial variable, the temporal variable, and normalize the amplitude of the solution according to the initial data. These rescaling relations and renormalization are nonlinear and thus are not captured by the ansatz (2.11) and the linearized equation (2.9).

To prove Theorem 6, we establish the nonlinear stability of ${{\bar{U}}}$ in the dynamic rescaling equation using weighted $L^{\infty }$ estimates. Since the stability estimates are standard [5, 11, 15] and the equation is local and quite simple, we do not present the proof here and refer it to Section 2.4 in the arXiv version [12] of this paper. Below, we prove Theorem 5.

Proof of Theorem 5

Recall ${{\bar{u}}} = \frac{1}{1 - t+ x^2}$ from (2.8). Using (2.9), we obtain

$$\begin{aligned} \begin{aligned} v(t, x)&= v_0(x) \exp \Big ( \int _0^t 2 \frac{1 }{1-s + x^2} ds \Big ) = v_0(x) \exp ( 2 \log (1 + x^2) - 2 \log (1 - t + x^2) ) \\&= v_0(x) \frac{ (1 + x^2)^2}{ (1 - t + x^2)^2 } = \tilde{v}(x) \frac{1}{(1-t)^2} ( {{\bar{U}}} ( \frac{x}{ (1-t)^{1/2}} ) )^2, \quad \tilde{v} = v_0(x) (1 + x^2)^2, \end{aligned} \end{aligned}$$

where ${{\bar{U}}}$ is given in (2.8). In particular, v blows up with a rate $(1-t)^{-2}$, which is even faster than that of ${{\bar{u}}}$. We remark that the exponent 2 in $(1-t)^{-2}$ is generic and does not relate to the coefficient 2 in (2.9) or the formulation of (2.2). We obtain the same exponent if we consider $u_t = c u^2$ for other constant $c>0$ instead of (2.2). Since $v_0(0) > 0$ and $v_0 \in C_c^0$, there exists $c, \delta >0$ such that $v_0(x) \ge c$ for $|x| \le \delta$. For any $p \in [1, \infty )$, we have

$$\begin{aligned} \begin{aligned} \int _{{\mathbb {R}}} |v|^p dx&\ge c \int _{ |x| \le \delta } (1-t)^{-2p} ( {{\bar{U}}} ( \frac{x}{ (1-t)^{1/2}} ) )^{2p} dx\\&= c (1-t)^{-2p+ 1/2} \int _{ |y| \le \delta (1-t)^{-1/2}} | {{\bar{U}}}(y)|^{2p} d y \\ || v(t)||_{L^p}&\gtrsim C(v_0, p) (1-t)^{-2 + \frac{1}{2p}}. \end{aligned} \end{aligned}$$

Recall ${{\bar{u}}}$ from (2.8). We have $|| {{\bar{u}}}(t) ||_p = C_p (1-t)^{-1 + \frac{1}{2p}}$. For $p \in [1, \infty )$, these estimates prove Theorem 5 . For $p=\infty$, the calculation is even simpler and thus is omitted. $\square$

Remark 2.1

For $v_0 \in C_c^{\infty }$ with $v_0(0) > 0$, since v(t) blows up faster than ${{\bar{u}}}$, it is expected that the relative instability $|| v(t)||_X / || {{\bar{u}}}||_X$ occurs in many norms X, e.g., the Sobolev norms $W^{k, p}$ and $X= C^{k, \alpha }$. This relative instability is generic for (2.9). Thus, using the linearized equation (2.9) around a blowup solution ${\bar{{\textbf{u}}}}$ is not suitable to study the stability of the profile (2.8).

2.3 1D models for the 3D Euler equations

In this section, we study the stability of the model problems for 3D Euler using notion of stability similar to that in [64].

Consider the De Gregorio model [23, 24] ((2.15) with $a=1$) and the generalized Constantin–Lax–Majda (gCLM) model [61]

$$\begin{aligned} \omega _t + a u \omega _x = u_x \omega , \quad u_x(\omega ) = H \omega , \quad x \in {\mathbb {R}}\mathrm { \ or \ } S^1, \end{aligned}$$

(2.15)

where H is the Hilbert transform and a is a parameter. We consider the following linearized equation for a singular solution ${{\bar{\omega }}}(t)$ that develops a finite time singularity at $T_*$

$$\begin{aligned} \partial _t \omega + a {{\bar{u}}} \omega _x + a u {{\bar{\omega }}}_x = {{\bar{u}}}_x \omega + u_x {{\bar{\omega }}}, \quad u_x = H \omega . \end{aligned}$$

(2.16)

Clearly, $\omega = \partial _x {{\bar{\omega }}}$ is a solution to (2.16). Following [64], we introduce the growth factor

$$\begin{aligned} \lambda _p(t) \triangleq \sup _{ \omega _0 \in L^p, \omega _0 \ne 0} \frac{ || \omega (t)||_p}{ || \omega _0||_p}, \quad p \in (1, \infty ). \end{aligned}$$

(2.17)

For $a=1$, in a joint work with Huang [15], we constructed a finite time blowup of the De Gregorio model ((2.15) with $a=1$) from $C_c^{\infty }$ initial data. The singular solution satisfies

$$\begin{aligned} {{\bar{\omega }}}(x, t) = C_{\omega }(t)^{-1} \Omega ( C_{\omega }(t) x, t), C_{\omega }(0) = 1, \lim _{t \rightarrow T_*} C_{\omega }(t) = 0, \Omega (x, t) = {{\bar{\Omega }}}(x) + {\tilde{\Omega }}(x, t), \end{aligned}$$

where $C_{\omega }(t)$ is decreasing, $\Omega ( \cdot , t) \in C^{\infty }$, ${{\bar{\Omega }}}$ is the approximate self-similar profile, and ${\tilde{\Omega }}(x, t)$ is a small perturbation. In particular, the estimates in [15] imply

$$\begin{aligned} | {\tilde{\Omega }}(x, t)| \lesssim |x|^{3/2}, \quad |{{\bar{\Omega }}}(x) - A x | \lesssim x^2 \end{aligned}$$

for some $A \ne 0$, where the implicit constants are time-independent. Therefore, for some small $\delta > 0$, we get $|\Omega (\delta , t)| \ge \frac{A}{2} \delta > 0$ for $t\in [0, T_*)$. For any $p\in [1, \infty )$, we obtain

$$\begin{aligned} || \partial _x {{\bar{\omega }}} ||_{L^p}&= C_{\omega }(t)^{-1/p} || \Omega _x(\cdot , t)||_p \gtrsim _p C_{\omega }(t)^{-1/p} \int _0^{\delta } |\Omega _x( y , t)| dy\\&\gtrsim _p C_{\omega }(t)^{-1/p} | \Omega ( \delta , t) | \\&\gtrsim _p C_{\omega }(t)^{-1/p} A \delta . \end{aligned}$$

Since $|| \partial _x {{\bar{\omega }}}_0 ||_{L^p} \ne 0$ and $C_{\omega }(t) \rightarrow 0$ as $t \rightarrow T_*$, we yield $\lambda _p(t) \rightarrow \infty$ (2.17) as $t \rightarrow T_*$.

On the other hand, nonlinear stability of these blowup solutions in some weighted $H^1$ norms has been established in [15] using the dynamic rescaling formulation [47, 54]. The nonlinear stability in [15] is established by analyzing the stability of the asymptotically (or approximate) self-similar blowup profile, which is very different from the linear stability in [64].

Similar discussions on the stability of the blowup solution in the dynamic rescaling equations and the instability of the blowup solution in the linearized equation apply to the singular solution of De Gregorio model [6], the gCLM model [5, 7, 15, 28, 30], and the Hou-Luo model [16].

2.4 The 3D Euler equations

Finally, we consider the 3D Euler equations. Suppose that ${\textbf{u}}(x, t)$ is a singular solution of the 3D Euler equations that blows up at a finite time $T_*$ with $|| {\textbf{u}}||_{L^2} < +\infty$. We have $\partial _{i} {\textbf{u}}_0 \ne 0$ for all i. If $\partial _{i} {\textbf{u}}_0 \equiv 0$ for some i, the initial velocity ${\textbf{u}}_0$ would have reduced to the two dimensional Euler equations, which could not blow up in a finite time.

For a domain without boundary, e.g. ${\mathbb {T}}^3$ or ${\mathbb {R}}^3$, the linearized equation (1.2) has exact solutions ${\textbf{v}}= \partial _i {\textbf{u}}$ for $i=1,2,3$, which was observed in [64] for the Navier Stokes equations. Suppose that X is some functional space equipped with a norm that is stronger than the $L^{\infty }$ norm, e.g. $X = L^{\infty }, C^{k, \alpha }, k \ge 0, \alpha \in (0, 1)$, or $X = H^s, s > \frac{3}{2}$, and it satisfies $\nabla {\textbf{u}}_0 \in X$. Since $\int _0^t ||\nabla {\textbf{u}}(s)||_{\infty } ds$ controls the blowup of the solution, we obtain

$$\begin{aligned} \infty = \limsup _{t \rightarrow T_*} \sum _{i=1}^3 \frac{ || \partial _i {\textbf{u}}(t)||_{L^{\infty }} }{ || \partial _i {\textbf{u}}_0||_X} \lesssim \limsup _{t \rightarrow T_*} \sum _{i=1}^3 \frac{ || \partial _i {\textbf{u}}(t)||_{X}}{ || \partial _i {\textbf{u}}_0||_X} \lesssim \limsup _{t \rightarrow T_*} \sup _{ {\textbf{v}}_0 \in X, {\textbf{v}}_0 \ne 0} \frac{ || {\textbf{v}}(t)||_{X}}{ || {\textbf{v}}_0||_X}. \end{aligned}$$

Under the notion of stability introduced in [64], the blowup is linearly unstable in the norm of X. Yet, this instability result is a direct consequence of the blowup criterion and does not use further properties of the blowup solution, e.g., the blowup profile and the blowup exponent.

3 Proof of Main Theorems

In this section, we will prove Theorems 1–3. Our idea is to weaken the regularity assumptions used in the proofs in [46, 63] and construct unstable solutions associated with the singular solutions in [11, 26, 27] by exploiting the special properties of these singular solutions.

Concretely, we first review the construction of the unstable solution to the linearized equations [46, 64] in Sect. 3.1 and the regularity assumptions of the singular solution used in [46, 64]. Then we present the properties that the singular solutions satisfy higher order regularity in the interior of the domain in Sect. 3.2. We defer their proofs to Sects. 4 and 5, which are based on the arguments and estimates in [11]. In Sect. 3.3, we use the higher order interior regularity of the solutions and localize the construction to the interior of the domain to solve the bicharacteristics-amplitude ODEs [46, 64]. Using the results in Sect. 3.3, in Sect. 3.4, we first relax the regularity assumptions in some steps in [46, 64]. Then we construct an axisymmetric unstable solution to (1.2) and prove Theorem 1. This is the most delicate part of the proof and we refer to more discussion at the beginning of Sect. 3.4. In Sects. 3.5, 3.6, we generalize the arguments in Sect. 3.4 to prove instability results in Boussinesq equations in Theorem 3 and Euler equations in ${\mathbb {R}}^3$ in Theorem 2.

Notations. We first introduce some notations to be used in the analysis. We use $(r, \vartheta , z)$ to denote the cylindrical coordinates in ${\mathbb {R}}^3$. The associated basis is

$$\begin{aligned} e_r = ( \cos \vartheta , \sin \vartheta , 0 ), \quad e_{\vartheta } = ( - \sin \vartheta , \cos \vartheta , 0), \quad e_z = (0, 0, 1). \end{aligned}$$

(3.1)

For x with coordinate $(x_r, x_{\vartheta }, x_z)$ and $A \subset {\mathbb {R}}^3$, we use $\tilde{x}, \tilde{A}$ to denote the poloidal component

$$\begin{aligned} \tilde{x} = (x_r, x_z) , \quad \tilde{A} = \{ \tilde{x} : x \in A \}. \end{aligned}$$

(3.2)

The poloidal component of the axisymmetric vorticity $\omega$ is defined as follows

$$\begin{aligned} \omega _p \triangleq \omega ^r e_r + \omega ^z e_z, \quad \omega = \omega ^r e_r + \omega ^{\vartheta } e_{\vartheta } + \omega ^z e_z. \end{aligned}$$

(3.3)

In the analysis of the axisymmetric Euler equations, for any 2D domain $\Sigma$ of (r, z), we abuse the notation and use

$$\begin{aligned} x \in \Sigma \quad \textrm{ if } \quad \tilde{x} = ( x_r, x_z ) \in \Sigma . \end{aligned}$$

(3.4)

For example, $x \in B_{(1,0)}(\delta )$ means $(x_r, x_z ) \in B_{(1,0)}(\delta )$, or equivalently, x in the annulus $B_{(1,0)}(\delta ) \times {\mathbb {R}}/ (2\pi {\mathbb {Z}})$. We abuse this notation since the flow is axisymmetric and thus many variables, e.g., $u^r, u^z, u^{\vartheta }, \omega ^{\vartheta }$, depend on (r, z) only.

3.1 The WKB expansion and the bicharacteristics-amplitude ODEs

The main idea in [46, 64] is to construct an approximate solution to (1.2) using a WKB expansion

$$\begin{aligned} v(t, x) \approx b(t, x) \exp ( \frac{ i S(t, x)}{\varepsilon } ) \end{aligned}$$

(3.5)

for sufficiently small $\varepsilon$, where $b(t, x) \in {\mathbb {R}}^3$ and S is a scalar, and the following bicharacteristics-amplitude ODE system (3.6)–(3.8) [46, 64]

$$\begin{aligned} {{\dot{\gamma }}}_t&= {\textbf{u}}(t, \gamma _t) , \quad \gamma _0 = x_0, \end{aligned}$$

(3.6)

$$\begin{aligned} {{\dot{\xi }}}_t&= -( \nabla {\textbf{u}})^T(t, \gamma _t) \xi _t, \end{aligned}$$

(3.7)

$$\begin{aligned} \dot{b}_t&= - (\nabla {\textbf{u}})(t, \gamma _t) b_t + 2 \frac{ \xi _t^T ( \nabla {\textbf{u}})(t, \gamma _t) b_t}{ |\xi _t|^2} \xi _t, \end{aligned}$$

(3.8)

with initial data $(x_0, \xi _0, b_0)$, where $(\nabla u)_{ij} = \partial _j u_i$. The regularity assumption ${\textbf{u}}\in C^0( [0, T], H^s), s > 9/2$ in [64] is mainly used to guarantee the solvability of the above ODEs with smooth dependence on the initial data.

The ODE system (3.6)–(3.8) has been derived in [35] to define the fluid Lyapunov exponent and used to study the stability of steady states of the Euler equations [34, 36]. The WKB expansion (3.5) was developed in [65] to study the spectrum of small oscillations in an ideal incompressible fluid. It has also been used to study the local stability conditions for the Euler equations [48].

For the sake of completeness, in Appendix 5.7, we begin with the WKB expansion (3.5) and then explain the use of the bicharacteristics-amplitude ODE system (3.6)–(3.8), which arise naturally in the construction of the approximate solution. We also explain the connections among the WKB expansion, the bicharacteristics-amplitude ODE system (3.6)–(3.8), and the growth of the unstable solution. From the review in Appendix 5.7, we have a few remarks.

Remark 3.1

• (a) From the proof in [64] and the simplified derivations in Appendix 5.7, the WKB construction and the high frequency (3.5) are mainly used to construct an approximate solution to (1.2) with a small error in the $L^p$ norm but not used to show the growth of the unstable solution.

• (b) The growth of the solution v and the linear instability are coupled with the growth of the vorticity via the ODE system (3.6)–(3.8) and (A.10).

• (c) As we mentioned in Sect. 2.4, for a domain without boundary, $\partial _i {\textbf{u}}, i=1,2,3$ are the exact solutions to (1.2) and blow up in a functional space X equipped with a norm stronger than the $L^{\infty }$ norm. These simple instability results do not use (3.5) and (3.6)–(3.8).

• (d) The argument in [64] has an advantage that several nonlocal terms become local. It is based on the characteristics and is local in nature. Due to this local property, we can relax the regularity assumptions in the proof in [64] for the singular solutions in [11, 26] and generalize it to prove Theorems 1–3.

3.2 Properties of the singular solutions

The singular solution to the 2D Boussinesq equations (1.5)–(1.6) constructed in [11] satisfies the following properties. The ${{\mathcal {C}}}^k$ norm in Theorem 7 is defined in (4.15). The reader should not confuse it with the standard $C^k$ norm.

Theorem 7

Let $\omega$ be the vorticity and $\theta$ be the density in the 2D Boussinesq equations described by (1.5)–(1.6). There exists $\alpha _0 > 0$ such that for $0< \alpha < \alpha _0$, the unique local solution of the 2D Boussinesq equations in the upper half plane develops a focusing asymptotically self-similar singularity in finite time $T_*$ for some initial data $\omega _0 \in C_c^{\alpha }({\mathbb {R}}_+^2), \theta _0 \in C_c^{1, \alpha }({\mathbb {R}}_+^2)$. Moreover, we have $\lim _{t \rightarrow T_*} || \nabla \theta (t)||_{\infty } = \infty$, the velocity field is in $C^{1, \alpha }$ with finite energy. For any $T < T_*$ and any compact domain $\Sigma$ in the interior of $\{ (x, y): x \ne 0, y > 0 \}$, we have $\theta _0 \in C^{50}(\Sigma )$ and $\omega , \nabla \theta , \frac{1}{ \sqrt{x^2 + y^2}} {\textbf{u}}\in L^{\infty }( [0, T], {{\mathcal {C}}}^{50} \cap C^{50}( \Sigma ) ), {\textbf{u}}\in L^{\infty }( [0, T], C^{50}(\Sigma ) )$.

The regularity ${{\mathcal {C}}}^{50}, C^{50}$ can be further improved to ${{\mathcal {C}}}^k, C^k$ with larger k directly by choosing smaller $\alpha _0$. The first part of the theorem about the blowup has been proved in [11]. To prove the regularity in the interior of the domain, we generalize the weighted energy estimates for the perturbation and the estimates of the approximate steady state in [11] to sufficiently high order. Since the weighted norms used in [11] and the energy estimates, e.g. ${{\mathcal {H}}}^k$ (see (4.14)), are comparable to the standard Sobolev norms $H^k$ in the interior of the domain, we establish the interior regularity using the embedding inequalities. See Sect. 4 for the proof.

In [11], the 3D axisymmetric Euler equations are studied in a cylinder $D = \{ (r,z): r \in [0,1], z \in {\mathbb {T}}\}, {\mathbb {T}}= {\mathbb {R}}/ ( 2 {\mathbb {Z}})$ that is periodic in z. Here, r, z are the cylindrical coordinates in ${\mathbb {R}}^3$. The equations are given below:

$$\begin{aligned} \partial _t (ru^{\vartheta }) + u^r (r u^{\vartheta })_r + u^z (r u^{\vartheta })_z = 0, \quad \partial _t \frac{\omega ^{\vartheta }}{r} + u^r ( \frac{\omega ^{\vartheta }}{r} )_r + u^z ( \frac{\omega ^{\vartheta }}{r})_z = \frac{1}{r^4} \partial _z( (r u^{\vartheta })^2 ), \end{aligned}$$

(3.9)

where $\omega ^{\vartheta }$ is the angular vorticity and $u^{\vartheta }$ is the angular velocity. The radial and the axial components of the velocity can be recovered from the Biot-Savart law

$$\begin{aligned} -(\partial _{rr} + \frac{1}{r} \partial _{r} +\partial _{zz}) \tilde{\psi } + \frac{1}{r^2} \tilde{\psi } = \omega ^{\vartheta }, \quad u^r = -\tilde{\psi }_z, \quad u^z = \tilde{\psi }_r + \frac{1}{r} \tilde{\psi } \end{aligned}$$

(3.10)

with a no-flow boundary condition on the solid boundary $r = 1$

$$\begin{aligned} \tilde{\psi }(1, z ) = 0 \end{aligned}$$

(3.11)

and a periodic boundary condition in z. For the Euler equations, we have the following results

Theorem 8

There exists $\alpha _0 > 0$ such that for $0< \alpha < \alpha _0$, the unique local solution of the 3D axisymmetric Euler equations in the cylinder $D = \{ r,z \in [0, 1] \times {\mathbb {T}}\}$ given by (3.9)–(3.11) develops a singularity in finite time $T_*$ for some initial data $\omega _0^{\vartheta } \in C^{\alpha }(D), u_0^{\vartheta } \in C^{1, \alpha }(D)$. The initial data $\omega _0^{\vartheta }, u_0^{\vartheta }$ are supported away from the symmetry axis $r=0$ with $u_0^{\vartheta } \ge 0$, $\omega _0^{\vartheta }$ is odd in z, $u_0^{\vartheta }$ is even in z, and the velocity field ${\textbf{u}}_0$ in each period has finite energy.

Moreover, the singular solution satisfies the following properties.

• (a) The poloidal component $\omega _p = \omega ^r e_r + \omega ^z e_z$ blows up $\lim _{t\rightarrow T_* } || \omega _p(t)||_{\infty } = \infty$.

• (b) There exists constants $0< 4 R_{1, \alpha }< R_{2, \alpha } < \frac{1}{4}$ such that for any particle within the support of $\omega ^{\vartheta }_0, u_0^{\vartheta }$, its trajectory up to the blowup time is within $B_{ (1, 0) }( R_{1,\alpha }) \cap D$.

• (c) For any compact domain $\Sigma$ in $\{ (r, z): r \in (0, 1), z \ne 0 \} \cap B_{ (1,0)}( R_{2,\alpha })$ and $T < T_*$, we have $u^{\vartheta }_0 \in C^{50}(\Sigma ), \omega ^{ \vartheta }, (u^{\vartheta })^2, u^r, u^z, u^{\vartheta } \in L^{\infty }( [0, T], C^{50}( \Sigma ) )$.

Except for result (c), the above theorem has been mostly proved in [11]. We recall from Remark 1.2 that the oversight $u_0^{\vartheta } \notin C^{1,\alpha }$ in [11] has been fixed in the updated arXiv version of [11]. See also Remark 5.5. The parameter $R_{2,\alpha }$ and domain $B_{(1,0)}(R_{2,\alpha })$ in the above theorem relate to the localized elliptic estimate. In particular, the cutoff function to localize the estimate is 1 in $B_{(1,0)}(R_{2,\alpha })$. One of the main difficulties in the proof is to show that $u^{\vartheta }$ is smooth in $\Sigma$. This does not follow from $(u^{\vartheta })^2 \in C^{50}(\Sigma )$ since $u^{\vartheta }$ has compact support and can degenerate in $\Sigma$. We use the property that $r u^{\vartheta }$ is transported along the flow to prove that it is smooth. See Sect. 5 for the proof.

The singular solution constructed in [26, 27] enjoys the following properties, which follow from the estimates in [26, 27].

Theorem 9

There exists $\alpha _0 > 0$ such that for $0< \alpha < \alpha _0$, the unique local solution of the axisymmetric Euler equations (3.9)–(3.10) in ${\mathbb {R}}^3$ without swirl $u^{\vartheta } \equiv 0$ develops a singularity in finite time $T_*$ for some initial data $\omega _0^{\vartheta } \in C_c^{\alpha }({\mathbb {R}}^3)$ odd in z with finite energy $|| {\textbf{u}}_0||_{L^2} < +\infty$. In addition, we have $u^r_r( t,0,0 ) > 0$ and

$$\begin{aligned} \int _0^{T_*} u_r^r( t, 0, 0) dt = \infty . \end{aligned}$$

(3.12)

For any compact domain $\Sigma \subset \{ (r, z): r >0, z \ne 0 \}$ and $T < T_*$, we have $\omega ^{\vartheta }, u^r, u^z \in L^{\infty }( [0, T], C^{50}( \Sigma ) )$.

In the blowup results in Theorem 7 and 8, $\nabla {\textbf{u}}$ also blows up at the singularity point. Since the blowup of $\nabla {\textbf{u}}$ implies the blowup of the solution, (3.12) can be seen as a blowup criterion for the singular solution in [26]. A similar one-point blowup criterion has been established to prove global regularity of the De Gregorio model for a large class of initial data in [6].

In the remaining part of this Section, we prove Theorems 1–3 using the important properties of the blowup solution in Theorems 7–9 and the argument in [46, 63]. We first prove Theorem 1.

3.3 Trajectory and the bicharacteristics-amplitude ODE

In this section, we solve the bicharacteristics-amplitude ODEs (3.6)–(3.8) in the interior of the domain. The main idea is to restrict the characteristics to the interior of the domain, where the singular solutions are smooth from Theorem 8–9, and then solve the ODEs using standard ODE theorems.

Due to the periodicity in z, we consider the domain within one period

$$\begin{aligned} D_1 \triangleq \{ (r,z) : r \in [0,1], |z| \le 1 \} . \end{aligned}$$

(3.13)

We further decompose $D_1$ into the two parts and introduce $\Upsilon$

$$\begin{aligned} \begin{aligned}&D_1^+ \triangleq \{ (r,z) : r \in [0,1], z \in [0, 1] \} , \quad D_1^- \triangleq \{ (r,z) : r \in [0,1], z \in [-1, 0] \} , \\&\Upsilon \triangleq \{ (r, z) : r = 1 \mathrm { \ or \ } z = 0 \}. \end{aligned} \end{aligned}$$

(3.14)

The set $\Upsilon$ denotes the boundary of the cylinder D and the symmetry plane $z = 0$.

Let ${\textbf{u}}$ be the velocity in Theorem 8. In the cylindrical coordinates $(r, \vartheta , z)$(3.1), we have ${\textbf{u}}= u^r e_r + u^{\vartheta } e_{\vartheta } + u^z e_z$. Since the singular solutions $\omega ^{\vartheta }, u^z$ in Theorem 8 are odd in z and we impose the no flow boundary condition (3.11), we obtain

$$\begin{aligned} {\textbf{u}}(t) \cdot n \Big |_{\Upsilon } = u^r(t) \cdot n^r + u^z(t) \cdot n^z = 0, \end{aligned}$$

(3.15)

where n is the normal vector of $\Upsilon$. Let ${\tilde{\gamma }}_t = (r_t, z_t)$ (3.2) be the (r, z) component of $\gamma _t$ in (3.6). Since the flow is axisymmetric, we have

$$\begin{aligned} \frac{d}{dt} r_t = u^r( r_t, z_t, t), \quad \frac{d}{dt} z_t = u^z( r_t, z_t, t), \quad \frac{d}{dt} {\tilde{\gamma }}_t = (u^r, u^z)({\tilde{\gamma }}_t, t). \end{aligned}$$

(3.16)

Thus, the angular coordinate $x_{0,\vartheta }$ of the initial data $x_0$ does not affect ${\tilde{\gamma }}_t$, and ${\tilde{\gamma }}_t$ depends on $\tilde{x}_0 = (r_0, z_0)$ only. Therefore, we have

$$\begin{aligned} {\tilde{\gamma }}_t( \tilde{x}_0 ) = {\tilde{\gamma }}_t( x_0 ) = (r_t, z_t), \quad \widetilde{ \gamma _t^{-1}(x) } = ( \widetilde{\gamma _t} )^{-1} (x) =( \widetilde{\gamma _t} )^{-1} ( \tilde{x}) . \end{aligned}$$

(3.17)

We have the following results for the system (3.6)–(3.8).

Lemma 3.2

Let $\gamma _t$ be the solution to (3.6) with initial data $x_0$, $T_*$ be the blowup time, $T < T_*$, and $D_1^{\pm }$ be the domains defined in (3.14). (a) For any $x_0 \in \Upsilon$ and $t \in [0, T_*)$, the trajectory $\gamma _t$ remains in $\Upsilon$; for any $x_0 \in D_1^{\pm } \backslash \Upsilon$ and $t \in [0, T_*)$, we have $\gamma _t \in D_1^{\pm } \backslash \Upsilon$. For any $t \in [0, T]$, $\gamma _t$ is invertible, and $\gamma _t, \gamma _t^{-1}$ are Lipschitz in time and the initial value.

Let $R_{1,\alpha }, R_{2,\alpha }$ be the radii in Theorem 8.

(b) Suppose that $x_0 \in ( D_1^{\pm } \backslash \Upsilon ) \cap \textrm{supp}( \omega _0 )$. There exists $\delta ( \tilde{x}_0, T) \in (0, \frac{1}{8})$ depending on $\tilde{x}_0, T$ and a compact set $\Sigma _2$, such that for any $t\in [0, T]$, we have

$$\begin{aligned} {\tilde{\gamma }}_t( B_{\tilde{x}_0 }( \delta ) ) \cup B_{ {\tilde{\gamma }}_t( \tilde{x}_0)}( \delta ) \subset \Sigma _2 \subset ( D_1^{\pm } \backslash \Upsilon ) \cap B_{(1,0)}(R_{2,\alpha }) . \end{aligned}$$

(3.18)

As a result, for initial data $z_0$ with $\tilde{z}_0 \in B_{ \tilde{x}_0}( \delta )$ and any $b_0, \xi _0$, there exist unique solutions $(\gamma _t, b_t, \xi _t)$ to (3.6)–(3.8) on $t\in [0, T]$. For $t \in [0, T]$, the functions $(\gamma _t, b_t, \xi _t)$ are Lipschitz in time and $C^4$ with respect to initial data $z_0$ with $\tilde{z}_0 \in B_{\tilde{x}_0}( \delta )$ and $b_0, \xi _0$, and $\gamma _t^{-1}(x)$ is Lipschitz in time and $C^4$ in x with $\tilde{x} \in {\tilde{\gamma }}_t( B_{\tilde{x}_0}( \delta ) ) \cup B_{{\tilde{\gamma }}_t( \tilde{x}_0)}(\delta )$.

In the above Theorem, we have used the notation (3.4). For example, $x_0 \in D_1^{\pm } \backslash \Upsilon$ means $\tilde{x}_0 \in D_1^{\pm } \backslash \Upsilon$. The domain of x with $\tilde{x} \in B_{\tilde{x}_0}(\delta )$ is the annulus $(r, z, \vartheta ) \in B_{\tilde{x}_0}(\delta ) \times {\mathbb {R}}/ (2\pi {\mathbb {Z}})$.

The ideas of the above Lemma are simple. Firstly, for any $x_0 \in D_1^{\pm } \backslash \Upsilon$, the trajectory $\gamma _t$ with $t \in [0, T]$ remains in $D_1^{\pm } \backslash \Upsilon$. Using the Lipschitz property of ${\tilde{\gamma }}_t, {\tilde{\gamma }}_t^{-1}$, we can find a neighborhood of ${\tilde{\gamma }}_t$ that still remains in $D_1^{\pm } \backslash \Upsilon$. We further restrict $\tilde{x}_0$ sufficiently close to (1, 0) and use the property that ${\textbf{u}}(x)$ is smooth for x with $\tilde{x} \in D_1^{\pm } \backslash \Upsilon \cap B_{(1,0)}(R_{2,\alpha })$ from Theorem 8 to solve (3.6)–(3.8).

Proof

Recall the notation $\tilde{x} = (r, z)$ from (3.2). Due to ${\textbf{u}}\in C^0( [0, T_*), C^{1,\alpha } )$ and the non-penetrated property (3.15), the results in (a) follow directly from the Cauchy-Lipschitz theorem.

Without loss of generality, we consider the domain $D_1^+ \backslash \Upsilon$. For any $x_0 \in ( D_1^{+} \backslash \Upsilon ) \cap \textrm{supp}( \omega _0 )$, from result (b) in Theorem 8 and (3.17), we know

$$\begin{aligned} {\tilde{\gamma }}_t(\tilde{x}_0) \in ( D_1^+ \backslash \Upsilon ) \cap B_{(1,0)}(R_{1,\alpha }), \quad t \in [0, T]. \end{aligned}$$

(3.19)

Since ${\tilde{\gamma }}_t(\tilde{x}_0)$ is continuous in t, using compactness, we have $\textrm{dist}( {\tilde{\gamma }}( \tilde{x}_0, [0, T]), \Upsilon ) > 0$. Let $L_{\gamma }$ be the Lipschitz constant of $\gamma _t, \gamma _t^{-1}$ on [0, T]. Denote

$$\begin{aligned} d_1 = \textrm{dist}( {\tilde{\gamma }}( \tilde{x}_0, [0, T]), \Upsilon ), \quad \delta _1 \triangleq \frac{1}{2} \min ( d_1, R_{1,\alpha }) > 0, \quad \delta =\min ( \frac{\delta _1}{ 2( L_{\gamma }+1)}, \frac{1}{16}). \end{aligned}$$

For $y = {\tilde{\gamma }}_t( \tilde{x}), \tilde{x} \in B_{ \tilde{x}_0}( \delta )$, using (3.19), we yield

$$\begin{aligned} \begin{aligned}&|y - {\tilde{\gamma }}_t( \tilde{x}_0)| \le L_{\gamma } | \tilde{x} -\tilde{x}_0 | \le L_{\gamma } \delta< \frac{\delta _1}{2}, \quad {\mathrm dist}(y, \Upsilon ) \ge {\mathrm dist}( {\tilde{\gamma }}_t( \tilde{x}_0), \Upsilon ) - \frac{\delta _1}{2} > \frac{\delta _1}{2}, \\&|y - (1,0)| < | {\tilde{\gamma }}_t( \tilde{x}_0) - (1,0)| + \frac{\delta _1}{2} \le \frac{3}{2} R_{1,\alpha }. \end{aligned} \end{aligned}$$

It follows that $y \in D_1^+ \backslash \Upsilon \cap B_{(1,0)}( \frac{3}{2} R_{1,\alpha })$. We define the compact set

$$\begin{aligned} \Sigma _2 = \{ \tilde{x} : \textrm{dist}(\tilde{x}, \Upsilon ) \ge \frac{1}{4} \delta _1 \} \cap {{\bar{D}}}_1^+ \cap {{\bar{B}}}_{(1,0)}( 2 R_{1,\alpha }). \end{aligned}$$

(3.20)

Recall from Theorem 8 that $R_{2,\alpha } > 4 R_{1,\alpha }$. The above derivations imply ${\tilde{\gamma }}_t( B_{ \tilde{x}_0}( \delta ) ) \subset \Sigma _2$. The proof of $B_{ {\tilde{\gamma }}_t( \tilde{x}_0)}( \delta ) \subset \Sigma _2$ follows from the same argument and is easier. We obtain (3.18).

Now, we consider (3.6)–(3.8) for initial data $z_0$ with $\tilde{z}_0 \in B_{\tilde{x}_0}( \delta )$ and $b_0, \xi _0$. Since $\Sigma _2$ is a compact set in $(D_1^+ \backslash \Upsilon ) \cap B_{(1,0)}(R_{2,\alpha })$, from Theorem 8, we have $u^r, u^z, u^{\vartheta } \in L^{\infty }( [0, T], C^{50}(\Sigma _2) )$. Since ${\tilde{\gamma }}_t( B_{\tilde{x}_0}( \delta )), B_{\tilde{x}_0}( \delta ) \subset \Sigma _2$ and ${\textbf{u}}(x)$ is smooth for x with $\tilde{x} \in \Sigma _2$, using the Cauchy-Lipschitz theorem, there exist unique solutions $(\gamma _t, b_t, \xi _t)$ to (3.6)–(3.8) on $t\in [0, T]$, and $\gamma _t, b_t, \xi _t$ are Lipschitz in time and $C^4$ with respect to the initial data.

Next, we consider the backward equation. Denote $\delta _2 = \frac{ \delta }{ L_{\gamma } + 1}$. Fix $t \le T$. For any $s \in [0, t]$, from (3.17) and (3.18), we get

$$\begin{aligned} {\tilde{\gamma }}_s^{-1} {\tilde{\gamma }}_t( B_{\tilde{x}_0}(\delta _2))= & {} {\tilde{\gamma }}_{t-s}( B_{\tilde{x}_0}(\delta _2)) \subset \Sigma _2, \quad {\tilde{\gamma }}_s^{-1} B_{ {\tilde{\gamma }}_t(\tilde{x}_0)}(\delta _2) \subset B_{ {\tilde{\gamma }}_{t-s}(\tilde{x}_0) }(L_{\gamma } \delta _2 )\\\subset & {} B_{ {\tilde{\gamma }}_{t-s}(\tilde{x}_0) }(\delta ) \subset \Sigma _2. \end{aligned}$$

From Theorem 8 and $u^r, u^z, u^{\vartheta } \in L^{\infty }( [0, T], C^{50}( \Sigma _2) )$, we can solve (3.6) backward on [0, t] for initial data $x_t$ with $\tilde{x}_t \in {\tilde{\gamma }}_t( B_{ \tilde{x}_0}( \delta _2 ) ) \cup B_{ {\tilde{\gamma }}_t(\tilde{x}_0)}(\delta _2) \subset \Sigma _2$, and $\gamma _t^{-1}$ is Lipschitz in time and $C^4$ in the initial data.

Finally, due to the inclusion

$$\begin{aligned} {\tilde{\gamma }}_t( B_{\tilde{x}_0}(\delta _2)) \cup ( B_{ {\tilde{\gamma }}_t( \tilde{x}_0) }(\delta _2)) \subset {\tilde{\gamma }}_t( B_{\tilde{x}_0}(\delta )) \cup ( B_{ {\tilde{\gamma }}_t( \tilde{x}_0) }(\delta )) \subset \Sigma _2, \quad t \in [0, T], \end{aligned}$$

we prove result (b) for $\Sigma _2$ defined in (3.20) and $\delta = \delta _2$. $\square$

3.4 Relaxation of $\beta _{\sigma }(t)$

In this section, we construct the axisymmetric unstable solution to (1.2) and prove Theorem 1. We first relax the regularity assumptions in some steps in [46, 64] in Propositions 3.3, 3.4. Then we discuss the properties of axisymmetric solutions and construct them in Sects. 3.4.1–3.4.4 using the ODE system (3.6)–(3.8). We localize the construction to the interior domain so that we can use Theorem 8. We show that the solution is unstable in Sect. 3.4.5. Various technicalities arise due to the localization. To grasp the main ideas of the constructions, the reader can skip some technical steps related to localization, such as (3.30), (3.36), and (3.44).

Recall the definition of $\beta _{\sigma }(t)$ from [46]

$$\begin{aligned} \beta _{\sigma }(t) = \sup _{ (x_0, b_0, {\tilde{\xi }}_0) \in D_1 \times {\mathbb {R}}^3 \times S^1, b_0 \cdot \xi _0 =0, |b_0| = r_0^{\sigma }} | r_t^{-\sigma } b_t(x_0, {\tilde{\xi }}_0, b_0)|, \end{aligned}$$

(3.21)

where $D_1$ is the domain for the Euler equations (3.13). Here, the notation $\xi _0 = {\tilde{\xi }}_0 \in S^1$ means that the initial data $\xi _0$ satisfies $\xi _{0} \cdot e_{\vartheta (x_0)} = 0$ and $( \xi _0 \cdot e_{r(x_0)} )^2 +( \xi _{0} \cdot e_z)^2 = 1$, where $e_{r(x_0)}, e_{\vartheta (x_0)}, e_z$ are the basis (3.1) associated with $x_0$. Since $\xi _{0} \cdot e_{\vartheta (x_0)}=0$, it relates to the notation (3.2).

We focus on the case $\sigma = 0$ and relax the domain $D_1$ (3.13) to $(D_1 \backslash \Upsilon ) \cap \textrm{supp}(\omega _0)$

$$\begin{aligned} \beta (t) = \sup _{ (x_0, b_0, {\tilde{\xi }}_0) \in ( D_1 \backslash \Upsilon ) \cap \textrm{supp}(\omega _0) \times {\mathbb {R}}^3 \times S^1, b_0 \cdot \xi _0 =0, |b_0| = 1 } | b_t(x_0, {\tilde{\xi }}_0, b_0)|, \end{aligned}$$

(3.22)

where $\omega _0$ is the vorticity of the singular solution in Theorem 8. From Lemma 3.2, for any $t< T_*, x_0 \in D_1\backslash \Upsilon , b_0 \in {\mathbb {R}}^3, {\tilde{\xi }}_0 \in S^1$, $b_t(x_0, {\tilde{\xi }}_0, b_0 )$ is well defined.

We have the following result, which modifies Proposition 2 in [46].

Proposition 3.3

Assume that ${\textbf{u}}$ is the singular solution in Theorem 8, $\omega$ is the associated vorticity, and $\omega _p$ is the poloidal component (3.3). For any $t \in (0, T_*)$, we have

$$\begin{aligned} || \omega _p( t, \cdot ) ||_{\infty } \le || \omega _p^{in} ||_{\infty } \beta (t)^2. \end{aligned}$$

Proof

We assume $|| \omega _p(t)||_{\infty } > 0$. Otherwise, the result is trivial. Since $\omega (t) \in C^{\alpha }$ and $|\omega |$ is even in z, using continuity and symmetry, we get

$$\begin{aligned} || \omega _p( t, \cdot ) ||_{\infty } = \sup _{ x \in D_1^+ \cap \textrm{supp}(\omega (t))} | \omega _p(t, x)| = \sup _{ x \in ( D_1^+ \backslash \Upsilon ) \cap \textrm{supp}(\omega (t))} | \omega _p(t, x)|. \end{aligned}$$

Now, for each $(t, x_t) \in (0, T_*) \times ( D_1^+ \backslash \Upsilon )$ with $|\omega (t, x_t)| > 0$, we can solve (3.6) backward on [0, t] with initial data $\gamma _t = x_t$. Since $x_t \in D_1^+\backslash \Upsilon$ and $|\omega (t, x_t)| > 0$, using (1.1) and a simple energy estimate along the trajectory implies $|\omega (0, x_0) | > 0$. Thus, we get $x_0 \in \textrm{supp}( \omega _0)$. From Lemma 3.2, we further obtain $x_0 \in ( D_1^+ \backslash \Upsilon ) \cap \textrm{supp}( \omega _0)$. Then we can solve (3.6)–(3.8) with initial data $x_0$ and any $b_0, \xi _0$ and solve (3.6)–(3.8) backward with initial data $x_t$ and any $b_t, \xi _t$.

We relax the definition of $\beta (t)$ since it suffices to consider $x_0 \in ( D_1^+ \backslash \Upsilon ) \cap \textrm{supp}( \omega _0) \subset ( D_1 \backslash \Upsilon ) \cap \textrm{supp}( \omega _0)$ instead of all $x_0 \in D_1$. The rest of the proof follows the same argument in [46]. $\square$

Next, we show that for the singular solution in Theorem 8, Proposition 3 in [46] remains true. Recall the definition of $\lambda _{p, \sigma }^{sym}$ from (1.4). We drop the domain D to simplify the notation.

Proposition 3.4

Let $t \in (0, T_*), p \in [ 1, \infty )$. Assume that ${\textbf{u}}$ is the singular solution in Theorem 8. Then we have $\beta (T) \lesssim _{\sigma } \lambda ^{sym}_{p, \sigma }(T)$ for any $\sigma \in {\mathbb {R}}$.

One of the difficulties in the proof is to construct an axisymmetric solution to (1.2).

Remark 3.5

The approximate solution and the initial data $v_{\varepsilon , \delta }^{in}$ to (1.2) constructed in [46]

$$\begin{aligned} v_{\varepsilon , \delta } = \varepsilon \textrm{ curl }\Big (\frac{b\times \xi }{ |\xi |^2} \varphi e^{iS / \varepsilon } \Big ) = i \varphi b e^{i S / \varepsilon } + \varepsilon c(x) e^{iS / \varepsilon } \triangleq A + B, \quad c(x) = \textrm{curl}( \frac{ b \times \xi }{ |\xi |^2} \varphi ) \end{aligned}$$

(3.23)

are not axisymmetric, where $b(t, x), \xi (t,x) \in {\mathbb {R}}^3$, $S, \varphi$ are scalar functions, and $\varepsilon$ is a small parameter. See equation (21) in [46]. To illustrate this point, we study the initial data more carefully. According to the construction in the proof of Proposition 3 in [46], for $t= 0$, we have $b(0, x) \equiv b_0, \xi (0, x) \equiv \xi _0$ for some

$$\begin{aligned} |b_0 | = 1, \quad |\xi _0| = 1, \quad b_0 \cdot \xi _0 = 0. \end{aligned}$$

(3.24)

In particular, $b, \xi$ are constant vectors. Moreover, $\varphi , S$ are independent of the angular variable $\vartheta$ [46], i.e. $\varphi (x) = \varphi (r, z), S(x) = S(r, z)$. Hence, we get

$$\begin{aligned} c(x) = \nabla \varphi \times \frac{b_0 \times \xi _0}{ |\xi _0|^2} = \nabla \varphi \times s_0, \quad s_0 \triangleq \frac{b_0 \times \xi _0}{ |\xi _0|^2}, \quad \partial _{\vartheta } A = 0. \end{aligned}$$

(3.25)

Suppose that $v_{\varepsilon , \delta }$ is axisymmetric (1.3). Then $v_{\varepsilon , \delta } \cdot \eta$ does not depend on $\vartheta$ for $\eta = e_r, e_{\vartheta }, e_z$ (3.1). Using these properties, (3.25), and $\partial _{\vartheta } e_r = e_{\vartheta }, \partial _{\vartheta } e_{\vartheta } = - e_r$, we get

$$\begin{aligned} 0= & {} \partial _{\vartheta } ( v_{\varepsilon , \delta } \cdot e_r ) = \partial _{\vartheta } ( (A+B) \cdot e_r) = A \cdot e_{\vartheta } + \partial _{\vartheta }( B \cdot e_r) \\= & {} A \cdot e_{\vartheta } + \varepsilon e^{iS / \varepsilon } \partial _{\vartheta } c(x) \cdot e_r- B \cdot e_{\vartheta }. \end{aligned}$$

Since the second and the third term have size $O(\varepsilon )$ and $\varepsilon$ is taken to $\varepsilon \rightarrow 0$ in [46], for sufficiently small $\varepsilon$, $A \cdot e_{\vartheta }$ and $\partial _{\vartheta }( B \cdot e_r)$ must be 0. Similarly, we get $A \cdot e_r = 0, \ \partial _{\vartheta }( B \cdot e_z) = 0$. Since the direction of A is given by $b_0$, it follows that $b_0 = (0, 0, b_{0, z}) = b_{0, z} e_z$. Note that $\varphi ( x) = \varphi (r, z)$ and $\nabla \varphi = \partial _r \varphi (r, z) e_r + \partial _z \varphi (r, z) e_z$. From (3.25) and $\partial _{\vartheta }( B \cdot e_z) = 0$, we get

$$\begin{aligned} \begin{aligned} c(x) \cdot e_z&= ( \partial _r \varphi e_r \times s_0 + \partial _z \varphi e_z \times s_0 ) \cdot e_z = \partial _r \varphi \cdot ( e_r \times s_0 ) \cdot e_z, \\ 0&= \partial _{\vartheta }( B \cdot e_z ) = \varepsilon e^{ iS / \varepsilon } \partial _{\vartheta }( c(x) \cdot e_z ) = \varepsilon e^{iS / \varepsilon }\partial _r \varphi \cdot ( \partial _{\vartheta } e_r \times s_0) \cdot e_z \\&= \varepsilon e^{iS / \varepsilon } \partial _r \varphi \cdot ( e_{\vartheta } \times s_0) \cdot e_z. \end{aligned} \end{aligned}$$

Since $b_0 =b_{0, 3} e_z$, we get $s_0 \cdot e_z =0, e_{\vartheta } \cdot e_z = 0$, which implies that $e_{\vartheta } \times s_0$ and $e_z$ are parallel. Then the above identity implies $e_{\vartheta } \times s_0 = 0$. Since $s_0$ is a constant vector and $\vartheta$ is arbitrary, we further obtain $s_0 = 0$, which contradicts (3.24) and (3.25).

The proof of Proposition 3.4 consists of several steps. Firstly, given $x_0, b_0, \xi _0$, we construct axisymmetric flows $\xi (t, x), b(t, x)$ and function S(t, x) using the PDE form of (3.6)–(3.8) such that $\xi (0, x_0) = \xi _0, b(0, x_0) = b_0, \nabla S = \xi$. Since the singular solution ${\textbf{u}}$ in Theorem 8 is only $C^{1,\alpha }$, these functions $\xi , b, S$ are not smooth enough to apply the argument in [46] to prove Proposition 3.4. Our key observation is that the solution (3.23) leading to the instability [46] is constructed locally along the trajectory of $x_0$. Thus, we can apply Lemma 3.2 and Theorem 8 to localize ${\textbf{u}}$ and obtain a much smoother localized velocity ${\textbf{u}}\cdot \chi$. Then we can obtain smooth $b, \xi , S$ and an axisymmetric velocity field given by (3.23). Finally, we show that b(T, x) can control $\beta (T)$ using the axisymmetric property of b. The remaining proof follows the argument in [46].

Before we present the proof, we need a simple Lemma for axisymmetric flows.

Lemma 3.6

Suppose that A(x), B(x) are axisymmetric flows (1.3), and $C(x) = C(r, z)$ is independent of $\vartheta$. Then $A \times B$, C(x)A, $\nabla \times A, \partial _r A, \partial _z A, \partial _{\vartheta } A$ are axisymmetric flows, and $A \cdot B$ is independent of $\vartheta$.

Proof

Since $e_r, e_{\vartheta }, e_z$ (3.1) are orthonormal basis, a simple calculation implies that $A \times B, C(r, z) A$ are axisymmetric and that $A \cdot B$ is independent of $\vartheta$. The property that the curl operator does not change axisymmetry is standard. For example, if the velocity ${\textbf{u}}$ is axisymmetric, the vorticity $\omega = \nabla \times {\textbf{u}}$ is also axisymmetric. The same reasoning and calculation apply to $\nabla \times A$. Since $\partial _r \eta = 0, \partial _z \eta = 0$ for $\eta = e_r, e_{\vartheta }, e_z$ and $\partial _{\vartheta } A = A^r(r, z) e_{\vartheta } - A^{\vartheta }(r, z) e_{r}$ for $A = A^r e_r + A^{\vartheta } e_{\vartheta } + A^z e_z$, we conclude that $\partial _rA, \partial _z A, \partial _{\vartheta } A$ are axisymmetric. $\square$

Proof of Proposition 3.4

Recall the poloidal component (3.2),(3.17)

$$\begin{aligned} \tilde{x} = (r , z), \quad {\tilde{\gamma }}_t = (r_t, z_t), \quad \tilde{A} = \{\tilde{a}: a \in A \}. \end{aligned}$$

(3.26)

We fix $T < T_*$. Suppose that $\beta (T) > 0$. Otherwise, the proof is trivial. Using the definition of (3.22) and result (b) in Theorem 8, for any $\eta > 0$, we can choose $(x_0, \xi _0, b_0)$ such that

$$\begin{aligned} x_0 \in (D_1 \backslash \Upsilon ) \cap \textrm{supp}(\omega _0) \subset B_{(1,0)}(1/4), \quad r_0 \ne 0, \ \xi _0 = {\tilde{\xi }}_0, \ \xi _0 \cdot b_0 = 0, \end{aligned}$$

(3.27)

and

$$\begin{aligned} 0 < \beta (T) \le (1 + \eta ) |b_T( x_0, {\tilde{\xi }}_0, b_0)|. \end{aligned}$$

(3.28)

We have $r_0 \ne 0$ since $x_0 \in B_{(1,0)}(1/4)$ implies $r_0 \ge \frac{3}{4}$. Denote

$$\begin{aligned} \vartheta _0 = x_{0,\vartheta }. \end{aligned}$$

(3.29)

Without loss of generality, we assume $x_0 \in D_1^+$. From Lemma 3.2, there exists $\delta > 0$ and a compact set $\Sigma _2$ such that (3.6)–(3.8) have a unique solution $( \gamma _t, b_t, \xi _t)$ on [0, T] for initial data x with $\tilde{x} \in B_{\tilde{x}_0}( \delta ), b_0, \xi _0$ and

$$\begin{aligned} {\tilde{\gamma }}_t( B_{\tilde{x}_0 }(\delta ) ) \cup B_{{\tilde{\gamma }}_t (\tilde{x}_0) }(\delta ) \subset \Sigma _2 \subset D_1^{+} \backslash \Upsilon \cap B_{(1,0)}(R_{2,\alpha }) , \quad t \in [0, T]. \end{aligned}$$

(3.30)

$\square$

3.4.1 Construction of axisymmetric functions

Our goal is to construct smooth (at least $C^4$) axisymmetric flows $\xi (t, x), b(t, x)$ satisfying (1.3) and function S(t, x) such that

$$\begin{aligned}&\xi (0, \tilde{x}, \vartheta _0 ) = \xi _0, \quad b(0,\tilde{x}, \vartheta _0 ) = b_0, \quad \xi (t, x) \cdot b(t, x) \equiv 0, \end{aligned}$$

(3.31)

$$\begin{aligned}&\xi (t, \gamma _t(\tilde{x} , \vartheta _0 )) = \xi _t( \tilde{x}, \vartheta _0,\xi _0 ), \quad b( t, \gamma _t(\tilde{x}, \vartheta _0)) = b_t( \tilde{x}, \vartheta _0, \xi _0, b_0) , \end{aligned}$$

(3.32)

$$\begin{aligned}&\nabla S(t, x) = \xi (t, x) , \quad \partial _{\theta } S(t, x) = \xi \cdot e_{\theta } = 0, \end{aligned}$$

(3.33)

for any $\tilde{x} \in B_{\tilde{x}_0}(\delta ), t \in [0, T]$, where $\vartheta _0=x_{0,\vartheta }$ (3.29) and $(\tilde{x}, \vartheta _0 )$ means $(r, \vartheta _0, z)$ in the cylindrical coordinates. Thus, $b(t, x), \xi (t, x)$ can be seen as the axisymmetric extensions of the solutions $\xi _t, b_t$ to the ODE (3.6)–(3.8) with initial data $(\tilde{x}, \vartheta _0),\xi _0, b_0$. We construct initial data as follows

$$\begin{aligned} \xi (0, x) = \xi _0^r e_r + \xi _0^z e_z, \quad b(0, x) = b_0^r e_r + b_0^{\vartheta } e_{\vartheta } + b_0^z e_z, \end{aligned}$$

(3.34)

where $e_{r(x_0)} = ( \cos \vartheta _0, \sin \vartheta _0, 0 ), \ e_{\vartheta (x_0)} = ( - \sin \vartheta _0, \cos \vartheta _0, 0 )$, and

$$\begin{aligned} \xi _0^r = \xi _0 \cdot e_{r(x_0)},\ \xi _0^z = \xi _0 \cdot e_z, \quad b_0^r = b_0 \cdot e_{r(x_0)}, \ b_0^{\vartheta } = b_0 \cdot e_{ \vartheta (x_0)}, \ b_0^z = b_0 \cdot e_z. \end{aligned}$$

The initial data $\xi (0, x), b(0, x)$ are axisymmetric and only depend on $x_{\vartheta }$ (3.1). From Lemma 3.6, $|\xi (0, x)|, |b(0,x)|, \xi (0, x) \cdot b(0, x)$ are independent of $\vartheta$. Using (3.27) and (3.34), we have

$$\begin{aligned}{} & {} \xi (0, \tilde{x}, \vartheta _0 ) = \xi _0, \ b(0, \tilde{x}, \vartheta _0 ) = b_0, \ |\xi (0, x)| = 1, \ | b(0, x)| = 1, \ \nonumber \\{} & {} \quad \xi (0, x) \cdot b(0, x) = \xi _0 \cdot b_0 = 0. \end{aligned}$$

(3.35)

3.4.2 Localization of the velocity

We want to construct $\xi (t, x), b(t, x)$ using (3.7)–(3.8) with the above initial data. Yet, the singular solution ${\textbf{u}}$ is only $C^{1,\alpha }$ and the resulting solutions $\xi , b$ are not smooth enough. To fix this problem, we localize the velocity. From (3.30), using compactness, we can find a smooth cutoff function $\chi _T(r, z)$ such that

$$\begin{aligned} \chi _T(\tilde{x}) = 1 , \quad \tilde{x} \in \Sigma _2, \quad \Sigma _2 \subset \textrm{supp}(\chi _T) =\Sigma _3 \subset D_1^{+} \backslash \Upsilon \cap B_{(1,0)}(R_{2,\alpha }) , \end{aligned}$$

(3.36)

where $\Sigma _3$ is another compact domain. Now, we modify the velocity ${\textbf{u}}$ as follows

$$\begin{aligned} {\textbf{u}}_T(t, x) \triangleq {\textbf{u}}(t, x) \chi _T(r, z). \end{aligned}$$

(3.37)

From Lemma 3.6 and Theorem 8, ${\textbf{u}}_T$ is axisymmetric and ${\textbf{u}}_T \in L^{\infty }( [0, T], C^{50}(D))$ is smooth in the whole domain.

3.4.3 Constructions of $b, \xi , S$

Consider the PDE (Eulerian) formulations of (3.7)–(3.8) with the modified velocity ${\textbf{u}}_T$

$$\begin{aligned} \begin{aligned} \partial _t \xi + {\textbf{u}}_T \cdot \nabla \xi&= - (\nabla {\textbf{u}}_T)^T \xi , \quad \partial _t b + {\textbf{u}}_T \cdot \nabla b = - (\nabla {\textbf{u}}_T) b + \frac{2 \xi ^T (\nabla {\textbf{u}}_T) b}{|\xi |^2} \xi \end{aligned} \end{aligned}$$

(3.38)

and initial data $\xi (0,\cdot ), b(0,\cdot )$. We will show that the evolution preserves the axisymmetry of $\xi , b$. For any axisymmetric functions g, f, using $\partial _{\vartheta } e_r = e_{\vartheta }, \partial _r e_{\vartheta } = -e_r$, we have

$$\begin{aligned} g \cdot \nabla f = (g^r \partial _r + \frac{g^{\vartheta }}{r} \partial _{\vartheta } + g^z \partial _z) f = \sum _{\alpha = \alpha , \vartheta , z}( g^r \partial _r + g^z \partial _z) f^{\alpha } \cdot e_{\alpha } + \frac{g^{\vartheta }}{r} ( f^r e_{\vartheta } - f^{\vartheta } e_{r}), \end{aligned}$$

which is axisymmetric. Therefore, we obtain

$$\begin{aligned} {\textbf{u}}_T \cdot \nabla \xi , \quad (\nabla {\textbf{u}}_T) \xi = \xi \cdot \nabla {\textbf{u}}_T, \quad {\textbf{u}}_T \cdot \nabla b, \quad (\nabla {\textbf{u}}_T) b \end{aligned}$$

are axisymmetric. Lemma 3.6 implies that $\xi \cdot (\nabla {\textbf{u}}_T) b, |\xi |^2 = \xi \cdot \xi$ are independent of $\vartheta$. Thus $\frac{ \xi ^T (\nabla {\textbf{u}}_T) b}{|\xi |^2} \xi$ is axisymmetric. Using the identity

$$\begin{aligned} - (\nabla {\textbf{u}}_T)^T \xi = ( \nabla {\textbf{u}}_T - (\nabla {\textbf{u}}_T)^T) \xi - (\nabla {\textbf{u}}_T ) \xi = (\nabla \times {\textbf{u}}_T) \times \xi - (\nabla {\textbf{u}}_T ) \xi \end{aligned}$$

and Lemma 3.6 again, we conclude that $- (\nabla {\textbf{u}}_T)^T \xi$ is axisymmetric. Therefore, the equations (3.38) preserves axisymmetry. From (3.38), it is easy to see that

$$\begin{aligned} \partial _t( \xi \cdot b) + {\textbf{u}}_T \cdot \nabla ( \xi \cdot b) = 0. \end{aligned}$$

Recall the initial data (3.34). From (3.35), we have $\xi (0, x) \cdot b(0, x) \equiv 0$. The above transport equation implies that $\xi (t, x) \cdot b(t, x) = 0$ in (3.31).

Next, we prove the identities in (3.32). First, for initial data x with $\tilde{x} \in B_{\tilde{x}_0}(\delta )$, due to (3.30) and ${\textbf{u}}_T = {\textbf{u}}$ in $\Sigma _2$ (3.36), (3.37), the flow maps on [0, T] generated by ${\textbf{u}}_T$ and ${\textbf{u}}$ are identical. Hence, we obtain

$$\begin{aligned} {\textbf{u}}( t, \gamma _t(x)) = {\textbf{u}}_T(t, \gamma _t(x)), \quad (\nabla {\textbf{u}})(t, \gamma _t(x)) = (\nabla {\textbf{u}})( t, \gamma _t(x)). \end{aligned}$$

Using (3.38) and the flow map $\gamma _t$ (3.6), we have

$$\begin{aligned}{} & {} \frac{d}{dt} \xi (t, \gamma _t(x)) = - (\nabla {\textbf{u}})^T \xi (t, \gamma _t(x)), \quad \\{} & {} \quad \frac{d}{dt} b(t, \gamma _t(x)) = - (\nabla {\textbf{u}}) b(t, \gamma _t(x)) + \frac{2 \xi ^T (\nabla {\textbf{u}}) b}{|\xi |^2} \xi (t, \gamma _t(x)) \end{aligned}$$

where $\nabla {\textbf{u}}$ is evaluated at $(t, \gamma _t(x))$. Thus, $\xi (t, \gamma _t(x))$ and $b(t, \gamma _t(x))$ satisfy the same ODE (3.7)–(3.8) for $\xi _t, b_t$. According to Lemma 3.2 and the discussion below (3.29), we can solve these ODEs for initial data x with $\tilde{x} \in B_{\tilde{x}_0}(\delta )$. Using (3.35), we get

$$\begin{aligned} \xi (0, \gamma _0(\tilde{x}, \vartheta _0)) = \xi _0 = \xi _t( \tilde{x}, \vartheta _0, \xi _0) |_{t=0}, \quad b(0, \gamma _0(\tilde{x}, \vartheta _0)) = b_0 = b_t( \tilde{x}, \vartheta _0, \xi _0) |_{t=0}. \end{aligned}$$

Using the uniqueness of ODEs, we obtain (3.32).

To construct S, following [46, 64] we solve the transport equation with the modified velocity ${\textbf{u}}_T$

$$\begin{aligned} \partial _t S + {\textbf{u}}_T \cdot \nabla S = 0, \quad S(0, x) = r \xi _0^r + z \xi _0^z. \end{aligned}$$

(3.39)

The equation for $\nabla S$ reads

$$\begin{aligned} \partial _t (\nabla S) + {\textbf{u}}_T \cdot \nabla ( \nabla S) = - (\nabla {\textbf{u}}_T)^T (\nabla S ), \quad (\nabla S)(0, x) = \xi _0^r e_r + \xi _0^z e_z = \xi (0, x). \end{aligned}$$

Comparing the above equations with (3.38), we yield $\nabla S(t, x) = \xi (t, x)$ for any x and $t \in [0, T]$.

Next, we consider $\partial _{\vartheta } S$. Since $\nabla S = \xi$ and ${\textbf{u}}_T$ are axisymmetric, using Lemma 3.6, we get

$$\begin{aligned} \partial _{\vartheta }( {\textbf{u}}_T \cdot \nabla S) =\partial _{\vartheta } ({\textbf{u}}_T \cdot \xi )= 0. \end{aligned}$$

Using (3.39) and $(\partial _{\vartheta } S )( 0, x)= 0$, we yield

$$\begin{aligned} \partial _t \partial _{\vartheta } S = 0, \quad \partial _{\vartheta } S (t, x) \equiv 0. \end{aligned}$$

This proves (3.33).

Since ${\textbf{u}}_T \in L^{\infty }([0, T], C^{50}(D) )$, $\xi (t, x), b(t, x), S(t, x)$ are smooth and at least $C^4$ in x.

3.4.4 Control of b(T, x)

We will show that b(T, x) can control $\beta (T)$ via (3.28).

Recall the poloidal notation (3.26). Let $x_T = \gamma _T(x_0)$ and $L_{\gamma } \ge 1$ be the Lipschitz constant of $\gamma _t, \gamma _t^{-1}$ on $[0, T] \times D_1$. From (3.28) and (3.32), we get

$$\begin{aligned} 0 < |b_T(x_0, b_0, \xi _0) | = |b(T, x_T)|. \end{aligned}$$

Using the continuity of $b(T, \cdot )$, there exists small $\delta _2$ with

$$\begin{aligned} \delta _2 \in (0, \frac{ \delta }{4 (L_{\gamma } + 1)^3} ) \end{aligned}$$

(3.40)

such that

$$\begin{aligned} (1-\eta ) |b_T(x_0, b_0, \xi _0)| = (1-\eta ) |b(T, x_T )|\le & {} \infty _{ \tilde{x} \in B_{ \tilde{x}_T(\delta _2) } } |b(T, \tilde{x}, x_{T,\vartheta } )|\nonumber \\= & {} \infty _{ x \in A_{x_T}(\delta _2) } |b(T, x)|. \end{aligned}$$

(3.41)

where we have used the continuity of b(T, x) in the inequality, and the axisymmetry property that |b(T, x)| is independent of $\vartheta$ in the third equality. Here, $A_{x_T}( \delta _2)= \{ x: \tilde{x} \in B_{\tilde{x}_T}(\delta _2) \}$ is an annulus. The above inequality reproduces Equation (19) in [46].

3.4.5 Construction of the axisymmetric velocity $v_{\varepsilon ,\delta }$

We follow [46, 64] to construct a cutoff function $\varphi$ so that we can localize b(T, x) to the domain where it is large using (3.41). Let $\varphi _T(x) = \varphi _T(r, z)$ be a smooth function supported in $A_{x_T}( \delta _2)$ with $|| \varphi _T ||_p = 1$. For any $t \in [0, T]$, we define

$$\begin{aligned} \varphi (t, x) \triangleq \varphi _T( \gamma _T \circ \gamma _t^{-1}(x)). \end{aligned}$$

(3.42)

Since $\varphi _T$ is independent of $\vartheta$, using (3.16) and (3.17), we know that the (r, z) component of $\gamma _T \circ \gamma _t^{-1}(x)$ only depends on $\tilde{x}$. Thus, we yield

$$\begin{aligned} \varphi (t, x) = \varphi _T( {\tilde{\gamma }}_T \circ {\tilde{\gamma }}_t^{-1}( \tilde{x})) \end{aligned}$$

and $\varphi (t, x)$ is independent of $\vartheta$.

Remark 3.7

We can also solve $\varphi (t, x)$ using the PDE similar to (3.38), (3.39)

$$\begin{aligned} \partial _t \varphi + {\textbf{u}}_T \cdot \nabla \varphi = 0, \quad \varphi (T, x) = \varphi _T(x). \end{aligned}$$

(3.43)

Tracking the support of $\varphi$ and using the argument similar to that in the proof of (3.32), one can show that these two constructions are the same.

Using (3.42) and (3.17), for $x \in \textrm{supp}( \varphi (t, \cdot ))$, we have $| {\tilde{\gamma }}_T \circ {\tilde{\gamma }}_t^{-1}(x) - {\tilde{\gamma }}_T(x_0)| \le \delta _2.$ Since ${\tilde{\gamma }}_T \circ {\tilde{\gamma }}_t^{-1}$ has Lipschitz constant $L_{\gamma }^2$, from (3.40), we get

$$\begin{aligned}{} & {} | \tilde{x} - {\tilde{\gamma }}_t(x_0)| \le L_{\gamma }^2 | {\tilde{\gamma }}_T \circ {\tilde{\gamma }}_t^{-1}(x) -{\tilde{\gamma }}_T(x_0)| \le L_{\gamma }^2 \delta _2, \quad \\{} & {} \quad \widetilde{\textrm{supp}( \varphi (t, \cdot ))} \subset B_{ {\tilde{\gamma }}_t(x_0)}( L_{\gamma }^2 \delta _2) \subset B_{ {\tilde{\gamma }}_t(x_0) }(\delta /2). \end{aligned}$$

Using (3.30), we further obtain

$$\begin{aligned} \widetilde{ \textrm{supp}( \varphi (t, \cdot ) ) } \subset \Sigma _2 \subset ( D_1^+ \backslash \Upsilon ) \cap B_{(1,0)}( R_{2,\alpha })\subset B_{(1,0)}(1/4) , \ t \in [0, T]. \end{aligned}$$

(3.44)

For fixed $\eta , \delta _2$, from Lemma 3.2, the function $\varphi$ is Lipschitz in time and $C^4$ in x on $[0, T] \times D_1$. Moreover, from (3.36), (3.37), we get

$$\begin{aligned} {\textbf{u}}_T(t, x) = {\textbf{u}}(t, x), \quad x \in \textrm{supp}( \varphi (t, \cdot )), \quad t \in [0, T]. \end{aligned}$$

(3.45)

Now, we follow [46, 64] to construct an approximate solution (3.23) via the WKB expansion. Since $\xi , b$ are axisymmetric flows and $S(t, x), \varphi (t,x), |\xi (t, x)|$ are independent of $\vartheta$, using Lemma 3.6 repeatedly, we yield that

$$\begin{aligned} b \times \xi , \quad \frac{b\times \xi }{|\xi |^2} \varphi e^{iS/\varepsilon }, \quad v_{\varepsilon , \eta } = \varepsilon \nabla \times ( \frac{b\times \xi }{|\xi |^2} \varphi e^{iS/\varepsilon }) \end{aligned}$$

are axisymmetric. We remark that $|\xi (t, x)|^{-1}$ is uniformly bounded on $[0, T] \times D_1$, which can be proved using the Lagrangian version of (3.38), the boundedness of $|\nabla {\textbf{u}}_T|$, and $|\xi (0, \cdot )| = |\xi _0| =1$ (3.34). Due to (3.44), $v_{\varepsilon , \eta }$ is supported in the interior of $D_1$ and $v_{\varepsilon , \eta } \cdot n = 0$ on $\partial D_1$.

Since $\textrm{supp}(v_{\varepsilon , \eta })\subset \textrm{supp}(\varphi )$, from (3.45), the localization of ${\textbf{u}}$ in (3.36) and (3.37) does not change the estimates of $v_{\varepsilon , \eta }$ in [46, 64]. Following the argument in [46, 64], we obtain that $v_{\varepsilon , \delta _2}$ is a solution to (1.2) with a small forcing term

$$\begin{aligned} \partial _t v_{\varepsilon , \delta _2} + ( {\textbf{u}}\cdot \nabla ) v_{\varepsilon , \delta _2} + ( v_{\varepsilon , \delta _2} \cdot \nabla ) {\textbf{u}}+ \nabla q_{\varepsilon , \delta _2} = R_{\varepsilon , \delta _2}. \end{aligned}$$

(3.46)

Moreover, we have the following estimates

$$\begin{aligned} \begin{aligned}&|| v_{\varepsilon , \delta _2}(T) ||_{L^p} \ge (1 - \eta ) |b(T, x_0, \xi _0)| - C_{\eta ,\delta _2} \varepsilon , \\&|| v_{\varepsilon , \delta _2}(0, \cdot )||_{L^p} \le 1 + C_{\eta , \delta _2} \varepsilon , \quad || R_{\varepsilon , \delta _2} ||_{L^p} \le C_{\eta , \delta _2} \varepsilon , \end{aligned} \end{aligned}$$

(3.47)

where $C_{\eta , \delta _2}$ is some constant independent of $\varepsilon$. The first two estimates are consequences of the leading order formula of $v_{\varepsilon , \eta }$ (3.23), (3.35), (3.41), and the conservation of $|| \varphi (t, \cdot )||_{L^p} =1$, which follows from the fact that $\varphi$ is transported by an incompressible flow, see e.g., (3.43). See also Appendix 5.7 for some formal derivations related to (3.46)–(3.47).

3.4.6 Symmetrization

An important observation is that $v_{\varepsilon , \delta _2}$ is only supported in the upper half domain $D_1^+ \backslash \Upsilon$ due to (3.44) and $\textrm{supp}( v_{\varepsilon , \delta _2} ) \subset \textrm{supp}( \varphi (t, \cdot ) )$. For the singular solution ${\textbf{u}}$ in Theorem 8, $\omega ^{\vartheta }(t)$ is odd and $u^{\vartheta }(t)$ is even in z, which induces the symmetry property (Sym) that $u^z(t)$ is odd and $u^{\vartheta }(t), u^r(t)$ are even in z. For vector $f = v_{\varepsilon , \delta _2}, R_{\varepsilon , \delta _2}$, we extend it to $D_1^-$ according to the same symmetry

$$\begin{aligned} {{\bar{f}}}^r = f^r(r, z) + f^r (r, -z), \quad {{\bar{f}}}^z = f^z(r, z) - f^z(r, -z), \quad {{\bar{f}}}^{\vartheta } = f^{\vartheta }(r, z ) + f^{\vartheta }(r, - z), \end{aligned}$$

where $f = f^r e_r+ f^{\vartheta } e_{\vartheta } + f^z e_z, {{\bar{f}}} = \bar{f}^r e_r+ {{\bar{f}}}^{\vartheta } e_{\vartheta } + {{\bar{f}}}^z e_z$. For the pressure $q_{\varepsilon , \delta _2}$ in (1.2), we extend it as an even function in z

$$\begin{aligned} {{\bar{q}}}_{\varepsilon , \delta _2} = q_{\varepsilon , \delta _2}(r, z) + q_{\varepsilon , \delta _2}(r, -z). \end{aligned}$$

The above symmetry properties are preserved by (1.1) and (1.2). We obtain that ${{\bar{v}}}_{\varepsilon , \delta _2}$ is a solution to (1.2) with pressure ${{\bar{q}}}_{\varepsilon , \delta _2}$ and forcing ${{\bar{R}}}_{\varepsilon , \delta _2}$ and enjoys the symmetry property (Sym). Since $\textrm{supp}( v_{\varepsilon , \delta _2} ) \in D_1^+$, ${{\bar{v}}}_{\varepsilon , \delta _2} - v_{\varepsilon , \delta _2}$ and $v_{\varepsilon , \delta _2}$ are disjoint, applying (3.47) yields

$$\begin{aligned} \begin{aligned}&||{{\bar{v}}}_{\varepsilon , \delta _2}(T) ||_{L^p} \ge 2 (1 - \eta ) |b(T, x_0, \xi _0)| - C_{\eta ,\delta _2} \varepsilon , \\&|| {{\bar{v}}}_{\varepsilon , \delta _2}(0, \cdot )||_{L^p} \le 2 + C_{\eta , \delta _2} \varepsilon , \quad || {{\bar{R}}}_{\varepsilon , \delta _2} ||_{L^p} \le C_{\eta , \delta _2} \varepsilon . \end{aligned} \end{aligned}$$

(3.48)

The last inequality on ${{\bar{R}}}_{\varepsilon ,\delta _2}$ follows from the triangle inequality. Let ${{\bar{v}}}(T)$ be the solution to (1.2) with initial data ${{\bar{v}}}_{\varepsilon , \delta _2}(0)$. Following the argument in [46, 64], we obtain

$$\begin{aligned} || {{\bar{v}}}(T) -{{\bar{v}}}_{\varepsilon , \delta _2}(T) ||_{L^p} \le C_{\eta , \delta _2} \varepsilon . \end{aligned}$$

(3.49)

Since the symmetry of ${{\bar{v}}}_{\varepsilon , \delta _2}(0)$ in z is preserved by (1.2), v(T) satisfies the symmetry (Sym).

3.4.7 Control of $\lambda _{p,\sigma }^{sym}$ for all power $\sigma$

Denote $\chi _2(x) = {\textbf{1}}_{ B_{(1,0)}( \frac{1}{2}) }(r, z)$. Since $\textrm{supp}( v_{\varepsilon , \delta _2}( t, \cdot ) )= \textrm{supp}( \varphi (t, \cdot ) ) \subset B_{ (1,0)}(1/4)$ (3.44) and ${{\bar{v}}}_{\varepsilon , \delta _2}$ is the symmetric extension of $v_{\varepsilon , \delta _2}$, we get $\chi _2 {{\bar{v}}}_{\varepsilon , \delta _2} ={{\bar{v}}}_{\varepsilon , \delta _2}$. Moreover, for $x \in \textrm{supp}( \chi _2) \cap D_1$, we get $r \in [1/2, 1]$. Then for any $\sigma \in {\mathbb {R}}$, using (3.47), we obtain

$$\begin{aligned} || r^{-\sigma } {{\bar{v}}}_{\varepsilon , \delta _2}(0, \cdot ) ||_{L^p} = || r^{-\sigma } \chi _2 {{\bar{v}}}_{\varepsilon , \delta _2}(0, \cdot ) ||_{L^p} \le C_{\sigma } || {{\bar{v}}}_{\varepsilon , \delta _2}(0, \cdot ) ||_{L^p} \le C_{\sigma } (2 + C_{\eta , \delta _2} \varepsilon ). \end{aligned}$$

Applying the above estimate, (3.41), (3.48), (3.49) and the definition (1.4), we yield

$$\begin{aligned} \begin{aligned} C_{\sigma }(2 + C_{\eta , \delta _2}) \lambda ^{sym}_{p, \sigma }(T)&\ge || r^{-\sigma } {{\bar{v}}}_{\varepsilon , \delta _2}(0, \cdot )||_{L^p} \lambda ^{sym}_{p, \sigma }(T) \\&\ge || r^{-\sigma } {{\bar{v}}}(T)||_{L^p} \ge || r^{-\sigma } \chi _2 {{\bar{v}}}(T)||_{L^p} \\&\ge \tilde{C}_{\sigma } || \chi _2 {{\bar{v}}}(T)||_{L^p} \ge \tilde{C}_{\sigma } ( || \chi _2 {{\bar{v}}}_{\varepsilon , \delta _2}(T) ||_{L^p} - || \chi _2 ( {{\bar{v}}}(T) -{{\bar{v}}}_{\varepsilon , \delta _2}(T) ) ||_{L^p} ) \\&\ge \tilde{C}_{\sigma } ( || {{\bar{v}}}_{\varepsilon , \delta _2}(T) ||_{L^p} - C_{\eta , \delta _2 } \varepsilon ) \\&\ge \tilde{C}_{\sigma } ( 2 (1-\eta ) b(T, x_0, \xi _0) - C_{\eta , \delta _2 } \varepsilon ) \ge \tilde{C}_{\sigma } \Big ( \frac{1-\eta }{1 + \eta } \beta (T) - C_{\eta , \delta _2 } \varepsilon \Big ). \end{aligned} \end{aligned}$$

Taking $\eta = 1/2$ and letting $\varepsilon \rightarrow 0$ conclude the proof. $\square$

Proof of Theorem 1

From Theorem 8, we have $\lim _{t \rightarrow T_*} || \omega _p(t) ||_{\infty } = \infty .$ Combining Propositions 3.3 and 3.4, we establish

$$\begin{aligned} \liminf _{t \rightarrow T_* } \lambda ^{sym}_{p, s}(t)^2 \ge C_{\sigma } \liminf _{ t \rightarrow T_*} \beta ^2(T) \ge C_{\sigma } \lim _{ t \rightarrow T_*} \frac{ || \omega _p(t) ||_{\infty } }{ || \omega _{p,0} ||_{\infty }} = \infty . \end{aligned}$$

We conclude the proof of Theorem 1. $\square$

3.5 Proof of Theorem 3

The proof of Theorem 3 is completely similar to that of Theorem 1 and is easier. We follow the arguments in [63]. Firstly, we note that there is a sign difference between the Boussinesq equations used in [11] (1.5) and [63]. In [63], the Boussinesq equations are given by

$$\begin{aligned} \theta _t + {\textbf{u}}\cdot \nabla \theta = 0, \quad {\textbf{u}}_t + {\textbf{u}}\cdot \nabla {\textbf{u}}+ \nabla p = (0, \theta )^T, \quad \nabla \cdot {\textbf{u}}= 0. \end{aligned}$$

(3.50)

The velocity-density formulation of (1.5) is the above equations with $(0, \theta )^T$ replaced by $(0, -\theta )^T$. Clearly, (1.5) and (3.50) are equivalent: $({\textbf{u}}, \theta )$ solves (1.5) if and only if $({\textbf{u}}, -\theta )$ solves (3.50). The linearized equation of (3.50) around a solution $({\textbf{u}}, \theta )$ of (3.50) is given by

$$\begin{aligned} \begin{aligned}&\partial _t \eta + {\textbf{u}}\cdot \nabla \eta + {\textbf{v}}\cdot \nabla \theta = 0, \quad \partial _t {\textbf{v}}+ {\textbf{u}}\cdot \nabla {\textbf{v}}+ {\textbf{v}}\cdot \nabla {\textbf{u}}+ \nabla q = (0, \eta )^T, \quad \textrm{div} \ {\textbf{v}}= 0, \end{aligned} \end{aligned}$$

(3.51)

which is also different from (1.7) with $(0, \eta )^T$ in (3.51) replaced by $(0, -\eta )^T$ in (1.7). Given solution $({\textbf{u}}, \theta )$ of (1.5) and $(v, \eta , {\textbf{u}}, \theta )$ satisfying (1.7), we obtain that $({\textbf{u}}, -\theta )$ is solution of (3.50) and $(v, -\eta , {\textbf{u}}, -\theta )$ satisfies (3.51). To keep the minimal changes of sign and other notations among this paper, [11], and [63], due to this connection, we use the following setting. Given a singular solution $({\textbf{u}}, - \theta )$ of (1.5) in Theorem 7, we obtain the solution $( {\textbf{u}}, \theta )$ of (3.50), which satisfies the same properties in Theorem 7, e.g., the blowup quantities and the regularity. Then we consider (3.50) and (3.51) in the following discussions so that the derivations and notations are consistent with those in [63].

The bicharacteristics-amplitude ODE system of (3.50) [63] read

$$\begin{aligned} {{\dot{\gamma }}}(t, x_0)&= {\textbf{u}}( t, \gamma (t, x_0)) , \end{aligned}$$

(3.52)

$$\begin{aligned} {{\dot{\xi }}}(t, x_0, \xi _0)&= - (\partial _x {\textbf{u}})^T \xi (t, x_0, \xi _0), \end{aligned}$$

(3.53)

$$\begin{aligned} \dot{b}( t, x_0, \xi _0)&= - (\partial _x \vec z) b + {\textbf{L}}b + (2 \frac{ \vec \xi ^T ( \partial _x \vec z) b }{|\xi |^2} - \frac{ \vec \xi \cdot ({\textbf{L}}b)}{ |\xi |^2} ) \vec \xi , \end{aligned}$$

(3.54)

where $\vec z \triangleq (\theta , {\textbf{u}})$, $b\in {\mathbb {R}}^3$, the matrix $\partial _x \vec z$, vector $\vec \xi$, and linear operator ${\textbf{L}}$ are given below

$$\begin{aligned} \partial _x \vec z \triangleq \left( \begin{array}{ccc} 0 &{} \partial _1 \theta &{} \partial _2 \theta \\ 0 &{} \partial _1 u_1 &{} \partial _2 u_1 \\ 0 &{} \partial _1 u_2 &{} \partial _2 u_2 \\ \end{array} \right) , \quad \vec \xi \triangleq \left( \begin{array}{c} 0 \\ \xi _1 \\ \xi _2 \\ \end{array} \right) , \quad {\textbf{L}}b \triangleq \left( \begin{array}{c} 0 \\ 0 \\ b_1 \\ \end{array} \right) . \end{aligned}$$

(3.55)

The initial data is given by $\gamma |_{t=0} = x_0, \xi |_{t = 0} = \xi _0 \in {\mathbb {R}}^2 \backslash \{ 0\}$ and $b|_{t = 0} = b_0 \in {\mathbb {R}}^3$. Denote

$$\begin{aligned} \Upsilon _2 \triangleq \{ (x, y) \in {\mathbb {R}}^2_+: x = 0 \mathrm { \ or \ } y = 0\}, \quad D = {\mathbb {R}}^2_+, \quad D^{\pm } \triangleq \{ (x, y): y \ge 0, \pm x \ge 0 \}. \end{aligned}$$

(3.56)

For the singular solution $({\textbf{u}}, -\theta )$ in Theorem 7 (then $({\textbf{u}}, \theta )$ solves (3.50)), since $\omega$ is odd, $\theta$ is even in x, and $v(x, 0) = 0$, we have

$$\begin{aligned} {\textbf{u}}\cdot n |_{\Upsilon _2} = 0, \end{aligned}$$

(3.57)

where n is the normal vector of $\Upsilon _2$. We first generalize Lemma 3.2 as follows.

Lemma 3.8

Let $\gamma _t$ be the solution to (3.52) with initial data $x_0$, $T_*$ be the blowup time, $T < T_*$, and $D^{\pm }$ be the domains defined in (3.56). (a) For any $x_0 \in \Upsilon _2$ and $t \in [0, T_*)$, its trajectory $\gamma _t$ remains in $\Upsilon _2$; for any $x_0 \in D_1^{\pm } \backslash \Upsilon _2$ and $t \in [0, T_*)$, we have $\gamma _t \in D^{\pm } \backslash \Upsilon _2$. For any $t \in [0, T]$, $\gamma _t$ is invertible, and $\gamma _t, \gamma _t^{-1}$ are Lipschitz in time and the initial value.

(b) For $x_0 \in D^{\pm } \backslash \Upsilon _2$, there exists $\delta (x_0, T) > 0$ depending on $x_0, T$ and a compact set $\Sigma _2$ such that

$$\begin{aligned} \gamma _t( B_{x_0 }( \delta ) ) \cup B_{ \gamma _t(x_0)}( \delta ) \subset \Sigma _2 \subset D^{\pm } \backslash \Upsilon _2 . \end{aligned}$$

(3.58)

As a result, for initial data $z_0 \in B_{x_0}( \delta )$ and any $b_0, \xi _0$, there exist a unique solution $(\gamma _t, b_t, \xi _t)$ to (3.52)–(3.54) on $t\in [0, T]$. The functions $(\gamma _t, b_t, \xi _t)$ are Lipschitz in time and $C^4$ with respect to initial data $z_0 \in B_{x_0}( \delta )$ and $b_0, \xi _0$, and $\gamma _t^{-1}(x)$ is Lipschitz in time and $C^4$ in $x \in \gamma _t( B_{x_0}( \delta ) ) \cup B_{\gamma _t(x_0)}(\delta )$.

Unlike Lemma 3.2 for the 3D Euler equations, in the above Lemma, since it is in 2D, we do not need to consider the angular variable $\vartheta$ and the poloidal component $\tilde{x}$ (3.2). Moreover, unlike (3.18), we do not restrict the initial data $x_0$ and the trajectory $\gamma _t(x_0)$ to a domain near the singularity (0, 0) since the velocity ${\textbf{u}}(t)$ in Theorem 7 is smooth in any interior compact domain in ${\mathbb {R}}_2^+$.

The proof of Lemma 3.8 follows from the non-penetrated condition (3.57), the regularity ${\textbf{u}}, \theta \in C^{1,\alpha }$ and ${\textbf{u}},\theta \in C^{50}(\Sigma )$ for any compact set $\Sigma \subset D^{\pm } \backslash \Upsilon _2$ from Theorem 7, and the same argument in the proof of Lemma 3.2.

We adopt the following notation from [63] by replacing the domain D by $D \backslash \Upsilon _2$

$$\begin{aligned} \alpha (T) \triangleq \sup _{ |b_0| = 1, | \xi _0| = 1, x_0 \in D \backslash \Upsilon _2, b_0 \cdot \vec \xi _0 = 0} | b(T, x_0, \xi _0, b_0)|. \end{aligned}$$

Recall from (3.55) that $b_0, \vec \xi _0 \in {\mathbb {R}}^3, \xi _0 \in {\mathbb {R}}^2$. From Lemma 3.8, for $x_0 \in D\backslash \Upsilon _2$, $b(T, x_0, \xi _0, b_0)$ and $\alpha (T)$ are well-defined. We modify Proposition 3.1 from [63] as follows.

Proposition 3.9

Assume that $({\textbf{u}}, -\theta )$ is the singular solution in Theorem 7. Then $({\textbf{u}}, \theta )$ is the singular solution of (3.50). For any $t \in (0, T_*)$, we have

$$\begin{aligned} ||\nabla \theta (T) ||_{\infty } \le || \nabla \theta _0||_{\infty } \alpha ^2(T). \end{aligned}$$

Note that $\nabla \theta \in C^{\alpha }$ is continuous, and we can solve (3.52)–(3.54) for $x_0 \in D^{\pm } \backslash \Upsilon _2$ from Lemma 3.8. The proof follows from the proof of Proposition 3.1 in [63] with minor modifications similar to those in the proof of Proposition 3.3. Thus, we omit the proof.

We modify Proposition 3.2 from [63] as follows.

Proposition 3.10

Assume that $({\textbf{u}}, -\theta )$ is the singular solution in Theorem 7. Then $({\textbf{u}}, \theta )$ is the singular solution of (3.50). For any $T \in (0, T_*)$ and $p \in (1, \infty )$, we have

$$\begin{aligned} \alpha (T) \le C_p \gamma ^{sym}_p(T). \end{aligned}$$

The proof follows from the argument in [63] and the argument in the proof of Theorem 3.4. The key point is that the approximate solution $( \eta _{\varepsilon , \delta }, v_{\varepsilon , \delta })$ constructed in [63] is similar to (3.23) and supported in a compact domain $\Sigma _2 \subset D^{\pm } \backslash \Upsilon _2$. See (3.44) for the case of the 3D Euler equations. The proof is much simpler since we do not need to construct an axisymmetric solution.

We give a sketch of the proof. We fix $T < T_*$. For any initial data $x_0 \in D^{\pm } \backslash \Upsilon _2$ and $b_0, \xi _0$ with $b_0 \cdot \vec \xi _0 = 0, |b_0|=1, |\xi _0|=1$, from Lemma 3.8, there exists $\delta > 0$ and a compact set $\Sigma _2$ such that (3.58) holds. Without loss of generality, we assume $x_0 \in D^+ \backslash \Upsilon _2$. We construct a smooth cutoff function $\chi _T$ similar to (3.36) such that

$$\begin{aligned} \chi _T(x) = 1, \quad x \in \Sigma _2, \quad \Sigma _2 \subset \textrm{supp}(\chi _T) = \Sigma _3 \subset D^{+} \backslash \Upsilon _2. \end{aligned}$$

We localize the singular solution $({\textbf{u}}, \theta )$ similar to (3.37) as follows

$$\begin{aligned} {\textbf{u}}_T(t, x) \triangleq {\textbf{u}}(t, x) \chi _T(x), \quad \theta _T(t, x) \triangleq \theta (t, x) \chi _T(x). \end{aligned}$$

(3.59)

From Theorem 7, we get ${\textbf{u}}_T, \theta _T \in L^{\infty }([0, T], C^{50}(D))$. Then we construct b(t, x), $\xi (t, x), \gamma (t, x)$ by solving the PDE (Eulerian) form of (3.52)–(3.54) with ${\textbf{u}}, \theta , \vec {z}$ replaced by ${\textbf{u}}_T, \theta _T, z_T = (\theta _T, {\textbf{u}}_T)$ using the following initial data

$$\begin{aligned} b(0, x) \equiv b_0, \quad \xi (0, x ) = \xi _0, \quad S(0, x) = x \cdot \xi _0. \end{aligned}$$

We choose $\delta _2 = \frac{\delta }{4 (1 + L_{\gamma })^3}$ similar to (3.40) and choose $\varphi _T$ that is supported in $B_{\delta _2}(\gamma _T(x_0))$ with $|| \varphi _T ||_{L^p}=1$. Then we construct a localized function with properties similar to (3.44)

$$\begin{aligned} \varphi (t, x) = \varphi _T( \gamma _T \circ \gamma _t^{-1}(x) ), \quad \textrm{supp}( \varphi (t, x)) \subset B_{\gamma _t(x_0)}(\delta / 2) \subset \Sigma _2. \end{aligned}$$

These functions $b(t,x), \xi (t,x), S(t,x), \varphi (t,x)$ are at least $C^4$ in the whole domain for $t \in [0, T]$. From (3.59), we have

$$\begin{aligned} {\textbf{u}}_T(t, x) = {\textbf{u}}(t, x), \quad \theta _T(t, x) = \theta (t, x), \quad x \in \textrm{supp}(\varphi (t)) \subset \Sigma _2, \quad t \in [0, T]. \end{aligned}$$

Using these functions $b, \xi , S, \varphi$, we follow [63] to construct the WKB solution, which is supported in $\textrm{supp}(\varphi (t)) \subset \Sigma _2$. Due to the above relation, the localization (3.59) does not change the estimates of the solution. We can further symmetrize the solution using the argument in Sect. 3.4.4. The rest of the proof follows [63].

One difference between our settings and those in [63] is that our domain ${\mathbb {R}}_2^+$ has boundary, while the domain in [63] is ${\mathbb {R}}^2$ or ${\mathbb {T}}^2$. In the proof of Proposition 3.10, this difference appears only in the elliptic estimate

$$\begin{aligned} \begin{aligned} - \Delta q = \nabla \cdot g, \ x \in {\mathbb {R}}_2^+, \quad - \frac{\partial q}{\partial n} = n \cdot g, \ \mathrm {\ on \ } \partial {\mathbb {R}}_2^+, \end{aligned} \end{aligned}$$

where n is the unit normal vector. In [63], there is no boundary and the second equation. In ${\mathbb {R}}_2^+$, the $L^p$ estimate

$$\begin{aligned} || \nabla q||_{L^p} \lesssim _p || g||_{L^p}, \quad p \in (1, \infty ) \end{aligned}$$

follows from the Poisson’s formula for q and the Calderon-Zygmund estimates of the kernel.

Now, we are in a position to prove Theorem 3. The proof is simpler than that in [63] since we do not require the blowup criterion on $\int _0^T || \nabla \theta ||_{\infty } dt$.

Proof of Theorem 3

From Theorem 7, we have $\lim _{t \rightarrow T_*} || \nabla \theta (t) ||_{\infty } = \infty .$ Combining Propositions 3.9 and 3.10, we establish

$$\begin{aligned} \liminf _{t \rightarrow T_* } \gamma ^{sym}_{p}(t)^2 \ge C_p \liminf _{ t \rightarrow T_*} \alpha ^2(T) \ge C_p \lim _{ t \rightarrow T_*} \frac{ || \nabla \theta (t) ||_{\infty } }{ || \nabla \theta _0 ||_{\infty }} = \infty . \end{aligned}$$

We conclude the proof of Theorem 3. $\square$

3.6 Proof of Theorem 2

For the singular solution [26], near the singularity $(r, z) = (0, 0)$, the flow moves down the z axis, and then travel outward in the r direction. See also Remark 2.1 in [26]. We will use the outward flow to prove Theorem 2. Denote

$$\begin{aligned} \begin{aligned} \Upsilon _3&\triangleq \{ (r, z) : r =0 \mathrm { \ or \ } z = 0 \}, \quad {\tilde{\beta }}_{\sigma }(t)&= \sup _{ \begin{array}{c} (x_0, b_0, {\tilde{\xi }}_0) \in ({\mathbb {R}}^3 \backslash \Upsilon _3) \times {\mathbb {R}}^3 \times S^1, \\ b_0 \cdot \xi _0 =0, |b_0| = r_0^{\sigma } \end{array} } | r_t^{-\sigma } b_t(x_0, {\tilde{\xi }}_0, b_0)|. \end{aligned} \end{aligned}$$

(3.60)

The definition of ${\tilde{\beta }}_{\sigma }(t)$ modifies (3.21) and is similar to (3.22). The velocity $u^r, u^z$ in Theorem 9 satisfies

$$\begin{aligned} {\textbf{u}}(t) \cdot n \Big |_{\Upsilon _3 } = u^r(t) \cdot n^r + u^z(t) \cdot n^z(t) = 0, \end{aligned}$$

(3.61)

and $(u^r, u^z)$ is smooth in ${\mathbb {R}}^3 \backslash \Upsilon _3$ and $u^{\vartheta } = 0$. In particular, $\gamma _t$ is a bijection from ${\mathbb {R}}^3 \backslash \Upsilon _3$ to ${\mathbb {R}}^3 \backslash \Upsilon _3$. Hence, we can generalize Lemma 3.2 to the current setting, and solve (3.6)–(3.8) in ${\mathbb {R}}^3 \backslash \Upsilon _3$ with solutions $b_t, \gamma _t, \xi _t, \gamma _t^{-1}$ that are $C^4$ on the initial data.

The following result is established in the proof of Proposition 2 in [46].

Proposition 3.11

For any $(T, x_T) \in (0, T_*) \times {\mathbb {R}}^3 \backslash \{ r = 0\}$ and $\sigma \in {\mathbb {R}}$, let $x_t$ be the backward solution of (3.6) from time T and $x_T$, $\omega _0 = \omega (0, x_0)$, $\xi _t$ be the solution of (3.7) with initial data $\xi _0 \cdot \omega _0 = 0, \xi _0 \ne 0, \xi _0 \cdot e_{\vartheta (x_0)} = 0$, and $b_t$ be a solution of (3.8) with initial data $b_0 = r_0^{\sigma } e_{\vartheta }$ and $b_0 \cdot \xi _0 = 0$. Then we have $r_0^{\sigma + 1} \le r_T |b_T|$.

Applying the above result to $x_T \in {\mathbb {R}}^3 \backslash \Upsilon _3 \subset {\mathbb {R}}^3 \backslash \{ r = 0\}$ and using definition (3.60), we yield

$$\begin{aligned} \frac{r_0^{\sigma +1}}{ r_T^{\sigma +1}} \le r_T^{-\sigma } |b_T| \le {\tilde{\beta }}_{\sigma }(T). \end{aligned}$$

Since $x_T = \gamma _T(x_0)$ is arbitrary in ${\mathbb {R}}^3 \backslash \Upsilon _3$ and $\gamma _T$ is a bijection from ${\mathbb {R}}^3 \backslash \Upsilon _3$ to itself, we derive $\sup _{ x_0 \in {\mathbb {R}}^3 \backslash \Upsilon _3} \frac{r_0^{\sigma +1}}{ r_T^{\sigma +1}} \le {\tilde{\beta }}_{\sigma }(T).$ Since ${\textbf{u}}\in C^{1,\alpha }$ and $\gamma _T(x)$ is Lipschitz in x, we get $\gamma _T( r_0, \vartheta _0, 0) = \lim _{ z \rightarrow 0} \gamma _T(r_0, \vartheta _0, z)$. Hence, we further obtain

$$\begin{aligned} \sup _{ x_0 \in {\mathbb {R}}^3 \backslash \{ r= 0 \} } \frac{r_0^{\sigma +1}}{ r_T^{\sigma +1}} \le {\tilde{\beta }}_{\sigma }(T). \end{aligned}$$

(3.62)

We have the following estimate for $r_T / r_0$. The idea is that the outgoing flow in the r direction near $(r, z) = (0, 0)$ generates rapid growth of $r_T / r_0$.

Lemma 3.12

Let ${\textbf{u}}$ be the singular solution in Theorem 9. Then for any $T < T_*$, we have

$$\begin{aligned} \sup _{ r_0 \ne 0} \frac{r_T}{r_0} \ge \exp \Big ( \frac{1}{2} \int _0^{T} u_r^r( t, 0,0) dt \Big ). \end{aligned}$$

Proof

Note that $u^r( t, 0, z) = 0$. For $T < T_*$, since $u^r(t) \in C^0( [0, T], C^{1,\alpha })$ and $u^r_r(t, 0, 0) > 0, t \in [0, T]$, there exists $\delta > 0$, such that

$$\begin{aligned} 0 < \frac{1}{2} u^r_r( t, 0, 0) \le \frac{u^r( t, r, 0 )}{r} \le 2 u^r_r( t, 0, 0) . \end{aligned}$$

(3.63)

for all $r \le \delta , t\in [0, T]$. Since $u^z( t, r, 0) = 0$, solving the r component of the ODE (3.6) backward with initial data $x_T = (r_T, 0), r_T = \delta /2$, we get that the trajectory is on $z = 0$ and

$$\begin{aligned} \frac{d}{dt} r_{T-t} = - u^r( T-t, r_{T-t}, 0) = - r_{T-t} \frac{u^r( T-t, r_{T-t}, 0) }{ r_{T-t}} \end{aligned}$$

Since $u^r(T-t, r, 0) \ge 0$ on $r \in [0, \delta ]$, $r_{T-t}$ is decreasing in t and $r_{T-t} \in [0, \delta ]$. Using the above ODE, (3.63), and Gronwall’s inequality, we obtain

$$\begin{aligned} r_0 \le \exp ( -\frac{1}{2}\int _0^T u_r^r( t,0,0) dt) r_T, \quad r_0 \ge \exp ( -2 \int _0^T u_r^r( t,0,0) dt) r_T > 0. \end{aligned}$$

The desired result follows. $\square$

For the singular solution in Theorem 9  , Proposition 3 in [46] remains true.

Proposition 3.13

Let $t \in (0, T_*), p \in (1, \infty ), \sigma \in (-\frac{2}{p^{\prime }}, \frac{2}{p} )$ and ${\textbf{u}}$ be the singular solution in Theorem 8. Then we have ${\tilde{\beta }}_p(T) \lesssim \lambda ^{sym}_{p, \sigma }(T)$.

From Theorem 9, for any $T < \infty$ and any compact domain $\Sigma \subset {\mathbb {R}}^3 \backslash \Upsilon _3$, we can localize ${\textbf{u}}$ using some cutoff function such that ${\textbf{u}}(t, x) \chi (x) = {\textbf{u}}(t, x)$ for $(x, t) \in \Sigma \times [0, T]$, and ${\textbf{u}}\chi$ is much smoother. The weighted estimate involving the weight $r^{-\sigma }$ in Lemma 4.1 in [46] does not require higher order regularity on ${\textbf{u}}$. Thus the proof follows from [46] and the proof of proposition 3.4.

Now, we are in a position to prove Theorem 2

Proof of Theorem 2

From Theorem 9, we have $\int _0^{T_*} u_r^r(t, 0,0) dt = \infty$. For $\sigma < -1$, $-\sigma - 1 > 0$, combining Lemma 3.12 and (3.62), we obtain

$$\begin{aligned} \lambda ^{sym}_{p, \sigma }(T)\ge & {} C {\tilde{\beta }}_{\sigma }(T) \ge C \sup _{r_0 \ne 0} (\frac{ r_0}{r_T})^{\sigma +1} = C (\sup _{r_0 \ne 0} \frac{r_T}{r_0})^{-1-\sigma } \ge C\exp ( \frac{ -1- \sigma }{2} \int _0^T u_r^r(t, 0, 0) dt). \end{aligned}$$

Letting $T \rightarrow T_*$, we complete the proof. $\square$

4 Properties of the Singular Solutions to the 2D Boussinesq Equations

In this Section, we prove Theorem 7 regarding the properties of the singular solutions to the 2D Boussinesq equations (1.5) constructed in [11]. In Sect. 5, we generalize these estimates to the 3D Euler equations with boundary. We will prove the higher-order interior regularity in Theorems 7–9 by generalizing the nonlinear stability estimates in [11] to the higher order and using embedding inequalities. These quantitative stability estimates can be useful for future study of the singular solution. Since the estimates essentially follow from similar estimates in [11], we will only summarize the estimates and refer the details to Section 4.1$-$4.4 in the arXiv version of this paper.

After the completion of this work, recently, the first author [8] established the higher-order interior regularity using another approach. This is done by performing weighted Hölder estimates of the physical equations directly with a BKM-type [1] continuation criterion.

4.1 Setup for the 2D Boussinesq equations

Firstly, we recall the setup from [11].

4.1.1 Dynamic rescaling formulation

The analysis of the singular solutions [11] is based on the dynamic rescaling formulation [47, 54]. To distinguish the solutions to (1.5)–(1.6) and the solutions to its dynamic rescaling formulation, we denote by $\omega _{phy}(x, t),$$\theta _{phy}(x,t), {\textbf{u}}_{phy}(x, t)$ the solutions of (1.5)–(1.6). Then it is easy to show that

$$\begin{aligned} \begin{aligned} \omega (x, \tau )&= C_{\omega }(\tau ) \omega _{phy}( C_l(\tau ) x, t(\tau ) ), \quad \theta (x , \tau ) = C_{\theta }(\tau ) \theta _{phy}( C_l(\tau ) x, t(\tau )), \\ {\textbf{u}}(x, \tau )&= C_{\omega }(\tau ) C_l(\tau )^{-1} {\textbf{u}}_{phy}(C_l(\tau ) x, t(\tau )) , \end{aligned} \end{aligned}$$

(4.1)

are the solutions to the dynamic rescaling equations

$$\begin{aligned} \begin{aligned} \omega _{\tau }(x, \tau ) + ( c_l(\tau ) {\textbf{x}}+ {\textbf{u}}) \cdot \nabla \omega&= c_{\omega }(\tau ) \omega + \theta _x , \qquad \theta _{\tau }(x , \tau )+ ( c_l(\tau ) {\textbf{x}}+ {\textbf{u}}) \cdot \nabla \theta = 0, \end{aligned} \end{aligned}$$

(4.2)

where ${\textbf{u}}= (u, v)^T = \nabla ^{\perp } (-\Delta )^{-1} \omega$, ${\textbf{x}}= (x, y)^T$,

$$\begin{aligned} \begin{aligned}&C_{\omega }(\tau ) = \exp \left( \int _0^{\tau } c_{\omega } (s) d \tau \right) , C_l(\tau ) = \exp \left( \int _0^{\tau } -c_l(s) ds \right) ,\\&\quad C_{\theta }(\tau ) = \exp \left( \int _0^{\tau } c_{\theta } (s) d \tau \right) , \end{aligned} \end{aligned}$$

(4.3)

$t(\tau ) = \int _0^{\tau } C_{\omega }(\tau ) d\tau$ and the rescaling parameter $c_l(\tau ), c_{\theta }(\tau ), c_{\omega }(\tau )$ satisfies

$$\begin{aligned} c_{\theta }(\tau ) = c_l(\tau ) + 2 c_{\omega }(\tau ). \end{aligned}$$

We have the freedom to choose the time-dependent scaling parameters $c_l(\tau ), c_{\omega }(\tau )$ according to some normalization conditions. Then (4.2) is completely determined and (4.2) is equivalent to the original equation using the relations (4.1)–(4.3), as long as $c_l(\tau ), c_{\omega }(\tau )$ remain finite. We refer more discussion about this reformulation for the 2D Boussinesq equations to [11].

The dynamic rescaling formulation [47, 54] is closely related to the modulation technique [42, 52, 55, 58, 59]. It has been a very effective tool to study singularity formation for many problems [3, 4, 42, 52, 55, 59]. Recently, it has been used to establish singularity formation in 3D incompressible Euler equations [11, 26, 27] and related models [5,6,7, 15, 15, 16, 28].

To simplify our presentation, we still use t to denote the rescaled time.

4.1.2 Polar coordinates and different variables

Consider the polar coordinates in ${\mathbb {R}}_2^+$

$$\begin{aligned} r = \sqrt{x^2 + y^2}, \quad \beta = \arctan (y / x), \quad R = r^{\alpha }. \end{aligned}$$

Let $\omega , \theta , \psi = (-\Delta )^{-1} \omega$ be the vorticity, density, and the stream function in (4.2). Denote

$$\begin{aligned}{} & {} \Omega (R, \beta , t) = \omega (x, y, t), \quad \Psi = \frac{1}{r^2} \psi , \quad \eta ( R, \beta , t) = (\theta _x) ( x, y, t), \nonumber \\{} & {} \quad \xi ( R, \beta , t) = (\theta _y)(x, y, t). \end{aligned}$$

(4.4)

Using the $(R, \beta )$ coordinates and the above new variables, we reformulate (4.2) as follows

$$\begin{aligned} \begin{aligned} \Omega _t + \alpha c_l R \partial _R \Omega + ({\textbf{u}}\cdot \nabla ) \Omega&= c_{\omega } \Omega + \eta , \\ \eta _t + \alpha c_l R \partial _R \eta + ({\textbf{u}}\cdot \nabla ) \eta&= (2 c_{\omega } - u_x) \eta - v_x \xi ,\\ \xi _t + \alpha c_l R \partial _R \xi + ({\textbf{u}}\cdot \nabla ) \xi&= (2 c_{\omega }- v_y) \xi - u_y \eta .\\ \end{aligned} \end{aligned}$$

(4.5)

The elliptic equation (1.6) reduces to the following for the modified stream function $\Psi$

$$\begin{aligned} - \alpha ^2 R^2 \partial _{R R} \Psi - \alpha (4+\alpha ) R \partial _R \Psi - \partial _{\beta \beta } \Psi - 4 \Psi = \Omega , \end{aligned}$$

(4.6)

with boundary conditions

$$\begin{aligned} \Psi (R,0) = \Psi (R, \pi /2) =0, \quad \lim _{R\rightarrow \infty } \Psi (R, \beta ) = 0. \end{aligned}$$

(4.7)

We consider the equations of $(\omega , \theta _x, \theta _y)$ in (4.5) since these variables have similar regularities.

The approximate steady state of (4.5) under the coordinates $(R, \beta )$ is given by

$$\begin{aligned} \begin{aligned} {\bar{\Omega }}(R, \beta )&= \frac{\alpha }{c} \Gamma (\beta ) \frac{ 3R }{ (1 + R)^2}, \quad {\bar{\eta }}(R, \beta ) = \frac{\alpha }{c} \Gamma (\beta ) \frac{ 6 R }{ (1 + R)^3} , \quad {\bar{c}}_l = \frac{1}{\alpha } + 3, \quad {\bar{c}}_{\omega } = -1 ,\\ \Gamma (\beta )&= (\cos (\beta ))^{\alpha }, \qquad c = \frac{2}{\pi } \int _0^{\pi /2} \Gamma (\beta ) \sin (2\beta ) d\beta . \end{aligned} \end{aligned}$$

(4.8)

We decompose a solution $({{\hat{\Omega }}}, {{\hat{\eta }}}, {{\hat{\xi }}}, {{\hat{c}}}_l, {{\hat{c}}}_{\omega })$ of (4.5) into the approximate steady state and their perturbations

$$\begin{aligned} {{\hat{\Omega }}} = {{\bar{\Omega }}} + \Omega , \quad {{\hat{\eta }}} = {{\bar{\eta }}} + \eta , \quad {{\hat{\xi }}} = {{\bar{\xi }}} + \xi , \quad {{\hat{c}}}_l = {{\bar{c}}}_l + c_l, \quad {{\hat{c}}}_{\omega } = {{\bar{c}}}_{\omega } + c_{\omega }. \end{aligned}$$

To uniquely determine the dynamic rescaling formulation, we impose the following normalization conditions on the perturbation of the rescaling parameters $c_l(t), c_{\omega }(t)$

$$\begin{aligned} c_{\omega }(t) = -\frac{2 }{\pi \alpha } L_{12}(\Omega (t))(0), \quad c_l(t) = - \frac{1-\alpha }{\alpha } \frac{2}{\pi \alpha }L_{12}(\Omega (t))(0)= \frac{1-\alpha }{\alpha } c_{\omega }(t), \end{aligned}$$

(4.9)

where $L_{12}(\cdot )$ is defined below in (4.10). We use $\Omega , \eta , \xi$ to denote the perturbation since we will mainly focus on the analysis of the perturbation in the rest of the paper. The reader should not confuse them with the solution to (4.5).

We introduce

$$\begin{aligned} \begin{aligned} L_{12}(\Omega )&\triangleq \int _R^{\infty } \int _0^{\pi /2} \frac{ \sin (2\beta ) \Omega (s, \beta ) }{s} ds d \beta , \quad \Psi _* \triangleq \Psi - \frac{ \sin ( 2\beta )}{ \pi \alpha } L_{12}(\Omega ). \end{aligned} \end{aligned}$$

(4.10)

The following decompositions of velocity $(U, V) = \nabla ^{\perp }(-\Delta )^{-1}\Omega$ in the $(R, \beta )$ coordinates are derived in Section 8.1 in [11]

$$\begin{aligned} \begin{aligned} U(\Psi )&= -\frac{2r\cos (\beta )}{\pi \alpha } L_{12}(\Omega ) - 2 r \sin (\beta ) \Psi _* - \alpha r \sin \beta D_R \Psi - r\cos \beta \partial _{\beta }\Psi _*, \\ V(\Psi )&= \frac{2r \sin (\beta )}{\pi \alpha } L_{12}(\Omega ) + 2 r \cos \beta \Psi _* + \alpha r \cos \beta D_R \Psi - r \sin \beta \partial _{\beta } \Psi _*, \end{aligned} \end{aligned}$$

(4.11)

where $\Psi$ is the solution of (4.6). For small $\alpha$, the $L_{12}$ terms capture the leading order terms (U, V), and $\Psi _*$ is the lower order part in $\Psi$. We estimate the lower order terms using the elliptic estimates in Propositions B.2, B.3. Moreover, using the formula of $\bar{\Omega }$ in (4.8), we have

$$\begin{aligned} \begin{aligned}&L_{12}({\bar{\Omega }}) = \frac{\pi }{2} \frac{3 \alpha }{1 + R} . \end{aligned} \end{aligned}$$

(4.12)

4.1.3 Weights and energy norms

We define the differential operators

$$\begin{aligned} D_R = R \partial _R, \quad D_{\beta } = \sin (2\beta ) \partial _{\beta }. \end{aligned}$$

We recall the following singular weights and norms ${{\mathcal {H}}}^k, {{\mathcal {C}}}^k$ from [11].

Definition 4.1

Recall $\Gamma (\beta ) = \cos ^{\alpha }(\beta )$. Let $\sigma = \frac{99}{100}, \gamma = 1 + \frac{\alpha }{10}$. Define $\varphi _i, \psi _i, \phi _i$ by

$$\begin{aligned} \begin{aligned} \psi _0&\triangleq \frac{3}{16}\left( \frac{(1+R)^3}{R^4} +\frac{3}{2} \frac{(1+R)^4}{R^3} \right) \Gamma (\beta )^{-1} , \quad \varphi _0 \triangleq \frac{(1+R)^3}{R^3} \sin (2\beta ), \\ \varphi _1&\triangleq \frac{(1+R)^4}{R^4} \sin (2\beta )^{ - \sigma }, \quad \varphi _2 \triangleq \frac{(1+R)^4}{R^4} \sin (2\beta )^{ - \gamma } , \\ \psi _1&\triangleq \frac{(1+R)^4}{R^4} ( \sin (\beta )\cos (\beta ) )^{-\sigma }, \quad \psi _2 \triangleq \frac{(1+R)^4}{R^4} \sin (\beta )^{-\sigma } \cos (\beta )^{-\gamma } , \\ \phi _1&\triangleq \frac{1+R}{R}, \quad \phi _2 \triangleq 1 + (R \sin (2\beta )^{\alpha })^{- \frac{1}{40}} , \quad \phi _{ij} = {\textbf{1}}_{i \ge 1} \phi _1 + {\textbf{1}}_{j\ge 1} \phi _2 . \\ \end{aligned} \end{aligned}$$

(4.13)

The special forms of $\psi _0, \varphi _0$ are designed carefully to exploit nonlocal cancellations in the linearized equations of (4.5) and are crucial for the linear stability analysis of the weighted $L^2$ part of the energy in (4.16). We define the weighted $H^k$ norms as follows

$$\begin{aligned} || f ||_{{{\mathcal {H}}}^m(\rho )} \triangleq \sum _{ 0\le k \le m} || \rho _1^{1/2} D^k_R f ||_{L^2} + \sum _{ \ i+ j \le m - 1 } || \rho _2^{1/2} D^{i}_R D^{j+1}_{\beta } f ||_{L^2} . \end{aligned}$$

(4.14)

Choosing $\rho _i = \varphi _i$ and $\rho _i = \psi _i, i= 1,2$, we get the ${{\mathcal {H}}}^m(\varphi )$ and ${{\mathcal {H}}}^m(\psi )$ norm, respectively. We simplify ${{\mathcal {H}}}^m(\varphi )$ as ${{\mathcal {H}}}^m$. The ${{\mathcal {H}}}^m$ norm is used for $\Omega , \eta$ and the ${{\mathcal {H}}}^k(\psi )$ norm for $\xi$.

We need the weighted $C^k$ norm to control $\xi$

$$\begin{aligned} \begin{aligned} || f ||_{{{\mathcal {C}}}^k}&\triangleq || f ||_{\infty } + \sum _{1 \le i \le k} ( || \phi _1 D_R^i f||_{\infty } + || \phi _2 D_{\beta }^i f ||_{\infty } ) \\&\quad + \sum _{ i, j \ge 1, i+ j \le k} || ( \phi _1 + \phi _2) D_R^i D_{\beta }^j f ||_{\infty }. \end{aligned} \end{aligned}$$

(4.15)

We remark that the second weights $\varphi _2, \psi _2, \phi _2$ are used to handle the angular derivatives. For mixed derivatives only involving $D_R$, we use the first weights $\varphi _1, \psi _1, \phi _1$.

We define the $L^2$-type energy with some parameters $\mu _i, \mu _{ij} > 0$ to be chosen

$$\begin{aligned} \begin{aligned} E_1^2(\Omega , \eta , \xi ) \triangleq&|| \Omega \varphi _0^{1/2}||_2^2 + || \eta \psi _0^{1/2}||_2^2 + \frac{81}{4\pi c} L^2_{12}(\Omega )(0 ) + \mu _1 ( || \Omega \varphi _1^{1/2}||_2^2 + || \eta \varphi _1^{1/2}||_2^2 ) \\&+ || \xi \psi _1^{1/2} ||_2^2 + \mu _2( || \Omega \varphi _1^{1/2}||_2^2 + || \eta \varphi _1^{1/2}||_2^2 ) + || D_{\beta }\xi \psi _2^{1/2}||_2^2 \\&+ \mu _3 ( || D_R \Omega \varphi _1^{1/2}||_2^2 + || D_R \eta \varphi _1^{1/2}||_2 + || D_R\xi \psi _1^{1/2}||_2^2 ) , \\ E_k^2(\Omega , \eta , \xi ) \triangleq&E_1^2 + \sum _{2 \le i \le k} \sum _{0 \le j \le i} \mu _{i, j} \left( || p_j^{1/2} D_R^{j} D^{i - j}_{\beta } \Omega ||_2^2 + || p_j^{1/2} D_R^j D^{i - j}_{\beta } \eta ||_2^2 \right. \\&\left. + || q_j^{1/2} D_R^j D^{i - j}_{\beta } \xi ||_2^2 \right) . \end{aligned} \end{aligned}$$

(4.16)

To estimate the velocity of the approximate steady state, we use the ${{\mathcal {W}}}^{l, \infty }$ norm [11, 26]

$$\begin{aligned} || f ||_{{{\mathcal {W}}}^{l,\infty }} \triangleq \sum _{0 \le k+ j \le l , j \ne 0} \Big | \Big | \sin (2\beta )^{- \frac{\alpha }{5}} \frac{ D_R^k D_{\beta }^j }{\frac{\alpha }{10} + \sin (2\beta )} f \Big |\Big |_{L^{\infty }} + \sum _{0 \le k \le l } \Big | \Big | D_R^k f \Big |\Big |_{L^{\infty }}. \end{aligned}$$

(4.17)

4.2 Nonlinear stability and finite time blowup

In Section 4.1$-$4.4 in the arXiv version of this paper [12], we generalize the third order nonlinear energy estimates of the perturbation in [11], which is essentially (4.19) with $k=3$, to the higher order version (large k). In particular, we fix $k=100$ and establish the following. There exist some absolute constants $\nu _{ij} > 0$ (for $E_{\cdot , \infty }$), $\mu _{ij},\mu _i > 0$ (for $E_k$ (4.16)) such that the energy given by

$$\begin{aligned} \begin{aligned} E( \Omega , \eta , \xi )&\triangleq ( E_k(\Omega , \eta , \xi )^2 + \alpha E_{k-2,\infty }(\xi )^2)^{1/2}, \quad k = 100, \\ E_{k, \infty }^2( \xi )&\triangleq || \xi ||_{\infty }^2 + \sum _{ i+ j \le k} \nu _{i j} || {{\mathcal {P}}}_{ij} \xi ||_{\infty }^2, \quad {{\mathcal {P}}}_{ij} \triangleq \phi _{ij} D_R^i D^j_{\beta } , \end{aligned} \end{aligned}$$

(4.18)

satisfies the following nonlinear energy estimates

$$\begin{aligned} \frac{1}{2} \frac{d}{dt} E^2(\Omega , \eta ,\xi ) \le -\frac{1}{15} E^2 + K \alpha ^{1/2} E^2 + K \alpha ^{-3/2} E^3 + K \alpha ^2 E . \end{aligned}$$

(4.19)

Since the estimates are essentially the same as those presented in [11], we do not present them here.

Using a standard bootstrap argument, we establish that there exists a small absolute constant $\alpha _1 < \frac{1}{1000}$ and $K_*$, such that if $E(\Omega (\cdot , 0), \eta (\cdot ,0), \xi (\cdot , 0)) < K_* \alpha ^2$, we have

$$\begin{aligned} E(\Omega (t), \eta (t), \xi (t) ) < K_* \alpha ^2 \end{aligned}$$

(4.20)

for all time $t>0$ and $\alpha < \alpha _1$. We refer the detailed bootstrap argument to [11].

Following the argument in [11], we obtain that $c_l(t), c_{\omega }(t)$ defined in (4.8), (4.9) satisfy

$$\begin{aligned} -\frac{3}{2}< c_{\omega }(t) + {{\bar{c}}}_{\omega }< -\frac{1}{2}, \quad \frac{1}{2\alpha } + 3< c_l + {{\bar{c}}}_l < \frac{2}{\alpha } + 3, \end{aligned}$$

where ${{\bar{c}}}_{\omega }, {{\bar{c}}}_l$ (4.8) denote the scaling parameters associated to the approximate steady state, and $c_{\omega }, c_l$ are the perturbations. In particular, $C_{\omega }(\tau ), C_l(\tau )$ defined in (4.3) remains finite for any $\tau < +\infty$ with bounds depending on $\tau , \alpha$ only.

Finally, we consider the regularity of the solutions $\omega + \bar{\omega }, \eta + {{\bar{\eta }}}, \xi + {{\bar{\xi }}}$ in the physical space using the relations (4.1), (4.3). Below, we show that $\frac{1}{r}( u + {{\bar{u}}}) \in {{\mathcal {C}}}^{k-2}$. Applying $\bar{L}_{12}(\Omega ) = \frac{\pi }{2} \frac{3\alpha }{1 + R}$ (4.12), the embedding in Proposition B.1, and Proposition B.3 to $U( {{\bar{\Psi }}})$ (4.11), we yield

$$\begin{aligned} \begin{aligned} || \frac{1}{r} U({{\bar{\Psi }}}) ||_{{{\mathcal {C}}}^k}&\lesssim || \frac{1}{1+R} ||_{{{\mathcal {C}}}^k} + || {{\bar{\Psi }}}_* ||_{ {{\mathcal {C}}}^k} + || D_R {{\bar{\Psi }}}||_{{{\mathcal {C}}}^k} + || \partial _{\beta } {{\bar{\Psi }}}_* ||_{{{\mathcal {C}}}^k} \\&\lesssim _{\alpha } 1 + || \frac{1+R}{R} {{\bar{\Psi }}}_* ||_{ {{\mathcal {W}}}^{k, \infty }} + || \frac{1+R}{R} D_R {{\bar{\Psi }}}||_{{{\mathcal {W}}}^{k, \infty }} + || \frac{1+R}{R} \partial _{\beta } {{\bar{\Psi }}}_* ||_{{{\mathcal {W}}}^{k, \infty }} \lesssim _{\alpha } 1. \end{aligned} \end{aligned}$$

(4.21)

For $U(\Psi )$, we first consider $L_{12}(\Omega )$ using Lemma C.4. Let $\chi$ be the radial cutoff function defined in Lemma C.4, which is constant near $r= 0$. Using Proposition B.1 and (4.20), we have

$$\begin{aligned} || L_{12}(\Omega )||_{{{\mathcal {C}}}^{k-2}} \lesssim || L_{12}( \Omega ) - \chi _1 L_{12}(\Omega )(0)||_{{{\mathcal {C}}}^{k-2}} + || \chi _1||_{{{\mathcal {C}}}^{k-2}} | L_{12}(\Omega )(0) | \lesssim _{\alpha } || \Omega ||_{{{\mathcal {H}}}^k}\lesssim _{\alpha } 1. \end{aligned}$$

Applying Propositions B.2 and B.1 to control the $\Psi , \Psi _*$ terms in $U(\Psi )$ (4.11), we get

$$\begin{aligned} || \frac{1}{r} U(\Psi )||_{ {{\mathcal {C}}}^{k-2}} \lesssim || L_{12}(\Omega )||_{{{\mathcal {C}}}^{k-2}} + || \Omega ||_{{{\mathcal {H}}}^k} \lesssim _{\alpha } 1. \end{aligned}$$

Similarly, using the estimates of the approximate steady state in Lemmas C.1, C.2, C.3, and Propositions B.1, B.3, we obtain

$$\begin{aligned} || \frac{1}{r} ( V(\Psi + {{\bar{\Psi }}}) ||_{{{\mathcal {C}}}^{k-2}} \lesssim _{\alpha } 1, \quad || {{\bar{\Omega }}}+ \Omega ||_{{{\mathcal {C}}}^{k-2}} \lesssim _{\alpha } 1, \quad || {{\bar{\eta }}} + \eta ||_{{{\mathcal {C}}}^{k-2}} \lesssim _{\alpha } 1, \quad || {{\bar{\xi }}} + \xi ||_{{{\mathcal {C}}}^{k-2}} \lesssim _{\alpha } 1. \end{aligned}$$

(4.22)

Since the $(R, \beta )$ coordinates of $(C_l x, C_l y)$ is $(C_l^{\alpha } R, \beta )$, using the rescaling relation (4.1), (4.4), in $(R,\beta )$ coordinates, we obtain

$$\begin{aligned} \Omega (R, \beta , \tau ) = C_{\omega }(\tau ) \omega _{phy}( C_l^{\alpha }(\tau ) R, \beta , t(\tau ) ), \quad \omega _{phy}(R, \beta , t(\tau ) ) = C_{\omega }^{-1}\Omega ( C_l^{-\alpha } R, \beta , \tau ). \end{aligned}$$

Similar relations apply for $\theta , {\textbf{u}}$. Applying (4.21), (4.22), the above relation, and $\rho ( \lambda R, \beta ) \lesssim C(\lambda ) \rho (R, \beta )$ for any weight $\rho$ in Definition 4.1, we have

$$\begin{aligned} \begin{aligned}&|| \omega _{ phy}(t(\tau )) ||_{{{\mathcal {C}}}^{k-2}} + || \theta _{x,phy}(t(\tau ) ) ||_{{{\mathcal {C}}}^{k-2}} + || \theta _{y,phy}(t(\tau ) ) ||_{{{\mathcal {C}}}^{k-2}} \\&\quad \quad + || \frac{1}{r} u_{phy} ||_{{{\mathcal {C}}}^{k-2}} + || \frac{1}{r} v_{phy} ||_{{{\mathcal {C}}}^{k-2}} \lesssim C( C_l( \tau ) , C_{\omega }(\tau ), \alpha , \tau ) \lesssim C(\alpha , \tau ) < +\infty . \end{aligned} \end{aligned}$$

(4.23)

To further estimate the $C^k$ regularity, we have the following simple embedding.

Lemma 4.2

Let $S\triangleq \{ (x, y): x \ne 0, y> 0\} = \{ (r, \beta ): r > 0, \beta \in (0, \pi /2) \cup (\pi /2, \pi )\}.$ For any compact domain $\Sigma \subset S$ and $l \ge 1$, we have

$$\begin{aligned} || f||_{C^{l-1}(\Sigma )} \lesssim _{l, \alpha , \Sigma } || f||_{{{\mathcal {C}}}^{l}}. \end{aligned}$$

Proof

Recall $D_R = R \partial _R$ and $R = r^{\alpha }$. Using the chain rule, we yield $r \partial _r = \alpha R \partial _R$. For any compact domain $\Sigma \subset S$, $i \ge 0$ and $p \in {\mathbb {R}}$, since $r \ne 0, \sin (\beta ), |\cos \beta | \in (0, 1)$, we obtain

$$\begin{aligned} | \partial _r^i r^{ p }| \lesssim _{ i, p, \Sigma } 1, \quad | \partial _{\beta }^i \sin ^p(\beta )| \lesssim _{i, p, \Sigma } 1, \quad | \partial _{\beta }^i | \cos (\beta )|^p | \lesssim _{i, p, \Sigma } 1. \end{aligned}$$

Recall the relation among $\partial _x, \partial _y, \partial _r, \partial _{\beta }$

$$\begin{aligned} \partial _x = \cos (\beta ) \partial _{r} -\frac{\sin (\beta )}{r} \partial _{\beta }, \quad \partial _y = \sin (\beta ) \partial _{r} + \frac{\cos (\beta )}{ r} \partial _{\beta }. \end{aligned}$$

Using the Leibniz rule, induction on l and the above estimate, for $i+j \le l$ and $(x, y) \in \Sigma$, we obtain

$$\begin{aligned} | \partial _x^i \partial _y^j f |&\lesssim _{l, \Sigma } \sum _{ m + n \le l} | \partial _r^m \partial _{\beta }^n f| \lesssim _{l, \Sigma } \sum _{ m + n \le l} | (r \partial _r )^m \partial _{\beta }^n f| \lesssim _{l, \alpha , \Sigma } \sum _{ m + n \le l} | D_R^m \partial _{\beta }^n f| \\&\lesssim _{l, \alpha , \Sigma } || f||_{{{\mathcal {C}}}^{l}}. \end{aligned}$$

It follows $f \in C^{l-1}( \Sigma )$. $\square$

Since ${\textbf{u}}= r \cdot \frac{1}{r } {\textbf{u}}$ and $r \in C^{k-2}( \Sigma )$, from (4.23) and Lemma 4.2, we further get ${\textbf{u}}\in C^{k-3}(\Sigma )$ for any compact set $\Sigma \subset \{ (x, y): x \ne 0, y>0 \}$. Using the above bootstrap estimates, e.g. (4.20), the regularity estimates, the arguments of localizing the initial data and that for the finite time blowup in [11], we prove Theorem 7. We refer these two arguments to [11].

5 Properties of the Singular Solution to the 3D Euler Equations

In [11], to generalize the blowup estimates from the 2D Boussinesq equations in ${\mathbb {R}}_2^+$ to the 3D axisymmetric Euler equations with boundary, we need the nonlinear energy estimates for the Boussinesq equations and two additional steps. The first step is to control the support of the solutions in the domain $(r, z) \in [0, 1] \times {\mathbb {T}}$ so that it does not touch the symmetry axis $r = 0$. The second step is to generalize the ${{\mathcal {H}}}^3$ elliptic estimates in the Boussinesq equations to the 3D Euler equations. See Section 1.3 and Section 9 in [11].

For higher order estimates of the singular solutions to the 3D Euler equations, we only need to generalize the ${{\mathcal {H}}}^3$ elliptic estimates to the ${{\mathcal {H}}}^k$ version since the first step does not involve higher order estimates and we have established the nonlinear energy estimates for the Boussinesq equations (4.19). Note that the ${{\mathcal {H}}}^3$ elliptic estimates in Proposition 9.9 in [11] is proved inductively with the weighted $L^2( \frac{(1+R)^4}{R^4})$ elliptic estimate being the based case. Therefore, its generalization to the ${{\mathcal {H}}}^k$ estimate in Proposition 5.2 below is straightforward.

These higher order estimates imply the interior regularity estimates of $\omega ^{\vartheta }, (u^{\vartheta })^2, u^r, u^z$ in Theorem 8. See Sect. 5.3. The estimate of $u^{\vartheta }$ does not follow from that of $(u^{\vartheta })^2$. In Sects. 5.5 and 5.6, we further estimate $u^{\vartheta }$.

The proof of Theorem 9 is similar and is mostly based on the estimates in [26, 27]. Thus, we will only sketch the proof.

5.1 Setup of the 3D axisymmetric Euler equations

We first review the basic setup of the 3D axisymmetric Euler equations from Section 9 in [11]. Recall the 3D axisymmetric Euler equations from (3.9)–(3.11) and the cylindrical coordinates $(r, \vartheta , z)$ (3.1) in ${\mathbb {R}}^3$. We introduce the following variables

$$\begin{aligned} \tilde{\theta }(r, z) \triangleq (r u^{\vartheta })^2, \quad \tilde{\omega }(r, z) = \omega ^{\vartheta } / r, \end{aligned}$$

(5.1)

new coordinates (x, y) centered at $r = 1, z= 0$, and its related polar coordinates

$$\begin{aligned} x = C_l(\tau )^{-1} z, \quad y = (1-r) C_l(\tau )^{-1}, \quad \rho = \sqrt{x^2 + y^2}, \quad \beta = \arctan (y/x) , \quad R = \rho ^{\alpha }, \end{aligned}$$

(5.2)

where $C_l(\tau )$ is defined below (5.5). The reader should not confuse the relation $R = \rho ^{\alpha }$ with $R = r^{\alpha }$ in the 2D Boussinesq. Since the domain $D = \{ (r, z): r \le 1, z \in {\mathbb {T}}\}$ of the equations (3.9)–(3.11) is periodic in z with period 2, we focus on one period

$$\begin{aligned} D_1 \triangleq \{ (r, z): r \le 1, |z| \le 1 \}. \end{aligned}$$

(5.3)

In the proof in [11], the variables ${\tilde{\omega }}, {\tilde{\theta }}$ (5.1) are the analog of $(\omega , \theta )$ in the 2D Boussinesq equations (1.5). The cylindrical coordinates (r, z) for the 3D Euler equations relate to (y, x) in the 2D Boussinesq equations (1.5) via the change of variables (5.2).

We consider the following dynamic rescaling formulation centered at $r = 1, z= 0$

$$\begin{aligned} \begin{aligned} \theta (x, y, \tau )&= C_{\theta }(\tau ) \tilde{\theta }( 1 - C_l(\tau ) y, C_l(\tau ) x , t(\tau ) ) = C_{\theta }(\tau ) {\tilde{\theta }} (r, z, t(\tau )) , \\ \omega (x, y, \tau )&= C_{\omega }(\tau ) \tilde{\omega }( 1 - C_l(\tau ) y, C_l(\tau ) x , t(\tau )) = C_{\omega }(\tau ) {\tilde{\omega }}( r, z, t(\tau )), \\ \psi (x, y, \tau )&= C_{\omega }(\tau ) C_l(\tau )^{-2} \tilde{\psi } (1 - C_l(\tau ) y, C_l(\tau ) x, t(\tau )) = C_{\omega }(\tau ) C_l(\tau )^{-2} {\tilde{\psi }}(r, z, t(\tau )), \end{aligned} \end{aligned}$$

(5.4)

where $C_l(\tau ), C_{\theta }(\tau ), C_{\omega }(\tau ), t(\tau )$ are given by $C_{\theta }(\tau ) = C_l^{-1}(\tau ) C^2_{\omega }(\tau )$,

$$\begin{aligned} \begin{aligned}&C_{\omega }(\tau ) = C_{\omega }(0) \exp \left( \int _0^{\tau } c_{\omega } (s) d \tau \right) , \ C_l(\tau ) =C_l(0) \exp \left( \int _0^{\tau } -c_l(s) ds \right) , \ \\&\quad t(\tau ) = \int _0^{\tau } C_{\omega }(\tau ) d\tau . \end{aligned} \end{aligned}$$

(5.5)

These rescaling relations are similar to those in (4.1)–(4.3). Denote

$$\begin{aligned}{} & {} \Psi (R,\beta ) = \frac{1}{\rho ^2} \psi (\rho , \beta ), \quad \Omega (R, \beta ) = \omega (\rho , \beta ), \quad \eta (R, \beta ) = (\theta _x)(\rho , \beta ), \nonumber \\{} & {} \quad \xi (R, \beta ) = (\theta _y)(\rho , \beta ). \end{aligned}$$

(5.6)

Since we rescale the cylinder $D_1 = \{ (r, z): r \le 1, |z|\le 1 \}$, the domain for (x, y) is

$$\begin{aligned} \tilde{D}_1 \triangleq \{ (x, y) : |x| \le C_l^{-1}, y \in [0, C_l^{-1}] \}. \end{aligned}$$

(5.7)

Using the above change of variables, one can reformulate the elliptic equation (3.10) as follows

$$\begin{aligned} \begin{aligned}&- \alpha ^2 R^2 \partial _{RR} \Psi - \alpha (4+\alpha ) R \partial _R \Psi - \partial _{\beta \beta } \Psi - 4 \Psi \\&\quad \quad + \frac{ C_l \rho }{r}( \sin (\beta ) (2 + \alpha D_R) \Psi + \cos (\beta ) \partial _{\beta } \Psi ) + \frac{C_l^2 \rho ^2}{r^2} \Psi = r \Omega , \end{aligned} \end{aligned}$$

(5.8)

with boundary condition of $\Psi$ (in the sector $R \le C_l^{-\alpha }$) given below

$$\begin{aligned} \Psi (R,0) = \Psi (R, \pi /2) =0. \end{aligned}$$

(5.9)

See Sections 9.1 and 9.2 [11] for the details.

Definition 5.1

We define the size of support of the rescaling variables $(\theta , \omega )$ (5.4)

$$\begin{aligned} S(\tau ) = \textrm{ess} \infty \{\rho : \theta (x, y,\tau ) =0, \omega (x, y, \tau ) = 0 \mathrm { \ for \ } x^2 + y^2 \ge \rho ^2 \}. \end{aligned}$$

Obviously, the support of $\Omega , \eta$ defined in (5.6) is $S(\tau )^{\alpha }$. After rescaling the spatial variable, the support of $(\tilde{\theta }, \tilde{\omega })$ (5.1), (3.9) satisfies

$$\begin{aligned} \textrm{supp} ( \tilde{\theta }(t(\tau )) ), \ \textrm{supp} ( \tilde{\omega }(t(\tau )) ) \subset \{ (r, z) : ( (r-1)^2 + z^2)^{1/2} \le C_l(\tau ) S(\tau ) \}. \end{aligned}$$

(5.10)

5.2 Localized elliptic estimates

Let $\chi _1(\cdot ): [0, \infty ) \rightarrow [0, 1]$ be a smooth cutoff function, such that $\chi _1(R) = 1$ for $R \le 1$, $\chi _1(R) = 0$ for $R \ge 2$ and $(D_R \chi _1)^2 \lesssim \chi _1$. This assumption can be satisfied if $\chi _1 = \chi _0^2$ where $\chi _0$ is another smooth cutoff function. Denote

$$\begin{aligned} \chi _{\lambda }(R) = \chi _1(R/ \lambda ), \quad \Psi _{\chi _{\lambda }} = \Psi \chi _{ \lambda } , \quad \Omega _{\chi _{\lambda }} = \Omega \chi _{\lambda }. \end{aligned}$$

(5.11)

In Section 9.2.2 in [11], we showed that the leading order part of $\Psi$ near 0 is captured by

$$\begin{aligned} L_{12}(Z_{\chi _{\lambda }})(0) = - L_{12}(\Omega )(0) + 4\alpha \int _0^{\pi /2} \Psi (0, \beta ) \sin (2\beta ) d \beta , \end{aligned}$$

(5.12)

when $\lambda \ge (S(\tau ))^{\alpha }$.

As discussed at the beginning of Sect. 5, we can generalize Proposition 9.9 in [11] as follows.

Proposition 5.2

Suppose that $\Psi$ is the solution of (5.8) and $\Omega \in {{\mathcal {H}}}^k$. There exists some absolute constant $\alpha _2$ and constant $\delta _k \in (0, 1/4)$, such that if $\alpha <\alpha _2$, $\lambda = \delta _k C_l^{-\alpha }, \ C_l S < \alpha \cdot \delta _k^{1/\alpha +1}$, we have

$$\begin{aligned} \begin{aligned}&\alpha ^2 || R^2 \partial _{RR} \Psi _{\chi _{\lambda }} ||_{{{\mathcal {H}}}^k} + \alpha || R \partial _{R \beta } \Psi _{\chi _{\lambda }} ||_{{{\mathcal {H}}}^k} +|| \partial _{\beta \beta } ( \Psi _{\chi _{\lambda }} \\&\quad \quad - \frac{\sin (2\beta ) }{\alpha \pi } (L_{12}(\Omega ) + \chi _1 L_{12}(Z_{\chi _{\lambda }})(0) ) ) ||_{{{\mathcal {H}}}^k} \lesssim _k || \Omega ||_{{{\mathcal {H}}}^k}, \\&| L_{12}(Z_{\chi _{\lambda }})(0) | \lesssim 3^{- \frac{1}{\alpha }} || \Omega \frac{1+R}{R}||_{L^2}. \end{aligned} \end{aligned}$$

In Proposition 9.9 in [11], we prove the case for $k=3$ with $\delta _k = 2^{-13}$. The following results generalize Proposition 9.11 from [11]. The conditions $\lambda = \delta _k C_l^{-\alpha }, C_l S< \alpha \delta _k^{1/\alpha + 1}$ guarantee that $\lambda \ge (S(\tau ))^{\alpha }$ in (5.12).

Proposition 5.3

Let ${\bar{\Psi }}_0(t)$ be the solution of (5.8) with source term $\Omega = {\bar{\Omega }}_0 = {\bar{\Omega }} \chi (R / \nu )$, and $\alpha _2, \delta _k$ be the constants in Proposition 5.2. If $\alpha < \alpha _2$, $\lambda = \delta _k C_l^{-\alpha }, \ C_l S< \alpha \delta _k^{1/\alpha + 1}, \ 2 \nu < \lambda$, we have

$$\begin{aligned} \begin{aligned}&\alpha || \frac{1+R}{R} D_R^2 {\bar{\Psi }}_{0,\chi _{\lambda }} ||_{{{\mathcal {W}}}^{k, \infty }} + \alpha || \frac{1+R}{R} R \partial _{R \beta } {\bar{\Psi }}_{0, \chi _{\lambda }} ||_{{{\mathcal {W}}}^{k, \infty }} \\&\quad \quad +||\frac{1+R}{R} \partial _{\beta \beta } ( {\bar{\Psi }}_{0,\chi _{\lambda }} - \frac{\sin (2\beta ) }{\alpha \pi } (L_{12}( {{\bar{\Omega }}}_0) + \chi _1 L_{12}( \bar{Z}_{\chi _{\lambda }})(0) ) ) ||_{{{\mathcal {W}}}^{k,\infty }} \lesssim _k \alpha , \\&| L_{12}( {{\bar{Z}}}_{\chi _{\lambda }})(0) | \lesssim 3^{- \frac{1}{\alpha }}, \end{aligned} \end{aligned}$$

where $L_{12}( {{\bar{Z}}}_{\chi _{\lambda }})(0)$ associated to $\bar{\Psi }_0$ is defined in (5.12).

The case of $k=5$ is Proposition 9.11 in [11]. The general case follows from a similar argument.

Choosing $k=100$ in Propositions 5.2 and 5.3 and using (5.11), we obtain the elliptic estimates for $\Psi (R, \beta ) = \Psi _{\chi _{\lambda }}(R, \beta ), R \le \lambda = \delta _{100} C_l^{-\alpha }$ in the dynamic rescaling equations. Using the relations (5.2) and (5.6) and rescaling the domain, we obtain that $R \le \lambda$ is equivalent to

$$\begin{aligned} \rho \le C_l^{-1} \delta _{100}^{1/\alpha }, \quad \rho C_l \le \delta _{100}^{1/\alpha }, \quad | (r, z) - (1, 0) | \le \delta _{100}^{1/100}. \end{aligned}$$

Thus, we have ${{\mathcal {H}}}^{100}$ estimate of the stream function ${\tilde{\psi }}$ (3.9) in the physical domain

$$\begin{aligned} B_{ (1, 0)}( R_{2,\alpha }), \quad R_{2,\alpha } = \delta _{100}^{1/\alpha } < 1/4. \end{aligned}$$

(5.13)

Now, we are in a position to prove Theorem 8. Denote

$$\begin{aligned} D_{R_2} \triangleq \{ (r, z) : r \in (0, 1), z \ne 0 \} \cap B_{(1,0)}(R_{2,\alpha }) , \quad \Upsilon \triangleq \{ (r, z) : r = 1 \mathrm {\ or \ } z = 0 \}. \end{aligned}$$

(5.14)

Remark 5.4

In later estimates, we will choose $\alpha$ to be very small and then choose S(0) to be very large. Finally, we choose $C_l(0)$ much smaller than $S(0)^{-1}, \alpha$. We treat $C_l(0)$ roughly as 0.

5.3 Blowup, control of the trajectory and the interior regularity

Recall from Definition 5.1 the size of support S(t) in the dynamic rescaling equations. Then $C_l(t) S(t)$ is the size of the support of the solution in the physical space. In [11], for some small $\alpha _0> 0$ and any $0< \alpha < \alpha _0$, we construct a class of $C^{\alpha }$ singular solutions with the following control of the support and trajectory. For a point within the support of the initial data $(\theta _0, \omega _0)$ (5.4) and with trajectory $(R(t), \beta (t))$, R(t) satisfies a uniform estimate

$$\begin{aligned} C_l(t) R(t)^{1/\alpha } \le C(\alpha , S(0)) C_l(0) \end{aligned}$$

(5.15)

for some constant $C(\alpha , S(0))$ up to the blowup time. See Section 9.3.5 in [11]. For initial data with support size S(0), we can pick $C_l(0)$ small enough such that

$$\begin{aligned} C_l(t) S(t) \le C( \alpha , S(0)) C_l(0) < R_{2, \alpha } / 8 \triangleq R_{1, \alpha } , \end{aligned}$$

(5.16)

where $R_{2,\alpha }$ is defined in (5.13). It follows

$$\begin{aligned} ( S(t))^{\alpha }< R_{1,\alpha }^{\alpha } C_l^{-\alpha }< (R_{2,\alpha } / 2)^{\alpha } C_l^{-\alpha } < \delta _{100} C_l^{-\alpha }. \end{aligned}$$

Thus, within the support of the solution, we can apply the high order elliptic estimates $(k=100)$ in Propositions 5.2 and 5.3 to estimate $\Psi (R, \beta )$.

As discussed at the beginning of Sect. 5, using the argument in [11] and the higher order elliptic estimates in Propositions 5.2 and 5.3, we can generalize the blowup results in Theorem 7 for the 2D Boussinesq equations to the 3D axisymmetric Euler equations. In particular, we have the control of the support and the trajectory (5.15)–(5.16) and obtain the following generalization of (4.21) and (4.22) for the solution $(\theta , \omega , \psi )$ in the dynamic rescaling formulation (5.4) of (3.9)

$$\begin{aligned} || \nabla \theta (\tau ) ||_{{{\mathcal {C}}}^{60}} + || \omega (\tau ) ||_{{{\mathcal {C}}}^{60}} + || \frac{1}{\rho } \nabla ( \psi (\tau ) \chi _{\lambda } ) ||_{{{\mathcal {C}}}^{60}} \lesssim _{\alpha } 1 . \end{aligned}$$

(5.17)

In general, $\theta , \omega , \psi$ are only defined in the bounded and rescaled domain (5.7). Since $\theta , \omega , \psi \chi _{\lambda }$ have compact support with $S(t) < \frac{1}{2} C_l^{-1}$ (5.16) or $(2 \lambda )^{1/\alpha } < \frac{1}{2} C_l^{-1}$ (see Lemma 5.2), these variables can be extended naturally to $(x, y) \in {\mathbb {R}}_+ \times {\mathbb {R}}$. Then the ${{\mathcal {C}}}^k$ norm (4.15) of these variables are well-defined. From (5.10) and (5.16), the solution ${\tilde{\theta }}(t, r, z), {\tilde{\omega }}(t,r, z)$ are supported in $B_{(1,0)}(R_{1,\alpha })\subset B_{(1,0)}(R_{2,\alpha })$. Since $\chi _{\lambda } = 1$ in $B_{(1,0)}(R_{2,\alpha })$, using (5.17), (3.10), the rescaling relation (5.4), (5.1), and estimates similar to those in Lemma 4.2, we yield

$$\begin{aligned} || {\tilde{\theta }}(t) ||_{C^{50}(\Sigma )} + || {\tilde{\omega }}(t) ||_{C^{50}(\Sigma )} + || u^r(t)||_{C^{50}(\Sigma )} + || u^z(t)||_{C^{50}(\Sigma )} \lesssim C( \alpha , \Sigma , C_l(\tau ), C_{\omega }(\tau ) ) \end{aligned}$$

(5.18)

for the compact domain $\Sigma \subset D_{R_2}$ (5.14). Since $r, \frac{1}{r}$ is smooth away from $r=0$, from (5.1), we yield $( u^{\vartheta })^2, \omega ^{\vartheta } \in C^{50}(\Sigma )$. We prove estimates for $\omega ^{\vartheta }, (u^{\vartheta })^2, u^r, u^z$ in result (c) in Theorem 8.

In the (r, z) coordinates, from (5.15), (5.16), and (5.2), for $(r_0, z_0) \in \textrm{supp}( {\tilde{\omega }}_0) \cup \textrm{supp}({\tilde{\theta }}_0) = \textrm{supp}(u_0^{\vartheta }) \cup \textrm{supp}( \omega _0^{\vartheta })$, we have

$$\begin{aligned} \gamma _t( r_0, z_0) \in B_{(1,0)}( R_{1,\alpha } ) . \end{aligned}$$

(5.19)

This proves result (b) in Theorem 8.

5.4 Result (a): Blowup of $\omega _p$

Recall the poloidal component of $\omega$ from (3.3)

$$\begin{aligned} \omega _p =\omega ^r e_r + \omega ^z e_z, \quad \omega ^r = - \partial _z u^{\vartheta }, \quad \omega ^z = \frac{1}{r} \partial _r( ru^{\vartheta }). \end{aligned}$$

From (5.4), (5.5), and (5.1), we get $\partial _x \theta (x, y, \tau ) = C_{\theta } C_l \partial _z {\tilde{\theta }} = C_{\omega }^2 \partial _z( (u^{\vartheta } / r)^2)$. It follows

$$\begin{aligned} I(\tau ) \triangleq \int _0^{ t(\tau )} || \partial _z ( \frac{ ( u^{\vartheta }(s) )^2 }{r^2} ) ||_{\infty } ds = \int _0^{\tau } C_{\omega }^{-2} || \partial _x \theta (x, y, s)||_{\infty } d s. \end{aligned}$$

The nonlinear stability result implies that $|| \partial _x \theta (x, y, s)||_{\infty } \approx || {{\bar{\theta }}}_x ||_{\infty } \gtrsim _{\alpha } 1$ and $C_{\omega }(\tau ) \le \exp ( - \tau / 2 )$. See Section 9.3.6 in [11] for the derivations. Since $u^{\vartheta }$ is supported in $B_{(1,0)}(1/4)$ and $r u^{\vartheta }(r, z, t)$ is transported (3.9), we obtain

$$\begin{aligned} || \partial _z ( \frac{ ( u^{\vartheta }(s) )^2 }{r^2} ) ||_{\infty } \lesssim || \partial _z u^{\vartheta }(s)||_{\infty } || r u^{\vartheta }(s ) ||_{\infty } \lesssim || \omega _p(s) ||_{\infty } || r u_0^{\vartheta } ||_{\infty }. \end{aligned}$$

Therefore, we establish

$$\begin{aligned} \int _0^{\tau } \exp ( s ) ds \lesssim _{\alpha } I(\tau ) = \int _0^{ t(\tau )} || \partial _z ( \frac{ ( u^{\vartheta }(s) )^2 }{r^2} ) ||_{\infty } ds \lesssim || r u_0^{\vartheta } ||_{\infty } \int _0^{ t(\tau )} || \omega _p(s) ||_{\infty } ds. \end{aligned}$$

Taking $\tau \rightarrow \infty$ yields $\int _0^{T_* } || \omega _p(s)||_{\infty } ds = \infty$, where $T_* = t(\infty ) < +\infty$ (5.5) is the blowup time.

5.5 Interior regularity of $u_0^{\vartheta }$

The smoothness of $u^{\vartheta }$ does not follow from $(u^{\vartheta })^2$ since $u^{\vartheta }$ can degenerate. In this section, we choose $u_0^{\vartheta }$ smooth in the interior of the domain. In Sect. 5.6, we show that the regularity can be propagated.

Let $\Sigma _1$ be any compact domain with

$$\begin{aligned} \Sigma _1 \subset \{ (x, y): x \ne 0, y > 0 \}. \end{aligned}$$

(5.20)

Remark 5.5

Recall from Remark 1.2 that we made a minor change of the approximate steady state of the 3D Euler equations in [14] and the updated arXiv version of [11], i.e. [10]. More precisely, in [10], we modify $\bar{\theta }_{old}$ used in [11] by ${{\bar{\theta }}}$ below

$$\begin{aligned} {{\bar{\theta }}}_{old} = \int _0^x {{\bar{\theta }}}_x( z, y) , \quad {{\bar{\theta }}} = 1 + \int _0^x {{\bar{\theta }}}_x(z, y) d z, \end{aligned}$$

(5.21)

where ${{\bar{\theta }}}_x(x, y) = {{\bar{\eta }}}(R, \beta )$ (4.8). See Eq (A.20) in [10]. This modification does not change $\nabla {{\bar{\theta }}}$, i.e. $\nabla {{\bar{\theta }}} = \nabla {{\bar{\theta }}}_{old}$, and we have ${{\bar{\theta }}} \in C^{1,\alpha }$. We remark that [10, 11] are essentially the same except for this minor change. In the following derivations, we use this new approximate steady state ${{\bar{\theta }}}$.

The initial data for $\theta$ in [10] (see Eq (9.55) in Sections 9.3.2 and 9.3.6 [10]) is chosen as

$$\begin{aligned} \theta _0(x, y) = {{\bar{\theta }}}_0(x, y) = \chi _1(R / \nu ) {{\bar{\theta }}}( x, y), \end{aligned}$$

where ${{\bar{\theta }}}$ is given in (5.21) and $\chi _1$ is some smooth cutoff function satisfying that $\chi _1^{1/2}$ is smooth. We have the smoothness of $\chi _1^{1/2}$ by choosing $\chi _1 = {\tilde{\chi }}_1^2$ for another smooth cutoff function ${\tilde{\chi }}_1$. Since ${{\bar{\theta }}}_x( x, y ) > 0$ for $x > 0$, ${{\bar{\theta }}}(0, y) \ge 1$ and ${{\bar{\theta }}}$ is even, we get ${{\bar{\theta }}} \ge 1.$

Using induction and the Leibniz rule, we get ${{\bar{\theta }}}^{1/2} \in C^{60}(\Sigma _1)$. Since ${{\bar{\theta }}}_0^{1/2} = {{\bar{\theta }}}^{1/2}$$\chi _1^{1/2}(R /\nu ), R \in C^{60}(\Sigma _1)$, and $\chi _1^{1/2}$ is smooth, we further obtain $\theta _0^{1/2}(x, y) = {{\bar{\theta }}}_0^{1/2}(x, y) \in C^{60}(\Sigma _1)$.

Since $\Sigma _1$ is an arbitrary compact domain with (5.20), using the relation among $\theta _0, {\tilde{\theta }}_0, u^{\vartheta }_0$ (5.1), (5.4) and the relation between the coordinate (r, z) and (x, y) in (5.2), we obtain $u_0^{\vartheta }(r, z) = \theta _0^{1/2} / r \in C^{60}(\Sigma )$ for any compact domain $\Sigma \subset D_{R_2}$ (5.14). Moreover, $u_0^{\vartheta }$ is even in z and this symmetry is preserved by (3.9).

5.6 Propagate the regularity of $u^{\vartheta }$

In Theorem 8, it remains to prove $u^{\vartheta }(t) \in L^{\infty }( [0, T],$$C^{50}(\Sigma ))$ for any compact set $\Sigma \subset D_{R_2}$ (5.14). Recall $\Upsilon$ from (5.14).

The idea is that if the domain $\Sigma$ is away from $\textrm{supp}( u^{\vartheta } )$, then $u^{\vartheta }$ vanishes and it is smooth. Otherwise, the trajectory $g_t$ (5.22) through $\Sigma$ can be contained in a compact set in $( D_1 \backslash \Upsilon ) \cap B_{(1,0)}( R_{2,\alpha })$ and is smooth according to Theorem 8. Since $r u^{\vartheta }$ is transported along the trajectory and the initial data $u^{\vartheta }_0$ is smooth, we then obtain that $u^{\vartheta }(t)$ is smooth in $\Sigma$.

Proof

Recall $D_1, \Upsilon$ from (5.3), (5.14). We fix $T< T_{*}$ and a compact set $\Sigma \subset ( D_1 \backslash \Upsilon ) \cap B_{(1,0)}(R_{2,\alpha })$. Consider the flow map $g_t: (r, z) \in D_1 \rightarrow D_1$ generated by $(u^r, u^z)$

$$\begin{aligned} \frac{d}{dt} g_t( r, z ) = ( u^r( g_t(r, z), t) , u^z( g_t(r, z), t ) , \quad g_0(r, z) = (r, z). \end{aligned}$$

(5.22)

It is the same as ${\tilde{\gamma }}_t$ in (3.16), (3.17). Since $u^r, u^z \in L^{\infty }( [0, T], C^{1,\alpha }(D_1))$, we can solve the above ODE with $g_t, g_t^{-1}$ being Lipschitz in (r, z). Due to the non-penetrated condition (3.15), we obtain that $g_t, g_t^{-1}$ are bijections from $D_1$ to $D_1$ and $D_1 \backslash \Upsilon$ to $D_1 \backslash \Upsilon$. One should not confuse (5.22) with (3.6). Denote $L_{g}$ by the Lipschitz constant of $g_t, g_t^{-1}$ for $t \in [0, T]$. Recall from (3.9) that

$$\begin{aligned} \partial _t (r u^{\vartheta }) + ( u^r \partial _r + u^z \partial _z ) (r u^{\vartheta }) = 0. \end{aligned}$$

We abuse the notation by denoting $x = (r, z)$. We get $r_t u^{\vartheta }( t, g_t(x)) = r_0 u^{\vartheta }_0( x)$. Inverting $g_t$ yields

$$\begin{aligned} r u^{\vartheta }( t, x) = r( g_t^{-1}(x) ) u^{\vartheta }_0( g_t^{-1}(x)). \end{aligned}$$

(5.23)

From result (b) in Theorem 8, we yield

$$\begin{aligned} \textrm{supp}( u^{\vartheta }(t)) \subset g_t( \textrm{supp}(u^{\vartheta }_0) ) \cap B_{(1,0)}(R_{1,\alpha }), \quad t \in [0, T_* ). \end{aligned}$$

(5.24)

Since $\Sigma$ is compact, it suffices to show that for any $x \in \Sigma$, there exists $\delta > 0$ such that $u^{\vartheta }(t) \in C^{50}(B_x(\delta ))$ with norm uniformly bounded on [0, T]. Since $g_t, g_t^{-1}$ are bijections and Lipschitz in t and x and $g_t^{-1} (\Sigma ) \cap \Upsilon = \emptyset$, we yield

$$\begin{aligned} \delta _1 \triangleq \min _{t \in [0, T]} {\mathrm dist}( g_t^{-1}(\Sigma ), \Upsilon ) > 0 . \end{aligned}$$

(5.25)

Now, we define

$$\begin{aligned} \begin{aligned}&\delta = \frac{1}{ 4 ( L_{g} + 1) } \min ( R_{1, \alpha }, \delta _1), \quad \Sigma _2 \triangleq \{ x: {\mathrm dist}( x, \Upsilon ) \ge \delta \} \cap {{\bar{B}}}_{(1,0)} ( 4 R_{1,\alpha } ) \cap {{\bar{D}}}_1, \\&S(t, \rho ) = \{ x: |x- y| \le \rho , y \in \textrm{supp}(u^{\vartheta }(t)) \} \cap D_1. \end{aligned} \end{aligned}$$

(5.26)

The set $S(t, \rho )$ is the $\rho$ neighborhood of $\textrm{supp}( u^{\vartheta }(t))$, and $\Sigma _2$ is a compact set in $D_1 \backslash \Upsilon \cap B_{(1,0)}( R_{2,\alpha })$. From result (c) in Theorem 8, we have $u^r, u^z \in L^{\infty } ( [0, T], C^{50}(\Sigma _2) )$.

If $x \in \Sigma \backslash S(t, 2 \delta )$, we get $u^{\vartheta }(t, x) = 0$ on $B_x( \delta )$ and thus $u^{\vartheta }(t) \in C^{50} (B_x(\delta ))$.

If $x \in \Sigma \cap S(t, 2 \delta ))$, from (5.24), we have $x = \gamma _t(x_0) + z, x_0 \in B_{(1,0)}(R_{1,\alpha }), |z| \le 2 \delta$. Hence, we get $B_x(\delta ) \subset B_{ \gamma _t(x_0)}(3\delta )$. Next, we show that the trajectory passing through $B_{ \gamma _t(x_0)}(3\delta )$ is contained in $\Sigma _2$. Recall that $L_{g}$ is the Lipschitz constant of $g_t, g_t^{-1}$ on [0, T]. For any $s \in [0, t]$ and $y = g_t(x_0) + z \in D_1, |z| \le 3\delta$, using (5.25), (5.26), we get

$$\begin{aligned} \begin{aligned} | g_s^{-1}(y) - g_s^{-1} g_t(x_0)|&\le L_{g} | y - g_t(x_0) | \le 3 L_{ g} \delta , \\ {\mathrm dist}( g_s^{-1} ( y), \Upsilon )&\ge {\mathrm dist}( g_s^{-1} g_t(x_0), \Upsilon ) -3 L_{ g} \delta \ge \delta _1 - 3 L_{ g} \delta > \delta , \\ | g_s^{-1} (y) - (1,0)|&\le | g_s^{-1} g_t(x_0) - (1,0)| + 3 L_{ g} \delta \le 3 L_{ g} \delta + R_{1, \alpha } \le 2 R_{1,\alpha }, \end{aligned} \end{aligned}$$

where we have used $g_{\tau }( x_0) \in B_{(1,0)}(R_{1,\alpha })$ from Theorem 8 for $x_0 \in \textrm{supp}( u^{\vartheta }_0)$ and $\tau \in [0, T]$. Hence, we establish

$$\begin{aligned} g_s^{-1} B_x(\delta ) \subset g_s^{-1} B_{\gamma _t(x_0)}( 3\delta ) \subset \Sigma _2, \quad s \in [0, t]. \end{aligned}$$

Since $u^r, u^z \in L^{\infty }( [0, T], C^{50}(\Sigma _2))$ (5.18), solving (5.22) backward with backward initial data in $B_x(\delta )$, we yield $g_t^{-1} \in C^{50}( B_x(\delta ))$, with bound depending on T and $\Sigma _2$. Since $r \in [1/2, 1]$ within the support of $u^{\vartheta }( \cdot )$, using (5.23), we prove $u^{\vartheta }(t) \in C^{50}(B_x(\delta ))$ with bound depending on $T, \Sigma _2$.

Combining both cases $x \in \Sigma \backslash S(t, 2\delta ), x \in \Sigma \cap S(t, 2\delta )$, we obtain $u^{\vartheta } \in L^{\infty }( [0, T],$$C^{50}( B_x(\delta ))$. Since $\delta$ is uniform for $x \in \Sigma$ and $\Sigma$ can be covered by finite balls with radius $\delta$, we obtain $u^{\vartheta } \in L^{\infty }( [0, T], C^{50}( \Sigma ) )$. $\square$

5.7 Proof of Theorem 9

The proof of Theorem 9 is similar and simpler than that of Theorem 8 since we do not need to control the trajectory and estimate the swirl $u^{\vartheta }$.

Proof

The first part of the theorem about the blowup result from some $\omega _0^{\vartheta } \in C_c^{\alpha }$ and $u^{\vartheta }_0 = 0$ has been proved in Theorems 1, 2 in [27]. Moreover, higher order estimates of the perturbation in the ${{\mathcal {H}}}^k$ norm for $k\ge 1$ and the profile have been established in Theorem 2 in [27]. Thus, the interior regularity $\omega ^{\vartheta }, u^r, u^z \in L^{\infty }( [0, T], C^{50}(D_2))$ in Theorem 9 follows from these higher order estimates and the argument in the proof of Theorem 7.

It remains to estimate $u_r^r(t, 0, 0)$. Let $(r, \vartheta , z)$ be the cylindrical coordinates in ${\mathbb {R}}^3$ (3.1), $\rho , R, \beta$ be the modified polar coordinates for (r, z) and $\Omega$ be the vorticity in the new coordinates

$$\begin{aligned} \beta = \arctan ( z / r), \quad \rho = (r^2 + z^2)^{1/2}, \quad R = \rho ^{\alpha }, \quad \Omega (R, \beta ) = \omega ^{\vartheta }(\rho , \beta ). \end{aligned}$$

(5.27)

Firstly, we show that

$$\begin{aligned}{} & {} u_r^r(0, 0) = - \frac{1}{2} L(\omega ^{\vartheta })(0) = - \frac{1}{2\alpha } L( \Omega )(0), \nonumber \\{} & {} \quad L(f)( r ) \triangleq \int _r^{\infty } \int _0^{\pi /2} \frac{ f( r, \beta ) \cos ^2(\beta ) \sin (\beta ) }{ r } d r d \beta . \end{aligned}$$

(5.28)

This can be obtained by following the derivations in [26, 27]. For the sake of completeness, we derive (5.28) in Appendix D using the formula ${\textbf{u}}= \nabla \times (-\Delta )^{-1} \omega$ in ${\mathbb {R}}^3$.

In [27], it is proved that the blowup solution $\Omega$ satisfies

$$\begin{aligned} \begin{aligned}&\Omega (R, \beta , t) = \frac{1}{\lambda (t)} \Xi ( \frac{R}{ \lambda ^{1+\delta }}, \beta , s ) , \quad \frac{ds}{dt} = \frac{1}{\lambda (t)}, \quad || \Xi ||_{L^{\infty }} \lesssim _{\alpha } 1, \\&\Xi = F + \varepsilon (\tau ) = F_* + \alpha ^2 g + \varepsilon (\tau ), \quad \frac{1}{\alpha } L(F)(0) =- 1 + O(\alpha ), \quad L(\varepsilon (\tau ))(0) \equiv 0, \end{aligned} \end{aligned}$$

(5.29)

for some rescaled time s and factor $\frac{T_*}{T_* - t} \lambda (t) \rightarrow 1$ as $t\rightarrow T_*$, where $T_*$ is the blowup time. Here $F = F_* + \alpha ^2\,g$ is the time-independent self-similar profile of (1.1) without swirl constructed in [26]. See Sections 2.3$-$2.5 in [27]. In particular, for $\alpha$ small enough, we get

$$\begin{aligned} \begin{aligned} u_r^r(0, 0, t)&=- \frac{1}{2 \alpha } L(\Omega )(0) = - \frac{1}{2 \alpha \lambda (t)} L( \Xi )(0) = - \frac{1}{2 \alpha \lambda (t)} L( F)(0) > 0, \\ u_r^r(t,0,0)&\gtrsim _{\alpha } || \Omega (t) ||_{L^{\infty }} = || \omega (t)||_{L^{\infty }}. \end{aligned} \end{aligned}$$

The last inequality is a consequence of that $u_r^r(t, 0,0)$ and $||\omega ^{\vartheta }||_{L^{\infty }} = || \omega ||_{L^{\infty }}$ have the same scaling and that the blowup is asymptotically self-similar. It follows $\int _0^{T_*} u_r^r(t, 0,0 )d t = \infty$. $\square$

Remark 5.6

In [26], the setup of the 3D axisymmetric Euler equations is not conventional and differs from (3.9)–(3.11) by a negative sign. See Section 2 in [26] for this difference. Therefore, in the current setting, the profile F for the vorticity is negative, and $\frac{1}{\alpha }L(F) (0) = -1 + O(\alpha )$, while the profile F is positive in [26, 27]. These changes do not affect the positive sign of $u^r_r(0,0,t)$.

Appendices

Appendix A. Review of the Construction of Unstable Solutions

We provide a brief review of the construction of the unstable solution in [46, 64] via a WKB expansion and explain the connections among the WKB expansion, the bicharacteristics-amplitude ODE system (3.6)–(3.8), and the growth of the unstable solution.

1.1 Construction of the approximate solution

Suppose that ${\textbf{u}}(t, x)$ is a singular solution of (1.1). Denote by $\gamma _t(x)$ the flow map

$$\begin{aligned} \frac{d}{dt} \gamma _t(x) = {\textbf{u}}( t, \gamma _t(x)), \quad \gamma _0(x) = x. \end{aligned}$$

(A.1)

The main idea in [64] is to construct an approximate solution to (1.2) using a WKB expansion

$$\begin{aligned} v(t, x) \approx b(t, x) \exp ( \frac{ i S(t, x)}{\varepsilon } ) \end{aligned}$$

(A.2)

for sufficiently small $\varepsilon$ and the characteristics of the flow, where $b(t, x) \in {\mathbb {R}}^3$ and S is a scalar. Plugging the above ansatz into (1.2), we obtain

$$\begin{aligned} R_{\varepsilon } = ( \partial _t + {\textbf{u}}\cdot \nabla + \nabla {\textbf{u}}) v = \frac{i}{\varepsilon }( \partial _t + {\textbf{u}}\cdot \nabla ) S \cdot b e^{ iS / \varepsilon } + ( \partial _t + {\textbf{u}}\cdot \nabla + \nabla {\textbf{u}}) b \cdot e^{i S / \varepsilon }, \end{aligned}$$

where $(\nabla {\textbf{u}}) f = f \cdot \nabla {\textbf{u}}= f_j \partial _j u_i e_i$. To eliminate the $O(\varepsilon ^{-1})$ term, one requires

$$\begin{aligned} (\partial _t + {\textbf{u}}\cdot \nabla ) S =0. \end{aligned}$$

(A.3)

Then we can rewrite $R_{\varepsilon }$ as follows

$$\begin{aligned} R_{\varepsilon } = (\partial _t + {\textbf{u}}\cdot \nabla + \nabla {\textbf{u}}) b \cdot e^{ i S/ \varepsilon } \triangleq F(t, x) \cdot e^{ i S/ \varepsilon } , \quad F \triangleq (\partial _t + {\textbf{u}}\cdot \nabla + \nabla {\textbf{u}}) b . \end{aligned}$$

(A.4)

An important observation in [64] is that for high frequency oscillation, i.e. small $\varepsilon$, the pressure term in (1.2) is almost local. We would like to construct (v, Q) such that

$$\begin{aligned} R_{\varepsilon } = F(t, x) e^{i S/ \varepsilon } = \nabla Q + E_{\varepsilon }, \end{aligned}$$

where $E_{\varepsilon }$ is a small error term. This is possible since Q is one order more regular than a highly oscillatory function $F(t, x) e^{i S / \varepsilon }$. By integration and exploiting the cancellation, Q can be of order $O(\epsilon )$. In fact, taking $\nabla \times$ on both sides, we obtain

$$\begin{aligned} \nabla \times R_{\varepsilon } = ( \nabla \times F) e^{i S / \varepsilon } + \frac{i}{\varepsilon } (\nabla S \times F) e^{i S / \varepsilon } = \nabla \times ( \nabla Q + E_{\varepsilon } ) = \nabla \times E_{\varepsilon }. \end{aligned}$$

To eliminate the $O(\varepsilon ^{-1})$ term, we require $\nabla S \times F = 0$, which implies $F = c(t, x) \nabla S$ for some scalar c(t, x). In this case, one can construct the pressure Q as follows

$$\begin{aligned} Q = - i \varepsilon c(t, x) e^{i S / e}. \end{aligned}$$

As a result, the error is given by

$$\begin{aligned} E_{\varepsilon } = R_{\varepsilon } - \nabla Q = c \nabla S e^{i S / \varepsilon } + i \varepsilon \cdot \nabla c \cdot e^{i S / \varepsilon } + i \varepsilon c \frac{ i \nabla S}{\varepsilon } e^{iS / \varepsilon } = i \varepsilon \cdot \nabla c \cdot e^{i S / \varepsilon }. \end{aligned}$$

(A.5)

Suppose that c is smooth, then the $L^p$ norm of the error $E_{\varepsilon }$ is small as $\varepsilon \rightarrow 0$.

From $F = c(t, x) \nabla S$ and (A.4), we yield

$$\begin{aligned} ( \partial _t + {\textbf{u}}\cdot \nabla + \nabla {\textbf{u}}) b = F(t, x) = c(t, x) (\nabla S)( t, x). \end{aligned}$$

Using the Lagrangian coordinates and the flow map $\gamma _t$ (A.1), we get

$$\begin{aligned} \partial _t b(t, \gamma _t(x)) = - ( \nabla {\textbf{u}}) b(t, \gamma _t(x)) + c(t, x) (\nabla S)(t, \gamma _t(x)). \end{aligned}$$

Denote

$$\begin{aligned} \xi _t( x) \triangleq (\nabla S)( t, \gamma _t(x)) , \quad b_t(x) \triangleq b(t, \gamma _t(x)) \;. \end{aligned}$$

(A.6)

The above equation reduces to

$$\begin{aligned} \frac{d}{dt} b_t = - (\nabla {\textbf{u}}) b_t + c(t, x) \xi _t . \end{aligned}$$

(A.7)

Next, we determine the equations for $b, \xi$. In order for v(t, x) to be incompressible, from the ansatz (A.2) and

$$\begin{aligned} \nabla \cdot v(t, x) = ( \nabla \cdot b ) e^{i S / \varepsilon } + \frac{i}{\varepsilon } b \cdot \nabla S e^{ i S /\varepsilon } \;, \end{aligned}$$

we require $b(t, x) \cdot (\nabla S)(t, x) = 0$ to eliminate the $O(\varepsilon ^{-1})$ term. In the Lagrangian coordinates, this condition is equivalent to enforcing

$$\begin{aligned} b(t, \gamma _t(x)) \cdot (\nabla S)( t, \gamma _t(x)) = b_t(x) \cdot \xi _t(x) = 0. \end{aligned}$$

(A.8)

Taking the gradient in the transport equation (A.3), we get

$$\begin{aligned} ( \partial _t + {\textbf{u}}\cdot \nabla ) \nabla S = - (\nabla {\textbf{u}})^T \nabla S. \end{aligned}$$

Using the Lagrangian coordinates and (A.6), we derive

$$\begin{aligned} \frac{d}{d t} \xi _t = \frac{d}{dt} (\nabla S)(t, \gamma _t(x)) = - (\nabla {\textbf{u}})^T (\nabla S )( t ,\gamma _t(x)) = - (\nabla {\textbf{u}})^T \xi _t. \end{aligned}$$

(A.9)

The incompressible condition (A.8) implies $\frac{d}{dt} (b_t \cdot \xi _t ) = 0$. Thus, from (A.7) and (A.9), we get

$$\begin{aligned} \langle c(t, x) \xi _t, \xi _t \rangle - \langle (\nabla u) b_t, \xi _t \rangle - \langle (\nabla {\textbf{u}})^T \xi _t, b_t \rangle = 0, \end{aligned}$$

where $\langle p, q \rangle = p_i q_i$. It follows that

$$\begin{aligned} c(t, x) = 2 \frac{ \xi _t^T ( \nabla {\textbf{u}}) b_t}{ | \xi _t|^2}. \end{aligned}$$

Thus, from (A.1),(A.7),(A.9), $\gamma _t, \xi _t, b_t$ satisfy the bicharacteristics-amplitude ODE system (3.6)–(3.8) of (1.1) [46, 64]

The above derivation reveals the main idea behind the construction of an approximate solution to (1.2) in [64] and the relationship between the WKB expansion (A.2) and the bicharacteristics-amplitude ODEs (3.6)–(3.8). The last step is to localize the solution v(t, x) to some trajectory and add a correction to v(t, x) (A.2) so that it is incompressible. We refer to [64] for the details.

1.2 Growth of the solution

The solution v(t, x) satisfies (1.2) up to an error similar to (A.5). Since $E_{\varepsilon }$ contains the highly oscillatory phase $e^{i S / \varepsilon }$, the error may not be small in $C^{k, \alpha }$ or $H^s$ norm. In [64], based on the WKB construction (A.2) and using the smallness of the error in the $L^p$ norm, the authors constructed an approximate solution to (1.2) with error controlled by $\varepsilon$. To prove the instability, they further showed the growth of v(t, x). From (A.2), the growth of $|| v||_p$ is due to $|| b_t||_p$. The authors showed that if the velocity ${\textbf{u}}(t, x)$ is smooth, the system (3.6)–(3.8) satisfies the following conservations along the characteristic $\gamma _t(x)$

$$\begin{aligned} \begin{aligned} \omega (t, \gamma _t(x) ) \cdot \xi _t&= \omega _0(x) \cdot \xi _0, \quad b_t \cdot \xi _t = \tilde{b}_t \cdot \xi _t, \quad ( b_t \times \tilde{b}_t) \cdot \xi _t = (b_0 \times \tilde{b}_0) \cdot \xi _0, \end{aligned} \end{aligned}$$

where $\omega = \nabla \times {\textbf{u}}$ is the vorticity of the blowup solution ${\textbf{u}}$, $\xi _t, b_t, \tilde{b}_t$ are the solution to (3.6)–(3.8) with initial data $x_0, \xi _0, b_0, \tilde{b}_0$, $b_0 \cdot \xi _0 = \tilde{b}_0 \cdot \xi _0 = 0$ and $b_0, \tilde{b}_0, \xi _0$ being linearly independent.

From the first and the third identity, formally, $b_t \times \tilde{b}_t$ plays a role similar to $\omega (t, \gamma _t(x))$. Indeed, using the above conservations, the authors further proved

$$\begin{aligned} || \omega (t, \cdot )||_{\infty } \le || \omega _0||_{L^{\infty }} \Big ( \sup _{ |b_0| = |\xi _0| = 1, x_0 \in \Omega , b_0 \cdot \xi _0 = 0} | b_t(x_0, \xi _0, b_0)| \Big )^2. \end{aligned}$$

(A.10)

According to the BKM blowup criterion, $|| \omega (t)||_{\infty }$ must blowup, which leads to the growth of $b_t$ and $|| v(t)||_{L^p}$ and implies linear instability.

Appendix B. Embedding Inequalities and Estimates of Nonlinear Terms

We have the following estimates for different norms. The first and last inequality generalize Proposition 7.6 in [11]. The second inequality is exactly Proposition 7.7 in [11]. The third inequality in (B.1) generalizes Lemma 7.11 in [11]. Since the proof essentially uses the estimates in [11], we omit the proof here and refer it to Appendix B in the arXiv version of this paper [12].

Proposition B.1

Let ${{\mathcal {C}}}^k$ and ${{\mathcal {W}}}^{k,\infty }$ be the norms defined in (4.15) and (4.17). For $k \ge 1$,

$$\begin{aligned} \begin{aligned} || f g||_{{{\mathcal {C}}}^k}&\lesssim || f||_{{{\mathcal {C}}}^k} || g||_{{{\mathcal {C}}}^k}, \quad || f g ||_{{{\mathcal {W}}}^{k,\infty }} \lesssim || f ||_{{{\mathcal {W}}}^{k,\infty }} || g||_{{{\mathcal {W}}}^{k, \infty }} , \\ || f||_{{{\mathcal {C}}}^{ k}}&\lesssim \alpha ^{-1/2} || f||_{ {{\mathcal {H}}}^{k+2}}, \quad || f||_{{{\mathcal {C}}}^k} \lesssim || \frac{1+R}{R} f ||_{{{\mathcal {W}}}^{k, \infty }}. \end{aligned} \end{aligned}$$

(B.1)

We have the following elliptic estimates for the stream function (4.10), (4.6).

Proposition B.2

Assume that $\alpha \le \frac{1}{4}$ and $\Omega \in {{\mathcal {H}}}^k, k \ge 3$. Let $\Psi$ be the solution to (4.6) with boundary condition (4.7). Then we have

$$\begin{aligned} \begin{aligned}&\alpha ^2 || R^2 \partial _{RR} \Psi ||_{{{\mathcal {H}}}^k} + \alpha || R \partial _{R \beta } \Psi ||_{{{\mathcal {H}}}^k} +|| \partial _{\beta \beta } (\Psi - \frac{1}{\alpha \pi } \sin (2\beta ) L_{12}(\Omega )) ||_{{{\mathcal {H}}}^k} \lesssim _k || \Omega ||_{{{\mathcal {H}}}^k}. \end{aligned} \end{aligned}$$

The above estimate with $k =3$ has been established in [11]. The general case $k \ge 3$ can be proved similarly. See also [26].

We have the following estimates for the velocity ${{\bar{u}}}$ of the approximate steady state.

Proposition B.3

For $\alpha \le \frac{1}{4}$ and $k \ge 5$, we have

$$\begin{aligned} \begin{aligned}&|| \frac{1+R}{ R} \partial _{\beta \beta } ( {\bar{\Psi }} - \frac{\sin (2\beta )}{\pi \alpha } L_{12}({\bar{\Omega }})) ||_{{{\mathcal {W}}}^{k+2,\infty }} \lesssim \alpha , \qquad || L_{12}({\bar{\Omega }})||_{{{\mathcal {W}}}^{k+2,\infty }} \lesssim \alpha , \\&\alpha || \frac{1+R}{R} D_R^2 {\bar{\Psi }} ||_{{{\mathcal {W}}}^{k,\infty }} + \alpha || \frac{1+R}{R} \partial _{\beta } D_R {\bar{\Psi }} ||_{{{\mathcal {W}}}^{k,\infty }} \\&\quad \quad + || \frac{1+R}{ R} \partial _{\beta \beta } ( {\bar{\Psi }} - \frac{\sin (2\beta )}{\pi \alpha } L_{12}({\bar{\Omega }})) ||_{{{\mathcal {W}}}^{k,\infty }} \lesssim \alpha \nonumber . \end{aligned} \end{aligned}$$

The case of $k = 5$ has been proved in Proposition 7.8 [11]. The general case $k \ge 5$ follows from a similar argument. See also [26].

Appendix C. Estimate of the Approximate Steady State

Recall from (4.4) that ${{\bar{\Omega }}}, {{\bar{\eta }}}, {{\bar{\xi }}}$ denote the approximate steady state ${{\bar{\omega }}}, {{\bar{\theta }}}_x, \bar{\theta }_y$ under the coordinates $(R, \beta )$, and the formula of ${\bar{\Omega }}, {\bar{\eta }}$ in (4.8).

$$\begin{aligned} {\bar{\Omega }} = \frac{\alpha }{c} \frac{3 R \Gamma (\beta ) }{(1+R)^2}, \quad {\bar{\eta }} = \frac{\alpha }{c} \frac{6 R \Gamma (\beta ) }{(1+R)^3} . \end{aligned}$$

(C.1)

We generalize Lemma A.6 in [11] from $k \le 3$ to any k below.

Lemma C.1

The following results apply to any $k \ge 0, 0 \le i + j \le k, j \ne 0$. (a) For $f = {\bar{\Omega }}, {\bar{\eta }}, {\bar{\Omega }} - D_R {\bar{\Omega }}, {\bar{\eta }} - D_R {\bar{\eta }}$, we have

$$\begin{aligned} | D_R^k f | \lesssim _k f , \quad |D_R^i D^j_{\beta } f | \lesssim _k \alpha \sin (\beta ) f. \end{aligned}$$

(C.2)

Recall the ${{\mathcal {W}}}^{k, \infty }$ norm (4.17). We generalize Lemma A.7 in [11] from $k = 7$ to any $k \ge 7$.

Lemma C.2

For any $k \ge 7$, it holds true that $\Gamma (\beta ),{\bar{\Omega }}, {\bar{\eta }} \in {{\mathcal {W}}}^{k, \infty }$ with

$$\begin{aligned} \begin{aligned} ||\frac{(1+R)^2}{R} {\bar{\Omega }}||_{{{\mathcal {W}}}^{k,\infty }} + || \frac{(1+R)^2}{R}{\bar{\eta }} ||_{{{\mathcal {W}}}^{k,\infty }} \lesssim _k \alpha , \quad || D_{\beta } {\bar{\Omega }}||_{{{\mathcal {W}}}^{k,\infty }} + || D_{\beta }{\bar{\eta }} ||_{{{\mathcal {W}}}^{k,\infty }} \lesssim _k \alpha ^2. \end{aligned} \end{aligned}$$

Recall the ${{\mathcal {K}}}^k$ norm (4.15). We generalize Lemma A.8 in [11] from $k= 5$ to any $k \ge 5$ below.

Lemma C.3

Assume that $0\le \alpha \le \frac{1}{1000}$. For $R \ge 0, \beta \in [0, \pi /2], k \ge 1$ and $i + j \le k$, we have

$$\begin{aligned}&| D^i_R D^j_{\beta } {\bar{\xi }} | \lesssim _k - {\bar{\xi }}, \quad | D^i_R D^j_{\beta } (3{\bar{\xi }} - R\partial _R {\bar{\xi }}) | \lesssim _k -{\bar{\xi }}, \\&|| {\bar{\xi }} ||_{{{\mathcal {C}}}^k} \lesssim || \frac{1+R}{R} ( 1 + ( R \sin ( 2 \beta )^{\alpha } )^{-\frac{1}{40} } ) {\bar{\xi }} ||_{L^{\infty }} \lesssim \alpha ^2, \end{aligned}$$

The proofs of Lemmas C.1–C.3 follows from the argument in [11], and thus are omitted.

For the $L_{12}$ operator (4.10), we generalize Lemma A.4 in [11] from ${{\mathcal {H}}}^3$ to its ${{\mathcal {H}}}^k$ version. The proof follows from a similar argument.

Lemma C.4

Let $\chi (\cdot ): [0, \infty ) \rightarrow [0, 1]$ be a smooth cutoff function, such that $\chi (R) = 1$ for $R \le 1$ and $\chi (R) = 0$ for $R \ge 2$. For $0 \le k \le n, 0\le l \le n-1, n \ge 3$, we have

$$\begin{aligned} \begin{aligned}&|| L_{12}(\Omega ) - L_{12}(\Omega )(0) \chi ||_{{{\mathcal {H}}}^n} + || D_R( L_{12}(\Omega ) - L_{12}(\Omega )(0) \chi ) ||_{{{\mathcal {H}}}^n} \lesssim _n || \Omega ||_{{{\mathcal {H}}}^n}, \\&|| D^k_R L_{12}(\Omega ) ||_{\infty } + || D^k_R ( L_{12}(\Omega ) -\chi L_{12}(\Omega )(0)) ||_{\infty } \lesssim _n || \Omega ||_{{{\mathcal {H}}}^n}. \end{aligned} \end{aligned}$$

(C.3)

Appendix D. Derivation of $u_r^r( 0,0)$

We derive the formula (5.28) for $u_r^r(0, 0)$ using the formula

$$\begin{aligned} {\textbf{u}}(x) = \nabla \times (-\Delta )^{-1} \omega = \frac{1}{4\pi } \int _{{\mathbb {R}}^3} \frac{\omega (y) \times (x- y)}{ |x-y|^3} dy. \end{aligned}$$

Recall the coordinates and change of variables (5.27)

$$\begin{aligned} \beta = \arctan ( z / r), \quad \rho = (r^2 + z^2)^{1/2}, \quad R = \rho ^{\alpha }, \quad \Omega (R, \beta ) = \omega ^{\vartheta }(\rho , \beta ), \end{aligned}$$

where $(r, \vartheta , z)$ is the cylindrical coordinates in ${\mathbb {R}}^3$ (3.1). Note that $u_r^r(0,0) = -\frac{1}{2} u_z^z(0,0)$ (3.10), we compute $u_z^z(0, 0)$. Since there is no swirl $u^{\vartheta } \equiv 0$, we get

$$\begin{aligned}{} & {} \omega = \omega ^{\vartheta } e_{\vartheta } = ( - \omega ^{\vartheta } \sin \vartheta , \omega ^{\vartheta } \cos \vartheta , 0), \\{} & {} \quad ( \omega \times (x - y) )_3 = - \omega ^{\vartheta } \sin (\vartheta ) (x_2 - y_2 ) - \omega ^{\vartheta } \cos (\vartheta ) (x_1 - y_1). \end{aligned}$$

Since the above formula is independent of $z= x_3$ and $\omega ^{\vartheta }(y)$ is odd in $y_3$, we yield

$$\begin{aligned} \partial _3 u^3 = \frac{1}{4\pi } \int _{{\mathbb {R}}^3} (\omega \times (x - y))_3 \partial _{x_3} \frac{1}{|x-y|^3} dy = \frac{1}{4\pi } \int _{{\mathbb {R}}^3} (\omega \times (x - y))_3 \frac{-3( x_3 - y_3)}{ |x-y|^5} dy. \end{aligned}$$

Evaluating at $x = 0$ and using

$$\begin{aligned} ( \omega \times ( - y) )_3 = \omega ^{\vartheta }( y) \sin (\vartheta ) y_2 + \omega ^{\vartheta } \cos (\vartheta ) y_1, = \omega ^{\vartheta }(y) r \end{aligned}$$

and $r = \rho \cos \beta , z = \rho \sin \beta , \beta \in [-\pi /2, \pi /2]$, we obtain

$$\begin{aligned} \begin{aligned} \partial _3 u^3(0, 0)&= \frac{3 }{4\pi } \int _{{\mathbb {R}}^3} \frac{\omega ^{\vartheta }(y) r y_3}{ |y|^5} d y = \frac{3}{4\pi } \int _0^{\infty }\int _0^{2\pi }\int _{{\mathbb {R}}} \frac{\omega ^{\vartheta }(y) r z }{ |y|^5} r d r d \vartheta d z \\&=\frac{3}{2} \int _{{\mathbb {R}}_+\times {\mathbb {R}}} \frac{\omega ^{\vartheta }(y) r^2 z }{ \rho ^5} d r d z \\&= \frac{3}{2} \int _0^{\infty } \int _{-\pi /2}^{\pi /2} \frac{\omega ^{\vartheta }(\rho , \beta ) \cos ^2(\beta ) \sin (\beta ) }{ \rho } d \rho d \beta \\&= 3 \int _0^{\infty } \int _{0}^{\pi /2} \frac{\omega ^{\vartheta }(\rho , \beta ) \cos ^2( \beta ) \sin (\beta ) }{ \rho } d \rho d \beta . \end{aligned} \end{aligned}$$

Using $u_r^r(0,0) = -\frac{1}{2}u_z^z(0,0)$ (3.10) and $\frac{ d \rho }{\rho } = \frac{1}{\alpha } \frac{dR}{R}$, we prove (5.28).