Maximal Fluctuations on Periodic Lattices: An Approach via Quantitative Wulff Inequalities

Abstract

We consider the Wulff problem arising from the study of the Heitmann–Radin energy of N atoms sitting on a periodic lattice. Combining the sharp quantitative Wulff inequality in the continuum setting with a notion of quantitative closeness between discrete and continuum energies, we provide very short proofs of fluctuation estimates of Voronoi-type sets associated with almost minimizers of the discrete problem about the continuum limit Wulff shape. In the particular case of exact energy minimizers, we recover the well-known, sharp $N^{3/4}$ scaling law for all considered planar lattices, as well as a sub-optimal scaling law for the cubic lattice in dimension $d\ge 3$.

1 Introduction

The crystallization problem amounts to prove that, in the limit of low temperatures and long time, the ground state configurations of certain atoms or molecules exhibit crystalline order. More precisely one considers N identical particles occupying the positions $x_{1},x_{2},\dots ,x_{N}\in \mathbb {R}^{d}$ and looks for the minimum of the energy

$$\begin{aligned} E_{N}(x_{1},x_{2},\dots x_{N})=\sum _{i<j}V_{2}(|x_{i}-x_{j}|), \end{aligned}$$

(1.1)

where $V_{2}$ is an interatomic two-body interaction potential. Physically meaningful potentials $V_{2}$ are repulsive at short range and attractive at long range, a paradigmatic example being the class of (p, 2p) Lennard–Jones potentials. Up to a normalization procedure which sets to 1 the optimal interatomic distance and to $-1$ the associated minimal energy, such a potential can be written as $V_{p,2p}(r)=r^{-2p}-2r^{-p}$. When $V_{2}=V_{p,2p}$ the minimizers of $E_{N}$ are very difficult to characterize and numerical simulations suggest that, up to surface relaxation effects, they sit on a periodic lattice (see for instance [27]). The problem can be highly simplified if instead one considers as interaction potential $V_{HR}(r)=\lim _{p\rightarrow +\infty }V_{p,2p}(r)$. The latter, known as the Heitmann–Radin sticky-disk potential, takes the form

$$\begin{aligned} V_{HR}(r)={\left\{ \begin{array}{ll} +\infty \, ,&{} 0<r<1\\ -1\, ,&{} r=1\\ 0\, ,&{}r>1,\\ \end{array}\right. } \end{aligned}$$

(1.2)

and it has been studied in the context of crystallization by Heitmann and Radin in [20]. With the choice $V_{2}=V_{HR}$ the crystallization problem becomes an optimal packing problem. In fact the infimum of $E_{N}$ is attained when the particles sit at the centers of hard spheres of radius 1 / 2 which maximize their mutual tangency. In [20] the authors prove that, in the two-dimensional case, the absolute minimizers of $E_{N}$ are subsets of the triangular lattice, up to rotation and translation (an alternative proof of this statement which makes use of discrete geometry arguments can be found in the recent paper by De Luca and Friesecke [8]). When not only two-body, but also three-body interactions (their role is that of favoring special bond angles) are taken into account, $E_{N}$ takes the form

$$\begin{aligned} E_{N}(x_{1},x_{2},\dots x_{N})=\sum _{i\le j}V_{2}~(|x_{i}-x_{j}|)+\sum _{i\le j\le k}V_{3}~(x_{i}-x_{j},x_{j}-x_{k}). \end{aligned}$$

(1.3)

If for instance $V_{3}$ favours either $2\pi /3$ or both $\pi /2$ and $\pi$ angles between consecutive bonds, it has been proved (under additional non-degeneracy conditions on $V_{3}$) that the system crystallizes on the honeycomb [21] or on the square lattice [22], respectively.

Finer geometric properties of the ground states of $E_{N}$ have been proved for instance in [9, 21, 22]. In particular, if ${\mathcal {L}}$ denotes the lattice on which the system crystallizes, it has been well understood that for configurations of particles sitting on a subset of ${\mathcal {L}}$, the energy $E_{N}$ can be written as a sum of bulk and surface contributions. In particular, if all the particles of a configuration X are sitting on the lattice ${\mathcal {L}}$, i.e., $X\subset {\mathcal {L}}$, observing that the energy per particle at a point $x\in X$ is minimal if all the nearest neighbors sites of x belong to the configuration X, one can easily derive that at leading order $E_{N}(X)\ge -C_{{\mathcal {L}}}N$, where $C_{{\mathcal {L}}}$ is the coordination number of the lattice ${\mathcal {L}}$ (i.e., the number of nearest neighboring sites of ${\mathcal {L}}$), which we here suppose to be independent of the site. This estimate can be easily proven to be optimal by computing $E_{N}$ at a configuration X which is maximally packed, that is such that it contains the maximal possible number of nearest neighbors. This argument suggests that finer properties of the minimizers of $E_{N}$ can be detected by studying the Gibbs excess energy of the system, that is the energy

$$\begin{aligned} {\mathcal {E}}_{N}(X):=E_{N}(X)+C_{{\mathcal {L}}}N. \end{aligned}$$

(1.4)

As not all the particles have the maximal amount of neighbors, the energy above is non-negative. Moreover, again computing ${\mathcal {E}}_{N}$ at maximally packed X one can see that ${\mathcal {E}}_{N}$ scales as $N^{\frac{d-1}{d}}$, a result that has been rigorously exploited for the first time in [1] (for $d=2$ and ${\mathcal {L}}$ the triangular lattice) and has led the authors to recognize ${\mathcal {E}}_{N}$ as a surface energy and then to prove that ${\mathcal {E}}_{N}$$\Gamma$-converges (in an appropriate topology which makes the functionals equi-coercive) to an anisotropic perimeter functional of the type

$$\begin{aligned} {\mathcal {F}}_{H}(A)=\int _{\partial ^{*} A}\Vert \nu _{A}\Vert _H\, d{{\mathcal {H}}}^{1},\ \end{aligned}$$

(1.5)

where H is a regular hexagon with unit area, $\partial ^{*} A$ denotes the reduced boundary of A on which a measure-theoretic normal $\nu _A$ is defined, and

$$\begin{aligned} \Vert \nu \Vert _{H}:=\sup \{x\cdot \nu :\,x\in H\},\quad \nu \in S^{1}. \end{aligned}$$

(1.6)

As a corollary of this result the authors show that, as $N\rightarrow +\infty$, any minimizing sequence of ${\mathcal {E}}_{N}$ converge (after being properly scaled and translated) to the unique minimizer H of ${\mathcal {F}}_H$ with unit-area constraint. The set H is the Wulff shape associated with (1.6) and the convergence can be understood as follows: one associates with each minimizing configuration $X=\{x_{1},x_{2},\dots ,x_{N}\}$ the measurable set $V(X)\subset \mathbb {R}^{2}$ given by the union of the Voronoi cells centered at the points of X and takes the convergence in the sense of the $L^{1}$ distance between the characteristic functions of V(X) and of H.

In contrast to the uniqueness of the Wulff shape (see [14, 25]) which minimises the macroscopic energy for fixed volume, the minimizers of the microscopic energy ${\mathcal {E}}_{N}$ present a generic non-uniqueness. Specifically one can prove the existence of a universal constant $K>0$, of a diverging sequence of natural numbers $(N_{j})_{j\in {\mathbb {N}}}$ and of a microscopic minimizer $X_{j}$ with $N_{j}$ particles which differ from the largest Wulff shape $H_{j}$, such that $H_{j}\cap {\mathcal {L}}\subset X_{j}$, by at most $K\, N_{j}^{3/4}$ particles, i.e.

$$\begin{aligned} |X_{j}~\triangle ~ (H_{j}\cap {\mathcal {L}})|\le K~N_{j}^{3/4}. \end{aligned}$$

(1.7)

Such a maximal asymptotic deviation, also known as maximal fluctuation estimate, has been first conjectured in [1] in the case of the crystallization on the triangular lattice and later proved in [6, 24]. The same estimate has been proved in [5, 22] for the square and the honeycomb lattices, respectively (see also [15, 16] for analogous results related to a model of ionic dimers).

The maximal fluctuation estimate can be seen as a quantitative version of a combinatorial isoperimetric-type inequality known as the edge isoperimetric inequality (EII). The relation between crystallization problems and EII has been first pointed out in [22]. In that paper the authors proved the maximal fluctuation estimate on the square lattice by finding, for each $N\in {\mathbb {N}}$ the solutions of the EII on that lattice. The same approach, based on the proof of the EII on the triangular and honeycomb lattices, has led to the proof of the $N^{3/4}$ law on those lattices.

Our approach to the proof of the maximal fluctuation inequality is different. The idea is that the asymptotic behavior for N large of the quantitative edge isoperimetric inequality can be obtained from its continuum counterpart, i.e., the quantitative version of the anisotropic isoperimetric inequality proved by Figalli et al. in [11] (see also [2, 4, 18]). In [11] the authors prove a quantitative stability for the anisotropic perimeter functional ${\mathcal {F}}_{W}$ given by

$$\begin{aligned} {\mathcal {F}}_{W}(D)=\int _{\partial ^* D} \Vert \nu \Vert _W\, d{{\mathcal {H}}}^{d-1}, \end{aligned}$$

(1.8)

where W is a convex set containing the origin and, for all $\nu \in S^{d-1}$, $\Vert \nu \Vert _{W}:=\sup \{x\cdot \nu :\,x\in W\}$. The set which minimizes the functional ${\mathcal {F}}_{W}$ among all measurable sets of volume $v>0$ (up to translations) is called the Wulff shape associated with $\Vert \nu \Vert _W$. This is the set $W_{v}$ obtained from W by an homothety which gives $|W_{v}|=v$. The quantitative isoperimetric inequality in [11] states the existence of a dimensional constant $C>0$ such that for every measurable set $D\subset \mathbb {R}^{d}$ with volume $v>0$ it holds that

$$\begin{aligned} \inf _{x\in \mathbb {R}^{d}}|D~\triangle ~(x+W_{v})|\le v\, \left( \frac{{\mathcal {F}}_{W}(D) - {\mathcal {F}}_{W}(W_v)}{{\mathcal {F}}_{W}(W_v)}\right) ^{\frac{1}{2}}. \end{aligned}$$

(1.9)

Roughly speaking an inequality like (1.7) can be obtained from (1.9) via a two step procedure. In the first step one identifies the discrete configuration $X=\{x_{1},x_{2},\dots ,x_{N}\}$ with a continuum measurable set $\zeta (X)$ chosen in such a way that $|X~\triangle ~ (x+W_{N}\cap {\mathcal {L}})|\lesssim |\zeta (X)~\triangle ~ (x+W_{N})|$. In the second step one looks for lower and upper bounds of ${\mathcal {E}}_{N}(X)-{\mathcal {E}}_{N}(\zeta (X))$. This procedure, described with more details in Sect. 2, leads for $d=2$ and in the case of the triangular, square and honeycomb lattice, to an estimate of the type

$$\begin{aligned} \inf _{x\in \mathbb {R}^{2}}|\zeta (X)~\triangle ~ (x+W_{N}\cap {\mathcal {L}})|\le C~N^{3/4}(1+{\mathcal {E}}_N(X) - \min {\mathcal {E}}_N)^{1/2}. \end{aligned}$$

(1.10)

It is worth noticing that our proof of the $N^{3/4}$ law neither produces the best constant, that can otherwise be found solving the EII, nor provides (or even relies on) any classification of the minimizers at a fixed N. However the estimate above is more general than the maximal fluctuation inequality as it generalises that to non ground state configurations and agrees with the $N^{3/4}$ law in for $X\in \hbox {arg min } {\mathcal {E}}_{N}$. Furthermore its proof is very elementary and avoids as much as possible the difficulties coming from the microscopic nature of the system. Our method can be generalised to any dimension. In Sect. 3.1 we show in the case of the lattice ${\mathbb {Z}}^{d}$ the asymptotic law $N^{1-\frac{1}{2d}}$ for minimizers. We remark that this scaling law has been independently obtained by Del Nin in his forthcoming PhD thesis [7].

Interestingly enough, our technique recovers the optimal asymptotic behaviour of the EII in dimension $d=2$, while it only provides a suboptimal estimate in dimension $d=3$ (and, quite likely, for any larger d). Indeed, it has been recently proved in [23] that the optimal estimate in dimension $d=3$ is, again, the $N^{3/4}$ law. The “loss of resolution” of our method can be explained, roughly speaking, as follows.

On the one hand, the minimizers of the discrete energy for any given N are very rigid. In all known cases, they are obtained as relatively small perturbations of “discrete Wulff shapes” that arise in connection with special values of N. The smallness of these allowed perturbations is one of the outcomes of EII, and is reflected in the sharp $N^{3/4}$ law.

On the other hand, the gap between the infima of the discrete and of the continuum energies allows larger shape fluctuations in the continuum setting, as estimated by the sharp quantitative Wulff inequality. This is the point where our method is mostly inaccurate.

In order to overcome this inaccuracy, we would need a lattice-based version of the sharp quantitative Wulff inequality. This seems to be an interesting question to be investigated in the future.

We finally remark that the results discussed in this paper pave the way to other stability results for functionals defined on points (lattices, stochastic lattices, graphs, data sets, etc.). Such results can be proven as a consequence of the already known stability for coarse grained continuum functionals and a specific approximation step that below takes the name of quantitative closeness.

2 Setting of the Problem and Preliminary Results

We denote by ${\mathcal {M}}$ the collection of all Lebesgue measurable subsets of $\mathbb {R}^{d}$. Given $E\in {\mathcal {M}}$ we denote by |E| its d-dimensional Lebesgue measure. Given X a countable set, we denote by $\#(X)$ the cardinality of X.

For $x\in \mathbb {R}^{d}$ and $r>0$ we denote by $B_{r}(x)$ the open ball of radius r centred at x. We set $B_{r}:=B_{r}(0)$ and denote by $S^{d-1}=\partial B_{1}$ the set of unitary vectors in $\mathbb {R}^{d}$. Throughout the paper we shall denote by C a positive constant whose value may change from line to line.

We denote by ${\mathcal {L}}\subset \mathbb {R}^{d}$ the set of vertices of a periodic tessellation of $\mathbb {R}^{d}$. Given $x\in {\mathcal {L}}$ we denote by $V(x):=\{y\in \mathbb {R}^{d}:\, |y-x|\le |y-z|,\, \forall z\in {\mathcal {L}}\}$ the Voronoi cell associated to ${\mathcal {L}}$ centred at x and by ${\mathcal {V}}({\mathcal {L}})=\{V(x), x\in {\mathcal {L}}\}$. Given $X\subset {\mathcal {L}}$ we set $V(X)=\bigcup _{x\in X}V(x)$ and $\mu _{{\mathcal {L}}}(X)=|V(X)|$ and we notice that the measure $\mu _{{\mathcal {L}}}$ is discrete and non-degenerate, in the sense that $\mu _{{\mathcal {L}}}(\{x\})$ takes only a finite number of positive values for all $x\in {\mathcal {L}}$. We denote by ${\mathcal {X}}$ the collection of all subsets $X\subset {\mathcal {L}}$ and for $N\in {\mathbb {N}}$ we further set ${\mathcal {X}}_{N}:=\{X\in {\mathcal {X}}:\, \#(X)=N\}$ . If ${\mathcal {E}}:{\mathcal {X}}\rightarrow [0,+\infty ]$ denotes an energy functional, we define the constrained energy ${\mathcal {E}}_{N}:{\mathcal {X}}\rightarrow [0,+\infty ]$ as

$$\begin{aligned} {\mathcal {E}}_{N}(X) = {\left\{ \begin{array}{ll} {\mathcal {E}}(X) &{} \text { if } X\in {\mathcal {X}}_{N},\\ +\infty &{} \text {otherwise,} \end{array}\right. } \end{aligned}$$

(2.11)

and assume that ${\mathcal {E}}_N$ is not identically $+\infty$.

Consider the functional ${\mathcal {F}}:{\mathcal {M}}\rightarrow [0,+\infty ]$ and assume that for any $v>0$ there exists a unique, up to null sets and translations, $W_v\in {\mathcal {M}}$ such that $|W_v| = v$ and ${\mathcal {F}}(W_v) = \min \{{\mathcal {F}}(D):\ D\in {\mathcal {M}},\ |D|=v \}>0$. Given $\varphi :[0,+\infty )\rightarrow [0,+\infty )$ a modulus of continuity (i.e. a continuous, strictly increasing function such that $\varphi (0)=0$), we say that ${\mathcal {F}}$ satisfies a $\varphi$-quantitative inequality if it holds that

$$\begin{aligned} \inf _{x\in \mathbb {R}^d}|D\triangle (x+W_v)| \le v\, \varphi \left( \frac{{\mathcal {F}}(D) - {\mathcal {F}}(W_v)}{{\mathcal {F}}(W_v)}\right) \qquad \text {for all }D\in {\mathcal {M}}\text { with } |D|=v, \nonumber \\ \end{aligned}$$

(2.12)

for all $v>0$.

The following sharp quantitative isoperimetric inequality for anisotropic perimeters has been proved in [11]:

Theorem 2.1

Let $W\subset \mathbb {R}^{d}$ be an open, bounded, convex set containing the origin and let

$$\begin{aligned} \Vert \nu \Vert _{W}:=\sup \{x\cdot \nu :\,x\in W\},\quad \nu \in S^{d-1}. \end{aligned}$$

Then the functional

$$\begin{aligned} {\mathcal {F}}(E)=\int _{\partial ^* D} \Vert \nu \Vert _W\, d{{\mathcal {H}}}^{d-1}, \end{aligned}$$

satisfies a $\varphi$-quantitative isoperimetric inequality with $W_{v}=v^{\frac{1}{d}}W$ and $\varphi (x)=C\sqrt{x}$.

2.1 Quantitative closeness

We say that the functional ${\mathcal {E}}_{N}$ in (2.11) is quantitatively close or Q-close to${\mathcal {F}}$ with respect to the map $\zeta :{\mathcal {X}}_{N}\rightarrow {\mathcal {M}}$ and the parameters $\alpha _{N},\beta _{N},\gamma _{N}\ge 0$ if for every $X\in {\mathcal {X}}_{N}$ such that

$$\begin{aligned} {\mathcal {E}}_N(X) \le \inf _{Y\in {\mathcal {X}}}{\mathcal {E}}_N(Y) + \alpha _{N}\,, \end{aligned}$$

(2.13)

the following two inequalities hold:

$$\begin{aligned}&{\mathcal {F}}(\zeta (X)) \le {\mathcal {E}}_N(X) + \beta _{N}\,, \end{aligned}$$

(2.14)

$$\begin{aligned}&\inf _{Y\in {\mathcal {X}}}{\mathcal {E}}_N(Y) \le \inf _{|D|=|\zeta (X)|}{\mathcal {F}}(D) + \gamma _{N}\,. \end{aligned}$$

(2.15)

We note that (2.13) and (2.14) imply the reverse of inequality (2.15) with $\alpha _{N}+\beta _{N}$ in place of $\gamma _{N}$.

Proposition 1

Let ${\mathcal {E}}_N$ be Q-close to ${\mathcal {F}}$, assume that ${\mathcal {F}}$ satisfies (2.12) and let $X\in {\mathcal {X}}_{N}$ be nonempty and such that (2.13) holds. Then, setting $v=|\zeta (X)|$, the following estimate holds

$$\begin{aligned} \inf _{x\in \mathbb {R}^d}|\zeta (X)\triangle (x+W_v)| \le v\, \varphi \left( \frac{\alpha _{N}+\beta _{N}+\gamma _{N}}{{\mathcal {F}}(W_v)}\right) . \end{aligned}$$

(2.16)

Proof

The proof of (2.16) is immediate, as

$$\begin{aligned} \inf _{x\in \mathbb {R}^d}|\zeta (X)\triangle (x+W_v)|&\le v\, \varphi \left( \frac{{\mathcal {F}}(\zeta (X)) - {\mathcal {F}}(W_v)}{{\mathcal {F}}(W_v)}\right) \\&\le v\, \varphi \left( \frac{{\mathcal {E}}_N(X) + \beta _{N}- \inf {\mathcal {E}}_N(X) + \gamma _{N}}{{\mathcal {F}}(W_v)}\right) \\&\le v\, \varphi \left( \frac{\alpha _{N}+\beta _{N}+ \gamma _{N}}{{\mathcal {F}}(W_v)}\right) . \end{aligned}$$

$\square$

3 Maximal Fluctuation Estimates

In this section we prove that in the case of the square, honeycomb and triangular lattices the Heitmann–Radin excess energy ${\mathcal {E}}_{N}$ of N particles is Q-close to an appropriate (and lattice dependent) anisotropic perimeter functional. According to Theorem 2.1, such functional satisfies a quantitative isoperimetric inequality which allows us to apply Proposition 1 and derive the maximal fluctuation estimate as a stability inequality for the functionals ${\mathcal {E}}_{N}$.

Before proceeding we set some notation that will be used later. Given a lattice ${\mathcal {L}}$ with unitary edge length, a set $X\subset {\mathcal {L}}$ and $x\in X$, we define the valence of x with respect to X as

$$\begin{aligned} \mathrm{{val}}(x,X)= \# \{y\in {\mathcal {L}}\setminus X:\ |y-x|=1\}\,. \end{aligned}$$

(3.17)

3.1 The d-dimensional cubic lattice

We call ${\mathcal {X}}$ and ${\mathcal {M}}$, respectively, the set of all finite subsets of points of the d-dimensional cubic lattice ${\mathcal {L}}={\mathbb {Z}}^d$ and the collection of measurable subsets of $\mathbb {R}^d$, as we have introduced in the previous section. For each $X\in {\mathcal {X}}$ we define

$$\begin{aligned} \zeta (X) = \bigcup _{x\in X} x + [-1/2,1/2]^d\,. \end{aligned}$$

The Heitmann–Radin excess energy of X takes the form

$$\begin{aligned} {\mathcal {E}}(X)=\sum _{x\in X}\mathrm{{val}}(x,X)\,. \end{aligned}$$

We consider the functional ${\mathcal {F}}:{\mathcal {M}}\rightarrow [0,+\infty ]$ to be finite only on sets D of bounded perimeter where it takes the form of an anisotropic perimeter functional, namely

$$\begin{aligned} {\mathcal {F}}(D) = P_1(D) = \int _{\partial ^* D} \Vert \nu \Vert _1\, d{{\mathcal {H}}}^1\,, \end{aligned}$$

where $\Vert \cdot \Vert _1$ denotes the $L^1$-norm in $\mathbb {R}^d$. According to the notation of Theorem 2.1, this norm coincides with the norm $\Vert \nu \Vert _{W}$ associated with the unitary cell of the lattice $W=(-1/2,1/2)^d$. It is well-known (see for instance [14, 25]) that for any $v>0$ the Wulff problem

$$\begin{aligned} \min _{|D|=v} P_1(D) \end{aligned}$$

has a unique (up to translations and null sets) solution $W_v = v^{\frac{1}{d}}\, [-1/2,1/2]^d$. Hence

$$\begin{aligned} \min _{|D|=v} P_1(D)=P_{1}(W_{v})=2dv^{(d-1)/d}\,. \end{aligned}$$

Moreover, by Theorem 2.1 the quantitative inequality

$$\begin{aligned} \inf _{x\in \mathbb {R}^d}|D\triangle (x+W_v)| \le c_1 v\, \left( \frac{P_1(D) - P_1(W_v)}{P_1(W_v)}\right) ^\frac{1}{2} \end{aligned}$$

(3.18)

holds for all $D\in {\mathcal {M}}$ with finite perimeter and $|D|=v$. Fix $N\in {\mathbb {N}}$ and let ${\mathcal {E}}_N$ be as in (2.11). We clearly have$|\zeta (X)| = \#(X)$ and ${\mathcal {F}}(\zeta (X)) = {\mathcal {E}}_N(X)$ whenever $X\in {\mathcal {X}}_{N}$. Moreover, (2.14) and (2.15) trivially hold with $\beta _{N}=0$ and

$$\begin{aligned} \gamma _{N}= \inf _{Y\in {\mathcal {X}}}{\mathcal {E}}_N(Y) - \inf _{|D|=N} {\mathcal {F}}(D). \end{aligned}$$

(3.19)

This shows that ${\mathcal {E}}_N$ is Q-close to ${\mathcal {F}}$ with parameters $\beta _{N}=0$ and $\gamma _{N}$ as in (3.19), and both are independent of $\alpha _{N}$. By Proposition 1 with $\varphi (s)=c_{1}\sqrt{s}$ and $v=N$ we get

$$\begin{aligned} \inf _{x\in \mathbb {R}^d} |V(X) \triangle (x+W_{N})| \le c_1 N \sqrt{\frac{\alpha _{N}+\gamma _{N}}{2dN^{1-1/d}}} = c_1\left( \frac{\alpha _{N}+\gamma _{N}}{2d}\right) ^{\frac{1}{2}}\ N^{\frac{d+1}{2d}}\,. \end{aligned}$$

(3.20)

We now proceed to estimate $\gamma _{N}$. Let $k\ge 0$ be the unique integer such that $k^d\le N< (k+1)^d$. It is not difficult to check that one can build a configuration $X_N$, such that

$$\begin{aligned} \zeta (X_N)=N\quad \text {and}\quad {\mathcal {E}}(X_N) \le 2d (k+1)^{d-1} \le 2dk^{d-1} + C_dk^{d-2}\,, \end{aligned}$$

where $C_d$ is a dimensional constant. The configuration $X_N$ is obtained by removing $(k+1)^d-N$ points from a cubical configuration made of $(k+1)^d$ points, in such a way that the energy does not increase. The algorithm for removing points starts from the point with coordinates all equal to $k+1$, then it removes points with $d-1$ coordinates equal to $k+1$ (and following the reverse order for the remaining one), then it removes points with $d-2$ coordinates equal to $k+1$ (following the reverse lexicographic order for the two remaining coordinates), and so on. It is not difficult to check that this procedure does not increase the energy of the resulting configuration of points. Hence we find

$$\begin{aligned} \gamma _{N}\le C_dN^{1-2/d}\,. \end{aligned}$$

(3.21)

By plugging (3.21) into (3.20) we finally obtain

$$\begin{aligned} \inf _{x\in \mathbb {R}^d} |V(X) \triangle (x+W_{N})|&\le c_1\left( \frac{\alpha _{N}+C_dN^{1-2/d}}{2d}\right) ^{\frac{1}{2}}\ N^{\frac{d+1}{2d}}\\&\le c_d\left( \alpha _{N}N^\frac{d+1}{d}+N^{2-1/d}\right) ^{\frac{1}{2}}\,. \end{aligned}$$

In particular, in the case $\alpha _N = 0$ we get

$$\begin{aligned} \inf _{x\in \mathbb {R}^d} |V(X) \triangle (x+W_{N})| \le c_dN^{1-\frac{1}{2d}}\,. \end{aligned}$$

Let us observe that, in dimension 2, we obtain the optimal fluctuation estimate $N^{3/4}$. However, in dimension $d\ge 3$ our method provides a sub-optimal fluctuation estimate $N^{1-\frac{1}{2d}}$. Indeed, we point out that the $N^{3/4}$ law has been proved for the lattice ${\mathbb {Z}}^3$ in [23].

3.2 The honeycomb lattice

We prove a fluctuation estimate for the Heitmann–Radin excess energy on the honeycomb lattice ${\mathcal {L}}$, that is,

$$\begin{aligned} {\mathcal {L}}= ({\mathbb {Z}}v_1 \oplus {\mathbb {Z}}v_2) \cup (e_2 + {\mathbb {Z}}v_1 \oplus {\mathbb {Z}}v_2)\,, \end{aligned}$$

where $v_1 = (\sqrt{3},0)$, $v_2 = (-\sqrt{3}/2,3/2)$, and $e_2 = (0,1)$. Note that each element of ${\mathcal {L}}$ has exactly three neighbors at distance 1. The Voronoi cell V(x) associated with ${\mathcal {L}}$ and centered at $x\in {\mathcal {L}}$ is an equilateral triangle of side length $\ell = \sqrt{3}$ and area $|V(x)| = \frac{3\sqrt{3}}{4}$, whose vertices belong to a dual hexagonal lattice of side length $\sqrt{3}$. This implies that $\mu _{\mathcal {L}}(\{x\}) = \frac{3\sqrt{3}}{4}$ for all $x\in {\mathcal {L}}$. We define the valence $\mathrm{{val}}(x,X)$ of a point x belonging to $X\subset {\mathcal {L}}$ as in (3.17). We introduce the energy

$$\begin{aligned} {\mathcal {E}}(X) = \sqrt{3} \sum _{x\in X} \mathrm{{val}}(x,X) \end{aligned}$$

and note that ut coincides with the Heitmann–Radin excess energy, up to the normalizing factor $\sqrt{3}$. In this section the functional ${\mathcal {F}}:{\mathcal {M}}\rightarrow [0,+\infty ]$ is finite only on those sets $D\subset \mathbb {R}^{2}$ of finite perimeter on which it takes the form

$$\begin{aligned} {\mathcal {F}}(D) = P_H(D) = \int _{\partial ^*D} \Vert \nu _D\Vert _H\, d{{\mathcal {H}}}^1\,. \end{aligned}$$

Here we use the notation $\Vert \cdot \Vert _H$ to denote, as in Theorem 2.1, the norm associated with the regular hexagon H having vertices on the six complex roots of the unity. For the functional ${\mathcal {F}}$, Theorem 2.1 holds true. We also set $\zeta (X) = V(X)$ for all $X\subset {\mathcal {X}}_{N}$. As before, given $v>0$ we have

$$\begin{aligned} \min _{|D|=v} P_H(D) = v^{\frac{1}{2}}\, P_H(\frac{1}{2\sqrt{3}}H), \end{aligned}$$

and we denote by $H_v=\frac{\sqrt{v}}{2\sqrt{3}}H$ the solution of the problem above having $|H_v|=v$. Since $\mu _{{\mathcal {L}}}(\{x\})=\frac{3\sqrt{3}}{4}$, we have for $X\in {\mathcal {X}}_N$

$$\begin{aligned} |\zeta (X)| = \frac{3\sqrt{3}}{4} \# X = \frac{3\sqrt{3} N}{4} \end{aligned}$$

and

$$\begin{aligned} {\mathcal {F}}(\zeta (X)) = {\mathcal {E}}(X)\,. \end{aligned}$$

As in the case of the square lattice, we immediately obtain (2.14) with $\beta _N = 0$. Let us set

$$\begin{aligned} \gamma _{N} = \inf _{Y\in {\mathcal {X}}} {\mathcal {E}}_{N}(Y) - \inf _{|D|=3\sqrt{3} N/4}{\mathcal {F}}(D)\,. \end{aligned}$$

We observe that ${\mathcal {E}}_N$ is Q-close to ${\mathcal {F}}$ with parameters $\alpha _N$, $\beta _N = 0$, and $\gamma _{N}$ given in the formula above. Thus we can apply Proposition 1 with $\varphi (s)=c_{1}\sqrt{(}s)$ and $v=3\sqrt{3} N/4$ to obtain that

$$\begin{aligned} \inf _{x\in \mathbb {R}^2} |V(X) \triangle (x{+}H_{3\sqrt{3} N/4})| {\le } \frac{3\sqrt{3}N}{4}\, \left( \frac{\alpha _{N}+ \gamma _{N}}{{\mathcal {F}}(H_{3\sqrt{3} N/4})}\right) ^{\frac{1}{2}} = c_2\frac{3}{4}\, \left( \frac{\alpha _{N}+ \gamma _{N}}{\sqrt{2}}\right) ^{\frac{1}{2}}\, N^{3/4}\,.\nonumber \\ \end{aligned}$$

(3.22)

Next we observe that $\zeta (X)$ coincides with $H_v$ when $N=\# X = 6k^2$, for some integer $k\ge 1$ and for $v=9\sqrt{3}k^2/4$, and note that in this case $H_v$ is a regular hexagon such that ${\mathcal {F}}(H_{v})=6\sqrt{3} k$. In the case $N\ge 6$ we take k as the integer such that $6k^2 \le N < 6(k+1)^2$ and we estimate

$$\begin{aligned} \gamma _N \le 6\sqrt{3}(k+1) - 6\sqrt{3}k = 6\sqrt{3}\,. \end{aligned}$$

Thanks to this estimate and to (3.22) we finally have

$$\begin{aligned} \inf _{x\in \mathbb {R}^2} |V(X) \triangle (x{+}H_{3\sqrt{3} N/4})| {\le } c_1\frac{3\sqrt{3}N}{4}\, \left( \frac{\alpha _{N}+ 6\sqrt{3}}{{\mathcal {F}}(H_v)}\right) ^{\frac{1}{2}} = c_1\frac{3}{4}\, \left( \frac{\alpha _{N}+ 6\sqrt{3}}{\sqrt{2}}\right) ^{\frac{1}{2}}\, N^{3/4}\,, \end{aligned}$$

which proves the $N^{3/4}$ law when there exists $\alpha >0$ such that $0\le \alpha _N \le \alpha$ for all N.

3.3 The triangular lattice

We define the triangular lattice as ${\mathcal {L}}= {\mathbb {Z}}e_1 \oplus {\mathbb {Z}}e_2$, with $e_1 = (0,1)$ and $e_2 = (1/2,\sqrt{3} /2)$. For each $x\in {\mathcal {L}}$, the Voronoi cell V(x) is the translated hexagon $x+\frac{1}{\sqrt{3}}H$, where H denotes the honeycomb lattice unitary cell already considered in the previous subsection. We thus have $|V(x)| = \sqrt{3}/2$. In order to define the map $\zeta$, it is convenient to construct a suitable “tent-like” function $f_X$ associated with each set $X\subset {\mathcal {X}}$, as follows. Given $x\in {\mathcal {L}}$ we consider the piecewise linear function $\varphi _x:\mathbb {R}^2\rightarrow \mathbb {R}$ such that $\varphi _x(x)=1$, $\varphi _x(y) = 0$ for all $y\in {\mathcal {L}}\setminus \{x\}$, and $\varphi$ is affine on every closed equilateral triangle with vertices on ${\mathcal {L}}$ and side length $=1$. In other words, $\varphi _x$ is the generic basis function of the $P^1$ finite elements defined on the triangular mesh. Then, for any $X\inf {\mathcal {X}}$ we set

$$\begin{aligned} f_X(y) = \sum _{x\in X}\varphi _x(y)\,. \end{aligned}$$

In the triangular lattice case, the Heitmann–Radin excess energy is given by

$$\begin{aligned} {\mathcal {E}}(X) = \frac{1}{2} \sum _{x\in X}\mathrm{{val}}(x,X),\qquad \forall \,X\in {\mathcal {X}}\,. \end{aligned}$$

We also define the map $\zeta$ as

$$\begin{aligned} \zeta (X) = \{y\in \mathbb {R}^2:\ f_X(y) > 1/2\}\,, \end{aligned}$$

for every $X\in {\mathcal {X}}$. We have the following proposition.

Proposition 2

For every $X\in {\mathcal {X}}$ it holds

$$\begin{aligned} {\mathcal {E}}(X) = \Vert \nabla f_X\Vert _{L^1} = P_H(\zeta (X))\,. \end{aligned}$$

(3.23)

Proof

Let us introduce the following notation: given $x,y\in {\mathcal {L}}$ with $d(x,y)=1$, we denote by $T_{xy}$ the equilateral triangle in the mesh with vertices x, y, z, such that the segment xz is obtained by counterclockwise rotating the segment xy by 60 degrees around x. By the definition of $f_X$, one can easily check that $\Vert \nabla f_X\Vert _{L^1(T_{xy})}=1/2$ if $x\in X$ and $y\notin X$. Therefore, for all $X\in {\mathcal {X}}_{N}$ we have

$$\begin{aligned} {\mathcal {E}}(X)&= \frac{1}{2} \sum _{x\in X} \#\{y\in {\mathcal {L}}\setminus X:\ d(x,y)=1\} \nonumber \\&= \sum _{x\in X}\sum _{{\mathop {d(x,y)=1}\limits ^{y\in {\mathcal {L}}\setminus X}}} \Vert \nabla f_X\Vert _{L^1(T_{xy})} = \Vert \nabla f_X\Vert _{L^1}\, . \end{aligned}$$

(3.24)

Some explanation about the previous identities is in order. We remark that $\nabla f_X$ is different from zero if and only if we consider the function $f_X$ restricted to an equilateral triangle whose vertices are not all contained in X, or in the complement of X. On such a “boundary triangle”, we have $|\nabla f_X| = \frac{2}{\sqrt{3}}$. Moreover, this collection of boundary triangles is in a one-to-one correspondence with pairs $(x,y)\in {\mathcal {L}}\times {\mathcal {L}}$ such that $x\in X$ and $y\notin X$, via the map $(x,y) \mapsto T_{xy}$. This explains the validity of the last two equalities and shows the first equality in (3.23). The second equality then follows from the fact that on every boundary triangle T, $\Vert \nabla f_X\Vert _{L^1(T)} = P_H(\zeta (X),T)$. $\square$

We are now going to check the assumptions of Proposition 1.

It is convenient to represent $\partial \zeta (X)$ as a 1-dimensional polyhedral chain, that is, as a finite union of oriented polygonal closed curves defined by ordered lists $\ell _h = (m_{h,1},\dots ,m_{h,j_h})$, $h=1,\dots , {\bar{h}}$ and $m_{h,j_h+1} = m_{h,1}$, where $m_{h,j}$ is a midpoint of an edge of ${\mathcal {L}}$ connecting a point of X with a point of ${\mathcal {L}}\setminus X$ in the 1-neighborhood of x (i.e., of an edge that “contributes” to the Heitmann–Radin energy of X) and each pair of consecutive points belongs to the same triangle of ${\mathcal {L}}$. We consider the discrete curvature measure associated with $\partial \zeta (X)$ and defined as a weighted sum of Dirac’s deltas concentrated on the set $M=\{m_{h,j}:\ h=1,\dots , {\bar{h}} \text { and } j=1,\dots ,j_h\}$. The weight of the curvature measure at every point $m_{h,j}\in M$ is the angle formed by the two vectors $m_{h,j+1} - m_{h,j}$ and $m_{h,j}-m_{h,j-1}$, that we denote from now on by $\kappa (m_{h,j})$. The possible values of $\kappa$ are $-\pi /3,0,\pi /3$. The following proposition holds true.

Proposition 3

Let $\gamma$ be the oriented, closed polygonal curve associated with a J-tuple $\ell = (m_1,\dots ,m_J)$ of points, with the following properties:

• (i) $J\ge 6$;

• (ii) $m_j$ is the midpoint of an edge of the triangular lattice ${\mathcal {L}}$, for all $1\le j\le J$;

• (iii) $m_j \ne m_{j'}$ for all $1\le j<j'\le J$ and, with the convention $m_{J+1}=m_1$, for all $j=1,\dots ,J$ the points $m_j$ and $m_{j+1}$ belong to the same closed equilateral triangle of ${\mathcal {L}}$;

• (iv) with the further convention $m_0 = m_J$, the angle formed by the two vectors $m_{j+1} - m_{j}$ and $m_{j}-m_{j-1}$ belongs to $\{-\pi /3,0,\pi /3\}$.

Then $\sum \nolimits _{j=1}^J \kappa (m_j) = \pm 2\pi$, where the sign is the one corresponding to the orientation of $\gamma$.

Proof

We observe that the polygonal $\gamma$ is necessarily simple, thanks to (iii) and (iv). Moreover, taking into account (iv), the property (i) is actually a necessary condition for $\gamma$ to be closed. The last statement then follows from the Gauss–Bonnet theorem. $\square$

By Proposition 3, assuming $X\in {\mathcal {X}}$ connected, we have

$$\begin{aligned} \sum _{h=1}^{{\bar{h}}} \sum _{j=1}^{j_h} \kappa (m_{h,j}) = 2\pi \big (1 - \#\hbox { holes of}\ \zeta (X)\big )\,. \end{aligned}$$

The area of an equilateral triangle whose height is 1 / 4 equals $\frac{1}{16\sqrt{3}}$, so that if we define $\tilde{\kappa }(m) = 3\kappa (m)/\pi$ we obtain $\tilde{\kappa }(m) \in \{-1,0,1\}$ and

$$\begin{aligned} |V(X)|-|\zeta (X)|&= \frac{1}{16\sqrt{3}} \sum _{h=1}^{{\bar{h}}} \sum _{j=1}^{j_h} \tilde{\kappa }(m_{h,j})\\&= \frac{\sqrt{3}}{16\pi }\sum _{h=1}^{{\bar{h}}} \sum _{j=1}^{j_h} \kappa (m_{h,j}) = \frac{\sqrt{3}}{8}\big (1 - \#\hbox { holes of}\ \zeta (X)\big )\,. \end{aligned}$$

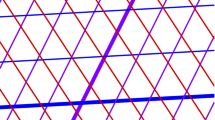
Note that the above decomposition is an immediate consequence of the fact that the signed area of the two triangles associated with a point $m_{h,j}$ (see Fig. 2) is given by $\frac{\tilde{\kappa }(m_{h,j})}{16\sqrt{3}}$.

Fig. 1

On the triangular lattice (small black discs), X (big black discs), V(X) (light grey region), $\partial V(X)$ (black line), $\partial \zeta (X)$ (black dotted line)

Fig. 2

A single contribution to the area difference $|V(X)| - |\zeta (X)|$ is given by pairs of triangles insisting on points $m_{h,j}$. The triangles are counted with positive sign if they are contained in V(X) (red color) and with negative sign if they are contained in the complement of V(X) (blue color)

Taking into account that $|V(X)| = \frac{\sqrt{3}}{2}N$ we find

$$\begin{aligned} |\zeta (X)| = \frac{\sqrt{3}}{2}N - \frac{\sqrt{3}}{8}\big (1 - \#\hbox { holes of}\ \zeta (X)\big ) \ge \frac{\sqrt{3}}{2}N - \frac{\sqrt{3}}{8}. \end{aligned}$$

We now set $v_N= \frac{\sqrt{3}}{2}N - \frac{\sqrt{3}}{8}$ and define

$$\begin{aligned} \gamma _{N}= \inf _{Y\in {\mathcal {X}}} {\mathcal {E}}_{N}(Y) - \inf _{|D|=v_N}P_H(D)\,. \end{aligned}$$

Then by the monotonicity of $v\mapsto \inf _{|D|=v}P_H(D)$, for every $X\in {\mathcal {X}}_N$ we have

$$\begin{aligned} \gamma _{N}\ge \inf _{Y\in {\mathcal {X}}} {\mathcal {E}}_{N}(Y) - \inf _{|D|=|\zeta (X)|}P_H(D)\,. \end{aligned}$$

Gathering together the results above, we have proved that the functional ${\mathcal {E}}_{N}$ is Q-close to $P_{H}$ with parameters $\alpha _{N}$, $\beta _{N}=0$ (by Proposition 2). We can apply Proposition 1 to deduce that

$$\begin{aligned} \inf _{x\in \mathbb {R}^d}|V(X)\triangle (x+H_{|\zeta (X)|})|&\le |\zeta (X)|\, \left( \frac{\alpha _{N}+\gamma _{N}}{P_H(H_{|\zeta (X)|})}\right) ^{1/2} \end{aligned}$$

(3.25)

where $H_{|\zeta (X)|}$ denotes the Wulff hexagon with area $|\zeta (X)|$.

In order to estimate $\gamma _{N}$ we now proceed as in the previous section. Let us set for any integer $k\ge 0$

$$\begin{aligned} N_k = 1 + 6+6\cdot 2 +\dots +6\cdot k = 3k^2 +3k+1\,. \end{aligned}$$

Given $N\in {\mathbb {N}}$, there exists a unique $k\ge 0$ such that

$$\begin{aligned} N_k \le N < N_{k+1}\,. \end{aligned}$$

Moreover, regular hexagons of side length $k+1$ can be obtained as the $\zeta$-image of suitable configurations of exactly $N_k$ points of the lattice. Hence we get the estimate

$$\begin{aligned} \inf _{Y\in {\mathcal {X}}} {\mathcal {E}}_{N}(Y) - \inf _{|D|=v_N}P_H(D)&\le \inf _{Y\in {\mathcal {X}}} {\mathcal {E}}_{N_{k+1}}(Y) - \inf _{|D|=v_N}P_H(D) \end{aligned}$$

(3.26)

$$\begin{aligned}&= 6(k+2) - \sqrt{24 v_N/\sqrt{3}} \end{aligned}$$

(3.27)

$$\begin{aligned}&\le \sqrt{12N -3}+9 - \sqrt{12 N - 1/8} \end{aligned}$$

(3.28)

$$\begin{aligned}&\le 9. \end{aligned}$$

(3.29)

We now combine (3.25) and (3.26) with the trivial estimate $|\zeta (X)|\le CN$ and we obtain

$$\begin{aligned} \inf _{x\in \mathbb {R}^2}|V(X)\triangle (x+H_{|\zeta (X)|})| \le c(\alpha _{N}+N^{\frac{3}{4}}(\sqrt{\alpha _{N}+1})) \end{aligned}$$

(3.30)

where $c>0$ is a fixed constant. This shows the $N^{3/4}$ law as soon as one takes $\alpha _{N}\le \alpha$ and $X\in {\mathcal {X}}_N$ connected.