Redox properties of PbO₂, IrO₂ and SnO₂ (110) surfaces with an adsorbed OH molecule: a chemical reactivity study in the grand canonical ensemble

Abstract

Employing the formalism of the joint density functional theory (JDFT) in the grand canonical ensemble, this paper studies the electronic structure and relative reactivity of an hydroxyl radical adsorbed on the surface of three different metal oxides that share the rutile-type structure and the (110) crystal plane; these materials are electrodes used in electrochemical advanced oxidation processes which consist in the generation of hydroxyl radicals, highly reactive species, that are able to oxidize organic compounds to CO$_2$, making these anodes efficient for wastewater treatment. By analyzing the changes in the average number of electrons as a function of the applied chemical potential at fixed external potential, we studied two reactivity indices from conceptual density functional theory: global and local softness, to help us understand the differences between these materials, additionally we propose a new scheme to approximate the redox properties of clean surfaces or surfaces in contact with different adsorbed molecules so that these values can be arranged in a relative potential scale which would allow direct comparison with experimental results.

1 Introduction

Tables of Standard Electrode Potentials are sources of valuable information for electrochemists because they contain information to evaluate solubility products, equilibrium and complexation constants and because, potentials are “really indices of free energies,” an ordered list of them can point out if a redox reaction will proceed spontaneously [1].

Having the ability to build a theoretical tool to obtain the redox properties of surfaces or surfaces in contact with different adsorbed molecules should be very helpful in the design of new materials because it could lead the way in proposing modifications of surfaces through metal doping or changing the nature of the adsorbates. Of course the task for building such a tool is monumental, because theoretically describing the behavior of an electrochemical solid–liquid interface requires to take into account processes occurring at a wide time and length scales. There are many efforts up to date to set up such kind of theoretical protocols (see Ref. [2] and references therein). Starting from the possible models, there are full cells set ups containing the two electrodes with opposite charges and the electrolyte; also, there are single cell models. In relation to the level of theory used, it ranges from classical Molecular Dynamics to ab initio Molecular Dynamics; in addition, there are also combined QM/MM like approaches. The time scale of the simulations and the size of the models depend greatly on the approximation used: $10^3$–$10^4$ atoms and around 10 ns for Classical Molecular Dynamics and near 100 atoms and up to 100 ps for ab initio Molecular Dynamics. One of the main challenges of the simulations in electrochemical interfaces is the presence of a finite surface charge that induces changes in the structure of the solvent and ions in its vicinity. Describing such changes requires a good sampling of the structures of the solvent and ions that imply larger times in the simulation or the use of enhanced sampling techniques; in addition to that, an accurate description of the electronic structure of the system is also recommended. The simulations can be done in different ensembles, the Grand Canonical $\mu$PT, the NVT or the NPT. In theoretical electrochemistry, treatments within Grand Canonical formalism require that electrons and chemical species are in contact with their corresponding constant chemical potential reservoirs. In this work, we introduce a calculation scheme for ordering the redox properties for this type of systems in a relative potential scale. It uses the Density Functional Theory in the Grand Canonical ensemble (GC-DFT) [3], a formalism that allows to carry out calculations of microscopic electrochemical systems in thermodynamic equilibrium since it is possible to set the temperature (T) and the chemical potential ($\mu {}$), in the same way as experiments do, where the electrochemical potential of the electrons is an independent variable and is associated with the potential imposed on the electrode. It also employs joint density funcional theory (JDFT) [4, 5] to describe electronic systems in thermodynamic equilibrium with a liquid environment. In our application of JDFT, only electrons are “grand canonical,” whereas the atomic species are only treated as a fixed external potential. The level of theory used to describe the system is a standard GGA exchange and correlation functional [6] using a half cell model using periodic conditions; the solvent is treated as a continuum polarizable media with monopole and dipole responses [7]. We should not expect that our approximation matches the actual redox potentials but as we will show, qualitative trends might be obtained with this scheme. We applied our ideas on metal oxides involved in electrochemical advanced oxidation processes that rely on the generation of hydroxyl radicals (OH$^{\cdot }$), which have a high oxidizing power at ambient temperature and atmospheric pressure, thus capable of oxidizing organic contaminants which make them efficient for wastewater treatment [8].

Metal oxide anodes are classified according to a model proposed by Comninellis [9] that is based in its catalytic power toward the oxygen evolution reaction (OER) into two types: active, and non active. IrO$_{2}$ surface presents a low overpotential for the OER and is considered as active, while SnO$_{2}$ and PbO$_{2}$ have high overpotentials and the oxidation of organic compounds is expected to take place. These three metal oxides will be used to test the proposed scheme. In a previous work [10], we studied the chemical reactivity of these solvated surfaces with two explicit water molecules according to the first step in the mechanism proposed by Comninellis [9]:

$$\begin{aligned} \mathrm{{M}} + \mathrm{{H}}_{2}\mathrm{{O}} \rightarrow \mathrm{{M}}(^{\bullet}\mathrm{{OH}}) + \mathrm{{H}}^{+} + \mathrm {e^-}{} \end{aligned}$$

(1)

where M denotes a metallic active site on the anode surface. We found that both molecules dissociate in H and OH hence, in this work our interest lies in the chemical reactivity of the systems when an OH molecule is adsorbed on the surface of the metallic oxide since these are the species that carry out the oxidation of the organic molecules:

$$\begin{aligned} \mathrm{{M}}(^{\cdot {}}\mathrm{{OH}}) + \mathrm{{R}} \rightarrow \mathrm{{M}} + \textit{m}\mathrm{{CO}}_{2} + \textit{n}\mathrm{{H}}_{2}\mathrm{{O}} + \mathrm{{H}}^{+} + \mathrm {e^-}{} \end{aligned}$$

(2)

where R is an organic compund and the anode acts as an inert reservoir of electrons, as pointed out by Marselli et al. [11]

2 Proposed scheme to approximate redox properties of surfaces

Sprik et al. [12, 13] developed a method to study an electrochemical half-reaction

$$\begin{aligned} X^{m} \rightarrow X^{m+\nu } + \nu \mathrm {e^-} \end{aligned}$$

(3)

where m and $\nu$ are integers with $\nu > 0$, in a grand canonical formulation where they limited the number of electronic states in the grand canonical partition function ($\Xi (T, \mu )$) to two, which are the ground state of the reduced and the oxidized system, with N and $N-\nu$ electrons, respectively

$$\begin{aligned} \Xi (T,\mu ;N_{I}) = \exp \left( \frac{N\mu }{k_\mathrm{{B}}T}\right) Q_{0}(T,N) + \exp \left( \frac{(N-\nu )\mu }{k_\mathrm{{B}}T}\right) Q_{0}(T,N-\nu ), \end{aligned}$$

(4)

here $k_\mathrm{{B}}$ is the Boltzmann constant and assuming that the temperature, T, is low compared to the electronic excitation energies, therefore $Q_{0}(T,N)$ and $Q_{0}(T,N-\nu )$ are the ground-state canonical partition functions for the N and $N-\nu$ electron systems, respectively.

To get an equation for the chemical potential in terms of the partition functions of both electronic systems, first they consider the expectation value of the number of electrons in the system to get the following expression

$$\begin{aligned} \left<N\right> \equiv k_\mathrm{{B}}T\left( \frac{\partial {\ln \Xi }}{\partial {\mu }}\right) _{T} = \frac{(N-\nu )+N\left( \frac{Q_{0}(T,N)}{Q_{0}(T,N-\nu )}\right) \exp (\frac{\nu \mu }{k_\mathrm{{B}}T})}{1+\left( \frac{Q_{0}(T,N)}{Q_{0}(T,N-\nu )}\right) \exp (\frac{\nu \mu }{k_\mathrm{{B}}T})} \end{aligned}$$

(5)

Subsequently, they define a fractional charge by taking the charge of the N-electron system as reference, $x \equiv N - \left<N\right>$, from which they obtain an equation of $\mu$ as a function of x

$$\begin{aligned} \mu = \frac{k_\mathrm{{B}}T}{\nu }\left( \ln {\frac{Q_{0}(T,N-\nu )}{Q_{0}(T,N)}} - \ln {\frac{x}{\nu -x}} \right) . \end{aligned}$$

(6)

With the free energy of each electronic system defined as $A_{N} = -k_\mathrm{{B}}T\ln {Q_{0}(T,N)}$, Eq. (6) can be rewritten in terms of the Helmholtz free energy of the oxidation reaction ($\Delta {A} = A_{N-\nu }-A_{N}$) as

$$\begin{aligned} \mu = -\frac{1}{\nu }\Delta {A} - \frac{k_\mathrm{{B}}T}{\nu } \ln {\frac{x}{\nu - x}}. \end{aligned}$$

(7)

By making the calculations at constant volume, the Helmholtz free energy difference can be taken as a Gibbs free energy difference in calculations at constant pressure. This approximation allows the use of the classical electrochemical relation $\Delta {G} = -\nu F\epsilon ^{0}$, with F the Faraday constant and $\epsilon ^{0}$ the experimental redox potential. Substituting this relation in Eq. (7), they get an expression that relates the chemical potential with $\epsilon ^{0}$

$$\begin{aligned} \mu = -F\epsilon ^{0}- \frac{k_\mathrm{{B}}T}{\nu } \ln {\frac{x}{\nu - x}} \end{aligned}$$

(8)

and from this equation one can see that when $x=\nu /2$, the value of chemical potential can be used to estimate the standard redox potential

$$\begin{aligned} \mu _{1/2} = -F\epsilon ^{0}. \end{aligned}$$

(9)

As the partition functions in Eq. (6) include contributions from the movements of the atoms in the system, Sprik et al. perform molecular dynamics where they consider an average of the ground states by taking into account the structural variations due to thermal fluctuations. They vary $\mu$ until they determine $\mu _{1/2}$ from a sigma-shaped variation of the fractional charge as a function of $\mu$, calling this method a numerical titration.

In this work, we propose to take the equilibrium geometries of the electronic systems in their respective ground states, so we can make calculations at fixed geometry varying $\mu$ inside the electrochemical window of experimental interest. This will allow us to get an estimation of the redox potential of each electrode. These values can be placed in a relative scale (vs. the standard hydrogen electrode) of redox potential which would give an estimation of the oxidizing power of an electrode with respect to an electrochemical reaction of interest. The scale can be directly compared to experimental values (in Volts) of compounds of interest as depicted in Fig. 1, and it should be useful to predict possible redox reactions.

Fig. 1

Schematic representation of the relative $\mu _{1/2}$ scale vs the standard hydrogen electrode in Volts, where oxidants and reductants go up and down the scale, respectively. MO$_{2}$ represents the electrochemical pair with a $-\mu _{1/2}^{2}$ redox potential of an electrode surface with $<N+1>^-$ and $<N>$ electrons, respectively. $X^{m}/X^{m+\nu }$ depicts any electrochemical pair with $-\mu _{1/2}^{1}$ as its experimental redox potential

3 Computational details

All calculations were performed under the joint density functional theory (JDFT) [14, 15] formalism and plane wave basis set with GBRV ultrasoft pseudopotentials [16] as implemented in the open-source density functional theory software, JDFTx [17]. Due to the radical nature of the OH and to explore the magnetic properties of these systems, spin polarized calculations were done with the Perdew–Burke–Ernzerhof (PBE) [6] exchange-correlation functional along with DFT-D2 pair-potential dispersion corrections [18] and without imposing the magnetic moment so that the final magnetic state always corresponds to the self-consistent result.

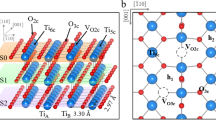
As in a previous work [10], the chosen metal oxides share the rutile-type structure and the most stable crystal face, the (110), [19,20,21] which is oxygen terminated Fig. 2. First it was done the optimization of lattice parameters and ionic positions of the bulk structures, then the metal oxide surfaces were constructed in a periodic, symmetric slab setup, as 2$\times$1 supercells with five layers of the metal atom and slab separation of 16 Å. Seven layers were also considered but we found almost no difference between both geometries.

Fig. 2

Schematic representation of the oxygen terminated (110) MO$_{2}$ surface where M = Pb, Ir, Sn. A unsaturated metal atom and B oxygen atom in a bridge position

In all models, lattice parameters were kept fixed and atomic positions of the two top layers were optimized, with the ionic Debye screening set to reflect 1 M concentration of electrolyte, employing the CANDLE [7] implicit solvation model. Afterward a molecule of OH was placed in a “flat” configuration (parallel to the surface plane) on top of one of the metal unsaturated atoms, then we performed the optimization of the top two layers of atoms with the molecule. With this geometry, we constructed inversion-symmetric slab models Fig. 3 and kept it fixed to study these systems under applied chemical potential ($\mu {}$) making single point calculations in the grand canonical formalism, using Fermi smearing at 298 K.

Fig. 3

Schematic representation of the inversion-symmetric slab model of MO$_{2}$ where M = Pb, Ir and Sn with an OH molecule on top of an unsaturated metal atom of the surface

The cutoff energy for the plane wave basis set was fixed at 32 Hartree for all calculations. The Brillouin zone was sampled with a Monkhorst-Pack [22] k-point mesh of $9 \times 9 \times 1$. The energy and forces convergence criteria were 10$^{-7}$ Hartree and 10$^{-4}$ Hartree/bohr, respectively. The calculations were performed employing truncated Coulomb potentials [23] and the auxiliary Hamiltonian method [24]. To facilitate the correlation of applied chemical potentials to the electrochemical scale, all values are reported relative to the standard hydrogen electrode (SHE) energy, $\mu -\mu _{SHE}$, where $\mu _{SHE} = -4.66$ eV as calibrated with the CANDLE solvation model for the PBE exchange-correlation functional [7]. As stated in the introduction, all these approximations should be enough to obtain at least qualitative trends as shown in previous works [24,25,26].

4 Results

4.1 Density of states, global and local softness of MO₂ surfaces with an adsorbed OH molecule

After optimization, the distances of the oxygen of the OH molecule to the unsaturated metal atom of the surface were 2.134, 2.016 and 1.928 Å for PbO$_{2}$, SnO$_{2}$ and IrO$_{2}$ surfaces, respectively. These results are in agreement with a previous work [27] where it was found that the OH is weakly adsorbed on the electrodes used for advanced electrochemical oxidation(PbO$_{2}$, SnO$_{2}$), in contrast to IrO$_2$ where the computed adsorption energy is larger and the OER takes place. All surfaces have a metallic character once the OH molecule is adsorbed as it is shown in Fig. 4. PbO$_{2}$ and SnO$_{2}$ density of states(DOS) have a similar shape. This happens due to the fact that these surfaces alone present different behaviors, SnO$_2$ is a semiconductor and PbO$_2$ is a metallic system but with low density of states around the Fermi level ($E_{f}$), consequently when an OH molecule is adsorbed its states contribute to the system around the $E_f$ in both surfaces giving them a similar shape, whereas IrO$_{2}$ has a metallic character with high density of states around the $E_{f}$ thus the adsorption of an OH molecule does not modify the shape of its DOS. It is worth mentioning this methodology allows to compare the DOS, aligning the eigenvalues with respect to the SHE rather than the standard alignment of the Fermi levels. This fact enables the possibility to correlate such differences directly with the experiment.

Fig. 4

Density of States per unit cell of the slab models with an OH molecule a PbO$_{2}$, b IrO$_{2}$ and c SnO$_{2}$. Black solid line and red dotted line denote the $\mu _{zc}$ (zero charge potential) and the Fermi level of each system, respectively

Table 1 contains the corresponding chemical potentials of zero charge of the three surfaces with an adsorbed OH molecule, where SnO$_{2}$ and PbO$_{2}$ have similar values. As expected from the experimental results of these two non active materials which have the same high overpotential for the OER, 1.90 V versus SHE in contrast with the low overpotential for IrO$_2$ surface, 1.52 V versus SHE [28]. The alignment with respect to the SHE reveals that the electronic states of both, SnO$_2$ and PbO$_2$, appear in the same energy region, that is why the chemical potentials of zero charge are similar. This can be rationalized, considering the similar nature of the electronic states involved for Sn and Pb, as main elements of the same family compared to Ir a transition metal atom.

Table 1 Potential of zero charge referred to the standard hydrogen electron ($\mu _{zc}$), in eV, for the metallic oxide surfaces with an adsorbed OH molecule

As in electrochemical experiments, employing GC-DFT coupled with JDFT allows us to impose a particular chemical potential and the average number of electrons $\left<N\right>$ of the system is obtained for each imposed chemical potential. We can evaluate the chemical reactivity of the systems by studying the changes in $\left<N\right>$ with respect to the changes in $\mu$. In this work, we will use two reactivity indices from Conceptual Density Functional Theory [29, 30] that were introduced by Yang and Parr [31]. The first one is a global reactivity index, called the global softness (S), defined as:

$$\begin{aligned} S = \left( \frac{\partial {\left<N\right>}}{\partial {\mu }} \right) _{T,v(\textbf{r})}. \end{aligned}$$

(10)

which indicates the chemical potential range where the system is more prone to exchange charge. The second one, is the local counterpart called the local softness ($s({\textbf {r}})$) [31] that shows the spatial regions of the system where a charge transfer can occur. The local softness is defined as:

$$\begin{aligned} s(\textbf{r}) = \left( \frac{\partial {\left<\rho (\textbf{r})\right>}}{\partial {\mu }} \right) _{T,v(\textbf{r})}, \end{aligned}$$

(11)

As can be seen from the previous equations, evaluating these quantities under the GC-DFT formalism is straight forward.

The $\left<N\right>$ as a function of $\mu$ for the studied oxides are shown in Fig. 5. According to the zero charge potentials of these surfaces(see Table 1) and remembering that at these potentials the surfaces incluiding the adsorbate are neutral, it is clear that the response of each one of the systems is different in the region where they lose electrons ($\mu < \mu _{zc}$) than in the one where they gain electrons ($\mu > \mu _{zc}$).

Fig. 5

Average number of electron difference, $\left<N\right>$– N$_{0}$, at applied chemical potential (eV), where $N_{0}$ is the number of electrons of the neutral system MO$_{2}$ with an OH molecule (with M = Pb, Ir, Sn)

From the data of $\left<N\right>$ as a function of $\mu$ (Fig. 5), the global softness for each system can be evaluated using a central finite difference approximation, the results are shown in Fig. 6. All the surfaces show a near constant global softness when $\mu < \mu _{zc}$, having a similar value for PbO$_2$ and SnO$_2$ surfaces and a lower value for IrO$_2$. The maxima of S for all the surfaces lie on the region where the systems gain electrons compared to their own neutral ones, i.e., where $\mu > \mu _{zc}$. The positions of the maxima are related to the $\mu _{zc}$ value for each surface. According to the global softness values, for all three systems, if we impose the chemical potential starting from the corresponding $\mu _{zc}$, all the systems will have a greater tendency to gain electrons than to lose them, having PbO$_2$ and SnO$_2$ a greater tendency than IrO$_2$.

Fig. 6

Softness in a.u. of the slab models MO$_{2}$ with an adsorbed OH molecule at applied chemical potential (eV)

To get information of which regions of the surfaces are involved in a charge transfer process when we change the chemical potential, we evaluated the local softness, $s(\textbf{r})$, for PbO$_2$ and IrO$_2$, because these two systems show different behavior in the oxidation of organic compounds. Figures 7 and 8 show, for different values of $\mu$, the local softness, the total charge of the surface and the local magnetization of the oxygen atom of the adsorbed OH molecule on PbO$_2$ and IrO$_2$ surfaces, respectively. For the PbO$_2$ case (Fig. 7), at $\mu > \mu _{zc}$, it can be observed that the local softness lies mainly over the adsorbed OH molecule and on the two oxygens in bridge position on the surface. At the beginning, while $\mu$ is increasing, the average number of electrons of the surface increases producing a more negative charge on the surface and also the local softness increases (Fig. 7d). Then at a certain point, even though the surface is still gaining electrons, the local softness decreases (Fig. 7h), losing capacity of trapping electrons on the OH and on the oxygens in bridge position( Fig. 7i). For IrO$_2$, also at $\mu > \mu _{zc}$, the local softness lies on the oxygen atoms of the surface and on the oxygen atom of the adsorbed OH. Again the local softness increases as $\mu$ increases until it reaches a certain $\mu$ value(Fig. 8d), then it starts to decrease but at a lower rate than in the PbO$_2$ surface. This behavior can be explained by the values of the global softness for these systems(Fig. 6).

Fig. 7

Local softness ($s(\textbf{r})$) at 0.06 a.u. of the slab model PbO$_{2}$ with an adsorbed OH molecule at applied chemical potential ($\mu$) in eV, charge of the supercell (q) and local magnetic moment (m) of the oxygen atom of the adsorbed OH molecule

Fig. 8

Local softness ($s(\textbf{r})$) at 0.06 a.u. of the slab model IrO$_{2}$ with an adsorbed OH molecule at applied chemical potential ($\mu$) in eV, charge of the supercell (q) and local magnetic moment (m) of the oxygen atom of the adsorbed OH molecule

4.2 Redox properties of MO$_{2}$ surfaces with an adsorbed OH molecule

As stated, considering the two states model in the grand canonical ensemble, $\mu _{1/2}$ corresponds to the redox potential. One can vary (impose) the chemical potential in order to obtain the average number of electrons. For systems in which the neutral and ionic species do not have close excited states, the plot of $\left<N\right>$ versus $\mu$ should look in principle like a sigmoid function, similar to a titration curve, from whom this method gets the name of numerical titration [13]. For the reduction half-reaction of $^{\bullet }{\text{OH}}$:

$$\begin{aligned} \mathrm {^\bullet}{\text{OH}} + \mathrm {e^-}{} \rightarrow \mathrm {OH^{-}}, \end{aligned}$$

(12)

we plotted the behavior of $\left<N\right>$ vs $\mu$ at different geometrical arrangements in Fig. 9. The analyzed region involves chemical potentials that are greater than the $\mu _{zc}$ for the $^{\bullet }{\text{OH}}$, i.e., the $^{\bullet }{\text{OH}}$ should gain electrons in this region. The $\left<N\right>$ were computed using the geometries of the $^{\bullet }{\text{OH}}$, $\mathrm {OH^{-}}$ or the optimized geometry at each chemical potential. As shown in Fig. 9a, the results of the average number of electrons at different potentials are similar despite the geometry used. The values obtained with the optimized geometry at each chemical potential can be fitted to a function $f(x) = (1 + e^{-a(x-b)})^{-1}$ with a = 118.529 and b =$-$1.42318, as displayed in Fig. 9b. Using this function, the reduction potential of $^{\bullet }{\text{OH}}$/$\mathrm {OH^{-}}$ is $-$1.42 eV, differing in 480 meV from the experimental value (1.90 V vs. SHE [32]).

Fig. 9

Average number of electrons difference from the neutral, $\left<N\right>- N_{0}$, as a function of the applied chemical potential ($\mu {}$), where $N_{0}$ is the number of electrons of $^{\bullet }{\text{OH}}$: a employing the $^{\bullet }{\text{OH}}$, $\mathrm {OH^{-}}$ geometries and performing a geometry optimization at each applied potential ($^{\bullet }{\text{OH}}$-$\mathrm {OH^{-}}$), respectively, and b fitted function to the $^{\bullet }{\text{OH}}$-$\mathrm {OH^{-}}$ data (solid blue line), function $f(x) = (1 + e^{-a(x-b)})^{-1}$ with a = 118.529 and b =$-$1.42318. Gray-dotted line indicates the gain of half average electron

To make this approximation viable for the redox properties of surfaces, we decided to study the changes in $\left<N\right>$ as a function of the chemical potential at a fixed geometry to avoid the geometry optimization cost of the system at each chemical potential. For the surfaces with an adsorbed OH, it is possible to obtain the reduction potential ($\epsilon _\mathrm{{red}}$) and the oxidation potential ($\epsilon _\mathrm{{ox}}$) according to the following half-reactions:

$$\begin{aligned} \mathrm { M(OH)}\left<N\right>+ \mathrm {e^-}{} \rightarrow \mathrm {M(OH)}\left<N+1\right>^{-} \end{aligned}$$

(13)

$$\begin{aligned} \mathrm {M(OH)}\left<N\right>\rightarrow \mathrm {M(OH)}\left<N-1\right>^{+} + \mathrm {e^-}{} \end{aligned}$$

(14)

where M(OH)$\left<N\right>$ is the state of the surface with an adsorbed OH with N electrons, M(OH)$\left<N+1\right>^{-}$ is the state with $N + 1$ electrons and M(OH)$\left<N-1\right>^{+}$ the state with $N - 1$ electrons. For the advanced electrochemical oxidation, $\epsilon _\mathrm{{red}}$ is the relevant quantity because these materials produce the oxidation of the organic compounds in solution.

As previously mentioned, according to the zero charge potentials of these surfaces, it is clear that the response of each one of the systems is different in the region where they lose electrons ($\mu < \mu _{zc}$, see Fig. 10a) than in the one where they gain electrons ($\mu > \mu _{zc}$, see Fig. 10b).

Fig. 10

Average number of electrons difference from the neutral, $\left<N\right>- N_{0}$, as a function of the applied chemical potential ($\mu {}$), where $N_{0}$ is the number of electrons of the neutral system MO$_2$ with an adsorbed OH molecule (where M = Pb, Ir, Sn). The colored solid lines are the fitted functions a $f(x) = ax + b$ in the loss region of electrons ($\mu < \mu _{zc}$) with a = 0.7256, b = 1.8839 for the PbO$_2$ surface, a = 0.4931, b = 0.6062 for IrO$_2$ and a = 0.6273, b = 1.6139 for SnO$_2$, and b a third degree polynomial $f(x) = ax^{3} + bx^{2} + cx + d$ in the gain region of electrons ($\mu _{zc} < \mu$) with a = 0.4913, b = 1.7810, c = 2.6342, d = 3.3407 for PbO$_2$, a = 0.0601, b = $-$0.6059, c = 0.1673, d = 1.2260 for IrO$_2$, a = 0.3652, b = 1.2280, c = 1.7080, d = 2.7132 for SnO$_2$. The dotted gray lines indicate the loss or gain of half average electron, respectively

In all cases, the data obtained can be fitted to a straight line for $\mu < \mu _{zc}$ and for the region where $\mu > \mu _{zc}$, the data were fitted using third degree polynomials. Using these functions, the $\mu _{1/2}$, i.e., the chemical potentials where the systems gain or lose half average electron, can be obtained corresponding to the respective potentials that are shown in Table 2. These values can be arranged in a potential scale, in Volts, to observe the relative oxidative or reductive power of the species(Fig. 11). From the scale it can be observed that for the neutral surfaces, SnO$_{2}$(OH) has the greatest oxidative power or ability to oxidize another species and IrO$_{2}$(OH) the smallest oxidative power. This trend can be correlated with experimental results [33, 34]. We can also observe that the positively charged surfaces have a greater oxidative power than their respective neutral one as expected.

Table 2 Oxidation Potential ($\epsilon _{ox}$) and reduction potential ($\epsilon _{red}$), referred to the standard hydrogen electrode, in eV, for MO$_2$ surfaces with an adsorbed OH molecule (where M = Pb, Ir, Sn) computed interpolating the values of $\left<N\right>-N_0 = -0.5$ and $\left<N\right>-N_0= 0.5$ using the $\left<N\right>= f(\mu {})$ curves, respectively. The potentials obtained by imposing the condition on the systems to have $N_0+1/2$ or $N_0-1/2$ electrons are also shown(see the text for details)

Instead of doing the $\left<N\right>$ versus $\mu$ curve to obtain the $\mu _{1/2}$ value, there is an alternative approach by calculating the Helmholtz free energy at a fixed $N=N_0+1/2$ or $N_0-1/2$ values. In this approach, rather than the grand potential the Helmholtz free energy is obtained at a fractional number of electrons with the same Fermi-Dirac smearing function. A detailed study of this scheme is in progress. The potentials obtained this way are also shown in Table 2. This approximation is less expensive and can be used to study a larger set of systems.

5 Conclusions

Our results showed that SnO$_{2}$ and PbO$_{2}$ surfaces with an adsorbed OH molecule have similiar electronic properties as redox potentials, DOS, local and global softness, which agree with the experimental similiar performance of the surfaces in the oxidation of organic compounds. The large difference of the computed reduction potential for IrO$_{2}$ compared to the ones computed for SnO$_{2}$ and PbO$_{2}$, is in line with the experimental result that IrO$_{2}$ should have a smaller oxidative power than the other metal oxides compared in this work. Despite all the approximations involved in the proposed scheme for arranging the redox properties of surfaces in a relative scale, qualitative trends can be obtained that explain the experimental behavior of these metal oxides. The use of better solvation models and density functional approximations might be necessary to improve the obtained results. We believe that the proposed scheme for computing the redox properties of surfaces or surfaces in contact with different adsorbants can be useful at least as a first screening to guide or propose modifications of the surfaces or the adsorbants.

Fig. 11

Potential scale (in V) referred to SHE, from the obtained potentials from the average number of electrons curves as a function of $\mu$ (Fig. 10), of the pairs MO$_{2}$(OH)$\left<N-1\right>^{+}$/MO$_{2}$(OH)$\left<N\right>$/MO$_{2}$(OH)$\left<N+1\right>^{-}$ where $\left<N\right>$ denotes the neutral structure with N electrons, $\left<N-1\right>$ the surface with one less electron and $\left<N+1\right>$ the surface with one more electron (with M = Ir, Sn, Pb). This Figure is only a schematic representation of the computed values