Diabatic potential energy curves for the $^4{\Pi}$ states of SH

Abstract

We present a diabatic representation of the potential energy curves (PECs) for the $^4{{\Pi}}$ states of $\mathrm {SH}$. Multireference, configuration interaction (MRCI) calculations were used to determine high-accuracy adiabatic PECs of both $\mathrm {SH}$ and ${\mathrm {SH}}^+$ from which the diabatic representation is constructed for $\mathrm {SH}$. The adiabatic PECs exhibit many avoided crossings due to strong Rydberg-valence mixing. We employ the block diagonalization method, an orthonormal rotation of the adiabatic Hamiltonian, to disentangle the valence autoionizing and Rydberg $^4\Pi$ states of $\mathrm {SH}$ by constructing a diabatic Hamiltonian. The diagonal elements of the diabatic Hamiltonian matrix at each nuclear geometry render the diabatic PECs and the off-diagonal elements are related to the state-to-state coupling. Care is taken to assure smooth variation and consistency of chemically significant molecular orbitals across the entire geometry domain.

1 Introduction

Several recent studies [1,2,3,4,5,6,7,8] have addressed the chemistry of $\mathrm {SH}$ and ${\mathrm {SH}}^+$ in the interstellar medium (ISM). The present work extends our recent calculations [8] related to an important destruction mechanism of ${\mathrm {SH}}^+$ and provides an overview of the methods we have employed.

Large concentrations of ${\mathrm {SH}}^+$ (sulfanylium) are observed in dense [4] and diffuse [2, 3] regions of the interstellar medium (ISM). Astrochemical models have assumed that the main formation mechanism of ${\mathrm {SH}}^+$ is the reaction of the atomic sulfur ion S$^+$ with H$_2$ [1]. This reaction is highly endothermic by 0.86 eV (9860 K). To overcome this endothermicity, turbulent dissipation, shocks, or shears are invoked. For that reason, the ${\mathrm {SH}}^+$ concentration is thought to provide a useful measure of turbulence in the diffuse ISM [3, 6]. In the photon-dominated environments in the ISM, where H$_2$ is vibrationally excited, the excess vibrational energy may overcome the endothermicity and facilitate the formation of ${\mathrm {SH}}^+$ from S$^+$ and H$_2$ [5].

The primary destruction mechanism for ${\mathrm {SH}}^+$ in the ISM is thought to be the process of Dissociative Recombination (DR) with electrons,

$$\begin{aligned} {\mathrm {SH}}^++ e^- \rightarrow {\mathrm {S}} + {\mathrm {H}}. \end{aligned}$$

(1)

For a full review of DR, which plays a critical role in determining the concentration of neutral species in many plasmas, we recommend books on the topic by Guberman [9, 10] and by Larsson and Orel [11]. Here we just note that a rate constant of $10^{-6}\,{\rm {cm}^3\,s^{-1}}$ for $T = 10\,$K is assigned to the ${\mathrm {SH}}^+$ reaction [Eq. (1)] in astrochemical databases [12, 13]. We also note that the destruction of ${\mathrm {SH}}^+$ by H$_2$ [1], the most abundant interstellar molecule, is not efficient because the reaction is endothermic; therefore, ${\mathrm {SH}}^+$ is not severely depleted by this process.

We have investigated the DR of several molecular ions [14,15,16] and recently undertook a careful study of ${\mathrm {SH}}^+$ [7, 8]. Rigorous calculations are quite complex and generally involve two phases. First, accurate potential energy curves (PECs) of the ion reactant and the neutral products are required. For the neutral products, the PECs and related coupling terms are usually presented using the diabatic formalism, a representation of the electronic Hamiltonian in which off-diagonal terms provide the necessary coupling between electron–molecular–ion scattering states and the neutral product states. These calculations rely on the electronic structure techniques of quantum chemistry. The second phase involves dynamics calculations, based on the PECs and their couplings. Multichannel Quantum Defect Theory (MCQDT or MQDT) [17] has been successfully employed in this phase to determine cross sections and rate constants [9, 18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36] that can be compared directly with experimental data.

Fig. 1

A generic schematic of the PECs required for modeling the two mechanisms for DR of a general ion AB$^+$ with an electron. In both panels the red PEC labeled AB$^{**}$ denotes an excited dissociating autoionizing neutral state of AB, and the blue PEC labeled AB$^+$ denotes the ground state of the ion. In the right panel the black dashed line depicts a bound Rydberg state of AB. Horizontal lines in the well of the ion and Rydberg state illustrate a low-lying vibrational level. The left panel illustrates the direct mechanism, in which the molecule can directly dissociate along the AB$^{**}$ channel. The right panel illustrates the indirect mechanism, in which an excited neutral Rydberg state facilitates the dissociation process by acting as an intermediate state

Figure (1) provides a simplified diagram of the DR process and the potential curves necessary to treat it. The left panel shows the PEC for the initial molecular ion (${\mathrm {SH}}^+$ in the present case) and a dissociating neutral state that leads to the final products. In fact, our recent work [8] suggests that two dissociating neutral states may play roles in the DR of ${\mathrm {SH}}^+$, for reasons described below.

The ground state of ${\mathrm {SH}}^+$ is denoted $X^3\Sigma ^-$, and its recombination with an electron can form $^{2,4}\Sigma$, $^{2,4}\Pi$, or $^{2,4}\Delta$ states of neutral ${\mathrm {SH}}$. In our early work on the DR of electrons with ${\mathrm {SH}}^+$ [7] we identified a dissociating autoionizing $^2\Pi$ state near the minimum of the ${\mathrm {SH}}^+(X^3\Sigma ^-)$ PEC (as depicted in Fig. (1)), leading us to first consider the doublet states as potential DR pathways. At the beginning of this study no experimental results for this reaction were available, but by the time the calculations were completed [8], we were able to compare our theoretical rate constants with experimental results obtained from the TSR-storage ring [37]. The theoretically determined rate constants for the DR of ${\mathrm {SH}}^+$ with electrons through the $^2\Pi$ states of $\mathrm {SH}$ at energies greater than $\sim$10 meV match very well with experiment [8]. However, at the very low energies of interest for the ISM (less than $\sim$10 meV), the calculated rates were about an order of magnitude less than the experimental values. This discrepancy led us to explore the $^4\Pi$ states of $\mathrm {SH}$ in order to identify additional pathways for DR. These new calculations are reported here; they also show dissociating autoionizing states in the region of the ground state of ${\mathrm {SH}}^+$. It seems likely that including the contribution of the $^4\Pi$ states to DR will improve the computed rate constants at low energies.

In the present work, only the electronic structure calculations and analysis needed to determine a diabatic representation of the $^4\Pi$ PECs of $\mathrm {SH}$ are reported. Calculations for the electronic state couplings, DR cross sections, and rate constants are in progress and will be the subject of a future publication. When the full analysis is complete, we expect it will provide important data for the astrochemical models that describe various environments in the ISM.

This paper is organized as follows. Part 2 describes the electronic structure techniques employed. The calculations include standard configuration interaction (CI) methods, which are used to determine adiabatic PECs. The diabatization process relies on our implementation [7, 8, 14,15,16] of the Block Diagonalization Method (BDM) [38, 39]. Application of the BDM or related diabatization methods [40] requires extra effort to insure the smooth variation of molecular orbitals (MOs) as the geometry of the molecule is varied. Throughout this article, we will highlight and refer to important MO occupations using equation numbers to simplify reading. In Part 3, we discuss how we achieve smoothly varying MOs. The determination of the resulting diabatic PECs is discussed in Part 4, and Part 5 contains concluding remarks.

2 Formalism

The adiabatic PECs result from standard multireference, configuration interaction (MRCI) quantum chemistry calculations. The calculations were completed using the 20 APR 2017 (R1) version of the GAMESS [41] suite.

2.1 The configuration interaction (CI) method

The configuration interaction (CI) method is well established throughout the literature. However, in order to establish the notation used throughout this article, we provide a very brief summary of the CI method, focusing on the details and nomenclature important for this study.

The CI electronic wavefunction for the $nth$ adiabatic state $\Psi _n$ can be written as a linear combination of the N expansion vectors that span the configuration space as shown in Eq. (2) [40, 42].

$$\begin{aligned} \Psi _n = \sum _i^N c_{\rm ni}\Phi _i \end{aligned}$$

(2)

These expansion vectors, denoted by $\Phi _i$, are the configuration state functions (CSFs), and the coefficient $c_{\rm ni}$ is related to the contribution of a particular CSF to the overall wavefunction such that $\sum _i^N |c_{\rm ni}|^2 = 1$.

Each CSF results from a linear combination of Slater determinants each, of which is constructed from the molecular orbitals (MOs) [42]. For high-accuracy PECs, like those presented in this work, N is a very large number on the order of $10^6$–$10^7$. The number of MOs varies based on the atomic orbital (AO) basis set but is typically on the order of $10^2$. These MOs are arranged into three subspaces: Frozen core, active, and virtual space (core, AS, VS respectively). The core consists of low-energy doubly-occupied MOs that are close to the nucleus. In the course of the calculation, electrons are never promoted out of the core. Active space MOs consist of doubly-occupied, singly-occupied, and un-occupied MOs. Electrons are excited within and out of the active space into the initially unoccupied virtual space. Often to conserve computer time (by reducing the total number of CSFs considered) the highest energy virtual MOs, those correlated to the core MOs, are frozen out of the calculation.

We employ two types of MRCI calculations in the present study. The most accurate, and time-intensive, CI wavefunction includes single and double excitations from the active space into the virtual space; MRCI-singles and doubles or the second-order CI (SOCI). The SOCI was used to determine the adiabatic states of ${\mathrm {SH}}^+$. An alternative to the SOCI wavefunction is to use only single excitations from the active space into the virtual space; MRCI-singles or the first-order CI (FOCI). The FOCI approximation uses far less computational resources ($N_{\mathrm {FOCI}} \ll N_{\mathrm {SOCI}}$), trading speed for accuracy, by losing electron correlation contributions to the final CI energies. However, one can still cautiously employ the FOCI, recouping some lost accuracy by using an active space large enough to regain some of the electronic correlation through double excitations within the active space itself [8, 15, 16].

The FOCI approximation was used to calculate the ground, valence, and Rydberg states of the $\mathrm {SH}$ radical presented in this article.

2.1.1 Calculation specifics and general MOcConfigurations for SH and SH⁺

For both $\mathrm {SH}$ and ${\mathrm {SH}}^+$ we used an optimized Dunning-style correlation-consistent basis set [43, 44] aug-cc-pVTZ (or ACCT) on both S and H. All calculations were completed in the $C_{2v}$ point group resulting in 73 MOs¹: 32 $A_1$, 7 $A_2$, 17 $B_1$, and 17 $B_2$. Use of the ACCT basis set resulted in two $\sigma$ and two $\pi$ molecular Rydberg orbitals having an $n=4$ localized character on S and one $\sigma$ Rydberg MO having $n=2$ character localized on H at all values of R, allowing these orbitals to be easily identified along the entire geometry domain.

Table 1 Electronic occupation of the ${\mathrm {SH}}^+(X^3\Sigma ^-)$ (ground) state in the traditional $C_{2v}$, $C_{\infty v}$, and the “simplified” notation used throughout the remainder of this article

Although our calculations were completed in the $C_{2v}$ point group, we use a simplified notation that borrows from the $C_{\infty v}$ point group and atomic chemistry notation to communicate chemical significance of the MOs. The simplified notation is interpreted from the electronic configuration of the ion ground state ${\mathrm {SH}}^+(X^3\Sigma ^-)$ and is related to the aforementioned point groups in Table 1. The numerical superscripts indicate electron occupations while the superscript “$*$” indicates an antibonding-type orbital. MOs numbered 1–5 represent the core orbitals that are always doubly occupied. The addition of an extra electron results in one of the $^{2,4}\Pi$ states discussed in this article.

The MOs employed to determine the ${\mathrm {SH}}(^4\Pi )$ states are optimized with Multi-Configuration Self-Consistent Field (MCSCF) calculations at each geometry of the neutral ground state ${\mathrm {SH}}(X^2\Pi )$; they are the same MOs used in our previous study [8] treating the ${\mathrm {SH}}(^2\Pi )$ states. The ${\mathrm {SH}}(^4\Pi )$ adiabatic separated atom limits determined with these optimized MOs showed greater accuracy ($|\Delta | \lesssim 0.1\,$eV) when compared to the spectroscopic levels reported by NIST [45] (see Table 3) than those determined with optimized MOs resulting from an MCSCF on the lowest ${\mathrm {SH}}(1^4\Pi )$ dissociating state.

The MCSCF calculations used to determine the 73 optimized MOs had five orbitals in the core and 10 in the active space. Full details of the calculation setup are given by us in reference [8]. A summary of how these optimized MOs are determined for each R and how we verify consistency at each R is given in Sect. 3.3. The resulting MCSCF calculations had 3 460 CSFs.

The ${\mathrm {SH}}(^4\Pi )$ states were generated using the FOCI approximation to the CI wavefunction. After an exhaustive analysis of various FOCI calculation sizes we settled on 5 frozen core, 15 active space (that includes the five lowest Rydberg and the five 3d MOs), 48 virtual MOs, and 5 frozen virtual MOs (those corresponding to the frozen core) by benchmarking our adiabatic separated atom limits against spectroscopic levels reported by NIST. The $^4\Pi$ FOCI calculation resulted in $1\,719\,948$ CSFs reproducing the atomic spectra of sulfur with great accuracy as shown in Table 3. The setup of the calculation, using the simplified notation, is illustrated in Eq. (3). All of the $^{2,4}\Pi$ states result from the ${\mathrm {SH}}^+$ configuration plus one extra electron occupying one of the open active space MOs.

$$ \underbrace {{({\text{core}})^{{10}} }}_{{{\text{Frozen}}\,{\text{on}}\,{\text{S}}}}\underbrace {{\overbrace {{(3s)^{2} ({\text{SH}})^{2} (\pi x)^{1} (\pi y)^{1} |({\text{SH}}*)}}^{{5\,{\text{Valence}}\,{\text{MOs}}}}\overbrace {{({\text{Rydberg}}) \ldots }}^{{5\,{\text{MOs}}}}\overbrace {{(3d) \ldots }}^{{5\,{\text{MOs}}}}}}_{{{\text{FOCI}}\,{\text{Calculation}}\,{\text{Active}}\,{\text{Space}}\,(15\,{\text{MOs}})}}\overbrace {{{\text{(VS}}) \ldots }}^{{53\,{\text{MOs}}}} $$

(3)

The SOCI wavefunction is used to determine the $X^3\Sigma$, $1^1\Delta$, and $1^3\Pi$ adiabatic states of ${\mathrm {SH}}^+$ in the same basis as above. For the ${\mathrm {SH}}^+$ SOCI the 3d MOs shown in Eq. (3) were moved to the virtual space leaving 5 frozen core, 10 active space, 53 virtual, and 5 frozen virtual MOs. These SOCI calculations resulted in 1 112 351 CSFs for the $X^3\Sigma$, 694 078 CSFs for the $1^1\Delta$, and 1 121 913 CSFs for the $1^3\Pi$ state. Optimized MCSCF MOs for each ion state were generated by the method outlined above in the state’s respective symmetry. However, because we are only interested in the lowest ionic state for each respective symmetry, we only included five MOs in the MCSCF active space.

The SOCI was also employed to compute the adiabatic energy of SH($X^2\Pi$) at $R = 1.36\, {\AA }$ and also to determine the vertical ionization potential $(T_e)$ from this ground state (see Ref. [8]) to the minimum of the ion ${\rm {SH}}^+$ ($R = 1.36\, {\AA }$ [8, 46, 47]) in order to correctly position the SOCI-calculated ${\mathrm {SH}}^+$ PECs relative to the FOCI-calculated $\mathrm {SH}$ PECs. Determination of $T_e$ and the vertical adjustment to the ion PECs is detailed in Sect. 4.2. This SOCI included 10 active space MOs, moving the five 3d MOs shown in Eq. (3) to the virtual space, resulting in $3\,114\,864\,$CSFs

The standard quantum chemistry calculations described above produce the adiabatic PECs. For applications like DR, where the states of interest are often embedded in the continuum, a rigorous diabatic representation rendering PECs like those illustrated in Fig. (1), as well as the state-to-state couplings, are required. In Sect. 4 we present the diabatic PECs for the $^4\Pi$ states of $\mathrm {SH}$.

2.2 Block diagonalization method (BDM)

The block diagonalization method (BDM) [38, 39], a method we have successfully employed in previous work [7, 8, 14,15,16], allows us to rigorously transform the large adiabatic Hamiltonian into a diabatic representation from which we determine the diabatic PECs and associated state-to-state coupling.

The number of CSFs comprising the CI (adiabatic) Hamiltonian is large (on the order of $10^6 - 10^7$). However, we can usually identify a small set of $N_\alpha$ CSFs or linear combinations of CSFs (Table 2 details the CSFs in the present study) that make a dominant contribution to $N_\alpha$ electronic states of interest. Then, $N_\alpha$ is the dimension of the square diabatic Hamiltonian $\mathbf {H}_\mathrm {dia}$.

The diabatic Hamiltonian $(N_\alpha \times N_\alpha )$ is a sub-block of the much larger $(N \times N)$ CI Hamiltonian. This block results from a series of rotation operations done on the CI Hamiltonian as illustrated in Fig. (2).

Fig. 2

Graphical interpretation of the block diagonalization method (BDM)

We arrive at $\mathbf {H}_{\mathrm {dia}}$ using the results of the conventional CI. First we construct a matrix $\mathbf {S}$ of the $N_\alpha$ CI coefficients (or linear combination of coefficients) $c_{ni}$ that comprise the $N_\alpha$ states of interest. We use $\mathbf {S}$ to construct the orthonormal matrix $\mathbf {T}$ defined by Eq. (4), where $(\dagger )$ represents the adjoint.

$$\begin{aligned} \mathbf {T} = \mathbf {S}^{-1}\left( \mathbf {S} \mathbf {S}^\dagger \right) ^{1/2} \end{aligned}$$

(4)

The diabatic Hamiltonian $\mathbf {H}_{\mathrm {dia}}$ is then given by Eq. (5)

$$\begin{aligned} \mathbf {H}_{\mathrm {dia}}= \mathbf {T}^\dagger \mathbf {E} \mathbf {T} \end{aligned}$$

(5)

where $\mathbf {E}$ represents the diagonal matrix with the adiabatic energies from the conventional MRCI. The diagonal elements of $\mathbf {H}_{\mathrm {dia}}$ are the resulting diabatic energies. The off-diagonal elements are related to the coupling between the diabatic states.

A successful application of the BDM requires that the MOs used in the final MRCI calculation vary smoothly as a function of nuclear geometry. In the next section (Sect. 3) we provide a detailed discussion about the interpretation and application of the MOs used in this study.

3 Electronic states of $\mathrm {SH}$ and smooth variation of MOs

In this section we schematically outline the electronic configurations (MO occupations) that give rise to the various states of interest using the simplified notation introduced in Sect. 2.1.1. We conclude the section by discussing how we assure a smooth transition from the chemical region (small internuclear separation R) to the separated atom limit (large R).

3.1 Valence states of SH

The bound ground state of the neutral complex, ${\mathrm {SH}}(X^2\Pi )$, is characterized by the configuration given in Eq. (6). The bound nature results from the doubly occupied (SH)-bonding MO and the unoccupied (SH$^*$)-antibonding MO.

$$\begin{aligned} (\text {core})^{10}\, (3s)^2\, ({\mathrm {SH}})^2\, {(\pi _x)^1\, (\pi _y)^2}\, {({\mathrm {SH}}^*)} \, {({\mathrm {Rydberg}})\,\ldots } \end{aligned}$$

(6)

Promotion of one of the electrons from the (SH) bonding MO to the (SH$^*$) antibonding MO results in the valence dissociating states, as indicated below in Eq. (7).

$$\begin{aligned} (\text {core})^{10}\, (3s)^2\, ({\mathrm {SH}})^1\, (\pi _x)^1\, (\pi _y)^2\, ({\mathrm {SH}}^*)^1 \, {({\mathrm {Rydberg}})\,\ldots } \end{aligned}$$

(7)

Dissociating states always have the (SH$^*$) MO occupied. In the present work, as well as in the $^2\Pi$ study [8], the lowest dissociating states, those of interest for DR of ${\mathrm {SH}}^+$ with electrons, maintain the same electronic configurations (occupied MOs) at every geometry. As the neutral complex transforms from a molecule to separated atoms the MOs numbered 7–10 in Table 1 smoothly transition from MOs to AOs centered on S or H. This transition is fully discussed in Sect. 3.3. At the separated atom limit the electronic configuration describing the lowest dissociating states (Eq. (7) in the molecular region) remains the same but the MOs have transformed into those shown in Eq. (8).

$$\begin{aligned} \overbrace{ (\text {core})^{10}\, (3s)^2\, \underbrace{(3p_z)^1 (3p_x)^1 (3p_y)^2}_{\text { Was (SH)} ^1 (\pi _x)^1 (\pi _y)^2} | \,{(\mathrm {Rydberg})\ldots } }^{\text {Sulfur Ground State: } {\mathrm {S}}(^3P) } \overbrace{ \underbrace{(1s_{\mathrm {H}})^1}_{\text {Was } ({\mathrm {SH}}^*)^1} }^{\text {Atomic } {\mathrm {H}}(^2S)} \end{aligned}$$

(8)

3.2 Rydberg states of $\mathrm {SH}$

Promotion of any of the electrons from the valence space into one of the Rydberg MOs results in a neutral state with Rydberg character. In this study, we encounter two types of Rydberg states: bound Rydberg states (a neutral state with an unoccupied anti-bonding MO and an occupied Rydberg MO) and dissociating states with Rydberg character (the anti-bonding MO and a Rydberg MO are occupied). The bound Rydberg states fall into two categories, ion core Rydberg and excited-state ion core Rydberg states.

Ion core Rydberg states consist of a ground-state ion core with a highly excited electron occupying an $n=4$ Rydberg MO localized on S. Eq. (9) depicts the MO occupations for ${\mathrm {SH}}{(1^4\Pi )}$ in the chemical region (small internuclear distances).

$$\begin{aligned} \overbrace{\underbrace{(\text {core})^{10}\, (3s)^2 ({\mathrm {SH}} )^2 (\pi _x)^1 (\pi _y)^1 ({\mathrm {SH}}^*)^0 }_{\text { SH } ^+\left( X\,^3\Sigma ^- \right) \text { Ion Core } (\text {C}_1)}|\,{(4p_y)}^1 }^{{\mathrm {SH}}(1^4\Pi ) \text { Rydberg State}} \end{aligned}$$

(9)

As noted for the valence states, at larger atomic distances the MOs smoothly transition, specifically the (SH) and (SH$^*$) to AOs centered on S and H respectively. This transition of MOs results in different MO occupations describing the same electronic state at different geometries. The MO and configurational transformation of the bound ion core Rydberg state illustrated by Eq. (9) is given in Eq. (10).

$$\begin{aligned} \overbrace{(\text {core})^{10}\, (3s)^2 \underbrace{(3p_z)^1 (3p_x)^1 (3p_y)^1}_{\text { Was (SH)}^2 (\pi _y)^1} | \,{(4p_y)}^1 }^{\text {Excited Sulfur: } {S(^5\it{P})}} ~ \overbrace{ \underbrace{(1s_{\mathrm {H}})^1}_{\text {Was}\, ({\mathrm {SH}}^*)^0}}^{\text {Atomic}\, {\mathrm {H}}(^2S)} \end{aligned}$$

(10)

We call attention to the initially doubly occupied (SH)-bonding MO transitioning to a singly occupied $3p_z$ AO centered on S and the initially un-occupied (SH$^*$)-antibonding MO transitioning to a singly occupied 1s AO centered on H. This transition is fully discussed in Sect. 3.3. The ${1}^4\Pi$ ion core Rydberg PEC and its ion parent ${\mathrm {SH}}^+(X^3\Sigma ^-)$ are colored green in Fig. (7). The corresponding ${2}^2\Pi$ ion core Rydberg PEC and the same parent ion are colored green in Fig. (8).

Excitation of electrons occupying the valence $(\mathrm {SH})$ and $\pi$ MOs in conjunction with an occupation of a Rydberg MO results in what we call the excited-state ion core Rydberg states. The configurations characterizing these states are depicted in Eqs. (11) and (12). Physically, the ${\mathrm {SH}}(3^2\Pi )$ Rydberg state has an ${\mathrm {SH}}^+(1^1\Delta )$ excited-state core as described by Eq. (11). The PECs of these states are colored red in Fig. (8).

$$\begin{aligned}&\overbrace{ (\text {core})^{10}\, (3s)^2 ({\mathrm {SH}} )^2\, (\pi _x)^2 (\pi _y)^0 \,({\mathrm {SH}}^*)^0 |\,(4p_x)^1 }^{{\mathrm {SH}}(3^2\Pi ) \text { Rydberg State }} \nonumber \\&\underbrace{ (\text {core})^{10}\, (3s)^2 ({\mathrm {SH}} )^2 \underbrace{(\pi _x)^0 (\pi _y)^2}_\text {Excited Core} ({\mathrm {SH}}^*)^0 }_{\text {SH}^+\left( 1^1\Delta \right) \text { Ion Core }} |\,(4p_x)^1 \end{aligned}$$

(11)

The ${\mathrm {SH}}(3^4\Pi )$ Rydberg state has an ${\mathrm {SH}}^+(1^3\Pi )$ excited-state core as described by Eq. (12). The PECs of these states are colored blue in Figs. (7) and (8).

$$\begin{aligned} \overbrace{ \underbrace{(\text {core})^{10}\, (3s)^2 \underbrace{{({\mathrm {SH}} )^1 (\pi _x)^1 (\pi _y)^2}}_{\text {Excited Core}} ({\mathrm {SH}}^*)^0 }_{\text {SH}^+\left( 1^3\Pi \right) \text { Ion Core}}|\,{(4s)}^1}^{{\mathrm {SH}}(3^4\Pi ) \text { Rydberg State}} \end{aligned}$$

(12)

Last are the dissociating states with Rydberg character. These are dissociating electronic states characterized by an occupied Rydberg MO. We untangled these types of Rydberg states during the analysis of the $^4\Pi$ states. We did not discover any in the analysis of the $^2\Pi$ states [8]. Eq. (13) provides an example of a dissociating Rydberg characterization. States of this nature typically have a singly occupied (SH$^*$) MO with one of the (4p) Rydberg MOs centered on S occupied.

$$\begin{aligned} (\text {core})^{10}\, (3s)^2\, ({\mathrm {SH}})^1\, (\pi _x)^1\, (\pi _y)^1\, ({\mathrm {SH}}^*)^1 \, {(4p)^1}\,\ldots \end{aligned}$$

(13)

The dissociating states with Rydberg character are labeled D$_2$ through D$_4$ in Fig. (7).

Understanding the MOs, how they are populated, and how they change as a function of geometry are prerequisite for obtaining a diabatic representation from the adiabatic PECs. The qualitative discussion above results from a rigorous understanding of the MOs generated by traditional methods. In the next section, we outline how assure a smooth transition of MOs from the small R chemical region to the large R separated atom limit.

3.3 Smooth variation of MOs

By examining isosurface plots [48], we found that the optimized MCSCF orbitals calculated at $R = 6.00$ Å corresponded very well with the separated-atom orbitals identified chemically in Sect. 3 (the respective atomic orbitals on S and H). Then, starting at $R = 6.00$ Å, we stepped down to smaller values of R by performing each new MCSCF using the orbitals from the previous step as the initial guess. We verified that this procedure gave smoothly varying orbitals by directly calculating pseudo-overlap matrix elements $\mathcal {O}_{ij}$ between the MOs at each geometry and those at the previously calculated geometry. $\mathcal {O}_{ij}$ is defined as the overlap between the $ith$ MO at a given geometry and a “translated” orbital formed by using the coefficients of the $jth$ MO at the previous geometry. The smoothness of the variation of the MOs is related to the extent to which $\mathcal {O}_{ij} \approx \delta _{ij}$ (the Kronecker delta function). For the calculations we did, we found that $\left| \mathcal {O}_{ii}\right| \ge 0.97$.

We use the absolute value sign because of the occasional unwanted sign changes. At several stages of the calculation, GAMESS checks the normalization of the MOs and sets the largest coefficient of each MO to be positive. Since the relative magnitude of the MO coefficients may depend on the internuclear separation, abrupt sign changes occasionally appeared as a function of R. Also, we found $\left| \mathcal {O}_{i \ne j}\right| \le 0.03$, with typical values $\left| \mathcal {O}_{i \ne j}\right| \lesssim 10^{-4}$. We took these results to be a confirmation that the MOs were sufficiently smooth allowing us to claim electronic configurational uniformity for each FOCI calculation.

Figure (3) illustrates the smooth variation of the molecular orbitals (SH) and (SH$^*$). In the chemical region (small R), these orbitals are bonding and antibonding, respectively. As R increases they make a smooth transition to a $3p_{z}$ centered on S and a 1s centered on H.

Fig. 3

Both rows of this figure show isosurface plots of two optimized MCSCF MOs in the active space of the FOCI calculation. For small R, the MO in the upper row corresponds to the SH-bonding (SH) orbital. As R increases this orbital smoothly transforms to a $3p_z$ atomic orbital centered on S. The MO in the second row corresponds to the antibonding orbital (SH$^{*}$). For large R this orbital transforms to a 1s atomic orbital centered on H. The two MOs shown above display the greatest variation between the chemical and the separated atom limits. These MOs suggest that $R=4.2\,$Å is nearly the separated limit

As first discussed in Sect. 3.2, the MO transformation shown in Fig. (3) results in geometry dependent electronic configurations when describing the Rydberg states. The two limits of the ${{\mathrm {SH}}(1}^4\Pi {)}$ ion core Rydberg state are depicted below where the underlined orbitals depict the geometry dependent occupations.

Bonding Region characterized by MO occupation:

$$\begin{aligned} (\text {core})^{10}(3s)^2\, \underline{({\mathrm {SH}})^2}\, (\pi _x)^1\, (\pi _y)^1\, \underline{({\mathrm {SH}}^*)^0}\,{(4s)^0\,(4p_x)^0\,(4p_z)^0\,} (4p_y)^1\,{\ldots } \end{aligned}$$

(14)

Separated Atom Region characterized by MO occupation:

$$\begin{aligned} (\text {core})^{10} (3s)^2\, \underline{(3p_z)^1}\, (3p_x)^1\, (3p_y)^1 \underline{(1s_{\mathrm {H}})^1} \, {(4s)^0\,(4p_x)^0\,(4p_z)^0\,}(4p_y)^1\,{\ldots } \end{aligned}$$

(15)

To assure that the occupations of the transforming MOs describing the ${{\mathrm {SH}}(1}^4\Pi )$ ion core Rydberg state varies smoothly with geometry, we track the occupation of the three MOs in question $[{\mathrm {(SH)}} \rightarrow (3p_z)\text {, } {\mathrm {(SH}^*)} \rightarrow (1s_{\mathrm {H}})\text {, and } 4p_y ]$. Figure (4) shows the initially doubly occupied (SH) and unoccupied (SH$^*$) MRCI natural MOs transitioning to a singly occupied ($3p_z$) on S and (1s) on H, respectively. The ($4p_y$-Ryd) remains singly occupied at all R giving the electronic state its Rydberg character. Occupancy of the other MOs remain independent of geometry.

Fig. 4

Occupations of the MRCI natural MOs describing the $^4\Pi$ core-Rydberg state as a function of geometry. We observe a smooth transition from the initially doubly occupied (SH) bonding MO to a singly occupied $3p_z$ AO centered on S. Similarly we observe a smooth transition from the initially unoccupied (SH$^*$)-antibonding MO to a singly occupied 1s AO centered on H. The $4p_y$ Rydberg MO (localized on S) remains singly occupied through the entire geometry domain giving the electronic state its Rydberg character. None of the other occupancies show geometry dependence

The occupations of the chemically transitioning MOs vary in a smooth predictable manner while the electronic state retains its Rydberg character through the entire geometry domain. Understanding this transition becomes important when tracking the CSFs resulting from the FOCI calculations across all geometries. The geometry dependence of the electronic occupations results in a geometry dependence of the CSFs (Fig. 5).

The geometry dependence of the CSFs describing the lowest $^4\Pi$ Rydberg states followed a predicable pattern that we can model through use of a geometry-dependent mixing angle $\gamma$ defined in Eq. (16) where the quantity in brackets represents the quotient of the respective MO occupancies at each geometry. The empirical model employed here is similar, in practice, to the model employed for the triple $\pi$-bond breaking in the co-linear ${\mathrm {N}_{2}\text {H}}$ system [16].

$$\begin{aligned} \gamma (R) = \arctan \left[ \dfrac{({\mathrm {SH}}^\star )}{(\mathrm {SH})}\right] ^2 \end{aligned}$$

(16)

Fig. 5

Graphical depiction of the geometry-dependent mixing angle from the empirical model shown in Eq. (16). The angle shows a smooth transition from the bonding to the separated atom limit

The contribution from the bound to separated atom electronic configurations (Eqs. (14), (15) respectively) to the overall lowest $^4\Pi$ ion core Rydberg electronic wavefunction can be modeled as a two CSF system as shown in Eq. (17) where $\Phi _{\mathrm {CR}}$ denotes the chemical region CSF characterized by Eq. 14 and $\Phi _{\mathrm {SA}}$ denotes the separated atom CSF characterized by Eq. (15)

$$\begin{aligned} \psi _{\mathrm {Ryd}}(R) = \cos \left[ 2\gamma \left( R\right) \right] \Phi _{\mathrm {CR}} + \sin \left[ \gamma \left( R\right) \right] \Phi _{\mathrm {SA}} \end{aligned}$$

(17)

In Fig. (6), we compare the prediction from this model and the actual contribution of the respective CSFs as determined by the final FOCI calculations. The electronic occupations that comprise the dominant CSFs describing R$_1$ are shown in Table 2.

Fig. 6

The left panel shows the prediction of the model in Eq. (17) for the contribution of the geometry-dependent CSFs to the $^4\Pi$ ion core Rydberg state as a function of geometry. The right panel shows the resulting contributions obtained from the final FOCI calculations. In both panels we denote the two CSFs as $\Phi _{\mathrm {CR}}$: the dominant CSF describing the lowest Rydberg in the chemical region (small R); and $\Phi _{\mathrm {SA}}$: the dominant CSF describing the lowest Rydberg in the separated atom (large R) region

4 Diabatic potential energy curves

4.1 Application of BDM to adiabatic PECs of SH

As discussed in Sect. 2.2, to employ the BDM one needs to identify $N_\alpha$ CSFs that make a dominant contribution to $N_\alpha$ eigenstates of the CI Hamiltonian across all geometries. Selecting the CSFs that have a dominant contribution to the states described in the diabatic subspace requires careful analysis and consideration of many individual CSFs. The specific CSFs that make large contributions to a given adiabatic state vary with geometry, making it challenging to choose a set that is satisfactory for all values of R.

In order to handle this situation we define what we call “super-CSFs”. This technique has proven useful in previous work by us [7, 8, 16]. A super-CSF is a linear combination of several CSFs combined in a way that gives a clear picture of the chemistry. Mathematically speaking, defining a super-CSFs is no more than a change of basis in a linear vector space. Super-CSFs became easier to identify from geometry to geometry than any one dominant CSFs because small sets of CSFs corresponding to the same MO occupancies often appeared with the same relative coefficients in several eigenvectors. In the simplest case, two CSFs, one can relate the relative coefficients to a mixing angle $\theta$, that is independent of R, and then define d

$$\begin{aligned} \Phi ^+&= \cos \theta \,\Phi _{1} + \sin \theta \,\Phi _{2} \nonumber \\ \Phi ^-&= -\sin \theta \,\Phi _{1} + \cos \theta \,\Phi _{2} \end{aligned}$$

(18)

where $\Phi ^+$ and $\Phi ^-$ represent the “super-CSFs” considered. The super-CSFs describing the states reported in Fig. (7) are of the form shown in Eq. (18) with mixing angles of $\pi /4$ and are detailed in Table 2.

Table 2 lists the 13 individual CSFs (represented as kets) that are used to define the $N_\alpha = 10$ diabatic space across the entire geometry domain. States labeled D$_1$–D$_3$ are described well by single CSFs while D$_4$ is represented well by a super-CSF (in a form like Eq. (18)).

The CSF combinations labeled 3d-R are attributed to a Rydberg state with an occupied 3d MO. The 3d MOs are not well described by our AO basis set so this adiabatic state is less accurate relative to the other states considered. Specifics about this state are not included in the results of this study. However, the 3d-R combination was required in the diabatization process because it represents a state that mixes with the well-described R$_2$ state in the chemical region.

The two Rydberg states, R$_1$ and R$_2$, as well as the state represented by the combination labeled 3d-R have the added complication of geometry dependent coefficients of the CSFs and super-CSFs as discussed in Sect. 3.2 and illustrated for R$_1$ in Figs. (4) and (6). We resolve this complication by digaonalizing the $6\times 6$ Rydberg sub-block of the $10\times 10$ diabatic matrix $\mathbf {H}_\mathrm {dia}$ after the formal diabatization process defined in Eq. (5). We previously employed this post-diabatization diagonalization of the Rydberg sub-block when treating the lowest $^2\Pi$ Rydberg state [8]. Presently, the Rydberg sub-block consists of the small and large R CSFs and super-CSFs for R$_1$, R$_2$, and 3d-R (six CSFs and super-CSFs in total). The two lowest eigenvectors of this diagonalization produce sensible R$_1$ and R$_2$ Rydberg states across the entire geometry domain.

Table 2 CSFs and super-CSFs used in the diabatization process

Determining which adiabatic electronic states to include in the diabatization also required careful consideration. At small values of R, both the valence and Rydberg states are approaching the repulsive wall, and we see very strong Rydberg-valence mixing between the states of interest (those described by our basis set) and those resulting from the MRCI calculation but not represented by electron occupations of active space MOs. We calculated the magnitude of the projection of each adiabatic state in the space spanned by the CSFs and super-CSFs. This procedure provided quantitative guidance for selecting the most appropriate adiabatic states. By trying several sets of CSFs with different values of $N_\alpha$, and selecting the set of adiabatic states with the largest projection values, we could systematically determine the appropriate parameters for the diabatization.

The coefficients of the CSFs in each adiabatic eigenvector were dependent on geometry, introducing uncertainty into the diabatization process. As the atomic separation (R) changed, the projections of some of the high-energy (adiabatic) eigenvectors onto the diabatic space changed; these states were therefore swapped in and out of the diabatization process. Whenever one of the higher adiabatic states in the diabatization changed, there was an unavoidable discontinuity in the diabatic curves. However, since these higher adiabatic states were only indirectly coupled to the states of interest, the effect was slight. To address this uncertainty we did extensive testing with different numbers of states (varying $N_\alpha$) to eliminate as many anomalies as possible without introducing new anomalies.

4.2 Results: diabatic PECs

By carefully crafting a set of chemically significant MOs and employing the technique of super-CSFs we are able to interpret the adiabatic results of the large FOCI calculations to produce a sensible diabatic representation of the $^4\Pi$ states of $\mathrm {SH}$. The resulting absolute diabatic energies are presented in Table 5 found in the appendix of this article. These absolute energies are the diagonal elements of $\mathbf {H}_\mathrm {dia}$ defined by Eq. (5), as described in Sect. 2.2, at each respective geometry. The off-diagonal elements of $\mathbf {H}_\mathrm {dia}$ are related to the state-to-state coupling that is required for the MQDT treatment of the DR process. These couplings and the MQDT calculations for the $^4\Pi$ states of $\mathrm {SH}$ will be the focus of a future publication.

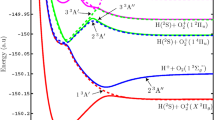
In Fig. (7), we graphically present our results for the $^4\Pi$ diabatic PECs of $\mathrm {SH}$. The adiabatic PECs resulting from the large active space calculations are shown with dashed lines, and the diabatic PECs are overlaid in solid colors. Figure (7) also shows the adiabatic SOCI potentials of $\mathrm {SH}^+$. The absolute energies of the ${\mathrm {SH}}^+$ SOCI PECs, which are provided in Table 6 in Appendix, are shifted up by 0.024384 Hartree (0.66352 eV) to accurately depict their positions relative to the adiabatic ${\mathrm {SH}}(X^2\Pi )$ ground state. This shift was determined by computing a large SOCI for the ${\mathrm {SH}}(X^2\Pi )$ state at the equilibrium position of the ion ($R=1.36\,$Å) then determining the energy value required to match the vertical ionization energy of the $\mathrm {SH}_{\mathrm {FOCI}}(X^2\Pi )$ to ${\mathrm {SH}}^+_\mathrm {SOCI}(X^3\Sigma ^-)$ excitation determined to be 0.347427563 Hartree (9.45399 eV) to the more accurate $\mathrm {SH}_\mathrm {SOCI}(X^2\Pi )$ to ${\mathrm {SH}}^+_\mathrm {SOCI}(X^3\Sigma ^-)$ excitation determined to be 0.37181154 Hartree ($10.11751\,$ eV), which is in good agreement with Dunlavey et al.’s [47] experimental value of $10.37\,$ eV and Park and Sun’s [49] computed value of $9.8657\,$ eV.

In the region of the repulsive wall $(R < 1.12\,{\AA })$ the dissociating autoionizing states and the bound Rydberg states [colored solid curves shown in Fig. (7)], experience strong Rydberg-valence mixing with highly excited states not well described by our AO basis set or the MRCI AS as defined in Eq. (3). The adiabatic PECs display many avoided crossings and up to 50 eigenvectors were needed to determine the extent of the mixing in this region as well as at larger separations. The adiabatic curves shown in Fig. (7) (23 of the 50+ roots calculated by GAMESS) represent the adiabatic states of interest as well as the continuum in which the quasi-discrete states are embedded. The network of adiabatic curves between C$_1$ and C$_2$ and above C$_2$ are described by a host of CSFs (five or more) with electron occupations in highly excited virtual space MOs. The rest of the adiabatic states seen show no direct coupling to the final diabatic states of interest.

Fig. 7

The high-accuracy adiabatic $^4\Pi$ curves are shown with black dashed lines. The diabatic PECs (the diagonal elements of $\mathbf {H}_\mathrm {dia}$ Eq. (5)) are overlaid with solid colored lines. The ${\mathrm {SH}}^+$ adiabatic ground state ($X^3\Sigma ^-$) denoted C$_1$ is colored green and the excited adiabatic state ($1^3\Pi$) denoted C$_2$ is colored blue. The solid green and blue diabatic Rydberg states are built on the corresponding ion cores C$_1$ and C$_2$. The adiabatic states exhibit many, some very large, avoided crossings typical of adiabatic PECs. The separated atom electronic configurations for all of the diabatic states (D$_1$–D$_4$, R$_1$, and R$_2$) as well as the adiabatic ionic states (C$_1$ and C$_2$) are listed in Table 3

Table 3 Comparison of excitation energies near the separated atom limits ($R = 6.0$Å) for the SH($^4\Pi$) and corresponding ion states compared to the atomic excitation energies reported on the NIST Atomic Spectra Database [45]

Fig. 8

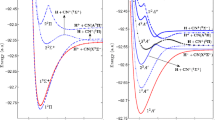
In this figure, we present the diabatic $^2\Pi$ ground and Rydberg PECs as dash-dot lines; these PECs were previously reported by Kashinski et al. [8]. The solid lines are the newly calculated $^4\Pi$ diabatic lowest dissociating state (D$_1$) and Rydberg states. The parent ion adiabatic states are shown as dashed lines. The $\mathrm {SH}(3\,^2\Pi )$ Rydberg (shown in dash-dot red) corresponds to the $\mathrm {SH}^+(1^1\Delta )$ ion shown in a red dash-dot line. The same color code is used in Fig. 7. The dotted vertical line is placed at $R=1.36\,$Å and corresponds to the minimum of the ground state of the ion $\mathrm {SH}^+(X\,^3\Sigma ^-)$. The vertical excitations reported in Table 4 are along this vertical line

Table 4 Comparison of excitation energies near the $\mathrm {SH}^+$ minimum ($R = 1.36$Å) from the SH($X^2\Pi$) diabatic PEC to the indicated diabatic $^{2,4}\Pi$ $\mathrm {SH}$ states

5 Concluding remarks

Large-scale MRCI electronic structure calculations have been completed to determine the $X^3\Sigma ^-$, and $1^3\Pi$ adiabatic PECs of $\mathrm {SH}^+$ and the $^4\Pi$ adiabatic PECs of $\mathrm {SH}$. Due to strong Rydberg-valence coupling the adiabatic PECs of $\mathrm {SH}$ displayed many strongly avoided crossings. By employing the block diagonalization method, with an understanding of the smoothly varying and well-crafted MOs, we were able to untangle the strongly mixed Rydberg and valence states and determine a sensible diabatic representation of the standard adiabatic $\mathrm {SH}$ PECs. The sensibility of the diabatic PECs is benchmarked by the good agreement of our vertical excitation energies $(T_e)$ at the ion minimum ($R=1.36\,$Å shown in Table 4) when compared to other theoretical treatments of $\mathrm {SH}$ [46, 49, 50] and the near separated-atom limit (shown in Table 3) when compared to experimental results [45] found in the literature. This good agreement validates our diabatization procedure.

Our previous work [8], focusing on the DR of $\mathrm {SH}^+$ with electrons through the $^2\Pi$ states of $\mathrm {SH}$, resulted in theoretical DR rate constants showing good agreement with experiment except for energies of interest for the ISM (less than $\sim$10 meV), were the rate constants fall below experimental values by about an order of magnitude. This discrepancy led us to explore the $^4\Pi$ states of $\mathrm {SH}$ in order to identify additional pathways for the DR process.

Through careful analysis of the geometry-dependent CSFs our diabatization method was able to uncover two bound low-lying $^4\Pi$ Rydberg states (R$_1$ and R$_2$) that result from two different ion cores (the $^3\Sigma ^-$ (C$_1$) and the $^3\Pi$ (C$_2$) respectively). Our method also uncovered several diabatic dissociating autoionizing states, including the lowest one, D$_1$, that crosses near the minimum of C$_1$, R$_1$, and R$_2$ as well as three others (D$_2$ through D$_4$) that cross near the minimum of C$_2$. These $^4\Pi$ PECs of $\mathrm {SH}$ are presented in Fig. (7).

Analysis of these PECs suggest an additional DR pathway through the dissociating autoionzing state D$_1$ due to its position relative to the minimum of ion C$_1$ and Rydbergs R$_1$ and R$_2$. R$_1$ and R$_2$ result from different ion cores highlighting the importance of multi-core effects on the DR process at low energies. We suggest the $^4\Pi$ states of $\mathrm {SH}$ will have a significant contribution to the DR of $\mathrm {SH}^+$ with electrons at low energies.

Work is in progress to extend our earlier calculations by applying the MQDT method to include contributions from the $^4\Pi$ states of $\mathrm {SH}$ to the DR of $\mathrm {SH}^+$ with electrons using the diabatic PECs presented in the present work and their associated state-to-state couplings. The results of these calculations will be the focus of a future publication.

Appendix

See Tables 5 and 6.

This appendix contains tables with our computationally determined results for the absolute diabatic potential energy values for the $\mathrm {SH}(^4\Pi )$ states as well as the absolute adiabatic energy values for the lowest $\mathrm {SH}^+$ states of indicated symmetry.

Table 5 Here we present the absolute diagonal elements of $\mathbf {H}_\mathrm {dia}$ defined in Eq. (5) resulting from our application of the block diagonalization method to the $\mathrm {SH}(^4\Pi )$ adiabatic potential energy curves (PECs). The numerical ordering of the $^4\Pi$ states is the order of occurrence vertically at $R = 1.36\,$Å. These diabatic PECs are plotted in Fig. (7)

Table 6 Here we present the absolute adiabatic energies for the lowest $\mathrm {SH}^+$ states of indicated symmetry. The PECs for the $\mathrm {SH}(X^3\Sigma ^-)$ and $\mathrm {SH}(1^1\Delta )$ states were previously plotted in ref. [8]. We add 0.24384 Hartree $(0.66352\,\text {eV})$ to these absolute energies before superimposing them on the diabatic $\mathrm {SH}(^4\Pi )$ PECs plotted in Fig. (7). This vertical shift is discussed in Sect. 4.2