1 The ambiguous nature of the chemical bond

In 1992, taking care to avoid understatement, Pauling expressed his view that “The concept of the chemical bond is the most valuable concept in chemistry. Its development over the past 150 years has been one of the greatest triumphs of the human intellect.” [1] However, just 15 years later, in a special issue of the Journal of Computational Chemistry entitled “90 Years of Chemical Bonding,” Frenking and Shaik commented that “we are still far from understanding the nature of the chemical bond” [2], which was echoed by Jacobsen, “many questions remain open in the quest for a unified and complete understanding of the true nature of the chemical bond” [3].

But is such a quest even meaningful? Jacobsen goes on to say that “it has become clear that the chemical bond per se does not exist. Each bond possesses its very own specific character,” [3]. Foroutan-Nejad et al. seem to share this view: “there is no general theoretical Scheme that may claim to encompass the description of all known types of chemical bonds.” [4]. Gillespie and Robinson go further: “a bond has no physical reality.” [5] Bader, as always is emphatic: “a ‘bond’ is neither measurable nor susceptible to theoretical definition.” [6] Instead of bonds, he speaks of “bonded interactions.”

Questioning the very concept of a chemical bond is not a recent development. Just a year after Pauling’s famous treatise [7], The Nature of the Chemical Bond, Allen and Shull noted that it is “extremely difficult to see factors significant in stabilizing a particular configuration of electrons and nuclei” [8].

This brings up a yet more fundamental issue of contention. Chemical bonds are typically viewed as linking atoms in molecules. But is it even meaningful to speak of atoms in molecules? Quantum chemistry views a molecule as a collection of electrons and nuclei. As Ivanic et al. pointed out, “the resolution of molecules in terms of atoms is not fundamental to rigorous physical theory.” [9] Parr et al. noted that the atoms-in-molecules concept is ambiguous and arbitrary [10], and Gilbert et al. put it succinctly, “There exists no quantum mechanical definition of an atom within a molecule and, therefore, any attempt to extract atomic identity is arbitrary.” [11]

Bader, developer of the Quantum Theory of Atoms in Molecules (QTAIM) [12, 13] naturally strongly disagrees [14]. However, while QTAIM is mathematically elegant, its relevance to chemical realities is increasingly being questioned [4, 15,16,17,18,19,20,21,22,23,24,25,26,27,28,29].

Can one aspire to explain the nature of bonds between atoms in molecules if it is not even established that there are indeed atoms in molecules? This dilemma has not prevented a variety of explanations of chemical bonding from being put forth: resonance, electronic charge buildup in internuclear regions, kinetic energy lowering, orbital interference, charge transfer, etc. Carbó-Dorca commented that “It might be almost impossible to describe in a short account the different manners by which the chemical bond has been described” [30].

In this brief overview, we have sought to demonstrate some fundamental disagreements that prevail in the area of chemical bonding. Our present objective is not to try to resolve any issues, but simply to provide some additional perspective.

2 Electrostatic potentials at nuclei of atoms and molecules

The electrostatic potential V0,A that is created at any nucleus A of a molecule by its electrons and the other nuclei is given rigorously, following Coulomb’s Law, by Eq. (1):

$$V_{{{0,}A}} = \sum\limits_{B \ne A} {\frac{{Z_{B} }}{{\left| {{\mathbf{R}}_{B} - {\mathbf{R}}_{A} } \right|}}} - \int {\frac{{\rho ({\mathbf{r}}){\text{d}}{\mathbf{r}}}}{{\left| {{\mathbf{r}} - {\mathbf{R}}_{A} } \right|}}}$$
(1)

RA is the position of nucleus A, having charge ZA, and RB and ZB are the position and charge of any other nucleus B; ρ(r) is the molecule’s electronic density. The two terms in Eq. (1) represent, respectively, the positive contribution of the other nuclei and the negative one of the electrons.

If A is the nucleus of just a single free atom, then the summation over other nuclei does not appear. The electrostatic potential V0 at the nucleus of a free atom is,

$$V_{{0}} = - \int {\frac{{\rho ({\mathbf{r}}){\text{d}}{\mathbf{r}}}}{{\mathbf{r}}}}$$
(2)

Now ρ(r) is the electronic density of the atom, and r is relative to its nucleus.

An important feature of the electrostatic potential is that it is a real physical property, an observable. It can be determined experimentally, by diffraction methods [31,32,33], as well as computationally.

It has been pointed out in the past that the electrostatic potential at the nucleus of a given atom is relatively insensitive to the atom’s molecular environment [34, 35]. We will now investigate this more extensively and in greater detail.

In Table 1 are the computed electrostatic potentials at the nuclei of the indicated atoms in a variety of molecules as well as in the free atoms. The calculations were carried out at the B3P86/6–311 + G(3df,2p) level, using Gaussian 09 [36].

Table 1 Computed electrostatic potentials at nuclei of indicated atoms
Full size table

The most striking feature of Table 1 is how little the electrostatic potential at an atom’s nucleus changes even in quite different environments, not only neutral molecules but ions as well. For example, the V0,A of the nitrogen atoms in Table 1 are all within 1.7% of the free atom value; this includes the nitrogen in the N3¯ and NO3¯ anions, in a series of neutral molecules of differing polarities, and in the NH4+ cation. For the chlorine atoms, the V0,A are within 0.6% of the free atom V0 in a series that includes the Cl¯ anion, the highly polar LiCl and several neutral covalent molecules, among them being Cl2.

This relative insensitivity to environment is particularly noteworthy because the two contributions to V0,A, the nuclear and the electronic, can change very considerably from one molecule to another. Consider, for instance, the carbon atoms in H2C=O and (H2N)2C=O. The nuclear and electronic contributions to the electrostatic potentials at the carbon nuclei are quite different in the two molecules:+ 4.496 and– 19.179 hartrees in H2C = O and + 9.916 and– 24.567 hartrees in (H2N)2C=O. Yet the net potentials at the carbon nuclei are nearly the same in both molecules, − 14.683 and − 14.651 hartrees, respectively (Table 1).

As another example, take the phosphorus in PF3 and Cl3P=O. The nuclear and electronic contributions to the potentials at the phosphorus nuclei in these molecules differ considerably: + 9.065 and − 63.101 hartrees in the former and + 16.414 and − 70.422 hartrees in the latter. However, the resulting net potentials at the phosphorus nuclei are very similar,− 54.036 and − 54.007 hartrees.

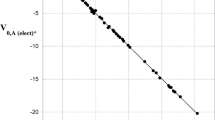
Table 1 and these examples can be interpreted as indicating that the electrostatic potential at the nucleus of an atom A in a molecule reflects almost entirely its own electronic density; the contributions of the other electrons and nuclei largely cancel. The electronic density of the atom undergoes some degree of polarization in forming the molecule and this has a minor effect upon its V0,A, which becomes more (less) negative as electronic charge is polarized toward (away from) the nucleus of A. V0,A is most negative when the atom A is part of an anion, least negative when part of a cation (Table 1). However, V0.A is in all cases very characteristic of the atom A, as can be seen in Table 1 and in the excellent correlation of the free atom V0 with their nuclear charges, Fig. 1.

Fig. 1
figure 1

Relationship between computed electrostatic potential at nucleus of free atom and nuclear charge, for atoms in Table 1 plus hydrogen atom. R2 = 0.9996

Full size image

Hydrogen is an exception to the generalization that V0,A values are relatively insensitive to molecular environment; its V0,H sometimes differs very considerably from that of the free atom, as shown in Table 2. This can be understood by recognizing that hydrogen has no inner electrons that can provide the basis for a relatively stable V0,H; its only electron is involved in bonding. The absence of inner electrons makes both the hydrogen atom and the hydrogen molecule atypical, as has been pointed out a number of times [29, 37,38,39,40]. (It is ironical that H2 has traditionally been used as the model for the covalent bond.)

Table 2 Computed electrostatic potentials at nuclei of hydrogen atoms
Full size table

It is tempting to try to rationalize the V0,A values in Table 1 in terms of electronegativities. On that basis, the electrostatic potential at the nucleus of an atom would be less (more) negative as the remainder of the molecule is more (less) electron attracting. In some instances, this does account for the observed V0.A. Thus, the carbon in CF4 has a less negative V0,C than does the carbon in CCl4. The nitrogen in pyrrole has a more negative V0,N than the one in NO2.

However, electronegativity does not explain all of the trends and patterns in Table 1. For example, why are the V0,A of many of the homonuclear diatomics less negative than for the free atoms? Why is it that in F2O, which combines the two most electronegative atoms, both V0,F and V0,O are less negative than for the free atoms? The lithium in LiF, LiH and LiCl is expected to be positive in character, yet in both LiF and LiH the potential at the lithium nucleus is more negative than in the free lithium atom.

3 Atomic and molecular energies from electrostatic potentials at nuclei

In 1962, Wilson used the Hellman–Feynman theorem [41, 42] to derive an exact formula for the energy of a molecule in terms of its electronic density [43]. This was two years prior to the Hohenberg–Kohn theorem [44], which established the electronic density as the fundamental determinant of all molecular properties.

It has subsequently been demonstrated that Wilson’s result can be re-formulated to give the energy of an N-electron molecule rigorously as a function of the electrostatic potentials at its nuclei [45, 46]:

$$E_{{{\text{mol}}}} = \sum\limits_{A} {z_{A} } \int\limits_{\lambda = 0}^{1} {\left[ {V_{0,A} (\lambda )} \right]_{N} {\text{d}}\lambda }$$
(3)

In Eq. (3), λ is a scaling parameter such that the charge on any nucleus Zi is λzi, where λ can vary between zero and one. In the actual molecule, λ = 1 and zi = Zi for each nucleus. The effect of λ is to make all of the nuclear charges increase in a concerted manner from zero to their true values.

The atomic version of Eq. (3) had already been introduced by Foldy [47] some years before Wilson’s work:

$$E_{{{\text{atom}}}} = \int\limits_{{Z^{\prime} = 0}}^{Z} {\left[ {V_{0} (Z^{\prime})} \right]_{N} {\text{d}}Z^{\prime}}$$
(4)

The actual application of eqs. (3) and (4) is challenging; e.g., the integrals are to be evaluated holding the numbers of electrons constant. Conceptually, however, these equations are quite significant. They show that the energy of an atom or molecule, which is a two-electron property, can be expressed rigorously in terms of the electrostatic potentials at the nuclei; these are one-electron properties but they evidently take account of electron–electron repulsion. This is a direct manifestation of the Hohenberg–Kohn theorem.

Furthermore, the molecular energy formula, Eq. (3), is simply the atomic formula, Eq. (4), summed over all of the constituent atoms. There are no explicit interaction or “mixing” terms. This is certainly consistent with the concept of atoms in molecules.

The difficulty of actually applying eqs. (3) and (4) has stimulated the development of a variety of approximate relationships between energies and electrostatic potentials at nuclei. There have been several reviews of this work [34, 35, 48,49,50,51,52,53].

An interesting aspect of this arises from the fact that approximate solutions of the Schrödinger equation often give V0 and V0,A more accurately than the total energies. For instance, Hartree–Fock atomic and molecular energies are correct through first-order but Hartree–Fock electrostatic potentials at nuclei are correct through second-order [49, 50, 54]. This means that Hartree–Fock V0 or V0,A inserted into an appropriate approximate E–V0 or E–V0,A relationship can produce energies that are better than Hartree–Fock, i.e., contain significant amounts of correlation energy. This has been demonstrated [49, 50, 55].

4 Energies of atoms in molecules

Equation (4) suggests an approximate proportionality between Eatom and \(ZV_{{0}}\), and Eq. (3) similarly suggests one between Emol and \(\sum\limits_{A} {Z_{A} V_{{{0,}A}} }\). We have investigated these possibilities, using the computed data in Tables 1 and 2 and the exact atomic and molecular energies in Tables 3 and 4.

Table 3 Properties of free atoms
Full size table
Table 4 Properties of molecules
Full size table

Figures 2 and 3 show that there are indeed excellent correlations between the exact Eatom and ZV0 for the atoms in Table 3 and between the exact Emol and \(\sum\limits_{A} {Z_{A} V_{{{0,}A}} }\) for the molecules in Table 4. R2 is 1.000 in both cases. Equations (5) and (6) describe these relationships.

$$E_{{{\text{atom}}}}\; { = 0}\;{\text{.4196(}}ZV_{{0}} ) - 0.1531$$
(5)
$$E_{{{\text{mol}}}}\; { = 0}\;{\text{.4199}}\left( {\sum\limits_{A} {Z_{A} V_{{{0,}A}} } } \right) - 1.050$$
(6)
Fig. 2
figure 2

Relationship between exact atomic energy and product ZV0 for atoms in Table 3. R2 = 1.0000

Full size image
Fig. 3
figure 3

Relationship between exact molecular energy and \(\sum\limits_{A} {{\text{Z}}_{A} {\text{V}}_{{{0,}A}} }\) for molecules in Table 4. R2 = 1.0000

Full size image

Note that the slopes of the lines are essentially the same, and they both go nearly through the origins.

Equation (5) is almost identical with an atomic energy formula that comes out of Thomas–Fermi theory [56, 58,59,60], which was a predecessor of Hohenberg–Kohn density functional theory; the Thomas–Fermi formula is,

$$E_{{{\text{atom}}}}\; { = }\;\frac{3}{7}{(}ZV_{{0}} ) = 0.4286{(}ZV_{{0}} )$$
(7)

Fraga showed that when Hartree–Fock V0 are used, Eq. (7) reproduces true atomic energies to within about 2% [61].

It was later demonstrated that Eq. (7) could be extended to molecules [62]:

$$E_{{{\text{mol}}}} = \frac{3}{7}\left( {\sum\limits_{A} {Z_{A} V_{{{0,}A}} } } \right) = 0.4286\left( {\sum\limits_{A} {{\text{Z}}_{A} {\text{V}}_{{{0,}A}} } } \right)$$
(8)

With Hartree–Fock V0,A, the errors are usually less than 2%.

Significantly better atomic and molecular energies are obtained with eqs. (5) and (6) and using the V0 and V0,A computed at our present B3P86/6–311 + G(3df,2p) level. For the atoms in Table 3, the average deviation from the exact energies is 0.89%; for the molecules in Table 4, it is 0.44%. While these errors are too large to allow reliable calculations of energy differences, e.g., dissociation energies, the results do indicate that eqs. (5) and (6) provide qualitatively meaningful atomic and molecular energies.

Both the rigorous molecular energy formula, Eq. (3), and the correlation in Eq. (6) express molecular energy entirely as a sum of atomic contributions. This suggests, as proposed some time ago [63], that the energy of a molecule can be apportioned between its constituent atoms in accordance with the ratio of each atom’s contribution to the sum of the contributions of all of the atoms. By that reasoning, the energy of atom M in the molecule is,

$$E_{{{\text{atom}},M}}\; { = }\;\left[ {\frac{{Z_{M} V_{{{0,}M}} }}{{\sum\nolimits_{{\text{A}}} {Z_{A} V_{{{0,}A}} } }}} \right]E_{{{\text{mol}}}}$$
(9)

Using the data in Tables 3 and 4, we have calculated the energies Eatom,M of the atoms in the molecules in Table 4. They are listed in Table 5. We have also found the differences ΔE between the energies of the atoms in the molecules and the free atoms, Eq. (10); these are also in Table 5.

$$\Delta E \, = \, E_{atom,M} - \, E_{atom}$$
(10)
Table 5 Calculated energies Eatom,M of atoms M in molecules, Eq. (9), and energy differences ΔE, Eq. (10)
Full size table

For homonuclear diatomics, each Eatom,M is simply half of Emol. It also follows from eqs. (9) and (10) that the sum of the ΔE for any molecule equals the atomization energy of that molecule, i.e., the energy needed to separate it into its constituent free atoms. For diatomics, this is the dissociation energy. Since we used the exact Eatom and Emol in eqs. (9) and (10), the sums of the ΔE in Table 5 must equal the exact atomization or dissociation energies of the molecules.

When an atom has ΔE < 0 in a particular molecule, its energy in that molecule is more negative than in the free state; ΔE > 0 indicates that the atom’s energy in the molecule is less negative than as a free atom. To some extent, the signs of the ΔE can be linked to the atoms’ electronegativities, the more electronegative having the more negative ΔE, but as with the V0,A values discussed earlier, the relationship to electronegativity is limited. Note, for instance, that in ClO the oxygen has ΔE = 0.000, while the ΔE of the chlorine is − 0.104 (Table 5).

5 Discussion and summary

The electrostatic potential at the nucleus of an atom A, labeled V0 for the free atom and V0,A when the atom is part of a molecule, is a key property of that atom. Its value changes remarkably little in going from one environment to another–free atom to nonpolar covalent to polar covalent to ionic–even though its nuclear and electronic components separately may vary considerably. The changes in these components largely cancel. The electrostatic potential at the nucleus can thus be viewed as qualitatively characterizing the atom, as shown in Table 1 and Fig. 1.

These observations bring to mind the "Quantum Chemical le Chatelier Principle" formulated by Mezey [64,65,66]. This states that when a molecule at equilibrium is subjected to a perturbation, such as a change in conformation, the effects upon the nuclear repulsion and electronic energies may be quite considerable but of similar magnitudes and opposite signs, so that they will approximately cancel. The total energy is relatively little affected.

The energies of atoms and molecules can be formulated, both rigorously and approximately, in terms of the electrostatic potentials at their nuclei. The molecular expressions are simply summations over the atomic contributions; there are no explicit interatomic ones. This provides a seemingly reasonable basis for estimating the energies of atoms in molecules.

We do not claim that the results that have been presented demonstrate conclusively the existence of atoms in molecules. It may be that this will never be definitively proven. However, a concept does not have to be rigorously established in order to be very useful, e.g., the laws of thermodynamics. It seems fair to say that our results provide strong indications that it is meaningful to view molecules and polyatomic ions as composed of atoms that keep their identities.