1 Introduction

Applications of computational chemistry using quantum mechanics, in the study of thermochemical properties, are among the most fundamental and useful information related to molecular systems [1]. It can be used in the study of the chemical reactivity [2], prediction of reaction barrier [3,4,5], and relative stability in gas-phase [6] or in solvent medium [7]. Fundamental electronic properties can be calculated using computational calculations, such as enthalpies of formation [8, 9], and proton and electron affinities [10, 11].

The critical feature of any proposed quantum model is its generality, and for practical purposes the model should be efficient and applicable to estimate the structure, energy, and other properties of atoms, molecules, molecular systems, and reaction processes [12]. This applicability presents two important goals to computational chemistry: (1) predict thermochemical parameters with reasonable accuracy and (2) at a lower computational cost.

Currently, many studies involving these two goals have employed combined strategies to approximate high-level correlated calculations and large basis set functions using a series of lower-level theoretical procedures and relatively smaller basis sets. Compound methodologies, such as Gaussian-n (\({n} = 1, 2, 3\), or 4) [13,14,15,16], Complete Basis Set (CBS-x, \({x} = 4\hbox {M}\), QB3, or APNO) [17,18,19], and Weizmann-n (Wn, \({n} =\,\)1–4) [20,21,22] approaches have been employed as a cost-effective alternative to the high-accuracy methods (Coupled Cluster or Multi-references methods).

They are used in a range of fields and have been capable of providing “chemical accuracy” (\(\approx \,1\) kcal mol\(^{-1}\)). Others theories combined with a compact effective pseudopotential have been successfully employed, considering the lower computational cost and performance [23,24,25,26].

Our group carried out the implementation of a compact effective pseudopotential (CEP) in the W1 method (1st version) [25], considering that the Weizmann-n methods are characterized by a rigorous well-defined series of ab initio calculations devoid of empirical adjustment parameters. The results obtained by this methodology (W1CEP) were close to the respective all electron calculations. The deviations from experimental data, with a 95% confidence, were in the range of \(\pm \, 3.4\) and \(\pm \, 4.0\)  kcal  mol\(^{-1}\) for W1 and W1CEP, respectively.

The objective of this manuscript is to present a modified W2 theory using Stuttgart/Dresden (SDD) RLC ECP basis set. According to Martin et al., the use of RLC ECP is recommended, for the following reasons (among others): (a) compact mathematical form, (b) ready availability in the commonly used quantum chemistry packages (Gaussian [27] for example), (c) consistent treatment of relativistic effects in all relevant rows of the periodic table, and (d) independence of the ECP on the valence basis set [28]. This modified methodology is referred to as W2SDD. The method employs the discretized version [29, 30] of the generator coordinate method (GCM) [31] to obtain the atomic basis sets in conjunction with relativistic pseudopotentials (Stuttgard relativistic large core basis set) [32]. The methodology (W2SDD) was used for calculating thermochemical properties. And in this work, we have applied it to the calculation of proton affinities and enthalpy of formation and, in particular, for studying the reaction between propene and hydrogen halide (F, Cl, Br, or I) at this level of theory. This reaction proceeds in accordance with Markovnikov’s rule. It is also reported, at the TDDFT level of theory, the calculation of electronic circular dichroism spectra of 2-halobutane. The ECD signal appears when propene is replaced by 1-butane in the above reaction.

2 Computational method

2.1 W2 theory

W2 theory is characterized by its accuracy in predicting fundamental thermochemical quantities. This theory successfully reproduces energies at CCSD(T)/CBS high level of theory. The theoretical results at this level come with a significant computational cost. Basically, the energy obtained in this theory is described by Eq. (1):

$$\begin{aligned} E_{{\rm CCSD(T)}/{\rm CBS}} \approx E_{{\rm SCF},\infty } + E_{{\rm COR,CCSD},\infty } +\,E_{{\rm COR,T,CCSD},\infty } + E_{\rm SRC} \end{aligned}$$
(1)

where the extrapolated energy components are: \(E_{{\rm SCF},\infty }\)—Hartree–Fock energy at the complete basis set limit, \(E_{{{\rm COR,CCSD}},\infty }\) – CCSD valence correlation energy at the complete basis set limit, \(E_{{{\rm COR,T,CCSD}},\infty }\) – CCSD(T) triple excitations contributions for the valence correlation energy obtained at the complete basis set limit, and \(E_{\rm SRC}\)—Scalar Relativistic Component obtained with and without core–valence correlations and scalar relativistic effects included with the Douglas–Kroll–Hess model. Additional terms are: \(E_{\rm ZPE}\), zero-point energy to account for the vibrational effect at 0 K and for deficiencies in the harmonic approximation. And \(E_{\rm SO}\), spin-orbit corrections considered for atoms [33].

The following steps are needed to derive the W2 energy—Eq. (1), considering the computational calculation:

Step1::

Molecular geometry optimization based on analytical energy gradients obtained at the B3LYP/cc-pVQZ+d level, where the \(+\,d\) denotes the addition of a set of d functions.

Step2::

Harmonic vibrational frequency calculation is performed at the optimized geometry obtained at Step 1. The theoretical vibrational frequencies are scaled by 0.893.

Step3::

Reoptimization of the molecular geometry at the B3LYP/cc-pVTZ+d level.

Step4::

Single-point calculations at the reoptimized molecular geometry at CCSD(T)/augh-cc-pVTZ+2df \((E3_{\rm level})\). The augh-cc-pVnZ (\({n} = {T}, Q\), or 5) basis set has different meanings for different elements of the periodic table. It is translated to cc-pVQZ for hydrogen and aug-cc-pVQZ for elements in the second and third periods, augmented with d and f orbitals.

Step5::

Single-point calculations at the reoptimized molecular geometry at CCSD(T)/augh-cc-pVQZ+2df (\(E4_{\rm level}\))

Step6::

Single-point calculations at the reoptimized molecular geometry at CCSD/augh-cc-pV5Z+2df (\(E5_{\rm level}\)).

Step7::

Single-point calculations at the reoptimized molecular geometry at CCSD(T,FC)/MTSmall, which is a completely decontracted cc-pVZT basis set [1].

Step8::

Single-point calculations at the reoptimized molecular geometry at CCSD(T,Full)/MTSmall with the Douglas–Kroll–Hess (DKH) model.

By Steps 7 and 8 the relativistic effects considering the difference between the CCSD(T,Full)/MTSmall and CCSD(T,FC)/MTSmall are obtained.

The infinite basis set limit terms—Eq. (1), are given by Eqs. (2)–(4) considering the extrapolation at SCF, CCSD valence correlation and contributions of triple excitations to the CCSD(T) valence correlation energies, respectively.

$$\begin{aligned}E_{{\rm SCF},\infty } = E5_{\rm SCF} - { \frac{ (E5_{\rm SCF} - E4_{\rm SCF})^2}{E5_{\rm SCF} - 2*E4_{\rm SCF} + E3_{\rm SCF}} } \end{aligned}$$
(2)
$$\begin{aligned} E_{{\rm COR,CCSD},\infty } = E5_{\rm CCSD} - E5_{\rm SCF} = +\, \frac{(E5_{\rm CCSD} - E5_{\rm SCF}) - (E3_{\rm CCSD} - E3_{\rm SCF})}{(5/4)^3 - 1} \end{aligned}$$
(3)
$$\begin{aligned}&E_{{\rm COR,T,CCSD},\infty } \nonumber \\&\quad = E4_{\rm CCSD(T)} - E4_{\rm CCSD} \nonumber \\&\qquad +\, { \frac{ ((E4_{\rm CCSD(T)} - E4_{\rm CCSD}) - ((E3_{\rm SD(T)} - E3_{\rm CCSD}) }{(4/3)^3 - 1} }. \end{aligned}$$
(4)

2.2 W2SDD theory

The W2SDD theory consists in generating a new function basis sets. These new sets are the basis sets employed at W2 theory, but now they are adapted with pseudopotential. The generator coordinate method, in its discretized version, has been very useful in the study of basis sets. The method can basically be described considering the monoelectronic function \(\psi (1)\) (atomic or molecular orbitals) described as an integral transform—Eq. 5,

$$\begin{aligned} \psi (1) = \int _0^\infty f(\alpha ) \phi (\alpha ,1) \hbox {d}\alpha \end{aligned}$$
(5)

where \(\alpha\), f(\(\alpha\)), and \(\phi (\alpha , 1)\) are the generator coordinate (exponent of the basis set), weight, and generator functions, respectively. The cc-pVTZ+d,cc-pVQZ+d, augh-cc-pVTZ+2df, augh-cc-pVQZ+2df, augh-cc-pV5Z+2df, and MTSmall basis sets adapted to the pseudopotential (SDD) were used as generator functions.

The procedure consists by: (1) uncontracting the basis sets, (2) eliminating the inner basis functions (they are described by the pseudopotential), and (3) searching for the new function basis sets.

For the minimization of a function (energy) of n variables (exponents), the Simplex algorithm [34] was used. This algorithm was adapted to the Gaussian program [27] to provide the minimum of energy, at the MP2 level of theory, considering the electronic ground state of the atom corresponding to the reoptimized new primitive functions (new exponents).

2.3 Mechanism for the hydrohalogenation of propene

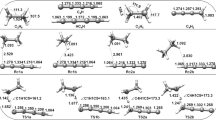
The W2SDD model was applied in the study of the mechanism for the hydrohalogenation of propene. The theoretical studies of the reaction mechanism between propylene and HX (\(\hbox {X} = \hbox {F}\), \(\hbox {C}\ell\), Br, and I) have involved the calculation of reactants, intermediary complexes, transition states, and products. Basically, the mechanism can be described by the following steps: (1) attack of HX on propylene; (2) a transition state is formed; (3) the halide attacks the carbocation intermediate; and (4) the product (according to the Markovnikov’s rule) is formed in a large amount [35, 36].

$$\begin{aligned}&\hbox {CH}_2 = \hbox {CHCH}_2 \,+\, \hbox {HX} \rightarrow [\hbox {TS}]^\# \rightarrow \hbox {CH}_3\mathrm{CHXCH}_3. \end{aligned}$$

2.4 Electronic circular dichroism

The replacement of propylene by 1-butene in the reaction with hydrogen halide, considering the process obeying Markovnikov’s rule, conducts to the formation of a molecule containing a chiral center, such as \(\hbox {CH}_3\hbox {C}^*\hbox {HXCH}_2\hbox {CH}_3\). To explore the chirality of these systems, we carried out the calculations of the electronic circular dichroism (ECD) spectra. ECD is an extremely powerful method for exploration of chirality and stereoselectivity of organic molecules and is based on differential absorption by a chiral molecule of left and right circularly polarized light in the UV and Visible regions [37].

The simulated ECD spectra can be obtained as the combination of the bands computed through theoretical calculations (TD-DFT). ECD signal intensity is theoretically related to the rotatory strength (R) quantity, which corresponds to to the intensity of an absorption band associated with the transition between \({|}\Psi _0{\rangle }\) and \({|}\Psi _i{\rangle }\)

$$\begin{aligned} f_{0 \rightarrow i} \propto \left[ \, \int \Psi _0 (\mathbf {r}) {\hat{\mu }} \Psi _i (\mathbf {r}) \hbox {d} \mathbf {r}\,\right] ^2 \end{aligned}$$
(6)

where \({\hat{\mu }}\) and \({\hat{m}}\) are the electric and magnetic dipole operators, respectively.

2.5 Non-covalent interactions (NCI) analysis

The non-covalent interactions [38] were calculated with the NCIPLOT software package [39]. This method indicates the kind of intermolecular interaction using the reduced density gradient (RDG) 2D plot. The repulsive forces are represented by a red color. In this case, the eigenvalue of the electron density Hessian (\(\lambda\)) is positive (\(\lambda\) > 0). For attractive forces, the sign of \(\lambda\) is negative (\(\lambda < 0\)) and is indicated by green and blue colors, the van der Walls and hydrogen interactions, respectively. Since van der Walls are weak interactions, \(\lambda\) in this case is close to zero.

3 Results and discussion

3.1 Function basis sets adapted to effective core potential

The uncontracted and unique function basis sets were used to obtain the primitive basis sets in conjunction with a pseudopotential (SDD/RCL/ECP). Figure 1a–c shows the weight function for (a) s, (b) p, and (c) d outermost atomic orbitals in Br atom. The SDD RLC pseudopotential acts at the right of the dashed lines. These regions define the core region. Gaussian functions in these regions are eliminated, and the smaller uncontracted Gaussian type orbitals (GTO) are obtained. The Simplex method is used in the search of the MP2 minimum energy of the electronic ground state. In an iterative process, optimizing the exponents of these GTO functions, until the convergence of energy is achieved. So, the new function basis sets adapted to the SDD/RLC/ECP will be used in all theoretical calculations.

Fig. 1
figure 1

Weight functions versus\(\hbox {ln}(\alpha )\) of the Br as, bp, and cd outermost atomic orbitals for the all-electron system

Full size image

3.2 Proton affinity

Table 1 shows the results of proton affinities (in \(\hbox {kcal mol}^{-1}\)) for a set of molecular systems containing F, \(\hbox {C}\ell\), Br, and I atoms. The results were obtained using the basis sets described in the previous section. A comparison between theoretical (using W2 and W2SDD theories) and experimental results is also presented. Our calculated values are close to the experimental results and the more sophisticated W2 data (when available). In Table 2, the differences between the experimental data and the W2SDD calculations are listed. W2SDD method yields the results comparable to experimental values (\(\approx 1\, \hbox {kcal mol}^{-1}\)). Calculations of more complex systems, using W2 approach, are impracticable with our computing resources.

Table 1 Experimental and calculated proton affinities (in kcal  mol\(^{-1}\))
Full size table
Table 2 Experimental and \(\Delta \hbox {W}2\)SDD proton affinities (in \(\hbox {kcal mol}^{-1}\))
Full size table

3.3 Enthalpies of formation

The small test sets of molecules were used to evaluate the performance of the enthalpies of formation using the W2 and W2SDD theories. The comparison of calculated and experimental enthalpies of formation (298 K, \(\hbox {kcal mol}^{-1}\)) for these molecular species is given in Table 3. The heat of formation at 0 K is given by [20]:

$$\begin{aligned}&\Delta _fH^o (AxByHz,0 K) \nonumber \\&\quad = x \cdot \Delta _fH^o (A,0 K) + y \cdot \Delta _fH^o (B,0 K) + \end{aligned}$$
(7)
$$\begin{aligned}&\qquad +\, z \cdot \Delta _fH^o (H,0 K) - \sum D_o \end{aligned}$$
(8)

where the values of the atomic \(\Delta _fH^o\) (obtained at CODATA database [41]) were employed and \(\sum D_o\) is the total atomization energy. The absolute deviations were determined as the difference between the experimental and calculated results, \(\Delta E = E_\mathrm{Exp} - E_\mathrm{Theor}\). Our calculated results are much closer to experiment than the W2 theory, where available. The poor results were obtained in two cases, for fluorine and iodine molecules. In the first case, the pseudopotential description is inadequate, and additional studies are needed for building a new basis function sets. For iodine molecule, the W2 method, given by Eq. (1), proves inadequate to fully characterize its enthalpy of formation. However, our result is compared with those given by all-electron calculations employing basis sets of high quality given by Jorge et al. [42].

Table 3 Comparison of calculated and experimental enthalpies of formation (\(\Delta _fH^0_\mathrm{gas}\)(298 K), in \(\hbox {kcal mol}^{-1}\)) for molecular species
Full size table

3.4 Free energy profile for the reaction coordinate between propene + HX, X = F, \(\hbox {Cl}\), Br, or I

The W2SDD gas-phase and solution phase free energies for all the studied molecular systems are given in Table 4. The table also presents the harmonic frequencies of the transition states. From these values, it is possible to build the free energy profile for the reaction mechanisms of propene and hydrogen halides (HX, X = F, \(\hbox {C}\ell\), Br, or I) in the gas-phase and simulated apolar medium, respectively. The transition state energy shows a decrease from X = F to I, both in gas-phase and in a solvated medium. This is an indication that the more diffuse the halide electronic cloud, the more stable the TS. In other words, it stabilizes the activation energy. Therefore, the last reaction occurs much more readily than the hydrogen fluoride addition. When analyzing the most stable products, the same behavior can be noticed from fluorine to iodine. All mechanisms are described by only one step through the corresponding transition state (Fig. 2). The enthalpy barriers, for the addition of hydrogen chloride to propene in gas-phase, at the W2SDD theory, is equal to 33.39  kcal mol\(^{-1}\). This calculated result is close to the different calculations obtained by Firme [45], considering a second-order mechanism, 33.57; 34.96, and 42.04  kcal mol\(^{-1}\) at \(\omega\)B97XD/6-311G++(d,p), \(\omega\)B97XD/def2-TZVP, and MP2/6-311G++(d,p) levels of theory, respectively.

Fig. 2
figure 2

Molecular geometry for the transition state (TS). The distances in parentheses are in Å  for gas-phase and in cyclohexane solvent, respectively

Full size image
Table 4 W2SDD gas-phase and solution phase free energies (in atomic units)
Full size table

3.5 Electronic circular dichroism: \(\hbox {CH}_3\hbox {CH}_2\hbox {CHXCH}_3\), X = F, \(\hbox {C}\ell\), Br, or I

Electronic circular dichroism spectra were calculated from of vertical excitation energies and rotatory strengths considering the first 15 excited states. The results were obtained at TD-DFT/PBE0/5BAS level of theory. The 5BAS corresponds to the adapted augh-cc-pV5Z+2df basis sets along the SDD/RLC/ECP. The calculations of electronic excitations in solvated environments (in cyclohexane) have been taken into account using the integral equation formalism for the polarizable continuum model (IEF-PCM) and including the relaxation provoked by reorientation of the solvent molecules around the halobutane. It was also added the D3 version of Grimme dispersion with Becke–Johnson damping [46]. The spectra were simulated into an ECD curve using Gaussian band shapes with half-width at 0.5 eV, as described in Fig. 3a, b, in gas-phase and in cyclohexane solvent, respectively. All molecular systems have the same geometrical configuration. In the ECD measurement, the absorption of linearly polarized light is orientation-dependent. So, in Fig. 3a, the ECD signal in molecular systems containing F and \(\hbox {C}\ell\) atoms shows the same behavior. The same phenomenon occurs for systems containing bromine and iodine atoms. The TD-DFT electronic circular dichroism spectrum of 2-chlorobutane shows a signal inversion between gas-phase and in cyclohexane solvent. Therefore, the apolar solvent affects the electronic distribution of this molecule.

Fig. 3
figure 3

Theoretical ECD spectra of 2-halobutane in a gas-phase and b cyclohexane solvent. Dashed and continuum lines represent spectral lines and simulated spectra using Lorentzian lineshape with half-width equal to 50 nm, respectively

Full size image

To assess the solvent influence, eight cyclohexane molecules were positioned around the solute, in the vertices of what would be a cubic box, at approximately a similar distance from the central solute molecule, as can be seen in Fig. 4. First, the geometry of this system was optimized employing a UFF force field [47]. Then, the ECD spectra, Fig. 5, were calculated using PBE0/cc-pVDZ for the whole system (solute/solvent), with the same settings as the previous calculations. The spectrum for 2-chlorobutane showed a signal inversion as did the IEF-PCM results. This suggests that the solvent generates an intrinsic condition and interacts with 2-chlorobutane. Thus, the solvent treatment is necessary and the implicit treatment was able to simulate de ECD spectrum. Also a cubic box approach showed that the disposition of solvent molecules is different for 2-fluorobutane and 2-chlorobutane.

Fig. 4
figure 4

a Representation of the cubic solvation with the position of the solvent molecules around the solute, before the optimization. Molecular geometries of b 2-flurobutane and c 2-chlorobutane in cyclohexane solvent, respectively

Full size image
Fig. 5
figure 5

Theoretical ECD spectra of a 2-fluorobutane and b 2-chlorobutane in cyclohexane solvent, respectively

Full size image

A NCI analysis was performed to investigate the interaction between solvent molecules and the halide molecules in the microsolvated system. The resulting volumes for 2-fluorobutane and 2-chlorobutane can be seen in Fig. 6. For both the molecules, the interactions are mostly of the van der Walls type. For the 2-chlorobutane, the interactions concentrate around the apolar portion of the molecule, having less interaction with the chlorine atom. However, in the 2-fluorobutane case, a much larger interaction between the solvent molecules and the fluorine atom can be observed. The specific signal can be attributed to the amount of interaction with the fluorine atom. The solvent shell cubic box treatment and NCI analysis was effective to describe the system and help in understanding the solvent effect and the signal difference between compounds with the same chirality in a ECD spectrum.

Fig. 6
figure 6

Non-covalent interaction (NCI) analysis of a 2-fluorobutane and b 2-chlorobutane

Full size image

All calculations were carried out with the Gaussian16 computer program [27].

4 Conclusion

An effective core potential, including relativistic effects, was adapted to W2 theory. The implementation, referred to as W2SDD, proved to be cost-effective (accuracy/computational cost) for both proton affinity and enthalpy of formation for a selected group of molecules containing halide atoms. This approach exhibits a performance similar to the all-electron W2 theory and can be applied in molecular systems where the original theory is prohibitive because of computational limitations. The cubic box microsolvation treatment proved to be a simple and effective tool to understand the systems studied and their ECD spectra. Studies are being carried out to investigate the ECD band signal and its inversion with solvation, including the ONIOM methodology.