1 Introduction

There are large number of allotropes for sulfur, and many of them are composed of homo-cyclic compounds [1, 2]. For instance, tetrathietane (S4) is one of these homo-cyclic sulfur allotropes that has not yet been separated in a pure state. S4 was observed in mixtures with other sulfur homo-cyclic compounds and characterized through Raman [3, 4], infrared [5, 6], UV–Vis [6,7,8,9,10] and mass [11,12,13] spectroscopy methods. According to this fact the molecule of O2 is paramagnetic and that of O4 is not, Lewis showed that oxygen gas is a mixture of O2 and O4 four-membered homo-cyclic (oxozone) molecules that is called liquid oxygen state, in 1924 [14]. In 2006, X-ray crystallography of this mixture oxygen has been proved that O4 is instable and its structure changes to O8 [15]. On the other hand, the S4 and O4 cyclic structures in pure state are still unknown; but dications and dianions of group (VI) elements such as S42+, Se42+, Te42+ and S42− are prepared in pure form and characterized by X-ray diffraction [16,17,18,19,20,21]. In particular, the geometrical parameters of S4 isomers have been studied in several researches, theoretically [22,23,24,25,26] and the relative energies of Sn (n = 2, 3, 4, 5, 6, 7, 8, 12) homo-cyclic, linear and non-cyclic structures were calculated and comprised with experimental data [27, 28]. O4 cyclic structure has been investigated theoretically, i.e., thermodynamic and kinetic of O4 cyclic structure stability [29, 30], transition states and activation energies of the O4 ring dissociation [31, 32], the shallow minimum of O4 in their potential surface [33]. Recently, the local minima of O4 molecule and the intermolecular complexes (O2)2 in singlet and triplet states have been studied and calculation results demonstrate that the O4 molecule is stable in D2d symmetry structures [34].

Many pieces of important experimental and computational information were revealed and analyzed to A4 tetra homo-cyclic compounds in the above-mentioned publication, but still stability in planar structure and the origin of non-planarity of the molecules in the series did not investigate any more. The pseudo-Jahn–Teller effect (PJTE) for non-degenerate states is the only source of structural instabilities and symmetry breaking phenomenon (SBP) as well [35, 36]. Planar structure instability concerning SBP has been reported, and PJTE has been employed to explain the origin of ring bending, puckering and twisting in the cyclic systems based on ground and excited states coupling [37,38,39,40,41,42,43,44,45,46,47,48,49,50,51]. Other researches were devoted to quench the PJTE by sandwiching two rings, cations, anions up and down to the folded rings and restore planarity of non-planar structures [40, 52, 53]. Recent investigations of the PJTE have also extended to three-dimensional systems [54, 55].

2 Computational details

Geometry optimization and then subsequent frequency calculations have been done for the A4 (A = O, S, Se, Te, Po) homo-cyclic series at the second-order Moller–Plesset (MP2) [56,57,58] level of theory with the cc-pVQZ basis set [59,60,61] and for Te and Po the cc-pVQZ-PP basis set and corresponding pseudo-potential [62,63,64] were employed; the basis sets will be referred to as cc-pVQZ-(PP) hereafter; both the planar (D4h) and non-planar (D2d) geometries have been considered for the neutral species. Geometry optimizations and frequency computations have also been carried out for the D2d non-planar singly and doubly charged anions and cations; for the singly charged species, the unrestricted formalism is used. The state averaged-complete active space self-consistent field (SA-CASSCF) wave-function method [65,66,67] with the cc-pVQZ-(PP) basis set was used to compute the adiabatic potential energy surfaces (APESs) along the b2u bending normal coordinate for the neutral species. Several active spaces, i.e., CAS(2,4), CAS(6,6), CAS(6,7) and CAS(10,9), have been checked for SA-CASSCF calculation, but based on our calculation results, six electrons and seven active orbitals that composed CAS(6,7) active space significantly were better than others to apply in the SA-CASSCF computation of the ground and excited states in the under-consideration series. All computations were carried out with the MOLPRO 2015 [68] electronic structure package.

3 Results and discussion

3.1 The symmetry breaking phenomenon in the A4 series

The geometries of the planar (D4h) and non-planar (D2d) equilibrium structure were optimized at the MP2/cc-pVQZ-(PP) level of theory. The bond length, bond angle and dihedral angle for the A4 (A = O, S, Se, Te, Po) series in the planar and equilibrium configurations are provided in Table 1. The imaginary frequency and corresponding normal mode displacements in Cartesian Z coordinates are also presented.

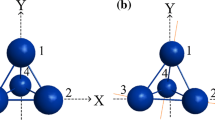
Table 1 Geometrical parameters of A4 (A = O, S, Se, Te, Po) compounds in planar and equilibrium configurations, the corresponding imaginary frequency and normal modes of planar instability in Cartesian Z
Full size table

An observed imaginary frequency along the b2u normal coordinate for the D4h configuration in A4 (A = O, S, Se, Te, Po) demonstrated that all of these homo-cyclic molecules are not stable in their planar configuration and subsequent bending in the A4 structures is caused by the PJTE. Therefore, the symmetry breaking phenomenon occurred, and their unstable planar configurations are bent from high symmetry (D4h) to the lower D2d stable symmetry equilibrium configuration (see Fig. 1).

Fig. 1
figure 1

Representative geometries for O4 in unstable high-symmetry planar configuration (D4h) and the stable bent (D2d) equilibrium geometry. Other A4 (A = O, S, Se, Te, Po) compounds adopt analogous geometries, see Table 1

Full size image

From Table 1, the bond of angle in the equilibrium configuration is increasing from O4 (87.83°) to Po4 (89.98°) and the dihedral angle value, which is the most illustrative parameter to show the bending in the A4 rings, also decreased from ± 10.22° to ± 1.40° from O4 to Po4. Regarding the imaginary frequency and normal mode values in Table 1, both these parameters are decreasing from the lighter molecule (O4) to the heavier (Po4) in the series.

A comparison between the geometrical parameters obtained with other expensive calculations would be of interest here. Based on Gadzhiev’s optimizations for a bent cyclic O4 (D2d symmetry) structure [34], the bond length at the CCSD(FC)/cc-pVTZ and CCSD(T)/cc-pCVTZ methods is ~ 1.45 Å, close to 1.48 Å. Moreover, the bond angles were reported to be 86.90° and 86.63° which are close to 87.83° as per the MP2/cc-pVQZ.

3.2 The pseudo-Jahn–Teller effect relevant to the A4 series

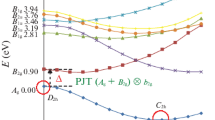
To explore the PJTE in the series of molecules, we need to examine the low-lying B2u excited states that contributes to the instability of the ground state. Therefore, the ground state (A1g) and six excited states (degenerate of Eg and Eu as well as non-degenerate B2g and B2u excited states) were computed in the planar configuration for each compound in the series. The MP2/cc-pVQZ planer geometries were used. Importantly, the corresponding energies along the coordinate of instability, i.e., \( b_{2u}\), were determined. The energy profiles along the \(Q_{{b_{2u} }}\) coordinate, referred to as the adiabatic potential energy surface (APES), are presented in Fig. 2.

Fig. 2
figure 2

The adiabatic potential energy surface (in eV) for the A4 (A = O, S, Se, Te, Po) homo-cyclic series along the b2u bending direction. Note the changing energy scale for A4 compounds. The normal modes were determined at the MP2/cc-pVQZ level of theory and the APES by CASSCF calculations (6,7)/cc-pVQZ-(PP) computations

Full size image

To help understand the nature of the low-lying electronic states, the SA-CASSCF wavefunction can be examined. Therefore, the main electronic configurations and their weight coefficients from CASSCF(6,7)/cc-pVQZ computations for the ground and six low-lying excited states in the planar configuration of the A4 (A = O, S, Se, Te, Po) compounds are presented in Table 2. The number inside the subscript brackets indicates that just one of the degenerate orbitals (eg and/or eu) contributes in the electronic configuration.

Table 2 Main electronic configurations and their coefficients of A4 (A = O, S, Se, Te, Po) compounds in the ground (A1g) and six low-lying degenerate and non-degenerate excited states
Full size table

Table 2 illustrates that the seven orbitals including 1a1g, 2eg, 2eu, 1b2g and 1b2u are contributing to the A4 series electronic configurations. The electronic configurations for O4 are significantly different as compared to other compounds in the series. However, Se4, Te4 and Po4 have similar electronic configurations in all state symmetries. S4 is similar to the heavier compounds (except for the degenerate Eu state). Moreover, the electronic configurations with the largest coefficient for the A1g ground and B2u excited states show clearly that an electron excitation from an orbital with b2u symmetry to an orbital with a1g symmetry occurred for all compounds. This fact rationalizes the logic of employing CAS (6,7) active space in the CASSCF calculation.

For all five A4 compounds, five excited states, i.e., degenerate Eg and Eu and non-degenerate B2g were located between the A1g ground and B2u excited states. The PJTE (1A1g + 1B2u) ⊗ b2u occurs for the A4 series due to mixing of the A1g ground and B2u excited states, and all other excited states lower than B2u do not contribute to the PJTE problem.

If the wavefunctions of the A1g ground and B2u excited states are denoted by \(|{\text{A}}_{{{\text{1g}}}}\) and \(|{\text{B}}_{{{\text{2u}}}}\), respectively, and \(2{\Delta }\) as the energy gap between them, then the instability condition for the ground state is given by

$$ {\Delta } < \left( {F_{{{\text{A}}_{{{\text{1g}}}} {\text{ B}}_{{{\text{2u}}}} }} } \right)^{2} /K_{0} $$
(1)

In Eq. (1), \(F_{{{\text{A}}_{{{\text{1g}}}} {\text{ B}}_{{{\text{2u}}}} }}\) is the linear vibronic coupling between the ground state and excited state

$$ F \equiv F_{{{\text{A}}_{{{\text{1g}}}} {\text{ B}}_{{{\text{2u}}}} }} = {\text{A}}_{{{\text{1g}}}} {|}\left( {\partial H/\partial Q} \right)_{0} {|}B_{{{\text{2u}}}} $$
(2)

\(H\) and \(Q\) are the Hamiltonian and the nuclear displacements, respectively. \(K_{0}\) is called the primary force constant and is given by

$$ K_{0} = {\text{A}}_{{{\text{1g}}}} {|}\left( {\partial^{2} H/\partial Q^{2} } \right)_{0} {\text{|A}}_{{{\text{1g}}}} $$
(3)

The vibronic coupling between these ground and excited states, which is denoted \( K\), the total force constant, is

$$ K = K_{0} - \left( {F_{{{\text{A}}_{{{\text{1g}}}} {\text{ B}}_{{{\text{2u}}}} }} } \right)^{2} /{\Delta } $$
(4)

Based on the instability condition and the subsequent bending, the curvature \(K\) of the APES, for A1g along \(Q_{{{\text{B}}_{{{\text{2u}}}} }}\), should be negative. Since the number of excited states in the system, in principles, is infinite, excited states with suitable symmetry that couple with the ground state in the direction of the \(b_{{{\text{2u}}}}\) instability can always be found. Therefore, corrections (designated as p) are used to suppress the effect of influence of relevant higher- and lower-energy excited states than effective excited state \((B_{{{\text{2u}}}} ) \) that are present in the system that are not in the \(Q\) direction. Thus, the primary force constant will reduce from \(K_{0}\) to \(K_{0} - p_{i}\), where \(p_{i} > 0\). To determine \(p_{i}\) values, the second-order perturbation theory correction to the energies of the two states (A1g and B2u) is indicated in a secular equation. The secular equation for the A4 homo-cyclic series is a 2 × 2 PJTE problem given by [35, 36]

$$ \left| {\begin{array}{*{20}c} {\frac{1}{2}\left( {K_{1} - p_{1} } \right)Q^{2} - \varepsilon } & {FQ} \\ {FQ} & {\frac{1}{2}\left( {K_{2} - p_{2} } \right)Q^{2} + {\Delta } - \varepsilon } \\ \end{array} } \right| = 0 $$
(5)

After solving the above equation, the roots are

$$ \varepsilon_{1,2} = \frac{1}{4}\left( {K_{1} - p_{1} + K_{2} - p_{2} } \right)Q^{2} + \frac{{\Delta }}{2} \pm \frac{1}{2}\sqrt {\left[ {\frac{1}{2}\left( {K_{1} - p_{1} - K_{2} + p_{2} } \right)Q^{2} - {\Delta }} \right]^{2} + 4F^{2} Q^{2} } $$
(6)

Figure 2 illustrates that the energy gap (\(2{\Delta }\)) between the ground state and the B2u excited state decreases from 6.12 eV in O4 to 2.29 eV in Po4. Additionally, the highest absolute value of the curvature in the ground state (i.e., instability of the ground state in the \(Q_{{b_{{{\text{2u}}}} }}\) direction) belongs to the O4 homo-cyclic compound and significantly decreases from O4 to Po4 an observation; which is in concordance with the variation of imaginary frequency along this mode, see Table 1. Moreover, the curvature of the B2u excited state (which mixes with the A1g ground state due to the PJTE (1A1g + 1B2u) ⊗ b2u decreases significantly from O4 to Po4.

3.3 Restoring planarity in A4 rings

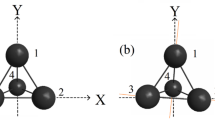
Planarization in the systems has been achieved without destroying their cyclic structure by adding or removing electrons [37]. To restore planarity in the series under-consideration, i.e., to quench the PJTE, the A4 (A = O, S, Se) molecules sandwiched two noble gas cations (NG+ = He+, Ne+, Ar+) above and below the plane A4 ring (σh plane), see Fig. 3. Density functional theory (DFT) with the B3LYP [67] functional and cc-pVTZ [59,60,61] basis set was employed for geometry optimization and harmonic frequency calculations for the (A4NG2)2+ complexes. The DFT computations were carried out with MOLPRO 2015, and the harmonic vibrational frequencies were computed numerically. The PJTE was suppressed in the (A4NG2)2+ complexes, and the presence of two NG+ ions forced the A4 system to be planar. On the other hand, if two H+ or Li+ cations were coordinated to the A4 bent system in the same manner as for NG+, the A4 ring did not return to planarity in the complexes.

Fig. 3
figure 3

The PJTE (1A1g + 1B2u) ⊗ b2u in the A4 (A = O, S, Se) series and effect suppressed by coordinating two noble gas cations (NG+ = He+, Ne+, Ar+) above and below the σh plane of the A4 (A = O, S, Se) rings

Full size image

Since coordinating the A4 ring by two noble gas cations was shown to quench the PJTE, i.e., restore the planarity of the ring, we considered the effects of adding (or removing) an electron or two electrons from A4 (A = O, S, Se, Te, Po). For geometrical parameters, imaginary frequencies and their normal displacements for the cations, anions and dianions of the A4 series, see Table 3.

Table 3 Geometrical parameters, imaginary frequencies (in cm−1) and normal modes along the b2u and distortion displacements of anion and dianion of the A4 (A = O, S, Se, Te, Po) compounds. All computations carried out at B3LYP/cc-pVTZ-(PP) level of theory
Full size table

From Table 3, it is seen that all calculated A4− anions show instability along similar \(b_{{{\text{2u}}}}\) normal displacement with same normal mode values as well as in their neutral A4 planar configurations (see Table 1), while imaginary frequency values in A4− are significantly less than relevant to A4, remarkably. Removing single or double electrons from homo-cyclic A4 systems (such as A4+ cations or A42+ dications) did not change their square structure as were in their neutral A4 planar configurations, while adding one or two electrons has distorted their structures to the new rhombus configuration.

The most interesting result of this calculation step is all dication A42+ forms are stable in their planar configuration. On the basis of restoring the planarity calculations, we can conclude that in both A42+ dication forms and (A4NG)2+ complexes ring planarity restore and were quenched the PJTE that triggers their bent configurations. Although in O4− and Po− anions geometry and frequency calculations were done, but adding an electron to other compounds in the under-consideration series makes them unstable in their hessian calculation.

3.4 Manipulation of the A4 series electronic configuration

To understand how removing two electrons from the A4 series affects their planarity, CASSCF (6,7) calculations have been done for the A42+ series. The results demonstrate that both electrons were removed from the b2u orbital (see Table 4). Moreover, there are no any electrons in the b2u orbital of the A1g ground state to contribute to the PJTE (1A1g + 1B2u) ⊗ b2u problem which is the reason for the instability in the A4 series planar configuration. In particular, the a1g−1 eu2 eu2 b2u1 electronic configuration which has the greatest weight coefficient for the A4 (A = S, Se, Te, Po) series in the B2u excited state has disappeared as given in Table 4 and Table 5 (although this electronic configuration remains for O42+, but its coefficient was reduced significantly in comparison with the neutral O4).

Table 4 Main electronic configurations and their coefficients of A42+ (A = O, S, Se, Te, Po) compounds in the ground (A1g) and B2u excited states
Full size table
Table 5 Main electronic configurations and their coefficients of the (S4H2)2+ and (S4He2)2+ complexes in the ground (A1g) and B2u excited states
Full size table

To explanation that how manipulation of A4 structure by sandwiching by two cations re-distorted the bent configuration of (A4NG)2+ complexes, electronic configuration calculations of (S4X2)2+ complexes (X = H, He) in the A1g ground and B2u excited states are presented in Table 5.

Table 5 illustrates that coordinating the S4 system with two H+ and He+ cations did not change the final occupancy of the (S4X2)2+ complexes. Additionally, sandwiching by two He+ cations occupies the a1g2 orbital in B2u excited state and the PJTE was perturbated. Likewise, coordinating the S4 bent ring with two Li+ cations occupies two UMOs of the S4 system. The frequency calculation for the (S4Li2)2+ complex shows that the number of imaginary frequencies increases to 4 in the S4 planar configuration. In other words, the coordination of lithium cations makes the S4 more unstable than its planar configuration.

Sandwiching two H+ to the S4 homo-cyclic system does not change the number of electrons and adds two protons to the (S4H2)2+ complex; thus, the PJTE is still active in (S4H2)2+ complex. From the above argument, one can rationalize that the manipulation of the electron configuration can only affect the SBP and the number protons do not contribute to causing the PJTE. B3LYP/cc-pVTZ optimizations and frequency calculations of S4 ring, S42+ dication, (S4H2)2+, and (S4He2)2+ complexes have been employed to figure out molecular orbital arrangements and electron transmission in Fig. 4. Due to removing two electrons from S4 ring in S42+ dication and sandwiching by two He+ cations in (S4He2)2+ complex, (4,7) and (8,7) active specie is replaced in CASSCF calculation of these systems, respectively.

Fig. 4
figure 4

Molecular orbital arrangements and electron excitation in S4, S42+, (S4H2)2+ and (S4H2)2+ complexes through B3LYP/cc-pVTZ optimizations and frequency calculations and CASSCF/cc-pVTZ computations [CAS(6,7) active specie are employed for both S4 and (S4H2)2+ systems and (4,7) and (8,7) were used for S42+ and (S4He2)2+, respectively]

Full size image

Figure 4 illustrates the similar molecular orbital arrangement and an electron excitation from the b2u orbital (HOMO) to the a1g orbital (LUMO + 1) in S4 neutral compound, and (S4H2)2+ complex (blue color line). Due to manipulation of the S4 electronic configuration in S42+ dication, and (S4He2)2+ complex, their electron excitations are completely different from S4 and (S4H2)2+. This fact shows that the PJTE (1A1g + 1B2u) ⊗ b2u for S4 neutral compound and (S4H2)2+ complex which effect quenched in S42+ dication, and (S4He2)2+ complex.

The PJTE occurs when a high occupied MO and a low unoccupied MO can interact under a geometrical distortion; the energy gap between the HOMO(b2u) and LUMO + 1(a1g) plays an important role in the PJTE (1A1g + 1B2u) ⊗ b2u. Therefore, the energy gap for both planar and bent configurations and the difference between them (in eV) for the A4 series are reported in Table 6.

Table 6 The energy gap between HOMO(b2u) and LUMO + 1(a1g) for planar (D4h) and bent (D2d) configurations and their difference for the A4 (A = O, S, Se, Te, Po) homo-cyclic series
Full size table

Due to the PJTE theorem, the increase in the energy gap between the HOMO(b2u) and LUMO + 1(a1g) results in the stabilization of the bent structure that undergoes a 5.35 − 6.27 eV increment in the series. While the PJTE is the only source of instability of the planar configuration, the stability increases from O to Po in the planar configuration of the four-membered homo-cyclic series. Indeed, we also can use the increment of the energy gap to show the PJTE reduction from O4 to Po4 in the A4 (A = O, S, Se, Te, Po) series.

4 Conclusions

Tetrathietane (S4) is a famous homo-cyclic sulfur allotrope that has not yet been separated in a pure state but characterized through different spectroscopy methods. Homo-cyclic structures of A4 (A = O, S, Se, Te, Po) are still unknown, but many of their dications are crystalized [16,17,18,19,20,21]. Toward understanding the structures of these four-member homo-cyclic compounds, geometry optimization and frequency computations have been carried out, and the results show that all A4 compounds under-consideration distort from the planar configurations (D4h symmetries) to bent equilibrium geometries with lower D2d symmetry. According to the adiabatic potential energy surfaces (APESs) along the \({Q}_{{b}_{2\mathrm{u}}}\) bending normal coordinate, the (1A1g + 1B2u) ⊗ b2u PJTE is the reason for the instability in the planar configuration. To restore planarity of the rings, two noble gas cations (NG+  = He+, Ne+, Ar+) were coordinated above and below the σh plane of the A4 (A = O, S, Se) ring and the (A4NG)2+ complexes became planar in their equilibrium configuration. Alternatively, removing one or two electrons from the rings (A4+, and A42+) quenched the PJTE that triggers their bending.