1 Introduction

Noncovalent interactions, dominant at large and intermediate intermolecular distances, are important in many fields of chemistry, physics and biology (see for instance Refs. [1–9]). They are typically represented as combination of various components emerging at various orders of the perturbation theory and defined as electrostatic (of either attractive or repulsive nature), exchange or size (of repulsive nature), induction and dispersion (of attractive nature) [10, 11]. When applicable, such representation allows to relate the most relevant interaction components with fundamental physical properties of the involved partners and then with their specific nature. For instance, due to the high value of the quadrupole moment of the benzene molecule (\(Q_{zz}= -8.45\) B) [12], the interaction of the \(\pi\) electron cloud of \({\text {C}}_{6}{\text {H}}_{6}\) with ions is predominantly electrostatic. Contrarily, when ions interact with molecules having a small quadrupole moment and a considerable molecular polarizability, as for instance the 1,3,5-trifluorobenzene [12–14], the intermolecular interaction is no longer dominated by the electrostatic term, but is mostly stabilized by dispersion and induction attraction [15]. This means that the presence of substituents in the aromatic ring of benzene can modulate, even at large distances, its ability to act as an electron donor [16]. In particular, the electron-donor capabilities of \({\text {C}}_{6}{\text {H}}_{6}\) are reversed when the 6 H atoms are substituted by 6 F atoms. The ability of the \(\pi\) cloud of \({\text {C}}_{6}{\text {H}}_{6}\) to act as an electron donor in the formation of hydrogen bonds has been widely investigated [17–20], while less information exists on the lone pair-\(\pi\) interaction, in spite of the important role played when the oxygen atom of water interacts with some aromatic residues in proteins [21]. The comparison of the behavior of \({\text {C}}_{6}{\text {H}}_{6}\) and \({\text {C}}_{6}{\text {F}}_{6}\) interacting with the same partners is particularly interesting because both molecules have quadrupole moments comparable in magnitude but opposite in sign. Moreover, they have comparable values of the polarizability [12–14] suggesting similar contributions of the dispersion and induction attraction when the aromatic molecules interact with the same partner. Accordingly, stabilization energies of the same order of magnitude can be expected for the \({\text {C}}_{6}{\text {H}}_{6}\)–\({\text {H}}_{2}\)O and the \({\text {C}}_{6}{\text {F}}_{6}\)–\({\text {H}}_{2}\)O aggregates. However, as the O lone pair points directly into the face of the \(\pi\) system in \({\text {C}}_{6}{\text {F}}_{6}\)–\({\text {H}}_{2}\)O, being the water dipole moment direction reversed respect to that of \({\text {C}}_{6}{\text {H}}_{6}\)–\({\text {H}}_{2}\)O, perturbative charge-transfer effects should play a different role in the two aggregates.

Unfortunately, an accurate characterization of the role played by the various interaction components is not easy, and the formulation of a proper energy function and of its dependence on the geometry of the molecular aggregate is a difficult task. Interaction energies are often calculated using the symmetry-adapted perturbation theory (SAPT) [22–24] and SAPT (DFT) [25, 26] methodologies, which allow a proper partition of the long-range intermolecular potential into basic components. However, weak interactions, as those involved in the aggregates that aromatic rings form with water molecules, must be calculated using very large basis sets. Indeed, previous studies [1, 27–31] have demonstrated that CCSD(T) calculations are required in order to obtain a reliable description of the interaction energies of the aggregates. As a consequence, in spite of the interest to describe the interaction in the complete configuration space, only the most stable structures are usually investigated. On the other hand, extensive molecular dynamics (MD) simulations can be performed only when a reliable formulation of the whole potential energy surface (PES) is available. The use of properly tested analytical functions is therefore crucial to describe the intermolecular interaction and the associated \(force field\) in the full space of configurations of various molecular systems and then to characterize their properties in different phases [32–34].

In the last years, some of us have proposed a semi-empirical potential model based on the separability of electrostatic (\(V_{{\text {el}}}\)), which include only permanent electric charge and/or permanent electric multipole contributions and nonelectrostatic (\(V_{{\text {nel}}}\)) interactions. The model defines the nonelectrostatic interaction by means of a sum of improved Lennard-Jones (ILJ) functions [35, 36], including only one additional parameter in comparison with the Lennard-Jones one. The ILJ function, depending on the balancing of positive (repulsion) and negative (attraction) contributions, properly accounts for the combination of size repulsion, dispersion and induction attraction, mixed terms and damping effects. In spite of the apparent simplicity of the model, namely the absence of explicit polarization and possibly charge-transfer effects, it has been applied successfully to describe both neutral and ionic intermolecular interactions in a variety of systems [37, 38]. In some test cases, the predicted data have been compared with results obtained from theoretical energy decomposition methods [39, 40]. In particular, an energy decomposition analysis according to Kitaura–Morokuma [41–43] (KM) scheme was used for the Na\(^{+}\)–benzene complex [39]. In our semi-empirical approach, all the contributions other than induction (polarization, charge transfer) are implicitly considered in the repulsion term (see for instance Ref. [44] and references therein). Therefore, the KM repulsion and charge-transfer terms were grouped and their sum was successfully compared with semi-empirical results. Although polarization and charge-transfer effects were not explicitly included in the formulation of the ILJ function, it was shown that their contribution could be corrected by fine-tuning of the β (see Sect. 3) parameter. In particular, in the Na\(^{+}\)–benzene case, a good agreement between the model predictions and ab initio results was found using low values of β. On the other hand, SAPT scheme analysis decomposition [22, 45] was applied to test the validity of the semi-empirical model for the halide–benzene clusters [40]. The obtained results showed that additional charge-transfer effects can be indirectly taken into account by changing the value of the \(\beta\) parameter in the ILJ function (see Sect. 3).

Recently, we have applied the potential model to investigate some benzene–hydrogen bond (\({\text {C}}_{6}{\text {H}}_{6}\)–H\(X\); \(X\) = O, S, N, C) interactions [46] considering the \({\text {H}}_{2}\)O–\({\text {C}}_{6}{\text {H}}_{6}\) [47], SH\(_{2}\)-\({\text {C}}_{6}{\text {H}}_{6}\) [46], NH\(_{3}\)–\({\text {C}}_{6}{\text {H}}_{6}\) [46] and CH\(_{4}\)–\({\text {C}}_{6}{\text {H}}_{6}\) [48] aggregates. A good agreement between the predicted values of both the minimum energy and the equilibrium geometry and available ab initio results was found [1, 27, 31, 49–52], indicating the validity of the model to describe the involved weak interactions, even when dispersion is the major source of attraction [48].

Due to the important role played by the interaction between aromatic molecules and water in determining the properties of biophysical systems [53], in the present investigation we are interested on the construction of a \({\text {C}}_{6}{\text {F}}_{6}\)–\({\text {H}}_{2}\)O force field, using a simple but reliable formulation and on its application to MD studies of the \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{n}\) (\(n= 1{\text {--}}6, 9{\text {--}}36\)) aggregates and of the solvation of \({\text {C}}_{6}{\text {F}}_{6}\). The paper has been organized as follows: In Sect. 2, the results of benchmark ab initio calculations are reported to check the validity of potential the model proposed. In Sect. 3, the steps followed to formulate the semi-empirical PES in effective atom–effective atom contributions are presented. MD results are shown in Sect. 4. Finally, concluding remarks are given in Sect. 5.

2 Benchmark ab initio calculations

In order to have reliable information from ab initio calculations of strength and range of both the out of plane lone pair-\(\pi\) and the in-plane hydrogen bond interactions between \({\text {H}}_{2}\)O and \({\text {C}}_{6}{\text {F}}_{6}\), three different approaches of the \({\text {H}}_{2}\)O molecule to \({\text {C}}_{6}{\text {F}}_{6}\) have been considered. Geometry optimizations have been computed at the MP2 [54, 55] level with the aug-cc-pVDZ basis set [56] using the Gaussian09 suite [57]. On the optimized structures, single-point coupled-cluster CCSD(T) [58–60] calculations using the aug-cc-pVTZ basis set [56] have been performed. The counterpoise correction [61, 62] for the basis set superposition error (BSSE) in the intermolecular interaction has been used. The equilibrium structures obtained are shown in Fig. 1.

Fig. 1
figure 1

Optimized structures of \({\text {C}}_{6}{\text {F}}_{6}\)–\({\text {H}}_{2}\)O from ab initio calculations at MP2/aug-cc-pVTZ level

Full size image

It has been found that the structure (a) has an interaction energy of −11.25 kJ mol−1 and that the distance from the O atom of \({\text {H}}_{2}\)O to the center of mass (c.m.) of \({\text {C}}_{6}{\text {F}}_{6}\) (\(R_{{\text {O--}}{\text {C}}_{6}{\text {F}}_{6}}\)) is equal to 2.9 Å. The (b) and (c) on plane structures have binding energies of −5.90 and −3.65 kJ mol−1, respectively, being the corresponding equilibrium \(R_{{\text {O--}}{\text {C}}_{6}{\text {F}}_{6}}\) distances equal to 5.34 and 5.87 Å, respectively.

Ab initio calculations at five different levels of theory, performed by Gallivan and Dougherty [63] for approaches of \({\text {H}}_{2}\)O along the C6 rotational axis of \({\text {C}}_{6}{\text {F}}_{6}\), report interaction energy values in the −6.99 to −16.32 kJ mol−1 range, associated with \(R_{{\text {O--}}{\text {C}}_{6}{\text {F}}_{6}}\) distances going from 2.94 to 3.50 Å. The value of −11.25 kJ mol−1 obtained here for structure (a) is in the range of energies calculated by Gallivan et al., while the value of \(R_{{\text {O}}{\text {--}}{\text {C}}_{6}{\text {F}}_{6}}= 2.9\) Å corresponds to the lower limit of the distances interval. The same value of 2.9 Å has been given by Amicangelo et al. [64] who reported BSSE-corrected energies estimated at the CCSD(T)/aug-cc-pVTZ level of calculation of −11.9 kJ mol−1 for an structure equivalent to the (a) one. On the other hand, matrix isolation infrared spectroscopy [64] provided experimental evidence of the most stable lone pair-\(\pi\) geometries in the \({\text {C}}_{6}{\text {F}}_{6}\)–\({\text {H}}_{2}\)O complex, being the peaks on the spectrum assigned to structures in which \({\text {H}}_{2}\)O is placed above the aromatic plane.

3 The formulation of the potential energy surface

An important purpose of the present investigation has been the formulation of the potential energy function with the chosen of effective parameters to describe, in the most simple and realistic way, the nonelectrostatic contribution of the \({\text {C}}_{6}{\text {F}}_{6}\)–\({\text {H}}_{2}\)O interaction by means of a sum of six O–C and six O–F effective energy terms. As anticipated, such formulation of the interaction is suitable to study the solvation phenomena of \({\text {C}}_{6}{\text {F}}_{6}\) by \({\text {H}}_{2}\)O. This target requires an accurate characterization of the interaction nature that, as indicated above, has been performed by assuming the total intermolecular potential energy (\(V_\mathrm{total}\)) decomposed in the so-called nonelectrostatic, \(V_{{\text {nel}}}\), and electrostatic, \(V_{{\text {el}}}\), partial contributions, which leads to an accurate intermolecular interaction partition [37, 47].

As a first step of the investigation, \(V_{{\text {nel}}}\) has been decomposed in molecule–aromatic bond contributions, by exploiting the decomposition of the \({\text {C}}_{6}{\text {F}}_{6}\) molecular polarizability, much higher than that of \({\text {H}}_{2}\)O, in twelve contributions associated with the bond polarizability tensors, each one having parallel and perpendicular components [65, 66],

$$\begin{aligned} V_{{\text {nel}}} =\sum _{i=1}^{6}V_{{\text {H}}_{2}{\text {O--}}({\text {CC}})_{i}}+ \sum _{i=1}^{6}V_{{\text {H}}_{2}{\text {O--}}({\text {CF}})_{i}} \end{aligned}$$
(1)

As usual, in our potential energy model, each term in Eq. 1 is described by means of the improved Lennard-Jones (ILJ) function [35, 36], given by,

$$\begin{aligned} V_{{\text {ILJ}}}(r,\gamma ) = \varepsilon (\gamma ) \left[ \frac{m}{n(r,\gamma )-m}\left( \frac{r_{0}(\gamma )}{r} \right) ^{n(r,\gamma )} - \frac{n(r,\gamma )}{n(r,\gamma )-m}\left( \frac{r_{0}(\gamma )}{r}\right) ^m \right] \end{aligned}$$
(2)

where \(r\) is the distance from two interaction centers, placed on the O atom of \({\text {H}}_{2}\)O and on the CC and the CF bonds, and \(\gamma\) is the angle that \(r\) forms with the bonds. The well depth, \(\varepsilon (\gamma )\), and the equilibrium distance, \(r_{0}(\gamma )\), for each interaction pair are modulated from the corresponding perpendicular (\(\varepsilon _{\perp }\), \(r_{0\perp }\)) and parallel (\(\varepsilon _{\parallel }\), \(r_{0\parallel }\)) values [46]). The values of such parameters can be anticipated by correlation formulas given in terms of the electronic polarizability (\(\alpha\)) of atoms, molecules and bond components. The procedure adopted has been described in detail elsewhere [67–69]. The \(n(r,\gamma )\) exponent, defining simultaneously the falloff of the molecule–bond repulsion and the strength of the attraction, is expressed as,

$$\begin{aligned} n(r,\gamma )= \beta +4.0 \left( \frac{r}{r_{0}(\gamma )}\right) ^2 \end{aligned}$$
(3)

where \(\beta\) is an adjustable parameter related to the hardness of the interacting partners, which adds flexibility to the potential energy function in comparison with the Lennard-Jones one [35]. The \(\beta\) parameter can be varied within a limited range of values, and preliminary estimates of \(\beta\) can be anticipated as suggested by Capitelli et al. [70]. The possibility of optimizing \(\beta\) not only adds flexibility to the potential function but also permits the combination of the ILJ function with different descriptions of the electrostatic interaction without modifying the relevant parameters of the potential energy function.

The initial guess parameters of the ILJ function are given in Table 1, and they can be tested and possibly improved by comparing the predictions from the model with ab initio results. However, the \(\varepsilon\) and \(r_{m}\) values can only be varied in limited ranges in order to maintain their relationship with the polarizability components and their physical meaning. As anticipated in Sect. 1, any marked disagreement between predictions and benchmark calculations [39, 40] would suggest the presence of additional interaction components that have not been taken into account in the model.

Table 1 Perpendicular and parallel molecule (effective atom)–bond components of the well depth (\(\varepsilon _{\perp }\), \(\varepsilon _{\parallel }\)) and of the equilibrium distances (\(r_{0\perp }\), \(r_{0\parallel }\)) for the two molecule–bond pairs
Full size table

The results obtained by combining \(V_{{\text {nel}}}\) using the standard value of \(\beta =8.5\) in Eq. 3 and the potential parameters of Table 1, with \(V_{{\text {el}}}\) calculated from the charge distribution computed with the ab initio methodology given in Sect. 2, indicate that while the interaction energy for the axial structure at equilibrium, equal to −12.81 kJ mol−1, is in a quite good agreement with the ab initio results of the previous section, those corresponding to the in-plane structures, equal to −2.22 and −2.23 kJ mol−1 for structures (b) and (c) (see Fig. 1), respectively, have lower energies. Due to the fact that the parameters given in the first row of Table 1 were also used to investigate the \({\text {C}}_{6}{\text {H}}_{6}\)–\({\text {H}}_{2}\)O interaction, such differences suggest that some additional charge-transfer and/or induction (polarization) effects, in comparison with those on \({\text {C}}_{6}{\text {H}}_{6}\)–\({\text {H}}_{2}\)O, are lacking in the formulation of the \({\text {C}}_{6}{\text {F}}_{6}\)–\({\text {H}}_{2}\)O potential. In fact, the environments created by \({\text {C}}_{6}{\text {H}}_{6}\) and \({\text {C}}_{6}{\text {F}}_{6}\) are different, originating different induction and charge-transfer stabilization effects when the aromatic molecules interact with water. In fact, the atomic charges on the \({\text {C}}_{6}{\text {F}}_{6}\)–\({\text {H}}_{2}\)O aggregates obtained with ab initio calculations differ from those of their isolated counterparts indicating that some charge transfer is occurring. Therefore, we have modified the formulation of the potential energy function to indirectly include the additional effects in \(V_{{\text {nel}}}\), adopting an effective atom(O)–effective atom (C and F) decomposition, more simple and easy to extend to the calculation of larger systems. These effects have been included by properly adjusting the potential parameters (see below). In this new formulation, \(V_{{\text {nel}}}\) described in Eq. 1 is replaced by

$$\begin{aligned} V_{{\text {nel}}} =\sum _{i=1}^{6}V_{{\text {O}}{\text {--}}({\text {C}})_{i}}+ \sum _{i=1}^{6}V_{{\text {O}}{\text {--}}({\text {F}})_{i}}, \end{aligned}$$
(4)

The corresponding O–C and O–F interaction contributions are formulated again by means of the ILJ functions (after removing the angular dependence). The corresponding parameters are given in Table 2.

Table 2 The well depth (\(\varepsilon\)) and the equilibrium distances (\(r_{0}\)) for the O–C and O–F pairs
Full size table

Values from Table 2 have been obtained starting, as usual, from the estimates performed exploiting the “effective” polarizability of C and F atoms bound in the \({\text {C}}_{6}{\text {F}}_{6}\) molecules and that of the water molecule. Note that polarizabilities of C and F atoms in the \({\text {C}}_{6}{\text {F}}_{6}\) molecule are considered as “effective” since they are different from those of the isolated gas phase atoms and because they must be compatible with both the global molecular polarizability and that associated with the C–F and C–C bond components.

\(V_{{\text {nel}}}\) has been paired with an alternative and more general representation of the electrostatic contribution, \(V_{{\text {el}}}\), that does not exhibit any unambiguous representation. As in our previous studies on ion-\({\text {C}}_{6}{\text {F}}_{6}\) systems [71], a total of eighteen point charges have been distributed on the \({\text {C}}_{6}{\text {F}}_{6}\) molecule frame (six placed on the F atoms and the remaining twelve at fixed distances from C atoms on both sides of the aromatic ring). Such distribution was chosen from the consideration that, asymptotically, \(V_{{\text {el}}}\) should correspond to the permanent dipole–permanent quadrupole interaction [71]. This leads to a charge of −0.12 a.u. on each F atom and to two positive charges of 0.06 a.u. separated by 0.137 Å on each C atom, placed on opposite sides of the aromatic plane. The electrostatic charge distribution of \({\text {H}}_{2}\)O, as in our previous studies, compatible with a dipole moment of 2.1 D (corresponding to that of each monomer on the water dimer) has been used to investigate the small clusters of the \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{n}\) type and a value of 2.4 D to study the solvation of hexafluorobenzene. This was motivated by the increase in the dipole moment of water when the number of involved molecules raises, possibly due to the increased role of polarization, charge-transfer and many body effects [72]. Moreover, the investigation of liquid water using the ILJ function demonstrated that a value of 2.4 D for the dipole moment of water, together with a value of 7.5 for the \(\beta\) parameter, allowed to reproduce the behavior of accurate radial distribution functions [73] and to predict mean potential energy and self-diffusion coefficients values in a good agreement with experimental results [36].

Benchmark CCSD(T) calculations on the three complexes (see Fig. 1) have been used again to fine-tune the estimated parameters in order to properly modulate the effect of the attraction in proximity of the equilibrium geometries. In particular, the \(r_{0}\) of the O–C pair has been increased of ca. 7 % while that of O–F has been decreased of ca. 5 %. It must be indicated that the corresponding value of \(\varepsilon\) has been modified consequently in order to maintain the same pair attraction contribution at long range [35]. With these new parameters, the calculated \({\text {C}}_{6}{\text {F}}_{6}\)–\({\text {H}}_{2}\)O interaction energies amount to −11.60, −5.88 and −3.87 kJ mol−1, for the (a), (b) and (c) structures, respectively. The internuclear distances have been found to be equal to 3.46 Å (structure a), 5.16 Å (structure b) and 5.78 Å (structure c). The predicted interaction energies are here in better agreement with the ab initio ones, with absolute differences equal to 0.35, 0.02 and 0.22 kJ mol−1 for the (a), (b) and (c) structures, respectively. The intermolecular distance for the equilibrium geometry of the most stable isomer is still overestimated with respect to the MP2 ones but in the range of other values found in the literature. The results so obtained here suggest that the potential model is able to describe structures corresponding to both axial and in-plane approaches of \({\text {H}}_{2}\)O–\({\text {C}}_{6}{\text {F}}_{6}\) in good agreement with highly correlated ab initio results and is then suitable to perform extensive MD simulations [63].

4 Molecular dynamics simulations

The \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{n}\) (\(n= 1\)–6, 9–36) small aggregates and the solvation of \({\text {C}}_{6}{\text {F}}_{6}\) surrounded by 400 \({\text {H}}_{2}\)O molecules are investigated by means of MD simulations. For the small aggregates, MD simulations have been performed in gas phase considering a NVE ensemble of particles, while for the solvation of hexafluorobenzene NVE simulations have been performed only to thermalize the system. The solvation of the system, once thermalized at different values of the temperature and at 1 bar of pressure, has been investigated using an isothermal–isobaric NpT ensemble, where the simulation cell can freely expand or contract. In this case, temperature and pressure are controlled using the Nosé–Hoover method [74] and by applying the Berendsen algorithm [75], respectively. Cubic periodic boundary conditions have been applied, and a cutoff radius of 11.5 Å has been considered in order to speed up the computation of the nonbonding interactions.

The equilibration of the systems to achieve the desired values of \(T\) and \(p\) has been performed for 0.3 ns, and the corresponding results have been excluded of the statistics carried out at the end of the simulation. Simulations along 5 ns (excluding equilibration) have been performed in all cases using a 0.001 ps time step. The electrostatic energy in the solvation process has been calculated by applying the Ewald sum [76], and in all the simulations, \({\text {C}}_{6}{\text {F}}_{6}\) has been kept rigid while the OH stretching and the HOH bending motions of water molecules have been allowed. For this purpose, an energy intramolecular term, expressed by means of harmonic functional expressions, has been added to the potential energy formulation [77]. MD calculations have been performed using the DL_POLY [78] program, where the subroutines of the potential and its derivatives have been implemented.

4.1 The \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{1{\text {--}}6}\) aggregates

The \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{1{\text {--}}6}\) equilibrium energies can be estimated by performing MD simulations at low values of the temperature, \(T\). As a matter of fact, an estimation of the equilibrium energy (without any contribution of kinetic energy and comparable with directly calculated binding energies), \(V_\mathrm{eq}\), can be obtained [79] from a linear extrapolation to \(T = 0\) K of the mean value of the configuration energy \(\overline{E_{\text {cfg}}}\) (i.e., the averaged potential energy of all the configurations attained along the simulation time) calculated at several (low) temperatures. Under these conditions, when no isomerization occurs, \(\overline{E_{\text {cfg}}}\) varies linearly with \(T\). The process of running consecutive MD simulations at decreasing temperatures can be regarded as a simulated annealing minimization [80]. However, given that this procedure can run into problems whenever the thermal energy is of the order of magnitude of the isomerization energy barriers, we judged better to extrapolate to 0 K the values of \(\overline{E_{\text {cfg}}}\), rather than running MD trajectories below 5 K.

For the smaller aggregate, \({\text {C}}_{6}{\text {F}}_{6}\)–\({\text {H}}_{2}\)O, the mean configuration energy values are represented as a function of the temperature in Fig. 2 (panel a), where the extrapolated value of the energy at \(T= 0\) K is also indicated. The obtained value of \(V_{\text {eq}}\), equal to −11.56 kJ mol−1, is in agreement with the value of −11.60 kJ mol−1 obtained from the static calculations performed at different values of the intermolecular distance (see the previous section). By increasing \(T\) it has been observed that the aggregate tends to dissociate at temperatures close to 80 K.

Fig. 2
figure 2

Mean value of the configuration energy, \(\overline{E_{\text {cfg}}}\), as a function of the temperature for the small \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{n=1{\text {--}}6}\) aggregates

Full size image

For the other aggregates, different initial configurations have been considered. At first, MD simulations have been performed at increasing values of \(T\) in order to allow isomerization when the chosen initial configuration is far away from the most stable structure of the aggregate. For instance, two different stable isomers have been detected for \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{2}\), one of them with the two water molecules placed on the same side of the aromatic plane (2\(\mid\)0 isomer), while in the second one the water molecules are placed in different sides of the \({\text {C}}_{6}{\text {F}}_{6}\) plane (1\(\mid\)1 isomer). Due to the fact that the interaction between water molecules, for several relative configurations, is stronger than the \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{2}\) one, the most stable isomer is the 2\(\mid\)0 one. In fact, the presence of the two \({\text {H}}_{2}\)O molecules on the same side of the aromatic plane favors the stabilization of the aggregate, reducing the dissociation probability. Moreover, if the initial configuration is the less stable, the aggregate remains in such configuration unless an isomerization process occurs, which requires an increase in the temperature. This means that, in spite of the fact that only the five lower temperatures are used in the linear extrapolation, a study to a wider range of \(T\) is needed. However, since different isomers have similar energies, the isomerization process often occurs at low temperatures.

Bearing in mind that our potential model predicts a \({\text {H}}_{2}\)O–\({\text {H}}_{2}\)O interaction energy of about 22 kJ mol−1 (see Ref. [72] and references therein), the higher stability of isomers having the water molecules placed on the same side of the aromatic plane is not surprising. As a matter of fact, the most stable isomers for \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{2{\text {--}}6}\) are those having all the \({\text {H}}_{2}\)O molecules grouped on the same side of the aromatic plane. The linear extrapolations of \(\overline{E_{\text {cfg}}}\) to \(T= 0\) K for the \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{2{\text {--}}6}\) aggregates are shown in Fig. 2 (panel b–f). As it can be seen in Fig. 2, for \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{2}\) (panel b) and \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{4}\) (panel d), \(\overline{E_{\text {cfg}}}\) varies linearly with \(T\) in the investigated range of temperatures, indicating the absence of isomerizations. On the contrary, the linearity of \(\overline{E_{\text {cfg}}}\) is disrupted for \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{3}\) (panel c) at temperatures about 40 K, which is indicative that such cluster tends to isomerize. By further increasing \(T\), \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{3}\) dissociates into \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{2}+{\text {H}}_{2}\)O.

MD simulations show that in the \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{1-5}\) aggregates, the \({\text {H}}_{2}\)O molecules tend to be grouped in a similar way as they do en pure water clusters at equilibrium [5, 72]. In particular, for \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{5}\), the five molecules of \({\text {H}}_{2}\)O are grouped through H-bonds forming a pentagon, which is placed parallel to the aromatic ring. This configuration is very stable, and in the range of temperatures investigated, no tendency to isomerize nor to dissociate has been observed. The variation of \(\overline{E_{\mathrm{cfg}}}\) with \(T\) for the \({\text {C}}_{6}{\text {F}}_{6}{\text {--}}({\text {H}}_{2}{\text {O}})_{5}\) and the \({\text {C}}_{6}{\text {F}}_{6}{\text {--}}({\text {H}}_{2}{\text {O}})_{6}\) aggregates is shown in panels (e) and (f) of Fig. 2, respectively.

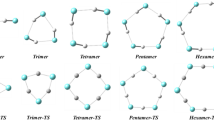
In general, the inspection of \(E_{\text {cfg}}\) at the different steps along the trajectory allows to see that the estimated value of \(V_{\text {eq}}\) is very close to the minimum value attained in the simulation. Accordingly, the geometry associated with the step with the lower value of \(E_{\text {cfg}}\) (more negative) should be very similar to the equilibrium one. Snapshots of these equilibrium-like structures are given in Fig. 3.

Fig. 3
figure 3

Predicted minimum structures for the \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{1{\text {--}}6}\) aggregates

Full size image

Additional analysis on the MD trajectories has been performed, focusing on the spatial disposition of the \({\text {H}}_{2}\)O molecules around \({\text {C}}_{6}{\text {F}}_{6}\). In order to do this, a three-dimensional probability density of the \({\text {H}}_{2}\)O molecules is constructed by transforming the outcome of the MD trajectories into spherical coordinates in an inertial reference frame. Probability isosurfaces (isovalue 0.5) of the \({\text {H}}_{2}\)O molecules in the aggregate illustrating the solvation shell are shown in Fig. 4 for \({\text {C}}_{6}{\text {F}}_{6}\)–\(({\text {H}}_{2}{\text {O}})_{4}\), \({\text {C}}_{6}{\text {F}}_{6}\)–\(({\text {H}}_{2}{\text {O}})_{5}\) and \({\text {C}}_{6}{\text {F}}_{6}\)–\(({\text {H}}_{2}{\text {O}})_{6}\) in the top, medium and lower panels, respectively. The solvent probability density is plotted using the VMD visualization software using the VolMap [81] tool included in the package.

Fig. 4
figure 4

Two views of the isosurface (isovalue 0.5) plot of the \({\text {H}}_{2}\)O probability density in the \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{4}\) (top panel), \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{5}\) (medium panel) and \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{6}\) (lower panel) aggregates. Results correspond to MD simulations at a temperature of 20 K

Full size image

As it can be observed in Fig. 4, only the \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{5}\) aggregate shows a probability density for the \({\text {H}}_{2}\)O molecules equal to zero at the center of the aromatic ring, as a consequence of the high stability of the aggregate in the conformation in which the five \({\text {H}}_{2}\)O are grouped forming a pentagonal structure. In spite of the high stability of \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{5}\), it has been observed that when a sixth molecule of \({\text {H}}_{2}\)O is added, the new molecule prefers to occupy positions close to the other ones, breaking the pentagonal configuration better than occupying positions on the opposite side of the aromatic ring (see Figs. 3, 4).

4.2 The formation of the \({\text {C}}_{6}{\text {F}}_{6}\) first solvation shell

By increasing the number of \({\text {H}}_{2}\)O molecules in the aggregates, a strong competition between \({\text {H}}_{2}\)O–\({\text {H}}_{2}\)O and \({\text {C}}_{6}{\text {F}}_{6}\)–\({\text {H}}_{2}\)O interactions is observed. As a matter of fact, in the previous section it has been shown that the symmetry of the distribution of the five molecules of water around \({\text {C}}_{6}{\text {F}}_{6}\) observed in the \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{5}\) aggregate is broken in \({\text {C}}_{6}{\text {F}}_{6}\)–\(({\text {H}}_{2}{\text {O}})_{6}\). This effect can be explained considering that one of the water molecules takes part in the formation of three hydrogen bonds.

In general, it has been observed that in the \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{n}\) aggregates, the \({\text {H}}_{2}\)O molecules often form a sort of cluster that then interacts with \({\text {C}}_{6}{\text {F}}_{6}\). This behavior has been clearly emphasized by increasing the number of water molecules, as can be observed in Fig. 5, where the probability isosurfaces (isovalue 0.5) of the \({\text {H}}_{2}\)O molecules in the \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{9}\) and \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{18}\) aggregates obtained at 20 K are shown in the left- and right-hand sides, respectively. In this figure, the tendency of the water molecules to form groups can be observed, being this behavior independent of the initial configuration considered. Such tendency, however, which also depends on \(T\), diminishes when the number of water molecules is high enough to complete the first solvation shell.

Fig. 5
figure 5

Isosurface (isovalue 0.5) plot of the \({\text {H}}_{2}\)O probability density in the \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{9}\) (left-hand side) and \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{18}\) (right-hand side). Results correspond to MD simulations at a temperature of 20 K

Full size image

By further increasing the number of water molecules up to 30, it has been evidenced that the most stable configuration is the one having all the water molecules in the same side of the aromatic ring. However, since the number of isomers having similar energies increases with the number of molecules of \({\text {H}}_{2}\)O, isomerizations to less stable configurations are observed even at low temperatures. For instance, for aggregates containing 30 \({\text {H}}_{2}\)O molecules, isomers forming an incomplete first solvation shell alternate with others having all the water molecules on the same side of the aromatic plane. Typical configurations of these structures are shown in Fig. 6. The one having all the water molecules on the same side of the aromatic ring is 0.5 eV stabler than the other.

Fig. 6
figure 6

Typical configurations of \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{30}\) attained along trajectories performed at 60 K of temperature

Full size image

The tendency to form incomplete solvation shells has also been observed for those aggregates containing 32 and 34 molecules of water. For \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{32}\) and \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{34}\), in spite of the fact that, often, only two and four molecules of water, respectively, are placed in the second solvation shell surrounding the first one, isomers with all the molecules placed on the same side of the aromatic ring are also observed. MD simulations show that the first solvation shell remains compact only when a minimum of 36 molecules of \({\text {H}}_{2}\)O surround \({\text {C}}_{6}{\text {F}}_{6}\). Three- and two-dimensional graphics of the probability density of the \({\text {H}}_{2}\)O molecules in the \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{36}\) aggregate are shown in Fig. 7. For this aggregate, 30 molecules tend to occupy positions in the first solvation shell, surrounding \({\text {C}}_{6}{\text {F}}_{6}\), while the remaining ones occupy positions in the second solvation shell.

Fig. 7
figure 7

Three-dimensional (left-hand side) and two-dimensional (right-hand side) isosurface (isovalue 0.5) plot of the \({\text {H}}_{2}\)O probability density in the \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{36}\) aggregate. Results correspond to MD simulations at a temperature of 20 K

Full size image

4.3 The solvation of \({\text {C}}_{6}{\text {F}}_{6}\)

The solvation of \({\text {C}}_{6}{\text {F}}_{6}\) has been studied by surrounding it with 400 molecules of \({\text {H}}_{2}\)O. Two representative initial configurations of the system have been considered, in one of them the 400 molecules of \({\text {H}}_{2}\)O have been placed on the same side of the aromatic ring, while in the other one the 400 molecules of water surround \({\text {C}}_{6}{\text {F}}_{6}\). MD simulations using the NpT ensemble have been performed at a pressure of 1 bar and at temperature values ranging from 275 to 350 K. The analysis of the results indicates that they are not affected by the initial configuration considered.

Due to the large size and the particular charge distribution of \({\text {C}}_{6}{\text {F}}_{6}\), the radial distribution functions should show not completely defined peaks. In fact, water molecules interact with \({\text {C}}_{6}{\text {F}}_{6}\) via two different mechanisms. In one of them, the lone pair of the O atom interacts with the positive charges placed on the C atoms of \({\text {C}}_{6}{\text {F}}_{6}\) (perpendicular approaches), while in the other the H atoms tend to form H-bonds with the aromatic molecule (equatorial approaches). Because of that, in the first solvation shell, those molecules approaching perpendicularly \({\text {C}}_{6}{\text {F}}_{6}\) are placed at shorter distances to the center of mass of \({\text {C}}_{6}{\text {F}}_{6}\) than those corresponding to equatorial approaches. This behavior, as can be seen in Fig. 8, is reflected in the \({\text {C}}_{6}{\text {F}}_{6}\)–O radial distribution function [RDF(\({\text {C}}_{6}{\text {F}}_{6}\)–O)]. The first double peak, centered at 4.225 Å and at 5.125 Å, is due to the molecules occupying mainly positions around the symmetry axis of the aromatic molecule and to the ones occupying equatorial positions, respectively. Obviously, the values of R where the peaks are centered cannot be considered as the actual values for axial and equatorial approaches, because intermediate approaches are also averaged in the RDF. This fact originates that the calculated first and second peaks appear at larger and shorter distances, respectively, than pure axial and equatorial approaches. Allesch et al. [53] define axial and equatorial regions considering limited regions (equatorial: 20° on both sides of the aromatic plane and axial: 20° around the C\(_{6}\) symmetry axis of \({\text {C}}_{6}{\text {F}}_{6}\)) and find peaks centered at 3.6 and 5.5 Å for axial and equatorial structures. Bearing in mind the above considerations, our results seem to be in agreement with those of Allesch et al. [53]. In spite of the fact that the double peak remains, as usually happens in the second solvation shell, it is less structured than the first one. According to the previous observations, the radial integration number does not show a clear plateau, being the coordination number not sharply defined (see Fig. 8). The coordination number has been calculated by integrating the two peaks of the RDF function assigned to the first solvation shell (\(R\) values from 3.5 to 6.5 Å). The result of the integration, equal to 30, is in good agreement with the results obtained in the previous section when the formation of the first solvation shell has been analyzed.

Fig. 8
figure 8

Radial distribution function RDF (\({\text {C}}_{6}{\text {F}}_{6}\)–O) representing the structure of the of the first and second solvation shells, derived from MD simulations performed at 300 K of temperature and 1 bar of pressure. The coordination number \(n(R)\), represented with a bold line, is also derived

Full size image

5 Conclusions

The evolution from the formation of small clusters \({\text {C}}_{6}{\text {F}}_{6}\)–(\({\text {H}}_{2}{\text {O}})_{n}\) to the solvation of \({\text {C}}_{6}{\text {F}}_{6}\) has been investigated by means of MD simulations. The intermolecular interaction energy has been constructed by assuming the separability of electrostatic and nonelectrostatic energies. The electrostatic energy reproduces the quadrupole–dipole interaction at large distances. On the other hand, the nonelectrostatic energy has been formulated using the ILJ function to obtain a representation of the force field suitable for MD simulations. In summary, for the small aggregates the hydration structure has been investigated using a NVE ensemble of particles, in which the total energy is conserved along the simulation. The binding energy of the small aggregates has been estimated by performing MD simulations at several low temperatures and extrapolating the values of the configuration (potential) energy to \(T = 0\,\text {K}\). A high tendency of the water molecules to form clusters that interact with \({\text {C}}_{6}{\text {F}}_{6}\) has been observed for the small aggregates. As a matter of fact, it has been found that the first solvation shell is only closed when the number of water molecules exceeds those needed to complete it. This fact evidences a high competition between \({\text {C}}_{6}{\text {F}}_{6}\)–\({\text {H}}_{2}\)O and \({\text {H}}_{2}\)O–\({\text {H}}_{2}\)O interactions. By solvating \({\text {C}}_{6}{\text {F}}_{6}\) by an ensemble of 400 water molecules, the radial distribution functions, obtained using a NpT ensemble of particles, have allowed to see the existence of two regions (axial and equatorial) in the first and second solvation shells. In spite of the fact that the radial integration number does not show a clear plateau and that the coordination number is not sharply defined, the comparison of the results of the solvated system with those for small aggregates allows to estimate a coordination number equal to 30.