Abstract
Based on the complex case, we present for commutative real Banach algebras \(\mathcal {R}\) several non-algebraic versions of the Arens-Royden theorem and the Shilov idempotent theorem. It will be shown that the Gelfand transform induces a group isomorphism of \(\mathcal {R}^{-1}/\exp \mathcal {R}\) onto \(C(X(\mathcal {R}), \tau )^{-1}/ \exp C(X(\mathcal {R}), \tau )\), where \(C(X(\mathcal {R}),\tau )\) is the algebra of \(\tau \)-symmetric complex-valued functions on the character space \(X(\mathcal {R} )\) of \(\mathcal {R}\) for some specific involution \(\tau \). We will also prove that for any \(\tau \)-symmetric closed-open subset of \(X(\mathcal {R})\) there is an idempotent e in \(\mathcal {R}\) whose Gelfand transform coincides with the characteristic function of E. We apply the real Arens-Royden theorem to show that the Bézout equation \(uf+vg=1\) has a solution in \(\mathcal {R}\) with u invertible if (and only if) it has such a solution in \(C(X(\mathcal {R}), \tau )\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let A be a commutative unital complex Banach algebra and denote by M(A) its spectrum; that is the set of all (non-zero) multiplicative \(\mathbb {C}\)-linear functionals on A. The classical Arens-Royden theorem reads as follows (see for example [1, 7]):
Theorem 0.1
(Arens-Royden)
- (1)
Suppose that for some \(f\in A\) the Gelfand transform \(\widehat{f}\) of f has a continuous logarithm on M(A). Then \(f=e^g\) for some \(g\in A\).
- (2)
Let \(f\in C(M(A),\mathbb {C})\). Suppose that \(f\not = 0\) on M(A). Then there exists \(g\in A^{-1}\) such that \(f/\widehat{g}\) has a continuous logarithm on M(A).
- (3)
The Gelfand transform induces a group isomorphism between the quotient groups \(A^{-1}/\exp A\) and \(C(M(A),\mathbb {C})^{-1}/ \exp C(M(A),\mathbb {C})\).
We are aware of only a couple of publications dealing with the extension of this theorem to real Banach algebras (see for example [2, 6]). The statements and proofs given there use some deep algebraic/topological terminology. Since these notions are difficult to understand by analysts and need a very profound background, we would like to present several, hopefully new, non-algebraic versions of the real variant of the Arens-Royden theorem. The idea is to deduce the real version via the complexification of the real Banach algebra \(\mathcal {R}\) and to use the property that the algebra \(\hat{\mathcal {R}}\) of Gelfand transforms of \(\mathcal {R}\) is a subalgebra of the algebra
of \(\tau \)-symmetric continuous functions for some specific involution on the character space \(X(\mathcal {R})\) of all real homomorphisms between \(\mathcal {R}\) and the real algebra \(^ \mathbb {R}{\mathbb {C}}\). Using the same methods, we shall also give a version of Shilov’s idempotent theorem for real Banach algebras.
2 Complexification of real Banach algebras
For the reader’s convenience, and mostly for notational reasons, we recall in this section the most fundamental results on real Banach algebras. All algebras considered are assumed to be commutative. Detailed proofs are presented for instance in the encyclopedic monograph [10].
If \(A=(A, +, \times ,\bullet _{\scriptscriptstyle s})\) is an algebra over \(\mathbb {C}\), then, by restricting the scalar multiplication \(\bullet \) to \( \mathbb {R}\), we obtain a real algebra, denoted by \(^{ \mathbb {R}}A\) or \(A_ \mathbb {R}\). The most easiest one is \(^ \mathbb {R}\mathbb {C}\), the \( \mathbb {R}\)-vector space/respectively algebra of complex numbers endowed with the real scalar product
We call \(A_ \mathbb {R}\) the real-ization of A. Here is now the well-known procedure to construct a complex algebra from a given real algebra (see for instance [5, 9, 11]).
Lemma 1.1
Let \(A=(A,+,\times ,{\mathop {\bullet }\limits _{\scriptscriptstyle \mathbb {R}}^{}}) \) be a real algebra. The complexification \(A_\mathbb {C}\) of A is the set \(A\times A\) endowed with the algebraic operations \(\oplus :A\times A\rightarrow A\), \(\otimes :A\times A\rightarrow A\) and \({\mathop {\bullet }\limits _{\scriptscriptstyle \mathbb {C}}^{}}:\mathbb {C}\times A\rightarrow A\), defined as follows: for \(\alpha , \beta \in \mathbb {R}\) and \(x,x',y,y'\in A\) let
Then,
- (1)
\(A_\mathbb {C}:=(A_\mathbb {C}, \oplus , \otimes , {\mathop {\bullet }\limits _{\scriptscriptstyle \mathbb {C}}^{}})\) is a complex algebra.
- (2)
The map \(\iota : {\left\{ \begin{array}{ll} A &{}\rightarrow A_\mathbb {C}\\ x&{}\mapsto (x,0)\end{array}\right. }\) is an \( \mathbb {R}\)-linear embedding of A into \(A_\mathbb {C}\).
- (3)
If A is a unital algebra with identity \({\varvec{1}}\), then so is \(A_\mathbb {C}\) with identity \((\varvec{1},0)\).
- (4)
In that case, \(x\in A\) is invertible in A if and only if (x, 0) is invertible in \(A_\mathbb {C}\).
- (5)
If \(\{x_\lambda :\lambda \in \Lambda \}\) is a basis for the real vector space A, then \(\{(x_\lambda ,0):\lambda \in \Lambda \}\) is such a basis for the complex vector space \(A_\mathbb {C}\).
Theorem 1.2
Let \((A,||\cdot ||)\) be a real Banach algebra. For \((u,v)\in A_\mathbb {C}\), let
and

Then
- (1)
\((A_\mathbb {C}, |\cdot |)\) is a real Banach algebra.
- (2)
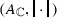 is a completely normed, complex algebra.
is a completely normed, complex algebra. - (3)
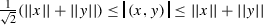 for any \((x,y)\in A_\mathbb {C}\).
for any \((x,y)\in A_\mathbb {C}\). - (4)
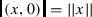 for each \(x\in A\).
for each \(x\in A\). - (5)
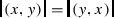 and
and 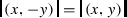 for every \(x,y\in A\).
for every \(x,y\in A\). - (6)
Any other norm \(|||\cdot |||\) for which \((A_\mathbb {C},|||\cdot |||)\) is a completely normed algebra satisfying (4), is equivalent with
 .
.
An important class of real algebras is given in the following example (see [8]). They play a fundamental role in the Gelfand theory of real Banach algebras.
Example 1.3
Let \(\tau \) be a continuous involution (that is \(\tau \circ \tau =\mathrm{id}\)) on the compact Hausdorff space X. Then the space
of all \(\tau \)-symmetric complex-valued continuous functions on X is a real Banach algebra when endowed with the supremum norm. Its complexification

is isomorphic and homeomorphic to \((C(X,\mathbb {C}), +, \times , \bullet _s,||\cdot ||_\infty )\), as is seen by using for each \(f\in C(X,\mathbb {C})\) the decomposition \(f=u_f+iv_f\), where
Proposition 1.4
Let \(\mathcal {R}\) be a commutative unital Banach algebra over \( \mathbb {R}\) and \(A=\mathcal {R}_\mathbb {C}\) its complexification. Let \(X(\mathcal {R})\) be the set of non-zero real algebra homomorphisms \(\chi : \mathcal {R}\rightarrow {^ \mathbb {R}\mathbb {C}}\) of \(\mathcal {R}\). Then, when endowed with the weak*-topology, \(X(\mathcal {R})\) is a compact Hausdorff space homeomorphic to M(A).
Proof
Consider the bijection
and its inversion which is given by \(\chi (f):=m(f,0)\). Since \(X(\mathcal {R})\) and M(A) are endowed with their associated Gelfand topologies, \(\chi _\lambda \rightarrow \chi \) implies \(\chi _\lambda (f)\rightarrow \chi (f)\) for every \(f\in \mathcal {R}\). Hence, for every \(f,g\in \mathcal {R}\),
We conclude that \(\Xi \) is a continuous map. The compactness of \(X(\mathcal {R})\) and the Hausdorff property of M(A) now imply that \(\Xi \) is a homeomorphism. \(\square \)
We shall call \(\Xi \) the canonical identification homeomorphism.
The main result on the relations between the maximal ideals and characters of a real Banach algebra (and which is a consequence of the Gelfand-Mazur theorem), reads as follows:
Theorem 1.5
Let \(\mathcal {R}\) be a commutative, unital Banach algebra over \( \mathbb {R}\). Then the following assertions hold:
- (1)
The kernel \(\ker \chi \) of any character \(\chi \in X(\mathcal {R})\) is a maximal ideal.
- (2)
Every maximal ideal M in \(\mathcal {R}\) of codimension 2 is the kernel of exactly two characters on \(\mathcal {R}\); namely some \(\chi \) and its complex conjugate \(\overline{\chi }\) defined by:
$$\begin{aligned} \overline{\chi }(f)=\overline{\chi (f)}. \end{aligned}$$ - (3)
Every maximal ideal M in \(\mathcal {R}\) of codimension 1 is the kernel of exactly one character \(\chi \) on \(\mathcal {R}\). In that case (and only in that case), \(\chi \in M_ \mathbb {R}(\mathcal {R})\), the set of nonzero real-valued multiplicative \( \mathbb {R}\)-linear functionals on \(\mathcal {R}\).
- (4)
Any maximal ideal M in \(\mathcal {R}\) either has codimension 1 or 2.
- (5)
\(X(\mathcal {R})\not =\emptyset \).
If I is an ideal in A, then \(^cI:=\{(f,-g): (f,g)\in I\}\) denotes the conjugate of I. The proof of the following Lemma, which is fundamental for us, is straightforward:
Lemma 1.6
Let \(\mathcal {R}\) be a commutative unital Banach algebra over \( \mathbb {R}\) and \(A=\mathcal {R}_\mathbb {C}\) its complexification. Consider the homeomorphisms \(\Xi : X(\mathcal {R})\rightarrow M(A)\) (defined above), and
and let E be the (possibly empty) set of fixed points of \(\tau \). To each \(m\in M(A)\) associate the map
Then
- (1)
\(m^*\in M(A)\) and \(\ker m^*={^c}\ker m\).
- (2)
The map
$$\begin{aligned} \tau ^*: {\left\{ \begin{array}{ll}M(A) &{}\rightarrow M(A)\\ m&{}\mapsto m^*\end{array}\right. } \end{aligned}$$is a homeomorphic involution (that is \(\tau ^*\circ \tau ^*=\mathrm{id}\))
- (3)
If \(\Xi (\chi )=m\), then \(\Xi (\overline{\chi })=m^*\); that is \(\Xi \circ \tau \circ \Xi ^{-1}=\tau ^*\).
- (4)
\(\Xi (E)\) coincides with the set of fixed points of \(\tau ^*\).
- (5)
\(E=\{\chi \in X(\mathcal {R}): \chi \hbox { is real-valued }\}\); that is \(E=M_ \mathbb {R}(\mathcal {R})\).
- (6)
\(E=\{\chi \in X(\mathcal {R}): \mathrm{codim}_{\, \mathbb {R}}\;\ker \chi =1\}\).
- (7)
\(E=\{\chi \in X(\mathcal {R}): \hat{f} (\chi )\in \mathbb {R}\;\hbox {for every } f\in \mathcal {R}\}\).
- (8)
\(\hat{\mathcal {R}}\subseteq C(X(\mathcal {R}), \tau )\).
3 Semi-simple real Banach algebras
Recall that a commutative unital Banach algebra A over \(\mathbb {K}= \mathbb {R}\) or \(\mathbb {C}\) is said to be semi-simple if its (Jacobson) radical \(\mathrm{rad}\; A\) (that is the intersection of all maximal ideals in A), is the zero ideal. Clearly, \(\mathrm{rad}\; A=\ker \Phi \), where
is the Gelfand homomorphism.
It is well known that a real commutative unital algebra \(\mathcal {R}\) is semi-simple if and only if \(\mathcal {R}_\mathbb {C}\) is semi-simple.
Following Kaplansky, the real-symmetric spectrum\(\sigma ^*_{\mathcal {R}}(x)\) of the element x in a real Banach algebra \(\mathcal {R}\) is defined as
and the real-symmetric spectral radius of \(x\in \mathcal {R}\) is given by
Recall that these spectra coincide with the image of the Gelfand transform of x (see [8]).
Lemma 2.1
Let A be a commutative unital Banach algebra over \( \mathbb {R}\) or \(\mathbb {C}\). Fix \(g\in A\) and \(r\in \mathrm{rad}\; A\). Then the following assertions hold:
- (1)
\(\varvec{1}+rg\in \exp A\).
- (2)
\(e^g+r\in \exp A\).
Proof
(1) Consider the series
Note that \(\root n \of {||r^ng^n||}\) converges to the spectral radius \(\rho _A(r g)\), respectively real-symmetric spectral radius \(\rho ^*_A(rg)\), of rg (see [8]). However, these radii are zero because \(rg\in \mathrm{rad }\;A\). We deduce that the series defining L converges absolutely in A. Hence \(e^L={\varvec{1}}+rg\).
(2) Use that \(e^g+r=e^g(\varvec{1}+ r e^{-g})\) and apply (1). \(\square \)
The next new result (roughly) tells us that for semi-simple algebras the Gelfand transformFootnote 1 of \(F\in \mathcal {R}_\mathbb {C}\) coincides with the Gelfand-transform \(\hat{f}\) of some \(f\in \mathcal {R}\) if and only if F is \(\tau ^*\)-symmetric. Note that for any \(f\in \mathcal {R}\), we have
where \(F=(f,0)\) and where \(\Xi :X(\mathcal {R})\rightarrow M(\mathcal {R}_\mathbb {C})\) is the canonical identification homeomorphism. Recall from Lemma 1.6 that \(\tau ^*\) is the involution \(m\mapsto m^*\) in \(M(\mathcal {R}_\mathbb {C})\) with \(m^*(f,g)=\overline{m(f,-g)}\). The following diagram illustrates the different maps appearing here:
Theorem 2.2
Let \(\mathcal {R}\) be a semi-simple commutative unital Banach algebra over \( \mathbb {R}\) and \(A=\mathcal {R}_\mathbb {C}\) its complexification. Given \(F=(u,v)\in A\), the following assertions are equivalent:
- (1)
There is \(f\in \mathcal {R}\) with \(\hat{f}= \widehat{F} \circ \Xi \).
- (2)
\(F=(f,0)\).
- (3)
\(\widehat{F}\circ \tau ^*=\overline{\widehat{F}}\).
The representation in (3) is called \(\tau ^*\)-symmetric.
Proof
(1) \(\Longrightarrow \) (2) Let \(\chi \in X(\mathcal {R})\). Then
Since the semi-simplicity of \(\mathcal {R}\) implies the one of \(\mathcal {R}_\mathbb {C}\) we conclude that \(F=(f,0)\).
(2) \(\Longrightarrow \) (3) Let \(m\in M(A)\). Then
(3) \(\Longrightarrow \) (2) Note that
and \(\overline{\widehat{F}(m)}= \overline{m(u,v)}\). Hence, by hypothesis, \(m(u,v)=m(u,-v)\) for every \(m\in M(A)\), from which we conclude that
The semi-simplicity of A now implies that \(v=0\) and so \(F=(u,0)\).
(2) \(\Longrightarrow \) (1) \(\widehat{F}(\Xi (\chi ))=\Xi (\chi )(f,0)=\chi (f)+i \chi (0)=\chi (f)=\hat{f}(\chi )\). \(\square \)
As a corollary, we have the the following useful result:
Corollary 2.3
Let \(\mathcal {R}\) be a semi-simple commutative unital Banach algebra over \( \mathbb {R}\) and \(A=\mathcal {R}_\mathbb {C}\) its complexification. Then the real algebra \(\hat{\mathcal {R}}\subseteq C(X(\mathcal {R}),\tau )\) can be identified with a subalgebra of \(C(M(A),\tau ^*)\).
Lemma 2.4
Let \(\mathcal {R}\) be a commutative unital Banach algebra over \( \mathbb {R}\) and \(A=\mathcal {R}_\mathbb {C}\) its complexification. Then, for all \(\widehat{F}\in \widehat{A}\), there is \(f\in \mathcal {R}\) such that
Proof
Let \(F=(u,v)\) with \(u,v\in \mathcal {R}\). Then, for \(\chi \in X(\mathcal {R})\) and \(m:=\Xi (\chi )\in M(A)\),
If we let \(f:=u^2+v^2\), then \(f\in \mathcal {R}\) and \(\hat{f}=Q\circ \Xi \) (by (2.1)). \(\square \)
4 The Arens-Royden Theorem for real Banach algebras
Theorem 3.1
(Real Arens-Royden) Let \(\mathcal {R}\) be a semi-simple commutative unital Banach algebra over \( \mathbb {R}\) and \(A=\mathcal {R}_\mathbb {C}\) its complexification. Then the following assertions hold:
- (1)
Let \(f\in \mathcal {R}\). Suppose that there is \(q\in C(M(A),\tau ^*)\) such that \(\hat{f}\circ \Xi ^{-1}=e^q\). Then \(f=e^g\) for some \(g\in \mathcal {R}\).
- (2)
Let \(f\in \mathcal {R}^{-1}\) and suppose there exists \(q\in C(M(A),\tau ^*)\) such that \(\hat{f} \circ \Xi ^{-1}=q^n\). Then there is \(g\in \mathcal {R}\) with \(f=g^n\).
- (3)
Every function \(Q\in C(M(A),\tau ^*)^{-1}\) has a factorization
$$\begin{aligned}Q=(\hat{f}\circ \Xi ^{-1})\; e^q\end{aligned}$$for some \(f\in \mathcal {R}^{-1}\) and \(q\in C(M(A),\tau ^*)\).
Proof
(1) Let \(F:=(f,0)\). By Theorem 2.2, \(\widehat{F}=\overline{\widehat{F}\circ \tau ^*}\). Since \(\widehat{F}= \hat{f}\circ \Xi ^{-1}\) (formula (2.1)), the hypotheses \(\hat{f}\circ \Xi ^{-1}=e^q\) now implies that
By the complex Arens-Royden Theorem 0.1 (1), there is \(a\in A\) such that \(e^a =F\) and, in particular, \(e^{\widehat{a}}= \widehat{F}=e^q\). We need to symmetrize a. Since \(e^{\widehat{a}-q}\equiv 1\), we deduce that for every \(m\in M(A)\),
Since the preimage \(E_k\) under the map \(\widehat{a}-q\) of each value \(2k\pi i\) is a closed-open subset of M(A), there exists finitely many \(k_n\in \mathbb {Z}\) such that
By the Shilov idempotent theorem for complex Banach algebras, [7, p.88], there is \(b\in A\) such that
Hence \(a-b\in A\) and \(\widehat{a}-\widehat{b}=q\). Moreover, since q is \(\tau ^*\) symmetric, the same holds for \(\widehat{a-b}\). Thus, by Theorem 2.2, there is \(g\in \mathcal {R}\) such that \(\hat{g}\circ \Xi ^{-1}=\widehat{a-b}\). Since we do have
we conclude that \(f= e^{g}\) (note that \(\mathcal {R}\) is semi-simple).
(2) This works similar as the point (1). First we note that q does not vanish on M(A), because \(\hat{f}\) does not vanish on \(X(\mathcal {R})\). Now, as above, with \(F=(f,0)\), \(\widehat{F}=q^n\). By the Corollary in [7, p. 88], there is \(a\in A\) with \(a^n=F\). Again, we need to symmetrize a. Since \(\widehat{a}^n/q^n\equiv 1\), we see that for every \(m\in M(A)\)
Thus, in the same way as in (1), there is \(b\in A\) with \(\widehat{b}= e^{-2k\pi i/n}\) on the preimage of \(e^{2k\pi i/n}\) with respect to \(\widehat{a}/q\). Hence \(ab\in A\) and \(\widehat{ab} =q\). Moreover, since q is \(\tau ^*\) symmetric, the same holds for \(\widehat{ab}\). Thus, by Theorem 2.2, there is \(g\in \mathcal {R}\) such that \(\hat{g}\circ \Xi ^{-1}=\widehat{ab}\). Consequently
and so, due to semi-simplicity of \(\mathcal {R}\), \(g^n= f\).
(3) By the complex Arens-Royden Theorem 0.1 (2), there is \(v\in A\) and \(k\in C(M(A),\mathbb {C})\) such that \(Q= \widehat{v} \; e^k\), where the Gelfand-transform is taken in A. Our goal is to achieve a similar \(\tau ^*\)-symmetric representation of Q in order to apply Theorem 2.2. Since Q is \(\tau ^*\)-symmetric, we have
Hence
Let
Then \(Q^2=w\, e^K\). Since \(\tau ^*\) is an involution, w and K belong to \(C(M(A),\tau ^*)\). By Lemma 2.4, \(w=\hat{g}\circ \Xi ^{-1}\) for some \(g\in \mathcal {R}\). If \(W=(g,0)\), then \(W\in A\) and \(\widehat{W} =w\). Thus, by construction,
In other words, the element W of A has a continuous square root in the space \(C(M(A),\mathbb {C})\). By a Corollary in [7, p. 88], W has a square root in A; that is, there is \(u\in A\) with \(W=u^2\). Let \(\tilde{q}:=e^{-K/2} \; Q\). Then \(\tilde{q}\in C(M(A),\tau ^*)^{-1}\) and \((\widehat{u}/\tilde{q})^2\equiv 1\) on M(A). Thus, there is a continuous sign-function s on M(A) such that \(\widehat{u}/\tilde{q}=s\). Since
are closed-open sets in M(A), there exists by Shilov’s idempotent theorem [7, p. 88] some \(p\in A\) with \(\widehat{p}=s\). Consequently, \(pu\in A\) and \(\widehat{pu}=\tilde{q}\) on M(A). Since \(\tilde{q}\) is \(\tau ^*\)-symmetric, we conclude from Theorem 2.2 that \(\widehat{pu}= \hat{f}\circ \Xi ^{-1}\) for some \(f\in \mathcal {R}\). Hence
Since \(\hat{f}\circ \Xi ^{-1}\not =0\) on M(A), \(\hat{f}\not =0\) on \(X(\mathcal {R})\) and so \(f\in \mathcal {R}^{-1}\). This yields the assertion of the Theorem that
for some \(K\in C(M(A),\tau ^*)\) and some invertible \(f\in \mathcal {R}\). \(\square \)
We shall now deduce a version of the Arens-Royden theorem that stays within the realm of real Banach algebras.
Let us point out that in the previous result the condition of semi-simplicity is not necessary. This is a consequence of the non semi-simple part of the next result by transfering it with the canonical identification homeomorphism \(\Xi \) from the \(\mathcal {R}\) setting to the \(\mathcal {R}_\mathbb {C}\)-setting.
Theorem 3.2
Let \(\mathcal {R}\) be commutative unital Banach algebra over \( \mathbb {R}\).
- (1)
Let \(f\in \mathcal {R}\). Suppose that there is (a \(\tau \)-symmetric function) \(q\in C(X(\mathcal {R}),\tau )\) satisfying \(q(\overline{\chi })=\overline{q(\chi )}\) such that \(\hat{f}=e^q\). Then \(f=e^g\) for some \(g\in \mathcal {R}\).
- (2)
Let \(f\in \mathcal {R}^{-1}\) and suppose there is (a \(\tau \)-symmetric function) \(q\in C(X(\mathcal {R}),\tau )\) satisfying \(q(\overline{\chi })=\overline{q(\chi )}\) such that \(\hat{f} =q^n\). Then there is \(g\in \mathcal {R}\) with \(f=g^n\).
- (3)
Given any \(\tau \)-symmetric zero-free function \(Q\in C(X(\mathcal {R}),\tau )\) satisfying \(Q(\overline{\chi })=\overline{Q(\chi )}\), there exists \(f\in \mathcal {R}^{-1}\) and a \(\tau \)-symmetric \(q\in C(X(\mathcal {R}),\tau )\) such that
$$\begin{aligned}Q= \hat{f}\; e^q.\end{aligned}$$
Proof
If \(\mathcal {R}\) is semi-simple we apply the previous Theorem. To this end, it suffices to consider the functions \(q^*:=q\circ \Xi ^{-1}\) and \(Q^*:=Q\circ \Xi ^{-1}\), which belong to \(C(M(A),\tau ^*)\) (due to Lemma 1.6), and conclude.
If \(\mathcal {R}\) is arbitrary with radical \(J:=\mathrm{rad}\; \mathcal {R}\), then we consider the quotient algebra \(\tilde{\mathcal {R}}:=\mathcal {R}/ J\). Now \(\tilde{\mathcal {R}}\) is a semi-simple algebra. Since J is closed, \(\tilde{\mathcal {R}}\) becomes a commutative, unital, real Banach algebra under the quotient norm. Since for the hull of J we have \(h(J)=X(\mathcal {R}/J)\), the adjoint \(\pi ^*: X(\mathcal {R}/J)\rightarrow X(\mathcal {R})\) of the quotient map \(\pi : \mathcal {R}\rightarrow \mathcal {R}/J\) is a homeomorphism. So we can identify these two character spaces and so we may also identify the Gelfand transform of \(f\in \mathcal {R}\) with that of its class \([f]\in \tilde{\mathcal {R}}\). Note that \(\widehat{f+r}=\widehat{f}\) for every \(r\in \mathrm{rad}\;\mathcal {R}\). An application of Step 1 now yields (for part (1)) \(g\in \mathcal {R}\) such that \([f]=e^{[g]}\). Hence \(f=e^g+r\) for some \(r\in \mathrm{rad}\; \mathcal {R}\). By Lemma 2.1, \(e^g+r\) is an exponential again. Hence \(f=e^L\) for some \(L\in \mathcal {R}\).
Similarily (for part (2)), there is \(g\in \mathcal {R}\) such that \([f]=[g]^n=[g^n]\). Hence \(f=g^n+r\) for some \(r\in \mathrm{rad}\;\mathcal {R}\). Since [f] is invertible in \(\tilde{\mathcal {R}}\), the same holds for [g] and therefore \(g^n\in \mathcal {R}^{-1}\). Thus \(fg^{-n}=1+rg^{-n}\). By Lemma 2.1, \(1+rg^{-n}\) is an exponential. We conclude that \(f=g^n e^L=(g e^{L/n}\big )^n\) for some \(L\in \mathcal {R}\).
For part (3), the semi-simple case yields \(q\in C(X(\tilde{\mathcal {R}}), \mathbb {C})= C(X(\mathcal {R}),\mathbb {C})\) and \([f]\in \tilde{\mathcal {R}}^{-1}\) such that \(Q=\widehat{[f]}\; e^q\). Since every representant \(f+r \) with \(r\in \mathrm{rad}\;\mathcal {R}\) is invertible in \(\mathcal {R}\), we obtain the assertion \(Q e^{-q}=\hat{f}\) for some \(f\in \mathcal {R}^{-1}\). \(\square \)
Given a commutative unital Banach algebra over \( \mathbb {R}\), let \(\mathcal {R}^\#\) denote the set of all invertible elements u in \(\mathcal {R}\) for which \(\hat{u}>0\) on \(E=M_ \mathbb {R}(\mathcal {R})\subseteq X(R)\), the set of real-valued characters on \(\mathcal {R}\). If \(E=\emptyset \), then \(\mathcal {R}^\#=\mathcal {R}^{-1}\). Here is now the final version of the Arens-Royden Theorem for real Banach algebras, which reflects Furutani’s algebraic version [6].
Theorem 3.3
Let \(\mathcal {R}\) be a commutative unital Banach algebra over \( \mathbb {R}\) and \(A=\mathcal {R}_\mathbb {C}\) its complexification. Then the Gelfand transform induces a group isomorphism between the three quotient spaces
- (1)
\(\mathcal {R}^{\#}/\exp \mathcal {R}\),
- (2)
\(C(X(\mathcal {R}), \tau )^{\#}/ \exp C(X(\mathcal {R}), \tau )\),
- (3)
\(C(M(A), \tau ^*)^{\#}/ \exp C(M(A), \tau ^*)\).
The same holds for the following bigger quotient spaces:
- (1’)
\(\mathcal {R}^{-1}/\exp \mathcal {R}\),
- (2’)
\(C(X(\mathcal {R}), \tau )^{-1}/ \exp C(X(\mathcal {R}), \tau )\),
- (3’)
\(C(M(A), \tau ^*)^{-1}/ \exp C(M(A), \tau ^*)\).
\(\square \)
Proof
First we note that \(\exp C(X(\mathcal {R}), \tau )\subseteq C(X(\mathcal {R}), \tau )^{\#}\), because every \(q\in C(X(\mathcal {R}),\tau )\) is real-valued on the fixed-point set E of \(\tau \), and so \(e^q>0\) there. Hence the map
is well-defined. Here we may replace on both sides \(B^{\#}\) by \(B^{-1}\). Note that [c] is the equivalence class of c in the quotient group \(C(X(\mathcal {R}), \tau )^{\#}/ \exp C(X(\mathcal {R}), \tau )\): \( c_1\sim c_2\Longleftrightarrow c_1 =e^d c_2\) for \(c_j\) and \(d\in C(X(\mathcal {R}), \tau )\). We claim that the kernel of \(\Phi \) is \(\exp \mathcal {R}\). In fact, let \(f\in \ker \Phi \); that is \(\hat{f}=e^q\) for some \(q\in C(X(\mathcal {R}), \tau )\), where \(f\in \mathcal {R}^{\#}\subseteq \mathcal {R}^{-1}\). Then, by Theorem 3.2 (1), there is \(g\in \mathcal {R}\) such that \(f=e^g\). Hence \(f\in \exp \mathcal {R}\), from which we deduce that \(\ker \Phi \subseteq \exp \mathcal {R}\). Since for \(h:=e^k\in \exp \mathcal {R}\) we have \(\Phi (h)=[\widehat{e^k}]=[e^{\hat{k}}]\), we conclude that \(\ker \Phi =\exp \mathcal {R}\).
To show the surjectivity of \(\Phi \), let \([Q]\in C(X(\mathcal {R}), \tau )^{\#}/ \exp C(X(\mathcal {R}), \tau )\), for some \(Q\in C(X(\mathcal {R}), \tau )^{\#}\). By Theorem 3.2 (3), there is \(q\in C(X(\mathcal {R}),\tau )\) and \(f\in \mathcal {R}^{-1}\) such that \(Q=e^q \hat{f}\). Since \(Q>0\) on E and q is real-valued on E, \(\hat{f}>0\) on E. Thus \(f\in \mathcal {R}^{\#}\) and \(\Phi (f)=[Q]\).
Putting all together, we have shown that \(C(X(\mathcal {R}), \tau )^{\#}/ \exp C(X(\mathcal {R}), \tau )\sim \mathcal {R}^{\#}/\exp \mathcal {R}\) as well as \(C(X(\mathcal {R}), \tau )^{-1}/ \exp C(X(\mathcal {R}), \tau )\sim \mathcal {R}^{-1}/\exp \mathcal {R}\).
The rest follows via the canonical identification homeomorphism \(\Xi \). \(\square \)
5 The Shilov idempotent theorem for real Banach algebras
If A is a complex commutative unital Banach algebra, then Shilov’s idempotent theorem [7, p.88] tells us that for every closed-open subset E in M(A) there is \(e\in A\) such that \(e^2=e\), \(\widehat{e}\equiv 1\) on E and \(\widehat{e}\equiv 0\) on \(M(A){\setminus } E\). Such a result, though, is not true for real Banach algebras: \(S:=\{m_r: m\in M(A)\}\) and \(\tilde{S}:=\{\overline{m_r}: m\in M(A)\}\) are two disjoint closed-open subsets of \(X(A_ \mathbb {R})\), (where \(m_r:A_ \mathbb {R}\rightarrow {^ \mathbb {R}\mathbb {C}}\) is the real homomorphism defined by \(m_r(a):=m(a)\)), but of course, if \(\hat{e}\) vanishes identically on S it vanishes identically on \(\tilde{S}\).
However, using the \(\tau ^*\)-symmetry of the Gelfand transform (Corollary 2.3), we obtain the following positive result:
Theorem 4.1
(Shilov’s idempotent Theorem for real algebras) Let \(\mathcal {R}\) be a commutative unital Banach algebra over \( \mathbb {R}\), \(A=\mathcal {R}_\mathbb {C}\) the complexification of \(\mathcal {R}\) and \(\Xi : X(\mathcal {R})\rightarrow M(A)\) the canonical identification homeomorphism.
- (1)
Suppose that C is a closed-open subset of M(A) satisfying
$$\begin{aligned} m\in C\Longleftrightarrow \tau ^*(m)\in C. \end{aligned}$$Then there exists a unique \(f\in \mathcal {R}\) such that \(f^2=f\), \(\hat{f}\circ \Xi ^{-1}\equiv 1\) on C and \(\hat{f}\circ \Xi ^{-1}\equiv 0\) on \(M(A){\setminus } C\).
- (2)
Suppose that S is a closed-open subset of \(X(\mathcal {R})\) satisfying
$$\begin{aligned} \chi \in S\Longleftrightarrow \overline{\chi }\in S. \end{aligned}$$Then there exists a unique \(e\in \mathcal {R}\) such that \(e^2=e\), \(\hat{e}\equiv 1\) on S and \(\hat{e}\equiv 0\) on \(X(\mathcal {R}){\setminus } S\).
Proof
We first assume that \(\mathcal {R}\) is semi-simple.
(1) By Shilov’s idempotent Theorem there is a unique \(F=(u,v)\in A\) such that \(F^2=F\), \(\widehat{F}\equiv 1\) on C and \(\widehat{F}\equiv 0\) on \(M(A){\setminus } C\). Now \(\widehat{F} \circ \tau ^*=\overline{\widehat{F}}\), because \(\tau ^*(m)\in C\) if and only if \(m\in C\). Hence, by Theorem 2.2, there is \(f\in \mathcal {R}\) with \(\hat{f}= \widehat{F} \circ \Xi \) and \(F=(f,0)\). Since \(F^2=(f,0)\otimes (f,0)=(f^2,0)\), we deduce that \(f^2=f\). Since two different \(f\in \mathcal {R}\) yield two different \(F=(f,0)\in A\), the uniqueness follows from the unicity of F.
(2) This is a direct consequence of (1) by setting \(C:=\Xi (S)\) and using Lemma 1.6 telling us that \(\Xi \circ \tau \circ \Xi ^{-1}=\tau ^*\), where \(\tau (\chi )=\overline{\chi }\) is the real-symmetric involution on \(X(\mathcal {R})\). In fact, the real-symmetry of S is equivalent to the \(\tau ^*\)-symmetry of C. Hence \(\hat{f}\circ \Xi ^{-1}\equiv 1\) on C implies that \(\hat{f} \equiv 1\) on S.
If \(\mathcal {R}\) is arbitrary with radical J, we proceed exactly as in the complex case. In fact, applying the semi-simple case to the quotient algebra \(\mathcal {R}/J\) (as we did it in the proof of Theorem 3.2) we get \(g\in \mathcal {R}\) such that \(g^2-g\in J\) and so that \(\hat{g}\equiv 1\) on S and \(\hat{g}\equiv 0\) on \(X(\mathcal {R}){\setminus } S\) (respectively \(\hat{g} \circ \Xi ^{-1}\equiv 1\) on C and \(\hat{g}\circ \Xi ^{-1}\equiv 0\) on \(M(A){\setminus } C\)). In particular, \(g-1/2\in \mathcal {R}^{-1}\). If \(x:=(g^2-g)(g-1/2)^{-2}\), then \(x\in J\) and therefore its real-symmetric spectral radius \(\rho ^*_\mathcal {R} (x)=0\). Hence the series
converges absolutely in \(\mathcal {R}\) to an element w satisfying \(w^2={\varvec{1}}-x\) and \(w-{\varvec{1}}\in J\). Now put \(e:=1/2+(g-1/2)w\). Then e is the desired idempotent. In fact, if \(x\in S\) then \(\hat{e}(x)= 1/2+(1-1/2)\cdot 1=1\) and if \(x\in X(\mathcal {R}){\setminus } S\), then \(\hat{e}(x)=1/2+(0-1/2)\cdot 1=0\). And, finally,
To prove uniqueness, let \(b,a\in \mathcal {R}\) satisfy \(\widehat{b}=\widehat{a}\) and \(a^2-a=b^2-b=0\). Since \(r:=a-b\in J\), we have the following equivalences in virtue of the invertibility of \(2b-\varvec{1}+r\) (note that its Gelfand transform is \(\pm 1\)):
\(\square \)
Remark
If \(\mathcal {R}\) is strictly real (that is if \(X(\mathcal {R})=M_ \mathbb {R}(\mathcal {R})\)), then condition \(\chi \in S\Longleftrightarrow \overline{\chi }\in S\) in Theorem 4.1 (2) is redundant.
6 An application to the solution of the Bézout equation with one invertible factor
We apply our version of the Arens-Royden theorem to extend from complex to real Banach algebras a result due to Corach and Suárez [3] on solutions of the Bézout equation with one invertible factor.
Theorem 5.1
Let \(\mathcal {R}\) be a commutative unital real Banach algebra and suppose that for a given pair \((f,g)\in \mathcal {R}^2\) there is a solution \((a,b)\in C(X(\mathcal {R}),\tau )^2\) to the equation \(a\hat{f} +b\hat{g}=1\), where a is zero-free on \(X(\mathcal {R})\). Then the Bézout equation \(uf+vg=1\) has a solution \((u,v)\in \mathcal {R}^2\) with u invertible.
Proof
Let \(a\hat{f} +b\hat{g}=1\) in \(C(X(\mathcal {R}),\tau )\) with a zero-free. Then there is \( c\in C(X(\mathcal {R}),\tau )\) such that \(d:=\hat{f}+c \hat{g}\not =0\) on \(X(\mathcal {R})\). By the real Arens-Royden Theorem 3.2 (3), \(d=\hat{r}e^q\) for some element r invertible in \(\mathcal {R}\) and some \(q\in C(X(\mathcal {R}),\tau )\).
Let \(E:=Z(\hat{g})\). Then E is \(\tau \)-symmetric. Since \(r\in \mathcal {R}\cap \mathcal {R}^{-1}\), we deduce that
Let R be the uniform closure in \(C(E,\tau )\) of \(\widehat{\mathcal {R}}|_E\). Since zero-sets of functions in \(\mathcal {R}\) are \(\mathcal {R}\)-convex, R is a natural uniformly closed subalgebra on E; that is \(X(R)=E\) (via evaluation functionals). By the Arens-Royden Theorem 3.2 (1), \(p\in \exp R\); that is \(p=e^s\) for some \(s\in R\). By the definition of R, there is a sequence \((a_n)\) in \(\mathcal {R}\) such that \(||\hat{a}_n-s||_E\rightarrow 0\). Hence \(||e^{\hat{a}_n}-e^s||_E\rightarrow 0\); that is \(||e^{\hat{a}_n}-\hat{f}/ \hat{r}||_E\rightarrow 0\). This in turn implies that \(e^{-\hat{a}_n}(e^{\hat{a}_n} -\hat{f}/ \hat{r})\rightarrow e^{-s} \cdot 0=0\) uniformly on E. Hence
It is now well-known that the condition \(||1-\hat{s} \hat{f}||_E<1\) for \(s\in \mathcal {R}^{-1}\) implies that \(uf+vg=1\) for some \((u,v)\in \mathcal {R}^2\) with u invertible; just look at the path \(t\mapsto (sf+t, g)\) in the set of invertible pairs in \(\mathcal {R}\) (see [4]). \(\square \)
Notes
In the following, we use the small \(\hat{}\) to denote the Gelfand-transform in \(\mathcal {R}\) and the widehat \(\;\widehat{}\;\) to represent the Gelfand-transform in \(\mathcal {R}_\mathbb {C}\).
References
Allan, G.: Introduction to Banach Spaces and Algebras. Oxford University Press, Oxford (2011)
Alling, N., Campbell, L.A.: Real Banach algebras. II. Math. Z. 125, 79–100 (1972)
Corach, G., Suárez, F.D.: Extension problems and stable rank in commutative Banach algebras. Topol. Appl. 21, 1–8 (1985)
Corach, G., Suárez, F.D.: On the stable range of uniform algebras and \(H^\infty \). Proc. Am. Math. Soc. 98, 607–610 (1986)
Dudley, R.M., Norvaiša, R.: Concrete Functional Calculus. Springer, New York (2011)
Furutani, K.: A note on the Arens-Royden theorem for real Banach algebras. TRU Math. 15, 19–22 (1979)
Gamelin, T.W.: Uniform Algebras. Chelsea, New York (1984)
Kulkarni, S.H., Limaye, B.V.: Real Function Algebras. Marcel Dekker, New York (1992)
Li, Bingren: Real Operator Algebras. World Scientific, New Jersey (2003)
Mortini, R., Rupp, R.: A Space Odyssey, Extension Problems and Stable Ranks—Accompanied by Introductory Chapters on Point-Set Topology and Banach Algebras– Textbook, Encylopedic Monograph, ca., pp. 2000 (in preparation)
Rickart, C.E.: General Theory of Banach Algebras. Krieger Publishing, Florida (1974)
Acknowledgements
Le premier auteur remercie l’UFR MIM (Mathématiques-Informatique-Mécanique) de l’université de Lorraine, Campus Metz, pour lui avoir donné la possibilité, via une mise à disposition, d’enseigner à l’Université du Luxembourg de 2017 à 2020. Un merci aussi à l’Université du Luxembourg pour avoir soutenu cette démarche.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Part of this work was done while the Rudolf Rupp enjoyed a sabbatical. He wants to thank the TH-Nürnberg for her support.
Rights and permissions
About this article
Cite this article
Mortini, R., Rupp, R. A revisit of the Arens-Royden and Shilov idempotent theorems for real Banach algebras. Math. Z. 294, 491–502 (2020). https://doi.org/10.1007/s00209-019-02294-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-019-02294-w
Keywords
- Real Banach algebras
- Complexifications and real-izations
- Group of invertible elements
- \(\tau \)-Symmetric
- Idempotents



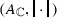 is a completely normed, complex algebra.
is a completely normed, complex algebra.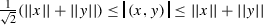 for any
for any 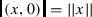 for each
for each 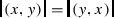 and
and 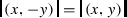 for every
for every  .
.