Elliptic points of the Drinfeld modular groups

Abstract

Let $K$ be an algebraic function field with constant field ${\mathbb {F}}_q$. Fix a place $\infty$ of $K$ of degree $\delta$ and let $A$ be the ring of elements of $K$ that are integral outside $\infty$. We give an explicit description of the elliptic points for the action of the Drinfeld modular group $G=GL_2(A)$ on the Drinfeld’s upper half-plane $\Omega$ and on the Drinfeld modular curve $G{\setminus }\Omega$. It is known that under the building map elliptic points are mapped onto vertices of the Bruhat–Tits tree of $G$. We show how such vertices can be determined by a simple condition on their stabilizers. Finally for the special case $\delta =1$ we obtain from this a surprising free product decomposition for $PGL_2(A)$.

1 Introduction

Let $K$ be an algebraic function field of one variable with constant field ${\mathbb {F}}_q$, the finite field of order $q$, and let $\infty$ be a fixed place of $K$ of degree $\delta$. Let $K_{\infty }$ be the completion of $K$ with respect to $\infty$ and let $C_{\infty }$ be the $\infty$-completion of an algebraic closure of $K_{\infty }$. The set $\Omega = C_{\infty } \backslash K_{\infty }$ is often referred to as Drinfeld’s upper half-plane. We denote the ring of all those elements of $K$ which are integral outside $\infty$ by $A$. (The simplest examples are $K={\mathbb {F}}_q(t)$ and $A={\mathbb {F}}_q[t]$.) The group $G=GL_2(A)$ plays a fundamental role [3] in the theory of Drinfeld modular curves. For this reason we will call $G$ a Drinfeld modular group. Drinfeld [3] has extended the classical theory of modular curves to the function field setting. Here ${\mathbb {Q}}, {\mathbb {R}}, {\mathbb {C}}$ are replaced by $K, K_{\infty }, C_{\infty }$, respectively. The roles of the classical upper half-plane, $\mathbb {H}$, (in ${\mathbb {C}}$) and the classical modular group, $SL_2({\mathbb {Z}})$, are assumed by $\Omega$ and $G$, respectively. The group $G$ acts as a set of linear fractional transformations on $\Omega$.

Let $S$ be a subgroup of $G$. We say that elements $\omega _1,\;\omega _2 \in \Omega$ are $S$ -equivalent if and only if $\omega _1=s(\omega _2)$, for some $s\in S$. For each subgroup $S$ of $G$ and $\omega \in \Omega$, let $S_{\omega }$ denote the stabilizer of $\omega$ in $S$.

Definition

The element $\omega \in \Omega$ is called an elliptic element of $S$ if $S_{\omega }$ is non-trivial, i.e. it does not consist entirely of scalar matrices. It is clear that $S$ acts on its set of elliptic elements, $E(S)$. We put $\mathop {{\mathrm {Ell}}}(S)=S\backslash E(S)$ and refer to its elements as the elliptic points of $S$.

Elliptic points are very important for a number of reasons. One of the purposes of Drinfeld’s theory is to provide an analytical description for the so-called Drinfeld modular curve, $G\backslash \Omega$ and hence $S\backslash \Omega$, for every finite index subgroup $S$. Of particular importance in this regard is, for example, the genus of such a curve whose evaluation usually depends on the Hurwitz formula [4, p. 87]. This relates the genera of $G \backslash \Omega$ and $S \backslash \Omega$ and contains terms coming from the ramification. But ramification in the covering $S \backslash \Omega \rightarrow G \backslash \Omega$ can only occur above elliptic points and cusps.

For $SL_2({\mathbb {Z}})$, it is a classical result that every element of $\mathbb {H}=\{z \in {\mathbb {C}}: \mathrm {Im}z > 0\}$ which is fixed by a non-scalar matrix is $SL_2({\mathbb {Z}})$-equivalent to one of $i,\rho \in \mathbb {H}$, where $i^2=-1$ and $\rho ^2+\rho +1=0$. Moreover every element of finite order in $SL_2({\mathbb {Z}})$ lies in the stabilizer of one of these “elliptic” elements. It follows then that $SL_2({\mathbb {Z}})$ has precisely two “elliptic points”. As we shall see the situation for Drinfeld modular groups is much more complicated.

Our first principal result provides a precise description of an elliptic element.

Theorem A

Fix any $\varepsilon \in {\mathbb {F}}_{q^2}\!\setminus \!{\mathbb {F}}_q$. An element $\omega \in \Omega$ is an elliptic element of $G$ if and only if

$$\begin{aligned} \omega =\frac{\varepsilon +s}{t} \end{aligned}$$

for some $s,t\in A\;(t\ne 0)$, for which

$$\begin{aligned} (\varepsilon ^q+s)(\varepsilon +s)=tt', \ { with } \ t' \in A. \end{aligned}$$

It follows that $G$ has elliptic elements if and only if $\delta$ is odd. Every elliptic element $\omega \in \Omega$ lies in ${\mathbb {F}}_{q^2}K \backslash K$. We deduce from Theorem A that the stabilizer $G_{\omega }$ of every elliptic $\omega \in \Omega$ is isomorphic to ${\mathbb {F}}_{q^2}^*$. We are also able to deduce that $|\mathop {{\mathrm {Ell}}}(G)|=L_K(-1)$, where $L_K(u)$ is the L-polynomial of $K$ [15, Section 5.1]. These deductions are already known [4, p. 50]. However our approach is more elementary than that of Gekeler. Moreover, we derive more precise information and interesting applications.

The Galois automorphism of ${\mathbb {F}}_{q^2}/{\mathbb {F}}_q$ extends to that of ${\mathbb {F}}_{q^2}K/K$ and gives rise to a conjugate map, $\omega \mapsto \overline{\omega }$, on $E(G)$. Many of our results depend on whether or not $\omega$ and $\overline{\omega }$ are $G$-conjugate. Of particular interest in this context is the subset of $\mathop {{\mathrm {Ell}}}(G)$ consisting of all those points corresponding to elliptic elements $\omega$ for which $\omega$ and $\overline{\omega }$ are $G$-equivalent. We are able to identify this subset with a certain group of involutions (see Theorem 3.8) and for this reason we denote it by $\mathop {{\mathrm {Ell}}}(G)_2$. It turns out, rather surprisingly perhaps, that $|\mathop {{\mathrm {Ell}}}(G)_2|$, as with $|\mathop {{\mathrm {Ell}}}(G)|$, does not depend on $A$, i.e. is independent of the particular choice of $\infty$. For $q\ge 8$ we can bound the size of $\mathop {{\mathrm {Ell}}}(G)_2$ from below, using arguments from algebraic number theory.

Associated with the group $GL_2(K_{\infty })$ is its Bruhat–Tits building which in this case is a tree, ${\mathcal {T}}$. See [14, Chapter II, Section 1]. From this $G$ inherits an action on ${\mathcal {T}}$. Most of our results involve the well-known building map

$$\begin{aligned} \lambda : \Omega \longrightarrow {\mathcal {T}}. \end{aligned}$$

See [4, p. 41], [5, p. 37]. Our next principal result elaborates on the way elliptic elements are mapped into ${\mathcal {T}}$ under the building map. It is known that, if $\omega \in E(G)$, then $\lambda (\omega )=v$, for some $v \in \mathop {{\mathrm {vert}}}({\mathcal {T}})$, and that $G_{\omega }\le G_v$. As usual $G_v$ denotes the stabilizer of the vertex $v$ of ${\mathcal {T}}$ in $G$. It is known [14, Proposition 2, p. 76] that $G_v$ is always finite. We prove the following.

Theorem B

Suppose that $\delta$ is odd.

• (a) Let $v \in \mathop {{\mathrm {vert}}}({\mathcal {T}})$. Then

  $$\begin{aligned} v = \lambda (\omega ),\; for\; some\; \omega \in E(G),\;\; {\textit{if}}\;\; and\;\; only\;\; {\textit{if}}\;\; q^2-1\; divides\; |G_v|. \end{aligned}$$

• (b) Suppose that $\omega \in E(G)$ and $\lambda (\omega )=v$.

  • (i) If $\omega ,\;\overline{\omega }$ are $G$-equivalent, then

    $$\begin{aligned} G_v \cong GL_2({\mathbb {F}}_q). \end{aligned}$$

  • (ii) Otherwise,

    $$\begin{aligned} G_v = G_{\omega } \cong {\mathbb {F}}_{q^2}^*. \end{aligned}$$

Let $\widetilde{v}$ denote the image in $\mathop {{\mathrm {vert}}}(G \backslash {\mathcal {T}})$ of a vertex $v$ of ${\mathcal {T}}$. We put $\widetilde{K}= {\mathbb {F}}_{q^2}K$.

Theorem C

If $\delta$ is odd, there exist bijections between the following sets

• (i) vertices $\widetilde{v}$ of $G{\setminus }{\mathcal {T}}$ such that $q^2 -1$ divides $|G_v|$;

• (ii) conjugacy classes (in $G$) of cyclic subgroups of $G$ of order $q^2 -1$;

• (iii) the orbits of the $Gal(\widetilde{K}/K)$-action on $\mathop {{\mathrm {Ell}}}(G)$.

In particular, among the uncountably many points of $G{\setminus }\Omega$ lying over any given vertex $\widetilde{v}$ of $G{\setminus }{\mathcal {T}}$ there are exactly

• one elliptic point if $G_v\cong GL_2({\mathbb {F}}_q)$;

• two ($Gal(\widetilde{K}/K)$-conjugate) elliptic points if $G_v\cong {\mathbb {F}}_{q^2}^*$;

• no elliptic points in all other cases.

Finally we focus our attention on the important special case where $\delta =1$. It can be shown that a vertex $v$ of ${\mathcal {T}}$ gives rise to an isolated vertex of $G \backslash {\mathcal {T}}$ when (and only when) $\delta =1$ and $v=\lambda (\omega )$ as in Theorem B. Isolated vertices are important for the following reason. If such a vertex and its incident edge arise from a vertex $v$ and incident edge $e$ of ${\mathcal {T}}$, then, from Bass–Serre theory [14, Theorem 13, p. 55],

where $H=G_v$ and $L=G_e$, the stabilizer of $e$. Combining this with the previously discussed results, we can prove our final principal result.

Theorem D

Suppose that $\delta =1$. Then there exists a subgroup $P$ such that

where

$$\begin{aligned} r=\frac{1}{2}(|\mathop {{\mathrm {Ell}}}(G)|-|\mathop {{\mathrm {Ell}}}(G)_2|). \end{aligned}$$

Moreover, if $q\ge 8$ is fixed, then $r$ grows exponentially with the genus of $K$.

This decomposition has a number of interesting consequences.

We recall that $A$ is an arithmetic Dedekind domain with $A^*={\mathbb {F}}_q^*$. In addition $\nu (a)\le 0$, for all $a \in A$. Moreover $\nu (a)=0$ if and only if $a \in {\mathbb {F}}_q^*$. By definition $Z$ consists of all the scalar matrices $\alpha I_2$, where $\alpha \in {\mathbb {F}}_q^*$. As usual, the degree of a prime ideal of $A$ or of a prime divisor of $K$ is the degree of its residue field over the constant field. By linear extension one obtains the degree of any ideal or divisor.

It is well known that if $\delta$ is odd, the place $\infty$ of $K$ has exactly one extension to $\widetilde{K}$, denoted by $\infty '$. In this case, $\widetilde{A}$ is the ring of all those elements of $\widetilde{K}$ which are integral outside $\infty '$. We note that, if $\varepsilon \in {\mathbb {F}}_{q^2}\backslash {\mathbb {F}}_q$, then $\widetilde{A}=A+\varepsilon A$. The action of $Gal(\widetilde{K}/K)$ on $\widetilde{K}$ is given by

$$\begin{aligned} \overline{a+\varepsilon b}=a+\varepsilon ^q b, \end{aligned}$$

where $a,b \in K$. Also, for any set $J$ in $\widetilde{K}$, for example if $J$ is an ideal of $\widetilde{A}$, we write $\overline{J}$ for the conjugate set $\{\overline{x}\ :\ x\in J\}$.

2 Elliptic elements on the Drinfeld upper halfplane $\Omega$

Before our first principal result we record some elementary properties of non-trivial elements of elliptic point stabilizers.

Lemma 2.1

Let $\omega \in \Omega$ be an elliptic element and let $M={\left[ \begin{array}{c@{\quad }c}a&{}b\\ c&{}d\end{array}\right] }$ be a non-scalar element of $G_{\omega }$. Then the minimal polynomial of $\omega$ over $K$ is

$$\begin{aligned} m_{\omega }(x)=x^2+\sigma x+\tau , \end{aligned}$$

where $\sigma =(d-a)/c$ and $\tau =-b/c$.

Proof

Follows from the fact that $M(\omega )=\omega$. Note that $bc\ne 0$, since $\omega \notin K$. $\square$

Before proceeding the following observation is critical.

The matrix $M \in G$ fixes $\omega \in \Omega$ if and only if ${\left[ \begin{array}{c}\omega \\ 1\end{array}\right] }$ is an eigenvector of $M$.

Lemma 2.2

Let $\omega \in \Omega$ be an elliptic point and let $M\in G_{\omega }$ be non-scalar. Then $\omega \in \widetilde{K}$, and ${\left[ \begin{array}{c} \omega \\ 1 \end{array}\right] }$ is an eigenvector of $M$ with eigenvalue $\varepsilon \in {\mathbb {F}}_{q^2}\!\setminus \!{\mathbb {F}}_q$.

Proof

Let

$$\begin{aligned} M= \left[ \begin{array}{c@{\quad }c} a&{}b\\ c&{}d \end{array}\right] . \end{aligned}$$

Then $bc\ne 0$ by Lemma 2.1. It follows that $K(\omega )$ is a quadratic extension of $K$. Now there exists $\varepsilon$ such that

$$\begin{aligned} a\omega +b=\varepsilon \omega \ \ \mathrm {and}\ \ c\omega +d=\varepsilon . \end{aligned}$$

Obviously $K(\omega )=K(\varepsilon )$. Moreover, $\varepsilon$ is an eigenvalue of $M$ and so

$$\begin{aligned} \varepsilon ^2+\eta \varepsilon +\rho =0, \end{aligned}$$

where $\eta =-(a+d)$ and $\rho =\mathop {{\mathrm {det}}}(M)=(ad-bc) \in {\mathbb {F}}_q^*$. Let $B$ denote the integral closure of $A$ in $K(\varepsilon )$. Since $M^{-1}\in G_{\omega }$ has eigenvalue $\varepsilon ^{-1}$, we have $\varepsilon ,\varepsilon ^{-1} \in B^*$. Now $\varepsilon \notin K_{\infty }$ (since $\omega \notin K_{\infty }$), so the place $\infty$ has only one extension $\infty '$ to $K(\varepsilon )$, and $B$ consists of the elements that are integral outside $\infty '$. Since $\varepsilon$ is invertible at all places outside $\infty '$, by the product formula it must also be invertible at $\infty '$ and hence a constant. So $\varepsilon$ is algebraic over ${\mathbb {F}}_q$ and since it generates a quadratic extension of $K$ we conclude that $\varepsilon \in {\mathbb {F}}_{q^2}\backslash {\mathbb {F}}_q$. Thus

$$\begin{aligned} K(\omega )=K(\varepsilon )=\widetilde{K}. \end{aligned}$$

$\square$

Proposition 2.3

[4, p. 50] Let $\omega$ be any elliptic element of any $G$. Then

$$\begin{aligned} G_{\omega } \cong {\mathbb {F}}_{q^2}^*. \end{aligned}$$

This isomorphism is given by mapping $M\in G_{\omega }$ to the eigenvalue of ${\left[ \begin{array}{c}\omega \\ 1\end{array}\right] }$ and it also respects addition of matrices.

Proof

By Lemma 2.2 ${\left[ \begin{array}{c}\omega \\ 1\end{array}\right] }$ is an eigenvector for all $M \in G_{\omega }$ with corresponding eigenvalue $\varepsilon \in {\mathbb {F}}_{q^2}^*$ depending on $M$. Applying $\tau \in Gal(\widetilde{K}/K)$, we see that ${\left[ \begin{array}{c}\overline{\omega }\\ 1\end{array}\right] }$ is an eigenvector with eigenvalue $\varepsilon ^q$. Hence there exists a matrix $X \in GL_2(\widetilde{K})$, such that, for all $M \in G_{\omega }$,

$$\begin{aligned} XMX^{-1}=\mathrm {diag}(\varepsilon ,\varepsilon ^q). \end{aligned}$$

There is therefore a monomorphism

$$\begin{aligned} G_{\omega } \hookrightarrow {\mathbb {F}}_{q^2}^*. \end{aligned}$$

To show that this map is surjective, we observe that by definition $G_{\omega }$ contains a nonscalar $N$ with eigenvalues $\mu ,\mu ^q \in {\mathbb {F}}_{q^2}\!\setminus \!{\mathbb {F}}_q$ and that for all $\alpha ,\beta \in {\mathbb {F}}_q$, with $(\alpha ,\beta ) \ne (0,0)$,

$$\begin{aligned} Y=\alpha I_2+\beta N \in G_{\omega }, \end{aligned}$$

and

$$\begin{aligned} XYX^{-1}=\mathrm {diag}(\alpha +\beta \mu ,\alpha +\beta \mu ^q). \end{aligned}$$

The result follows. $\square$

For an alternative proof of Proposition 2.3 see [4, p. 50].

Corollary 2.4

[4, p. 50] $G$ has elliptic elements if and only if $\delta$ is odd.

Proof

If $\omega$ is an elliptic element then, by definition, $\omega \notin K_{\infty }$. By the proof of Lemma 2.2 there exists $\varepsilon \in {\mathbb {F}}_{q^2}\backslash {\mathbb {F}}_q$ such that $\varepsilon \notin K_{\infty }$. In addition,

$$\begin{aligned} {\mathbb {F}}_{q^2} \subseteq K_{\infty }\; \Longleftrightarrow \; \delta \;\quad \mathrm {is\;even}. \end{aligned}$$

On the other hand, if $\delta$ is odd, every $\varepsilon \in {\mathbb {F}}_{q^2} \backslash {\mathbb {F}}_q$ is fixed by

$$\begin{aligned} M=\left[ \begin{array}{c@{\quad }c} \varepsilon ^q +\varepsilon &{} -\varepsilon ^{q+1}\\ 1 &{} 0\end{array}\right] , \end{aligned}$$

and hence elliptic. $\square$

Actually, one can give a precise description of the elliptic elements of $G$.

Theorem 2.5

Let $\delta$ be odd. Fix any $\varepsilon \in {\mathbb {F}}_{q^2}\!\setminus \!{\mathbb {F}}_q$. Then $\omega$ is an elliptic element of $G$ if and only if

$$\begin{aligned} \omega =\frac{\varepsilon +s}{t} \end{aligned}$$

for some $s,t\in A\;(t\ne 0)$, for which

$$\begin{aligned} (\varepsilon ^q+s)(\varepsilon +s)=tt', \ \hbox {with} \ t' \in A. \end{aligned}$$

Proof

Suppose $\omega =\frac{\varepsilon +s}{t}$ as above. Let

$$\begin{aligned} M_0=\left[ \begin{array}{c@{\quad }c}s'&{}-t'\\ t&{}-s\end{array}\right] , \end{aligned}$$

where $s'=(\varepsilon +\varepsilon ^q)+s$. Then it is easily verified that (non-scalar) $M_0\in G_{\omega }$. Moreover $M_0$ has eigenvalues $\varepsilon$ and $\varepsilon ^q$ and determinant $\varepsilon ^{q+1}\in {\mathbb {F}}_q^*$.

Conversely, let $\omega \in \Omega$ be elliptic. By Proposition 2.3 we can choose $M={\left[ \begin{array}{c@{\quad }c}a&{}b\\ c&{}d\end{array}\right] }$ in $G_{\omega }$ such that $\varepsilon (M)=\varepsilon$. Then from the proof of Lemma 2.2

$$\begin{aligned} \omega =(\varepsilon -d)/c. \end{aligned}$$

Now $M(\omega )=\omega$ and so

$$\begin{aligned} c\omega ^2+(d-a)\omega -b=0. \end{aligned}$$

Let $\omega '$ be the other root of this quadratic equation. Then $\omega '=\frac{\varepsilon ^q +s}{t}$ and

$$\begin{aligned} \omega \omega '=-b/c=(\varepsilon ^q-d)(\varepsilon -d)/c^2. \end{aligned}$$

Thus the condition is satisfied with $s=-d$ and $t=c$. $\square$

If $\omega =\frac{\varepsilon +s}{t}$ is elliptic and $M\in G_\omega$, then from $M\omega =\omega$ one immediately obtains $M\overline{\omega }=\overline{\omega }$. So the conjugate $\overline{\omega }=\frac{\varepsilon ^q +s}{t}$ is also elliptic with the same stabilizer, i.e.

$$\begin{aligned} G_{\overline{\omega }}=G_{\omega }. \end{aligned}$$

A finer analysis of this in the next three sections will lead to some interesting group-theoretic consequences. Among many others we will need the following easy intermediate result.

Lemma 2.6

If $\delta$ is odd, mapping $\{\omega , \overline{\omega }\}$ to $G_{\omega }=G_{\overline{\omega }}$ is a natural bijection between the unordered pairs $\{\omega , \overline{\omega }\}$ of conjugate elliptic points and cyclic subgroups of $G$ of order $q^2 -1$.

Proof

The inverse map is given by mapping the cyclic subgroup to its two fixed points $\{\omega , \overline{\omega }\}$. These are indeed elliptic. If not, they would lie in $K_\infty$, and consequently the eigenvalue of the eigenvector ${\left[ \begin{array}{c}\omega \\ 1\end{array}\right] }$ would be in $K_\infty \cap {\mathbb {F}}_{q^2}^*={\mathbb {F}}_q^*$, in contradiction to the order of the subgroup. $\square$

Lemma 2.6 also shows that if $\delta$ is odd, then the intersection of any two cyclic subgroups of $G$ of order $q^2 -1$ is exactly $Z$.

We conclude this section with a further restriction on the factor $t$ in Theorem 2.5 which we make use of later on.

Lemma 2.7

Let $\omega =\frac{\varepsilon +s}{t}\in \Omega$ be an elliptic element as in Theorem 2.5. Then

• (a) $\deg ({\mathfrak {p}})$ is even for every prime ideal ${\mathfrak {p}}$ of $A$ that divides $tA$.

• (b) $\nu (t)$ is even.

Proof

(a) Let ${\mathfrak {p}}$ be a prime ideal of $A$ of odd degree. Then ${\mathfrak {p}}$ is inert in $\widetilde{A}$. Let $\widetilde{{\mathfrak {p}}}$ be the prime ideal in $\widetilde{A}$ above ${\mathfrak {p}}$. If ${\mathfrak {p}}$ divides $(t)$ in $A$, then $\widetilde{{\mathfrak {p}}}$ divides $(\varepsilon +s)(\varepsilon ^q +s)$ in $\widetilde{A}$. Since $\widetilde{{\mathfrak {p}}}$ is a prime ideal, it must divide one of the two factors. Applying the Frobenius automorphism of $\widetilde{K}/K$, it also divides the other factor. Hence $\widetilde{{\mathfrak {p}}}$ divides $(\varepsilon -\varepsilon ^q) =\widetilde{A}$, a contradiction.

(b) By (a) and the product formula $\delta \nu (t)$ is even, and $\delta$ is odd by Corollary 2.4. $\square$

3 Elliptic points on the Drinfeld modular curve $G{\setminus }\Omega$

In view of Corollary 2.4 we assume throughout this section that $\delta$ is odd.

Central to the definition of $G \backslash \Omega$ is the following equivalence relation.

Definition

Let $\omega _1, \omega _2 \in \Omega$. We say that $\omega _1,\omega _2$ are $G$ -equivalent, written $\omega _1 \equiv \omega _2$, if and only if there exists $g \in G$ such that

$$\begin{aligned} \omega _1=g(\omega _2). \end{aligned}$$

If $\omega _1=g(\omega _2)$ then

$$\begin{aligned} gG_{\omega _2}g^{-1}=G_{\omega _1}. \end{aligned}$$

It follows that $G$-equivalent points of $\Omega$ have isomorphic stabilizers in $G$. As we shall see the converse does not hold.

It is clear that $G$ acts on its elliptic points, $E(G)$. We denote the set of equivalence classes by $\mathop {{\mathrm {Ell}}}(G)$. The elements of this set are referred to as the elliptic points of $G$.

In particular if $\delta$ is odd, then from Theorem 2.5 every $\varepsilon \in {\mathbb {F}}_{q^2}\setminus {\mathbb {F}}_q$ is an elliptic point of $G$. Moreover, if $\varepsilon$ and $\varepsilon '$ are any two elements of ${\mathbb {F}}_{q^2}\backslash {\mathbb {F}}_q$, then $\varepsilon '=\alpha \varepsilon +\beta$ for some $\alpha \in {\mathbb {F}}_q^*,\; \beta \in {\mathbb {F}}_q$ and hence

$$\begin{aligned} \varepsilon \equiv \varepsilon '. \end{aligned}$$

In particular, $\varepsilon \equiv \overline{\varepsilon }$. However, this does not always hold for general elliptic points. For an arbitrary elliptic point $\omega$ we will investigate later the precise conditions under which $\omega$ and $\overline{\omega }$ are $G$-equivalent. (They are not always equivalent despite the fact that $G_{\omega }=G_{\overline{\omega }}$.)

Lemma 3.1

Let

$$\begin{aligned} \omega =\frac{\varepsilon +s}{t} \end{aligned}$$

be an elliptic element, where $\varepsilon ,s,t$ are as defined in Theorem 2.5. Then

• (a) $J_{\omega }:=t A+(\varepsilon +s)A\; \trianglelefteq \; \widetilde{A}$.

• (b) The ideal $J_{\omega }$ does not depend on the choice of $\varepsilon \in {\mathbb {F}}_{q^2}\!\setminus \!{\mathbb {F}}_q$.

Proof

• (a) It suffices to prove that $\varepsilon J_{\omega }\subseteq J_{\omega }$. Now

  $$\begin{aligned} \varepsilon t=t(\varepsilon +s)-st \in J_{\omega }. \end{aligned}$$

  On the other hand,

  $$\begin{aligned} \varepsilon (\varepsilon +s)=(\varepsilon +\varepsilon ^q)(\varepsilon +s) -(\varepsilon ^q+s) (\varepsilon +s)+s(\varepsilon +s) \in J_{\omega }, \end{aligned}$$

  by the properties of $\varepsilon ,s,t$.

• (b) Choosing a different $\varepsilon '\in {\mathbb {F}}_{q^2}\!\setminus \!{\mathbb {F}}_q$, there exist $\alpha \in {\mathbb {F}}_q^*$ and $\beta \in {\mathbb {F}}_q$ with $\varepsilon '=\alpha \varepsilon +\beta$. So $\omega =\frac{\varepsilon '-\beta +\alpha s}{\alpha t}$, which gives the same ideal. $\square$

Let $A_0$ denote $A$ or $\widetilde{A}$. If $I,I'$ are ideals in $A_0$, we write

$$\begin{aligned} I \sim _{A_0} I' \Longleftrightarrow aI=bI', \end{aligned}$$

for some non-zero $a,b \in A_0$.

Our next result is crucial since it enables us to identify $\mathop {{\mathrm {Ell}}}(G)$ with a subgroup of $\mathrm {Cl}(\widetilde{A})$.

Lemma 3.2

Let $\omega$ and $\omega '$ be elliptic elements of $G$. Then

$$\begin{aligned} \omega \equiv \omega ' \;\Longleftrightarrow \; J_{\omega } \sim _{\widetilde{A}}J_{\omega '}. \end{aligned}$$

Proof

Let $\omega =\frac{\varepsilon +s}{t}$ and $\omega '= \frac{\varepsilon +s'}{t'}$. Then

$$\begin{aligned} tA+(\varepsilon +s)A\sim _{\widetilde{A}} t'A+(\varepsilon +s')A \end{aligned}$$

if and only if there exist $a,b,c,d \in A$ with $ad-bc \in {\mathbb {F}}_q^*$ and a non-zero $\rho \in \widetilde{K}$ such that

$$\begin{aligned} \rho t'=(at+b(\varepsilon +s))\;\ \mathrm {and}\;\ \rho (\varepsilon +s')=(ct+d(\varepsilon +s)). \end{aligned}$$

$\square$

Mapping an elliptic element $\omega$ to the ideal class $[J_{\omega }]\in \mathrm {Cl}(\widetilde{A})$ induces by Lemma 3.2 an injective map from $\mathop {{\mathrm {Ell}}}(G)$ into $\mathrm {Cl}(\widetilde{A})$. In order to describe its image, we need the norm map $N$ from ideals of $\widetilde{A}$ to ideals of $A$, and also from divisors of $\widetilde{K}$ to divisors of $K$.

If $\widetilde{P}$ is a prime ideal of $\widetilde{A}$, then $N(\widetilde{P})=P^{f(\widetilde{P}/P)}$ where $P=\widetilde{P}\cap A$ is the underlying prime ideal of $A$ and $f(\widetilde{P}/P)$ is the inertia degree. This definition is then canonically extended to products. (See [17, Ch. V, §11, p. 306].) Analogously for divisors (cf. [12, p. 82]).

In our simple situation we can equivalently say: If $J\trianglelefteq \widetilde{A}$, then $N(J)$ is the $A$-ideal $J\overline{J}\cap A$.

Actually, $N(J)$ is also the $A$-ideal generated by all norms of elements in $J$ [17, Ch. V, §11, Lemma 3, p. 307], but this is not completely obvious. And in practice it is more awkward to handle than the other properties.

The norm map $N$ induces group homomorphisms

$$\begin{aligned} \overline{N}: \mathrm {Cl}(\widetilde{A})\longrightarrow \mathrm {Cl}(A) \end{aligned}$$

and

$$\begin{aligned} \overline{N}: \mathrm {Cl}^0(\widetilde{K})\longrightarrow \mathrm {Cl}^0(K). \end{aligned}$$

Since $\delta$ is odd, both norm maps are surjective. As $\infty$ is inert in $\widetilde{K}$ by [12, Proposition 8.13], we can apply [11, Proposition 2.2] which tells us that $\overline{N}$ is surjective onto $\mathrm {Cl}(A)$. The surjectivity onto $\mathrm {Cl}^0(K)$ is known from the theory of Jacobian varieties. Alternatively, by [11, Lemma 1.2] we have

$$\begin{aligned} |\mathrm {Cl}(\widetilde{A})|=\delta |\mathrm {Cl}^0(\widetilde{K})|\ \;\mathrm {and}\ \;|\mathrm {Cl}(A)|=\delta |\mathrm {Cl}^0(K)|. \end{aligned}$$

So one surjectivity implies the other one.

Our next goal is to show that the kernel of $\overline{N}$ is the image of $\mathop {{\mathrm {Ell}}}(G)$. The following description of an element of $\mathrm {Cl}(\widetilde{A})$ is essential for our purposes.

Lemma 3.3

Let $J \trianglelefteq \widetilde{A}$. Then, for any fixed $\varepsilon \in {\mathbb {F}}_{q^2} \backslash {\mathbb {F}}_q$, there exist $a\in A$ and an ideal $I \trianglelefteq A$ such that

$$\begin{aligned} J \sim _{\widetilde{A}} J'=I+(\varepsilon +a) A. \end{aligned}$$

Moreover $J' \cap A= I$ and $N(J')=I$.

Proof

Now $\widetilde{A}=A+\varepsilon A$ and so, by [2, Chapter VII, Section 4.10, Proposition 24], there exists $a,b \in A$ and an $A$-module $I'$, $A$-isomorphic to an $A$-ideal such that

$$\begin{aligned} J=I'+(a+\varepsilon b) A. \end{aligned}$$

Since $A$ is Dedekind there are two possibilities.

(a) :

$I'=x A,\; {\textit{for}}\; {\textit{some}}\; {\textit{nonzero}}\; x\in \widetilde{A}$:

Then

$$\begin{aligned} J \sim _{\widetilde{A}} \overline{x}J. \end{aligned}$$

By multiplying by another term in $A$ (to “clear denominators”) we may assume that $x \in A$.

(b) :

$I'= Ax+Ay,\; {\textit{with}}\; ey=fx\ne 0,\;{\textit{where}}\;x,y \in \widetilde{A}\;{\textit{and}}\; e,f \in A$:

Replacing $J$ with $fy^{-1}J$ and then “clearing denominators” as above we may assume that $x,y \in A$.

From now on we replace $I'$ with $I$, where $I\trianglelefteq A$. Let $i\in I$. Then $i\varepsilon \in J$ and so $i=bb'$, where $b' \in A$. On the other hand $\varepsilon (a+\varepsilon b) \in J$, and since $\varepsilon ^2 =\alpha \varepsilon +\beta$ with $\alpha ,\beta \in {\mathbb {F}}_q$, this implies $a=bb''$, where $b'' \in A$. We now replace $J$ with $J'=b^{-1}J$, which has the desired form.

Moreover, $J'\cap A= I$ is obvious. Finally,

$$\begin{aligned} J'\overline{J'}=I^2+I(\varepsilon -a)+I(\varepsilon ^q -a)+ (\varepsilon -a)(\varepsilon ^q -a)A \subseteq I^2+I\widetilde{A}+(J'\cap A)\subseteq I\widetilde{A}. \end{aligned}$$

Conversely, $J'\overline{J'}$ contains $I(\varepsilon -a)-I(\varepsilon ^q -a)$, and hence $I(\varepsilon -\varepsilon ^q)=I\widetilde{A}$. So together $J'\overline{J'}=I\widetilde{A}$ and thus $N(J')=I$. $\square$

Theorem 3.4

Mapping an elliptic element $\omega$ to the ideal class $[J_{\omega }]$ in $\mathrm {Cl}(\widetilde{A})$ induces a bijection between $\mathop {{\mathrm {Ell}}}(G)$ and the kernel of the surjective norm map $\overline{N}: \mathrm {Cl}(\widetilde{A}) \longrightarrow \mathrm {Cl}(A)$.

Proof

If $\omega =\frac{\varepsilon +s}{t}$ is elliptic, then the ideal $J_{\omega }=tA+(\varepsilon +s)A$ from Lemma 3.1 has norm $tA$ by Lemma 3.3. So $[J_{\omega }]$ lies in the kernel of $\overline{N}$.

Conversely, we represent each element $[J]$ of $\mathrm {Cl}(\widetilde{A})$ by an ideal $J$ of the form given by Lemma 3.3. Then $[J] \in \mathrm {Ker}\;\overline{N}$ if and only if $N(J)=I$ is principal, i.e. if and only if

$$\begin{aligned} J=A c+A(a+\varepsilon ), \end{aligned}$$

for some non-zero $a,c \in A$.

Note that, if $J$ is of this form, then $(a+\varepsilon ) (a+\varepsilon ^q)=cc'$, for some $c' \in A$, since $J\cap A=I$. Suppose that $A c+A a\ne A$. Then there exists a prime $\widetilde{A}$-ideal, ${\mathfrak {p}}$, containing $a,c$. Thus $(a+\varepsilon )(a+\varepsilon ^q) \in {\mathfrak {p}}$ and so $\varepsilon \in {\mathfrak {p}}$, which implies that ${\mathfrak {p}}=\widetilde{A}$. Hence $A c+A a=A$ and so $J$ is determined by the elliptic point $\omega =(a+\varepsilon )/c$. (See Theorem 2.5.) $\square$

So far, $|\mathop {{\mathrm {Ell}}}(G)|$ seems to depend on the ring $A$, of which there are infinitely many non-isomorphic ones in the same function field $K$. But one can go one step further.

Lemma 3.5

The canonical map from $\mathrm {Cl}^0(\widetilde{K})$ to $\mathrm {Cl}(\widetilde{A})$ restricts to an isomorphism of abelian groups between the kernel of $\overline{N}: \mathrm {Cl}^0(\widetilde{K}) \longrightarrow \mathrm {Cl}^0(K)$ and the kernel of $\overline{N}: \mathrm {Cl}(\widetilde{A}) \longrightarrow \mathrm {Cl}(A)$.

Proof

Mapping the divisor $\prod \limits P^{e_P}$ of $\widetilde{K}$ to the fractional ideal $\prod \nolimits _{P\ne \infty }P^{e_P}$ of $\widetilde{A}$ induces an isomorphism from ${\mathrm {Cl}}^0(\widetilde{K})$ to a subgroup of index $\delta$ in ${\mathrm {Cl}}(\widetilde{A})$, namely to the classes consisting of ideals whose degrees are divisible by $\delta$. (Compare [12, Proposition 14.1].) But the degree of every principal ideal of $A$ obviously is divisible by $\delta$. So if the ideal class $[J]$ is in the kernel of $\overline{N}$, then $\delta$ divides $\deg (N(J))=2\deg (J)$ and hence $\deg (J)$ since $\delta$ is odd. Now one easily verifies that the map induces the desired isomorphism. $\square$

Corollary 3.6

[4, p. 50] With the above notation,

$$\begin{aligned} |\mathop {{\mathrm {Ell}}}(G)|=L_K(-1). \end{aligned}$$

Proof

Combining Theorem 3.4 and Lemma 3.5 with [15, Theorem V.1.15 (c), (f)], we have

$$\begin{aligned} |\mathop {{\mathrm {Ell}}}(G)|=\frac{|\mathrm {Cl^0}(\widetilde{K})|}{|\mathrm {Cl^0}(K)|} =\frac{L_{\widetilde{K}}(1)}{L_K(1)}=L_K(-1). \end{aligned}$$

$\square$

Corollary 3.6 (as well as Proposition 2.3 and Corollary 2.4) is already known [4, p. 50]. However our approach is more elementary than that of Gekeler. In particular it avoids any mention of the fact that $G\backslash \Omega$ is a component of the moduli scheme for Drinfeld $A$-modules of rank $2$. In addition, at this stage we don’t yet need the building map $\lambda : \Omega \longrightarrow {\mathcal {T}}$, where ${\mathcal {T}}$ is the Bruhat–Tits tree associated with $G$. (See [14, Chapter II, Section 1.1], [4, p. 41].)

The remaining results in this section will elaborate on the structure of $\mathop {{\mathrm {Ell}}}(G)$.

Lemma 3.7

• (a) For $q\ge 4$ there exists only one non-rational function field $K$ with $|\mathop {{\mathrm {Ell}}}(G)|=1$, namely

  $$\begin{aligned} K={\mathbb {F}}_4(x,y)\ \ \hbox { with}\ \ y^2 +y=x^3. \end{aligned}$$

• (b) More generally, for any positive integer $n$ there are only finitely many nonrational function fields $K$ with $q\ge 3$ and $|\mathop {{\mathrm {Ell}}}(G)|=n$.

Proof

Using Corollary 3.6 and the Riemann Hypothesis for function fields [15, Theorem 5.2.1], [15, Theorem 5.1.15(e)] we have

$$\begin{aligned} n=|\mathop {{\mathrm {Ell}}}(G)|=L_K(-1) \ge (\sqrt{q}-1)^{2g}. \end{aligned}$$

For given $n$ this bounds $q$, and for $q>4$ it also bounds $g$.

In particular, $n=1$ is only possible for $q\le 4$; and if $n=1$ for $q=4$, then necessarily $L_K(u)=(1+2u)^{2g}$.

A function field $K$ over ${\mathbb {F}}_q$ with $L_K(u)=(1+\sqrt{q}u)^{2g}$ is called maximal. Equivalently, a maximal function field is a function field with $q+1+2g\sqrt{q}$ places of degree $1$.

By Ihara’s Theorem [15, Proposition 5.3.3] the genus of a maximal function field is bounded by $g\le \frac{q-\sqrt{q}}{2}$. For $q=4$ this leaves only the possibility $g=1$. But it is well known that $y^2+y=x^3$ is the only elliptic function field over ${\mathbb {F}}_4$ with $L$-polynomial $(1+2u)^2$. Alternatively one could invoke [13, Theorem] here. This finishes the proof of (a).

For (b) we still have to take care of the cases $q=3$ and $4$. We exploit the following lower bound for the class number from [15, Exercise 5.8, p. 213]

$$\begin{aligned} L_K(1)\ge \frac{q-1}{2}\cdot \frac{q^{2g}+1-2gq^g}{g(q^{g+1}-1)}\ge \frac{q-1}{2}\cdot \frac{q^{2g}-2gq^g}{gq^{g+1}}= \frac{q-1}{2} \left( \frac{q^{g-1}}{g}-\frac{2}{q}\right) . \end{aligned}$$

Applied to the field $\widetilde{K}$ this yields

$$\begin{aligned} L_{\widetilde{K}}(1)\ge \frac{c\cdot q^{2g}}{g} \end{aligned}$$

where $c$ is a nonzero constant depending on $q$. Combined with the upper bound

$$\begin{aligned} L_K(1)\le (\sqrt{q}+1)^{2g} \end{aligned}$$

from the Riemann Hypothesis [15, Theorem 5.2.1], [15, Theorem 5.1.15(e)] this shows

$$\begin{aligned} |\mathop {{\mathrm {Ell}}}(G)|=\frac{L_{\widetilde{K}}(1)}{L_K(1)}\ge \frac{c\cdot q^{2g}}{g(\sqrt{q}+1)^{2g}}. \end{aligned}$$

So $|\mathop {{\mathrm {Ell}}}(G)|$ goes to infinity with $g$ provided $q\ge 3$. $\square$

We apply Lemma 3.2 to the cases for which $L_K(-1)=1$. (One such is the genus zero case $K={\mathbb {F}}_q(T)$.) Let $\varepsilon \in {\mathbb {F}}_{q^2} \backslash {\mathbb {F}}_q$. Then, if $\omega$ is any elliptic point, there exists $g \in G$ such that $g(\omega )=\varepsilon$. In particular, then $\omega \equiv \overline{\omega }$ for all elliptic points.

We will determine now when this happens in general. By Lemma 3.3 we have

$$\begin{aligned} J_{\omega }J_{\overline{\omega }}=J_{\omega }\overline{J_{\omega }}= N(J_{\omega })\widetilde{A}=t\widetilde{A}. \end{aligned}$$

It follows that in $\mathrm {Cl}(\widetilde{A})$

$$\begin{aligned}{}[J_{\overline{\omega }}]=[J_{\omega }]^{-1}. \end{aligned}$$

Hence

$$\begin{aligned} \omega \equiv \overline{\omega }\Longleftrightarrow [J_{\omega }]^2=1 \end{aligned}$$

in $\mathrm {Cl}(\widetilde{A})$, or equivalently, in $\mathrm {Cl}^0(\widetilde{K})$.

Definition

Let $\mathop {{\mathrm {Ell}}}(G)_2$ be the subset of $\mathop {{\mathrm {Ell}}}(G)$ consisting of those orbits of elliptic elements for which $\overline{\omega } \equiv \omega$.

We have just proved the following result.

Theorem 3.8

The bijection between $\mathop {{\mathrm {Ell}}}(G)$ and the kernel of the norm map $\overline{N}$ described in Theorem 3.4 restricts to a bijection between $\mathop {{\mathrm {Ell}}}(G)_2$ and the $2$-torsion subgroup of the kernel of $\overline{N}$ in $\mathrm {Cl}(\widetilde{A})$, or by Lemma 3.5 equivalently, the $2$-torsion subgroup of the kernel of $\overline{N}$ in $\mathrm {Cl}^0(\widetilde{K})$.

In particular, $|\mathop {{\mathrm {Ell}}}(G)|$ and $|\mathop {{\mathrm {Ell}}}(G)_2|$ only depend on $K$, not on the choice of the place $\infty$ (apart from the general condition that $\delta$ has to be odd).

Hence if $\mathop {{\mathrm {Ell}}}(G)=\mathop {{\mathrm {Ell}}}(G)_2$ (for example, when $L_K(-1)=1$) it follows that $\omega \equiv \overline{\omega }$ for all $\omega \in E(G)$. On the other hand we can prove the following.

Theorem 3.9

• (a) For $q\ge 8$ there are only two function fields $K$ of genus $g>0$ for which $\mathop {{\mathrm {Ell}}}(G)=\mathop {{\mathrm {Ell}}}(G)_2$, namely

  $$\begin{aligned} K={\mathbb {F}}_9(x,y)\ \ with\ \ y^3+y=x^4\ \ (genus\;3) \end{aligned}$$

  and

  $$\begin{aligned} K={\mathbb {F}}_9(x,y)\ \ with\ \ y^2=x^3-x\ \ (genus\;1). \end{aligned}$$

• (b) For fixed $q\ge 8$ we have $\lim \limits _{g\rightarrow \infty } \frac{|\mathop {{\mathrm {Ell}}}(G)_2|}{|\mathop {{\mathrm {Ell}}}(G)|}=0$.

Proof

(a) By Corollary 3.6 and the Riemann Hypothesis for function fields [15, Theorem 5.2.1], [15, Theorem 5.1.15(e)]

$$\begin{aligned} |\mathop {{\mathrm {Ell}}}(G)|=L_K(-1) \ge (\sqrt{q}-1)^{2g}. \end{aligned}$$

On the other hand, the $2$-torsion rank of an abelian variety of dimension $g$ is bounded by $2g$, and even by $g$ if the characteristic is $2$. Applying this to $\mathrm {Cl}^0(\widetilde{K})$ (compare [12, Chapter 11]) we get

$$\begin{aligned} |\mathop {{\mathrm {Ell}}}(G)_2| \le 2^{2g}, \end{aligned}$$

and even $|\mathop {{\mathrm {Ell}}}(G)_2| \le 2^g$ if the characteristic is $2$. This proves both claims if $q>9$ and also if $q=8$.

For the remaining case $q=9$ we note that by the same argument $|\mathop {{\mathrm {Ell}}}(G)|=|\mathop {{\mathrm {Ell}}}(G)_2|$ is only possible if $L_K(u)=(1+3u)^{2g}$, that is, if $K$ is a maximal function field. Then Ihara’s Theorem [15, Proposition 5.3.3] implies $g\le 3$. Moreover, $g=2$ is not possible, because then $K$ would be hyperelliptic, i.e. a double covering of a rational function field ${\mathbb {F}}_9(T)$, and hence could have at most $2(9+1)<22$ places of degree $1$.

By [13, Theorem] there is a unique maximal function field of genus 3 over ${\mathbb {F}}_9$, namely ${\mathbb {F}}_9(x,y)$ with $y^3 +y=x^4$. Furthermore, by [13, Lemma 1] this function field has $\mathrm {Cl}^0(K)\cong \bigoplus _{i=1}^{6}{\mathbb {Z}}/4{\mathbb {Z}}$. Since $L_{\widetilde{K}}(t)=(1-9t)^6$, by the same argument we have $\mathrm {Cl}^0(\widetilde{K})\cong \bigoplus _{i=1}^{6}{\mathbb {Z}}/8{\mathbb {Z}}$, and hence the kernel of the norm map is indeed isomorphic to $\bigoplus _{i=1}^{6}{\mathbb {Z}}/2{\mathbb {Z}}$.

For $g=1$ we use the well-known fact that $y^2=x^3-x$ is the only elliptic function field over ${\mathbb {F}}_9$ with $L$-polynomial $(1+3u)^2$ or some explicit calculations with Weierstrass equations.

Finally, to prove claim (b) for $q=9$ we bound $|\mathop {{\mathrm {Ell}}}(G)|$ from below by exactly the same procedure as in the proof of Lemma 3.7. Then $\frac{|\mathop {{\mathrm {Ell}}}(G)_2|}{|\mathop {{\mathrm {Ell}}}(G)|}\le \frac{g\cdot 8^{2g}}{c\cdot 9^{2g}}$, which goes to 0. $\square$

When $q>9$ and $g>0$ therefore $G$ has an elliptic point $\omega _0$ which is not equivalent to $\overline{\omega _0}$. As we shall see in the next two sections, points like these have a special significance for the Bruhat–Tits tree and the structure of $G$.

Remark 3.10

It is not clear whether for $q\le 7$ there are only finitely many function fields $K$ with $\mathop {{\mathrm {Ell}}}(G)=\mathop {{\mathrm {Ell}}}(G)_2$. And even if one could prove finiteness, the actual determination of all such fields would be a tedious task.

Let us consider the special case where $K$ is a quadratic extension of a rational function field ${\mathbb {F}}_q(T)$, that is, $K$ is hyperelliptic or possibly elliptic. In this case the degree $4$ Galois extension $\widetilde{K}/{\mathbb {F}}_q(T)$ has $3$ intermediate extensions, namely $K$, ${\mathbb {F}}_{q^2}(T)$, and the unramified quadratic twist of $K$, which we denote by $K'$.

Now the kernel of the norm map from $\mathrm {Cl}^0(\widetilde{K})$ to $\mathrm {Cl}^0(K)$ is isomorphic to $\mathrm {Cl}^0(K')$. So the determination of all hyperelliptic $K$ with $\mathop {{\mathrm {Ell}}}(G)=\mathop {{\mathrm {Ell}}}(G)_2$ is equivalent to the determination of all hyperelliptic function fields with divisor class group of exponent $2$.

For the more special case where in addition a degree $1$ place of ${\mathbb {F}}_q(T)$ is ramified in $K'$ this is the goal of the paper [1]. But even then case-by-case arguments and a computer search were needed.

More importantly, on the way from [1, Theorem 21] to [1, Theorem 37] several cases, including among others for $h=8$ the cases $q=5$, $g=2$ and $q=3$, $g=3,4$ as well as $q=2$, $4\le g\le 8$ seem to have got lost, and consequently the main result of that paper is incomplete. Without claim for completeness we point out some missing elliptic function fields $K'$ with ${\mathrm {Cl}}^0(K')\cong {\mathbb {Z}}/2{\mathbb {Z}}\oplus {\mathbb {Z}}/2{\mathbb {Z}}$, to wit

$$\begin{aligned} K'&= {\mathbb {F}}_3(x,y) \hbox { with } y^2=x^3-x,\\ K'&= {\mathbb {F}}_5(x,y) \hbox { with } y^2=x^3+x,\\ K'&= {\mathbb {F}}_7(x,y) \hbox { with } y^2=x^3-1,\\ K'&= {\mathbb {F}}_9(x,y) \hbox { with } y^2=x^3-\sqrt{-1}x. \end{aligned}$$

The last example is the unramified quadratic twist of the exceptional $K$ in Theorem 3.9(a).

4 The images of elliptic points on the Bruhat–Tits tree ${\mathcal {T}}$

Associated with the group $GL_2(K_{\infty })$ is its Bruhat–Tits building which in this case is a $(q^{\delta }+1)$-regular tree, ${\mathcal {T}}$. The most convenient description for our purposes is the one in [14, Chapter II, Section 1]. See also [5, Section 1.3]. The vertices of ${\mathcal {T}}$ are the homothety classes of ${\mathcal {O}}_\infty$-lattices of rank $2$ in $K_\infty \oplus K_\infty$. Two such vertices are joined by an edge if they contain lattices $L_1$ and $L_2$ such that $L_2$ is a maximal ${\mathcal {O}}_\infty$-sublattice of $L_1$. This definition is of course symmetric, because then $\pi L_1$ is a maximal sublattice of $L_2$.

Via its natural embedding into $GL_2(K_\infty )$, the group $G$ acts on ${\mathcal {T}}$ without inversion [14, Corollary, p. 75]. Classical Bass–Serre theory [14, Theorem 13, p. 55] shows how the structure of $G$ can be derived from that of the quotient graph $G\backslash {\mathcal {T}}$. The structure of this quotient is described in [14, Theorem 9, p. 106]. (Serre’s approach uses the theory of vector bundles. For a more elementary approach see [7, Theorem 4.7].) In the sequel we will write $v$ and $e$ for vertices respectively edges of ${\mathcal {T}}$ and $\widetilde{v}$ and $\widetilde{e}$ for their images in $G\backslash {\mathcal {T}}$.

A central object in the study of Drinfeld’s half-plane is the building map

$$\begin{aligned} \lambda : \Omega \longrightarrow {\mathcal {T}}. \end{aligned}$$

See [4, p. 41], [5, Section 1.5]. We only mention the facts that we need and refer to the literature for a thorough description.

If $|\cdot |$ denotes the multiplicative valuation on $C_\infty$, then every $\omega \in \Omega$ defines a norm $v_\omega (u,v):=|u\omega +v|$ on the vector space $K_\infty \oplus K_\infty$. By a theorem of Goldman and Iwahori there are two types of such norms. If the unit ball of $v_\omega$ is an ${\mathcal {O}}_\infty$-lattice $L$ in $K_\infty \oplus K_\infty$, then $\lambda (\omega )$ is the vertex of ${\mathcal {T}}$ given by the homothety class of $L$. In all other cases $v_\omega$ is a “convex combination” of two norms that are of the former type and belong to two neighbouring vertices. Correspondingly $\lambda$ then maps $\omega$ to a point on the edge joining these two vertices.

Another important feature is that $\lambda$ respects the actions of $GL_2(K_\infty )$ on $\Omega$ and ${\mathcal {T}}$, that is

$$\begin{aligned} \lambda (g(\omega ))=g(\lambda (\omega )). \end{aligned}$$

In particular, $\lambda$ induces a map from the quotient space $G{\setminus }\Omega$ to the quotient graph $G{\setminus }{\mathcal {T}}$. Important information about $G{\setminus }\Omega$ is encoded in the (in a certain sense) simpler object $G{\setminus }{\mathcal {T}}$ (see for example [5]). Here we explore this theme with respect to elliptic points.

Lemma 4.1

If $\omega \in \Omega$ is an elliptic element, then $\lambda (\omega )$ is a vertex of ${\mathcal {T}}$ and $G_{\omega }$ is a subgroup of $G_{\lambda (\omega )}$. Moreover, $\lambda (\omega )= \lambda (\overline{\omega })$.

Proof

If $\delta$ is odd, for every $\varepsilon \in {\mathbb {F}}_{q^2}\setminus {\mathbb {F}}_q$ the associated norm $v_{\varepsilon }((u,v))=|u\varepsilon +v|$ on $K_\infty \oplus K_\infty$ obviously is the maximum norm $\max \{|u|,|v|\}$, whose unit ball is the standard lattice ${\mathcal {O}}_\infty \oplus {\mathcal {O}}_\infty$. So all $\varepsilon \in {\mathbb {F}}_{q^2}\setminus {\mathbb {F}}_q$ map to the standard vertex in ${\mathcal {T}}$.

Now if $\omega$ is any elliptic point, by Theorem 2.5 we have $\omega =\frac{\varepsilon +s}{t}$ and $\overline{\omega }=\frac{\varepsilon ^q +s}{t}$ for suitable $s,t\in A$. So under $\lambda$ both, $\omega$ and $\overline{\omega }$ map to the same vertex of ${\mathcal {T}}$, namely the image of the standard vertex under the action of ${1\ s\atopwithdelims ()0\ t}\in GL_2(K_\infty )$.

The fact $G_\omega \le G_{\lambda (\omega )}$ is clear. (See also [5, (1.5.3), p. 37].) $\square$

We recall [14, Proposition 2, p. 76] that the elements of finite order in $G$ are precisely those in

$$\begin{aligned} \bigcup _{v \in \mathop {{\mathrm {vert}}}({\mathcal {T}})}G_v. \end{aligned}$$

We note that

$$\begin{aligned} Z\le G_e\cap G_\omega , \end{aligned}$$

for all $e \in \mathop {{\mathrm {edge}}}({\mathcal {T}})$ and $\omega \in E(G)$. Hence $q-1$ divides all $|G_v|$.

Let $\omega \in E(G)$. Then we know that $G_{\omega } \le G_{\lambda (\omega )}$ and consequently $q^2-1$ divides $|G_{\lambda (\omega )}|$, by Proposition 2.3. One of the main aims of this section is to establish the converse of this result. However, for that we need a few lemmata.

Lemma 4.2

Let $M\in G_v$. Then the eigenvalues of $M$ lie in ${\mathbb {F}}_{q^2}$.

Proof

The characteristic polynomial of $M$ is

$$\begin{aligned} t^2-\tau t+\eta , \end{aligned}$$

where $\tau =\mathrm {tr}(M)$ and $\eta =\mathop {{\mathrm {det}}}(M)\in {\mathbb {F}}_q^*$. Now $M$ has finite order and so $\tau$ lies in the algebraic closure of ${\mathbb {F}}_q$ in $A$ which is ${\mathbb {F}}_q$. $\square$

Lemma 4.3

Let $w \in \mathop {{\mathrm {vert}}}({\mathcal {T}})\cup \mathop {{\mathrm {edge}}}({\mathcal {T}})$. Suppose that $M_1,M_2$ are matrices in $G_w$. If

$$\begin{aligned} \mathop {{\mathrm {det}}}(\alpha _1M_1+\alpha _2M_2) \in {\mathbb {F}}_q^*, \end{aligned}$$

where $\alpha _1,\alpha _2 \in {\mathbb {F}}_q$, then

$$\begin{aligned} \alpha _1M_1+\alpha _2M_2 \in G_w. \end{aligned}$$

Proof

If $M_i$ fixes a vertex, that is, a lattice class $\Lambda$, then because of $M_i \in GL_2(A)$ by [14, II.1.3 Lemma 1, p. 76] it fixes any underlying lattice $L$. Thus $\alpha _1 M_1 +\alpha _2 M_2$ is an endomorphism of $L$. But since its determinant is invertible in ${\mathcal {O}}_{\infty }$, it actually is an automorphism of $L$. So it fixes the same lattice class. $\square$

As is clear from the proof of Proposition 2.3, Lemma 4.3 also holds for $G_{\omega }$, where $\omega \in E(G)$. Our next result shows that, when $v=\lambda (\omega )$, the structure of $G_v$ can be determined completely.

Proposition 4.4

Let $\omega \in \Omega$ be an elliptic element, and let let $v=\lambda (\omega )$ be its image under the building map. There are two possibilities.

• (i) If $\omega \not \equiv \overline{\omega }$, then

  $$\begin{aligned} G_v=G_{\omega } \cong {\mathbb {F}}_{q^2}^*, \end{aligned}$$

  in which case $|\;G_v|=q^2-1$.

• (ii) If $\omega \equiv \overline{\omega }$, then

  $$\begin{aligned} G_v \cong GL_2({\mathbb {F}}_q), \end{aligned}$$

  in which case $|\;G_v|=q(q-1)^2(q+1)$.

Proof

By Proposition 2.3 and Lemma 4.1, $G_{\omega }\cong {\mathbb {F}}_{q^2}^*$ and $G_{\omega } \le G_v$. By [10, Corollary 2.12] there are only two possibilities, namely $G_v=G_{\omega } \cong {\mathbb {F}}_{q^2}^*$ or $G_v \cong GL_2({\mathbb {F}}_q)$.

If $M\omega =\overline{\omega }$, then $M$ lies in $G_v$ (by Lemma 4.1) but not in $G_{\omega }$; so $G_v \cong GL_2({\mathbb {F}}_q)$. To see the converse fix a generator $M_1$ of $G_{\omega }$. Then there is another generator $M_2$ of $G_{\omega }$ that has the same characteristic polynomial. Hence $M_1$ and $M_2$ are conjugate in $G_v \cong GL_2({\mathbb {F}}_q)$, say by the matrix $M_3$. Since $M_3$ respects the fixed points of $G_{\omega }$, we have $M_3 \omega =\overline{\omega }$. $\square$

Our next lemma highlights the importance of the $q^2-1$ as a feature of our results.

Lemma 4.5

For a vertex stabilizer $G_v$ the following three statements are equivalent:

• (i) $q^2 -1$ divides $|G_v|$.

• (ii) $G_v$ contains a matrix whose eigenvalues are not in ${\mathbb {F}}_q$.

• (iii) $G_v$ contains a cyclic subgroup of order $q^2-1$.

Proof

$\mathrm{(i)}\Rightarrow \mathrm{(ii)}$: If $q+1$ is divisible by an odd prime $r$, then $r$ divides neither $q$ nor $q-1$. Let $M\in G_v$ be an element of order $r$. From the order we see that the eigenvalues of $M$ cannot be in ${\mathbb {F}}_q$. If $q+1$ is not divisible by any odd prime, then it is divisible by $4$. If $G_v$ contains an element of order $4$, we can argue as before. If not, we fix a $2$-Sylow subgroup of $P$ of $G_v$, which then is necessarily of exponent $2$ and hence abelian. So all matrices in $P$ can be simultaneously diagonalized. Since the eigenvalues can only be $1$ and $-1$, there are only $4$ such diagonal matrices. But the order of $P$ is divisible by $8$, a contradiction.

$\mathrm{(ii)}\Rightarrow \mathrm{(iii)}$: If the eigenvalues of $M$ are not in ${\mathbb {F}}_q$, then by Lemma 4.2 they are in ${\mathbb {F}}_{q^2}\!\setminus \!{\mathbb {F}}_q$. Let

$$\begin{aligned} I(M)= \left\{ \alpha I_2+\beta M: \alpha ,\beta \in {\mathbb {F}}_q^*,\; (\alpha ,\beta ) \ne (0,0)\right\} . \end{aligned}$$

By Lemma 4.3 then $I(M) \le G_v$. Part (iii) follows since $I(M) \cong {\mathbb {F}}_{q^2}^*$.

$\mathrm{(iii)}\Rightarrow \mathrm{(i)}$ is trivial. $\square$

For some $q$ (for example $q=4$) every subgroup of $G$ of order $q^2-1$ is cyclic. On the other hand for the case $q=3$ the embedding of $A_4$ in $PGL_2({\mathbb {F}}_3)$ gives rise to a subgroup $S$ of $G$ containing $Z$ of order $8$ for which $S/Z$ is not cyclic.

In Lemma 4.5 the condition (i) can be replaced by

$$\begin{aligned} \mathrm{(i)}'\;\;|G_v|\;{\textit{is}}\;{\textit{divisible}}\;{\textit{by}}\;q+1\;(q\ne 3)\;{\textit{and}}\;8\;(q=3). \end{aligned}$$

Here the restriction when $q=3$ is necessary. It is well-known [14, p. 86] that, when $A={\mathbb {F}}_3[t]$, there is a vertex $v'$ for which

• (1) $|G_{v'}|=12$,

• (2) every matrix in $G_{v'}$ has eigenvalues in ${\mathbb {F}}_3^*$.

We note that the proof of Lemma 4.5 shows that when, $q \ne 3$, the following implication holds.

$$\begin{aligned} q+1\;{\textit{divides}}\;|G_v| \Rightarrow q^2-1\; {\textit{divides}} \; |G_v|. \end{aligned}$$

As stated above the main aim in this section is to prove that the converse of Proposition 4.4 holds. We will prove that, if $q^2-1$ divides $|G_v|$, then $v=\lambda (\omega )$ for some elliptic point $\omega \in E(G)$. We require one more lemma.

Lemma 4.6

Let $\delta$ be odd and let $M\in G$ be a matrix of finite order whose eigenvalues are not in ${\mathbb {F}}_q$. Then

• (i) $M$ does not fix any edges of ${\mathcal {T}}$.

• (ii) $M$ fixes exactly one vertex of ${\mathcal {T}}$.

Proof

(i) Suppose that $M$ fixes an edge. Then there exists a matrix $P\in GL_2(K_{\infty })$ that maps this edge to the standard edge whose stabilizer is $Z_\infty \cdot \mathcal{J}$ where $Z_\infty$ is the centre of $GL_2(K_\infty )$ and $\mathcal{J}$ is the Iwahori group

$$\begin{aligned} \mathcal{J}=\left\{ {a\quad b\atopwithdelims ()c\quad d}\in GL_2({\mathcal {O}}_\infty )\ :\ c\in \pi {\mathcal {O}}_\infty \right\} . \end{aligned}$$

From the determinant we see that $P$ conjugates $M$ into $\mathcal{J}$. Let $\widetilde{M}\in \mathcal{J}$ be this conjugate of $M$. Then the characteristic polynomial $X^2 -\tau X+\eta$ of $\widetilde{M}$ is irreducible over ${\mathbb {F}}_q$, and hence over ${\mathbb {F}}_{q^{\delta }}$ if $\delta$ is odd.

On the other hand, reducing $\widetilde{M}$ modulo the maximal ideal of ${\mathcal {O}}_{\infty }$ we obtain a matrix with the same characteristic polynomial. But the reduced matrix has the form ${a\ b\atopwithdelims ()0\ d}$ with entries in ${\mathbb {F}}_{q^{\delta }}$. So its characteristic polynomial splits over ${\mathbb {F}}_{q^{\delta }}$, a contradiction.

(ii) By [14, Proposition 2, p. 79] $M$ fixes at least one vertex. If $M$ fixes two different vertices of ${\mathcal {T}}$, then it fixes the whole geodesic on ${\mathcal {T}}$ between these two vertices and hence at least one edge in contradiction to (i). $\square$

By the way, Lemma 4.6(ii) provides an alternative proof of the claim in Lemma 4.1 that $\lambda (\omega )=\lambda (\overline{\omega })$.

We now come to the principal results of this section.

Theorem 4.7

Let $\delta$ be odd and let $v \in \mathop {{\mathrm {vert}}}({\mathcal {T}})$. Then

$$\begin{aligned} v = \lambda (\omega ),\; {\textit{for}}\; {\textit{some}}\; \omega \in E(G),\;\; {\textit{if}}\;\; {\textit{and}}\;\; {\textit{only}}\;\; {\textit{if}}\;\; q^2-1\; {\textit{divides}}\; |G_v|. \end{aligned}$$

Proof

If $v=\lambda (\omega )$ for some $\omega \in E(G)$, then $q^2 -1$ divides $|G_v|$ by Proposition 4.4.

Conversely, assume that $q^2 -1$ divides $|G_v|$. Then $G_v$ contains a cyclic subgroup $C$ of order $q^2 -1$ by Lemma 4.5. By Lemma 2.6 this subgroup $C$ fixes an elliptic point $\omega \in E(G)$. Again by Proposition 4.4 we know that $q^2 -1$ divides $|G_{v'}|$ for $v'=\lambda (\omega )$. Since $C$ is contained in $G_v$ and $G_{v'}$, Lemma 4.6 implies $v'=v$. $\square$

Theorem 4.8

If $\delta$ is odd, there exist natural bijections between the following sets

• (i) vertices $\widetilde{v}$ of $G{\setminus }{\mathcal {T}}$ such that $q^2 -1$ divides $|G_v|$;

• (ii) conjugacy classes (in $G$) of cyclic subgroups of $G$ of order $q^2 -1$;

• (iii) the orbits of the $Gal(\widetilde{K}/K)$-action on $\mathop {{\mathrm {Ell}}}(G)$.

Proof

We first establish the bijection between (i) and (ii). Let $v$ be a vertex of ${\mathcal {T}}$ with image $\widetilde{v}$ in $G{\setminus }{\mathcal {T}}$. If $G_v\cong {\mathbb {F}}_{q^2}^*$, this is such a cyclic subgroup of order $q^2 -1$, and the stabilizers of the other lifts of $\widetilde{v}$ to $\mathop {{\mathrm {vert}}}({\mathcal {T}})$ are exactly the conjugates of $G_v$. A similar argument applies if $G_v \cong GL_2({\mathbb {F}}_q)$. Of course, then $G_v$ has several cyclic subgroups of order $q^2 -1$, but they are all conjugate (already in $G_v$).

Conversely, let $C$ be a cyclic subgroup of $G$ of order $q^2 -1$. By Lemma 4.6 it fixes exactly one vertex of ${\mathcal {T}}$. So its conjugacy class fixes exactly one vertex of $G{\setminus }{\mathcal {T}}$.

The bijection between (ii) and (iii) follows by applying the action of $G$ to the bijection in Lemma 2.6. $\square$

Remark 4.9

Theorem 4.8 (in combination with Proposition 4.4) implies in particular that over every vertex $\widetilde{v}$ of $G{\setminus }{\mathcal {T}}$ with $G_v\cong GL_2({\mathbb {F}}_q)$ there lies exactly one elliptic point of $G{\setminus }\Omega$; and over every vertex $\widetilde{v}$ of $G{\setminus }{\mathcal {T}}$ with $G_v\cong {\mathbb {F}}_{q^2}^*$ lie two ($Gal(\widetilde{K}/K)$-conjugate) elliptic points of $G{\setminus }\Omega$.

But when considering the building map $\lambda :\Omega \rightarrow {\mathcal {T}}$, over every vertex $v$ of ${\mathcal {T}}$ with $G_v\cong GL_2({\mathbb {F}}_q)$ there lie $q(q-1)$ elliptic points on $\Omega$, in $q(q-1)/2$ pairs of $Gal(\widetilde{K}/K)$-conjugate elliptic points, corresponding to the $q(q-1)/2$ different cyclic subgroups of order $q^2 -1$ in $GL_2({\mathbb {F}}_q)$. (Compare Lemmas 2.6 and 4.6.) Over every vertex $v$ of ${\mathcal {T}}$ with $G_v\cong {\mathbb {F}}_{q^2}^*$ we again have one pair of $Gal(\widetilde{K}/K)$-conjugate elliptic points on $\Omega$.

One should not forget however that there also are uncountably many non-elliptic points lying over each of these vertices, as for every vertex $v$ of ${\mathcal {T}}$ there are uncountably many points of $\Omega$ mapping to $v$ under the building map.

A much more general statement than Proposition 4.4, namely the complete classification of all possible types of vertex stabilizers for any constant field (not just for ${\mathbb {F}}_q$) and for any $\delta$ is given in [10].

5 Isolated vertices and amalgams

A vertex $\widetilde{v}$ of the quotient graph $G\backslash {\mathcal {T}}$ is called isolated if there is only one edge of $G\backslash {\mathcal {T}}$ attached to it. Obviously this is equivalent to $G_v$ acting transitively on the $q^{\delta }+1$ edges of ${\mathcal {T}}$ attached to $v$.

Theorem 5.1

Let $v\in \mathop {{\mathrm {vert}}}({\mathcal {T}})$. Then $\widetilde{v}$ is an isolated vertex of $G\backslash {\mathcal {T}}$ if and only if the following two conditions both hold:

• (i) $\delta =1$,

• (ii) $G_v$ satisfies any of the three equivalent conditions of Lemma 4.5.

Proof

Assume first that $\delta =1$ and $G_v$ contains a cyclic group of order $q^2 -1$. Then by Lemma 4.6 none of the elements outside $Z$ can fix an edge. So $G_v$ acts transitively on the $q+1$ edges adjacent to $v$, and $\widetilde{v}$ is isolated.

Now assume conversely that $\widetilde{v}$ is isolated. Then $G_v$ acts transitively on the $q^{\delta }+1$ edges emanating from $v$. So $|G_v|$ is divisible by $(q-1)(q^{\delta }+1)$.

If $q^{\delta }+1$ is divisible by an odd prime $r$, then $r$ divides neither $q$ nor $q-1$. Let $M\in G_v$ be an element of order $r$. From the order we see that the eigenvalues of $M$ cannot be in ${\mathbb {F}}_q$. But by Lemma 4.2 they are in ${\mathbb {F}}_{q^2}$, so $r$ divides $q+1$. Together with $r$ dividing $q^{\delta }+1$ this implies that $\delta$ is odd. If $\delta$ were bigger than $1$, then $G_v$ would act transitively on at least $q^3 +1$ edges. But $|G_v/Z|\le q^3 -q$ by Proposition 4.4.

If $q^{\delta }+1$ is not divisible by any odd prime, then it is divisible by $4$, and hence $q$ is congruent to $3$ modulo $4$ and $\delta$ is odd. As above we obtain $\delta =1$. Moreover, $q+1$ divides $|G_v|$ because it divides $q^{\delta }+1$. $\square$

Combining Theorem 5.1 with Theorem 4.8 we obtain the following

Corollary 5.2

Let $\delta =1$. Then the building map induces a bijection between the $Gal(\widetilde{K}/K)$-orbits on elliptic points of $G\setminus \Omega$ and the isolated vertices of $G\setminus {\mathcal {T}}$ with the properties described in Proposition 4.4.

The number of isolated vertices with stabilizer isomorphic to $GL_2({\mathbb {F}}_q)$ (resp. to ${\mathbb {F}}_{q^2}^*$) is $|\mathop {{\mathrm {Ell}}}(G)_2|$ (resp. $r=\frac{1}{2}(|\mathop {{\mathrm {Ell}}}(G)|-|\mathop {{\mathrm {Ell}}}(G)_2|)$). In particular, these numbers only depend on $K$, not on the choice of the degree one place $\infty$.

We also record a graph-theoretic property of isolated vertices.

Proposition 5.3

• (a) Let $\delta$ be odd and let $v_1,v_2 \in \mathop {{\mathrm {vert}}}({\mathcal {T}})$, where $|G_{v_i}|$ is divisible by $q^2-1$, $(i=1,2)$. Then the (geodesic) distance between $v_1$ and $v_2$ (in ${\mathcal {T}}$) and consequently the distance between $\widetilde{v_1}$ and $\widetilde{v_2}$ (in $G\backslash {\mathcal {T}}$) is even.

• (b) The distance between any two isolated vertices of $G{\setminus }{\mathcal {T}}$ is even.

Proof

(a) By Theorem 4.7 there exist $\omega _i \in E(G)$ with $v_i =\lambda (\omega _i)$, ($i=1,2$). Fix $\varepsilon \in {\mathbb {F}}_{q^2}\setminus {\mathbb {F}}_q$. By Theorem 2.5 we can write $\omega _i =\frac{\varepsilon +s_i}{t_i}$ with $s_i ,t_i \in A$. Thus $\omega _2 =M(\omega _1)$ with

$$\begin{aligned} M= \left[ \begin{array}{c@{\quad }c} 1 &{} s_2\\ 0 &{} t_2 \end{array}\right] \left[ \begin{array}{c@{\quad }c} t_1 &{} -s_1\\ 0 &{} 1 \end{array}\right] \in GL_2(K_\infty ). \end{aligned}$$

Consequently $v_2 =M(v_1)$ by [GR, (1.5.3)]. Let $d(v_1,v_2)$ be the distance between $v_1$ and $v_2$. Then by [14, Corollary, p. 75] and Lemma 2.7(b)

$$\begin{aligned} d(v_1,v_2) \equiv \nu (\mathop {{\mathrm {det}}}(M))\equiv \nu (t_1)+\nu (t_2)\equiv 0\;(\mathop {{\mathrm {mod}}}2). \end{aligned}$$

Part (b) follows from part (a) and Theorem 5.1. $\square$

The principal group-theoretic consequence of Theorem 5.1 is the following.

Theorem 5.4

Suppose that $\delta =1$ and that $\widetilde{v}$ is an isolated vertex of $G\backslash {\mathcal {T}}$. There are two possibilities.

• (i) If $G_v \cong GL_2({\mathbb {F}}_q)$, then there exists a subgroup $H$ of $G$ such that

  

  where $B_2({\mathbb {F}}_q)$ is the usual Borel subgroup of $GL_2({\mathbb {F}}_q)$ (of order $q(q-1)^2$).

• (ii) If $G_v\cong {\mathbb {F}}_{q^2}^*$, then there exists a subgroup $H$ of $G$ for which

  

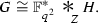
  Hence

  

  where $H'=H/Z$.

In both cases $H$ can be chosen such that it contains all upper triangular matrices from $G$.

Proof

Bass–Serre theory [14, Theorem 13, p. 55] presents $G$ as the fundamental group of a graph of groups [14, p. 42] given by a lift

$$\begin{aligned} j: {\mathcal {T}}_0\longrightarrow {\mathcal {T}}, \end{aligned}$$

where ${\mathcal {T}}_0$ is a maximal subtree of $G\backslash {\mathcal {T}}$. We can choose $j({\mathcal {T}}_0)$ such that it contains all vertices $\Lambda _n$ with

$$\begin{aligned} L_n :={\mathcal {O}}_{\infty }\oplus \pi ^n {\mathcal {O}}_{\infty } \end{aligned}$$

for sufficiently big $n$. These map to one of the infinite half-lines of $G\backslash {\mathcal {T}}$.

Now let $v$ be the vertex of $j({\mathcal {T}}_0)$ that maps to $\widetilde{v}$ and let $e$ be the edge of $j({\mathcal {T}}_0)$ incident with $v$. As $\widetilde{v}$ is isolated in $G \backslash {\mathcal {T}}$, we have $|G_v:G_e|=q+1$. By Bass–Serre theory [14, p. 42] we have

where $H$ is the fundamental group of the graph of groups obtained from $G\backslash {\mathcal {T}}$ by removing the isolated vertex $\widetilde{v}$ and the edge incident with it. In particular, $H$ contains all stabilizers of all vertices of $j({\mathcal {T}}_0)$ that are different from $v$. So by our construction $H$ contains

$$\begin{aligned} G_{\Lambda _n}= \left\{ {a\quad b\atopwithdelims ()0\quad d}\in GL_2(A)\ :\ \nu (b)\ge -n\right\} \end{aligned}$$

for all sufficiently big $n$, and hence $H$ contains all upper triangular matrices. $\square$

When $\delta =1$ a decomposition of type (i) always occurs because the standard vertex has stabilizer $GL_2({\mathbb {F}}_q)$. More interesting decompositions occur when there are isolated vertices of type (ii).

Theorem 5.5

Suppose that $\delta =1$. Then there exists a subgroup $P$ of $PGL_2(A)$ for which the following free product decomposition holds

where

$$\begin{aligned} 2r=|\mathop {{\mathrm {Ell}}}(G)|-|\mathop {{\mathrm {Ell}}}(G)_2|. \end{aligned}$$

Actually, $P$ can be chosen in such a way that it contains all upper triangular matrices from $PGL_2(A)$.

Moreover $r$ is maximal in the following sense. Suppose that $C$ is a cyclic subgroup of $PGL_2(A)$ of order $q+1$ for which

Then there exists $v \in \mathop {{\mathrm {vert}}}({\mathcal {T}})$ such that

• (i) $G_v \cong {\mathbb {F}}_{q^2}$,

• (ii) $\psi (G_v)=C$, where $\psi : G \rightarrow PGL_2(A)$ is the natural map.

Proof

Let

$$\begin{aligned} \widetilde{V}=\{\widetilde{v} \in \mathop {{\mathrm {vert}}}(G \backslash {\mathcal {T}}):\; G_v \cong {\mathbb {F}}_{q^2}^*\}. \end{aligned}$$

Let $\widetilde{v_1},\;\widetilde{v_2} \in \widetilde{V}$. Then, by Theorem 4.7, $G_{v_i}=G_{\omega _i}$, for some $\omega _i \in E(G)$, where $\omega _i \not \equiv \overline{\omega _i}$, ($i=1,2$). If $\widetilde{v_1}=\widetilde{v_2}$, then $v_2=g(v_1)$, for some $g \in G$, so that $G_{\omega _2}=gG_{\omega _1}g^{-1}=G_{g(\omega _1)}$. It follows that $\{\omega _2,\;\overline{\omega _2}\}=\{g(\omega _1), \;g(\overline{\omega _1})\}$.

On the other hand if $\omega _j (\ne \overline{\omega _j}) \in E(G)$ and $S_j=\{\omega _j\;\overline{\omega _j}\}$, where $j=3,4$, then for all $g \in G$ either $S_3=g(S_4)$ or $S_3 \cap g(S_4) = \emptyset$. By Corollary 5.2 we have $|\widetilde{V}| =r$, where $r$ is defined as above.

The free product decomposition is a consequence of an iteration of the process described in the proof of Theorem 5.4(ii).

For the last part of the theorem $C$, under $\psi$, lifts to a cyclic subgroup $C'$ of $G$ of order $q^2-1$. Now by [14, Proposition 2, p. 76] $C' \le G_v$, for some $v \in \mathop {{\mathrm {vert}}}( {\mathcal {T}})$. Then by Theorem 4.7 there are two possibilities for $G_v$, described in Proposition 4.4. Either $G_v=C'$ in which case we are finished, or $G_v\cong PGL_2({\mathbb {F}}_q)$. In the latter case the canonical map from $PGL_2(A)$ onto $C$ restricts to an epimorphism

$$\begin{aligned} PGL_2({\mathbb {F}}_q)\twoheadrightarrow C. \end{aligned}$$

This gives the desired contradiction. $\square$

Theorem 5.6

• (a) For $q\ge 8$ and $g>0$ there exist exactly two rings $A$ (up to isomorphism) such that all isolated vertices of $GL_2(A){\setminus }{\mathcal {T}}$ have stabilizers isomorphic to $GL_2({\mathbb {F}}_q)$, namely $A={\mathbb {F}}_9[x,y]$ with $y^3+y=x^4$ (genus $3$) or with $y^2=x^3-x$ (genus $1$).

• (b) For fixed $q\ge 8$ the number $r$ of free factors in Theorem 5.5 grows exponentially with $g$. More precisely, for $q\ge 8$ and all cases of positive genus except the two discussed in part (a) we have

  $$\begin{aligned} r\ge \frac{1}{4}(\sqrt{q}-1)^{2g}>\frac{3^g}{4}. \end{aligned}$$

Proof

(a) From Theorem 3.9(a) we know already that there are only two fields $K$ with these properties. For any choice of the place $\infty$ of degree $1$ we get a ring $A$ with this property. It remains to show that different choices of $\infty$ give isomorphic rings.

For the genus $3$ case we use that by [15, Exercise 6.10] the automorphism group of a Hermitian function field (that is, a function field ${\mathbb {F}}_{q^2}(x,y)$ with $y^q+y=x^{q+1}$) acts transitively on its places of degree $1$. So different choices of $\infty$ will lead to isomorphic rings $A$.

The elliptic case can be seen by some easy calculations with Weierstrass equations.

(b) If $\mathop {{\mathrm {Ell}}}(G)_2$ is strictly smaller than $\mathop {{\mathrm {Ell}}}(G)$, then, because of the group structure, it has index at least $2$. Hence, if there are elements of order bigger than $2$ in $\mathop {{\mathrm {Ell}}}(G)$, their number is at least $\frac{1}{2}L_K(-1)\ge \frac{1}{2}(\sqrt{q}-1)^{2g}$. So in that case the number of isolated vertices with cyclic stabilizer is at least $\frac{1}{4}(\sqrt{q}-1)^{2g}$, which for $q\ge 8$ is bigger than $\frac{1}{4}3^g$. $\square$

Remark 5.7

• (a) It is, of course, well possible that the group $PGL_2(A)$ also splits off other free factors than those stipulated by Theorem 5.5. Let for example $A={\mathbb {F}}_9[x,y]$ with $y^2 =x^3 -x$. Then $r=0$, but from Takahashi’s results [16] one obtains that in this case $PGL_2(A)$ is a free product of $10$ infinite groups.

• (b) By the same arguments as in the proof of Theorem 5.6(b), for $q\in \{5,7\}$ we still have $r>\frac{1}{4}(\frac{3}{2})^g$ provided $r$ is not zero. (Compare Remark 3.10.)

• (c) Theorem 5.5 has a number of interesting consequences. For example suppose that $r\ge 2$ and that $q \equiv -1\;(\mathop {{\mathrm {mod}}}6)$. Then there exists an epimorphism

  $$\begin{aligned} \theta : PGL_2(A) \twoheadrightarrow PSL_2({\mathbb {Z}}), \end{aligned}$$

  since

  

Example 5.8

Let

$$\begin{aligned} A={\mathbb {F}}_2[x,y]\ \ \ \hbox {with}\ \ \ y^2 +y=x^3 +x+1. \end{aligned}$$

This elliptic curve has exactly one rational point, namely the one at infinity. So $L_K(u)=1-2u+2u^2$, and thus $L_K(-1)=5$ and $r=2$. More precisely,

where (cf. Takahashi [16], [8, Theorem 5.3] or (the proof of) [9, Lemma 5.2 (c)]). Since the normal hull of $B_2(A)$ in $GL_2(A)$ contains all elements from $\varDelta (\infty )$, we see that a finite group can be generated by two elements of order $3$ if and only if it is the quotient of this $GL_2(A)$ by a normal non-congruence subgroup of level $A$. For results on which classical finite simple groups can be generated by two elements of order $3$ see [6, Corollary 1.8].

Example 5.9

Let

$$\begin{aligned} A={\mathbb {F}}_7[x,y]\ \ \ \hbox {with}\ \ \ y^2 =x^3 +4. \end{aligned}$$

Then $L_K(u)=1-5u+7u^2$. Thus $L_K(-1)=13$ and $r=6$. So there exists a surjective homomorphism from $GL_2(A)$ to any finite (or infinite) group that is generated by at most $6$ elements of orders dividing $8$. More precisely, by Takahashi’s description of the quotient graph (cf. [16]) we have

where $\varDelta (0)$, $\varDelta (\infty )$ are infinite subgroups and, again, $\varDelta (\infty )$ contains all upper triangular matrices (modulo $Z$).

In particular, there exists a normal non-congruence subgroup $N$ of level $A$ such that $G/N$ is isomorphic to the permutation group of Rubik’s cube (which is generated by $6$ elements of order $4$). Recall that the order of that permutation group is roughly $43\times 10^{18}$.