1 Introduction

With the development and utilization of new energy sources as well as the development of power grid technology, the power system with centralized and single power supply as the main feature has problems such as stability and unsuitability for remote areas [1, 2]. Microgrids is the mainstream direction of future grid development. Microgrids is not only the transition from traditional power grid to smart grid, but also an indispensable and important part of the future smart grid construction [3]. Microgrids is a single controllable entity, which can be composed of multiple DG according to the communication topology network. Among them, DG and loads are connected to the large power grid through switches and common coupling points, which can effectively reduce the impact of intermittent power sources on the large power grid. The development of microgrids is closely related to advanced control technology, and communication technology, which is currently the focus of research and development [4].

Microgrids control can be divided into primary control, secondary control and tertiary control. The primary control includes current inner loop control and droop control. The secondary control is used to compensate the voltage and frequency deviation caused by the primary control, which is divided into centralized, decentralized and distributed control. The tertiary control is generally the energy management control of microgrids. The small signal dynamic model of microgrids based on droop control was studied in [5]. Genetic algorithm is used to optimize the operation characteristics of the microgrids, which improve the dynamic performance of the system, however, the propose controller does not restore the voltage and frequency to the reference value. Decentralized control to restore voltage and frequency of islanded microgrids are used in [6,7,8]. The adopted method only needs local information, which reduce the complexity of communication. However, it is difficult to coordinate the global information and affects the overall control goal because a single DG cannot obtain information from other DGs in decentralized control. Distributed secondary control for islanded microgrids to restore voltage and frequency are adopted in [9,10,11]. This method is based on a multi-agent system and realizes mutual coordination among DGs through sparse network communication, which eliminate the impact of single-point failure on the system. In particular, a pinning-based hierarchical and distributed secondary cooperative control strategy for AC microgrids clusters is proposed in [11]. It can realize many control objectives including frequency, voltage restore, active and reactive power sharing.

In the secondary voltage and frequency control of the microgrids, the system convergence speed depends on the convergence time of the designed controller. Fully distributed and adaptive control methods to restore the voltage and frequency of microgrids are adopted in [9, 12, 13]. The proposed control schemes belong to finite time control problems, and the convergence speed of the system needs to be further improved. Therefore, it is more practical to study the finite time recovery of voltage and frequency. A distributed robust finite time secondary voltage and frequency controller based on the feedback linearization method are designed in [11, 14,15,16]. The designed controllers have good robustness and anti-disturbance performance. However, the output constraints and plug and play function are not considered. In [17] a new mesh topology is used to secondary control on voltage and frequency within a finite time, and the proposed controller supports plug and play function. In [15, 18, 19], finite time sliding mode control is used for secondary control of voltage and frequency of microgrids, so as to maintain the stability of the system and accelerate the convergence speed. However, sliding mode control contains differential operation and requires a large amount of calculation, as well as exists obvious chattering phenomenon. A secondary voltage control method based on extended state Kalman filter and fast terminal sliding mode is proposed [20]. The extended state Kalman filter was used to accurately estimate the state information of model, and the fast terminal sliding mode control is used to accelerate the convergence speed of the system. However, the problem of secondary frequency recovery and active power sharing are not considered. Wang et al. [21] proposed a distributed fixed time control scheme for DC microgrids based on dynamic average consistency to achieve current sharing between converters and voltage regulation of DC buses. The proposed controllers do not need to deliver the output current data to the neighbors and sample the voltage of the DC bus, making them easier to be implemented in practice. In [22] based on the prescribed performance control approach, a secondary control scheme is developed for DC microgrids, current sharing among the converters and voltage regulation of the DC bus are achieved while the prescribed transient performance is guaranteed. The evolution of both the bus voltage error and the current sharing error can be constrained within a predefined imposed bound.

The state constrained problem generally exists in the actual system. If the system does not meet the constraints, it will not only degrade the system security performance, but even make the whole system unstable. In microgrids, the actual physical states such as voltage and frequency are usually inevitably constrained to a certain extent. At the same time, transmitting information (error, etc.) in the network is also necessary to limit due to the limitations of network bandwidth and transmission rate. In [23], the secondary control problem of AC microgrids with voltage and frequency constraints is studied. The model predictive control method is used to solve the problem of state constraints. In [24], the distributed robust control method is adopted to ensure the frequency constraint of the microgrids and maintain the resilience operation of the microgrids.

To address the aforementioned issues of the existing literature, an adaptive fuzzy fixed time secondary voltage controller and secondary frequency controller which considers state constraints are designed in this paper. Firstly, based on the multi-agent consensus method, each DG is regarded as a nonlinear agent, and the agents communicate through a sparse network. The feedback linearization is used to deal with nonlinear systems, and those unknown variables after feedback linearization are approximated by adaptive fuzzy system to improve the adaptive ability. Secondly, a new sliding mode surface and sliding mode approach law is designed, so that the voltage quickly converges to the reference value within a fixed time. The fixed time convergence does not depend on the initial state of the system, and it only depends on the parameters of the designed controller. Then the fixed-time voltage and frequency reference tracking can be achieved before the desired maximum settling-time. Finally, the problem of voltage constraint being considered, the Barrier Lyapunov Function (BLF) is used to constrain the voltage error, so that the output voltage is constrained within the preset range. A secondary frequency controller based on the control barrier function is designed to constrain the output frequency within a preset range. The controllers designed can ensure the sharing of active power and reactive power.

The rest of this paper is structured as follows: Sect. 2 is the preliminaries knowledge and problem formulation, introducing graph theory knowledge, related lemmas, and the large-signal dynamic model of distributed power based on inverters; In Sect. 3 the fixed time secondary voltage controller is designed; In Sect. 4 the secondary frequency is designed; Sect. 5 is the simulation and result analysis to verify the effectiveness of the proposed controller; Sect. 6 is the conclusion.

2 Preliminaries knowledge and problem formulation

2.1 Graph theory

The microgrids can be regarded as a multi-agent system, and its distributed consensus coordination control can be represented by directed graphs and undirected graphs. Suppose a graph is \(G(V,E)\), where the set of vertices \(V = \{ {\overline{\nu }}_{1\;} {\overline{\nu }}_{2\;} \cdots \;{\overline{\nu }}_{n} \}\) and the set of edges \(E \subset V \times V\), \(\times\) represent the Cartesian product. The matrix \(A = [a_{ij} ] \in R^{N \times N}\) is the adjacency matrix of the graph G, in which \(a_{ij}\) represents the weight coefficient of the edge in G. If and only if \(({\overline{\nu }}_{j} ,{\overline{\nu }}_{i} ) \in E\), it means that vertex j can receive information from vertex i, otherwise \(a_{ij} = 0\). In the graph, the degree of a vertex refers to the number of edges connected to the vertex. For directed graphs, there are in degree and out degree. In degree is the number of edges that start from \({\overline{\nu }}_{i}\), and out degree is the number of edges that point to \({\overline{\nu }}_{i}\). In addition, the penetration matrix D and the graph Laplace matrix L are defined as:\(D = {\text{diag}}(\overline{d}_{1} , \cdots ,\overline{d}_{N} ) \in R^{N \times N}\), \(L = D - A \in R^{N \times N}\), respectively. According to the definition of the matrix D: \(\overline{d}_{i} = \sum\limits_{j = 1}^{N} {a_{ij} }\) [25].

2.2 Large signal dynamic model of distributed generation based on inverter

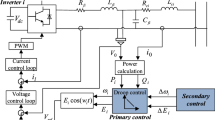
The control block diagram of the ith inverter of AC microgrids is shown in Fig. 1, which includes DC sources, inverter, PWM module, power calculation module, voltage and current controllers [26].

Fig. 1
figure 1

Control block diagram of the ith inverter of microgrids DG

Full size image

In Fig. 1, \(v_{{{\text{o}}i}}\), \(i_{{{\text{o}}i}}\) is the output voltage and current of the ith RLC filter circuit. \(v_{{{\text{od}}i}} {,} v_{{{\text{oq}}i}}\) is the d-q component of the output voltage of the ith RLC filter circuit. \(i_{{{\text{od}}i}} , i_{{{\text{oq}}i}}\) is the d-q component of the output current of the ith RLC filter circuit. \(v_{{{\text{od}}i}}^{*} , v_{{{\text{oq}}i}}^{*}\) is the voltage d-q component generated by the ith droop control. \(\omega_{i}\) is angular frequency generated by the ith droop control. \(v_{{{\text{id}}i}} {,} v_{{{\text{iq}}i}}\) is the d-q component of the input voltage of the ith inverter. \(i_{{{\text{id}}i}} {,} i_{{{\text{iq}}i}}\) is the d-q component of the output current of the ith inverter. \(P_{i}\), \(Q_{i}\) is the active power and reactive power output by the ith low-pass filter circuit. \(v_{{{\text{b}}i}}\) is the bus voltage of the ith DG. \(v_{{{\text{bd}}i}} \;{,}\;v_{{{\text{bq}}i}}\) is the d-q transformation of the bus voltage at the common coupling point connected to the grid.

\(\omega_{{{\text{n}}i}}\), \(v_{{{\text{n}}i}}\) is the rated angular frequency and voltage of the ith DG. \(i_{{{\text{id}}i}} {,} i_{{{\text{iq}}i}}\), \(L_{{{\text{f}}i}} ,\;C_{{{\text{f}}i}}\) is the resistance, inductance and capacitance of the ith RLC filter. \(R_{{{\text{c}}i}} ,\;L_{{{\text{c}}i}}\) is the resistance and inductance of the ith coupling line.\(k_{Pi}^{{}}\),\(k_{Qi}^{{}}\) is the frequency and voltage droop control coefficients.

\(P_{i}\), \(Q_{i}\), \(\omega_{{{\text{n}}i}}\), \(v_{{{\text{n}}i}}\) are the inputs to the droop control; \(v_{{{\text{od}}i}}^{*} , v_{{{\text{oq}}i}}^{*}\),\(\omega_{i}\) are the outputs to the droop control. \(\omega_{{{\text{n}}i}}\), \(v_{{{\text{n}}i}}\) are the inputs to the secondary control; \(\omega_{{{\text{ref}}}} ,\;v_{{{\text{ref}}}}\) are the outputs to the secondary control. \(v_{{{\text{od}}i}}^{*} , v_{{{\text{oq}}i}}^{*}\), \(i_{{{\text{id}}i}} {,} i_{{{\text{iq}}i}}\),\(v_{{{\text{od}}i}} {,} v_{{{\text{oq}}i}}\), \(i_{{{\text{od}}i}} , i_{{{\text{oq}}i}}\) are the inputs to the voltage and current controller; \(v_{{{\text{id}}i}} {,} v_{{{\text{iq}}i}}\) are the outputs to the voltage and current controller.

For voltage source inverter, the dynamic models of LC filter circuit, coupling circuit and voltage and current control circuit are studied in [27]. The large signal state space model of DG shown in Fig. 1 can be written as:

$$ \begin{gathered} \dot{x}_{i} = f_{i} (x_{i} ) + g_{i} (x_{i} )u_{i} + k_{i} (x_{i} )d_{i} \\ = \overline{f}_{i} (x_{i} ) + g_{i} (x_{i} )u_{i} \\ y_{i} = h_{i} (x_{i} ) \\ \end{gathered} $$
(1)

where,\(x_{i} = [\delta_{i} \;P_{i} \;Q_{i} \;\phi_{{{\text{d}}i}} \;\phi_{{{\text{q}}i}} \;\gamma_{{{\text{d}}i}} \;\gamma_{{{\text{q}}i}} \;i_{{{\text{id}}i}} \;i_{{{\text{iq}}i}} \;v_{{{\text{od}}i}} \;v_{{{\text{oq}}i}} \;i_{{{\text{od}}i}} \;i_{{{\text{oq}}i}} ]\) is state, \(d_{i} = [\omega_{{{\text{com}}}} \;v_{{{\text{bd}}i}} \;v_{{{\text{bq}}i}} ]^{\rm T}\) is disturbance, \(u_{i}\) is input, \(y_{i}\) is the output. The meaning of each variables and \(f_{i} (x_{i} ),\;g_{i} (x_{i} ),\;k_{i} (x_{i} ),h_{i} (x_{i} )\) are shown in [28].

For secondary voltage control, the input and output are: \(u_{i} = V_{{{\text{n}}i}}\) and \(y_{i} = v_{{{\text{od}}i}}\), respectively. For secondary frequency control, the input and output are: \(u_{i} = \omega_{{{\text{n}}i}}\) and \(y_{i} = \omega_{i}\), respectively. The droop control equation as follows:

$$ \omega_{i} = \omega_{{{\text{n}}i}} - k_{Pi} P_{i} $$
(2)
$$ v_{{{\text{od}}i}}^{*} = V_{{{\text{n}}i}} - k_{Qi}^{{}} Q_{i} $$
(3)
$$ v_{{{\text{oq}}i}}^{*} = 0 $$
(4)

where, \(k_{Pi}^{{}}\), \(k_{Qi}^{{}}\) are the droop control coefficients, \(P_{i}\) and \(Q_{i}\) can be obtained from (5), (6):

$$ P_{i} = \frac{{\omega_{{{\text{c}}i}} }}{{s + \omega_{{{\text{c}}i}} }}(v_{{{\text{od}}i}} i_{{{\text{od}}i}} + v_{{{\text{oq}}i}} i_{{{\text{oq}}i}} ) $$
(5)
$$ Q_{i} = \frac{{\omega_{{{\text{c}}i}} }}{{s + \omega_{{{\text{c}}i}} }}(v_{{{\text{oq}}i}} i_{{{\text{od}}i}} - v_{{{\text{od}}i}} i_{{{\text{oq}}i}} ) $$
(6)

where, \(\omega_{{{\text{c}}i}}\) is the cut off frequency of the low pass filter.

The microgrids can realize power sharing after drooping control, but drooping control is differential adjustment, which cannot make the output voltage and frequency accurately reach the reference value, so the voltage and frequency need to be adjusted again.

3 Design of distributed secondary voltage controller

The secondary voltage control of the microgrids is a tracking problem. In this section, the distributed secondary voltage fixed time controller will be first designed to make the output voltage \(v_{{{\text{od}}i}}\) reach consensus (\(\overline{v}_{{{\text{od}}1}} = \overline{v}_{{{\text{od}}2}} \cdots = \overline{v}_{{{\text{od}}N}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {v_{{{\text{od}}i}} }\)) through error tracking. For each nonlinear system, the Lie derivative method is used to feedback linearize the system, and the unknown part of the system is approximated by adaptive fuzzy system (\(\hat{F}_{i} (x_{i} ) = {\hat{\boldsymbol{\psi }}}_{i}^{\rm T} {{\varvec{\updelta}}}_{i} ({\mathbf{e}}_{i} )\)). Secondly, a new sliding mode surface and sliding mode approach law are designed to make the voltage converge in a fixed time (\(T(x_{0} ) \le T_{\max } = \frac{1}{\mu (r - 1)} + \frac{1}{\mathchar'26\mkern-10mu\lambda (1 - h)} = \frac{2}{{\overline{\mu }_{i} (q - 1)}} + \frac{4}{{\overline{\mathchar'26\mkern-10mu\lambda }_{i} }}\)). Finally, considering the problem of state constraints, BLF is used to design the controller to make the state of the system constraint within the preset range (\(- \kappa_{i} \le e_{i,1} \le \kappa_{i}\)). In microgrids, it is difficult to achieve reactive power sharing due to mismatched line impedance. Accurate voltage control will lead to unequal sharing of reactive power, so voltage recovery and accurate sharing of reactive power can be achieved by considering the average consistency of voltage.

Suppose the output is \(y_{i,1} = y_{i} = \overline{v}_{{{\text{od}}i}}\), where, \(\overline{v}_{{{\text{od}}i}}\) is the average value of output voltage of all DGs, which meets the following requirements under steady state conditions: \(\overline{v}_{{{\text{od}}1}} = \overline{v}_{{{\text{od}}2}} \cdots = \overline{v}_{{{\text{od}}N}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {v_{{{\text{od}}i}} }\), \(v_{{{\text{od}}i}} = v_{{{\text{od}}i}}^{*}\) [29].

The nonlinear system (1) is feedback linearized by Lie derivative method:

$$ \dot{y}_{i,1} = y_{i,2} $$
(7)
$$ \dot{y}_{i,2} = \overline{v}_{i} = F_{i} (x_{i} ) + G_{i} (x_{i} )u_{i} $$
(8)

where, \( F_{i} (x_{i} ) = L_{{\bar{f}_{i} }}^{2} h_{i} (x_{i} ) = \frac{{\partial (L_{{\bar{f}_{i} }} h_{i} )}}{{\partial x_{i} }}\bar{f}_{i} (x_{i} ) = ( - \omega _{i}^{2} - \frac{{k_{{{\text{Pc}}i}} k_{{{\text{Pv}}i}} + 1}}{{C_{{{\text{f}}i}} L_{{{\text{f}}i}} }} - \frac{1}{{C_{{{\text{f}}i}} L_{{{\text{c}}i}} }})\bar{v}_{{{\text{od}}i}} + \frac{{R_{{{\text{c}}i}} }}{{C_{{{\text{f}}i}} L_{{{\text{c}}i}} }}i_{{{\text{od}}i}} - \frac{{2\omega _{i} }}{{C_{{{\text{f}}i}} }}i_{{{\text{oq}}i}} - \frac{{R_{{{\text{f}}i}} + k_{{{\text{Pc}}i}} }}{{C_{{{\text{f}}i}} L_{{{\text{f}}i}} }}i_{{{\text{id}}i}} + \frac{{2\omega _{i} - \omega _{{\text{b}}} }}{{C_{{{\text{f}}i}} }}i_{{{\text{iq}}i}} - \frac{{k_{{{\text{Pc}}i}} k_{{{\text{Pv}}i}} k_{{Qi}}^{{}} }}{{C_{{{\text{f}}i}} L_{{{\text{f}}i}} }}Q_{i} + \frac{{k_{{{\text{Pc}}i}} k_{{{\text{Iv}}i}} }}{{C_{{{\text{f}}i}} L_{{{\text{f}}i}} }}\phi _{{{\text{d}}i}} + \frac{{k_{{{\text{Ic}}i}} }}{{C_{{{\text{f}}i}} L_{{{\text{f}}i}} }}\gamma _{{{\text{d}}i}} + \frac{{v_{{{\text{bd}}i}} }}{{C_{{{\text{f}}i}} L_{{{\text{c}}i}} }} + \frac{{k_{{{\text{Pc}}i}} }}{{C_{{{\text{f}}i}} L_{{{\text{f}}i}} }}H_{i} i_{{{\text{od}}i}} \), \(G_{i} {(}x_{i} {) = }L_{gi} L_{{\overline{f}_{i} }} h_{i} {(}x_{i} {) = }\frac{{\partial (L_{{\overline{f}_{i} }} h_{i} )}}{{\partial x_{i} }}g_{i} {(}x_{i} {) = }\frac{{k_{{{\text{Pc}}i}} k_{{{\text{Pv}}i}} }}{{C_{{{\text{f}}i}} L_{{{\text{f}}i}} }}\), where \(\omega_{{\text{b}}}\) is the rated frequency of the microgrids; \(k_{{{\text{Pc}}i}} ,k_{{{\text{Pv}}i}} ,k_{{{\text{Ic}}i}} ,k_{{{\text{Iv}}i}}\) represents the proportion and integral gain of voltage and current control loops respectively [20].

Using the consensus protocol, the error function of DG output voltage is designed as follows:

$$ \begin{gathered} e_{i,1} = \sum\limits_{{j \in N_{i} }} {a_{ij} (y_{i,1} - y_{j,1} )} + b_{i} (y_{i,1} - y_{0} ) + \\ \sum\limits_{{j \in N_{i} }} {a_{ij} (k_{Qi}^{{}} Q_{i} - k_{Qj}^{{}} Q_{j} )} \\ \end{gathered} $$
(9)
$$ \begin{gathered} e_{i,2} = \sum\limits_{{j \in N_{i} }} {a_{ij} (y_{i,2} - y_{j,2} )} + b_{i} (y_{i,2} - \dot{y}_{0} ) + \\ \sum\limits_{{j \in N_{i} }} {a_{ij} (k_{Qi}^{{}} \dot{Q}_{i} - k_{Qj}^{{}} \dot{Q}_{j} )} \\ \end{gathered} $$
(10)

where, \(y_{0} = v_{{{\text{ref}}}}\),\(\dot{y}_{0} = 0\),\(\dot{e}_{i,1} = e_{i,2}\),\(b_{i} \ge 0\) are the control gains, and \(N_{i}\) is the communication neighborhood set of the ith controller. When the error tends to zero, there are \(y_{i,1} = y_{j,1} = y_{0}\), \(k_{Qi}^{{}} Q_{i} = k_{Qj}^{{}} Q_{j}\), that is, \(\frac{1}{N}\sum\limits_{i = 1}^{N} {v_{{{\text{od}}i}} } = v_{{{\text{ref}}}}\). The accurate sharing of reactive power is realized.

Derivate (8) and substitute (6) into it:

$$ \dot{e}_{i,2} = \overline{d}_{i} (\overline{v}_{i} - \overline{v}_{j} ) + b_{i} \overline{v}_{i} + \overline{d}_{i} (k_{Qi}^{{}} \ddot{Q}_{i} - k_{Qj}^{{}} \ddot{Q}_{j} ) $$
(11)

where, \(\overline{d}_{i} = \sum\limits_{j = 1}^{N} {a_{ij} }\).

3.1 Controller design and improvement of the sliding surface

Select NTSM (Nonsingular terminal sliding mode):

$$ s_{i} = e_{i,2} + k^{\prime}_{1} |e_{i,1} |^{\alpha } {\text{sign}}(e_{i,1} ),\;\;i = 1, \cdot \cdot \cdot ,N $$
(12)

where, constant \(k^{\prime}_{1} > 0\), \(0 < \alpha < 1\) is the coefficient of sliding mode surface.

BLF is a control method to solve the state constraint problems of system [30]. In the actual operation process, the state variables of the system are subject to certain restrictions due to the influence of actuators. In order to restrict the system state strictly converging to the desired state, BLF can be constructed to stabilize the system so that the state of the system is always within the given constraint ranges.

The constraint range of tracking error is:

$$ - \kappa_{i} \le e_{i,1} \le \kappa_{i} $$
(13)

where, constant \(\kappa_{i} > 0\).

The error is normalized as follows:

$$ \eta_{i} = \frac{{e_{i,1} }}{{\kappa_{i} }} $$
(14)

The proposed sliding surface can be rewritten as:

$$ s_{i} = e_{i,2} + k_{1} |\eta_{i} |^{\alpha } {\text{sign}}(\eta_{i} ),\;\;i = 1, \cdot \cdot \cdot ,N $$
(15)

where, variable \(k_{1} = k^{\prime}_{1} |\kappa_{i} |^{\alpha }\).

Deriving (15) and substituting Eqs. (11) and (8) into it:

$$ \dot{s}_{i} = (\overline{d}_{i} + b_{i} )[F_{i} (x_{i} ) + G_{i} (x_{i} )u_{i} ] - \overline{d}_{i} \overline{v}_{j} + k_{1} \alpha \left| {\eta_{i} } \right|^{\alpha - 1} \dot{\eta }_{i} $$
(16)

Consider the BLF candidate as:

$$ V_{1i} = \frac{1}{2} \cdot \frac{{s_{i}^{2} }}{{1 - \eta_{i}^{2} }} $$
(17)

For the feedback linearization system (8), based on the NTSM (12), as well as considering the state constraints, the BLF method is adopted for design controller as:

$$ \begin{gathered} u_{i} = \frac{1}{{G_{i} {(}x_{i} {)}(\overline{d}_{i} + b_{i} )}}[( - (\overline{d}_{i} + b_{i} )\hat{F}_{i} {(}x_{i} {) + }\overline{d}_{i} \overline{v}_{j} + \sum\limits_{i = 1}^{n} {\frac{{s_{i} \eta_{i} \dot{\eta }_{i} }}{{1 - \eta_{i}^{2} }}} \\ - (k_{1} \alpha \left| {\eta_{i} } \right|^{\alpha - 1} \dot{\eta }_{i} + \zeta \left| {s_{i} } \right|^{1/2} {\text{sign}}(s_{i} ) + k_{2} \left| {s_{i} } \right|^{q} {\text{sign}}(s_{i} ))] \\ \end{gathered} $$
(18)

where, \(\zeta > 0,\;k_{2} > 0,\;q > 1\), \(\hat{F}_{i} {(}x_{i} {)}\) is the estimate of \(F_{i} (x_{i} )\), \(- \zeta \left| {s_{i} } \right|^{1/2} {\text{sign}}(s_{i} ) - k_{2} \left| {s_{i} } \right|^{q} {\text{sign}}(s_{i} )\) is designed sliding mode approach law.

From (16) and (18), it is known that:

$$ \begin{gathered} \dot{s}_{i} = (\overline{d}_{i} + b_{i} )(F_{i} (x_{i} ) - \hat{F}_{i} (x_{i} )) - \frac{{s_{i} \eta_{i} \dot{\eta }_{i} }}{{1 - \eta_{i}^{2} }} - \\ \zeta \left| {s_{i} } \right|^{1/2} {\text{sign}}(s_{i} ) - k_{2} \left| {s_{i} } \right|^{q} {\text{sign}}(s_{i} ) \\ \end{gathered} $$
(19)

3.2 Adaptive fuzzy estimation of system uncertainty

Because some unknown variables and parameter variations are involved in the system (8), the adaptive fuzzy system is used for estimation. It is expressed in the form of fuzzy function as follows:

$$ F_{i} (x_{i} ) = {{\varvec{\uppsi}}}_{i}^{\rm T} {{\varvec{\updelta}}}_{i} ({\mathbf{e}}_{i} {)} + \vartheta_{i} $$
(20)

where, \({\mathbf{e}}_{i} = [e_{i,1} \;e_{i,2} ]^{\rm T}\), \({{\varvec{\uppsi}}}_{i} = [\psi_{i1}^{{}} ,\;\psi_{i2}^{{}} ,\; \cdots ,\;\psi_{iM}^{{}} ]^{\rm T}\) is the weight vector of the fuzzy system, and \({{\varvec{\updelta}}}_{i} ({\mathbf{e}}_{i} ) = [\delta_{i,1} ({\mathbf{e}}_{i} ),\delta_{i,2} ({\mathbf{e}}_{i} ), \cdots ,\delta_{{i,M_{i} }} ({\mathbf{e}}_{i} )]^{\rm T}\) is the fuzzy basis function vector. \(\delta_{i,j} ({\mathbf{e}}_{i} ) = \frac{{\prod\limits_{\varsigma = 1}^{2} {\xi_{{F_{\varsigma }^{i,j} }} (e_{i\varsigma }^{{}} )} }}{{\sum\limits_{j = 1}^{{M_{i} }} {\prod\limits_{\varsigma = 1}^{2} {\xi_{{F_{\varsigma }^{i,j} }} (e_{i\varsigma }^{{}} )} } }}\), \(\varsigma = 1,2\), where \(\xi_{{F_{\varsigma }^{i,j} }} (e_{i\varsigma }^{{}} )\) is the membership function and Mi is the total number of fuzzy rules. \(\vartheta_{i}\) is the minimum fuzzy approximation error.

It can be obtained from (20):

$$ \hat{F}_{i} (x_{i} ) = {\hat{\boldsymbol{\psi }}}_{i}^{\rm T} {{\varvec{\updelta}}}_{i} ({\mathbf{e}}_{i} ) $$
(21)

where, \(\tilde{F}_{i} (x_{i} ) = F_{i} (x_{i} ) - \hat{F}_{i} (x_{i} )\), \({\hat{\boldsymbol{\psi }}}_{i}\) is the estimate of \({{\varvec{\uppsi}}}_{i}\).

Select the adaptive law as:

$$ {\dot{\hat{\boldsymbol{\psi }}}}_{i} = l_{1i} \sum\limits_{i = 1}^{n} {\frac{{(\overline{d}_{i} + b_{i} )s_{i} }}{{1 - \eta_{i}^{2} }}} \delta_{i} ({\mathbf{e}}_{i} ) - 2l_{1i} l_{2i} {\hat{\boldsymbol{\psi }}}_{i} $$
(22)

where, \(l_{1i}\),\(l_{2i} > 0\).

3.3 Proof of stability

Select BLF as follows:

$$ V_{i} = V_{1i} + \frac{1}{{2l_{1i} }}{\tilde{\boldsymbol{\psi }}}_{i}^{\rm T} {\tilde{\boldsymbol{\psi }}}_{i} $$
(23)

where, \({\tilde{\boldsymbol{\psi }}}_{i} = {{\varvec{\uppsi}}}_{i} - {\hat{\boldsymbol{\psi }}}_{i}\), \({\tilde{\boldsymbol{\psi }}}_{i}\) is the estimation error of the weight vector.

Derivate (23) and substitute Eq. (19) into it:

$$ \begin{gathered} \dot{V}_{i} = \frac{{s_{i}^{2} \eta_{i} \dot{\eta }_{i} }}{{(1 - \eta_{i}^{2} )^{2} }} + \frac{{s_{i} \dot{s}_{i} }}{{1 - \eta_{i}^{2} }} + \frac{1}{{l_{1i} }}{\tilde{\boldsymbol{\psi }}}_{i}^{\rm T} {\dot{\tilde{\boldsymbol{\psi }}}}_{i} \\ { = }\frac{{s_{i} }}{{1 - \eta_{i}^{2} }}[(\overline{d}_{i} + b_{i} )(F_{i} (x_{i} ) - \hat{F}_{i} (x_{i} )) - \\ \zeta \left| {s_{i} } \right|^{1/2} {\text{sign}}(s_{i} ) - k_{2} \left| {s_{i} } \right|^{q} {\text{sign}}(s_{i} )] + \frac{{{\tilde{\boldsymbol{\psi }}}_{i}^{\rm T} {\dot{\tilde{\boldsymbol{\psi }}}}_{i} }}{{l_{1i} }} \\ \end{gathered} $$
(24)

Sort out (24) and substitute Eq. (22) into it:

$$ \begin{gathered} \dot{V}_{i} = \frac{{s_{i} }}{{1 - \eta_{i}^{2} }}[(\overline{d}_{i} + b_{i} )(\tilde{F}_{i} (x_{i} ) - {\tilde{\boldsymbol{\psi }}}_{i}^{\rm T} {{\varvec{\updelta}}}_{i} ({\mathbf{e}}_{i} )) - \\ \zeta \left| {s_{i} } \right|^{\frac{1}{2}} {\text{sign}}(s_{i} ) - k_{2} \left| {s_{i} } \right|^{q} {\text{sign}}(s_{i} )]{ + 2}l_{2i} {\tilde{\boldsymbol{\psi }}}_{i}^{\rm T} {\hat{\boldsymbol{\psi }}}_{i} \\ = \frac{{s_{i} }}{{1 - \eta_{i}^{2} }}[(\overline{d}_{i} + b_{i} )\vartheta_{i} - \zeta |s_{i} |^{1/2} {\text{sign}}(s_{i} ) - \\ k_{2} \left| {s_{i} } \right|^{q} {\text{sign}}(s_{i} ))] + 2l_{2i} {\tilde{\boldsymbol{\psi }}}_{i}^{\rm T} {\hat{\boldsymbol{\psi }}}_{i} \\ \end{gathered} $$
(25)

Lemma 1

[31]: For \(\forall \upsilon\), the following inequality holds:

$$ \hat{\upsilon }^{\rm T} \tilde{\upsilon } \le \frac{1}{2}\upsilon^{\rm T} \upsilon - \frac{1}{2}\tilde{\upsilon }^{\rm T} \tilde{\upsilon } $$
(26)

where, \(\hat{\upsilon }\) and \(\tilde{\upsilon }\) are the estimation and estimation error of \(\upsilon\) respectively, \(\tilde{\upsilon } = \upsilon - \hat{\upsilon }\).

According to Lemma 1 and Eq. (25), it can be known that:

$$ \begin{gathered} \dot{V}_{i} \le \frac{{(\overline{d}_{i} + b_{i} )\vartheta_{i} s_{i} }}{{(1 - \eta_{i}^{2} )}} - \frac{1}{{1 - \eta_{i}^{2} }}\zeta |s_{i} |^{3/2} - \\ \frac{1}{{1 - \eta_{i}^{2} }}k_{2} \left| {s_{i} } \right|^{q + 1} + l_{2i} ({{\varvec{\uppsi}}}_{i}^{\rm T} {{\varvec{\uppsi}}}_{i} - {\tilde{\boldsymbol{\psi }}}_{i}^{\rm T} {\tilde{\boldsymbol{\psi }}}_{i} ) \\ \le \frac{{A_{1i} s_{i} }}{{1 - \eta_{i}^{2} }} - \frac{1}{{1 - \eta_{i}^{2} }}\zeta |s_{i} |^{3/2} - \\ \frac{1}{{1 - \eta_{i}^{2} }}k_{2} \left| {s_{i} } \right|^{q + 1} - l_{2i} {\tilde{\boldsymbol{\psi }}}_{i}^{\rm T} {\tilde{\boldsymbol{\psi }}}_{i} + A_{2i} \\ \end{gathered} $$
(27)

where, \(A_{1i} = (\overline{d}_{i} + b_{i} )\vartheta_{i}\), \(A_{2i} = l_{2i} {{\varvec{\uppsi}}}_{i}^{\rm T} {{\varvec{\uppsi}}}_{i}\).

For Eq. (27), the following inequality holds:

$$ \begin{aligned} &\dot{V}_{i} \le - (1 - \eta _{i}^{2} )^{{\frac{{q - 1}}{2}}} \left( {k_{2} - \frac{{A_{{1i}} }}{{2|s_{i} |^{q} }}} \right)\frac{{|s_{i} |^{{q + 1}} }}{{(1 - \eta _{i}^{2} )^{{\frac{{q + 1}}{2}}} }} - \\ &\qquad(1 - \eta _{i}^{2} )^{{ - \frac{1}{4}}} \left( {\zeta - \frac{{A_{{1i}} }}{{2|s_{i} |^{{1/2}} }}} \right)\frac{{|s_{i} |^{{3/2}} }}{{(1 - \eta _{i}^{2} )^{{\frac{3}{4}}} }} - l_{{2i}} {\tilde{\boldsymbol{\psi }}}_{i}^{{\rm T}} {\tilde{\boldsymbol{\psi }}}_{i} + A_{{2i}} \\ &\quad\le - 2^{{\frac{{q + 1}}{2}}} (1 - \eta _{i}^{2} )^{{\frac{{q - 1}}{2}}} \left( {k_{2} - \frac{{A_{{1i}} }}{{2|s_{i} |^{q} }}} \right)V_{{i1}}^{{\frac{{q + 1}}{2}}} - \\ &\qquad 2^{{\frac{3}{4}}} (1 - \eta _{i}^{2} )^{{ - \frac{1}{4}}} \left( {\zeta - \frac{{A_{{1i}} }}{{2|s_{i} |^{{1/2}} }}} \right)V_{{i1}}^{{\frac{3}{4}}} + A_{{2i}} \\ \end{aligned} $$
(28)

Lemma 2

[32]: if \(\beta_{1} ,\beta_{2} , \cdots \beta_{n}\) is n non-negative numbers, constants \(\chi \in (0,1]\) and \(\varphi \in (1, + \infty )\), then:

$$ \sum\limits_{i = 1}^{n} {\beta_{i}^{\chi } } \ge (\sum\limits_{i = 1}^{n} {\beta_{i} } )^{\chi } $$
(29)
$$ \sum\limits_{i = 1}^{n} {\beta_{i}^{\varphi } } \ge n^{1 - \varphi } (\sum\limits_{i = 1}^{n} {\beta_{i} } )^{\varphi } $$
(30)

According to inequality (28) and lemma 2, there are:

$$ \dot{V}_{i} \le - \overline{\mu }_{i} V_{i}^{{\frac{q + 1}{2}}} - \overline{\mathchar'26\mkern-10mu\lambda }_{i} V_{i}^{\frac{3}{4}} + A_{2i} $$
(31)

where, \(\overline{\mu }_{i} = 2(1 - \eta_{i}^{2} )^{{\frac{q - 1}{2}}} \left(k_{2} - \frac{{A_{1i} }}{{2|s_{i} |^{q} }}\right)\), \(\overline{\mathchar'26\mkern-10mu\lambda }_{i} = 2^{\frac{3}{4}} (1 - \eta_{i}^{2} )^{{ - \frac{1}{4}}} \left(\zeta - \frac{{A_{1i} }}{{2|s_{i} |^{1/2} }}\right)\).

Lemma 3

[33]: Consider the following continuous nonlinear system:

$$ \dot{x} = f(x),\;x(0) = x_{0} ,\;x \in R^{n} $$
(32)

where \(f\;:\;R \times R^{n} \to R^{n}\) is a nonlinear function, which can be discontinuous. The solutions of (32) are understood in the sense of Filippov. Assume the origin is an equilibrium point of (32).

Definition 1

[33]: The origin of (32) is said to be practical fixed-time stable if it is globally finite-time stable and the settling-time function \(V(x)\) is globally bounded, i.e., \(\exists T_{\max } > 0:T(x_{0} ) \le T_{\max } ,\;\forall x_{0} \in R^{n}\).

Assuming that if there exists a continuous radially unbounded and positive definite function \(V:R^{n} \to R_{ + } \cup \{ 0\}\) such that 1) \(V(x) = 0 \Leftrightarrow x = 0\); 2) any solution \(x(t)\) of (32) satisfies the inequality:

$$ D^{*} V(x(t)) \le - \mu V^{r} (x(t)) - \mathchar'26\mkern-10mu\lambda V^{\hbar } (x(t)) + \ell $$
(33)

where denote by \(D^{*} V(x)\) the upper right-hand derivative of a function \(V(x)\), constants \(\mu > 0,\;\mathchar'26\mkern-10mu\lambda > 0\), \(r > 1\), \(0 < \hbar < 1\),\(0 < \ell < \infty\). Then the origin of system (32) is practical fixed-time stable and the settling time can be estimated as:

$$ T(x_{0} ) \le T_{\max } = \frac{1}{\mu (r - 1)} + \frac{1}{\mathchar'26\mkern-10mu\lambda (1 - h)},\;\forall x_{0} \in R^{n} $$
(34)

According to Lemma 3, the designed controller is practical fixed-time stable and it can be seen from inequality (31), the settling time can be estimated as:

$$ T(x_{0} ) \le T_{\max } = \frac{1}{\mu (r - 1)} + \frac{1}{\mathchar'26\mkern-10mu\lambda (1 - h)} = \frac{2}{{\overline{\mu }_{i} (q - 1)}} + \frac{4}{{\overline{\mathchar'26\mkern-10mu\lambda }_{i} }} $$
(35)

where \(r = \frac{q + 1}{2},\;h = \frac{3}{4}\).

This completes the proof.

Figure 2 is a block diagram of secondary voltage control. It can be seen from the Fig. 2 that when the DG is running, the control input is updated at all times.

Fig. 2
figure 2

Block diagram of fixed time secondary voltage control

Full size image

4 Design of distributed secondary frequency controller

In this section, the secondary frequency control is designed to make \(\omega_{i} \to \omega_{{{\text{ref}}}}\) to compensate for the frequency deviation caused by droop control, and let the follower follow the leader to make the frequency consensus within fixed time and make the frequency within constraint range, that is:

$$ \mathop {\lim }\limits_{t \to T} (\omega_{i} - \omega_{j} ) = 0 \Leftrightarrow \omega_{i} = \omega_{j} ,\;\forall t \ge T,\;\forall i,j \in N $$
(36)

The active power is sharing according to the rated capacity ratio of DG in the following proportion:

$$ k_{P1}^{{}} P_{1} = k_{P2}^{{}} P_{2} = \cdots = k_{Pi}^{{}} P_{i} $$
$$ \begin{gathered} \mathop {\lim }\limits_{t \to T} (k_{Pi}^{{}} P_{i} - k_{Pj}^{{}} P_{j} ) = 0 \hfill \\ \Leftrightarrow k_{Pi}^{{}} P_{i} = k_{Pj}^{{}} P_{j} ,\;\forall t \ge T,\;\forall i,j \in N \hfill \\ \end{gathered} $$
(37)

In order to restore the distributed secondary frequency, the derivation of (8) is:

$$ \dot{\omega }_{i} = \dot{\omega }_{{{\text{n}}i}} - k_{Pi}^{{}} \dot{P}_{i} = u_{\omega i} $$
(38)

In order to achieve accurate power sharing, assume:

$$ u_{{{\text{p}}i}} = k_{Pi}^{{}} \dot{P}_{i} $$
(39)

Considering the state constraints, the auxiliary controller is designed as follows:

$$ \begin{aligned} u_{{\omega i}} = & - K_{\omega } \left[ {\sum\limits_{{j \in N_{i} }} {a_{{ij}} \left| {\omega _{i} - \omega _{j} } \right|^{{c_{{\text{w}}} }} {\text{sign}}(\omega _{i} - \omega _{j} )} } \right. \\ & \left.\vphantom{\sum\limits_{{j \in N_{i} }}} { + b_{i} \left| {\omega _{i} - \omega _{{{\text{ref}}}} } \right|^{{c_{{\text{n}}} }} {\text{sign}}(\omega _{i} - \omega _{{{\text{ref}}}} )} \right] \\ \end{aligned} $$
(40)
$$ u_{{{\text{p}}i}} = - g_{{\text{p}}} \left[\sum\limits_{{j \in N_{i} }} {a_{ij} \left| {k_{pi}^{{}} P_{i} - k_{pj}^{{}} P_{j} } \right|^{{c_{{\text{p}}} }} {\text{sign}}(k_{pi}^{{}} P_{i} - k_{pj}^{{}} P_{j} )} \right] $$
(41)

where, \(g_{{\text{p}}} > 0\), \(0 < c_{{\text{w}}} < 1,\;0 < c_{{\text{p}}} < 1,\;c_{{\text{n}}} > 1\).

The state constraints are:

$$ K_{{\upomega }} = \left\{ \begin{gathered} \;\;\;\;\;\;\;\;\;\;k_{{\upomega }} \;\;\;\;\;\;\;\;,\;\;if\;0 \le t \le \overline{t} \hfill \\ \frac{{k_{{\text{b}}} }}{{\varepsilon_{{\upomega }}^{2} - \left| {\omega_{i} - \omega_{j} } \right|^{2} }},\;\;if\;t \ge \overline{t} \hfill \\ \end{gathered} \right. $$
(42)

where, \(k_{{\upomega }} > 0,\;k_{{\text{b}}} > 0\), \(\overline{t}\) is the auxiliary time variable, which can be selected according to the required control, and \(\varepsilon_{{\upomega }} > 0\) is the error constraint boundary between \(\omega_{i}\) and \(\omega_{j}\), which satisfies \(\left| {\omega_{i} - \omega_{j} } \right| < \varepsilon_{{\upomega }}\).

According to (37), (38), the frequency secondary control input is:

$$ \omega_{{{\text{n}}i}} = \int {(u_{{{\upomega }i}} + u_{pi} )} dt $$
(43)

The designed secondary frequency controller can realize frequency recovery and active power sharing within fixed time, and the output frequency is constrained effectively, so it has good robustness and anti-disturbance performance. The block diagram of secondary frequency control is shown in Fig. 3. It can be seen from the Fig. 3 that when the DG is running, the control input is updated at any times.

Fig. 3
figure 3

Block diagram of fixed time secondary frequency control

Full size image

Figure 3 shows that the secondary frequency control consists of two parts. The first part of the controller will realize the steady tracking of the reference frequency. At the same time, it can ensure the fast convergence of the frequency in a fixed time and the stable operation within the constraint range. The second part is to ensure the sharing of active power. The first part and the second part is added and integrated to form a frequency secondary controller, and is sent into the DG.

5 Simulation and result analysis

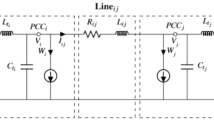
In this section, under the environment of MATLAB/SimPowerSystems software, an island AC microgrids with DC voltage source of 800 V, the inverter voltage of 380 V, and frequency 50 Hz is built. The effectiveness of the designed secondary voltage and frequency controller is verified through load variations, impedance line fails, and large disturbance. The communication block diagram of DG is shown in Fig. 4, which is composed of DG, load and RL line [34]. The sparse network communication of bidirectional directed graph is adopted to reduce the sensitivity of the system to faults. The communication topology is shown in Fig. 5, the reference of voltage and frequency is input to DG1 as the leader. Some parameters of the DG model, load and RL circuit are shown in Tables 1 and 2. Table 3 is the control parameter of the proposed scheme.

Fig. 4
figure 4

Simplified block diagram of AC microgrids

Full size image
Fig. 5
figure 5

Communication topology diagram of DG

Full size image
Table 1 Model parameters of DG
Full size table
Table 2 Some parameters of load and RL line
Full size table
Table 3 Parameters of the proposed control scheme
Full size table

The membership function used in adaptive fuzzy estimation is:

$$ \xi_{{F_{\varsigma }^{i,j} }} (e_{i\varsigma }^{{}} ) = \exp \left[\frac{{ - (e_{i\varsigma }^{{}} + 2 - 0.5j)^{2} }}{2} \right],j = 1,\; \cdots ,\;7 $$

5.1 Under load variations and impedance line fails

In order to verify the performance of the proposed secondary control under load variations and impedance line fails, it is assumed that: \(\overline{t} = 1\) s when t = 0.0 s, only the primary control is used; when t = 0.5 s, the secondary control is activated, and the proposed controller starts to run; when t = 1 s, load 2 is increased by 50%; when t = 1.5 s, load 3 is reduced by 25%; when t = 2.5 s, load 1 is increased by 50%; when t = 3.0 s, load 1 returns to its original value; when t = 3.5 s, Line 3 is disconnected; when t = 4.0 s, Line 3 is reconnected. The simulation result of secondary voltage and frequency control is shown in Fig. 6.

Fig. 6
figure 6

Output average voltage and frequency and active and reactive power

Full size image

It can be seen from Fig. 6 that with droop control only, although the voltage and frequency can be gradual stability stable, they have not reach the reference value. After the maximum change of average voltage and frequency is about 0.2V and 0.14Hz, the system remains stable for about 0.4 s, the system has good robustness. Active and reactive power are sharing accurately in proportion.

The uncertainty of the fuzzy approximation system is shown in Fig. 7.

Fig. 7
figure 7

Tuzzy approximation \(F_{i} (x_{i} )\)

Full size image

It can be seen from Fig. 7 that the adaptive fuzzy system has a good approximation effect for \(F_{i} (x_{i} )\).

Therefore, when the load variations and the impedance line fails, the output error of the designed controller is always within the preset range \(- 10 < e_{i,1} < 10\) and \(- 0.2 < e_{\omega i} < 0.2\) under the BLF constrained.

5.2 Performance verification of state constraints under large disturbance

Due to load sudden change, disturbance and other factor, it may be caused large transient variations of voltage and frequency, which may have a serious impact on system performance. Therefore, it is necessary to verify the output restricting capacity of the designed secondary voltage and frequency controller under large disturbance. Suppose that when t = 1.5 s, load 2 increased by 50%. When t = 2.5 s, load 3 is decreases by 25%. When t = 3.5 s, load 1 is increased by 5 times and compared with the traditional secondary voltage and frequency control without output constraints, the communication topology diagram still adopts the mode of Fig. 5. The simulation results are shown in Figs. 8 and 9.

Fig. 8
figure 8

Traditional secondary voltage and frequency control without output constraints

Full size image
Fig. 9
figure 9

Secondary voltage and frequency control considering output constraints

Full size image

Figure 8a, d shows the traditional secondary voltage and frequency control without output constraints and their error respectively. It can be seen from Fig. 8b, d that when the load variations little, both the voltage and the frequency error are within the restricted range. When the load variations greatly, where e3,1 is the maximum error secondary voltage control and \(e_{\omega 1}\) is the maximum error of the secondary frequency control respectively. The maximum voltage error e3,1 is 14 and exceeds the preset error \(- 10 < e_{i,1} < 10\), and the maximum frequency error \(e_{\omega 1}\) is 0.25 and exceeds the preset error \(- 0.2 < e_{\omega i} < 0.2\).

Figure 9a–d are the errors of the secondary voltage and frequency control considering output constraints. It can be seen from Fig. 9b, d that when the load variations greatly, the maximum error of voltage and frequency are within the preset constraint ranges \(- 10 < e_{i,1} < 10\) and \(- 0.2 < e_{\omega i} < 0.2\). The simulation results shows that the designed secondary controller has strong constrain ability on the system output.

5.3 Verification of practically fixed time convergence characteristics

To verify the convergence properties of the practically fixed time presented in this paper, the scheme presented in this paper is compared with the asymptotic time method proposed in [34] and the finite time method proposed in [35], respectively, as shown in Fig. 10.

Fig. 10
figure 10

Comparison of secondary voltage and frequency control

Full size image

As shown in Fig. 10, under the same initial conditions, the convergence time \(T(x_{0} )\) of the output voltage and frequency by the practically fixed-time method in this paper are about 0.2 s and 0.15 s, respectively, which do not exceed \(T_{\max }\) of 1.09 s and 0.95 s (They are computed by control parameters). The convergence time of output voltage and frequency by the asymptotic time method proposed in [34] are about 1.2 s and 0.8 s, respectively. The convergence time of output voltage and frequency by the finite time method proposed in [35] are about 0.4 s and 0.3 s, respectively. By comparison, the scheme proposed in this paper has faster convergence speed and better performance.

5.4 Controller performance testing for communication link fault

To verify the stability of the proposed controller under communication link fault, it is assumed that \(t = 1.5{\text{s}}\), load 4 increases by 10%, and at \(t = 2.5{\text{s}}\), load 4 restores to its initial set value. When \(t = 3.5{\text{s}}\), Communication between DG4 and DG1 is disconnected, Fig. 11 is a communication topology diagram under communication link fault and the simulation results are shown in Fig. 12.

Fig. 11
figure 11

Communication topology diagram under communication link fault

Full size image
Fig. 12
figure 12

Distributed secondary control under communication link fault

Full size image

From Fig. 12, it can be seen that the voltage and frequency are always within \(370{\text{V}} < v_{{{\text{od}}i}} < 390{\text{V}}\), \(49.8{\text{Hz}} < \omega_{i} < 50.2{\text{Hz}}\), and even under communication link fault, the system has good state constrained performance. When the load increases or decreases, the system can adjust the frequency and voltage in a short period of time, and restore the voltage and frequency to the reference values. The convergence time \(T(x_{0} )\) of the output voltage and frequency are about 0.5 s and 0.7 s, respectively, which do not exceed \(T_{\max }\) of 1.09 s and 0.95 s. The proposed method has good capabilities.

6 Conclusion

Aiming at the deviation problem caused by droop control, an adaptive fuzzy fixed time secondary voltage controller and secondary frequency controller considering state constraints are proposed. Multi-agent consensus control method is adopted to accurately track the reference input of voltage and frequency. The adaptive fuzzy system is used to approximate the unknown variables part of the system; the new sliding mode control is used to realize the global fixed time convergence of the system. Considering the problem of state constraints, a voltage controller is designed based on BLF function to the tracking error is within a preset range to constraint the output voltage. The frequency controller is designed based on the control barrier function to make the tracking error in the preset range to constraint the output frequency. The simulation results show that under the conditions of load variations, impedance line fault, and large disturbance, compared with the traditional secondary control, the proposed controller makes the system converge in a fixed time and has the ability of state constraint.

As future works the microgrids control under network attack should be considered, and time-varying BLF method is also a future work to improve the ability of system.