1 Introduction

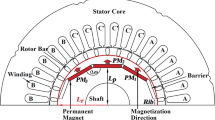
Linear permanent magnet motors (LFPMMs) are used in different fields such as flywheel energy storage system, hybrid vehicle system (HEVs), wind turbines, and medical and domestic applications. Moreover, LFPMMs are inherently suitable for high-performance applications, i.e., direct-drive systems and where low noise and smooth torque are imperative requirements [1,2,3,4]. Generally, LFPMMs are divided into single-sided, double-sided and multi-stage motors. Radii of stator and rotor and existing of teeth for stator compose special types of LFPMMs. Single-sided structures are used less than double-sided structures because double-sided structures have some advantages rather than single-sided, such as the output energy can be increased to twice compared with the single-sided linear flux machines. In addition, double-sided structure for LFPMM produces an equilibrium force in the center of motor and obstacles vibration and distortion in the middle of this motor building. Figure 1 shows LPMIADSSM that involved in cored and coreless structure. Eliminating cores lead to reduce the core loss and machine volume; therefore, coreless structures are preferred compared with cored structures, and in this paper, the coreless structure is considered; however, this method presented in this paper can be implemented for cored structure.

Fig. 1
figure 1

Cross section of LPMIADSSM: a cored b coreless

Full size image

Analytical model based on sub-domain method is a fast, proven and accurate model; in industrial applications, it is faster than numeric models and are more significant for reducing the time of simulations, which have the same accuracy as the numeric method; this analysis facilitates evaluating the arbitrary motor in different geometric structure values; therefore, analytical models are suggested because they are faster than numeric model and this method can help the users to understand all of interplays in motor, opposite of numerical method that everything is vague and user cannot have a deep realization of the motor behavior and the output results depend on the mesh sizes. The sub-domain method is one of the useful analytic methods investigated in this paper [5,6,7,8]. In this method, all the machine areas are divided into an appropriate sub-region and the partial differential equations (PDEs) in each sub-region are defined according to the Maxwell equations. Based on superposition method, the flux density for each sub-region is obtained by considering the PMs and armature current effects separately. Some articles used the analytical model for considering only PMs’ excitation (open-circuit mode) [9,10,11] and some other ones considered only armature reaction (AR) effects [12], and in more accurate analysis both of them has been considered [13,14,15,16] (Table 1).

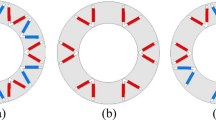
Table 1 Components of the magnetization patterns
Full size table

To obtain the accurate results, permeability for cores should not be infinite, and infinite permeability lead to obtain zero magnetic field intensity. It means that there is no any reduction of magneto-motive force in length of flux path in the cores that considers infinite permeability for cores [17], but the proposed method in this article is able to take an account finite permeability for cores and its effect on the flux distribution. Different magnetization patterns are used in the permanent magnet machines that in previous studies parallel magnetization pattern has been reported in some articles [18,19,20,21] and Halbach magnetization patterns in [22]. In the previous papers, they have not been concentrated on whole state magnetization [23,24,25,26], but in this article whole different arrays of magnetization are considered and calculated.

For summarizing the analytical method in this paper, it can be mentioned that this paper considers finite permeability for cores, variety magnetization patterns and both PM and AR effects on the magnetic flux density.

For reminding, this paper is divided to five sections; in section I have been presented past works. In section II the 2-D analytical model of linear permanent magnet synchronous motor with double mover, assumptions and reasonings for solution problem is expressed and subsections of this part explains proposed motor and calculates mentioned parameters at above. In section III, the presented results of analytical model are compared with FEA model (numerical solution). In the last part is brought concluded explanation of whole article.

2 Methodology and assumptions

At the first step of solution, some assumptions are considered as follows:

  • End effects are ignored, i.e., the motor is assumed to have infinite axial length.

  • The magnetic flux density has only vertical and horizontal components; this implies that the magnetic vector potential has only axial component.

  • All the materials are isotropic.

  • The all media have finite permeability.

  • The motor has slot-less stator structure.

  • The airspace between the magnets has the same permeability as the magnets.

  • Eddy current reaction field is neglected.

For obtaining the PDEs in each sub-region in the LPMIADSSMs, the investigated algorithm is demonstrated as follows:

  • Utilized the assumptions as mentioned.

  • Dividing the motor area to the appropriate sub-domain.

  • By Poisson and Laplace equation, PDEs of system are introduced.

  • For obtaining the unknown constants coefficients in the magnetic flux density, boundary conditions are applied.

  • Calculating the expansion Fourier for the current density in the winding sub-region and PM magnetization patterns for obtaining the Poisson equations.

  • After knowing constant coefficient for each sub-region, the magnetic flux density is able to be calculated.

  • Comparison between the obtained analytic method results and FEM results is made to validate the model.

2.1 Finding the PDEs in each sub-regions

Figure 2 divides different regions for the LPMIADSSMs; in fact, the winding is in direction of y and magnetization patterns of PMS are in the z and x directions.

Fig. 2
figure 2

Dividing of LPMIADSSMs

Full size image

The simplified Maxwell equation, which is applied to each sub-region to find the magnetic vector potential, is shown in Eq. 1.

$$ - \nabla^{2} {\varvec{A}}_{y}^{i} = \mu_{r} {\varvec{J}}_{y}^{i} + \mu_{0} \nabla \times {\varvec{M}} $$
(1)

It is noted that in the PM sub-region J = 0, in the winding sub-region M = 0 and for other regions both of J and M are zero. Based on solving differential equation method, it is necessary to find the homogeneous solution for (1). To achieve this aim, separation variables are applied; therefore, in the i = FAG, SAG, FE, SE, FR, SR, S, the magnetic vector potential is obtained as follows that \(\alpha_{n} = n\pi /\tau_{p}\) where \(\tau_{p}\) is pole pitch.

$$ - \nabla^{2} {\varvec{A}}_{y}^{i} = 0 $$
(2)
$$ \begin{aligned} \varvec{A}_{y}^{i} \left( {x,z} \right) = & \sum\limits_{{n = 1}}^{\infty } {\left( {a_{n}^{i} sinh\left( {\alpha _{n} z} \right) + b_{n}^{i} {\text{cosh}}\left( {\alpha _{n} z} \right)} \right)} cos\left( {\alpha _{n} x} \right) \\ & + \left( {c_{n}^{i} sinh\left( {\alpha _{n} z} \right) + d_{n}^{i} {\text{cosh}}\left( {\alpha _{n} z} \right)} \right)sin\left( {\alpha _{n} x} \right) \\ \end{aligned} $$
(3)

Magnetic flux density is obtained for each sub-region by using curl from magnetic vector potential (\(B = \nabla \times A\)); component of horizontal and z is obtained:

$$ B_{x}^{i} \left( {x,z} \right) = \frac{{\partial A_{y}^{i} }}{\partial z} $$
(4)
$$ B_{z}^{i} \left( {x,z} \right) = \frac{{ - \partial A_{y}^{i} }}{\partial x} $$
(5)

Strength field in (7), (8) is written:

\(H_{x}^{i} = \frac{{B_{x}^{i} }}{{\mu_{0} \mu_{r}^{i} }} - \frac{M}{{\mu_{r}^{i} }}\) (6) For regions winding Fw and SW that after solving Eq. 7, relation 8 will occur.

$$ - \nabla ^{2} \varvec{A}_{y}^{i} = - \mu _{0} \varvec{J}_{y}^{i} $$
(7)
$$ \begin{aligned} \user2{A}_{y}^{i} \left( {x,z} \right) & = \mathop \sum \limits_{{n = 1}}^{\infty } \left( {a_{n}^{i} sinh\left( {\alpha _{n} z} \right) + b_{n}^{i} \cosh \left( {\alpha _{n} z} \right) + \mu _{0} J_{{2n}} /\alpha _{i}^{2} } \right)cos\left( {\alpha _{n} x} \right)~ \\ & \quad + \left( {c_{n}^{i} sinh\left( {\alpha _{n} z} \right) + d_{n}^{i} \cosh \left( {\alpha _{n} z} \right) + \mu _{0} J_{{1n}} /\alpha _{i}^{2} } \right)sin\left( {\alpha _{n} x} \right) \\ \end{aligned} $$
(8)

where Fourier expansion for current density in winding region is:

$$ {\varvec{J}}_{y}^{i} \left( {x,t} \right) = \mathop \sum \limits_{n = 1}^{\infty } J_{1n} sin\left( {\alpha_{n} x} \right) + J_{2n} cos\left( {\alpha_{n} x} \right) $$
(9)

For FPM and SPM, the relation similar to other regions is written:

$$ - \nabla^{2} {\varvec{A}}_{y}^{i} = \mu_{0} \nabla \times {\varvec{M}} $$
(10)

Magnetic vector potential is the sum of private and general answer, but there is a difference in other regions, because the PMs and movers move; therefore x changes to \(x_{new}\) where v shows the linear velocity of movers and PMs:

$$ x_{new} = x - d $$
(11)

That:

$$ d = vt + d_{0} $$
(12)

Corresponding to mentioned procedure, for magnetic potential vector in FPM and SPM we have:

$$ \begin{aligned} A_{y}^{i} \left( {x,z} \right) & = \sum\limits_{{n = 1}}^{\infty } {\left( {a_{n}^{i} \sinh \left( {\alpha _{n} z} \right) + b_{n}^{i} \cosh \left( {\alpha _{n} z} \right) + \mu _{0} J_{{2n}} /\alpha _{i}^{2} } \right)} \cos \left( {\alpha _{n} x} \right) \\ & \quad + \left( {c_{n}^{i} \sinh \left( {\alpha _{n} z} \right) + d_{n}^{i} \cosh \left( {\alpha _{n} z} \right) + \mu _{0} J_{{1n}} /\alpha _{i}^{2} } \right)\sin \left( {\alpha _{n} x} \right)\end{aligned}$$
(13)

where vector of M is extracted from Fourier expansion of shape of magnetization with respect to displacement:

$$ {\varvec{M}} = \mathop \sum \limits_{n = 1}^{\infty } m_{xn} cos\left( {\alpha_{n} x} \right) + m_{yn} sin\left( {\alpha_{n} x} \right) $$
(14)

Each sub-region has 4 unknown variables, which by applying the boundary conditions is similar to Table 2, in intersection between each two sub-regions; this variable can be found. Boundary conditions clarify that vertical components of the magnetic flux density and horizontal components of magnetic field intensity must be continued in the intersection of two sub-regions as:

Table 2 Boundary conditions for intersection of regions
Full size table

3 Flux density distribution due to PM and AR

The simulations were obtained in the presence of winding and PM conditions separately. Firstly, the flux density due to PM in all of regions will be calculated and compared with the results of FEM.

The horizontal and vertical components of flux density according to Table 3 at the center of each-region for the different magnetization are shown in different figures that all the evaluations are done in static model and at the special time. Simulated results for analytic model and FEM in all the regions for ideal Halbach pattern are illustrated in Fig. 3, two-segment Halbach pattern in Fig. 4, parallel pattern in Fig. 5 and bar magnet in the shifting direction pattern in Fig. 6 for horizontal and vertical component; moreover, this motor is examined when there's only winding and neglects the effect of PM; therefore, for each region results of FEM and analytical method in Fig. 7 are compared together. Finally, superposition theory can be used to calculate the effect of either PM or winding at the same time. The interesting point in the three Halbach magnetization patterns is related to the magnetic flux path that it passes mainly through the PMs and the magnetic flux in the rotor is negligible, and it is possible to replace the rotor with other material having less weight, less volume and cheaper than the ferromagnetic materials. Also, it is evident that the ideal Halbach magnetization includes less THD compared with other magnetization patterns.

Table 3 Specifications of studied LPMIADSSM
Full size table
Fig. 3
figure 3figure 3

Distribution of flux density for ideal Halbach magnetization: a Flux density horizontal component of FR, b flux density vertical component of FR, c flux density horizontal component of FPM, d flux density vertical component of FPM, e flux density horizontal component of FAG, f flux density vertical component of FAG, g flux density horizontal component of FW, h flux density vertical component of FW, I flux density horizontal component of S, J flux density vertical component of S, k flux density horizontal component of SW, L flux density vertical component of SW, m flux density horizontal component of SAG, n flux density vertical component of SAG, o flux density horizontal component of SPM, p flux density vertical component of SPM, Q flux density horizontal component of SR, R flux density vertical component of SR

Full size image
Fig. 4
figure 4figure 4

Distribution of flux density for two-segment Halbach magnetization: a Flux density horizontal component of FR, b Flux density vertical component of FR, c Flux density horizontal component of FPM, d Flux density vertical component of FPM, e Flux density horizontal component of FAG, f Flux density vertical component of FAG, g Flux density horizontal component of FW, h Flux density vertical component of FW, I Flux density horizontal component of S, J Flux density vertical component of S, k Flux density horizontal component of SW, L Flux density vertical component of SW, m Flux density horizontal component of SAG, n Flux density vertical component of SAG, o Flux density horizontal component of SPM, p Flux density vertical component of SPM, Q Flux density horizontal component of SR, R Flux density vertical component of SR

Full size image
Fig. 5
figure 5figure 5

Distribution of flux density for parallel magnetization: a Flux density horizontal component of FR, b Flux density vertical component of FR, c Flux density horizontal component of FPM, d Flux density vertical component of FPM, e Flux density horizontal component of FAG, f Flux density vertical component of FAG, g Flux density horizontal component of FW, h Flux density vertical component of FW I Flux density horizontal component of S J Flux density vertical component of S, k Flux density horizontal component of SW L, Flux density vertical component of SW, m Flux density horizontal component of SAG, n Flux density vertical component of SAG, o Flux density horizontal component of SPM, p Flux density vertical component of SPM, Q) Flux density horizontal component of SR, R Flux density vertical component of SR

Full size image
Fig. 6
figure 6figure 6

Distribution of flux density for bar magnet in the shifting direction magnetization: a Flux density horizontal component of FR, b Flux density vertical component of FR, c Flux density horizontal component of FPM, d Flux density vertical component of FPM, e Flux density horizontal component of FAG, f Flux density vertical component of FAG, g Flux density horizontal component of FW, h Flux density vertical component of FW, I Flux density horizontal component of S, J Flux density vertical component of S, k Flux density horizontal component of SW, L Flux density vertical component of SW, m Flux density horizontal component of SAG, n Flux density vertical component of SAG, o Flux density horizontal component of SPM, p Flux density vertical component of SPM, Q Flux density horizontal component of SR, R Flux density vertical component of SR

Full size image
Fig. 7
figure 7figure 7

Distribution of flux density for only AR: a Flux density horizontal component of FR, b Flux density vertical component of FR, c Flux density horizontal component of FPM, d Flux density vertical component of FPM, e Flux density horizontal component of FAG, f Flux density vertical component of FAG, g Flux density horizontal component of FW, h Flux density vertical component of FW, I Flux density horizontal component of S, J Flux density vertical component of S, k Flux density horizontal component of SW, L Flux density vertical component of SW, m Flux density horizontal component of SAG, n Flux density vertical component of SAG, o Flux density horizontal component of SPM, p Flux density vertical component of SPM, Q Flux density horizontal component of SR, R Flux density vertical component of SR [16]

Full size image

Another exciting point in the simulation procedure is related to the time of the simulation that for the analytical model it is 14 times less than the numerical one. It means in the design stage optimization problem includes too many iterations, and times can be saved by implementing the analytical model, if possible, instead of the numerical model.

4 Conclusion

This paper concentrated on analytical model to calculate magnetic flux density for LPMIADSSMs. Sub-domain method based on partial differential equations is applied due to its accuracy and speed of obtaining answers, and by this model, the effects of AR and PMs with different magnetization patterns on distribution of flux density in all sub-regions are scrutinized. Finally, the results for both PM and AR are validated by FEM extracted by Maxwell software.