1 Introduction

Hydropower stations, both reservoir and pumped-storage, undertake the task of expanding market profits and maintaining power grid frequency stability [1]. It is essential and urgent for both power generators and grid managers to determine the change in FMHS and forecast its power generation when the energy storage is in infancy, such as South-West China [2]. Unfortunately, research in this cognate area remains sparse. Furthermore, the alteration of generation output in real-time to respond to frequency fluctuations introduces significant random fluctuations into the series [3], which increases the challenge posed by this problem.

Referring to determine the generation schedules for the hydropower station, scholars have provided two main ideas: One is establishing an optimal problem, whose input is inflow and load demand and constrained with market rules, transmission capacity, reservoir and plant safety, etc. [4, 5]. This problem is always multi-stage, non-linear with multiple objectives [6], whose parameters are stochastic and always be solved by some simplified, linearized methods [7]. As for FMHS, there is acceptable deviation between the linearized solution and actual operation of the power stations [8]. Although non-linear evolutionary algorithms may reduce the error, it may consume more time and RAM [9]. The other, time series analysis and prediction based on date-driven models, has become more popular because of its simplicity, low data requirement, and robustness. They can be used to extract implicit information directly from historical data with less time cost and RAM usage [10,11,12]. Yong-qi Liu, et al. derived reservoir operation rule based on Bayesian deep learning method under the influences of parameter and inflow uncertainty, whose experimental result is better than that of traditional optimal models [13]. Majid Dehghani, et al. coupled an adaptive neuro-fuzzy inference system (ANFIS) with gray wolf optimization to forecast the hydropower generation and obtained better effects than single ANFIS [14]. The factors influencing FMHS are comprehensive, the relationships between them are gray, and the weights of influences therein are fuzzy, these force us to mine rules only with the help of original signals (OS). However, more work needs to be done to achieve suitable accuracy.

ANN is an important branch of data mining and artificial intelligence technology, which can establish the correlation between inputs and outputs by learning large amounts of data than traditional mathematical statistical model [15]. There are more than ten ANNs applied in variety of areas for time series prediction [16,17,18]. Shi et al. proposed a two-stage electricity price forecasting scheme with two ANNs [19]. Saâdaoui, et al. forecast electricity spot prices with ANN and a regression model, the model shows great superiority in time cost and data dependency [20]. Similarly, Zhe Wang solved building thermal load prediction by developing deep learning ANN model, whose physics-based prediction is also constrained by the model and input complexity [21]. In hydrology, powerful learning performance makes it an important means of inflow forecasting [22, 23], which has been considered as global problems in time series analysis. Different algorithms show different performances along the changes in series characteristics, and none of them is omnipotent across all prediction problems. For instance, with its simple structure, high precision, and easy implementation, BP has been one of the most widely used ANNs since 1986, but it depends too much on learning samples and is too slow. ELM is a learning algorithm based on the feed-forward neural network, allowing rapid learning, good generation performance, and strong non-linear capabilities [24]. However, the accuracy of ELM in regression calculation is lower than BP. Another advanced algorithm GRNN is established by using radial basis function neurons and liner neurons, which shows stronger mapping ability in non-linear problems with more complex calculation [25].

With the increasing complexity of the OS, single ANN algorithm cannot satisfy the task, so researchers seek to improve accuracy and accelerate the solution using hybrid forecasting models. The main strategy can be summarized thus: (a) selecting optimal inputs for their predictive model with feature selection to accelerate the process [26, 27], (b) coupling with optimization algorithms to determine connection weights [28], and (c) reducing complexity or extract characteristic values of the OS invoking the “decomposition-and-ensemble” principle [29], whereby the OS is decomposed into several intrinsic mode functions (IMFs) and residual (Re), and the prediction results of the complete sequence can be obtained by summation or clustering after prediction [30, 31]. The common decomposition methods are wavelet transform (WT) [32], empirical mode decomposition (EMD) [33], and EEMD [34]. In our study, optimal input selection was accomplished with autocorrelation analysis (ACA), the parameters of various ANNs were determined by whale optimal algorithm (WOA) [35], and EEMD was applied to decompose the OS.

EEMD is an effective method that can separate the curve with its intricate mathematical relationship into several curves with a relatively clear, simple mathematical relationship to mining data features [36, 37]. Compared to WT, it can adaptively decompose the OS in a step-by-step manner according to the extreme values [38]. Meanwhile, it prevents mode mixing in EMD with white noise efficiently, but is ill-conditioned in terms of end effects, which will distort the decomposed sub-series [39]. Few researchers paid attention to this key issue. For instance, Liu Huimin and Hao Guo-Cheng, etc., only discussed the steps and advantages of the “decomposition-and-ensemble” principle with EEMD, but the end effects were ignored [37, 40]. The mirror method, which copies extrema [41] or flips complete cycle [42] and then adds these to beginning and end points, is a simple but effective way to alleviate end effects. However, the generation of FMHS is pseudo-periodic sequences, so it is difficult to identify the periodic component and calibrate a typical wave equation. Besides this, symmetric extension is adopted to alleviate the end effects [43]. Unfortunately, the end points of FMHS signals represent the generation at the beginning and end of the day, and symmetric extension may destroy the distribution characteristics of the OS. Last but not the least, forecasting methods, which extend the OS with one or multi-step ahead forecasting by AI technology, such as support vector regression (SVR) [44], are applied to alleviate the end effects. However, there are some shortcomings arising therefrom in multi-step forecasting, and the time consumed by calibrating SVR parameters is also non-negligible [45]. Inspired by these, we alleviate the end effect by coupling mean generating function (MGF) with ELM, which takes account of both accuracy and calculation rate.

Other researchers have paid more attention to improving single networks through OS decomposition or parameter optimization and then compared with each other or the original network [46, 47]. For some physical quantities with significant differences between different periods, such as seasonal tidal level [48], wind speed [29], and river runoff [22, 31],predictions with a single network attempt to maintain their accuracy [49]. In recent years, adaptive selection and complementarity of various networks seem to be becoming more popular. Tan Qiao-feng, et al. compared the performance of ANFIS, SVM and seasonal first-order autoregressive (SVR (1)) models in flood and dry seasons and then recommended the use of different models to forecast monthly runoff [50], which undoubtedly provided a new solution. de Mattos Neto et al. also applied different networks for establishing adaptive forecasting system [51]. It is found that the generation of FMHS has prominent seasonality, and even then there remain significant differences between two adjacent days; therefore, we switch optimal algorithm adaptively from a variety of ANNs to prevent these effects. The complete annual series of FMHS consists of over 30,000 elements, and the tremendous amount of computation makes it inevitable that a parallel computing strategy is introduced [52] to the adaptive learning process.

In summary, the main contributions are listed as follows: First, an accurate and efficient forecasting model is established, which provides a new avenue to determine dispatch schedules of FMHS. Second, standard EEMD is improved to reduce mode mixing caused by end effects, so that the sub-series are as simple as possible. Finally, a new concept adaptively involving mixing of multiple ANNs is introduced. Various scenarios are set to confirm that this hybrid model can give full play to the advantages of each ANN. The rest of the study is organized as follows: Section 2 covers improvements to standard EEMD and data pre-processing. Section 3 introduces the ANN and algorithms and outlines the hybrid forecasting model. Section 4 covers the prediction effect using a case study from Sichuan Province, China. Section 5 discusses the necessity of the improved EEMD strategy and adaptive combination of various ANNs, and Section 6 concludes.

2 Improvement of EEMD

EEMD is developed from EMD to overcome issues around mode mixing, so the result of EEMD, IMFs and Re, will follow two rules [53].

  1. a)

    The difference of the number of extreme points (\(Ne\)) and zero-crossing points (\(Nz\)) is not more than 1 in the whole series, that is,

    $$ Nz - 1 \le Ne \le Nz + 1. $$
    (1)
  2. b)

    The mean value of upper and lower envelopes is 0 at any point, that is,

    $$ {{\left[ {f_{\max } \left( t \right) + f_{\min } \left( t \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {f_{\max } \left( t \right) + f_{\min } \left( t \right)} \right]} 2}} \right. \kern-\nulldelimiterspace} 2} = 0. $$
    (2)

The basic hypothesis of EEDM is any OS \(x\left( t \right)\) is expressed as the sum of several IMFs and Re, that is,

$$ x\left( t \right) = \sum\limits_{i = 1}^{n} {IMF_{i} \left( t \right) + R_{n} \left( t \right)} , $$
(3)

where \(R_{n} \left( t \right)\) denotes Re, \(n\) is the total of IMF, and \(i\) is index of IMFs.

The basic sifting algorithm for EMD and EEMD is described as follows:

Step 1. Find the location of all extreme points in \(x\left( t \right)\).

Step 2. Determine the upper and lower envelope according to local maximum and minimum, respectively, with cubic spline interpolation and then calculate their mean value:

$$ m_{1} \left( t \right) = {{\left[ {u\left( t \right){ + }l\left( t \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {u\left( t \right){ + }l\left( t \right)} \right]} 2}} \right. \kern-\nulldelimiterspace} 2}, $$
(4)

where \(u\left( t \right)\) and \(l\left( t \right)\) are upper and lower envelope, respectively.

Step 3. The difference between OS and the mean value is calculated, that is,

$$ h_{1} \left( t \right) = x\left( t \right) - m_{1} \left( t \right). $$
(5)

Step 4. If \(h_{1} \left( t \right)\) is satisfied with the rules in (1) and (2), set \(IMF_{1} \left( t \right) = h_{1} \left( t \right)\), else, set \(x\left( t \right){ = }h_{1} \left( t \right)\) and go to Step 1.

Step 5. Subtract the derived IMF from \(x\left( t \right)\), that is,

$$ x^{\prime}\left( t \right) = x\left( t \right) - IMF_{m} \left( t \right). $$
(6)

Then go to Step 1, the \(x^{\prime}\left( t \right)\) is defined as the Re.

Step 6. Stop the sifting process when the Re from Step 5 becomes a monotonic function and there is no new IMF.

The EEMD algorithm adds white noise (WN) that will cancel into the OS many times; this has proved effective in overcoming mode mixing. The signal combined with OS and WN is described as:

$$ s\left( t \right) = x\left( t \right) + \left\{ {w_{k} \left( t \right)} \right\}_{k = 1}^{K} , $$
(7)

where \(w_{k} \left( t \right)\) is the white noise, and\(K\) and \(k\) are the total number and serial number of WN, respectively. The reconstruction signal (RS) \(s\left( t \right)\) also is expressed as (3) through the EMD algorithm.

As mentioned above, end effects are another issue in EMD, and it has not been completely overcome through EEMD; furthermore, these may cause distortion of the envelope and then gradually “pollute” other IMFs. To obtain ‘purer’ IMFs, the mean generating function (MGF) is applied to select different forms of OS and extend them, thus achieving comprehensive extension of the curve by non-linear weighted reconstructed (NWR), as shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of boundary extension method of improved EEMD

Full size image

Given a signal \(x\left( t \right)\) with length \(2N\left( {N > 3} \right)\), the improved EEMD proceeds as follows:

Step 1. The data on the left are reordered, forming \(XT\left( N \right)\), where the index \(n\) is between 1 and \(N\) from the middle to the left. Then, \(XT\left( N \right)\) is divided into two parts according to the parity of \(n\), that is,

$$ \left\{ {\begin{array}{*{20}c} {XT_{1} = XT\left( p \right)} & {p = 1:2:N} \\ {XT_{2} = XT\left( q \right)} & {q = 2:2:N} \\ \end{array} } \right., $$
(8)

where \(X_{L,1}\) and \(X_{L,2}\) are two sequences composed of elements whose indices are odd and even, respectively.

Step 2. Forecast \(XT_{1}\) and \(XT_{2}\) with ELM, that is,

$$ \left\{ {\begin{array}{*{20}c} {XT_{1} \left( {p^{\prime}} \right) = a_{1} + f_{1} \left[ {XT_{1} \left( {p - 1} \right),XT_{1} \left( {p - 2} \right), \cdots ,XT_{1} \left( {p - p^{ * } } \right)} \right]} & {p > p^{ * } } \\ {XT_{2} \left( {q^{\prime}} \right) = a_{2} + f_{2} \left[ {XT_{2} \left( {q - 1} \right),XT_{2} \left( {q - 2} \right), \cdots ,XT_{2} \left( {q - q^{ * } } \right)} \right]} & {q > q^{ * } } \\ \end{array} } \right., $$
(9)

where \(a_{1}\) and \(a_{2}\) are parameters of ELM, \(f_{1}\) and \(f_{2}\) represent the fitting function, \(p^{ * }\) and \(q^{ * }\) denote the lag order of \(XT_{1}\) and \(XT_{2}\), respectively;\(p^{ * }\) and \(q^{ * }\) are determined during training of the ELM.

Step 3. Establish an NWR model between predicted and actual values at index-\(n\), that is,

$$ X\left( n \right) = \alpha \left( n \right) \times XT_{1} \left( n \right) + \beta \left( n \right) \times XT_{2} \left( n \right), $$
(10)

where \(\alpha \left( n \right)\) and \(\beta \left( n \right)\) are on-line weighting coefficients determined during training of the ELM.

Step 4. Repeat ELM until the sequence is extended outwards by K, which is the length of the wave crest/valley: this point is the “new” end of the signal.

Step 5. Decompose the extend sequence in Step 4 by EEMD and remove the extended part of each IMF: the remaining part is the Re of the OS.

Step 6. Set the data to the right as \(XT\left( N \right)\), repeat Steps 1 to 5, to obtain the complete IMF of the OS.

The process of improved EEMD can be evaluated as shown in Fig. 2. During the decomposition process, the new, real signal value is constantly added to adjust the extended data set dynamically. We extend the left half with the current historical value and the right half with ELM in Steps 2 to 4, so that the information of OS is entirely usable.

Fig. 2
figure 2

Flow chart through the improved EEMD method

Full size image

3 Hybrid forecasting model

In our hybrid forecasting model, data pre-processing is accomplished by improved EEMD (as described in Section 2); the ANN models chosen are ELM, BP, and GRNN; the number of neurons in each hidden layer of ELM and BP and spread factor of GRNN is optimized by WOA.

The ELM, BP, GRNN, and WOA are described as follows:

  1. a)

    ELM is a learning algorithm based on the feed-forward neural network, given a sample set \(\left\{ {\left[ {x\left( j \right),y\left( j \right)} \right]|x\left( j \right) \in R_{c} ,x\left( j \right) \in R_{d} ,j = 1,2, \cdots ,N_{s} } \right\}\), where \(c\) and \(d\) are the number of neurons in input and output layers, respectively, and \(N_{s}\) denotes the number of elements, the ELM can be described thus:

    $$ y\left( j \right) = \sum\limits_{h = 1}^{{N_{h} }} {\theta_{h,j} G\left[ {\omega_{j,h} \cdot x\left( j \right) + b_{h} } \right]} ,j = 1,2, \cdots ,N_{s} , $$
    (11)

    where \(N_{h}\) denotes the number of neurons in the hidden layers, \(\omega_{j,h}\) is the connection weight between the \(jth\) neuron in the input layer and the \(hth\) neuron in the hidden layer, \(\theta_{h,j}\) denotes the connection weight between the \(hth\) neuron in the hidden layer and the \(jth\) neuron in the output layer, \(G\left( \cdot \right)\) is the activation function, and \(h\) is index pertaining to the neurons in the hidden layer.

  2. b)

    BP is one of the most widely used ANNs, and it can achieve good accuracy after training. For the sample set above, the BP can be described as follows:

    $$ z\left( h \right) = G\left[ {\sum\limits_{j = 1}^{{N_{s} - 1}} {\omega_{j,h} \cdot x\left( j \right) - \xi_{h} } } \right], $$
    (12)
    $$ y\left( j \right) = G\left[ {\sum\limits_{j = 1}^{{N_{s} - 1}} {\theta_{h,j} \cdot z\left( h \right) - \xi_{j} } } \right], $$
    (13)

    where \(z\left( h \right)\) denotes the output from the hidden layer, \(\xi_{h}\),\(\xi_{j}\) are thresholds for the hidden and output layers, and other parameters have the same meaning as above.

  3. c)

    GRNN is an improvement on the radial function network, which is established using radial basis function neurons and liner neurons. The input vector is \(X_{G} = \left\{ {x\left( j \right)|j = 1,2, \cdots ,N_{s} } \right\}\), and the predicted value of GRNN (also called the output vector) is \(Y_{G} = \left\{ {y\left( j \right)|j = 1,2, \cdots ,N_{s} } \right\}\), the procedure of the GRNN model can be represented as

    $$ E\left[ {Y_{G} |X_{G} } \right] = \frac{{\int_{ - \infty }^{\infty } {Y_{G} f\left( {Y_{G} ,X_{G} } \right)dX_{G} } }}{{\int_{ - \infty }^{\infty } {f\left( {Y_{G} ,X_{G} } \right)dX_{G} } }}, $$
    (14)

    where \(E\left[ {Y_{G} |X_{G} } \right]\) is the expected value of the output and input vectors; \(f\left( \cdot \right)\) is the joint probability density function.

    The GRNN contains an input layer, pattern layer, summation layer, and output layer. The pattern Gaussian function \(p\left( g \right)\) between input layer and pattern layer is given by

    $$ p\left( g \right) = \exp \left[ { - \frac{{\left[ {X_{G} - X\left( g \right)} \right]^{T} \left[ {X_{G} - X\left( g \right)} \right]}}{{2\sigma^{2} }}} \right] \, \left( {g = 1,2, \cdots ,N_{G} } \right), $$
    (15)

    where \(\sigma\) denotes the smoothing parameter, \(X\left( g \right)\) is a specific training vector of neuron \(g\) in the pattern layer, and \(N_{G}\) is number of pattern neurons. (Other parameters have the same meaning as above.)

    The summation layer computes the sum of pattern layer outputs with two summations, namely \(Sum_{s}\) and \(Sum_{\omega }\): The former computes arithmetic sum, and the latter computes the weight sum. The transfer function can be represented as

    $$ Sum_{s} = \sum\limits_{g = 1} {p\left( g \right)} , $$
    (16)
    $$ Sum_{\omega } = \sum\limits_{g = 1} {\omega_{g} p\left( g \right)} . $$
    (17)

    Finally, the output of the GRNN can be calculated as follows:

    $$ Y_{G} = {{Sum_{s} } \mathord{\left/ {\vphantom {{Sum_{s} } {Sum_{\omega } }}} \right. \kern-\nulldelimiterspace} {Sum_{\omega } }}. $$
    (18)
  4. d)

    The WOA is inspired by the strategy of the spiral rise and cyclic updating seen in humpback whale predation paths. The renewal process of an individual can be described as follows:

    $$ \overrightarrow {S} = \left| {\overrightarrow {C} \cdot \overrightarrow {{s^{ * } }} \left( m \right) - \overrightarrow {s} \left( m \right)} \right|, $$
    (19)
    $$ \overrightarrow {s} \left( {m{ + }1} \right){ = }\overrightarrow {{s^{ * } }} - \overrightarrow {A} \cdot \overrightarrow {D} , $$
    (20)

    where \(\overrightarrow {S}\) indicates the current position, \(\overrightarrow {{s^{*} }}\) is the position vector of the best solution obtained so far, \(\overrightarrow {s}\) is the position vector, \(\overrightarrow {A}\) and \(\overrightarrow {C}\) represent coefficient vectors, and \(m\) indicates the current iteration. The vector \(\overrightarrow {{s^{*} }}\) will be updated in each iteration if there is a better solution.

Vectors \(\overrightarrow {A}\) and \(\overrightarrow {C}\) are calculated as follows:

$$ \overrightarrow {A} = 2\overrightarrow {a} \cdot \overrightarrow {r} - \overrightarrow {a} , $$
(21)
$$ \overrightarrow {C} = 2 \cdot \overrightarrow {r} , $$
(22)

where \(\overrightarrow {a}\) is linearly decreased from 2 to 0, and \(\overrightarrow {r}\) is a random vector on [0, 1]

The helical motion of a humpback whale can be described by:

$$ \overrightarrow {s} \left( {m + 1} \right) = \overrightarrow {{S^{\prime}}} \cdot e^{bl} \cdot \cos \left( {2\pi l} \right) + \overrightarrow {{s^{*} }} \left( m \right), $$
(23)

where \(\overrightarrow {{S^{\prime}}} { = }\left| {\overrightarrow {s} \left( m \right) - \overrightarrow {{s^{*} }} \left( m \right)} \right|\) and indicates the distance between vectors \(\overrightarrow {s} \left( m \right)\) and \(\overrightarrow {{s^{*} }} \left( m \right)\), \(b\) is a constant defining the shape of the logarithmic spiral, l is a random number on \(\left[ { - 1,1} \right]\). (Other parameters have the same meaning as above.)

Equations (20) and (23) are to be satisfied simultaneously that is the probability of each of them is 50%, so the position update during optimization is described as follows:

$$ \left\{ {\begin{array}{*{20}l} {\overrightarrow {s} \left( {m{ + }1} \right){ = }\overrightarrow {{s^{ * } }} - \overrightarrow {A} \cdot \overrightarrow {D} } & {if \, p_{W} < 0.5} \\ {\overrightarrow {s} \left( {m + 1} \right) = \overrightarrow {{S^{\prime}}} \cdot e^{bl} \cdot \cos \left( {2\pi l} \right) + \overrightarrow {{s^{*} }} \left( m \right)} & {if \, p_{W} \ge 0.5} \\ \end{array} } \right., $$
(24)

where \(p_{W}\) is a random number on [0, 1].

With the help of improved EEMD and WOA, all three ANNs can accomplish the task independently, although there are differences in accuracy and time consumption. In particular, the deviation is mostly concentrated in the adjacent two days with seasonal alternation or severe load change; however, different ANNs show different performances in the same period. Therefore, an ANN adaptive switching strategy is introduced to prevent the effects of seasonality and mutation as described below.

Firstly, one-step ahead time series prediction with ELM, BP, and GRNN is accomplished independently, and after 96 repetitions, the predicted daily curve can be obtained. Then, these results can be used for evaluating prediction performance, and the best will be chosen for 96-step prediction the day after. When updating information, this cycle continues until completing the forecast results of the whole year. It is noticed that the calculation of the three ANNs is parallel, so the adaptive evaluation and switching do not cost too much time and resources.

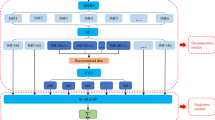
The advantage of ANN adaptive switching is such that there are obvious improvements compared with the deviation above and it provides a convenient path to real-time generation forecasting of FMHS. The specific steps of hybrid forecasting model based on improved EEMD and ANNs adaptive switching are described as follows and shown in Fig. 3.

Fig. 3
figure 3

Flow chart through the hybrid forecasting model based on improved EEMD and ANNs

Full size image

Step 1. Pre-process the OS with improved EEMD as described in Section 2, then delete decomposition results of the extended section, retain the remaining IMFs and Re.

Step 2. Forecast IMFs and Re time-by-time using ELM, BP, and GRNN while optimizing the model parameters by WOA. The predicted value for each period in any IMF or Re is the best result of the three ANN algorithms (adaptively speaking).

Step 3. Compute the arithmetic sum of the predicted values of all IMFs and Re and output it as a result.

Step 4. Evaluate the prediction performance of the hybrid model with appropriate error evaluation indices.

4 Case study

To verify the effectiveness of the proposed model, an experiment was conducted in PBG, one of the major FMHSs in Sichuan Province, China. PBG consists of a reservoir with a retained water volume of 5.12 billion m3 and a hydropower plant with an installed capacity of 3600 MW. In the Dadu Basin, more than five other runoff hydropower stations are located downstream of PBG, whose inflows are directly affected by generation at PBG. The operation of PBG is supposed to satisfy the requirements imposed by the electricity energy market and grid frequency modulation in Sichuan, and the latter usually has strong randomness.

4.1 Data source

The monitoring system deployed in this power plant provides convenience in terms of data acquisition. The intact real-time generation data of PBG in 2018 are employed as the OS. The sampling interval is set to 15 min, and the beginning and end times is set as 00:15 and 24:00 daily. There are 96 samples collected daily, giving a total of 35,040 pieces in this experiment (Table 1). As mentioned above, the generation of FMHS is dependent on both precipitation and load demand, so the whole sample is divided into four parts by season, and we selected 96 from a typical day in each part, giving a total of 384 samples for forecasting and model testing. The generation process of PBG on ordinary days is shown in Fig. 4. The daily generation process of PBG is governed by a bimodal curve akin to the system load demand, but more random fluctuations are added thereto. It is certain that the OS will be more complex and irregular, and there is huge difficulty in forecasting samples with sufficient accuracy.

Table 1 Detailed description of data sources
Full size table
Fig. 4
figure 4

The generation process of PBG in typical days

Full size image

4.2 Model description

ELM, BP, and GRNN are important branches of supervised learning algorithms, which show strong dependence on the training sample set. The shortage of samples may make it challenging to cover all data features and cause a large deviation at key points. On the contrary, too much repetition of invalid training will reduce the efficiency of the algorithm. It is necessary for the success of supervised learning to determine the appropriate size of training sample and select the input which has a strong correlation to the target as far as possible. So, the similarity between samples is first identified to define the model structure with the help of autocorrelation analysis (ACA).

The generation sequence of FMHS is the result of responding to load demand. Autocorrelation of load demand comes from the same climate characteristics (including precipitation, temperature, etc.) in any season. The signal of FMHS exhibits the same characteristics and can be described by its autocorrelation coefficient (AC). Firstly, we show interest in the autocorrelation between days. The autocorrelation of daily average generation demonstrates a significant downward trend with the increase in date interval, as shown in Fig. 5(a). Then, we pay more attention to the correlation between intraday periods, as shown in Fig. 5(b). AC over 0.5 between days and 0.8 between intraday periods, respectively, is regarded as a strong correlation, so we infer that there is a strong correlation between the generation of FMHS in 14- and 8-day periods.

Fig. 5
figure 5

Autocorrelation analysis of the FMHS signal, a autocorrelation between days; b autocorrelation between intraday periods

Full size image

Based on the ACA, the generation process of PBG in the next day was selected as the prediction target and the samples of the first 14 days formed the training set. The input of the model was the generation of the first eight periods. Therefore, in the forecasting models by ANN this time, the number of neurons in input layer and output layer is 8 and 1, respectively. Furthermore, we set the training times, learning rate, and convergence accuracy of BP to 1000, 0.01, and 0.00001, respectively. The activation function \(G\left( \cdot \right)\) in (11) was chosen to be “sig,” and in (12), (13), we chose “tansing” and “purelin,” respectively. The number of neurons in the hidden layers of ELM and BP, and smoothing parameter \(\sigma\) in (15) of GRNN is optimized by WOA. The optimization of the improved EEMD, WOA and adaptive ANN switching processes was accomplished using the MATLAB™ platform, run on a computer with an Intel® Core™ i7 processor (2.70 GHz) and 8 GB of RAM.

The efficiency of a forecasting model is always reflected by prediction experiments with large-scale, long-range samples and described through a series of error evaluation indicators. In our experiment, four typical days (Fig. 4) (including 384 samples) and the power generation signal of PBG in 2018 (a total of 35,040 samples) were selected for model testing. The error evaluation indicators used are mean absolute percent error (MAPE), mean absolute error (MAE), root mean square error (RMSE), and concordance index (CI):

$$ MAPE = \frac{1}{{N_{s} }}\sum\limits_{j = 1}^{{N_{s} }} {\left| {\frac{{\widehat{y}\left( j \right) - y\left( j \right)}}{y\left( j \right)}} \right|} \times 100 $$
(25)
$$ MAE = \frac{1}{{N_{s} }}\sum\limits_{j = 1}^{{N_{s} }} {\left| {\widehat{y}\left( j \right) - y\left( j \right)} \right|} $$
(26)
$$ RSME = \sqrt {\frac{1}{{N_{s} }}\sum\limits_{j = 1}^{{N_{s} }} {\left[ {\widehat{y}\left( j \right) - y\left( j \right)} \right]}^{2} } $$
(27)
$$ CI = 1 - \frac{{\sum\limits_{{j = 1}}^{{N_{s} }} {\left[ {\widehat{y}\left( j \right) - y\left( j \right)} \right]} ^{2} }}{{\sum\nolimits_{{j = 1}}^{{N_{s} }} {\left[ {\left| {\overline{y} - \widehat{y}\left( j \right)} \right| + \left| {\overline{y} - y\left( j \right)} \right|} \right]^{2} } }} $$
(28)

where \(\widehat{y}\left( j \right)\) is the forecast value of sample, and\( \overline{y} {\text{ = }}\frac{1}{{N_{s} }}\sum\nolimits_{{j = 1}}^{{N_{s} }} {y\left( j \right)} \) is the mean of the signals. (Other parameters have the same meaning as above.)

4.3 Calculated result

Data pre-processing was conducted with improved EEMD: The OS was decomposed into 14 IMFs and Re (Fig. 6). Limited by space, we only displayed decomposed results of 16 days in 2018, which consist of 1536 data points.

Fig. 6
figure 6

Rendering of improved EEMD (partial)

Full size image

The forecasting results of typical days with the hybrid model are shown in Fig. 7. Limited by space, the results for the whole year are not shown. The calculated results for error evaluation in typical days and 2018 are listed in Tables 2 and 3, respectively. It took 56 s and 807 s to run forecasts of four specific days and the whole year.

Fig. 7
figure 7

Forecast result: the PBG generation process in typical days

Full size image
Table 2 Calculated results for error evaluation in typical days
Full size table
Table 3 Calculated results for error evaluation in 2018
Full size table

Good effect was realized with the hybrid forecasting model based on improved EEMD and ANNs both in typical days and on the whole year. In particular, the MAPE of the whole year was only 8.38% and the IA was more than 0.99, but only took around 15 min, which shows the model could be used for the prediction of extensive, complex signals. As for intraday samples, the model performed best in autumn, corresponding to the flood period in Dadu River, which conforms with the original intention of developing generation forecasting for this FMHS. The forecasting accuracy of CI was greater than 0.95 at a time–cost of only less than one minute, which provides sufficient decision-making for dispatch scheduling of CHSs. The improved EEMD and adaptive combination of various ANNs strategy are the key to successful prediction, as discussed in Section 5.

5 Discussion

To analyze the necessity of data pre-processing with improved EEMD, generation signals in typical days are taken as the OS, and three scenarios are set as follows:

Scenario 1 The OS was forecast directly by ELM, BP, and GRNN without pre-processing, and we described them as Scenario 1-a, Scenario 1-b, and Scenario 1-c, respectively, according to different ANN algorithms used.

Scenario 2 The OS was forecast by ELM, BP, and GRNN after decomposition with standard EEMD, and we described them as Scenario 2-a, Scenario 2-b, and Scenario 2-c, respectively, according to different ANN algorithms used.

Scenario 3 The OS was forecast by ELM, BP, and GRNN after decomposition with improved EEMD, and we described them as Scenario 3-a, Scenario 3-b, and Scenario 3-c, respectively, according to different ANN algorithms used.

It is important to note that the model structures are kept the same as mentioned in Section 4-(B), and the ANN parameters are all optimized by WOA in Scenario 1–3. The error is still represented by MAPE, MAE, RSME, and CI. Calculated results for error evaluation of Scenario 1–3 and time cost are listed in Tables 4, 5 and 6, respectively.

Table 4 Calculated results for error evaluation and time in Scenario 1
Full size table
Table 5 Calculated results for error evaluation and time in Scenario 2
Full size table
Table 6 Calculated results for error evaluation and time in Scenario 3
Full size table

The predicted values appear very disordered in Scenario 1 as shown in Fig. 8. Using the same ANN algorithm, the data pre-processing based on a decomposition strategy brought significant improvements in accuracy across all seasons. Compared with the predicted result in Scenario 1, the MASE of typical days in spring, summer, and winter was reduced by over 50%, especially in winter, where it was decreased by 68.4% (that in autumn was further improved based on an already high accuracy). The accuracy was also improved by nearly 10% in terms of CI. The calculated results of the OS in Fig. 6 with standard EEMD are shown in Fig. 10. The OS was decomposed into ten IMFs and Re.

Fig. 8
figure 8

Comparison between predicted values and OS in Scenario 1

Full size image
Fig. 9
figure 9

Comparison between predicted values and OS in Scenario 2

Full size image
Fig. 10
figure 10

Rendering of original EEMD (partial)

Full size image

Compared with the improved EEMD, the decomposition by the standard algorithm is not thorough, and there is apparent mode mixing. Specifically, starting from IMF4 in Fig. 10, the amplitudes of different parts of each IMF are incongruent, a fact particularly obvious at the end points on both sides. While in Fig. 6, the amplitudes of each component exhibit no significant differences in all periods. The end-effect causes aliasing between adjacent modes with standard EEMD, which blurs the distinction between signals. In terms of time cost, decomposition reduces the complexity of each signal, and the ANN model has the higher efficiency when predicting simple curves, so the calculation time is reduced.

In Scenario 3, the end-point effect and mode mixing are solved by improved EEMD, and there are greater improvements to the accuracy with both ELM, BP, and GRNN in Scenario 2. Since the new decomposition method needs to extend the end points of the curve, it naturally takes a certain amount of time. It is noteworthy that the prediction and calculation time in this scenario are similar to those of the proposed hybrid model, even better in specific seasons. All such outputs are realized using the BP ANN. It is questionable that the OS can be forecast accurately only by BP after pre-processing with improved EEMD: It is useless for complex mixing of ANNs.

As shown in Fig. 11, there is no doubt that BP has done a good job in many periods that is why much of the hybrid result is made up of BP outputs. In response to the issue mentioned above, the forecast set from a typical day of each season is expanded to the month of that day and is set as Scenario 4. In this scenario, the data pre-processing, model structure, parameter optimization, and error representation are consistent with Scenario 3. Calculated results for error evaluation of Scenario 4 are listed in Table 7.

Fig. 11
figure 11

Comparison between predicted values and OS in Scenario 3

Full size image
Table 7 Calculated results for error evaluation in Scenario 4
Full size table

When observing Table 7, the best model is not consistent in different seasons and months, as is the case in Scenario 1, that is, no one method is better than the others at all seasons. Therefore, the corresponding optimal model in different seasons, months, dates, and periods is selected for forecasting to give full play to the advantages of each model, learning from each other, and further improving the prediction accuracy of the model, which is the main benefit of hybrid forecasting.

It has been proved in Scenario 4 that the rolling competition between ELM, BP, and GRNN is indispensable in the process of forecasting. Finally, we expand the forecast set to the whole year of 2018 (the aforementioned OS), which is set as Scenario 5. It can be predicted with the proposed hybrid ANN algorithm and ELM, BP, and GRNN, respectively, after data pre-processing by improved EEMD. Calculated results for error evaluation and time cost of this scenario are listed in Table 8, and the change of index between the single and hybrid ANN algorithm is calculated, as shown in parentheses.

Table 8 Calculated results for error evaluation in Scenario 5
Full size table

The hybrid model in the prediction of complex sequences shows obvious superiority. It caused at least 15% reduction in MAPE and MSE, and more than 48% compared to GRNN. As for CI, the hybrid model also showed certain improvements, which represents the advantage in curve fitting of the model. In practice, the calculation and adaptive switching of the three ANNs are run in parallel, so the hybrid model costs a little more time than others, but this difference is negligible considering the massive size of the samples.

The previous analysis shows the necessity of coupling EEMD with BP, ELM, and GRNN in an adaptive switching strategy for forecasting generation of FMHS. We forecast \(XT_{1}\) and \(XT_{2}\) in Eq. (9) with SVR instead of ELM to alleviate the end effects, on the contrary, the rest of hybrid model remains unchanged, expressed as EEMD-SVR- ANNs; the previous hybrid model is expressed as EEMD-ELM- ANNs. In addition, the penalty factor C and kernel function parameter ε are determined by WOA [54]. The same set with Scenario 5 is forecast to compare the performance differences between the two models. Calculated results for error evaluation and time cost of the two are listed in Table 9.

Table 9 Comparison of the two hybrid forecasting models
Full size table

SVR-based EEMD also decomposes the OS into 14 pure IMFs and one Re, whose shapes are similar to that in Fig. 6. Due to the limitation of word-count, it will not be displayed here repeatedly. SVR with appropriate parameters shows advantage in sequence fitting, as evinced by the reduction in error and improvement of CI. However, it is uneconomical to exchange nearly three times the time consumption for less than 1% improvement in accuracy; therefore, the hybrid forecasting model we proposed is a solution that balances calculation accuracy and time consumption.

Finally, a hybrid forecasting model that couples improved EEMD and various ANNs in an adaptive switching strategy was developed to solve the problem of prediction of a seasonal, highly fluctuating sequence. The algorithms involved in the model including EEMD, BP, ELM, GRNN, and WOA all have mature toolboxes available on the MATLAB™ platform. With sufficient improvement and combination, the whole process of adaptive calculation was realized. When the OS changes, users only need to adjust the number of input and output layers of the ANN through ACA, and other parameters remain as descripted in Section 4, B. Furthermore, our model can be applied in forecasting time series with fewer elements and significant regularities, such as monthly runoff, energy or electricity prices, and soil temperature.

6 Conclusion

A hybrid forecasting model to determine real-time generator schedules of the FMHS in HPHPS is proposed. The generation signal of FMHS is rich in gray fuzziness, randomness, and volatility, so standard EEMD is improved to prevent end effects and mode mixing; it is then used to split and simplify the original signal. In the proposed model, each IMF and Re are forecast with the best algorithm among ELM, BP, and GRNN (adaptively applied in different periods). In addition, the key parameters of three ANNs are optimized with WOA, and four error indicators are employed to evaluate the efficacy of predictions using the proposed model.

The intact generation process of PBG (a typical FMHS in Sichuan, China) in 2018 that comprises 35,040 samples is selected to model training and testing. The structure and application of the model are described. The calculated error indicators in typical days and the whole year suggest its efficacy. To illustrate the effectiveness of the decomposition and the adopted hybrid strategy, five scenarios are set determined by different data pre-processing methods and sizes of forecast set. After much discussion, the hybrid forecasting model has obvious advantages in accuracy. When used to predict complete samples, there is at least a 15% reduction in MAPE and MSE and a certain improvement in CI. As for computational efficiency, the time demand satisfies the need for decision-making among both generator and grid manager.

As for determining the optimal model structure in Section 4, researchers have attempted to select best inputs that have more similar characteristics to forecasts set by gray-relationship analysis, the K-means algorithm, random forest technique, etc. Although the same goal has been achieved through ACA in the present work, the topics mentioned above are worthy of future investigation.