1 Introduction

Large complex systems usually contain subsystems in which some of the variables change more rapidly than others. Multirate methods have been proposed to make the solution of these systems more efficient by solving each subsystem with different time-step sizes according to the subsystems’ time constants. The need for multirate solutions exists across disciplines. For example, in chemistry it is possible to use the separation of time scales to simulate the dynamics of macromolecules, a simulation whose computational complexity is enormous [1, 2]. This paper will focus on the application of a multirate technique in an electric power system with a novel asynchronous implementation.

In complex modern power systems, with online and real-time operation and control, solution speed can be critical, so multirate concepts in electrical engineering have been considered for some time. In the late 1950s, they were used to make digital controllers operate at higher rates than the basic sampling rate of the system [3, 4]. In the 1970s, multirate methods were proposed by Gear [5] for the solution of differential equations to model systems with widely varying time responses. In power systems, multirate methods have been considered since the 1980s for hybrid simulations, where the well-known electromagnetic transients program (EMTP) was combined with a transient stability program for AC systems (TSP) [6,7,8].

Within the context of electromagnetic transient (EMT) solutions, multirate was initially proposed by Semlyem et al. [9] in 1993 to improve simulation efficiency. A more general approach was proposed by Moreira and Marti [10] in 2005 and by Moreira et al. [11] in 2006 within the MATE solution framework [12,13,14]. More recently, Arjen et al. [15], in 2015, showed the inclusion of hybrid simulation techniques in stability-type and EMT simulation tools for a better transient stability assessment than the common alternatives. In 2016, Haddadi et al. [16] presented the time warping (TW) technique, which allows adapting a simulation in an EMT solver or a steady-state solver, accelerating the simulation without a loss of precision. New methodologies have been proposed for multirate (MR) simulation solvers as simulation tools have become more essential for electrical engineers. In 2018 [17], an overview of state-of-the-art solutions to interface power systems and information and communication technology simulators was presented. Finally, an interesting work [18] was presented in 2019, wherein the technique denominated multirate mixed solver is used as an iterative solver for the nonlinear elements and a conventional non-iterative linear solver for the other elements. It should be noted that the multirate mixed solver methodology requires using an exactly integer multiple of time-steps between subsystems, and subsystems must be separated by transmission line delays.

MATE combines the principles of multinode Thévenin equivalents [19], diakoptics [20], and modified nodal analysis [21] to partition a system into subsystems that may have their own solution method and their own solution step size. The MATE solution involves three steps: (1) the subsystems are solved independently (possibly in parallel processors), (2) then the currents in the links joining the subsystems are calculated using Thévenin equivalents for the subsystems, and (3) the link currents are injected back into the subsystems. For linear systems, this process gives identical results to performing a full-system simultaneous solution with no iterations.

This paper advances the state-of-the-art in solving multirate systems represented by EMTP models within the MATE solution framework by using multiple and non-multiple time-step sizes. Compared to previous multirate formulations, the proposed method relaxes two restrictions of these formulations: one, that the subsystems must be separated by transmission line delays; and two, that the time-step sizes of the subsystems must be multiples of each other [18]. The proposed solution accepts any arbitrary time-step in any of the subsystems and the updating of the subsystems is done asynchronously within the MATE framework, while still maintaining a simultaneous solution with no iterations. This is possible because the EMTP models calculate the future history sources using the solution at the present time point. When a particular subsystem needs updating, the other subsystems are represented by a Thévenin source and a Thévenin impedance. The Thévenin source is interpolated between a past and a future time point. It is assumed that the Thévenin impedance does not change between interpolation steps. To avoid sampling problems associated with combining multiple-step-size signals, numerical conditioning of the variables exchanged must be provided to avoid aliasing and imaging issues.

The proposed method in this paper is denominated A-MATE-multirate and has been prototyped in MATLAB code. This paper is organized as follows. The MATE methodology is presented in the context of its application to multirate simulation in Sect. 2. Multirate simulation is discussed in detail in Sect. 3. Results are presented in Sect. 4, showing the efficiency and accuracy of the proposed method.

2 Review of MATE

The MATE framework and the corresponding detailed equations for EMTP solutions are described in [10,11,12,13,14]. A summary of the procedure is presented below. In the MATE solution, the full network is divided into independent subnetworks connected through link branches. Although the link branches can be any element in the normal single-rate MATE solution, in this work, for A-MATE-Multirate, the link branches will be restricted to being resistances to avoid having time constants in the links. Consider the system in Fig. 1, which has three subsystems and three branch links.

Fig. 1
figure 1

Sample system for MATE explanation

Full size image

The system in Fig. 1 can be represented by a set of hybrids modified nodal equations as follows:

$$ \left[ {\begin{array}{*{20}r} \hfill {Y_{1} } & \hfill 0 & \hfill 0 & \hfill {C_{1} } \\ \hfill 0 & \hfill {Y_{2} } & \hfill 0 & \hfill {C_{2} } \\ \hfill 0 & \hfill 0 & \hfill {Y_{3} } & \hfill {C_{3} } \\ \hfill {C_{1}^{T} } & \hfill {C_{2}^{T} } & \hfill {C_{3}^{T} } & \hfill { - z} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {V_{1} } \\ {V_{2} } \\ {V_{3} } \\ {I_{L} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {h_{1} } \\ {h_{2} } \\ {h_{3} } \\ 0 \\ \end{array} } \right] $$
(1)

For the three subsystems j = 1, 2, and 3, Yj, Vj, and hj are, respectively, the admittance matrices, the nodal voltages, and the sum of history and external current sources. For simplicity, all sources will be referred to as “history sources” although they also include external independent sources. Matrices Cj capture the connectivity between subsystems. The links are modeled by their branch equations: IL is the links’ current vector that has all the ilink, and z is a diagonal matrix with the link impedances (resistances). In order to solve (1), Gaussian elimination can be applied to the rows that have the link currents IL, yielding the new set of equations

$$ \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & {Y_{1}^{ - 1} C_{1} } \\ 0 & 1 & 0 & {Y_{2}^{ - 1} C_{2} } \\ 0 & 0 & 1 & {Y_{3}^{ - 1} C_{3} } \\ 0 & 0 & 0 & {Z_{{{\text{Total}}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {V_{1} } \\ {V_{2} } \\ {V_{3} } \\ {I_{L} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {e_{1} } \\ {e_{2} } \\ {e_{3} } \\ {E_{L} } \\ \end{array} } \right] $$
(2)

where ej are the internal node voltages of each subnetwork. Notice that

$$ e_{j} = Y_{j}^{ - 1} h_{j} $$
(3)

Denoting eTh,j the Thévenin voltages of the subnetworks as seen from the link nodes, EL can be defined as the sum of the subsystems’ Thévenin sources:

$$ E_{{\text{L}}} = e_{{\text{Th,1}}} + e_{{\text{Th,2}}} + e_{{\text{Th,3}}} $$
(4)

ZTotal is a matrix with all the impedances, that is, the subsystems’ Thévenin impedances, ZTh,j, plus the link impedances

$$ Z_{{{\text{Total}}}} = Z_{{\text{Th,1}}} + Z_{{\text{Th,2}}} + Z_{{\text{Th,3}}} + z $$
(5)

Considering the connectivity matrices C results in,

$$ e_{{\text{Th,j}}} = C_{j}^{T} e_{j} $$
(6)
$$ Z_{{{\text{Th,}}j}} = C_{j}^{T} Y_{j}^{ - 1} C_{j} $$
(7)

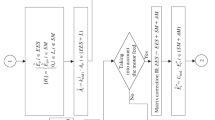
For the normal MATE solution (equal time-step), the process described below is used to solve each subsystem at a given time, t. A key aspect of this process is that in EMTP modeling, the history sources to be used in the next time point are calculated from the solution at the present time point. The solution process is as follows:

  1. (1)

    Solve for the link currents using the Thévenin voltages eTh,j calculated in the previous time point. From (2),

    $$ I_{{\text{L}}} = Z_{{{\text{Total}}}}^{ - 1} E_{{\text{L}}} $$
    (8)
  2. (2)

    Update the internal node voltages of every subsystem to obtain the actual voltages by injecting the link currents into the corresponding nodes. This is performed from (2),

    $$ V_{j} = e_{j} - Y_{j}^{ - 1} C_{j} I_{{\text{L}}} $$
    (9)
  3. (3)

    Compute the history sources hj of the subsystems for the next solution point t = t + Δt.

  4. (4)

    Obtain the Thévenin voltages of the subsystems for the solution at time t = t + Δt considering the subsystems as isolated from the other subnetworks using (6).

  5. (5)

    Advance the solution time by t = t + Δt and return to step 1 until the end of simulation time is reached.

3 A-MATE-multirate solution

In the proposed A-MATE-multirate methodology, each subsystem can be solved with a different time-step size. At the end of each subsystem’s internal solution step, the subsystem is updated by the effect of the other subsystems.

When updating an internal subsystem, the external subsystems are represented by Thévenin equivalents interpolated to match the time point at which the internal subsystem is being updated. It can be observed from (9) that the actual voltages of a given subsystem are a function of its internal voltages, the admittance matrix, the connectivity matrix, and the link’s current vector. The vector of internal voltages, ej, is obtained from voltages interpolated for the time point of the subsystem being updated; Y and C are pre-calculated; the links’ current vector IL depends on known data (Thévenin impedances, link’s impedances, Thévenin source vectors), (4), (6), and (8).

3.1 The rate change errors

In multirate systems, various simulation processes running at different sampling rates are solved together. For this to happen, interface variables from slower to faster processes must be interpolated, whereas those from faster to slower processes must be decimated, although the proposed A-MATE-multirate technique will relax the requirement of multiplicity of the time-steps. Assume, for simplicity in the following analysis, that there are two interconnected subsystems in Fig. 2, denominated the fast subsystem and the slow subsystem, where the time-step of the slow subsystem ΔT is M times that of the fast subsystem Δt.

Fig. 2
figure 2

Single-channel multirate scheme

Full size image

The interpolation procedure by a factor M that preserves the information content of the interpolated signal consists of inserting M − 1 samples of zero value between adjacent samples. The decimation process of a sequence by a factor M is performed by retaining only one of each group of M consecutive samples. These sampling rate conversions may introduce two types of errors: imaging and aliasing. Interpolation produces imaging that must be removed by passing the interpolated sequence through a low-pass filter. To avoid the aliasing produced by decimation, the signal must be low-pass filtered so that its bandwidth is reduced M times. The anti-imaging and anti-aliasing processing is also illustrated in Fig. 2 for two interconnected subsystems. In this scheme, called single channel, it is assumed that the high frequencies that are filtered out are of no interest. Reference [22] presents a detailed theory of the frequency-domain multirate considerations.

3.2 Thévenin equivalents during interpolation and decimation

As noted above, when an internal subsystem is ready for updating, the other external subsystems are represented by their Thévenin equivalents as seen by the interconnecting links. The Thévenin equivalents of these external subsystems are calculated from interpolation if they are slower than the updating system, or from decimation if they are faster than the updating system.

For explanation purposes, before describing the general case of arbitrary time-step ratios, the simpler case of decimation and interpolation for time-steps that are multiples of each other is first presented.

3.2.1 Thévenin equivalents for interpolation

In practice, interpolation is not performed by the insertion of zero-value samples between known samples. Instead of this, linear interpolation is used, since it simultaneously acts as a low-pass filter. When updating a given subsystem, the history terms h and the Thévenin voltages eTh for the solution of the next time point of this subsystem are calculated. This means that a future sample of any eTh is known at all the times, making it possible to use a linear interpolation. The solution points needed to update of a fast internal subsystem will lie between two known points of the Thévenin voltages of a slower external subsystem. If an external slow subsystem with a time-step equal to ΔT is to be interpolated by a factor M, then the interpolated Thévenin voltages eTh,lin obtained from the Thévenin voltages eTh are given by

$$ e_{{\text{Th,lin}}} \left( t \right) = e_{{{\text{Th}}}} \left( k \right) + \frac{{e_{{{\text{Th}}}} \left( {k + 1} \right) - e_{{{\text{Th}}}} \left( k \right)}}{\Delta T}\left( {n\Delta t - k\Delta T} \right), \, Mk\Delta t \le n\Delta t \le \left( {k + 1} \right)M\Delta t \, $$
(10)

where k is the discrete time counter of the external slow subsystem corresponding to time t = kΔT and n is the eTh,lin’s discrete time counter corresponding to t = nΔt. Note that eTh,lin is a sequence of Thévenin voltages with time-step equal to ΔT/M, and it is the information that the fast internal subsystem must be updated. The interpolation process by a factor M is graphically illustrated in Fig. 3.

Fig. 3
figure 3

Time line of two consecutive solution points for a particular Thévenin voltage eTh of a given subsystem

Full size image

In order to interpret linear interpolation as a linear filtering process, the impulse response for the linear interpolator hlinear and its Fourier transform Hlinear [22] are considered in (11):

$$ h_{{{\text{linear}}}} \left( n \right) = \left\{ {\begin{array}{*{20}l} {1 - {{\left| n \right|} \mathord{\left/ {\vphantom {{\left| n \right|} {M,}}} \right. \kern-\nulldelimiterspace} {M,}}} \hfill & {\left| n \right| < M} \hfill \\ {0,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} ,\,H_{{{\text{linear}}}} \left( \omega \right) = \frac{1}{M}\left[ {\frac{{\sin \left( {\omega M/2} \right)}}{{\sin \left( {\omega /2} \right)}}} \right]^{2} } \right. $$
(11)

where hlinear, which is a triangular pulse, has a length L = 2 M − 1. For M = 3, the performance of the linear interpolator in Fig. 4 can be assessed by comparing its frequency response Hlinear (ω) in (11) to that of the ideal low-pass filter Hideal(ω), which is theoretically derived from the ideal discrete time interpolator [22].

Fig. 4
figure 4

Linear interpolation as a low-pass filter for M = 3

Full size image

The purpose of the interpolation filter is to remove the images of the zero-valued interpolated signal while leaving the frequencies below π/M unaltered, leading to a good performance when the spectrum of the interpolated signal is negligible for ω greater than π/M. Note that linear interpolation is appropriate if the original sampling rate is several times the Nyquist rate due to the decaying behavior of the response. This occurs when the original continuous-time signal has been oversampled [23], which is the case in EMTP solutions, where the signals are oversampled in order to compensate for the distortion introduced by the discretization rule [19].

An example of linear interpolation is presented to clarify the aforementioned concepts. Consider the signal f1(t) = e−t shown in Fig. 5a, which has a sampling frequency Fs = 2 Hz (Δt = 0.5 s) and length of 10 samples. This signal is interpolated by a factor 3 by inserting two zero valued samples between samples of f(t), yielding to the signal f2(t) shown in Fig. 5b, which has a length of 30 samples. For an interpolation factor M = 3, the impulse response of the linear interpolator is hlinear = {1/3, 2/3, 1, 2/3, 1/3}, and the length in samples is L = 5; when this sequence is convolved with f2(t) the signal f3(t) in Fig. 5c is obtained. The length of the convolved signal is 34 samples (30 + 5 − 1). Note the delay of 2 samples in the interpolated signal. This interpolator acts as a FIR filter, which has a delay of (L − 1)/2 samples. Note that when linear interpolation is performed directly (without convolution) as in Fig. 3, this delay in not present.

Fig. 5
figure 5

Sequences in time domain of linear interpolation through convolution process for M = 3

Full size image

The Fourier transforms of the original signal, the signal interpolated with zeros and the filtered signal are depicted in Fig. 6a–c, respectively. The spectra images due to the interpolation can be appreciated in Fig. 6b, and in Fig. 6c, it can be seen that the spectra images have been removed.

Fig. 6
figure 6

Magnitude spectra of the time sequences of the linear interpolation example for M = 3

Full size image

3.2.2 Thévenin equivalents for decimation

In EMTP simulations, the signals are oversampled in order to compensate for the distortion introduced by the discretization rule (e.g., trapezoidal) [19]. Consider that the interconnected subsystems in Fig. 2 have fmax,slow and fmax,fast as maximum frequencies to be simulated and that the corresponding Nyquist frequencies are

$$ F_{{\text{Ny,slow}}} = {1 \mathord{\left/ {\vphantom {1 {\left( {2\Delta T} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {2\Delta T} \right)}},\,F_{{\text{Ny,fast}}} = {1 \mathord{\left/ {\vphantom {1 {\left( {2\Delta t} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {2\Delta t} \right)}}\;{\text{with}}\;\Delta T = M\Delta t. $$
(13)

If the maximum frequency to be simulated by the fast subsystem is below the Nyquist frequency of the slow subsystem, i.e., fmax,fast ≤ FNy,slow, then the sampling frequency of the slow subsystem is sufficient for representing the transients originating in the fast subsystem. This condition is shown graphically in Fig. 7. This is a common situation when the ratios of the time-steps on the order of a few tens.

Fig. 7
figure 7

Multirate frequency scheme with no decimation-filtering needed

Full size image

When decimating signals, previous works [8, 9] proposed averaging the fast signals (low-pass filtering) before being used by a slower subsystem; these references do not consider the time-step ratio between subsystems. In the present paper, the size of this ratio is considered to save computational time by avoiding unnecessary averages. In the case of Fig. 7, when the combined solution is capable of representing the desired fast transients in the slow subsystem, direct simple decimation without averaging is recommended. For example, assume a fast subsystem with 10 kHz as the maximum frequency to be observed (fmax,fast), connected to a slower system whose fNy is 10 kHz. By making the fast subsystem’s fNy say 50 kHz for accurate representation of the 10 kHz components; this system can be decimated to fit the slower connected subsystem’s fNy (10 kHz) with no need of filtering. Transients will appear on the slower side with low resolution, but no aliasing will appear in the slower subsystem.

The decimation process produces aliasing if the maximum frequency of the signal to decimate is not limited to the frequency interval |f|< FNy,slow. The approach proposed in this paper to attenuate high frequencies is smoothing through fitting techniques, specifically by using the Savitzky–Golay filter.

Savitzky–Golay filtering Not all electrical networks include conveniently located long transmission lines that can be used as links to separate subsystems; the method presented in this paper does not have this restriction, but does require filtering to eliminate the injection of frequency components from the fast system which are beyond the bandwidth of the slow system. Filters such as FIR filters used in earlier works introduce a phase delay which is undesirable in the here proposed simultaneous solution. The smoothing filter provided by Savitzky–Golay avoids this problem [24]. This filter uses a generalized moving average procedure with coefficients which attempt to fit a polynomial of a specified order. In the presented proposal, order-one averaging (straight line) is used over a specified number of samples. The MATLAB function sgolayfilt [25] is used to implement a Savitzky–Golay smoothing filter. To use sgolayfilt, an odd-length number of samples must be chosen. The function internally computes the smoothing polynomial coefficients, performs delay alignment, and is careful of transient effects at the start and end of the data record. The larger the number of high frequency cycles in the filter window, the better it will behave, since the straight line will tend to lay on the average of these waves.

3.2.3 Arbitrary time-steps

By relaxing the constraint of using integer time-step multiples between subsystems, as required in previous works, flexibility and generality are increased. One example is when interfacing solutions from samplers that run at fixed time-steps. In simulation, for a general-purpose solver like the EMTP, the user should have the freedom to choose the most adequate time-step for each subsystem. Although the user can specify arbitrary time-steps, for the purpose of exchanging information between subsystems, while avoiding aliasing in signal processing, rational ratios are used in the interpolation and decimation of the Thévenin equivalents.

Consider the two interconnected subsystems A and C in Fig. 8a. The ratios between their time-steps, 3 µs and 7.5 µs, are not integer, but can be expressed as rational fractions, 2/5 and 5/2. These fractions are shown in Fig. 8a, where subsystem A requires eTh,C-1 from C to be updated, and C requires eTh,A-2 from A to be updated. In this case, eTh,A-2 is interpolated by a factor of 2 and then decimated by a factor of 5, whereas eTh,C-1 is interpolated by a factor of 5 and then decimated by a factor of 2.

Fig. 8
figure 8

Rate conversion by a rational factor, a system, b interpolations and decimations between the subsystems A and C, c interpolations between the subsystems A and C

Full size image

To avoid aliasing, the interpolated values not used in the decimation process are needed when a low-pass filter is used, since the filtering includes these samples; for example, the Savitzky–Golay filter is applied over these samples when needed. When no aliasing is expected, the interpolation points are those points shown as decimated values in Fig. 8b; there is no point in calculating samples that are going to be discarded. This is shown in Fig. 8c, where the time-steps are very close to each other, thus falling into the special category explained in item 2 above (no filtering required).

3.2.3.1 Scheduling and synchronization

For synchronization of the partitioned system, it is necessary to identify the sequence in which each subsystem must be solved. In this work, this is done according to the size of the time-step of the subsystems; an algorithm decides the sequence for solving each subsystem. We follow an asynchronous updating approach where the link currents are calculated according to the needs of the “internal” subsystem to be updated due to the presence of the “external” subsystems. Figure 9 illustrates the updating sequence, according to the time-step sizes, for the three subsystems in Fig. 8. First, subsystem A is solved at t = 3 µs with subsystems B and C represented by interpolated sources. Then, subsystem B is solved at t = 5 µs with interpolated sources from subsystems A and C. Then, A is solved again in the mentioned way. Then, C is solved at t = 7.5 µs with interpolated sources from subsystems A and B. The updating sequence is repeated until the end of the simulation. Remember that one future sample of each Thévenin voltage source is known at all times.

Fig. 9
figure 9

Time scheduling in the subsystem’s simulation

Full size image

There might be certain instants of time t when all subsystems call for updates at the same time. For our example, this occurs every 15 µs. However, this does not mean that all subsystems are solved simultaneously at those instants, as in the traditional EMTP multirate simulation [19]. Instead, in the here presented method, the solution of each subsystem is carried out in isolation of the other subsystems and only the Thévenin equivalents of the neighboring subsystems are used. As a result, these solution points are not different from the other solution points that do not coincide in time. This is critical for the parallel implementation of the A-MATE-multirate algorithm.

3.2.3.2 Partitioning points and time-step selection for A-MATE-multirate

The optimum partitioning points for the application of A-MATE-multirate depend on the time constants of different regions of the system. In many cases, there are clear regions with different time constants. One such example is a subsystem consisting of power electronics components. Here, the commutation needs of the valves will determine the time-step size needed for simulating this subsystem [26]. In a general case, the dominant eigenvalues of different subsystems can be used as criteria for subsystem partitioning and time-step selection [9, 27,28,29,30].

The normal MATE algorithm solves a large system by splitting the system into smaller subsystems which are first solved separately and then combined with each other through the solution of the subsystem of links interconnecting the subsystems. The subsystem of links is solved by representing the individual subsystems using Thévenin equivalents. The individual subsystems can be solved by using different numerical integration rules [11] and different integration time-step sizes, if necessary. This allows exploiting the integrations rule attributes best suited to the particular subsystem’s characteristics [26].

4 Test cases

4.1 Multirate circuit

The A-MATE-multirate scheme is tested on the three-subsystem circuit shown in Fig. 10. The parameters of the circuit are: R1 = 0.01 Ω, L1 = 1 µH, C1 = 1 µF, R2 = 1 Ω, L2 = 1 µH, R3 = 5 Ω, L3 = 25 µH, and the links resistances are RLink = 10 Ω. This circuit is based on the circuit presented in [8, 9]. The system is energized at t = 0 by applying a sinusoidal voltage vs = cos(2π60t). Fast transients are triggered by having an initial charge of 1.0 V in capacitor C1 of subsystem A.

Fig. 10
figure 10

Electric circuit for multirate simulation

Full size image

It can be seen that the fast transient propagates to the entire network and assesses the accuracy of the waveforms depending on the time-steps selected for the different subsystems; the trapezoidal integration rule is used for this simulation. For these tests, the unpartitioned solution with a very small time-step of 0.1 µs will be considered the reference solution. To show the effect of using inadequate equal time-steps for the entire circuit, additional single-rate simulations were performed with Δt = 1.125 µs and Δt = 8.75 µs. Figure 11 shows the voltage across one element of every subsystem: capacitor C1, inductor L2, and inductor L3 for each equal-rate simulation. The results in Fig. 11 show that the results with these larger time resolutions give poor representations.

Fig. 11
figure 11

Single-rate simulations for different time-steps: a voltage across C1, b voltage across L2, and c voltage across L3

Full size image

Next, the resolution of Δt = 0.1 µs will be retained for subsystem A only, while the time-steps for subsystems B and C are set to 1.125 µs and 8.75 µs, respectively. The ratios among the time-steps of the subsystems are shown in Table 1 and are derived as shown in Fig. 8. Some of these ratios can be further reduced. For example, the ratio from A to C is 4/350 but could also be 2/175. The reason to keep it at 4/350 is that interpolation by a factor of 4 is required for the solution of subsystem B anyway, and there is no need to perform interpolation by a factor of 2 to obtain points that have already been calculated. Similar situations occur for other ratios.

Table 1 Rational multiples between subsystems
Full size table

The results obtained using the indicated larger time-steps for subsystems B and C are shown in Fig. 12. As can be seen in this figure, the voltages at C1 and L2 are superimposed with the reference results. These results show that although both waveforms have the same frequency, the subsystems are capable of reproducing the waveforms without a loss of accuracy using different time-steps. The Nyquist frequency of subsystem B is greater than the frequency of the transient originated in subsystem A, as stated in Sect. 3.2, and therefore, direct interpolation can be performed, as in Fig. 8c. Note that there is no aliasing in subsystem B when decimating subsystem A.

Fig. 12
figure 12

Multirate simulations. a Voltage across C1, b voltage across L2

Full size image

The voltage at L3 is strongly aliased (the high frequency of subsystem A is shown as a fake lower frequency) as shown by the dashed line in Fig. 13. To reduce the aliasing eTh,A is smoothed with the Savitzky–Golay filter. From the ratios in Table 1, it can be seen that the interpolation factor of eTh,C is 350. Since the sgolayfilt function works on odd samples, the filtering process is performed every 351 samples. Figure 13 shows the propagation of the fast transient to subsystem C. When attenuated, the leftover behavior is only due to the voltage source. While updating only the solution of subsystem C with the filtered signal, the results in A and B remain unaltered as in Fig. 12. Note that even with the aliasing present, the solution of the subsystems is not unstable. This is due to the properties of the EMTP implicit integration as opposed to open integration or iteration schemes.

Fig. 13
figure 13

Voltage across the inductor L3 during the multirate simulation with and without smoothing the Thévenin equivalent from the fast subsystem

Full size image

4.2 Multirate system

Now, the A-MATE-multirate method is tested on the network shown in Fig. 14. This network is based on the Simulink example denominated the “Simple 6 Pulse HVDC Transmission System” [25]. The test system is separated into two subsystems; one is naturally “slow” and the other is naturally “fast”. By maintaining the constraint imposed by the fast subsystem, the time-step (Δt) will be fixed at 5.5 µs for this subsystem.

Fig. 14
figure 14

Rectifier test system

Full size image

In order to validate the proposed methodology, the time-step is increased in the slow subsystem (MΔt) by increasing M, and the results compared to a reference solution, that is, when M = 1. This increment of M can be performed in two ways: (1) by using integers yielding time-steps multiples of the fast subsystem and (2) by using non-integers producing non-multiple time-steps of the fast subsystem, thus proving the unconstrained of using integer multiples time-step between subsystems, as required in previous works. Below, implementation for integers multiple time-steps is first tested and then the proposed A-MATE-multirate simulation is provided.

4.2.1 Multiple time-steps

The time-step sizes used between subsystems are shown in Table 2. Please note that M is increased from 1 to 10 in increments of 1 and from 10 to 50 in increments of 10. As noted above, the time-step for the fast subsystem (Δt) will be fixed at 5.5 µs. Therefore, the resulting time-steps used for the slow subsystem are multiples of the time-step used in the fast subsystem.

Table 2 Multiple time-steps between subsystems
Full size table
Table 3 Multiple and non-multiple time-step sizes between subsystems
Full size table

The DC load current (ic,M) of the fast subsystem and the source current of the slow subsystem (is,M) will be used for the analysis. Figure 15 shows the multirate simulations for the DC load current (ic,M). In Fig. 15a, it can be seen that transients are well reproduced, and the zoom in Fig. 15b shows that as M increases, the difference between simulations also increases at the same rate. The absolute error of ic,M with respect to reference solution ic,1 is shown in Fig. 16a for the transient state and in Fig. 16b for the steady state. Although there is some noticeable shifting of the wave forms, these error levels are acceptable, considering that the slow subsystem time-step has increased up to 50 times.

Fig. 15
figure 15

a DC load current (ic,M) for multiple time-steps, b zoom of the DC load current

Full size image
Fig. 16
figure 16

Absolute error of ic,M with respect to reference solution, ic,1. a Transient state, b steady state

Full size image

The slow subsystem in Fig. 17 presents phase A of the source current (is,M) for multiple time-steps. As can be seen in Fig. 17a, the transient in this subsystem is also well reproduced.

Fig. 17
figure 17

a Phase A of the source current (is,M) for multiple time-steps, b zoom of the source current

Full size image

The zoom of Fig. 17b clearly shows the increasing process of M for the time-step of the slow subsystem. Figure 17b also shows that as M increases, the difference between simulations also increases at the same rate; this is an expected result.

Similar to the fast subsystem, the absolute error of is,M with respect to reference solution is,1 is shown in Fig. 18a for the transient state and in Fig. 18b for the steady state. This error is calculated by downsampling the reference solution is,1 according to each solution is,M. There is also some noticeable shifting of the wave forms due to the integration rule. However, these error levels are acceptable, considering that the slow subsystem time-step has increased up to 50 times.

Fig. 18
figure 18

Absolute error of is,M with respect to reference solution, is,1 a Transient state, b steady state

Full size image

4.2.2 Non-multiple time-steps

The time-steps used between subsystems are now shown in Table 3. In this case, M is increased from 1 to 10 in increments of 1, producing multiple time-step sizes of the fast subsystem. Additionally, three non-integer values have been added for M between each integer, producing non-multiple time-step sizes of the fast subsystem.

In this way, there are both multiple and non-multiple time-step sizes of the fast subsystem. Once again, the time-step size for the fast subsystem (Δt) will be also fixed at 5.5 µs. The DC load current (ic,M) of the fast subsystem and the source current of the slow subsystem (is,M) will be used for the analysis.

Figure 19 shows the multirate simulations for the DC load current (ic,M) for multiple and non-multiple time-step sizes. Figure 19a shows that transients are well reproduced, and the zoom in Fig. 19b shows that as M increases, the difference between simulations also increases at the same rate, demonstrating that the proposed methodology works well even in non-multiple time-step sizes.

Fig. 19
figure 19

a DC load current (ic,M) for multiple and non-multiple time-steps, b zoom of the DC load current

Full size image

The absolute error of (ic,M) with respect to reference solution ic,1 is shown in Fig. 20a for the transient state and in Fig. 20b for the steady state. Once again, there is some noticeable shifting of the wave forms; however, these error levels are acceptable, considering that the slow subsystem time-step has increased up to 10 times.

Fig. 20
figure 20

Absolute error of ic,M with respect to reference solution, ic,1. a Transient state, b steady state

Full size image

Figure 21 presents phase A of the source current (is,M) for multiple and non-multiple time-step sizes. In Fig. 21a, it can be seen that transients in this subsystem are also well reproduced for both multiple and non-multiple time-step sizes.

Fig. 21
figure 21

a Phase A of the source current (is,M) for multiple and non-multiple time-steps, b zoom of the source current

Full size image

In the zoom of Fig. 21b, the increasing process of M for the time-step of the slow subsystem can be clearly observed. Figure 21b also shows that as M increases, the difference between simulations also increases at the same rate. Note that the simulations of the source current (is,M) for non-multiples (subscripts a, b, and c) are exactly between the results using multiple time-step sizes, demonstrating the asynchronous feature of the A-MATE-multirate method.

The absolute error of is,M with respect to reference solution is,1 cannot be calculated because the sampling rate is not multiple between simulations. However, due to the behavior of the simulations, it should be similar to Fig. 18.

5 Discussion

Large complex systems usually contain subsystems in which some of the variables change more rapidly than others. Therefore, multirate methods have been proposed to make the solution of these systems more efficient by solving each subsystem with different time-step sizes, according to the subsystems’ time constants. In this sense, the calculated results for multirate simulations in Sect. 4 consistently show that the presented A-MATE-multirate method is a valid approach.

The MATE-MR method was first presented in [26], with particular attention to the effect of combining different integration rules for representing the slow and the fast subsystems and by using multiple time-step sizes. This paper presents the novel A-MATE-multirate method which accepts any arbitrary time-step multiple and non-multiple in any of the subsystems and need not be separated by transmission line delays, unlike previous multirate formulations. For example, in 2019 [18], a multirate method was proposed in which the subsystems must be separated by transmission line delays and the time-steps of the subsystems must be multiples of each other.

The main feature of the A-MATE-multirate is that it allows finding the most appropriate time-step sizes for the simulating of the subsystems. The fast subsystem regularly imposes the constraint of the time-step size, but if the slow subsystem is small, it is possible through the proposed method to use the smaller time-step size for the simulation, thus increasing the accuracy of the result. Therefore, this method can find the most optimal unrestricted time-step, and moreover, subsystems need not be separated by transmission line delays, thus increasing the scope of the method.

Therefore, the features of the A-MATE-multirate method facilitate its application in a parallel and/or real-time simulation in which each processor can use the smallest time-step possible. As regards the processors, two scenarios can be highlighted:

  1. (1)

    A HIL simulation, in which a physic element has a fixed frequency-sampling rate, e.g., a DSP. In this case, the processors could be configured as follows:

    • If a subsystem is assigned to a single processor, and this subsystem represents a small network, then its time-step size could be decreased as much as possible to approximate the execution time of other processors, thus increasing the precision of the simulation.

    • If a given time-step size is the most appropriate for one sector of a big network, and this step size is much bigger than that of other sectors, then a large part of this network could be simulated in a single processor. Therefore, the simulated sub-network could be as large as possible, as long as the execution time of this processor is similar to that of other processors.

  2. (2)

    Simulation without restrictions.

In this case, it is possible to split the network by grouping small networks or sub-networks in such a way that some sub-networks involve fast reacting elements and other sub-networks slow reacting elements. The advantage here is that there would be no restriction to synchronizing the execution time of each processor, as the smallest time-step size could be selected by rearranging some sub-networks.

6 Conclusions

The A-MATE-multirate methodology for combining several subsystems solved with different time-step sizes was presented. Conditioning of the signals exchanged between subsystems is performed using filters for the decimation of the fast subsystems when updating the slow subsystems, and for the interpolation of the slow subsystems when updating the fast subsystems. The effectiveness of the proposed methodology was demonstrated with examples. The main findings are as follows:

  1. (1)

    The A-MATE-multirate method can be used to combine subsystems which must be solved with multiple or non-multiple time-step sizes and need not be separated by transmission line delays, thus relaxing the requirement of previous multirate techniques, in which the solution time-step sizes of different systems must be multiples of each other and the subsystems must be separated by transmissions lines.

  2. (2)

    The paper introduces the concept of asynchronous updating, in which each subsystem is updated according to its own internal clock, providing an asynchronous simultaneous solution without iterations between subsystems.

  3. (3)

    The obtained testing results with the A-MATE-multirate technique and the single rate solution show similar accuracy. The error levels were acceptable, considering that in one case, the slow subsystem time-step size had increased even up to 50 times.

  4. (4)

    The performance of a multirate simulation depends on the number of links, the size of the subsystems, and the complexity of each subsystem’s solution.

  5. (5)

    The examples presented in this paper were chosen to address the issues involved in the application of this methodology. However, it can be applied for the modeling of any electric power system.

  6. (6)

    An important application of A-MATE-multirate is the simulation of power electronic converter stations interfaced to the bulk power grid. In this case, the transmission system can be solved with larger time-step sizes as if the converter system were not connected, while the converter system can be solved with a much smaller step size to account for the action of the commutating valves.