Hybrid fault diagnosis algorithms for transmission lines

Abstract

This paper presents a fault location method for transmission lines with the application of a mono-objective optimization technique using the ellipsoid algorithm with voltage and current data of both terminals. The fault detection is performed using the stationary wavelet transform and Parseval’s theorem, and the classification was conducted with the application of artificial neural networks. The minimization of the objective function defined for the short and long transmission line models provides not only the distance to the fault point, but also the fault resistance value. Many short-circuit situations simulated in the alternative transients program are tested with variations in the fault type, adjustments in the distance to the fault point, and fault resistance. The results of the algorithm applied to real faults in the electrical system of Brazil are also presented and compared to the values obtained with a classic fault location algorithm. According to the observations, the adopted formulation achieves the pre-established objectives, with mean errors of fault location for the real cases lower than 2% of the line length.

1 Introduction

A fault location method for transmission lines is required by electric companies to assist them in providing quality services to their consumers, the reduction of operational costs, and to avoid paying fines to the regulatory agencies.

Among factors that affect electrical system performance are the faults or short circuits in components and equipment, especially when these are permanent, requiring the deployment of a maintenance team to perform the necessary repairs. Among the faults, those that occur in transmission lines—which can be extensive and sometimes difficult to access—play a prominent role. When the fault is permanent, the line is taken out of service. In some cases, the system does not reach the appropriate service status, causing unwanted blackouts.

To reduce the consequences, as soon as a fault occurs in a transmission line, immediate actions should be taken for its location and repair. The location step, i.e., determining the location where the fault occurred, is critical for the services to be restored because the faster and more precise it is, the shorter is the repair time [1].

Fig. 1

Fault location algorithm

Table 1 Line parameters and sources used for the simulated faults

In [2, 3], the use of two terminals considering the representation in the phase domain instead of using symmetrical components was proposed, with non-synchronized data. The main advantages of this representation are that the type of fault does not have to be known, and it is applicable for untransposed lines, since any general impedance matrix can be considered. Conversely, without considering the line’s capacitances, these algorithms may show greater errors for long lines. In [4] a methodology is presented for untransposed lines, using the $\pi$ model. Some works have focused on other aspects of the problem, such as line parameter errors [5,6,7,8], which have introduced techniques that do not need the line parameters to evaluate the fault distance. The technique proposed in [9] introduced a fault location method for mixed lines—overhead lines and cables.

This study presents the results of the application of an ellipsoid optimization algorithm for the fault location in a transmission line simulated in the Alternative Transients Program (ATP) [10], and in real situations of the Brazilian electrical system, obtained by digital event recorders or digital relays with oscillography facilities of a Brazilian power company. Two objective functions (OFs) are presented: one for the short transmission line model that ignores the capacitance and another that considers the long line model with the hyperbolic corrections. The method presented is based on symmetrical components of the fault circuit, considering the transposed line and the synchronized data. For the method’s correct performance, the fault needs to be identified.

In addition to the distance to the fault, the application of the method proposed provides the estimated fault resistance value. This information is important for the maintenance team because, according to the results obtained, its value indicates the nature of the fault. High fault resistance values are associated with fire and vegetation in the area, whereas the low values are related to short circuits caused by overvoltages from atmospheric discharge (AD). The steps required by the fault location program were developed in MATLAB.

2 Initial considerations

Before solving the problem with the minimization of the OF, the application of pre-processing routines is necessary for the preparation of the data. Figure 1 presents the basic steps involved in the developed fault location program, showing the main steps to be executed. The process starts with the reading of the input data, i.e., the voltages and currents in the two line terminals contained in a file, which could be the output of the ATP or in COMTRADE format [11]. Next, the fault instant is determined to allow the separation of the pre and post-fault periods. The pre-conditioning of these signals is then performed with a low-pass filter, the 100 Hz second-order Butterworth filter, to remove the higher frequencies. After this step, the input data were interpolated to obtain the sampling rate desired. In this case, the number of points per cycle (NPC) [12] of the fundamental frequency (60 Hz) is 16.

To estimate the phasors associated with the fundamental frequency, the least-squares method by Sachdev and Baribeau [13] was used. The next step is fault classification, to select the voltage and current phasors involved in the short circuit and the OF that will be used by the algorithm for the location. Finally, the last step is the application of the algorithm to estimate the distance to the fault point and the fault resistance through the minimization of the OF.

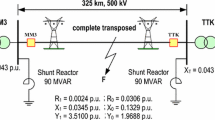
For the analysis and routine tests of the locator, a database was created with the faults simulated with the ATP program considering a 200 km and 138 kV three-phase transmission line. The transmission line parameters and the data from the equivalent sources are listed in Table 1 and the line configuration is shown in Fig. 2. The fault detection, classification and location algorithms were also submitted to nine real faults obtained by digital event recorders. The fault location was confirmed by the maintenance team.

Fig. 2

Line configuration

Fig. 3

Determination of Parseval’s energy with the dC1 coefficients

3 Fault detection and classification

3.1 Fault detection

In the fault detection step, the stationary wavelet transform (SWT) [14, 15] and Parseval’s theorem were applied [16]. Initially, the samples of input data were normalized considering the maximum peak value, which was recorded during the first two cycles when the electrical system was operating in the pre-fault period. Next, the fourth-order Daubechies mother wavelet (db4) was used at its first decomposition level for the extraction of high-frequency signals called the detail coefficient dC1. Other wavelets were tested [17], and the db4 at its first decomposition level proved to be efficient for the extraction of high-frequency characteristics.

With the dC1 detail coefficients, the energy E is calculated based on Parseval’s theorem, according to Eq. (1).

$$\begin{aligned} {E}=\mathop \sum \limits _{{n}=1}^{N} \hbox {dC}1^{2}\left( {n} \right) \end{aligned}$$

(1)

The calculation is performed by a moving window, equal in length to the NPC, through dC1, with a step for sample displacement. Figure 3 presents the evolution of an original current signal going through the previously described steps.

For the fault detection, the data of the energy of detail coefficient (E) are selected, which refer to the signals of three-phase currents, and then the occurrence of fault is identified in any of the three phases according to Eq. (2).

$$\begin{aligned} {E}\left( {{n}+1} \right) -{E}\left( {n} \right) >\Delta _{E} \end{aligned}$$

(2)

where n corresponds to the n$\mathrm{th}$ sample of the energy of the detail coefficient E, and ${\varvec{\Delta }}_\mathbf{E}$ corresponds to the energy variation that indicates the fault detection. The fault detector allows the separation of the signals in sets of data so the fault voltages and currents are properly used in the OF for the fault location.

Fig. 4

Different types of faults: a single phase-to-ground (AG, BG or CG); b two-phase (AB, AC, BC); c three-phase (ABC); d two phase-to-ground (ABG, ACG or BCG)

3.2 Fault classification

This step classifies the disturbances using the artificial neural networks (ANNs) [18, 19]. The set of data is subdivided into one training set and one validation set. The latter is used to evaluate the ANN during the training phase. This procedure is necessary to avoid the overtraining of the ANN. In this situation, the training process should be interrupted when the smallest mean square error for the validation set is achieved during the training phase. The sizes of the training and validation sets correspond to 80 and 20% of all examples of the data set, respectively. In the training and validation sets, the fault conditions presented to the ANNs were randomly arranged in the file.

Figure 4 details the types of faults investigated here, where the different types of faults, the location of the fault F, the distance at which the fault d occurred from terminal S and fault resistances R $_\mathbf{F}$ are presented.

A set of scenarios for ANN training was generated, considering nine points along the transmission line were selected as points for the application of fault situations. The combination of these positions with the variations of two fault incidence angles ($0{^{\circ }}\hbox { and }90{^{\circ }}$) and the three line-to-ground fault resistances (0, 30 and 100 $\Omega$) or with the three line-to-line fault resistances (0, 1 and 5 $\Omega$) used resulted in 54 situations for each fault type. Three data windows were considered after the detection of the fault situation (fault start). Hence, the data set is formed by 1620 patterns (9 fault locations $\times$ 3 fault resistances $\times$ 2 fault incidence angles $\times$ 3 data windows $\times$ 10 fault types).

The fault voltage and current phasor moduli were employed soon after the detection (extracted with the least-squares method) as the initial values considered in the first data window from the total of three windows. Window 1 contains four fault voltage samples (VA $_\mathbf{F}$, VA $_{{\varvec{F}}+1}$, VA $_{{\varvec{F}}+2}$, VA $_{{\varvec{F}}+3}$, VB $_{{\varvec{F}}}$, VB $_{{\varvec{F}}+1}$, VB $_{{\varvec{F}}+2}$, VB $_{{\varvec{F}}+ 3}$, VC $_{{\varvec{F}}}$, VC $_{{\varvec{F}}+1}$, VC $_{{\varvec{F}}+2}$, and VC $_{{\varvec{F}}+3}$,). This window also contains the four samples related to the fault currents (IA $_{{\varvec{F}}}$, IA $_{{\varvec{F}}+1}$ , IA $_{{\varvec{F}}+2}$, IA $_{{\varvec{F}}+3}$, IB $_{{\varvec{F}}}$, IB $_{{\varvec{F}}+1}$, IB $_{{\varvec{F}}+2}$, IB $_{{\varvec{F}}+3}$, IC $_{{\varvec{F}}}$, IC $_{{\varvec{F}}+1}$, IC $_{{\varvec{F}}+2}$, and IC $_{{\varvec{F}}+3}$,) with the respective expected response of the neural network for a fault situation along the transmission line (${S}_{1}$, ${S}_{2}$, ${S}_{3}$, and ${S}_{4})$. The other windows are obtained with the displacement of a sample in the data set. Similar to what occurs in the detection step; the phasors are normalized in relation to the maximum peak value that is registered during the first two cycles when the electrical system is operating in the pre-fault period. Table 2 shows the expected responses of the neural network from the function of the fault type in the training phase.

Table 2 Neural network output from the function of the fault type

Fig. 5

Line voltages and currents for CG fault

In the validation phase, it was stipulated that the outputs ($\hbox {S}_{i}$) observed in the range of −1 to 0.5 ($0\le \hbox {S}_{i}<0.5$) indicate a normal situation and that the values in the range of 0.5–1.0 ($0.5\le \hbox {S}_{i\le }1.0$) indicate a fault.

The characteristics of the network were determined experimentally with multilayer perceptron (MLP) topology, backpropagation supervised learning method, and Levenberg–Marquardt training algorithm. The activation function is the tangent sigmoid and the 24-16-4 neural network architecture was selected.

Figure 5 shows the voltage and current signals for a real fault case caused by atmospheric discharge. The transmission line is 500 kV and 342.7 km long. The neural network classified the event correctly as CG

Table 3 shows the outputs of the ANN for nine real fault cases, which obtained 100% of right responses in the classification. Special attention is drawn to the fact that the neural networks had been trained with the data from a line simulated in the ATP with different impedance, extension, and short-circuit characteristics in relation to real cases. When compared to those of the real cases, the results are different from what is usually presented in literature, where the neural network is applied to files generated from the same transmission line where it had been trained [20, 21]. This demonstrates the generalization capability of the developed methodology.

Table 3 Neural network outputs: real faults

3.3 Fault location: ellipsoid algorithm

The fault location is performed using a mono-objective optimization technique with the ellipsoid algorithm. The intuitive idea of the algorithm, i.e., the exclusion of semi-spaces [22], consists in enclosing the optimal solution with an ellipsoid. With this ellipsoid, cuts are performed that are always generating smaller ellipsoids until a degenerate ellipsoid is achieved over the optimal point, which will be its center.

The basic ellipsoid algorithm is described by the following recursive equations that generate a sequence of x $_\mathbf{k}$ points

$$\begin{aligned} x_{k+1} =x_k -\beta _1 \frac{Q_k g_k }{(g_k Q_k g_k )^{1/2}}\end{aligned}$$

(3)

$$\begin{aligned} Q_{k+1} =\beta _2 \left( {Q_k -\frac{\beta _3 (Q_k g_k )(Q_k g_k )^{T}}{g_k^T Q_k g_k }} \right) \end{aligned}$$

(4)

With

$$\begin{aligned} \beta _1 =\frac{1}{(n+1)}\quad \beta _2 =\frac{n^{2}}{(n^{2}+1)}\quad \beta _3 =\frac{2}{(n+1)} \end{aligned}$$

(5)

Vector g $_\mathbf{k}$ is the subgradient of the most violated constraint, or if x $_\mathbf{k}$ is in the feasible region, a subgradient of the OF f $_{0}$(x $_\mathbf{k})$ in that point. Figure 6 presents the evolution of the ellipsoids for a simulated fault at 20 km and with fault resistance of 20 $\Omega$ in a transmission line.

Fig. 6

Example of ellipsoid evolution—6 iterations

4 Objective function for the fault location

To find the fault location, OFs were created based on symmetrical components dependent on the different fault types (single-phase, two-phase, two-phase-to-ground, and three-phase) using data from the two terminals of the monitored transmission line. Thus,

$$\begin{aligned} F=F\left( {x,Z_1 } \right) \end{aligned}$$

(6)

where x is the fault point, R $_{{\varvec{F}}}$ is the fault resistance.

Fig. 7

Circuit for AG fault

4.1 Short line model-(OPT-short)

As an example of how to obtain the OF in a three-phase transmission line, consider the phase A fault to ground, represented in the diagram of Fig. 7.

The indexes 0, 1, and 2 indicate the components of the zero, positive, and negative sequences, respectively. In the short line model, ${{I}}_{Sm}^ ={I}_{Sm}^{F}$ and ${I}_{Rm}^ ={I}_{Rm}^{F}$, where m = 0, 1, 2. With the application of Kirchhoff’s voltage law,

$$\begin{aligned}&{V}_{S0} +{V}_{S1} +{V}_{S2} -{xZ}_1 \left( {{I}_{S1} +{I}_{S2} } \right) -{xZ}_0 {I}_{S0} \nonumber \\&\quad -3{R}_{F} \left( {{I}_{S1} +{I}_{R1}}\right) =0 \end{aligned}$$

(7)

Table 4 Objective functions for short line model

Table 5 Objective functions for long line model

Adding and subtracting $xZ_1 I_{S0}$

$$\begin{aligned}&{V}_{S0} +{V}_{S1} +{V}_{S2} -{xZ}_1 \left( {{I}_{S0} +{I}_{S1} +{I}_{S2} } \right) -{xI}_{S0} \left( {{Z}_0 -{Z}_1 } \right) \nonumber \\&\quad -3{R}_{F} \left( {{I}_{S1} +{I}_{R1} } \right) =0 \end{aligned}$$

(8)

Given that

$$\begin{aligned} {V}_{S0} +{V}_{S1} +{V}_{S2} ={V}_{S} \end{aligned}$$

$$\begin{aligned} {I}_{S0} +{I}_{S1} +{I}_{S2} ={I}_{S} \end{aligned}$$

(9)

The result is

$$\begin{aligned} {V}_{S}\,-\,{xZ}_1 \left( {{I}_{S} +\frac{{Z}_0 -{Z}_1 }{{Z}_1 }{I}_{S0} } \right) \,-\,3{R}_{F} \left( {{I}_{S1} +{I}_{R1} } \right) =0 \end{aligned}$$

(10)

It can be written that

$$\begin{aligned} {V}_{S}^{M} - {V}_{S}^{C} =0 \end{aligned}$$

(11)

where

$$\begin{aligned} {V}_{S}^{C} ={xZ}_1 \left( {{I}_{S} +\frac{{Z}_0 -{Z}_1 }{{Z}_1 }{I}_{S0} } \right) +3{R}_{F} \left( {{I}_{S1} +{I}_{R1} } \right) \end{aligned}$$

(12)

and $\mathop V\nolimits _S^M$ and $\mathop V\nolimits _S^C$ are the measured and calculated voltages in terminal S, respectively.

Using the square of the modulus of Eq. (11), the result is

$$\begin{aligned} {F}\left( {{x,R}_{F} } \right) =\left| {{V}_{ S}^{M} -{V}_{S}^{C} } \right| ^{2} \end{aligned}$$

(13)

i.e.,

$$\begin{aligned}&{F}( {{x,R}_{F} })\nonumber \\&\quad =Re\left( {\left( {V_S -xZ_1 \left( {I_S +\frac{Z_0 -Z_1 }{Z_1 }I_{S0} } \right) -3R_F \left( {I_{S1+} I_{R1} } \right) } \right) } \right) ^{2}\nonumber \\&\qquad +\,Im\left( {\left( {V_S -xZ_1 \left( {I_S +\frac{Z_0 -Z_1 }{Z_1 }I_{S0} } \right) -3R_F \left( {I_{S1+} I_{R1} } \right) } \right) } \right) ^{2}\nonumber \\ \end{aligned}$$

(14)

Table 4 contains the objective functions according to the fault type.

4.2 Long line model-(OPT-long)

For the long line model, consider Fig. 7 with the parameters distributed along the transmission line resulting in the hyperbolic equations. The OF, in which the minimum point is the fault location, is given by Table 5.

$$\begin{aligned} {V}_{S0}^{F}= & {} \hbox {cosh} \left( {{\varvec{\gamma }} _0 {x}} \right) {V}_{S0} -{Z}_{C0} \hbox {sinh}\left( {{\varvec{\gamma }} _0 {x}} \right) {I}_{S0}\\ {V}_{S1}^{F}= & {} \hbox {cosh} \left( {{\varvec{\gamma }} _1 {x}} \right) {V}_{S1} -{Z}_{C1} \hbox {sinh}\left( {{\varvec{\gamma }} _1 {x}} \right) {I}_{S1}\\ {V}_{S2}^{F}= & {} \hbox {cosh} \left( {{\varvec{\gamma }} _2 {x}} \right) {V}_{S2} -{Z}_{C2} \hbox {sinh}\left( {{\varvec{\gamma }} _2 {x}} \right) {I}_{S2}\\ {I}_{S1}^{F}= & {} \frac{\hbox {sinh} \left( {{\varvec{\gamma }} _1 {x}} \right) {I}_{S1} }{{Z}_{C1}}- {\hbox {cosh}}\left( {{{\varvec{\gamma }}} _1 {x}} \right) {{I}_{S1}}\\ {I}_{R1}^{F}= & {} \frac{\hbox {sinh} \left( {{\varvec{\gamma }} _1 {x}} \right) {V}_{R1} }{{Z}_{C1} }-\hbox {cosh}\left( {{\varvec{\gamma }} _1 {x}} \right) {I}_{R1}\\ {{I}_{S2}^{F}}= & {} \frac{\hbox {sinh} \left( {{\varvec{\gamma }} _2 {x}} \right) {I}_{S2} }{{Z}_{C1} }-\hbox {cosh}\left( {{\varvec{\gamma }} _2 {x}} \right) {I}_\mathrm{S2}\\ {I}_{R2}^{F}= & {} \frac{\hbox {sinh} \left( {{\varvec{\gamma }} _2 {x}} \right) {V}_{R2} }{{Z}_{C2} }-\hbox {cosh}\left( {{\varvec{\gamma }} _2 {x}} \right) {I}_{R2}\\ \end{aligned}$$

5 Results obtained

5.1 Simulated signals

After the fault detection and classification, the ellipsoid algorithm is applied to find the fault location and calculate the fault resistance. Figure 8 shows the OF for AG fault with fault resistance of 20 $\Omega$ at 100 km from terminal S considering the short line model. Figure 9 presents the evolution of the value of the function, and Fig. 10 shows the evolution of the algorithm for the determination of the distance to the fault and the calculation of the fault resistance. For the results with simulated data, the 200 km long, 138 kV line with the characteristics of Table 1 and Fig. 2 was used.

Fig. 8

Objective function for AG fault

Fig. 9

Evolution of the objective

Fig. 10

Evolution of the variables distance to fault (X) and fault resistance R $_{F}$

Figure 9 indicates that the algorithm rapidly converges to the minimum of the function with initial oscillations of the variables, which decrease as the algorithm evolves, as shown by Fig. 10.

To better compare the performance of the proposed method, two other location methods were implemented: one for transposed lines and synchronized data—Johns et al. [23] and the other for untransposed lines and non-synchronized data—Douglas et al. [3]. The error is expressed in function of the total length of the line, given by

$$\begin{aligned} e(\% ) = \left| {\frac{{({\text {estimated}}\;{\text {location}} - {\text {real}}\;{\text {location}}) \times 100}}{{{\text {line}}\;{\text {length}}}}} \right| \end{aligned}$$

(15)

Figures 11 and 12 present the location errors obtained for AG fault in different points in the transmission lines for the fault resistances of 20 and 100 $\Omega$ using the OF for the short line model (OPT-Short) and long line model (OPT-Long). Figure 13 presents the algorithm errors when BC faults are applied along the line, with fault resistance of 5 $\Omega$. Table 6 shows the average and maximum errors produced by the algorithms.

Fig. 11

Location errors—AG fault—${R}_{F}=20$ $\Omega$

Fig. 12

Location errors—AG fault—${R}_{F}=100$ $\Omega$

Fig. 13

Location errors—BC fault—${R}_{F}=5$ $\Omega$

Table 6 Errors produced by the algorithms

The algorithms produced errors lower than 1.5%, except for the short line model algorithm, which had errors up to 3.25%. The optimization algorithm based on the long line model produced, in the average, the lowest errors. The optimization algorithm based on the short line model and the method proposed in [3] produced slightly higher errors for not predicting the line’s capacitances.

The fault location algorithm proposed is based on sequence components and on the assumption that complete transposition is satisfied for the transmission line. The line in Fig. 2 was simulated as not transposed in the ATP and the results were presented in Table 7, for BC faults along the line, with fault resistance of 5 $\Omega$.

The sampling frequency is 960 Hz for data in the simulation, that is, 16 sampling points for each power frequency cycle. The phase-angle difference between two adjacent sampling points is $22.5{^{\circ }}$. A synchronism error of $45{^{\circ }}$, between S and R terminals, was induced for AG faults with fault resistance equal to 20 $\Omega$ along the transmission line. Results are shown in Table 7.

Table 7 Errors due to transposition and synchronism

For the untransposed line, except the method proposed in [3], which considers, in its modeling, the line’s non-transposition, the errors increased. Nevertheless, the methods may be used for fault location. For non-synchronized data, the method in [3] continued to produce the errors shown in Table 6. The optimization algorithm turned out to be synchronism-sensitive, with an increase in the errors. The method presented in [23], on the other hand, produced greater errors due to the data’s non-synchronism.

Figure 14 presents the fault resistance value estimated for two cycles after short-circuit at 80 km with a resistance of 20 $\Omega$, from the optimization algorithm using the short line model. Figure 15 shows fault resistance values estimated for various fault points along the transmission line for AG faults with fault resistance values of 20 and 100 $\Omega$.

Fig. 14

Estimated fault resistance—evolution

Fig. 15

Estimated values for fault resistance—simulations for 20 and 100 $\Omega$

The long line model is the most precise one, producing, for values of 100 and 20 $\Omega$, a maximum deviation of 3.1 and 3.2 $\Omega$, respectively.

5.2 Real signals

The location program was applied to real short-circuit cases in the electrical system of Brazil for the OF using the short and long line models. Results are shown in Table 8.

Table 8 Estimation for real cases

Although the simulated cases resulted in smaller errors for the long line model, the same did not occur for the real cases, where the mean errors were similar with 1.90% for the short line model and 1.92% for the long line model. The average error presented by methods proposed in [3] and [23] was of 3.23 and 2.15%, respectively. Differences observed with regard to the results of simulated data, in which the long line algorithm had a better performance, were not repeated in real cases. Possibly the combination of errors due to errors in the line parameters, non-transposition, errors of the potential and current transformers had an influence on the algorithms’ responses, reducing the differences between the results. However, the values obtained demonstrate the viability of the application of the algorithms proposed to real short-circuit cases.

In relation to the fault resistance value, it can be observed that small values are associated with atmospheric discharge, and average values of approximately 25 $\Omega$ are associated with fires. To obtain a more conclusive answer for the agent that caused the short circuit and the fault resistance value, more tests are required.

For fault location methods that apply phasors of two line terminals in practical cases, estimations that present error up to 2% of the line extension are considered good. This value is based on the experience of engineers who work with fault location. Therefore, the method proposed led to good results for most analyzed cases of Table 4.

6 Conclusions

This study presented an algorithm for the fault location and determination of fault resistance in transmission lines. In the detection step, the db4 SWT is used and with its detail coefficients dC1, Parseval’s energy is calculated. In the classification step, a neural network is used, where the inputs are the voltage and current phasor moduli of the analyzed event whose topography was defined after a series of tests. The observations indicate the correct classification for the real cases tested even though the network was trained with short-circuit files from a transmission line simulated in the ATP. In the fault location and determination of fault resistance, the ellipsoid optimization algorithm was applied to the selected OF based on the fault type, which proved to be fast and stable.

For the short line model, data simulated in the ATP were applied with an average error smaller than 1.5% for the 200-km line with the estimation of the distance and resistance of the fault. For the long line model, the average error was lower than 0.5%. When applied to real cases, the average errors obtained with the two line models were similar and slightly lower than those presented with the classic algorithm [23], with the mean value lower than 2%, thus demonstrating its viability for practical applications. The estimated fault resistance values in real cases can be associated with their cause, which in the cases presented were atmospheric discharge and fire; however, a larger database is still necessary for more conclusive analyses.