Job search under asymmetric information: endogenous wage dispersion and unemployment stigma

Abstract

We present a model of directed job search with asymmetric information regarding worker type. While job applicants know their productivity type, firms can only observe the duration of unemployment as well as a noisy signal of worker type. Firms can offer an unscreened wage or a wage that is conditioned on passing the screening and the duration of unemployment. This framework leads to three possible equilibria which depend on model parameter values. We describe the circumstances under which each equilibrium may result and the empirical implications of each equilibrium. Our model sheds light into wage scarring, unemployment duration, wage dispersion and firm-wage sorting, as well as the effects of unemployment insurance and minimum wages on search behavior and the distribution of wages.

1 Introduction

Going back decades, researchers have developed models of asymmetric information to explore labor market transitions, the consequences of unemployment, and the distribution of wages. These models leverage the key insight that firms extrapolate information about a worker based on his unemployment status as well as the duration of his unemployment spell. For example, Lazear (1984) creates a model in which firms have better information about their own workers than those at other firms. Consequently, workers that are fired or laid off are presumed to be of lower productivity than those who remain employed. Vishwanath (1989) explores a setting in which unemployed workers search for a job and face a wage offer distribution that is assumed to decline with unemployment duration due to the stigma associated with unemployment duration. In Lockwood (1991), workers become unemployable, at a fixed wage, after an extended spell of unemployment because firms perceive the worker as being of low expected productivity.

While these models explore some of the consequences of asymmetric information for workers, they generally assume an exogenous wage offer distribution as opposed to allowing the set of available wage offers to endogenously vary with the time spent looking for work. In addition, existing models do not show how asymmetric information about worker types might lead to endogenous heterogeneity across firms in the types of workers hired and wages offered. On the other hand, models of wage dispersion and employer–employee sorting as in Shimer (2005) and Burdett and Mortensen (1998) typically resort to imperfections in the labor market other than asymmetric information, such as coordination and search frictions.

In this paper, we develop a general equilibrium model of job search with asymmetric information that matches a wide range of observed patterns of wage dispersion, sorting and unemployment stigma in the labor market. In our model, job applicants differ in productivity, which is privately known by the worker. Workers are aware of all job advertisements and can direct their application to whichever provides highest expected utility. Employers advertise either that they are willing to hire all applicants at a given wage or that they will only hire applicants who pass a screening test, who are then paid a wage that may depend on their duration in unemployment. Competition among firms ensures that in equilibrium, the advertised wage equals the expected productivity of the hired workers. Thus, friction arises in this economy due to the private knowledge of worker type and the imperfect ability of firms to screen that type.

Equilibria of three types can arise. In the separating equilibrium, all high-productivity workers apply to the screened high-wage job, while all low-productivity workers apply to a non-selective, low-wage job. In downward pooling equilibria, some or all high-productivity workers join all the low-productivity workers in applying for the non-selective job. While this offers a lower wage, this is compensated by guarantee of fast employment. In both types of equilibria, unemployment duration conveys no additional information and does not affect wages.

The most intriguing behavior comes in upward pooling equilibria. Here, all workers initially apply to the screened job. High-productivity workers are more likely to obtain the job, so the quality of the applicant pool, along with the advertised wage, declines with unemployment duration. After a sufficient reduction in applicant quality, the low-productivity workers become indifferent between the screened and the non-selective jobs, employing a mixed strategy. From this point on, workers of both types exit at similar rates, so the wages remain constant with respect to unemployment duration.

Our model provides a variety of insights into the duration of unemployment, the distribution of wages, the sorting of heterogeneous workers across employers, and the impacts of unemployment insurance and minimum wages. Previewing the findings, we provide conditions under which the search behavior of low-skilled workers leads to both genuine wage dispersion and positive sorting between workers and firms—workers of the same productivity type that are hired by different employers may receive different wages, and high-wage firms always hire better-quality workers on average. Our model also implies that unemployment can have a causal negative impact on realized wages. We examine situations in which the labor market clears from top down, with the highest wage jobs being filled first, as well as situations in which the market clears from bottom up. We explore how the quality of the applicant pool affects the distribution of wages for both high- and low-ability workers. Finally, we use our model to examine the effect of unemployment insurance and minimum wages on job search and the distribution of wages.

In the remainder of the paper, we outline prior theoretical literature in Sect. 2. We then describe our model in Sect. 3 and characterize its equilibria in Sect. 4, along with discussion of several extensions. In Sect. 5, we summarize existing empirical evidence in light of our model as well as the types of settings in which each of the equilibria is likely to occur. We next consider in Sect. 6 the impact in our environment of two common labor market policies, unemployment benefits and minimum wages. Section 7 then concludes. All proofs are presented in “Appendix.”

2 Prior theoretical literature

Our work primarily contributes to the literature studying the so-called “rational stigma” of unemployment duration, first explored in the theoretical models of Vishwanath (1989) and Lockwood (1991), and more recently in Gonzalez and Shi (2010) as well as contemporary work of Doppelt (2015), Fernandez-Blanco and Gomes (2017), Fernandez-Blanco and Preugschat (2015), and Jarosch and Pilossoph (2015). In each of these models, workers are less likely to be hired the longer they have been unemployed, and in some cases, the average wage falls as well.¹ Recent work focuses on whether this duration dependence occurs at the individual level (longer spells reduce the chances for a given worker) or whether it only occurs in aggregate due to dynamic selection (workers with low chances remain unemployed for longer spells).

Our model differs in key ways from prior and contemporary literature. First, our model underscores that duration dependence in the wage and hazard to reemployment is not inevitable, occurring only in the full upward pooling equilibrium. When screening is more accurate, workers are more similar in their productivity, or the population is skewed toward one type, other equilibria can occur with constant wages over the unemployment spell.

Second, we show that even when duration dependence occurs (in the full upward pooling equilibrium), both reemployment hazard rates and wages eventually plateau after initially falling. This is in contrast to many models in which the hazard rates and wages continue to decline over time.

Third, other papers effectively assume symmetric information. Gonzalez and Shi (2010) and Fernandez-Blanco and Preugschat (2015) assume that workers do not know their own type, so that firms and workers glean the same information from the worker’s unemployment spell. In Lockwood (1991), Doppelt (2015) and Jarosch and Pilossoph (2015), workers have no choice in where they direct job applications, so they cannot take advantage of any private information. Vishwanath (1989) only models the worker’s search process while the distribution of wage offers is exogenously given, thus becoming a dynamic decision problem rather than a game with asymmetric information.

In our environment, participants are asymmetrically informed: workers perfectly know their type and the set of advertised jobs, but firms can only make imperfect inferences about applicant types. It is significant that duration dependence can occur in such a setting. Informed workers have the option to direct their search to jobs that are commensurate with their skill. If directed applications perfectly sort workers, then firms learn nothing from unemployment duration and impose no penalty for it. Indeed, Fernandez-Blanco and Gomes (2017) also assume asymmetric information with fully informed workers; however, their setting yields only a separating equilibrium with no duration dependence, conditional upon worker type.

Fourth, all workers in our model have positive marginal product. This demonstrates that duration dependence need not rely on the existence of unproductive workers as is the case in most of the models cited above. In most of these, marginal product is either non-positive or strictly less than the leisure benefit of unemployment. In Fernandez-Blanco and Gomes (2017), firms specialize with different levels of capital, and it is inefficient to use lower-productivity workers with larger amounts of capital. In Sect. 5, we explore settings in which a binding minimum wage or generous unemployment benefit makes the employment of low-productivity workers unprofitable.

Fifth, we contribute to the wage dispersion literature by demonstrating that asymmetric information about worker quality alone can lead to dispersed wages, even conditional on the worker’s type and length of unemployment. Other models that generate wage dispersion require worker heterogeneity (Albrecht and Axell 1984), on-the-job search (Burdett and Mortensen 1998), search coordination frictions (Burdett and Mortensen 1998; Shimer 2005; Albrecht et al. 2006), or expiring unemployment insurance benefits (Akin and Platt 2012). Our framework highlights the role of asymmetric information as a labor market friction that induces wage dispersion. It is worth noting that other papers on rational stigma do not feature wage dispersion.

Screening of applicants has also been introduced into macro-labor search models (e.g., Ravenna and Walsh 2012; Villena-Roldán 2012; Wolthoff 2017) to provide better micro-foundations of the matching process. In these models, interviews perfectly reveal a worker’s productivity, preventing the information asymmetry that we study. On the other hand, they only permit firms to hire one worker per vacancy, which is costly to post, creating a congestion externality that is not present in our setting where firms can potentially hire all applicants. Both Ravenna and Walsh (2012) and Villena-Roldán (2012) predict that wages decline in the length of unemployment spell because the best workers are hired more quickly, but the mechanism differs from ours. In Ravenna and Walsh (2012), this is because the best workers always generate positive surplus and will be hired, while lower-efficiency workers only get hired after a lucky draw of their stochastic productivity. In Villena-Roldán (2012), each vacancy receives a stochastic number of applications, so the most productive workers are more likely to beat other applicants in a given vacancy.²

3 Model

3.1 Environment

We consider a competitive labor market consisting of a large number of firms and a continuum of workers of measure 1. Workers initially differ only in their marginal productivity, known only to the worker himself, which is $p_h$ for fraction $\eta \in (0,1)$ of new entrants to the job market, and $p_\ell < p_h$ for the remainder. Time is discrete, and the horizon is infinite. Future payoffs are discounted with a common discount factor of $\beta$.

Firms are ex-ante identical and engage in wage competition to maximize profit. Firms move first, each simultaneously posting a wage and the criteria used for selecting workers (to be described momentarily). We consider as if each firm only posts one wage, paying all selected workers that wage forever thereafter. Each firm commits at time 0 to its posted wage contract,³ including wage w(t) and hiring policies, and only hire in their chosen period t. Given that firms earn zero expected profit in equilibrium, this is without loss of generality.

Job advertisements are public knowledge and are used by workers to direct their search. In the unscreened job, employers commit to accept any applicant without screening and without regard to the number of periods $t \in \mathbb {N}$ that the worker has searched for a job (his duration of unemployment). Of course, these employers correctly anticipate that their applicants will have a lower marginal product, paying a commensurate wage $w_u$.

For a screened job, the applicant is only hired if he passes a screening test (for instance, through interviews, aptitude tests, background checks, or reference verification), which has an accuracy of $\gamma > \frac{1}{2}$. That is, with probability $\gamma$, the test reports the true productivity of the worker, while with probability $1 - \gamma$, the test misreports the productivity. The employer then pays the hired worker wage $w_s(t)$, which may depend on unemployment duration $t \in \mathbb {N}$, since it indicates how many times he has failed a screening prior to the current attempt.⁴

Fig. 1

Timing of events

Workers apply to posted jobs repeatedly (with one application per period) until they are hired according to the posted policies. Workers are risk neutral in monetary payoffs, and receive utility with a monetary equivalent of b dollars from leisure or unemployment benefits while searching for a job. We assume that the screening test is independent across firms and across periods. As a consequence, a worker that fails the screening test in period t may nevertheless pass the test in period $t+1$.

To ensure that employment is socially optimal, we assume $p_\ell > b$. Once hired, we assume that the job continues indefinitely at the specified wage. For the reader’s convenience, we summarize the timing of events in Fig. 1. Note the job advertisement is non-rival, allowing a firm to hire multiple workers from one ad.

3.2 Workers

Every period, a worker who does not have a job must decide where to direct his application, whether to the screened job or the unscreened job. The decision for a high-productivity worker who has been unemployed for t periods can be expressed recursively in the following Bellman equation:

$$\begin{aligned} U_h(t) = b + \beta \max \left\{ \gamma \frac{w_s(t)}{1 - \beta } + (1- \gamma ) U_h(t+1) , \; \frac{w_u}{1 - \beta } \right\} . \end{aligned}$$

(1)

Each period, the worker receives leisure utility b, and applies to whichever job advertisement (for which he is eligible) offers the highest expected payoff. If he applies to an unscreened job, he is hired for sure at wage $w_u$. If he applies to the screened job, he is hired with probability $\gamma$; otherwise, after failing the test, he must continue his search. Workers who are hired in period t start working and receive wage from period $t+1$ on.

The expected payoff for a low-productivity worker who has been unemployed for t periods can be similarly expressed:

$$\begin{aligned} U_\ell (t) = b + \beta \max \left\{ (1 - \gamma ) \frac{w_s(t)}{1 - \beta } + \gamma U_\ell (t+1) , \; \frac{w_u}{1 - \beta } \right\} . \end{aligned}$$

(2)

The key distinction is in the probability of passing the screening. For the low-productivity worker, this occurs with probability $1 - \gamma$, as the test mistakenly identifies him as having high productivity.

Each worker of productivity $i \in \{h, \ell \}$ and unemployment duration t must choose a search strategy of where to direct his application that day. To permit mixed strategies, we represent this strategy $\sigma _i(t) \in [0,1]$ as the probability of applying to the screened job.

3.3 Population law of motion

The search strategy of workers at time t will impact the composition of unemployed workers in the market thereafter. Indeed, employers will be highly interested in how the population of each type of workers evolves the longer they remain in the market, as it affects the average productivity of job applicants.

Let $f_h(t)$ and $f_\ell (t)$ denote the number of workers of each productivity type remaining in the market after t periods of time. Recall that $f_h(0) = \eta$ and $f_\ell (0) = 1 - \eta$. The populations of workers obey the following laws of motion:

$$\begin{aligned} f_h(t+1)= & {} (1 - \gamma ) \sigma _h(t) f_h(t), \end{aligned}$$

(3)

$$\begin{aligned} f_\ell (t+1)= & {} \gamma \sigma _\ell (t) f_\ell (t). \end{aligned}$$

(4)

In both equations, the left-hand side, $f_i(t+1)$, is the population of workers with productivity i and unemployment duration $t+1$. On the right-hand side, the fraction $1 - \sigma _i(t)$ will be offered the unscreened job and exit the market. Thus, only the fraction $\sigma _i(t)$ who applied to the screened job could potentially remain in the market, and then only if they fail the screening test, which happens with probability $1 - \gamma$ for those with high productivity and $\gamma$ for those with low productivity.

3.4 Employers

In a competitive labor market with free entry by employers, each hiring firm must pay workers their expected marginal product.⁵ Employers are able to hire all candidates, provided they pass the screening test if required by the employer. The expected profit from a given advertisement depends on two factors. First, employers must estimate the ex-ante expected productivity of their job applicants, which they infer from the search strategy $\sigma _i(t)$ and population of workers $f_i(t)$.

Ex ante, the expected profit for an employer offering a screened job to workers who have been unemployed for t periods is:

$$\begin{aligned} \Pi _s(t) \equiv \frac{1}{1 - \beta } \left[ \sigma _h(t) f_h(t) \gamma (p_h - w_s(t)) + \sigma _\ell (t) f_\ell (t) (1 - \gamma ) (p_\ell - w_s(t)) \right] .\quad \end{aligned}$$

(5)

This computes the measure of each type of worker ($\sigma _i(t) f_i(t)$) times the probability that the worker passes the screening test ($\gamma$ or $1 - \gamma$), multiplied by the profit per worker. If a worker of either type fails the screening test, the firm earns zero profit.

The expected profit for an employer offering an unscreened job is similarly computed, only without any chance of being rejected since no screening occurs:

$$\begin{aligned} \Pi _u \equiv \frac{1}{1 - \beta } \sum _{t \in \mathbb {N}} (1 - \sigma _h(t)) f_h(t) (p_h - w_u) + (1 - \sigma _\ell (t)) f_\ell (t) (p_\ell - w_u). \end{aligned}$$

(6)

For a given job, workers of both types are paid the same advertised wage. Even employers who screen workers are not able to perfectly distinguish the types; those who pass the screen look identical, even though $\sigma _\ell (t) f_\ell (t) (1 - \gamma )$ of them have low productivity.

3.5 Equilibrium

The equilibrium concept we use is subgame perfect Nash equilibrium, with firms simultaneously moving first, followed by an infinite sequence of simultaneous moves by workers. An equilibrium consists of a sequence of posted screened wages, $w_s(t) \in \mathbb {R}$; a posted unscreened wage, $w_u \in \mathbb {R}$; worker populations $f_h(t)$ and $f_\ell (t)$; and search strategies $\sigma _h(t)$ and $\sigma _\ell (t)$ for each $t \in \mathbb {N}$, such that:

• 1. Ex-ante profit of employers from offering $w_s(t)$ or $w_u$ is zero. No firm can profit from unilateral deviation, offering a different wage schedule.

• 2. Workers optimally choose their application strategy, meaning:

  • (a) $\sigma _h(t) = 1$ if $(1- \gamma ) U_h(t+1) > \frac{w_u - \gamma w_s(t)}{1 - \beta }$.

  • (b) $\sigma _h(t) = 0$ if $(1- \gamma ) U_h(t+1) < \frac{w_u - \gamma w_s(t)}{1 - \beta }$.

  • (c) $\sigma _\ell (t) = 1$ if $\gamma U_\ell (t+1) > \frac{w_u - (1 - \gamma ) w_s(t)}{1 - \beta }$.

  • (d) $\sigma _\ell (t) = 0$ if $\gamma U_\ell (t+1) < \frac{w_u - (1 - \gamma ) w_s(t)}{1 - \beta }$.

• 3. The evolution of worker populations reflects the realized acceptance of job offers as stated in Eqs. (3) and (4).

The first condition imposes zero profits on firms, which one can view as shorthand for Bertrand competition among potential employers for a given advertisement.⁶ The second condition requires workers to optimize on the equilibrium set of job applications, while still allowing for mixed strategies. The third condition imposes that the quality of workers with any unemployment duration t is consistent with the hirings that would have occurred before t.

4 Equilibrium characterization

As we examine equilibrium behavior, we can first rule out certain possibilities. First, the first equilibrium requirement pins down the wages that can be offered as indicated below. Furthermore, these wages must be at least as large as the unemployment benefit b. This places a lower bound on the utility of all workers and ensures that workers prefer to apply each period rather than abstain from search.

Lemma 1

In equilibrium,

$$\begin{aligned} w_s(t)&= \frac{\gamma \sigma _h(t) f_h(t) p_h + (1 - \gamma ) \sigma _\ell (t) f_\ell (t) p_\ell }{\gamma \sigma _h(t) f_h(t) + (1 - \gamma ) \sigma _\ell (t) f_\ell (t)}\end{aligned}$$

(7)

$$\begin{aligned} w_u&=\frac{\sum _{t \in \mathbb {N}} (1 - \sigma _h(t)) f_h(t) p_h + (1 - \sigma _\ell (t)) f_\ell (t) p_\ell }{\sum _{t \in \mathbb {N}} (1 - \sigma _h(t)) f_h(t) + (1 - \sigma _\ell (t)) f_\ell (t)}. \end{aligned}$$

(8)

Moreover, $w_h(t) \ge p_\ell$ and $w_u \ge p_\ell$; thus $U_i(t) > \frac{b}{1 - \beta }$.

Second, high-productivity workers have weakly higher expected utility than low-productivity workers at any point in time. This is because they have equal payoffs in the unscreened market and are more likely to secure a screened job.

Lemma 2

In equilibrium, $U_h(t) \ge U_\ell (t)$.

Third, if any fraction of high-productivity workers apply to an unscreened job, all low-productivity workers of the same unemployment duration must apply to the unscreened job. Since the low-productivity workers are less likely to be hired at a screened job, they cannot be more inclined to apply there than those who are more likely to be hired.

Lemma 3

In equilibrium, if $\sigma _h(t) < 1$ then $\sigma _\ell (t) = 0$.

The preceding lemmas greatly reduce the candidates for equilibrium. Indeed, only three possibilities exist, distinguished by whether workers of one type imitate the other type. In a separating equilibrium, no imitation occurs: all high-productivity workers apply to screened jobs, while all low-productivity workers apply to unscreened jobs. In an upward pooling equilibrium, the high-productivity workers behave the same, but low-productivity workers imitate them by apply to screened jobs. Finally, the reverse occurs in a downward pooling equilibrium, with high-productivity workers imitating the low-productivity workers by applying to unscreened jobs. Further nuance arises in both pooling equilibria based on whether the imitating group strictly prefers doing so (full pooling), or is indifferent and mixes between the two job types (partial pooling).

4.1 Separating equilibrium

We begin our characterization of these equilibria with the separating equilibrium, where workers immediately segregate themselves into distinct labor markets. Low-productivity workers all apply for the unscreened job and are immediately hired at wage $p_\ell$. High-productivity workers all apply for screened jobs, but must repeatedly apply until they pass the screening interview. Of course, firms realize that they are only interviewing high-quality candidates, but have committed to reject applicants who fail the screening process. As a result, screened workers are all paid the same wage $p_h$ regardless of when they are hired; there is no wage scarring.

Proposition 1

The separating equilibrium, where

$$\begin{aligned} w_s(t)&= p_h \end{aligned}$$

(9)

$$\begin{aligned} w_u&=p_\ell \end{aligned}$$

(10)

$$\begin{aligned} \sigma _h(t)&= 1 \end{aligned}$$

(11)

$$\begin{aligned} \sigma _\ell (t)&= 0 \end{aligned}$$

(12)

$$\begin{aligned} f_h(t)&= \eta (1 - \gamma )^t \end{aligned}$$

(13)

$$\begin{aligned} f_\ell (t)&= {\left\{ \begin{array}{ll} 1 - \eta &{} \quad \mathrm{if} \; t = 0 \\ 0 &{} \quad \mathrm{if} \; t > 0, \end{array}\right. } \end{aligned}$$

(14)

exists if and only if:

$$\begin{aligned} \gamma \ge \frac{(1 - \beta )(p_\ell - b)}{p_h - p_\ell + (1 - \beta )(p_\ell - b)} \quad \text { and } \quad \gamma \ge \frac{p_h - p_\ell }{p_h - p_\ell + (1 - \beta )(p_\ell - b)}.\quad \end{aligned}$$

(15)

The two conditions in (15) are incentive compatibility constraints for the high- and low-productivity workers, respectively, ensuring that the former prefer applying to the screened job, while the latter prefer the unscreened job. Intuitively, the separating equilibrium occurs when the screening process is highly accurate. For instance, if $\gamma = 1$, both conditions are clearly satisfied.

The other parameters determine the required threshold of accuracy. For instance, if workers are very patient ($\beta \rightarrow 1$), then the right-hand side of the second constraint approaches 1. That is, patient low-productivity workers are tempted to repeatedly apply to the screened wage, accepting longer unemployment for a chance at higher wages. Only a highly accurate screening test can discourage this strategy by reducing their chance of success.

In a similar vein, if low-productivity workers are barely covering their outside option ($p_\ell \rightarrow b$), the right-hand side of the second constraint again approaches 1. The low-productivity workers gain very little by taking an immediate unscreened job and are thus tempted to take their chances in the screened job market unless the screening test is likely to reject them.

Finally, as workers look more homogenous ($p_\ell \rightarrow p_h$), the right-hand side of the first constraint approaches 1. This is because the unscreened wage draws close to the screened wage, so high-productivity workers are tempted to take the non-selective job immediately rather than risk being falsely screened. With high enough accuracy, however, they remain willing to take the chance for the higher wage.

This equilibrium not only matches workers to jobs that are commensurate with their skills, but it does so in the quickest possible time frame. Moreover, the worker’s choice of where to apply fully communicates that worker’s private information; the time he spent on the market provides no additional information. As a result, wages are held constant regardless of hiring date.

One may wonder why not all high-type workers get hired in period 1, since all low-type workers are hired in period 0, ensuring that all unemployed in period 1 are of high type. However, since unscreened wages are not conditioned on the screening interview or the duration of unemployment, any unscreened wage meant to attract high types in period 1 will in fact attract all workers in period 0, leading to losses for the firm that posted such a wage. Thus, firms’ best response is to commit to hire only those that pass the screening test, even though the failing applicants have the same productivity. In Sect. 4.6, we consider the possibility of duration-contingent unscreened job offers.

4.2 Upward pooling equilibrium

Next, we examine the upward pooling equilibrium. Here, all high-productivity workers apply for the screened jobs, but either some or all of the low-productivity workers also try their luck at screened jobs. If all workers initially apply to the screened job (i.e., full pooling), the screening leads firms to cherry pick a disproportionate number of high-productivity workers. Thus, the quality of the remaining pool of unemployed workers is falling, so the wages offered also fall over time.

Eventually, the wage falls low enough that some low-productivity workers are willing to apply to unscreened jobs (i.e., partial pooling). Since hiring is guaranteed in the unscreened market, this equalizes the rate at which both types of workers are hired, maintaining a constant proportion of each and steady wages in both markets thereafter.

Proposition 2

An upward pooling equilibrium, where

$$\begin{aligned} w_s(t)\equiv & {} {\left\{ \begin{array}{ll} \frac{\eta (1 - \gamma )^{t}\gamma p_h + (1 - \eta ) \gamma ^{t}(1-\gamma ) p_\ell }{\eta (1 - \gamma )^{t}\gamma + (1 - \eta ) \gamma ^{t}(1-\gamma ) } &{}\quad \text { for }\;t < T \\ p_\ell + \frac{\gamma (1 - \beta ) (p_\ell - b)}{1 - \gamma } &{}\quad \mathrm{for }\;t \ge T \\ \end{array}\right. }\end{aligned}$$

(16)

$$\begin{aligned} w_u= & {} p_\ell \end{aligned}$$

(17)

$$\begin{aligned} \sigma _h(t)= & {} 1 \mathrm{for all }\;t\end{aligned}$$

(18)

$$\begin{aligned} \sigma _\ell (t)= & {} {\left\{ \begin{array}{ll} 1 &{}\quad \mathrm{for }\;t < T \\ \left( \frac{1 - \gamma }{\gamma } \right) ^T Q &{}\quad \mathrm{for }\;t = T \\ \frac{1 - \gamma }{\gamma } &{} \quad \mathrm{for }\;t > T \\ \end{array}\right. }\end{aligned}$$

(19)

$$\begin{aligned} f_h(t)= & {} \eta (1 - \gamma )^t \quad \mathrm{for\,all }\;t \end{aligned}$$

(20)

$$\begin{aligned} f_\ell (t)= & {} {\left\{ \begin{array}{ll} (1-\eta ) \gamma ^t &{} \quad \mathrm{for }\;t \le T \\ (1-\eta ) Q \gamma (1 - \gamma )^{t-1} &{} \quad \mathrm{for }\;t > T \end{array}\right. }\end{aligned}$$

(21)

$$\begin{aligned} Q\equiv & {} \frac{\eta }{1-\eta } \cdot \frac{(1 - \gamma ) (p_h-p_\ell )- \gamma (1 - \beta ) (p_\ell -b)}{ (1 - \gamma )(1 - \beta ) (p_\ell -b)}\end{aligned}$$

(22)

$$\begin{aligned} T\equiv & {} \max \left\{ 0, \left\lceil \frac{\ln Q }{\ln (\gamma /(1 - \gamma ) )} \right\rceil \right\} , \end{aligned}$$

(23)

exists if and only if $Q >0$.

The requirement that $Q > 0$ ensures that low-productivity workers are willing to apply to screened jobs. Since the denominator of Q is always positive, one only needs to check the sign of the numerator. This is equivalent to $\gamma < \frac{p_h - p_\ell }{p_h - p_\ell + (1 - \beta )(p_\ell - b)}$, which is the opposite of the incentive compatibility constraint on low-productivity workers in the separating equilibrium [the second constraint in (15)].⁷

The degree of pooling is determined by T, which determines the lowest positive integer for which $\left( \frac{1 - \gamma }{\gamma } \right) ^T Q \le 1$. If $T = 0$, the equilibrium always remains in a partial pooling phase, with low-productivity workers indifferent between the jobs, using a mixed strategy across both. Note that the mixed strategy and offered wages at each job remain constant for $t > T$, which is necessary to maintain indifference throughout the partial pooling phase.

If $T > 0$, then initially all workers strictly prefer the screened job and fully pool in applying there for the first $t < T$ periods. This screening will hire disproportionately from the high-productivity workers, worsening the pool of future applicants and their wages. This wage scarring continues with a longer unemployment spell, but stops after period T when the partial pooling phase begins.

When full pooling occurs, the low-wage firms will only end up hiring workers later in their unemployment spell. High-wage firms will vary depending on which wages they offer. The market clears from top to bottom, meaning that the firms offering the highest wages will get the workers with shortest job search (and more of them). Firms that offer lower screened wages will see fewer total applicants, interview them later in their search spell, and accept a smaller percentage of the applicants.

The full pooling phase ($T > 0$) occurs if and only if $Q > 1$, which is equivalent to $\eta \ge \frac{(1-\gamma )(1-\beta )(p_\ell -b)}{(1-\gamma )(p_h-p_\ell )+(1-2\gamma )(1-\beta )(p_\ell -b)}$. This is most likely to occur when there are more high-productivity workers (large $\eta$), the screening mechanism is not very precise (small $\gamma$), or the gains from employing low-productivity workers are minimal ($p_\ell$ is closer to b than to $p_h$). In effect, low-productivity workers are hoping to be mistaken for high-productivity workers; and when there are a lot of the latter, the employer will infer that those who pass the screen are more likely to be highly productive. In effect, the more productive workers pass on a positive externality to the less productive workers by raising the posterior beliefs of employers.

4.3 Downward pooling equilibria

Finally, we examine downward pooling equilibria. These consist of all low-productivity workers applying and being hired to the unscreened job, while some or all of the high-productivity workers imitate them by initially applying to the unscreened job. With full downward pooling, all workers take the unscreened job, and the market empties in period 0. With partial downward pooling, the high types randomize between screened and unscreened jobs in period 0; those who are not hired continue in the screened market thereafter.

Proposition 3

A downward pooling equilibrium, where

$$\begin{aligned} w_s(t)&= p_h \quad \mathrm{for\,all }\;t \\ w_u&= {\left\{ \begin{array}{ll} \eta p_h + (1 - \eta ) p_\ell &{} \quad \mathrm{if } \; S = 0 \\ b + \frac{(p_h - b) \gamma }{1 - \beta (1 - \gamma )} &{} \quad \mathrm{if } \; S> 0 \end{array}\right. }\\ \sigma _h(t)&= {\left\{ \begin{array}{ll} S &{}\quad \mathrm{for }\;t = 0 \\ 1 &{}\quad \mathrm{for }\;t> 0 \\ \end{array}\right. }\\ \sigma _\ell (t)&= 0 \quad \mathrm{for\,all }\;t \\ f_h(t)&= {\left\{ \begin{array}{ll} \eta &{}\quad \mathrm{if } \; t = 0 \\ \eta S (1 - \gamma )^t &{}\quad \mathrm{if }\; t> 0 \end{array}\right. }\\ f_\ell (t)&= {\left\{ \begin{array}{ll} 1 - \eta &{} \quad \text { if } \; t = 0 \\ 0 &{} \quad \text { if } \; t > 0, \end{array}\right. } \end{aligned}$$

exists for $S = 0$ if and only if $\varDelta \ge 0$ and exists for $S = \varDelta$ if and only if $0 \le \varDelta \le 1$, where

$$\begin{aligned} \varDelta \equiv 1 - \frac{(1-\eta )}{\eta (p_h - b)} \left( \frac{ (p_h - p_\ell ) \gamma }{(1-\beta ) (1-\gamma )} - (p_\ell - b) \right) . \end{aligned}$$

(24)

In this notation, the parameter $\varDelta$ determines which equilibria can occur. As discussed in the next subsection, both partial and full downward pooling equilibria exist when $\varDelta \in [0,1]$. The variable S indicates the fraction of high-productivity applications to the screened job in period 0. When $S = 0$, full pooling occurs in the unscreened job. The requirement that $\varDelta \ge 0$ is equivalent to:

$$\begin{aligned} \gamma \le \frac{(1-\beta )\left( \eta (p_h-p_\ell )+p_\ell -b \right) }{(1- \beta \eta )(p_h-p_\ell )+(1-\beta )(p_\ell -b)}. \end{aligned}$$

(25)

This ensures that high-productivity workers prefer applying to the unscreened job, even if the best wage $p_h$ is offered at the screened job. This is most likely to hold when the screening interview is less accurate (low $\gamma$), when most worker have high productivity (high $\eta$), or when worker productivity is more homogeneous ($p_\ell$ is closer to $p_h$).

When $S = \varDelta$, high-productivity workers only partially pool in the unscreened job. As with full pooling, $\varDelta \ge 0$ is required for this equilibrium to exist, so that high-productivity workers are initially willing to apply to the unscreened job. Additionally, $\varDelta \le 1$ is required to ensure that high-productivity workers are also willing to apply to the screened job. If this condition fails, the unscreened job would be enticing to the high-productivity workers even if the lowest wage of $p_\ell$ were offered. This condition is equivalent to:

$$\begin{aligned} \gamma \ge \frac{(1 - \beta )(p_\ell - b)}{p_h - p_\ell + (1 - \beta )(p_\ell - b)} \end{aligned}$$

(26)

Of course, this is the same as the first condition in (15), required for the existence of a separating equilibrium.

4.4 Existence and uniqueness

One virtue of our model is that each of the three equilibria—separating, upward pooling, and downward pooling—is plausibly related to empirical behavior. Parameter values determine which can arise, as already specified in Propositions 1, 2 and 3. Here, we verify that an equilibrium always exists, and identify conditions under which multiple equilibria can exist, as summarized in the following corollary.

Corollary 1

An equilibrium always exists. Indeed,

• 1. If $\varDelta < 0$, then exactly one upward pooling or separating equilibrium exists.

• 2. If $\varDelta \in [0,1]$, then the partial downward pooling equilibrium, the full downward pooling equilibrium, and exactly one upward pooling or separating equilibrium exist.

• 3. If $\varDelta > 1$, then only the full downward pooling equilibrium exists.

First, note that the separating, partial upward pooling, and full upward pooling equilibria are mutually exclusive: one and only one of them occurs if $\varDelta \le 1$.

Second, it is worth noting that when $\varDelta = 0$, the full and partial downward pooling equilibria coincide (and indeed, the wage $w_u$ is the same in both its listed cases). On the other hand, when $\varDelta = 1$, the partial downward pooling equilibrium coincides with the separating equilibrium. Thus, in these knife-edge cases, exactly two equilibria will exist.

Finally, when $\varDelta \in (0,1)$, three equilibria exist. Indeed, the full downward pooling equilibrium exists whenever the partial downward pooling equilibrium does. In this context, multiple equilibria indicate that individual payoffs are affected by aggregate search decisions because of their effect on wages. A high-productivity worker may be willing to quickly obtain an unscreened job so long as many other high-productivity workers apply and drive up the wage. But if not, the unscreened wage will be too low to entice him for the screened market. Essentially, in each equilibrium, the workers are coordinating on a shared, correct belief about how the others will direct their applications.

Figure 2 illustrates the preceding result. Having normalized $p_h = 1$, we compare which equilibria exist depending on the initial composition of workers ($\eta$, on the vertical axis), the precision of the screening ($\gamma$, on the horizontal axis), and the relative productivity of low workers ($p_\ell$, across the panels). Although b and $\beta$ are held constant in this figure, an increase in either one has similar effect to a decrease in $p_\ell$. For these parameters, note that $\varDelta = 1$ when $p_\ell = 0.932$ and $\gamma = 0.5$, pictured in Panel E.

Fig. 2

Equilibrium existence. Each region indicates whether a separating (S), upward pooling (U), or downward pooling (D) equilibrium exists, depending on the initial fraction of high-productivity workers (vertical axis), the precision of screening (horizontal axis), and the productivity of low workers relative to high workers (panel), with other parameters set at $p_h = 1$, $b = 0.25$, and $\beta = 0.9$. In the U regions, full upward pooling exists iff $\eta$ lies above the dotted line, while partial upward pooling exists otherwise. In the D regions, full downward pooling always exists. Partial downward pooling exists only in $U + D$ or $S + D$

Several striking features are readily observed. First, with a highly precise test, only the separating equilibrium exists, regardless of other parameters. Intuitively, low-productivity workers find it useless to apply at the screened job, since success is so unlikely, yet high-productivity workers are likely to be hired in the first several attempts. Moreover, with a more narrow gap in productivity between workers (moving from Panels A–E), the separating equilibrium can be sustained even with less precise screening. Compressed productivity also compresses wages, offering low-productivity workers less reward for imitating the high-productivity workers.

Second, when nearly all workers are highly productive, downward pooling equilibria exist. The few low-productivity workers do not dilute wages much, giving the high-productivity workers little incentive to apply to screened jobs and risk a delay in being hired. However, with more balance in the initial pool of workers, downward pooling can no longer be sustained. This is particularly true when there is a wider gap in productivity, or when screening is more precise.

Indeed, it is noteworthy that the downward pooling equilibria can only play a significant role in the extremes, where low- and high-productivity workers are quite similar, few low-productivity workers are in the market, or screening is quite ineffective. Moreover, the separating equilibrium requires extremes in either highly similar productivities or highly effective screening.

This means that for more moderate parameterizations, the unique equilibrium generates upward pooling. Indeed, the dotted line in the U region distinguishes the full upward pooling (for $\eta$ above the line) from partial upward pooling; note that this region is larger with a greater productivity gap or less precise screening.

4.5 Efficiency

We next examine the efficiency of the various equilibria by several metrics. The first we consider is to rank equilibria according to total welfare (the objective of a utilitarian social planner). Since the firms earn zero profits, this is equivalent to the weighted sum of the workers’ present discounted expected utility.

On this metric, our results are straightforward: the social planner wants workers employed as quickly as possible, since they contribute strictly more to welfare when working ($p_h$ or $p_\ell$) than when unemployed (b), while their wages once employed are irrelevant. Thus, full downward pooling is clearly best, since all workers are immediately hired. This is followed by partial downward pooling, separating, partial upward pooling, and then full upward pooling. This ordering occurs because total welfare falls as more workers apply to the screened job and thus delay their employment. Even so, a social planner may have more nuanced objectives—perhaps including how closely workers’ wages follow their marginal productivity—for which downward pooling equilibria are less desirable.

Even by the utilitarian standard, raising total welfare may require reducing one worker’s expected utility in order to increase another’s by a larger amount. In practice, the losers in this redistribution may oppose and prevent the intervention. Thus, we consider a weaker standard of whether one equilibrium Pareto dominates another. No one should object if a social planner imposes a method of directing applications that strictly benefits some worker while harming none.

By this standard, a partial downward pooling equilibrium is always dominated by full downward pooling: both high- and low-productivity workers prefer the latter. In the former, the unscreened wage is strictly lower, and since high-productivity workers are indifferent about the screened wage, it does not increase expected utility.

Similarly, a partial upward pooling equilibrium is always dominated by a separating market, since low-productivity workers receive the same utility and high-productivity workers use the same strategy but are paid more in the latter. Of course, a separating equilibrium never exists when an upward pooling equilibrium does, since low-productivity workers would deviate to apply for the screened job if it offered $w_s = p_h$. Thus, while imposing a separating equilibrium offers a Pareto improvement, the separation cannot be enforced so long as the social planner does not know the type of individual workers.

Enforcement of full downward pooling is much easier, as the social planner could insist and verify that all workers are paid identically. Compared to a separating equilibrium, this would help low-productivity workers with a higher wage in the same amount of search time. High-productivity workers would dislike the lower wage in downward pooling, but would also conserve on search time. When (25) holds, the reduced search outweighs the lower wage. Thus, full downward pooling Pareto dominates separating whenever the former equilibrium exists; otherwise, the two cannot be Pareto ranked.⁸

4.6 Model extensions

We conclude by considering some dimensions on which our model can be generalized. First, our model depicts all workers as entering the market in period 0; however, nothing would change if successive cohorts of workers entered the market every period. We already assume that the duration of unemployment, t, is easily observable, which also immediately reveals the cohort of the worker. Thus, workers cannot pretend to have been unemployed for a shorter period (to mix with younger cohorts). Moreover, workers discount future payoffs, and the equilibrium wage always weakly declines; so no worker would want to pretend to be unemployed for a longer period (to mix with older cohorts). Rather, each cohort would be treated independently as depicted in our base model.

Second, our base model features only two types of workers, but similar behavior emerges with additional types (with lower-productivity workers having less chance of passing the screening). The analog of a separating equilibrium would have all the highest type applying to the screened job, with all others applying to the unscreened job. Upward pooling would occur if additional types attempt the screened applications; again, the pool quality and wage will fall with unemployment duration, until eventually only the best two types remain in the screened market. Downward pooling would have everyone pooling in the unscreened market (with perhaps some of the highest type submitting screened applications).

Third, we assume that each worker’s application is always evaluated by an employer, which omits a common search friction where some workers fail to match with a potential employer.⁹ Our model can readily accommodate a probability of matching that is less than one, which would have two effects. First, the value of future search is reduced, which is similar in impact to a smaller discount factor. Second, the market never fully empties of either type, since missed opportunities to match will prolong their participation. While this matching probability adds more notation, we still obtain a similar set of possible equilibria.

Fourth, we impose that the unscreened wage does not vary with the applicant’s unemployment duration, making it truly unscreened. Effectively, firms are fully committed to unconditionally hire any applicant at the posted wage $w_u$, without examining their resume, interviewing them, or determining their unemployment duration. This assumption also simplifies the dynamic problem by holding one option constant throughout. Even without this restriction, it is worth noting that the unscreened wage would either remain constant always, or increase at most twice in a row to empty the market.¹⁰ Indeed, the upward pooling equilibria of our baseline model are completely unaffected by the introduction of duration-varying unscreened jobs, since both types remain in the market indefinitely. Close analogs to the separating and downward pooling equilibria occur as well, with two potential alterations. First, after all low-productivity workers exit in period 0, firms can offer the unscreened wage $w_u(1) = p_h$ instead of $p_\ell$, allowing the remaining high-productivity workers to exit in period 1 rather than slowly exit after repeated attempts at screened jobs. Second, the exact parameters required to sustain a particular equilibrium will differ, since duration-varying unscreened wages will change the outside option of continued search.¹¹ Even so, the full downward pooling equilibrium still exists whenever partial downward pooling does (along with an upward pooling or separating equilibrium), as in the baseline model.

Finally, we restrict screening firms to only offer a job to those who pass. Alternatively, firms could post two wages: $w_s(t)$ for those who pass the test, and a consolation wage $w_c(t)$ for those who fail. The latter would reflect both the average productivity of failing candidates and their willingness to accept the offer. In the presence of consolation offers, no worker would apply to the unscreened wage—by pursuing the consolation wage, they obtain at least as much as the unscreened wage plus a chance to pass the screening in the same period. Thus, consolation offers take the place of unscreened jobs, with workers choosing between accepting a consolation offer or waiting to apply to screened job again next period. This leads to qualitatively similar equilibria as in our base model, with upward pooling if some or all low-productivity workers reject the consolation offer in an attempt to pass future screening, and downward pooling if some or all high-productivity workers accept the consolation offer.

5 Empirical implications

Our theory is able to explain a variety of well-documented empirical phenomena. First, our model sheds light on the reasons for wage dispersion in the initial realized wages of workers with the same skill in the same market. Second and related to our first point, our model predicts that unemployment can lead to wage scarring in certain situations. Third, our model can explain why some labor markets clear from top down (with the best workers finding employment first), while others clear from bottom up. Fourth, we can explain differences across markets in the initial wages offered to workers.

As we discuss the empirical relevance of our work, we will touch on each of the equilibria present in our model with the exception of the partial downward pooling equilibrium. We do not focus on this equilibrium since when it exists, the Pareto dominating full downward equilibrium also exists as well as either an upward pooling or separating equilibrium. If any coordination mechanisms existed to select a better equilibrium, the partial downward equilibrium would never result. Furthermore, the implications of the partial downward equilibrium tend to be similar to those of the full downward equilibrium.

Because empirical implications of our model can differ across the separating, downward pooling, partial upward pooling, and full upward pooling equilibria, it is helpful to summarize the parameter values of our model under which each type of equilibrium is most likely. Table 1 provides this information in a concise format. Similarly, Table 2 outlines how the empirical implications of our model vary across equilibria.

Table 1 Model parameter values by equilibrium type

Table 2 Empirical implication by equilibrium type

5.1 Wage dispersion and positive firm-worker sorting

In our model, unconditional wage dispersion exists because of heterogeneity in worker skill. High-ability workers receive higher wages in expectation than low-ability workers in all equilibria besides the full downward pooling equilibrium. In the separating equilibrium, this is the only source of wage heterogeneity. This result is unsurprising given that the separating equilibrium occurs in settings in which firms are able to measure worker skill with high precision.

In upward pooling equilibria, however, firms have less precise measures of worker skill, leading to wage heterogeneity among workers with the same skill—so-called genuine wage dispersion. Firms post different wages because the information they possess (by observing unemployment duration and screening results) indicates that workers differ in their expected marginal productivity. However, due to randomization in search strategies as well as luck in the interview process, equivalently skilled workers will end up at firms offering different wages.

This wage dispersion is empirically relevant, with economists observing that some firms pay systematically higher wages than other firms, even controlling for worker skill via worker fixed effects, as in Abowd et al. (1999). In the empirical literature on the employer size-wage premium, researchers find a wage premium associated with working in large firms or establishments (Moore 1911; Brown and Medoff 1989; Idson and Feaster 1990; Velenchik 1997), even after controlling for observed and unobserved job or worker characteristics, as in Gibson and Stillman (2009) and Troske (1999). Similarly, a more recent literature has documented persistent wage gains associated with exporting firms (Bernard and Jensen 1995, 2004; Schank et al. 2007) that cannot be explained by observable differences, such as plant heterogeneity, region and industry factors, as well as unobserved worker effects.

Consistent with the predictions of the full upward pooling equilibrium, recent empirical literature finds positive sorting between firms and workers (e.g., Abowd et al. 2014). By this we mean that high-ability workers, on average, go to firms that pay high wages. This sorting occurs not because of any complementarity between the ability of the worker and production process of the firm. Rather it occurs because firms that engage in screening have higher-productivity workers on average and high-ability workers are more likely to pass the screening. Empirically, researchers have found that large firms and exporting firms offer a wage premium to identically productive workers and hire better workers on average. Our model can thus explain the simultaneous occurrences of wage dispersion and positive firm-worker sorting.

5.2 Wage scarring

In the full upward pooling equilibrium, the wages of both high- and low-ability workers initially decline with unemployment duration, since the expected productivity of job applicants falls as the best workers find jobs first. Thus, the same phenomenon that implies wage dispersion also implies wage scarring. By this, we mean that time in unemployment has a causal negative effect on the eventual wage a given worker receives. In other equilibria, wage scarring does not occur because the quality of the pool of applicants to the screened and unscreened jobs remains constant.¹²

The full upward pooling equilibrium is consistent with the findings of Kroft et al. (2012), who perform an experimental audit study to show that employer screening plays an important role in generating duration dependence. Employers use the unemployment spell length as a signal of unobserved worker productivity, and are less likely to use it in weak labor markets when this signal is less informative. Similarly, Eriksson and Rooth (2014) find employers attach a negative value to contemporary unemployment spells lasting at least nine months, suggesting that employers use this as a signal of a worker’s productivity. In observational studies, Arranz et al. (2005), Gregory and Jukes (2001), and Belzil (1995) all provide evidence that realized wages decline with unemployment duration. Overall, the empirical evidence is consistent with wage scarring, suggesting that many labor markets may exhibit conditions conducive for the full upward pooling equilibrium.

5.3 Market clearing

Our model makes predictions regarding whether high- or low-ability workers find employment first. Under the full downward pooling equilibrium, workers of both high and low ability are immediately hired. In contrast, under the separating equilibrium, low-ability workers find employment first since they apply to unscreened jobs. High-ability workers take longer to find employment since they only apply to screened jobs and may be rejected several times during their search. Hence, the market clears from bottom up.

In the full upward pooling equilibrium, high-ability workers are disproportionately likely to find employment in the early periods at the highest paying jobs. Low-productivity workers also apply to screened jobs, but are hired less often. Consequently, the market clears from top down. In the partial upward pooling equilibrium, workers of either productivity exit at the same rate in all periods $t > 0$; however, hiring in period $t = 0$ will disproportionately favor either high or low types, depending on which are more abundant in the initial worker population.

Our model thus relates the order of market clearing to primitive market parameters, such as the precision of signaling and the percentage of high-type workers in the pool of job applicants. Unfortunately, to the best of our knowledge, there have not been any empirical studies on the relationship between worker productivity and unemployment duration, probably due to the difficulty in measuring the former.

5.4 Pool quality externalities

When firms’ screening technology is sufficiently informative, the wage a worker can expect to receive does not depend on the distribution of ability in her market. Because only high-ability workers have a strong chance of finding a high-wage job, workers self-select to the jobs which match their capabilities. This is what we observe in the separating equilibrium.

When the screening technology is less precise, however, the distribution of ability has important effects on the expected earnings of both high- and low-ability workers. Wages not only depend on the worker’s own type but also on the fraction of high-ability applicants to the screened job (in upward pooling equilibria) or the unscreened job (in downward pooling equilibria). Low-productivity workers always benefit from more high-productivity colleagues applying to the same job.

Empirical support for applicant pool externalities is provided by results from the literature on the inter-industry wage differences, where workers in industries with a high proportion of talents earn an wage premium. Dickens and Katz (1987b) and Krueger and Summers (1988) examine individual-level data for the USA and find large and persistent inter-industry wage differentials for seemingly identical workers on similar jobs, even after controlling for unobserved worker heterogeneities using the fixed effects approach. Dickens and Katz (1987a) examine industry characteristics and show that workers in high-wage industries also have higher average education levels, which is consistent with externalities arising from highly educated peers in the industry.

Our model also provides an alternative interpretation of the empirical results from the human capital spillovers literature. Moretti (2004a) and Rosenthal and Strange (2008) find that wages for workers rise with the average education level of the labor market, even controlling for the worker’s own education. Moretti (2004b) find that productivity of plants in cities that experience large increases in the share of college graduates rises more than the productivity of similar plants in cities that experience small increases in the share of college graduates. In addition, these productivity gains are offset by increased labor costs, consistent with the prediction that the higher average productivities are exactly matched by higher wages in our model. Our model indicates that this need not be caused by direct spillovers due to worker interaction (since actual productivity is constant), but could arise from an informational externality where less productive workers are compensated more generously because of the difficulty of distinguishing them from more numerous high-productivity workers.

6 Policy interventions

In this section, we evaluate the model behavior under two common labor market policies, both of which can shut down the unscreened labor market. First, low-productivity workers may prefer unemployment to accepting a job that pays their marginal product: $b > p_\ell$. This could arise through generous unemployment benefits, disability payments, or early retirement. Second, a binding minimum wage may forbid employers from paying workers $p_\ell$, even if it is their marginal product. Either policy leads to similar results, which we report below. In addition, this environment brings our model closer to that of Lockwood (1991), only still allowing for wage offers to endogenously vary with the unemployment spell.

6.1 Generous unemployment benefits

First, we examine the case where $p_h> b > p_\ell$. Clearly, no worker of either type is willing to accept an unscreened job that pays less than the unemployment benefit. However, if one considers resignation to permanent unemployment benefits as the alternative to repeated attempts at applying to the screened job, then the possible equilibria are analogous to those in Sect. 4.

We begin by noting that a separating equilibrium, in which all high-productivity workers apply to the screened job while all low-productivity workers resign their search, can never occur. If it did, the offered wage would be $w_s(t) = p_h$, so a low-productivity worker would be choosing between $\frac{b}{1 - \beta }$ and $U_\ell = b + \beta \left( (1 - \gamma ) \frac{p_h}{1 - \beta } + \gamma U_\ell \right)$. Solving for search utility $U_\ell$ and comparing this would indicate that resigning is strictly preferred only if:

$$\begin{aligned} \frac{b}{1 - \beta }> \frac{p_h}{1 - \beta } + \frac{b - p_h}{1 - \beta \gamma } \quad \Longrightarrow \quad \beta (1 - \gamma ) (b - p_h) > 0. \end{aligned}$$

(27)

This is only true if unemployment benefits are so generous that even the high-productivity workers who are paid their marginal product also want to resign, which is ruled out by assumption.

Next, consider the upward pooling equilibrium. As before, some or all of the low-productivity workers apply for the screened job each period. However, those who do not resign and exit the market permanently. This results in the following equilibrium solution:

$$\begin{aligned} w_s(t)\equiv & {} {\left\{ \begin{array}{ll} \frac{\eta (1 - \gamma )^{t}\gamma p_h + (1 - \eta ) \gamma ^{t}(1-\gamma )p_\ell }{\eta (1 - \gamma )^{t}\gamma + (1 - \eta ) \gamma ^{t} (1-\gamma )} &{}\quad \text { for }\;t < T \\ b &{}\quad \text { for }\;t \ge T \\ \end{array}\right. }\end{aligned}$$

(28)

$$\begin{aligned} \sigma _h(t)= & {} 1 \end{aligned}$$

(29)

$$\begin{aligned} \sigma _\ell (t)= & {} {\left\{ \begin{array}{ll} 1 &{}\quad \text { for }\;t < T \\ \left( \frac{1 - \gamma }{\gamma } \right) ^T Q_b &{}\quad \text { for }\;t = T \\ \frac{1 - \gamma }{\gamma } &{}\quad \text { for }\;t > T \\ \end{array}\right. }\end{aligned}$$

(30)

$$\begin{aligned} f_h(t)= & {} \eta (1 - \gamma )^t \qquad \qquad \text { for all }\;t \end{aligned}$$

(31)

$$\begin{aligned} f_\ell (t)= & {} {\left\{ \begin{array}{ll} (1-\eta ) \gamma ^t &{}\quad \text { for }\;t < T \\ (1-\eta ) Q_b \gamma (1 - \gamma )^{t-T} &{}\quad \text { for }\;t \ge T \end{array}\right. }\end{aligned}$$

(32)

$$\begin{aligned} Q_b\equiv & {} \frac{\eta }{1-\eta } \cdot \frac{\gamma (p_h-b)}{ (1 - \gamma ) (b - p_\ell )}\end{aligned}$$

(33)

$$\begin{aligned} T\equiv & {} \max \left\{ 0, \left\lceil \frac{\ln Q_b }{\ln (\gamma /(1 - \gamma ) )} \right\rceil \right\} . \end{aligned}$$

(34)

As before, it is possible that initially all workers fully pool, applying for the screened job. This occurs so long as $Q_b > 1$. However, once the proportion of high-productivity workers is drawn down, partial pooling sets in. If the proportion was low enough that $Q_b \le 1$, partial upward pooling occurs throughout. During that phase, low-productivity workers must be indifferent, which can only occur if $p_h = b$ (derived from Eq. 27 holding with equality). This makes the high-productivity workers indifferent as well. However, the equilibrium assigns all high-productivity workers to search, while mixing the low-productivity workers just enough to maintain the necessary wage that makes them indifferent. Note that an upward pooling equilibria will always exist, since necessarily $Q_b > 0$.

The downward pooling equilibria are unaltered from Sect. 4, with some or all high-productivity workers joining all the unproductive workers in applying to the unscreened job. However, full downward pooling additionally requires $\eta p_h + (1 - \eta ) p_\ell \ge b$, which would fail if unemployment benefits exceed the average productivity in the market.

In light of these results, consider the policy implications of increasing the generosity of unemployment benefits. Suppose that the initial policy satisfied $p_\ell > b$, and a separating equilibrium occurred. Holding the other parameters fixed at any value, as benefits increase, the equilibrium first changes to a partial upward pooling equilibrium, then eventually to a full upward pooling equilibrium. Then, as b becomes larger than $p_\ell$, the full upward pooling equilibrium continues, but with a large enough increase in b, the partial upward pooling equilibrium takes over again.¹³

Fig. 3

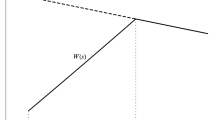
Change in wages as unemployment benefits rise. The solid line depicts the highest screened wage, while the dashed line indicates the lowest screened wage. The unscreened wage appears as the dotted line. Parameters besides b are set at $p_h = 1$, $p_\ell = 0.75$, $\gamma = 0.8$, $\eta = 0.5$ and $\beta = 0.9$

In terms of the effect on wages (illustrated in a numerical example in Fig. 3), note that the unscreened wage is constant at $p_\ell$ right up until $b > p_\ell$, when it ceases to be offered. The screened wage would start at $p_h$ for all t in the separating equilibrium. When partial upward pooling emerges, the screened wage begins to fall until full upward pooling emerges. At that point, the wages of the earliest hires (w(0)) stay constant, while wages continue to fall for all those hired later. This continues until $b = p_\ell$, where the unscreened wage coincides with the lowest screened wage. With further increases in b, later wages begin to rise. Once partial upward pooling re-emerges, the (only) offered wage will continue to rise.

Thus, the generosity of unemployment benefits can have a profound effect on sorting and wage dispersion in the market. Increasing benefits will encourage screened applications by low-productivity workers; by diluting the applicant pool, greater generosity will decrease screened wages and lengthen the duration of full upward pooling. Eventually, further benefit generosity will shut down the unscreened market and decrease wage dispersion, but this also leads to increasing populations of permanently unemployed workers.

Increasing generosity also reduces efficiency in the labor market, encouraging low-productivity workers to delay employment and creating greater mismatch between the wages and productivity of individual workers. Moreover, if unemployment benefits must be financed through taxes, these transfers do not contribute to welfare and can prevent some workers from ever becoming productive.

The primary testable implication of our model with regard to unemployment insurance is that more generous unemployment benefits will tend to prolong search behavior and lead to higher unemployment. The empirical literature is largely consistent with this theory, including recent work by Rothstein (2011), Farber and Valleta (2013) and Farber et al. (2015). To our knowledge, however, researchers have not yet examined how increasing the generosity of unemployment insurance differentially affects the wages of high- and low-ability job applicants.

6.2 Binding minimum wage

Next, consider an environment in which firms are required to pay at least $m > p_\ell$ to any employee. We also assume that $m > b$; if not, the solution precisely follows the preceding analysis on unemployment insurance.

The minimum wage disrupts the upward pooling or separating equilibria precisely because the intended wage $w_u = p_\ell$ is no longer legal, while the legal wage is unprofitable if it only attracts low-productivity workers. This effectively shuts down the market for unscreened jobs, leaving workers to decide between applying for screened jobs or resigning their search in favor of unemployment benefits. However, since the workers still receive the unemployment benefit each period they are unsuccessful at applying for the screened job, it is a dominant strategy for both types to apply to screened job as long as it is offered.

This eliminates the possibility of a separating or partial upward pooling equilibrium, where some or all of the low-productivity workers give up on applying to the screened job. However, a variant of a full upward pooling equilibrium exists. Here, all workers apply to the screened job for as long as it is offered—but it will not be offered to workers with a long enough employment spell, which occurs when the expected marginal product of applicants falls below the minimum wage. This equilibrium takes the following form:

$$\begin{aligned} w_s(t)\equiv & {} {\left\{ \begin{array}{ll} \frac{\eta (1 - \gamma )^{t}\gamma p_h + (1 - \eta ) \gamma ^{t}(1-\gamma ) p_\ell }{\eta (1 - \gamma )^{t}\gamma + (1 - \eta ) \gamma ^{t}(1-\gamma ) } &{}\quad \text { for }\; t < T \\ \emptyset &{}\quad \text { for }\; t \ge T \\ \end{array}\right. }\end{aligned}$$

(35)

$$\begin{aligned} \sigma _h(t)= & {} \sigma _\ell (t) = {\left\{ \begin{array}{ll} 1 &{}\quad \text { for }\; t < T \\ 0 &{}\quad \text { for }\; t \ge T \\ \end{array}\right. }\end{aligned}$$

(36)

$$\begin{aligned} f_h(t)= & {} {\left\{ \begin{array}{ll} \eta (1 - \gamma )^t &{}\quad \text { for }\; t < T \\ 0 &{}\quad \text { for }\; t \ge T \\ \end{array}\right. } \end{aligned}$$

(37)

$$\begin{aligned} f_\ell (t)= & {} {\left\{ \begin{array}{ll} \eta \gamma ^t &{}\quad \text { for } t < T \\ 0 &{}\quad \text { for } t \ge T \\ \end{array}\right. } \end{aligned}$$

(38)

where $T \equiv \left\lceil \frac{\ln Q_m }{\ln (\gamma /(1 - \gamma ))} \right\rceil$ and $Q_m \equiv \frac{\eta }{1 - \eta } \cdot \frac{\gamma (p_h - m)}{(1 - \gamma )(m - p_\ell )}$. If $Q_m < 1$, then $T < 0$, meaning no jobs are offered and all workers live on unemployment insurance. Otherwise, all workers continually reapply for the screened job as long as they are offered, with wages falling (until hitting the minimum wage) for those who are hired later in their unemployment spell.

The unscreened market can be active in a downward pooling equilibria, which exist (unchanged from Sect. 4.3) so long as the equilibrium unscreened wage is legal. In full downward pooling, the average productivity must exceed the minimum wage ($\eta p_h + (1 - \eta ) p_\ell \ge m$). In partial downward pooling, the wage that makes high-productivity workers indifferent must exceed the minimum wage $\left( b + \frac{(p_h - b) \gamma }{1 - \beta (1 - \gamma )} \ge m\right)$. In either case, the conditions in Proposition 3 must also hold.

As we consider comparative statics with respect to m, the curious outcome is that a minimum wage can drastically alter the equilibrium behavior as it becomes binding. When $m \le p_\ell$ it has no effect in any of the three equilibria from Sect. 4. But as soon as it crosses $m > p_\ell$ by even a small margin, the separating and partial upward pooling equilibria cease to exist, and the full upward pooling equilibria discretely changes, loosing the unscreened market and replacing it with a lower stream of unemployment benefits. Indeed, if the market were in a separating or partial upward pooling equilibrium before the minimum wage increases, it is not obvious whether a full upward pooling or a downward pooling equilibrium is more likely to emerge, since neither is close to the original equilibria. Note that for a sufficiently high minimum wage, the downward pooling equilibria eventually cease to exist, leaving only the full upward pooling equilibrium.

If the full upward pooling equilibrium initially emerges, note that $Q_m \rightarrow \infty$ when $m \rightarrow p_\ell$. Thus, for a low minimum wage, the screened market would continue nearly indefinitely (with wages approaching m). If the minimum wage increases further, $Q_m$ and T will fall, causing the screened market to shut down earlier. This unambiguously harms all workers in terms of ex-ante utility. Anyone who gets a job will be paid the same as they would have under a lower m, while those who might have passed the test later in their search will no longer be given the opportunity.

A large empirical literature examines the impacts of the minimum wage on employment levels. Counter to our and many other models, the aggregate employment effects of the minimum wage tend to be small, at least in the USA (see, for example, Dube et al. 2010). Nevertheless, it is not clear whether the minimum wage has been increased above the productivities of low-type workers in the market. DiNardo et al. (1996) present evidence that the decline in the real value of the minimum wage between 1979 and 1988 led to substantial increases in the dispersion of wages, particularly among women. This finding is consistent with our model.

7 Conclusion

In conclusion, we develop a model of job search with asymmetric information that sheds novel insights into a variety of labor market phenomena. In particular, our model provides insights into the settings in which we are likely to observe wage dispersion, wage scarring, job market clearing, and applicant pool externalities. Furthermore, our model sheds insights into how unemployment benefits and binding minimum wages affect not only patterns of optimal search but also upon the distribution of wages for both high- and low-skill workers. As a consequence, our paper provides a single plausible and parsimonious framework to understand labor market patterns that earlier had required several models to explain.

Our findings suggest fruitful avenues of future research for empirical researchers. For example, our model suggests that a sufficiently large increase in the minimum wage would likely increase job search for the lowest skilled applicants. Furthermore, it could also adversely affect the wages of high-skilled applicants. Neither of these and a variety of other implications have yet been tested.

On the theoretical front, researchers could generalize our model in a variety of ways. For example, one could allow workers to have imperfect information regarding their own skill. Consequently, workers as well as firms could obtain more information about their type during job search. One could also make it costly for firms to post jobs or introduce other frictions to the matching process between firms and workers. It is likely that such extensions might preclude analytical solutions but could likely be solved numerically.

A Proofs

1.1 Proof of Lemma 1

Each advertisement must earn zero profits in expectation. Equation 7 is obtained by setting $\Pi _s(t) = 0$ and solving for $w_s(t)$ in Eq. 5; likewise, Eq. 8 is obtained by setting $\Pi _u(t) = 0$ and solving for $w_u$ in Eq. 6. Since these are each a weighted average of $p_h$ and $p_\ell$, both of which are strictly greater than b, we know that $w_j(t) \ge p_\ell > b$. Thus, the benefit from search, $U_i(t)$, always exceeds the benefit from perpetual delay, $\frac{b}{1 - \beta }$.$\square$

1.2 Proof of Lemma 2

We examine four possible strategy profiles in period t, depending on which job each type of worker applies to.

First, suppose that workers with an unemployment duration t and both productivities weakly prefer applying to the unscreened job. In that case, $U_h(t) = U_\ell (t) = \frac{w_u}{1 - \beta }$ without regard to the next period utility.

Next, suppose that high-productivity workers strictly prefer the screened job, while low-productivity workers weakly prefer the unscreened job. Then,

$$\begin{aligned} U_h(t) = b + \beta \left( \gamma \frac{w_s(t)}{1 - \beta } + (1 - \gamma ) U_h(t+1) \right) > b + \beta \frac{w_u}{1 - \beta } = U_\ell (t), \end{aligned}$$

where the inequality comes from the strict preferences of high-productivity workers, while the latter equality comes from the fact that the low-productivity workers prefer the unscreened job. Thus, $U_h(t) > U_\ell (t)$.

Next, suppose that low-productivity workers strictly prefer the screened job, while high-productivity workers strictly prefer the unscreened job. This requires that $\sigma _\ell (t) = 1$ and $\sigma _h(t) = 0$. Since no high-productivity workers apply to the screened job, and in accordance with Lemma 1, $w_s(t) = p_\ell$. The unscreened wage, on the other hand, has some high-productivity applicants (though other periods may also include low-productivity workers); thus, $w_u > p_\ell$. Moreover, since $\sigma _h(t) = 0$, no high-productivity workers are unemployed in the subsequent period: $f_h(q) = 0$ for all $q > t$. Thus, $w_s(q) = p_\ell$ for all $q > t$.

Since a low-productivity worker will face the same wages from that point on, his problem becomes stationary, so that $U_\ell (t) = U_\ell (q)$ for all $q \ge t$, and would employ the same strictly preferred strategy $\sigma _\ell (q) = 1$ in each subsequent period. This produces utility:

$$\begin{aligned} U_\ell (q) = b + \beta \left( \frac{(1- \gamma )p_\ell }{1 - \beta } + \gamma U_\ell (q)\right) \quad \Longrightarrow \quad U_\ell (q) = \frac{(1 - \beta ) b + \beta (1- \gamma ) p_\ell }{(1 - \beta )(1 - \beta \gamma )}. \end{aligned}$$

(39)

But applying to the unscreened advertisement in period t would provide $b + \frac{w_u}{1 - \beta }$. Since $b < p_\ell \le w_u$, we find:

$$\begin{aligned} {\begin{matrix} b + \frac{w_u}{1 - \beta } &{}= \frac{(1 - \beta ) b - \beta \gamma (1 - \beta ) b+ \beta (1 - \beta \gamma ) w_u}{(1 - \beta )(1 - \beta \gamma )} \\ &{}> \frac{(1 - \beta ) b - \beta \gamma (1 - \beta ) p_\ell + \beta (1 - \beta \gamma ) p_\ell }{(1 - \beta )(1 - \beta \gamma )} = \frac{(1 - \beta ) b + \beta (1- \gamma ) p_\ell }{(1 - \beta )(1 - \beta \gamma )}. \end{matrix}} \end{aligned}$$

(40)

The unscreened wage provides strictly more utility than the screened wage, contradicting $\sigma _\ell (q) = 1$. Thus, it is not possible for this case to occur.

Finally, consider the case where both types of workers prefer the screened job, with strict preference for low-productivity workers. First, assume that $U_h(t+1) \ge U_\ell (t +1)$. This implies:

$$\begin{aligned} b + \beta \left( (1 - \gamma ) \frac{w_s(t)}{1 - \beta } + \gamma U_h(t+1) \right) \ge b + \beta \left( (1 - \gamma ) \frac{w_s(t)}{1 - \beta } + \gamma U_\ell (t+1) \right) . \end{aligned}$$

(41)

Because the workers do not abstain from job search, we know that $\frac{w_s(t)}{1 - \beta } \ge U_h(t+1)$. Moreover, $\gamma > 1/2$, so

$$\begin{aligned} \beta (2 \gamma - 1) \left( \frac{w_s(t)}{1 - \beta } - U_h(t+1) \right) \ge 0. \end{aligned}$$

(42)

Thus, by adding the left-hand side of Eq. 42 to the left-hand side of Eq. 41, we obtain

$$\begin{aligned} b + \beta \left( \gamma \frac{w_s(t)}{1 - \beta } + (1 - \gamma ) U_h(t+1)\right) \ge b + \beta \left( (1 - \gamma ) \frac{w_s(t)}{1 - \beta } + \gamma U_\ell (t+1) \right) . \end{aligned}$$

By definition, this is $U_h(t) \ge U_\ell (t)$. Thus, if $U_h(t+1) \ge U_\ell (t +1)$, then $U_h(t) \ge U_\ell (t)$.

With that established, recall that we have already shown that $U_h(q) \ge U_\ell (q)$ if low-productivity workers weakly prefer the unscreened job in period q. Thus, if this occurs at any period $q > t$, we then know that $U_h(t) \ge U_\ell (t)$ in the prior periods when both types prefer the screened job.

Suppose instead that in every period $q \ge t$, low-productivity workers strictly prefer the screened job and high-productivity workers weakly prefer the screened job. This requires that $\sigma _\ell (q) = 1$. We assume that $\sigma _h(q) > 0$ for all q; otherwise, the same contradiction occurs as when high-productivity workers strictly prefer the unscreened job. Given these strategies, $f_\ell (q) = f_\ell (t) \gamma ^{q - t}$, while $f_h(q) = f_h(t) (1- \gamma )^{q - t} \prod _{j=t}^q \sigma _h(j)$. Let $\theta = \frac{f_h(t)}{f_\ell (t)}$. Thus, substituting these into the expression in Lemma 1 and rearranging, the screened wage for all $q \ge t$ is:

$$\begin{aligned} w(q) = \frac{p_\ell + p_h \theta \left( \frac{1 - \gamma }{\gamma } \right) ^{q - t - 1} \prod _{j=t}^q \sigma _h(j)}{1 + \theta \left( \frac{1 - \gamma }{\gamma } \right) ^{q - t - 1} \prod _{j=t}^q \sigma _h(j)}. \end{aligned}$$

Denote $\mu _q \equiv \left( \frac{1 - \gamma }{\gamma } \right) ^{q - t - 1} \prod _{j=t}^q \sigma _h(j)$. Since $\gamma \in (1/2, 1]$, then $\frac{1 - \gamma }{\gamma } \in [0, 1)$. Moreover, $\sigma _h(j) \in (0,1]$. Thus, $\lim _{q \rightarrow \infty } \mu _q = 0$, and therefore $\lim _{q \rightarrow \infty } w(q) = p_\ell$.

Indeed, the screened wage monotonically falls: $w(q) > w(q+1)$. This is because $\mu _q > \mu _{q+1}$, so:

$$\begin{aligned}&p_h> p_\ell \quad \Longleftrightarrow \quad p_h ( \mu _q - \mu _{q+1} )> p_\ell ( \mu _q -\mu _{q+1} )\\&\quad \Longleftrightarrow \quad p_\ell + p_h \mu _q - p_h \mu _{q+1} + p_h \mu _q \mu _{q+1}> p_\ell + p_\ell \mu _q - p_\ell \mu _{q+1} + p_h \mu _q \mu _{q+1}\\&\quad \Longleftrightarrow \quad (1 -\mu _{q+1}) ( p_\ell + p_h \mu _q)> (1 -\mu _{q}) ( p_\ell + p_h \mu _{q+1})\\&\quad \Longleftrightarrow \quad \frac{p_\ell + p_h \mu _q}{1 -\mu _{q}}> \frac{ p_\ell + p_h \mu _{q+1}}{1 -\mu _{q+1}} \Longleftrightarrow \quad w(q) > w(q+1). \end{aligned}$$

Since $\sigma _\ell (q) = 1$ for all $q \ge t$, we also note that the utility of low-productivity workers approaches the stationary solution where $w_s = p_\ell$ depicted in Eq. 39; that is, $\lim _{q \rightarrow \infty } U_\ell (q) = \frac{(1-\beta ) b + (1 - \gamma ) p_\ell }{(1-\beta )(1 - \beta \gamma )}$. This means that for q sufficiently large, $U_\ell (q)$ is arbitrarily close to the right-hand side of Eq. 40. Yet applying to the unscreened job would provide utility $b + \frac{w_u}{1 - \beta }$, where $w_u \ge p_\ell$. By the same comparison in Eq. 40, applying to the unscreened job is strictly better at such a q, contradicting $\sigma _\ell (q) = 1$. Thus, it is not possible in equilibrium for both types to prefer the screened job indefinitely.

Thus, we conclude that $U_h(t) \ge U_\ell (t)$ for all t.$\square$

1.3 Proof of Lemma 3

Suppose $\sigma _h(t) < 1$ for high-productivity workers and $\sigma _\ell (t) > 0$ for low-productivity workers with an unemployment duration of t.

The high-productivity worker must be indifferent or strictly prefer the unscreened wage, so the following must hold:

$$\begin{aligned} \gamma w_s(t) + (1 - \beta )(1- \gamma ) U_h(t+1) \le w_u. \end{aligned}$$

The low-productivity worker must be indifferent or strictly prefer the screened wage, yielding:

$$\begin{aligned} (1- \gamma ) w_s(t) + (1 - \beta ) \gamma U_\ell (t+1) \ge w_u. \end{aligned}$$

But combining these, this implies that

$$\begin{aligned} \gamma w_s(t) + (1 - \beta )(1- \gamma ) U_h(t+1) \le (1- \gamma ) w_s(t) + (1 - \beta ) \gamma U_\ell (t+1). \end{aligned}$$

which, with rearrangement becomes:

$$\begin{aligned} \left( w_s(t) - (1 - \beta ) U_\ell (t+1) \right) \le \frac{1- \gamma }{\gamma } \left( w_s(t) - (1 - \beta ) U_h(t+1) \right) . \end{aligned}$$

Since $\gamma \in (1/2,0)$, we note that $\frac{1- \gamma }{\gamma } \in (0,1)$, so:

$$\begin{aligned} w_s(t) - (1 - \beta ) U_\ell (t+1) < w_s(t) - (1 - \beta ) U_h(t+1). \end{aligned}$$

Thus, $U_h(t+1) < U_\ell (t+1)$, which contradicts Lemma 2.$\square$

1.4 Proof of Proposition 1

First, note that under the proposed equilibrium, both firms earn zero profit (paying the marginal product to hired workers) as required in Lemma 1, and a positive measure of workers apply to both types of jobs. Moreover, the solutions to $f_h(t)$ and $f_\ell (t)$ follow directly from the proposed $\sigma _h(t)$ and $\sigma _\ell (t)$. All that remains to be shown is that neither type of worker will want to deviate from the proposed search strategy.

For a low-productivity worker, his equilibrium expected utility is: $U_\ell = b + \beta \frac{p_\ell }{1 - \beta }$. If he were to apply to the screened job, his expected utility would be: $b + \beta \left( (1 - \gamma ) \frac{p_h}{1 - \beta } + \gamma \left( b + \frac{\beta p_\ell }{1 - \beta } \right) \right)$. The comparison of these two show that the low-productivity worker will chose the unscreened job if and only if:

$$\begin{aligned} (1 - \beta \gamma ) p_\ell \ge (1 - \gamma ) p_h + (1 - \beta ) \gamma b , \end{aligned}$$

which, with rearrangement, is equivalent to the second condition in Eq. 15.

For a high-productivity worker, his equilibrium expected utility is: $U_h(t) = \frac{(1 - \beta ) b + \beta \gamma p_h}{(1 - \beta )(1 - \beta + \beta \gamma )}$. Applying to the unscreened job would provide $b + \beta \frac{p_\ell }{1 - \beta }$. Comparing these, we find that the worker will choose the screened job if and only if:

$$\begin{aligned} (1 - \beta )(1 - \gamma ) b + \gamma p_h \ge (1 - \beta + \beta \gamma ) p_\ell , \end{aligned}$$

which, with rearrangement, is equivalent to the first condition in Eq. 15.$\square$

1.5 Proof of Proposition 2

First, consider the partial pooling phase for $t > T$. The proposed equilibrium recommends that low-productivity workers use a mixed strategy, which requires indifference across the two job advertisements. From the unscreened job, his expected utility is: $U_\ell = b + \beta \frac{p_\ell }{1 - \beta }$. Applying to the screened job, his expected utility would be: $b + \beta \left( (1 - \gamma ) \frac{w_s(t)}{1 - \beta } + \gamma \left( b + \frac{\beta p_\ell }{1 - \beta } \right) \right)$. By setting these equal and solving for $w_s(t)$, we obtain the equilibrium wage for $t \ge T$ in Eq. 16. By Lemma 3, if low workers are indifferent then high workers strictly prefer the screened job.

At the same time, this wage must earn zero profits as required in Lemma 1. The marginal product of the average hired worker is: $( \gamma f_h(t) p_h + (1 - \gamma ) \sigma _\ell (t) f_\ell (t) p_\ell ) / ( \gamma f_h(t) + (1 - \gamma ) \sigma _\ell (t) f_\ell (t) )$. By equating this productivity to the preceding wage and solving for $\sigma _\ell (t)$, we obtain:

$$\begin{aligned} \sigma _\ell (t) = \frac{ ((1 - \gamma ) p_h + (1 - \beta ) \gamma b - (1 - \beta \gamma ) p_\ell ) f_h(t)}{(1 - \beta ) (1 - \gamma ) (p_\ell - b) f_\ell (t)}. \end{aligned}$$

(43)

The solution to $f_h(t)$ is straightforward since $\sigma _h(t) = 1$. For $t > T$, the solution to $f_\ell (t)$ is found by substituting for $f_h(t)$ and $\sigma _\ell (t)$ into the law of motion in Eq. 4. This in turn can be substituted back into Eq. 43 to obtain the equilibrium $\sigma _\ell (t) = (1 - \gamma ) / \gamma$ for $t>T$. Note that $\sigma _\ell (t) \in [0,1)$ because $\gamma > \frac{1}{2}$.

In period T, the first two paragraphs of the proof still apply: indifference pins down the screened wage and therefore pins down the fraction of low-productivity workers applying for the screened job, $\sigma _\ell (T)$. However, since $\sigma _\ell (t) = 1$ for all $t < T$, the population $f_\ell (t) = (1 - \eta ) \gamma ^t$ for all $t \le T$. When $f_\ell (T)$ is substituted into Eq. 43, this yields $\sigma _\ell (T) = \left( \frac{1 - \gamma }{\gamma } \right) ^T Q$. Note that if $Q < 0$, this is not a mixed strategy and the equilibrium cannot occur for any T. Also, the definition of T ensures that T is the lowest positive integer for which $\left( \frac{1 - \gamma }{\gamma } \right) ^T Q \le 1$, so $\sigma _\ell (T) \le 1$.

Now, we turn to the full pooling phase (which occurs if $T > 0$). For $t < T$, the population $f_h(t)$ and $f_\ell (t)$ follow directly from $\sigma _h(t) = \sigma _\ell (t) = 1$, and the wage is determined by the zero profit condition. What remains is to verify that low-productivity workers will strictly prefer to apply to the screened jobs in this range; from there, it follows from Lemma 3 that the high-productivity workers also prefer applying to the screened job.

Consider the choice of a low-productivity worker at period $T - 1$. From the unscreened job, his expected utility is: $U_\ell = b + \beta \frac{p_\ell }{1 - \beta }$. Applying to the screened job, his expected utility would be: $b + \beta \left( (1 - \gamma ) \frac{w(T-1)}{1 - \beta } + \gamma \left( b + \frac{\beta p_\ell }{1 - \beta } \right) \right)$. In comparing these, the screened job is strictly preferred if:

$$\begin{aligned} (1 - \gamma ) \frac{\eta (1 - \gamma )^{T-2} p_h + (1 - \eta ) \gamma ^{T-2} p_\ell }{\eta (1 - \gamma )^{T-2} + (1 - \eta ) \gamma ^{T-2} } + \gamma \left( (1 - \beta ) b + \beta p_\ell \right) > p_\ell \end{aligned}$$

This rearranges to become $1 < \left( \frac{1 - \gamma }{\gamma } \right) ^{T-1} Q$. Since T is chosen as the smallest integer for which this condition does not hold, then for $T - 1$, it must hold.

For each preceding period, $t < T - 1$, $U_\ell (t) > U_\ell (T - 1)$ because there is the same chance of passing the screening in period t, but there is also the option value of the $T - t - 2$ periods thereafter. Thus, the relative benefit of applying to the screened job is only strengthened in preceding periods.

Note that a firm cannot profitably deviate from this equilibrium: any posting (screened or unscreened) offering higher wages than an existing option will earn negative profits, and any posting offering lower wages will attract no workers.$\square$

1.6 Proof of Proposition 3

In either downward pooling equilibrium, the wages and population of workers follow mechanically from the proposed strategy $\sigma _\ell (t)$ and $\sigma _h(t)$.

First, consider a full downward pooling equilibrium, with $S = 0$. We only need to verify that all workers prefer applying to the unscreened job. For instance, if a high-productivity worker applies to the screened job in period 0 but returns to the unscreened job if he fails the interview, he obtains:

$$\begin{aligned} \frac{\gamma p_h}{1-\beta }+(1-\gamma )\left( b+\beta \frac{ w_u}{1-\beta }\right) \le \frac{w_u}{1-\beta }. \end{aligned}$$

(44)

After substituting for $w_u = \eta p_h + (1- \eta ) p_\ell$ and rearranging, this condition becomes (25), or equivalently, $\varDelta \ge 0$. If this holds, Lemma 3 ensures that low-productivity workers also prefer applying to the unscreened job. Note that if $w_s = p_h$ is not sufficient to entice the high-productivity workers, then any lower wage would also fail to do so (e.g., if the firms lowered the wage seeking positive profits, or if the low-productivity workers were also enticed to apply).

Next, consider a partial downward pooling equilibrium, with $S = \varDelta$. To obtain zero profits as required by Lemma 1, the unscreened wage must equal $w_u = \frac{\eta (1 - S) p_h + (1- \eta ) p_\ell }{\eta (1 - S) + (1- \eta )}$. For the high-productivity workers to be indifferent between the two job applications, the utility from always applying to the screened job must equal the utility from applying to the unscreened job:

$$\begin{aligned} \frac{(1 - \beta ) b + \beta \gamma p_h}{(1 - \beta )(1 - \beta + \beta \gamma )} = b + \frac{\beta w_u}{1-\beta }. \end{aligned}$$

(45)

We then insert $w_u$ into this equation and solve for S, whose unique solution is $\varDelta$. Of course, to be used as a mixed strategy, we must have $\varDelta \in [0,1]$. In all future periods, the high-productivity workers face the same indifference, so they can fully apply to the screened job. Again by Lemma 3, since high-productivity workers are indifferent between the two jobs, low-productivity workers will prefer the unscreened job.

Note that a firm cannot profitably deviate from this equilibrium: any posting (screened or unscreened) offering higher wages than an existing option will earn negative profits, and any posting offering lower wages will attract no workers.$\square$

1.7 Proof of Corollary 1

First, we establish that the separating equilibrium and the partial and full upward pooling equilibria each require $\varDelta \le 1$, which is equivalent to the first condition in (15). This is explicitly stated for the separating equilibrium in Proposition 1, but it is also needed for the upward pooling equilibria to exist. If it were violated, this condition rearranges to $(1 - \beta )(p_\ell - b) > \frac{\gamma }{1 - \gamma } (p_h - p_\ell )$, and thus, the upward pooling wage for $t \ge T$ would be:

$$\begin{aligned} w_s(t) \equiv p_\ell + \frac{\gamma (1 - \beta ) (p_\ell - b)}{1 - \gamma }> p_\ell + \left( \frac{\gamma }{1 - \gamma } \right) ^2 (p_h - p_\ell ) > p_\ell + p _h - p_\ell = p_h, \end{aligned}$$

where the first inequality comes from substitution of the condition and the second comes from $\gamma > 1/2$. This wage is greater than the marginal product of all workers, resulting in negative profits. In sum, all three equilibria cannot exist when the condition is violated.

Now suppose that parameters are such that $\varDelta \le 1$ is satisfied. Note that an upward pooling equilibrium exists if $Q > 0$, while a separating equilibrium exists if $\frac{p_h - p_\ell }{p_h - b - \beta (p_\ell - b)} \le \gamma$, which by rearrangement is equivalent to $Q \le 0$. Moreover, a full upward pooling equilibrium exists iff $Q > 1$, while a partial upward pooling equilibrium exists iff $Q \in (0,1]$. Thus, the separating equilibrium and the upward pooling equilibria are mutually exclusive, but one always exists if $\varDelta \ge 0$.

The existence of downward pooling equilibria is simply restated from Proposition 3. Note that for any $\varDelta$ there exists an equilibrium, because the full downward pooling equilibrium exists iff $\varDelta \ge 0$, while a separating or upward pooling equilibrium exists iff $\varDelta \le 1$.$\square$