Inefficient liquidity provision

Abstract

We prove that in competitive market economies with no insurance for idiosyncratic risks, agents will always overinvest in illiquid long-term assets and underinvest in short-term liquid assets. We take as our setting the seminal model of Diamond and Dybvig (J Polit Econ 91(3):401–419, 1983), who first posed the question in a tractable model. We reach such a simple conclusion under mild conditions because we stick to the basic competitive market framework, avoiding the banks and intermediaries that Diamond and Dybvig (1983) and others introduced.

1 Introduction

The Emergency Economic Stabilization Act of 2008 stated that its goal was “to restore liquidity and stability to the financial system of the United States.” To this end, the act originally gave the Treasury authority to purchase up to $\$700$ billion in illiquid “troubled assets.” Indeed, it now seems clear that before the late 2000s crisis, financial institutions systematically overinvested in illiquid assets and underinvested in safe, liquid assets. Should this pattern surprise us? In general, do agents in competitive markets systematically choose to provide too little liquidity?

Diamond and Dybvig (1983) provide the seminal analysis on the trade-off between safe, short-term assets and higher-yielding, long-term assets that may be illiquid in the short run. The tension is that while investors want high average returns, they may experience liquidity shocks and require cash before the maturity of their long-term investments. With access to a sufficiently rich set of assets, competitive equilibrium in such economies is efficient, and investors achieve optimal liquidity insurance. However, as Diamond and Dybvig (1983) observe, this set of assets would need to contain derivatives that condition payments on the needs of individual investors. As liquidity needs often are private information or difficult to observe, competitive asset markets of this kind will likely be limited.

The basic Diamond and Dybvig (1983) framework consists of three periods and two technologies, a high-yielding one that takes two periods to mature and a one period storage technology that is “liquid” in the sense that in the middle period its resources are available to consume. In the first period, the ex ante identical agents divide their resources between the two technologies. In the second period, agents may consume and trade bonds, but they cannot liquidate long-term investments. In the third period, returns are realized, and the agents consume. Uncertainty and the need for insurance stem from the fact that in the second period agents face random liquidity shocks. In particular, agents randomly differ in how they discount future utility; that is, they differ in impatience. The sudden impatience represents, for example, the possibility that an investor might experience a random medical problem or that a financial firm might have to honor a credit default swap. We extend this idiosyncratic risk to allow for aggregate risk: Both the fraction of the population at each impatience level and the long-term return are stochastic. Consequently, the interest rate that emerges in the middle period is also stochastic.

At this point in their analysis, Diamond and Dybvig (1983) took a sharp turn. They moved away from competitive and anonymous markets and introduced banks and financial intermediaries. Their paper shows that such institutions may improve upon stark incomplete markets by offering incentive compatible contracts to investors. In the original Diamond and Dybvig (1983) model, a standard bank deposit contract is incentive compatible and sufficient for optimal insurance, even when liquidity needs are private information. The Diamond and Dybvig (1983) analysis is famous for a nasty side effect of bank deposit contracts: Their model exhibits multiple equilibria. While one equilibrium yields optimal insurance, the other consists of a bank run, which is worse than autarky. So, in overcoming the private information problem, the market becomes fundamentally fragile.

While most related papers follow the lead of Diamond and Dybvig (1983) and study bank runs or intermediary contracting problems, we return to the simpler setting consisting of just individual investors and competitive asset markets. We answer our original question by showing that in our Diamond–Dybvig setting, agents always underinvest in short-term, liquid assets.

We require two mild assumptions: (1) Absolute risk aversion is nonincreasing. (2) Ex ante, investors place more weight on their future impatient selves than on their future patient selves. Almost all commonly used utility functions satisfy (1); Arrow (1965) wrote that violations of decreasing absolute risk aversion are problematic. Assumption (2) is simply the embodiment of liquidity shocks being emergencies, which are associated with high marginal utility, all else equal.

Our main result (Theorem 1) is that under (1) and (2), all incomplete markets competitive equilibria are constrained inefficient: agents overinvest in the illiquid, long-term technology. The investors would all be better off ex ante if they each decided to shift some resources from the longer illiquid investment to the liquid investment. That welfare rises is surprising: weighting their impatient selves more, that is, realizing liquidity shocks are emergencies, the investors were already allocating extra to the short-term technology as insurance against liquidity shocks. However, in equilibrium, they do not allocate enough.

A pecuniary externality is at play. When every individual shifts resources from long-term to short-term, they depress the middle period interest rates, reallocating resources from middle period lenders (individuals who turned out to be patient) to borrowers (individuals who turned out to be impatient). When an individual shifts his own resources from long-term to short-term, he is shifting money from the last period to the middle period whether or not he turns out to be impatient.¹

A key step in deriving the inefficiency of competitive investment is proving that the interest rate between the last two periods falls when agents get richer in the penultimate period and poorer in the final period. To sign this static, it suffices to show that the resulting two period economies always display stability, so we are able to employ the results of Geanakoplos and Walsh (2016), who show that in two good, I agent economies with common Bernoulli utilities and common endowments but arbitrary heterogeneous discounts, nonincreasing absolute risk aversion guarantees stability.

Our analysis contributes to the existing literature on liquidity provision in three main ways. First, most papers following Diamond and Dybvig (1983) study the intermediary contracting problem, the interaction of intermediaries, or security design. We show that the welfare and policy results of this literature arise in a simple competitive equilibrium setting. We suggest that the main implications and lessons stem simply from market incompleteness, and not from private information mechanism design. Second, we employ weaker assumptions in proving overinvestment in the long-term technology. While our main assumption is nonincreasing absolute risk aversion, previous authors impose some combination of CRRA u, homothetic u, numerical bounds on relative risk aversion, and bounds on the long-term return. Third, unlike previous studies, we allow for aggregate risk in the fraction of the population that turns out to be impatient (as well as in the long-term return), which makes the interest rate random.

The paper concludes with an extension in which the investors may in the middle period liquidate the long-term technology. In states where the fraction of impatient agents is particularly high, the long-term return is low, or the liquidation return is high, the interest rate rises to a level that induces the agents to liquidate part of the long-term technology. This fire sale of productive assets is a tangible manifestation of underinvestment in the short-term technology. Theorem 2 shows that the fire sale economy also exhibits constrained inefficient liquidity underprovision. In a numerical example, forcing agents to provide more liquidity initially and thus to curtail investment in the more productive long-term asset actually increases total production in crisis states of the world: Fire sales decline at a rate faster than the increase in liquidity.²

2 Related literature

Economists have long discussed the tension financial institutions face in deciding between safe, liquid reserves and more profitable but illiquid long-term investments. In their Yale College economics textbook, Fairchild et al. (1937) write,

The banker is impelled by two counteracting motives, profits and safety. The bank derives its profits principally from the making of loans and discounts, and the larger its portfolio of loans and discounts the larger in general will its profits be. But as loans and discounts are made, cash is immediately withdrawn or deposits are created or the bank’s note issues are increased. Thus, the reserve ratio falls, and the bank’s condition becomes proportionately less safe. To the banker’s desire for profits is thus opposed the necessity of keeping a safe ratio between the reserve and the demand liabilities. (p. 439)

Diamond and Dybvig (1983) provide the most famous mathematical treatment of this topic. They observe, as do we, that standard competitive markets will be inefficient without state contingent assets. However, rather than addressing constrained efficiency or possible beneficial market interventions, these authors analyze the ability of bank deposit contracts to insure investors and famously observe that such intermediary contracts introduce the possibility of a bank run equilibrium, which is worse than autarky.

Also, the original Diamond–Dybvig preference structure is quite particular. They assume that impatient types have the utility function $u\left( c_{1}\right)$ and that patient types have the utility function $u\left( c_{1}+c_{2}\right)$, where $c_{1}$ and $c_{2}$ are first and second period consumption. We suppose that both types have the utility function $u\left( c_{1}\right) +\beta u\left( c_{2}\right)$, where $\beta$ is lower for the impatient agents. Furthermore, unlike Diamond and Dybvig (1983), we require neither a quantitative bound on relative risk aversion nor a cross-restriction on the long-term asset return and the size of the preference shock.

Jacklin (1987) extends Diamond and Dybvig (1983) along two dimensions. First, he considers both the original Diamond–Dybvig preferences and a preference specification similar to the one we employ. Second, he compares the risk sharing properties of standard bank deposit contracts with those of an economy in which agents trade equity shares in a firm that makes the initial long-run/short-run portfolio decision. When agents cannot trade bank deposits, deposit contracts welfare dominate allocations from competitive equity markets because second-best insurance calls for a wedge between the marginal rate of substitution and the technological rate of return. With competitive, laissez-faire asset markets, investor trade erodes such wedges. Indeed, when agents can retrade bank deposits, allocations from the two mechanisms coincide. For this reason, Jacklin (1987) policy suggestion is the “prohibition of a frictionless credit market,” in the presence of an existing bank deposit arrangement.

Farhi et al. (2009) effectively argue, however, that the characterization of Jacklin (1987) is too stark. In their model, intermediaries compete to design liquidity insurance mechanisms for investors. The catch is that the resulting contracts are non-exclusive in the sense that the intermediaries cannot stop their customers from trading bonds among themselves. With more preference generality than in Jacklin (1987), these authors order by welfare a taxonomy of insurance arrangements. First-best ($\text{ SP }^{1}$) allocations maximize ex ante utility subject to resource constraints. Second-best ($\text{ SP }^{2}$) allocations honor both resource and incentive compatibility constraints. With the original Diamond–Dybvig preferences, $\text{ SP }^{1}$ and $\text{ SP }^{2}$ coincide. When profit maximizing intermediaries compete to insure the agents, Farhi et al. (2009) refer to the situation as $\text{ CE }^{2}$. As competition drives profits to zero, $\text{ CE }^{2}$ coincides with $\text{ SP }^{2}$. That is, subject to the private information constraint, the government cannot improve on competitive insurance markets. $\text{ CE }^{3}$ arises when price-taking intermediaries compete and investors can privately trade in competitive bond markets. The observation of Jacklin (1987) is basically that $\text{ CE }^{3}$ is worse than $\text{ SP }^{2}$ (and $\text{ CE }^{2}$) and that preventing private retrading improves welfare. Market forces are effectively an additional constraint.

In contrast, Farhi et al. (2009) show that $\text{ CE }^{3}$ is inefficient beyond its distinction from $\text{ CE }^{2}$. Specifically, they characterize the third best ($\text{ SP }^{3}$), in which the planner maximizes utility subject to resource constraints, incentive constraints (regarding liquidity preferences), and constraints that prevent investor side trades at the corresponding market prices. $\text{ SP }^{3}$ is worse than $\text{ SP }^{2}$ because it entails more constraints. $\text{ SP }^{3}$ is, however, better than $\text{ CE }^{3}$ because unlike the price-taking intermediaries, the planner understands how his contracts affect the private market interest rate. In short, the allocations of CE$^{3}$ suffer due to a pecuniary externality. The key theorem of Farhi et al. (2009) explains how simple liquidity controls on intermediaries drive the economy from $\text{ CE }^{3}$ to $\text{ SP }^{3}$. They show that if the impatient agents have, all else equal, more (less) ex ante utility weight, then $\text{ CE }^{3}$ underprovides (overprovides) liquidity. However, to sign the link between initial investment and ex ante utility in any case, the authors require either preference homotheticity or a bound on the liquidity shock variance. Thus, our analysis is distinct both in that we study the case without intermediaries and require just nonincreasing absolute risk aversion.

Bhattacharya and Gale (1987) study a related setting in which intermediaries insure agents who want to consume either early or late. However, at the time of initial investment, each intermediary is uncertain about the fraction of “early diers” he will face and wants to insure against having too many of them. Consequently, the model of Bhattacharya and Gale (1987) is mathematically similar to the general Diamond–Dybvig setting but has intermediaries instead of individual investors as its agents. In the parlance of Farhi et al. (2009), the focus of Bhattacharya and Gale (1987) is a characterization of $\text{ SP }^{2}$. In particular, they show how different assumptions regarding preferences affect the sign of the optimal wedge between the technological return and the effective interest rate. Also, they observe that Walrasian interbank markets exhibit “free-rider” problems, but they do not formalize this argument.

Finally, using the original Diamond–Dybvig preferences, Yared (2013) also considers a case without intermediaries. In his model, agents cannot commit to honoring debt contracts, but the government can issue bonds for trade (financed by taxes). When the government issues a sufficient number of bonds, the economy is equivalent to one with unconstrained, uncontingent trade between agents. In this case, the equilibrium allocations are inefficient. However, by restricting the supply of bonds, the government effectively imposes a $t=1$ borrowing constraint and under certain conditions can implement the first best. The borrowing constraint helps because it forces agents to store more initially. So, Yared (2013) also derives an overinvestment result. Our analysis is distinct from his because (i) he uses the original Diamond–Dybvig preference/shock assumptions, (ii) his policy intervention involves using fiscal policy to set a borrowing constraint in the middle period of the model, and (iii) he does not allow for aggregate risk.³

3 Model

Consider an economy consisting of three time periods, $t\in \left\{ 0,1,2\right\}$, and a unit mass of ex ante identical investors. There is a single consumption good in each time period, and each agent is endowed with $e>0$ units of the good at $t=0$. At $t=0$, each agent allocates his endowment between two investment technologies. The first is a one period saving technology that yields a gross return of 1 at $t=1$. The second is a long-term illiquid investment that gives a gross return of $R_{s}>0$ at $t=2$ in aggregate state $s\in S$, where $S\ge 1$. Let x and y denote the respective allocations to the short- and long-term assets. Let $e_{s1}\left( x\right)$ and $e_{s2}\left( x\right)$ denote the $t=1$ and $t=2$ endowments conditional on liquid investment x in state s. By definition, $e_{s1}\left( x\right) =x$ and $e_{s2}\left( x\right) =R_{s}\left( e-x\right) =R_{s}y$.⁴ At $t=1$, the agents trade one period, riskless bonds in competitive, anonymous markets.

While investors do not consume at $t=0$, they derive utility from consumption at $t=1$ and $t=2$ according to the twice continuously differentiable Bernoulli utility function u, which satisfies $u^{\prime }>0$, $u^{\prime \prime }<0$, and $\lim _{x\downarrow 0}u^{\prime }\left( x\right) =\infty$. At $t=0$, the agents face two forms of uncertainty. First, agents randomly have different tastes for consumption at $t=1$ and $t=2$. That is, they have different degrees of impatience, and each investor learns his type at $t=1$. Second, there is aggregate risk concerning the probability distribution of types and the $t=2$ return. As the $t=1$ interest rate depends on the distribution of types, this uncertainty introduces interest rate risk.

Suppose there are $I>1$ impatience types indexed by i. Type i is distinguished by the pair $\left( w^{i},\beta ^{i}\right) \gg 0$. We suppose the state s, $t=1$ present value utility of impatience type i is

$$\begin{aligned} w^{i}\left[ u\left( c_{s1}^{i}\right) +\beta ^{i}u\left( c_{s2}^{i}\right) \right] , \end{aligned}$$

where $c_{st}^{i}$ is the consumption of type i at $t\in \left\{ 1,2\right\}$ in state $s\in S$. Parameter $\beta ^{i}$ represents the patience of type i. If $\beta ^{i}<\beta ^{j},$ then i is more impatient than j. Parameter $w^{i}$ weights the utility of different types. If in addition to $\beta ^{i}<\beta ^{j}$ we also have $w^{i}\beta ^{i}\ge w^{j} \beta ^{j},$ then ex ante type i is valued more than type j, because the present value weights are higher for i in period 1 and at least as high in period 2. We suppose that impatience increases because of emergencies, which increase the utility of contemporaneous consumption. The case with $w^{i} \beta ^{i}=w^{j}\beta ^{j}$ corresponds to the one described in footnote 5 of independent and equally likely emergencies each period.⁵

There are S possible type distributions: $\varPi _{1},\ldots ,\varPi _{S}$, where $\varPi _{s}=\left( \pi _{s}^{1},\ldots ,\pi _{s}^{I}\right)$ and $\pi _{s}^{i}$ is the probability of becoming type i conditional on distribution s. Let $P_{s}>0$ be the $t=0$ probability of realizing distribution s at $t=1$. Assume, as usual, that $\pi _{s}^{i}$ is both the probability of becoming type i as well as the fraction of agents that realize type i. By relabeling the impatience types as necessary, it is without loss of generality to order the agents as follows: $\beta ^{1}<\cdots <\beta ^{I}$.

Let $q_{s}$ be the $t=1$ price of a bond paying 1 at $t=2$. As the agents are the same ex ante, they choose the same x at $t=0$ and thus have identical endowments at $t=1$ and $t=2$. However, because they differ in impatience, they trade in bonds at $t=1$. The type distribution determines the gains from trade and thus the market clearing interest rate. Hence, the bond price has an s subscript. Define $\mathbf {q}\equiv \left( q_{1} ,\ldots ,q_{S}\right)$. Let $b_{s}^{i}$ denote the bond holdings of type i conditional on state s. The $t=0$ budget set of an agent is thus

$$\begin{aligned} \widetilde{\mathcal {B}}\left( \mathbf {q},e\right) =\left\{ \begin{array} [l]{l} \left( \left( x,y\right) ,\left( c_{s1}^{i},c_{s2}^{i},b_{s}^{i}\right) _{s\in S}^{i\in I}\right) \in \mathbb {R}_{+}^{2}\times \mathbb {R} ^{3SI}\left| \ \forall i\in I,s\in S\right. \\ x+y\le e,\\ c_{s1}^{i}+q_{s}b_{s}^{i}\le x,\ c_{s2}^{i}\le R_{s}y+b_{s}^{i},\\ c_{s1}^{i},c_{s2}^{i}\ge 0 \end{array} \right\} . \end{aligned}$$

Note that because there are no bond market frictions, it is without loss of generality to assume that the agents simultaneously trade $t=1$ and $t=2$ consumption goods at respective prices 1 and $q_{s}$. Conditional on $\left( x,y\right)$ and aggregate state s, the setting becomes a classic I agent, two good endowment economy. We can ignore bond holdings and write the budget set as

$$\begin{aligned} \mathcal {B}\left( \mathbf {q},e\right) =\left\{ \begin{array} [l]{l} \left( \left( x,y\right) ,\left( c_{s1}^{i},c_{s2}^{i}\right) _{s\in S}^{i\in I}\right) \in \mathbb {R}_{+}^{2}\times \mathbb {R}_{+}^{2SI}\left| \ \forall i\in I,s\in S\right. \\ x+y\le e,\\ c_{s1}^{i}+q_{s}c_{s2}^{i}\le x+q_{s}R_{s}y \end{array} \right\} . \end{aligned}$$

The $t=0$ problem of each investor is thus

$$\begin{aligned} \max _{\left( x,y\right) ,\left( c_{s1}^{i},c_{s2}^{i}\right) _{s\in S}^{i\in I}} {\displaystyle \sum _{s=1}^{S}} P_{s} {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}w^{i}\left[ u\left( c_{s1}^{i}\right) +\beta ^{i}u\left( c_{s2}^{i}\right) \right] \hbox { such}\ \hbox { that}\nonumber \\ \left( \left( x,y\right) ,\left( c_{s1}^{i},c_{s2}^{i}\right) _{s\in S}^{i\in I}\right) \in \mathcal {B}\left( \mathbf {q},e\right) . \end{aligned}$$

(1)

Given e, define $c_{st}^{i}\left( x,q_{s}\right)$ to be time t consumption demand at bond price $q_{s}$ and endowment $\left( x,R_{s}\left( e-x\right) \right)$. We now define competitive equilibrium.

Definition 1

(Competitive equilibrium) Competitive equilibrium consists of prices $q_{s}^{*}$ ($\forall s\in S$), a short-term asset investment $x^{*}$ (liquidity), and consumption choices $c_{st}^{i*}=c_{st}^{i}\left( x^{*},q_{s}^{*}\right)$ ($\forall i\in I,\ s\in S$, $t\in \left\{ 1,2\right\}$) such that:

• 1. Given prices, $\left( \left( x^{*},e-x^{*}\right) ,\left( c_{s1}^{i*},c_{s2}^{i*}\right) _{i\in I}^{s\in S}\right)$ solves the $t=0$ investor problem (1).

• 2. Markets clear for all $s\in S$:

  $$\begin{aligned} {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}c_{s1}^{i*}&=x^{*}\\ {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}c_{s2}^{i*}&=R_{s}\left( e-x^{*}\right) . \end{aligned}$$

From the assumptions on u, competitive equilibrium exists, and in equilibrium there is an interior solution for liquidity:

Proposition 1

(Existence) A competitive equilibrium exists and $x^{*}\in \left( 0,e\right)$.

Proposition 1 stems from the following observation: as x approaches 0, the interest rate diverges to infinity in all states, encouraging high investment in x. As x approaches e, the gross interest rate goes to 0, encouraging high investment in y. By continuity, there is an intermediate x that constitutes an equilibrium.⁶

Note that Diamond and Dybvig (1983) assume there are two types and that patient and impatient utility are, respectively, $\rho u\left( c_{1} +c_{2}\right)$ and $u\left( c_{1}\right)$, where $\rho <1$, $\rho R>1$, and relative risk aversion is greater than or equal to 1. While our specification is not technically a generalization of the classical Diamond–Dybvig one, our general setting exhibits the same tensions and trade-offs as those of the classical model. Moreover, our version is the standard representation of time variation in “taste” for consumption. In the classical setting, patient and impatient agents have qualitatively different preferences: while for the former $c_{1}$ and $c_{2}$ are perfect substitutes, for the latter $t=2$ goods are completely useless. In contrast, we follow Jacklin (1987), Bhattacharya and Gale (1987), and Farhi et al. (2009) and analyze the case in which $t=1$ and $t=2$ goods are imperfect substitutes for both types.

4 Welfare analysis

As there are not complete $t=0$ insurance markets for emergency risk, competitive equilibrium is not ex ante Pareto efficient. In this section, we show that equilibrium is also constrained inefficient ( 1): decreasing absolute risk aversion implies investors systematically underinvest in liquidity.

Once agents have chosen their initial investment x, the economy reduces to a simple collection of S two period economies. Observe that after each agent chooses x,  his budget set in each state s if he is of impatience type i reduces to

$$\begin{aligned} \mathcal {B}\left( q_{s},e,x,s\right) =\left\{ \left( c_{s1}^{i},c_{s2} ^{i}\right) \in \mathbb {R}_{+}^{2}|\ c_{s1}^{i}+q_{s}c_{s2}^{i}\le x+q_{s}R_{s}\left( e-x\right) \right\} . \end{aligned}$$

We now define competitive equilibrium conditional on x:

Definition 2

(Competitive equilibrium conditional on x) Competitive equilibrium conditional on x consists of prices $q_{s}\left( x\right)$ ($\forall s\in S$) and consumption choices $c_{st}^{i}\left( x\right) =c_{st}^{i}\left( x,q_{s}\left( x\right) \right) (\forall i\in I, s\in S, t\in \left\{ 1,2\right\}$) such that:

• 1. Given $q_{s}\left( x\right)$, we have $(c_{s1} ^{i}\left( x\right) ,c_{s2}^{i}\left( x\right) )\in \mathcal {B}\left( q_{s}\left( x\right) ,e,x,s\right)$, and $(c_{1},c_{2} )\in \mathcal {B}\left( q_{s}\left( x\right) ,e,x,s\right)$ implies

  $$\begin{aligned} w^{i}\left[ u\left( c_{s1}^{i}\left( x\right) \right) +\beta ^{i}u\left( c_{s2}^{i}\left( x\right) \right) \right] \ge w^{i}\left[ u\left( c_{1}\right) +\beta ^{i}u\left( c_{2}^{i}\right) \right] . \end{aligned}$$

• 2. Markets clear for all $s\in S$:

  $$\begin{aligned} {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}c_{s1}^{i}\left( x\right)&=x\\ {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}c_{s2}^{i}\left( x\right)&=R_{s}\left( e-x\right) . \end{aligned}$$

Given arbitrary bond prices $\mathbf {q}$ and liquidity x, we can define ex ante utility $V\left( x,\mathbf {q}\right)$:

$$\begin{aligned}&V\left( x,\mathbf {q}\right) =\max _{\left( c_{s1}^{i},c_{s2}^{i}\right) _{s\in S}^{i\in I}} {\displaystyle \sum _{s=1}^{S}} P_{s} {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}w^{i}\left[ u\left( c_{s1}^{i}\right) +\beta ^{i}u\left( c_{s2}^{i}\right) \right] \hbox { such} \hbox { that}\nonumber \\&\quad \left( c_{s1}^{i},c_{s2}^{i}\right) \in \mathcal {B}\left( q_{s} ,e,x,s\right) . \end{aligned}$$

(2)

Therefore, conditional on x equilibrium ex ante utility is $V\left( x,\mathbf {q}\left( x\right) \right)$, and competitive equilibrium ex ante utility is $V\left( x^{*},\mathbf {q}\left( x^{*}\right) \right)$. Consider now the $t=0$ problem of a benevolent planner who is able to force all of the investors into a particular short-term savings level x but then must stand idly by while markets clear. The planner can anticipate that each agent will wind up with expected utility $V\left( x,\mathbf {q}\left( x\right) \right)$. As his policy affects all agents, the planner, unlike the atomistic individuals, internalizes how x impacts $q_{s}$ across different realizations of $\varPi _{s}$. Geanakoplos and Polemarchakis (1986) described a method for proving that generically in these types of situations with incomplete markets, the planner can improve utility by choosing x that differs from competitive equilibrium. Here we sharpen that conclusion by proving that the planner can always improve utility by increasing x beyond competitive equilibrium $x^{*}$.

Define $a\left( \cdot \right) \equiv -u^{\prime \prime }\left( \cdot \right) /u^{\prime }\left( \cdot \right)$ to be the Arrow–Pratt measure of absolute risk aversion. u satisfies declining absolute risk aversion (DARA) if $a\left( c\right) \ge a\left( c^{\prime }\right)$ whenever $c\le c^{\prime }$. We now state our main result.

Theorem 1

Suppose (i) u satisfies DARA and (ii) if $\beta ^{i}\le \beta ^{j}$ then $w^{i}\beta ^{i}\ge w^{j}\beta ^{j}$. Then every competitive equilibrium is ex ante constrained inefficient. In particular, all investors could be made better off by collectively allocating more to the short-term asset: the function $V:(0,e)\times \mathbb {R} _{++}^{S}\rightarrow \mathbb {R}$ is differentiable, and at every equilibrium $x^{*}\in (0,e)$ and

$$\begin{aligned} \left. \frac{\hbox {d}}{\hbox {d}{x}}V\left( x,\mathbf {q}\left( x\right) \right) \right| _{x=x^{*}}>0. \end{aligned}$$

Proof

See Appendix A.3. $\square$

Condition (ii) says, essentially, that agents put more ex ante weight on their impatient selves than on their patient selves, which causes them to choose higher x than if they put equal weight on their future selves. The theorem says that, despite this, they would all be better off if they all chose still higher x (and thus lower y). In short, condition (ii) and DARA imply overinvestment in the long-term, illiquid asset. Furthermore, one can show that interest rates are highest exactly when the fraction of impatient agents is highest. Hence, investors realize that they are most likely to become impatient exactly when borrowing rates will be highest. These high rates in impatient times incline them to allocate more to the short investment than they would have otherwise. But, as Theorem 1 tells us, the investors do not allocate enough to the short-term asset: no one agent affects the interest rate, which is the tool by which all are made better off collectively.

Intuitively, increasing liquidity above $x^{*}$ has two effects. First, by stability the interest rate falls (the price of $t=2$ goods rises) as the relative supply of $t=1$ goods rises. For all realizations of s, the falling rate redistributes from the lenders (the patient agents) to the borrowers (the impatient agents). As there is more utility weight on the impatient agents, ex ante utility increases (as does ex post utility, on average). The second effect is that each agent’s $t=1$ ($t=2$) endowment rises (falls). In states where the interest rate is high, this effect actually benefits all agents, holding constant the price. When the interest rate is low, everyone is hurt. The question is, what is the overall balance of these endowment effects? Can they overwhelm the beneficial redistribution effect? The answer is no. As we see in the Date 0 Lemma (Lemma 1), this balancing is exactly the margin on which each agent is choosing x to begin with. At $x^{*}$, these endowment effects completely wash out. Only the redistribution effect remains, which means increasing liquidity (local to $x^{*}$) unambiguously improves utility ex ante.

A key step in proving Theorem 1 is establishing stability of equilibrium, which follows from the results of Geanakoplos and Walsh (2016). They show that utility separability, DARA, common endowments, and common Bernoulli utilities are sufficient for uniqueness and stability in two good, I agent economies, which are what emerge in the present analysis after x is chosen and uncertainty is resolved. The key step in proving stability is in establishing that total demand for $t=2$ goods is downward sloping in q for any x and realization of s. Why is DARA sufficient for downward sloping demand? Proving sufficiency amounts to showing that the income effects of relatively impatient agents are not too strong. Patient agents, who are savers, necessarily have downward sloping demand: The substitution effect in the Slutsky equation is negative by separability and concavity, and the income effect term is negative because they are buyers of $t=2$ goods. For very impatient agents, however, the income effect may be positive because the most impatient agents are borrowing (they are sellers of $t=2$ goods). DARA is sufficient for showing that the total income effect is negative. Specifically, this assumption ensures that the patient agents have the largest (absolute value) income effects. Why? The most patient agents consume the most $t=2$ goods. If $a\left( c\right) \ge a\left( c^{\prime }\right)$ whenever $c\le c^{\prime }$, these agents have the least sensitive marginal utility of consumption for these goods. If you give an investor a splash of income, he allocates between $t=1$ and $t=2$ goods, keeping constant the ratio of marginal utilities. With highly insensitive marginal utility for $t=2$ goods, a patient agent will change consumption of $t=2$ goods a lot just to the maintain the ratio. See Appendix A.1 and Geanakoplos and Walsh (2016) for more details.

Curtailing short-term investment is not always the right intervention. If instead of condition (ii) we assume $w^{1}\le w^{2}\le \cdots \le w^{N}$, then there is always underinvestment in the long-term technology, which we prove as Theorem 3 in Appendix. If the w’s satisfy Eq. 8 in Appendix, then equilibrium is constrained efficient. Is Eq. 8 a knife-edge case? When $S=1$, we can prove the answer is yes: Theorem 4 in Appendix considers the classical case of no aggregate risk about the fraction of the population that turns out to be impatient. We prove that equilibrium is unique, and for almost all ex ante weights $(w^{1} ,\ldots ,w^{I})$ individuals place on their future patient and impatient selves, equilibrium is constrained inefficient: everybody could be made better off if everybody shifted investment one way or the other.⁷

In comparison with the existing literature, our assumption of DARA is weaker than those employed in previous papers, which impose some combination of CRRA u, homothetic u, numerical bounds on relative risk aversion, and restrictions on $R_{s}$. Some variation of condition (ii) has been needed in previous papers to establish underinvestment in liquidity. A special case is $w^{i}=1/\beta ^{i}$, which implies $w^{1}\beta ^{1}=\cdots =w^{I}\beta ^{I}=1$. $w^{i}=1/\beta ^{i}$ corresponds to the “liquidity shock” case from Farhi et al. (2009) and is similar to the original Diamond–Dybvig specification. Finally, while most other papers emphasize the role of banks or intermediaries in creating inefficiencies, we derive and sign constrained inefficiency in a simple setting consisting of just anonymous trade in competitive asset markets.

5 Fire sales

We now change the model so that agents are able to liquidate the long-term investment at a fire sale rate at $t=1$. In particular, after uncertainty is resolved, an agent may liquidate an amount $L_{s}^{i}$, where $0\le L_{s} ^{i}\le y$. Doing so yields a fire sale return of $r_{s}L_{s}^{i}$ at $t=1$, where $r_{s}>0$, and means that the agent’s $t=2$ endowment falls to $R_{s}\left( y-L_{s}^{i}\right)$. The $t=0$ problem of each investor thus becomes

$$\begin{aligned}&\max _{\left( x,y\right) ,\left( c_{s1}^{i},c_{s2}^{i},L_{s}^{i}\right) _{s\in S}^{i\in I}} {\displaystyle \sum _{s=1}^{S}} P_{s} {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}w^{i}\left[ u\left( c_{s1}^{i}\right) +\beta ^{i}u\left( c_{s2}^{i}\right) \right] \mathrm{such \quad that} \\&\quad \left( \left( x,y\right) ,\left( c_{s1}^{i},c_{s2}^{i},L_{s}^{i}\right) _{s\in S}^{i\in I}\right) \in \mathcal {B}_{L}\left( \mathbf {q},e\right) \\&\mathcal {B}_{L}\left( \mathbf {q},e\right) =\left\{ \begin{array} [l]{l} \left( \left( x,y\right) ,\left( c_{s1}^{i},c_{s2}^{i},L_{s}^{i}\right) _{s\in S}^{i\in I}\right) \in \mathbb {R}_{+}^{2}\times \mathbb {R}_{+} ^{3SI}\left| \ \forall i\in I,s\in S\right. \\ x+y\le e\\ 0\le L_{s}^{i}\le y\\ c_{s1}^{i}+q_{s}c_{s2}^{i}\le \left( x+r_{s}L_{s}^{i}\right) +q_{s} R_{s}\left( y-L_{s}^{i}\right) \end{array} \right\} . \end{aligned}$$

Let $L_{s}= {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}L_{s}^{i}$ be the total fire sale liquidation. Competitive equilibrium is as in Definition 1, except the market clearing conditions become

$$\begin{aligned} {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}c_{s1}^{i}&=x+r_{s}L_{s}\nonumber \\ {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}c_{s2}^{i}&=R_{s}\left( e-x-L_{s}\right) . \end{aligned}$$

(3)

Fig. 1

Varying the liquidation value (r) in the fire sales model

Fig. 2

Varying the initial level of liquidity (x). The solid lines correspond to the case with $r = .9$. The dotted lines correspond to the case without fire sales. The vertical lines correspond to the equilibrium levels of liquidity

In contrast with the $r_{s}=0$ version in which liquidation is impossible, here a high interest rate ($1/q_{s}$) induces $t=1$ liquidation, resulting in a decline in $t=2$ production. Indeed, if $1/q_{s}>R_{s}/r_{s}$ in state s, agents would fully liquidate the long-term technology, consuming at $t=2$ only via the bond market. This complete fire sale, however, could never be an equilibrium because it would violate $t=2$ market clearing (3). Therefore, in state s of the fire sale equilibrium either $1/q_{s} =R_{s}/r_{s}$ and agents are indifferent to liquidation or $1/q_{s} <R_{s}/r_{s}$ and $L_{s}=0$. Because agents are indifferent in fire sale states, it is straightforward to extend the proof of Theorem 1 to the fire sale economy, yielding Theorem 2.

Theorem 2

Suppose (i) u satisfies DARA, (ii) if $\beta ^{i}\le \beta ^{j}$ then $w^{i}\beta ^{i}\ge w^{j}\beta ^{j}$, and (iii) there is at least one state without fire sales (e.g., $r_{s}=0$ for some $s\in S$). Then every competitive equilibrium with fire sales is ex ante constrained inefficient. In particular, all investors could be made strictly better off by collectively allocating more to the short-term asset.

Proof

See Appendix A.4. $\square$

5.1 Numerical fire sale example

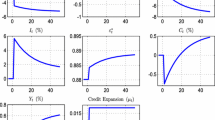
Consider the special case where there are two types, impatient and patient ($\rho ^{I}>\rho ^{P}$, where $\rho ^{i}=1/\beta ^{i}$), and two aggregate states, normal and crisis ($\pi _{N}^{I}<\pi _{C}^{I}$). R and r are constant across states. Let $u\left( c\right) =\log \left( c\right)$, $\left( \rho ^{I},\rho ^{P}\right) =\left( 2,1\right)$, $R=1.5$, $\left( \pi _{C} ^{I},\pi _{N}^{I}\right) =\left( .5,.1\right)$, $\left( P_{C} ,P_{N}\right) =\left( .1,.9\right)$, and $e=1$. In Fig. 1, we see that as liquidation recovery r increases past roughly .8, the agents liquidate part of the long-term technology in the crisis state. And, in anticipation of this option, all else equal, initial liquid short-term investment x declines. The decline in short-term liquid investment, coupled with the fire sale option, generates endogenous volatility in $t=2$ production. Note, however, that the possibility of liquidation actually increases ex ante utility, as we see in Fig. 1: The fire sale caps the interest rate at R / r and effectively improves insurance.

Fig. 3

Bond prices, varying the liquidation value (r) and the initial level of liquidity (x). The vertical line corresponds to the equilibrium level of liquidity. $r=.9$ in the right pane

Figure 2 shows what happens with the imposition of various initial liquidity levels. Increasing x decreases the interest rate in normal times (Fig. 3) and improves utility, up to a point. Most interestingly, we see that while increasing x mechanically decreases the $t=2$ endowment in normal times, the additional liquidity actually increases production in crisis times. The reason is that fire sales decline faster than the fall in long-term investment. Therefore, a liquidity floor not only improves welfare for the investors but also increases output in the worst states of the world.

6 Conclusion

In our generalized version of the seminal Diamond–Dybvig model, incomplete but anonymous and competitive markets yield constrained inefficient allocations. Specifically, investors underprovide the market with liquidity: If they were to collectively invest less in long-term illiquid assets, they would all achieve better insurance and higher ex ante utility. We allow for uncertainty in the liquidity shock distribution and the long-term return, which creates aggregate interest rate risk. Our key assumptions are just that (i) all else equal, investors experiencing liquidity shocks have higher marginal utility of consumption and (ii) absolute risk aversion is nonincreasing in consumption. An intuitive and common argument is that financial institutions and investors overinvest in high-yielding but illiquid assets. We have shown that this overinvestment holds across a number of important dimensions of generality.

Appendix

1.1 Geanakoplos and Walsh (2016) results for the two good, I agent economy

This section rehashes the results of Geanakoplos and Walsh (2016), which we use in proving our theorems. Consider the economy that exists after liquidity x has been chosen and all uncertainty has resolved. To simplify notation, drop reference to x and s. This economy consists of the I impatience types, where $\pi ^{i}$ is the fraction of i types, and two goods, $t=1$ consumption ($c_{1}^{i}$) and $t=2$ consumption ($c_{2}^{i}$). The agents have the identical endowment $\left( e_{1},e_{2}\right) \gg 0$. Stars denote competitive equilibrium quantities. The utility function of impatience type $i\in I$ is $u\left( c_{1}^{i}\right) +\beta ^{i}u\left( c_{2}^{i}\right)$, where u is twice continuously differentiable, $u^{\prime }>0$, $u^{\prime \prime }<0$, and $\lim _{x\downarrow 0}u^{\prime }\left( x\right) =\infty$. u satisfies DARA if $a\left( c\right) \ge a\left( c^{\prime }\right)$ whenever $c\le c^{\prime }$, where $a\left( \cdot \right) \equiv -u^{\prime \prime }\left( \cdot \right) /u^{\prime }\left( \cdot \right)$. The agents are ordered by patience: $\beta ^{1}<\cdots <\beta ^{I}$. The budget constraint is $c_{1}^{i}+qc_{2}^{i}\le e_{1}+qe_{2}$. Define $D\left( q\right) \equiv \sum _{i=1}^{I} \pi ^{i}c_{2}^{i}\left( \left( e_{1},e_{2}\right) ,q\right)$ to be market demand for $t=2$ goods, where $c_{2}^{i}\left( \left( e_{1},e_{2}\right) ,q\right)$ is type i’s demand at price q. From Geanakoplos and Walsh (2016), we have the following result:

Proposition 2

Suppose u satisfies DARA. Then equilibrium is unique and the following hold:

• 1. $c_{1}^{1*}>\cdots >c_{1}^{I*}$.

• 2. $c_{2}^{1*}<\cdots <c_{2}^{I*}$.

• 3. $\rho ^{1}u^{\prime }\left( c_{1}^{1*}\right)>\cdots >\rho ^{I}u^{\prime }\left( c_{1}^{I*}\right) ,$ where $\rho ^{i}=1/\beta ^{i}$.

• 4. Demand is downward sloping: $D^{\prime }\left( q^{*}\right) <0$.

• 5. Equilibrium is stable: $\partial q^{*}/\partial e_{1}>0$ and $\partial q^{*}/\partial e_{2}<0.$

• 6. $q^{*}$ is continuously differentiable in $\left( e_{1} ,e_{2}\right)$, and $c_{t}^{i}$ is continuously differentiable in $\left( e_{1},e_{2}\right)$ and q.

Proof

Parts 1, 2, 4, and 5 are proved in Geanakoplos and Walsh (2016). Part 3 follows immediately from Part 1 and the Euler equations, $q=\beta ^{i} u^{\prime }\left( c_{2}^{i}\right) /u^{\prime }\left( c_{1}^{i}\right)$, which hold at the optimum by the assumptions on u. The properties in Part 6 are standard, following from the twice continuous differentiability of u, the Euler equation, market clearing conditions, and the implicit function theorem. $\square$

Intuitively, when absolute risk aversion is decreasing, then the derivative of consumption with respect to wealth is increasing in consumption: $\partial c_{2}^{i}/\partial \omega$ rises monotonically in $c_{2}^{i}$, meaning buyers have the strongest income effects. It follows that demand is downward sloping, which implies stability.

1.2 Statement and Proof of the Date 0 Lemma (Lemma 1)

Lemma 1

(Date 0 Lemma) At competitive equilibrium, the partial derivative of ex ante utility with respect to liquidity is 0:

$$\begin{aligned} \left. \frac{\partial }{\partial x}V\left( x,\mathbf {q}\left( x\right) \right) \right| _{x=x^{*}}=0 \end{aligned}$$

Proof

Plugging the budget constraint into Eq. 2, ex ante utility is

$$\begin{aligned} V\left( x,\mathbf {q}\left( x\right) \right)= & {} \max _{c_{s2}^{i}\ge 0} {\displaystyle \sum _{s=1}^{S}} P_{s} {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}w^{i}\left( u\left( x+q_{s}\left( x\right) R_{s}\left( e-x\right) -q_{s}\left( x\right) c_{s2}^{i}\right) \right. \\&\left. +\,\beta ^{i}u\left( c_{s2}^{i}\right) \right) , \end{aligned}$$

so by the envelope theorem

$$\begin{aligned} \frac{\partial V}{\partial x}= {\displaystyle \sum _{s=1}^{S}} P_{s} {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}w^{i}u^{\prime }\left( c_{s1}^{i}\left( x,q_{s}\left( x\right) \right) \right) \left( 1-q_{s}\left( x\right) R_{s}\right) . \end{aligned}$$

(4)

Similarly, plugging in the budget constraint, for any $\mathbf {q}$ the agent problem (1) becomes

$$\begin{aligned} \max _{x\in \left[ 0,e\right] ,c_{s2}^{i}\ge 0} {\displaystyle \sum _{s=1}^{S}} P_{s} {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}w^{i}\left( u\left( x+q_{s}R_{s}\left( e-x\right) -q_{s} c_{s2}^{i}\right) +\beta ^{i}u\left( c_{s2}^{i}\right) \right) , \end{aligned}$$

and the x FOC is

$$\begin{aligned} 0= {\displaystyle \sum _{s=1}^{S}} P_{s} {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}w^{i}u^{\prime }\left( c_{s1}^{i}\left( x,q_{s}\right) \right) \left( 1-q_{s}R_{s}\right) . \end{aligned}$$

(5)

By the concavity of the problem and $x^{*}\in \left( 0,e\right)$ (see Proposition 1), the FOC holds in equilibrium. Since the right-hand sides of (5) and (4) coincide at $x=x^{*}$ in equilibrium, we have

$$\begin{aligned} \left. \frac{\partial }{\partial x}V\left( x,\mathbf {q}\left( x\right) \right) \right| _{x=x^{*}}=0. \end{aligned}$$

$\square$

1.3 Proof of Theorem 1

Plugging the budget constraint into Eq. 2 and optimizing over $c_{s2}^{i}$, ex ante utility is

$$\begin{aligned}&V\left( x,\mathbf {q}\left( x\right) \right) \nonumber \\&= {\displaystyle \sum _{s=1}^{S}} P_{s} {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}w^{i}\left( \begin{array} [c]{c} u\left( x+q_{s}\left( x\right) R_{s}\left( e-x\right) -q_{s}\left( x\right) c_{s2}^{i}\left( x,q_{s}\left( x\right) \right) \right) \\ +\,\beta ^{i}u\left( c_{s2}^{i}\left( x,q_{s}\left( x\right) \right) \right) \end{array} \right) . \end{aligned}$$

(6)

By Part 6 of Proposition 2, $V:(0,e)\times \mathbb {R} _{++}^{S}\rightarrow \mathbb {R}$ is well defined and differentiable. By the chain rule,

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}x}V=\frac{\partial V}{\partial x}+ {\displaystyle \sum _{s=1}^{S}} q_{s}^{\prime }\left( x\right) \frac{\partial V}{\partial q_{s}}. \end{aligned}$$

By the Date 0 Lemma (Lemma 1), at $x=x^{*}$ the first term on the right-hand side is 0, so

$$\begin{aligned} \left. \frac{\mathrm{d}}{\mathrm{d}x}V\left( x,\mathbf {q}\left( x\right) \right) \right| _{x=x^{*}}= {\displaystyle \sum _{s=1}^{S}} q_{s}^{\prime }\left( x^{*}\right) \frac{\partial V\left( x^{*},\mathbf {q}\left( x^{*}\right) \right) }{\partial q_{s}}. \end{aligned}$$

Since $x^{*}\in \left( 0,e\right)$ by Proposition 1 and since DARA holds, $q_{s}^{\prime }\left( x^{*}\right) >0$ by stability (Part 5 of Proposition 2). Thus, the theorem follows provided for all $s\in S$

$$\begin{aligned} \left. \frac{\partial V\left( x,\mathbf {q}\left( x\right) \right) }{\partial q_{s}}\right| _{x=x^{*}}>0. \end{aligned}$$

From Eq. 6, we have

$$\begin{aligned} \left. \frac{\partial V\left( x,\mathbf {q}\left( x\right) \right) }{\partial q_{s}}\right| _{x=x^{*}}=P_{s} {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}w^{i}\beta ^{i}\rho ^{i}u^{\prime }\left( c_{s1}^{i*}\right) \left( R_{s}\left( e-x^{*}\right) -c_{s2}^{i*}\right) , \end{aligned}$$

(7)

where $\rho ^{i}=1/\beta ^{i}$. By premise (ii) of the theorem and Proposition 2 (Parts 2 and 3), $\left( w^{i}\beta ^{i}\rho ^{i}u^{\prime }\left( c_{s1}^{i*}\right) \right) ^{i\in I}$ and $\left( R_{s}\left( e-x^{*}\right) -c_{s2}^{i*}\right) ^{i\in I}$ are both strictly decreasing sequences. By interpreting type $i\in I$ as a random variable drawn with probability $\pi _{s}^{i}$, these sequences are strictly decreasing functions of the random variable (call them $f\left( i\right)$ and $g\left( i\right)$, respectively), and we can write the weighted summation in Eq. 7 as expectation with respect to $\varPi _{s}$:

$$\begin{aligned} E_{\varPi _{s}}\left[ w^{i}\beta ^{i}\rho ^{i}u^{\prime }\left( c_{s1}^{i*}\right) \left( R_{s}\left( e-x^{*}\right) -c_{s2}^{i*}\right) \right] =E_{\varPi _{s}}\left[ f\left( i\right) g\left( i\right) \right] . \end{aligned}$$

Since the functions are strictly decreasing, the Chebyshev Sum Inequality⁸ gives us

$$\begin{aligned} E_{\varPi _{s}}\left[ f\left( i\right) g\left( i\right) \right] >E_{\varPi _{s} }\left[ f\left( i\right) \right] E_{\varPi _{s}}\left[ g\left( i\right) \right] . \end{aligned}$$

So, the theorem follows from market clearing:

$$\begin{aligned} E_{\varPi _{s}}\left[ g\left( i\right) \right] = {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}\left( R_{s}\left( e-x^{*}\right) -c_{s2}^{i*}\right) =0. \end{aligned}$$

Intuitively, since $w^{i}\beta ^{i}\rho ^{i}u^{\prime }\left( c_{s1}^{i*}\right)$ and $R_{s}\left( e-x^{*}\right) -c_{s2}^{i*}$ have the same order, they have positive covariance. Since the expectation of $R_{s}\left( e-x^{*}\right) -c_{s2}^{i*}$ is 0 by market clearing, positive covariance implies the expectation of the product is positive:

$$\begin{aligned} 0&<cov_{\varPi _{s}}\left[ f\left( i\right) ,g\left( i\right) \right] =E_{\varPi _{s}}\left[ f\left( i\right) g\left( i\right) \right] -E_{\varPi _{s}}\left[ f\left( i\right) \right] E_{\varPi _{s}}\left[ g\left( i\right) \right] \\&=E_{\varPi _{s}}\left[ f\left( i\right) g\left( i\right) \right] . \end{aligned}$$

$\square$

1.4 Proof of Theorem 2

Given two observations, the proof of Theorem 1 can be easily adapted to prove Theorem 2. First, the Date 0 Lemma (Lemma 1) still holds with fire sales. To see this, let $q_{s}\left( x\right)$ denote the conditional on x equilibrium price without fire sales, and let $\widetilde{q}_{s}\left( x\right)$ denote the equilibrium price with fire sales. If $1/q_{s}>R_{s}/r_{s}$, then once fire sales are allowed agents will choose $L_{s}^{i}=e-x$. In this case, markets will not clear in $t=2$. So, if $1/q_{s}\left( x\right) \ge R_{s}/r_{s}$, then $\widetilde{q}_{s}\left( x\right) =r_{s}/R_{s}$ and agents are indifferent to the level of $L_{s}^{i}$. If $1/q_{s}<R_{s}/r_{s}$, then income is maximized by choosing $L_{s}^{i}=0$, and $q_{s}\left( x\right) =\widetilde{q}_{s}\left( x\right)$. From the perspective of the price-taking agents, in equilibrium the economy is as if there were no fire sales. Therefore, since there is one state without fire sales, we will have $x^{*}\in \left( 0,e\right)$ (by the argument for Proposition 1) and the x FOC (5) will hold in equilibrium.

Second, even though $\widetilde{q}_{s}\left( x\right)$ is non-differentiable at $x\$if$\ 1/q_{s}\left( x\right) =R_{s}/r_{s}$, $\widetilde{q}_{s}\left( x\right)$ is always right differentiable in equilibrium. In states where $1/q_{s}<R_{s}/r_{s}$, $L_{s}^{i}=0$ binds and DARA ensures the interest rate falls as x rises, which only makes $L_{s} ^{i}=0$ bind more. If $1/q_{s}>R_{s}/r_{s}$, then the interest rate $1/\widetilde{q}_{s}\left( x\right)$ is stuck at $R_{s}/r_{s}$, even with a little more liquidity (since $q_{s}\left( x\right)$ is continuous). If $1/q_{s}=R_{s}/r_{s}$ and agents are exactly indifferent to using fires or not, then increasing x pushes down the interest rate and makes them strictly prefer to not liquidate any of the long-term asset.

We can now sign the ex ante utility impact of a small increase in x (at $x^{*}$) in the fire sales economy. Holding prices constant, the state-by-state reallocation of endowments has no impact on utility by the Date 0 Lemma (Lemma 1). In the strict fire sale states, the interest rate is constant and there is no price effect on utility. In the strict and indifferent $L_{s}^{i}=0$ states (there is at least one by assumption), it is as if there were no fire sales, and the proof of Theorem 1 goes through.$\square$

1.5 Statement and Proof of Theorem 3

Theorem 3

Suppose (i) u satisfies DARA and (ii) if $\beta ^{i}\le \beta ^{j}$ then $w^{i}\le w^{j}$. Then competitive equilibrium is ex ante constrained inefficient. In particular, all investors could be made better off by collectively allocating more to the long-term asset:

$$\begin{aligned} \left. \frac{\mathrm{d}}{\mathrm{d}x}V\left( x,\mathbf {q}\left( x\right) \right) \right| _{x=x^{*}}<0. \end{aligned}$$

Proof

Using $\beta ^{i}\rho ^{i}=1$ and the fact that $\left( w^{i}u^{\prime }\left( c_{s1}^{i*}\right) \right) ^{i\in I}$ and $\left( R_{s}\left( e-x^{*}\right) -c_{s2}^{i*}\right) ^{i\in I}$ are, respectively, strictly increasing and decreasing [Part 1 of Proposition 2 and premise (ii)], Theorem 3 follows from the proof of Theorem 1.$\square$

1.6 Statement and Proof of Theorem 4

From the proofs of Theorems 1 and 3, we can now see that there is either over or underinvestment unless $(w^{1},\ldots ,w^{I})$ is such that

$$\begin{aligned} {\displaystyle \sum _{s=1}^{S}} P_{s}q_{s}^{\prime }\left( x^{*}\right) {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}w^{i}u^{\prime }\left( c_{s1}^{i*}\right) \left( R_{s}\left( e-x^{*}\right) -c_{s2}^{i*}\right) =0, \end{aligned}$$

(8)

which seems like a knife-edge case. This insight gives rise to the following theorem, which takes up the classical case of no aggregate uncertainty about the fraction of agents who are impatient. In this case, there is a unique equilibrium, which is generically constrained inefficient (though we do not say whether because of overinvestment or because of underinvestment).

Theorem 4

Suppose there is no aggregate uncertainty, $S=1$. Suppose u satisfies DARA and is three times continuously differentiable. Then there is a unique equilibrium. Fix arbitrary discounts $0<\beta ^{1}<\cdots <\beta ^{I}$, productivity $R>0$, and the probabilities $\pi _{s}^{i}$. Then for almost every choice of $(w^{1},\ldots ,w^{I})\in \mathbb {R} _{++}^{I}$, the unique competitive equilibrium is ex ante constrained inefficient

Proof

By the assumption on u, $q_{s}\left( x\right)$ and consumptions $c_{st}^{i}\left( x\right)$ are twice continuously differentiable functions of $x\in (0,e)$. Hence, we can define the continuously differentiable function $F:(0,e)\times \mathbb {R} _{++}^{I}\rightarrow \mathbb {R} ^{2}$ by

$$\begin{aligned} F(x,w)=\left( F_{1}(x,w),F_{2}(x,w)\right) , \end{aligned}$$

where

$$\begin{aligned} F_{1}(x,w)&= {\displaystyle \sum _{s=1}^{S}} P_{s} {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}w^{i}u^{\prime }\left( c_{s1}^{i}\left( x\right) \right) \left( 1-Rq_{s}(x)\right) \\ F_{2}(x,w)&= {\displaystyle \sum _{s=1}^{S}} P_{s}\left( \frac{\partial }{\partial x}q_{s}\left( x\right) \right) {\displaystyle \sum _{i=1}^{I}} \pi _{s}^{i}w^{i}u^{\prime }\left( c_{s1}^{i}\left( x\right) \right) [R(e-x)-c_{s2}^{i}\left( x\right) ], \end{aligned}$$

and $w=(w^{1},\ldots ,w^{I})$. Equilibrium occurs when $F_{1}(x,w)=0$ and constrained inefficiency when $F_{2}(x,w)\ne 0$ also.

First, we show that whenever $F_{1}(x,w)=0$, the derivative $\partial F_{1}(x,w)/\partial x<0$. The reason is that $\partial q_{s}(x)/\partial x>0$ (by Proposition 2), and with no aggregate uncertainty, $1-Rq_{s}(x)=0$. It follows that there must be a unique equilibrium, since any function like $F_{1}(x|w)$ that always crosses the x-axis with negative slope can only cross once.

We now demonstrate that whenever the two-dimensional function $F(x,w)=0$, the derivative matrix $D_{(x,w)}F$ has column rank 2. Note first that the most impatient agent 1 must always be a seller of good 2, hence $[R(e-x)-c_{s2} ^{i}\left( x\right) ]>0$ for all s. It follows that $\partial F_{2}(x,w)/\partial w^{1}>0.$ Moreover, when $1-Rq_{s}(x)=0$ for all s (as must happen when there is one future aggregate state), $\partial F_{1}(x,w)/\partial w^{1}=0.$ We already saw that $\partial F_{1} (x,w)/\partial x<0.$ Hence,

$$\begin{aligned} D_{x,w^{1}}F=\left[ \begin{array} [c]{cc} - &{}\quad 0\\ ? &{}\quad + \end{array} \right] \end{aligned}$$

has full rank.

This rank argument shows that the two-dimensional function F is transverse to 0,  $F\pitchfork 0,$ that is whenever $F(x,w)=0$, the derivative matrix $D_{(x,w)}F$ has column rank 2. Then since the functions F are continuously differentiable, by the transversality theorem, for almost all $w\in \mathbb {R} _{++}^{I}$, we have $F_{w}\pitchfork 0,$ where $F_{w}(x)\equiv F(x,w)$. But $D_{x}F_{w}(x)$ is a $2\times 1$ matrix and thus can never have rank 2. Hence, for almost all w, $F_{w}(x)$ is never 0, which means that whenever the top expression $F_{1}$ is 0, the bottom expression $F_{2}$ is nonzero. It then follows that for almost all w,  every equilibrium is constrained inefficient. $\square$