Existence of equilibrium in OLG economies with increasing returns

Abstract

We consider a standard overlapping generations (OLG) economy with a simple demographic structure where a new cohort of agents appears at each period and whose economic activity is extended over two successive periods, and finitely many firms may be active. The production possibilities are described by a sequence of production set-valued mappings and the main innovation comes from the fact that we allow for increasing returns to scale of more general type of non-convexities. To describe the behavior of the firms, we consider loss-free pricing rules, which cover the case of the average pricing rule, the competitive behavior when the firms have convex production sets, and the competitive behavior with quantity constraints à la Dehez–Drèze. We prove the existence of an equilibrium under assumptions, which are at the same level of generality than the ones for the existence in an exchange OLG economy.

1 Introduction

Overlapping generations models are studied both in microeconomics and in macroeconomics to analyze intertemporal phenomena. These models involve infinitely many dates, goods and consumers. This double infinity is source of many unobservable phenomenons in standard Arrow-Debreu economies even with an infinite-dimensional commodity space.

Regarding the production side, a firm may benefit from increasing returns, which have their sources in economies of scale, internal or external to the firm, resulting in an increase of its average productivity. On one side, internal economies of scale come from the expansion of the firm itself, that is its average costs depend on its size. They can be achieved through technical economies related to a large machinery and equipments resulting in a production of large scale, technological developments, labor division, splitting tasks according to the specialization of the workforce, managerial economies of scale, showing the importance of trained and qualified employees who are able to take quicker and better decisions. Indeed, good managers are able to find new methods and equipments, more profitable to the firm, cutting wastes and allowing for more efficiency in terms of time and thus reducing production costs. Bigger firms have more possibilities to enjoy financial economies of scale since they are more favorable to loans at lower rates than the smaller ones, leading to additional resources and opportunities to raise their scale.

On the other side, external economies of scale occur outside of the firm, in this case its average costs do not depend on its size; however, they can be internal to the industry to which it belongs. This corresponds to the way Marshall (1920) treats increasing returns: external to the firm but internal to the industry. An important source of external economies of scale is knowledge spillover that benefit industrial clusters. Indeed workers of different firms can easily interact and share their ideas and knowledges, allowing firms to take advantage of improvements of human capital, inventions, and technical successes of other firms. Thus production depends not only on commodity resources but also on know-how. These informal channels and knowledge diffusions are not costly but critical for success, in particular to innovative industries, and these advantages are greater if the industry is larger and more concentrated. Models of endogenous growth consider externalities that might be introduced for example via the level of human capital, which are source of increasing returns at the aggregate level. For instance, Romer (1986) proposed an alternative view on long-run growth driven by the accumulation of knowledge, which has an increasing marginal product on the production of consumption good, thus increasing returns to scale.

We thus plan to study a standard overlapping generations model with production allowing increasing returns to scale and a behavior of the producers, which goes beyond the competitive one. Indeed, increasing returns to scale are sources of non-convexities in production, which make the profit maximizing behavior at given prices meaningless. In this line, it is necessary to model the behavior of producers beyond the profit maximizing one.

The basic model is the one introduced by Balasko and Shell (1980, 1981), Balasko et al. (1980), see also Tvede (2010) for a very intuitive approach. The production knowledge of a producer is described by generalized production correspondences, which define the possible outputs at one date given the vector of inputs consumed at the previous date. This sequential approach of the production allows to consider innovation along the time and heterogeneity of producers.

The equilibrium concept is the standard one but for the behavior of the producers since we do not assume that the production sets are convex. In models allowing for non-convex technologies, the firms follow general pricing rules to describe a large range of possible behaviors including the profit maximizing behavior at given prices. The literature considers pricing rules which associate a set of admissible prices to a weakly efficient production. For a comprehensive introduction see Bonnisseau and Cornet (1988), Cornet (1988), Dierker et al. (1985), Villar (2000). We also remark that this pricing rule modelization allows encompassing models with intermediate goods, imperfect competition and increasing returns at the aggregate level as in Benhabib and Farmer (1994). Indeed, it is equivalent to a unique firm following a markup pricing rule. Since the production is defined in a recursive way, we propose to define also the pricing rule recursively, so that the prices for two successive dates depend on the production possibilities for these two dates and not for the other ones.

We consider loss-free pricing rules, meaning that the firms are restricted to get a nonnegative profit over two successive periods. This covers the case of the average pricing rule, the competitive behavior when the firms have convex production sets, and the competitive behavior with quantity constraints à la Dehez and Drèze (1988a, b).

Contrary to the case of a constant return technology, it is crucial to determine how profits (or losses) of producers are distributed among consumers. Indeed, the optimality of the equilibrium allocation depends on the repartition scheme. In this first paper, we only consider private ownership economies and we assume that the shares are given exogenously. These allocation of the shares can be interpreted as the result of a bequest process between the old and young generations. It would be meaningful to introduce a stock market at each date allowing the old generation to sell the shares to the young generation but this is not an obvious matter. Indeed, contrary to the case of a finite economy where the stock market is innocuous in absence of uncertainty, the stock market leads in OLG economies to a complete transfer of the intertemporal profit to the first generation, which is not economically relevant. Then it seems necessary for understanding the role of the stock market in OLG economies to introduce a durable (capital) commodity which is beyond the scope of this paper (See Magill and Quinzii 1999).

In this paper, we provide an existence result under sufficient conditions at the same level of generality than those for an exchange OLG economy. On the production side, we need to assume the free-disposal condition as for the standard results in finite economies. On the pricing rule, we just need a continuity condition.

In the last section, we show by mean of a numerical example with a production function with a fixed cost that the average pricing rule can dominate the marginal cost pricing rule in the long run. Indeed, the welfare of the consumers at the steady-state equilibrium associated to the marginal cost pricing rule is smaller than the one associated to the average pricing rule in the long run when the initial price is large enough. This phenomenon is due to the accumulation of the input commodity leading the average price to converge to the marginal cost and the fixed cost to become negligible with respect to the level of production.

2 Description of the model

We consider an economy with infinitely many dates $(t=1, 2,\ldots )$. For all $t\in {\mathbb {N}}^*$, there exists a finite set ${\mathcal {L}}_t$ of commodities available in the world. We denote $\#{\mathcal {L}}_t=L_t$.

2.1 Consumers

At each period $t\in {\mathbb {N}}$ (including at period 0), a finite and non-empty set of consumers ${\mathcal {I}}_t$, called generation t, are born. We denote $\#{\mathcal {I}}_t= I_t$ and ${\mathcal {I}}=\cup _{t\in {\mathbb {N}}}{\mathcal {I}}_t$. Each individual lives two periods (an agent born at period t lives at t and $t+1$ and is assumed to have no economic activity before t and after $t+1$).

The consumption set of each individual $i\in {\mathcal {I}}_t$, $t \ge 1$ is the subset $X^i = {\mathbb {R}}^{L_t }_+\times {\mathbb {R}}^{L_{t+1}}_+$. Thus consumption of each consumer of generation t is limited to his lifetime t and $t+1$. The consumption set of consumers of generation 0 is ${\mathbb {R}}^{L_1}_+$.

Consumers preferences are represented by a utility function $u^i: X^i\rightarrow {\mathbb {R}}$.

The vector $e^i\in {\mathbb {R}}^{L_t}_{++}\times {\mathbb {R}}^{L_{t+1}}_{++}$ represents the initial endowment of the agent i of the generation t, which is null outside his lifetime.

2.2 Producers

We assume the set of producers ${\mathcal {J}}$ to be finite. We denote $\#{\mathcal {J}}=J$. The firms may operate at some periods and close down at other periods of time, at no cost.

The production possibilities are represented by set-valued production mappings which associate to a given vector of inputs at date t, a set of possible outputs produced at the next period. This supposes that the production process takes time, the consumption of an input at date t has no influence on the output at this date. For each firm j, $(F^j_t)_{t=1}^\infty$ is a sequence of mappings from $-{\mathbb {R}}_+^{L_t}$ to ${\mathbb {R}}^{L_{t+1}}$.

For a given inputs vector $z^j_t$, $F^j_t(z^j_t)$ is the set of possible vector of outputs the firm can produce. We do not assume the nonnegativity of the output vectors in order to allow for productions with free disposal, but the hypothesis we posit later in the next section will show that only the nonnegative output vectors will be relevant.

Let us associate with each firm j at each period t an elementary production set $Z^j_t$ defined by:

$$\begin{aligned} Z^j_t= \left\{ \left( z_t^j, \zeta _{t+1}^j\right) \in -{\mathbb {R}}_+^{L_t} \times {\mathbb {R}}^{L_{t+1}} \mid \zeta _{t+1}^j \in F_t^j \left( z_t^j\right) \right\} \end{aligned}$$

Notice that $Z_j^t$ is the graph of the mapping $F^j_t$. We define the global inter-temporal production set of firm j by:

$$\begin{aligned} Y^j=\left\{ \left( y_t^j\right) _{t=1}^\infty \in \prod _{t=1}^\infty {\mathbb {R}}^{L_t} \mid \forall t, \exists \left( z_t^j, \zeta _{t+1}^j\right) \in Z_t^j : y^j_t= z_t^j + \zeta _t^j \hbox { with } \zeta _1^j=0\right\} \end{aligned}$$

2.3 Feasibility condition

An allocation $((x^i)_{i \in {\mathcal {I}}}, (y^j)_{j \in {\mathcal {J}}}) \in \prod _{t=0}^\infty \prod _{i \in {\mathcal {I}}_t} X^i \times \prod _{j \in {\mathcal {J}}} Y^j$ is feasible if for all $t \in {\mathbb {N}}^*$, it satisfies the market-clearing condition:

$$\begin{aligned} \sum _{i\in {\mathcal {I}}_{t-1}\cup {\mathcal {I}}_t} x^i_t=\sum _{i\in {\mathcal {I}}_{t-1}\cup {\mathcal {I}}_t} e^i_t+\sum _{j\in {\mathcal {J}}} y^j_t \end{aligned}$$

(1)

We denote by ${\mathcal {A(E)}}$ the set of feasible allocations.

2.4 Pricing rule

The price vector p is an element of $\prod _{t=1}^\infty {\mathbb {R}}_+^{L_t}$, and $p_{th}$ is the market price of the commodity h at date t.

Since the model we consider allows for increasing returns, we describe the behavior of the producers by general pricing rules. See Cornet (1988), Dierker et al. (1985), Villar (2000) for surveys on the representation of economic behavior of producers by pricing rules. Since the production possibilities are defined in a recursive way, we define the pricing rule in a similar way. This approach corresponds to the idea that at each period, newly born individuals appear, taking part to the economic decisions thus to the determination of productions carried over their lifetime.

For a producer j at a period t, the pricing rule $\varphi ^j_t$ is a set-valued mapping defined on the set of weakly efficient productions of $Z^j_t$ with values in ${\mathbb {R}}^{L_t}_+ \times {\mathbb {R}}^{L_{t+1}}_+$. So, given a weakly efficient production $y^j \in Y^j$ and a price p, the pair $(y^j,p)$ is compatible with the behavior of the jth producer if for all t, $(p_t,p_{t+1}) \in \varphi ^j_t (z^j_t, \zeta ^j_{t+1})$ where $(z^j_t, \zeta ^j_{t+1}) \in Z^j_t$ and $y^j_t = z^j_t + \zeta ^j_t$.

A state $((y^j), p)$ is called a production equilibrium if for all t, each firm $j \in {\mathcal {J}}$ finds acceptable the price $(p_t, p_{t+1})$ according to its pricing rule for the given weakly production plan $(y^j)$, that is for all $j \in {\mathcal {J}}$, for all t, $(p_t, p_{t+1}) \in \varphi ^j_t( z^{j}_t, \zeta ^{j}_{t+1} )$, where $( z^{j}_t, \zeta ^{j}_{t+1} ) \in Z^j_t$ and $y^{j}_t =z^{j}_t + \zeta ^{j}_t$.

We assume a private ownership economy. Each agent $i \in {\mathcal {I}}_t$ holds a share $\theta ^{ij}\ge 0$ of the firm j such that for all j, $\sum _{i\in {\mathcal {I}}_t}\theta ^{ij}=1$. These shares on firms profits can be seen as the result of a bequest process over time, transmitted by old to young generations at each period.

2.5 Equilibrium

We are now able to state the definition of an equilibrium in this overlapping generations economy with production.

Definition 1

An equilibrium in the OLG economy ${\mathcal {E}}$ is an element $(p^*, (x^{i*}), (y^{j*})) \in \prod _{t=1}^\infty {\mathbb {R}}^{L_t}_+ \times \prod _{i \in {\mathcal {I}}} X^i \times \prod _{j \in {\mathcal {J}}} Y^j$ such that:

• (a) for all $t \in {\mathbb {N}}^*$, for all $i \in {\mathcal {I}}_t$, $x^{i*}$ is a maximal element of $u^i$ in the budget set:

  $$\begin{aligned}&\left\{ x^i \in X^i \mid p^*_t \cdot x^i_t + p^*_{t+1} \cdot x^i_{t+1} \le p^*_t \cdot e^i_t + p^*_{t+1} \cdot e^i_{t+1} \right. \\&\quad \left. + \sum _{j \in {\mathcal {J}}}\theta ^{ij}\left( p^*_t \cdot z^{j*}_t+p^*_{t+1} \cdot \zeta ^{j*}_{t+1}\right) \right\} , \end{aligned}$$

  where $( z^{j*}_t, \zeta ^{j*}_{t+1} ) \in Z^j_t$ and $y^{j*}_t =z^{j*}_t + \zeta ^{j*}_t$ for all t, and, for all $i \in {\mathcal {I}}_0$, $x^{i*}$ is a maximal element of $u^i$ in the budget set $\{x^i \in X^i \mid p^*_1 \cdot x^i_1 \le p^*_1 \cdot e^i_1\};$

• (b) for all $j \in {\mathcal {J}}$, for all t, $(p^*_t, p^*_{t+1}) \in \varphi ^j_t( z^{j*}_t, \zeta ^{j*}_{t+1} )$;

• (c) for all $t\in {\mathbb {N}}^*$, $\sum _{i\in {\mathcal {I}}_{t-1}\cup {\mathcal {I}}_t} x^{i*}_t=\sum _{i\in {\mathcal {I}}_{t-1}\cup {\mathcal {I}}_t} e^i_t+\sum _{j\in {\mathcal {J}}} y^{j*}_t$.

An equilibrium is thus a list of prices and allocations such that: (a) every consumer maximizes her utility at given prices within her budget set; (b) all the firms are at equilibrium at $((y^{j*}), p^*)$; and (c) all markets clear at every date $t \in {\mathbb {N}}^*$.

3 Existence of equilibrium

We consider standard assumptions on the consumption side.

Assumption C

• (a) For all $t\in {\mathbb {N}}^*$, for all individuals $i\in {\mathcal {I}}_t$, $X^i={\mathbb {R}}^{L_t}_+\times {\mathbb {R}}^{L_t+1}_+$ and for all $i \in {\mathcal {I}}_0$, $X^i= {\mathbb {R}}^{L_1}_+$.

• (b) For all individuals in ${\mathcal {I}}$, $u^i$ is continuous, quasi-concave and locally non-satiated;

• (c) For all $t\in {\mathbb {N}}^*$, there exists $i_0(t)\in {\mathcal {I}}_t$ such that for all $x_t \in {\mathbb {R}}^{L_t}_+$, $u^{i_0(t)}(x_t, \cdot )$ is locally non-satiated and $i_1(t)\in {\mathcal {I}}_t$ such that for all $x_{t+1} \in {\mathbb {R}}^{L_{t+1}}_+$, $u^{i_1(t)}(\cdot , x_{t+1})$ is locally non-satiated.

Assumption E

For all $t\in {\mathbb {N}}^*$, for all $i \in {\mathcal {I}}_t$, $e^i \in {\mathbb {R}}^{L_t}_{++}\times {\mathbb {R}}^{L_t+1}_{++}$ and for all $i \in {\mathcal {I}}_0$, $e^i \in {\mathbb {R}}^{L_1}_{++}$.

We posit the following assumption on the production mappings.

Assumption F

• (a) For all $(j,t) \in {\mathcal {J}}\times {\mathbb {N}}^*$, $F_t^j$ has a closed graph;

• (b) for all $z^j_t \in - {\mathbb {R}}^{L_t}_+$, $0 \in F_t^j (z^j_t)$;

• (c) for all $z^j_t \in - {\mathbb {R}}^{L_t}_+$, $F^j_t(z^j_t) \cap {\mathbb {R}}^{L_{t+1}}_+$ is bounded;

• (d) for all $z^j_t, z^{j\prime }_t \in - {\mathbb {R}}^{L_t}_+$, if $z_j^t \le z^{j\prime }_t$ then $F^j_t(z^{j\prime }_t) \subset F^j_t(z_j^t)$;

• (e) $F^j_t(z^j_t) = (F^j_t(z^j_t) \cap {\mathbb {R}}^{L_{t+1}}_+) - {\mathbb {R}}^{L_{t+1}}_+$.

Assumption F implies that $Y^j$ is closed for the product topology and satisfies the possibility of inaction and the free-disposal assumption. The set of weakly efficient production plans coincides then with the frontier of the production set. Furthermore, negative outputs correspond to the disposal of some part of the production. We do not make assumptions on the returns to scale, thus increasing returns are allowed.

We make the following regularity condition on the pricing rule. It merely means that the pricing rule is continuous and at least one nonzero price vector is associated to each weakly efficient production. Condition (b) says that the price of an output vanishes if the output is disposed off.

Assumption PR

For all $(j,t) \in {\mathcal {J}}\times {\mathbb {N}}^*$,

• (a) $\varphi ^j_t$ has a closed graph and for all $(z^j_t, \zeta ^j_{t+1}) \in \partial Z^j_t$, $\varphi ^j_t (z^j_t, \zeta ^j_{t+1})$ is a closed convex cone in ${\mathbb {R}}^{L_t}_+ \times {\mathbb {R}}^{L_{t+1}}_+$ different from $\{(0,0)\}$;

• (b) for all $(z^j_t, \zeta ^j_{t+1}) \in \partial Z^j_t$, for all $(p_t, p_{t+1}) \in \varphi ^j_t (z^j_t, \zeta ^j_{t+1})$, if $\zeta _{t+1,k}<0$ then $p_{t+1,k}=0$.

Although losses are possible in the presence of increasing returns, we will particularly focus on loss-free pricing rules: Only combinations of prices and productions yielding nonnegative profits will be found acceptable by the producers.

Assumption LF

(Loss-free assumption) For all $(j,t) \in {\mathcal {J}}\times {\mathbb {N}}$, for all $(z^{j}_t, \zeta ^{j}_{t+1}) \in Z^j_t$, for all $(p_t, p_{t+1}) \in \varphi ^j_t(z^j_t, \zeta ^j_{t+1})$,

$$\begin{aligned} p_t \cdot z^j_t+ p_{t+1} \cdot \zeta ^j_{t+1} \ge 0 \end{aligned}$$

Assumption LF is naturally associated with firms operating in unregulated markets where inaction is possible: in this way, whenever the markets conditions are not advantageous, the owners of the firms can always decide to close them down without incurring any cost, thus profits are guaranteed to remain nonnegative.

Remark 1

Although we are considering firms eventually operating over all periods, we can interpret our description of the production sector as a sequence of firms operating only for two successive dates t and $t+1$ as in Tvede (2010). We can also encompass firms operating only at some periods by setting $F^j_t$ equal to $-{\mathbb {R}}^{L_{t+1}}_+$ for the period where the firm is inactive.

Pricing rules satisfying Assumptions PR and LF always exist. Villar (2000) has pointed out two main examples: the markup pricing rule, whose particular case is the average cost pricing rule, and the constrained profit maximization, which results in combinations of prices and productions such that no other combinations using fewer inputs but yielding to higher profits are possible. Constrained profit maximization can be used to model the behavior of firms where increasing returns are due to fixed costs or to the use of a fixed capital like land or machinery.

Remark 2

Note that in many OLG models, increasing returns are associated to imperfect competitions. The structure of the market consists of considering two sectors of production: one for intermediate goods and the other one for final goods. For example, in Benhabib and Farmer (1994), firms in the sector of final goods operate under perfect competition, while each intermediate goods producer has a monopoly power over the good it produces. This formalization allows then for the application of competitive behavior approach on the production sector despite the increasing returns to scale. This imperfect competition structure, takes into account the market power that firms with increasing returns possess, allowing them to make positive profit. Actually, by merging the intermediate and final goods sectors, we get an equivalent model with a firm exhibiting increasing returns to scale and following a markup pricing rule, the markup being directly related to the market power of the intermediate good sector.

The main result of this paper is the following:

Theorem 1

Under Assumptions C, E, F, PR and LF, the OLG economy ${\mathcal {E}}$ has an equilibrium.

Remark 3

This result encompasses the known existence results for OLG exchange economies. Indeed, it suffices to consider that there is only one producer with a constant production correspondence $F_t$ defined by $F_t(z_t)= - {\mathbb {R}}^{L_{t+1}}_+$ and the pricing rule corresponding to the competitive behavior, that is,

$$\begin{aligned} \varphi _t\left( z_t, \zeta _{t+1}\right) = \left\{ \left( p_t, p_{t+1}\right) \in {\mathbb {R}}^{L_{t}}_+ \times {\mathbb {R}}^{L_{t+1}}_+ \mid p_t \cdot z_t + p_{t+1} \cdot \zeta _{t+1} =0\right\} . \end{aligned}$$

Remark 4

If we further assume that $F^j_t$ has a convex graph for all (j, t) and that the pricing rule $\varphi ^j_t$ describes the competitive behavior, that is,

$$\begin{aligned} \varphi ^j_t(z^j_t, \zeta ^j_{t+1})= & {} \left\{ (p_t, p_{t+1}) \in {\mathbb {R}}^{L_{t}}_+ \times {\mathbb {R}}^{L_{t+1}}_+ \mid p_t \cdot z^j_t + p_{t+1} \cdot \zeta ^j_{t+1} \ge p_t \cdot z^{j\prime }_t \right. \\&+\left. p_{t+1} \cdot \zeta ^{j\prime }_{t+1}, \forall \left( z^{j\prime }_t, \zeta ^{j\prime }_{t+1}\right) \in Z^j_t\right\} , \end{aligned}$$

then Assumptions PR and LF are satisfied and Theorem 1 gives the existence of a competitive equilibrium in the OLG economy.

Remark 5

Note that Assumption PR(b) implies that for all $t \in {\mathbb {N}}^*$, for all $k \in {\mathcal {L}}_{t+1}$, then $\zeta ^{j*}_{t+1,k} \ge 0$ if commodity k is desirable by at least one consumer of generation t or $t+1$. So, even if we do not a priori exclude negative quantities of output when we define the production mappings, at equilibrium, the production of an output is always nonnegative for desirable commodities.

4 Equilibrium in truncated economies

We will proceed as for exchange economies (see Balasko et al. 1980) to establish the existence of equilibrium in ${\mathcal {E}}$. To get a concept which is stable under the truncation and has a closed graph property, we need to introduce the pseudo-equilibrium as an intermediary tool. Furthermore, to deal carefully with the truncated production sets, we have to extend the free-disposal assumption over the whole periods. We first show the existence of pseudo-equilibrium in the truncated economies with a finite horizon

$$\begin{aligned} {\mathcal {E}}_{\tau }=\left( \left( u^{\tau i}, X^{\tau i}, e^{\tau i}, \theta ^i\right) _{i \in {\mathcal {I}}^{\tau -1}_0}, \left( Y^{tj}, \tilde{\varphi }^{tj}\right) _{\buildrel {t=1, \ldots , \tau -1}\over {j \in {\mathcal {J}}}}\right) \end{aligned}$$

then we prove that prices and allocations remain in a compact space of a suitable linear space equipped with the right topology, and we finally show that a cluster point is an equilibrium of the OLG economy.

Notations. Let $\tau \ge 2$ be an integer. The truncated economy ${\mathcal {E}}_{\tau }$ is defined as follows:

• ${\mathcal {I}}_0^{\tau -1}= \cup _{t=0}^{\tau -1} {\mathcal {I}}_t$ is the set of all the individuals born up to period $\tau -1$.

• For each $i \in {\mathcal {I}}_1$,

• $X^{\tau i} = \{x \in \prod _{t=1}^\tau {\mathbb {R}}^{L_t}_+ \mid x_{t^{\prime }}=0, \forall {t^{\prime }}>1\}$

• $u^{\tau i}$, from $X^{\tau i}$ to ${\mathbb {R}}$, is defined by $u^{\tau i} (x) = u^i (x_1)$

• $e^{\tau i} = (e^{\tau i}_{t^{\prime }})_{{t^{\prime }}=1}^{\tau } \in \prod _{t=1}^\tau {\mathbb {R}}^{L_t}_+$ is defined by $e^{\tau i}_1=e^i_1$, and $e^{\tau i}_{t^{\prime }}=0$ if ${t^{\prime }}>1$.

• For each $t=1, \ldots , \tau -1$, for each $i \in {\mathcal {I}}_t$,

• $X^{\tau i} = \{x \in \prod _{t=1}^\tau {\mathbb {R}}^{L_t}_+ \mid x_{t^{\prime }}=0, \forall {t^{\prime }}\ne t, t+1\}$

• $u^{\tau i}$, from $X^{\tau i}$ to ${\mathbb {R}}$, is defined by $u^{\tau i}(x) = u^i (x_t, x_{t+1})$

• $e^{\tau i}= (e^{\tau i}_{t^{\prime }})_{{t^{\prime }}=1}^{\tau } \in \prod _{t=1}^\tau {\mathbb {R}}^{L_t}_+$ is defined by $e^{\tau i}_t=e^i_t$, $e^{\tau i}_{t+1}=e^i_{t+1}$ and $e^{\tau i}_{t^{\prime }}=0$ if ${t^{\prime }}\ne t, t+1$.

For each t, we choose an arbitrary closed convex cone $C_t$, called free-disposal cone, included in ${\mathbb {R}}^{L_t}_{++} \cup \{0\}$ containing $\mathbf{1}^t = (1,\ldots ,1) \in {\mathbb {R}}^{L_t}_{++} \cup \{0\}$ in its interior. We denote by $C_t^+$ the positive polar cone of $C_t$ ¹.

We define the extended production set $Y^{tj}$ for $t=1, \ldots , \tau -1$ as follows:

$$\begin{aligned} Y^{tj}= \left\{ \left( y_{{t^{\prime }}}^{tj}\right) _{{t^{\prime }}=1}^{\tau } \in \prod _{{t^{\prime }}=1}^\tau {\mathbb {R}}^{L_{t^{\prime }}} \mid \left( y_t^{tj}, y_{t+1}^{tj}\right) \in Z_t^j, \forall {t^{\prime }}\ne t, t+1, y^{tj}_{t^{\prime }}\in -C_{t^{\prime }}\right\} \end{aligned}$$

This extension is necessary since the existence result for economies with non-convex production sets require that the production sets satisfy the free-disposal assumption or at least a weak form of it, namely, with our notations the fact that $Y^{tj} - \prod _{{t^{\prime }}=1}^\tau C_{t^{\prime }}=Y^{tj}$. We also extend the pricing rules as follows: for all $y^{tj} \in \partial Y_{tj}$,

$$\begin{aligned} \tilde{\varphi }^{tj}\left( y^{tj}\right) = \left\{ p \in \prod _{{t^{\prime }}=1}^\tau C_t^+ \mid \left( p_t, p_{t+1}\right) \in \varphi ^j_t \left( y^{tj}_t,y^{tj}_{t+1}\right) , p_{t^{\prime }}\cdot y^{tj}_{t^{\prime }}=0, \forall {t^{\prime }}\ne t, t+1\right\} \end{aligned}$$

We thus extend the production sets into $\prod _{{t^{\prime }}=1}^\tau {\mathbb {R}}^{L_{t^{\prime }}}$, but we focus only on the production at date t and restrict the activity at dates $t^\prime \ne t$ to the free disposal at zero cost. Since $C_t \subset {\mathbb {R}}^{L_t}_{++} \cup \{0\}$ for all t, we also remark that if $p \in \tilde{\varphi }^{tj}(y^{tj})$ and $p_{t^{\prime }}\in {\mathbb {R}}^{L_{t^{\prime }}}_+\setminus \{0\}$ for some ${t^{\prime }}\ne t, t+1$, then $y^{tj}_{t^{\prime }}=0$. Note that if $p \in \tilde{\varphi }^{tj} (y^{tj})$, $p \cdot y^{tj}= p_t \cdot y^{tj}_t + p_{t+1} \cdot y^{tj}_{t+1}$. So, the extension does not change the profit.

We now define a pseudo-equilibrium.

Definition 2

A pseudo-equilibrium in the truncated economy ${{\mathcal {E}}}_\tau$ is an element $(p^*, (x^{i*}), (y^{tj*})) \in \prod _{t=1}^\tau C_t^+ \times \prod _{i \in {\mathcal {I}}_0^{\tau -1}} X^{\tau i} \times \prod _{j \in {\mathcal {J}}} \prod _{t=1}^{\tau -1} Y^{tj}$ such that:

• (a) for all $t=1, 2,\ldots ,\tau -1$, for all $i \in {\mathcal {I}}_t$, $x^{i*}$ is a maximal element of $u^{\tau i}$ in the budget set

  $$\begin{aligned} \left\{ x^i \in X^{\tau i} \mid p^* \cdot x^i \le p^* \cdot e^{\tau i} + \sum _{j \in {\mathcal {J}}}\sum _{t=1}^{\tau -1} \theta ^{ij}_t p^* \cdot y^{tj*}\right\} ; \end{aligned}$$

  for all $i \in {\mathcal {I}}_0$, $x^{i*}$ is a maximal element of $u^{\tau i}$ in the budget set $\{x^i \in X^{\tau i} \mid p^* \cdot x^i \le p^* \cdot e^{\tau i}\}$;

• (b) for all $j \in {\mathcal {J}}$, for all $t=1, \ldots , \tau -1$, $p^* \in \tilde{\varphi }^{t j} (y^{tj*})$;

• (c) For all $t=1, \ldots , \tau -1$, $\sum _{i\in {\mathcal {I}}^{\tau -1}_0} x^{i*}_t=\sum _{i\in {\mathcal {I}}_0^{\tau -1}} e^{\tau i}_t + \sum _{j\in {\mathcal {J}}} \sum _{{t^{\prime }}=1}^{\tau -1} y^{{t^{\prime }}j*}_t$ and $\sum _{i\in {\mathcal {I}}^{\tau -1}_0} x^{i*}_\tau \le \sum _{i \in {\mathcal {I}}_0^{\tau -1}} e^{\tau i}_\tau + \sum _{i \in {\mathcal {I}}_\tau } e^{i}_\tau + \sum _{j\in {\mathcal {J}}} \sum _{{t^{\prime }}=1}^{\tau -1} y^{{t^{\prime }}j*}_\tau$

Remark 6

In the definition of a pseudo-equilibrium, the price $p^*$ is supposed to be in $\prod _{t=1}^\tau C_t^+$. Actually, we remark that it belongs to the smaller set $\prod _{t=1}^\tau {\mathbb {R}}^{L_t}_+$. This is a consequence of Condition (b) and the fact that $\varphi ^j_t$ takes its values in ${\mathbb {R}}^{L_t}_+ \times {\mathbb {R}}^{L_{t+1}}_+$. Consequently, we deduce from the definition of $\tilde{\varphi }^{tj}$ that at equilibrium $y^{tj*}_{t^{\prime }}=0$ for all ${t^{\prime }}\ne t, t+1$.

Remark 7

The difference between a pseudo-equilibrium and an equilibrium is that we do not require the market-clearing condition at the last period $\tau$ and we artificially increase the initial endowments by adding those of the consumers of the generation $\tau$. So, an equilibrium of ${\mathcal {E}}_\tau$ is clearly a pseudo-equilibrium. This particular feature is useful to show below that if $\tau ^\prime > \tau$, then the restriction of a pseudo-equilibrium of $\mathcal {E}_{\tau ^\prime }$ to the $\tau -1$ first generations is a pseudo-equilibrium of ${\mathcal {E}}_\tau$.

Indeed, let $\bar{\tau } > \tau$ and $(p^*, (x^{i*}), (y^{tj*}))$ be a pseudo-equilibrium in the economy ${\mathcal {E}}_{\bar{\tau }}$, then we show that the price and the allocations restricted to the $\tau$ first periods $\left( q^*, (\chi ^{i*})_{i \in {\mathcal {I}}_0^{\tau -1}}, (\xi ^{tj*})_{\buildrel {j \in {\mathcal {J}}}\over { t=1,\ldots ,\tau -1}}\right)$ defined by

• $q^*=(p^*_t)_{t=1}^\tau$,

• for all $i \in {\mathcal {I}}_0^{\tau -1}$, $\chi ^{i*}= (x^{i*}_t)_{t=1}^\tau$,

• for all $j \in {\mathcal {J}}$, for all $t=1, \ldots , \tau -1$, $\xi ^{tj*}=(y^{tj*}_{t^{\prime }})_{{t^{\prime }}=1}^\tau$,

is a pseudo-equilibrium in the economy ${\mathcal {E}}_{\tau }$.

From the definition of a pseudo-equilibrium, we just have to look at Condition (c) for the period $\tau$. Since $(p^*, (x^{i*}), (y^{tj*}))$ is a pseudo-equilibrium in the economy ${\mathcal {E}}_{\bar{\tau }}$ and $\bar{\tau } >\tau$, one has:

$$\begin{aligned} \sum _{i\in {\mathcal {I}}^{\bar{\tau }-1}_0} x^{i*}_\tau =\sum _{i\in {\mathcal {I}}_0^{\bar{\tau }-1}} e^{\bar{\tau } i}_\tau + \sum _{j\in {\mathcal {J}}} \sum _{{t^{\prime }}=1}^{\bar{\tau } -1} y^{{t^{\prime }}j*}_\tau \end{aligned}$$

From the definition of $X^{\bar{\tau } i}$, for all $i \in \cup _{t=\tau +1}^{\bar{\tau }-1} {\mathcal {I}}_t$, $x^{i*}_\tau =0$. From the definition of $e^{\bar{\tau } i}$, for all $i \in \cup _{t=\tau +1}^{\bar{\tau }-1} {\mathcal {I}}_t$, $e^{\bar{\tau } i}_\tau =0$. From the previous remark, for all ${t^{\prime }}= \tau +1, \ldots , \bar{\tau } -1$, for all j, $y^{{t^{\prime }}j*}_\tau =0$. Furthermore, for all j, $y^{\tau j*}_\tau \le 0$ and for all $i \in {\mathcal {I}}_\tau$, $x^{i*}_\tau \ge 0$. So, one deduces that:

$$\begin{aligned} \sum _{i\in {\mathcal {I}}^{\bar{\tau }-1}_0} x^{i*}_\tau =\sum _{i\in {\mathcal {I}}^{ \tau -1}_0} x^{i*}_\tau + \sum _{i\in {\mathcal {I}}_ \tau } x^{i*}_\tau =\sum _{i\in {\mathcal {I}}^{ \tau -1}_0} e^{\bar{\tau } i}_\tau + \sum _{i\in {\mathcal {I}}_ \tau } e^{\bar{\tau } i}_\tau + \sum _{j\in {\mathcal {J}}} \sum _{{t^{\prime }}=1}^{ \tau -1} y^{{t^{\prime }}j*}_\tau + \sum _{j\in {\mathcal {J}}} y^{\tau j*}_\tau \end{aligned}$$

which implies that :

$$\begin{aligned} \sum _{i\in {\mathcal {I}}^{ \tau -1}_0} x^{i*}_\tau \le \sum _{i\in {\mathcal {I}}^{ \tau -1}_0} e^{\bar{\tau } i}_\tau + \sum _{i\in {\mathcal {I}}_ \tau } e^{\bar{\tau } i}_\tau + \sum _{j\in {\mathcal {J}}} \sum _{{t^{\prime }}=1}^{ \tau -1} y^{{t^{\prime }}j*}_\tau \end{aligned}$$

So we get Condition (c) for the period $\tau$ since $x^{i*}_\tau = \chi _\tau ^{i*}$ and $e^{\bar{\tau } i}_\tau = e^{ \tau i}_\tau$ for all $i \in {\mathcal {I}}^{ \tau -1}_0$ and $e^{\bar{\tau } i}_\tau = e^{ i}_\tau$ for all $i \in {\mathcal {I}}_\tau$.

Since the truncated economy ${\mathcal {E}}_\tau$ does not satisfy the strong survival assumption but its weak form, we are going to deduce the existence of pseudo-equilibrium from a quasi-equilibrium.

Definition 3

A quasi-equilibrium in the truncated economy ${\mathcal {E}}_\tau$ is a list $(p^*, (x^{i*}), (y^{tj*}))$ in $\prod _{t=1}^\tau C_t^+ \times \prod _{i \in {\mathcal {I}}_0^{\tau -1}} X^{\tau i} \times \prod _{j \in {\mathcal {J}}} \prod _{t=1}^{\tau -1} Y^{tj}$ satisfying:

• (a) for all $t=1,2 \ldots \tau -1$, $x^{i*}$ is an element of the budget set:

  $$\begin{aligned} \left\{ x^i \in X^{\tau i} \mid p^* \cdot x_i^* \le p^* \cdot e^{\tau i} + \sum _{j \in {\mathcal {J}}}\sum _{t=1}^{\tau -1} \theta ^{ij}_t p^* \cdot y^{tj*}\right\} \end{aligned}$$

  and for all $x^{i}\in X^{\tau i}$, if $p^* \cdot x_i < p^* \cdot e^{\tau i} + \sum _{j \in {\mathcal {J}}}\sum _{t=1}^{\tau -1} \theta ^{ij}_t p^* \cdot y^{t j}$, then $u^{\tau i}(x^i) \le u^{\tau i}(x^{i*})$. for all $i \in {\mathcal {I}}_0$, $x^{i*} \in \{x^i \in X^i \mid p^* \cdot x^i \le p^* \cdot e^{\tau i}\}$ and for all $x^{i}\in X^{\tau i}$, if $p^* \cdot x^i < p^* \cdot e^{\tau i}$, then $u^{\tau i}(x^i) \le u^{\tau i}(x^{i*})$,

• (b) for all $j \in {\mathcal {J}}$, for all $t=1, \ldots , \tau -1$, $p^* \in \tilde{\varphi }^{\tau j} (y^{tj*})$;

• (c) $\sum _{i\in {\mathcal {I}}^{\tau -1}_0} x^{i*}=\sum _{i\in {\mathcal {I}}_0^{\tau -1}} e^i + \sum _{j\in {\mathcal {J}}} \sum _{t=1}^{\tau -1} y^{tj*}$;

• (d) $p^* \ne 0$.

Proposition 1

Under the assumptions of Theorem 1, for all $\tau \ge 2$, there exists a quasi-equilibrium of the economy ${\mathcal {E}}_\tau$.

Proof

The proof is based on the fact that ${\mathcal {E}}_\tau$ satisfies the necessary assumption of the existence of a (quasi)-equilibrium. See Bonnisseau and Cornet (1988) for the existence of equilibrium with bounded losses pricing rules and in particular of loss-free pricing rules, Gourdel (1995) for the existence of quasi-equilibrium and the way to go from quasi-equilibrium to equilibrium, and Bonnisseau and Jamin (2008) for the existence of equilibrium with a weaker version of the free-disposal assumption.

Indeed, the existence of quasi-equilibrium is ensured by Assumptions (C) and (E), and the facts that :

• $\tilde{\varphi }^{tj}$ satisfies Assumption (PR)(a) since $\varphi ^{j}_t$ satisfies this assumption and $C_t$ is a closed convex cone.

• for all $(y^{tj} )\in \prod \partial Y^{tj}$, if $p \in \cap _{j\in {\mathcal {J}}} \cap _{t=1}^{\tau -1} \tilde{\varphi }^{tj}(y^{tj})$, $p \cdot e^{\tau i} + \sum _{j \in {\mathcal {J}}}\sum _{t=1}^{\tau -1} \theta ^{ij}_t p\cdot y^{t j}\ge 0$, thanks to Assumptions (LF) and (E), and the definition of $\tilde{\varphi }^{tj}$.

• $Y^{tj} - \prod _{{t^{\prime }}=1}^\tau C_{t^{\prime }}= Y^{tj}$ (free disposal)

and the boundedness assumption stated by the following lemma. $\square$

Let $e \in \prod _{t \in {\mathbb {N}}^*} {\mathbb {R}}^{L_t}_+$ defined by $e_t = \sum _{i \in {\mathcal {I}}_t \cup {\mathcal {I}}_{t-1}} e^i_t$. Let $e^\prime \in \prod _{t \in {\mathbb {N}}^*} {\mathbb {R}}^{L_t}_+$ such that $e^\prime \ge e$. We denote by $\tilde{{\mathcal {A}}}({\mathcal {E}}_\tau (e^\prime ))$, the set of allocations satisfying the market-clearing condition for a pseudo-equilibrium (Condition (c) of Definition 2) for the economy ${\mathcal {E}}_\tau$. We establish that feasible allocations are bounded for all greater initial endowments. For all t, let $\mathbf{1}^t$ be the vector of ${\mathbb {R}}^{L_t}$ with all its coordinates equal to 1.

Lemma 1

For all $e^\prime \ge e$, for all $j \in {\mathcal {J}}$, there exists a sequence of nonnegative real numbers $(m^{tj})$ such that for all $\tau$, for all $((x^i),(y^{tj})) \in \tilde{{\mathcal {A}}}({\mathcal {E}}_\tau (e^\prime ))$, for all $i \in {\mathcal {I}}_0^{\tau -1}$, for all $t =1, \ldots , \tau -1$,

$$\begin{aligned} 0 \le x^i_t \le e^\prime _t + \left( \sum _{j \in {\mathcal {J}}} m^{tj}\right) \mathbf{1}^t; \end{aligned}$$

for all $j \in {\mathcal {J}}$, for all $t= 1, \ldots ,t-1$,   for all ${t^{\prime }}\ne t+1$,

$$\begin{aligned} 0\ge & {} y_{t^{\prime }}^{t j} \ge -e^\prime _{t^{\prime }}- \sum _{j \in {\mathcal {J}}} m^{{t^{\prime }}j} \mathbf{1}^{t^{\prime }},\\ m^{(t+1)j} \mathbf{1}^{t+1}\ge & {} y_{t+1}^{t j} \ge -e^\prime _{t+1} - \sum _{j \in {\mathcal {J}}} m^{(t+1) j} \mathbf{1}^{t+1}. \end{aligned}$$

Proof

Let $((x^i),(y^{tj}))$ be an element of $\tilde{{\mathcal {A}}}(\mathcal {E_\tau }(e^\prime ))$. Then, for all $t=1, \ldots , \tau$,

$$\begin{aligned} \sum _{i\in {\mathcal {I}}^{\tau -1}_0} x^{i}_t \le e^\prime _t + \sum _{j\in {\mathcal {J}}} \sum _{{t^{\prime }}=1}^{\tau -1} y^{{t^{\prime }}j}_t \end{aligned}$$

For all $j \in {\mathcal {J}}$, we define the sequence $(m^{tj})$ as follows: $m^{1j}=0$ and $m^{t+1 j}$ is a positive real number so that:

$F^j_t(-e^\prime _t-\sum _{j \in {\mathcal {J}}} m^{tj} \mathbf{1}^t) \subset m^{t+1 j}\mathbf{1}^{t+1} - {\mathbb {R}}^{L_{t+1}}_+$.

Such real number exists from the boundedness Assumption F(c). Since $0\le \sum _{i\in {\mathcal {I}}^{\tau -1}_0} x^i_1$, we get $\sum _{j \in {\mathcal {J}}} y_1^{1j}+ \sum _{j \in {\mathcal {J}}} \sum ^{\tau -1}_{t=2} y_1^{tj} \ge -e^\prime _1$. Since for all $j \in {\mathcal {J}}$, $y_1^{1j} \le 0$ and for all $t =1, \ldots , \tau -1$, $y_1^{tj} \le 0$, we obtain $0 \ge y_1^{1j} \ge -e^\prime _1$, for all j and $0 \ge y_1^{tj} \ge -e^\prime _1$ for all t.

For the second period, we have:

$$\begin{aligned} \sum _{j \in {\mathcal {J}}} y_2^{1j}+ \sum _{j \in {\mathcal {J}}} y_2^{2j}+ \sum _{j \in {\mathcal {J}}} \sum ^{\tau -1}_{t=3} y_2^{tj} \ge -e^\prime _2 \end{aligned}$$

For all $j \in {\mathcal {J}}$, $y_2^{2j} \le 0$ and for all $t =3, \ldots , \tau - 1$, $y_2^{tj} \le 0$. From the above inequalities and Assumption F(d), $y_2^{1j} \in F^j_1(y_1^{1j})\subset F^j_1(-e^\prime _1) \subset m^{2 j}\mathbf{1}^{2} - {\mathbb {R}}^{L_{2}}_+$. Thus, for all $j \in {\mathcal {J}}$,

$0 \ge y_2^{tj} \ge -e^\prime _2 - \sum _{j \in {\mathcal {J}}} m^{2j} \mathbf{1}^2$, for all $t=2,\ldots ,\tau -1$,

By an induction argument taking into account the definition of the sequences $(m^{tj})$ we prove the result for all period.

For the consumptions, since they are all nonnegative,

$$\begin{aligned} 0 \le x^i \le \sum _{i^\prime \in {\mathcal {I}}^{\tau -1}_0} x^{i^\prime }. \end{aligned}$$

So, for all t,

$$\begin{aligned} 0 \le x^i_t \le e^\prime _t + \sum _{j \in {\mathcal {J}}} \sum _{{t^{\prime }}=1}^{\tau -1} y_t^{{t^{\prime }}j} \le e^\prime _t + \sum _{j \in {\mathcal {J}}} y_t^{t-1 j} \le e^\prime _t + \sum _{j \in {\mathcal {J}}} m^{t j} \mathbf{1}^t \end{aligned}$$

$\square$

The following lemma ensures that a quasi-equilibrium of $\mathcal E_\tau$ is an equilibrium.

Lemma 2

If $(p^{*}, (x^{i*}), (y^{tj*}))$ is a quasi-equilibrium of ${\mathcal {E}}_\tau$, then $p^{*}_t \ne 0$ for all t and $(p^{*}, (x^{i*}), (y^{tj*}))$ is an equilibrium.

Proof

Since the utility functions are continuous, the condition for a quasi-equilibrium $(p^{*}, (x^{i*}), (y^{tj*}))$ to be an equilibrium is that the individual wealth is strictly above the subsistence level, that is: $w^{i*}=p^* \cdot e^{\tau i} + \sum _{j \in {\mathcal {J}}}\theta ^{ij}_t p^*\cdot y^{tj*}> \inf p^*. X^{\tau i}$, for all $i \in {\mathcal {I}}_0^{\tau -1}$. As already remarked (See Remark 6), $p^* \in \prod _{t=1}^\tau {\mathbb {R}}^{L_t}_+$, so $\inf p^*. X^{\tau i}=0$. Hence, from Assumptions E and LF, it suffices to show that $p^*_t \ne 0$ for all $t=1, \ldots , \tau$.

Suppose that there exists t such that $p^*_t = 0$. Knowing that $p^*$ is not equal to 0, there exists $\bar{t}$ such that $p^*_{\bar{t}} \ne 0$ and $p^*_{\bar{t}+1}=0$ or $p^*_{\bar{t}} = 0$ and $p^*_{\bar{t}+1} \ne 0$. We deal with the first case, the proof being the same for the second case.

Since $p^*_{\bar{t}} \in {\mathbb {R}}^{L_{\bar{t}}}_+ \setminus \{0\}$, the consumer $i_1$ in ${\mathcal {I}}_{\bar{t}}$ given by Assumption C(c) has a strictly positive wealth $w^{i_1*} > 0$. Then $(x^{i_1*}_{\bar{t}}, x^{i_1*}_{\bar{t}+1})$ belongs to the demand of consumer $i_1$ that maximizes the utility function under the budget constraint. Then, the local non-satiation of the partial utility function $u^{i_1}(x^{i_1*}_{\bar{t}},\cdot )$ [Assumption C(c)] implies that $p^*_{\bar{t}+1} \ne 0$.

Thus, necessarily $p^*_t\ne 0$ for all t, and $w^{i*} > \inf p^*. X^{\tau i}=0$. $\square$

From Remark 2, an equilibrium is a pseudo-equilibrium, thus we have proved the following result.

Proposition 2

Under the Assumptions of Theorem 1, for all $\tau \ge 2$, there exists a pseudo-equilibrium of the economy ${\mathcal {E}}_\tau$.

In the following lemma, we provide two properties of the pseudo-equilibrium, which will be useful for the limit argument in the next section. In the following, a nonzero price $p^*$ is normalized so that $\sum _{t=1}^\tau \sum _{\ell \in L_t} p^*_{t\ell }=1$.

Lemma 3

If $(p^{*}, (x^{i*}), (y^{tj*})$ is a pseudo-equilibrium of ${\mathcal {E}}_\tau$, then $p^{*}_t \ne 0$ for all $t=1, \ldots , \tau$.

The set of pseudo-equilibria of the economy ${\mathcal {E}}_\tau$ with a normalized price is closed.

Proof

The first part uses the same argument as for Lemma 2.

We now consider a sequence of pseudo-equilibria $(p^{\nu }, (x^{i\nu }), (y^{tj\nu }))$ converging to $(\bar{p}, (\bar{x}^{i}), (\bar{y}^{tj})$. We prove that $(\bar{p}, (\bar{x}^{i}), (\bar{y}^{tj})$ is also a pseudo-equilibrium.

It is easy to establish that $(\bar{p}, (\bar{x}^{i}), (\bar{y}^{tj}))$ satisfies Condition (b) in Definition 2, since $\tilde{\varphi }^{\tau j}$ has closed graph, and also the condition (c). So it remains to show that the condition (a) is also satisfied.

Denote by $(w^{i \nu })$ the associated wealth sequence and by $\bar{w}^{i}$ its limit. One easily shows that the budget constraint is satisfied by $\bar{x}^i$. If $\bar{w}^i >0$, then $\bar{x}^i$ maximizes the utility function under the budget constraint. Indeed, if $\bar{p} \cdot x^i < \bar{w}^{i}$, then for $\nu$ large enough, $p^\nu \cdot x^i \le w^{i\nu }$. But this implies that $u^i(x^i) \le u^i(x^{i \nu })$, and by the continuity of $u^i$, $u^{i}(x^i) \le u^{i}(\bar{x}^{i})$. If $\bar{p} \cdot x^i = \bar{w}^{i} > 0$, let $\lambda < 1$, and then $\bar{p} \cdot (\lambda x^i) < \bar{w}^{i}$. So, from above, $u^i(\lambda x^i) \le u^i(\bar{x}^{i})$. Using again the continuity of $u^i$, $u^{i}(x^i)= \lim _{\lambda \rightarrow 1} u^i(\lambda x^i) \le u^{i}(\bar{x}^{i})$.

Let us now prove that $\bar{p}_t \ne 0$, for all t. Since $\bar{p}\ne 0$ by normalization, there exists t such that $\bar{p}_t \ne 0$. Hence, for the consumer $i_0(t) \in {\mathcal {I}}_t$ and $i_1 (t-1) \in {\mathcal {I}}_{ t-1}$, $\bar{w}^{i_0(t)} > 0$ and $\bar{w}^{i_1(t-1)} > 0$. So the agents $i_0 (t)$ and $i_1(t-1)$ are utility maximizer hence, from Assumption C(c), $\bar{p}_{t+1} \ne 0$ and $\bar{p}_{t-1} \ne 0$. Doing again the same argument, we conclude that the prices at each period are different from 0.

Since $\bar{p}_t \ne 0$, for all t, $\bar{w}^i >0$ for all consumers, hence all of them are maximizing utility under the budget constraint at the price $\bar{p}$, which proves that $(\bar{p}, (\bar{x}^{i}), (\bar{y}^{tj})$ is a pseudo-equilibrium. $\square$

5 From truncated equilibria to equilibrium

The proof of Theorem 1 consists of considering a sequence of pseudo-equilibria in the truncated economy with an horizon increasing to infinity. First, we establish that the sequence of normalized equilibrium prices in the truncated economies remains in a compact set for the product topology on $\prod _{t=1}^\infty {\mathbb {R}}^{L_t}$. Then we show that the sequence of T-equilibrium remains in a compact set and we prove that a cluster point is an equilibrium of the OLG economy ${\mathcal {E}}$.

From the previous section, for all $T\ge 2$, there exists a T-equilibrium $(p^{T}, (x^{iT}), (y^{tjT}))$ of the economy ${\mathcal {E}}_T$. Since we have proved in the previous section (see Lemma 2) that $p^T_1 \ne 0$, we normalize $p^T$ so that $\sum _{\ell \in L_1} p^T_{1 \ell }=1$.

We extend the price and the allocations to the whole space $\prod _{t=1}^\infty {\mathbb {R}}^{L_t}$ by adding zeros for the missing components without modifying the notations. So, now the sequences $(p^{T})$, $(x^{iT})$ and $(y^{tjT})$ are in $\prod _{t=1}^\infty {\mathbb {R}}^{L_t}$.

We now prove that the sequence of prices $(p^T)$ remains in a compact subset of $\prod _{t=1}^\infty {\mathbb {R}}^{L_t}$.

Lemma 4

For all t, there exists $\tilde{k}_t \in {\mathbb {R}}_+$ such that for all T, $0 \le p^T_t \le \tilde{k}_t \mathbf{1}^t$.

Proof

If it is not true, there exist $\bar{t}$ and an increasing sequence $(T^\nu )$ such that $p^{T^\nu }_{\bar{t}} \ge \nu \mathbf{1}^{\bar{t}}$. Let $\tau > \bar{t} + 2$. We assume without any loss of generality that $T^\nu > \tau$ for all $\nu$.

Now we consider the restriction to the $\tau$ first period of the $T^\nu$-equilibrium $(p^{T^\nu }, (x^{iT^\nu }), (y^{tjT^\nu }))$:

• for all $i \in {\mathcal {I}}_0^{\tau -1}$, $x^{i \nu }$ is the restriction of $x^{i T^\nu }$ to $\prod _{t=1}^{\tau } {\mathbb {R}}^{L_t}$;

• for all $j \in {\mathcal {J}}$, for all $t=1, \ldots , \tau -1$, $y^{tj\nu }$ is the restriction of $y^{tjT^\nu }$ to $\prod _{t=1}^{\tau } {\mathbb {R}}^{L_t}$;

• $p^\nu$ is the restriction of $p^{T^\nu }$ to $\prod _{t=1}^{\tau } {\mathbb {R}}^{L_t}$.

From Remark 7 in the previous section, $(p^\nu ,(x^{i \nu }),(y^{tj\nu }))$ is a pseudo-equilibrium of the truncated economy ${\mathcal {E}}_\tau$. We now renormalize the price $p^\nu$ as follows:

$$\begin{aligned} \pi ^\nu = \frac{1}{\sum _{t=1}^\tau \sum _{\ell \in L_t} p^\nu _{t \ell }}p^\nu \end{aligned}$$

Since $\pi ^\nu$ is nonnegative, the sequence remains in the simplex of $\prod _{t=1}^{\tau } {\mathbb {R}}^{L_t}$, which is compact. From Lemma 1, the sequence $((x^{i \nu }),(y^{tj\nu }))$ remains in the compact subset $\tilde{ {\mathcal {A}}} ({\mathcal {E}}_\tau (e))$. So the sequence $(\pi ^\nu ,(x^{i \nu }),(y^{tj\nu }))$ has a cluster point $(\bar{\pi },(\bar{x}^{i }),(\bar{y}^{tj}))$. From Lemma 3, $(\bar{\pi },(\bar{x}^{i }),(\bar{y}^{tj}))$ is also a pseudo-equilibrium of the truncated economy ${\mathcal {E}}_\tau$. But $\bar{\pi }_1=0$ since $(\sum _{t=1}^\tau \sum _{\ell \in L_t} p^\nu _{t \ell })$ converges to $+ \infty$ and $0 \le p^\nu _{1 \ell } \le 1$ for all $\ell \in L_1$. Hence we get a contradiction since Lemma 3 shows that for all $t=1, \ldots , \tau$, $\bar{\pi }_t \ne 0$. $\square$

Proof of Theorem 1

From Lemma 1 and the above lemma, the sequence of T-equilibrium of ${\mathcal {E}}_T$, $(p^{T}, (x^{iT}), (y^{tjT}))$, remains in a compact set for the product topology of $\prod _{t=1}^\infty {\mathbb {R}}^{L_t} \times \prod _{{t^{\prime }}=1}^\infty \prod _{i \in {\mathcal {I}}_{t^{\prime }}} \prod _{t=1}^\infty {\mathbb {R}}^{L_t} \times \prod _{j \in {\mathcal {J}}} \prod _{{t^{\prime }}=1}^\infty \prod _{t=1}^\infty {\mathbb {R}}^{L_t}$. Since this is a countable product of finite dimensional spaces, the product topology is metrizable on the compact sets and there exists a subsequence $(p^{T^\nu }, (x^{iT^\nu }), (y^{tjT^\nu }))$ of $(p^{T}, (x^{iT}), (y^{tjT}))$, which converges to $(p^*, (x^{i*}), (y^{tj*}))$. We recall that the convergence for the product topology implies the usual convergence when we consider only a finite number of components.

For each $\tau \ge 2$, for $\nu$ large enough, the restriction of $(p^{T^\nu }, (x^{iT^\nu }), (y^{tjT^\nu }))$ to the $\tau$ first periods is a pseudo-equilibrium of ${\mathcal {E}}_\tau$ see Remark 7 and it converges to the restriction of $(p^*, (x^{i*}), (y^{tj*}))$ to the $\tau$ first periods. From Lemma 3, this restriction is a pseudo-equilibrium of ${\mathcal {E}}_\tau$. From Definition 2 and the notations above, one deduces that $(p^*, (\xi ^{i*}), (y^{j*}))$ defined as follows in an equilibrium for the OLG economy ${\mathcal {E}}$:

• for all $t \ge 1$, for all $i \in {\mathcal {I}}_t$, $\xi ^{i*}= (x^{i*}_t, x^{i *}_{t+1})$ and for all $i \in {\mathcal {I}}_0$, $\xi ^{i*}= x^{i*}_1$;

• for all $j \in {\mathcal {J}}$ for all $t \ge 1$, $z^{j*}_t= y^{tj*}_t$, $\zeta ^{j*}_{t+1}= y^{tj*}_{t+1}$ and $y^{j*}_t = z^{j*}_t + \zeta _t^{j*}$ with $\zeta _0^{j*}=0$.

$\square$

6 A numerical example

Let us consider a simple case of stationary OLG economy with one individual per generation, a single firm and a single commodity at each period. Thus, at every date $t \ge 1$, $\vert {\mathcal {L}}_t \vert =1$, and $\vert {\mathcal {I}}_t \vert =1$.

All consumers are identical except the old consumer at date $t=0$. Their consumption set is $X= {\mathbb {R}}^2_{+}$, their initial endowment vector $(e^y>0, e^o>0)$, and their utility function $u: X \rightarrow {\mathbb {R}}$ is defined by $u(x^y_t,x^o_{t})= a \ln x^y_t+ (1-a) \ln x^o_{t}$, $0\le a \le 1$. The consumption set of the consumer born at date $t=0$, who is old at date $t=1$, is ${\mathbb {R}}_{+}$.

The firm is described by a production function $f: -{\mathbb {R}}_+\rightarrow {\mathbb {R}}$ which transforms the good at date t into the good at date $t+1$ with a fixed cost and then a constant marginal cost.

$$\begin{aligned} f(z_t)={\left\{ \begin{array}{ll} -\gamma \left( z_t-\hat{z}\right) , &{} \text {if }z_t \le \hat{z} \le 0\\ \ 0, &{} \text {if }\hat{z} \le z_t \le 0 \end{array}\right. } \end{aligned}$$

where $\gamma > 1$, $\hat{z}<0$.

This technology clearly exhibits strict increasing returns to scale due to the fixed cost $\hat{z}$.

The price vector p is an element of ${\mathbb {R}}^2_+$. Define the relative price: $\pi _{t}= \frac{p_t}{p_{t+1}}$. We assume that the producer follows the average cost pricing: $p_t z_t + p_{t+1} \zeta _{t+1}=0$, or in term of relative prices: $\pi _t z_t + \zeta _{t+1}=0$.

Each consumer t is maximizing her utility function $u^t$ under her budget constraint. Given a price $(p_t, p_{t+1})$, the consumer t’s demand is:

$$\begin{aligned} \left\{ \begin{array}{ll} x^y_t=\frac{a w^t}{p_t}=a\left( e^y+\frac{e^o}{\pi _t}\right) \\ x^o_{t}= \frac{(1-a)w^t}{p_{t+1}} =(1-a)\left( \pi _t e^y+e^o\right) \end{array} \right. \end{aligned}$$

Clearly, if the relative price $\pi _t$ increases, the agent will decrease his consumption when young and increase it when old. His lifetime utility is an increasing function of $\pi _t \ge 0$. However, we note that at each period t, the relative price $\pi _t$ cannot be too small. Indeed, if we let $\pi _t$ tend to $0^+$ at date t, the consumption of young $x^y_t$ will be infinitely high while the total resource at each date is finite.

Whenever $z_t\le \hat{z}$, the firm can decide to produce $\zeta _{t+1}=-\gamma (z_t-\hat{z})$ following an average cost pricing. Thus we can write: $\zeta _{t+1}= -\pi _t z_t$ and:

• $\zeta _{t+1}= \frac{\gamma \hat{z} \pi _t }{\pi _t-\gamma }$

• $z_t= - \frac{\gamma \hat{z}}{\pi _t-\gamma }$

Remark 8

• (1) $z_t$ and $\zeta _{t+1}$ are well defined whenever $\pi _t < \gamma$;

• (2) for all $t \ge 0$, for $\pi _t \in (0, \gamma )$, $\zeta _{t+1}>0$ and $z_t<0$, in addition, $\zeta _{t+1}$ is an increasing function of $\pi _t$;

• (3) $\lim _{\pi _t \rightarrow \gamma ^-} \zeta _{t+1}= \lim _{\pi _t \rightarrow \gamma ^-} \frac{\gamma \hat{y} \pi _t }{\pi _t-\gamma }=+\infty$

• (4) In case of constant returns to scale, that is no fixed cost, it is known that the firm, while maximizing its profit, would exhibit a discontinuous supply function at $\gamma$. The fixed cost associated with the average cost pricing leads to a smooth supply function on the range $(0, \gamma )$.

The sequence of prices $(p^*_{t})$ is an equilibrium price system if the sequence of relative prices $(\pi ^*_{t})$ is a solution of the following recursive equation:

$$\begin{aligned} (1-a) e^y \left( \pi _{t-1}-1\right) - \frac{\gamma \hat{y} }{\pi _{t-1}-\gamma } \pi _{t-1}= a e^o \left( 1-\frac{1}{\pi _t}\right) -\frac{\gamma \hat{y}}{\pi _t-\gamma } \end{aligned}$$

with $\pi _t \in (0,\gamma )$ for all $t\ge 1$, $\gamma >1$, $0 \ge \hat{y} \ge -e^y$.

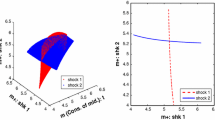
Figure 1 represents the graph associated with this equation in the space $(\pi _{t-1}, \pi _t)$ for the particular case where $\gamma =4$, the initial endowment when young $e^y= 2$, the initial endowment when old $e= 0.8$, the propension to consume when young $a= 0.02$, the fixed cost $\hat{z}= -1$. Here, the consumer is ready to invest in the production since his endowment is large enough when young and his preferences put a higher weight when old.

Fig. 1

Graph of the equilibrium price equation

We have multiple steady-states equilibria: a low and stable steady state $\pi ^* < 1$ and $\pi ^{**}=1$ which is not stable. Suppose that at each date $t_0$, $\pi _{t_0} <1$, then the economy will display a succession of inflationary equilibria since all the following prices will be below 1 and will be decreasing to the low steady state $\pi ^*$. If we instead have $\pi _{t_0} >1$, then the successive price $\pi _{t_0+1} >1$ so are all the following prices. This case will lead to a non-stationary equilibria where the relative prices will increase and tend to the marginal price $\gamma$ without reaching it, that is: $1 < \pi _{t_0} < \pi _{t_0+1} < \ldots < \gamma$. Thus from period $t_0$, the production will be increasing, so will be the welfare of all the successive generations since they will benefit from a deflation: $p_{t_0} > p_{t_0+1} > \ldots$. Thus the successive equilibrium converges toward an equilibrium of a fictitious economy without fixed cost and a marginal cost equals to $\gamma$. Numerically, we get $u^*=0.255$, $u^{**}=0.595$ and $\bar{u}=1.597$ are respectively the utility levels at $\pi ^*$, $\pi ^{**}$ and the limit of the utility level when $\pi (t)$ converges to $\gamma$.

Remark 9

Note that a steady-state equilibrium exists if the producer follows the marginal pricing rule even if it generates losses. Indeed, the demand would be:

$$\begin{aligned} \left\{ \begin{array}{ll} x^y_t=a\left( e^y+ \hat{z}+ \frac{e^o}{\gamma }\right) \\ x^o_{t}= (1-a)\left( \gamma \left( e^y+\hat{z}\right) + e^o\right) \end{array} \right. \end{aligned}$$

The corresponding market-clearing equation gives a positive production equals to 0.768, and the associated utility is 0.344 which is clearly lower than $u^{**}$ thus lower than $\bar{u}$. This shows that the average pricing rule can dominate the marginal cost pricing rule in the long run by initiating a growth path when the initial relative price is large enough.