Subjective evaluation versus public information

Abstract

This paper studies a principal–agent relation in which the principal’s private information about the agent’s effort choice is more accurate than a noisy public performance measure. For some contingencies the optimal contract has to specify ex post inefficiencies in the form of inefficient termination (firing the agent) or wasteful activities that are formally equivalent to third-party payments (money burning). Under the optimal contract, the use of these instruments depends not only on the precision of public information but also on job characteristics. Money burning is used at most in addition to firing and only if the loss from termination is small. The agent’s wage may depend only on the principal’s report and not on the public signal. Nonetheless, public information is valuable as it facilitates truthful subjective evaluation by the principal.

1 Introduction

In the textbook moral hazard problem, the agent chooses some unobservable effort, and the only information about his success is some noisy but objective performance measure which is verifiable by outsiders. As Prendergast (1999) has pointed out, however, most people do not work in jobs like these. Rather, many firms use subjective performance evaluations.

This paper studies subjective performance evaluation in a single interaction between a risk-neutral principal and a risk-neutral agent with limited liability. The principal may use a publicly verifiable but noisy objective performance signal to provide effort incentives for the agent. But, he privately receives more accurate information about the output produced by the agent. This information is not observable by outsiders and in this sense ‘subjective’. We show that the optimal contract always relies not only on the public performance measure but also on subjective evaluation by the principal. Therefore, it has to address two incentive problems. On the one hand, the agent must be given incentives to exert effort. On the other hand, the principal has to be incentivized to report his information truthfully: giving a bad performance evaluation must be costly for the principal if the performance is in fact good; otherwise, the principal would be tempted to report bad performance to save on wage costs. Thus some ex post inefficiencies are unavoidable.

The literature has studied two different solutions to the incentive problem of truthful subjective evaluation. First, Kahn and Huberman (1988) study up-or-out contracts in a dynamic setting where in an initial period the agent should acquire some firm specific human capital. The agent chooses an effort to learn, and then the principal privately receives information about the agent’s success. In the optimal contract, the principal commits ex ante either to promote the agent and pay a high wage, or else to end the relationship by firing the agent.¹ By firing the agent the principal foregoes the output from the human capital investment. This prevents him from giving a bad performance evaluation when the agent was successful by the commitment to fire upon announcing a bad performance evaluation. There is an ex post inefficiency, however, since the agent is fired after a bad evaluation, even if it would be ex post optimal to keep him.

Second, MacLeod (2003) considers contracts that directly specify a certain amount of ex post inefficiencies. In the following we refer to this type of wasteful activities as “money burning”, because they are formally equivalent to payments to a passive third party.² But, more generally, money burning may also represent the monetary equivalent of organizational conflict in the form of strikes or sabotage, costly litigation, and non-pecuniary penalties. Through money burning the principal’s profit can be made independent of his performance evaluation. He thus has no incentive to give bad evaluations to safe costs. But money burning is required whenever a bad evaluation lowers the agent’s wage.³

Prematurely terminating the relation by firing the agent destroys some part of the output generated by the agent’s effort. We show that this is a more efficient incentive device for subjective performance evaluation than money burning. The latter can occur under the optimal contract, but only as a secondary instrument in addition to firing the agent. Therefore, termination should be more frequently observed than money burning. Our analysis further shows that the use of these instruments depends not only on the precision of public information but also on job characteristics that affect the cost of firing the agent.⁴

Money burning and firing have subtly different implications for the incentives of the principal: The principal’s cost of burning one dollar does not depend on the agent’s success or failure, but the principal’s cost from firing the agent often depends on how successful the agent was. Whether or not the agent’s success increases the principal’s cost of firing can depend on the type of occupation. In jobs requiring little specific human capital, the value of continuing or terminating the relationship is likely to be independent of the agent’s current success. Then money burning and firing share essentially the same properties. For such occupations, money burning can be motivated as a shortcut for the termination of a valuable work relationship (MacLeod 2003). On the other hand, many jobs require specific human capital, and the cost of firing the agent is higher when he was successful and has acquired it, as in Kahn and Huberman (1988). Similarly, Schmitz (2002) studies a buyer–seller relationship where the seller (agent) produces a good, the quality of which depends on the seller’s effort, but only the buyer (principal) knows his true willingness to pay for the good. Here ‘firing’ corresponds to the buyer not buying the good after it has been produced, and the principal’s loss from not buying the good depends on the realized quality of the good.⁵

To describe the dependence between the principal’s cost of firing and the agent’s success in a straightforward way, we assume that upon firing the principal loses a fraction $\alpha$ of the output produced by the agent. The parameter $\alpha$ may capture characteristics of the agent’s job, such as the importance of job specific human capital, or the degree to which the project is finished when the principal decides on firing. When the agent can easily be replaced and the job requires little or no specific human capital, $\alpha$ will be low. In contrast, in the relation between a buyer and a single irreplaceable seller studied in Schmitz (2002), the buyer loses all the potential gains from trade when he decides not to buy; in this setting $\alpha$ equals one.

We show that, under our assumption that upon firing the principal loses the fraction $\alpha$ of the output produced by the agent, firing is the more cost-effective instrument, and the principal will prefer firing over money burning. Since the costs of firing are high when the agent was in fact successful, a commitment to fire the agent after a bad performance evaluation gives the principal strong incentives to report successes truthfully. Moreover, the costs of this commitment are relatively low, since on the equilibrium path the principal will give a bad report only if the agent was, after all, not successful, and hence firing him is not that costly for the principal.⁶ Only a bounded amount of incentives, however, can be generated by firing if $\alpha$ is small. The principal then cannot be given strong incentives for truthful revelation of his information, since he will not lose much after firing the agent. In this situation he has to resort to money burning.⁷

We also provide several insights into the interaction between subjective and objective performance evaluation. If the principal receives his private information before the less informative public signal becomes available, the agent’s wage schedule is not uniquely determined. It can be chosen in such a way that wages are contingent exclusively on subjective evaluation and do not depend on the public performance measure. This does not mean, however, that public information is useless. While it is not directly used to incentivize the agent, it facilitates providing incentives for truthful subjective evaluation by the principal. We show that for this reason the principal’s payoff is increasing in the precision of public information.

In contrast, if the principal’s information arrives after the public signal, the agent’s wage schedule is uniquely determined by the optimal contract and it necessarily depends on both types of performance measures. This is so because the principal in this case faces an ex post truthtelling constraint for each single realization of the public signal rather than an ex ante constraint in expectation of the public signal. Perhaps surprisingly, however, it turns out that for the principal’s payoff it does not matter whether he receives his private information earlier or later than the realization of public information.

By the latter observation, the principal has no incentive to acquire information early on. But, we also discuss a slight extension of our model where the fraction of output lost due to project termination changes over time. When the timing of subjective evaluation can be selected by the principal, he will report when the fraction of output lost due to project termination is high enough such that no money burning is necessary to solve the incentive problem of truthful subjective evaluation. This reinforces our argument that money burning is a less attractive instrument than firing the agent in contracting problems with subjective evaluations.

1.1 Related literature

As described above, our paper contributes to the literature on optimal contracting with subjective evaluation by comparing the use of project termination with money burning activities.⁸ From this literature, Schmitz (2002) and Khalil et al. (2015) are most closely related to our paper. Schmitz (2002) allows the use of both project termination and money burning and assumes, as is natural in his buyer–seller setting, that the complete output produced by the agent (seller) is lost when the principal (buyer) terminates the relation. In his setting, the optimal contract never involves any money burning. Khalil et al. (2015) study a related issue in an adverse selection model. In their model, the agent knows the productivity of his effort, and the principal receives some subjective information about the agent’s type. If the principal receives his information before the agent chooses his effort, the optimal contract specifies an effort that depends on the agent’s report about his type and on the principal’s report. In particular, there is a rescaling of the project to a lower level of effort and wage if the agent reports a low productivity but the principal’s signal indicates a high productivity. Khalil et al. (2015) find that this rescaling is superior to money burning.

There are several differences between their result and our comparison of firing versus money burning. First, rescaling as in Khalil et al. (2015) presupposes that the principal receives his private information before the agent chooses his effort. Therefore the principal strictly prefers to receive his information early. In our moral hazard setting, the principal’s private information is a signal about the effort chosen by the agent, and thus necessarily becomes available only after the effort has been chosen. Moreover, in our setting the principal has no incentive to acquire information early; in contrast, he will strictly prefer to acquire information late if the fraction of output lost upon firing is increasing over time.

Second, rescaling works in Khalil et al. (2015) since different types of the agent trade off producing output and receiving wages at different rates. In contrast, firing works in our model since the principal’s expected cost from firing depends on his private signal. This has implications concerning the set of implementable contracts. In Khalil et al. (2015) the principal’s incentive constraints jointly imply that they hold with equality in every possible state, such that the principal will always be indifferent between his reports. As in MacLeod (2003), this indifference of the principal is an implication of the principal’s incentive constraints. In contrast, in our setting the principal’s incentive constraints can all be fulfilled without the principal ever being indifferent between sending different reports. This is possible even in the absence of public information because the principal’s cost of firing depends on his private information. As in a standard adverse selection model, in the optimal contract the principal’s incentive constraint after having received bad news is slack, while the principal’s incentive constraint after having received favorable information is binding. The latter, however, is an implication of optimality of the contract, and not of implementability alone.

Rajan and Reichelstein (2009) examine the interaction between objective and subjective performance indicators in bonus pool arrangements. In their analysis the total amount of money in the bonus pool can depend on objective performance indicators. The principal’s subjective evaluation then determines the fraction of the bonus pool that is paid out to the agent while the remainder is diverted to a third party. In our context, a bonus pool is not an optimal arrangement because the principal can also fire the agent. Typically, therefore the total amount that the principal has to pay to the agent and to a third party depends not only on objective but also on subjective performance measures. Also Zabojnik (2014) studies the interaction between objective and subjective performance indicators. He considers a setting where workers initially do not know their own abilities. Therefore, subjective evaluations have a feedback role: giving a bad evaluation is costly for the principal since the agent infers he has low ability and lowers his future efforts. In contrast, we focus on a moral hazard setting where the agent’s ability is commonly known.

Two recent contributions on optimal contracting with subjective evaluation include Lang (2013) and Sonne and Sebald (2012). In Lang (2013) the principal can justify subjective evaluation by sending a costly message. Sonne and Sebald (2012) consider a behavioral economics model in which unfair subjective evaluation by the principal induces a costly conflict with the agent. Similarly to money burning this may help the principal to truthfully commit to a higher wage.

Subjective evaluations have also been studied in models of repeated interactions, where intertemporal incentives for truthful revelation play a key role.⁹ Baker et al. (1994) and Pearce and Stacchetti (1998) study the combination of subjective and objective performance measures in infinitely repeated interactions; the focus of these papers differ from ours since thy impose exogenous assumptions on the set of admissible contracts that imply that, in the stage game, the private information of the principal cannot be used. While their focus is on the provision of intertemporal incentives to solve the principal’s incentive constraints, we study the optimal contract in a one-shot relation without any exogenous restrictions on the set of admissible contracts.

1.2 Structure of contents

The paper is organized as follows. Section 2 introduces the model. Section 3 uses the revelation principle to formulate the contract design problem. As a benchmark, we show in Sect. 4 that under unlimited liability, the principal can implement the first-best effort and extract the full surplus. Section 5 introduces limited liability of the agent and contains the core results of the paper, which are illustrated by an example in Sect. 6. Whereas the main part of the paper assumes that the principal reports his information before the public signal is realized, in Sect. 7 we show that the principal realizes the same payoff if he reports ex post, which implies that the principal has no incentive to acquire information early. Moreover, Sect. 7 also contains the extension of the model where the fraction of output lost upon firing is growing over time. Under this assumption, the principal will always report late enough such that no money burning is needed in the optimal contract. We summarize our results and discuss extensions in Sect. 8. All formal proofs are collected in an appendix.

2 The model

There is one principal and one agent, who are both risk-neutral. At some initial date the principal offers the agent an employment contract for a joint project. The agent’s outside option payoff at the contracting stage is normalized to zero. After being employed, the agent chooses some effort $e\in E \equiv [0, 1]$. From this effort choice the principal receives at some future date the (expected) output or benefit $x = x_{H}$ with probability e and $x = x_{L}$ with probability $1-e$, where $0< x_{L} < x_{H}$. The agent’s monetary equivalent of his disutility of effort is $c\left( e\right)$. His choice of effort is not observable, neither to outsiders nor to the principal. The principal pays the agent the wage w at the end of their contractual relationship.

After the agent has chosen e, the principal privately observes whether the (expected) output will be $x_L$ or $x_H$. The interpretation of $x_L$ and $x_H$ as signals of expected output allows for the possibility that the principal does not perfectly observe the realization of output before the contracting relation ends. The principal’s information and the realization of output are not publicly observable. The output or benefit received by the principal may, for example, represent the quality of a good or service whose private value is difficult to determine.¹⁰ The output may also represent the money-streams from a project, which may not be verifiable. For instance, if the principal operates in several businesses it may be impossible to ascribe money-streams to a particular project.¹¹ But we assume that there is an imprecise public signal $s\in \left\{ s_{L},s_{H}\right\}$, which is observable by outsiders and therefore verifiable. The public signal is correct with probability $\sigma \in (1/2, 1)$: if the output is $x_i$ the public signal is $s_i$ with probability $\sigma > 1/2$ and $s_j \ne s_i$ with probability $1-\sigma < 1/2$. Thus, the principal’s information is more precise than the public signal. In fact, his signal is a sufficient statistic in the sense that there is no additional information in the public signal. Nonetheless, public information is useful for the principal because the terms of a contract with the agent be made contingent directly on the public signal, whereas this is not possible for the principal’s private information. Only in the limit $\sigma \rightarrow 1$ our setup becomes equivalent to the standard principal–agent setting, where output is publicly observed and not only by the principal.¹²

The principal can prematurely terminate the project after observing the expected output. He thereby forgoes some part of the output so that his loss is increasing in the expected output. For simplicity, we assume that by firing the agent the principal destroys a fraction $\alpha \in \left( 0 ,1\right]$ of output.¹³ In a procurement relation, for instance, the principal may exit the relation by not accepting the services or goods produced by the agent. Similarly, in an employment relation, dismissing the agent may generate a loss of output because the agent still has to perform some additional contractible tasks to finish the job after his effort investment. Since these tasks are contractible, we can simply normalize the agent’s labor cost for this part of the project to zero. In what follows we use the terms ‘firing the agent’ and ‘terminating the project’ synonymously.

The parameter $\alpha$ indicates the extent to which the project is already completed when termination occurs. It may also reflect the delay cost from replacing the agent by another one to complete the job. In a buyer–seller relation, for example, where the principal refuses to trade after the agent has finished production of a good, $\alpha = 1$ as in Schmitz (2002). The agent’s gross payoff from being dismissed is equal to zero. But, because the termination decision is observable and contractible, his wage could be made contingent on whether the project is completed or not.¹⁴ We allow for stochastic contracts and denote by $\theta \in [0, 1]$ the probability that the project is prematurely terminated.

The inefficiency of premature project termination may be used to provide incentives for information revelation and effort choice (cf. Kahn and Huberman 1988). A similar incentive device is deleting some part of the surplus through ‘money burning’ activities. This may simply be achieved through some monetary payment to a passive third party. Alternatively, it can also present the cash equivalent of a (contractible) non-monetary penalty that harms one party but does not benefit the other party. For example, one of the parties may be degraded in rank or suffer a reputation loss. Further, as pointed out by MacLeod (2003), in a repeated relationship money burning may take the form of destructive equilibrium conflict that reduces the surplus from future trade. We permit money burning to be included as an incentive device in the contract. Without loss of generality, we assume that only the principal engages in money burning and denote its amount by $b \ge 0$.¹⁵

The agent’s effort cost $c(\cdot )$ satisfies $c\left( 0\right) = 0$ and $c^{\prime }\left( e\right) > 0$, $c^{\prime \prime }\left( e\right) >0$ for all $e > 0$. Further

$$\begin{aligned} c^{\prime }\left( 0\right) = 0, \quad c^{\prime }\left( 1\right) > x_H - x_L. \end{aligned}$$

(1)

Assumption (1) is sufficient to eliminate corner solutions for the agent’s effort when the agent’s remuneration is not restricted to be non-negative. For the analysis of the limited liability case, in which wages have to be non-negative, we assume in addition that

$$\begin{aligned} c^{\prime \prime \prime }\left( e\right) \ge 0, \quad c^{\prime \prime }\left( 0\right) < \frac{\sigma }{1-\sigma } \left( x_{H}-x_{L}\right) . \end{aligned}$$

(2)

These conditions avoid corner solutions with zero effort under limited liability. In addition, the first condition in (2) guarantees that the second–order conditions for the principal’s optimization problem are satisfied.¹⁶

The agent’s utility is $w-c\left( e\right)$, and the principal’s utility is $x\left( 1-\alpha \theta \right) -w - b$. If the agent’s effort were contractible and in the absence of limited liability restrictions, it would be chosen to maximize the expected joint surplus

$$\begin{aligned} S(e) \equiv e \, x_{H}+\left( 1-e\right) x_{L}-c\left( e\right) , \end{aligned}$$

(3)

which is obtained by setting $\theta = b = 0$. The first order condition

$$\begin{aligned} x_{H} - x_{L} = c^{\prime }\left( \tilde{e}\right) , \end{aligned}$$

(4)

thus determines the first-best effort level $\tilde{e}$, and the first-best surplus is $S(\tilde{e})$.

3 Contract design

In our setting, optimal contract design stipulates that the contracting parties publicly report their information whenever they observe new information (see Myerson 1986). Therefore, we consider contracts that require the principal to choose some verifiable message after observing the realization of output. By the revelation principle (Myerson 1979), it is sufficient to consider messages that enable the principal to report simply some output $\hat{x} \in \{ \hat{x}_L, \hat{x}_H \}$. Since the terms of the contract can be conditioned on the report, the principal’s subjective evaluation of performance complements the objective performance measure provided by the public signal.

Fig. 1

The sequence of events

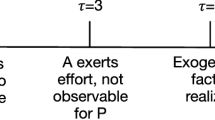
We first consider the case where the principal observes output and chooses a report before the public signal realizes. We discuss an alternative timing in Sect. 7. In Sects. 4, 5 and 6 the sequence of events is as follows: After a contract has been signed in stage $t = 0$, the agent chooses his effort e in stage $t = 1$. Then in stage $t = 2$ the principal observes the realization of output $x \in \left\{ x_{L}, x_{H}\right\}$ and reports $\hat{x} \in \left\{ \hat{x}_{L}, \hat{x}_{H}\right\}$. In stage $t = 3$ the contract is executed after the public signal s is observed. Figure 1 summarizes the sequence of events.

A contract specifies the wage, the probability of firing the agent before project completion, and the amount of money-burning contingent on the public signal s and the principal’s report $\hat{x}$. Let $\theta _{ij}$ denote the probability of firing when the public signal is $s_i$ and the principal’s report is $\hat{x}_j$. Similarly, $w_{ij}$ is the wage and $b_{ij}$ represents money burning if the public signal is $s_i$ and the report is $\hat{x}_j$. Note that, since the agent is risk-neutral, there is no loss of generality by not conditioning his wage on whether he is fired or not.¹⁷ Let

$$\begin{aligned}&w = \left( w_{HH},w_{HL},w_{LH},w_{LL}\right) , \quad \theta = \left( \theta _{HH},\theta _{HL},\theta _{LH},\theta _{LL}\right) , \nonumber \\&\text {and} \quad b = \left( b_{HH},b_{HL},b_{LH},b_{LL}\right) . \end{aligned}$$

(5)

A contract $\gamma = (w, \theta , b)$ then has to satisfy $\gamma \in \Gamma \equiv \left\{ (w, \theta , b) \in \mathbb {R}^{12} \vert \, b \ge 0, \,\theta \right. \left. \in [0,1]^4 \right\}$.

If the principal observes the output $x_L$ and reports $\hat{x}_j$ in stage 2, he receives the expected payoff

$$\begin{aligned} V_L(\gamma , \hat{x}_j)\equiv & {} \sigma \left[ (1 - \alpha \, \theta _{Lj}) x_L - w_{Lj} - b_{Lj}\right] \nonumber \\&+\,(1-\sigma ) \left[ (1 - \alpha \, \theta _{Hj}) x_L - w_{Hj} - b_{Hj}\right] , \end{aligned}$$

(6)

because the public signal in stage 3 is $s_L$ with probability $\sigma$ and $s_H$ with probability $1 - \sigma$. Analogously, if the output realization is $x_H$, the principal’s payoff is equal to

$$\begin{aligned} V_H(\gamma , \hat{x}_j)\equiv & {} \sigma \left[ (1 - \alpha \, \theta _{Hj}) x_H - w_{Hj} - b_{Hj}\right] \nonumber \\&+ (1-\sigma ) \left[ (1 - \alpha \, \theta _{Lj}) x_H - w_{Lj} - b_{Lj}\right] \end{aligned}$$

(7)

when he reports $\hat{x}_j$.

By the revelation principle, we can restrict ourselves to contracts that satisfy the incentive compatibility constraints

$$\begin{aligned} V_L(\gamma , \hat{x}_L) \ge V_L(\gamma , \hat{x}_H), \quad V_H(\gamma , \hat{x}_H) \ge V_H(\gamma , \hat{x}_L). \end{aligned}$$

(8)

These constraints ensure that reporting truthfully is optimal for the principal. In what follows, we refer to the principal’s incentive compatibility constraints in (8) as the ICP constraints. Since the principal reports truthfully in stage 2, his ex ante expected payoff at the contracting stage is

$$\begin{aligned} V(\gamma , e) \equiv e\, V_H(\gamma , \hat{x}_H) + (1-e)\, V_L(\gamma , \hat{x}_L). \end{aligned}$$

(9)

Truthful reporting by the principal also implies that the agent’s expected wage is

$$\begin{aligned} U_L(\gamma ) \equiv \sigma \, w_{LL} + (1-\sigma ) w_{HL} \end{aligned}$$

(10)

if the principal observes $x_L$, and

$$\begin{aligned} U_H(\gamma ) \equiv \sigma \, w_{HH} + (1-\sigma ) w_{LH} \end{aligned}$$

(11)

otherwise. Therefore, the agent’s ex ante payoff is

$$\begin{aligned} U(\gamma , e) \equiv e\, U_H(\gamma ) + (1-e)\, U_L(\gamma ) - c(e) \end{aligned}$$

(12)

at the contracting stage.¹⁸

Since effort is not observable, the agent chooses e in stage 1 to maximize his expected payoff in (12). This implies that e is determined by the first order condition¹⁹

$$\begin{aligned} U_H(\gamma ) - U_L(\gamma ) = c'(e). \end{aligned}$$

(13)

This condition ensures that e maximizes $U(\gamma , e)$ because $U(\gamma , e)$ is strictly concave in e. In what follows, we refer to the incentive compatibility condition for the agent’s effort in (13) as the ICA constraint.

At the contracting stage, the principal proposes a contract $\gamma$ that the agent can either accept or reject. As the agent’s outside option payoff is zero, he accepts the contract if it satisfies his individual rationality constraint

$$\begin{aligned} U(\gamma , e) \ge 0. \end{aligned}$$

(14)

In the following we refer to (14) as the IRA constraint.

4 Unlimited liability contracts

In this section, we briefly consider as a benchmark the optimal contract in the absence of non-negativity restrictions on the wage schedule w. Thus the agent is not protected by limited liability and he may face a penalty $w_{ij} < 0$ for some realization $(s_i, x_j)$ of the public signal and output. In this situation the principal’s problem is

$$\begin{aligned} \max _{(\gamma , e) \in \Gamma \times E} \, V(\gamma , e) \quad \text {subject to (8), (13), and (14) } \end{aligned}$$

(15)

because he has to satisfy the ICP, ICA, and IRA constraints.

As is well-known (see e.g. Harris and Raviv 1979), with a risk-neutral agent and without limited liability restrictions the principal is able to appropriate the first-best surplus by making the agent the residual claimant in the relationship. This can be done by ignoring the principal’s information and conditioning the agent’s wage exclusively on the public signal s. This explains the following observation:

Proposition 1

Let $(\gamma ,e)$ solve problem (15). Then $\theta =b=0\$and the wages can be chosen such that $\gamma$ ignores the principal’s information:

$$\begin{aligned} w_{HH}=w_{HL},\quad w_{LL}=w_{LH}. \end{aligned}$$

Moreover, e is equal to the first-best effort $\tilde{e}$ and the principal’s payoff $V(\gamma ,\tilde{e})$ is equal to the first-best surplus $S(\tilde{e})$.

Under unlimited liability, subjective evaluation by the principal plays no role, independently of the precision of the public signal.²⁰ Therefore, the principal actually has no incentive to supervise the agent to acquire information about the future realization of output. It is important for this result that negative wage payments are feasible, because the wage $w_{LL}=w_{LH}$ in Proposition 1 is negative. Indeed, it tends to minus infinity in the limit $\sigma \rightarrow 1/2$ where the public signal becomes uninformative.²¹

5 Limited liability contracts

We now turn to the more interesting case where the agent is protected by limited liability. Thus the principal has to obey the additional constraint that the agent’s wage cannot be negative and so his problem becomes

$$\begin{aligned} \max _{(\gamma , e) \in \Gamma \times E} \, V(\gamma , e) \quad \text {subject to (8), (13), (14) and } w \ge 0. \end{aligned}$$

(16)

In what follows, we analyze how the principal’s subjective information affects the terms of the contract $\gamma$ and the agent’s effort e. Since the principal’s information is more accurate than the public signal, the Informativeness Principle of Holmstrom (1979) suggests that his information should be used in determining the agent’s pay. This principle, however, is not directly applicable in the present context because the principal’s observation of performance is not publicly verifiable. Nonetheless, even though subjective evaluation is constrained by the ICP conditions, we will show that it will always be used in an optimal contract.

The following proposition establishes some characteristics of the solution to problem (16) that hold independently of the precision of the public signal:

Proposition 2

The solution $(\gamma ,e)$ of problem (16) has the following properties. (a) The agent’s wage is zero whenever the principal reports low output, i.e. $w_{HL}=w_{LL}=0$. The wages $w_{HH}\ge 0$ and $w_{LH}\ge 0$ are (not uniquely) determined by

$$\begin{aligned} \sigma w_{HH}+(1-\sigma )w_{LH}=c^{\prime }(e). \end{aligned}$$

(17)

(b) The agent is not fired and money burning does not occur whenever the principal reports high output. Further, there is no money burning if the principal’s report of low output is confirmed by the public signal. That is,

$$\begin{aligned} \theta _{HH}=b_{HH}=\theta _{LH}=b_{LH}=b_{LL}=0. \end{aligned}$$

(18)

(c) If money burning takes place after the principal’s report of low output is not confirmed by the public signal, then the agent also is fired with probability one, i.e. $b_{HL}>0$ implies $\theta _{HL}=1$.

(d) The agent’s effort e depends on firing $\theta$ and money burning b according to

$$\begin{aligned} c^{\prime }(e) = \sigma \left( \alpha \, \theta _{HL}\,x_{H}+b_{HL}\right) +\left( 1-\sigma \right) \alpha \theta _{LL}x_{H}. \end{aligned}$$

(19)

By part (a) of Proposition 2, the agent’s wage payment can be positive only if the principal reports that output is high. Since the principal’s information is more accurate than the public signal, this is the most efficient way of providing effort incentives as required by the ICA constraint (13). The observation is in line with Hayes and Schaefer (2000) who empirically find that, controlling for publicly observable performance measures, current CEO compensation predicts future firm performance. Further, (17) allows the principal to set $w_{HH} = w_{LH}=c^{\prime }(e)$ in an optimal contract. This together with $w_{HL}=w_{LL} =0$ means that the agent’s remuneration w can be chosen such that it depends only on the principal’s report and not at all on the public signal.

The remaining parts of Proposition 2 are implications of the ICP constraints (8). Here the relevant constraint is that the principal should have no incentive to underreport output, i.e. to claim that output is low while it is in fact high. This explains why according to part (b) there are no ex post inefficiencies if the principal reports high output.²² Inefficiencies serve only to deter the principal from falsely reporting low output. By committing the principal to pay a positive wage for high output they create effort incentives for the agent. As a result, the agent’s effort choice is related to the principal’s cost of firing and money burning as stated in part (d).

An implication of part (b) is that money burning can be optimal at most when the principal reports low output, but the public signal is high. Part (c) shows that in this event the agent is also fired with probability one, i.e. money burning is used only as an additional instrument if the constraint $\theta _{HL} \le 1$ is binding. Burning money is less attractive than firing to deter the principal from underreporting. This finding is similar to an observation by Khalil et al. (2015), who show that in their model output and effort distortions are more effective than burning money. To understand the intuition in our setting, note that the agent’s expected wage for high output in (17) is identical to the principal’s costs of money burning and firing on the r.h.s. of (19). Suppose the principal wants to increase the agent’s expected wage for high output to provide stronger effort incentives. He could do this without violating the ICP constraints e.g. by increasing $b_{HL}$ by some $\epsilon > 0$. This would cost him $\epsilon$ in the event that output is low but the public signal is high. Alternatively, the principal could achieve the same effort effect by raising $\theta _{HL}$ to $\theta '_{HL}$ so that $\alpha \, \theta _{HL}\,x_{H}$ is increased by $\epsilon$. His firing cost in the event of low output with a high public signal is then $\alpha \theta '_{HL} x_L < \alpha \theta '_{HL} x_H = \alpha \, \theta _{HL}\,x_{H} + \epsilon$. Thus, the firing cost increases by less than $\epsilon$. Firing serves as a incentive device to deter underreporting when output is high, but firing actually occurs only if output is low. In contrast with money burning firing costs are output dependent. This makes them a cheaper incentive device than money burning.

Proposition 2 already determines a substantial part of the variables in an optimal contract. In addition, it shows that $b_{HL}$ should be used only if the instrument $\theta _{HL}$ is exhausted in the sense that $\theta _{HL}=1$. Proposition 2 does not, however, help to compare the instruments $\theta _{LL}$ and $b_{HL}$. As we show in our next Lemma, their relative attractiveness turns out to depend on the precision of the public signal. Define the critical value

$$\begin{aligned} \bar{\sigma }\equiv \frac{\sqrt{x_{H}}}{\sqrt{x_{H}}+\sqrt{x_{L}}}. \end{aligned}$$

(20)

Note that $1/2<\bar{\sigma }<1$.

Lemma 1

Let $\left( \gamma ,e\right)$ solve problem (16). Then

• (a) $\theta _{LL}=0$ if $\sigma >\bar{\sigma }$;

• (b) if $\sigma <\bar{\sigma }$, $b_{HL}>0$ implies $\theta _{LL}=1$ and $\theta _{LL} > 0$ implies $\theta _{HL}=1$.

Lemma 1 further simplifies our analysis of problem (16). By part (a), there will be no project termination if both output and the public signal are low and the public signal is sufficiently informative: $\theta _{LL}$ is zero. It is then cheaper to deter the principal from underreporting by making him burn money, that is, by using the instrument $b_{HL}$. In fact, if the public signal is sufficiently informative, using $b_{HL}$ is attractive for two reasons. First, there is only a small chance that the public signal is high when output is low; therefore also the likelihood that the principal actually has to pay $b_{HL}$ is low. Second, $b_{HL}$ is quite effective in deterring the principal from underreporting if the public signal is sufficiently informative: given that output is high, the public signal is likely to be high as well; thus if the principal underreports, he has to pay $b_{HL}$ with high probability. As long as $\sigma >\bar{\sigma }$, these considerations outweigh the countervailing consideration (related to those in the discussion of Proposition 2) that burning money is less effective than firing.

If $\sigma <\bar{\sigma }$, however, these countervailing considerations make $\theta _{LL}$ a more attractive instrument than $b_{HL}$. Therefore, by part (b) of Lemma 1, if the public signal is not very informative, there is no money burning unless the agent is fired with probability one if the public signal correctly indicates low output. The second statement in part (b), shows a similar ranking for the variables $\theta _{LL}$ and $\theta _{HL}$. Roughly speaking, it means that the principal should first use $\theta _{HL}$ before using $\theta _{LL}$.

Together with our previous findings, the following proposition characterizes the optimal contract for the case where the public signal is sufficiently precise.

Proposition 3

Let $(\gamma ,e)$ solve problem (16). Suppose that $\sigma >\bar{\sigma }$. Then, irrespective of $\alpha$, $\theta _{LL} = 0$. After the principal’s report of low output is not confirmed by the public signal, money burning occurs if and only if the loss from firing the agent is sufficiently small. More specifically, there exists a critical $\bar{\alpha }\in (0,1)$ such

• (a) $b_{HL}>0$ and $\theta _{HL}=1$ if $\alpha <\bar{\alpha }$;

• (b) and $b_{HL}= 0$ and $\theta _{HL} \in (0, 1]$ if $\alpha \ge \bar{\alpha }$.

From Propositions 2 and 3 we conclude that as long as the public signal is sufficiently accurate, project termination and money burning occur if and only if the public signal conflicts with the principal’s report that output is low. When this happens, the public signal of high output is actually incorrect because the principal always reports truthfully. But, to credibly overrule the public signal, the principal has to be committed to some action that reduces his payoff.

Proposition 3 also shows that project termination and money burning are clearly ranked as incentive devices for truthful reporting: Money burning occurs only as a secondary instrument when the probability of firing the agent cannot be further increased because it is already equal to one. Indeed, money burning is not used at all in an optimal contract if $\alpha \ge \bar{\alpha }$, which means that the loss from terminating the project is relatively high. As we show below in Proposition 5, the principal’s expected payoff is increasing in $\alpha$ if $\alpha < \bar{\alpha }$, whereas for $\alpha \ge \bar{\alpha }$ it does not depend on $\alpha$. Thus, if the principal could choose the parameter $\alpha$, he would select some $\alpha \in [\bar{\alpha }, 1]$.²³ Over this range, he does not have to resort to money burning and $\alpha \theta _{HL}$ is a constant: when $\alpha$ increases, it is optimal to reduce $\theta _{HL}$ proportionally so that the expected loss from firing does not change.

Interestingly, under the conditions of Proposition 3, we have $\theta _{LL} = 0$ but $\theta _{HL} > 0$, i.e. an employee with a less favorable public signal can be less likely to be fired. The explanation of this perhaps counterintuitive result is that our analysis focuses on firing as an incentive device for the principal to report truthfully, rather than for the agent to exert effort. In our model the agent can be punished for low output only by setting his wage equal to zero. If firing would inflict some additional loss on the agent, then by firing the principal could further punish for low output and so enhance the agent’s effort incentives. Thus, extending our model e.g. by a reputation loss of the agent from being fired may imply that not only $\theta _{HL} > 0$ but also $\theta _{LL} > 0$.

But even within the framework of our model, the prediction of how the probability of firing depends on the public signal is ambiguous. On the one hand, under the conditions of Proposition 3 the probability of firing is higher when the public signal is high, because firing occurs only if the principal is contradicted by a public signal that falsely indicates high output. Yet, the likelihood for this to happen is relatively small since the public signal is relatively precise for $\sigma > \bar{\sigma }$. On the other hand, Proposition 4 (a) below shows for the case $\sigma < \bar{\sigma }$ that $\theta _{HL}=\theta _{LL}=1$ for low values of $\alpha$. In this case, the probability of firing is actually lower when the public signal is high than when it is low. To see this, note that the agent is fired if and only if the principal’s signal is low. But given that the principal’s signal is low, it is more likely that also the objective signal is low because $\sigma > 1/2$. In summary, the relation between the probability of firing and the public signal is not clear–cut and depends on the parameters $\sigma$ and $\alpha$. This ambiguity is in line with the empirical observation that the significance of the turnover–performance relation for CEOs is fairly small: as Murphy (1999) concludes in a survey on executive compensation, better performance according to verifiable measures empirically decreases the probability of termination, but this effect is economically small. A possible explanation might be that not only public performance measures but also subjective evaluations are important for dismissing a CEO.

Our next result shows that the properties of the optimal contract are similar, albeit slightly more complicated, in the case where the public signal is rather imprecise:

Proposition 4

Let $(\gamma ,e)$ solve problem (16). Suppose that $\sigma <\bar{\sigma }$. Then there exist critical values $\bar{\alpha }_{1}$ and $\bar{\alpha }_{2}$, with $0<\bar{\alpha }_{1}< \bar{\alpha }_{2}<1$, such that

• (a) $b_{HL}>0$ and $\theta _{HL}=\theta _{LL}=1$ if $\alpha <\bar{\alpha }_{1}$;

• (b) $b_{HL}=0, \theta _{LL} \in (0, 1]$ and $\theta _{HL}=1$ if $\alpha \in \left( \bar{\alpha }_{1},\bar{ \alpha }_{2}\right)$;

• (c) and $b_{HL}=\theta _{LL}=0$ and $\theta _{HL} \in (0, 1]$ if $\alpha > \bar{\alpha }_{2}$.

The main difference with Proposition 3 is that now the principal may have to fire the agent even if the public signal corroborates his report of low output. The reason is that the principal must be given additional incentives not to underreport if the public signal is relatively imprecise. But note that money burning never occurs if the public signal agrees with the principal’s report of low output, because $b_{LL} = 0$ by Proposition 2 (b).

Again, the incentive devices for truthful evaluation are hierarchically ordered. After the principal states low output, money burning is optimal only if at the same time the project is terminated with certainty. This is the case if the loss of output from firing the agent is rather low as $\alpha < \bar{\alpha }_1$. For higher values of $\alpha$ the loss from project termination is sufficient to keep the principal from underreporting and so money burning is suboptimal. But also the termination probabilities $\theta _{LL}$ and $\theta _{HL}$ are ranked as $\theta _{LL}$ can be positive only if $\theta _{HL} = 1$. Indeed, this happens for intermediate values of $\alpha$ in the interval $\left( \bar{\alpha }_{1},\bar{ \alpha }_{2}\right)$. In contrast, if $\alpha > \bar{\alpha }_{2}$ the principal has to fire the agent with positive probability only if the public signal $s = s_H$ provides no support for his evaluation $\hat{x} = \hat{x}_L$.

Our next result in this section shows that the principal benefits from increases in the parameters $\sigma$ and $\alpha$.

Proposition 5

Let $(\gamma ,e)$ solve problem (16). Then the principal’s payoff $V(\gamma ,e)$ is strictly increasing in $\sigma$. Moreover, $\partial V(\gamma ,e)/\partial \alpha > 0$ over the range where $\theta _{HL}=1$ in Propositions 3 and 4, and $\partial V(\gamma ,e)/\partial \alpha = 0$ if $\theta _{HL} < 1$.

The direct effect of a more precise public signal is not that it allows providing stronger incentives for the agent’s effort choice. Indeed, our conclusion from Proposition 2 shows that under an optimal contract the agent’s remuneration can be chosen to be independent of the public signal. The reason that the principal gains from an increase in $\sigma$ is that it relaxes his ICP constraints for truthful subjective evaluation. If the public signal becomes more accurate, it becomes easier to punish the principal for underreporting. As a consequence, the expected loss from money burning or project termination is reduced. For example, if $\sigma > \bar{\sigma }$ such losses occur by Proposition 3 only if the public signal $s_H$ is incorrect because the true output is $x_L$. As $\sigma$ increases, the likelihood of an incorrect signal decreases and therefore expected losses are reduced. In fact, in the limit $\sigma \rightarrow 1$ the expected loss from money burning or project termination tends to zero.

At first sight it may look paradoxical that the principal gains if firing the agent generates a higher loss of output. But again the intuition is that this relaxes the ICP conditions. Whenever $\theta _{HL} = 1$, an increase in $\alpha$ makes the principal better off because this allows him to reduce the less effective incentive instruments $b_{HL}$ or $\theta _{LL}$. This argument no longer holds if for high values of $\alpha$ it becomes optimal to set $\theta _{HL} < 1$ and $b_{HL} = \theta _{LL} =0$. Then the principal simply keeps $\alpha \theta _{HL}$ constant and so the expected loss from firing the agent does not depend on $\alpha$.

We conclude this section by investigating how the parameter $\alpha$ affects money burning $b_{HL}$ and the agent’s effort e in the optimal contract. Recall that, by Propositions 3 and 4, $b_{HL}>0$ over the range $\left[ 0,\bar{\alpha }\right)$ for $\sigma >\bar{\sigma }$, and over the range $\left[ 0,\bar{\alpha }_{1}\right)$ for $\sigma <\bar{\sigma }$.

Proposition 6

Let $\left( \gamma ,e\right)$ solve problem (16). Then $b_{HL}$ and e are both strictly decreasing in $\alpha$ over the range where $b_{HL}>0$ in Propositions 3 and 4. However, e is not monotone in $\alpha :$ there exists an $\varepsilon >0$ such that the optimal effort is strictly increasing in $\alpha$ over the interval $\left( \bar{\alpha },\bar{\alpha } +\varepsilon \right)$ if $\sigma >\bar{\sigma }$, and over the interval $\left( \bar{\alpha }_{1},\bar{\alpha }_{1}+\varepsilon \right)$ if $\sigma <\bar{\sigma }$.

Proposition 6 implies that the expected wage, which by Proposition 2 equals $ec^{\prime }\left( e\right)$, is also not monotone in $\alpha$. In the next section, we illustrate and explain Proposition 6 by an example.

6 An example

In this section we illustrate the solution of the principal’s problem (16) under limited liability by a numerical example for the case $\sigma > \bar{\sigma }$. Let

$$\begin{aligned} c(e) = 5 e^2/2, \quad x_L = 6, \quad x_H = 10, \quad \sigma = 3/4. \end{aligned}$$

(21)

Notice that $\sigma > \bar{\sigma }$ because $\bar{\sigma }\approx 0.5645$. Further, the first-best effort is $\tilde{e} = 4/5$.

The proof of Proposition 2 shows that we can ignore the IRA constraint (14) and the first of the two ICP constraints in (8). Since the optimal contract $\gamma$ satisfies (18) and $\theta _{LL} = 0$ by Lemma 1 (a), the principal’s ex ante payoff $V(\gamma , e)$ simplifies for the specification in (21) to

$$\begin{aligned} 6 + 4 \, e - \frac{e}{4} \left( 3 w_{HH} + w_{LH} \right) - \frac{1-e}{4}\left( 6 \alpha \,\theta _{HL} + b_{HL}\right) . \end{aligned}$$

(22)

Similarly, the second ICP constraint in (8) becomes

$$\begin{aligned} {30 \alpha \,\theta _{HL} + 3 b_{HL}} \ge {3 w_{HH} + w_{LH}}, \end{aligned}$$

(23)

and the ICA constraint (13) reduces to

$$\begin{aligned} 3 w_{HH} + w_{LH} = 20 e. \end{aligned}$$

(24)

The principal’s problem is therefore to choose e and $(w_{HH}, w_{LH}, \theta _{HL}, b_{HL}) \ge 0$ to maximize his payoff in (22) subject to (23), (24), and $\theta _{HL} \le 1$.²⁴

It is a bit tedious but straightforward to derive the solution of this optimization problem from the Kuhn–Tucker conditions: The critical value $\bar{\alpha }$ mentioned Proposition 3 is given by $\bar{\alpha }= 7/33$, and the solution for $(e, \theta _{HL}, b_{HL})$ is

$$\begin{aligned} e = \frac{7- 3 \alpha }{20}, \quad \theta _{HL} = 1, \quad b_{HL} = \frac{7- 33 \alpha }{3}, \quad \text {if} \quad \alpha \le \bar{\alpha }, \end{aligned}$$

(25)

and

$$\begin{aligned} e = \min \left[ \frac{3 \alpha }{2} , \frac{3}{8}\right] , \quad \theta _{HL} = \min \left[ 1, \frac{1}{4 \alpha } \right] , \quad b_{HL} = 0, \quad \text {if} \quad \alpha \ge \bar{\alpha }. \end{aligned}$$

(26)

The wages $w_{HH} \ge 0$ and $w_{LH} \ge 0$ are determined by (24) together with the solution for the agent’s effort e in (25) and (26), respectively.

Fig. 2

Solution variables $(e, \theta _{HL}, b_{HL})$

As Fig. 2 illustrates, the solution variables $(e, \theta _{HL}, b_{HL})$ are continuous functions of the parameter $\alpha$. But these functions have a kink at $\alpha = \bar{\alpha }$ and at $\alpha = 1/4 > \bar{\alpha }$. The kinks can occur at those values of $\alpha$ where the constraints $b_{HL} \ge 0$ and $\theta _{HL} \le 1$ become binding. Indeed, for $\alpha \in (\bar{\alpha }, 1/4)$ these constraints are both binding so that $b_{HL}$ and $\theta _{HL}$ remain constant within this interval. For $\alpha < \bar{\alpha }$ only the constraint $\theta _{HL} \le 1$ is binding and $b_{HL}$ is strictly decreasing in $\alpha$. Similarly, $\theta _{HL}$ is strictly decreasing when for $\alpha > 1/4$ only the constraint $b_{HL} \ge 0$ is binding .

Figure 2 also illustrates the result of Proposition 6 that the agent’s effort e is not a monotone function of $\alpha$. It is decreasing over the interval $[ 0 , \bar{\alpha })$, increasing over the interval $[\bar{\alpha }, 1/4)$, and constant for $\alpha \ge 1/4$. This is so because the agent’s effort incentive is positively related to the principal’s willingness to incur an efficiency loss after reporting low output. As long as $b_{HL} > 0$, an increase in the cost of project termination makes it optimal for the principal to reduce the amount of money burning at a rate that requires also reducing the agent’s effort. In contrast, over the range where we have a corner solution with $b_{HL} = 0$ and $\theta _{HL} = 1$, the principal’s cost of reporting low output necessarily increases with $\alpha$ and so he can provide stronger incentives for the agent. Finally, if $\theta _{HL} < 1$, the principal optimally adjusts to a higher value of the parameter $\alpha$ by keeping $\alpha \theta _{HL}$ constant. Thus the expected cost of project termination and, therefore, also the agent’s effort are not changed.

7 The timing of evaluation

We now consider the alternative timing of events where the principal becomes informed about the output realization after the public signal is observed. This means the sequence of events in Fig. 1 is reversed in stages $t = 2$ and $t = 3$. Whereas this does not affect the ICA and IRA constraints for the agent, the principal’s ICP constraints have to be reformulated because at the reporting stage he already knows the public signal.

If the principal observes the output $x_L$ and reports $\hat{x}_j$ in stage 3, his payoff depends on whether in stage 2 the public signal has been $s_L$ or $s_H$ according to

$$\begin{aligned} \begin{aligned} V_L(\gamma , \hat{x}_j\vert s_L)&\equiv (1 - \alpha \, \theta _{Lj}) x_L - w_{Lj} - b_{Lj} , \\ V_L(\gamma , \hat{x}_j\vert s_H)&\equiv (1 - \alpha \, \theta _{Hj}) x_L - w_{Hj} - b_{Hj}. \end{aligned} \end{aligned}$$

(27)

Similarly, his payoffs after observing $x_H$ depend on the public signal and are equal to

$$\begin{aligned} \begin{aligned} V_H(\gamma , \hat{x}_j \vert s_H)&\equiv (1 - \alpha \, \theta _{Hj}) x_H - w_{Hj} - b_{Hj}, \\ V_H(\gamma , \hat{x}_j \vert s_L)&\equiv (1 - \alpha \, \theta _{Lj}) x_H - w_{Lj} - b_{Lj}. \end{aligned} \end{aligned}$$

(28)

The ICP constraints for truthful reporting in the four possible (x, s)–constellations therefore are

$$\begin{aligned} \begin{aligned} V_L(\gamma , \hat{x}_L\vert s_L) \ge V_L(\gamma , \hat{x}_H\vert s_L),&\,&V_L(\gamma , \hat{x}_L\vert s_H) \ge V_L(\gamma , \hat{x}_H\vert s_H),\\ V_H(\gamma , \hat{x}_H\vert s_H) \ge V_H(\gamma , \hat{x}_L\vert s_H),&\,&V_H(\gamma , \hat{x}_H\vert s_L) \ge V_H(\gamma , \hat{x}_L\vert s_L). \end{aligned} \end{aligned}$$

(29)

Obviously, in comparison with the previous ICP conditions in (8) these constraints are more restrictive: The principal now has to report truthfully ex post for each realization of the public signal, while under (8) this is required only ex ante in expectation. Therefore, whenever $\gamma$ satisfies the ICP conditions in (29) it also satisfies these conditions in (8).

When the principal observes output after the realization of the public signal, his contracting problem becomes

$$\begin{aligned} \max _{(\gamma , e) \in \Gamma \times E} \, V(\gamma , e) \quad \text {subject to (29), (13), (14) and } w \ge 0. \end{aligned}$$

(30)

The only difference between this problem and problem (16) in Sect. 5 is that the ex ante ICP constraints (8) are replaced by the ex post constraints (29).

It is easy to see that in the case of unlimited liability contracts, which we studied in Sect. 4, it does not matter for the principal whether he reports his evaluation before or after the realization of the public signal. This is so because by Proposition 1 he can appropriate the first-best surplus by setting $b = \theta = 0$ and using a wage schedule that is independent of his evaluation. The same contract thus trivially satisfies also the ICP constraints for ex post reporting.²⁵ Perhaps more surprising is the following observation that also with limited liability the time at which the principal observes and reports output is irrelevant for his payoff.

Proposition 7

Let $(\gamma , e)$ solve problem (16). Then $\gamma$ satisfies the ICP constraints in (29), and therefore $(\gamma , e)$ also solves problem (30) if and only if $w_{LH} = \alpha \theta _{LL} x_H$ in (17). Thus for the principal’s payoff it does not matter whether he observes the realization of output before or after the public signal.

As part (a) of Proposition 2 shows, the agent’s remuneration is not uniquely determined by the solution of problem (16). This degree of freedom turns out to be sufficient for meeting also the more restrictive requirements for ex post truthful reporting. By (17) and (19), Proposition 7 implies that the agent’s wages in the solution of problem (30) satisfy

$$\begin{aligned} w_{HH} = \alpha \, \theta _{HL}\,x_{H}+b_{HL}, \quad w_{LH} = \alpha \theta _{LL} x_H. \end{aligned}$$

(31)

The payments $w_{HL}$ and $w_{LL}$ are zero by Proposition 2 (a). Thus the agent is never rewarded by a positive wage if the principal submits an unfavorable evaluation $\hat{x}_L$. If, however, he reports $\hat{x}_H$ the public signal becomes decisive because $w_{HH} > w_{LH}$ by Propositions 3 and 4. In contrast with our findings for ex ante reporting, the agent’s wage schedule now necessarily depends not only on the principal’s report but also on the public signal.

In our analysis the timing of subjective evaluation by the principal is exogenous. But from Proposition 7 we can draw some immediate conclusions for environments in which the principal can decide at which stage he evaluates the agent. Since the timing is irrelevant for his payoff, the principal has no incentive to acquire information at an early stage. Indeed, a slight modification of our model leads to the conclusion that delaying his report may even increase his payoff. Suppose that the parameter $\alpha$, which presents the degree of project completion, increases over time. For instance, in the model of Kahn and Huberman (1988) it makes sense to assume that the principal’s loss from firing the agent is highest when the worker’s firm specific human capital acquisition is nearly completed so that his output would soon become available. Replacing such a worker would delay production and is more costly than replacing a worker in a relatively early stage of his training. In such situations, we can conclude from Propositions 3–5 that the principal gains from postponing the agent’s evaluation as long as $\alpha$ lies in the range where $\theta _{HL} = 1$. Of course, the argument goes the other way round if $\alpha$ is decreasing over time, which may happen if the principal is able to appropriate some fraction of the output even after firing the agent. In this case the principal would optimally receive information early. In either case, the optimal time of reporting occurs when $\alpha$ is sufficiently large so that $\theta _{HL} < 1$. Interestingly, then money burning is no longer needed to prevent underreporting by the principal. Thus, if the timing of evaluation can be freely selected, reporting low output requires the principal to terminate the project and dismiss the agent with a positive probability, but he is not forced to burn money in addition.

8 Conclusions

We have studied a principal–agent relation where the principal possesses more accurate information about the outcome of the agent’s effort than a publicly verifiable performance measure. Despite being noisier than the principal’s information, public information is helpful to reduce the ex post inefficiencies that are unavoidably associated with subjective evaluation. As long as the public performance measure is not too imprecise, such inefficiencies occur only if the principal’s subjective evaluation is contradictory to the public signal. In general, the presence of public information relaxes the principal’s incentive compatibility constraints for truthful subjective evaluation.

Our analysis further shows that there is a clear pecking–order of the instruments that can be used to support truthful subjective evaluation. We show that ‘firing’ the agent, thereby destroying some part of the output, is more efficient than ‘burning money’. When the efficiency loss from firing is large enough, an optimal contract makes no use of money burning. Also, money burning is not optimal as long as there is a positive probability that the agent is not fired.

The problem of subjective performance evaluation consists of creating effort incentives for the agent and, at the same time, incentives for truthful reporting by the principal. This double incentive problem can be extended to a setting with more than one agent where the principal’s private information is about some aggregate measure such as the sum or the mean of the efforts.

As is standard in the literature on subjective evaluation, in our model the principal does not have to invest in information acquisition. An additional moral hazard problem occurs, however, if the principal’s information acquisition is costly and not observable. How this problem interacts with the other two incentive problems of subjective evaluation may be an interesting subject of further research.

Appendix

Proof of Proposition 1

Suppose that $\theta =b=0$, $w_{HH}=w_{HL}$, and $w_{LH}=w_{LL}$. Then the principal’s incentive constraints (8) are obviously satisfied. Let the difference of the wages satisfy

$$\begin{aligned} w_{HH}-w_{LL}=\frac{c^{\prime }\left( \tilde{e}\right) }{2\sigma -1}. \end{aligned}$$

(32)

Then by (13) the agent will choose the first-best effort $\tilde{e}$. In addition, by unlimited liability one can choose the wage $w_{LL}$ such that the agent’s individual rationality constraint holds with equality:

$$\begin{aligned} w_{LL}=c\left( \tilde{e}\right) -\left[ \frac{1-\sigma }{2\sigma -1}+\tilde{e}\right] c^{\prime }\left( \tilde{e}\right) . \end{aligned}$$

(33)

This contract implements the first-best effort $\tilde{e}$. Moreover, the principal’s payoff is equal to the first-best surplus $S\left( \tilde{e}\right)$ because the agent receives his outside option payoff. Obviously, the payoff of the principal cannot be higher; thus the contract considered here is optimal. Moreover, any optimal contract must implement the first-best effort $\tilde{e}$, for otherwise the principal’s payoff must be lower than the first-best surplus $S\left( \tilde{e}\right)$.

It remains to show that $\theta =b=0$ in any optimal contract. By assumption (1), $\tilde{e}\in \left( 0,1\right)$. Since $\sigma <1$, this implies that all four possible combinations of output and the public signal occur with positive possibility. Therefore, whenever $\theta \not =0$ or $b\not =0$, total surplus is below the first-best surplus $S\left( \tilde{e}\right)$, and hence the principal’s payoff is below $S\left( \tilde{e} \right)$ as well. $\square$

Proof of Proposition 2

The agent’s utility is

$$\begin{aligned} U\left( \gamma ,e\right) =\max _{e^{\prime }}U\left( \gamma ,e^{\prime }\right) \ge U\left( \gamma ,0\right) . \end{aligned}$$

(34)

Since $w\ge 0$ and $c\left( 0\right) =0$, $U\left( \gamma ,0\right) \ge 0$. Thus, in what follows we can ignore constraint (14) because it is automatically satisfied.

If $\left( \gamma ,e\right)$ solves problem (16), then obviously $\gamma$ must maximize $V(\gamma ,e)$ subject to the constraints in (16) when e is treated as a fixed parameter. The latter is a linear optimization problem since $V\left( \gamma ,e\right)$ and all constraints are linear in $\gamma$, and the Kuhn–Tucker conditions are both necessary and sufficient for a maximum. Following a standard method, we temporarily ignore that $\gamma$ has to satisfy the inequality $V_{L}\left( \gamma , \hat{x}_{L}\right) \ge V_{L}\left( \gamma ,\hat{x} _{H}\right)$ in (8), and show below that this constraint is automatically satisfied. Consider the Lagrangian

$$\begin{aligned} L \equiv V(\gamma ,e)+\lambda \left( V_{H}(\gamma ,\hat{x}_{H})-V_{H}(\gamma ,\hat{x}_{L})\right) +\mu \left( U_{H}(\gamma )-U_{L}(\gamma )-c^{\prime }(e)\right) \end{aligned}$$

(35)

with $\lambda \ge 0$. Note that $\mu >0$ as the agent’s incentive constraint must be binding.

Straightforward differentiation shows that $w_{HL}= w_{LL} = 0$ because

$$\begin{aligned} \frac{\partial L}{\partial w_{HL}}= & {} -\left( 1-e\right) \left( 1-\sigma \right) +\lambda \sigma -\mu \left( 1-\sigma \right) < \frac{\partial L}{\partial b_{HL}}=-\left( 1-e\right) \left( 1-\sigma \right) +\lambda \sigma , \nonumber \\\end{aligned}$$

(36)

$$\begin{aligned} \frac{\partial L}{\partial w_{LL}}= & {} -\left( 1-e\right) \sigma +\lambda \left( 1-\sigma \right) -\mu \sigma < \frac{\partial L}{\partial b_{LL}}=-\left( 1-e\right) \sigma +\lambda \left( 1-\sigma \right) . \end{aligned}$$

(37)

Moreover, $\theta _{HH}=b_{HH}=\theta _{LH}=b_{LH}=0$ because

$$\begin{aligned} \frac{\partial L}{\partial \theta _{HH}}= & {} \alpha x_{H} \, \frac{\partial L}{\partial b_{HH}} =- \alpha \sigma x_{H}\left( e + \lambda \right) <0, \end{aligned}$$

(38)

$$\begin{aligned} \frac{\partial L}{\partial \theta _{LH}}= & {} \alpha x_{H} \, \frac{\partial L}{\partial b_{LH}} =- \alpha \left( 1-\sigma \right) x_{H}\left( e +\lambda \right) <0. \end{aligned}$$

(39)

Finally, $b_{LL}=0$ because $\sigma > 1/2$ implies that

$$\begin{aligned} \frac{\partial L}{\partial b_{LL}} =-\left( 1-e\right) \sigma +\lambda \left( 1-\sigma \right) < \frac{\partial L}{\partial b_{HL}} =-\left( 1-e\right) \left( 1-\sigma \right) +\lambda \sigma . \end{aligned}$$

(40)

The above arguments prove part (b) of the proposition. To complete the proof of part (a), note that the agent’s incentive constraint (13) reduces to (17), because $w_{HL}= w_{LL} = 0$. Changing $w_{HH}$ and $w_{LH}$ such that Eq. (17) continues to hold leaves the principal’s payoff constant and does not interfere with any of the constraints. Therefore, the optimal wages $w_{HH}$ and $w_{LH}$ are not unique.

To prove part (c), note that $b_{HL}>0$ implies

$$\begin{aligned} \frac{\partial L}{\partial b_{HL}}=-\left( 1-e\right) \left( 1-\sigma \right) +\lambda \sigma =0, \end{aligned}$$

(41)

and thus $\lambda = {\left( 1-e\right) \left( 1-\sigma \right) }/{\sigma }$. This implies

$$\begin{aligned} \frac{\partial L}{\partial \theta _{HL}}= & {} -\left( 1-e\right) \left( 1-\sigma \right) \alpha x_{L}+\lambda \sigma \alpha x_{H} \end{aligned}$$

(42)

$$\begin{aligned}= & {} \left( 1-e\right) \left( 1-\sigma \right) \alpha \left( x_{H} - x_{L}\right) >0. \end{aligned}$$

(43)

Therefore $b_{HL}>0$ implies $\theta _{HL}=1$.

We now show that, as claimed above, only the second inequality in the ICP constraints (8) is binding. By parts (a) and (b), the principal’s incentive constraint $V_{H}(\gamma ,\hat{x} _{H})\ge V_{H}(\gamma ,\hat{x}_{L})$ in (8) simplifies to

$$\begin{aligned} \sigma w_{HH}+\left( 1-\sigma \right) w_{LH}\le \sigma \left( \theta _{HL}\alpha x_{H}+b_{HL}\right) +\left( 1-\sigma \right) \theta _{LL}\alpha x_{H}. \end{aligned}$$

(44)

Suppose this constraint is not binding. Then $\theta _{HL}$ must be strictly positive, since by limited liability the left hand side of (44) is non-negative, and by part (c) the right hand side can be positive only if $\theta _{HL}>0$. Thus one must have ${\partial L}/{\partial \theta _{HL}} \ge 0$, and by (42) this implies $\lambda > 0$. This proves that the constraint (44) must be binding and $V_{H}(\gamma ,\hat{x}_{H}) \ge V_{H}(\gamma ,\hat{x}_{L})$ must hold with equality.

Using part (a) and (b) the inequality $V_{L}(\gamma ,\hat{x}_{L})\ge V_{L}(\gamma ,\hat{x}_{H})$ in (8) reduces to

$$\begin{aligned} \left( 1-\sigma \right) \left( \theta _{HL}\alpha x_{L}+b_{HL}\right) +\sigma \theta _{LL}\alpha x_{L}\le \sigma w_{LH}+\left( 1-\sigma \right) w_{HH}. \end{aligned}$$

(45)

Since (44) is binding,

$$\begin{aligned}&\sigma w_{LH}+\left( 1-\sigma \right) w_{HH} =\frac{2\sigma -1}{\sigma } w_{LH}+\frac{1-\sigma }{\sigma }\left[ \sigma \left( \alpha \theta _{HL}x_{H}+b_{HL}\right) \right. \nonumber \\&\left. \qquad +\left( 1-\sigma \right) \alpha \theta _{LL}x_{H}\right] \nonumber \\&\quad \ge \left( 1-\sigma \right) \left( \alpha \theta _{HL}x_{H}+b_{HL}\right) +\frac{\left( 1-\sigma \right) ^{2}}{\sigma }\alpha \theta _{LL}x_{H} \end{aligned}$$

(46)

where the inequality follows from $w_{LH}\ge 0$. Subtracting the left hand side of (45) shows that

$$\begin{aligned}&\sigma w_{LH}+\left( 1-\sigma \right) w_{HH}-\left( \left( 1-\sigma \right) \left( \theta _{HL}\alpha x_{L}+b_{HL}\right) +\sigma \theta _{LL}\alpha x_{L}\right) \nonumber \\&\quad \ge \left( 1-\sigma \right) \alpha \theta _{HL}\left( x_{H}-x_{L}\right) +\left[ {\left( 1-\sigma \right) ^{2}}x_{H}/{\sigma } -\sigma x_{L}\right] \alpha \theta _{LL}. \end{aligned}$$

(47)

If $\theta _{LL}=0$, this implies that (45) is satisfied. Similarly, if $\left( 1-\sigma \right) ^{2}x_{H}/\sigma \ge \sigma x_{L}$, (45) is satisfied. To complete the argument, we show that one cannot have that $\left( 1-\sigma \right) ^{2}x_{H}/\sigma <\sigma x_{L}$ and $\theta _{LL}>0$. Indeed, $\theta _{LL}>0$ implies

$$\begin{aligned} \frac{\partial L}{\partial \theta _{LL}}=-\left( 1-e\right) \sigma \alpha x_{L}+\lambda \left( 1-\sigma \right) \alpha x_{H}\ge 0, \end{aligned}$$

(48)

and so

$$\begin{aligned} \lambda \ge \frac{\left( 1-e\right) \sigma x_{L}}{\left( 1-\sigma \right) x_{H}}. \end{aligned}$$

(49)

By the first equality in (41) this implies

$$\begin{aligned} \frac{\partial L}{\partial b_{HL}}\ge \left( 1-e\right) \left[ -\left( 1-\sigma \right) +\frac{\sigma x_{L}}{\left( 1-\sigma \right) x_{H}}\sigma \right] > 0, \end{aligned}$$

(50)

where the second inequality holds if $\left( 1-\sigma \right) ^{2}x_{H}/\sigma <\sigma x_{L}$. Since this would imply $b_{HL} = \infty$, we have shown that $\theta _{LL} = 0$ if $\left( 1-\sigma \right) ^{2}x_{H}/\sigma <\sigma x_{L}$.

Finally, statement (d) directly follows by combining (17) with (44), which holds with equality as shown above. $\square$

Proof of Lemma 1

(a) As shown in the last part of the proof Proposition 2, $\theta _{LL} = 0$ if $\left( 1-\sigma \right) ^{2}x_{H}/\sigma <\sigma x_{L}$. As this inequality is equivalent to $\sigma > \bar{\sigma }$, this proves part (a).

(b) Let $b_{HL}>0$ and $\sigma <\bar{\sigma }$. Then ${\partial L}/{\partial b_{HL}} = 0$ and so by the second equality in (36)

$$\begin{aligned} \lambda =\frac{\left( 1-e\right) \left( 1-\sigma \right) }{\sigma }. \end{aligned}$$

(51)

By the equality in (48) this implies

$$\begin{aligned} \frac{\partial L}{\partial \theta _{LL}}= & {} -\left( 1-e\right) \sigma \alpha x_{L}+\frac{\left( 1-e\right) \left( 1-\sigma \right) }{\sigma }\left( 1-\sigma \right) \alpha x_{H} \end{aligned}$$

(52)

$$\begin{aligned}= & {} \left( 1-e\right) \alpha \left[ -\sigma x_{L}+\frac{\left( 1-\sigma \right) }{\sigma }\left( 1-\sigma \right) x_{H}\right] > 0, \end{aligned}$$

(53)

where the last inequality holds because $\sigma <\bar{\sigma }$. Therefore, $\theta _{LL}=1$.

As shown in the proof of Proposition 2, $\theta _{LL}>0$ implies (49). Therefore, by (42)

$$\begin{aligned} \frac{\partial L}{\partial \theta _{HL}}\ge & {} -\left( 1-e\right) \left( 1-\sigma \right) \alpha x_{L}+\frac{\left( 1-e\right) \sigma x_{L}}{\left( 1-\sigma \right) x_{H}}\sigma \alpha x_{H} \end{aligned}$$

(54)

$$\begin{aligned}= & {} \left( 1-e\right) \alpha x_{L}\frac{2\sigma -1}{1-\sigma }>0. \end{aligned}$$

(55)

Therefore $\theta _{LL}>0$ implies $\theta _{HL}=1$. $\square$

Proof of Proposition 3

We substitute out all choice variable except e from the principal’s problem, and then optimize with respect to e. By parts (a) and (b) of Proposition 2, the principal’s profit $V\left( e,\gamma \right)$ equals

$$\begin{aligned} e x_{H}+\left( 1-e\right) x_{L}-e c^{\prime }\left( e\right) -\left( 1-e\right) \left[ \left( 1-\sigma \right) \left( \alpha \theta _{HL}x_{L}+b_{HL}\right) +\sigma \theta _{LL}\alpha x_{L}\right] . \end{aligned}$$

(56)

By Lemma 1, $\theta _{LL}=0$ and hence by (19),

$$\begin{aligned} \sigma \left( \alpha \, \theta _{HL}\,x_{H}+b_{HL}\right) =c^{\prime }(e). \end{aligned}$$

(57)

There are two possible cases. First, suppose that $\sigma \alpha x_{H}\ge c^{\prime }\left( e\right)$. This is equivalent to $e \le \hat{e}$, where $\hat{e} \equiv c^{\prime -1}\left( \sigma \alpha x_{H}\right)$. In this case, (57) and Proposition 2 (c) imply that $b_{HL}=0$ and $\theta _{HL}=c^{\prime }\left( e\right) /\left( \sigma \alpha x_{H}\right)$. Profit equals

$$\begin{aligned} \phi _{1}\left( e\right) \equiv e x_{H}+\left( 1-e\right) x_{L}-\left[ ec^{\prime }\left( e\right) +\left( 1-e\right) \left( 1-\sigma \right) \frac{c^{\prime }(e)x_{L}}{\sigma x_{H}}\right] . \end{aligned}$$

(58)

Second, suppose that $\sigma \alpha x_{H} < c^{\prime }\left( e\right) ,\$or, equivalently, $e>\hat{e}$. Then $\theta _{HL}=1$ and so by (57) $b_{HL} = {c^{\prime }(e)}/{\sigma }-\alpha x_{H}>0$. In this case, the principal’s payoff is

$$\begin{aligned} \phi _{2}\left( e\right) \equiv e x_{H}+\left( 1-e\right) x_{L}- ec^{\prime }\left( e\right) - \left( 1-e\right) \left( 1-\sigma \right) \left[ \frac{c^{\prime }(e)}{\sigma }-\alpha \left( x_{H}-x_{L}\right) \right] . \end{aligned}$$

(59)

Note that $\phi _{1}\left( e\right) \le \phi _{2}\left( e\right)$ if and only if $c^{\prime }\left( e\right) \le \sigma \alpha x_{H}$. Therefore, the principal’s payoff as a function of e can be written as

$$\begin{aligned} \tilde{V}\left( e\right) \equiv \min \left\{ \phi _{1}\left( e\right) ,\phi _{2}\left( e\right) \right\} . \end{aligned}$$

(60)

The functions $\phi _{1}$ and $\phi _{2}$ are strictly concave in e.²⁶ The minimum of two strictly concave functions is strictly concave, hence $\tilde{V}$ is strictly concave.

Differentiating $\phi _{2}$ yields

$$\begin{aligned} \phi _{2}^{\prime }\left( e\right) = x_{H}-x_{L}-\frac{2\sigma -1}{\sigma } c^{\prime }\left( e\right) -\left[ e + \left( 1-e\right) \frac{\left( 1-\sigma \right) }{\sigma }\right] c^{\prime \prime }\left( e\right) -\alpha \left( 1-\sigma \right) \left( x_{H}-x_{L}\right) . \end{aligned}$$

(61)

Define $e_{2}^{*}$ implicitly by $\phi _{2}^{\prime }\left( e_{2}^{*}\right) =0$. Since $\phi _{2}$ is strictly concave, $e_{2}^{*}$ is unique. Since $c^{\prime \prime \prime }(e) \ge 0$ and $c^{\prime }(0) = 0$, $e c^{\prime \prime }(e) \ge c^{\prime }(e)$ for all e. By (1) therefore $c^{\prime \prime }(1) \ge c^{\prime }(1) > x_H - x_L$. This implies $\phi _{2}^{\prime }\left( 1\right) <0$ and so $e_{2}^{*}<1$.

If $e_{2}^{*}>\hat{e}$, then $e_{2}^{*}$ maximizes the principal’s payoff $\tilde{V}\left( e\right)$. Moreover, if the optimal contract involves $b_{HL}>0$, then $e_{2}^{*}> \hat{e}$. We use the intermediate value theorem to show that $e_{2}^{*}> \hat{e}$ if and only if $\alpha$ is strictly smaller than a critical value $\bar{\alpha }\in \left( 0,1\right)$. The argument proceeds in three steps:

• 1. At $\alpha =0$, $\phi _{2}^{\prime }\left( 0\right) >0$ by assumptions (1) and (2). Moreover, if $\alpha =0$, the critical value $\hat{e}$ equals zero. Therefore, if $\alpha =0$, then $e_{2}^{*} > \hat{e}$.

• 2. The critical value $\hat{e}$ is continuous and strictly increasing in $\alpha$. Moreover, $e_{2}^{*}$ is continuous and strictly decreasing in $\alpha$:

  $$\begin{aligned} \frac{de_{2}^{*}}{\mathrm{d}\alpha }=-\frac{{\partial \phi _{2}^{\prime } \left( e_{2}^{*}\right) }/{\partial \alpha }}{\phi _{2}^{\prime \prime } \left( e_{2}^{*}\right) }=\frac{\left( 1-\sigma \right) \left( x_{H}-x_{L}\right) }{\phi _{2}^{\prime \prime }\left( e_{2}^{*}\right) } <0. \end{aligned}$$

  (62)

• 3. If $\alpha =1$, $e_{2}^{*}$ solves

  $$\begin{aligned} \frac{2\sigma -1}{\sigma }c^{\prime }\left( e_{2}^{*}\right) +\left[ e_{2}^{*}+\left( 1-e_{2}^{*}\right) \frac{\left( 1-\sigma \right) }{ \sigma }\right] c^{\prime \prime }\left( e_{2}^{*}\right) =\sigma \left( x_{H}-x_{L}\right) . \end{aligned}$$

  (63)

  Since $c^{\prime \prime \prime }\left( e\right) \ge 0 = c^{\prime }\left( 0\right)$, we have $ec^{\prime \prime }\left( e\right) \ge c^{\prime }\left( e\right)$ and thus

  $$\begin{aligned} \left[ \frac{2\sigma -1}{\sigma }+1\right] c^{\prime }\left( e_{2}^{*}\right) <\sigma \left( x_{H}-x_{L}\right) . \end{aligned}$$

  (64)

  By $\sigma >1/2$, it follows that $c^{\prime }\left( e_{2}^{*}\right) <\sigma x_{H}$. We conclude that, if $\alpha =1$, $c^{\prime }\left( e_{2}^{*}\right) <\sigma \alpha x_{H}$ and thus $e_{2}^{*}<\hat{e}$.

From steps 1–3, it follows that there exists a critical value $\bar{\alpha } \in \left( 0,1\right)$ such that $e^{*}>\hat{e}$ holds if and only if $\alpha <\bar{\alpha }$. As argued above, this implies that $b_{HL} > 0$ if and only if $\alpha <\bar{\alpha }$. $\square$

Proof of Proposition 4

There are three cases corresponding to statements (a), (b) and (c). First, suppose that $c^{\prime }\left( e\right) \le \sigma \alpha x_{H}$, or equivalently, $e\le \hat{e}=c^{\prime -1}\left( \alpha \sigma x_{H}\right)$. Then, by Proposition 2 (c) and (d), $\theta _{HL}=c^{\prime }\left( e\right) /\left( \sigma \alpha x_{H}\right)$ and $\theta _{LL}=b_{HL}=0$. Profit equals $\phi _{1}\left( e\right)$, as defined in the proof of Proposition 3. Second, suppose that $\sigma \alpha x_{H}<c^{\prime }\left( e\right) \le \alpha x_{H}$. This is equivalent to $e\in \left( \hat{e},\bar{e}\right] ,\$where $\bar{e}:=c^{\prime -1}\left( \alpha x_{H}\right)$. In this case $\theta _{HL}=1$, and $b_{HL}=0$, and $\theta _{LL}=\left[ c^{\prime }(e)-\sigma \alpha x_{H}\right] /\left[ \left( 1-\sigma \right) \alpha x_{H}\right]$. Using (56), the principal’s profit is

$$\begin{aligned} \phi _{3}\left( e\right) \equiv ex_{H}+\left( 1-e\right) x_{L}-ec^{\prime }\left( e\right) -\left( 1-e\right) \left[ \frac{\sigma x_{L}}{\left( 1-\sigma \right) x_{H}}c^{\prime }(e)-\alpha x_{L}\frac{2\sigma -1}{1-\sigma }\right] . \end{aligned}$$

(65)

Third, suppose that $c^{\prime }\left( e\right) >\alpha x_{H}$, or, equivalently, $e>\bar{e}$. Then $\theta _{LL}=\theta _{HL}=1$ and $b_{HL}=\left( c^{\prime }(e)-\alpha x_{H}\right) /\sigma$, and profit equals

$$\begin{aligned} \phi _{4}\left( e\right) \equiv ex_{H}+\left( 1-e\right) x_{L}-ec^{\prime }\left( e\right) -\left( 1-e\right) \left[ \alpha x_{L}+\frac{\left( 1-\sigma \right) \left( c^{\prime }(e)-\alpha x_{H}\right) }{\sigma }\right] . \end{aligned}$$

(66)

Note that $\phi _{1}\left( e\right) \le \phi _{3}\left( e\right)$ if and only if $c^{\prime }(e) \le \sigma \alpha x_H$. Moreover $\phi _{3}\left( e\right) \le \phi _{4}\left( e\right)$ if and only if $c^{\prime }(e) \le \alpha x_H$. Thus $c^{\prime }\left( e\right) \le \alpha \sigma x_{H}$ if and only if $\phi _{1}\left( e\right) =\min \left\{ \phi _{1}\left( e\right) ,\phi _{3}\left( e\right) ,\phi _{4}\left( e\right) \right\}$. Moreover, $\sigma \alpha x_{H}<c^{\prime }\left( e\right) \le \sigma x_{H}$ if and only if $\phi _{3}\left( e\right) <\phi _{1}\left( e\right)$ and $\phi _{3}\left( e\right) \le \phi _{4}\left( e\right)$. Therefore, the principal’s payoff can be written

$$\begin{aligned} \tilde{V}\left( e\right) =\min \left\{ \phi _{1}\left( e\right) ,\phi _{3}\left( e\right) ,\phi _{4}\left( e\right) \right\} . \end{aligned}$$

(67)

The functions $\phi _{1}$, $\phi _{3}$, and $\phi _{4}$ are strictly concave in e.²⁷ Therefore, $\tilde{V}$ is strictly concave in e.

Define $e_{4}^{*}$ implicitly by $\phi _{4}^{\prime }\left( e_{4}^{*}\right) =0$. Since $\phi _{4}$ is strictly concave, $e_{4}^{*}$ is unique. By assumption (1), $e_{4}^{*}<1$. If $e_{4}^{*} > \bar{e}$, then $e_{4}^{*}$ maximizes $\tilde{V}\left( e\right)$. Moreover, if the optimal contract involves $b_{HL}>0$, then $e_{4}^{*}>\bar{e}$.

We use the intermediate value theorem to show that $e_{4}^{*}>\bar{e}$ if and only if $\alpha$ is strictly smaller than a critical value $\bar{\alpha } _{1}\in \left( 0, 1\right)$. The argument proceeds in three steps:

• 1. If $\alpha =0$, $\phi _{4}^{\prime }\left( 0\right) >0 = \bar{e}$. Thus if $\alpha =0$, $e_{4}^{*}>\bar{e}$.

• 2. $e_{4}^{*}$ is continuous and strictly decreasing in $\alpha$. Moreover, $\bar{e}=c^{\prime -1}\left( \alpha x_{H}\right)$ is continuous and strictly increasing in $\alpha$.

• 3. At $\alpha =1$, $e_{4}^{*}$ solves

  $$\begin{aligned} x_{H}=c^{\prime }\left( e_{4}^{*}\right) + \left[ e_{4}^{*}\sigma +\left( 1-e_{4}^{*}\right) \left( 1-\sigma \right) \right] c^{\prime \prime }\left( e_{4}^{*}\right) \frac{\sigma }{2 \sigma -1}. \end{aligned}$$

  (68)

  Therefore, at $\alpha =1$, $\alpha x_{H}>c^{\prime }\left( e_{4}^{*}\right)$ and so $e_{4}^{*} < \bar{e}$.

Thus there exists an $\bar{\alpha }_{1}\in \left( 0,1\right)$ such that if $\alpha =\bar{\alpha }_{1}$, $e_{4}^{*}$ $=\bar{e}$. For all $\alpha <\bar{\alpha }_{1}$, the optimal effort is $e_{4}^{*}>\bar{e};$ moreover $b_{HL}>0$ and $\theta _{HL}=\theta _{LL}=1$. On the other hand, for all $\alpha \ge \bar{\alpha }_{1}$, $b_{HL}=0$.

It remains to show that there exists $\bar{\alpha }_{2}\in \left( \bar{\alpha } _{1},1\right)$ such that $\theta _{LL}>0$ if and only if $\alpha <\bar{\alpha }_{2}$. Note that $\theta _{LL}>0$ if and only $\phi _{3}^{\prime }\left( \hat{e}\right) >0$. To see this, first suppose that $\phi _{3}^{\prime }\left( \hat{e}\right) \le 0$. Then $\tilde{V}\left( e\right) < \tilde{V}\left( \hat{e}\right)$ for all $e>\hat{e}$ since $\tilde{V}(\cdot )$ is strictly concave. Hence the optimal effort is no larger than $\hat{e}$ and $\theta _{LL}=0$. Second, if $\phi _{3}^{\prime }\left( \hat{e}\right) >0$, then the optimal effort is strictly bigger than $\hat{e}$ and $\theta _{LL}>0$.

We use the intermediate value theorem to show that there exists $\bar{\alpha }_{2} \in \left( \bar{\alpha }_{1}, 1\right)$ such that $\phi _{3}^{\prime }\left( \hat{e}\right) >0$ if and only if $\alpha <\bar{\alpha }_{2}$. The argument proceeds in three steps:

• 1. By definition of $\bar{\alpha }_{1}$, if $\alpha =\bar{\alpha }_{1}$, then $\phi _{4}^{\prime }\left( e_{4}^{*}\right) =\phi _{4}^{\prime }\left( \bar{e}\right) =0$. Since $\phi _{3}$ and $\tilde{V}$ are strictly concave, and $\bar{e}>\hat{e}$, it follows that $\phi _{4}^{\prime }\left( \bar{e} \right) \le \phi _{3}^{\prime }\left( \bar{e}\right) <\phi _{3}^{\prime }\left( \hat{e}\right)$. Therefore, if $\alpha =\bar{\alpha }_{1}$, then $\phi _{3}^{\prime }\left( \hat{e}\right) >0$.

• 2. $\phi _{3}^{\prime }\left( \hat{e}\right)$ is continuous and strictly decreasing in $\alpha :$

  $$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\alpha }\phi _{3}^{\prime }\left( \hat{e}\right) =\left[ \frac{ \partial }{\partial \alpha }\phi _{3}^{\prime }\left( e\right) \right] _{e= \hat{e}}+\phi _{3}^{\prime \prime }\left( \hat{e}\right) \frac{\mathrm{d}\hat{e}}{ \mathrm{d}\alpha }<0. \end{aligned}$$

  (69)

• 3. Suppose $\alpha =1$. Since $e c^{\prime \prime }\left( e\right) \ge c^{\prime }\left( e\right)$,

  $$\begin{aligned} \phi _{3}^{\prime }\left( \hat{e}\right)= & {} x_{H}-x_{L}-x_{L}\frac{2\sigma -1}{1-\sigma }-\left[ 1-\frac{\sigma x_{L}}{\left( 1-\sigma \right) x_{H}} \right] c^{\prime }\left( \hat{e}\right) \end{aligned}$$

  (70)
  $$\begin{aligned}&-\left[ \hat{e}+\left( 1-\hat{e}\right) \frac{\sigma x_{L}}{\left( 1-\sigma \right) x_{H}}\right] c^{\prime \prime }\left( \hat{e}\right) \end{aligned}$$

  (71)
  $$\begin{aligned}< & {} x_{H}-x_{L}-x_{L}\frac{2\sigma -1}{1-\sigma }-\left[ 2-\frac{\sigma x_{L} }{\left( 1-\sigma \right) x_{H}}\right] \sigma x_{H} \end{aligned}$$

  (72)
  $$\begin{aligned}= & {} x_{H}-2\sigma x_{H}-\sigma x_{L}<0. \end{aligned}$$

  (73)

  Hence if $\alpha =1$, then $\phi _{3}^{\prime }\left( \hat{e}\right) <0$.

$\square$

Proof of Proposition 5

The principal’s expected payoff $\tilde{V}\left( e\right)$ defined in (60) and (67) is strictly increasing in $\sigma$ because the functions $\phi _1, \phi _2, \phi _3$ and $\phi _4$ are strictly increasing in $\sigma$. If $\theta _{HL} < 1$, then $\tilde{V}\left( e\right) = \phi _1(e)$, as defined in (58), and therefore $\partial \tilde{V}\left( e\right) /\partial \alpha = 0$. If $\theta _{HL} = 1$, then $\tilde{V}\left( e\right) = \phi _2(e)$ in the case of Proposition 3 and $\partial \tilde{V}\left( e\right) /\partial \alpha > 0$ because $\phi _2$ is strictly increasing in $\alpha$. In the case of Proposition 4, $\tilde{V}\left( e\right) = \min \left\{ \phi _3(e), \phi _4(e)\right\}$. As $\sigma < \bar{\sigma }$, $\phi _3$ and $\phi _4$ are strictly increasing in $\alpha$ and so $\partial \tilde{V}\left( e\right) /\partial \alpha > 0$. $\square$

Proof of Proposition 6

Suppose $\sigma >\bar{\sigma }$. By Proposition 3, $b_{HL}$ is strictly positive if and only if $\alpha <\bar{\alpha }$. Moreover, the proof of Proposition 3 establishes that, when $\alpha <\bar{\alpha }$, the profit maximizing effort is equal to $e_{2}^{*}$ which is strictly decreasing in $\alpha$ [see Eq. (62)], and $\theta _{HL}=1$ and $\theta _{LL}=0$. By Eq. (19) it follows that

$$\begin{aligned} b_{HL}=\frac{c^{\prime }\left( e_{2}^{*}\right) }{\sigma }-\alpha x_{H}, \end{aligned}$$

(74)

which is strictly decreasing in $\alpha$.

By the proof of Proposition 3, the principal’s profit from implementing effort e is $\tilde{V}\left( e\right) =\phi _{1}\left( e\right)$ if $e\le \hat{e}\equiv c^{\prime -1}\left( \sigma \alpha x_{H}\right)$, and $\tilde{V}\left( e\right) =\phi _{2}\left( e\right)$ if $e>\hat{e}$. We show that there exists an $\varepsilon ^{\prime }>0$ such that, if $\alpha \in \left( \bar{\alpha },\bar{\alpha }+\varepsilon ^{\prime }\right)$, the profit maximizing effort is equal to $\hat{e}$ and thus strictly increasing in $\alpha$.

Since $\tilde{V}\left( e\right)$ is strictly concave in e, it is sufficient to prove that $\phi _{1}^{\prime }\left( \hat{e}\right)>0>\phi _{2}^{\prime }\left( \hat{e}\right)$ if $\alpha \in \left( \bar{\alpha } ,\bar{\alpha }+\varepsilon ^{\prime }\right)$ for some $\varepsilon ^{\prime }>0$. Straightforward calculations show that

$$\begin{aligned} \phi _{1}\left( e\right) -\phi _{2}\left( e\right) =-\left( 1-e\right) \left( 1-\sigma \right) \left[ \frac{c^{\prime }(e)}{\sigma }\left( \frac{x_{L}}{x_{H}}-1\right) +\alpha \left( x_{H}-x_{L}\right) \right] . \end{aligned}$$

(75)

Since $\phi _{1}\left( \hat{e}\right) =\phi _{2}\left( \hat{e}\right)$,

$$\begin{aligned} \frac{c^{\prime }(\hat{e})}{\sigma }\left( \frac{x_{L}}{x_{H}}-1\right) +\alpha \left( x_{H}-x_{L}\right) =0. \end{aligned}$$

(76)

Moreover, if $\alpha =\bar{\alpha }$, then $\phi _{2}^{\prime }\left( \hat{e}\right) =0$ by construction of $\bar{\alpha }$. Thus $\alpha =\bar{\alpha }$ implies

$$\begin{aligned} \phi _{1}^{\prime }\left( \hat{e}\right) =\phi _{1}^{\prime }\left( \hat{e}\right) -\phi _{2}^{\prime }\left( \hat{e}\right) =-\left( 1-\hat{e}\right) \left( 1-\sigma \right) \frac{c^{\prime \prime }(\hat{e})}{\sigma }\left( \frac{x_{L}}{x_{H}}-1\right) >0. \end{aligned}$$

(77)

By continuity, there exists $\varepsilon ^{\prime }>0$ such that $\phi _{1}^{\prime }\left( \hat{e}\right) >0$ when $\alpha \in \left( \bar{\alpha },\bar{\alpha }+\varepsilon ^{\prime }\right)$. It remains to show that $\phi _{2}^{\prime }\left( \hat{e}\right) <0$ when $\alpha \in \left( \bar{\alpha },\bar{\alpha }+\varepsilon ^{\prime }\right)$. Equation (61) implies that $\phi _{2}^{\prime }\left( e\right)$ is strictly decreasing in $\alpha$ (holding e constant). Moreover, $\hat{e}$ is strictly increasing in $\alpha$, and $\phi _{2}^{\prime \prime }\left( e\right) <0$. Since $\alpha =\bar{\alpha }$ implies $\phi _{2}^{\prime }\left( \hat{e}\right) =0$, it follows that $\phi _{2}^{\prime }\left( \hat{e}\right) <0$ when $\alpha \in \left( \bar{\alpha },\bar{\alpha }+\varepsilon ^{\prime }\right)$.

Suppose $\sigma <\bar{\sigma }$. By Proposition 4, $b_{HL}$ is strictly positive if and only if $\alpha <\bar{\alpha }_{1}$. Moreover, the proof of Proposition 4 establishes that, when $\alpha <\bar{\alpha }_{1}$, the profit maximizing effort is equal to $e_{4}^{*}$ which is strictly decreasing in $\alpha$, and $\theta _{LL}=\theta _{HL}=1$. By Eq. (19), it follows that

$$\begin{aligned} b_{HL}=\frac{c^{\prime }\left( e_{4}^{*}\right) -\alpha x_{H}}{\sigma }, \end{aligned}$$

(78)

which is strictly decreasing in $\alpha$.

By the proof of Proposition 4, the principal’s profit from implementing effort e is $\tilde{V}\left( e\right) =\phi _{1}\left( e\right)$ if $e\le \hat{e}$, $\tilde{V}\left( e\right) =\phi _{3}\left( e\right)$ if $\hat{e}<e\le \bar{e}\equiv c^{\prime -1}\left( \alpha x_{H}\right)$, and $\tilde{V}\left( e\right) =\phi _{4}\left( e\right)$ if $e>\bar{e}$. We show that there exists an $\varepsilon ^{\prime \prime }>0$ such that, if $\alpha \in \left( \bar{\alpha }_{1},\bar{\alpha }_{1} +\varepsilon ^{\prime \prime }\right)$, the profit maximizing effort is equal to $\bar{e}$ and thus strictly increasing in $\alpha$.

Since $\tilde{V}\left( e\right)$ is strictly concave in e, it is sufficient to prove that $\phi _{3}^{\prime }\left( \bar{e}\right)>0>\phi _{4}^{\prime }\left( \bar{e}\right)$ if $\alpha \in \left( \bar{\alpha } _{1},\bar{\alpha }_{1}+\varepsilon ^{\prime \prime }\right)$ for some $\varepsilon ^{\prime \prime }>0$. Straightforward calculations show that

$$\begin{aligned} \phi _{3}\left( e\right) -\phi _{4}\left( e\right) =-\left( 1-e\right) \left[ \frac{\sigma x_{L}}{\left( 1-\sigma \right) x_{H}}c^{\prime }(e)-\alpha x_{L}\frac{\sigma }{1-\sigma } -\frac{\left( 1-\sigma \right) \left( c^{\prime }(e)-\alpha x_{H}\right) }{\sigma }\right] .\nonumber \\ \end{aligned}$$

(79)

Since $\phi _{3}\left( \bar{e}\right) =\phi _{4}\left( \bar{e}\right)$,

$$\begin{aligned} \frac{\sigma x_{L}}{\left( 1-\sigma \right) x_{H}}c^{\prime }(\bar{e})-\alpha x_{L}\frac{\sigma }{1-\sigma }-\frac{\left( 1-\sigma \right) \left( c^{\prime }(\bar{e})-\alpha x_{H}\right) }{\sigma }=0. \end{aligned}$$

(80)

Suppose that $\alpha =\bar{\alpha }_{1}$. Then $\phi _{4}^{\prime }\left( \bar{e}\right) =0$ by construction of $\bar{\alpha }_{1}$. Thus

$$\begin{aligned} \phi _{3}^{\prime }\left( \bar{e}\right) =\phi _{3}^{\prime }\left( \bar{e}\right) -\phi _{4}^{\prime }\left( \bar{e}\right) =-\left( 1-\bar{e}\right) \left( \frac{\sigma x_{L}}{\left( 1-\sigma \right) x_{H}} -\frac{\left( 1-\sigma \right) }{\sigma }\right) c^{\prime \prime }(\bar{e}) \end{aligned}$$

(81)

which is strictly positive since $\sigma <\bar{\sigma }$. By continuity, there exists some $\varepsilon ^{\prime \prime }>0$ such that $\phi _{3}^{\prime }\left( \bar{e}\right) >0$ when $\alpha \in \left( \bar{\alpha }_{1},\bar{\alpha }_{1}+\varepsilon ^{\prime \prime }\right)$. It remains to show that $\phi _{4}^{\prime }\left( \bar{e}\right) <0$ when $\alpha \in \left( \bar{\alpha }_{1},\bar{\alpha }_{1}+\varepsilon ^{\prime \prime }\right)$. Equation (66) implies that $\frac{\partial }{\partial \alpha }\phi _{4}^{\prime }\left( e\right) =x_{L}-\frac{1-\sigma }{\sigma }x_{H}<0$, where the inequality follows from $\sigma <\bar{\sigma }$. That is, $\phi _{4}^{\prime }\left( e\right)$ is strictly decreasing in $\alpha$ (holding e constant). Moreover, $\bar{e}$ is strictly increasing in $\alpha$, and $\phi _{4}^{\prime \prime }\left( e\right) <0$. Since $\alpha =\bar{\alpha }_{1}$ implies $\phi _{4}^{\prime }\left( \bar{e}\right) =0$, it follows that $\phi _{4}^{\prime }\left( \bar{e}\right) <0$ when $\alpha \in \left( \bar{\alpha }_{1},\bar{\alpha }_{1}+\varepsilon ^{\prime \prime }\right)$.

Setting $\varepsilon :=\min \left\{ \varepsilon ^{\prime },\varepsilon ^{\prime \prime }\right\}$ concludes the proof. $\square$

Proof of Proposition 7

Since $(\gamma , e)$ solves problem (16), $\gamma$ satisfies (18) and $w_{LL} = w_{HL} = 0$ by Proposition 2 (a). This reduces the constraints in (29) to

$$\begin{aligned} V_L(\gamma , \hat{x}_L\vert s_L) - V_L(\gamma , \hat{x}_H\vert s_L)= & {} w_{LH}- \alpha \theta _{LL} x_L \ge 0, \end{aligned}$$

(82)

$$\begin{aligned} V_L(\gamma , \hat{x}_L\vert s_H) - V_L(\gamma , \hat{x}_H\vert s_H)= & {} w_{HH} -\alpha \,\theta _{HL}\, x_L - b_{HL} \ge 0, \end{aligned}$$

(83)

$$\begin{aligned} V_H(\gamma , \hat{x}_H\vert s_H) - V_H(\gamma , \hat{x}_L\vert s_H)= & {} \alpha \, \theta _{HL}\,x_H + b_{HL} - w_{HH} \ge 0, \end{aligned}$$

(84)

$$\begin{aligned} V_H(\gamma , \hat{x}_H\vert s_L) - V_H(\gamma , \hat{x}_L\vert s_L)= & {} \alpha \theta _{LL} x_H- w_{LH} \ge 0. \end{aligned}$$

(85)

Further, (17) and (19) imply

$$\begin{aligned} \sigma w_{HH} + (1-\sigma ) w_{LH} = \sigma (\alpha \,\theta _{HL}\, x_H + b_{HL}) + (1-\sigma )\alpha \,\theta _{LL}\, x_H. \end{aligned}$$

(86)

By (85) $w_{LH} \le \alpha \theta _{LL} x_H$. Suppose that this inequality is strict, i.e. $w_{LH} < \alpha \theta _{LL} x_H$. Then (86) implies that $w_{HH} > \alpha \,\theta _{HL}\, x_H + b_{HL}$, a contradiction to (84). This proves that the constraints in (29) cannot be satisfied if $w_{LH} \ne \alpha \theta _{LL} x_H$.

Now let $w_{LH} = \alpha \theta _{LL} x_H$. Then (82) and (85) hold because $x_L < x_H$. As $w_{LH} = \alpha \theta _{LL} x_H$, (86) implies

$$\begin{aligned} w_{HH} = \alpha \,\theta _{HL}\, x_H + b_{HL}. \end{aligned}$$

(87)

Thus the equality holds in (84), and the strict inequality holds in (83) because $x_L < x_H$. This proves that (82)–(85) are satisfied if $(\gamma , e)$ solves problem (16) with $w_{LH} = \alpha \theta _{LL} x_H$ and $w_{HH} = \alpha \,\theta _{HL}\, x_H + b_{HL}$. $\square$