Optimal banking contracts and financial fragility

Abstract

We study a finite-depositor version of the Diamond–Dybvig model of financial intermediation in which the bank and all depositors observe withdrawals as they occur. We derive the constrained efficient allocation of resources in closed form and show that this allocation provides liquidity insurance to depositors. The contractual arrangement that decentralizes this allocation resembles a standard bank deposit with a demandable debt-like structure. When withdrawals are unusually high, however, depositors who withdraw relatively late experience significant losses. This contractual arrangement can be fragile, admitting another equilibrium in which depositors run on the bank by withdrawing funds regardless of their liquidity needs.

1 Introduction

Banks and other financial intermediaries engage in maturity transformation by issuing short-term liabilities while investing in assets whose full return is realized over a longer time horizon. In fact, much of an intermediary’s liabilities are usually payable on demand, meaning that a holder is entitled to request immediate repayment. These liabilities are also debt-like in the sense that the value of a claim is typically not contingent on the precise timing of withdrawal; during normal times, all holders receive the “face value” of their claim. During episodes of high withdrawal demand, however, claims that are repaid late in the process can be subjected to considerable discounts. Such intermediation arrangements often appear to be fragile in the sense of being susceptible to runs—events in which liability holders rush en masse to redeem their claims and, as a result, resources are allocated inefficiently. In this paper, we provide a model of financial intermediation that accounts for all of these features simultaneously. We follow Green and Lin (2003), Peck and Shell (2003) and others in that we place no restrictions on financial arrangements or the allocation of resources other than those explicitly specified as part of the environment.

Arrangements based on maturity transformation and debt-like liabilities are not limited to retail banking; they are widespread and integral parts of the modern financial system. A number of such arrangements experienced events resembling a run during the recent financial crisis, including wholesale deposits, brokerage accounts, repurchase agreements and money market mutual funds, to name a few.¹ Regulatory reform efforts in the wake of the crisis have focused on limiting maturity transformation by requiring financial institutions to more closely align the maturity structure of their assets with that of their liabilities and to limit the debt-like features of some contracts. Evaluating the desirability of such reforms requires having a theory of financial arrangements based on maturity transformation that explains why these arrangements arise and what social benefits they offer.

Diamond and Dybvig (1983) laid the foundations for such a theory by identifying important elements of an economic environment in which financial intermediaries play a socially valuable role while being susceptible to runs. In their model, high-return investment takes time to mature and agents have random needs for immediate liquidity. A risk-sharing arrangement resembling a bank can improve the allocation of resources in this setting. The fact that a depositor’s liquidity needs are private information requires the bank to allow depositors to choose when to withdraw their funds. This ability to choose, in turn, creates the potential for inefficient withdrawals and fragility. However, private information alone is not enough to explain the fragility of financial arrangements as an equilibrium outcome. Diamond and Dybvig hint at two other elements that would be needed for this theory to successfully explain fragility: (i) some form of first-come, first-served (or sequential service) constraint and (ii) a degree of aggregate uncertainty about the total demand for liquidity. While the role of these additional elements was discussed informally in Diamond and Dybvig’s seminal work, the precise details of the arguments were left mostly unexplored.

Starting with Wallace (1988), a literature has developed that attempts to explicitly model these elements of the theory and investigate the extent to which fragility is an inherent feature of banking and other financial arrangements.² The approach in this literature is to fully specify the physical environment and to derive the predicted outcomes by solving an allocation problem with no further restrictions on what can be attained. Two important lessons have emerged. First, fragility obtains only if the payouts associated with some of an institution’s short-term liabilities are relatively insensitive to the state of aggregate liquidity demand. In addition, the information available to depositors when making withdrawal decisions interacts with the payout structure in subtle ways to determine the fragility of an arrangement.

The relative insensitivity of payouts in these models is a direct consequence of sequential service. A bank learns about the level of aggregate liquidity demand by observing individual depositors’ actions. In the absence of sequential service, the bank would fully observe this demand before redeeming any liabilities and would set payouts accordingly. Under standard assumptions on preferences, the resulting allocation would give depositors no incentive to run. However, when withdrawals happen sequentially and depositors must be served as they arrive, the bank has less information when payouts are made, and hence, these payouts are necessarily less responsive to underlying conditions. As more withdrawals occur, the bank will gradually learn the level of aggregate liquidity demand and adjust payouts to withdrawing depositors accordingly. In such a setting, information about a depositor’s position in the withdrawal order becomes critical to her decision. With no information, each depositor will consider it equally likely that she occupies each possible position in this order. All depositors will then make the same comparison between the expected utilities of withdrawing early and of withdrawing late. If each depositor has some information about her own position, on the other hand, each will face a different decision problem. The information structure thus determines the nature of the strategic interaction between depositors and therefore influences the scope for fragility.

Previous work has derived different results from different combinations of assumptions about sequential service and the information structure. Green and Lin (2003) present one reasonable formulation and show that, under certain conditions, the optimal banking arrangement is not fragile. In their model, all depositors report to the bank sequentially and either withdraw their deposit or communicate that they do not currently wish to withdraw. Depositors have some information about their likely position in the withdrawal order when they make this decision. The bank conditions the payout to a withdrawing depositor on all previous reports: Subsequent withdrawals are adjusted downward if a depositor makes an early withdrawal and upward if she instead reports that she will not withdraw early. In this way, the payouts to depositors may be highly sensitive to the pattern of withdrawal decisions. Green and Lin show that this sensitivity can be sufficient to rule out bank runs as an equilibrium outcome. Peck and Shell (2003) consider the case where depositors have no information about their place in the withdrawal order and assume that only those depositors intending to withdraw report to the bank. Under this alternative specification, they show that bank runs can arise in equilibrium.³

In this paper, we propose an alternative environment that shares many features of these earlier specifications but modifies some that we regard as extreme and perhaps unrealistic. In contrast to Green and Lin (2003), we assume that depositors only report to the bank when they wish to withdraw. In this respect, we follow Peck and Shell (2003), who state that “[i]t is hard to imagine people visiting their bank for the purpose of telling them that they are not interested in making any transactions at the present time.” Additionally, we depart from the previous literature by assuming that each depositor can observe how many withdrawals have already occurred when deciding whether to withdraw. As a result, they can calculate exactly how much they will receive if they choose to withdraw, instead of facing uncertainty that is only resolved after the withdrawal decision has been made, as in both Green and Lin (2003) and Peck and Shell (2003).

We show that this new specification of the environment induces some properties in the banking arrangement that resemble those observed in reality. In particular, the bank’s payout schedule is initially almost completely insensitive to the pattern of withdrawal decisions and, in this sense, displays the debt-like property that is common in demand-deposit contracts. Furthermore, in situations where withdrawal demand becomes unusually high, depositors who are late to withdraw suffer significant discounts relative to the face value of their deposits, a type of “partial suspension of convertibility” that Wallace (1990) argues was a common feature of historical banking panics.⁴ We also show that the frictions in our environment can restrict the flow of information sufficiently to make a run on the bank consistent with equilibrium. The key ingredient for this result is that when the bank only observes the actions of depositors who withdraw, it is relatively slow to react to a situation in which aggregate withdrawal demand is high, as occurs when depositors run on the bank. This slow reaction is anticipated by depositors and creates an incentive for those who have the opportunity to be relatively early in the withdrawal order to withdraw regardless of their liquidity needs. Based on these findings, we conclude that several common features of banking—the face-value property of demand deposits, sharp discounts during crises and fragility—may have the same fundamental source: the gradual revelation of information inherent in a withdrawal process that takes place sequentially.

The paper is organized as follows. Section 2 describes the environment, including our specification of sequential service and the information structure. Section 3 derives the efficient allocation of resources in the absence of private information, which serves as a useful benchmark in the rest of the analysis. Section 4 returns to the case of private information and describes a banking arrangement that aims to implement this allocation. Section 5 studies financial fragility and demonstrates that a bank run can arise in our environment. Section 6 offers some concluding remarks.

2 The environment

There are two time periods, indexed by $t\in \left\{ 0,1\right\}$, and a finite number I of depositors. There is a single good that can be consumed in each period. Let $c_{i}=\left( c_{i}^{0},c_{i}^{1}\right) \in \mathbb {R} _{+}^{2}$ denote the consumption of depositor i in each period. A depositor’s preferences depend on her type $\omega _{i}\in \left\{ 0,1\right\}$. If $\omega _{i}=0,$ the depositor is impatient and only cares about consumption in period 0. If $\omega _{i}=1,$ the depositor is patient and cares about the sum of her consumption in the two periods. Depositor i’s utility level is given by

$$\begin{aligned} u\left( c_{i}^{0}+\omega _{i}c_{i}^{1}\right) =\frac{1}{1-\gamma }\left( c_{i}^{0}+\omega _{i}c_{i}^{1}\right) ^{1-\gamma }. \end{aligned}$$

(1)

As in Diamond and Dybvig (1983), we assume the coefficient of relative risk aversion $\gamma$ is greater than unity. Each depositor’s type $\omega _{i}$ is an independent draw from a Bernoulli distribution, where $\pi$ is the probability of being impatient, and is private information. Let $\omega =\left( \omega _{1},\ldots ,\omega _{I}\right)$ denote the vector of types for all depositors and let $\varOmega$ denote the set $\left\{ 0,1\right\}$, so that we have $\omega _{i}\in \varOmega$ and $\omega \in \varOmega ^{I}$.

We use $\theta \left( \omega \right)$ to denote the total number of patient depositors in the profile $\omega ,$ that is

$$\begin{aligned} \theta \left( \omega \right) =\sum _{i=1}^{I}\omega _{i}. \end{aligned}$$

Let $p\left( \theta \right)$ denote the probability of the set of profiles $\omega$ in which there are exactly $\theta$ patient depositors. Since types are independent across depositors, $\theta$ is a binomial random variable and we have

$$\begin{aligned} p\left( \theta \right) =C\left( I,\theta \right) \left( 1-\pi \right) ^{\theta }\pi ^{I-\theta }, \end{aligned}$$

(2)

where C is the standard combinatorial function

$$\begin{aligned} C\left( I,\theta \right) =\frac{I!}{\theta !\left( I-\theta \right) !}. \end{aligned}$$

(3)

There is also a bank that has an endowment of I units of the good at the beginning of date 0 and aims to distribute these resources to maximize depositors’ expected utility.⁵ A depositor can withdraw from the bank either in period 0 or in period 1,  but not both. Depositors are isolated from each other, and goods must be consumed immediately after withdrawal. These assumptions imply that no markets exist in which depositors could trade after withdrawing; a depositor simply consumes what she receives from the bank (see Wallace 1988, on this point). Each unit of the good that is not consumed in period 0 is transformed into $R>1$ units of the good in period 1.

Depositors’ opportunities to withdraw in period 0 arrive sequentially in a randomly determined fashion, with each depositor equally likely to occupy each position in the sequence. When her opportunity arrives, a depositor is able to observe how many withdrawals have already been made. She does not, however, observe the decisions of any depositors who have already chosen not to withdraw in period 0. Likewise, the bank only observes depositors’ actions when they withdraw. In other words, the bank always knows how many withdrawals it has already processed, but it has no information about depositors who may have already chosen not to withdraw in period 0, nor about depositors who have not yet had an opportunity to withdraw.

When a depositor withdraws, the amount she receives can depend only on the information currently available to the bank. This sequential service constraint limits the ability of the bank to make payouts contingent on the demand for early withdrawals. Consider, for example, the first depositor to withdraw in period 0. When she arrives, the bank only knows that at least one depositor is withdrawing; it has no other information that can be used to make inferences about the total number of early withdrawals that will take place. The consumption this depositor receives must, therefore, be the same for all outcomes in which at least one withdrawal occurs; let $x_{1}$ denote this amount. Similarly, let $x_{n}$ denote the amount of consumption received by the nth depositor to withdraw in period 0, which must be the same for all outcomes in which at least n early withdrawals occur. The restrictions imposed by the sequential service constraint thus imply that the period-0 actions of the bank can be fully described using a payout schedule $x=\left\{ x_{n}\right\} _{n=1}^{I}$. This schedule must satisfy the feasibility constraints

$$\begin{aligned} \sum \limits _{n=1}^{I}x_{n}\le I\quad \text {and} \quad x_{n}\ge 0\quad \text { for all }n. \end{aligned}$$

(4)

Notice that the sequence x is a contingent plan; it specifies the period- 0 payouts the bank will make in all possible scenarios, including the one where all I depositors withdraw early. If fewer than I depositors withdraw in period 0,  some of these payouts will not be made. After all depositors have had an opportunity to withdraw in period 0,  the bank observes that the period has ended and the economy moves to period 1. At this point, the bank knows how many depositors have not yet withdrawn. Since depositors are risk averse, efficiency requires that the bank divide the matured assets in period 1 evenly among these depositors. As a result, the operation of the bank in our environment is completely summarized by the period-0 payout schedule x.

Our formulation of the sequential service constraint differs from that in Wallace (1988, 1990) and Green and Lin (2003). In those papers, each depositor contacts the bank in period 0 and announces whether or not she wishes to withdraw. In such a setting, the period-0 payout received by a depositor can depend on the entire sequence of withdrawal decisions made up to that point. We instead follow Peck and Shell (2003) in assuming that the bank only observes the decisions of those depositors who have chosen to withdraw. This formulation slows down the flow of information about the level of total withdrawal demand to the bank and, in so doing, places stronger restrictions on the payout schedule as described above. In the sections that follow, we show how this slower flow of information to the bank has important implications for the form of optimal banking arrangements and for financial fragility.

We also depart from most of the existing literature by assuming that each depositor is able to observe the number of withdrawals that have already taken place when her opportunity to withdraw arises.⁶ In Green and Lin (2003), a depositor observes a signal correlated with her position in the sequence of withdrawal opportunities before making her decision. However, because she does not observe actions taken by the depositors before her in this sequence, she will typically be uncertain about the number of withdrawals that have already been made and, hence, about the amount she would receive from the bank if she chose to withdraw. In Peck and Shell (2003), a depositor receives no information about her position in the sequence or the actions of other depositors. Since the bank necessarily observes the actions of those depositors with whom it interacts, both of these approaches imply that a depositor has less information than the bank about the withdrawal history. This asymmetry raises the question of whether the bank might choose to communicate its information to a depositor before she makes her choice or whether a depositor could change her decision after seeing the amount offered by the bank. (See Nosal and Wallace 2009 for an analysis of the former issue.) Under our approach, in contrast, depositors and the bank observe exactly the same information about the withdrawal history; there is no scope for the bank to either provide or withhold information about this history to depositors.

3 The efficient allocation

We begin our analysis by deriving the efficient allocation of resources in an environment that is identical to the one just described, but where the preference type $\omega _{i}$ can be observed by the bank when depositor i has her opportunity to withdraw. This allocation will be a useful benchmark in subsequent sections when we study the equilibria of a game played by depositors with private information.

Given the form of preferences (1) and the return $R>1$ on investment, efficiency clearly requires that a depositor consume in period 0 if and only if she is impatient. When the bank can observe types $\omega _{i},$ therefore, it will only permit impatient depositors to withdraw in the early period. Let $z_{m}$ denote the amount of resources that the bank has remaining after serving m depositors in period 0 under the payout schedule x,  so that $z_{0}=I$ and

$$\begin{aligned} z_{m}=I-\sum _{n=1}^{m}x_{n}\quad \,\, \text {for }m=1,\ldots I-1. \end{aligned}$$

(5)

The bank’s objective function can then be written as

$$\begin{aligned} \sum _{\theta =1}^{I}p\left( \theta \right) \left( \sum \limits _{n=1}^{I-\theta }u\left( x_{n}\right) +\theta u\left( \frac{ Rz_{I-\theta }}{\theta }\right) \right) +p\left( 0\right) \left( \sum \limits _{n=1}^{I-1}u\left( x_{n}\right) +u\left( z_{I-1}\right) \right) . \end{aligned}$$

(6)

The efficient payout schedule is the sequence $\left\{ x_{n}^{*}\right\}$ that maximizes (6) subject to the feasibility constraints in (4) and the definition in (5). To solve for the efficient schedule, we reformulate (6) as a dynamic programming problem. Define the following conditional probabilities:

$$\begin{aligned} q_{n}={\mathrm {Prob}}\left[ I-\theta \left( \omega \right) \ge n\ |\ I-\theta \left( \omega \right) \ge n-1\right] . \end{aligned}$$

After the bank has encountered $n-1$ impatient depositors in period $0, q_{n}$ is the probability that it will meet at least one more. Using the binomial density in (2), this conditional probability can be written as

$$\begin{aligned} q_{n}=\frac{\sum \nolimits _{\theta =0}^{I-n}p\left( \theta \right) }{ \sum \nolimits _{\theta =0}^{I-n+1}p\left( \theta \right) }. \end{aligned}$$

We can then derive the efficient payout schedule $x_{n}$ as a function of these probabilities $q_{n}$.

Proposition 1

The efficient payout schedule sets

$$\begin{aligned} x_{n}^{*}=\frac{z_{n-1}^{*}}{\left( \phi _{n}\right) ^{\frac{1}{ \gamma }}+1} \qquad \text {for }n=1,\ldots ,I, \end{aligned}$$

where the sequence $\left\{ z_{n}^{*}\right\}$ is defined by using $\left\{ x_{n}^{*}\right\}$ in (5) and $\left\{ \phi _{n}\right\}$ is defined recursively by $\phi _{I}=0$ and

$$\begin{aligned} \phi _{n}=q_{n+1}\left( \phi _{n+1}{}^{\frac{1}{\gamma }}+1\right) ^{\gamma }+\left( 1-q_{n+1}\right) \left( I-n\right) ^{\gamma }R^{1-\gamma } \end{aligned}$$

for $n=1,\ldots ,I-1$.

The proposition shows how the fraction of the remaining resources $z_{n-1}$ that the nth impatient depositor will receive depends on the remaining conditional probabilities $q_{n+1}, q_{n+2},$ etc., as well as on the parameters R and $\gamma$. A proof of the proposition is given in the appendix.

Example

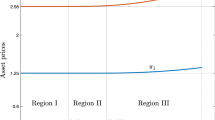
Figure 1 plots the efficient payout schedule for the parameter values $R=1.1, \gamma =6,$ and $\pi =0.5$ when there are 20 depositors (in panel a) and 200 depositors (in panel b). The lower curve in each panel represents, for each value of n, the consumption $x_{n}^{*}$ that the nth impatient depositor will receive in period 0. The upper curve represents the level of consumption that all patient depositors will receive in period 1 if there is a total of $n-1$ impatient depositors. The fact that this latter curve lies everywhere above the former has the following interpretation. Consider the last depositor in the sequence of period-0 withdrawal opportunities, and let the number of impatient depositors before her be given by $n-1$. If she is impatient, she will receive $x_{n}^{*}$, from the lower curve in the figure; if she is patient, she will receive the consumption allocated to patient depositors when there are a total of $n-1$ impatient depositors, which is the corresponding point on the upper curve. The figure shows that the last depositor in the sequence always consumes more when she is patient than when she is impatient, regardless of the types of the other depositors. Notice that this feature does not necessarily hold for other depositors. The first depositor in the sequence, for example, consumes $x_{1}$ if she is impatient and can end up receiving any point on the upper curve if she is patient, depending on the total number of impatient depositors. In panel (a), for example, she will consume more than $x_{1}$ when she is patient if the number of impatient depositors turns out to be less than 12, but otherwise she will consume less. $\square$

Fig. 1

Efficient payout schedule. a 20 depositors. b 200 depositors

Using the solution given in Proposition 1, we can derive some properties of the efficient payout schedule. First, we establish that this schedule offers depositors liquidity insurance in the sense that the benefit of the return R on investment is shared by all depositors, even those who consume before this return is realized. In a model with no aggregate uncertainty, Diamond and Dybvig (1983) showed how $\gamma >1$ implies that the efficient level of consumption for all impatient depositors is greater than the per-capita value of the bank’s assets in period 0. When there is aggregate uncertainty, as in our model here, the definition of liquidity insurance must be adjusted because different impatient depositors consume under different circumstances. In this case, we say that a payout schedule x offers liquidity insurance to the nth impatient depositor if

$$\begin{aligned} x_{n}>\frac{z_{n-1}}{I-n+1}, \end{aligned}$$

(7)

that is, if the amount given to this depositor is larger than the value of the bank’s remaining resources divided by the number of depositors who have not yet withdrawn. The following result shows that $x^{*}$ satisfies this expression for all values of n up to $I-1$. A proof is given in the appendix.⁷

Proposition 2

The efficient payout schedule $x^{*}$ offers liquidity insurance in the sense of (7) for $n=1,\ldots ,I-1$.

This result has important implications for the shape of the efficient payout schedule as depicted in the lower lines of Fig. 1. When more depositors consume in the early period, before the return R is realized, providing liquidity insurance for this group becomes more costly in terms of lowering the consumption of patient depositors as a group. The bank’s efficient response to an increase in the likely number of impatient depositors is, therefore, to decrease the consumption of all remaining depositors. As additional withdrawals take place in period 0,  the bank becomes more pessimistic about the total number of impatient depositors. As shown in the figure, the bank adjusts to this new information by setting the payout $x_{n+1}^{*}$ lower than $x_{n}^{*}$. The following proposition shows that this monotonicity is a general feature of the efficient payout schedule.

Proposition 3

The efficient payout schedule is strictly decreasing, with $x_{n+1}^{*}<x_{n}^{*}$ for $n=1,\ldots ,I-1$.

Proof

From Proposition 1, we know that the efficient payout schedule satisfies

$$\begin{aligned} x_{n}^{*}=\frac{z_{n-1}^{*}}{\phi _{n}{}^{\frac{1}{\gamma }}+1} \quad \text { and } \quad x_{n+1}^{*}=\frac{z_{n}^{*}}{ \phi _{n+1}{}^{\frac{1}{\gamma }}+1}, \end{aligned}$$

where

$$\begin{aligned} z_{n}^{*}=z_{n-1}^{*}-x_{n}^{*}. \end{aligned}$$

Combining these expressions yields

$$\begin{aligned} x_{n+1}^{*}=x_{n}^{*}\frac{\phi _{n}{}^{\frac{1}{\gamma }}}{\phi _{n+1}{}^{\frac{1}{\gamma }}+1}. \end{aligned}$$

Using the second inequality in Lemma 1 (in the appendix), it follows immediately that $x_{n+1}^{*}<x_{n}^{*}$ for $n=1,\ldots ,I-1$. $\square$

Figure 1 also indicates that the schedule $x^{*}$ is initially quite flat, with $x_{1}^{*}$ very close in value to $x_{2}^{*}, x_{3}^{*},$ and several more payouts. Only as the number of early withdrawals becomes larger do the downward adjustments in $x_{n}^{*}$ become visible. In other words, depositors withdrawing in period 0 are initially treated similarly, each receiving close to what might be considered the “face value” of their deposit. This property emerges from the fact that, initially, withdrawals provide relatively little information to the bank about the total number of impatient depositors and, hence, have little impact on the efficient payout.

To understand this property better, consider the example in panel (a) of the figure. The total number of impatient depositors in this example is likely to be close to 10,  since each of the 20 depositors has a 1 / 2 probability of being impatient. When the first early withdrawal takes place, the bank learns that at least one depositor is impatient, which rules out the (extremely unlikely) event that all 20 depositors are patient. The bank’s belief about the distribution of $\theta$ is only slightly changed by this information, which leads it to set the payout for the next impatient depositor, $x_{2}^{*},$ only slightly different from $x_{1}^{*}$. More generally, the continuation probability $q_{n+1}$ is very close to 1 for small values of n,  which implies that the bank is almost certain that additional withdrawals will be made. Since depositors are risk averse, the efficient plan will approximately equalize the values of all payments that are nearly certain to be made. As the number of depositors $I\$increases, the information content of an additional withdrawal when n is small decreases because the fraction of depositors who are patient is less likely to deviate significantly from its mean. As a result, the payout schedule is initially flatter when I is larger, as illustrated in panel (b) of the figure.⁸

As the proportion of the population that has withdrawn in period 0 increases, additional withdrawals become more informative about the value of $\theta$. After 10 withdrawals have taken place in panel (a), for example, the continuation probability $q_{11}$ has fallen to 0.7. At this point, there is significant uncertainty about whether or not an additional early withdrawal will be made. If another depositor arrives to withdraw, the bank’s belief about $\theta$ changes significantly and, as a result, the payout $x_{11}^{*}$ is noticeably lower than $x_{10}^{*}$. As illustrated in the figure, these changes become larger and larger as n increases toward the total number of depositors I. This part of the curves resembles what Wallace (1990) calls a “partial suspension of convertibility,” in which some depositors receive significantly less than the face value of their deposits when the realized demand for early withdrawal is high.

4 Banking

We now return to the environment in which preference types $\omega _{i}$ are private information. In this setting, the only way for the bank to make a depositor’s consumption contingent on $\omega _{i}$ is to allow her to choose the period in which she withdraws. We consider the following banking arrangement: Each depositor chooses whether to withdraw early or late based on her own preference type and on the number of withdrawals that have already been made when her opportunity arrives, and the bank makes payouts according to the schedule $x^{*}$ derived in Proposition 1. This arrangement creates a withdrawal game for depositors; the remainder of the paper is devoted to studying the equilibria of this game.⁹

4.1 The withdrawal game

A depositor chooses a withdrawal strategy, which assigns a withdrawal period (either 0 or 1) to each combination of her preference type $\omega _{i}$ and the number n representing the opportunity to make the nth withdrawal in period 0,

$$\begin{aligned} y_{i}=\varOmega \times \left\{ 1,\ldots ,I\right\} \rightarrow \left\{ 0,1\right\} . \end{aligned}$$

We use y to denote a profile of strategies, one for each depositor, and $y_{-i}$ to denote the strategies of all depositors except i.

Our interest is in the Bayesian Nash equilibria of the withdrawal game, where each depositor chooses the strategy $y_{i}$ that maximizes her expected utility while correctly anticipating the strategies $y_{-i}$ of other depositors.¹⁰ We study symmetric equilibria, in which all depositors follow the same strategy. Different depositors may still take different actions, of course, as their preference types and withdrawal opportunities will differ.

As described above, impatient depositors only care about consumption in period 0, and hence, the individual best response to any strategy profile $y_{-i}$ will satisfy $y_{i}\left( 0,n\right) =0$ for all n. In other words, we only need to check what a depositor will choose to do when she is patient.

Consider the decision faced by a patient depositor who has an opportunity to make the nth withdrawal in period 0. If she chooses to withdraw, she will receive $x_{n}^{*}$. If she waits, the amount she receives at $t=1$ will depend on the total number of withdrawals that take place in period 0,  which is not yet known. Let $\widehat{\theta }$ denote the number of depositors who wait until $t=1$ to withdraw in this case, including herself. Then, $I-\widehat{\theta }$ will be the total number of early withdrawals. Note that $\widehat{\theta }$ is a random variable that depends on both the number of patient depositors $\theta$ and the profile of withdrawal strategies followed by the other depositors, $y_{-i}$. Let $p_{n}\left( \widehat{\theta };y_{-i}\right)$ denote the posterior probability this depositor, using Bayes’ rule, assigns to the event that exactly $\widehat{ \theta }$ depositors (including herself) wait until $t=1$ to withdraw. Given this belief, she computes the expected utility of waiting to withdraw, denoted $\mu \left( n;y_{-i}\right)$, as

$$\begin{aligned} \mu \left( n;y_{-i}\right) \equiv \sum _{\widehat{\theta }=1}^{I}p_{n}\left( \widehat{\theta };y_{-i}\right) u\left( \frac{Rz_{I-\widehat{\theta }}}{ \widehat{\theta }}\right) . \end{aligned}$$

(8)

An equilibrium of the withdrawal game is a strategy profile $y^{*}$ satisfying

$$\begin{aligned} y_{i}^{*}\left( \omega _{i},n\right) =\left\{ \begin{array}{ccl} 0 &{} \ &{} \hbox { if } \omega _{i}=0 \hbox { or } u\left( x_{n}^{*}\right) >\mu \left( n;y_{-i}^{*}\right) \\ 1 &{} &{} \hbox { if } \omega _{i}=1 \hbox { and } u\left( x_{n}^{*}\right) <\mu \left( n;y_{-i}^{*}\right) \end{array} \right\} \text { for all }n,\text { for all }i. \end{aligned}$$

In other words, each depositor is optimally choosing when to withdraw given her beliefs about the total number of early withdrawals, and those beliefs are consistent with the actions prescribed in the equilibrium strategy profile $y^{*}$. Impatient depositors always withdraw early, and patient depositors withdraw early when the value of the available payout, $u\left( x_{n}^{*}\right) ,$ exceeds the expected value of waiting, $\mu \left( n;y_{-i}^{*}\right)$. Note that when a patient agent is indifferent, because $u\left( x_{n}^{*}\right) =\mu \left( n;y_{-i}^{*}\right) ,$ either action ($y_{i}=0$ or $y_{i}=1$) is consistent with equilibrium.

4.2 Incentive compatibility

One strategy of particular interest is the no-run strategy, in which a depositor withdraws early if and only if she is impatient

$$\begin{aligned} y_{i}^{0}\left( \omega _{i},n\right) =\omega _{i}\quad \text {for all }n. \end{aligned}$$

(9)

Let $y^{0}$ denote the no-run strategy profile. If $y^{0}$ is an equilibrium of the withdrawal game, this equilibrium achieves the efficient allocation of resources derived in Sect. 3.

In this case, the number of depositors who wait to withdraw, $\widehat{ \theta },$ is the same as the number of patient depositors $\theta$. A depositor’s initial belief about $\theta$ is given by (2). To illustrate how the posterior beliefs $p_{n}\left( \theta ;y_{-i}^{0}\right)$ are formed, suppose that $n=1,$ meaning that no withdrawals have occurred yet. This situation could arise because the depositor is first in the sequence of withdrawal opportunities, in which case it would convey no information about $\theta$. However, it also could arise because the depositor is later in the sequence but all of the depositors before her were patient, in which case $\theta$ is likely to be high. The depositor weighs the relative likelihood of these different situations in updating her belief about $\theta$ according to Bayes’ rule.

More generally, suppose a patient depositor observes that $n-1$ withdrawals have already been made when her opportunity to withdraw arrives. Define $Z_{k}^{n-1}$ to be the set of all type profiles $\omega$ in which there is a patient depositor in the kth position with exactly $n-1$ impatient depositors in the first $k-1$ positions, that is,

$$\begin{aligned} Z_{k}^{n-1}=\left\{ \omega :\omega _{k}=1\wedge \quad \sum \limits _{j=1}^{k-1}\left( 1-\omega _{j}\right) =n-1\right\} . \end{aligned}$$

The depositor knows that the realized profile $\omega$ must lie in this set for some value of k. The following proposition derives her posterior belief about the number of patient depositors $\theta ;$ a proof of the result is given in the appendix.

Proposition 4

A patient depositor who anticipates that all other depositors are following (9) and who has the opportunity to make the nth withdrawal in period 0 will assign probability

$$\begin{aligned} p_{n}\left( \theta ;y_{-i}^{0}\right) =\rho _{n}\left( \theta ;I\right) \equiv \frac{\sum \nolimits _{\omega \in \left\{ \omega :\theta \left( \omega \right) =\theta \right\} }\left( p\left( \omega \right) \sum \nolimits _{k=n}^{I}{\mathcal {I}}_{\left\{ \omega \in Z_{k}^{n-1}\right\} }\right) }{\sum \nolimits _{\omega \in \varOmega ^{I}}\left( p\left( \omega \right) \sum \nolimits _{k=n}^{I}{\mathcal {I}}_{\left\{ \omega \in Z_{k}^{n-1}\right\} }\right) } \end{aligned}$$

to the event that exactly $\theta$ of the I depositors are patient, where ${\mathcal {I}}_{\left\{ A\right\} }$ is the indicator function for the set A.

Using the distribution $p_{n}\left( \theta ;y_{-i}^{0}\right) ,$ we can obtain the value of $\mu \left( n;y_{-i}^{0}\right)$ from equation (8). The no-run strategy profile is an equilibrium of the withdrawal game if and only if:

$$\begin{aligned} u\left( x_{n}^{*}\right) \le \mu \left( n;y_{-i}^{0}\right) \quad \text {for }n=1,\ldots ,I. \end{aligned}$$

(10)

The left-hand side of these inequalities represents the value of withdrawing early and receiving the payout $x_{n}^{*}$ for sure. The right-hand side is the expected utility of waiting to withdraw when all other depositors are following (9). When these inequalities are satisfied for all values of n,  a patient depositor will find it optimal to withdraw in period 1 regardless of the number of withdrawals that have taken place when her opportunity arrives in period 0. As a result, there is an equilibrium of the withdrawal game in which all depositors follow the strategy (9) and the efficient allocation of resources obtains. In this case, we say that the efficient allocation is incentive compatible.

Our focus in the rest of the paper is on situations in which the efficient allocation is incentive compatible. We follow an approach that is common in the literature by first solving for the efficient payout schedule $x^{*}$ without imposing the incentive compatibility conditions, using Proposition 1, and then verifying that the solution satisfies (10). Note that the constraints imposed by private information are not binding on the efficient allocation of resources in these cases. This fact illustrates the benefits of banking arrangements that resemble demand-deposit contracts, in which depositors are allowed to choose when to withdraw their funds from the bank. As in Diamond and Dybvig (1983) and others, such an arrangement allows the bank to potentially achieve the same allocation of resources it would choose if it could directly observe each individual depositor’s consumption preferences when she arrives. However, such arrangements may also open the door to financial fragility in the sense of admitting other equilibria in which some patient depositors “run” on the bank and withdraw in period 0, leading to an inferior allocation. In the next section, we investigate whether such fragility can arise in our model and what forms it may take.

5 Fragility

In this section, we investigate whether the withdrawal game defined above can have other Bayesian Nash equilibria, in which some depositors choose to withdraw in period 0 even when they are patient. If such equilibria exist, the bank is fragile in the sense that attempting to implement the efficient allocation of resources using the arrangement described above could lead to an inefficient outcome that resembles a run on the bank. We first show that there cannot be an equilibrium in which all depositors attempt to withdraw early. We then construct an example of a partial-run equilibrium, in which some patient depositors withdraw early but others do not.

5.1 No full-run equilibrium

The type of bank run studied in most of the literature has all depositors attempting to withdraw their funds in the early period.¹¹ We refer to this strategy profile,

$$\begin{aligned} y_{i}\left( \omega _{i},n\right) =0\quad \text {for all }\omega _{i},n,\text { for all }i, \end{aligned}$$

(11)

as a full run. It is fairly easy to see that a full run cannot be part of an equilibrium in our model. Consider a depositor with $n=I,$ meaning that all of the other $I-1$ depositors have already withdrawn when her opportunity to withdraw in period 0 arises. If she chooses to withdraw in period 0, she will receive all of the bank’s remaining resources, $z_{I-1}^{*}$. If she waits until period 1 to withdraw, however, she will receive the matured value of these resources $Rz_{I-1}^{*}$. Because $R>1,$ a patient depositor in this situation would always strictly prefer to wait to withdraw. In other words, the full-run strategy (11) is strictly dominated by a strategy with $y_{i}\left( 1,I\right) =1$ and, hence, cannot be part of an equilibrium. The following proposition records this result.

Proposition 5

There is no equilibrium in which depositors play the strategy profile in expression (11).

This aspect of our model is similar in spirit to one of the key features of Green and Lin (2003). In their setting, depositors receive a signal about their position in the sequence of withdrawal opportunities. If a depositor’s signal indicates that she is very likely to be last in this sequence, she faces a decision that is similar to the one described above and will strictly prefer to wait until period 1 if she is patient. Depositors in our model do not observe their place in the sequence; however, a depositor who observes that everyone else has already withdrawn can readily infer she is in the last position. For this reason, the Green–Lin logic for this last depositor applies in our setting as well and a full-run equilibrium cannot exist. Green and Lin (2003) then use a backward-induction argument to show that the no-run strategy profile is the unique equilibrium in their setting; no type of run equilibrium can exist. In the next subsection, we show this stronger result does not hold in our environment.

5.2 Partial-run equilibria

Proposition 5 shows that if a run equilibrium exists in our environment, it must be partial, with only some depositors participating. One possibility is for depositors to run until the total number of withdrawals reaches some critical level and then for the run to stop. Consider the following class of strategy profiles

$$\begin{aligned} y_{i}^{\bar{n}}\left( \omega _{i},n\right) =\left\{ \begin{array}{l} 0 \\ \omega _{i} \end{array} \,\, \text { for } \begin{array}{l} n\le \bar{n} \\ n>\bar{n} \end{array} \right. \quad \text {for some }1\le \bar{n}\le I-1,\quad \text {for all }i. \end{aligned}$$

(12)

Note that setting $\bar{n}=0$ would correspond to a no-run strategy profile in (9), while setting $\bar{n}=I$ would correspond to a full-run strategy profile in (11). For values of $\bar{n}$ between 1 and $I-1,$ this profile represents a partial run.

Recall that $\widehat{\theta }$ denotes the total number of depositors who wait until period 1 to withdraw. Under a partial-run strategy profile, $\widehat{\theta }$ is bounded above by $\min [\theta ,I-\bar{n}]$. The realized value of $\widehat{\theta }$ will be less than the number of patient depositors $\theta$ if one or more of the first $\bar{n}$ depositors in the decision order is patient and, following (12), withdraws in period 0.

To determine whether (12) is consistent with equilibrium for some positive value of $\bar{n}$, we need to compare the expected utility a depositor receives from following this strategy to the expected utility associated with deviating. In particular, for $n\le \bar{n},$ we need to consider whether a patient depositor would be better off waiting until period 1 to withdraw, while for $n>\bar{n}$ we need to consider whether a patient depositor would be better off withdrawing in period 0. We address these two cases in turn.

(i) $n\le \bar{n}:$ If the depositor follows the strategy in (12), she will withdraw early and receive $x_{n}^{*}$. If she deviates, she will receive the period-2 payout associated with $\widehat{\theta }$ depositors waiting to withdraw. Comparing the expected utility of these two outcomes requires deriving the depositor’s belief about $\widehat{\theta }$ under the assumption that $\left( i\right)$ she is patient, $\left( ii\right)$ all other depositors follow the strategy profile in (12), and $\left( iii\right)$ she deviates from (12) and waits until period 1. In this case, the value of n fully reveals the depositor’s position in the sequence of withdrawal opportunities: She must be the nth depositor to decide. It does not, however, give her any information about the profile of types $\omega$. The depositor knows that at least $\bar{n}$ depositors will withdraw early and that the remaining $I- \bar{n}-1$ depositors will each withdraw early if and only if they are impatient.¹² Her posterior belief about $\widehat{\theta }$ is then given by

$$\begin{aligned} p_{n}\left( \widehat{\theta };y_{-i}^{\bar{n}}\right) =0\text { for }\widehat{\theta }=0 \quad \text {or } \quad \widehat{\theta }>I-\bar{n} \quad \text { and } \quad n\le \bar{n} \end{aligned}$$

(13)

and

$$\begin{aligned} p_{n}\left( \widehat{\theta };y_{-i}^{\bar{n}}\right)&=C\left( I-\bar{n}-1, \widehat{\theta }-1\right) \pi ^{I-\bar{n}-\widehat{\theta }}\left( 1-\pi \right) ^{\widehat{\theta }-1} \nonumber \\&\quad \text {for }\widehat{\theta }=\left\{ 1,\ldots ,I-\bar{n} \right\} \quad \text { and } \quad n\le \bar{n}, \end{aligned}$$

(14)

where C is the combinatorial function (3). In other words, the depositor knows that $\widehat{\theta }$ will be at least 1 (herself) and can be up to $I-\bar{n}$ if all of the other depositors who do not participate in the run are patient. The types of these other depositors are i.i.d. Bernoulli trials. Notice that $p_{n}\left( \widehat{\theta };y_{-i}^{ \bar{n}}\right)$ is independent of n for all $n<\bar{n};$ the depositor’s precise position in the sequence of withdrawals does not affect her posterior belief about $\widehat{\theta }$ in this case.

The expected utility of deviating from (12) and withdrawing in period 1 is given by $\mu \left( n;y_{-i}^{\bar{n}}\right)$ as defined in (8), using the distribution $p_{n}\left( \widehat{\theta };y_{-i}^{ \bar{n}}\right)$ presented in (13)–(14). A necessary condition for (12) to be consistent with equilibrium is that

$$\begin{aligned} u\left( x_{n}^{*}\right) \ge \mu \left( n;y_{-i}^{\bar{n}}\right) \quad \text { for } n\le \bar{n}. \end{aligned}$$

Notice that $\mu \left( n;y_{-i}^{\bar{n}}\right)$ is independent of n for $n\le \bar{n},$ while Proposition 3 establishes that $u\left( x_{n}^{*}\right)$ is strictly decreasing in n. Therefore, the condition above will be satisfied for all $n\le \bar{n}$ if and only if it is satisfied for $\bar{n}$, that is,

$$\begin{aligned} u\left( x_{\bar{n}}^{*}\right) \ge \mu \left( \bar{n};y_{-i}^{\bar{n} }\right) . \end{aligned}$$

(15)

When this condition holds, a depositor who expects all other depositors to follow the strategy in (12) and observes a value of n less than or equal to $\bar{n}$ will also be willing to follow (12). In other words, (15) is a necessary condition for the strategy profile $y^{\bar{ n}}$ to be an equilibrium. We record this result, which is useful for constructing the examples below, as a proposition.

Proposition 6

If the strategy profile $y^{\bar{n}}$ is an equilibrium, then $u\left( x_{\bar{n}}^{*}\right) \ge \mu \left( \bar{n} ;y_{-i}^{\bar{n}}\right)$.

(ii) $n>\bar{n}:$ When the depositor’s opportunity to withdraw arrives later, after the run has ended, she can no longer be certain about her position in the sequence of withdrawal opportunities. Instead, she must form beliefs about how many of the $I-\bar{n}$ no-run depositors are impatient and what her position within the sequence of these depositors might be. This inference problem is similar in structure to the one discussed in the context of incentive compatibility in Sect. 3. In this case, the depositor’s posterior belief about $\widehat{\theta }$ is given by

$$\begin{aligned} p_{n}\left( \widehat{\theta };y_{-i}^{\bar{n}}\right) =\rho _{n-\bar{n} }\left( \widehat{\theta };I-\bar{n}\right) \quad \text {for } \widehat{\theta }=\left\{ 1,\ldots ,I-\bar{n}\right\} \quad \text { and }\quad n>\bar{n}. \end{aligned}$$

(16)

The expression $\rho _{n-\bar{n}}\left( \widehat{\theta };I-\bar{n}\right)$ is the probability distribution presented in Proposition 4 applied to the subset of $I-\bar{n}$ depositors who do not participate in the run. Note that the index on this distribution is adjusted from n to $n-\bar{n}$, since the depositor in question observes $n-1-\bar{ n}$ withdrawals from the $I-\bar{n}$ no-run depositors.

A patient depositor following the strategy in (12) would wait until period 1 to withdraw and would have expected utility given by $\mu \left( n;y_{-i}^{\bar{n}}\right)$ from (8), with the distribution $p_{n}\left( \widehat{\theta };y_{-i}^{\bar{n}}\right)$ now given by (16). If she instead deviates and withdraws early, she will receive $x_{n}^{*}$ for sure. The strategy profile $y^{\bar{n}}$ is consistent with a best response for these depositors if

$$\begin{aligned} u\left( x_{n}^{*}\right) \le \mu \left( n;y_{-i}^{\bar{n}}\right) \quad \text {for }n=\bar{n}+1,\ldots ,I. \end{aligned}$$

(17)

If conditions (15) and (17) both hold for some $\bar{n}$ with $1\le \bar{n}\le I-1$, the partial-run strategy profile (12) based on that value of $\bar{n}$ is a Bayesian Nash equilibrium of the withdrawal game. Our main result in this section is that, for some parameter values, such a partial-run equilibrium exists.

Proposition 7

There exist parameter values such that the efficient payout schedule $x^{*}$ both $\left( i\right)$ generates an incentive compatible allocation and $\left( ii\right)$ admits a partial-run equilibrium with $1\le \bar{n}\le I-1$.

The proof is by example. We present the example in the next subsection, followed by a detailed discussion of the intuition behind it.

5.3 An example

Our example is based on the same parameter values that were used to illustrate the efficient allocation in panel (a) of Fig. 1: $I=20$, $R=1.1, \gamma =6,$ and $\pi =0.5$.¹³ Figure 2 plots three curves, two of which are simply the utility associated with the consumption levels plotted in the earlier figure. The third curve is an auxiliary function $\mu \left( n;y_{-i}^{n}\right)$. This curve gives the expected utility from waiting to withdraw for a patient depositor who has the opportunity to make the nth withdrawal in period 0 under the assumption that all of the depositors before her are running but all of the depositors after her are not. In other words, this curve measures the value of deviating from the strategy profile $y^{n}$ for the last depositor who participates in this partial run.

Fig. 2

A partial-run equilibrium

The figure shows the necessary condition identified in Proposition 6—that $u\left( x_{\bar{n}}^{*}\right) \ge \mu \left( \bar{n};y_{-i}^{\bar{n}}\right)$ hold—to be satisfied for any potential cutoff value $\bar{n}$ between 7 and 16. Let us concentrate attention on the partial-run strategy with the largest possible threshold, in this case $\bar{n}=16$. The fact that the necessary condition holds implies that depositors with $n\le 16$ will all chose to play according to the partial-run strategy profile $y^{16}$. Hence, to show that $y^{16}$ is an equilibrium strategy profile, we only need to show that depositors with $n>16$ will also prefer to follow this strategy, which specifies that they wait until period 1 if patient. This is done in Fig. 3, where the upper curve plots the incentive to run

$$\begin{aligned} u\left( x_{n}^{*}\right) -\mu \left( n;y_{-i}^{16}\right) \end{aligned}$$

for all n between 1 and 20.¹⁴ The discussion above demonstrated that this value must be positive for n between 1 and 16;  this fact is also reflected in Fig. 3. The new information in the figure is that the expression is negative for $n=17$ through 20,  which verifies that a patient depositor who has any one of these opportunities to withdraw in period 0 would choose to wait, in accordance with the candidate equilibrium strategy profile. Hence, the figure establishes that strategy profile (12) with $\bar{n}=16$ comprises an equilibrium of the withdrawal game.

Fig. 3

Incentive to run

Figure 3 also verifies that the efficient allocation is incentive compatible in this example. The lower curve in the figure plots

$$\begin{aligned} u\left( x_{n}^{*}\right) -\mu \left( n;y_{-i}^{0}\right) ; \end{aligned}$$

that is, the gain in expected utility from running for each value of n under the assumption that all other depositors follow the no-run strategy. The fact that this line is negative everywhere demonstrates that the no-run strategy profile is also an equilibrium of the withdrawal game. Together, the two curves in Fig. 3 thus establish the result in Proposition 7. It is worth emphasizing that there is nothing special about the parameter values used in this example; it is easy to construct similar examples using a wide range of parameter values.

5.4 Intuition

To gain intuition for why the partial-run strategy profile in (12) is an equilibrium, it is useful to examine the behavior of the “critical” depositor whose opportunity to withdraw in period 0 is $\bar{n}$. This depositor follows the run strategy even though she believes that no one after her will run. This type of behavior is inconsistent with equilibrium under Green and Lin’s (2003) formulation of the sequential service constraint, a fact that is crucial for their backward-induction argument. Understanding why it can arise here thus illustrates a key difference between our environment and theirs.

Suppose we compare this depositor’s equilibrium belief about the number of early withdrawals with the beliefs used by the bank in designing the payout schedule $x^{*}$. The efficient payout $x_{16}^{*}$ depends on the probability that there will be a 17th early withdrawal (and an 18th, and so on). Given that the bank expects only impatient agents to withdraw early, and each depositor has an independent, one-half probability of being impatient, the bank considers a 17th early withdrawal fairly unlikely. When faced with a 16th early withdrawal, the bank believes that the four depositors it has not yet seen are likely to have already had their opportunities to withdraw and decided to wait because they are patient. In this sense, the bank is “optimistic” that the 16th early withdrawal will be the last one and the payout $x_{16}^{*}$ is chosen based on this optimism.

In the partial-run equilibrium, however, the depositor making the 16th withdrawal recognizes that a run is underway and the number of early withdrawals is thus likely to be much larger than the number of impatient depositors. Importantly, she knows that four depositors have not yet had the opportunity to contact the bank in period 0. She expects that, on average, two of these depositors will be impatient, and hence, she realizes that the early withdrawals are unlikely to end with her. Any additional withdrawals will further deplete the bank’s resources, lowering the consumption she would receive if she were to wait and withdraw in period 1. Her more pessimistic belief about the number of early withdrawals thus makes running—and accepting the payout based on the bank’s optimistic belief—an attractive strategy.¹⁵

Notice how the limited flow of information implied by our formulation of the sequential service constraint makes this divergence in beliefs possible. When a depositor makes the 16th withdrawal, the bank does not know that she is the 16th depositor to have an opportunity to withdraw. In fact, the payout schedule $x^{*}$ is based on the belief that if a 16th impatient depositor withdraws, she is likely to be the last depositor to decide. In Green and Lin (2003), in contrast, patient depositors are expected to announce to the bank that they will not withdraw when their turn in the order comes. Under this specification, both the bank and the depositor will know that there are four depositors who still have an opportunity to contact the bank in period 0. Since types are independent, if these depositors will report truthfully then the bank and the depositor must have the same belief about the number of additional early withdrawals, regardless of what strategies the earlier depositors have followed.¹⁶ Because of this agreement in beliefs, the payout offered to each depositor in the Green–Lin setup appears “appropriate” given her beliefs and, as a result, she will choose to report truthfully. This reasoning is central to the unique implementation result in Green and Lin (2003). In contrast, the divergence in beliefs in our model arises naturally whenever one or more depositors follow a non-truthful strategy. The example presented here shows how this divergence in beliefs can be strong enough to generate a run equilibrium in the withdrawal game.

5.5 Discussion

In earlier work (Ennis and Keister 2009), we showed that partial-run equilibria can arise in the model with Green and Lin’s (2003) formulation of the sequential service constraint when depositors’ preference types are correlated. The intuition behind this earlier result is similar to that described for our example above. In particular, in both cases there is a critical depositor who chooses to run even though she expects everyone after her to report truthfully. The payout to this depositor is designed based on the expectation that her withdrawal will likely be the last one in period 0, while the critical depositor believes that additional early withdrawals are very likely. As described above, this divergence in beliefs makes withdrawing early, and receiving the payout based on the more optimistic belief, an attractive choice. The difference in beliefs was generated by the correlation structure of types in our earlier work, while in the present paper it is generated by the fact that the bank does not observe the actions of depositors who choose not to withdraw.

This insight about the importance of divergent beliefs is likely to prove useful for studying fragility in other environments. Suppose for example, that both the bank and depositors observe some measure of the “time” that elapses between two withdrawals and use this information to make inferences about the number of depositors who have already chosen not to withdraw. Depending on the distribution of depositors’ arrival times at the bank, agents may or may not have significantly more information on which to base their decisions in such a setting. The efficient allocation would be much more complex: A depositor’s consumption would in general depend not only on her position in the withdrawal order, but also on the precise time she arrives at the bank and the times at which all previous withdrawals were made. A banking arrangement that implements this type of allocation might bear less resemblance to a standard demand-deposit contract than the arrangement we study here. Nevertheless, it seems likely that the degree to which depositors’ beliefs about the number of additional early withdrawals during a run diverge from those used by the bank in designing payouts will be critical for determining whether a run equilibrium exists. Extending our analysis to such alternative environments is an interesting avenue for future research.

One feature our model shares with much of the existing literature is the fact that a run is observationally equivalent to an event that occurs with positive probability under the no-run strategy profile (that is, an event in which many depositors are impatient). In other words, the bank can never actually be sure that a run is taking place, even ex post. ¹⁷ There is, however, a difference in how quickly the bank is able to infer that something unusual is happening. In our setting, a run is initially equivalent to almost all events under the no-run strategy profile. Suppose depositors follow the partial-run strategy profile in (12). As the first few depositors arrive to withdraw, the bank is only able to infer that at least a few depositors are withdrawing, an event that is very likely to happen under the no-run strategy profile as well. In the Green and Lin (2003) specification of the sequential service constraint, in contrast, the bank will observe the fact that no depositors are choosing to wait to withdraw, which is unlikely to occur if depositors are following the no-run strategy profile. Relative to the Green–Lin approach, our specification slows down the flow of information about depositors’ strategies to the bank. This slower flow of information makes the bank slower to react to a surge in early withdrawals, which in turn tends to increase the incentive for individual depositors to participate in a run.

Our approach of allowing a depositor to observe the number of withdrawals that have already been made when her opportunity to withdraw arrives gives the withdrawal game a more dynamic flavor than much of the existing literature. It also potentially opens the door to issues of signaling, in which a depositor takes into account the effect her action will have on the actions of subsequent depositors (see Andolfatto et al. 2007). Such effects play a minimal role in our setting, however, because depositors only observe withdrawals and receive no information when another depositor chooses not to withdraw. Under the strategy profile $y^{\bar{n}}$, for example, there is no way for the depositor with the first opportunity to withdraw to “signal” that she is deviating from this profile. If she chooses not to participate in the run, this action is unobserved and the next depositor, observing that no withdrawals have taken place yet, will incorrectly infer that she has the first opportunity to withdraw. Similarly, if a patient depositor deviates from the no-run strategy profile by withdrawing early, other depositors will infer that she was impatient rather than suspecting a deviation. For these reasons, many of the complications typically associated with dynamic games do not arise in our setting.

We have followed a common approach in the literature by assuming the bank makes payouts according to the efficient schedule $x^{*}$ and asking whether the resulting withdrawal game admits a run equilibrium. If the bank placed positive probability on the event of a run, it might follow a different plan. For example, it might choose a payout schedule x that is less efficient than $x^{*}$ when depositors follow the no-run strategy profile $y^{0},$ but mitigates the effects of a run if one occurs. If the probability of a run is large enough, the bank may further alter the payout schedule to make it “run proof” in the sense that the only equilibrium strategy profile is $y^{0}$ (see Cooper and Ross 1998; Ennis and Keister 2006). Alternatively, the bank might consider other, more complex contractual arrangements that attempt to solicit additional information from depositors about play in the withdrawal game (see, e.g., Andolfatto et al. 2014; Cavalcanti and Monteiro 2011). In this sense, our result that the withdrawal game based on the efficient payout schedule $x^{*}$ has a (partial) run equilibrium can serve as a starting point for further investigation of financial fragility and its implications in the environment we have introduced here.

6 Concluding remarks

We study a model of financial intermediation in the tradition of Diamond and Dybvig (1983) with some novel features. In our environment, a depositor’s actions are observed by both the bank and other depositors, but only when she withdraws. We show this specification of sequential service is tractable and generates results that are intuitive and perhaps more realistic than those in the existing literature. Depositors, for example, are able to learn before making a decision what payout they would receive by withdrawing. Moreover, even though our approach allows for very complex patterns of payouts, the optimal arrangement resembles in many ways a traditional banking contract. Under this arrangement, depositors who withdraw early in the course of events all receive approximately the face value of their deposits. If the number of withdrawals becomes unexpectedly large, however, depositors begin experiencing significant discounts in what they receive from the bank.

In addition to highlighting the debt-like features of the optimal contract, we show that this arrangement is fragile in the sense of being susceptible to a self-fulfilling run by depositors. A run in our setting is necessarily partial, with only some depositors participating. The previous literature has shown that in environments similar to ours, fragility may not arise if contractual arrangements are sufficiently flexible. Our specification of the environment suggests that the debt-like features of banking contracts and financial fragility may have a common origin in the gradual revelation of information that is inherent in banking arrangements.

Appendix: Proofs

Proposition 1

The efficient payout schedule sets

$$\begin{aligned} x_{n}^{*}=\frac{z_{n-1}^{*}}{\left( \phi _{n}\right) ^{\frac{1}{ \gamma }}+1} \quad \text {for }n=1,\ldots ,I, \end{aligned}$$

where the sequence $\left\{ z_{n}^{*}\right\}$ is defined by using $\left\{ x_{n}^{*}\right\}$ in (5) and $\left\{ \phi _{n}\right\}$ is defined recursively by $\phi _{I}=0$ and

$$\begin{aligned} \phi _{n}=q_{n+1}\left( \phi _{n+1}{}^{\frac{1}{\gamma }}+1\right) ^{\gamma }+\left( 1-q_{n+1}\right) \left( I-n\right) ^{\gamma }R^{1-\gamma } \end{aligned}$$

for $n=1,\ldots ,I-1$. $\square$

Proof

Let $V_{n}$ denote the sum of the expected utilities of all depositors who have not yet consumed when the bank encounters the nth impatient depositor, conditional on the bank allocating the available resources $z_{n-1}$ efficiently among these depositors. These values must satisfy the following recursive equation:

$$\begin{aligned} V_{n}\left( z_{n-1}\right) =\max _{\left\{ x_{n}\right\} }\ \left\{ \begin{array}{l} \frac{\left( x_{n}\right) ^{1-\gamma }}{1-\gamma }+q_{n+1}V_{n+1}\left( z_{n-1}-x_{n}\right) + \\ \left( 1-q_{n+1}\right) \left( I-n\right) \frac{1}{1-\gamma }\left( \frac{ R\left( z_{n-1}-x_{n}\right) }{I-n}\right) ^{1-\gamma } \end{array} \right\} , \end{aligned}$$

(18)

for $n=1,\ldots I$.

If all I depositors are impatient, the bank will give all of the remaining resources to the last depositor when she reports. We therefore have the following terminal condition

$$\begin{aligned} V_{I}\left( z_{I-1}\right) =\frac{1}{1-\gamma }\left( z_{I-1}\right) ^{1-\gamma }. \end{aligned}$$

The combination of this equation, the initial condition $z_{0}=I,$ and Eq. (18) constitutes the dynamic programming problem whose solution gives the efficient payout schedule.

Consider the decision problem faced by the bank if it faces an $\left( I-1\right) ^{th}$ impatient depositor. Given $z_{I-2},$ the maximization problem in (18) reduces to

$$\begin{aligned} \max _{\left\{ x_{I-1}\right\} }\ \frac{\left( x_{I-1}\right) ^{1-\gamma }}{ 1-\gamma }+q_{I}\frac{\left( z_{I-2}-x_{I-1}\right) ^{1-\gamma }}{1-\gamma } +\left( 1-q_{I}\right) \frac{\left( R\left( z_{I-2}-x_{I-1}\right) \right) }{ 1-\gamma }^{1-\gamma }. \end{aligned}$$

The solution to this problem sets

$$\begin{aligned} x_{I-1}=\frac{z_{I-2}}{\left( \phi _{I-1}\right) ^{\frac{1}{\gamma }}+1}, \end{aligned}$$

where

$$\begin{aligned} \phi _{I-1}\equiv q_{I}+\left( 1-q_{I}\right) R^{1-\gamma }. \end{aligned}$$

(19)

Substituting the solution back in the objective function and doing some straightforward algebra yields the value function

$$\begin{aligned} V_{I-1}\left( z_{I-2}\right) =\frac{\left( z_{I-2}\right) ^{1-\gamma }}{ 1-\gamma }\left( \left( \phi _{I-1}\right) ^{\frac{1}{\gamma }}+1\right) ^{\gamma }. \end{aligned}$$

The function $V_{I-1}$ captures the utility of the last two depositors to report to the bank in the event that at least $I-1$ depositors are impatient. In this case, the $\left( I-1\right) ^{th}$ depositor to report is necessarily impatient. The Ith may also be impatient, reporting in period 0,  or patient, in which case she will report in period 1. The probabilities of these events (given by $q_{I}$) are contained in the constant $\phi _{I-1}$.

It is straightforward to use this same procedure to show that, for any $n<I,$ the solution to the maximization problem in (18) sets

$$\begin{aligned} x_{n}=\frac{z_{n-1}}{\phi _{n}{}^{\frac{1}{\gamma }}+1}, \end{aligned}$$

where

$$\begin{aligned} \phi _{n}=q_{n+1}\left( \phi _{n+1}{}^{\frac{1}{\gamma }}+1\right) ^{\gamma }+\left( 1-q_{n+1}\right) \left( I-n\right) ^{\gamma }R^{1-\gamma }. \end{aligned}$$

(20)

Note that condition (19) emerges naturally from (20) using the “terminal” value $\phi _{I}=0$. $\square$

Proposition 2

The efficient payout schedule $x^{*}$ offers liquidity insurance in the sense of (7) for $n=1,\ldots ,I-1$.

Proving this proposition requires showing that

$$\begin{aligned} x_{n}^{*}=\frac{z_{n-1}^{*}}{\left( \phi _{n}\right) ^{\frac{1}{ \gamma }}+1}>\frac{z_{n-1}^{*}}{I-n+1} \end{aligned}$$

or, equivalently,

$$\begin{aligned} \phi _{n}{}^{\frac{1}{\gamma }}<I-n \end{aligned}$$

holds for $n=1,\ldots ,I-1$. These inequalities are established as part of the following lemma:

Lemma 1

The inequalities

$$\begin{aligned} \left( I-n\right) R^{\frac{1-\gamma }{\gamma }}<\phi _{n}{}^{\frac{1}{\gamma }}<\phi _{n+1}{}^{\frac{1}{\gamma }}+1\le I-n \end{aligned}$$

(21)

hold for $n=1,\ldots I-1$. $\square$

Proof of the lemma:

The proof is by backward induction. First, consider the case of $n=I-1$. Proposition 1 defines $\phi _{I}=0$ and

$$\begin{aligned} \phi _{I-1}=q_{I}+\left( 1-q_{I}\right) R^{1-\gamma }. \end{aligned}$$

Note that $R>1$ and $\gamma >1$ implies $R^{1-\gamma }<1$. Together with the fact that $0<q_{I}<1,$ these definitions thus imply

$$\begin{aligned} R^{\frac{1-\gamma }{\gamma }}<\phi _{I-1}{}^{\frac{1}{\gamma }}<\phi _{I}{}^{ \frac{1}{\gamma }}+1=1, \end{aligned}$$

which shows that (21) holds for $n=I-1$.

Next, suppose (21) holds for some $n\le I-1;$ we need to show that the set of inequalities then also holds for $n-1$. Together with $R^{\frac{ 1-\gamma }{\gamma }}<1,$ the first inequality in (21) implies

$$\begin{aligned} \left( I-n+1\right) R^{\frac{1-\gamma }{\gamma }}<\phi _{n}{}^{\frac{1}{ \gamma }}+1. \end{aligned}$$

From the definition of $\phi$ in Proposition 1, we have

$$\begin{aligned} \phi _{n-1}=q_{n}\left( \phi _{n}{}^{\frac{1}{\gamma }}+1\right) ^{\gamma }+\left( 1-q_{n}\right) \left( I-n+1\right) ^{\gamma }R^{1-\gamma }. \end{aligned}$$

Since $0<q_{n}<1,$ these last two expressions imply

$$\begin{aligned} \left( I-n+1\right) ^{\gamma }R^{1-\gamma }<\phi _{n-1}<\left( \phi _{n}{}^{ \frac{1}{\gamma }}+1\right) ^{\gamma } \end{aligned}$$

or

$$\begin{aligned} \left( I-n+1\right) R^{\frac{1-\gamma }{\gamma }}<\phi _{n-1}{}^{\frac{1}{ \gamma }}<\phi _{n}{}^{\frac{1}{\gamma }}+1, \end{aligned}$$

which establishes that the first two inequalities in (21) hold for $n-1$ as well. Turning to the third inequality in (21), the assumption that this inequality holds for n, 

$$\begin{aligned} \phi _{n+1}{}^{\frac{1}{\gamma }}+1\le I-n, \end{aligned}$$

combined with the definition of $\phi _{n}$ in Proposition 1 implies

$$\begin{aligned} \phi _{n}\le & {} q_{n+1}\left( I-n\right) ^{\gamma }+\left( 1-q_{n}\right) \left( I-n\right) ^{\gamma }R^{1-\gamma } \\< & {} q_{n+1}\left( I-n\right) ^{\gamma }+\left( 1-q_{n}\right) \left( I-n\right) ^{\gamma } \\= & {} \left( I-n\right) ^{\gamma }. \end{aligned}$$

The inequality $\phi _{n}<\left( I-n\right) ^{\gamma }$ can be rewritten as

$$\begin{aligned} \phi _{n}{}^{\frac{1}{\gamma }}+1<I-\left( n-1\right) , \end{aligned}$$

which establishes that the third inequality in (21) also holds for $n-1,$ as desired.¹⁸ $\square$

Proposition 4

A patient depositor who anticipates that all other depositors are following (9) and who has the opportunity to make the nth withdrawal in period 0 will assign probability

$$\begin{aligned} p_{n}\left( \theta ;y^{0}\right) =\rho _{n}\left( \theta ;I\right) \equiv \frac{\sum \nolimits _{\omega \in \left\{ \omega :\theta \left( \omega \right) =\theta \right\} }\left( p\left( \omega \right) \sum \nolimits _{k=n}^{I} {\mathcal {I}}_{\left\{ \omega \in Z_{k}^{n-1}\right\} }\right) }{ \sum \nolimits _{\omega \in \varOmega ^{I}}\left( p\left( \omega \right) \sum \nolimits _{k=n}^{I}{\mathcal {I}}_{\left\{ \omega \in Z_{k}^{n-1}\right\} }\right) } \end{aligned}$$

to the event that exactly $\theta$ of the I depositors are patient, where ${\mathcal {I}}_{\left\{ A\right\} }$ is the indicator function for the set A. $\square$

Proof

Let $\sigma$ denote the depositor’s position in the sequence of withdrawal opportunities in period 0;  recall that this position is not observed by the depositor. The depositor is concerned with two independent random events: the ordered sequence of preference types $\omega$ and her position $\sigma$ in the order, which is drawn from the uniform distribution on $\left\{ 1,\ldots I\right\}$. The probability of a pair $\left( \omega ,\sigma \right)$ is given by

$$\begin{aligned} P\left( \omega ,\sigma \right) =\frac{p\left( \omega \right) }{I}, \end{aligned}$$

where

$$\begin{aligned} p\left( \omega \right) =\left( 1-\pi \right) ^{\theta \left( \omega \right) }\pi ^{I-\theta \left( \omega \right) }. \end{aligned}$$

Recall that we have defined $Z_{k}^{n-1}$ as the set of all type profiles $\omega$ in which there is a patient depositor in the kth position with exactly $n-1$ impatient depositors ahead of her in the order. Now define the events

$$\begin{aligned} B_{k}^{n-1}= & {} \left\{ \left( \omega ,\sigma \right) :\omega \in Z_{k}^{n-1}\right\} , \\ C_{k}= & {} \left\{ \left( \omega ,\sigma \right) :\sigma =k\right\} , \end{aligned}$$

and

$$\begin{aligned} A_{k}^{n-1}=B_{k}^{n-1}\cap C_{k}. \end{aligned}$$

The event $A_{k}^{n-1}$ is the set of pairs $\left( \omega ,\sigma \right)$ in which the depositor in question is in the kth position with exactly $n-1$ impatient depositors ahead of her in the order. Note that since the events $B_{k}^{n-1}$ and $C_{k}$ are independent and $P\left( C_{k}\right) =1/I$ for all values of k,  we have

$$\begin{aligned} P\left( A_{k}^{n-1}\right) =\frac{P\left( B_{k}^{n-1}\right) }{I} =\sum \limits _{\omega \in \varOmega ^{I}}\frac{p\left( \omega \right) \mathcal {I }_{\left\{ \omega \in Z_{k}^{n-1}\right\} }}{I}. \end{aligned}$$

The union

$$\begin{aligned} A^{n-1}=\bigcup \limits _{k=n}^{I}A_{k}^{n-1} \end{aligned}$$

contains all of the profiles $\omega$ that the depositor in question considers to be possible together with the positions $\sigma$ that she could conceivably occupy in each profile. Because the sets $A_{k}^{n-1}$ are disjoint for different values of k,  we have

$$\begin{aligned} P\left( A^{n-1}\right)= & {} \sum \limits _{k=n}^{I}P\left( A_{k}^{n-1}\right) \nonumber \\= & {} \sum \limits _{k=n}^{I}\sum \limits _{\omega \in \varOmega ^{I}}\frac{p\left( \omega \right) {\mathcal {I}}_{\left\{ \omega \in Z_{k}^{n-1}\right\} }}{I}\nonumber \\= & {} \sum \limits _{\omega \in \varOmega ^{I}}p\left( \omega \right) \sum \limits _{k=n}^{I}\frac{{\mathcal {I}}_{\left\{ \omega \in Z_{k}^{n-1}\right\} }}{I}. \end{aligned}$$

(22)

In other words, the probability of the set $A^{n-1}$ can be obtained by summing the probabilities of all profiles $\omega ,$ each weighted by the fraction of the I positions in the order that match the observed criteria (that is, have a patient depositor with exactly $n-1$ impatient depositors ahead of her in the order). Notice that any profile $\omega$ that is not in the set $Z_{k}^{n-1}$ for some value of k receives zero weight in this sum.

Next, define

$$\begin{aligned} D^{\omega }=\left\{ \left( \widehat{\omega },\sigma \right) :\widehat{\omega }=\omega \right\} . \end{aligned}$$

The set $D^{\omega }$ contains all of the pairs $\left( \omega ,\sigma \right)$ that correspond to a particular profile of preference types $\omega$. It is straightforward to see that the prior probability of this set is given by $p\left( \omega \right)$. The posterior probability we want to calculate is

$$\begin{aligned} P\left( D^{\omega }\ |\ A^{n-1}\right) , \end{aligned}$$

that is, the probability of a particular profile $\omega$ conditional on the depositor observing that there are $n-1$ impatient depositors ahead of her in the order. Applying Bayes’ rule yields

$$\begin{aligned} P\left( D^{\omega }\ |\ A^{n-1}\right) =\frac{P\left( A^{n-1}\ |\ D^{\omega }\right) P\left( D^{\omega }\right) }{P\left( A^{n-1}\right) }. \end{aligned}$$

(23)

By definition

$$\begin{aligned} P\left( A^{n-1}\ |\ D^{\omega }\right) P\left( D^{\omega }\right) =P\left( A^{n-1}\cap D^{\omega }\right) =P\left( \bigcup \limits _{k=n}^{I}\left( \left( B_{k}^{n-1}\cap D^{\omega }\right) \cap C_{k}\right) \right) . \end{aligned}$$

(24)

For a given profile $\omega ,$ we have

$$\begin{aligned} B_{k}^{n-1}\cap D^{\omega }=\left\{ \begin{array}{l@{\quad }l@{\quad }l} \varnothing &{} B_{k}^{n-1}=\varnothing \\ \varnothing &{} \text {if }\, \omega \notin Z_{k}^{n-1} \\ D^{\omega } &{} \omega \in Z_{k}^{n-1} \end{array} \right\} , \end{aligned}$$

Again using the fact that $\sigma$ is independent of $\omega$ and that $P\left( C_{k}\right) =1/I$ for all k, this implies

$$\begin{aligned} P\left( A^{n-1}\cap D^{\omega }\right) =P\left( D^{\omega }\right) \frac{ \sum \nolimits _{k=n}^{I}{\mathcal {I}}_{\left\{ \omega \in Z_{k}^{n-1}\right\} }}{ I}. \end{aligned}$$

(25)

In other words, the probability of the intersection of the sets $A^{n-1}$ and $D^{\omega }$ is equal to the probability of $D^{\omega }$ multiplied by the fraction of the I positions in the order that the depositor could conceivably occupy when the realized profile is $\omega$.

Substituting (22), (24) and (25) in expression (23) yields the posterior belief over profiles $\omega ,$

$$\begin{aligned} P\left( D^{\omega }\ |\ A^{n-1}\right) =\frac{p\left( \omega \right) \sum \nolimits _{k=n}^{I}{\mathcal {I}}_{\left\{ \omega \in Z_{k}^{n-1}\right\} }}{ \sum \nolimits _{\omega \in \varOmega ^{I}}\left( p\left( \omega \right) \sum \nolimits _{k=n}^{I}{\mathcal {I}}_{\left\{ \omega \in Z_{k}^{n-1}\right\} }\right) }. \end{aligned}$$

This expression shows that the posterior probability of a profile $\omega$ is proportional to its prior probability multiplied by the fraction of positions in the order the depositor could conceivably occupy if $\omega$ were the true profile.

Finally, the posterior probability distribution over $\theta ,$ the number of patient depositors, is given by

$$\begin{aligned} p_{n}\left( \theta ;I\right) =\sum \limits _{\left\{ \omega :\theta \left( \omega \right) =\theta \right\} }P\left( D^{\omega }\ |\ A^{n-1}\right) . \end{aligned}$$

$\square$