Analysis of 3D interaction of a blast wave with a finite wall

Abstract

The aim of this study is to characterize the interaction of a shock wave with an obstacle. The effect of the length of the obstacle on the shock wave propagation and maximum overpressure is investigated. Several previous studies investigated the use of obstacles such as porous materials, grids, pseudo-perforated walls, triangular wedges, or multi-obstacles as a way to mitigate blast intensity. Here, the focus is on the interaction of an incident shock wave on a single-plate obstacle. This obstacle can be seen as a wall or a low-rise building. The paper presents a small-scale experimental study. The blast wave is created by the detonation of a hemispherical gaseous charge. It is characterized by pressure sensors and a high-speed camera. The pressure sensors record the overpressure and arrival time. The propagation, reflection, and diffraction of the shock wave are analyzed from the pictures produced during the visualization tests.

1 Introduction

In the literature, the interaction of a shock wave with an obstruction is analyzed according to the different properties of the obstruction. Thus, the isolated obstacle in a highly compressible flow and in the presence of a shock wave can be examined either as an absorbing element or as a perfectly rigid and reflective element. When the obstacle is assumed to be perfectly reflecting, its geometry and dimensions are the parameters chosen to determine its influence on the properties of the transmitted and reflected waves. Maillot et al. [1] experimentally measured the height of the Mach stem appearing downstream of a semi-cylindrical obstacle with a radius of half the hemispherical explosive charge (gas mixture, propane–oxygen). In addition, they noted that overpressure was reduced by about 30% close downstream of the obstacle compared to free-field values, but then increased under the effect of the appearance of the Mach stem (approximately 50 mm downstream of the semi-cylindrical obstacle with a radius of 23 mm) and later recovered its value in free-field conditions. The Mach stem was considered as the sole cause of the maximum overpressure increase since the infinite length of the semi-cylindrical obstacle makes the diffraction of the shock wave take place in a two-dimensional plane. Therefore, there is no lateral wave that could produce overpressure.

Complex geometries have been analyzed in order to mitigate the incident shock wave. Sha et al. [2] investigated numerically the influence of obstacle geometry on the attenuation of a shock wave. By first studying the effect of the thickness of a rectangular obstacle, they observed that the narrower the obstacle, the faster the attenuation of the incident shock wave. Thus, in order to have the thinnest possible edge while keeping a physically rigid structure, they chose a triangular shape for the obstacle. They then studied the effect of the inclination of the downstream and upstream parts of the triangular obstacle. They found that the inclination of the downstream face had no influence, whereas the upstream face of the triangular obstacle attenuated the shock wave. Thus, by comparing their results with the experimental shock tube tests by Gongora-Orozco et al. [3] for the same obstacle heights and inter-obstacle gap, they showed that triangular obstacles with an obtuse slope on the windward side are more effective than rectangular obstacles in terms of attenuation of the incident shock wave.

In [4], Sochet et al. studied the effect of the inclination of the leading and trailing edges of protective walls on the overpressure of blast waves for angles between $20^{\circ }$ and $90^{\circ }$. It was found that a $90^{\circ }$ angle on the upstream face of the protective barrier had a shielding effect, reducing the maximum downstream overpressure but producing strong reflected overpressures. The $90^{\circ }$ angle on the upstream face also avoided the formation of a Mach stem before the incident wave reaches the top of the barrier. A $90^{\circ }$ angle on the downstream face of the barrier had the advantage of creating a large expansion wave, which also reduced the maximum overpressure. Blast wall protection was experimentally studied by Rose et al. [5, 6], and particular attention was paid to the “shadow” region above the ground downstream of the wall. According to Borgers and al. [7] using numerical means, the “shadow” region represents at least four times the height of the wall.

This paper presents an experimental study of the interaction of a spherical blast wave with an isolated obstacle (called “wall” in the following). Particular attention was paid to the maximum overpressure evolution on the ground downstream of the wall. The only parameter studied was the obstacle length perpendicular to the direction of the shock wave propagation. The chosen walls and the experimental setup are presented in the first part. In the second part, the maximum overpressure is analyzed and is broken down according to its different sources. Then, in the third part a maximum overpressure calculation is suggested to compute the effects downstream of the obstacles.

2 Experimental facilities

2.1 Experimental setup

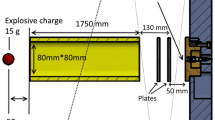
The experiments were carried out at small scale. The explosion is produced by detonating a gaseous charge (propane–oxygen stoichiometric mixture) in a hemispherical soap bubble. With a radius of 60 mm, the mass $m_{{\mathrm {c}}}$ of the hemispherical charge is $6.2882\times 10^{-4}$ kg. The energy produced by the explosion of this volume of gas is $6.85\times 10^{-3}$ MJ. This gaseous explosive charge at small scale is well documented in the literature and can be used as a model. It was used by Rokhy and Soury [8] to validate their numerical method by comparing the experimental results of Sauvan et al. [9] in a confined room with their simulation. The ignition device and the experimental bench are the same as those used in Maillot et al. [1]. This system was optimized to ensure good repeatability. Figure 1 illustrates this repeatability with an example of three overpressure measurements in free field at 203 mm from the center of the explosive charge.

Fig. 1

Overlay of three overpressure measurements in free field

In addition to repeatability, each test had to satisfy a validation criterion. This criterion is a tolerance of 5% on the maximum overpressure measured by a pressure sensor positioned in free field and compared to a reference value. Therefore, all the experimental measurements presented have a constant error margin of 5%.

The flat table, called detonation table, is perforated, in order to install the ignition device and pressure sensors (Fig. 2). Ignition is created by discharging a high voltage to sublimate a tinned copper wire between two electrodes. Sochet et al. [10] provide details on this ignition method.

Visualizations were performed using the shadowgraph method PILS (Pure In Line Shadowscopy) detailed in Hargather et al. [11]. In this method, the light source is coaxial with the optical axis. Light rays are deflected through the shock wave and produce shadows on the retro-reflective screen positioned behind the studied area (Fig. 2). However, the divergence of the light rays forces an optical correction as given by Dewey [12] to measure the free-field propagation of the shock wave. This correction of the shock wave ray depends on the distance between the observed phenomenon and the camera, and on the position of the charge center. In the present study, the parallax error was estimated by the shock wave speed from the pressure sensors and the measurements from the visualization. The parallax error was found to be 1.5%.

Fig. 2

Experimental bench schema

2.2 Experimental equipment

The pressure sensors used to measure the properties of the blast wave are piezoelectric PCB 113B26. Acquisition was recorded from 1 ms before the explosion until 5 ms after the explosion with a sampling rate of 1 MHz. In the present study, the pressure sensors are positioned in the axis passing by the center of the charge and the center of the obstacle to simplify the analysis, including one probe isolated in free field (Fig. 2). The distance between each sensor is 100 mm. The first sensor is located between the obstacle and the center of the explosive charge, 103 mm from the latter.

Shock wave visualizations were performed with a high-speed camera Phantom V7.3. In all the experiments, the sample rate was 16,877 pps and the image resolution was $688 \times 456$ pixels. With this resolution, an area of $570 \times 217~\hbox {mm}^2$ can be visualized. The manufacturer of the fast camera guarantees that there is no distortion, except for images exported in JPEG format due to compression. Hence, once the videos had been recorded, they were exported in AVI format and then processed using the open-source software imageJ.

2.3 Obstacles

In this study, the shock wave interacts with a single obstacle/wall. The nomenclature of the wall dimensions is detailed in Fig. 3 with t for thickness, L for length, H for height, and $R_{{\mathrm {upstream}}}$ the distance between the center of the charge and the upstream face of the wall. In all configurations, $R_{{\mathrm {upstream}}}$, t, and H remain constant at $R_{{\mathrm {upstream}}}= 144~\hbox {mm}$, $t=18~\hbox {mm}$, and $H=82~\hbox {mm}$. The length L varies from 82 to 500 mm. The dimensions of the obstacles and their position in relation to the explosive charge make it possible to represent on a small scale an IED (Improvised Explosive Device) explosion facing a fence wall.

Fig. 3

Dimension nomenclature of obstacles

The classification of all the walls is presented in Table 1.

Table 1 Classification of obstacles

Fig. 4

Relative difference of the maximum overpressure

3 Analysis of the maximum overpressure

When the incident spherical blast wave, called incident wave (IW), interacts with a finite wall, one part is reflected, and one part diffracts around each face of the obstacle (the two sides and top, see Fig. 3). Around the lateral faces, this part of the blast wave is called lateral wave (LW); the wave diffracting on the top face is called bypass wave (BW). In this study, the maximum overpressure $\varDelta P_{{\mathrm {max}}}$ is the main blast wave property analyzed. It was measured at different positions in only one direction (studied direction, Figs. 2 and 3). Measurements were then compared to the free field values $\varDelta P_{{\mathrm {max, FF}}}$, i.e., when there is no obstruction. One way to compare these measures is to use the relative difference RD. The relative difference of the maximum overpressure is defined as follows:

$$\begin{aligned} {{\mathrm {RD}}} = \frac{\varDelta P_{{\mathrm {max}}}-\varDelta P_{{\mathrm {max, FF}}}}{\varDelta P_{{\mathrm {max, FF}}}}\times 100 \end{aligned}$$

(1)

In order to compare experiments at different scales, the reduced distance Z is used throughout this study to express the maximum overpressure and the arrival time evolution, since it has been demonstrated that small-scale experiments are correlated with large-scale experiments (Rigby et al. [13], Dewey and Sochet [14]) using scaled values. In this study, the reduced distance was calculated by dividing R by the cubic root of the charge mass $m_{{\mathrm {c}}}$:

$$\begin{aligned} Z = \frac{R}{\root 3 \of {m_{{\mathrm {c}}}}} \end{aligned}$$

(2)

The relative difference of the maximum overpressure RD ($\varDelta P_{{\mathrm {max}}}$) downstream of the obstacles presented in Table 1 is plotted against the reduced distance Z in Fig. 4.

As shown in Fig. 4, there are different shapes of overpressure evolution downstream of the obstacles. The wall length L governs these differences. Hence, the obstacles were split into three categories:

• $H \le L < 1.5~H$, or equivalently 82 mm $\le L < 150$ mm

• $1.5~H \le L < 3~H$, or 150 mm $\le L < 250$ mm

• $L > 3~H$, or $L > 250$ mm

In the first category ($H \le L < 1.5~H$), increasing the obstacle length increases the maximum overpressure following the initial attenuation. In the second category ($1.5~H \le L < 3~H$), increasing L delays reaching the positive phase of the relative difference RD ($\varDelta P_{{\mathrm {max}}}$) downstream of the obstacles. In the third category ($L \ge 3~H$), the values of the relative difference of the maximum overpressure remain negative. Here, the mitigation effect is greater than in the other categories. Wall-18-250-82 seems to represent the transition criteria from $Z =7~\hbox {m}\cdot \hbox {kg}^{-1/3}$ because its relative maximum overpressure difference reaches positive values. One can note that the maximum overpressure attenuation is 80% at the nearest pressure sensor downstream of the wall. Contrary to the claims of Borgers et al. [7], the “shadow” region here is estimated to be only once the height of the wall H.

3.1 Retrieval of different overpressure sources

Based on what has been described above, it is interesting to investigate which phenomena are responsible for such a difference between the three obstacle categories. In this section, it is assumed that the overpressures produced by shock waves that consecutively reach a given position add up perfectly. Figure 5 illustrates this assumption. In this illustration, a first shock wave produces a first overpressure. Later, a second shock wave produces a second overpressure. Finally, the resulting overpressure is the sum of the overpressures produced by the two shock waves.

Fig. 5

Schematic illustration of the assumption concerning the sum of overpressures

Fig. 6

Overpressure time history at $0.4786~\hbox {m}\cdot \hbox {kg}^{-1/3}$ (H/2) downstream of the obstacles

Table 2 What Fig. 6 demonstrates

Figure 6 shows the overpressure time history at the distance H/2 downstream of three obstacles, i.e., in its shadow area, one from each category. The obstacles are Wall-18-82-82, Wall-18-168-82, and Wall-18-350-82. The relative differences of the maximum value of each overpressure profile are visible in Fig. 4 at $Z=2.37~\hbox {m}\cdot \hbox {kg}^{-1/3}$.

Figure 6 demonstrates several things which are detailed in Table 2. Finally, one can see that there are three different shock wave schemes:

• The shock wave is a bypass wave BW.

• The shock wave is a couple of lateral waves LWs.

• The shock wave is a combination of the bypass wave BW and the lateral waves LWs.

3.2 Bypass wave BW

The so-called bypass wave is the part of the incident wave that diffracts on the upper side of the obstacle and reflects on the ground. Hence, the bypath path depends on the obstacle height. However, in this study, all the obstacles are the same height: 82 mm. So, the bypass wave BW trajectory is expected to be the same for each obstacle. As the bypass wave does not use the straightway Z, it is expressed against a new reduced distance, the reduced bypass path:

$$\begin{aligned} \begin{aligned} Z_{{\mathrm {bypass}}}&= \sqrt{Z_{{\mathrm {upstream}}}^2+\left( \frac{H}{\root 3 \of {m_{{\mathrm {c}}}}}\right) ^2}\\&\quad +t+ \sqrt{\left( \frac{H}{\root 3 \of {m_{{\mathrm {c}}}}}\right) ^2+Z_{{\mathrm {downstream}}}^2} \end{aligned} \end{aligned}$$

(3)

where $Z_{{\mathrm {upstream}}}$ is the reduced scale of the distance $R_{{\mathrm {upstream}}}$ and $Z_{{\mathrm {downstream}}}$ is the reduced distance downstream of the obstacle.

In order to estimate the bypass wave effects as accurately as possible, arrival time and overpressure are presented only downstream of the obstacles whose length exceeds 250 mm, i.e., obstacles from the third category (see Fig. 7).

Fig. 7

Measurements of the properties of the bypass wave BW downstream of the obstacles

As expected, the measured properties are the same downstream of these obstacles. From these measurements, evolution laws can be expressed for a reduced bypass path ranging from $3.2~\hbox {m}\cdot \hbox {kg}^{-1/3}$ to $12.7~\hbox {m}\cdot \hbox {kg}^{-1/3}$. The arrival time and the maximum overpressure of the bypass wave BW are given in (4) and (5), respectively:

$$\begin{aligned}&T_{{\mathrm {a, BW}}} = \frac{0.2477~Z_{{\mathrm {bypass}}}^2+0.3261~Z_{{\mathrm {bypass}}} -0.4416}{Z_{{\mathrm {bypass}}}+4.187} \end{aligned}$$

(4)

$$\begin{aligned}&\frac{\varDelta P_{{\mathrm {max, BW}}}}{P_0} = \frac{0.605~Z_{{\mathrm {bypass}}}-1.473}{Z_{{\mathrm {bypass}}}^2 -6.522~Z_{{\mathrm {bypass}}}+19.92} \end{aligned}$$

(5)

3.3 Lateral waves LWs

The lateral waves are the couple of shock waves that diffract around each lateral face of the obstacle and thus apply a side-on pressure. Unlike the bypass wave, the lateral waves depend on the obstacle length, the only parameter that changes between each obstacle. Hence, the path of the lateral waves varies with the obstacles. Figure 8 shows the properties of the lateral waves against the reduced lateral path $Z_{{\mathrm {lateral}}}$ ranging from 2.6 to $13.9~\hbox {m}\cdot \hbox {kg}^{-1/3}$. The reduced lateral path is expressed as follows:

$$\begin{aligned} \begin{aligned} Z_{{\mathrm {lateral}}}&= \sqrt{Z_{{\mathrm {upstream}}}^2+\left( \frac{L}{2\root 3 \of {m_{{\mathrm {c}}}}}\right) ^2}\\&\quad +t+ \sqrt{\left( \frac{L}{2\root 3 \of {m_{{\mathrm {c}} }}}\right) ^2+Z_{{\mathrm {downstream}}}^2} \end{aligned} \end{aligned}$$

(6)

Fig. 8

Measurements of the properties of the lateral waves LWs downstream of the obstacles

The arrival time evolution is linear and its fitted curve equation is:

$$\begin{aligned} T_{{\mathrm {a, LW}}} = 0.2223~Z_{{\mathrm {lateral}}}-0.3068 \end{aligned}$$

(7)

The maximum overpressure produced by the lateral waves LWs corresponds to this evolution equation:

$$\begin{aligned} \frac{\varDelta P_{{\mathrm {max, LW}}}}{P_0} = 8.774~Z_{{\mathrm {lateral}}}^{-2.636} \end{aligned}$$

(8)

3.4 Combination bypass wave/lateral waves

When the bypass wave and the lateral waves arrive at the same time, they interact and create a combination wave. Figure 9 illustrates conditions that make the lateral waves and the bypass wave interact, using data from the pressure sensor analysis. This area is called the interaction area.

Fig. 9

Obstacle lengths and their downstream area where the bypass wave and the lateral waves interact

Figure 9 is interesting because it shows that the interaction area evolves with the three categories of obstacles. In the first category ($H \le L < 1.5~H$), the lateral waves interact together before interacting with the bypass wave. It follows that the interaction area is constant. In the second category ($1.5~H \le L < 3~H$), the lateral waves and the bypass wave interact together almost at the same time. As a result, the interaction area is closer downstream obstacles of the second category than downstream obstacles in the first category. Lastly, in the third category ($L \ge 3~H$), the lateral waves interact together but they arrive later than the bypass wave. Once they have merged, they will catch up with the bypass wave. Therefore, the greater the length of the obstacle, the farther the interaction zone is from the obstacle.

Fig. 10

Maximum overpressure produced by the bypass and lateral waves interaction downstream of the obstacles

The maximum overpressure measured in the interaction area is plotted against the reduced distance downstream obstacles in Fig. 10. Here the reduced distance range, where the lateral waves LWs interact with the bypass wave BW downstream of the obstacles, is from 1.7 to $10.5~\hbox {m}\cdot \hbox {kg}^{-1/3}$. The curve fitting the maximum overpressure in Fig. 10 is given by the following equation:

$$\begin{aligned} \begin{aligned}&\frac{\varDelta P_{{\mathrm {max, BW-LW}}}}{P_0}(Z_{{\mathrm {downstream}}}) \\&\quad =\frac{25.6}{Z_{{\mathrm {downstream}}}^2+10.53~Z_{{\mathrm {downstream}}}+4.156} \end{aligned} \end{aligned}$$

(9)

4 Maximum overpressure calculation

Now that the maximum overpressure produced by the bypass and the lateral waves individually is known, the maximum overpressure downstream of a wall can be estimated by combining these tendency equations. However, Fig. 6 shows that the overpressure of the bypass shock wave and the lateral waves overpressure all add up. Therefore, if the arrival time of the fastest shock wave is close to the arrival time of the slowest wave, the addition of their overpressure increases the maximum overpressure of the signal. Hence, in the maximum overpressure calculation, the difference in arrival time $\varDelta T_{{\mathrm {a}}}$ between shock waves must be taken into account.

The maximum overpressure calculation depends on the category of obstacles and is calculated only at the pressure sensors position. Moreover, the purpose of this calculation is to suggest a phenomenological analysis, not to propose an accurate estimate of the maximum overpressure downstream of a wall. The calculation results may therefore contain large errors.

4.1 First category ($H \le L < 1.5~H$)

In the first category, the lateral waves LWs go around the wall before the bypass wave BW does. Figure 11 shows the evolution of these waves at four consecutive times after the explosion downstream of the obstacles in the first category (Wall-18-100-82 in this example). In pictures (a), (b), and (c), the bypass wave BW becomes smaller and smaller with time until it disappears in picture (d). As one can see, the bypass wave BW is connected to wave W2. Wave W2 is created by the interaction of the two lateral waves. It means that when lateral waves interact together, they become stronger so that they can be dominant with respect to the bypass wave. Therefore, the bypass wave is absorbed by wave W2. The same thing seems to occur for wave W1 [in fact, there are two W1 waves, as is shown in picture (d)]. This W1 wave is created by the interaction of the bypass wave with each lateral wave. Only one lateral wave should be visible because the bypass by the lateral sides is symmetric. However, both lateral waves are visible because of the parallax. One can note that the wave structure formed by the reflected wave RW, the bypass wave BW, and wave W2 resembles a terminal double-Mach reflection TerDM [15].

Fig. 11

Organization and evolution of shock waves downstream of the obstacle Wall-18-100-82

Now that interaction between the lateral waves and the bypass wave has been detailed downstream of the obstacles in the first category, a maximum overpressure calculation is proposed. For the first category, the maximum overpressure calculation depends on the distance downstream of the obstacle:

• At $R_{{\mathrm {downstream}}} < H$

  $$\begin{aligned} \varDelta P_{{\mathrm {max}}} (Z_{{\mathrm {downstream}}})=\varDelta P_{{\mathrm {max,LW}}} (Z_{{\mathrm {lateral}}}) \end{aligned}$$

  (10)

• At $R_{{\mathrm {downstream}}} > H$

  $$\begin{aligned} \begin{aligned} \varDelta P_{{\mathrm {max}}} (Z_{{\mathrm {downstream}}})&=\varDelta P_{{\mathrm {max,BW-LW}}} (Z_{{\mathrm {downstream}}})\\&\quad -\varDelta P_{{\mathrm {max, LW}}} (Z_{{\mathrm {lateral}}}) \end{aligned}\nonumber \\ \end{aligned}$$

  (11)

with $\varDelta P_{{\mathrm {max, LW}}}$ and $\varDelta P_{{\mathrm {max, BW-LW}}}$ calculated from (8) and  (9), respectively.

Figure 12 proposes a comparison between the measured maximum overpressure and the calculation from (10) and (11) downstream of the obstacles in the first category. The error produced by the calculation is within the interval [$-25.6$%; 13.2%].

Fig. 12

Comparison between experimental and calculated results of the maximum overpressure in category 1

4.2 Second category ($1.5~H \le L < 3~H$)

In the second category of obstacles, the lateral waves LWs go around the obstacle more or less at the same time as the bypass wave does. Therefore, each lateral wave interacts with the other lateral wave as it interacts with the bypass wave. As a result, this new combination produces a maximum overpressure higher than downstream of the obstacles in the first category.

• At $R_{{\mathrm {downstream}}} < H$

  $$\begin{aligned} \varDelta P_{{\mathrm {max}}} (Z_{{\mathrm {downstream}}})=2~\varDelta P_{{\mathrm {max,LW}}} (Z_{{\mathrm {lateral}}}) \end{aligned}$$

  (12)

• At $R_{{\mathrm {downstream}}} > H$

  $$\begin{aligned} \begin{aligned} \varDelta P_{{\mathrm {max}}} (Z_{{\mathrm {downstream}}})&=\varDelta P_{{\mathrm {max,BW-LW}}} (Z_{{\mathrm {downstream}}})\\&\quad -\varDelta P_{{\mathrm {max, LW}}} (Z_{{\mathrm {lateral}}}) \end{aligned}\nonumber \\ \end{aligned}$$

  (13)

Figure 13 illustrates the maximum overpressure downstream of the obstacles in the second category from experimental measurement and calculation (12, 13). The error produced by the calculation is within the interval [$-25.3$%; 19.1%].

Fig. 13

Comparison between experimental and calculated results of the maximum overpressure in category 2

Fig. 14

Comparison between experimental and calculated results of the maximum overpressure in the category 3

4.3 Third category ($L \ge 3~H$)

In the third category, the length of the obstacle is large enough to delay the lateral waves LWs as they do not disturb the bypass wave BW nor its reflection on the ground RW. Hence, the maximum overpressure is produced by the bypass wave (5). Nevertheless, the lateral waves interact together and form a new wave (W2 in Fig. 11). This wave travels faster than the bypass wave, even if its reflection becomes irregular and forms a Mach stem. Therefore, in the third category, as the overpressure produced by the lateral waves is added to the overpressure produced by the bypass wave, the maximum overpressure depends on the delay between the bypass wave and the lateral waves until they interact all together. Having $\varDelta T_{{\mathrm {a}}}$($Z_{{\mathrm {downstream}}}$) = $T_{{\mathrm {a, BW}}}$($Z_{{\mathrm {bypass}}}$)–$T_{{\mathrm {a, LW}}}$($Z_{{\mathrm {lateral}}}$),

• While $\varDelta T_{{\mathrm {a}}}>$ 0.07 ms

  $$\begin{aligned} \varDelta P_{{\mathrm {max}}} (Z_{{\mathrm {downstream}}})= \varDelta P_{{\mathrm {max, BW}}} (Z_{{\mathrm {bypass}}}) \end{aligned}$$

  (14)

• Then

  $$\begin{aligned} \begin{aligned} \varDelta P_{{\mathrm {max}}} (Z_{{\mathrm {downstream}}})&= \varDelta P_{{\mathrm {max, FF}}} (Z_{{\mathrm {bypass}}})\\&\quad -\varDelta P_{{\mathrm {max, BW}}} (Z_{{\mathrm {bypass}}}) \end{aligned} \end{aligned}$$

  (15)

with $\varDelta P_{{\mathrm {max, FF}}}$ the maximum overpressure law without obstruction.

Figure 14 shows the maximum overpressure calculated from (14) and (15) and the measured maximum overpressure values. The error produced by the calculation is within the interval [$-16.4$%; 16.1%]. Here, the estimate of the maximum overpressure is better than for the calculation of the first two categories. This can be explained by the fact that the lateral waves do not act on the maximum overpressure.

5 Conclusion

In this study, the interaction of an isolated finite-dimensional wall with a spherical blast wave has been investigated in order to understand the effects of its lateral dimension (length). Using different obstacles of the same height (82 mm) and for a range of lengths from 82 to 500 mm, the influence of the obstacle length on the maximum overpressure was determined. It was observed that the protective effect occurs in the area close downstream of the obstacle. The maximum protection zone extends over a distance close to the height of the walls H projected to the ground downstream of them. However, depending on the length of the walls, the protective effect does not last. Indeed, downstream of an obstacle whose length $L < 3~H$, the maximum overpressure becomes much stronger (up to 40%) than in free field. Therefore, it is assumed that this mitigation is canceled by lateral waves when they have caught up with the bypass wave. One can hypothesize that the maximum overpressure is mitigated downstream of an “infinite” obstacle because there is no lateral wave.

Thanks to the distinction between the overpressure produced by the bypass wave and the overpressures produced by the lateral waves in the overpressure measured by each pressure sensor, a calculation of the maximum overpressure is proposed depending on the obstacle length. The difference between measurement and calculation is reasonable ($-25$% to +20% error). Finally, this paper proposes an analysis of phenomena observed downstream of a wall, considering the effect of the bypass wave and the lateral waves on the maximum overpressure.