1 Introduction

This paper describes the analysis of measurements of blast waves produced by a series of small-scale hemispherical stoichiometric, rich, and lean propane/oxygen charges. The total mass of each charge was less than 1 g. The purpose of these experiments was to demonstrate and evaluate the ability to consistently produce small-scale gaseous explosions and to determine whether the classical blast scaling laws were applicable. If these objectives could be achieved, it would validate the use of small-scale laboratory experiments to study the physical properties and effects of larger-scale planned and accidental gaseous explosions.

2 Experimental procedures

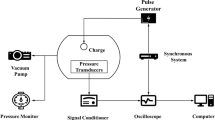
The procedures used to generate and measure the propane/oxygen explosions are described in detail by Sochet and Maillot [1], which also includes a comprehensive compendium of previous studies of gaseous explosions. The experiments were carried out on a horizontal plate. The pre-mixed propane and oxygen was injected though a small hole in the plate covered by a thin film of soap solution. Pressure was applied until the resulting hemispherical bubble reached a desired radius: 0.05 m for the experiments described here.

Each explosion was centrally initiated by application of a high voltage to an exploding wire inserted through the hole in the plate. The initiator consisted of a thin copper wire welded to tungsten electrodes. The applied voltage came from the discharge of capacitors (7 kV, \(8\,\upmu \hbox {F}\)) which instantaneously melted the wire and created a plasma. The estimated energy release was 50–60 J.

The plate on which the explosions occurred was made of Trespa®. The material is a compact high-pressure laminate (HPL) based on thermosetting resins homogeneously reinforced with natural fibres and manufactured under high pressure and high temperature. The thickness of the plate was 20 mm. The plate was isolated from the supporting structure by rubber pads, and each gauge was isolated from the plate by a rubber gasket.

Three explosive mixtures were studied: a stoichiometric propane/oxygen mixture, a lean mixture with a reduced amount of propane, and a rich mixture with an excess of propane. In each case, the mass of the charge was determined by the hemispherical volume with a radius of 0.05 m. The stoichiometric charge, \(\hbox {C}_{3}\hbox {H}_{8} + 5\hbox {O}_{2}\), consisted of 0.0798 g propane plus 0.2903 g oxygen for a total mass of 0.3702 g. The lean charge, \(\hbox {C}_{3}\hbox {H}_{8} + 6.25\hbox {O}_{2}\), consisted of 0.0661 g propane plus 0.3003 g oxygen for a total mass of 0.3664 g. The rich charge, \(\hbox {C}_{3}\hbox {H}_{8} +4.17\hbox {O}_{2}\), consisted of 0.0926 g propane plus 0.2810 g oxygen for a total mass of 0.3736 g. The above masses were those used in the subsequent analyses, and the number of decimal places does not imply the accuracy of their measurement.

Between three and five experiments were carried out with each mixture. The results from the experiments with each mixture were consistent and have been combined for the subsequent analyses.

The hydrostatic pressure in the blast wave generated by each explosion was measured by an array of piezoelectric transducers (Kistler 603 B and PCB 113B26) flush mounted in the high-pressure laminated plate. Fourteen transducers were used at distances from the centre of the charge ranging from 0.145 to 0.904 m. The resulting signals were digitally recorded at a frequency of 1 MHz. A typical record of the signal from such a measurement is shown in Fig. 1.

It can be seen in Fig. 1 that the increase in pressure to its maximum value is not as rapid as would be expected at a shock front. It was hypothesized that there were two possible reasons for this finite rise time. It might be associated with the transition time as the shock passes over the face of the gauge, or it might be due to the mechanical inertia of the components of the transducer together with the frequency response of the associated electronics. The rise times to the first maximum for the stoichiometric measurements ranged randomly from 8 to \(1.7\,\upmu \hbox {s}\) with a mean of \(1.2\,\upmu \hbox {s}\) and did not appear to be related to the shock velocities at the gauge positions. It was therefore assumed that the finite rise time was principally due to the inertia and frequency response of the transducer systems.

Fig. 1
figure 1

The pressure–time signal from the piezoelectric transducer at a distance of 0.684 m from the centre of a stoichiometric propane/oxygen mixture (\(\hbox {C}_{3}\hbox {H}_{8} + 5\hbox {O}_{2}\)) with a total mass of 0.37 g

Full size image

The pressure–time histories at many radii showed the second shock arriving in the positive phase before the pressure had returned to the ambient value. This is a characteristic of gaseous explosions, unlike that for most solid explosives for which the second shock arrives in the negative phase close to the pressure minimum.

Many of the gauge signals, such as Fig. 1, show a number of small oscillations after the maximum value. It is not clear whether this is due to small pressure variations behind the primary shock or “ringing” of the transducer and its electronics. It was concluded that because of their small magnitude, the oscillations were not relevant in the subsequent analyses.

3 Analyses

Two types of analyses were applied to the data derived from the transducers: an analysis of the primary shock time-of-arrival (TOA) at each gauge position and an analysis of the pressure–time history recorded by each gauge.

3.1 Shock time-of-arrival analysis

The TOA of the primary shock at each gauge location was selected as the first pressure reading showing a measureable value above zero, e.g., the time of the most left-hand data point in Fig. 1. The resulting radius–time data were least-squares-fitted to

$$\begin{aligned} R_{\mathrm {S}}=A+a_{0}t_{\mathrm {S}}+B\mathrm {ln}\left( 1+a_{0}t_{\mathrm {S}} \right) +C\sqrt{\mathrm {ln}(1+a_{0}t_{\mathrm {S}}),} \end{aligned}$$
(1)

where \(R_{\mathrm {S}}\) is the radial distance of the shock from the centre of the explosion, \(t_{\mathrm {S}}\) the time-of-arrival of the shock, A, B, and C the fitted coefficients, and \(a_{0}\) the ambient sound speed. It may be noted that as \(t_{\mathrm {S}} \rightarrow \infty \,\hbox { d}R_{\mathrm {S}}/\hbox {d}t \rightarrow a_{{0}}\), the ambient sound speed. This equation was first proposed by Dewey [2], and its application is described in detail by Dewey in [3]. It has been used extensively to analyse the blast waves from a large number of centred explosions.

The least-squares fit of (1) to the radius–time data, in which the radius, R, was measured in metres, the time, t, in milliseconds, and the sound speed, \(a_{{0}}\), in metres per millisecond, for the stoichiometric explosions is illustrated in Fig. 2, with the resulting fitted coefficients \(A = 0.02\), \(B = 835\), and \(C = 10\).

Fig. 2
figure 2

Radial distance from the centre of the stoichiometric explosion versus the measured times of shock arrival and the least-squares fit to (1)

Full size image

The Mach number of the shock at any time was calculated by differentiating (1), viz.,

$$\begin{aligned} M_{\mathrm {S}}= & {} \frac{1}{a_{0}}\frac{\mathrm {d}R_{\mathrm {S}}}{\mathrm {d}t_{\mathrm {S}}}\nonumber \\= & {} \left( 1+\frac{B}{1+a_{0}t_{\mathrm {S}}}+\frac{C}{2\left( 1+a_{0}t_{\mathrm {S}} \right) \sqrt{\mathrm {ln}\left( 1+a_{0}t_{\mathrm {S}} \right) } } \right) .\nonumber \\ \end{aligned}$$
(2)

The values of the shock Mach number, \(M_{\mathrm {S}}\), obtained from (2) can be used in the Rankine–Hugoniot relationships to determine all of the physical properties immediately behind the shock, as described by Dewey [4]. The Rankine–Hugoniot relationship

$$\begin{aligned} \frac{{\mathrm {OP}}_{\mathrm {S}}}{P_{0}}=\frac{7}{6}\left( M_{\mathrm {S}}^{2}-1 \right) \end{aligned}$$
(3)

was used to determine the peak hydrostatic overpressure, \(\hbox {OP}_{\mathrm {S}}\), in terms of the ambient pressure, \(P_{\mathrm {0}}\), assuming the ratio of specific heats \(\gamma = 1.4\), at radial distances from the centres of the propane/oxygen explosions. The result for the stoichiometric explosions is plotted in Fig. 3.

Fig. 3
figure 3

Peak hydrostatic overpressure versus radial distance for the stoichiometric explosions determined from the shock time-of-arrival measurements

Full size image

3.2 Overpressure–time histories analysis

Inspection of the overpressure–time measurement illustrated in Fig. 1, which is typical of all such measurements, shows that it is difficult to determine exactly the peak hydrostatic overpressure immediately behind the shock from such a record because of the finite response time of the transducer and the associated electronics. Decreasing the response time may not solve this problem due to ringing of the gauge system which may cause overshoot of the peak value. It has been found that a reliable way to overcome this problem is to least-squares-fit the recorded measurements in the positive phase to the modified Friedlander equation

$$\begin{aligned} \mathrm {OP}={\mathrm {OP}}_{\mathrm {S}}\cdot \mathrm {e}^{-\propto t}\left( 1-\frac{t}{t^{+}} \right) , \end{aligned}$$
(4)

where OP is the hydrostatic overpressure at a time t after the arrival of the shock, \(\hbox {OP}_{\mathrm {S}}\) the peak overpressure immediately behind the shock, \(\alpha \) a factor of the exponential coefficient, and \(t^{+}\) the duration of the positive phase when the pressure is greater than the ambient pressure; \(\hbox {OP}_{\mathrm {S}}\), \(\alpha \), and \(t^{+}\) are the least-squares-fitted coefficients. An unmodified form of this equation

$$\begin{aligned} \mathrm {OP}={\mathrm {OP}}_{\mathrm {S}}\cdot \mathrm {e}^{-\frac{t}{t^{+}}}\left( 1-\frac{t}{t^{+}} \right) , \end{aligned}$$
(5)

for which there are only two fitted coefficients, \(\hbox {OP}_{\mathrm {S}}\) and \(t^{+}\), was first used by G. I. Taylor to describe the shape of a blast and first reported by his student Friedlander [5]. The properties of (4) and (5) are described in detail by Dewey [6].

It has been found that the Friedlander equation (5), in which the constant in the exponential coefficient is \(1/t^{{+}}\), is a good descriptor of the pressure–time histories of blast waves from explosives such as TNT for the region in which the peak hydrostatic overpressure is less than 1 atm, but not in regions with higher peak pressures. The modified form of the equation, (4), is a good descriptor of the shape of blast waves from most explosives over a wide range of peak overpressures.

The data from each of the pressure–time measurements of the blast waves from the propane/oxygen explosions were truncated from a few measurement points before the pressure maximum and up to the arrival of the second shock. This truncation eliminated most of the points within the relatively slow rise time that was assumed to be due to the frequency response of the transducer. This was an arbitrary choice, but the high density of the measurement points meant that addition or removal of a few points in this region had no significant effect on the subsequent analysis.

The truncated data from each of the pressure–time measurements were least-squares-fitted to the modified Friedlander equation (4). A result of such a least-squares fit is shown in Fig. 4.

Fig. 4
figure 4

Least-squares fit of the modified Friedlander equation (4), to the truncated measured data from the gauge at 0.255 m from the explosion of the rich propane/oxygen mixture, where \(t_{{0}}\) is the time-of-arrival of the shock at the gauge

Full size image

The excellent way, in which the modified Friedlander equation is able to describe the pressure–time measurement illustrated in Fig. 4, is typical of all the least-squares fits to the gauge measurements of the blast waves from the stoichiometric, rich, and lean propane/oxygen mixtures.

The fitted coefficients, \(\hbox {OP}_{\mathrm {S}}\), were assumed to be the best determinations of the peak hydrostatic overpressures available from the pressure–time measurements.

3.2.1 Positive phase impulse

The pressure–time measurements were also used to determine the positive phase impulses at each gauge position. This could be done in two ways: (a) by summing the overpressure measurements and multiplying by the time interval between measurements and (b) by integrating the modified Friedlander equation, viz.,

$$\begin{aligned} I_{+}=\sum \limits _{0}^{t^{+}} {\mathrm {OP}\cdot \Delta t,} \end{aligned}$$
(6)

and

$$\begin{aligned} I_{+}= & {} \int _{0}^{t^{+}} {\mathrm {OP}}_{\mathrm {S}}\cdot \mathrm {e}^{-\propto t}\left( 1-\frac{t}{t^{+}} \right) \mathrm {d}t\nonumber \\= & {} \frac{{\mathrm {OP}}_{\mathrm {S}}}{\alpha ^{2}t^{+}}\left( \mathrm {e}^{-\alpha t^{+}}+\alpha t^{+}-1 \right) , \end{aligned}$$
(7)

where OP is the measured hydrostatic overpressure at a time t after the arrival of the shock, \(\Delta t\) the time interval between each pressure measurement, \({\hbox {OP}}_{\mathrm {S}}\) the peak hydrostatic overpressure immediately behind the shock, and \(t^{+}\) the positive phase duration.

Applying (6) to the data plotted in Fig. 4 gives \(I_{+} = 0.0417\,\hbox {atm}\,\hbox {ms}\). Applying (7) using the fitted coefficients of the least-squares fit of those data to the modified Friedlander equation gives \(I_{+} = 0.0461\,\hbox {atm}\). In the subsequent analyses, (7) was used to calculate the positive phase impulse for each gauge position.

Fig. 5
figure 5

Calculated positive phase impulse versus radius and the least-squares fit to a three-parameter exponential equation for the rich mixture explosions

Full size image

The calculated positive phase impulses at all gauge locations for the rich mixture explosions are plotted as functions of radius in Fig. 5, with their least-squares fit to a three-parameter exponential equation

$$\begin{aligned} I_{+}=0.0167+0.1698\mathrm {e}^{-6.0032R}, \end{aligned}$$
(8)

where \(I_{+}\) is the positive phase impulse (atm ms) and R is the radial distance from the charge centre in metres.

3.2.2 Pressure–time parameters as functions of radius

Least-squares-fitting the pressure–time histories to the modified Friedlander equation provided three fitted parameters at each gauge location: \(\hbox {OP}_{\mathrm {S}}\) the peak hydrostatic overpressure, \(\alpha \) the exponential coefficient, and \(t^{{+}}\) the positive phase duration. The values of each of these parameters for the lean mixture explosions are plotted as functions of radius in Figs. 6, 7, and 8.

The peak hydrostatic overpressures and the exponential coefficients as functions of radius were least-squares-fitted to a three-parameter exponential decay equation, and the positive phase durations were fitted to a three-parameter exponential increase equation. These results are also plotted in the figures.

Fig. 6
figure 6

Peak hydrostatic overpressure, \(\hbox {OP}_{\mathrm {S}}\) (atm), versus radius, R (m), from the modified Friedlander fits to the data from the lean mixture explosions, and the least-squares fit to \(\hbox {OP}_{\mathrm {S}} = 0.1425+6.8562\,\hbox {exp}(-8.8741{R})\)

Full size image
Fig. 7
figure 7

The exponential coefficients, \(\alpha \) (\(\hbox {ms}^{{-1}})\), from the modified Friedlander fits to the data from the lean mixture explosions versus radius, R (m), and the least-squares fit to \(\alpha = 1.7338 + 23.1445\,\hbox {exp}(-6.5195R)\)

Full size image
Fig. 8
figure 8

The positive phase durations, \(t^{{+}}\) (ms), from the modified Friedlander fits to the data from the lean mixture explosions versus radius, R (m), and the least-squares fit to \(t^{+} = 0.0266 + 0.3511(1 - \hbox {exp}(-2.{1285R})\)

Full size image

3.3 Comparison of shock time-of-arrival and pressure–time analyses

The peak hydrostatic overpressures were determined by using two different analysis techniques: the analysis of the shock time-of-arrival, as illustrated in Sect. 3.1, and by analysis of the pressure–time measurements, as illustrated in Sect. 3.2. The results of these two methods applied to the data from the lean mixture explosions are compared in Fig. 9.

Fig. 9
figure 9

A comparison of the peak hydrostatic overpressure versus radius from the shock time-of-arrival analysis with that from the modified Friedlander fits to the pressure–time measurements using the data from the lean mixture explosions

Full size image

3.4 Summary

The analyses described in the above sections were applied to the measurements of each of the blast waves generated by the three propane/oxygen mixtures: stoichiometric, rich, and lean. The results of the analyses illustrated above were selected from some of each of these mixtures. The quality of the results was similar for all the mixtures. All of the results from the analyses are available for download from https://doi.org/10.5683/SP2/VHN1UQ. They are also provided here as Electronic Supplementary Material.

The measurements for each mixture were obtained from a series of three to five explosions. From an inspection of the measurements, it was not possible to distinguish the results from the different experiments, indicating that there was a high degree of reproducibility.

4 Comparison of results

All of the experiments discussed here were carried out with charges of the same volume, viz., a hemisphere with a radius of 0.05 m. As a result, the total masses and the masses of the propane and oxygen were different for each series of experiments. This means that a direct comparison of the measured results has little meaning. To make a valid comparison of the blast waves from the different mixtures, it is necessary to scale the results to charges of the same mass. This was done using Hopkinson scaling (Hopkinson [7]; Dewey [3]), viz.,

$$\begin{aligned} R_{1}=R_{2}\left( \frac{W_{1}}{W_{2}} \right) ^{1/3}, \end{aligned}$$
(9)

where \(R_{{1}}\) is the distance of a measured blast wave property from the centre of an explosive charge of mass \(W_{{1}}\) and \(R_{{2}}\) is the distance at which the same property will occur from a charge of mass \(W_{{2}}\). The ambient pressure and temperature at the time of each gaseous explosion were not measured, and so Sachs scaling (Sachs [8]; Dewey [3]), which accounts for differences in these properties, was not applied. Equation (9), with \(W_{{1}}\) set to 1 kg and \(W_{{2}}\) equal to the mass of propane in each of the gaseous mixtures, was applied to the experimental results so that they could be appropriately compared.

The masses of propane used in the three experimental series were: stoichiometric 0.07984 g, lean 0.06607 g, and rich 0.09265 g. Using these charge masses in (9) and setting \(W_{{1}} = 1\,\hbox {kg}\) gave the following scaling factors that could be applied to the measured radii: stoichiometric \(S_{\mathrm {S}} =23.2234\), lean \(S_{\mathrm {L}} = 24.7361\), and rich \(S_{\mathrm {R}} = 22.0996\).

Applying these scaling factors to the peak hydrostatic overpressures as a function of radius obtained from the shock velocity analyses gives the results shown in Fig. 10.

Fig. 10
figure 10

Peak hydrostatic overpressures from the stoichiometric, rich, and lean gaseous explosions versus radius scaled to 1 kg of propane

Full size image

It can be seen that the overpressures from the lean explosions are higher than those from the other two mixtures. The overpressures from the rich explosions are significantly less at short radii, but gradually gain and eventually surpass those from the other explosions at longer radii. These differences are as might be expected. For the lean explosions, there is an excess of oxygen leading perhaps to a more efficient detonation with all the propane being consumed. For the rich explosions, there is a deficiency of oxygen so that 20% of the propane is not consumed in the detonations, resulting in lower overpressures at short radii. However, the unconsumed propane will mix with atmospheric oxygen in the turbulent contact region where the detonation products mix with the ambient air. This causes afterburning, as seen with other oxygen deficient explosives such as TNT, and this enhances the blast wave at longer radii.

Fig. 11
figure 11

Positive phase impulses for the three gaseous mixtures versus radius scaled to 1-kg propane

Full size image

The positive phase impulses of the blast waves from the three gaseous mixtures are plotted in Fig. 11 as functions of radius scaled to 1 kg of propane based on the amount of propane contained in each mixture. The impulse from the rich mixture is slightly less than that from the stoichiometric mixture, which is to be expected because 20% of the propane in the rich mixture would not have been consumed in the detonation because of the lack of oxygen.

The impulse from the lean mixture appears to be significantly higher than that from the stoichiometric mixture. Because this was an unexpected result, the analysis of the data from the lean explosion was carefully rechecked and appears to be an accurate representation of the experimental measurements. The excess oxygen in the lean explosions may have resulted in a more efficient detonation, and the expanding detonation products would have contained the 20% unconsumed oxygen. These factors may have contributed to the observed increase in impulse.

Many of these issues may be clarified using CFD to numerically simulate blast waves from gaseous explosions, in which the detonation processes and gas ratios can be adjusted in the initial conditions of the simulation.

5 Comparison with ProBlast interface

Dewey [9] describes an Excel©  interface, ProBlast, that provides the physical properties of blast waves generated by propane explosions. The interface was developed using measurements of the blast wave produced by a nominal 20-ton propane/oxygen mixture. The estimated total charge mass of this explosion was 19,281 kg. The results from the small-scale explosions, described above, have been compared with the predictions of the interface.

The mass of propane in the stoichiometric explosion, 0.0798 g, was input in the interface. The atmospheric pressure and temperature at the time of the explosion were not measured, and the values used in the interface were 99.6 kPa, the mean atmospheric pressure for the altitude at which the explosions were carried out, and \(15\,^{{\circ }}\hbox {C}\). Comparisons of the time-of-arrival of the primary shock for the stoichiometric explosion, the peak hydrostatic overpressures obtained from the radius–time analysis and from the gauges as functions of radius for the three explosive mixtures, and the pressure–time measurement at 0.255 m from the centres of the stoichiometric explosion are shown in Figs. 12, 13, 14, 15, and 16.

Fig. 12
figure 12

Shock time-of-arrival versus radius for the stoichiometric explosion as measured and as calculated by ProBlast

Full size image
Fig. 13
figure 13

Peak hydrostatic overpressure versus radius for the stoichiometric explosion as calculated from the shock time-of-arrival, as determined by the modified Friedlander fits to the pressure–time measurements, and as calculated by ProBlast

Full size image
Fig. 14
figure 14

Hydrostatic overpressure versus time at 0.255 m from the centre of the stoichiometric explosion for the modified Friedlander fit to the gauge measurement and from ProBlast

Full size image
Fig. 15
figure 15

Peak hydrostatic overpressure versus radius for the rich explosion, comparing the measured results with the output values from ProBlast using the full mass of propane and 80% of the mass

Full size image
Fig. 16
figure 16

Peak hydrostatic overpressure versus radius for the lean explosions, comparing the measured results with the output values from ProBlast

Full size image

6 Discussion and conclusions

The time histories of the hydrostatic pressures in the blast waves generated by the surface burst explosions of stoichiometric, rich, and lean mixtures of propane and oxygen with total masses of approximately 0.35 g have been measured using arrays of flush-mounted piezoelectric transducers. Details of these experiments are described by Sochet and Maillot [1].

The times-of-arrival of the primary shocks at the gauge positions were analysed for each of the explosions to determine the shock velocities, from which the values of the physical properties immediately behind the shocks were calculated using the Rankine–Hugoniot relationships, as described by Dewey [4].

The pressure–time measurements between the primary and second shocks from all the gauges were least-squares-fitted to the modified Friedlander equation (4). The result for one of the measurements is shown in Fig. 4. The excellent agreement between the least-squares fit and the measured pressures illustrated in the figure was similar at all the gauge positions for the three explosive mixtures. The three coefficients provided by the fits to the modified Friedlander equation are: the peak hydrostatic overpressure, \(\hbox {OP}_{\mathrm {S}}\), the exponential coefficient, \(\upalpha \), and the positive phase duration, \(t^{{+}}\). These three coefficients were used in the subsequent analyses to determine components such as the positive phase impulse, as illustrated in Fig. 11.

Comparisons of the measurements of the peak hydrostatic pressures and the positive phase impulses of the blast waves from the three explosive mixtures scaled to a unit mass of propane show that the wave from the rich mixture was slightly weaker than that from the stoichiometric mixture. This is to be expected because the lack of oxygen in the rich mixture means that only 80% can be detonated. However, the undetonated 20% is able to be burned as the detonation products mix with atmospheric oxygen causing some enhancement of the blast wave at large radii. Both the peak hydrostatic pressures and positive phase impulses from the lean mixture appear to be significantly higher than those from the stoichiometric mixture. This result was unexpected and may indicate a more efficient detonation when there is an excess of oxygen.

The measurements from the small-scale explosions have been compared with the predictions from the ProBlast interface after input of the propane masses, the ambient atmospheric pressure and temperature, and 80% of the charge mass for the rich explosions. In all cases, the agreement between the predictions and the measurements was very good. The ProBlast interface was developed using measurements of a nominal 20-ton propane/oxygen charge, and the approximate mass of the small-scale charges was 0.35 g. The good agreement therefore validates Hopkinson’s and Sachs’ scaling for propane/oxygen explosions over many orders of magnitude of charge mass. It also validates the use of small-scale explosions to determine the physical properties and the effects of much larger, and usually accidental, explosions.

The Friedlander equation (5) and the modified equation (4), used to analyse the pressure–time measurements, are described in Sect. 3.2 where it is pointed out that for solid explosives such as TNT the unmodified equation is only valid to describe the pressure–time measurements for which the peak hydrostatic overpressure is less than about 1 atm. At higher peak pressures, it is necessary to use the modified equation. In regions where the unmodified equation is valid, the exponential coefficient, \(\alpha \), in the modified equation must approximately equal \(1/t^{{+}}\), where \(t^{{+}}\) is the positive phase duration.

To investigate this feature for the blast waves from the stoichiometric explosions, the fitted coefficients \(\alpha \) and \(1/t^{{+}}\) from the least-squares fits to the modified Friedlander equation were analysed as functions of radius and were least-squares-fitted to a three-parameter exponential decay function. The results are plotted in Fig. 17. From this figure, it can be seen that the two parameters are equal at a radius of approximately 0.24 m where the peak hydrostatic overpressure is approximately 0.8 atm, and this is the only region in which the unmodified Friedlander equation can be used to describe the pressure–time history of the blast wave from the gaseous mixture.

Fig. 17
figure 17

Exponential coefficient and inverse positive phase duration as functions of radius for the stoichiometric explosions

Full size image

In the above sections, the results of the analyses of the pressure–time measurements of the blast waves produced by the stoichiometric, rich, and lean propane/oxygen mixtures have been illustrated in each case with results from only one of the mixtures. The measured data and the analyses for all the mixtures may be downloaded from https://doi.org/10.5683/SP2/VHN1UQ. They are also provided here as Electronic Supplementary Material.

It should be noted that the highest hydrostatic overpressures measured in the experiments were less than three atmospheres and so any conclusions from the subsequent analyses may be applicable only in the mid- and long-range distances from the explosions. It has been assumed that all the shocks studied were sufficiently weak that the ideal gas equations of state were valid in the shock transitions.