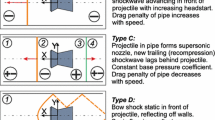
Abstract
Projectile accelerations above \(500~\hbox {ms}^{-2}\) are commonly encountered in aerodynamic applications, but suitable validation data are rare in this regime. Experimental transonic velocity range data for a sphere decelerating under its own drag have been used to validate a numerical model for decelerating objects. The validated model is then used to explore the flow field ahead of objects decelerating from supersonic to subsonic Mach numbers. To model the non-inertial frame of the projectile, source terms were included in the momentum and energy equations in a computational fluid dynamics model. In decelerating cases, the bow shock formed in supersonic flight persists in the subsonic regime. The differences in the flow field between the steady and unsteady cases are explained using the concept of flow history. In the experiment, a tubular insert was present near the observation window in the ballistic range. The insert was numerically modelled, and it is shown that the resulting bow shock behaviour can be explained in terms of the Kantrowitz criterion, in conjunction with flow history. The RAE2822 aerofoil was used to explore the effects of shock overtaking and propagation during deceleration from supersonic to low subsonic Mach numbers. In this case, the bow shock wave persists from the initial supersonic speed to projectile Mach numbers lower than 0.4. The expansion wave and tail shock are shown to overtake the decelerating projectile and propagate forward, behind the bow shock.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Objectives
The study of the unsteady aerodynamics of accelerating bodies has increasingly become a subject of interest in recent years. It has become clear that using steady-state assumptions in the design of air and land vehicles, as well as modelling missile dynamics, can result in incorrect engineering solutions to practical problems. Therefore, an improved understanding of the flow around an accelerating object is required. In recent years, numerical methods have become available which provide better insights into unsteady aerodynamic problems.
Accelerating bodies may be modelled in an absolute inertial frame, or in a body-fixed non-inertial frame, as described below. The non-inertial frame has been chosen for implementation in \(\hbox {ANSYS}^{\textregistered }\) FluentFootnote 1 for present purposes. One objective of this paper is to validate the implementation against experimental data. For this purpose, velocity-dependent drag is also included. Since decelerating objects are able to sustain bow shocks at subsonic projectile speeds [1, 2], stand-off distances at subsonic projectile speeds are modelled. Then, since the ballistic range in which the data were gathered contains a tubular insert near the observation window, a wall boundary is included, with the objective of understanding the behaviour of the bow shock wave generated by a decelerating projectile passing through a tube. Finally, overtaking waves are investigated using the RAE2822 aerofoil profile.
1.2 Review summary
Most of the early work on acceleration (and deceleration) was directed towards understanding the drag on spheres falling under gravity. Basset [3] developed the concept of a history force, which refers to the fact that the development of a boundary layer over an accelerating particle in a fluid depends on the temporal history of fluid elements in the local field. This formulation was later generalized for compressible fluids [4].
Boundary layer development for moving walls was originally solved analytically by Blasius [5], Görtler [6], and Schlichting [7], usually with a focus on impulsive start. Since the drag on spheres in relatively viscous fluids is of industrial interest, most studies are for low-Reynolds-number objects in incompressible fluids [8, 9]. Recent contributions have been made by Combrinck et al. [10].
The concept of added mass, defined as the ratio of the drag force on the body to the acceleration, proved to be useful in acceleration cases and was originally developed in the work of Lagally [11] and Taylor [12].
It should be noted that the cases of interest in this study are those in which an object decelerates in stagnant air. A frame of reference attached to the decelerating object is not an inertial frame, and the Galilean frame transformation for constant inter-frame velocities is not applicable [13]. This is an important factor, because it is Galilean invariance that allows the results from a stationary model in a constant-speed wind tunnel to be applied to a constant-speed model moving in stationary air. Flow over a model in a wind-tunnel start-up experiment is not equivalent to flow over a decelerating or accelerating aircraft. The insights gained from experiments using transient wind-tunnel conditions may, however, be useful.
Transonic work on tunnel start-up has been largely related to prediction of inlet starting in hypersonic tunnels, directed at research in propulsion and scramjets. CFD has been used to investigate the prediction of the aerodynamics of a start-up [14,15,16]; earlier work on a successful duct start-up is based on the Kantrowitz criterion for supercritical flow through a converging duct [17].
Very little work has been carried out in the absolute frame. Sawyer and Sullivan measured lift on a balsa wing accelerated on a moving cart [18]. In the current paper, only rectilinear acceleration is considered. It is noted that the fields of aeroelasticity and turbine engines deal to a certain extent with small-scale acceleration, but are not relevant in the present case.
Railgun and rocket sled experiment data are rarely available. However, ballistic range data, where available, prove to be useful: shock stand-off distance for spheres decelerating through the transonic regime was modelled by using relative frame acceleration terms by Saito et al. [2], in 2011, to which we will refer. One set of very relevant experiments is the development of the Bloodhound Supersonic Car [19], which will attempt to set a new land speed record in the near future, but for which data are not currently publicly available.
A CFD study on rectilinear and parabolic acceleration was published by Inoue et al. [20], in 1997, but no experimental data were available for comparison. Forsberg et al. [21], in 2003, implemented an inertial frame numerical scheme and validated it, demonstrating that the drag on a flare configuration accelerating through the transonic region was approximately 20% lower than the steady drag at the same instantaneous Mach numbers. The flow field history and shock effects on accelerating and decelerating aerofoils in the transonic range have been modelled by Roohani and Skews [1, 22, 23].
We note here that basic theory has been covered for gravitational terms [24] and rotational acceleration has been reviewed: Owczarek [25], Greenspan [26], Boubnov and Golitsyn [27], and expanded by Kageyama and Hyodo [28]. Development of the Euler and Navier–Stokes equations for constant pure rotation and variable pure rotation, in both incompressible and compressible flows, has been carried out by Combrinck et al. [10, 29,30,31] based on the Kageyama–Hyodo modified Galilean operator derivation. This has allowed the development of the laminar boundary layer equations for a surface accelerating parallel to its own plane, validated through reproduction of the Blasius profile, showing that boundary layer thickness increases with acceleration and decreases with deceleration [10, 32]. The resulting equations have recently been applied to aero-ballistic motion, with an exploration of the Magnus force on a rotating body [31].
Frankl [33] provided slender-body theory for constant rectilinear acceleration, and Lilley et al. [34] presented Mach line methodology for qualitative understanding of acceleration effects. The transformation of the Navier–Stokes equations under arbitrary acceleration has been covered by Forsberg et al. [21] and Gledhill et al. [13, 35].
The deceleration case chosen for validation is that of Saito et al. [2]. Starr et al. [36] provide ballistic range results for experiments in which the steady state was approached as closely as possible through careful selection of the model mass and launch velocity. It is noted that the literature contains wide-ranging work on steady-state stand-off distance, for example [37]. Summaries are provided by, for example, Anderson [38].
1.3 Test cases
In the present paper, Fluent results are compared with the data of Saito et al. [2]. It has been established that the mass of 0.127 kg given by Saito et al. [2] was the combined mass of the sphere and the sabot (T. Saito, private communication, 2017). The mass of the spherical projectile without the sabot was approximately 0.0165 kg, which is the mass that is used in the present investigation. Saito et al. [2] established that a shock continues to propagate ahead of the sphere even when the sphere has decelerated to subsonic speeds and provided both experimental and numerical data in support. Further experimental evidence of the shock at subsonic projectile speeds has been provided by Kikuchi et al. [39], also in a ballistic range experiment.
Subsequently, comparison is made between steady and unsteady data and the shock stand-off distance is measured. The flow dynamics is further investigated after the sphere slows down and reaches subsonic velocities under its own drag. As separation shocks on the sphere complicate the flow, shock waves are also examined in simulations of a decelerating RAE2822 aerofoil. Constant values of deceleration have been used to provide further insights into the shock stand-off distance in the transient cases.
2 Methodology
2.1 Numerical method
A numerical technique was developed in Fluent for analysis of unsteady aerodynamic problems, and this case is designed for comparison with the numerical and experimental models from Saito et al. [2] in order to validate the numerical technique in Fluent. Source terms have been added in the momentum and energy conservation equations in the non-inertial frame [13, 22] attached to the sphere. A velocity-dependent drag (VDD) model is used: at each time step, the drag force is determined and the deceleration calculated. The projectile velocity is updated and provided as input to the solver. At the far-field boundary, the external fluid velocity in the projectile frame is updated to match the instantaneous sphere velocity in the inertial laboratory frame. These modifications are implemented with Fluent user-defined functions.
Axisymmetric flow is assumed. This is justified in order to simplify the nature of the wake behind the body and also because Saito et al. [2] used an axisymmetric model to compare with their experimental results and found no significant difference between the bow shock stand-off distance in their viscous and inviscid numerical results. This was also confirmed during this investigation. Mesh independence was ensured by comparing stand-off distances with different grids and by comparing inviscid results from a different mesh with viscous results using the mesh chosen for this investigation shown in Fig. 1. Finally, in order to ensure that the bow shock was captured accurately and that the results were mesh independent, grid adaption was used.
Wall \(y^+\) is the non-dimensional normal distance from the centre of the first grid cell adjacent to the wall. In this study, the size of the grid near the wall was chosen to ensure that the wall \(y^+\) was always between 30 and 300 in the range of Mach numbers encountered by the sphere during its decelerating flight. Under these \(y^+\) values, the law of the wall is used to analyse the near wall flow. However, if through grid adaption the cells near the wall are refined such that the \(y^+\) values fall below 30, the analysis becomes inaccurate. Therefore, in order to avoid this no grid adaption is performed on the surface of the sphere, but from 5 mm in front of the sphere. This can be seen in Fig. 2b.
The refinement is designed to be very sensitive and depends on gradients of pressure, temperature, density, and velocity. If at any point the gradient of any of these parameters was more than 0.05% of the maximum gradient for that parameter in the domain, the mesh at that point was refined. The coarsening of the mesh only took place if the gradient was below 0.03% of the maximum gradient in the domain. The velocity-dependent drag simulation may be sensitive to grid changes during adaption. For this reason, the grid is fully adapted in a preliminary transient model, and the resulting grid, shown in Fig. 2a, is used unchanged during the final transient simulation.
A complete set of simulations was conducted with a density-based solver. The Spalart–Allmaras turbulence model was used as it is a reliable model for transonic external aerodynamic flows. However, it must be noted that since in this study it has already been shown that viscosity does not play a significant role in determining shock stand-off distance, many of the standard turbulence models would have been adequate. Sutherland’s law for relating viscosity to temperature was used. The atmospheric pressure was taken as 99 kPa and the ambient temperature as 288.15 K to match the experiment (T. Saito, private communication, 2017).
A characteristic Riemann pressure far-field boundary condition was used at the far-field boundary of the domain, using instantaneous projectile velocities as described above. The solution method formulation used was implicit. A Courant number of 1 was chosen with a time step size of \(10^{-5}~\hbox {s}\). The residual monitors used for the computation were continuity, energy, x-velocity, y-velocity, and turbulent viscosity. Drag in N was also used as a monitor. The drag was not non-dimensionalized because in unsteady accelerating flow the reference velocity u keeps changing and this is part of the \(\frac{1}{2} \rho _\infty u^2\) term used to non-dimensionalize the drag.
2.2 Sphere
The initial purpose of the study is to provide a numerical analysis of the flow field in front of a projectile, decelerated from supersonic velocities under its own drag, firstly for validation purposes and secondly to understand the effects of the passage of the projectile through a tube, since the experiment contained a tubular insert at the observation window. The sphere is 30 mm in diameter and has a mass \(m = 0.0165~\hbox {kg}\) (T. Saito, private communication, 2017). It was launched at three different initial Mach numbers \(M_{0}\): 1.25, 1.19, and 1.13. For the present work, only \(M_{0} = 1.25\) has been studied. Note that in the present study, M is the Mach number of the projectile unless otherwise stated.
Steady-state results for the sphere in flight at different constant velocities are first compared to experimental results in the literature from Starr et al. [36]. The unsteady results are then compared to experimental and numerical results from Saito et al. [2]. This is to validate the CFD code used. The investigation then focuses on pressure waves that propagate in front of the sphere while decelerating in subsonic flight.
In the ballistic range experiment, the sphere passes through the centre of a tube with diameter 0.600 m in the region of the observation window, at which the final measurement is taken (see Fig. 12). This wall was included in numerical models by Saito et al. [2]. For the present work, it has been constructed in the grid shown in Fig. 3, with a wall length of 0.120 m on either side of the centre of the sphere. The length of the tube in the experiment is not known, and both numerical models are approximations.
2.3 Kantrowitz criterion
It is noted that the Kantrowitz criterion [17, 40] governs the start-up conditions of supersonic wind tunnels and may be influential in the different, but related, case of a supersonic sphere flying through a tube. The Kantrowitz limit \(M_{\mathrm{K}}\) for fluid choking in a semi-infinite tube is given [41] as follows:
where \(A_{\mathrm{i}}\) is the inlet area, \(A_{\mathrm{t}}\) is the throat area, \(\gamma \) is the ratio of the specific heat capacities of air at ambient temperature, and \(M_{2}\) is given by (2). For a free stream Mach number M, steady-state shocks will exist within a semi-infinite tube for \(M>M_{\mathrm{K}}\) but will be expelled from the inlet for \(M<M_{\mathrm{K}}\). Assuming that it is reasonable to consider the throat area to be approximated by \(A_{\mathrm{t}}=A_{\mathrm{i}}-\pi {r_{\mathrm{p}}}^2\), where \(r_{\mathrm{p}}\) is the radius of the projectile, we obtain \(M_{\mathrm{K}}\approx 1.06\). This factor will be kept in mind in interpreting the results below.
2.4 RAE2822 aerofoil
In order to explore the aerodynamic effects resulting from blunt objects decelerating through \(M=1\), results from an RAE2822 aerofoil under constant deceleration were compared to the sphere results. The RAE2822 geometry is plotted in Fig. 4, and the grid and its far-field boundaries are shown in Fig. 5a, with details shown in Fig. 5b. There are 210 cells from the leading edge to the trailing edge of each surface. The grid is composed of 126,900 cells. The domain extends approximately 56 chord lengths upstream to 88 chord lengths downstream and 64 chord lengths away from the upper and lower surfaces. Wall \(y^+\) is between 40 and 70 over most of the surface at \(M = 0.5\), which provides reasonable \(y^+\) values over the transient range between Mach numbers 0.3 and 1.6. All far-field boundaries were pressure far-field boundaries. The aerofoil is at an angle of attack of \(2.79^\circ \). The same solver conditions were used as for the sphere case, with the exception that the initial velocity and pressure were Mach number 1.6 and 101,325 Pa, respectively. The aerofoil was decelerated at a constant value of \(1041~\hbox {ms}^{-2}\) (approximately 106 g). A time step of \(10^{-3}~\hbox {s}\) was used for these simulations based on the larger cell sizes.
Similar constant-deceleration simulations were run for the sphere geometry above, with a time step of \(10^{-5}~\hbox {s}\), and the same physical conditions as for other sphere simulations, to explore the effects of the decay of the shock wave at subsonic speeds.
3 Results
3.1 Sphere
3.1.1 Free stream analysis
A flow field showing the bow shock in front of the sphere, decelerating at Mach number 1.10 under its own drag, is illustrated in Fig. 6. The shock stand-off distance is the distance between the point of inflection of the bow shock and the nose of the sphere and will be referred to as delta (\(\delta \)). In order to non-dimensionalize this distance, it is divided by the radius or diameter of the sphere, \(\delta /R\) or \(\delta /D\).
For the purposes of validating the steady-state operation of our model, we compared steady-state results from Fluent with the experimental data of Starr et al. [36] and the steady-state numerical calculations of Saito et al. [2]. This is shown in Fig. 7. The empty squares in the figure show the experimental results, and the crosses show the results from Fluent, for a temperature of 300 K. The dark squares are the numerical results from Saito et al. [2]. There is a very good correlation between the steady-state results from Fluent and these experimental and numerical results from the literature. Therefore, the choice of turbulence model, the mesh, and the type of grid adaption used were reasonable as they match experimental results.
A very important aspect of this research is comparison of shock stand-off distances between the steady and unsteady cases. In Fig. 8, pressure profiles from the steady and the unsteady cases are compared at the same Mach number. The pressure profiles are shown as a function of x, measured from the centre of the sphere along the axis of symmetry. The steady state is a constant-velocity case at Mach number 1.03, and in the unsteady scenario, the sphere is decelerating under its own drag at Mach number 1.03 when its initial velocity was Mach number 1.25. From the pressure profiles, it is observed that the shock stand-off distance for the unsteady decelerating case is smaller than for the corresponding steady-state scenario.
In Fig. 9, the data obtained from Fluent and Saito et al. [2] are compared. The purpose of this is first of all to obtain a comparison between steady and unsteady data in Fluent and then to compare the unsteady data from Fluent with unsteady data from Saito et al. In the figure, the stand-off distance is expressed in terms of \(\delta /R\), which is the distance divided by the sphere radius. This is plotted against the Mach number M at which the sphere travels. Steady-state data from Fluent are represented by a bold line. The agreement between the Fluent transient results and the numerical results of Saito et al. is very good, and there is a reasonable agreement with the experimental data, validating the Fluent numerical transient technique.
In Fig. 10, shock profiles are plotted for the transient case in which the initial Mach number is 1.25, for times at which the instantaneous Mach number of the projectile is supersonic. The shocks become weaker as time passes, and the Mach number is reduced. In Fig. 11, additional pressure profiles are provided for subsonic sphere Mach numbers. It is interesting to note that at Mach numbers equal to and less than 1, where under steady-state conditions no shock would be present, a bow shock exists in these unsteady conditions.
3.1.2 Effects of a tubular insert within the ballistic range
In the ballistic range experiments, a tubular insert was included at the second of two observation windows. A diagram of the ballistic range will be found in the original paper ([2], figs. 2 and 3). Measurements of initial speed were taken from the first observation window, at approximately 6 m from the starting point of the acceleration tube. Measurements of final speed were taken at the second observation window, which is approximately 9.7 m from the starting point of the acceleration tube. The insert only covered part of the flight path and was a cylinder of 600 mm diameter centred on the axis of symmetry of the ballistic range tank (T. Saito, private communication, 2017).
For the purposes of CFD simulation, it was assumed by Saito et al. (a) that the tube was of finite length 240 mm and (b) that the relative positions of the end points of the tube and the projectile did not change during the simulation. We have made the same assumptions for the purposes of comparison and have used the configuration to investigate the effects of a wall modelled in this way. A schematic diagram of the tubular insert geometry as used in the simulation is shown in Fig. 12. Note that the simulation domain (Fig. 3) only extends from the axis of symmetry to the internal wall of the tubular insert.
Schematic diagram of the simulation geometry of the tubular insert ([2], T. Saito, private communication, 2017). All measurements are in mm
The presence of this tubular wall is now considered. The grid in Fig. 3, which includes a slip or no-slip wall at 0.3 m from the axis, was used to model both steady-state and velocity-dependent drag (VDD) cases. Note that the end points of the wall do not change their position relative to the sphere, as the grid remains fixed in the projectile frame. This is modelled in the same way in the simulations of Saito et al. [2]. However, this is not a true representation of the ballistic range, where the sphere flies past the edges of the tube as it moves through the insert, but it is a simplified numerical approximation. In order to provide a better model of the relative motion of the sphere and the tube in the ballistic range, a velocity boundary condition can be imposed at the tube wall. In the following paragraphs, this is referred to as a “moving wall”.
The shock stand-off distances for these cases have been compared to previous data in Fig. 13. The stand-off distance for the decelerating case is significantly larger when the wall is included than the free stream stand-off distance \(\delta \) for \(M\,{<}\,1.03\) for an inviscid model and for \(M\,{<}\,1.02\) for the viscous moving wall model.
To investigate the cause of the sudden increase in \(\delta \) as M decreases, pressure contours for a case including the insert wall are shown in Fig. 14. The curved domain boundary, following that of Saito et al., is seen at the top of each figure. The wall extends only along the straight line at the top of the domain shown.
Below the Mach number 1.02, the bow shock starts to move towards the left boundary. This behaviour is not inconsistent with the approximate behaviour indicated by the Kantrowitz limit \(M_{\mathrm{K}}\) for this tube in (1) and (2), which indicates that steady-state shocks would be expelled from a semi-infinite tube with these dimensions for \(M<1.06\). The instantaneous Mach number at which shock expulsion begins is lower than \(M_{\mathrm{K}}\) because the shock expulsion is delayed by the flow history effects in transient cases. Further discussion of the flow history effects appears below.
3.1.3 Constant-acceleration cases
Additional insights into decelerating sphere flow fields in the free stream can be provided by simulating cases at a constant deceleration. Stand-off distances for two cases in which deceleration is fixed at \(a=-\,1041~\hbox {ms}^{-2}\) and \(a=-\,2082~\hbox {ms}^{-2}\) are illustrated in Fig. 15. As expected, values of \(\delta /R\) tend towards the steady state as the absolute value of deceleration decreases.
When the flow field around the sphere is inspected for constant deceleration, some new phenomena are observed. Flow fields for the sphere decelerating from Mach number 1.25 are shown in Fig. 16; in this case, the magnitude of the deceleration is at a constant value of \(1041~\hbox {ms}^{-2}\).
A bow shock is observed for \(M = 1.05\) (Fig. 16a). The bow shock persists for lower instantaneous Mach numbers.
Note that the shock attached to the sphere surface has not overtaken the sphere in this range of projectile Mach numbers (Fig. 16) and therefore does not contribute to steep waves upstream of the sphere.
3.2 RAE 2822 aerofoil
Additional insights into the way in which the shock waves decay as the relative speed of the object frame decreases have been gained by expanding on earlier work on aerofoils [42]. In the following figures, this is illustrated for comparison with the sphere flow fields above.
In the right-hand column of Fig. 17, the familiar steady-state behaviour of the flow field around a transonic aerofoil is shown. No bow shock is observed below Mach number 1. Flow fields for deceleration from Mach number 1.60 are shown in the left-hand column of Fig. 17. The bow shock at the instantaneous Mach number of 1.05 has a considerably smaller stand-off distance than the steady-state value. At \(M=0.98\), a bow shock persists. By \(M=0.75\), the bow wave is still present. The bow wave and other features are now moving faster than the aerofoil, and it can be seen that at \(M=0.75\) the tail shock is beginning to overtake the aerofoil.
By the time \(M=0.65\) is reached, the remnants of the tail shock have completely overtaken the aerofoil and form an acoustic feature ahead of the aerofoil nose; in addition, the decaying bow wave feature has propagated many chord lengths away from the nose. We now proceed to explore the nature of these features.
In Fig. 18, the pressure profile for \(M = 1.05\) shows the bow shock. The profile for \(M = 0.98\) also indicates the steep pressure structure associated with the bow shock. At \(M = 0.75\), the steep wave has propagated further away from the nose, but the pressure behind it has dropped below the undisturbed upstream pressure. Reference to Fig. 17c confirms that this drop is associated with the expansion wave, which has overtaken the decelerating aerofoil. When the aerofoil has decelerated to \(M = 0.65\), the tail shock has overtaken the aerofoil and is visible as the pressure rise 2 m in front of the nose in Fig. 18.
The position of the inflection point in the bow wave can be calculated and is plotted as the stand-off distance \(\delta \) in Fig. 19. An inflection point is illustrated as a solid circle in Fig. 18 for \(M = 0.65\). The stand-off distance for the steady state has been computed in the same way for comparison, and the bow shock exists only for supersonic projectile Mach numbers. During deceleration of the aerofoil, the bow shock persists below \(M = 1.0\) and stand-off distance \(\delta \) can be tracked all the way down to \(M = 0.4\) in the present data. Further observation was limited by the domain boundary.
To emphasize the way in which the wave outruns the aerofoil, the shock and aerofoil positions can be transformed to the absolute frame. The positions in this frame of the aerofoil nose, \(x_{\mathrm{P}}\), and the bow shock, \(x_{\mathrm{b}}\), are shown in Fig. 20. The wave continues to propagate forward, while the projectile slows down, explaining the increasing stand-off distance. We now investigate whether the wave is an acoustic wave, propagating at the speed of sound, or whether it is a shock wave.
To assist in understanding the nature of the wave, we calculate the speed of the wave \(v_{\mathrm{b}}\) from the time derivative \(\mathrm {d}x_{\mathrm{b}}/\mathrm {d}t\) of the bow shock position. The results are shown in Fig. 21 as open circles. The speed of sound in undisturbed air, c, is shown as a solid line. Calculations of \(v_{\mathrm{b}}\) for \(t > 0.3~\hbox {s}\), resulting in projectile Mach number \(M < 0.4\), are subject to error due to the grid size in the simulation, but in the range shown, the speed of the wave is above the speed of sound.
To investigate whether this wave is indeed still a shock, the shock speed \(v_{\mathrm{RH}}\) can be calculated from the Rankine–Hugoniot jump conditions from the measured pressures on either side of the wave. These pressures are available in the simulation. The speed \(v_{\mathrm{RH}}\) is also shown in Fig. 21 (solid circles). The comparison between \(v_{\mathrm{b}}\), \(v_{\mathrm{RH}}\), and c indicates that the wave is behaving as a shock wave down to subsonic projectile Mach numbers as low as Mach number 0.4.
At a given fixed position ahead of the aerofoil nose, the pressure due to the wave passage can be extracted from the data. Samples are shown in Fig. 22 for a position approximately 2.1 m in front of the aerofoil nose. The initial overpressure is due to the bow shock, and the subsequent drop in pressure is due to the overtaking expansion wave. The second small shock is related to the overtaking tail shock structure.
4 Discussion
4.1 Free stream sphere model
The performance of Fluent for steady-state shock stand-off distance calculation has been validated by comparison with the experimental results of Starr et al. [36].
The first objective of this investigation was to validate the technique developed in Fluent for modelling acceleration of objects in stationary air. This has been accomplished, since good correlation with the experimental and numerical results of Saito et al. [2] was achieved using a free stream model.
The concept of flow history refers, in the present context, to the fact that when an object is accelerated in a compressible fluid, the flow field does not have time to stabilize at any specific Mach number, but retains features associated with an earlier time. In comparison with the expected steady-state condition at a given Mach number, the bow shock stand-off distance \(\delta \) under deceleration was found to be reduced. This is because in the case of deceleration, the flow field is retaining some of the characteristics of an earlier time when the Mach number was higher. At higher Mach numbers, the stand-off distance is smaller, and therefore, the current transient flow field would be expected to exhibit a smaller stand-off distance.
4.2 Effect of tubular insert boundary conditions
In the ballistic range experiments, a tubular insert was placed near the observation window, and the effects of this insert were modelled numerically by Saito et al. by creating a reflecting wall at 0.30 m from the axis. A similar inviscid Fluent model was constructed. Initial simulations showed that the stand-off distance rose sharply for \(M<1.03\) in comparison with the Fluent free stream data and the experimental data. To test the effect of the wall boundary condition, a velocity was imposed at the wall in a fully viscous simulation to provide a better approximation of the relative motion of the projectile and the wall. In this simulation, the stand-off distance only started rising for \(M<1.02\). This can be explained in terms of the Kantrowitz criterion, bearing in mind that the transient effects due to flow history would affect the Mach number at which the shock is expelled from the tube. In steady-state conditions, the value of \(M_{\mathrm{K}}\), which is the Mach number below which the shock can only exist outside the tube, is approximately 1.06 for the geometry of this case. This is higher than the transient Mach numbers at which the shock starts to exit the tube in the numerical simulations. In fact, the shock arrives outside the tube at subsonic Mach numbers. In terms of flow history, this can be explained by the fact that the bow shock does not have sufficient time to travel to the end of the tube at \(M_{\mathrm{K}}\). By the time the shock reaches the end of the tube, the sphere has already decelerated to a subsonic Mach number. It would be valuable to explore the phenomenon of shock expulsion behaviour further for these transient cases.
The ballistic range experiments have been modelled with velocity-dependent drag. CFD models with constant deceleration have been used to show that the reduction in the stand-off distance \(\delta \) in comparison with the steady-state case is dependent on the magnitude of the deceleration, as would be expected from the flow history concept.
4.3 RAE2822 aerofoil
The flow fields associated with a decelerating aerofoil with the RAE2822 profile have been investigated in order to develop a better understanding of the way shocks and waves overtake a decelerating projectile. This is necessary because the separation shocks present on the sphere complicate the overtaking process.
In the ballistic range sphere cases, when the projectile speed dropped below Mach number 1, the decaying bow shock waves persisted down to \(M = 0.981\), as was shown by Saito et al. [2] and Kikuchi et al. [39]. In the aerofoil case, we demonstrate, using the validated CFD, that the wave persists down to at least \(M = 0.4\). This wave propagates upstream at a speed above the speed of sound in undisturbed air, while the aerofoil slows down and falls behind as its speed drops below the speed of sound. The wave front speed is consistent with the speed obtained from the pressure ratio across the wave using the Rankine–Hugoniot jump conditions. This suggests that the wave is still a shock down to at least \(M = 0.4\) based on the available data in this case.
At a station in the relative frame approximately 2 m ahead of the nose, the time evolution of the pressure shows the arrival of the bow shock, the expansion fan, and the overtaking tail shock, at consecutive times. These waves have some qualitative similarities to blast waves and propagate independently of the projectile, which has been left behind.
5 Conclusions
Shock stand-off distance has been modelled in the body-fixed frame, with both free stream and tubular wall conditions, in Fluent for a sphere decelerating under its own drag. Reduction in the stand-off distance due to deceleration was observed and has been explained in terms of flow history.
The steady-state Fluent model has been validated with the experimental data of Starr et al. [36]. The Fluent transient free stream model of an accelerating object has been validated with the ballistic range experimental data, and numerical model, of Saito et al. [2].
This provides one of the few experimental validations for objects accelerating into undisturbed fluid in the compressible flow regime. This validation provides a foundation for the investigation of the effects of significant acceleration in the transonic speed range and therefore has implications for understanding transient loads on aircraft and missiles.
In the experiment, a tubular insert was present at the observation window in the ballistic range. Below Mach number 1.03, the shock is expelled from the tube. This is considered to be related to the Kantrowitz criterion, which would account for steady-state shock expulsion at a flow speed of Mach number 1.06 for these conditions. One reason that the observed Mach number is lower is that flow history would delay the Kantrowitz effect.
During deceleration, at subsonic instantaneous projectile Mach numbers, the bow shock persists and propagates ahead of the decelerating object. The transient subsonic flow fields therefore have a completely different nature from steady-state subsonic flow fields at the same Mach number because they contain features related to supersonic flow, due to flow history effects.
For the RAE2822 aerofoil profile under constant deceleration of 106 g from Mach number 1.6, it has been demonstrated that the bow shock wave persists down to projectile Mach number 0.4 and possibly lower Mach numbers. The expansion wave associated with the aerofoil, and the tail shock, both travel forward over the wall surface and overtake the aerofoil. Upstream pressure profiles clearly show the resulting progression of the bow shock, followed by a significant expansion, followed by the remnants of the tail shock, propagating forward in front of the decelerating projectile.
There is considerable scope for new work in understanding acceleration effects in internal flow, as shown by the results with the tube wall above, and in analysing flow features propagating ahead of subsonic projectiles decelerating from supersonic speeds.
Notes
Fluent, Inc., version 6.3 User and Tutorial Guides, 2007; \(\hbox {ANSYS}^{\textregistered }\) Fluent User’s Guide Release 18 and intervening Releases; Images used courtesy of ANSYS, Inc.
References
Roohani, H., Skews, B.: The influence of acceleration and deceleration on shock wave movement on and around airfoils in transonic flight. Shock Waves 19, 297–305 (2009). https://doi.org/10.1007/s00193-009-0207-9
Saito, T., Hatanaka, K., Yamashita, H., Ogawa, T., Obayashi, S., Takayama, K.: Shock stand-off distance of a solid sphere decelerating in transonic velocity range. Shock Waves 21, 483–489 (2011). https://doi.org/10.1007/s00193-011-0323-1
Basset, B.: Treatise on Hydrodynamics. Deighton, Bell, & Co., Cambridge (1888)
Parmar, M., Haselbacher, A., Balachandar, S.: Generalized Basset–Boussinesq–Oseen equation for unsteady forces on a sphere in a compressible flow. Phys. Rev. Lett. 106, 084501 (2011). https://doi.org/10.1103/PhysRevLett.106.084501
Blasius, H.: Grenzschichten in Flüssigkeiten mit kleiner Reibung. Z. Math. Phys. 56, 1–37 (1908). English translation in NACA-TM-1256
Görtler, H.: Verdrängungswirkung der laminaren grenzschicht und druckwiderstand. Ing. Arch. 14, 286–305 (1944). https://doi.org/10.1007/BF02085962
Schlichting, H.: Boundary Layer Theory, 8th edn. Springer, Berlin (2000). https://doi.org/10.1007/978-3-642-85829-1
Coles, D., Hirst, E.: Computation of turbulent boundary layers. 1968 AFOSR-IFP-Stanford Conference, vol. II. Stanford University, Stanford, CA (1969)
Piomelli, U., Yuan, J.: Numerical simulations of spatially developing, accelerating boundary layers. Phys. Fluids 25, 101304 (2013). https://doi.org/10.1063/1.4825033
Combrinck, M., Dala, L., Lipatov, I.: Non-inertial forces in aero-ballistic flow and boundary layer equations. R&D J. S. Afr. Inst. Mech. Eng. 33, 85–96 (2017)
Lagally, M.: Berechnung der Kräfte und Momente, die strömende Flüssigkeiten auf ihre Begrentung ausüben. Z. Angew. Math. Mech. 2, 409–422 (1922). https://doi.org/10.1002/zamm.19220020601
Taylor, G.: The energy of a body moving in an infinite fluid, with application to airships. Proc. R. Soc. Lond. Ser. A 120, 13–21 (1928). https://doi.org/10.1098/rspa.1928.0131
Gledhill, I., Roohani, H., Forsberg, K., Eliasson, P., Skews, B., Nordström, J.: Theoretical treatment of fluid flow for accelerating bodies. Theor. Comput. Fluid Dyn. 30, 449–467 (2016). https://doi.org/10.1007/s00162-016-0382-0
Tahir, R., Mölder, S., Timofeev, E.: Unsteady starting of high Mach number air inlets—a CFD study. 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Huntsville, AL, AIAA Paper 2003-5191 (2003). https://doi.org/10.2514/6.2003-5191
Mölder, S., Timofeev, E., Tahir, R.: Flow starting in high compression hypersonic air inlets by mass spillage. 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Fort Lauderdale, FL, AIAA Paper 2004-4130 (2004). https://doi.org/10.2514/6.2004-4130
Najafiyazdi, A., Tahir, R., Timofeev, E., Mölder, S.: Analytical and numerical study of flow starting in supersonic inlets by mass spillage. 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cincinnati, OH, AIAA Paper 2007-5072 (2007). https://doi.org/10.2514/6.2007-5072
Kantrowitz, A., Donaldson, C.: Preliminary investigation of supersonic diffusers. Technical Report, National Advisory Committee for Aeronautics, ACR-L5D20 (1945)
Sawyer, R., Sullivan, J.: Lift response of a rectangular wing undergoing a step change in forward speed. AIAA J. 28, 1306–1307 (1990). https://doi.org/10.2514/3.25209
Evans, B., Rose, C.: Simulating the aerodynamic characteristics of the Land Speed Record vehicle BLOODHOUND SSC. J. Automob. Eng. 228, 1124–1141 (2014). https://doi.org/10.1177/0954407013511071
Inoue, O., Sakai, T., Nishida, M.: Focusing shock waves generated by an accelerating projectile. Fluid Dyn. Res. 21, 403–416 (1997). https://doi.org/10.1016/S0169-5983(97)00026-9
Forsberg, K., Gledhill, I., Eliasson, P., Nordström, J.: Investigations of acceleration effects on missile aerodynamics using CFD. 21st Applied Aerodynamics Conference, Orlando, FL, AIAA Paper 2003-4084 (2003). https://doi.org/10.2514/6.2003-4084
Roohani, H., Skews, B.: Unsteady aerodynamic effects experienced by aerofoils during acceleration and retardation. Proc. I MechE Part G J. Aerosp. Eng. 222, 631–636 (2008). https://doi.org/10.1243/09544100JAERO280
Roohani, H., Skews, B.: Shock wave profiles on a transonic wing during acceleration. 27th International Symposium on Shock Waves, 30596 (2009)
Landau, L.D., Lifshitz, E.M.: Fluid Mechanics. Pergamon Press, Oxford (1959)
Owczarek, J.: Fundamentals of Gas Dynamics. International Textbook Company, Scranton, PA (1964)
Greenspan, H.: The Theory of Rotating Fluids. Cambridge University Press, Cambridge (1990)
Boubnov, B.M., Golitsyn, G.: Convection in Rotating Fluids. Springer, Berlin (1995). https://doi.org/10.1007/978-94-011-0243-8
Kageyama, A., Hyodo, M.: Eulerian derivation of the Coriolis force. Geochem. Geophys. Geosyst. 7, Q02009 (2006). https://doi.org/10.1029/2005GC001132
Combrinck, M., Dala, L.: Eulerian derivations of noninertial Navier–Stokes equations. 29th Congress of the International Council of the Aeronautical Sciences 0577 (2014)
Combrinck, M., Dala, L., Lipatov, I.: Eulerian derivation of non-inertial Navier–Stokes equations for compressible flow in constant, pure rotation. HEFAT2015, 11th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics, 20–23 July 2015, Kruger National Park, South Africa (2015)
Combrink, M., Dala, L., Lipatov, I.: Eulerian derivation of non-inertial Navier–Stokes and boundary layer equations for incompressible flow in constant pure rotation. Eur. J. Mech. B/Fluids 65, 10–30 (2017). https://doi.org/10.1016/j.euromechflu.2016.12.012
Combrinck, M., Dala, L., Lipatov, I.: Boundary layer response to arbitrary acceleration. 12th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics, 11 to 13 July 2016, Malaga, Spain (2016)
Frankl, F.: Effect of the acceleration of elongated bodies of revolution upon the resistance in a compressible flow. Technical Report, National Advisory Committee for Aeronautics, Report NACA TM 1230 (1949)
Lilley, G., Westley, R., Yates, A., Busing, J.: Some aspects of noise from supersonic aircraft. J. R. Aeronaut. Soc. Coll. Aeronaut. Rep. 57, 396–414 (1953). https://doi.org/10.1017/S036839310012526X
Gledhill, I., Forsberg, K., Eliasson, P., Baloyi, J., Nordström, J.: Investigation of acceleration effects on missile aerodynamics using computational fluid dynamics. Aerosp. Sci. Technol. 13, 197–203 (2009). https://doi.org/10.1016/j.ast.2009.04.008
Starr, R., Bailey, A., Varner, M.: Shock detachment distance at near sonic speeds. AIAA J. 14, 537–539 (1976). https://doi.org/10.2514/3.7124
Billig, F.: Shock-wave shapes around spherical- and cylindrical-nosed bodies. J. Spacecr. Rockets 4, 822–823 (1967). https://doi.org/10.2514/3.28969
Anderson, J.: Hypersonic and High-Temperature Gas Dynamics, 2nd edn. American Institute of Aeronautics and Astronautics, Reston (2002). https://doi.org/10.2514/4.861956
Kikuchi, T., Takayama, K., Igra, D., Falcovitz, J.: Shock standoff distance over spheres in unsteady flows. 30th International Symposium on Shock Waves, vol. 1, pp. 275–278 (2017). https://doi.org/10.1007/978-3-319-46213-4_45
Katz, J., Yon, S., Rogers, S.: Impulsive start of a symmetric airfoil at high angle of attack. AIAA J. 34, 225–230 (1996). https://doi.org/10.2514/3.13054
Hill, P., Peterson, C.: Mechanics and Thermodynamics of Propulsion, 2nd edn. Addison-Wesley Publishing Co., Reading, MA (1992)
Roohani, H., Skews, B.: Effect of acceleration on shockwave dynamics of aerofoils during transonic flight. 26th International Symposium on Shock Waves A3351 (2007)
Acknowledgements
The very helpful information provided by T. Saito and his team is acknowledged with gratitude. One of the authors (I.M.A. Gledhill) acknowledges the generous grant of the CSIR (Council for Scientific and Industrial Research), South Africa, without which the collaboration could not have been accomplished. The financial assistance of the National Research Foundation (NRF) towards this research is hereby acknowledged. Opinions expressed, and conclusions arrived at, are those of the author and are not necessarily to be attributed to the NRF. ANSYS, ANSYS Workbench, AUTODYN, CFX, Fluent and any and all ANSYS, Inc., brand, product, service and feature names, logos and slogans are registered trademarks or trademarks of ANSYS, Inc., or its subsidiaries in the USA or other countries. All other brand, product, service and feature names, or trademarks are the property of their respective owners.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by A. Sasoh and A. Higgins.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Roohani, H., Gledhill, I.M.A., Mahomed, I. et al. Bow shock stand-off distance for subsonic decelerating bodies. Shock Waves 30, 115–129 (2020). https://doi.org/10.1007/s00193-019-00921-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00193-019-00921-3