High-order fully implicit solver for all-speed fluid dynamics

Abstract

We introduce a novel Newton–Krylov (NK)-based fully implicit algorithm for solving fluid flows in a wide range of flow conditions—from variable density nearly incompressible to supersonic shock dynamics. The key enabling feature of our all-speed solver is the ability to efficiently solve conservation laws by choosing a set of independent variables that produce a well-conditioned Jacobian matrix for the linear iterations of the global nonlinear iterative solver. In particular, instead of choosing to discretize the conservative variables (density, momentum, total energy), which is traditionally used in Eulerian high-speed compressible fluid dynamics, we demonstrate superior performance by discretizing the primitive variables—pressure–velocity–temperature in the very low-Mach flow limits or density–velocity–temperature/entropy in the shock dynamics range. Moreover, our method allows us to avoid direct inversion of the mass matrix in discrete time derivatives, which is usually an additional source for stiffness, especially pronounced when going to very high-order schemes with non-orthogonal basis functions. Here, we show robust solutions obtained for discontinuous finite element discretization up to seventh-order accuracy. Another important aspect of the solution algorithm is the Advection Upstream Splitting Method (AUSM), adopted to compute numerical fluxes within our reconstructed discontinuous Galerkin (rDG) spatial discretization scheme. The use of the low-Mach modification of the hyperbolic flux operator is found to be necessary for enabling robust simulations of very stiff liquids and metals for Mach numbers below $M=10^{-5}$, which is well known to be very computationally challenging for compressible solvers. We demonstrate that our fully implicit rDG-NK solver with the ${\mathrm{AUSM}}^{+}$-up flux treatment produces efficient and high-resolution numerical solutions at all speeds, ranging from vanishing Mach numbers to transonic and supersonic, without substantial modifications of the solution procedures. (At high speed, we add limiting and use a simpler preconditioning of the Krylov solver.) Numerical examples include nearly incompressible constant-property flow past a backward-facing step with heat transfer, low-Mach variable-property channel flow of water at supercritical state, phase change and melt pool dynamics for laser spot welding and selective laser melting in additive manufacturing, and Mach 3 flow in a wind tunnel with a step.

1 Introduction and background

It is a common practice in computational fluid dynamics (CFD) to utilize different numerical algorithms when solving fluid flows at low and high speeds. At low speed, very often, the compressibility is ignored, rendering either a fully incompressible (divergence-free, isochoric) formulation [1, 2], or variations of the acoustic filtering approach (low-Mach approximations) [3]. This generates families of numerical algorithms that solve for pressure (or Lagrange multiplier functions in projection algorithms [1, 4]), which are substantially different from what is commonly used at high-speed flows, evolving conservative (mass, momentum, and total energy) variables [5, 6].

There are a few reasons why conservative-variable compressible solvers are ineffective at very low speeds. To start with, timescales associated with acoustics are substantially faster than those of convection, resulting in commonly used explicit time discretizations to be highly inefficient. There are a few more effective operator-splitting algorithms (e.g., implicit continuous-fluid Eulerian (ICE) family [7] and numerous variations) that enable more efficient solution procedures to implicitly step over acoustics. These algorithms are commonly referred to as “all-speed,” but in practice they are mostly used for subsonic compressible flows. Applying implicitly discretized high-speed conservative-form compressible methods is difficult, because the density is nearly constant in time ($\rho \approx$ const), and the total energy is dominated by internal energy ($\frac{\mathbf {v}^2}{2} \ll {\mathfrak {u}}$). This results in very ill-conditioned linear algebra at vanishing Mach numbers. In addition, numerical discretizations become grossly inaccurate at $M \rightarrow 0$ limit, as the pressure gradient term in the momentum equation is scaled as $\sim \frac{1}{M^2}$, becoming numerically unresolvable in the range of $M<10^{-2}$. There were a few important developments in the 1990s that were focused on improving the solvability of compressible solvers in the low-Mach number limit, including the work by Turkel [8], Choi and Merkle [9], Weiss and Smith [10], and Van Leer et al. [11]. These methods design the local preconditioning to alter the characteristics of the governing equations, thereby improving the accuracy of the pressure gradient evaluations. Probably the most productive and practical improvement in the flux accuracy in compressible solvers at vanishing Mach numbers is due to Meng-Sing Liou and his Advection Upstream Splitting Method (AUSM). Low-Mach modifications of the AUSM family were proposed in [12,13,14,15,16]. The most complete version of the AUSM scheme was presented in [17], which employed asymptotic analysis to formally derive proper scalings for the numerical fluxes in the limit of small Mach numbers. A few more recent studies on this subject are presented in [18,19,20,21,22].

In the present work, we attempt to resolve some of the difficulties fully compressible solvers encounter at low-Mach numbers by utilizing Meng-Sing Liou’s ${\mathrm{AUSM}}^{+}$-up (for flux accuracy) and combining it with a fully implicit Jacobian-free Newton Krylov (JFNK) reconstructed Discontinuous Galerkin (rDG) method (for efficiency, accuracy, and the ability to step over acoustic timescales). Jacobian-free Newton–Krylov methods have been shown to be very effective at rendering accurate solutions to nonlinear PDEs when tight-coupling and accurate resolution of multiple timescales is a must. For the most comprehensive overview of JFNK and numerous preconditioning techniques, we refer to Knoll and Keyes [23] and references within. Recent applications of the physics-based preconditioning to compressible fluid dynamics are discussed in [24, 25]. The key aspect of JFNK, which we would like to emphasize here, is that one can choose any independent set of variables for spatial discretization, while still solving for conserved (mass, momentum, and total energy) quantities/equations in the global nonlinear iterative procedure. Since in the low-Mach limit the density is nearly constant (or very strongly coupled to pressure for liquids), using it as a prime discretization variable is generally a bad choice. Similarly, specific total energy should be avoided, since in the low-Mach limit the thermal energy totally overwhelms the kinetic energy portion of the total energy, which usually produces very ill-conditioned Jacobian matrices that are extremely difficult to precondition. Instead, for our DG discretization, we utilize pressure, velocity, and temperature. This choice of independent variables is also beneficial, because many low-Mach-number solvers are constructed around solving the pressure Poisson equation, and a substantial body of experience for solving elliptic/parabolic systems can be utilized when designing preconditioning techniques. Discussion of preconditioning for iterative Krylov methods is beyond the scope of the present work, and we refer to our recent work in [26] for additional details. Finally, we show that within the JFNK, we can avoid direct inversion of the mass matrices, which are known to become very stiff/ill-conditioned for high-order non-orthogonal basis functions. We found that using DG with the Taylor basis functions up to seventh order does not impact the performance of the underlying linear solvers in the wide range of flow conditions considered in this work.

Here, we demonstrate that our basic all-speed solution algorithm is essentially the same at both vanishing Mach numbers and supersonic flow conditions with the only differences being: (1) engaging a solution field limiter when strong shocks are present and (2) activating a different preconditioning approach for the Krylov solver. (For low speed, the Schur-complement-based approach [26] is proven to be scalable and cost-effective, while for high speed, a simpler element-block-diagonal strategy works well.) Here, we use a variation of the unstructured-mesh Barth–Jesperson (BJ) [6, 27] limiter, modified to work robustly with the Newton-based iterative algorithm (avoiding the well-known non-differentiability issue of the BJ limiter) and with the $\hbox {P}_n\hbox {P}_m$ DG solution reconstruction procedure. Numerical demonstrations are designed to cover all-speed range, including constant-density nearly incompressible flows (Sect. 4.2), variable density, viscosity, conductivity, and specific heat stiff-liquid (supercritical water) flows at very low Mach conditions (Sect. 4.3), solid–liquid phase change and Marangoni convection in direct energy heating applications (Sect. 4.4), and, finally, strong-shock Mach 3 flows (Sect. 4.5).

The method is implemented and tested within LLNL’s ALE3D code [28, 29]. ALE3D is a multi-physics numerical simulation tool, focusing on modeling hydrodynamics and structural mechanics in all-speed multi-material applications. Additional ALE3D features include heat conduction, chemical kinetics and species diffusion, incompressible flow, a wide range of material models, chemistry models, multi-phase flow, and magneto-hydrodynamics for long (implicit)- and short (explicit)-timescale applications.

The rest of the paper is organized as follows. First, we describe the mathematical and physical models in Sect. 2. An overview of the numerical algorithm, with a dive-in to describe our nonlinear residuals for conservation laws solved in a general primitive-variable formulation within Newton–Krylov solution procedure, is presented in Sect. 3. Numerical examples are given in Sect. 4, followed by concluding remarks in Sect. 5.

2 Governing equations

2.1 Conservation laws

We are interested in solving the compressible Navier–Stokes and energy equations, defined as:

$$\begin{aligned} \begin{array}{l} \underline{\text{ Mass } \text{ conservation }} \\ \partial _{_{{t}}} {\rho } + \partial _{_{{j}}} \left( {\rho } {{\mathbf{v }}}_{_{{j}}} \right) = 0,\\ \underline{\text{ Momentum } \text{ conservation }} \\ \partial _{_{{t}}} {\rho }{{\mathbf{v }}}_{_{{i}}} + \partial _{_{{j}}} \left( {\rho } {{\mathbf{v }}}_{_{{i}}} {{\mathbf{v }}}_{_{{j}}} +{P} -\varvec{\tau }_{_{i,j}}\right) = \left( {\rho }-{\rho }_{_\mathrm{h}}\right) \mathbf{g}_{_{i}}, ~~~~~~~~~~~~ \\ \underline{\text{ Total } \text{ energy } \text{ conservation }} \\ \partial _{_{{t}}} {\rho } {e} + \partial _{_{{j}}} \left( \left[ {\rho } {e} + {P} - \varvec{\tau }_{_{i,j}}\right] {{\mathbf{v }}}_{_{{j}}} + \mathbf{q}_{_{j}} \right) = {{\mathbf{v }}}_{_{{k}}} \left( {\rho }-{\rho }_{_\mathrm{h}}\right) \mathbf{g}_{_{k}}, \end{array} \end{aligned}$$

(1)

where t, ${\mathbf{r }}=\left( x,y,z\right)$, $\rho$, ${\mathbf{v }}$, P, T, $e={\mathfrak {u}}+\frac{{\mathbf{v }}^2}{2}$, and ${\mathbf{g }}$ are time, Cartesian coordinates, density, material velocity vector, pressure, temperature, specific total energy, and gravitational vector, respectively. Note that the subtracted hydraulic head is based on reference density $\rho _{_{\mathrm{h}}}$. The deviatoric viscous stress tensor can be expressed as [30]

$$\begin{aligned} \varvec{\tau }_{_{i,j}}= 2 \mu {{\mathcal {S}}}_{_{i,j}} + \underbrace{\left( \varsigma - \frac{2}{3} \mu \right) }_{\lambda } \partial _{_k} {{\mathbf{v }}}_{_{{k}}} \delta _{_{ij}}, \end{aligned}$$

(2)

where $\mu$ and $\lambda$ are the first and second Lamé parameters, respectively, while $\varsigma$ is the bulk viscosity. All viscosities are Stokesian, i.e., $\lambda =-\frac{2}{3} \mu$ and $\varsigma =0$, and, generally, temperature and pressure dependent. The strain rate tensor is defined as

$$\begin{aligned} {{\mathcal {S}}}_{_{i,j}} = \frac{1}{2} \left( \partial _{_j} {{\mathbf{v }}}_{_{{i}}}+ \partial _{_i} {{\mathbf{v }}}_{_{{j}}} \right) . \end{aligned}$$

(3)

We will use Fourier’s law for heat conduction, $\mathbf{q}_{_{j}}=-{\kappa } \partial _{_{{j}}} {T}$, where the coefficient of thermal conductivity $\kappa$ is generally temperature and pressure dependent.

In incompressible/low-Mach formulations, it is customary to solve for the specific internal energy (${\mathfrak {u}}$) equation, which can be written as

$$\begin{aligned} \begin{array}{l} \underline{\text{ Internal } \text{ energy } \text{ formulation }} \\ \partial _{_{{t}}} {\rho } {{\mathfrak {u}}}\! +\! \partial _{_{{j}}} \left( \left[ {\rho } {{\mathfrak {u}}} \!-\! \varvec{\tau }_{_{i,j}}\right] {{\mathbf{v }}}_{_{{j}}} \!+\!\mathbf{q}_{_{j}} \right) \! +\! P \partial _{_{{k}}} {{\mathbf{v }}}_{_{{k}}}= {{\mathbf{v }}}_{_{{k}}} \left( {\rho }-{\rho }_{_\mathrm{h}}\right) {{\mathbf{g }}}_{_k}. \end{array}\nonumber \\ \end{aligned}$$

(4)

This alternative energy equation formulation is mathematically equivalent to the total energy conservation (1), though for a majority of all-speed flow solvers, (4) is preferable due to generally better conditioning at low speed. With our Newton–Krylov framework (Sect. 3), both formulations behave equally well numerically. It is also instructive to note that we account for viscous heating and do not ignore pressure work [the last term on the l.h.s. of (4)], i.e., maintaining a fully compressible formulation.

2.2 Dimensionless form

When solving the governing equations (1), it is highly desirable to properly scale the equations, to ensure solvability of the nonlinear and linear solvers involved in the Newton–Krylov-based fully implicit framework, Sect. 3. We define the following basic length, velocity, density, viscosity, thermal conductivity, pressure, temperature,¹ specific internal energy, specific heat, and isobaric compressibility scaling/reference parameters:

$$\begin{aligned} L,~ \bar{v},~ \bar{\rho },~ \bar{\mu },~ \bar{\kappa },~ P_{_\mathrm{R}},~ \bar{T},~ T_{_\mathrm{R}}, \Delta T_{_\mathrm{g}},~ {\mathfrak {u}}_{_\mathrm{R}},~ \bar{C}_{_p}, \text{ and } \bar{\beta }. \end{aligned}$$

(5)

With these, the rest of the scaling parameters are

$$\begin{aligned} \begin{array}{c} \bar{t}=\frac{L}{\bar{v}},~ \bar{P} = \bar{\rho } \bar{v}^2,~ \bar{{\mathfrak {u}}}=\bar{C}_{_p} \bar{T},~ \bar{\nu } = \frac{\bar{\mu }}{\bar{\rho }}, \text{ and } \bar{\alpha }=\frac{\bar{\kappa }}{\bar{\rho } \bar{C}_{_p}}, \end{array} \end{aligned}$$

(6)

where $\nu$, $C_{_p}$, and $\alpha$ are kinematic viscosity, isobaric specific heat, and thermal diffusivity, respectively. The dimensionless pressure, temperature, and specific internal energy functions are defined as

$$\begin{aligned} \tilde{P}=\frac{P-P_{_\mathrm{R}}}{\bar{P}},~\tilde{T}=\frac{T-T_{_\mathrm{R}}}{\bar{T}}, \text{ and } \tilde{{\mathfrak {u}}}=\frac{{\mathfrak {u}}-{\mathfrak {u}}_{_\mathrm{R}}}{\bar{\mathfrak {u}}}. \end{aligned}$$

(7)

Importantly, the reference pressure ($P_{_\mathrm{R}}$), temperature ($T_{_\mathrm{R}}$), and specific internal energies (${\mathfrak {u}}_{_\mathrm{R}}$) are necessary to avoid round-off errors when operating in the supercritical thermodynamic states $\left[ P\ge 22.1~\mathrm{MPa}, T\ge 647~\mathrm{K} \right]$, see Sects. 2.3.2 and 4.3.

With these, the governing equations (1) become:

$$\begin{aligned}&\begin{array}{l} \underline{\text{ Mass } \text{ conservation }} \\ \partial _{_{\hat{t}}} \hat{\rho } + \partial _{_{\hat{j}}} \left( \hat{\rho } \hat{{\mathbf{v }}}_{_{{j}}} \right) = 0,\\ \underline{\text{ Momentum } \text{ conservation }} \\ \partial _{_{\hat{t}}} \hat{\rho } \hat{{\mathbf{v }}}_{_{{i}}} + \partial _{_{\hat{j}}} \left( \hat{\rho } \hat{{\mathbf{v }}}_{_{{i}}} \hat{{\mathbf{v }}}_{_{{j}}} +\tilde{P} -\tilde{\varvec{\tau }}_{_{i,j}} \right) = \left( \hat{\rho }-\hat{\rho }_{_\mathrm{h}}\right) \hat{{\mathbf{g }}}_{_i}, ~~~~~~~~~~~~ \end{array} \end{aligned}$$

(8)

$$\begin{aligned}&\begin{array}{l} \underline{\text{ Total } \text{ energy } \text{ conservation }} \\ \partial _{_{\hat{t}}} \hat{\rho } \hat{e} + \partial _{_{\hat{j}}} \left( \left[ \hat{\rho } \hat{e} + \epsilon _{_\mathrm{E}}\left( \hat{P}_{_{\mathrm{R}}} + \tilde{P} - \tilde{\varvec{\tau }}_{_{i,j}} \right) \right] \hat{{\mathbf{v }}}_{_{{j}}} + \tilde{\mathbf{q}}_{_{j}} \right) \\ \quad = \epsilon _{_\mathrm{E}}\hat{{\mathbf{v }}}_{_{{k}}} \left( \hat{\rho }-\hat{\rho }_{_\mathrm{h}}\right) \hat{{\mathbf{g }}}_{_k}, \end{array} \end{aligned}$$

(9)

where the dimensionless variables are defined as:

$$\begin{aligned} \begin{aligned}&\hat{t}=\frac{t}{\bar{t}},~ \hat{{\mathbf{x }}}=\frac{{\mathbf{x }}}{L},~ \hat{\rho }=\frac{\rho }{\bar{\rho }},~ \hat{\rho }_{_\mathrm{h}}=\frac{\rho _{_\mathrm{h}}}{\bar{\rho }},~ \hat{{\mathbf{v }}}=\frac{{\mathbf{v }}}{\bar{v}},\\&\hat{T}=\frac{T}{\bar{T}},~ \hat{{\mathbf{g }}}=\frac{\mathrm{Gr}}{\mathrm{Re}^2 \hat{\beta } \bar{\beta } \Delta T_{_\mathrm{g}}},~ \hat{\beta } = \frac{\beta }{\bar{\beta }}, \\&\hat{e}= \frac{e}{\bar{{\mathfrak {u}}}},~ \hat{\mu }= \frac{\mu }{\bar{\mu }}, ~\tilde{\mu } = \frac{\hat{\mu }}{\mathrm{Re}},~ \hat{\varvec{\tau }}=\frac{\varvec{\tau } L}{\bar{\mu }\bar{v}},~ \tilde{\varvec{\tau }}=\frac{\hat{\varvec{\tau }}}{\mathrm{Re}},\\&\hat{\kappa }=\frac{\kappa }{\bar{\kappa } },~ \tilde{\kappa }=\frac{\hat{\kappa }}{\mathrm{Re}~\mathrm{Pr}},~ \hat{\mathbf{q}}=\frac{\mathbf{q }L}{\bar{\kappa }},~ \tilde{\mathbf{q}}=\frac{\hat{\mathbf{q}}}{\mathrm{Re}~\mathrm{Pr}}. \end{aligned} \end{aligned}$$

(10)

The dimensionless internal energy equation can be written as:

$$\begin{aligned} \begin{array}{l} \underline{\text{ Internal } \text{ energy } \text{ formulation }} \\ \partial _{_{\hat{t}}} \hat{\rho } \hat{{\mathfrak {u}}} + \partial _{_{\hat{j}}} \left( \left[ \hat{\rho } \hat{{\mathfrak {u}}} - \epsilon _{_\mathrm{E}}\tilde{\tau }_{_{i,j}} \right] \hat{{\mathbf{v }}}_{_{{j}}} +\tilde{\mathbf{q}}_{_{j}} \right) \\ \quad +\epsilon _{_\mathrm{E}}\left( \hat{P}_{_\mathrm{r}} + \tilde{P}\right) \partial _{_{\hat{k}}} \hat{{\mathbf{v }}}_{_{{k}}} = \epsilon _{_\mathrm{E}}\hat{{\mathbf{v }}}_{_{{k}}} \left( \hat{\rho }-\hat{\rho }_{_\mathrm{h}}\right) \hat{{\mathbf{g }}}_{_k}. \end{array} \end{aligned}$$

(11)

The classical fluid dynamics scaling numbers in the above formulation—the Reynolds, the Prandtl, the Grashof, and the Rayleigh numbers—are defined by scaling parameters as:

$$\begin{aligned} { \begin{array}{c} \mathrm{Re}=\frac{\bar{\rho } \bar{v}L}{\bar{\mu }},~ \mathrm{Pr}= \frac{\bar{\nu }}{\bar{\alpha }},~ \mathrm{Gr}= \frac{g\bar{\beta } \Delta T_{_\mathrm{g}} L^3}{\bar{\nu }^2},~\text{ and }~ \mathrm{Ra}= \mathrm{Gr}~\mathrm{Pr}. \end{array} } \end{aligned}$$

(12)

Finally, due to the fully compressible formulation used here, there is one more scaling parameter, which represents the ratio of kinetic and thermal energies, defined as:

$$\begin{aligned} \epsilon _{_\mathrm{E}}=\frac{\bar{v}^2}{\bar{{\mathfrak {u}}}}. \end{aligned}$$

(13)

This parameter appears in energy equations as a factor for viscous heating and pressure work terms.

2.3 Equations of state

2.3.1 Isothermal sphere polytropic EoS

To represent nearly incompressible fluids, we use a simple constant-property compressible material formulation, with the following polytropic equation of state:

$$\begin{aligned} P=P_{_\mathrm{R}}+ \bar{c}_{_\mathrm{s}}^2 \rho ^{^{\left( \frac{n+1}{n}\right) }}, \end{aligned}$$

(14)

where $\bar{c}_{_\mathrm{s}}$ is a specified (constant) speed of sound, while n is the polytropic index. We are considering a polytrope with index $n=+\infty$, which corresponds to what is called an isothermal sphere. With this EoS, pressure and temperature are decoupled (which generally simplifies the preconditioning), and the dynamic viscosity ($\bar{\mu }$) and thermal conductivity ($\bar{\kappa }$) are chosen to be constant. In addition, we assume thermally perfect gas formulation for specific internal energy,

$$\begin{aligned} {\mathfrak {u}}= {\mathfrak {u}}_{_\mathrm{R}}+ \bar{C}_{_v} \left( T- T_{_\mathrm{R}} \right) , \end{aligned}$$

(15)

where $\bar{C}_{_v}$ is the given constant. Note, for this EoS, $\left. \frac{\partial \rho }{\partial T}\right| _{P}=0$ and $\bar{C}_{_p}=\bar{C}_{_v}$. This equation of state is used in the numerical examples of Sects. 4.2 and 4.4.

Fig. 1

Temperature dependence of material properties for water, for selected pressures above critical point, based on IAPWS-IF97 [31]

2.3.2 Supercritical water EoS

To demonstrate the performance of our solver for numerically stiff fluids with variable properties at the nearly incompressible limit, we use water in a supercritical state. The equation of state is based on the “International Association for the Properties of Water and Steam, Industrial Formulation 1997” (IAPWS-IF97) [31], and is briefly described in Appendix. It is instructive to note that in the temperature range of interest (from 650 to 750 K, see example in Sect. 4.3), density, dynamic viscosity, and thermal conductivity vary significantly (Fig. 1). The speed of sound is very high (the peak Mach number is below $10^{-5}$), rendering incompressible approximations inappropriate.

2.3.3 $\gamma$-gas EoS

Our final EoS is the ideal gas law, defined as

$$\begin{aligned} P=\rho {\mathfrak {u}}\left( \gamma -1\right) =\rho RT, ~~~ \gamma =\frac{\bar{C}_{_p}}{\bar{C}_{_v}}, \end{aligned}$$

(16)

where $R=\frac{R_{\mathrm{u}}}{{{\mathcal {M}}}}=\bar{C}_{_p}-\bar{C}_{_v}$ is the specific gas constant, with the universal gas constant $R_{\mathrm{u}} \approx 8.31446 \frac{\mathrm{J}}{{\mathrm{mol}}\, {\mathrm{K}}}$ and ${{\mathcal {M}}}$ is the molecular weight of the gas. Perfect gas assumption (15) is used for ${\mathfrak {u}}\left( T\right)$. This EoS is used for the manufactured solution problem in Sect. 4.1 and in the high-speed flow example of Sect. 4.5.

3 Numerical algorithm

3.1 Reconstructed discontinuous Galerkin (rDG)

In this section, we describe the discontinuous finite element method used for our space discretization. We start with some background information and brief review of the previous work in Sects. 3.1.1 and 3.1.2. Then, we focus on describing different choices for solution vectors and a way to avoid explicitly forming and inverting mass matrices in Sect. 3.1.3—these are new technical contributions of the present work, which improves the robustness of the method at the limits of vanishing Mach numbers, as well as when utilizing the high-order non-orthogonal basis functions.

3.1.1 Background

For space discretization, we utilize the reconstructed Discontinuous Galerkin method (rDG), which was originally introduced in [32] and further developed in [33,34,35,36,37,38,39,40,41,42] for solving nonlinear mixed hyperbolic-parabolic systems of governing equations. The idea originated from the pioneering work by van Leer et al. [43], where a consistent discretization of the parabolic operator in diffusion equations was developed using the so-called inter-cell recovery. The method was extended to generic hyperbolic systems with source terms in [25, 44], adding an “in-cell recovery” operator. Dumbser et al. [45,46,47] introduced an extension with least-squares recovery, making the algorithm practical for unstructured grid discretizations. They have also coined the term $\hbox {P}_{n}\hbox {P}_m$ discretization² for a Discontinuous Galerkin method.

The computational domain $\varOmega$ is subdivided into a collection of non-overlapping elements, $\varOmega _{_e}$. The set of independent variables $\mathbb {V}$ is represented in the broken Sobolev space $\mathbb {V}^{^{(p)}}_{_{h}}$, consisting of discontinuous vector-values polynomial functions of degree p,

$$\begin{aligned} \mathbb {V}^{^{(p)}}_{_{h}} = \left\{ \upsilon _{_h} \in \left[ \mathcal {L}_{_2} \left( \varOmega \right) \right] ^{^m} : \left. \upsilon _{_h} \right| _{_{\varOmega _{_e}}} \in \left[ \mathcal {V}^{^m}_{_p} \right] \forall \varOmega _{_e} \in \varOmega \right\} , \end{aligned}$$

(17)

where m is the dimension of the unknown vector and $\mathcal {V}_{_p}$ is the space of all polynomials of degree $\le p$. Numerical polynomial solutions $\mathbf{V}_{_h}^{^{(p)}}$ in each element are expressed using a chosen set of basis functions $\mathcal {B}_{_{(k)}}\left( {\mathbf{x }}\right)$, as

$$\begin{aligned} \mathbf{V}_{_h}^{^{(p)}}\left( {\mathbf{x }},t\right) = \sum \limits _{k=0}^{p-1} \mathbf{V}_{_{(k)_{_e}}} \left( t\right) \mathcal {B}_{_{(k)}} \left( {\mathbf{x }}\right) +\mathcal {O}\left( h^{^p}\right) , \end{aligned}$$

(18)

where $\mathbf{V}_{_{(k)_{_e}}}$ denotes the solved-for degrees of freedom (DoF) in an element e. These degrees of freedom constitute the solution vector for the Newton–Krylov nonlinear solver, to be discussed in Sect. 3.3.2. We will introduce the choices for $\mathbf{V}$ in Sect. 3.1.3. To contrast, the vector of conservative variables can also be discretized using basis functions $\mathcal {B}_{_{(k)}}\left( {\mathbf{x }}\right)$,

$$\begin{aligned} \mathbf{U}_{_h}^{^{(p)}}\left( {\mathbf{x }},t\right) = \sum \limits _{k=0}^{p-1} \mathbf{U}_{_{(k)_{_e}}} \left( t\right) \mathcal {B}_{_{(k)}} \left( {\mathbf{x }}\right) +\mathcal {O}\left( h^{^p}\right) . \end{aligned}$$

(19)

Though, in our fully implicit solution algorithm, we do not need $\mathbf{U}_{_{(k)_{_e}}}$ (these are “auxiliary” quantities, never explicitly evaluated), as will be shown in Sect. 3.1.3.

The basic DG method is defined by the following weak formulation, which is obtained by inserting (19) into governing equations (1), multiplying by a test function , integrating over an element $\varOmega _{_e}$, and then performing an integration by parts,

(20)

where $\mathbf{U}^{^{(p)}}_{_h}$ and are represented by piecewise-polynomial functions of degree p, which are discontinuous between the cell interfaces, and ${\mathbf{n }}=n_{_j}$ denotes the unit outward normal vector of the element face $\varGamma _{_e}$ (i.e., the boundary of $\varOmega _{_e}$). By $\mathbf{F}$ and $\mathbf{D}$, we denote the hyperbolic and parabolic vectors in (1), respectively, while $\mathbf{S}$ represents the vector of source terms.

The local residual function $\mathbf{R}^{^{(p)}}_{_h} \left( \mathbf{U}^{^{(p)}}_{_h}\right)$ defines an inner product of the solution residue representation (with a chosen set of basis functions) and the test functions . In our solution procedure (Sect. 3.3), we are minimizing this inner product, which makes our approach a particular case of the method of Mean Weighted Residuals (MWR).

3.1.2 Basis functions

In this work, we utilize the Taylor-series-based functions to represent both the test and basis functions. In 2D, these are

(21)

where $\Delta x= \frac{x_{_\mathrm{max}}-x_{_\mathrm{min}}}{2}$, $\Delta y= \frac{y_{_\mathrm{max}}-y_{_\mathrm{min}}}{2}$, and $x_{_\mathrm{max}}$, $x_{_\mathrm{min}}$, $y_{_\mathrm{max}}$, and $y_{_\mathrm{min}}$ are the maximum and minimum coordinates in the cell $\varOmega _{_e}$ in the x- and y-direction, respectively.³

This choice is different from our previous work [42], where we utilized a Petrov–Galerkin discretization with orthogonal tensor-product Legendre-polynomial-based basis/test functions that are defined in reference space. There are a few important advantages of the Taylor basis functions in the context of implementation and practical simulations. These include the simplicity to generalize to arbitrary high-order (here, we implemented and tested the method up to the seventh-order accuracy, Sect. 4.1), more straightforward way to implement boundary conditions involving spatial derivatives (like those involved in Marangoni convection, Sect. 4.4.1), as well as compatibility with the limiting procedures used here (Sect. 3.4). Notably, since the method does not require forming and inverting mass matrices to evaluate time derivatives, there is no substantial downside of non-orthogonality, which is normally a concern for going to very high-order versions of the algorithm. Even though non-orthogonality does lead to slightly less diagonally dominant Jacobian matrices, no significant impact on the method convergence is found.

3.1.3 Choices for the solution vector

It is very important to properly choose the set of solution variables, as this will greatly influence the solvability of the linear algebra utilized in the Krylov iterations of our Newton–Krylov algorithm, Sect. 3.3.2. The naïve choice of using conservative variables, $\mathbf{V}=\mathbf{U}$, where $\mathbf{U}=\left( \rho , \rho \mathbf {v}, \rho e\right) ^{{\intercal }}$, is a good one only for high-speed flows, but becomes degenerate at the limit of vanishing Mach numbers. We found that the choice of

$$\begin{aligned} \mathbf{V}=\left( P, \mathbf {v}, T \right) ^{^{\intercal }} \end{aligned}$$

(22)

works well at both low- and high-speed ranges. This set of $\mathbf{V}$ will be denoted as $\left( P \mathbf{v} T\right)$-formulation hereafter. At high speed, it is slightly worse-conditioned than the set of conservative variables, denoted as $\left( \rho \mathbf{m} E\right)$-formulation (i.e., resulting in slightly more Krylov iterations needed per unpreconditioned linear step), but it works best at the vanishing Mach number range. The other two options used in this work are

$$\begin{aligned} \mathbf{V}=\left( \rho , \mathbf {v}, T\right) ^{\intercal }~~ {\text{ and }}~~ \mathbf{V}=\left( \rho , \mathbf {v}, \epsilon \right) ^{\intercal }, \end{aligned}$$

(23)

where $\epsilon =\frac{P}{\rho ^{\gamma }}$ is $\gamma$-gas’s entropy production. These formulations (denoted as $\left( \rho \mathbf{v} T\right)$ and $\left( \rho \mathbf{v} \epsilon \right)$) are found to be advantageous over both $\left( P \mathbf{v} T\right)$- and $\left( \rho \mathbf{m} E\right)$-formulations for shock dynamics.

The choice of the primitive variables in $\left( P \mathbf{v} T\right)$-formulation has additional advantages from the point of view of setting boundary conditions, as the practically useful boundary conditions involve enforcing either the Dirichlet or the Neumann BC on pressure, temperature, and velocity. This is not that simple when the primary variables being evolved are density, momentum, and total energy, as an additional nonlinear solver must be utilized to enforce the desired boundary states, for a generic equation of state.

With the basis/test functions () and solution vector ($\mathbf{V}$) chosen, the eth element’s residual vector can be written as:

(24)

where $\mathbf{W}$ is an integral vector, denoting a product of the mass matrix ($\mathbf M$) and the conservative vector ($\mathbf U$), and representing the element’s total mass, momentum, and energy. Importantly, the vector $\mathbf{W}$ can be evaluated directly from the solved-for degrees of freedom $\mathbf{V}_{(k)_{_e}}^{^R}$ using the in-cell reconstructed solution representation and a quadrature-point integration rule,

(25)

where $N_g$ and $\omega _g$ are the total number and the weights of the quadrature integration points, respectively; $\left| \mathbb {J}_{g_e} \right|$ is the determinant of the element’s Jacobian matrix evaluated at a quadrature point $\mathbf{r}_g$; are the basis functions of the nth order evaluated at a quadrature point $\mathbf{r}_g$; and $\mathbf{U}_{_{_g}}$ is a value of the conservative variable (specific density, momentum vector, and specific total energy) evaluated at a quadrature point $\mathbf{r}_g$ using the primitive-variable in-cell solution representation by (18) and an appropriate equation of state. Notably, neither the mass matrix$\mathbf{M}$nor the degrees of freedom of the conservative vector$\mathbf{U}_{_{(k)_{_e}}}$are explicitly evaluated (and inverted) during the computation of the element’s nonlinear residual vector $\mathbf{R}_{(k)_{_e}}$. Moreover, the mass matrix might be non-orthogonal (which is the case for the Taylor basis function rDG discretization of order $p>1$). Inversion of the non-orthogonal mass matrices for high-order schemes is known to result in more ill-conditioned global Jacobian matrices [defined by (39) in Sect. 3.3.2], which is avoided here.

The in-cell high-order polynomial solution is obtained by applying the ${\mathrm{rDG}_{{P_{_{N}}P_{_{M}}}}}$ reconstruction, whose solution can be broken up into a “solved-for” portion ($\hbox {P}_N$) and a “reconstructed” portion ($\hbox {P}_M$),

$$\begin{aligned} \mathbf{V}_{_h}^{\mathrm{R}}\left( {\mathbf{x }},t\right)= & {} \underbrace{\sum \limits _{k=0}^{N-1} \mathbf{V}_{_{(k)_{_e}}} \left( t\right) \mathcal {B}_{_{(k)}} \left( {\mathbf{x }}\right) }_{{{{\text{ Solved-for, } \hbox {P}_N}}}}\nonumber \\&+ \underbrace{\sum \limits _{k=N}^{M-1} \mathbf{V}_{_{(k)_{_e}}} \left( t\right) \mathcal {B}_{_{(k)}} \left( {\mathbf{x }}\right) }_{{{{\text{ Reconstructed, } \hbox {P}_M}}}}+\mathcal {O}\left( h^{^{M-1}}\right) . \end{aligned}$$

(26)

Diffusion fluxes in the face integration terms of (24) are evaluated using the inter-cell reconstruction. Computation of hyperbolic fluxes is discussed in Sect. 3.2. Both in-cell and inter-cell reconstructions are beyond the scope of the present manuscript, and we refer to [32, 33, 37, 42] for detail description of the method. Here, we are utilizing rDG discretizations denoted as ${\mathrm{rDG}_{{P_{_{0}}P_{_{1}}}}}$ (second-order accurate, finite-volume), ${\mathrm{rDG}_{{P_{_{1}}P_{_{3}}}}}$ and ${\mathrm{rDG}_{{P_{_{2}}P_{_{3}}}}}$ (both fourth-order accurate), ${\mathrm{rDG}_{{P_{_{2}}P_{_{4}}}}}$ (fifth-order accurate), and the ${\mathrm{rDG}_{{P_{_{4}}P_{_{6}}}}}$ (seventh-order accurate).

At high-speed flow conditions, the reconstructed solution requires limiting. A brief summary of the limiting algorithm and how it is made consistent with the Newton-based solution procedure are described in Sect. 3.4.

3.2 Advection Upstream Splitting Method (AUSM)

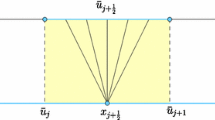
To evaluate the numerical hyperbolic fluxes $\mathbf{F}_{_j}$ in the face integration terms of (24), we are using Meng-Sing Liou’s ${\mathrm{AUSM}}^{+}$-up  scheme [19]. First, at each quadrature point g of an element’s faces $\varGamma _{_e}$, we compute the solutions “from-inside” ($\mathrm L$) and “from-outside” ($\mathrm R$) using the in-cell reconstructed DG profiles (26) from elements sharing the face under consideration, $\mathbf{V}_{_{g}}^{^\mathrm{L/R}}$. Then, as in all schemes of the AUSM family, the flux is split into convective and pressure parts,

(27)

where

$$\begin{aligned}&\dot{m}_{_{\mathrm{I},g}}= a_{_{\mathrm{I},g}} M_{_{\mathrm{I},g}} \frac{\rho _{_g}^{\mathrm{R}}+ \rho _{_g}^{\mathrm{L}} - {{\mathcal {S}}} \left( M_{_{\mathrm{I},g}}\right) \left( \rho _{_g}^{\mathrm{R}}-\rho _{_g}^{\mathrm{L}}\right) }{2}, \end{aligned}$$

(28)

$$\begin{aligned}&M_{_{\mathrm{I},g}} = {{\mathcal {M}}}_{(4)}^{+} \left( M_{_{\mathrm{L},g}} \right) +{{\mathcal {M}}}_{(4)}^{-} \left( M_{_{\mathrm{R},g}} \right) - \Delta _{_u} \left( p_{_g}^{\mathrm{R}}-p_{_g}^{\mathrm{L}}\right) ,\nonumber \\&p_{_{\mathrm{I},g}} = \frac{1}{2} \left( {{\mathcal {P}}}^{+}_{(5)} \left( M_{_{\mathrm{L},g}}, \alpha _{_p} \right) p_{_g}^{\mathrm{L}} + {{\mathcal {P}}}^{-}_{(5)} \left( M_{_{\mathrm{R},g}}, \alpha _{_p} \right) p_{_g}^{\mathrm{R}} \right) , \end{aligned}$$

(29)

$$\begin{aligned}&\varDelta _{_u} = \frac{K_{_p} }{f_{a}} \frac{\max \left( 1-\sigma _{_p} \bar{M}^{^2},0\right) }{\rho _{_{\mathrm{I},g}} a_{_{\mathrm{I},g}}^2},\nonumber \\&\varDelta _{_p} = K_{_u} {{\mathcal {P}}}^{+}_{(5)} \left( M_{_{\mathrm{L},g}}, \alpha _{_p} \right) {{\mathcal {P}}}^{-}_{(5)} \left( M_{_{\mathrm{R},g}}, \alpha _{_p} \right) \nonumber \\&\qquad \quad \quad \times \left( \rho _{_g}^\mathrm{R}+ \rho _{_g}^\mathrm{L} \right) f_{_a} a_{_{\mathrm{I},g}} \left( v_{_{n,\mathrm{R}}}-v_{_{n,\mathrm{L}}}\right) , \end{aligned}$$

(30)

$$\begin{aligned}&\bar{M}^{^2} = \frac{ v^2_{_{n,\mathrm{L}}} +v^2_{_{n,\mathrm{R}}} }{2 a_{_{\mathrm{I},g}}^2},~~~ \rho _{_{\mathrm{I},g}} = \frac{\rho _{_g}^\mathrm{R}+ \rho _{_g}^\mathrm{L}}{2},~~~ a_{_{\mathrm{I},g}} = \frac{a_{_g}^\mathrm{R}+ a_{_g}^\mathrm{L}}{2},\nonumber \\&v_{_{n,\mathrm{L|R}}}= \mathbf{v}_{_g}^{^\mathrm{L|R}} \cdot \mathbf{n},~~~ M_{_{\mathrm{L|R},g}}= \left| \frac{ v_{_{n,\mathrm{L|R}}} }{a_{_{\mathrm{I},g}}}\right| , \end{aligned}$$

(31)

and the constants are $K_{_p}=\frac{1}{4}$, $K_{_u}=\frac{3}{4}$, and $\sigma _{_p}=1$. The “smoothing” function introduced here makes (27) and (28) differentiable, and better suited for the Newton-based method utilized here,

$$\begin{aligned} {{\mathcal {S}}} \left( M_{_{\mathrm{I},g}}\right) = \left\{ \begin{array}{l@{\quad }l} 1 &{} \text{ if }\; M_{_{\mathrm{I},g}}>M_{_s}\\ -1 &{} \text{ if }\; M_{_{\mathrm{I},g}}<-M_{_s}\\ \sin \left( \frac{\pi M_{_{\mathrm{I},g}}}{M_{_s}}\right) &{}\text{ otherwise } \end{array} \right. . \end{aligned}$$

(32)

This formulation is found to work well within Newton iterations. The original formulation [19] can be recovered by setting

$$\begin{aligned} {{\mathcal {S}}} \left( M_{_{\mathrm{I},g}}\right) = \left\{ \begin{array}{l@{\quad }l} 1 &{} \text{ if }\; M_{_{\mathrm{I},g}}>0\\ -1 &{}\text{ otherwise } \end{array} \right. . \end{aligned}$$

(33)

In (27)–(31), $\mathbf{v}^\mathrm{L|R}_{_g}$, ${{\mathcal {H}}}^\mathrm{L|R}_{_g}$, $\rho ^\mathrm{L|R}_{_g}$, $p^{\mathrm{L}|R}_{_g}$, and $a^\mathrm{L|R}_{_g}$ are the face quadrature point reconstructed solutions for material velocity, specific enthalpy, density, pressure, and speed of sound, respectively. We refer to [19] for definitions of functions ${{\mathcal {M}}}_{(4)}^{\pm }$ and ${{\mathcal {P}}}_{(5)}^{\pm }$.

By setting $f_a=1$ and $\alpha _{_p}=\frac{3}{16}$, the basic ${\mathrm{AUSM}}^{+}$-up  scheme is recovered. It will be used for high-speed flow (example in Sect. 4.5). The low-Mach version of the scheme will be used in all the remaining examples, defined by modifying $f_a$ and $\alpha _{_p}$ as described in [19], i.e.,

$$\begin{aligned}&f_a = M_{_\mathrm{o}}\left( 2-M_{_\mathrm{o}}\right) ,~~M^2_{_\mathrm{o}}=\min \left( 1, \max \left( \bar{M}^{^2} , M^2_{_\mathrm{co}}\right) \right) \nonumber \\&\quad \mathrm{and }~~\alpha _{_p} = \frac{3}{16} \left( -4 + 5 f^2_a \right) \end{aligned}$$

(34)

and $M_{_\mathrm{co}}$ is a problem-dependent cut-off parameter. The scaling factor $f_a$ is designed to modify the local numerical speed of sound, which allows the scheme to maintain its accuracy and robustness, as has been shown by asymptotic analysis at the $M \rightarrow 0$ limit in [19]. In most of the low-speed examples here, we set $M_{_s}=\min \left( 10^{-4}, M_{_\mathrm{co}}\right)$. As demonstrated in Sects. 4.2, 4.3 and 4.4, in combination with NK fully implicit scheme, robust and accurate solutions are obtained without additional local preconditioning matrix included in the time derivative terms.

The other Riemann solvers used here for comparison are the local Lax–Friedrichs (LLF) and the Harten/Lax/van Leer (HLL), see [5] for details.

3.3 NK fully implicit solver

In this section, we briefly outline the time discretization, as well as the nonlinear and linear solvers, and preconditioners used in our implicit Newton–Krylov-based solution algorithm.

3.3.1 Time discretization

Residual vector with the method-of-lines diagonally implicit Runge–Kutta (DIRK) time discretization of (24) can be written as

(35)

where s is the total number of implicit Runge–Kutta (IRK) stages, while ${\textsf {a}}_{_{mr}}$ and ${\textsf {b}}_{_{r}}$ are the stage and the main scheme weights, respectively. By , we denote the PDE operators and source terms [face and domain integral terms in (24)]. We refer to [42] for definitions of $\alpha$, $\beta$, ${\textsf {a}}_{_{mr}}$, and ${\textsf {b}}_{_{r}}$ for the second-order Backward Differentiation Formula ($\hbox {BDF}_2$), and the third- to fifth-order Explicit Singly Diagonal Implicit Runge–Kutta ($\hbox {ESDIRK}_{3,4,5}$) schemes, which are utilized in the present study. We would like to highlight that no direct mass matrix evaluation and inversion are needed for time derivatives. Instead, we evaluate $\mathbf{W}^{^{[m]}}$ as described in (25).

3.3.2 Newton–Krylov

Each stage of the IRK (35) requires a solution of the nonlinear system in the form

(36)

where

(37)

is a solution vector that includes all K degrees of freedom for all variables in all $\mathrm N_{_\mathrm{cells}}$ computational cells. It is instructive to emphasize that the reconstructed DoFs ($k=K, \ldots , K_R-1$) of (26) are not a part of the solution vector.

The nonlinear system (36) is solved with Newton’s method [23], iteratively, as a sequence of linear problems defined by

(38)

The matrix $\mathbb {J}^{^a}$ is the Jacobian of the ath Newton’s iteration, and is the update vector. Each $_{(i,j)}$th element of the Jacobian matrix is a partial derivative of the ith equation with respect to the jth variable:

$$\begin{aligned} \mathbb {J}_{_{i,j}} \equiv \frac{\partial \mathrm{res}_{_i}}{\partial {{\mathcal {X}}}_{_j}}. \end{aligned}$$

(39)

The linear system (38) is solved for , and the new Newton’s iteration value for is then computed as

(40)

where $\lambda ^{^a}$ is the step length determined by a line search⁴ procedure [49], while is the search direction. Newton’s iterations on are continued until the convergence criterion

(41)

is satisfied. The nonlinear tolerance $\mathrm{tol}_{_\mathrm{N}}$ is varied from $10^{-3}$ to $10^{-8}$.

To solve the linear problem given by (38), we use the Arnoldi-based Generalized Minimal RESidual method⁵ (GMRES) [50]. Since the GMRES does not require individual elements of the Jacobian matrix $\mathbb {J}$, the matrix never needs to be explicitly constructed. Instead, only matrix-vector multiplications $\mathbb {J} {\varvec{\kappa }}$ are needed, where ${{\varvec{\kappa }}}$ are Krylov vectors. The action of the Jacobian matrix is approximated in the Jacobian-free manner by Fréchet derivatives

(42)

(see [23] for choosing $\varepsilon$). Here, we use the inexact Newton’s method [23], solving to a tight tolerance only when the added accuracy matters, i.e., when it affects the convergence of the Newton’s iterations. This is accomplished by making the convergence of the linear residual proportional to the nonlinear residual:

(43)

where $\nu _{_a}$ is computed as described in [51].

3.3.3 Preconditioning

It is well known that GMRES needs preconditioning to keep the number of iterations relatively small and to prevent the storage and CPU time from becoming prohibitive. We are using the right-preconditioned form of the linear system [52],

(44)

where $\mathbb {P}^{-1}$ approximates $\mathbb {J}^{-1}$. The right-preconditioned version of (42) is

(45)

• 1. Direct solver The most robust but not scalable preconditioner is to choose $\mathbb {P}=\mathbb {J}$, and to apply a global direct solver.⁶ This approach does require the Jacobian evaluation, for which we use finite differencing with solution perturbations, as described in [26]. Since re-assembling the Jacobian matrix every Newton iteration is prohibitively expensive, we lag (freeze) the Jacobian matrix over several nonlinear solutions. We use the GMRES iteration count to detect when the current Jacobian is no longer a good approximation. When it exceeds the specified threshold (typically 20–50 Krylov iterations) within a given Newton iteration, we re-evaluate the Jacobian. For some problems (like those in Sect. 4.1 or 4.2), only a few Jacobian re-evaluations are needed over the whole transient. For very nonlinear problems, involving phase change and melt pool formation, the Jacobian is re-evaluated almost every time step. In these cases, some substantial speed-up procedures can be applied. For example, in the tests of Sect. 4.4, we can identify the molten-steel elements, and the Jacobian re-evaluation is applied only in these elements, where we know a substantial change in the solution state has occured, in addition, we can ignore the Jacobian elements that are below the prescribed threshold,

  $$\begin{aligned} \left| \mathbb {J}_{_{i,j}} \right| <\epsilon _{_{\mathbb {J}}} \left| \mathbb {J}_{_{i,i}} \right| , \end{aligned}$$

  where $\mathbb {J}_{_{i,i}}$ is the value of the diagonal element, and the threshold $\epsilon _{_{\mathbb {J}}}$ is typically set to be $<10^{-4}$. Depending on the problem solved, this will shrink the size of the preconditioning matrix $\mathbb {P}$ down to 30%, which helps in both the memory storage and the computational time to factorize it.

• 2. ${{\textit{Physics-block Schur complement }}\left( \mathbf{v} P- \mathbf{v} T\right) }$ Using direct solver preconditioner is prohibitively expensive for large problems. Instead, in [26], we have developed a scalable iterative solver, which is based on the physics-based approximate block factorization. For the Navier–Stokes equations, we can decompose the $3 \times 3$$\left( P \mathbf{v} T\right)$ block system into a sequence of two $2 \times 2$ block subsystems (the velocity-pressure, $\mathbf{v} P$, and the velocity-temperature, $\mathbf{v} T$, sub-blocks), using the Schur complement. The problem reduces to a sequence of scalar solvers amenable to multigrid algorithms. It is instructive to note that solving for the first $2 \times 2$$\left( \mathbf{v} P \right)$ block is akin to Chorin’s predictor–corrector projection algorithm [53] or to the incompressible-flow SIMPLE/Uzawa solvers [2]. The second $2 \times 2$$\left( \mathbf{v} T \right)$ block is necessary when the coupling to temperature cannot be ignored, as in the case of the complex equations of state (Sect. 4.3) or the melting-solidification problems (Sect. 4.4). Detail discussion of scalable iterative preconditioners is beyond the scope of this work. We refer to [26] for a description and performance evaluations of different approximate block factorization preconditioners developed for rDG-based fully implicit solvers, including the demonstration of the weak and strong scalings on large-scale problems solved using up to 10,000 CPU cores.

• 3. Element block-diagonal (EBD) This preconditioner is useful when the simulation time step does not substantially exceed both the material and the acoustic CFL numbers, i.e., $\max (\mathrm{CFL}_{_\mathrm{aco}}, \mathrm{CFL}_{_\mathrm{mat}}) \le 20$, like in the shock dynamics example of Sect. 4.5. In these cases, the global preconditioners are not cost-effective. In the EBD, we decompose the global solution vector into smaller local solution sub-vectors, containing only unknowns (DoFs) associated with a given mesh element, and ignoring long-range element-to-element coupling, when the approximate Jacobian sub-blocks are assembled. These smaller sub-blocks can be inverted, for each element, at each Krylov iteration. (In fact, we use the LU-factorization once, right after the approximate Jacobian is evaluated, storing the factorized sub-blocks for each element, and applying very inexpensive back-substitution only when the preconditioned Krylov vector needs to be turned back to the GMRES solver.) The re-evaluation of the local preconditioning matrices is done similarly to the above global preconditioners (using the finite differencing with perturbations), but the cost for assembling the block-diagonal sub-matrices is significantly lower, as many neighbor-to-neighbor coupling Jacobian elements are ignored.

3.4 Directional BJ limiter

To enable discontinuous solutions in high-speed applications, we utilize limiters that modify the in-cell high-order polynomial representation of the solution vector (26) as

$$\begin{aligned} \mathbf{V}_{_h}^{{\mathrm{R,L}}}\left( {\mathbf{x }},t\right)= & {} \underbrace{\sum \limits _{k=0}^{K-1} \mathbf{V}_{_{(k)_{_e}}} \left( t\right) \mathcal {B}_{_{(k)}} \left( {\mathbf{x }}\right) }_{{\text{ Solved-for }}}\nonumber \\&+ \underbrace{\sum \limits _{k=K}^{K_R-1} \overbrace{\alpha _{_{(k)_{_e}}}}^{{\text{ Limiters }}} \left( \mathbf{V}_{_h}^{\mathrm{R}} \right) \mathbf{V}_{_{(k)_{_e}}} \left( t\right) \mathcal {B}_{_{(k)}} \left( {\mathbf{x }}\right) }_{{\text{ Reconstructed }}}, \end{aligned}$$

(46)

where $\alpha _{_{(k)_{_e}}}$ is the limiter for the kth DoF in the element e. In this work, we restrict the discussion to the second-order ${\mathrm{rDG}_{{P_{_{0}}P_{_{1}}}}}$. Limiting the higher-order schemes will be presented elsewhere.

The vertex-based limiting of the finite-volume solution on unstructured mesh was introduced by Barth and Jesperson (BJ) in [27]. Recently, the hierarchical version of the BJ limiter for discontinuous Galerkin methods was developed by Kuzmin [54]. These limiters are unidirectional, i.e., $\alpha _{_{(1)_{_e}}}=\alpha _{_{(2)_{_e}}}=\alpha ^{{(1)}}_{_e}$, for the ${\mathrm{rDG}_{{P_{_{0}}P_{_{1}}}}}$ in two dimensions. In this study, we use the following “directional” modification (denoted hereafter as $\hbox {BJ}_\mathrm{dir}$), which seems to work well with our fully implicit solver.

First, we follow Barth and Jesperson [27], computing the limited solution at the ith vertex of the element e as

$$\begin{aligned} \begin{aligned}&\alpha _{_{i,e}}^{^{(1)}} = \left\{ \begin{array}{l@{\quad }l} f_{_\mathrm{BJ}} \left( \frac{\mathbf{V}_{_{(0)_i}}^{^\mathrm{max}}-\mathbf{V}_{_{(0)_e}}}{\mathbf{V}^{^\mathrm{U}}_{_{(0)_{i,e}}}-\mathbf{V}_{_{(0)_e}}} \right) , &{} \text{ if }\; \mathbf{V}_{_{(0)_{i,e}}}>\mathbf{V}_{_{(0)_e}} \\ f_{_\mathrm{BJ}} \left( \frac{\mathbf{V}_{_{(0)_i}}^{^\mathrm{min}}-\mathbf{V}_{_{(0)_e}}}{\mathbf{V}^{^\mathrm{U}}_{_{(0)_{i,e}}}-\mathbf{V}_{_{(0)_e}}} \right) , &{} \text{ if }\; \mathbf{V}_{_{(0)_{i,e}}}<\mathbf{V}_{_{(0)_e}} \\ 1, &{} {\mathrm{otherwise}} \\ \end{array} \right. ,\\ \\&\text{ where }~ f_{_\mathrm{BJ}} \left( \frac{\varDelta _{+}}{\varDelta _{-}}\right) = \min \left( 1,\frac{\varDelta _{+}}{\varDelta _{-}} \right) \end{aligned} \end{aligned}$$

(47)

and

$$\begin{aligned} \mathbf{V}^{^\mathrm{L}}_{_{(0)_{i,e}}}=\mathbf{V}_{_{(0)_e}}+\alpha _{_i} \left( \mathbf{V}^{^\mathrm{U}}_{_{(0)_{i,e}}}-\mathbf{V}_{_{(0)_e}} \right) . \end{aligned}$$

(48)

By $\mathbf{V}^{^\mathrm{U}}_{_{(0)_{i,e}}}$ and $\mathbf{V}^{^\mathrm{L}}_{_{(0)_{i,e}}}$, we denote the unlimited and the limited reconstructed solutions at the ith vertex of the element e, respectively, while the $\mathbf{V}_{_{(0)_i}}^{^\mathrm{max}}$ and $\mathbf{V}_{_{(0)_i}}^{^\mathrm{min}}$ are the maximum and minimum values of $\mathbf{V}_{_{(0)_{\varepsilon }}}$ in the subset of elements $\left\{ \varepsilon \in {{\mathcal {V}}}_{_i} \right\}$ sharing the ith vertex. In [27], the limiter $\alpha ^{{(1)}}_{_e}$ was computed by taking the minimum of $\alpha _{_{i,e}}^{^{(1)}}$ over all vertices of the element e. Instead, we consider a subset of sub-elements $\left<e,i,j \right>$ (in two dimensions), where i and j are the face-sharing vertices of the element e. At each vertex of the triangular sub-element, we have the reconstructed solutions $\left<\mathbf{V}_{_{(0)_e}}, \mathbf{V}^{^\mathrm{L}}_{_{(0)_{i,e}}}, \mathbf{V}^{^\mathrm{L}}_{_{(0)_{j,e}}} \right>$, allowing us to compute the slopes $\delta _{_x}^{\left<e,i,j \right>}$ and $\delta _{_y}^{\left<e,i,j \right>}$. These slopes can be converted to the slope limiters as

$$\begin{aligned} \alpha ^{\left<e,i,j \right>}_{_{x|y}} = \left\{ \begin{array}{l@{\quad }l} \frac{\delta _{_{x|y}}^{\left<e,i,j \right>}}{\mathbf{V}_{_{(1|2)_e}}} &{} \text{ if }\; \left| \mathbf{V}_{_{(1|2)_e}} \right| > 10^{-13}\\ 1 &{} \text{ otherwise } \end{array} \right. . \end{aligned}$$

(49)

The final directional slope limiters are taken as the minima of the $\alpha ^{\left<e,i,j \right>}_{_{x|y}}$ over all sub-elements composing an element e.

The BJ-based limiters are non-differentiable, which is known to be a problem for Newton-based iterative algorithms. We have numerically verified that without a proper measure, the Newton iterations might stall and fail to produce a converged solution at some time steps and mesh resolutions. A few improvements are known, like replacing the MinMod version of the $f_{_\mathrm{BJ}}$ in (47) with the van-Albada-inspired limiter (differentiable) introduced by Venkatakrishnan⁷ [55], and some others, as discussed in [56]. However, these modifications cannot make the whole procedure differentiable, as the vertex-by-vertex “if” statements (a major cause of the non-differentiability) cannot be eliminated. Instead, to prevent the “stalling” of nonlinear iterations, we use the following strategy:

• Within the NK algorithm, the limiters are computed only for the first $m_{_\mathrm{L}}$ Newton iterations, $\alpha _{_{(1)_{_e}}}^{^{(m\le m_{_\mathrm{L}})}}$.

• For all nonlinear iterations $m>m_{_\mathrm{L}}$, the limiters are fixed at the value computed using the solution at the end of the $m_{_\mathrm{L}}$th iteration, i.e., $\alpha _{_{(k)_{_e}}} =f \left( \mathbf{V}^{^{m_{_\mathrm{L}}}} \right)$.

For the shock dynamics test case in Sect. 4.5, $m_{_\mathrm{L}}=3$ worked well. Once the limiter is “frozen,” nonlinear iterations are found to rapidly converge with one or two more iterations to the chosen nonlinear tolerance of $\hbox {tol}_{_\mathrm{N}}=10^{-7}$.

Finally, we would like to point out that the choice of the solution variables, i.e., $\left( P \mathbf{v} T\right)$, $\left( \rho \mathbf{m} E\right)$, $\left( \rho \mathbf{v} T\right)$, or $\left( \rho \mathbf{v} \epsilon \right)$, has an effect on the boundness and monotonicity of the solution. This is because the above-discussed BJ limiter enforces boundness for the variables it is applied on. Thus, if one solves for the conservative variables, i.e., density, momentum, and total energy, these are the flow variables that are being slope-limited. On the other hand, in practical simulations, we would like the primitive variables, i.e., pressure, density/temperature, and velocity, to be monotone. As discussed by Kuzmin [54], the bounding of conservative variables does not guarantee monotonicity of the non-conservative variables. This requires the design of compatible slope limiters, which is not straightforward for high-order DG. Solving directly for the variables needed to be monotone allows us to avoid these complications.

Fig. 2

Snapshots of the manufactured solution for temperature (left) and Mach number/velocity field (right), using two mesh resolutions, at time $t=0.13$. Computation with the ${\mathrm{rDG}_{{P_{_{2}}P_{_{4}}}}}$ and $\hbox {ESDIRK}_5$ discretization schemes

Table 1 Parameters of the manufactured solution

4 Numerical examples

Our numerical demonstration test suite is designed to show that the method is capable of producing robust high-order accurate solutions to very difficult problems in a wide range of flow conditions and fluid velocities, ranging from nearly incompressible, variable density, to transonic and supersonic regimes; from the forced and natural convection heat transfer in channels (Sects. 4.2 and 4.3), phase change (melting/solidification) thermocapillary convection in metals (Sect. 4.4), to shock dynamics in wind tunnels (Sect. 4.5). The core numerical algorithm/space–time discretization is the same for all flow speeds, with the main differences in how the linear solver is preconditioned, and whether the solution limiting algorithm is activated.

4.1 Manufactured solution

We start with a manufactured solution, as introduced in [42], to verify the method convergence to high order. In two dimensions, the following solution field is manufactured for temperature, pressure, and velocity:

$$\begin{aligned} \begin{aligned} T\left( x,y,t\right)&= \bar{{\mathcal {T}}}+ \left( \delta {{\mathcal {T}}}_{_0}+a_{_{T}} \sin \left( 2 \pi t \right) \right) \cos \left( 2 \pi \left( x + \omega _{_{1}}t \right) \right) \\&\quad \sin \left( 2 \pi \left( y + \omega _{_{2}}t \right) \right) \\ P\left( x,y,t\right)&=\bar{{\mathcal {P}}}+ \left( \delta {{\mathcal {P}}}_{_0}+a_{_{P}} \sin \left( 2 \pi t \right) \right) \sin \left( 2 \pi \left( x + \omega _{_{1}}t \right) \right) \\&\quad \cos \left( 2 \pi \left( y + \omega _{_{2}}t \right) \right) \\ v_{_{1}}\left( x,y,t\right)&= \left( \delta {{\mathcal {V}}}_{_0}+a_{_{v}} \sin \left( 2 \pi t \right) \right) \cos \left( 2 \pi \left( x +\omega _{_{1}}t \right) \right) \\&\quad \sin \left( 2 \pi \left( y + \omega _{_{2}}t \right) \right) \\ v_{_{2}}\left( x,y,t\right)&= \left( \delta {{\mathcal {V}}}_{_0}+a_{_{v}} \sin \left( 2 \pi t \right) \right) \sin \left( 2 \pi \left( x + \omega _{_{1}}t \right) \right) \\&\quad \cos \left( 2 \pi \left( y + \omega _{_{2}}t \right) \right) \end{aligned}, \end{aligned}$$

(50)

where $\bar{{\mathcal {T}}}$, $\bar{{\mathcal {P}}}$, $\delta {{\mathcal {T}}}_{_0}$, $\delta {{\mathcal {P}}}_{_0}$, $\delta {{\mathcal {V}}}_{_0}$, $a_{_{T}}$, $a_{_{P}}$, $a_{_{v}}$, $\omega _{_{1}}$, and $\omega _{_{2}}$ are given constants. This solution corresponds to translating (with velocity ${\mathbf{w }}=\left( \omega _{_{1}}, \omega _{_{2}}\right)$) and oscillating (with amplitudes $a_{_{T}}$, $a_{_{P}}$, and $a_{_{v}}$) waves. Snapshots of the solution for $t=0.13$ are shown in Fig. 2 for two mesh resolutions.

For testing and convergence measurements, we used the $\gamma$-gas law EoS, Sect. 2.3.3, with constant viscosity and thermal conductivity. Parameters of the test problem are summarized in Table 1. To generate the solution (50), the source terms⁸ are added to the r.h.s. of (1). The computational domain was set as described in [42] to produce non-uniform meshes, as shown in Fig. 2. Dirichlet boundary conditions are applied for all flow variables at all domain boundaries.

Fig. 3

Space convergence for different reconstruction ${\mathrm{rDG}_{{P_{_{n}}P_{_{m}}}}}$ space discretization schemes. Solution with the $\hbox {ESDIRK}_5$ time discretization, at $t=0.02$. ${\mathfrak L}_{_1}$-norms of errors versus the total number of the solved-for DoFs per variable

The computational results for mesh convergence in space are summarized in Fig. 3, measuring the ${\mathfrak L}_1$-norms of error for temperature and velocity magnitude using the $\left( P \mathbf{v} T\right)$-formulation with very small time steps and the fifth-order accurate $\hbox {ESDIRK}_5$ scheme, to minimize contributions from time discretization errors, as we are interested in the spatial convergence. As one can clearly see, we obtained nearly theoretical convergence rates for both the Navier–Stokes (NS) and the Euler formulations, for all tested reconstruction schemes, up to the seventh order. As one can also see from Fig. 2, the high-order ${\mathrm{rDG}_{{P_{_{n}}P_{_{m}}}}}$ is capable of resolving/capturing subcell-size vortical structures with very high accuracy.

It is also instructive to note the benefits of the reconstruction. In particular, for the same total number of the solved-for DoFs, the fourth-order-accurate ${\mathrm{rDG}_{{P_{_{1}}P_{_{3}}}}}$ (three solved-for plus seven reconstructed DoFs) results in a slightly more accurate solution than the fourth-order-accurate ${\mathrm{rDG}_{{P_{_{2}}P_{_{3}}}}}$ (six solved-for plus four reconstructed DoFs) scheme.⁹ More on the advantages of the reconstruction for implicit solvers (the bandwidth of the Jacobian matrices and the total size of the solution vectors) can be found in [26, 42].

4.2 Nearly incompressible backward-facing step

In our second numerical example, we demonstrate how the method performs in the limit of vanishing Mach numbers, by simulating incompressible-flow separation in a channel with a backward-facing step. As a benchmark, we use numerical results from [58], which were obtained with the third-order accurate in-space and the second-order accurate in-time Crank–Nicholson incompressible finite-difference method. In addition, the data from [57] will be used to compare with experiments for the reattachment length.

We consider a laminar flow of compressible fluid in the channel with a step $H=1$ and an expansion ratio $\mathrm{ER}=1.5$, defined as $\mathrm{ER}=\frac{R_{_\mathrm{h}}+H}{H}$, where $R_{_\mathrm{h}}$ is a hydraulic radius.¹⁰ At the beginning of the simulation, the fluid is motionless, with an initial temperature $\hat{T}=0$. At the inlet, the following pulsating parabolic velocity profile is enforced:

$$\begin{aligned}&\hat{{\mathbf{v }}}^\mathrm{(inlet)} \left( \hat{x}, \hat{y}, \hat{t}\right) \nonumber \\&\quad = 4\left( 1+{{\mathcal {A}}}_\mathrm{p} \sin \left( \pi \frac{\hat{t}}{\tau _\mathrm{p}}\right) \right) \frac{\hat{y} L}{ R_\mathrm{h}} \left( 1- \frac{\hat{y} L}{ R_\mathrm{h}}\right) , \end{aligned}$$

(51)

where ${{\mathcal {A}}}_\mathrm{p}$ and $\tau _\mathrm{p}$ are the amplitude and the period of a pulse, respectively. For most of the simulations, we use ${{\mathcal {A}}}_\mathrm{p}=0$. The pressure is fixed at the outlet. The lower wall is heated, by ramping its temperature to $\hat{T}=1$. All remaining walls of the channel are kept adiabatic. The computational domain was set with a length of 10 step heights upstream of the step and a length of 50 downstream thereof. The mesh was uniform, with 17,000 elements in total, which is substantially finer than the mesh of $\approx 2000$ elements used in the reference solution by [58]. The Reynolds number based on the step height $\mathrm{Re}_{_{H}}$ is varied from 2 to 500. The Prandtl number was fixed at $\mathrm{Pr}=0.7$. To approximate incompressible-fluid behavior, we set a very high speed of sound for the EoS from Sect. 2.3.1, varying $\bar{c}_{_\mathrm{s}}$ in the range from 10 to $10^7$, which corresponds to a peak Mach number ($\bar{M}=\frac{\bar{v}}{\bar{c}_{_\mathrm{s}}}$) in the range from $\bar{M}=0.1$ to $10^{{-7}}$. Most of the simulations shown here are performed using the $\left( P \mathbf{v} T\right)$-formulation, with $\bar{c}_{_\mathrm{s}}=10^4$ and setting ${\mathrm{AUSM}}^{+}$-up’s cut-off Mach number in (34) to $M_{_\mathrm{co}}=10^{-4}$. For space discretization, we used the fourth- and the fifth-order-accurate ${\mathrm{rDG}_{{P_{_{2}}P_{_{3}}}}}$ and ${\mathrm{rDG}_{{P_{_{2}}P_{_{4}}}}}$ space discretization schemes, which were combined with the second-order-accurate $\hbox {BDF}_2$ time discretization scheme. All simulations were started with small time steps, which is required to resolve the initial pressure wave dynamics. Then, the time steps were smoothly increased as the flow develops, since we are looking for steady-state solutions. At the end of the simulations, the time step¹¹ corresponded to $\mathrm{CFL}_{_\mathrm{aco}}>\left( 10^{5}\ldots 10^7 \right)$ (depending on $\bar{c}_s$) and $\mathrm{CFL}_{_\mathrm{mat}}\sim 384$, i.e., we were stepping over both acoustic and material timescales, which is allowable with our fully implicit method.

Fig. 4

Dynamics of the velocity magnitude field and streamlines for the nearly incompressible ($\bar{M}=10^{-4}$) backward-facing step problem with $\mathrm{Re}_{_{H}}=500$, $\mathrm{Pr}=0.7$, and $\mathrm{ER}=1.5$. Solution using the ${\mathrm{rDG}_{{P_{_{2}}P_{_{3}}}}}$ and $\hbox {BDF}_2$ schemes on a mesh with 17,000 elements

Fig. 5

Steady-state temperature (top) and velocity/streamlines (bottom) fields, for the nearly incompressible ($\bar{M}=10^{^{-4}}$) backward-facing step problem with $\mathrm{Pr}=0.7$ and $\mathrm{ER}=1.5$. Solution using the ${\mathrm{rDG}_{{P_{_{2}}P_{_{3}}}}}$ and the $\hbox {BDF}_2$ schemes on a mesh with 17,000 elements

Fig. 6

Influence of Reynolds number on the local heat transfer coefficient and the position of the reattachment point. ${\mathrm{ER}}=1.5$, $\mathrm{Pr}=0.7$, $\bar{M}=10^{-4}$

Fig. 7

Variation of the reattachment length with the Reynolds number for different values of expansion ratios. Comparison with the experimental data by Armaly et al. [57]. Steady-state solutions using $\bar{M}=10^{-4}$ and the ${\mathrm{rDG}_{{P_{_{2}}P_{_{4}}}}}$ and the $\hbox {BDF}_2$ schemes on a mesh with 17,000 elements

It is instructive to note that setting boundary conditions with the $\left( P \mathbf{v} T\right)$-formulation was rather straightforward. At solid walls and inlet, we applied a Dirichlet condition for velocity components and either the Dirichlet or the Neumann (heat flux) boundary conditions for temperature, which is easy, since these are the variables we are solving for in the $\left( P \mathbf{v} T\right)$-formulation. No pressure boundary condition is applied, to avoid over-specification. At the exit, we applied the Dirichlet BC for pressure, the Neumann (zero-flux) BC for temperature, and no velocity BC is needed. Setting similar boundary conditions using non-primitive-variable formulations (like the conservative-variable $\left( \rho \mathbf{m} E\right)$-formulation) is complicated and would require additional nonlinear solvers to enforce the desired BC states.

Computational results are presented in Figs. 4, 5, and 6. The flow quickly separates right after the step. At relatively high Reynolds numbers, there are numerous eddies that are evolved in time and pushed away with the flow (Fig. 4). At steady state, only one vortex right after the step exists, with the flow separation point moving further away from the step as the Reynolds number is increased (Fig. 5).

The steady-state Nusselt number distribution along the heated wall is plotted in Fig. 6. As one can see, the peak value of the heat transfer coefficient is consistently located right after the reattachment point, which is an expected result. It is worth pointing out that in the lower-resolution results by [58], only the $\mathrm{Re}_H=500$ case exhibited this behavior. We believe this is either because of the insufficient resolution ([58] used a coarser mesh and a lower-order accurate discretization) or because the true steady states were not achieved. Our simulations indicate that until the true steady state is attained, the peak Nusselt number might oscillate around the flow reattachment point.

Fig. 8

Steady-state Mach number and streamline fields for different $\bar{M}$ numbers (0.1, $10^{-3}$ and $10^{-6}$). Solutions using the $\left( P \mathbf{v} T\right)$-formulation with the ${\mathrm{rDG}_{{P_{_{2}}P_{_{4}}}}}$, for $\mathrm{Re}_H=600$ and $\mathrm{ER}=\frac{1}{2}$

Fig. 9

Dynamics of the velocity magnitude and streamlines for one period of the pulsating-flow example. Simulation with the $\left( P \mathbf{v} T\right)$-formulation, using the ${\mathrm{rDG}_{{P_{_{2}}P_{_{4}}}}}$ and the $\hbox {ESDIRK}_5$ schemes, advancing with the time step of $\Delta \hat{t}=10$. $\bar{M}=10^{-3}$, ${{\mathcal {A}}}_\mathrm{p}=\frac{9}{10}$, $\tau _\mathrm{p}=10^2$, and $\mathrm{Re}_H=600$

Fig. 10

Convergence of the nonlinear solver in the limit of vanishing Mach numbers, for different solution vector formulations, $\left( P \mathbf{v} T\right)$ or $\left( \rho \mathbf{v} T\right)$, and ${\mathrm{AUSM}}^{+}$-up solver, basic or all-speed. Relative error at ath iteration is defined as . Convergence is shown for five time steps $\Delta \hat{t}=10$, using the ${\mathrm{rDG}_{{P_{_{2}}P_{_{4}}}}}$ and the $\hbox {BDF}_2$ schemes. ${{\mathcal {A}}}_\mathrm{p}=\frac{9}{10}$, $\tau _\mathrm{p}=10^2$, and $\mathrm{Re}_H=600$

In Fig. 7, we show the dependence of the reattachment length on Reynolds number and compare with the experimental data from [57]. Note that the Reynolds number is based on the hydraulic diameter $D_\mathrm{h}=2 R_\mathrm{h}$, as this is what has been used in experimental data and other numerical simulations [59, 60]. The results are found to be consistent with other numerical studies, and also in excellent agreement with experiments. Some deviation at the high Reynolds number range is also consistent with findings from [59], and most probably due to the discrepancies in the computational versus experimental setups (geometry, inlet velocity profile, etc.), but not exceeding 15%, which is within the overall accuracy of the experimental data.

Since the problem at hand is nearly incompressible, and the EoS from Sect. 2.3.1 allows us to “dial” the sound speed $\bar{c}_{_\mathrm{s}}$ and corresponding Mach numbers $\bar{M}=\frac{\bar{v}}{\bar{c}_{_\mathrm{s}}}$, the current approach should be viewed as a method of artificial compressibility [61, 62]. The numerical solutions are insensitive to Mach numbers, as long as $\bar{M} \le 0.1$. This is demonstrated in Fig. 8. Thus, the “dialing-down” of the sound speed should be interpreted as a preconditioning technique, since the governing equations are degenerate at the limit $\bar{M} \rightarrow$ 0, as one can see from the dimensionless momentum equation (8) rewritten as

$$\begin{aligned} \partial _{_{\hat{t}}} \hat{\rho } \hat{{\mathbf{v }}}_{_{{i}}} + \partial _{_{\hat{j}}} \left( \hat{\rho } \hat{{\mathbf{v }}}_{_{{i}}} \hat{{\mathbf{v }}}_{_{{j}}} +\underbrace{\frac{\hat{\rho }}{\bar{M}^{^2}} }_{{\begin{array}{l}{\mathrm{Degenerate}} \\ {\mathrm{at}}~ M\rightarrow 0\end{array}}} - \frac{\hat{\varvec{\tau }}_{_{i,j}}}{\mathrm{Re}} \right) = \left( \hat{\rho }-\hat{\rho }_{_\mathrm{h}}\right) \hat{{\mathbf{g }}}_{_i}, \end{aligned}$$

(52)

where we used (14). The $\sim \frac{1}{\bar{M}^{^2}}$ pressure gradient degeneracy of the compressible formulations is well known and most recently discussed in [18,19,20,21,22]. The hyperbolic flux (Riemann-solver) fixes, like those introduced in these studies, are found effective and necessary to enable simulations with Mach numbers as low as $\bar{M} \approx 10^{-3}$. By combining the high-order rDG spatial discretizations with the primitive-variable $\left( P \mathbf{v} T\right)$-formulation described in Sect. 3.1, we can obtain robust solutions when the Mach numbers are as low as $\bar{M}=10^{-7}$. Note that as shown in [22, 63], condition numbers of the unpreconditioned Jacobian matrix at this limit are incredibly large, which might make the linear algebra unsolvable.

To demonstrate performance/conditioning of the underlying linear algebra for different choices of the solved-for variables and the Riemann solvers, we use the pulsating-flow example, by setting the period of the inlet velocity oscillation to $\tau _\mathrm{p}=100$ and varying the amplitude ${{\mathcal {A}}}_\mathrm{p}$ in (51). This test problem is similar to what is used in [60]. We start from the pre-computed steady-state solutions. At time zero, a slow-transient sinusoidal pulse of the inlet velocity is applied. Snapshots of the velocity field and streamlines for ${{\mathcal {A}}}_\mathrm{p}=\frac{9}{10}$ are shown in Fig. 9. To solve the nonlinear systems arising from our space–time discretization, we applied the inexact Newton method [51], solved with the linesearch algorithm based on the polynomial secant minimization, as implemented in PETSc [64]. The Jacobian matrix is evaluated with finite differencing, at the beginning of the transient, and fixed during the testing. To avoid the ambiguity associated with iterative preconditioning of the GMRES, for these tests, we are using the direct solver (SuperLU-DIST) as a preconditioner for Krylov iterations. The nonlinear iteration tolerance is set to $\mathrm{tol}_{_\mathrm{N}}=10^{-5}$. At the first Newton iteration, linear tolerance is set to $10^{-4}$, tightening with the following nonlinear iterations, as discussed in [51]. Simulations are performed with time step $\Delta \hat{t}=10$, chosen to resolve the pulse in the inlet velocity, resulting in the material $\mathrm{CFL}_{_\mathrm{mat}}=384$, the acoustic $\mathrm{CFL}_{_\mathrm{aco}}$ up to $10^8$, and the viscous/thermal Fourier numbers¹²$\mathrm{Fo}_{_{\mu }}=25$ and $\mathrm{Fo}_{_{\kappa }}=35$, respectively, for the chosen mesh resolution.

As shown in Fig. 10, the nonlinear solver converged typically within 3–5 iterations. When using the all-speed ${\mathrm{AUSM}}^{+}$-up combined with the $\left( P \mathbf{v} T\right)$-formulation, we can reliably converge for Mach numbers as low as $\bar{M}=10^{-7}$. While the number of linear iterations does steadily increase with the reduction in the Mach number, both the linear solver and the Newton method do reliably converge to the chosen set of tolerances. Without the all-speed modification (i.e., with the basic ${\mathrm{AUSM}}^{+}$-up), the linear solver fails when the $\bar{M}$ number is below $10^{-4}$.

Table 2 On the low-Mach number limits of the pseudo-compressible method with different numerical discretization schemes, for the pulsating-flow backward-facing step example

To show the importance of the chosen set of solution variables, we performed similar simulations with the $\left( \rho \mathbf{v} T\right)$-formulation. It is well recognized that using density as a primary solution unknown leads to more ill-conditioned Jacobian matrices at the limit of vanishing Mach numbers [65], as the density is nearly constant. This is confirmed by our numerical analysis. As one can see from Fig. 10, the method converges well for Mach numbers $10^{-2}$ and higher. At lower Mach numbers, the linear solver failed to converge. We stop linear iterations when the count of Krylov iterations exceeds 150, even if the specified linear tolerance is not attained, proceeding to the next Newton iteration.¹³ For this test problem, with $\bar{M}=10^{-3}$, we are still able to converge nonlinear iterations, but at significant computational cost. With even lower Mach numbers, the nonlinear iterations also fail.

Finally, we summarize the observable limits of the lowest Mach numbers that allowed convergent Newton–Krylov solution procedures in Table 2 for several tested solution variable formulations and approximate Riemann solvers. The all-speed ${\mathrm{AUSM}}^{+}$-up with the $\left( P \mathbf{v} T\right)$-formulation is clearly the most effective algorithm and is recommended when such a low Mach number is dictated by the real material equation of state and flow configuration. This will be demonstrated in our next numerical example.

4.3 Unstably stratified flows of supercritical water in heated horizontal channels

In the third numerical test, we demonstrate the performance of our solver for variable-density nearly incompressible flow of supercritical water in a channel. These simulations are very difficult, since the fluid density is a strong function of temperature, varying almost threefold in the temperature range of interest (from $\sim 660$ to 710 K), which means that the compressibility of the fluid cannot be ignored. Moreover, all other thermodynamic and transport properties (heat capacity, sound speed, viscosity, and thermal conductivity) are also strongly temperature dependent (Fig. 1), necessitating a tight tolerance of the nonlinear solver to properly resolve all the physics in the limit of very low Mach numbers. We utilize the IAPWS-IF97 equation of state, implemented as described in Sect. 2.3.2 and Appendix. No approximations/simplifications in the governing equations are made, keeping the formulation fully compressible. Preconditioning by artificially “dialing-down” speed of sound is not possible. To our knowledge, these are first-of-a-kind attempts to numerically simulate mixed convection of fully compressible supercritical fluids in channels.

The problem is formulated as follows. We consider a two-dimensional channel 1 cm wide and 20 cm long. Water in a supercritical state ($P=25\,\hbox {MPa}$, $T=660\,\hbox {K}$) enters the channel with a speed of about 6.7 mm/s, corresponding to $\mathrm{Re}=500$. The first 12 cm of the channel is heated from below (by setting the bottom wall temperature at $T_{_\mathrm{bot}}=710\,\hbox {K}$) and cooled from above ($T_{_\mathrm{top}}=660\,\hbox {K}$). The last 8 cm of the channel walls are kept adiabatic. The channel is horizontal, with gravity pointing downwards, and the magnitude corresponding to the specified $\mathrm{Ra}$ number varied up to $10^8$. The boundary conditions are: (1) parabolic velocity profile and constant temperature $T_{_\mathrm{inflow}}=660\,\hbox {K}$ at the channel inlet; (2) constant-pressure, Neumann temperature BC at the exit; and (3) no-slip velocity at the channels top and bottom walls. When Dirichlet velocity boundary conditions are applied, no BC for pressure is necessary. Similarly, when Dirichlet BC is applied for pressure, no BC is needed for velocity, to prevent over-specification of the boundary conditions, since the fully compressible method is utilized. Initial conditions were constant temperature $T_{_\mathrm{init}}=660\,\hbox {K}$, parabolic velocity profile, and linear axial pressure gradient, corresponding to the incompressible-fluid analytical solution for channel flows. We have numerically verified that this solution is maintained for isothermal conditions. (It can also be achieved starting from an initially zero-velocity state.) Simulations were started by smoothly increasing the bottom temperature to the specified value (typically over 100 s of the simulation time). This results in the development of a thermal boundary layer, which, depending on the strength of the gravity, might result in the formation of hydrodynamic instabilities. This disrupts the viscous boundary layer, creating dynamic Rayleigh–Bénard convection loops, which are detached by the action of the forced convection and consequently transported downstream.

Fig. 11

Dynamics of the density field, for a mixed forced/natural convection flow of supercritical water in a heated horizontal channel. $\mathrm{Re}=500$, $\mathrm{Ra}=10^8$

Fig. 12

Snapshot of velocity, temperature, Mach number, and pressure function distributions, for a mixed forced/natural convection flow of supercritical water in a heated horizontal channel, at $t=61\,\hbox {s}$. $\mathrm{Re}=500$, $\mathrm{Ra}=10^8$

Fig. 13

The effect of gravity ($\mathrm{Ra}$ number) on flow pattern and stability of the boundary layer

The simulations are performed using the fourth-order-accurate ${\mathrm{rDG}_{{P_{_{1}}P_{_{3}}}}}$ space discretization scheme and the third-order-accurate $\hbox {ESDIRK}_3$ time discretization scheme. The mesh consists of approximately 70,000 elements, partitioned on 288 cores, with a finer mesh near the horizontal walls to more accurately resolve temperature gradients due to the heating/cooling. The time step was varied to resolve dynamic timescales associated with the evolution of eddies formed due to unstable thermal stratification. The peak CFL and Fourier numbers were at the range of $\mathrm{CFL}_{_\mathrm{aco}}=2 \times 10^7$, $\mathrm{CFL}_{_\mathrm{mat}}=200$, $\mathrm{Fo}_{_{\mu }}=1000$, and $\mathrm{Fo}_{_{\kappa }}=500$. Since the method is unconditionally stable, the time step size is dictated by the accuracy requirement rather than by the stability restrictions. The problem is solved to the nonlinear tolerance $\mathrm{tol}_{_\mathrm{N}}=10^{-6}$, which typically converged within five to eight Newton iterations.

Computational results are presented in Figs. 11, 12, and 13. Typical unstably stratified flow pattern development is shown in Fig. 11, depicting the density field at a very high Rayleigh number of $10^8$. As one can see, the thermal boundary layer quickly becomes unstable, forming numerous small-scale plumes about 1 cm downstream of the inlet, which are transported by the flow downstream. The top boundary layer is stably stratified. The plumes tend to merge and grow in size, breaching the core of the channel flow roughly 5 cm downstream of the inlet. We would like to note the significant density variations, which are almost a threefold change in magnitude. At this high Rayleigh number, the flow pattern becomes chaotic, corresponding to transition from soft to hard turbulence.

As one can see from Fig. 12, the Mach number is very low, $\bar{M}<10^{-4}$, which makes the problem extremely hard to solve. The use of the low-Mach modification for the ${\mathrm{AUSM}}^{+}$-up scheme and solving in $\left( P \mathbf{v} T\right)$-form were essential. Without the low-Mach modification, the linear and nonlinear solvers failed to converge. The use of the $\left( \rho \mathbf{v} T\right)$ formulation also resulted in non-converged solutions, due to very tight pressure-density coupling and ill-conditioned Jacobian matrices.

Finally, we show the effect of the Rayleigh number in Fig. 13. It can be seen that lowering the $\mathrm{Ra}$ number increases the boundary layer development length. In fact, for our heating length of only 12 diameters, the instability does not occur below $\mathrm{Ra}=5 \times 10^6$. Moreover, there is a clear tendency of the reduction in the resolved vortex length scales with larger gravity effects.

Fig. 14

Formulation of the stationary laser spot welding problem. Samples of the meshes and domain partitioning. Top: laser power distribution for $Q_{_\mathrm{L}}=1200\,\hbox {W}$. Bottom-left: the base (thick lines) and the coarsest-used (thin lines) meshes (${{\mathcal {R}}}1$ and ${{\mathcal {R}}}4$); bottom-right: domain partitioning (572 cores) for the finest-used mesh ${{\mathcal {R}}}32$. Isolines of the solidus temperature are shown for the cases of $Q_{_\mathrm{L}}=4000\,\hbox {W}$ (in red) and $Q_{_\mathrm{L}}=1200\,\hbox {W}$ (in black), at the simulation time of $t=2\,\hbox {s}$

4.4 Laser melting physics

In our next two examples, we demonstrate the method’s ability to solve phase change problems in applications related to direct energy heating. First, we show an example of stationary laser spot welding, Sect. 4.4.1, followed by the selective laser melting related to the powder bed fusion (PBF) processes in 3D additive manufacturing [66], Sect. 4.4.2. In addition to stiff acoustic waves due to the extremely low compressibility of metals, the applications of interest require the incorporation of Marangoni convection, making the coupling of velocity and temperature fields very tight, which is very difficult to resolve with conventional CFD methods.

We use the homogeneous equilibrium phase change model to represent melting/solidification, as described in [26, 42]. The approach incorporates latent heat into the equation of state’s ${\mathfrak {u}}\left( T\right)$ relationship, with two distinct melting temperatures (liquidus and solidus, $T_{_\mathrm{L}}$ and $T_{_\mathrm{S}}$); and introduces a “mushy” zone, enforcing “no-velocity” conditions when transitioning from the liquid to the solid states. We use a combination of (a) the Darcy-law-like interfacial drag force model, to mimic the processes of dendritic structure formation, and (b) the variable viscosity model, which significantly enhances viscous stresses in the material’s solid state to inhibit its motion. The approach originates from the work by Voller and Prakash [67], which has been evolved into more sophisticated formulations, like those described in [68]. Our approach differs from the previous work in that we use the method of artificial compressibility [1] with high-order space–time discretization, enabling very accurate resolution of melt pool dynamics within a tightly coupled Newton–Krylov iterative procedure.

Table 3 Parameters and physical constants for laser melting physics examples

The metals are treated as compressible materials, with the equation of state described in Sect. 2.3.1 and a very high sound speed to represent nearly incompressible material states of metallic alloys. All simulations shown here are done with the $\left( P \mathbf{v} T\right)$-formulation. The all-speed ${\mathrm{AUSM}}^{+}$-up scheme is essential to accurately resolve pressure gradients at the limit of vanishing Mach numbers. This is in contrast to incompressible formulations, based on Picard-iteration, SIMPLE-family implicit solvers used in [67,68,69,70]. Our long-term goal is to enable a seamless simulation of both laser-induced rapid melt pool formation and dynamics with all the relevant physics included (metal evaporation, recoil pressure effects, and inert gas convection above the free surface), which we believe can only be done in a fully compressible computational modeling framework.

4.4.1 Stationary laser spot welding

This numerical example is taken from the work by Ehlen et al. [68], who studied the melt pool shapes formed during laser spot welding. The simulations are performed on a two-dimensional $\left( r, z\right)$ axisymmetrical computational domain as shown in Fig. 14. The domain is $\left( 20 \times 16\right) \,\hbox {mm}$ in size. The free surface is assumed to be flat (interface dynamics is currently ignored), and the convection of the inert gas above the surface is not directly modeled.¹⁴ The effective radius of the Gaussian-shaped laser source was $R_{_\mathrm{laser}}=4\,\hbox {mm}$. The total power of the laser $Q_{_\mathrm{L}}$ is deposited at the free surface as

$$\begin{aligned}&q_{_\mathrm{laser}}\left( r\right) = q_{_\mathrm{max}} \exp \left( -2 \frac{r^2}{R^2_{_\mathrm{laser}}}\right) ,\nonumber \\&\quad \text{ where }~ q_{_\mathrm{max}} = Q_{_\mathrm{L}} \frac{\left( 1+\coth \frac{R^2_{_{D}}}{R^2_{_\mathrm{laser}}}\right) }{\pi R^2_{_{D}}}, \end{aligned}$$

(53)

and $R_{_{D}}$ is the radial size of the computational domain. At the top (free) surface, we applied nonlinear heat flux boundary conditions for the energy equation, combining the laser energy deposition with losses due to thermal radiation, convection-to-air, and evaporative cooling:

$$\begin{aligned} q_{_\mathrm{fs}} \left( r, t, T \right)= & {} q_{_\mathrm{laser}} -\underbrace{q_{_\mathrm{radiation}}}_{\varepsilon _{_\mathrm{b}} \sigma _{_\mathrm{b}} \left( T^4-T_{_\mathrm{a}}^4\right) } -\underbrace{q_{_\mathrm{convection}}}_{\alpha _{_\mathrm{conv}} \left( T-T_{_\mathrm{a}}\right) } \nonumber \\&-\underbrace{q_{_\mathrm{evaporation}}}_{\Delta H_{_\mathrm{v}} J_{_\mathrm{v}} f\left( T\right) }, \end{aligned}$$

(54)

where

$$\begin{aligned} \begin{aligned}&J_{_\mathrm{v}}=0.82 {{\mathcal {A}}} \frac{ {{\mathcal {P}}}\left( T\right) }{\sqrt{2 \pi {{\mathcal {M}}} R T}},\\&{{\mathcal {P}}}\left( T\right) = 0.54 P_{_\mathrm{a}} \exp \left[ \frac{-\lambda _{_{\mathrm{e}}}}{K_{_\mathrm{B}}} \left( \frac{1}{T}-\frac{1}{T_{_\mathrm{b}}}\right) \right] ,\\&\quad \text{ and }~~~ f\left( T\right) = \left\{ \begin{array}{ll} 0 &{}\quad \text{ if }~T<T_{_\mathrm{b}} \\ 1 &{}\quad \text{ if }~T>T_{_\mathrm{b}}+\delta T_{_\mathrm{b}} \\ \frac{1}{2} \left[ 1-\cos \left( \frac{T-T_{_\mathrm{b}}}{\delta T_{_\mathrm{b}}} \pi \right) \right] &{}\quad \text{ otherwise } \end{array}\right. . \end{aligned} \end{aligned}$$

(55)

All parameters of the models used here are summarized in Table 3.

The following traction (Marangoni-driven) boundary condition is applied for the momentum equations:

$$\begin{aligned} \tau _{_{rz, {\mathrm{Mara}}}}^\mathrm{BC} \left( r, t, \mathbf{v}, T \right) = \mu _{_\mathrm{m}} \frac{\partial v_r}{\partial z} = \frac{\partial \sigma }{\partial T} \frac{\partial T}{\partial r} + \sum \limits _i \frac{\partial \sigma }{\partial {\textsf {a}}_{_i}} \frac{\partial {\textsf {a}}_{_i}}{\partial r},\nonumber \\ \end{aligned}$$

(56)

where $\tau _{_{rz, \mathrm Mara}}^\mathrm{BC}$ is a free-surface shear stress enforced as (traction) nonlinear boundary conditions, implemented at the spatial discretization order consistent with the chosen ${\mathrm{rDG}_{{P_{_{n}}P_{_{m}}}}}$ scheme; $\mu _{_\mathrm{m}}$ is the dynamic viscosity of the metallic alloy; $\sigma$ denotes the surface tension, while ${\textsf {a}}_{_i}$ refers to the thermodynamic activity of the ith alloy component. Following [68], we ignore solutal contributions to the surface traction forces (56) by setting $\frac{\partial \sigma }{\partial {\textsf {a}}_{_i}}=0$. However, the impurities are still accounted for by the thermal Marangoni coefficient, as defined by Sahoo et al. [71],

$$\begin{aligned}&\frac{\partial \sigma }{\partial T} \left( T, {\textsf {a}}_{_\mathrm{s}}\right) \nonumber \\&\quad = \left. \frac{\partial \sigma }{\partial T}\right| _{{\textsf {a}}_{_\mathrm{s}}=0}+ \frac{\Delta H_{_0} \varGamma _{_\mathrm{s}}}{T} \frac{K_{_\mathrm{seg}}}{1+K_{_\mathrm{seg}}}-\varGamma _{_\mathrm{s}} R \ln \left( 1+K_{_\mathrm{seg}}\right) \nonumber \\\\&\qquad \text{ and }~~~K_{_\mathrm{seg}}= \kappa _e {\textsf {a}}_{_\mathrm{s}} \exp \left( \frac{\Delta H_{_0}}{RT}\right) ,\nonumber \end{aligned}$$

(57)

where ${\textsf {a}}_{_\mathrm{s}}$ is the (variable) sulfur activity (in wt%). All model parameters are defined in Table 3. As shown in Fig. 15, by adding ${\textsf {a}}_{_\mathrm{s}}$, the sign of the Marangoni coefficient is reversed at the so-called critical temperature, causing the “reverse Marangoni” effects and very interesting fluid dynamics/hydrodynamic instabilities.

First, we performed simulations on a sequence of meshes, labeled as ${{\mathcal {R}}}1$ to ${{\mathcal {R}}}32$, with the finest corresponding to approximately 230,000 elements.¹⁵ Figure 14 shows a comparison of the base mesh (${{\mathcal {R}}}1$) and one of the refined meshes (${{\mathcal {R}}}4$). The figure also shows the boundary of the melt pool, which is uniformly refined. The governing equations (1) are modified to account for axisymmetry by using a conservative cylindrical approach “$\left( r^{\alpha } \mathbf{U}\right)$,” as described in [72].

Fig. 15

Dependence of the Marangoni coefficient on sulfur activity

The governing equations (1) are cast in the dimensionless form (8) and (11), choosing as a length scale the laser’s effective radius, $L=R_{_\mathrm{laser}}$, and using the following thermocapillary-based velocity scale:

$$\begin{aligned} \bar{v}= \mathrm{Fr} \cdot \sqrt{\left| f\right| _{_\mathrm{Ma}} L}, ~~~\text{ and }~~~ \left| f\right| _{_\mathrm{Ma}}=\left| \left. \frac{\partial \sigma }{\partial T}\right| _{{\textsf {a}}_{_\mathrm{s}}=0} \right| \frac{\Delta T_{_\mathrm{g}} \bar{\mathrm{Pr}}}{\bar{\rho } L^2}. \end{aligned}$$

(58)

The rest of the scaling parameters (5) are $\bar{\rho }=\rho _{_\mathrm{m}}$, $\bar{\mu }=\mu _{_\mathrm{m,l}}$, $\bar{\kappa }=\kappa _{_\mathrm{m}}$, $P_{_\mathrm{R}}=0$, $T_{_\mathrm{R}}=T_{_\mathrm{S}}$, $\bar{T}=\Delta T_{_\mathrm{g}}=T_{_\mathrm{b}}-T_{_\mathrm{S}}$, ${\mathfrak {u}}_{_\mathrm{R}}=0$, $\bar{C}_{_P}=C_{_{p_\mathrm{m}}}$, and $\bar{\beta }=\beta _{_\mathrm{m}}$. The Marangoni number is related to the Reynolds number as

$$\begin{aligned} \mathrm{Ma}=\frac{\mathrm{Re}^2}{\mathrm{Fr}^2}, \end{aligned}$$

(59)

where we set the Froude number to $\mathrm{Fr}=1$. The dimensionless numbers are summarized in Table 4. The sound speed in the EoS (14) was set to $\bar{c}_{_\mathrm{s}}=\bar{v}\times 10^4$, which results in a peak of Mach number well below $10^{-2}$, approximating the nearly incompressible behavior of metallic alloys.

Table 4 Dimensionless numbers for the stationary laser spot welding (LSW, Sect. 4.4.1) and the selected laser melting (SLM, Sect. 4.4.2)

Fig. 16

Snapshots of temperature (left), velocity (right), and melting front for selected time frames of 2D axisymmetric laser spot welding with the laser power $Q_{_\mathrm{L}}=1.2\,\hbox {kW}$. Example of the “V”-shape melt pool (with stable melt pool dynamics)

Fig. 17

Snapshots of temperature (left), velocity (right), and melting front for selected time frames of 2D axisymmetric laser spot welding with the laser power $Q_{_\mathrm{L}}=2\,\hbox {kW}$. Example of the “W”-shape melt pool (melt pool dynamics with hydrodynamic instabilities due to reverse Marangoni convection). Isolines corresponding to the critical temperature are shown in white

Fig. 18

Snapshots of temperature (left), velocity (right), and melting front for selected time frames of 2D axisymmetric laser spot welding with the laser power $Q_{_\mathrm{L}}=4\,\hbox {kW}$. Example of the “W”-shape melt pool (melt pool dynamics with boiling and hydrodynamic instabilities due to reverse Marangoni convection). Isolines corresponding to the critical temperature are shown in white

Computational results obtained with ${\mathrm{rDG}_{{P_{_{2}}P_{_{3}}}}}$ and $\hbox {BDF}_2$ discretizations on mesh ${{\mathcal {R}}}10$ are shown in Figs. 16, 17, and 18. For all computations, the tolerance of the Newton iterations was set to $10^{-7}$, converging on average with 7 to 10 nonlinear iterations and less than 25 Krylov iterations per linear step. The simulation’s time step was set to resolve material velocity scales ($\mathrm{CFL}_{_\mathrm{mat}}=1$), stepping over acoustic and viscous stress timescales. The sulfur activity was set to ${\textsf {a}}_{_\mathrm{s}}=1.4 \times 10^{-2}\,\hbox {wt}\%$.

More in-depth discussion of these simulations will be presented elsewhere. Here, we place the focus on the robustness and accuracy of our algorithm, and its ability to capture hydrodynamic instabilities in numerically very stiff modeling framework.

By increasing the power of the laser, the free-surface temperature of the melt pool becomes hotter. For relatively low laser power, $Q_{_\mathrm{L}}=1.2$ kW in Fig. 16, the melt pool resembles the “V”-shape [68]. The critical temperature is reached at the center of the melt pool, forming a very small clockwise rotating vortex near the axisymmetry boundary. The rest of the melt pool moves in the counterclockwise direction, driven by thermocapillary forces pointing to the center of the melt pool.

Flow dynamics become even more interesting when the power of the laser was increased to 2 kW, shown in Fig. 17. In this case, the central clockwise rotating vortex is comparable with the outer counterclockwise rotating one. The two eddies are separated by the reversed traction spot, corresponding to the critical temperature at the surface. The plume of the liquid metal is hydrodynamically unstable. At the beginning of the melt pool formation, the shape resembles a “W”, consistent with what is reported in [68]. It is instructive to note that in order to capture hydrodynamic instabilities with the second-order ${\mathrm{rDG}_{{P_{_{0}}P_{_{1}}}}}$ scheme, one needs a very fine mesh (${{\mathcal {R}}}32$ and higher). With the fourth-order ${\mathrm{rDG}_{{P_{_{1}}P_{_{3}}}}}$ and ${\mathrm{rDG}_{{P_{_{2}}P_{_{3}}}}}$ schemes, adequate hydrodynamically unstable solutions are obtained on the coarsest mesh ${{\mathcal {R}}}4$ (3600 elements in total), which clearly indicates the advantages of using high-order-accurate schemes for these types of applications.

At the highest laser power of 4 kW, shown in Fig. 18, the surface reaches the boiling temperature. Even though we are ignoring mass transfer due to the evaporation of metal, the cooling effects are effectively represented by (55), which adds a very stiff nonlinear boundary condition to the energy equation. The condition numbers of the underlying linear algebra are extremely high. Nevertheless, we are able to obtain converged numerical solutions on very fine meshes. In comparison with similar simulations in [68], which used a fixed-grid uniform-mesh $60 \times 40$ (no mesh refinement was attempted), we can refine the mesh and obtained converged solutions at all investigated laser powers. (In [68], numerical instabilities were reported at the transitional-to-“W”-shape laser powers of $Q_{_\mathrm{L}}=1.5\,\hbox {kW}$.)

A three-dimensional example with the ${\mathrm{rDG}_{{P_{_{0}}P_{_{1}}}}}$ is shown in Fig. 19. In this simulation, the melt pool dynamics is driven by gravity forces only, as we ignored Marangoni convection. In this case, the melt pool formed is close to the hemispherical shape, and the peak velocity is only 1 cm/s. This is dramatically different from the Marangoni-driven convection in Figs. 16, 17, and 18, where the peak velocity at the free surface is near 1 m/s. We found that these gravity-only simulations behave much better numerically, which was evident from the convergence rates for Newton iterations, as well as from the total number of Krylov iterations per Newton iteration. More detailed analysis of the computational results and performance (convergence) of our nonlinear solver will be presented elsewhere.

Fig. 19

Snapshot of the temperature (left slice and top surface), velocity (right slice), and melting front, for 3D stationary spot laser welding. Simulation using ${\mathrm{rDG}_{{P_{_{0}}P_{_{1}}}}}$ and $\hbox {BDF}_2$, on a mesh with 3.7M elements (17M DoFs). The laser’s effective radius is 4 mm, and the effective power $Q_{_\mathrm{L}}$ is 2 kW. Partitioning with 540 cores is also shown (left-bottom). Thermocapillary convection is ignored. The effects of radiative heat transfer and evaporative cooling are accounted for

Fig. 20

Snapshots of the free-surface temperature (in K), melting front, and critical-temperature isolines for selected time frames of the laser-induced melting of stainless steel in additive manufacturing applications. The laser spot of $Q_{_\mathrm{L}}=100\,\hbox {W}$ in power and effective radius of $100\,\upmu \hbox {m}$ is moving with 2 m/s over the test section in a “Z”-shape pattern. Test section, computational domain with 3M elements (15M DoFs) and partitioning with 360 cores are shown at the right-bottom

Fig. 21

Snapshots of the free-surface velocity (in m/s), melting front, and critical-temperature isolines for selected time frames of laser-induced melting of stainless steel in additive manufacturing applications. The laser spot is moving with 2 m/s in a “Z”-shape pattern

4.4.2 Selective laser melting

In the next example, we show three-dimensional simulations of a dynamically moving laser spot, which is related to applications in additive manufacturing. Modeling of the free-surface and laser power deposition is similar to the previous example of Sect. 4.4.1. The size and power of the laser are, however, smaller, $R_{_\mathrm{laser}}=100\,\upmu \hbox {m}$ and $Q_{_\mathrm{L}}=100$ W. The computational domain (shown in Fig. 20) has a uniformly refined $\left( 1\times 1\right) \,\hbox {mm}^2$ test section at the center. The laser is moving with the speed of 2 m/s, which is typical for laser configuration in powder bed fusion (PBF). The laser is moving in a “Z”-pattern during the first 2.4 ms and then stops. The dimensionless numbers corresponding to the melt pool convection are considerably smaller than those of the stationary spot welding (LSW) case (shown in Table 3). All material properties were the same as those in Sect. 4.4.1. The sulfur activity was set to ${\textsf {a}}_{_\mathrm{s}}=1.4 \times 10^{-2}\,\hbox {wt}\%$. For all the simulations, we used the second-order accurate ${\mathrm{rDG}_{{P_{_{0}}P_{_{1}}}}}$ space discretization and the $\hbox {BDF}_2$ time discretization with the scalable iterative preconditioner as described in [26].

In difference to the LSW case, the melt pool shape was shallow (Fig. 20) due to relatively short residence time of the material exposure to direct heating. No fully developed flow dynamics pattern is established before the material re-solidified. Nevertheless, the peak surface velocity in the melt pool was even higher, $\approx$1.4 m/s, as compared to $\approx 0.75$ m/s in the LSW case (Fig. 21). This is because the density of the laser energy deposition is higher, and the temperature gradients causing thermocapillary convection are also higher.

We found that our solver converged well and the whole transient was effectively executed in a reasonable time, under 24 hrs of wall-clock time, for the mesh of 3 million degrees of freedom and partitioning with 360 cores. This is in contrast to an explicit time discretization solver [66], which is not scalable and required weeks to a month for similar-resolution simulations. This makes our computational tool useful for practical applications of interest, enabling a sensitivity study on the effects of the laser configuration. We refer to [26, 42] for discussion of the method’s performance. More in-depth discussion of these types of simulations (physics, applications, convergence/accuracy) will be presented elsewhere.

Fig. 22

Sample of the corner-refined mesh (4032 elements) and partitioning with 32 cores

Fig. 23

Dynamics of the Mach field, using $\left( \rho \mathbf{v} \epsilon \right)$-formulation. Solution using ${\mathrm{rDG}_{{P_{_{0}}P_{_{1}}}}}$, ${\mathrm{AUSM}}^{+}$-up, and $\hbox {BDF}_2$, with 260,000 elements, 360 cores, and $\hbox {CFL}=1$

Fig. 24

Mach fields at $\hat{t}=4$, comparing $\left( \rho \mathbf{v} \epsilon \right)$-, $\left( \rho \mathbf{v} T\right)$-, and $\left( P \mathbf{v} T\right)$-formulations. Solutions using ${\mathrm{rDG}_{{P_{_{0}}P_{_{1}}}}}$, ${\mathrm{AUSM}}^{+}$-up, and $\hbox {BDF}_2$, with 260,000 elements, 360 cores, and $\hbox {CFL}=1$

Fig. 25

Snapshot of the pressure (P), density ($\rho$), and entropy production fields ($\epsilon$), for $\hat{t}=4$, using the $\left( \rho \mathbf{v} \epsilon \right)$-formulation. Solution using the ${\mathrm{rDG}_{{P_{_{0}}P_{_{1}}}}}$, the ${\mathrm{AUSM}}^{+}$-up, and the $\hbox {BDF}_2$, with 260,000 elements, 360 cores, and $\hbox {CFL}=1$

4.5 Mach 3 wind tunnel with a step

The final numerical test demonstrates the performance of our fully implicit Newton–Krylov solver for supersonic flow. This is a range of flow conditions typically requiring totally different simulation tools. We will show that our solver works very well for these flow speeds, which is very important when seamless simulations spanning wildly different flow conditions are required.

We will use a canonical example of flow in a wind tunnel with a step, which was originally introduced by Emery [73] in 1968. More recently, Woodward and Colella [74] used this test to evaluate the performance of a number of explicit finite-volume schemes. This benchmark test is particularly interesting because it highlights the algorithm’s ability to capture relatively strong shocks ($M=3$), as well as contact discontinuities with instabilities, and the formation/dynamics of the Mach stem pattern. The problem has a singular point, labeled in Fig. 22, leading to errors in the entropy field downstream of the corner. Here, we will not use any numerical fix, such as the one described in [74]. Instead, we refine the mesh near the corner, as shown in Fig. 22, which is known to reduce these errors.

We have tested three formulations for the solution vector, $\mathbf{V}=\left( P \mathbf{v} T\right)$, $\left( \rho \mathbf{v} T\right)$, and $\left( \rho \mathbf{v} \epsilon \right)$, where $\epsilon$ denotes entropy production. All three formulations work well, with the entropy-production-based approach (Fig. 23) resulting in the least noisy solution and the lowest entropy errors due to the singular point at the corner. Simulations are performed using the second-order in-space ${\mathrm{rDG}_{{P_{_{0}}P_{_{1}}}}}$ scheme with the modified Barth–Jesperson limiting ($\hbox {BJ}_\mathrm{dir}$), which was adapted to our fully implicit Newton-based time discretization, as described in Sect. 3.4. For numerical flux evaluation, we use the ${\mathrm{AUSM}}^{+}$-up scheme. We numerically verified that the shocks are captured within two to three cells, while contact discontinuities are described within four to five cells. Simulations are started with time steps corresponding to $\hbox {CFL}=1$ and slowly increased to $\hbox {CFL}=2$ after $\hat{t}=2$, which corresponds to the time when very slow flow dynamics is established. Both the $\hbox {BDF}_2$ and the $\hbox {ESDIRK}_3$ schemes worked well, with the $\hbox {ESDIRK}_3$ producing sharper solutions under high CFL numbers. Even though the method is unconditionally stable, we limit simulations to $\hbox {CFL}=2$ because we would like to accurately resolve the Kelvin–Helmholtz instability of the contact discontinuity formed at the Mach stem. In addition, we use the element block-diagonal (EBD) preconditioning, which performs best for relatively small CFL numbers, Sect. 3.3.3 [63].

Dynamics of the Mach number field is shown in Fig. 24. All flow features are captured well, consistent with a known solution by other schemes [74]. Comparison of the Mach field for time $\hat{t}=4$ is shown in Fig. 24, using three tested formulations for $\mathbf{V}$. The computed fields are visually indistinguishable. (More detail comparison will be presented elsewhere, showing that the $\left( \rho \mathbf{v} \epsilon \right)$-formulation is slightly better than the other two formulations). Figure 25 presents pressure, density, and entropy production fields, using the $\left( \rho \mathbf{v} \epsilon \right)$-formulation. The Kelvin–Helmholtz instability is visible in both the density and the entropy field. In addition, we would like to point out that for the chosen mesh resolution (corresponding to effectively $\Delta h=\frac{1}{320}$), the entropy errors and related spurious Mach stem are very small and barely distinguishable.

Fig. 26

Zoom-in of the Mach field in the neighborhood of the Mach stem, for $\hat{t}=4$, using the $\left( \rho \mathbf{v} \epsilon \right)$-formulation and two different approximate Riemann solvers. The solutions utilized the ${\mathrm{rDG}_{{P_{_{0}}P_{_{1}}}}}$ and the $\hbox {BDF}_2$, with 260,000 elements, 288 cores, and $\hbox {CFL}=2$

In Fig. 26, we show a comparison of the solutions with two different approximate Riemann solvers, using the $\left( \rho \mathbf{v} \epsilon \right)$-formulation. Our implicit solver works fine with both schemes. However, the ${\mathrm{AUSM}}^{+}$-up results in a less diffusive solution.

Fig. 27

Convergence of the nonlinear solver for different limiters. The relative error $\epsilon _{_{{\mathcal {X}}}}$ is defined in Fig. 10. Five time steps with $\hbox {CFL}=1$ and $\hbox {BDF}_2$. The solutions utilized the $\left( \rho \mathbf{v} \epsilon \right)$-formulation, the all-speed ${\mathrm{AUSM}}^{+}$-up, and the ${\mathrm{rDG}_{{P_{_{0}}P_{_{1}}}}}$, on the mesh with 4000 elements. The nonlinear tolerance was $\mathrm{tol}_{_\mathrm{N}}=10^{-5}$

Finally, in Fig. 27, we demonstrate an example of the solution when the Newton method had difficulty to converge to the prescribed tolerance. In this case, the non-differentiable Barth–Jespersen (BJ) limiter results in a “stalled” solution. This happens when, at certain elements, the states of the limiter become “locked” in a repeated pattern at a sequence of the nonlinear iterations. In Fig. 27, this happened at the last three time steps. There is a very noticeable repeated pattern in the history of the relative error. These stalled states can be broken by “freezing” the limiter, as described in Sect. 3.4 and demonstrated in Fig. 27. It is instructive to note that having non-differentiable limiter does not mean you will always stall. In fact, the same transient with slightly different (but also non-differentiable) limiters does not result in the non-convergent nonlinear solver, as shown in Fig. 27 using the $\hbox {BJ}_\mathrm{dir}$ and the Venka limiters. Our experience shows that freezing the limiter would always result in a good convergence of the Newton method, for all tested non-differentiable limiters.¹⁶

5 Concluding remarks

The main technical contribution of this work is a new treatment of the time discretization operator in the Newton–Krylov Discontinuous Galerkin-based fully implicit numerical method for the modeling of fluid dynamics at all speeds. The approach avoids explicit reconstruction of the degrees of freedom for the conservative vector $\mathbf{U}$ and computation/inversion of the mass matrix. Instead, we are using integration with quadrature rule, computing contributions-to-the-nonlinear-residuals of the time derivatives for an element’s mass, momentum, and energy, evaluated directly from the solved-for vector of unknowns, $\mathbf{V}$. This vector is chosen based on conditioning/solvability of the underlying linear algebra. The choice of the pressure-velocity-temperature works well at all speeds, ranging from the nearly incompressible to supersonic shock dynamics. The low-speed flux modification (here, with the ${\mathrm{AUSM}}^{+}$-up scheme) is found to be essential for flux evaluations at vanishing Mach numbers, allowing us to perform robust simulations of variable-density supercritical water in nuclear reactor safety applications and metallic alloy laser-induced melting/solidification in additive manufacturing, with the peak Mach number as low as $10^{-7}$. The same scheme with minor modifications works for shock dynamics applications, which makes the presented approach very valuable when a seamless all-speed flow capability is necessary.

Another valuable technical contribution is related to the treatment of non-differentiable limiters within Newton–Krylov iterative procedure, which allows a robust convergence of the Newton-based nonlinear solver in the shock dynamics application range. Here, we used the Barth–Jespersen (BJ) limiters, modified to account for spatial directions.

We have demonstrated the robustness and accuracy of the approach using two canonical benchmark problems (a) the backward-facing step in the nearly incompressible regime and (b) the Emery test in the supersonic flow regime; and two examples of very difficult flows with (c) mixed convection of the fully compressible low-Mach variable-density supercritical water in a channel, and (d) laser-induced phase change in metallic alloys. The two latter examples feature very interesting hydrodynamic instabilities, demonstrating the advantages of using high-order space-time discretization incorporated in a robust and efficient fully implicit computational framework.

Appendix: IAPWS-IF97

To represent water in a supercritical thermodynamic state, we use the “International Association for the Properties of Water and Steam, Industrial Formulation 1997” (IAPWS-IF97) [31]. Above the fluid’s critical point, i.e.,

$$\begin{aligned} \left[ \begin{array}{cll} P &{}\ge &{} P_{_\mathrm{c}}=22.064~\mathrm{MPa} \\ T &{}\ge &{} T_{_\mathrm{c}}=647.096~\mathrm{K} \\ &{}&{}\rho _{_{_\mathrm{c}}}=322~\mathrm{\frac{kg}{m^3}} \end{array} \right] , \end{aligned}$$

(60)

the pressure can be represented as a function of density and temperature, as

$$\begin{aligned} \tilde{P} \left( \hat{\rho }, \tilde{T} \right)= & {} \frac{\rho _{_{_{\mathrm{c}}}} T_{_{\mathrm{c}}} R}{\bar{P}} \delta ^{^2} \phi _{_{\delta }}-\bar{P}_{_{\mathrm{R}}}, \end{aligned}$$

(61)

where $R=461.526$$\mathrm{\frac{J}{kg~K}}$ is the specific gas constant, while dimensionless density ($\delta$) and inverse of temperature ($\theta$) are defined as:

$$\begin{aligned} \delta \left( \hat{\rho }\right) = \frac{\hat{\rho }}{\hat{ \rho }_{_{_{\mathrm{c}}}}} \text{ and } \theta \left( \tilde{T} \right) =\frac{\hat{T}_{_{\mathrm{c}}}}{\tilde{T}+\hat{T}_{_R}}. \end{aligned}$$

(62)

The dimensionless specific internal energy ($\tilde{{\mathfrak {u}}}$), specific isobaric heat capacity ($\hat{C}_p$), speed of sound ($\hat{c}_s$), and isobaric compressibility ($\hat{\beta }$) can be written as:

$$\begin{aligned} \begin{aligned}&\tilde{{\mathfrak {u}}} = \frac{T_{_c} R}{\bar{{\mathfrak {u}}}} \phi _{_{\theta }}- \hat{{\mathfrak {u}}}_{_R},\\&\hat{C}_p = \left( \frac{\delta \phi _{_{\delta }} \left( 1-\theta \frac{\phi _{_{\delta \theta }}}{\phi _{_{\delta }}}\right) ^2}{2+ \delta \frac{\phi _{_{\delta \delta }}}{\phi _{_{\delta }}}}-\theta ^2 \phi _{_{\theta \theta }} \right) \frac{R}{\bar{C}_{_p}},\\&\hat{c}_s = \left( 2 \phi _{_{\delta }}+ \delta \left[ \phi _{_{\delta \delta }}- \frac{\left( \phi _{_{\delta }} - \theta \phi _{_{\delta \theta }} \right) ^2 }{\theta ^2 \phi _{_{\theta \theta }}} \right] \right) \frac{\delta }{\theta } \frac{T_{_{\mathrm{c}}} R}{ \bar{v}^2},\\&\hat{\beta } =-\frac{\theta \phi _{_{\delta }}}{\left( 2 \phi _{_{\delta }}+\delta \phi _{_{\delta \delta }}\right) \hat{T}_{_{\mathrm{c}}}}, \end{aligned} \end{aligned}$$

(63)

where $\phi$ is the dimensionless Helmholtz free energy:

$$\begin{aligned} \phi \left( \delta , \theta \right) = a_{_{(1)}} \ln \delta + \sum \limits _{i=2}^{40} a_{_{(i)}} \delta ^{^{b_{_{(i)}}}} \theta ^{^{c_{_{(i)}}}}, \end{aligned}$$

(64)

while $\phi _{_{\delta }}$, $\phi _{_{\theta }}$, $\phi _{_{\delta \delta }}$, $\phi _{_{\delta \theta }}$, and $\phi _{_{\theta \theta }}$ are its first and second derivatives relative to $\delta$ and $\theta$. The coefficients $a_{_{(n)}}$ and exponents $b_{_{(n)}}$ and $c_{_{(n)}}$ are given in [31].

Dynamic viscosity and thermal conductivity are nonlinear functions of temperature and density and defined as

$$\begin{aligned} \begin{aligned}&\tilde{\mu } \left( \hat{\rho }, \tilde{T}\right) = \frac{\mu _{_\mathrm{dg}} \left( \tilde{T}\right) \times \mu _{_\mathrm{fd}}\left( \hat{\rho }, \tilde{T}\right) \times \mu _{_\mathrm{ce}} }{\bar{\mu } \bar{\mathrm{Re}}},\\&\tilde{\kappa } \left( \hat{\rho }, \tilde{T}\right) = \frac{\kappa _{_\mathrm{dg}} \left( \tilde{T}\right) \times \kappa _{_\mathrm{fd}}\left( \hat{\rho }, \tilde{T}\right) + \kappa _{_\mathrm{ce}} }{\bar{\kappa } \bar{\mathrm{Re}} \bar{\mathrm{Pr}} }. \end{aligned} \end{aligned}$$

(65)

Viscosities and thermal conductivities in the dilute-gas limit ($\mu _{_\mathrm{dg}}$ and $\kappa _{_\mathrm{dg}}$), and contributions due to finite density ($\mu _{_\mathrm{fd}}$ and $\kappa _{_\mathrm{fd}}$) are described in [75, 76]. In the present study, we will ignore critical enhancement factors, $\mu _{_\mathrm{ce}}=1$ and $\kappa _{_\mathrm{ce}}=0$, as these are relatively unimportant in the range of thermodynamic states of interest.

Special care must be taken to properly code (63)–(65), as these might become prohibitively expensive to be used in implicit solvers. We have optimized all these computations to be compatible with discontinuous Galerkin-based residual evaluations (Sect. 3.1). As described in Sect. 3.1, our nonlinear solver is formulated in terms of DG degrees of freedom for pressure ($\tilde{P}$), velocity ($\hat{{\mathbf{v }}}$), and temperature ($\tilde{T}$). This would require the application of a Newton solver to first evaluate $\hat{\rho }\left( \tilde{P}, \tilde{T}\right)$, for (61), before evaluating the rest of the thermodynamic variables using analytical (63). We used quadruple precision (16-bit) for (61)–(65), as this improves the conditioning and overall convergence of the Newton–Krylov algorithm. The performance of our nonlinear solver using this optimized equation of state is comparable (only two or three times more expensive) to the performance of the solver employed with simpler analytical forms of equation of state (e.g., Sect. 2.3.1).

Finally, we would like to note that the scaling properties $\bar{\rho }$, $\bar{\mu }$, $\bar{\kappa }$, and $\bar{C}_{_p}$ are chosen as evaluated at the reference state $\left( P_{_{\mathrm{R}}}, T_{_{\mathrm{R}}}\right)$.