Abstract
The transition boundary separating the region of regular reflection from the regions of single-, transitional-, and double-Mach reflections for a planar shock wave moving in air and interacting with an inclined wedge in a shock tube is studied by both analytical methods and computational-fluid-dynamic simulations. The analytical solution for regular reflection and the corresponding solutions from the extreme-angle (detachment), sonic, and mechanical-equilibrium transition criteria by von Neumann (Oblique reflection of shocks, Explosive Research Report No. 12, Navy Department, Bureau of Ordnance, U.S. Dept. Comm. Tech. Serv. No. PB37079 (1943). Also, John von Neumann, Collected Works, Pergamon Press 6, 238–299, 1963) are first revisited and revised. The boundary between regular and Mach reflection is then determined numerically using an advanced computational-fluid-dynamics algorithm to solve Euler’s inviscid equations for unsteady motion in two spatial dimensions. This numerical transition boundary is determined by post-processing many closely stationed flow-field simulations, to determine the transition point when the Mach stem of the Mach-reflection pattern just disappears and this pattern then transcends into that of regular reflection. The new numerical transition boundary is shown to agree well with von Neumann’s closely spaced sonic and extreme-angle boundaries for weak incident shock Mach numbers from 1.0 to 1.6, but this new boundary trends upward and above von Neumann’s sonic and extreme-angle boundaries by a couple of degrees at larger shock Mach numbers from 1.6 to 4.0. Furthermore, the new numerically determined transition boundary is shown to agree well with very few available experimental data obtained from previous experiments designed to reflect two symmetrical moving oblique shock waves along a plane without a shear or boundary layer.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Regular- and Mach-reflection flow-field patterns from the interaction of a moving planar shock wave with a wedge in air. These four examples were produced using the computational-fluid-dynamics algorithm described in Sect. 3.2
The interaction of a moving planar shock wave with an inclined wedge in a shock tube produces four basic shock-reflection configurations or patterns, as shown in Fig. 1 for air (computed as a polytropic gas). The type of pattern depends on the speed or Mach number \(M_{\mathrm{i}}\) of the incident shock wave and the angle \(\theta _{\mathrm{w}}\) of the wedge, as shown in Fig. 2 for air (\(\gamma = 7/5\)). Regular reflection (RR) is composed of the planar incident shock along with the straight and curved reflected shock which are joined at the wedge surface. As the shocks propagate this two-shock confluence point moves along the wedge surface. RR occurs at large wedge angles for strong shocks and also at small wedge angles for weak shocks.
In single Mach reflection (SMR), the confluence of the incident planar shock and curved reflected shock occurs above the wedge, and a third shock called the Mach stem extends from the confluence point to the wedge surface. In addition, from the triple-shock confluence point, a curved shear layer called the slip stream trails the moving triple point and shocks. SMR occurs typically at small wedge angles.
Regions of regular- and Mach-reflection patterns separated by analytical and experimental transition boundaries for air and diatomic gases
Double Mach reflection (DMR) features two triple shock confluence points, each with a nearly straight slip stream, and the latter has a distinct kink (“k” in Fig. 1). In transitional Mach reflection (TMR), the second triple point is barely visible and occurs as a slight kink in the reflected shock, and a second slip stream is not always observable. The slight kink in the TMR patterns is more noticeable near the TMR–DMR boundary and disappears near the SMR–TMR boundary (Fig. 2). Note that the markers “d” and “k” in Fig. 1 indicate the locations on the reflected shock of the front of the disturbance or signal that emanates from the wedge corner and surface.
The basic irregular Mach-reflection (MR) pattern was discovered in double-spark separated discharges made in 1878 by Ernst Mach [1], from observations of smeared carbon soot patterns on coated glass plates exposed to the shock-induced flow field. The four patterns of regular, single-Mach, transitional-Mach, and double-Mach reflections were discovered in shock-tube experiments in air in the 1940s and 1950s by Smith [2] and White [3]. Two-shock regular-reflection and three-shock Mach-reflection configurations were studied theoretically in the 1940s by von Neumann [4,5,6], Courant and Friedrichs [7], and Bleakney and Taub [8], and in the 1950s by Cabannes [9] and Kawamura and Saito [10].
The regions and boundaries between regular and Mach reflection patterns were introduced in Fig. 2, in a graph of the wedge angle versus the incident shock Mach number. As mentioned earlier, regular reflections occur typically at larger wedge angles and single-Mach reflections occur typically at smaller wedge angles. The influence of the incident shock strength is also important, as depicted in the figure. Double- and transitional-Mach reflections occur in the mid to lower range of wedge angles and at large incident shock Mach numbers. The two upper transition boundaries are based on the two criteria of mechanical equilibrium and detachment, and they originate from von Neumann [5]. These two boundaries establish three regions: one upper region for regular reflection only, one adjacent dual region for either regular reflection or Mach reflection (TMR and DMR), and one lower region for only Mach reflection (SMR, TMR, and DMR). The two other boundaries that subdivide the region of Mach reflection (MR) into the regions of SMR, TMR, and DMR are the results of research by Ben-Dor and Glass [11, 12]. For additional information on shock waves and Mach reflection, see the books by Ben-Dor [13] and Glass and Sislian [14]. Ben-Dor includes another weak Mach-reflection configuration called von Neumann reflection (vNR), which resembles an SMR pattern with a band of compression waves near the triple point, a curved Mach stem, and a barely noticeable slip stream. The region of vNR occurs at the left side of the SMR region, but no boundary between vNR and SMR is available to illustrate the vNR region in Fig. 2. The paper by Semenov, Berezkina, and Krassovskaya [15] provides a more recent and extensive classification of Mach-reflection configurations.
The experimental data presented in Fig. 2 come from detailed investigations aimed specifically at finding the transition boundary between regular and Mach reflections. Shadowgraph and schlieren photographs were taken of moving shocks interacting with wedges in a shock tube for various wedge angles and incident shock Mach numbers near the boundary between regular and Mach reflections, to locate the points along the transition boundary at which the Mach-stem length just diminishes to zero. Various incident and reflected shock angles were measured from these photographs and plotted as a means to determine the experimental transition boundary. The papers of relevance by Smith [2], White [3], Bleakney and Taub [8], Kawamura and Saito [10], Henderson and Lozzi [16], Henderson and Siegenthaler [17], Walker et al. [18], Lock and Dewey [19], and Kobayashi et al. [20] provide details of their experimental methods and data-processing techniques.
All of the transition boundaries between the various shock-reflection patterns shown in Fig. 2 are the result of analytical methods using the theory of shock waves moving in a polytropic gas (\(\gamma =7/5\)), and the presence of a combined viscous and thermal boundary layer on the wedge surface is ignored. All of the experimental transition-boundary data shown in the figure stem from shock-tube experiments using air as the working gas and wedges with smoothly machined surfaces. Nonetheless, a combined viscous and thermal boundary layer is produced behind the incident and reflected shocks on the wedge surface. Furthermore, the transition boundary from the string of experimental data, shown in Fig. 2, clearly lies below the closely spaced sonic and extreme-angle boundaries of von Neumann [5]. The resulting persistence of regular reflection across von Neumann’s mechanical-equilibrium, sonic, and extreme-angle boundaries, downward into the Mach-reflection region by a few degrees, is normally attributed to the presence of the boundary layer on the wedge surface in the experiments and the lack thereof in analytical predictions of the transition boundaries. Although this explanation is fairly well accepted, additional supporting evidence is desirable to validate these RR to MR transition boundaries. The papers by Bleakney and Taub [8], Hornung [21], Henderson et al. [22], and Adachi et al. [23] provide additional information.
The goals of this and a subsequent study are to provide more detailed information and understanding related to the persistence of regular reflection past the von Neumann extreme-angle boundary into the Mach-reflection region, which can be explained partly but maybe not fully by the presence of the boundary layer on the wedge surface. In these complementary studies, the transition boundary between regular and Mach reflection will be determined numerically using an advanced computational-fluid-dynamics algorithm to solve both the Euler and Navier–Stokes equations for unsteady two-dimensional shock interactions with a wedge in air at various shock Mach numbers and wedge angles, combined with effective post-processing techniques to accurately determine each local RR to MR transition-boundary point from a collection of closely stationed computational flow fields. The transition boundary is systematically examined and extended for incident shock Mach numbers ranging from 1.0 to 4.0. The first of these studies reported herein focuses on the case of solving Euler’s equations for inviscid and compressible flow, without a boundary layer on the wedge surface, and developing sophisticated and accurate flow-field post-processing techniques, whereas a subsequent companion paper will focus on the second case of solving the Navier–Stokes equations for viscous and heat-conducting flows, with a boundary layer on the wedge surface. The boundary layer can be turned off and on in computational studies more easily than modifying experimental shock-tube facilities, and this should facilitate the evaluation of the viscous effects on the transition boundary between regular and Mach reflection.
2 Analytical solutions
2.1 Solution for regular reflection
Consider a moving planar shock wave interacting with an inclined wedge with a known angle \(\theta _{\mathrm{w}}\), as illustrated in Fig. 3. The incident shock (\(S_{\mathrm{i}}\)) moves into a quiescent fluid (gas or liquid) in region (1) with known pre-shock flow properties (e.g., pressure \(p_1\), density \(\rho _1\), sound speed \(a_1\), temperature \(T_1\), and flow velocity \(u_1=0\) m/s). Let the strength of this incident shock be specified by its speed \(V_{\mathrm{i}}\) or Mach number \(M_{\mathrm{i}}=V_{\mathrm{i}}/a_1\). Based on the given value of \(M_{\mathrm{i}}\), and knowledge of the fluid properties and its equation of state, all of the flow properties in region (2) can be determined (i.e., \(p_2\), \(\rho _2\), \(a_2\), \(T_2\), \(u_2=u_1+\varDelta u_{\mathrm{i}}\), in which \(\varDelta u_{\mathrm{i}}\) is the flow speed induced by the incident shock). If the reflected shock Mach number \(M_{\mathrm{r}}\) and its angle \(\theta _{\mathrm{r}}\) with the wedge surface were also known, then the knowledge of the fluid properties and its equation of state could be used to subsequently determine all of the flow properties in region (3) (i.e., \(p_3\), \(\rho _3\), \(a_3\), \(T_3\), \(u_3\)).
Regular-reflection pattern showing moving shocks, flow-field regions, and various shock and wedge angles
For regular reflection to occur, the reflected shock (\(S_{\mathrm{r}}\)) must remain attached to the incident shock (\(S_{\mathrm{i}}\)) at the wedge surface. Hence, the speed \(V_{\mathrm{i}}/\!\sin (\theta _{\mathrm{i}})=V_{\mathrm{i}}/\!\cos (\theta _{\mathrm{w}})\) of the incident shock along the wedge surface must be matched to the speed \(V_{\mathrm{r}}\) of the reflected shock along the wedge. This requirement yields
in which the second term on the right side of the equation results from the interaction of the reflected shock with the flow field in region (2). The component of the induced flow (\(u_2=u_1+\varDelta u_{\mathrm{i}}=\varDelta u_{\mathrm{i}}\)) by the incident shock in region (2) that is directed normal to but toward the wedge surface is given by \(\varDelta u_{\mathrm{i}}\cos \left( \theta _{\mathrm{i}}\right) \). This component must be countered by the component of the induced flow from the reflected shock that is normal to but away from the wedge surface, so that no flow enters the nonporous wedge surface. This requirement yields
The flow along the wedge surface in region (3) can be determined from
by considering the components of both shock-induced flows in the direction parallel to the wedge surface.
Solutions for shock-wave reflections from a wedge in polytropic air
Equations (1) to (3) apply to arbitrary gases or fluids, and the physical properties of a specific fluid enter the problem only through the shock-jump conditions. In the case of a polytropic gas, the conventional Rankine–Hugoniot equations (Thompson [24]) for the incident shock are summarized as
in which \(\gamma \) is the specific heat ratio. Similar equations apply to the reflected shock, with appropriate subscript changes (i.e., \(2\rightarrow 3\), \(1\rightarrow 2\), \(\text {i}\rightarrow \text {r}\)).
Several solutions for regular reflection for the case of polytropic air are illustrated in Fig. 4. For polytropic air, the reflected shock angle \(\theta _{\mathrm{r}}\) is varied from 0\(^{\circ }\) to 180\(^{\circ }-\theta _{\mathrm{i}}\), and the reflected shock speed \(V_{\mathrm{r}}\) is then calculated by means of (1) for the specified incident shock Mach number \(M_{\mathrm{i}}=2\), which also yields the value of \(\varDelta u_{\mathrm{i}}\) from using (7). The calculations are done three times for wedge angles \(\theta _{\mathrm{w}}=70^{\circ }\), 50.59\(^{\circ }\), and 40\(^{\circ }\), or shock angles \(\theta _{\mathrm{i}}=90^{\circ }-\theta _{\mathrm{w}}=20^{\circ }\), 39.41\(^{\circ }\), and 50\(^{\circ }\), giving the three curves shown in Fig. 4. The value of \(V_{\mathrm{r}}\) releases the value of \(\varDelta u_{\mathrm{r}}\) by means of (7) with appropriate subscripts. An error is constructed from (2) as
When this error equals zero, a solution for regular reflection occurs. For the case of polytropic air with the incident shock angle \(\theta _{\mathrm{i}}=20^{\circ }\), the weak reflected shock solution (well-known from oblique shock-reflection theory) with the values of \(V_{\mathrm{r}}\) and \(\theta _{\mathrm{r}}\) corresponds to location (a) in the figure, the strong reflected shock solution corresponds to location (b), and a nonphysical solution occurs at location (c). For the shock angle \(\theta _{\mathrm{i}}=39.41^{\circ }\), the solutions (a) and (b) merge and yield the same values for \(V_{\mathrm{r}}\) and \(\theta _{\mathrm{r}}\), which corresponds to von Neumann’s extreme angle (detachment criterion) at which regular reflection switches to Mach reflection. For the incident shock angle \(\theta _{\mathrm{i}}=50^{\circ }\), the weak and strong shock solutions are imaginary and nonphysical and regular reflection cannot occur, replaced instead by Mach reflection.
A simple analytical solution for regular reflection can be derived for the case of the polytropic gas. The reflected shock angle \(\theta _{\mathrm{r}}\) is eliminated first from (1) and (2). For this solution, the reflected shock Mach number takes the form of a cubic polynomial (e.g., in \(V_{\mathrm{r}}^2\)). However, the nonphysical solution given by \(V_{\mathrm{r}}-V_{\mathrm{i}}+\varDelta u_{\mathrm{i}}=0\) or \(p_3-p_1=0\) can be factored out so that the solution for the reflected shock speed \(V_{\mathrm{r}}\) reduces to a quadratic polynomial in terms of \(V_{\mathrm{r}}^2\). The derivation is complicated and tedious. The quadratic polynomial, its coefficients, and the solution for the square of the reflected shock Mach number \(M_{\mathrm{r}}^2=V_{\mathrm{r}}^2/a_2^2\) are
in terms of the input specification of incident shock Mach number \(M_{\mathrm{i}}\) and wedge angle \(\theta _{\mathrm{w}}\). The weak and strong shock solutions correspond to the negative and positive signs in (10), respectively. The solution for the reflected shock angle follows from (2), and the pressure \(p_3\) behind the reflected shock is given by (11). The regular-reflection solution was derived first by von Neumann [5] and reproduced later by others like Polachek and Seeger [25] and Henderson [26]. They adopt the transformed plane of steady flow with a supersonic flow imposed down the wedge into the incident shock to make the self-similar shock-reflection pattern stationary. These conventional equations are well illustrated by previous researchers [5, 8, 10, 13, 16, 25,26,27]. However, the derivation using (1) to (2) for moving shocks is simpler and less cumbersome than using the conventional equations in the form employed by previous researchers.
2.2 Solution for the extreme-angle boundary
The solution for the extreme angle by von Neumann [5] can be obtained from (10) by setting the discriminant \(b^2-c^2\) to zero, when the two roots merge for the weak and strong reflected shocks. After substantial manipulation, the cubic polynomial in \(\cos \left( \theta _{\mathrm{w}}\right) \), its coefficients, and the physically realistic solution for the shock and wedge angles \(\theta _{\mathrm{i}}\) and \(\theta _{\mathrm{w}}\), shown in Fig. 3, are
in terms of the input specification of the incident shock Mach number \(M_{\mathrm{i}}\) or inverse shock density ratio in term \(d_{\mathrm{i}}\). This revision of the extreme-angle or detachment boundary derived originally by von Neumann [5] is given herein as a cubic polynomial in terms of the wedge angle \(\cos \left( \theta _{\mathrm{w}}\right) \) and incident shock angle \(\sin \left( \theta _{\mathrm{i}}\right) \). In the previous work of von Neumann [5], and others like Polachek and Seeger [25] and Henderson [26], the solutions were given as a cubic polynomial in terms of the incident shock angle squared, that is, \(\sin ^2\!\left( \theta _{\mathrm{i}}\right) \). The extreme-angle boundary in Fig. 2 was calculated using (14).
The derivative \(\mathrm{d}\sin \left( \theta _{\mathrm{w}}\right) /\mathrm{d}M_{\mathrm{i}}\) is required later in this study. This derivative is obtained from (12) as
The cubic polynomial given by (12) in terms of \(\cos \left( \theta _{\mathrm{w}} \right) \) can be rearranged into a quadratic polynomial for the density ratio \(\rho _2/\rho _1\) as a function of the wedge angle \(\theta _{\mathrm{w}}\) or \(\cos \left( \theta _{\mathrm{w}}\right) \). This quadratic polynomial, its coefficients, and the solutions for the density ratio and incident shock Mach number are summarized as
The input values of the wedge angle lie in the restricted range \(0\le \cos \left( \theta _{\mathrm{w}}\right) \le \sqrt{\left( 3-\gamma \right) /4}\), and the physically realistic solutions for the density ratio lie in the range \(1\le \rho _2/\rho _1\le \left( \gamma +1\right) / \left( \gamma -1\right) \), corresponding to the shock Mach number range \(1\le M_{\mathrm{i}}\le \infty \).
The upper value of the wedge-angle range corresponds to a maximum in the wedge angle versus shock Mach number \(M_{\mathrm{i}}\), which is barely visible in Fig. 2 near \(M_{\mathrm{i}} \approx 2.48\), but marked with the short line crossing the extreme-angle boundary. This maximum wedge angle is obtained by setting the discriminant \(b^2-4ac\) in (18) equal to zero. The maximum wedge angle and the corresponding density ratio and shock Mach number are
which are all functions of the specific heat ratio only. When \(\gamma =7/5\), the three previous equations yield values of \(\theta _{\mathrm{w}}=50.7685^{\circ }\), \(\rho _2/\rho _1 = 3.31238\), and \(M_{\mathrm{i}}=2.48239\), respectively.
2.3 Solution for the sonic boundary
The analytical solution for the boundary between regular and Mach reflection is based on the sonic criterion first proposed by von Neumann [5], and the first analytical solution as a quintic polynomial in terms of \(\sin ^2\left( \theta _{\mathrm{i}}\right) \) was given by Henderson [26]. For the case of the wave motion shown in Fig. 3, the corner disturbance is assumed to move at the speed of sound and convected by the flow along the wedge surface. It just overtakes the moving point of coalescence of the incident and reflected shocks along the wedge surface, yielding the expression \(u_3+a_3=V_{\mathrm{i}}{/}\cos \left( \theta _{\mathrm{w}}\right) \). The analytical solution that is derived from this sonic criterion takes the simpler form of a quartic polynomial in terms of \(\cos ^2\left( \theta _{\mathrm{w}}\right) \). This polynomial, its coefficients and the physically realistic solution for the wedge and shock angles \(\theta _{\mathrm{w}}\) and \(\theta _{\mathrm{i}}\), shown in Fig. 3, are summarized by
The sonic boundary is almost indistinguishable from the extreme-angle boundary, as shown in Fig. 2, differing by less than a half of a degree for each given value of the shock strength.
2.4 Solution for the mechanical-equilibrium boundary
The solution for the mechanical-equilibrium boundary of von Neumann [5] starts with the three-shock pattern of Mach reflection, as shown in Fig. 5. This upper boundary for the dual region of regular and Mach reflection (Fig. 2) occurs when the triple-point trajectory angle \(\chi \) diminishes to zero, the Mach stem diminishes to an infinitesimal height, and the slip stream collapses onto the wedge surface.
Mach-reflection pattern showing moving shocks, slip stream, triple-point trajectory angle \(\chi \), and flow-field regions
The Mach stem of infinitesimal length moves along the wedge with a speed \(V_{\mathrm{m}}=V_{\mathrm{i}}/\sin \left( \theta _{\mathrm{i}}\right) \), produces a post-shock pressure \(p_4=p_3=p_1+p_1\frac{2\gamma }{\gamma +1}\left( M_{\mathrm{m}}^2-1\right) \), which is set equal to the pressure \(p_3\) on the other side of the slip stream and behind the reflected shock. This results in a reflected shock Mach number given by
This equation is substituted into (9) to eliminate \(M_{\mathrm{r}}\), so that the remaining equation can be solved for an expression for the mechanical-equilibrium boundary in terms of the wedge angle \(\theta _{\mathrm{w}}\) versus the incident shock Mach number \(M_{\mathrm{i}}\). After considerable manipulation, the resulting quadratic polynomial in terms of \(\cos ^2\!\left( \theta _{\mathrm{w}}\right) \), its coefficients, and the physically realistic solutions for the angles \(\theta _{\mathrm{w}}\) and \(\theta _{\mathrm{i}}\) are summarized as
This revised solution of von Neumann [5] was used to plot the mechanical-equilibrium boundary in Fig. 2.
The mechanical-equilibrium boundary touches the extreme-angle boundary and shares the same slope at one location in the plane of \(\theta _{\mathrm{w}}\) versus \(M_{\mathrm{i}}\), as can be seen in Fig. 2. This point of contact can be obtained by combining (12) and (26) to eliminate \(\cos \left( \theta _{\mathrm{w}} \right) \). The solution for the incident shock strength \(\rho _2/\rho _1\) in terms of the variable \(z=\frac{\gamma +1}{2}\!\left( \rho _2/\rho _1-1\right) \) is then given by the quartic polynomial
followed by the solutions for the density ratio and incident shock Mach number (once z is determined). For a polytropic gas with \(\gamma =7/5\), the solutions are given by \(z=0.944980\), \(\rho _2/\rho _1=1.78748\), \(M_{\mathrm{i}}=1.45658\), and then \(\theta _{\mathrm{w}}=48.5876^{\circ }\) from either (14) or (27).
3 Computational fluid dynamics solutions
3.1 Equations for two-dimensional unsteady and inviscid gas flows
The partial differential equations for solving unsteady compressible and inviscid gas flows in two spatial dimensions of interest here, for the determination of the unsteady flow fields from regular and Mach reflections from a wedge without a boundary layer, are given by
in matrix form, where t denotes the time, \(\vec {\nabla }\) is the vector differential operator and \({\vec {\mathbf{F}}} = (\mathbf {F}, \mathbf {G})\) is the total solution flux dyad. The three column vectors
contain the conserved quantities (mass, momentum, energy) and the corresponding inviscid fluxes (in the x- and y-coordinate directions), whereas T denotes the matrix transpose. In addition, p, \(\rho \), u, and v are the usual symbols for the gas pressure, density, and flow velocities in the x- and y-coordinate directions. The total energy is the sum of the internal and kinetic energies, given by \(e=\varepsilon +(u^2+v^2)/2\). For a polytropic or perfect gas, the internal energy \(\varepsilon =c_vT\), the enthalpy \(h=e+p/\rho =c_pT\), and the equation of state is given by \(p=\rho RT\), in which R and T denote the specific gas constant and temperature. The specific heats at constant pressure and volume are \(c_p=\gamma R/(\gamma -1)\) and \(c_v=R/ \left( \gamma -1\right) \), and the specific heat ratio is \(\gamma =c_p/c_v\). The previous partial differential equations are normally called Euler’s equations (Thompson [24]), which are used to represent unsteady compressible flow problems that are inviscid and non-turbulent, as required herein.
The molecular weight of dry air used in this research is \(M_\mathrm{air}=28.9655\) kg/mol, and the specific gas constant for air follows as \(R_\mathrm{air}=\mathcal{R}/M_\mathrm{air}=287.048\) J/kg K. The mixture specific heat is \(c_{p_\mathrm{air}}=1004.59\) J/kg K at 295 K, and the specific heat ratio of air follows as \(\gamma _\mathrm{air}=c_{p_\mathrm{air}}/\left( c_{p_\mathrm{air}}-R_\mathrm{air}\right) =1.4004\), which is frequently rounded to the value 1.40. These properties of dry air are used in this study, with the value of the specific heat ratio of air reduced slightly to \(\gamma _\mathrm{air}=7/5\), with \(c_{p_\mathrm{air}}=\gamma _\mathrm{air} R_\mathrm{air}/(\gamma _\mathrm{air}-1)\), which conform to the specific case of a diatomic gas.
3.2 Computational-fluid-dynamics algorithm
The partial differential equations, along with the equation of state and thermodynamic properties of air, presented in Sect. 3.1, are solved numerically to determine the unsteady flow field from the interaction of a planar shock with an inclined wedge. The modern computational-fluid-dynamics (CFD) solution algorithm developed by Groth and co-researchers [28,29,30,31,32,33,34,35,36] is used to generate these shock-reflection computations or simulations. This numerical algorithm or computer code is robust and provides high-resolution solutions. The stability and accuracy of the solution method, including the AMR procedure, used herein for shock-reflection phenomena was established previously for shock-reflection applications by Hryniewicki et al. [28] and for other applications by McDonald et al. [29], Gao et al. [33], Gao and Groth [35], and Sachdev et al. [36]. The mesh resolution adopted herein for the calculation of the transition boundary between regular and Mach reflection is based on this previous investigation. The primary features of this algorithm relevant to this study are described briefly in Sects. 3.2.1 to 3.2.3.
3.2.1 Finite-volume method
A finite-volume method is used in the spatial discretization of the Euler equations given by (31). Such schemes represent and evaluate a set of partial differential equations as a system of algebraic equations, and the flow properties are calculated at discrete places on a meshed geometry, as described in the book of LeVeque [37]. In two spatial dimensions, the finite-volume method reduces to a finite-area method. Equation (31) is multiplied by \(\mathrm{d}x\,\mathrm{d}y\) and two integrations are included. The first term \(\int _y\!\int _x\left( \partial {\mathbf {U}}/\partial t \right) \,\mathrm{d}x\,\mathrm{d}y\) reduces to the integral \(\int _A\left( \partial {\mathbf {U}}/\partial t\right) \,\mathrm{d}A\) over an arbitrary area A. The last term \(\int _y \int _x( \vec {\nabla }\!\cdot {\vec {\mathbf{F}}}) \mathrm{d}x \mathrm{d}y\) can be converted into a single integral for a closed path around the area A using the divergence or Green’s theorem. Equation (31) then reduces to
in which \(\varGamma \) denotes the closed path and \(\vec {n}\) is the outward unit vector that is normal to the control surface of interest. Let the arbitrary shaped area A in this equation be replaced by a cell of finite area from our computational mesh of quadrilateral shaped cells. One of these cells with the side lengths and normal vectors denoted by \(\varDelta \ell _k\) and \(\vec {n}_k\) with \(k=1,2,\ldots ,4\) is illustrated in Fig. 6. For this quadrilateral cell, using the mid-point rule (for second-order accuracy) for the integration, (35) then reduces to the semi-discrete algebraic form
in which \({\bar{\mathbf{U}}}_{i,j}=A^{-1}\!\int _A{\mathbf {U}}_{i,j}\,\mathrm{d}A\) is the cell-averaged value. Solution methods pertaining to two-dimensional cells that include a curved boundary have been developed by Ivan and Groth [38]. Finite-volume methods have an important attribute of being conservative of the elements of \({\mathbf {U}}\), because the flux crossing a boundary into one cell is identical to that leaving the abutting cell via the same boundary, and these fluxes are directly related to the time rate of change of the vector of conserved solution variables \({\mathbf {U}}\) within each cell.
Quadrilateral cell for the finite-volume method
The conventional steps are reviewed for advancing the cell-averaged solution of \({\bar{\mathbf{U}}}_{i,j}\) for cell (i, j) from time t to \(t+\varDelta t\) using (36). Second-order accurate solution reconstruction within the cell is given by
in which the solution is represented as a linear function that is dependent on the two solution derivatives \(a_{i,j}\) and \(b_{i,j}\) in the x- and y-coordinate directions determined by a least-squares fit to the data from the four adjacent cells (with \(\varPhi _{i,j}=1\)). This reconstruction enables the evaluation of \({\mathbf {U}}_{i,j}^{(k)}\) at the four centers of the quadrilateral edges. These four edge values \({\mathbf {U}}_{i,j}^{(k)}\) and the corresponding four edge values \({\mathbf {U}}_{i\pm 1,j\pm 1}^{(k')}\) of the neighbouring cells can agree or differ discontinuously, providing the basis of calculating the flux \({\vec {\mathbf{F}}}\) across each cell boundary by solving a cell-edge corresponding Riemann problem. This least-squares piecewise solution reconstruction procedure is explained by Barth [39]. The slope limiter \(\varPhi _{i,j}\) of Venkatakrishnan [40] is employed herein to provide values in the range 0 to 1 for (37), to ensure solution monotonicity near discontinuities, whereas second-order spatial accuracy with \(\varPhi _{i,j}=1\) is maintained in smooth flow-field regions. The numerical flux at each cell interface between abutting cells is evaluated using the approximate Riemann solver of Harten, Lax, and van Leer [41], with the improvements suggested by Einfeldt [42].
A second-order, predictor-corrector, time-marching scheme is applied to reliably and efficiently integrate the semi-discrete form of (36) in time. The physical time step \(\varDelta t\) for advancing the solution in time for all cells simultaneously is obtained by considering the inviscid Courant–Friedrichs–Lewy (CFL) criterion. The time step is given by \(\varDelta t = n_{\mathrm{CFL}} \varDelta \ell _{\mathrm{min}} / (|\vec {V}| + a)_{\mathrm{max}}\), in which the CFL number \(n_{\mathrm{CFL}}=0.60\) in this study, the flow-velocity magnitude \(|\vec {V}|=\sqrt{u^2+v^2}\), the sound speed \(a=\sqrt{\gamma p / \rho }\), and the minimum and maximum values are obtained from a global search through all cells in the computational domain.
3.2.2 Anisotropic block-based adaptive mesh refinement
The spatial discretization of the partial differential equations is implemented on a computational grid that subdivides the physical domain into a finite representation of geometric cells. To achieve the desired level of solution accuracy for a given numerical scheme, a minimum spatial resolution is required to capture pertinent features of the flow field with sufficient detail and precision. While a uniformly dense grid tessellation is a simple strategy to meet this demand, it is inefficient computationally and inherently over-resolves localized regions of homogeneity within a complex flow field.
Refinement and coarsening of a block with 8-by-8 cells during (i) anisotropic AMR in the \(\xi \)-direction, (ii) anisotropic AMR in the \(\zeta \)-direction and (iii) isotropic AMR
In this research, the finite-volume scheme outlined earlier is used in conjunction with anisotropic block-based adaptive mesh refinement (AMR) coming from the work of Williamschen and Groth [31] and Zhang and Groth [32], as illustrated in Figs. 7 and 8. The cell-averaged solution quantities defined within quadrilateral computational cells are embedded in structured, body-fitted grid blocks. Automatic and local solution-directed mesh adaptation of the individual grid blocks is performed independently in each of the \(\xi \) and \(\zeta \) computational coordinate directions when dealing with strong anisotropic flow features, as shown in Fig. 7. A flexible block-based hierarchical binary tree data structure is used to facilitate this approach. The coarsening and refinement of grid blocks is performed once every six time steps in this study, and this is achieved using physics-based refinement criteria according to local spatial gradients of both fluid density and flow velocity.
Grid blocks at various stages of a DMR simulation (\(M_{\mathrm{i}}=4.0\), \(\theta _{\mathrm{w}}=43.0^\circ \), \(n_{\mathrm{r}}=10\)): a solution initialization, b initial anisotropic AMR application, c early interaction of incident shock with a wedge, and d late interaction
The benefits and capabilities of dynamic mesh adaptation via anisotropic AMR with \(n_{\mathrm{r}}\) levels of refinement is demonstrated in Fig. 8. The initial mesh at time zero consists of only two grid blocks depicted in Fig. 8a, and each grid block consists of a set of 8-by-8 cells that are not displayed. The shock discontinuity is shown as a vertical dashed line in the first block. Before the flow-field computations begin, anisotropic AMR is implemented to refine the grid blocks around the shock discontinuity, and these results are shown in Fig. 8b. During the computations, the shock-on-wedge flow field evolves with time, and so does the mesh, tracking and helping to accurately define all complicated features of the flow field. Grid blocks are illustrated at early and late times in Fig. 8c, d, respectively. These four mesh snapshots correspond to the DMR flow-field configuration computed and shown earlier in Fig. 1d.
A square grid block with equal side lengths \(\varDelta \ell \) and 8-by-8 interior cells features initial cell side lengths of \(2^{-3}\varDelta \ell \), for the zeroth level of refinement. For \(n_{\mathrm{r}}\) levels of refinement the smallest cell side length is reduced to \(2^{-n_{\mathrm{r}}-3}\varDelta \ell \). For \(n_{\mathrm{r}}=10\), this corresponds to the smallest cell side of \(1.22{\times }10^{-4}\varDelta \ell \) and a refinement factor \(2^{n_{\mathrm{r}}+3}\) given by 8192. The number of refinement levels is specified at the beginning of each CFD flow-field simulation, and \(n_{\mathrm{r}}\) varies from 10 to 13 in this study to generate flow-field simulations with a high spatial resolution.
3.2.3 Parallel implementation
The CFD solution technique used herein lends itself naturally to parallelization via block-based domain decomposition, implemented with the C ++ programming language and Message Passing Interface (MPI) library. The self-similar solution blocks are distributed equally amongst available processors within a homogeneous multiprocessor architecture, with more than one block permitted per core.
3.3 Problem specification and solution initialization
The computational domain, boundaries, dimensions,and initial conditions ahead of the incident shock wave in region (1), are documented in Fig. 9. The flow properties behind the incident shock in region (2) are obtained using the Rankine–Hugoniot jump conditions given by (4) through (7). The wedge length of 1.2 m was selected so the incident shock could interact and move along the wedge a distance of 1.0 m for all computed flow-field simulations with incident shock Mach numbers \(M_{\mathrm{i}}\) ranging from 1.0 to 4.0. The 1.0 m height and horizontal pre-wedge distances ensured that the reflected wave would not reach the upper and left boundaries during all CFD flow-field simulations.
Initial and boundary conditions for the numerical simulation of unsteady shock-wave reflections from a wedge
Reference points \(\left( M_{\mathrm{i}}^\star ,\sin \left( \theta _{\mathrm{w}}^\star \right) \right) \) along von Neumann’s extreme-angle boundary between RR and MR for air, and a superimposed (\(\alpha \), \(\beta \))-coordinate system showing the locations of CFD flow-field simulations normal to the extreme-angle boundary
4 Methodology for determining the numerical transition boundary between RR and MR
The transition boundary between regular reflection(RR) and Mach reflection (MR), determined analytically by von Neumann [5] based on the extreme-angle or detachment criterion, given by (12) to (14) and shown in Fig. 2, is examined by performing detailed numerical or CFD flow-field simulations of planar shock reflections from an inclined wedge. The methodology for determining the numerical transition boundary precisely from CFD flow-field simulations requires the following: (i) RR and MR (SMR, TMR, and DMR) flow fields concentrated about a point on a previous analytical transition boundary are computed accurately and (ii) the wedge angle \(\theta _{\mathrm{w}}\) and incident Mach number \(M_{\mathrm{i}}\) for a point on the resulting numerical transition boundary are then computed accurately based on the disappearance of the Mach stem from the MR pattern and the first occurrence of the RR configuration. The first requirement is well met using the CFD algorithm described in the previous section. For the second requirement, a methodology for post-processing the CFD flow fields is developed and described below to permit the determination of numerous coordinate points \(\left( M_{\mathrm{i}},\theta _{\mathrm{w}}\right) \) along the numerical transition boundary with an accuracy that is much superior than that achievable by human inspection and interpretation of CFD flow-field images (and also by human interpretation of experimental flow-field photographs).
4.1 Selected \(\left( M_{\mathrm{i}},\theta _{\mathrm{w}}\right) \)-coordinates for CFD simulations
Von Neumann’s [5] transition boundary between RR and MR (SMR, TMR, and DMR), based on the extreme-angle or detachment criterion, is used as a starting point for the determination of the numerical transition boundary based on CFD flow-field simulations. Twenty coordinate points along this transition boundary were selected, as given in Table 1. These points along the transition boundary are also plotted and numbered in Fig. 10 as the sine of the wedge angle \(\theta _{\mathrm{w}}\) versus the incident Mach number \(M_{\mathrm{i}}\). At each reference point (\(M_{\mathrm{i}}^\star \!,\,\sin \left( \theta _{\mathrm{w}}^\star \right) \)) on the extreme-angle boundary, a set of coordinate points \(\left( M_{\mathrm{i}},\sin \left( \theta _{\mathrm{w}}\right) \right) \) normal to and crossing the extreme-angle boundary are specified for the CFD flow-field simulations, as marked with “\(\times \)” signs at points 6 and 15 in the Fig. 10. These points, which define the CFD simulations, are determined using an \(\left( \alpha ,\beta \right) \)-coordinate system that is translated from the origin \(\left( M_{\mathrm{i}}=1,\sin \left( \theta _{\mathrm{w}}\right) =0\right) \) to one of the points (e.g., number 6), and then rotated such that the \(\alpha \)-abscissa and \(\beta \)-ordinate are, respectively, perpendicular and parallel to the extreme-angle boundary. The transformation that renders the CFD simulation points is
in which \(\phi ^\star \) is the rotation angle and \({\mathrm {d}}\sin \left( \theta _{\mathrm{w}} \right) /{\mathrm {d}}M_{\mathrm{i}}\) denotes the slope of the extreme-angle boundary at the reference coordinates \(M_{\mathrm{i}}^\star \) and \(\sin \left( \theta _{\mathrm{w}}^\star \right) \). This derivative was defined previously by (16). The CFD simulation points are obtained by setting the parameter \(\beta =0\) in the transformation equations. The parameter \(\alpha \) is then varied such that the CFD simulation points become concentrated in the vicinity of the numerical transition boundary where the Mach stem disappears, which might occur below (\(\alpha >0\)), on (\(\alpha =0\)), or above (\(\alpha <0\)) the extreme-angle transition boundary.
4.2 Mach-stem length and triple-point angle
A characteristic length of the Mach stem is required for the determination of the numerical or CFD transition boundary because this length in Mach-reflection configurations diminishes to zero as the flow-field simulations are computed closer and closer to the numerical transition boundary. The characteristic length \(L'\) selected for this study is depicted in Fig. 11 for the case of a single Mach reflection. This physical length is given by \(L'=V_{\mathrm{m}}\delta t -V_{\mathrm{i}}\delta t/\cos \left( \theta _{\mathrm{w}}\right) \), in which \(V_{\mathrm{m}}\) denotes the speed of the foot of the Mach stem along the wedge surface, \(V_{\mathrm{i}}/\cos \left( \theta _{\mathrm{w}}\right) \) is the speed of the incident shock along the wedge, and \(\delta t\) denotes the time increment after the incident shock first encounters the wedge apex and a regular- or Mach-reflection pattern begins.
Characteristic length \(L'\) of the Mach stem
The physical length \(L'\) as defined above is inconvenient because it increases continuously from zero with increasing time (\(\delta t\)). Hence, the length is normalized by dividing it by \(V_{\mathrm{i}}\,\delta t/\cos \left( \theta _{\mathrm{w}}\right) \) to overcome this difficulty and one then obtains the normalized length
which is constant for the case of a self-similar flow field. In the case of a regular-reflection configuration (without a Mach stem), this normalized length L should be zero. The normalized length is calculated for each CFD flow-field simulation of regular and Mach reflection patterns, as described in Sects. 4.3 to 4.5.
The angle \(\chi \) between the wedge surface and the triple-point trajectory, defined in Fig. 11, is given by
This important relationship between L and \(\chi \) is derived by assuming that the incident shock and Mach stem are straight lines and the Mach stem is perpendicular to the wedge surface.
Capturing the incident shock-front transition by probing the upper boundary cells to determine the transition pressure and flow-field locations
4.3 Incident shock trajectory and speed
The trajectory and speed of the incident shock are determined by post-processing data obtained from each CFD flow-field simulation, rather than accepting the theoretical shock speed based on the Rankine–Hugoniot equations that were used to initialize the CFD simulation. In the CFD simulations, which are based on solving Euler’s equations for inviscid flow, the incident shock front is a rapid transition of flow-field properties typically spread over 3 to 12 cells in this study due to numerical viscosity. (Note that there is no physical viscosity in these cases.) The objective is to determine the distance–time trajectory of the center of the incident shock-front transition and calculate therefrom the shock-front speed as the time derivative of the trajectory distance–time data.
The data collected from each CFD simulation to calculate the incident shock trajectory and speed are briefly described first. During each CFD simulation, all of the cells along the upper boundary, as illustrated in Fig. 12, are probed every time step just before AMR is activated (i.e., at every sixth time step), in the order of the cells ahead to behind the incident shock. This probing is done using the set of specified pressures
in which \(p_1^{\star }\) and \(p_2^{\star }\) are the theoretical pre- and post-shock pressures, and \(K=20\) is a convenient number when the number of discrete incident shock-front data points varies from 3 to 12. On each sweep k, the pressure \(\hat{p}_k\) is compared to the cell pressure \(p_\mathrm{cell}\). If \(\hat{p}_k>p_\mathrm{cell}\), the sweep continues to the next cell. When \(\hat{p}_k<p_\mathrm{cell}\), all relevant cell data for defining the incident shock transition are stored for post-processing, and the sweep of probing successive cells for pressure level k is terminated. This probing scheme of successive upper boundary cells effectively captures the incident shock-front transition as a collection of discrete pressure–distance data at a given time step, as also illustrated in Fig. 12. The sweeps for the \(\hat{p_k}\) levels can gather repeated data from the same cell. All redundant data are not needed to define the shock-front transition, so they are eliminated from the collected data sets.
The continuous shock-front transition can be constructed by means of a curve fit to the collected data, as shown by the dashed line through the discrete pressure–distance data. Then, the location \(x_\text {c}\) of the center of this transition, where the pressure is given by \(p_\text {c}=\frac{1}{2}\left( p_1^{\star }+p_2^{\star }\right) \), can be obtained, as depicted by the vertical dashed line in Fig. 12. Note that \(p_2^{\star }\) is the theoretical Rankine–Hugoniot pressure stemming from the specification of the incident shock Mach number \(M_{\mathrm{i}}\) used to initiate the computational flow-field simulations.
The shock-front transition is constructed from the interior cell pressures defined by \(p_i\), with \(i=1,2,\ldots ,n\), versus the cell center distances \(z_i=x_i-x_\mathrm{apex}\) along the upper boundary of the computational domain. The symbol n denotes the total number of discrete cell distances and pressures in the shock transition and \(x_\mathrm{apex}\) is the horizontal distance of the wedge apex on the lower boundary. The center of the shock-front transition propagates through the upper boundary cells with centers located by the coordinates (\(x_{i,j}\), \(y_{i,j}\)), in which the indices i and j denote the arrangement of the cells in the x and y directions. The variations in the vertical cell distances \(y_{i,j}\) from the upper wall do not influence the incident shock-front trajectory and speed because the shock-front is assumed normal to the upper boundary, so j and \(y_{i,j}\) are omitted from the analysis and equations.
The continuous transition \(z=z(p)\) of the incident shock front can be represented for convenience as
with the property averages defined by
The three unknown coefficients in this curve-fit equation, denoted by \(\hat{\alpha }\), \(\hat{\beta }\), and \(\hat{\gamma }\), are determined by means of a standard least-squares fitting method. Note that this logarithmic form of the curve-fit equation occurs in theoretical shock-front transitions obtained by Rankine [43] for heat conduction only and Taylor [44] and Becker [45] for both heat conduction and dynamic viscosity, although the shock-front structure in the CFD simulations originates from numerical viscosity (i.e., from ensuring non-oscillatory solution behaviour).
The global error is defined as the sum of the squares of the local errors and given by
and the weights \(w_i\) used in this study are defined by
The square of the weights \(w_i^2\) ranges from a maximum value of 7, when \(\left( z_i-z_o'\right) {/}\varDelta z_o\) is zero or close to zero, to much smaller values when \(\left( z_i-z_o'\right) {/}\varDelta z_o\) becomes large. Illustrations of \(z_o'\), \(z_i-z_o'\), and \(\varDelta z_o\) are shown in Fig. 13.
Definitions of \(p_o\), \(\varDelta p_o\), \(z_o'\), \(z_o\) and \(\varDelta z_o\) for the incident shock-front transition
The objective of the curve fit is to construct a continuous shock-front transition from the discrete distance \(z_i\) versus pressure \(p_i\) data and therefrom determine the location \(z_o\) on the transition for some specified pressure \(p_o\) (normally the center value). In this process, an approximate value of \(z_o\) is denoted by \(z_o'\), and it is obtained from the intersection of two straight lines; one for the constant pressure \(p_o\) and the other that joins the two coordinates pairs (\(z_i\),\(p_i\)) and (\(z_{i+1},p_{i+1}\)) that bracket the specified value of \(p_o\). Also defined in Fig. 13 are the terms \(\varDelta z_o=z_{i+1}-z_i\) and \(\varDelta p_o=p_{i+1}-p_i\), such that \(z_o'=z_i+\varDelta z_o \left( p_o-p_i\right) {/}\varDelta p_o\). When the curve fit has been constructed, the more accurate value of the distance \(z_o\) on the shock-front transition is calculated by means of (44) with the pressure \(p=p_o\). For the center of the shock-front transition, \(z = z_o \rightarrow z_\text {c}\) for \(p=p_o \rightarrow p_\text {c}=\frac{1}{2}\left( p_1^{\star }+p_2^{\star }\right) \).
In the standard least-square curve fit, the three derivatives \(\partial E/\partial \hat{\alpha }\), \(\partial E/\partial \hat{\beta }\), and \(\partial E/\partial \hat{\gamma }\) of (48) are determined and set to zero, and this procedural step yields the matrix equation
for the solution of \(\hat{\alpha }\), \(\hat{\beta }\), and \(\hat{\gamma }\). The elements of the square matrix and right-hand vector are given by
and these are averages like those defined earlier by (45)–(47). The solution of (50) follows as
for the curve-fit coefficients. Note that when the curve fit is done without using weights (i.e., \(w_i^2=1\)), then \(c=0\), \(e=0\), \(f=1\), and \(i=0\) from (53), (55), (56), and (59), such that the coefficient \(\hat{\gamma }\) is then equal to zero. This occurs because of the specific curve-fit construction given by (44).
The resulting continuous shock-front transitions of the incident shock by the preceding curve fits to CFD flow-field data are illustrated in Fig. 14 for three different reference points RP-4, 8, and 16 with different \(\alpha \) values of 0.005, 0.005, and 0.0 (normal to the extreme-angle transition boundary). Shown also are the interpolated shock-front transition centers from using \(p=p_\text {c}=\frac{1}{2}\left( p_1^{\star }+p_2^{\star }\right) \) to obtain \(z=z_\text {c}\) using (44). These results were chosen from CFD runs with different shock Mach numbers to illustrate the shock-front constructions for the cases when the number of discrete distance–pressure data were 11, 6, and 4 for reference points RP-4, 8, and 16, respectively. These illustrations are typical of all curve fits for the incident-shock front. The curve-fit expression given by (44) is successful in capturing the incident shock-front transitions.
Continuous transitions of the incident shock front in air, constructed by curve fits using discrete CFD flow-field data, when the AMR level \(n_{\mathrm{r}} = 10\)
The trajectory of the incident shock front, along the upper boundary during a CFD run, starts before the wedge apex and ends when the shock progresses along the upper boundary by the distance (1 m)\(\cos (\theta _{\mathrm{w}})\), which equals 1 m along the wedge surface. The trajectory consists of numerous \(z_\text {c}\) values determined at every sixth time step during the CFD run. Such results are illustrated in Fig. 15 for the reference points RP-3, 10, and 18 with different values of \(\alpha =0.005\), \(-0.023\), and 0.0, respectively. Each shock-front trajectory is plotted as a chain of numerous small dots, each dot corresponding to the time t at which the shock-front curve-fit equation gave the transition center value \(z_\text {c}\).
The three shock-front trajectories that are presented in Fig. 15 for the incident shock are typical of those obtained in this study for all of the reference points and different values of \(\alpha \). The shock-front trajectories look extremely linear. However, the actual advancement of the center of the incident shock in the CFD simulations is always forward but somewhat nonuniform or jerky with distance. This jerkiness in movement is very small and it decreases when the CFD time steps (\(\varDelta t\)) are reduced. Hence, trajectory jerkiness is less severe when using more levels of AMR in the CFD simulations, and also when flow-field simulations contain complex flow structures with larger flow velocities and sound speeds, because the time steps are thereby reduced.
Incident shock-front trajectories in air as chains of 4699, 4131, and 4702 dots for RP-3, 10, and 18, respectively, when the AMR level \(n_{\mathrm{r}} = 11\)
The curve fit to the incident shock trajectory data \(z_i=(z_{\mathrm{c},i},~t_i)\) is given by the second-order polynomial
along with relevant intermediate equations and the solution for the curve-fit coefficients \(\hat{a}\) and \(\hat{b}\). The first-order solution is obtained by setting \(\hat{b}=0\) in (63)–(65). The data used for the incident shock-front curve fits are always confined to the region of z from 10 cm to the end of the computer run when the incident shock reaches the final distance of about \(z_\mathrm{e}=(1~\mathrm {m})\cos \left( \theta _{\mathrm{w}}\right) \) along the top boundary, or a corresponding distance along the wedge of 1 m. The curve fits are more accurate when the distance–time data correspond to the incident shock reflecting from the wedge surface, because the time steps are then smaller than when the incident shock has not yet reached the wedge apex.
The goodness of the curve fit is tied closely to the standard deviation of the data from the fitted curve, which is calculated as \(\sigma _z=\left[ \frac{1}{m}\sum _{i=1}^m\left\{ z(t_i)-z_i\right\} ^2\right] ^{1/2}\), for which m is the number of \(\left( z_i,t_i\right) \) data pairs. For the incident shock in this study, the standard deviations were approximately 18, 9, and 4 microns for AMR levels \(n_{\mathrm{r}}=10\), 11, and 12, respectively, which correspond to about 1/8 of the size of the smallest computational cell edges within the flow field.
The incident shock-front velocity follows from the derivative of (63), and it is given by
in which \(t_\mathrm{e}\) is the time at the end of the computer run corresponding to the final distance \(z_\mathrm{e}\). For the trajectory data illustrated in Fig. 15 for reference points RP-3, 10, and 18, the post-processing of the CFD simulations via (66) yielded incident shock-front velocities of 352.151, 590.216, and 1205.028 m/s. These computed values are in excellent agreement with the corresponding theoretical values from the Rankine–Hugoniot equations that were utilized to initiate the computer runs, differing by 0.02, 0.008, and 0.005%, respectively. Although the incident shock-front trajectories in the CFD simulations are extremely linear and a straight-line fit could have been used to fit the data instead of the second-order polynomial, the second term \(2\,\hat{b}\,t_\mathrm{e} \ll \hat{a}\) in (66), such that the incident shock velocity \(V_{\mathrm{i}}\) is dictated primarily by the value of \(\hat{a}\).
4.4 Mach-stem trajectory and speed
The objective is to determine the distance–time trajectory of the center of the Mach-stem shock front along the wedge and calculate therefrom the Mach-stem speed from the time derivative of this trajectory. Although the process is similar to that for the incident shock front in the previous section, there are some significant differences to explain and difficulties to overcome.
During the collection of CFD simulation data that are used to perform the Mach-stem trajectory calculations, all of the cells along the wedge surface, in the order of the cells ahead to behind the Mach stem, are probed for each time step just before AMR is activated (i.e., every sixth time level), as illustrated in Fig. 16. This probing procedure is done with the set of specified pressures
in which \(p_1^{\star }\) and \(p_2^{\star }\) are the pre- and post-shock pressures of the incident shock front, and \(K=20\) is a convenient number as used previously in (43). The pressure difference between pressure levels (i.e., \(p_{k+1}-p_k\)) remains the same as that used for the incident shock front, but the pressure range has been increased substantially from \(K-1\) to 3K, because the Mach-stem shock (when it occurs) is not only stronger than the incident shock but its post-shock pressure \(p_3^{\star }\) is also unknown. These additional upper sweeps are required to ensure that the entire shock-front transition is captured at each time level of interest, as depicted in Fig. 16.
Capturing the Mach-stem shock-front transition by probing the cells along the wedge to determine the transition pressures and flow-field locations
The data collected from the cell centers consist primarily of the cell pressures \(p_{i,j}\) and locations (\(x_{i,j}\),\(y_{i,j}\)). These data are converted into the pressures \(p_i\) (j is ignored) and the distances \(z_i\), along the lower boundary before the wedge apex and then along the inclined wedge surface, by means of
with relevant information shown in Fig. 16. Note that
so that the calculations of the hypotenuse h, small angle \(\omega \) and \(h\cos \left( \omega \right) \) are not required, because \(h\cos \left( \omega \right) \) in (68) is replaced by the results of (70). The first calculation of \(z_i\) covers the case of the incident shock front moving along the lower boundary, and this is equivalent to that used for the incident shock front moving along the upper boundary. The second calculation of \(z_i\) is for the case of regular reflection (without a Mach stem) when the incident shock front contacts and moves along the wedge surface, and the distance extrapolation to the wedge surface is vertically downward or parallel to the incident shock front. The third calculation of \(z_i\) covers the last case of Mach reflection when the Mach stem contacts the wedge surface and the extrapolation is parallel to the foot of the Mach stem, which is assumed normal to the wedge surface.
Each set of discrete pressure \(p_i\) versus distance \(z_i\) data for the incident or Mach-stem shock front at the wedge surface is numbered \(i=1,2,\ldots ,n''\), and it contains repeated data (i.e., same shock-front pressures and locations). These redundant data are not needed to define the shock front, so they are removed, and the number of data \(n''\) is thereby reduced to \(n'\). This data set still contains additional data collected from the flow-field behind the shock front, stemming from the upper sweeps that pass the shock-front transition, as shown in Fig. 16. These extraneous data are also removed from the data set by doing the calculations
from \(i=3,4,\ldots ,n'-1\). If the ratio r of the current cell-center separation by the average separation is less than 1.1 for \(3\le i\le n'-1\), then all of the data are kept and \(n=n'\). However, if \(r>1.1\) for a particular value of i, then the calculations stop and \(n=i\). This truncates all of the extraneous data behind the shock front, because \(n'\) is reduced to n. The data set (\(z_i,p_i\)), \(i=1,2,\ldots ,n\) now contains data only for the shock-front transition at the wedge surface. Note that this previous procedure is effective in capturing the shock-front transition data, because the AMR in the CFD algorithm concentrates cells of small widths within and near shock fronts.
The continuous shock-front transition \(z=z(p)\) for the incident-shock or Mach-stem data is then obtained using the curve-fit equation
with the post-shock pressure \(p_3^{\star }\) replacing \(p_2^{\star }\) in (44)–(47). This post-shock pressure and the curve fit to the shock-front data are determined in the following manner. A value of \(p_3^{\star }\) is guessed to be slightly greater than \(p_n\) from the shock-front data set. The curve-fit coefficients \(\hat{\alpha }\), \(\hat{\beta }\), and \(\hat{\gamma }\) in (72) are determined using (50)–(62) with \(p_3^{\star }\) replacing \(p_2^{\star }\). The corresponding global error E is then calculated using (48), with \(p_3^{\star }\) replacing \(p_2^{\star }\), and the derivative
is calculated. This derivative should be negative if the value of \(p_3^{\star }\) is sufficiently close to that of \(p_n\). The value of \(p_3^{\star }\) is then increased and the procedure is repeated until the derivative changes to a positive value. When this occurs the minimum in the global error E has been bracketed between the last two choices of \(p_3^{\star }\), as illustrated in Fig. 17. A cubic polynomial is then constructed between the two data points with known slopes that bracket the global-error minimum to determine the new estimate of \(p_3^{\star }\), which is obtained by setting the derivative of the cubic polynomial to zero. The global error E can also be calculated for this new estimate of \(p_3^{\star }\). The process is iterative by applying the cubic polynomial between points that bracket the minimum more closely, yielding a final accurate result for \(p_3^{\star }\). When this iteration is finished, the curve fit of the shock front is also completed, and the value of the shock-front center \(z_\text {c}\) is obtained using \(p=p_\text {c}=\frac{1}{2}\left( p_1^{\star }+p_3^{\star } \right) \) in (72).
Determining the post-shock pressure \(p_3^{\star }\) and curve fit of the Mach-stem shock front by minimizing the global error
Continuous transitions of the Mach-stem shock front in air, constructed by curve fits using CFD flow-field data, when the AMR level \(n_{\mathrm{r}}=11\)
The resulting continuous shock-front transitions of the Mach stem by the preceding curve fits to CFD flow-field data are illustrated in Fig. 18 for reference points RP-3, 9, and 17 using different alpha values of 0.015, 0.004 and \(-0.0138\) (normal to the extreme-angle transition boundary). Shown also are the interpolated shock-front transition centers from using \(p=p_\text {c}=\frac{1}{2}\left( p_1^{\star }+p_3^{\star }\right) \) to obtain \(z=z_\text {c}\) in (72). These shock-front constructions are for three cases with discrete distance–pressure shock transition data of 10, 6, and 4 for reference points RP-3, 9, and 17, respectively. These constructions are typical of all curve fits for the Mach stem occurring in this study. It is readily apparent that the curve fit given by (72) successfully captures the Mach-stem shock-front transitions.
The trajectory of the center of the shock front of the Mach stem along the wedge surface during a CFD run, from its start at the wedge apex and ending when it progresses along the wedge surface by about 1 m, is obtained from numerous \(z_\text {c}\) values determined at every sixth time level during the CFD run. Such results are illustrated in Fig. 19 for three different reference points RP-3, 8, and 19, with different values of alpha 0.005, 0.004, and 0.0, respectively. Each shock-front trajectory is plotted as a chain of numerous small dots, each dot corresponding to the time t at which the curve fit gave the center value \(z_\text {c}\). The Mach-stem trajectories are slightly kinked at the wedge apex (\(z=0\) cm), because the shock speed along the lower boundary before the wedge apex essentially equals that of the incident shock, but later along the wedge surface the Mach-stem shock is stronger than the incident shock and its speed is larger.
Mach-stem shock-front trajectories in air as a chain of 4689, 3972, and 4464 dots for RP-3, 8, and 19, respectively, when the AMR level \(n_{\mathrm{r}}=11\)
The three shock-front trajectories that are presented in Fig. 19 for the Mach stem are typical of those obtained in this study for all of the reference points and different values of \(\alpha \). The two portions of each shock-front trajectory are almost linear, and the actual advancement of the center of the Mach-stem transition in the CFD simulations is always forward but jerky with distance, very similar to that for the motion of the incident shock along the upper boundary. The speed of the Mach stem along the wedge surface is determined by fitting a second-degree polynomial to the distance–time data, as given earlier by (63) for the incident shock wave. The distance–time data used for this curve fit spans the distances along the wedge from 50 cm to the end of the CFD run at 100 cm, or slightly larger because the Mach stem is ahead of the incident shock front. The time derivative of the curve fit then yields the Mach-stem speed \(V_{\mathrm{m}}=\hat{a}+2\hat{b}\mathrm{t}_\mathrm{e}\) at the end of the shock-front trajectory.
The goodness of the polynomial fit is tied closely to the standard deviation of the data from the second-order curve fit, and the standard deviations given by \(\sigma _z=\left[ \frac{1}{m}\sum _{i=1}^m\left\{ z(t_i)-z_i\right\} ^2\right] ^{1/2}\) can vary markedly for the case of the Mach stem, in contrast to those reported earlier for the incident shock. For regular reflection from the wedge surface, the standard deviations are typically 2 to 4 times as high as those for the incident shock. For Mach reflections with large Mach stems that emerge and stabilize rapidly as the wedge apex is encountered and passed, the standard deviations are 2 to 20 times higher than those for the incident shock. However, for Mach reflections close to the numerically determined transition boundary, the emergence of an extremely small Mach stem and its stabilization with distance along the wedge is somewhat erratic, and the standard deviations are much larger as a result. In such cases, the Mach stem can either emerge suddenly and then decelerate or it can emerge slowly and then accelerate to a final speed. The distance–time trajectories of such Mach stems are somewhat curved and the use of a second-order polynomial curve fit to these trajectories yields smaller standard deviations of the data from the fitted curves in comparison to those computed from a first-order polynomial curve fit.
Mach-stem length L versus parameter \(\alpha \) for RP-3, 7, 11, 15, and 18 in air, when the AMR level \(n_{\mathrm{r}}=12\)
4.5 Determination of numerical transition boundary between RR and MR from CFD flow-field data
The methodology and related post-processing tools developed and described in the previous Sects. 4.1 to 4.4 are now combined to determine the numerical transition boundary between regular and Mach reflections by processing the CFD flow-field data for the 20 reference points defined earlier in Table 1 and shown previously in Fig. 10.
Five plots of the Mach-stem length L versus the parameter \(\alpha \) (normal to von Neumann’s extreme-angle boundary) are shown in Fig. 20 for reference points RP-3, 7, 11, 15, and 18. Each plot originates from the post-processing of numerous closely spaced CFD flow fields around the numerical transition boundary, such that the transition value \(\alpha _\mathrm{c}\) can be obtained accurately when the Mach-stem length L from Mach reflection patterns diminishes to zero and the Mach reflection configurations first switch into that of a regular reflection.
The method of obtaining the numerical transition boundary from such L versus \(\alpha \) plots is explained. Two sets of post-processed data are determined for each plot shown in Fig. 20. The first data set originates from calculations for which all shock reflection patterns from the wedge surface are assumed to be regular reflection, and the data for \(z_i\) in the post-processing phase is mapped downward onto the wedge surface, parallel to the incident shock wave, as illustrated earlier in Fig. 16. Some of these data are shown on the left side of the five plots in Fig. 20 as the white-filled circles, and they are labelled RR for regular reflection. The second data set originates from calculations for which all shock reflection patterns from the wedge surface are assumed to be Mach reflection, and the data for \(z_i\) in the post-processing phase are mapped onto the wedge surface, normal to the surface and parallel to the Mach stem (if it exists or it does not), as also illustrated earlier in Fig. 16. Some of these data are shown on the right side of the five plots in Fig. 20 as the black-filled circles or black dots, and they are labelled MR for Mach reflection. The average value of the left-most data (before the left-most vertical dashed line) for the RR white-filled circles in each plot is calculated, denoted by \(\overline{L}_\text {rr}\), and shown as a horizontal dashed line in each plot given in Fig. 20. The average value of the left-most data for the MR black dots (not shown on the left side of each plot) is also calculated, denoted by \(\overline{L}_\text {mr}\), and shown as another horizontal dashed line. Both averages are nearly zero because they correspond to regular-reflection patterns, the average \(\overline{L}_\text {mr}\) is always lower than \(\overline{L}_\text {rr}\), and the differences between the two are noticeable only for incident shock Mach numbers \(M_\mathrm{i}\) between 1.1 to 1.7 and wedge angles from 40\(^{\circ }\) to 50\(^{\circ }\).
The data for the case of regular reflection (white-filled circles) are more sensitive to the emergence of the Mach stem than the data for the case of Mach reflection (black dots). For the case of the mapping of \(z_i\) downward onto the wedge surface (parallel to the incident shock), a disturbance must have a speed slightly larger than the incident shock speed \(V_{\mathrm{i}}\) to emerge as a partial or full Mach stem. For the other case of the mapping of \(z_i\) normal to the wedge surface (parallel to the Mach stem), a disturbance must have a speed slightly larger than \(V_{\mathrm{i}}/\cos \left( \theta _\mathrm{w}\right) \) to emerge as a partial or full Mach stem.
As \(\alpha \) increases in the plots shown in Fig. 20, the regular-reflection data, therefore, indicate the early or premature arrival of the onset of Mach reflection, whereas the Mach reflection data indicate the late or delayed arrival of the onset of Mach reflection. Hence, the first indication in the regular-reflection data of a disturbance or Mach stem is flagged, and shown by the left-most vertical dashed line among the white-filled circles in the plots in Fig. 20. Furthermore, the delayed indication in the Mach-reflection data of a strong change to a Mach stem is correspondingly flagged, and shown by the right-most vertical dashed line among the black dots.
These two flag placements are based on changes in the data by about two or more standard deviations from the average values of \(\overline{L}_\text {rr}\) and \(\overline{L}_\text {mr}\). The numerical transition-boundary value of \(\alpha \), denoted by \(\alpha _\mathrm{c}\), is simply taken as the center value or average of the early and late indications of the emergence of a Mach stem. Furthermore, once the center value \(\alpha _\text {c}\) has been determined, only the regular-reflection data (white-filled circles) are plotted on the left-hand side of this center value, and only the Mach-reflection data (black dots) are plotted on the right-hand side, as illustrated in all five of the plots in Fig. 20.
The plots of L versus \(\alpha \) for incident shock Mach numbers \(M_\mathrm{i}\) ranging from 1.0 to 1.5, before the dual region of regular and Mach reflection shown in Fig. 10, exhibit fairly gradually and smoothly changing values of L from large values in the Mach reflection region to zero (or nearly zero) as the numerical transition boundary is approached. Such changes are observable in Fig. 20a, b. This also means that the change in the size of the Mach stem from Mach to regular reflection is also fairly smooth and gradual, occurring over a wide range of \(\alpha \) values, and diminishes slowly to zero as the transition boundary is approached.
For the case of higher incident shock Mach numbers from 1.5 to 4.0 (and upward), in the dual region of regular and Mach reflection, the reduction in the size of the Mach stem from Mach to regular reflection is much more rapid and even discontinuous, occurring over a narrow range of \(\alpha \) values. Such changes are observable in Fig. 20c–e. Such nearly discontinuous Mach-stem changes from Mach to regular reflection at the transition boundary, from a sizable Mach stem to no Mach stem, were noticed and explained in the early experimental results and theoretical research by Bleakney and Taub [8] and Kawamura and Saito [10].
The L versus \(\alpha \) results presented in this research for the stronger incident shocks are smoothed somewhat through the numerical transition boundary from the numerical computations that ensure solution monotonicity near discontinuities. Note that the width of this smearing is reduced when the accuracy of the CFD simulations is improved by increasing the number of AMR levels. The 12 refinement levels for AMR used in this research were carefully selected by assessment testing to ensure that the numerical transition boundary was accurately defined and essentially independent of the mesh densities used in the CFD simulations. Further discussion of CFD flow-field convergence and solution accuracy is provided in Sect. 4.6.
Transition from Mach to regular reflection for RP-5 in air (\(M_{\mathrm{i}}^\star = 1.089\), \(\theta _{\mathrm{w}}^\star = 35.8945^\circ \), \(n_{\mathrm{r}} = 12\))
Transition from Mach to regular reflection for RP-16 in air (\(M_{\mathrm{i}}^\star = 3.0\), \(\theta _{\mathrm{w}}^\star = 50.7032^\circ \), \(n_{\mathrm{r}} = 12\))
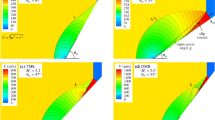
Contoured flow-field images from CFD simulations for Mach reflection changing to regular reflection are presented in Figs. 21 and 22 for reference points RP-5 and RP-16, respectively. Each collection of four images is arranged normal to von Neumann’s extreme-angle transition boundary and features in sequence two Mach-reflection patterns with diminishing Mach-stem lengths, then the pattern at the numerical transition boundary when the Mach stem just disappears, and finally one regular-reflection pattern just beyond this transition boundary. These images are focused on the shock-reflection patterns close to the wedge surface, and the lengths of 5 mm and 5 cm that are included in Figs. 21 and 22 provide a reference length scale.
The two Mach-reflection patterns in Fig. 21 are presented at values of \(\alpha =0.015\) and 0.0075, which are rather far from the numerical transition-boundary value of \(\alpha _\text {c}=0.0001\), because the Mach stem and slip stream are otherwise too small to be easily observed by the human eye for \(\alpha \) values much closer to the numerical transition boundary. The opposite is true of the results presented in Fig. 22. In this case, the two Mach-reflection patterns with a Mach stem and slip stream at \(\alpha =-0.0126\) and \(-0.0138\) close to the numerical transition boundary of \(\alpha _\text {c}=-0.0154\) are much more pronounced, because these results occur in the dual region where either Mach or regular reflection can occur.
The triple-point trajectory angles \(\chi \), corresponding to the Mach-reflection patterns in Figs. 21a and 22a with the largest Mach stems, are given by \(0.100^{\circ }\) and \(1.98^{\circ }\), respectively. The triple-point angles for the Mach-reflection patterns in Figs. 21b and 22b, with slightly smaller Mach stems (i.e., closer to the transition boundary), are given by \(0.0245^\circ \) and \(0.908^\circ \), respectively. These angles were calculated using (42) and the information on L and \(\theta _{\mathrm{w}}\) provided in the captions. These calculated values of \(\chi \) are more precise than those measured directly from enlarged CFD flow-field images, such as those in Figs. 21 and 22.
The numerical transition-boundary points from post-processing all of the CFD flow-field data for the 20 reference points on von Neumann’s extreme-angle transition boundary are summarized in Table 2. The values of the transition value \(\alpha _\text {c}\) from data like those shown in Fig. 20, and the corresponding incident shock Mach number \(M_\mathrm{i}\) and wedge angle \(\theta _\mathrm{w}\) calculated using (38) and (39), appear in columns 4 to 6.
4.6 Study of mesh refinement on solution accuracy
An investigation was performed to determine the effects of mesh refinement on the accuracy of the CFD flow-field solutions and the subsequent post-processing determination of the new numerical transition boundary between regular and Mach reflections. The assessment was performed to evaluate the resolution requirements for the 20 selected reference points (Table 1) to yield the set of 20 transition points for the transition value \(\alpha _\text {c}\), related incident shock Mach number \(M_{\mathrm{i}}\) and related wedge angle \(\theta _{\mathrm{w}}\) reported in Table 2. This study demonstrates that the mesh was sufficiently refined at 12 levels of anisotropic adaptive mesh refinement (AMR) such that the final results for the new numerical transition boundary were converged (i.e., grid independent) and could, therefore, be considered accurate.
Four plots of the normalized Mach-stem length L versus the parameter \(\alpha \) for AMR levels \(n_{\mathrm{r}}=10\), 11, 12, and 13 are presented in Figs. 23 and 24 for reference points RP-5 and 16, respectively. The results for RP-5 are typical of all reference points for incident shock Mach numbers in the range \(1.0<M_{\mathrm{i}}<1.6\), for which the new numerical transition boundary agrees well with the closely spaced sonic and extreme-angle boundaries of von Neumann [5]. The results for RP-16 are typical of all reference points for incident shock Mach numbers in the range \(1.6<M_{\mathrm{i}}<4.0\), for which the new numerical transition boundary trends slightly but significantly above the closely spaced sonic and extreme-angle boundaries into the dual region of regular and Mach reflections.
As the mesh is refined from AMR levels \(n_{\mathrm{r}}=10\) to 13 for reference points RP-5 and 16 in Figs. 23 and 24, (i) the two averages \(\overline{L}_\text {rr}\) and \(\overline{L}_\text {mr}\) become more equal and converge toward the true value of zero, (ii) the vertical variations in the data for regular reflection (white-filled circles) diminish substantially (especially for RP-1 to 8), (iii) the vertical variations in the data for Mach reflection (black dots) diminish marginally, (iv) the bottom transition region between regular and Mach reflections becomes narrower (RP-5) and sharper (RP-16), (v) the early and late indicators of the emergence of a Mach stem, denoted by the two outer vertical dashed lines, contract for increasing mesh refinement levels of AMR, (vi) the average of these early and late indications for RP-5, given by the center dashed-line labelled \(\alpha _\text {c}\), shifts slightly rightward (towards the extreme-angle boundary), less and less as the value of \(\alpha _\text {c}\) converges to a nearly constant value between the sonic and extreme-angle boundaries, and (vii) the average of these early and late indications for RP-16, given by the center dashed-line labelled \(\alpha _\text {c}\), shifts slightly leftward (away from both the sonic and extreme-angle boundaries), less and less as the value of \(\alpha _\text {c}\) converges to a nearly constant value.
Mach-stem length L versus parameter \(\alpha \) for RP-5 in air, when the AMR level \(n_{\mathrm{r}}=10\), 11, 12, and 13
Mach-stem length L versus parameter \(\alpha \) for RP-16 in air, when the AMR level \(n_{\mathrm{r}}=10\), 11, 12, and 13
The small changes in the transition values of \(\alpha _\text {c}\) with increasing mesh refinement, as shown in Figs. 23 and 24 for reference points RP-5 and 16 with AMR levels \(n_{\mathrm{r}}=10\) to 13, are not significant in changing the numerically determined transition-boundary points \((M_{\mathrm{i}}, \theta _{\mathrm{w}})\) presented in Table 2. If the early and late vertical dashed-line indicators of the emergence of the Mach stem in the plots of L versus \(\alpha \) are considered as error bars on the transition value of \(\alpha _\text {c}\), then the results presented in Table 2 for \(M_{\mathrm{i}}\) and \(\theta _{\mathrm{w}}\) are accurate in the worst cases to within \({\pm }0.22\) and \({\pm }0.27\)%, for all 20 reference points selected along von Neumann’s extreme-angle transition boundary. The resulting error bars on symbols used to plot the incident shock Mach number \(M_{\mathrm{i}}\) versus the wedge angle \(\theta _{\mathrm{w}}\) for the numerically determined transition points (like data shown in Fig. 2) are not noticeable, because they would each be covered by the white-filled circle or black-dot markers.
The use of 12 levels of AMR is considered sufficient to accurately determine the new transition boundary separating regular and Mach reflections in this research. This conclusion is based on the present mesh refinement study on CFD solution accuracy, in conjunction with the preceding results presented in Sects. 4.3 and 4.4 that illustrate the high accuracy of the post-processing method in the computations of the incident and Mach shock speeds \(V_{\mathrm{i}}\) and \(V_{\mathrm{m}}\). At the mesh resolution of 12 levels of AMR, the predicted CFD flow-field solutions and post-processed transition-boundary points are considered as essentially independent of the mesh densities used for the CFD simulations.
5 Experimental transition boundary for regular to Mach reflections without a boundary layer
Experimental data are collected herein to verify the numerical transition boundary between regular and Mach reflection from a wedge, for the specific case when no shear or boundary layer exists on the inclined reflecting surface. Only seven such experimental results have been published.
Smith [46] in 1959 was the first researcher to propagate a shock wave at an almost constant speed \(V_\mathrm{i}\) or shock Mach number \(M_\mathrm{i}\) along a rectangular shock-tube channel and then reflect this planar shock from an angled channel end. His experimental setup is illustrated in Fig. 25 for the case of Mach reflection. The two reflected shocks from the two angled channel ends interact by reflecting from each other along the channel center plane. The reflected shock angle with the channel centerline is shown in the figure as \(\theta _\mathrm{i}\), and the wedge angle is given by \(\theta _\mathrm{w}=90^{\circ }-\theta _\mathrm{i}\). Because the shock reflecting surface behind the two reflecting shocks is gaseous and moving behind the shocks, no boundary or shear layer is produced at the reflecting surface. As a consequence, regular and Mach reflection processes are essentially inviscid, without the shear effect of viscosity and heat transfer by conduction at an otherwise rigid and stationary material surface. To determine the transition boundary between regular and Mach reflection, the channel-end angle \(\theta _\text {e}\) must be changed gradually from one shock-tube experiment to the next (normally for the same incident shock strength), so that the Mach stem diminishes to zero and regular reflection just begins.
Mach reflection in a shock tube with a wedge-shaped or angled reflecting duct end
Henderson and Lozzi [16, 27] adopted this shock-tube technique of Smith [46] for some of their work in 1975 and 1979. Experimental results to be used later in this research, in terms of the incident shock Mach number \(M_\mathrm{i}\) and wedge angle \(\theta _\mathrm{w}\), were extracted from various diagrams and figures in the papers of Smith [46] and Henderson and Lozzi [16, 27]. These final results are presented in Table 3.
Mach reflection in a bifurcated shock tube where the upper and lower ducts rejoin
Regular to Mach reflection transition boundary in air without a shear or boundary layer (inviscid). The numerical transition boundary determined in this research is defined by the string of 20 white-filled circles
Barbosa and Skews [47] in 2002 criticized the technique of Smith [46] with an angled shock-tube end as being too small in size and lacking interpretation accuracy. Instead, they built a large shock tube with a channel that first bifurcates into two equal-sized diverging ducts, which slowly bend back together, and finally rejoin, as illustrated in Fig. 26. Two equal-strength shocks emerging from the upper and lower ducts come together and reflect from each other. Maintaining a constant gas temperature in the long upper and lower ducts before experiments was difficult, but overcome.
The final shock reflection process for the case of a wedge angle of 40\(^{\circ }\) from Barbosa and Skews [47] is depicted in Fig. 26, for the case of Mach reflection. The shock reflecting surface is gaseous and moving behind the reflecting shocks, as in Smith’s apparatus, such that no shear or boundary layer is produced. Hence, the shock reflection process is essentially inviscid. The strengths of the incident shock waves are systematically varied to make the Mach stem length approach zero to determine the transition between regular and Mach reflection. Further bifurcated shock-tube experiments using 20\(^{\circ }\) and 48\(^{\circ }\) wedge angles with inviscid, gaseous reflecting surfaces were performed in 2011 by Herron and Skews [48]. The experimental results for the incident shock Mach numbers \(M_\mathrm{i}\) and wedge angles \(\theta _\mathrm{w}\) used in these studies are taken directly from the papers by Barbosa and Skews [47] and Herron and Skews [48]. These results are also included in Table 3.
6 Discussion of the new numerical transition boundary between regular and Mach reflections
The numerical transition boundary between regular and Mach reflections from flow-field simulations using CFD techniques described in Sect. 3, for an inclined wedge without a boundary layer, and using post-processing tools described in Sect. 4, are plotted as a sequence of white-filled circles in Fig. 27. This is done for all 20 reference points selected along von Neumann’s extreme-angle transition boundary in Sect. 4.1, and the data were taken directly from earlier results collected in Table 2.
For low incident shock Mach numbers \(M_\mathrm{i}\) ranging from 1.0 to 1.6, the numerical transition boundary is in excellent agreement with the analytical results of von Neumann [5] for the sonic and extreme-angle transition boundaries, which are very close together. However, for higher Mach numbers from 1.6 to 4.0, the numerical transition boundary trends slightly higher than the sonic and extreme-angle boundaries by as much as 1.6\(^{\circ }\). This upward shift of the numerical transition boundary above the closely spaced sonic and extreme-angle boundaries occurs only in the dual region where either regular or Mach reflection can occur. The upward trend of this numerical transition boundary (inviscid, no boundary layer) in the dual region is somewhat unanticipated, because it was expected that the numerical transition boundary would be in close agreement with the closely spaced sonic and extreme-angle transition boundaries of von Neumann [5].
Transition-boundary results for regular to Mach reflections from shock-tube experiments with inclined surfaces that are gaseous and moving without a shear or boundary layer behind the shocks, as described in Sect. 5 and given in Table 3, are included in Fig. 27. Most of these experimental results are for low incident shock Mach numbers \(M_\mathrm{i}\) below 1.4. These results are in good agreement with von Neumann’s analytical and closely spaced sonic and extreme-angle transition boundaries, and also in good agreement with our results for the new numerical transition boundary. The numerical transition boundary, in the range \(1.0<M_{\mathrm{i}}<1.6\), is not sufficiently accurate to provide a definitive conclusion as to whether it agrees better with either the sonic or extreme-angle boundary, primarily because the sonic and extreme-angle boundaries are so close together. However, the new numerical transition boundary typically lies between the closely spaced sonic and extreme-angle boundaries for this lower range of incident shock Mach numbers.
One shock-tube result from Henderson and Lozzi [16] for \(M_\mathrm{i}=1.88\pm 0.07\) with \(\theta _{\mathrm{w}}=51.0^\circ \pm 0.5^\circ \) lies inside the dual region of regular and Mach reflection. This result is \(0.6^\circ \) above the extreme-angle boundary, which is definitively above von Neumann’s closely spaced analytical sonic and extreme-angle boundaries. This result, however, is in good agreement with the new numerical transition boundary. Unfortunately, experimental shock-tube results like those of Smith [46], Henderson and Lozzi [16, 27], Barbosa and Skews [47], and Herron and Skews [48] are not available at higher incident shock Mach numbers to provide a more conclusive confirmation that the new numerical transition boundary for inviscid gas flows is a better transition boundary than those of von Neumann for the closely spaced sonic and extreme-angle boundaries.
A numerical and experimental study by Previtali et al. [49] for a moving incident shock interacting with straight and concave tipped wedges contains information that is relevant to the present paper. The CFD simulations and visual inspections of enlarged flow-field images to determine Mach and regular reflection patterns for the case of the straight wedge without a surface boundary layer (inviscid flow) in a diatomic and polytropic gas illustrate that the transition from Mach to regular reflection occurs very close to the closely spaced sonic and extreme-angle boundaries of von Neumann, for the case of their four incident shock Mach numbers \(M_{\mathrm{i}}\) of 1.5, 2.0, 2.5, and 3.0 connected to the dual region. Their four transition-boundary points lie much closer to the closely spaced sonic and extreme-angle boundaries than to our new numerical transition boundary. As a consequence, the authors of this paper conclude that the four transition-boundary points of Previtali, Timofeev, and Kleine do not support or confirm our new numerical RR to MR transition boundary within the dual region. The reasons for the differences between Previtali, Timofeev, and Kleine and our results are not clear, but they use short wedge lengths of 5 cm versus our more appropriate 100 cm, and they perform visual inspections of enlarged flow-field images to determine Mach and regular reflection patterns versus our methodology (Sect. 4) of capturing refined shock-front output data in conjunction with accurate post-processing analyses.
The new numerical transition boundary between regular and Mach reflection clearly does not agree with the mechanical-equilibrium boundary of von Neumann [5] for the present case of unsteady or pseudo-steady flows for a moving incident shock interacting with an inclined wedge (as can be seen in Fig. 27). However, for the case of steady supersonic flows over wedges, the two transition boundaries for MR to RR and RR to MR are known to be roughly close to von Neumann’s mechanical-equilibrium and sonic or extreme-angle boundaries, respectively, that encompass the dual region. Hysteresis effects involving the changing back and forth between regular and Mach reflection patterns by slow cyclic changes in the wedge angle are known to occur, as studied by Ben-Dor [13] and Ivanov et al. [50]. Such hysteresis effects do not occur for the case of a moving planar shock interacting with an inclined wedge of fixed wedge angle. Hornung [21] provides more information about the differences between shock-wave reflections from wedges for unsteady or pseudo-steady flow (i.e., with a moving shock) and those for steady or quasi-steady supersonic flow reflections from a wedge.
7 Conclusions
The three sets of analytical equations to determine the RR to MR transition boundaries for von Neumann’s sonic, extreme-angle, and mechanical-equilibrium criteria were revised and shortened, and relevant details of their contact point and maximum values were also provided. These results have been included because of their importance to the new results for the numerical transition boundary between regular reflection (RR) and Mach reflection (MR) for the case of moving planar shock waves interacting with an inclined wedge.
An accurate and systematic methodology for determining the numerical transition boundary between RR and MR from CFD flow-field simulations without a boundary layer on the wedge surface was well established in this study, including important details of sophisticated procedures for calculating the speeds of the incident shock and Mach stem, calculating the normalized (self-similar) Mach-stem length, and extracting the numerical transition-boundary point from closely packed CFD flow-fields across but normal to von Neumann’s extreme-angle boundary. The procedure was applied for the case of polytropic air at the 20 reference points defined earlier in Sect. 4.1. These 20 numerical transition-boundary points (\(M_{\mathrm{i}}\),\(\theta _\mathrm{w}\)) given in Table 2 have been determined with an accuracy superior to that possible by human inspection and interpretation of numerical images from simulated flow fields and experimental photographs from experiments.
The numerical transition boundary for inviscid flow along the wedge surface agrees well with the closely spaced analytical sonic and extreme-angle boundaries of von Neumann [5] for low incident shock Mach numbers from 1.0 to 1.6, as might be expected. However, this boundary trends unexpectedly slightly upward by as much as 1.6\(^{\circ }\) above the extreme-angle boundary at larger incident shock Mach numbers from 1.6 to 4.0. Although this upward trend is small, it is noticeable, significant, and confirmed by one experiment by Henderson and Lozzi [16]. For inviscid flow along the wedge surface, with no boundary layer, stronger Mach reflections, therefore, persist upward from the Mach-reflection region into the dual region of regular and Mach reflection patterns (Fig. 27). This is exactly the opposite behaviour of what occurs for the case for shock reflections with a viscous and thermal boundary layer on the wedge surface, where regular reflections persist downward into the Mach reflection region (Fig. 2). Hence, for shock reflections with a boundary layer on the wedge surface, the persistence of regular reflection occurs from the regular reflection region across the entire dual region and the new numerical transition boundary, over the closely spaced sonic and extreme-angle transition boundaries, and down into the Mach-reflection regions of TMR and DMR. The experimental persistence is, therefore, larger than previously understood, in that it is now considered to progress past the new numerical transition boundary, instead of only the lower sonic and extreme-angle transition boundaries. The experimental results of shock reflections from a wedge with a boundary layer are illustrated in Fig. 2, and those of the other case without a boundary layer are illustrated in Fig. 27.
The physical mechanism and reasons for the upward shift in the new numerical RR to MR transition boundary, above von Neumann’s closely spaced sonic and extreme-angle boundaries, in the dual RR and MR region (\(1.6<M_\mathrm{i}<4.0\)), is not yet fully understood. Systematic grid convergence studies and post-processing analyses of the CFD flow-field solutions have ruled out numerical errors as a possible source or cause of this small upward shift. The string of 20 white-filled circles for the new numerical transition boundary originates from a large number of carefully and systematically conducted unsteady CFD flow-field simulations. The transition-boundary points, as a string of data, are neither erratic nor random in behaviour; instead, they occur in a uniform and systematic manner (Fig. 27). The new numerical transition boundary has been generated by high-resolution CFD simulations which account fully for the unsteady shock-reflection process from the inclined wedge surface, unlike the analytical boundaries which are based on quasi-steady theory with straight shock fronts. The effects of the corner disturbance speed and shape are included in these computations, as are those of the curved reflected shock when the corner disturbance overtakes the incident shock in RR and the triple point in MR, and the slip stream can be straight or curved. Consequently, it should not necessarily be expected that the new numerical transition boundary will agree well with the closely spaced sonic and extreme-angle boundaries for larger incident shock Mach numbers corresponding to the dual RR and MR region. Von Neumann’s transition boundaries, based on the sonic and extreme-angle criteria, stem from fairly simple analytical considerations in which the incident, reflected and Mach-stem shocks are all assumed planar or straight, and the slip stream is also assumed straight. Moreover, von Neumann’s analytical formulations ignore the corner disturbance totally for the extreme-angle boundary, and the corner signal is assumed to move at the speed of sound superposed on the flow for the other case of the sonic transition boundary. More detailed physical reasons for the small but significant upward shift in the new numerical transition boundary into the dual region of RR to MR are currently being investigated for possible publication later.
As a recap, the occurrences of regular and/or Mach reflection in various ranges of the wedge angle \(\theta _{\mathrm{w}}\), for inviscid flows without a boundary layer and viscous flows with a boundary layer, are summarized in Tables 4 and 5. These tables pertain to incident shock Mach numbers in the ranges \(1.0< M_{\mathrm{i}} < 1.55\) before the dual region of RR and MR, and \(M_{\mathrm{i}}>1.55\) for the dual region, respectively. In these tables, the new symbols \(\theta _\text {sb}\), \(\theta _\text {eab}\), \(\theta _\text {meb}\), and \(\theta _\text {nb}\) denote the respective wedge angles for the sonic, extreme-angle, mechanical-equilibrium and new numerical transition boundaries. In addition, \(\theta _\text {exp}^\text {if}\) and \(\theta _\text {exp}^\text {vf}\) denote the transition boundaries from the string of experimental results without and with a boundary layer on the wedge surface, respectively, corresponding to inviscid and viscous flows. The tabulated regions of RR and MR stem from previous and current studies.
In a planned follow-on study, the persistence of regular reflection across both the new numerical transition boundary and sonic and extreme-angle transition boundaries (inviscid) into the Mach reflection region will be explored. This study will involve the solution of the Navier–Stokes equations for shock reflections from an inclined wedge with a combined viscous and thermal boundary layer on the wedge surface. The objective will be to develop a better understanding of why the experimental results (with a wedge boundary layer) shown in Fig. 2 persist noticeably below von Neumann’s sonic and extreme-angle transition boundaries and to explore the effects of the wedge length on this persistence.
References
Mach, E.: Über den verlauf der funkenwellen in der ebene und im raume. Sitzungsber. Akad. Wiss. Wien. (II, Abth), 77, 819–838 (1878)
Smith, L.G.: Photographic investigation of the reflection of plane shocks in air, Division 2, National Defence Research Committee of the Office of Scientific Research and Development, OSRD Rep. No. 6271 (1945)
White, D.R.: An experimental survey of the Mach reflection of shock waves, Technical Report II-10, Department of Physics, Princeton University, Aug. 1951. Also, Proceedings of the Second Midwestern Conference on Fluid Mechanics, March 17–19, 1952, Ohio State University, Engineering Experiment Station Bulletin 149, 21(3), 253–259 (1952)
von Neumann, J.: Theory of shock waves, Progress Report, Division 8, National Defence Research Committee of the Office of Scientific Research and Development, U.S. Dept. Comm. Tech. Serv. No. PB32719 (1943). Also, John von Neumann, Collected Works, Pergamon Press, 6, 178–202 (1963)
von Neumann, J.: Oblique reflection of shocks, Explosive Research Report No. 12, Navy Department, Bureau of Ordnance, U.S. Dept. Comm. Tech. Serv. No. PB37079 (1943). Also, John von Neumann, Collected Works, Pergamon Press 6, 238–299 (1963)
von Neumann, J.: Refraction, intersection and reflection of shock waves, paper delivered at a conference on Shock Waves and Supersonic Flow on 19 March 1945 at Princeton University (1945). Also, John von Neumann, Collected Works, Pergamon Press 6, 300–308 (1963)
Courant, R., Friedrichs, K.O.: Supersonic Flow and Shock Waves. Wiley Interscience Publishers, New York (1948)
Bleakney, W., Taub, A.H.: Interaction of shock waves. Rev. Mod. Phys. 21(4), 584–605 (1949)
Cabannes, H.: Lois de la réflexion des ondes de choc dans les écoulements plans non stationnaires, O.N.E.R.A. 80, 1–29 (1955)
Kawamura, R., Saito, H.: Reflection of shock waves: 1. Pseudostationary case. J. Phys. Soc. Jpn. 11(5), 584–592 (1956)
Ben-Dor, G., Glass, I.I.: Domains and boundaries of non-stationary oblique shock-wave reflexions. 1: Diatomic gas. J. Fluid Mech. 92(3), 459–496 (1979)
Ben-Dor, G., Glass, I.I.: Domains and boundaries of non-stationary oblique shock-wave reflexions. 2: Monatomic gas. J. Fluid Mech. 96(4), 735–756 (1980)
Ben-Dor, G.: Shock Wave Reflection Phenomena, 1e, 2e. Springer-Verlag Books, Berlin (1991, 2007)
Glass, I.I., Sislian, J.P.: Nonstationary Flows and Shock Waves. Clarendon Press, Oxford (1994)
Semenov, A.N., Berezkina, M.K., Krassovskaya, I.V.: Classification of pseudo-steady shock wave reflection types. Shock Waves 22(4), 307–316 (2012)
Henderson, L.F., Lozzi, A.: Experiments on transition of Mach reflexion. J. Fluid Mech. 68, 139–155 (1975)
Henderson, L.F., Siegenthaler, A.: Experiments on the diffraction of weak blast waves: the von Neumann paradox. Proc. R. Soc. Lond. A 369(1739), 537–555 (1980)
Walker, D.K., Dewey, J.M., Scotten, L.N.: Observation of density discontinuities behind reflected shocks close to the transition from regular to Mach reflection. J. Appl. Phys. 53(3), 1398–1400 (1982)
Lock, G.D., Dewey, J.M.: An experimental investigation of the sonic criterion for transition from regular to Mach reflection of weak shock waves. Exp. Fluids 7(5), 289–292 (1989)
Kobayashi, S., Adachi, T., Suzuki, T.: On the unsteady transition phenomenon of weak shock waves. Theor. Appl. Mech. 49, 271–278 (2000)
Hornung, H.: Regular and Mach reflection of shock waves. Ann. Rev. Fluid Mech. 18, 33–58 (1986)
Henderson, L.F., Takayama, K., Crutchfield, W.Y., Itabashi, S.: The persistence of regular reflection during strong shock diffraction over rigid ramps. J. Fluid Mech. 431, 273–296 (2001)
Adachi, T., Sakurai, A., Kobayashi, S.: Effect of boundary layer on Mach reflection over a wedge surface. Shock Waves 11(4), 271–278 (2002)
Thompson, P.A.: Compressible-Fluid Dynamics. Rensselaer Polytechnic Institute Press, New York (1988)
Polachek, H., Seeger, R.J.: Shockwave interactions. In: Emmons, H.W. (ed.) Fundamental of Gas Dynamics. High Speed Aerodynamics and Jet Propulsion, Vol III, pp. 482–525 (1958)
Henderson, L.F.: Regions and boundaries of diffracting shock wave systems. ZAMM 67(2), 73–86 (1987)
Henderson, L.F., Lozzi, A.: Further experiments on transition to Mach reflexion. J. Fluid Mech. 94, 541–559 (1979)
Hryniewicki, M.K., Groth, C.P.T., Gottlieb, J.J.: Parallel implicit anisotropic block-based adaptive mesh refinement finite-volume scheme for the study of fully resolved oblique shock wave reflections. Shock Waves 25(4), 371–386 (2015)
McDonald, J.G., Sachdev, J.S., Groth, C.P.T.: Application of Gaussian moment closure to microscale flows with moving embedded boundaries. AIAA J. 52(9), 1839–1857 (2014)
Northrup, S.A., Groth, C.P.T.: Parallel implicit adaptive mesh refinement scheme for unsteady fully-compressible reactive flows. AIAA Paper 2013-2433 (2013)
Williamschen, M.J., Groth, C.P.T.: Parallel anisotropic block-based adaptive mesh algorithm for three-dimensional flows. AIAA Paper 2013-2442 (2013)
Zhang, J.Z., Groth, C.P.T.: Parallel high-order anisotropic block-based adaptive mesh refinement finite-volume scheme. AIAA Paper 2011-3695 (2011)
Gao, X., Northrup, S., Groth, C.P.T.: Parallel solution-adaptive method for two-dimensional non-premixed combusting flows. Prog. Comput. Fluid Dyn. 11(2), 76–95 (2011)
Gao, X., Groth, C.P.T.: A parallel solution-adaptive scheme for three-dimensional turbulent non-premixed combusting flows. J. Comput. Phys. 229(9), 3250–3275 (2010)
Gao, X., Groth, C.P.T.: A parallel adaptive mesh refinement algorithm for predicting turbulent non-premixed combusting flows. Int. J. Comput. Fluid Dyn. 20(5), 349–357 (2006)
Sachdev, J.S., Groth, C.P.T., Gottlieb, J.J.: A parallel solution-adaptive scheme for multi-phase core flows in solid propellant rocket motors. Int. J. Comput. Fluid Dyn. 19(2), 159–177 (2005)
LeVeque, R.: Finite Volume Methods for Hyperbolic Problems. Cambridge University Press, Cambridge (2002)
Ivan, L., Groth, C.P.T.: High-order solution-adaptive central essentially non-oscillatory (CENO) method for viscous flows. J. Comput. Phys. 257(A), 860–862 (2014)
Barth, T.J.: Recent developments in high order k-exact reconstruction on unstructured meshes. AIAA Paper 93-0668 (1993)
Venkatakrishnan, V.: On the accuracy of limiters and convergence to steady state solutions. AIAA Paper 93-0880 (1993)
Harten, A., Lax, P.D., Van Leer, B.: On upstream differencing and Godunov-type schemes for hyperbolic conservation laws. SIAM Rev. 25(1), 35–61 (1983)
Einfeldt, B.: On Godunov-type methods for gas dynamics. SIAM J. Numer. Anal. 25(2), 294–318 (1988)
Rankine, W.J.M.: On the thermodynamic theory of waves of finite longitudinal disturbance. Philos. Trans. R. Soc. 160, 277–288 (1870)
Taylor, G.I.: The conditions necessary for discontinuous motion in gases. Proc. R. Soc. Lond. A 84(571), 371–377 (1910)
Becker, R., Stoßwelle und detonation. Z. Phys. 8, 321–362 (1922). Also, English translation, NACA TM No. 505 (1929)
Smith, W.R.: Mutual reflection of two shock waves of arbitrary strengths. Phys. Fluids 2(5), 533–541 (1959)
Barbosa, F.J., Skews, B.W.: Experimental confirmation of the von Neumann theory of shock wave reflection transition. J. Fluid Mech. 472(1), 263–282 (2002)
Herron, T., Skews, B.W.: On the persistence of regular reflection. Shock Waves 21(6), 573–578 (2011)
Previtali, F.A., Timofeev, E., Kleine, H.: On unsteady shock wave reflections from wedges with straight and concave tips. AIAA Paper 2015-2642 (2015)
Ivanov, M.S., Gimelshein, S.F., Beylich, A.E.: Hysteresis effect in stationary reflection of shock waves. Phys. Fluids 7(4), 685–667 (1995)
Acknowledgements
The contributions of Lucie Freret in making the anisotropic algorithm of AMR more efficient are greatly appreciated. Computational resources for performing all of the calculations reported in this research were provided by the SciNet High-Performance Computing Consortium at the University of Toronto and Compute/Calcul Canada, through funding from the Canada Foundation for Innovation (CFI) and the Province of Ontario, Canada.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by B. Skews.
Rights and permissions
About this article
Cite this article
Hryniewicki, M.K., Gottlieb, J.J. & Groth, C.P.T. Transition boundary between regular and Mach reflections for a moving shock interacting with a wedge in inviscid and polytropic air. Shock Waves 27, 523–550 (2017). https://doi.org/10.1007/s00193-016-0697-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00193-016-0697-1