1 Introduction

Parachutes are effective decelerators for descent and recovery of aerospace vehicles in terrestrial and planetary missions. Particularly, a number of parachute-based decelerator systems were tested for different Mars missions, including the Viking landers in the 1970s, and later the Mars Pathfinder mission [1, 2]. Suitability in terms of compact storage and easy deployment are the prime advantages of parachutes in this regard. For such applications, parachutes are usually deployed at supersonic speeds. Parachutes are intrinsically non-rigid, and at supersonic speeds compressible flow with shocks sets up complex fluid-structure interactions that critically affects their aerodynamics and stability [3, 4]. From early supersonic wind tunnel experiments, inherently unsteady and asymmetric shock structures ahead of the parachute were observed. The associated fluid-structural interactions can cause severe alterations to the effective drag area of the parachute, and the propagation of vibrations can also result in structural failure [4, 5]. Much of these studies were aimed at achieving the aerodynamic drag and stability coefficients that were essential for designing the parachutes. More details regarding the fluid and structural dynamics were elaborated upon by recent experimental work from NASA, using advanced tools such as high-speed schlieren, PIV, and high-speed imaging followed by photogrammetry [7, 9]. The results clearly showed the complex behavior, including unsteady shocks, associated changes to the frontal area of the parachute, and effects of the suspension lines that connect it to the base of the vehicle. Computational studies were carried out using a coupled approach, where the large eddy analysis of turbulent fluid dynamics was integrated with structural modeling of the flexible parachute. The computational tools could capture the physics of the phenomena as well as the experiments [6]. The fundamental unsteady shock behavior is well represented by a rigid hemispherical shell facing a supersonic flow [4]. A valid approach to understand the fluid mechanics has been to study the flow ahead of a rigid hemispherical shell at different supersonic Mach numbers [5]. The effect of suspension lines and the base of the payload were also studied by rigid body models [8]. With increasing interest for various missions involving spacecraft recovery, including landing on Mars in particular, it is crucial to fundamentally understand the unsteady fluid dynamics ahead of the parachute system. Experiments were carried out recently by Kawamura and Mizukaki in JAXA’s supersonic wind tunnel on a hemispherical shell facing supersonic flow at Mach numbers ranging from 2 to 4 [10]. High-speed schlieren images showed sustained shock pulsation cycles for Mach numbers greater than two. Although a possible mechanism for the shock unsteadiness was proposed, it remains unverified due to limited visualization of the whole flow field in their experiments. Experimental efforts have been continuing, using diagnostics such as pressure-sensitive paints (PSP) to further observe this flow field [11].

Despite these studies, the basic mechanism responsible for shock oscillations ahead of a hemispherical shell remains unresolved. The prime objective of this work was to clarify the underlying physics responsible for unsteady shock oscillations ahead of a hemispherical shell placed in a supersonic flow of Mach number 4.0 by three-dimensional solutions to the compressible Navier–Stokes equations using the 3D unstructured solver FaSTAR, developed by JAXA [12, 13]. The flow and geometry conditions are chosen to closely represent the experiments by Kawamura and Mizukaki [10]. The computational method is verified by a comparison of experimental and numerical schlieren images. Shock oscillations are evident in the numerical simulations, and from the detailed three-dimensional flow field, the mechanism for sustained shock oscillations is explained.

A topological similar flow field is represented by a number of studies on forward-facing nose cavities (mostly cylindrical in shape) placed in high Mach number flows. A significant application of forward facing nose cavities is for thermal protection from severe nose heating of vehicles at high Mach numbers [15, 16]. Shock oscillations were consistently observed for these flows as well. Especially, when considering supersonic pitot measurements in hypersonic facilities, the shock oscillations ahead of the pitot cavity interfere with the signals and hinder their analysis [17]. Mainly, principles of cavity resonance using a Helmholtz resonator model have been used to model these oscillations [14, 18, 19]. A simple result that comes out of this analysis is that the shock oscillates at the resonant frequency of the cavity which can be related to the geometry and flow field variables. The frequency of oscillation is given by (1).

$$\begin{aligned} f_s=\frac{\sqrt{\gamma RT_0}}{4(L+\delta )} , \end{aligned}$$
(1)

where \(\gamma \) and R are the ratio of specific heats and the gas constant, respectively. Since the flow within the cavity is assumed to be relatively stagnant, the temperature approaches the stagnation temperature of the flow, \(T_\mathrm {0}\). L is the length of the cavity, and \(\delta \) is the shock stand-off distance. This result, based on the study of shock oscillations ahead of cylindrical cavities, can be extended to the domain of shock oscillations ahead of the hemispherical shell. However, the fact that the flow field through a hemispherical shell is dominantly three-dimensional, while the models for cylindrical cavities have treated them as quasi-1D, has to be kept in mind.

This article is organized into two sections. First, the method of numerical simulations, the geometry, the grid, and boundary conditions are explained. Then, the results, comparison with experiments, grid dependence study, and the description of the mechanism for shock oscillations are elaborated upon.

2 Numerical method

The full three-dimensional, compressible Navier–Stokes equations are solved using fast aerodynamic routines (FaSTAR), a CFD code developed by JAXA, Japan. The capabilities as well as code validation on simple and complex flow scenarios have been described in detail by Hashimoto et al. [12, 13]. FaSTAR integrates the basic fluid dynamic equations by a cell-centered finite volume method. The equation of state for an ideal gas relates the pressure, density, and temperatures of the flow field. The coefficient of viscosity is calculated by the Sutherland’s formula. The code employs MUSCL type linear data reconstruction, and the numerical fluxes are evaluated by the AUSM+ scheme with minmod limiter. The Green–Gauss method is used for evaluating the gradients in numerical fluxes and viscous terms. The LU-SGS (lower/upper symmetric Gauss Seidel) method is used for time integration. The solutions are accurate to second order in both time and space.

The computations are carried out on a PC-cluster system developed by the authors. The system has 24 parallel computing elements (Processing Elements or PE) with 2.67 GB of memory per element. Intel’s Core i7-3930K (3.20 GHz) processors are used in the PCs that compose the cluster.

2.1 Geometry and grid

The geometry consists of a hemispherical shell placed within a cuboidal volume, and the extent of the cuboid is made far enough to minimize the effect of boundaries. The hemispherical cavity has an internal diameter of 80 mm, and the shell thickness is 2.1 mm. The boundaries of the cuboid extend from \(-500\) to 500 mm, in the y and z directions, with the origin on the center point of the concave hemispherical surface. The supersonic free stream is directed along the x axis, and the boundaries are located 300 mm upstream and 500 mm downstream of the center.

Fig. 1
figure 1

Details of the computational grid. a The overall computational grid as viewed in the x-z plane, b a view of the dense mesh close to the hemispherical shell

Full size image

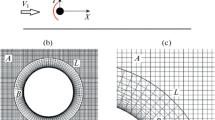
The computational volume is discretized into dominantly hexahedral mesh elements using an automatic hexahedral mesh generator HexaGrid [20]. Simulations are carried out on multiple grids of increasing refinement. Refinement is achieved by doubling the overall mesh density from the coarse to the finer grid. At the finest grid, the total number of mesh elements are about 8 million cells. A comparative study indicating that the solutions are indeed grid converged is further discussed in Sect. 3.3. All results and discussions here on are for the finest grid. Figure 1a clearly depicts the computational grid as seen along the x–z plane, and Fig. 1b is a zoomed version showing the fine mesh near the model. The grid consists of coarse elements near the boundaries. The mesh density is gradually made fine, with the finest mesh density near the model. Body-fitted prismatic elements are used near the walls of the model to capture the near-wall flow accurately. In general, the mesh elements are cubical volumes of size 1.05 mm at the outer regions, and close to the model they are of 0.53 mm in size. The cells closest to the wall are at a distance of 0.045 mm normal to it.

2.2 Boundary and initial conditions

The boundary and initial conditions are chosen corresponding to the experimental conditions as described in Kawamura and Mizukaki [10]. A Mach 4.0 supersonic free stream is incident upon the model from left to right, with stagnation pressure and temperature conditions as described in Table 1. The Reynolds number corresponding to the free stream conditions, with the model diameter D being the reference length, is \(3.45\times 10^6\). The outer boundaries and the downstream boundary are such that they allow a supersonic free stream without reflections of any shocks back into the computational domain. The computations are started with the initial condition that the flow has free stream values everywhere, which is somewhat unphysical. However, after an initial stage the flow features settle to what has been observed in experiments, as described in Sect. 3.2.

Table 1 Table of flow conditions
Full size table

3 Results and discussions

The flow equations are integrated in space and time beginning with the initial condition that the flow is Mach 4.0 everywhere. The initial transients that correspond to this non-physical start of the flow involve large variations in the shock structure ahead of the cavity. Within a duration of 5 ms, the flow settles down to a configuration that has an axisymmetric shock which oscillates with low amplitude. This flow configuration is termed as Flow Configuration A. This configuration is unstable and the flow switches at about 20 ms to a second configuration that has a complicated asymmetric shock structure, involves large-amplitude pulsations, and is termed as Flow Configuration B. The simulations are carried out for a duration of 45 ms. First, we discuss the detailed structure of Flow Configuration A and Flow Configuration B. The numerical results are validated by comparing a sequence of schlieren images obtained experimentally and from the computations. The grid dependence study is also described.

3.1 Flow topologies

Figure 2a is a numerical schlieren along the x–y plane, obtained by taking the gradient of density along the x direction, which corresponds to the knife edge being placed vertically. This figure depicts Flow Configuration A which appears at about 5 ms after the start of the simulation, and persists for about 15 ms. As evident from the figure, the shock \(S_{0}\) is nearly axisymmetric, and the flow is largely subsonic between the shock and the cavity. Small vortices can be observed within the cavity, which play a dominant role in destabilizing this configuration as detailed in Sect. 3.4. The flow turns supersonic again as it passes around the lip of the cavity through the expansion fan (EF). This quasi-steady state of the flow has small-amplitude shock oscillations. The distance of the shock from the innermost point in the convex side of the cavity is termed \(L_\mathrm {1}\), which is about 67.4 mm in this case.

Figure 2b, on the other hand, represents the flow features when the shock is deformed to the maximum extent during the non-stationary large-amplitude shock pulsation cycles (the second stage of the flow), which is referred to as Flow Configuration B. The flow is three-dimensional, and only the x–y cross-section is represented in the figure. The shock \(S_\mathrm {1}\) is completely deformed and is thrust outwards into the supersonic free stream. The distance between the farthest extent of this shock and the center of the convex cavity is \(L_\mathrm {2}\). The maximum \(L_\mathrm {2}\) encountered during the computations is 111.2 mm, about 1.65 times \(L_\mathrm {1}\). The shape of the shock \(S_\mathrm {1}\) is such that it can no longer ensure subsonic flow on the lower end of the cavity, thus shock \(S_\mathrm {2}\) forms to ensure proper flow turning and pressure matching conditions at the lower rim of the cavity. Therefore, the flow passing at the lower end of the cavity passes through two shocks (\(S_\mathrm {1}\) and \(S_\mathrm {2}\)), while at the upper end \(S_\mathrm {1}\) is far away from the cavity lip. This establishes a pressure differential along the cavity from the lower end to the upper end, causing the flow to accelerate along the cavity from bottom to top (as marked by the arrow), and intercept the flow from \(S_\mathrm {1}\) as a supersonic jet. This causes the shock \(S_\mathrm {3}\) to develop. Consequently, the jet-like flow from the cavity is turned and spills out of the top lip. Within the confines of the cavity there are two flows of differing entropies and temperatures, one stream that has passed through two shocks, and another that has passed only through one shock. These two different streams generate a shear layer with large vortical activity termed as the mixing region (MR). This region is clearly visible when vorticity contours are discussed in Sect. 3.4. Near the lower lip, the movement of individual shocks \(S_\mathrm {1}\) and \(S_\mathrm {2}\) during the shock pulsations can produce various flow configurations depending on Edney’s criteria for shock-shock interactions [21]. Several combinations of oblique shocks, Mach stem, expansion fans, and slip lines (SL) are produced as a result of such interactions.

Fig. 2
figure 2

Numerical schlieren of a Flow Configuration A and b Flow Configuration B. \(S_\mathrm {0}\), \(S_\mathrm {1}\), \(S_\mathrm {2}\) shocks, MR mixing region, SL slip line/shear layer, \(L_\mathrm {1}\), \(L_\mathrm {2}\) shock stand-off distance

Full size image

The shock shape during the second stage of the flow is highly unsteady, and undergoes large amplitude pulsations. This particular flow picture is close to the maximum amplitude of the shock deformation, after which the structure collapses. The shocks are drawn closer to the cavity as in Flow Configuration A. Thereafter, the next cycle begins with the shock deforming and shock stand-off distance increasing. The mechanism of these self-sustained pulsations are explained in detail in Sect. 3.4.

The description of the flow as understood from the numerical schlieren images is further enhanced by plotting the streamlines at those particular instants of the flow, as shown in Fig. 3a, b. The lines are colored by the local Mach number of the locations along which they traverse. This brings out the Mach number distribution within the flows as well as emphasizes features such as the three-dimensionality of the shock shape and vortices.

Fig. 3
figure 3

Streamline plot of a Flow Configuration A and b Flow Configuration B

Full size image

Clearly visible in Fig. 3a, is the axisymmetric shock \(S_\mathrm {0}\) corresponding to Flow Configuration A. The flow is subsonic within the cavity until it is accelerated to supersonic velocities at the outer rim of the cavity. Figure 3b evidently shows that the shock shape and the ensuing flow are highly three-dimensional in Flow Configuration B. The shock \(S_\mathrm {1}\) is unable to make the flow subsonic at the lower rim of the cavity, and \(S_\mathrm {2}\) is formed as a consequence. The directional jet-like flow accelerating to supersonic Mach number from the lower end to the upper rim of the cavity is unmistakable. The shock \(S_\mathrm {3}\) caused by the collision of two opposing flows is also clearly visible.

Fig. 4
figure 4

A comparison of the experimental schlieren images (a–e) with the numerical schlieren images (d–j)

Full size image

3.2 Comparison with experiments

Figure 4 compares a series of schlieren images obtained from experiments to those extracted from the current numerical calculations. The experimental schlieren images are obtained from the experimental setup described in [10]. There are a few factors to be considered when making this comparison. The experimental schlieren images are line of sight integrated versions of density gradient variations in the test section. Since the hemispherical shell generates a three-dimensional shock structure, correspondingly the shock appears thicker, and shocks of different directions are also captured in a single frame. The numerical schlieren image on the other hand is a slice of the density gradient field, hence the shocks appear crisp, and the flow features of only that slice are visible. The shock thickness seen in the numerical schlieren image is limited by the grid resolution, and appears thicker than it actually is. The flow starting process is different in the experiment and numerical simulation. However, the different stages, such as the appearance of Flow Configuration A, transition to Flow Configuration B, and large amplitude pulsations of Flow Configuration B, are observed in both. Thus, to make a time series comparison, a particular instant of time is chosen when the nearly axisymmetric shock in Flow Configuration A shows a small deformation indicating the start of transition to Flow Configuration B, as is clearly observed in Fig. 4a, f respectively, and this time is referred to as \(t_\mathrm {ref}\). The experimental schlieren images are taken at an interval of 200 \(\upmu \)s, while the numerical results are obtained at about 15.5 \(\upmu \)s, and the image sequences are taken so as to correspond as closely as possible with each other. The series of five experimental images show a duration of flow starting from the transition of Flow Configuration A (Fig. 4a) to one complete cycle of the large amplitude shock pulsation in Fig. 4f. Figure 4b is an intermediate stage in the transition where the shock \(S_\mathrm {0}\) has undergone significant deformation but has not yet split into the three shock structure that is seen in the Fig. 4c. Figure 4c is the first appearance of the Flow Configuration B with all the corresponding shock structures as described in Sect. 3.1. The shock \(S_\mathrm {1}\) is deformed to the maximum extent. Shocks \(S_\mathrm {2}\) and \(S_\mathrm {3}\) are also visible. Figure 4d shows the shocks retreating back, and the shock stand-off distance \(L_\mathrm {2}\) has decreased before reaching the second maximum of the next cycle in Fig. 4e. From the numerical schlieren images, Fig. 4f–j, the close correspondence in the shapes and appearance of the shocks at the respective instances is unmistakable. The numerical schlieren images also depict the same sequence of events starting from the transition of Flow Configuration A to Flow Configuration B (Fig. 4g, h ) and the full cycle of large amplitude shock oscillation (Fig. 4h–j). The frequency of large amplitude shock oscillation as estimated from the sequence of experimental schlieren images is about 833 Hz (\(\pm \)20 %), given that schlieren images are available only at relatively large time intervals. The frequencies of shock oscillations in the non-stationary phase, as shown from the pressure data sampled at the center point of the hemispherical shell, are 869 and 853 Hz (which is described in Sect. 3.5). There is thus a close match (within 3 %) between the frequency of oscillations established from experiments and numerical simulations. Qualitative features of the flow like shock shapes of \(S_\mathrm {1}\), \(S_\mathrm {2}\), \(S_\mathrm {3}\), the MR, and the shock interactions at the bottom of the cavity are well represented in the numerical schlieren images. Some features such as the SL appear smeared because of the grid, however, they are present at the corresponding locations. A difference of 20 % can be observed in the evaluation of \(L_\mathrm {2}\) from the numerical and experimental schlieren. The grid resolution, as described in Sect. 2.1, is one of the prime reason for this difference, contributing a maximum of 8 %. The shock deformation is caused by interactions between shock and vortices in the cavity. However, there are inherent difficulties in capturing these dynamics by a numerical code on a finite grid size with the limitations posed by hardware capabilities. Considering them, and the fact that the qualitative features and the essential physics including the frequency of oscillations is well captured by the CFD code, it is confirmed that the results from the numerical code agree well, and are an accurate enough representation of the experimental results.

Fig. 5
figure 5

A comparison between a numerical schlieren image using the fine grid (mesh density twice that of the coarse grid), and b numerical schlieren image using the coarse grid

Full size image

3.3 Comparison of grids

Figure 5 compares numerical schlieren for the coarse and the fine grid, with mesh density being doubled for the fine grid. Clearly, the shock appears thicker and small scale vortices are smeared out in Fig. 5b in comparison with Fig. 5a. However, the overall structure of the flow remains the same in both the figures. The shock stand-off distance \(L_\mathrm {2}\) shows a small difference of 8 % between the two compared to change in grid spacing which is double (100 % increase) in the coarser grid. Thus, further refinement would not change the flow features or shock shapes appreciably. Besides, both the simulations show the same features of the flow including the appearance of Flow Configuration A, the transition to Flow Configuration B, and the shock pulsations. Thus, it is concluded that for the present case, the finest grid with 8 million cells is fine enough to accurately represent the flow features.

Having validated the numerical simulations against experimental findings, and confirmed that the solutions are also grid independent, we further discuss the unsteady characteristics of the flow from vorticity contours, cavity pressure, and shock stand-off distance calculations.

3.4 Mechanism of unsteadiness and shock oscillations

We find that mutual interaction of shock with vortices that are generated by it, and amplified by the cavity in a loop are the reason for the destabilization of Flow Configuration A and the sustained pulsations of Flow Configuration B. Thus, this mechanism is described in detail with the aid of vorticity contours, which reveal the structure of the vortices and their dynamics clearly. The vorticity contours are superimposed on gray shades of the numerical schlieren so that shocks as well as vortices are evident.

Fig. 6
figure 6

Sequence of events leading to the destabilization of Flow Configuration A

Full size image

3.4.1 Mechanism of destabilization of Flow Configuration A

The set of images in Fig. 6 show the sequence of events leading to the destabilization of Flow Configuration A. The mechanism pertaining to the growth of significant deformation to the shock \(S_\mathrm {0}\) that ultimately leads to the establishment of Flow Configuration B is described in Sect. 3.4.2. The images are mid-plane x–y cross-sections of vorticity contours that are superimposed on the numerical schlieren. Thus, what is seen are the cross-sections of vortex tubes in space. The color map shows that negative vortices are colored towards the blue end of the spectrum, while positive vortices are colored towards the red end. In this case, clockwise rotations as looking into the paper correspond to positive vortices, and anti-clockwise rotations are negative. These images are taken from a time duration beginning at about 13.5 ms lasting to 14 ms from the start of the simulation (referred to as \(t_\mathrm {0}\)). After the initial transients associated with the unphysical flow start of this system, Flow Configuration A is established at about 5 ms, and lasts until about 15 ms. Thus, it is expected that the mechanism responsible for destabilization of Flow Configuration A should be clearly observable during the duration at which these images are analyzed. These demarcations in the unsteady flow field are also clearly observable in the pressure traces and shock stand-off distance calculations detailed in Sect. 3.5 and shown in Figs. 8 and 9.

Figure 6a shows the Flow Configuration A and the vorticity contours associated with it. The curved shock \(S_\mathrm {0}\) ahead of the cavity generates a number of vortex tubes extending into the cavity. Vortices, termed clockwise vortices (CV) and anti-clockwise vortices (ACV), are of similar magnitudes and nearly equal in number, such that the total vorticity within the cavity is nearly zero at this moment. This shock undergoes small amplitude shock oscillations(SSO) along the x direction in response to pressure waves emanating from the shock, reflecting at the cavity wall, and reaching back to the shock. This oscillation happens through Fig. 6a–f, but since the amplitude is small, they are not so apparent in the figures. The behavior of these vortices during such oscillations has to be noticed in particular among the images. It can be seen that the vortex tubes that were attached to the shock in Fig. 6a, have become free to be convected by the flow in Fig. 6c. These free vortices are convected by the flow as it spills over along the outer rim of the cavity. As the vortices move close to the shock towards the edge of the cavity, they perturb the shock shape slightly. This perturbation is clear on close observation of the sequence of Fig. 6c–e, as the vortex CV gets pulled out of the cavity. It is important to notice that an ACV is left back in the cavity while CV is convected out. More vortex tubes are again generated in the next cycle as seen in Fig. 6f, but now a small finite ACV still remains in the cavity. Over the course of many such oscillations this counter clockwise rotation in the cavity builds up and amplifies, bringing out a pronounced rotation to the flow in the cavity and in response the shock shape undergoes large deformation moving towards Flow Configuration B.

3.4.2 Establishment and sustainment of Flow Configuration B

Figure 7 shows the sequence of events starting from the point that a significant counter clockwise vorticity remains within the cavity to the establishment of Flow Configuration B, which then repeats cyclically as the shocks undergo large amplitude shock pulsations. Flow Configuration B appears for the first time at 23.16 ms after the start of the simulation (\(t_\mathrm {0}+23.16\) ms), and these images cover the later part of the transition from Flow Configuration A to Flow Configuration B, starting from \(t_\mathrm {0}+17.47\) ms to \(t_\mathrm {0}+23.16\) ms.

Fig. 7
figure 7

Sequence of events leading to the establishment of Flow Configuration B

Full size image

A significant anti-clockwise vorticity (ACV) has been formed in the cavity in Fig. 7a, which lends a slight rotation to the flow in the cavity moving from the lower rim to the upper rim (denoted by a thin curved arrow). Once this rotation sets in, further series of events seek to enhance this rotation as more and more ACVs are held back in the cavity while CV vortices are preferentially convected out. This effect can be seen clearly in Fig. 7b, where three ACVs can be seen clearly while one CV is being pushed out of the cavity region. With this, the magnitude of rotation within the cavity also increases, as shown by a thicker arrow. A slight deformation of the shock as the flow between the cavity starts to rotate in a counter clockwise manner is also visible. With further strengthening of this rotation in Fig. 7c, the shock deformation is more pronounced and clearly observable. Since the sense of rotation is anti-clockwise, the flow from the upper rim pushes the shock \(S_\mathrm {0}\) away from it. A significant point to notice here is that as soon as the shock deformation becomes pronounced, the pressure distribution gets altered to amplify this situation. Since the shock is pushed to a farther distance away near the upper rim of the cavity, the spillage at that section increases, and at the same time, static pressure drops in comparison to the lower rim. The flow within the cavity at this stage is still subsonic, although it accelerates from lower to the upper rim along the cavity walls. This condition continues to grow as the shock gets pushed outward near the upper rim. Just before the maximum amplitude, the shock gets so deformed that the shock configuration switches to a two shock configuration where \(S_\mathrm {1}\) is thrust far into the free stream at the upper end, and \(S_\mathrm {2}\) appears distinctly at the lower rim to aid flow turning and pressure matching. A preview of this is already seen in Fig. 7c, where there is an oblique arm of the shock extending from the center of the cavity to the upper rim and a nearly normal arm at the lower half of the cavity. At some point, the acceleration becomes large enough to accelerate the flow to supersonic velocity, and this flow as it leaves the upper rim interacts with the oncoming flow from \(S_\mathrm {1}\), forming the shock \(S_\mathrm {3}\). At this point, the shock configurations are at the maximum amplitude in a given cycle of pulsation. This configuration has been described extensively as Flow Configuration B. The rotation within the cavity is at the maximum, and a very large counter clockwise vortex that sits within the MR is clearly visible in Fig. 7d. Since the shock \(S_\mathrm {1}\) is now at the farthest location, there is a large spilling of mass from the upper end of the cavity, which in its force pulls out this large ACV from the cavity. As this ACV is shed out from the cavity, the shock structure falls back towards the cavity. However, since the shock deformation is very significant, and a preferential sense of rotation is established within the cavity, the flow does not return to Flow Configuration A. Large amplitude shock pulsations are sustained where the flow moves from Fig. 7a–d, wherein the shock gets deformed, pushed out, and as a large vortex is shed from the cavity, it falls back.

At this point it is necessary to emphasize that full three-dimensional numerical simulations have been carried out. For the sake of clear explanations, images used are slices of the three-dimensional flow field. The three dimensionality of the flow field is clearly shown in Fig. 3. In this context, shock \(S_\mathrm {0}\) in Flow Configuration A has been described as nearly axisymmetric in an average sense, and minor three-dimensional deformations of the shock structure are present as the shock responds to the small vortices present between the shock and the hemispherical shell. Similarly, it needs to be clarified that the appearance of Flow Configuration B in this particular case is such that there is a preference towards rotation in the counter-clockwise sense; hence the shock structure gets deformed towards the upper lip of the shell. Once the deformation occurs, then that configuration persists as the shock becomes completely asymmetric, and a preferential pressure gradient is established along the hemispherical shell. But, this is not a strict condition, and it is equally likely that the deformation can happen at any location along the circumference of the hemisphere in other similar cases. So the shocks \(S_\mathrm {1}\) and \(S_\mathrm {3}\) can be located at the lower lip or along the sides, as the case may be. Hence, to be clear, if shocks \(S_\mathrm {1}\) and \(S_\mathrm {3}\) are located at the upper lip, then shock \(S_\mathrm {2}\) will be located at the lower lip, with a preferential flow rotation along the shell in the anti-clockwise sense. In a different case, it is equally possible that if shocks \(S_\mathrm {1}\) and \(S_\mathrm {3}\) are located at the lower lip, then shock \(S_\mathrm {2}\) will be located at the upper lip, with a preferential flow rotation along the shell in the clockwise sense.

It is also important to clarify that the full compressible Navier–Stokes equations are solved on a three-dimensional grid without invoking any turbulence model. From the description, it is very clear that it is crucial to capture the unsteady interactions between vortices and shocks to describe the mechanism of these shock oscillations. There are limitations to existing turbulence models in accurately capturing such complex flow scenarios [22]. On the other hand, direct numerical simulation (DNS) or large eddy simulation (LES) demands a large number of grid elements and require extensive computational capabilities. However, it is evident from the comparison of experiments and numerical simulations that the current computations do accurately capture the flow field. Previous studies on similar geometries have also observed this fact [8]. Some observations to be noted are that the mechanism of destabilization of Flow Configuration A is dependent on the amplification of vortices that are generated by the curved shock. The current simulation does capture this mechanism, but is limited by the grid resolution. Many more interactions of sub-grid scale vortices may not have been captured. To some extent, this might have affected the manner of transition either forwarding or delaying it. However, once Flow Configuration A is destabilized, further dynamics are governed by large-scale vortices that are of the same order as the diameter of the shell, which are very well captured in these simulations. Thus, the shock pulsations themselves are not affected much by the neglect of sub-grid scale vortices. It is shown clearly in Sect. 3.2 that the flow features and frequencies of shock pulsations are well represented in the numerical computations.

Fig. 8
figure 8

a Pressure and shock stand-off distance traces with b their Fourier transforms during the initial stages of the flow

Full size image

The stages of the flow and the cyclic oscillations leave their imprints upon the pressure of the cavity, which is sampled at the center of the convex surface of the cavity from the unsteady results. The shock stand-off distances \(L_\mathrm {1}\) and \(L_\mathrm {2}\) can also be calculated. By analyzing these signals using Fourier transforms, information on preferred frequencies can be understood.

3.5 Analysis of pressure and shock stand-off distance

Figure 8a is a plot of the signals extracted from numerical simulations, of the pressure at the center of the convex surface, and of the shock stand-off distance (\(L_\mathrm {1}\) or \(L_\mathrm {2}\) as the case maybe), from the start of the simulation till the end of Flow Configuration A. The pressure is sampled from the start of the simulations. The shock stand-off distance is calculated only after the flow settles to Flow Configuration A, after 9.3 ms. The initial very large variations in the pressure is due to the transients from the non-physical start of the flow and take a while to settle. Flow configuration A appears after 5 ms and is clearly shown in the figure. The average pressure is nearly steady, and small fluctuations are imposed due to shock oscillations. Similarly, during the same time, the shock stand-off distance also fluctuates about the mean with small amplitude. The pressure fluctuations have a lag of about 0.18 ms to the corresponding shock motions. This is expected since the pressure waves have to be transmitted through the space of the cavity, and they also experience a certain degree of attenuation due to large scale fluid motion within the cavity. The average temperature within the cavity at this stage is 290 K, and the corresponding acoustic speed is 341 m/s. For the given size of the cavity, the time interval for pressure wave transmission is about 0.20 ms, which is similar to the amount of lag between the pressure and shock stand-off distance signals. Since the amplitude of oscillations are small, the column resonance model where it is taken that the pressure wave has a resonant wavelength that is four times the shock stand-off distance \(L_\mathrm {1}\), should apply. The frequency of oscillation corresponding to the average shock stand-off distance of 67.4 mm is 1.27 kHz, as computed from (1). Figure 8b shows the frequency spectrum obtained by taking the Fourier transform of both pressure and shock stand-off distance signals. The sampling rate for pressure signals is at 340 kHz, and a total of 8192 sampling points are available giving a frequency resolution of 41.5 Hz. The sampling rate (68.1 kHz) as well as the number of sampling points (2048) is less for the shock stand-off distance signals, which yield a frequency resolution of 33.3 Hz. Disregarding the very low frequency signals which correspond to the non-zero average, it can be clearly observed that there are frequency peaks at 1.26 kHz for the pressure signal and 1.39 kHz for the shock stand-off distance signal. These numbers agree well with the frequency evaluated from the Helmholtz resonator model (difference between the frequency for the pressure oscillation and the estimate from the model is 1 %). The flow transition to Flow Configuration B involving large-amplitude shock pulsations can be observed in the traces of pressure and shock stand-off distance after about 17.5 ms.

Fig. 9
figure 9

a Pressure and shock stand-off distance traces with b their Fourier transforms during the later stages of the flow

Full size image

From 20 ms onwards large-amplitude non-stationary shock pulsations are observed. The traces of shock stand-off distance and cavity pressure are shown in Fig. 9a, and the Fourier transform of these signals in Fig. 9b. Clearly, the amplitude of oscillatory signals are much larger than for Flow Configuration A. The average shock stand-off distance is 90 mm, while the maximum achieved during the simulations is 111.2 mm, about 1.65 times larger than the shock stand-off distance during Flow Configuration A. From the time trace of the signals it is clear that these pulsations are non-stationary, i.e., they do not have a persistent characteristic from one cycle to the next. However, the repetition of an increase of shock stand-off distance, followed by its collapse is evident. So, the Fourier transform is composed of a cluster of frequencies. Two prominent peaks (again setting aside low frequencies corresponding to the average), are at 869 and 853 Hz, respectively. Since these shock oscillations are large (as high as 4.5 mm), the application of Helmholtz resonator model is questionable. However, it can still be considered for estimating the frequencies since the basic mechanism of these oscillations is still due to interactions of pressure waves and vortices. Considering that there is a larger spillage at this configuration, the average temperature within the cavity drops to 271 K and the acoustic speed to 330 m/s. If the average shock stand-off distance during the pulsation is considered, then the resonance frequency estimated from (1) is 916.7 Hz. Whereas, if the maximum shock stand-off distance is considered, it is 741.9 Hz. Thus, it can be seen that the frequencies are good estimates of the actual observations. A difference of 5.5 % exists due to the large-amplitude non-stationary characteristics of these pulsations, which cannot be easily modeled with the assumptions of the Helmholtz resonator model. Hence, the Helmholtz resonator model is useful to predict the frequencies of shock oscillations quite accurately in the Flow Configuration A, and to a very good estimation in the case of Flow Configuration B.

4 Conclusions

The main objective of this study was to clarify the flow mechanism for shock oscillations ahead of the cavity of a hemispherical shell open to a supersonic free stream using numerical tools. This flow configuration is particularly important for understanding the flow ahead of parachute decelerators during the descent stage of atmospheric entry of aerospace vehicles. The full compressible Navier–Stokes equations were solved using the finite volume CFD code FaSTAR (developed by JAXA). The results discussed in this article were derived from a grid converged solution on a grid of 8 million hexahedral cells, computed using a PC-based cluster system developed in-house. The simulations were conducted for a free-stream Mach number of 4.0 corresponding to experiments carried out by Kawamura and Mizukaki [10], and the numerical results are in good agreement with the experimental observations. The key conclusions from this study are as follows:

  • Two flow configurations are observed. Flow Configuration A where the shock ahead of the cavity is axisymmetric and oscillates at small amplitudes. Flow configuration B where the shock is asymmetric, highly deformed, thrust into the free stream on one side by as much as 1.65 times Flow Configuration A, and undergoes large amplitude non-stationary shock pulsations.

  • The preferential accumulation and amplification of one kind of vortices generated at the shock due to the dynamics of the cavity results in inducing a rotation that deforms the shock. This enhancement of vortices, its interaction with the shock, and final shedding sustain the large amplitude pulsations.

  • The cavity resonance model is able to predict the shock oscillations with good accuracy during Flow Configuration A (1.27 kHz). However, in Flow Configuration B the prediction is a good estimate 916.7 Hz compared to the numerical results (859 and 863 Hz).

Further studies are being conducted to ascertain whether this mechanism prevails in cavities of different shapes as well.