1 Introduction

In this paper, the initial development of a supersonic jet shear layer is examined in both the free jet and impinging jet. The focus is on the region closest to the nozzle exit to understand the initial state of the naturally thin, unforced shear layer. In particular, high-momentum, steady microjet injection at the nozzle lip is used to modify the shear layer with the intention of dampening the growth of large-scale structures naturally observed in both laminar- and turbulent-free shear layers [4]. We adopt the view that these structures are the product of, or can be modeled as, linear instability waves of the inflectional velocity profile [5, 14, 20, 22]. These structures, or instability waves, derive their energy from the shear in the mean flow. Evidence has shown that these waves can be used to model the sound producing mechanisms of turbulent mixing in subsonic and supersonic jets [7, 19, 20]. Hence, a control method, presumably with the ultimate goal of noise reduction, would seek to modify the mean flow in a manner that reduces the growth of these structures. A logical approach would then be to thicken the mean velocity profile such that there is a reduction in shear to feed the growth of the instability waves. This is the route that has been taken in the current study in which microjet injection is applied to supersonic (\(M_{j} = 1.5\)) free and impinging jets.

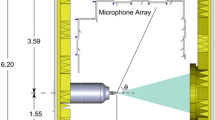
Although the dominant noise sources are drastically different for the free jet and for a resonating flow such as the impinging jet, they are both governed by large-scale, coherent motion. In an impinging jet, much like that of the free jet or shear layer, natural instabilities in the shear layer are amplified as they convect downstream. As these structures impinge on a flat plate normal to the jet axis, they generate acoustic waves which, in the case of the supersonic jet, travel upstream through the ambient. These acoustic waves then interact with the naturally unstable shear layer, reinforcing and amplifying the growth of the large-scale structures. When a phase lock occurs between the upward propagating acoustics and the production of coherent structures in the shear layer, jet resonance occurs. This is referred to as a feedback loop [15] and is shown schematically in Fig. 1. Jet resonance leads to intense, discrete “impingement tones”. This leads to many undesirable side effects including significantly increased noise levels and high unsteady pressure loads on the impingement surface [3]. Similar to a control mechanism in a free jet, we wish to attenuate the growth of these structures and disrupt the feedback loop.

Fig. 1
figure 1

Impinging jet schematic

Full size image

Applications of both active and passive control of supersonic jets have been extensively studied over several decades. Passive methods of control that have been explored include tabs [16], modified nozzle geometries [24] and chevrons [1]. Active methods include co-flow [17], counter-flow [18], and the method discussed here, steady microjet injection at the nozzle lip [2]. As the primary goal of each of these methods is the direct modification of the shear layer at the nozzle exit, it is critical to understand the baseline shear layer characteristics and how these are modified by the application of a particular control scheme. To this end, we conduct particle image velocimetry (PIV) zoomed in around the nozzle exit. Here, we examine the modification to the mean flow, specifically in terms of shear layer growth and vorticity distribution. The near-field acoustics are also compared with and without microjet injection for the free and the impinging jet. As we have argued that the noise sources are inextricably connected with the stability waves, we also compute the stability characteristics using the extracted velocity profiles from PIV.

2 Experimental setup

2.1 Jet facility

The experiments were conducted at the STOVL supersonic jet facility of the Florida Center for Advanced Aero-Propulsion (FCAAP) Laboratory at the Florida State University. This is a blow-down type facility primarily used to study the flow field and effects of jet-induced phenomena on STOVL aircraft. It consists of high-pressure (2 MPa) reservoirs with a combined storage volume of 10 m\(^3\). Air from the storage tanks is regulated to the desired stagnation pressure and heated through an inline electric heater before leading to a stagnation chamber. Here, the flow passes through a series of flow conditioning screens before it is expanded through the nozzle. The facility is capable of reaching Mach 2.2 and a temperature ratio \(T_{0}/T_\mathrm{amb}\) of 2.3, where \(T_{0}\) and \(T_\mathrm{amb}\) are the stagnation and ambient temperature, respectively.

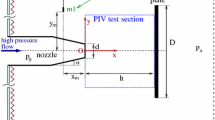
The current studies were conducted with an ideally expanded Mach 1.5 axisymmetric nozzle at a temperature ratio of 1.0. The Mach 1.5 nozzle is designed using a fifth-order polynomial converging to a throat diameter \((d)\) of 25.4 mm, and a \(3^{\circ }\) conical portion diverging to the design exit diameter \((d_\mathrm{e})\) of 27.5 mm. A circular flat plate, the lift plate, with a diameter \((D)\) 254 mm \((10~d)\), is fit flush with the nozzle exit for a canonical simulation of the underside of a STOVL aircraft. The ground plane is connected to a hydraulic lift, allowing it to simulate an impinging jet for standoff distances \(1 < h/d < 40\). The ground plane was removed for the free jet case. A schematic of the experimental setup is shown in Fig. 2. All data are presented in cylindrical coordinates \((r,\theta ,x)\), with the origin taken to be at the nozzle exit. The method of active flow control studied in this experiment is steady microjet injection at the nozzle lip. The lift plate, representing the under surface of an aircraft, is fitted with 16 microjets circumferentially spaced around the nozzle exit, as shown in Fig. 2. These microjets are manufactured using 400 \(\upmu \)m steel tubes oriented at \(60^{\circ }\) with respect to the main jet axis. The microjets are connected to one large reservoir maintained at 690 kPa, nozzle pressure ratio (NPR) 6.8. The primary stagnation chamber is connected to four secondary plenum chambers that act as a source to four microjets each. Extensive parametric studies have been done to optimize the microjet arrangement, including number, diameter, angle and spacing for the same experimental arrangement. The current microjet configuration was chosen based on the results of Lou [8]. Namely, a \(60^{\circ }\) injection angle was found to yield the best results in terms of noise suppression for the impinging jet over the widest range of impingement heights. For a fixed microjet diameter of 400 \(\upmu \)m and the nozzle used in the current experiment, little change was observed in the structure of the streamwise vortices created by the microjet injection by increasing the number of jets from 16 to 32. This also had negligible effect on noise suppression. There was, however, appreciable modification and corresponding noise reduction in 16 jets as opposed to eight. Hence, for the specific geometry of the current study, the parameters chosen in the current study are considered optimal. More details can be found in [8]. Previous microjet control results on similar geometries have shown significant reduction, especially in the case of impinging jets, on the noise characteristics of the main jet at a combined mass flow of only 0.5 % of the main jet [2, 3].

Fig. 2
figure 2

STOVL experimental setup

Full size image

2.2 Acoustic measurements

For the impinging jet, acoustic measurements were taken using a near-field microphone (B&K Type 4939 coupled with a Type 2670 preamplifier powered with a Nexus Conditioning Amplifier Type 2690). The microphone is located at a radial location of \(r/d = 15\) along the centerline of the jet and flush with the nozzle exit. For the free jet case, microphones were placed at a radius of \(r/d = 15\) at observer angles of \(\phi = 90^{\circ }\) and \(30^{\circ }\). Here, we define \(\phi \) to be the angle measured from the downstream jet axis. The signals from the microphones were filtered at 30 kHz through Stanford Research Systems SR640 Dual Low-pass Filters and then simultaneously sampled at 70 Hz using a National Instruments Data Acquisition card (PXI-6133) and a PC running LabVIEW software. The data were processed using 100 averaged FFTs with a 75 % overlap and a Hanning window function.

2.3 Particle image velocimetry

PIV was used to obtain the streamwise velocity field near the nozzle exit along the central jet axis. A modified Wright Nebulizer was used to generate small, approximately \(0.5~\upmu \)m, oil droplets as seed for the primary jet. In addition, the ambient air was seeded with smoke particles (\(\sim \)1–5 \(\upmu \)m) produced by a Rosco 1600 fog generator. For the PIV measurements, an Nd:YAG laser (Spectra-Physics, 400 mJ) was used for flow field illumination. The laser pulse was passed through a combination of spherical and cylindrical lenses to produce a light sheet approximately 1.5 mm thick. The images were recorded by a CCD camera (Kodak ES 1.0) with a 1k \(\times \) 1k resolution. The image pair acquisition rate was 15 Hz with a pulse separation of 1.25 \(\upmu \)s. A total of 1,000 images pairs were acquired and processed for each case to ensure convergence of second-order statistics. The image pairs were processed using a multipass algorithm with a final interrogation region of \(32 \times 32\) pixels with a \(50~\%\) overlap. This yields a spatial resolution of \(0.043~d\) for the current field of view of \(2.5d \times 2.5d\). A schematic of the PIV setup is shown in Fig. 3 which also shows the PIV region for the current study. For these experiments, the images were zoomed in around the nozzle exit to better resolve the shear layer characteristics.

Fig. 3
figure 3

PIV setup

Full size image

There are several possible sources of error in any PIV experiment. We attempt to address a few of those here. To examine errors due to particle slip, we follow the analysis presented by Mei [9]. Namely, we examine the cutoff Stokes number for the seed particles obtained by modeling the frequency response of the particle. We use the corresponding cutoff time constant and compare that to the local time scale of the fluid. Within the main jet, based on an average particle size of \(0.5~\upmu \)m, the cutoff time constant is \(\sim \)4.8 \(\upmu \)s. Using the centerline jet velocity \(U_{j}\), and the nozzle diameter \(d\) as the respective velocity and length scales, the corresponding fluid time scale is \(\sim \)58 \(\upmu \)s. As the fluid time scale is significantly larger than the particle time scale, it is expected that the particle will respond sufficiently fast to accurately track the fluid velocity. Here, it is important to note that the main jet is seeded with smaller sized particles than the ambient air. Due to entrainment, the larger particles from the ambient air will become engulfed in the shear layer. For simplicity, we treat the particles as independent systems. We choose the local length scale to again be the jet diameter \(d\). While a more appropriate length scale may be the local shear layer width \(\delta \), these will be on the same order where significant entrainment of the ambient particles has occurred. The local velocity scale is chosen to be an average convection velocity of \(0.6~U_{j}\), consistent with estimated propagation speed of large-scale structures within the shear layer (see Sect. 4). With these parameters, the local fluid time scale is \(\sim \)98 \(\upmu \)s. Assuming an average particle size of \(2~\upmu \)m, the corresponding cutoff time constant is \(\sim \)76 \(\upmu \)s. As the cutoff time constant is now on the same order as the fluid time scale, we would expect significant errors in particle slip. Larger particle size will also significantly increase the estimated error as the cutoff time constant is proportional to the square of the particle diameter [9]. Note that realistically, the turbulent shear layer would contain a mixture of the ambient seed and main jet seed particles, rather than the homogeneous assumption made for this simplified analysis. To consider the disparity of particle size, we examine the correlation error following the method proposed by Timmins [23]. To examine the uncertainty in correlation error we choose particle image size, particle seeding density, shear rate and particle displacement as the contributors to error. These parameters are examined in the raw and processed image files and an uncertainty surface is generated that is then used to estimate the error. Particularly, as the error analysis includes the apparent particle image size, the size discrepancy between the ambient and main jet seed is considered. The resultant estimated error computed for the impinging jet is given in Fig. 4. As expected, we see the largest error (\(<\)10 m/s) within the jet shear layer. Other major contributors occur in the vicinity of the weak shock structure within the jet column, although this error is much lower (\(<\)4 m/s) than that observed in the shear layer. Taking the average convection velocity to be \(0.6~U_{j}\), the maximum error within the shear layer is estimated to be \(\sim \)3.5 % of ideal.

Fig. 4
figure 4

Estimated PIV correlation error in velocity magnitude. Contour is of percent error with respect to the jet exit velocity \(U_j\)

Full size image

3 Results and discussion

To develop an effective and efficient active flow control technique, it is critical to examine the initial condition of the jet shear layer and determine its effect on the near-field acoustics, velocity field, shear layer growth and its stability. In the following sections, these parameters are discussed with a focus on how microjet-based flow control alters the characteristics of the shear layer in both the free and the impinging jet.

3.1 Jet acoustics

This section provides a brief summary of the effects of microjet injection on the noise characteristics of supersonic jets. Details of previous studies can be found in aforementioned references [2, 3, 8]. First, we examine the attenuation associated with an impinging jet. All acoustic spectra are presented as sound pressure levels (SPL) in decibels (dB, ref: 20 \(\upmu \)Pa) as a function of jet Strouhal number, \(St = fd/U_{j}\), where \(f\) is the frequency in Hz. Figure 5 shows the near-field acoustic spectra obtained for an impinging jet with and without microjet control. The baseline, uncontrolled case is characterized by high amplitude, discrete impingement tones associated with jet resonance. This resonance is due to a coupling, or phase lock, between the large-scale coherent structures in the jet shear layer and the upward propagating acoustics. The application of high-momentum microjet injection, shown as the “With Control” case in Fig. 5, nearly eliminates the dominant tone, albeit at the expense of creating a less energetic tone at a higher frequency. There is also an appreciable reduction in broadband levels, indicating that the effect of control is not merely a disruption of the feedback loop. This leads to a reduction in the overall sound pressure levels (OASPL) of 8.9 dB.

Fig. 5
figure 5

Impinging jet acoustic spectra with and without microjet control

Full size image

In the case of the nearly ideally expanded free jet, there are of course no discrete tones. However, at this stage, it is prudent to examine the effect of the lift plate on the uncontrolled free jet noise spectra. As shown in Fig. 2, the microjet control is embedded in the lift plate. Hence, the baseline, uncontrolled case will also be that with the lift plate attached. Figure 6 compares free jet noise at angles of \(\phi = 90^{\circ }\) and \(30^{\circ }\). with and without the lift plate.

Fig. 6
figure 6

Effect of lift plate on free jet noise. , with lift plate, black line, no lift plate

Full size image

The acoustic spectra without the lift plate are as expected. Namely, the turbulent mixing component from the large-scale structures at the end of the potential core leads to a low-frequency, broadband peak in the spectra at St \({\,\sim \,}\) 0.2. At \(\phi = 90^{\circ }\) to the jet axis, there is a broad, high-frequency hump. Note that, as the divergent portion of the nozzle is a straight conic section with a sharp transition at the nozzle throat, the jet plume will inevitably contain a weak shock structure. The evidence of this is shown in Fig. 6 as broadband shock associated noise near St\(\sim \)0.4. The effect of placing the lift plate at the nozzle exit is also shown in Fig. 6. We see that the general shape of the spectra is similar at both polar angles. However, there is a slight increase in broadband levels and also the emergence of discrete tones in the spectra. Due to entrainment, the presence of the lift plate can locally drop the ambient pressure at the nozzle exit, leading to a slight underexpansion of the nozzle. This, coupled with the effect of a large reflecting surface, allows for the generation of the tones seen in Fig. 6. As was the case with the impinging jet, with the application of microjets, we aim to reduce or eliminate the discrete tones similarly associated with a type of feedback mechanism. In addition, we also aim to reduce broadband levels, specifically in the peak radiation direction of \(\phi = 30^{\circ }\).

Figure 7 shows the effect of microjet control on the free jet spectra. First, in examining the effect of control on radiation at \(\phi = 90^{\circ }\), we see that there is little to no effect on the broadband shock associated noise. This is expected as the microjets themselves will cause a weak shock structure in the jet plume. There is seen to be a reduction in the broadband component associated with turbulent mixing. Typically, modifications at the nozzle exit can potentially add to this component observed upstream and at \(\phi = 90^{\circ }\) with respect to the jet axis. This has been reported for several control strategies that modify the shear layer at the nozzle exit, such as chevrons and microjets [1]. However, as shown in Fig. 6, the presence of the lift plate itself increases this turbulence. Hence, the application of microjets counteracts the effect of the lift plate on this component of jet noise. This leads to a reduction in OASPL at \(\phi = 90^{\circ }\) of 1.2 dB.

Fig. 7
figure 7

Free jet acoustic spectra with and without microjet control. , No control, black line, with control. Solid and dashed lines represent \(\phi = 30^{\circ }\) and \(90^{\circ }\), respectively

Full size image

Typically, the main focus of any free jet control strategy is to reduce the radiation in the peak noise direction, \(\phi \sim 30^{\circ }\). To this end, injection at the nozzle exit aims to attenuate the growth of natural instabilities in the shear layer that lead to the generation of large-scale, spatially coherent structures that are presumed responsible for the dominant noise component. First, we note that Fig. 7 shows the elimination of the discrete tones associated with the presence of the lift plate. In addition, we observe an appreciable decrease in broadband levels at \(\phi = 30^{\circ }\). This indicates that we have modified the initial shear layer in some manner that has led to a reduction in the large, energetic structures that radiate in this direction. To quantify, there is a reduction in OASPL of 4.5 dB. To examine this further, we conduct an in depth analysis of the velocity field and resultant stability characteristics.

3.2 Velocity field

To examine the shear layer characteristics of the free and the supersonic impinging jet, both with and without microjet control, planar streamwise velocity contours were measured using PIV. These are shown in Fig. 8. All cases correspond to a Mach 1.5 nearly ideally expanded jet operating at NPR 3.7 and all impinging jet studies were conducted at \(h/d = 4\). It should be noted, especially for the impinging jet, that as the goal of the current study was to focus on the initial shear layer characteristics, the impingement region is not in the field of view.

Fig. 8
figure 8

Average streamwise velocity contours for the free and the impinging jet with and without microjet control. a Free jet-no control, b Free jet-with control, c Impinging jet-no control, d Impinging jet-with control

Full size image

The free jet case with no control, Fig. 8a, is characterized by an initially thin shear layer near the nozzle exit, which gradually thickens downstream due to turbulent diffusion and entrainment. The weak shock cell structure present in Fig. 8a (see Fig. 9 for a centerline profile) is due primarily to the nozzle design and the effects of entrainment locally reducing the back pressure at the nozzle exit. Figure 8b shows the velocity contour of the free jet with control applied. The mean velocity within the jet core is not much affected; however, weak oblique shocks can faintly be seen near the jet exit plane due to microjet injection. In comparing the development of the shear layer, it is evident that the microjet injection has had a significant effect. With control applied, a rapid thickening of the shear layer is observed, and the shear layer is seen to be thicker through the majority of the profile shown here. Similar observations can be made in the case of the impinging jet. In comparing Fig. 8a,c for the baseline flowfield (no control), the average velocity in the core of the jet looks nearly identical for the free and the impinging jet. For the impinging jet, the shear layer develops in a similar constant manner; however, the spreading rate is increased. This is indicative of the oscillatory nature of the flow field which will cause a thickening of the shear layer in the average. Again, in Fig. 8d, the effect of microjet injection is seen in the presence of weak oblique shocks within the jet core. Also, the trend observed in the free jet is repeated with a rapid growth of the shear layer near the nozzle exit and point of injection. Downstream of the initial nonlinear thickening, the shear layer stabilizes and the growth rate appears to asymptote. To further examine the effect of microjet injection on the mean streamwise velocity within the jet core, centerline profiles are extracted for the free jet case. These are presented in Fig. 9 with and without microjet control. Note that, the case of the impinging jet is nearly identical and is not repeated here. For the baseline case, Fig. 9 shows a slight oscillation in the centerline velocity. As previously mentioned, the presence of the lift plate causes the jet to operate in a slightly underexpanded condition. Hence, the velocity increases just outside the nozzle as the jet further expands. Note that, even the baseline flowfield is especially complex as the conical divergent portion of the nozzle does not require that the velocity vector is identically parallel to the jet axis at the nozzle exit. In addition, the slope discontinuity at the throat can create a shock that persists throughout the nozzle and into the jet core [13].

Fig. 9
figure 9

Free jet centerline average streamwise velocity with and without microjet control

Full size image

The oblique shock created with microjet injection is apparent in Fig. 9 for the “With Control” case. Here, the jet does not undergo full expansion as in the baseline case before it encounters the oblique shock. This is evident in the double oscillation pattern shown with microjet control.

3.3 Vorticity profiles

In addition to the velocity contours, it is useful to examine the vorticity distribution concentrated within the viscous shear layer, especially in a comparison of microjet injection. Considering the flow is essentially parallel, the main component of vorticity is the variation of the streamwise velocity in the radial direction. Here, the main conclusion to be drawn is that the thickening of the shear layer with microjet control leads to a reduction in the azimuthal vorticity in both the free and the impinging jet. Hence, as a first-order approximation, the vorticity can be expressed as \(\varOmega _{\theta }\sim U_{j}/\delta \), where \(U_{j}\) is jet axial velocity, \(\varOmega _{\theta }\) is azimuthal vorticity and \(\delta \) is the shear layer thickness. As shown in Figs. 8 and 9, the magnitude of the velocity within the jet core is only minimally affected by the microjet control. Thus, considering \(U_{j}\) approximately constant, any increase in shear layer thickness should lead to a reduction in peak azimuthal vorticity. Figures 10 and 11 show the corresponding azimuthal vorticity contours of the free and the impinging jet with and without control. Azimuthal vorticity profiles are computed for axial locations \(x/d = 0.5, 1.0, 1.5\) and 2.0 and non-dimensionalized based on jet radius and centerline velocity. As expected, in both cases, the peak azimuthal vorticity is significantly reduced, especially in the direct vicinity of the nozzle exit. Considerable reduction is seen up to 1.5 diameters downstream of the nozzle exit. At 2 diameters downstream, little reduction is seen in the vorticity. This is largely due to the fact that, at this axial position, the shear layer thickness is approximately equal in both cases. At \(x/d = 0.5\), similar reduction is seen in both the free and the impinging jet.

Fig. 10
figure 10

Free jet vorticity profiles normalized by jet half width, \(R_{1/2}\), and centerline velocity, \(U_j\). a \(x/d = 0.5\), b \(x/d = 1.0\), c \(x/d = 1.5\), d \(x/d = 2.0\)

Full size image
Fig. 11
figure 11

Impinging jet vorticity profiles normalized by jet half width, \(R_{1/2}\), and centerline velocity, \(U_j\). a \(x/d = 0.5\), b \(x/d = 1.0\), c \(x/d = 1.5\), d \(x/d = 2.0\)

Full size image

Also seen in the vorticity profiles in Figs. 10b and 11b is slight asymmetry. The strong streamwise vortices produced by microjet injection form along the high-speed side of the jet shear layer [1]. This creates an asymmetric distribution in azimuthal vorticity closer to the nozzle exit where these streamwise vortices form. However, as they convect downstream, these vortices diffuse with the jet shear layer and merge together. This leads to an eventual azimuthally homogeneous flow and a return to symmetry in the vorticity profiles at \(x/d=2\).

3.4 Shear layer characteristics

To examine the effect of microjet injection and its direct modification of the shear layer, the shear layer profiles and growth rates are determined. Figures 12 and 13 compare the shear layer thicknesses for the free and the impinging jet, respectively. Here, the shear layer thickness has been defined as \(\delta = r_{90} - r_{10}\), where \(r_{90}\) and \(r_{10}\) are the radial location where the streamwise velocity is 90 and 10 % of the jet velocity, respectively. With no control in both cases (free as well as impinging jet), it is shown that the shear layer grows at an approximately linear rate over the entire axial range shown. The small, localized deviations from the linear fit are largely due to the presence of the weak shock structures as shown in the velocity profiles in Figs. 8 and 9.

Fig. 12
figure 12

Free jet shear layer growth

Full size image
Fig. 13
figure 13

Impinging jet shear layer growth

Full size image

In comparing the baseline case with the control case for both the free and the impinging jet, a significant difference is observed in the evolution of the shear layer. As previously mentioned when examining the streamwise velocity contours, the shear layer is much thicker in the case of microjet injection. The initial thickening of the shear layer is seen in the nonlinear region of Figs. 12 and 13. At a given axial position downstream, however, the shear layer thickness trends to an asymptotic linear profile similar to that observed in the no control case. The principal difference here is that although there exists a rapid thickening, the fully developed linear growth rate is smaller in both cases with applied control. Although not discussed here, microjets have been shown to induce streamwise vorticity and nearly the same growth rate change was observed in the axial variation of streamwise vorticity with microjet injection on a Mach 0.9 jet [1]. In this case, the decay of streamwise vorticity experienced a rate change at nearly the same axial position. Thus, we conclude that the initial thickening of the shear layer with microjet injection is likely due to the generation of these strong streamwise vortices. After some prescribed position downstream, the mutual interaction of the counter-rotating vortex pairs combined with viscous effects will cause their eventual decay, resulting in a thickened shear layer with a lower growth rate. Of course the location at which this occurs will be highly dependent on the initial state of the uncontrolled shear layer, as well as the microjet spacing and supply pressure.

The trend to a lower growth rate is an important parameter as it indicates that microjet control has had a stabilizing effect on the inherent instabilities of the shear flow. To quantify these results, the shear layer axial growth rate, \(d\delta /dx\), for the free and the impinging jet, is 0.10 and 0.11, respectively. As the two flows are quite similar in the region very near the nozzle exit, the baseline growth rates are very similar. With microjet injection, in the fully developed linear region, \(d\delta /dx\) is reduced to 0.08 and 0.06, respectively. Again, the reduction in shear layer growth is similar in both cases, although for the impinging jet, the initial nonlinear region extends slightly further downstream.

The linear growth rate of the shear layer thickness is indicative of a self-preserving flow. In this case, it is expected that all dimensionless quantities will depend only on a local similarity variable, and not explicitly on the axial position. For the axisymmetric jet, the similarity variable is taken to be \(\eta = (r - R_{1/2})/\delta \) with \(u/U_{j} = f(\eta )\). Here, \(r\) is the radial position, \(R_{1/2}\) is the radial position where the jet velocity is half of the centerline velocity, and \(\delta \) is again the shear layer thickness at the given axial position. Figure 14 shows the normalized velocity \(u/U_{j}\) plotted as a function of the similarity variable \(\eta \). For both the free and the impinging jet cases of no control, the profiles at all four axial positions collapse nearly identically onto a single similarity solution. This coincides with the observed linear growth rate of the shear layer for the no control case in Fig. 14a, c. It is interesting to note that even in the impinging jet, where the feedback mechanism dominates the unsteady flow field, the initial mixing region still shows similarity. The results are, however, different for the profiles with microjet injection. As shown in Fig. 14b, d, while the similarity profiles collapse identically for the last three axial positions, the profile at \(x/d = 0.5\) does not. This is again consistent with axial variation in the shear layer thickness. The incipient nonlinear shear layer growth due to microjet injection prevents self-similarity. However, downstream, once the initial conditions have decayed, the mixing region grows linearly with distance and similarity is achieved. These results were used to construct the linear fits of the shear layer thickness of Figs. 12 and 13. As previously explained, the nonlinear shear layer growth prevents self-similarity. Thus, the similarity profiles with control were plotted for each axial position until convergence with downstream locations was achieved. It was found that, for the free jet, the solution collapsed at \(x/d = 0.62\) and for the impinging jet at \(x/d = 0.82\). These axial positions were then considered as the start of the linear region. The linear fit was then constructed from this point downstream. As the profiles without control collapse identically, the entire region was plotted with a linear fit.

Fig. 14
figure 14

Similarity profiles for the free and the impinging jet, with and without microjet control. a Free jet-no control, b Free jet-with control, c Impinging jet-no control, d Impinging jet-with control

Full size image

4 Stability analysis

We have thus far discussed the effect of microjet injection on the aeroacoustics, velocity field, vorticity distribution and shear layer growth. It has been reasoned that an initial thickening of the shear layer with microjet injection reduces the shear layer growth in both the free and the impinging jet. The acoustics reveal that microjet control leads to a reduction in radiated noise in the free jet and an attenuation of the impingement tones and broadband levels for the impinging jet. We now explore the stability characteristics of the velocity profiles to further gain insight into how the manipulation of the shear layer modifies the natural Kelvin–Helmholtz instabilities.

The importance of large-scale, spatially coherent structures on the radiated noise has become apparent in several studies [7, 20, 21]. It is believed that these structures are a major contributor to jet noise at low angles with respect to the jet axis. There is a connection between these coherent structures, referred to as wave packets [7] and stability waves determined from modal solutions to the disturbance equations deriving their energy from the mean flow. Here, we complete a linear stability analysis using velocity profiles obtained from PIV and attempt to relate the theoretical results to the observed behavior previously reported. The stability analysis closely follows that described by Morris [11]. Namely, we assume that the primitive variables may be decomposed as \(\mathbf {q} = \bar{\mathbf {q}} + \mathbf {q}'\). where \(\mathbf {q} = [\rho u_{x} u_{r} u_{\theta } p]^\mathrm{T}\), \(\bar{\mathbf {q}}\) denotes the time-averaged quantities obtained from PIV, and \(\mathbf {q}'\) denotes the linear perturbations. Note that for the mean flow, we assume the jet to be ideally expanded and hence the pressure uniform and we estimate the density from the Crocco–Busemann relation [11]. Assuming inviscid disturbances, we linearize the Euler equations in which the density disturbance equation becomes decoupled. In the present analysis, we analyze each axial position independently. Hence, in our formulation, we neglect the mean flow divergence and assume that all axial derivatives (\(\partial /\partial x\)) are identically zero. This is the weakly parallel flow assumption. We further assume that the only nonzero velocity component is the axial component, and that it is only a function of radial position (i.e., \(\bar{u}_{i} = \bar{u}_{x}(r)\)). We now represent the disturbance by a normal modes solution as

$$\begin{aligned} \mathbf {q}'=\hat{\mathbf {q}}(r)\exp [i(\alpha x+m\theta - \omega t)]. \end{aligned}$$
(1)

Here, \(\hat{\mathbf {q}}(r)\) is a shape function describing the radial distribution of the disturbance and the argument of the exponential is a phase function describing the axial, azimuthal and temporal oscillations. In the phase function, \(\alpha \) is the axial wavenumber, \(m\) is the azimuthal mode number and \(\omega \) is the radian frequency. On substitution into the disturbance equations, we may combine all the shape functions into a single ordinary differential equation describing the pressure shape function, \(\hat{p}\).

$$\begin{aligned} \frac{d^{2}\hat{p}}{dr^{2}}&- \left[ \frac{2\alpha d\bar{u}_{x}/dr}{\alpha \bar{u}_{x} - \omega } + \frac{d\bar{\rho }/dr}{\bar{\rho }} - \frac{1}{r} \right] \frac{d\hat{p}}{dr}\nonumber \\&- \left[ \frac{m^{2}}{r^{2}} + \alpha ^{2} - \frac{\bar{\rho }}{\gamma \bar{p}} (\alpha \bar{u}_{x} - \omega )^{2} \right] \hat{p} = 0 \end{aligned}$$
(2)

This is referred to as the compressible Rayleigh equation. A detailed derivation of (2) may be found in [10, 11, 22]. Here, \(\bar{u}_{x}\) refers to the mean streamwise radial velocity profile at each axial position obtained from PIV and \(\bar{\rho }\) is the corresponding density profile estimated from Crocco–Busemann. \(\gamma \) is the ratio of specific heats and is taken to be \(1.4\). \(\bar{p}\) is the ideally expanded pressure given by \(\bar{p} = \rho _{j}(U_{j}/M_{j})^{2}/\gamma \). For the spatial stability problem that is most applicable for convectively unstable flows such as a jet or shear flow, (2) becomes an eigenvalue problem for the complex wavenumber \(\alpha \). For a specified \(m\) and \(\omega \), we can solve for \(\alpha \) by matching the specified boundary conditions as \(r \rightarrow 0\) and \(r \rightarrow \infty \). If we define \(\alpha = \alpha _{r} + i \alpha _{i}\), where \(i = \sqrt{-1}\), then \(\alpha _{r}\) is the number of oscillations per unit length and \(\alpha _{i}\) is the axial growth rate. The jet is then unstable for all \(\alpha _{i} < 0\) and we can determine the convection speed of the instabilities as \(c_{ph} = \omega /\alpha _{r}\). We determine the boundary conditions by noting that within the potential core, as \(r \rightarrow 0\), and in the far-field as \(r \rightarrow \infty \), the radial derivatives of the mean axial velocity and density become zero. Hence, (2) becomes a Bessel’s equation. By requiring that the pressure eigenfunction \(\hat{p}\) is bounded at \(r = 0\) and \(\infty \), we can directly write the boundary conditions as

$$\begin{aligned} \hat{p}(r) \sim I_{m}\left( \sqrt{\alpha ^{2} - \frac{\bar{\rho }}{\gamma \bar{p}} (\alpha \bar{u}_{x} - \omega )^{2}} r \right) \end{aligned}$$
(3)

as \(r \rightarrow 0\), and

$$\begin{aligned} \hat{p}(r) \sim K_{m}\left( \sqrt{\alpha ^{2} - \frac{\bar{\rho }}{\gamma \bar{p}} (\alpha \bar{u}_{x} - \omega )^{2}} r \right) \end{aligned}$$
(4)

as \(r\rightarrow \infty \), where \(I_{m}\) and \(K_{m}\) are the modified Bessel functions of the first and second kind, respectively. To solve (2), we use a shooting method. To this end, we integrate using a variable step fourth-order Runge–Kutta with an initial guess for \(\alpha \) from the specified boundary conditions at the jet centerline (\(r = 0.01~d\) to avoid the singularity at the origin) and the far-field. We then match solutions at the nozzle lip line \(R_{j} = d/2\) and iterate upon \(\alpha \) until \(\hat{p}\) and \(d\hat{p}/d r\) are continuous there. The iteration on \(\alpha \) is carried out using Newton–Rhapson (the system is expanded to accommodate the \(\alpha \) derivative) until \(| \alpha ^{n+1} - \alpha ^{n} | < 10^{-9}\).

To provide an analytical representation of the velocity profile, we estimate the velocity as

$$\begin{aligned} \bar{u}_{x}(r) = {\left\{ \begin{array}{ll} U_{j}, &{}\quad r < h\\ U_{j}\exp \left[ -\ln (2)\displaystyle {\frac{(r - h)^{2}}{b^{2}}}\right] , &{}\quad r \ge h. \end{array}\right. } \end{aligned}$$
(5)

Here, \(U_{j}\) is the centerline velocity and \(h\) and \(b\) are parameters that are determined from a least-squares fit. A sample profile used in the stability calculation is provided in Fig. 15 for the baseline free jet at \(x/d = 0.5\). It is seen that (5) accurately approximates the physical velocity profile. Example stability calculations for the profile shown in Fig. 15 are also shown in Figs. 16 and 17. It is shown in Fig. 16 that the jet is unstable over a wide \(St\) range, being most unstable for \(St \sim 0.4\) for both the axisymmetric (\(m = 0\)) and helical (\(m = 1\)) mode. At this Mach number (\(M_{j} = 1.5\)), the two modes have similar growth rates, with the \(m = 1\) mode being slightly dominant. It is worth noting that the jet is most unstable for \(St \sim 0.4\), which is also the peak \(St\) in the free jet spectra observed at \(\phi = 90^{\circ }\).

Fig. 15
figure 15

Sample profile for \(\bar{u}_{x}(r)\) used in the stability calculation for the baseline free jet at \(x/d = 0.5\). The parameters in (5) are \(h = 0.4617\) and \(b = 0.0754\). The symbols are velocity values obtained from PIV and the solid line is (5)

Full size image
Fig. 16
figure 16

Example unstable growth rate versus jet Strouhal number (\(St = fd/U_{j}\)). This is computed for the free jet baseline flow at \(x/d = 0.5\). Solid and dashed lines represent \(m = 0\) and \(m = 1\) respectively

Full size image
Fig. 17
figure 17

Example convection velocity \(c_{ph}\) versus jet Strouhal number computed for the free jet baseline flow at \(x/d = 0.5\). Solid and dashed lines represent \(m = 0\) and \(m = 1,\) respectively

Full size image

The convection velocity, \(c_{ph} = \omega /\alpha _{r}\), of the Kelvin–Helmholtz instabilities is bound by \(0 < c_{ph} \le U_{j}\). For the same profile, this is shown in Fig. 17 for the helical and axisymmetric mode. For the peak \(St \sim 0.4\), \(c_{ph} \sim 0.6U_{j}\) and \(0.65U_{j}\) for the \(m=1\) and \(m=0\) modes, respectively.

To describe the axial evolution of the natural instabilities, we further examine the growth rates at \(x/d = 2.0\). This is shown in Fig. 18. Contrary to Fig. 16 for a profile close to the nozzle exit, there is a large difference between the \(m = 0\) and \(m = 1\) mode, with the \(m = 1\) mode having a significantly larger growth rate. The helical mode has a slightly lower \(St\) at peak \(-\alpha _{i}\), however, both \(m = 0\) and \(m = 1\) occur near \(St \sim 0.2\). While the growth rates of both modes decrease with axial distance, the \(m = 0\) mode decreases much more rapidly than the \(m = 1\) mode. There is also a slight increase in convection velocity. This is quantified in Fig. 19. The \(m = 1\) mode still propagates at \(c_{ph} \sim 0.6U_{j}\) for the peak unstable growth rate. However, the convection velocity of the \(m = 0\) mode increases slightly to \(c_{ph} \sim 0.75U_{j}\). In addition, further claim to support there is a connection between radiated noise and instability waves, the broadband peak seen in Fig. 7 for \(\phi = 30^{\circ }\) occurs in the same \(St\) range as the most unstable growth rates.

Fig. 18
figure 18

Unstable growth rate versus \(St\) for the baseline free jet at \(x/d = 2.0\). Solid and dashed lines represent \(m = 0\) and \(m = 1,\) respectively

Full size image
Fig. 19
figure 19

Convection velocity versus \(St\) for the baseline free jet at \(x/d = 2.0\). Solid and dashed lines represent \(m = 0\) and \(m = 1,\) respectively

Full size image

We are now able to compare the effect of microjet control on the jet instability purely by examining the resultant shear layer profiles. Note that, one further assumption has been made to analyze the profiles with microjet injection. As microjets induce strong counter-rotating vortices oriented parallel to the jet axis, the resultant flow profile is not strictly a function of radial position alone. There is an azimuthal dependence that arises from the corrugated nature of the velocity profile as observed from the \(r-\theta \) plane. Throughout the current work, as well as in the present stability analysis, we have neglected this azimuthal dependence, by explicitly assuming that the shear layer thickness, \(\delta = f(r) \ne f(r,\theta )\). The same can be said with regard to the jet half width. In addition, as the convection velocity is only minimally affected by the shear layer profile and is nominally \(0.6U_{j} \sim 0.7U_{j}\), we only present results of unstable growth rates.

First, we examine the effect of microjet control on the free jet at \(x/d = 0.5\). Recall that the baseline case was presented in Fig. 16. Figure 20 compares the effect of microjet control on \(\alpha _{i}\) for the \(m = 0\) mode. The same comparison for the \(m = 1\) mode is shown in Fig. 21.

Fig. 20
figure 20

Comparison on microjet control on the unstable growth rate for the \(m=0\) mode for the free jet at \(x/d = 0.5\). Solid and dashed lines represent no control and with control, respectively

Full size image
Fig. 21
figure 21

Comparison on microjet control on the unstable growth rate for the \(m=1\) mode for the free jet at \(x/d = 0.5\). Solid and dashed lines represent no control and with control, respectively

Full size image

For both cases, we see that the thickening of the shear layer profile (see Fig. 12) leads to an appreciable reduction in the magnitude of the unstable growth rates. There is also a shift to a slightly lower frequency for maximum \(-\alpha _{i}\). While the low-frequency content is largely unaffected, the region of \(St\) for \(-\alpha _{i} > 0\) is decreased. The reduction in growth rate agrees with the shear layer growth observed in Fig. 12. In fact, Morris [12] used a model based on the superposition of instability waves to capture turbulent shear layer growth, providing a direct relationship between spatial growth rates, \(\alpha _{i}\) and \(\delta (x)\). Hence, based on the reduction in \(-\alpha _{i}\), we can say that we have likely reduced the receptivity of the shear layer which leads to the reduction in spreading rate.

Continuing further downstream, we examine the evolution of instabilities with microjet control (without, of course, including any history effects as \(\alpha \ne \alpha (x)\) in our model). Figures 22 and 23 show the effect of microjet control on the unstable growth rates computed at \(x/d = 2.0\) for the \(m=0\) and \(m=1\) mode, respectively. We observe similar trends discussed at \(x/d = 0.5\). Namely, the growth rates for both modes with control are again reduced. However, here we see that the reduction is not as drastic. This is still consistent with the growth of the shear layer width shown in Fig. 12. As we move downstream, the two profiles and their corresponding computed growth rates become similar. At \(x/d = 2.0\), we also observe that the \(m=1\) mode is dominant. While these results are intuitive and support the observations in the PIV data, by disregarding the history effects we may be missing significant information. The initial thickening of the shear layer with microjet control, and then its trend towards a lower, linear growth rate, is responsible for the eventual merging of the shear layer profiles at some axial position downstream. However, in this analysis, we consider each axial position independent from any other. Thus, our model does not include the initial effects seen in Fig. 12. Perhaps a more accurate method would be to include these effects by allowing \(\alpha \) to vary with \(x\) and replacing \(\alpha x\) in the phase function of (1) with \(\int _{x} \alpha ~dx\). Note that in this case the shape function also becomes a mild function of \(x\). This formulation results in the parabolized stability equations [6] and may be explored further in future work.

Fig. 22
figure 22

Comparison on microjet control on the unstable growth rate for the \(m=0\) mode for the free jet at \(x/d = 2.0\). Solid and dashed lines represent no control and with control, respectively

Full size image
Fig. 23
figure 23

Comparison on microjet control on the unstable growth rate for the \(m=1\) mode for the free jet at \(x/d = 2.0\). Solid and dashed lines represent no control and with control, respectively

Full size image

The above analysis was strictly for the free jet. For the present investigation near the nozzle exit, we could carry out the same analysis for the impinging jet. This would, of course, consider only downward propagating instability waves that are convectively unstable. We have already seen that the microjets alter the mean flow in a similar manner for both the free and the impinging jet. Thus, as the velocity profiles are similar, that analysis produces nearly identical results with the free jet data already presented. However, in self-excited flows such as the impinging jet, perhaps an absolute instability occurs as opposed to the convective instability considered thus far [11]. This may be explored further in future work.

5 Conclusions

The effect of microjet control on the shear layer characteristics of supersonic free and impinging jets is examined through near-field acoustics, particle image velocimetry and linear stability analysis. It is reasoned that the development of the shear layer particularly close to the nozzle exit plays an important role in the natural instabilities and their growth. We find that in both the impinging jet as well as the free jet, microjet injection is characterized by an initial rapid thickening of the shear layer. This initial region is followed by a fully developed region in which the shear layer thickness grows linearly with axial distance and the shear layer profiles are self-similar. In addition, with control, the linear shear layer growth rate beyond the initial nonlinear region is relatively reduced. Although the noise sources in free and impinging jets are quite different, the modification to the mean flow is similar. As a result, we observe appreciable reduction in sound pressure levels for both cases. For the impinging jet, there is a drastic reduction in impingement tones accompanied with a reduction in broadband levels. Although the current control scheme was not optimized for a free jet, we still observe an overall reduction of 4.5 dB for a free jet in the peak radiation direction. Linear stability analysis conducted on the velocity profiles extracted from PIV reveals that the thickening of the shear layer leads to a reduction in unstable growth rates. This is especially the case near the nozzle exit where the baseline shear layer is very thin. We conclude that microjet injection is not only a viable method for control in disrupting the feedback mechanism inherent in resonant flow fields such as the impinging jet, but it is also able to favorably modify the coherent structures and turbulent mixing believed responsible for the dominant noise source in free jets.