1 Introduction

With the development of multi-GNSS, especially the BDS and Galileo satellites with multi-frequency designed signal structure, the differential code bias (DCB) has begun to receive increasing interest in the multi-frequency multi-GNSS community (Lou et al. 2015). It is generally acknowledged that the DCB is a hardware delay caused by the signal traveling through the instruments on satellite and receiver side, which may cause a ranging error up to several meters. And the DCB plays an important role in GNSS ionospheric modeling, undifferenced ambiguity resolution, as well as the high-precision multi-frequency GNSS data processing (Lanyi and Roth 1988; Wilson and Mannucci 1993; Gu et al. 2013; Gu 2013).

Great efforts have been made to the estimation of the DCB constant part, as well as the modeling of the DCB variation, each make their own contributions (Zhong et al. 2016; Xiang and Gao 2017; Zha et al. 2019; Zhang et al. 2019; Gu et al. 2020). Notably the work of Montenbruck et al. (2014) and Wang et al. (2016) has begun to routinely provide DCB products of multi-frequency multi-GNSS since 2013, while Gong et al. (2018) and Zheng et al. (2019) have gone one step further by modeling the BDS signal distortion biases caused by different correlator spaces and front-end designs of receivers. The signal distortion biases are related to receiver models and will decrease the accuracy of DCB estimation when using inhomogeneous receivers, such as receivers from MGEX network.

Obviously, attributed to the achievements and the ongoing efforts of researchers, the reliable products and models of DCB are expected to be publicly available. However, there was no consensus on an acceptable solution for the GLONASS DCB up to now. Unlike code division multiple access (CDMA) used by GPS, BDS and Galileo, etc., the GLONASS signals are modulated with frequency division multiple access (FDMA) up to now (ICD-GLONASS 2008; Revnivykh 2010). Since the DCB is related to signal modulation and frequency, the receiver code biases of GLONASS are varying for different satellites due to FDMA, and consequently increase the difficulty for high precision GLONASS data processing. It is noted that by taking the frequency dependence of GLONASS DCB into consideration, the so-called inter-frequency bias (IFB) is usually further estimated besides the DCB parameter.

The earliest studies of GLONASS IFB may date back to 2000s. Tsujii et al. (2000) pointed out that the IFB can cause an error on the order of a few meters for a zero-baseline experiment. Al-Shaery et al. (2013) proposed an algorithm to effectively fix ambiguity by calibrating inter-channel phase bias for GNSS RTK. Based on the residual analysis of precise point positioning (PPP), Shi et al. (2013) estimated undifferenced GLONASS pseudo-range IFB for 133 receivers from five manufacturers and pointed out that the IFB is not only dependent on the receiver type, but also have a strong correlation with the receiver firmware. Yasyukevich et al. (2015) founded that there are systematic variations on the determination of the absolute total electron content by using GLONASS data. By comparison the results of GPS/GLONASS combined ionospheric modeling with and without GLONASS IFB estimated, Zhang et al. (2017a, b) argued that the GLONASS IFB would introduce a frequency-dependent error ranged from 0.53 to 1.13 TECU. Moreover, a co-stations experiment was carried out by Zhang et al. (2017a, b) to analyze the characteristics of GLONASS P1P2 pseudo-range IFB, and the result demonstrated that the GLONASS IFBs cannot be absorbed by the receiver DCB during ionosphere modeling.

DCB is originally treated as by-product of global GNSS ionospheric delay modeling in Ionosphere Working Group (Iono-WG) by the international GNSS service (IGS). Typically, the DCB/IFB is estimated along with ionospheric delay spherical-harmonic (SH) modeling based on geometry-free combination (GF). It was until 2012, the IGS has issued a call for participation in IGS bias and calibration working group (BCWG), and providing the GNSS bias products to cope with the multi-frequency multi-GNSS data processing (Schaer 2012; Johnston et al. 2017). However, concerning the GLONASS IFB solution, a GPS-like approach was usually involved. In other words, the varying of GLONASS receiver code bias for different satellites was absorbed in the data processing (Hauschild and Montenbruck 2016; Wang et al. 2016). More recently, for the flexibility of GNSS bias transformations, the CODE analysis center (AC) has developed an observable-specific signal bias (OSB) approach as an extension to the traditional DCB solution. In this study, the GLONASS IFB of each satellite was simply treated as a common parameter for all stations (Villiger et al. 2019). Notably, the FDMA-aware GLONASS bias products are actually provided by two individual AC, i.e., CODE and GFZ in the SINEX-bias format via ftp://cddis.gsfc.nasa.gov/pub/gps/products/mgex/. However, for the CODE products, only the ionosphere-free (IF) combination IFB of P1 and P2 is available (Prange et al., 2020), while it is founded that the GLONASS IFB of GFZ on both frequencies are identical for the same receiver-satellite pair (Männel et al., 2020). On the other hand, there is no combined GLONASS IFB products up to our knowledge. In summary, we can conclude that there is lack of consensus on a standard solution for the GLONASS IFB.

To fully access the capabilities of multi-frequency GNSS, the undifferenced and uncombined data processing model is promoted, in which all undifferenced and uncombined available signals from variety of frequencies of multi-GNSS are incorporated in a uniform parameter estimation system directly (Schönemann et al. 2011; Gu et al. 2013). Focusing on the ionospheric delay parameterization in the undifferenced and uncombined GNSS data processing model, the DESIGN (DEterministic plus Stochastic Ionosphere model for GNss) is further developed by Shi et al. (2013), Lou et al. (2015), and Zhao et al. (2019). In this contribution, we extended the undifferenced and uncombined data processing model with DESIGN to GLONASS IFB solution. This paper is organized as follows: firstly, the mathematic models of IFB with traditional SH ionospheric delay modeling solution and undifferenced and uncombined solution are introduced, while the datum effect in the two IFB solutions is analyzed. In addition, the products of CODE and GFZ are also compared. To verify the efficiency of these two IFB solutions, numerical experiments of both regional and global network were carried out with two-month data under different ionosphere activity status. Finally, we presented our conclusion.

2 Notation

In this paper, we adopt the following conventions: matrices and vectors are denoted in bold form, while scalars are denoted in regular form. And the term in its bold form stands for the corresponding vector, e.g., \({{\varvec{P}}}_{{\varvec{r}},{\varvec{f}}}={\left(\begin{array}{cc}\begin{array}{cc}{\stackrel{\sim }{P}}_{r,f}^{1}& {\stackrel{\sim }{P}}_{r,f}^{2}\end{array}& \begin{array}{cc}\cdots & {\stackrel{\sim }{P}}_{r,f}^{j}\end{array}\end{array}\right)}^{T}\) and \({{\varvec{N}}}_{{\varvec{r}}, {\varvec{f}}}={\left(\begin{array}{cc}\begin{array}{cc}{N}_{r,f}^{1}& {N}_{r,f}^{2}\end{array}& \begin{array}{cc}\cdots & {N}_{r,f}^{j}\end{array}\end{array}\right)}^{T}\) are the pseudo-range observation minus calculated (OMC) vector and the ambiguity vector for receiver \(r\) on frequency \(f\) for different satellite \(j\). For more details concerning these vectors, we refer to Sect. 3. In addition, a few symbols and notions are defined for future reference: \(\otimes \) are the Kronecker product (Rao. 1973); and the notions are defined as

$${{\varvec{z}}}_{{\varvec{s}}}={\left(\begin{array}{cc}\begin{array}{cc}0& 0\end{array}& \begin{array}{cc}\cdots & 0\end{array}\end{array}\right)}^{T}$$
(1)
$${{\varvec{u}}}_{{\varvec{s}}}={\left(\begin{array}{cc}\begin{array}{cc}1& 1\end{array}& \begin{array}{cc}\cdots & 1\end{array}\end{array}\right)}^{T}$$
(2)
$${{\varvec{Z}}}_{{\varvec{s}}}=\left(\begin{array}{ccc}0& \cdots & 0\\ \vdots & \ddots & \vdots \\ 0& \cdots & 0\end{array}\right)$$
(3)
$${{\varvec{U}}}_{{\varvec{s}}}=\left(\begin{array}{ccc}1& \cdots & 0\\ \vdots & \ddots & \vdots \\ 0& \cdots & 1\end{array}\right)$$
(4)
$$diag({\varvec{a}})=\left(\begin{array}{cc}\begin{array}{cc}\begin{array}{c}\begin{array}{c}{a}_{1}\\ 0\end{array}\\ \begin{array}{c}\vdots \\ 0\end{array}\end{array}& \begin{array}{c}\begin{array}{c}0\\ {a}_{2}\end{array}\\ \begin{array}{c}\vdots \\ 0\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\begin{array}{c}\cdots \\ \cdots \end{array}\\ \begin{array}{c}\ddots \\ \cdots \end{array}\end{array}& \begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ \begin{array}{c}\vdots \\ {a}_{n}\end{array}\end{array}\end{array}\end{array}\right)$$
(5)
$${{\varvec{J}}}_{{\varvec{i}}{\varvec{j}}}=\left(\begin{array}{cc}{J}_{ij}^{i}& -{J}_{ij}^{j}\end{array}\right)=\left(\begin{array}{cc}\frac{{f}_{i}^{2}}{{f}_{i}^{2}-{f}_{j}^{2}}& \frac{-{f}_{j}^{2}}{{f}_{i}^{2}-{f}_{j}^{2}}\end{array}\right)$$
(6)

thus, \({{\varvec{z}}}_{{\varvec{s}}}\) is a \(s\) by \(1\) vector with zero entries and \({{\varvec{u}}}_{{\varvec{s}}}\) is a \(s\) by \(1\) vector with one entries, while \({{\varvec{Z}}}_{{\varvec{s}}}\) is a \(s\) by \(s\) matrix with zero entries and \({{\varvec{U}}}_{{\varvec{s}}}\) is a \(s\) by \(s\) identity matrix, and \(\mathrm{diag}({\varvec{a}})\) denotes the diagonal matrix with the elements of vector \({\varvec{a}}={\left(\begin{array}{cc}\begin{array}{cc}{a}_{1}& {a}_{2}\end{array}& \begin{array}{cc}\cdots & {a}_{n}\end{array}\end{array}\right)}^{T}\) on the main diagonal. The dimensions and lengths of such vectors will generally be obvious from context. \({{\varvec{J}}}_{{\varvec{i}}{\varvec{j}}}\) is the IF transformation matrix for observation on frequency \(i,j\left(i\ne j\right)\).

3 Method

The basic observations of the GNSS pseudo-range and carrier phase are described as follows (Teunissen and Montenbruck 2017):

$$\left.\begin{array}{c}{P}_{r,f}^{s}={\rho }_{r}^{s}+{t}_{r}-{t}^{s}+{\alpha }_{r}^{s}{T}_{z}+\frac{40.3{\gamma }_{r}^{s}}{{f}^{2}}{I}_{r}^{s}+{b}_{r,f}-{b}^{s,f}+{\varepsilon }_{P}\\ {\Phi }_{r,f}^{s}={\rho }_{r}^{s}+{t}_{r}-{t}^{s}+{\alpha }_{r}^{s}{T}_{z}-\frac{40.3{\gamma }_{r}^{s}}{{f}^{2}}{I}_{r}^{s}+{\lambda }_{f}{N}_{r,f}^{s}+{\varepsilon }_{\Phi }\end{array}\right\}$$
(7)

where \({P}_{r,f}^{s}\) and \({\Phi }_{r,f}^{s}\) are the pseudo-range and carrier phase on frequency f from receiver r to satellite s in metric units;\({\rho }_{r}^{s}\) is the geometric distance for specific satellite s and receiver r pair;\({t}_{r}\) and \({t}^{s}\) denote the clock offset for receiver and clock, respectively;\({{\alpha }}_{\mathrm{r}}^{\mathrm{s}}\) and \({T}_{z}\) stand for the mapping function and the zenith tropospheric delay, respectively; \({\gamma }_{r}^{s}\) is the mapping function, and \({I}_{r}^{s}\) is the zenith total election content at the signal Ionospheric Pierce Point (IPP); \({b}^{s,f}\) and \({b}_{r,f}\) are the frequency-dependent code bias delay for satellite and receiver, respectively; \({N}_{r,f}^{s}\) denotes the float ambiguity in the cycle unit, and \(\lambda \) is the corresponding wavelength; \({\varepsilon }_{p}\), \({\varepsilon }_{\Phi }\) denote the measurement noise together with the un-model multipath error for pseudo-range and carrier phase, respectively. Meanwhile, satellite orbit errors, the phase center corrections, relative effect, earth rotation error, phase-windup as well as the loading effects are assumed to be corrected in Eq. (7).

Considering the FDMA signals for GLONASS, the receiver code bias \({b}_{r,f}\) is satellite frequency related, thus cannot be separated from the satellite code bias \({b}^{s,f}\)(Shi et al. 2018). Then, by defining the inter-frequency bias (IFB) for GLONASS

$$\mathrm{IFB}_{r,f}^{s}={b}_{r,f}-{b}^{s,f}$$
(8)

and assume that \({t}^{s}\) is exactly known with IGS precise ephemeris, thus Eq. (7) can be rewritten as

$$\left.\begin{array}{c}{P}_{r,f}^{s}={\rho }_{r}^{s}+{t}_{r}+{\alpha }_{r}^{s}{T}_{z}+\frac{40.3{\gamma }_{r}^{s}}{{f}^{2}}{I}_{r}^{s}+\mathrm{IFB}_{r,f}^{s}+{\varepsilon }_{P}\\ {\Phi }_{r,f}^{s}={\rho }_{r}^{s}+{t}_{r}+{\alpha }_{r}^{s}{T}_{z}-\frac{40.3{\gamma }_{r}^{s}}{{f}^{2}}{I}_{r}^{s}+{\lambda }_{f}{N}_{r,f}^{s}+{\varepsilon }_{\Phi }\end{array}\right\}$$
(9)

Though that the IFB usually contains both constant and variable parts as DCB as we have pointed out in the introduction, the variable part was neglected for the large noise of pseudorange measurements.

3.1 Spherical-harmonic ionospheric delay modeling

The GLONASS IFB can be also estimated along with the global or regional ionospheric delay SH modeling based on GF combination. By definition, the GF combination is derived from Eq. (9) with the dual-frequency observations:

$$\left.\begin{array}{c}{P}_{\mathrm{GF},r}^{s}=\left(\frac{1}{{f}_{1}^{2}}-\frac{1}{{f}_{2}^{2}}\right)40.3{\gamma }_{r}^{s}{I}_{r}^{s}+\mathrm{IFB}_{\mathrm{GF},r}^{s}+{\varepsilon }_{{P}_{\mathrm{GF}}}\\ {\Phi }_{\mathrm{GF},r}^{s}=-\left(\frac{1}{{f}_{1}^{2}}-\frac{1}{{f}_{2}^{2}}\right)40.3{\gamma }_{r}^{s}{I}_{r}^{s}+{N}_{\mathrm{GF},r}^{s}+{\varepsilon }_{{\Phi }_{\mathrm{GF}}}\end{array}\right\}$$
(10)

in which

$$\left.\begin{array}{c}\mathrm{IFB}_{\mathrm{GF},r}^{s}=\mathrm{IFB}_{r,1}^{s}-\mathrm{IFB}_{r,2}^{s}\\ {N}_{\mathrm{GF},r}^{s}={\lambda }_{1}{N}_{r,f}^{s}-{\lambda }_{2}{N}_{r,f}^{s}\end{array}\right\}$$
(11)

Since \(\mathrm{IFB}_{\mathrm{GF},r}^{s}\) and \({N}_{\mathrm{GF},r}^{s}\) can be safely regarded as constant without cycle-slip, \({P}_{\mathrm{GF},r}^{s}\) is usually smoothed by \({\Phi }_{\mathrm{GF},r}^{s}\) to remove the noise of pseudo-range based on the Hatch filter (Hatch 1982):

$${\stackrel{-}{P}}_{\mathrm{GF},r}^{s}\left(i+1\right)=\frac{i}{i+1}\left({\stackrel{-}{P}}_{\mathrm{GF},r}^{s}\left(i\right)-\Delta {\Phi }_{\mathrm{GF},r}^{s}\left(i+1\right)\right)+\frac{1}{i+1}{P}_{\mathrm{GF},r}^{s}\left(i+1\right)$$
(12)

with

$$\left.\begin{array}{c}{\stackrel{-}{P}}_{\mathrm{GF},r}^{s}\left(1\right)={P}_{\mathrm{GF},r}^{s}\left(1\right)\\ \Delta {\Phi }_{\mathrm{GF},r}^{s}\left(i+1\right)={\Phi }_{\mathrm{GF},r}^{s}\left(i+1\right)-{\Phi }_{\mathrm{GF},r}^{s}\left(i\right)\end{array}\right\}$$
(13)

In this case, we can deduce that

$${\stackrel{-}{P}}_{\mathrm{GF},r}^{s}\left(i+1\right)=\frac{1}{i+1}\sum_{m=1}^{i+1}\left({P}_{\mathrm{GF},r}^{s}\left(m\right)+{\Phi }_{\mathrm{GF},r}^{s}\left(m\right)\right)-{\Phi }_{\mathrm{GF},r}^{s}\left(i+1\right)$$
(14)

By substituting Eq. (10) into (14), and regarding \(\mathrm{IFB}_{\mathrm{GF},r}^{s}\) and \({N}_{\mathrm{GF},r}^{s}\) as constant, we have

$${\stackrel{-}{P}}_{\mathrm{GF},r}^{s}=\left(\frac{1}{{f}_{1}^{2}}-\frac{1}{{f}_{2}^{2}}\right)40.3{\gamma }_{r}^{s}{I}_{r}^{s}+\mathrm{IFB}_{\mathrm{GF},r}^{s}+{\varepsilon }_{{\stackrel{-}{P}}_{\mathrm{GF}}}$$
(15)

in which

$${\varepsilon }_{{\stackrel{-}{P}}_{\mathrm{GF}}}=\frac{1}{i+1}\sum_{m=1}^{i+1}\left({\varepsilon }_{{P}_{\mathrm{GF}}}+{\varepsilon }_{{\Phi }_{\mathrm{GF}}}\right)-{\varepsilon }_{{\Phi }_{\mathrm{GF}}}$$
(16)
$$D\left({\varepsilon }_{{\stackrel{-}{P}}_{\mathrm{GF}}}\right)=\frac{{\delta }_{{P}_{\mathrm{GF}}}^{2}+{\delta }_{{\Phi }_{\mathrm{GF}}}^{2}}{i+1}+{\delta }_{{\Phi }_{\mathrm{GF}}}^{2}\approx \frac{{\delta }_{{P}_{\mathrm{GF}}}^{2}}{i+1}+{\delta }_{{\Phi }_{\mathrm{GF}}}^{2}$$
(17)

thus, the noise of smoothed pseudo-range GF observation can be reduced as the epochs accumulated, i.e., \(i+1\).

Without loss of generality, suppose \(j\) satellites are tracked by \(k\) receivers simultaneously, i.e., \(s\in \left(\begin{array}{ccc}1& \ldots & j\end{array}\right)\) and \(r\in \left(\begin{array}{ccc}1& \ldots & k\end{array}\right)\), then the GLONASS IFB solution based on regional ionospheric delay modeling in the matrix–vector form based on Eq. (15) can be written as

$${\left(\begin{array}{ccc}{{\varvec{P}}}_{{\varvec{G}}{\varvec{F}},1}& \cdots & {{\varvec{P}}}_{{\varvec{G}}{\varvec{F}},{\varvec{k}}}\end{array}\right)}^{T}={\varvec{A}}\bullet {\left(\begin{array}{cc}{\varvec{I}}& {{\varvec{I}}{\varvec{F}}{\varvec{B}}}_{{\varvec{G}}{\varvec{F}}}\end{array}\right)}^{T}$$
(18)
$${\varvec{A}}=\left(\begin{array}{cc}\left(\frac{1}{{f}_{1}^{2}}-\frac{1}{{f}_{2}^{2}}\right)40.3{\gamma }_{r}^{s}\bullet {{\varvec{U}}}_{{\varvec{j}}\bullet {\varvec{k}}}& {{\varvec{U}}}_{{\varvec{j}}\bullet {\varvec{k}}}\end{array}\right)$$
(19)

in which the vertical ionospheric delay \(I\) is further constrained with SH expansion (Schaer, 1999)

$${I}_{\beta ,s}=\sum_{n=0}^{{n}_{\mathrm{max}}}\sum_{m=0}^{n}{\stackrel{\sim }{P}}_{nm}\left(sin\beta \right)\left({\stackrel{\sim }{C}}_{nm}cos\left(ms\right)+{\stackrel{\sim }{S}}_{nm}sin\left(ms\right)\right)$$
(20)

where \(\beta \) and \(s\) are the geomagnetic latitude and sun-fixed longitude of the interception point of the line of sight; \({n}_{\mathrm{max}}\) is the maximum degree of the SH expansion; \({\stackrel{\sim }{P}}_{nm}\) is the normalized associated Legendre function of degree \(n\) and order \(m\); \({\stackrel{\sim }{C}}_{nm}\) and \({\stackrel{\sim }{S}}_{nm}\) are the unknown SH coefficients and Global Ionosphere Map (GIM) parameters, respectively (Schaer 1999).

Still, the design matrix corresponding to \({{\varvec{I}}{\varvec{F}}{\varvec{B}}}_{{\varvec{G}}{\varvec{F}}}\), i.e., \({{\varvec{U}}}_{{\varvec{j}}\bullet {\varvec{k}}}\) is an identical matrix. Thus, the columns of the design matrix for ionospheric delay can be expressed as a linear combination of \({{\varvec{U}}}_{{\varvec{j}}\bullet {\varvec{k}}}\), regardless the ionospheric delay constrain involved, e.g., SH constrain in this study. Fortunately, the design matrix for ionospheric delay is mapping function \({\gamma }_{r}^{s}\), and geometry terms, i.e., \(\beta \) and \(s\) related, while since these terms are changing over epochs, \({{\varvec{I}}{\varvec{F}}{\varvec{B}}}_{{\varvec{G}}{\varvec{F}}}\) can be separated from the \({\varvec{I}}\) in a multi-epoch solution.

3.2 Undifferenced uncombined PPP

Focusing our attention on the IFB parameters, it is assumed that the geometric distance \({\rho }_{r}^{s}\) and the tropospheric delay \({\alpha }_{r}^{s}{T}_{z}\) are exactly known, and only dual frequency is involved here. Then the model (9) can be further simplified

$$\left.\begin{array}{c}{\stackrel{\sim }{P}}_{r,f}^{s}={t}_{r}+\frac{40.3{\gamma }_{r}^{s}}{{f}^{2}}{I}_{r}^{s}+\mathrm{IFB}_{r,f}^{s}+{\varepsilon }_{P}\\ {\stackrel{\sim }{\Phi }}_{r,f}^{s}={t}_{r}-\frac{40.3{\gamma }_{r}^{s}}{{f}^{2}}{I}_{r}^{s}+{\lambda }_{f}{N}_{r,f}^{s}+{\varepsilon }_{\Phi }\end{array}\right\}$$
(21)

in which \(\stackrel{\sim }{P}\) and \(\stackrel{\sim }{\Phi }\) are the observation minus calculation (OMC) for pseudo-range and carrier-phase, respectively, i.e., \(\stackrel{\sim }{P}=P-\rho -{\alpha }_{r}^{s}{T}_{z}\) and \(\stackrel{\sim }{\Phi }=\Phi -\rho -{\alpha }_{r}^{s}{T}_{z}\).

In the case that the receiver r tracked j satellites simultaneously, i.e., \(s\in \left(\begin{array}{ccc}1& \ldots & j\end{array}\right)\), the GLONASS IFB solution model based on the undifferenced and uncombined observation in the matrix–vector form based on Eq. (21) can be written as

$${\left(\begin{array}{cc}\begin{array}{cc}{{\varvec{P}}}_{{\varvec{r}},1}& {{\varvec{P}}}_{{\varvec{r}},2}\end{array}& \begin{array}{cc}{{\varvec{\Phi}}}_{{\varvec{r}},1}& {{\varvec{\Phi}}}_{{\varvec{r}},2}\end{array}\end{array}\right)}^{T}={{\varvec{A}}}_{{\varvec{r}}}\bullet {\left(\begin{array}{cc}\begin{array}{cc}{t}_{r}& {\varvec{I}}\end{array}& \begin{array}{cc}{\varvec{I}}{\varvec{F}}{\varvec{B}}& {\varvec{N}}\end{array}\end{array}\right)}^{T}$$
(22)
$${{\varvec{A}}}_{{\varvec{r}}}=\left(\begin{array}{cc}\begin{array}{cc}{{\varvec{u}}}_{4{\varvec{j}}}& \left(\begin{array}{c}40.3\\ -40.3\end{array}\right)\otimes \left(\begin{array}{c}diag(\frac{{{\varvec{\gamma}}}_{{\varvec{r}}}^{{\varvec{s}}}}{{{\varvec{f}}}_{1}^{2}})\\ diag(\frac{{{\varvec{\gamma}}}_{{\varvec{r}}}^{{\varvec{s}}}}{{{\varvec{f}}}_{2}^{2}})\end{array}\right)\end{array}& \begin{array}{cc}\left(\begin{array}{c}{{\varvec{U}}}_{2{\varvec{j}}}\\ {{\varvec{Z}}}_{2{\varvec{j}}}\end{array}\right)& \left(\begin{array}{c}{{\varvec{Z}}}_{2{\varvec{j}}}\\ {\lambda }_{f}{{\varvec{U}}}_{2{\varvec{j}}}\end{array}\right)\end{array}\end{array}\right)$$
(23)

The model expressed as Eqs. (22) and (23) is a typical singular system due to the linear dependence of the parameters \({t}_{r}\), \({\varvec{I}}\) and \({\varvec{I}}{\varvec{F}}{\varvec{B}}\) (Welsch 1979; Gu et al. 2013).

Concerning the datum deficiency of ionospheric delay \({I}_{r}^{s}\), it can be regularized by applying its temporal and spatial constrains, as well as a priori ionospheric delay model as discussed by Zhao et al. (2019). In this study, the DESIGN model is adopted in the ionospheric delay constrain:

$$\left.\begin{array}{c}{I}_{r}^{s}={a}_{0}+{a}_{1}dL+{a}_{2}dB+{a}_{3}d{L}^{2}+{a}_{4}d{B}^{2}+{r}_{r}^{s}\\ {\stackrel{\sim }{I}}_{r}^{s}={a}_{0}+{a}_{1}dL+{a}_{2}dB+{a}_{3}d{L}^{2}+{a}_{4}d{B}^{2}+{r}_{r}^{s}+{\varepsilon }_{{\stackrel{\sim }{I}}_{r}^{s}}\end{array}\right\}$$
(24)

where \({a}_{i}\) (\(i\in \left(\begin{array}{ccc}0& \ldots & 4\end{array}\right)\)) are the coefficients that describe the deterministic behavior of ionospheric delay; \({r}_{r}^{s}\) is the residual ionospheric effect for each satellite that describes the stochastic behavior of ionospheric delay; dL, dB are the longitude and latitude differences between the IPP and the approximate location of station, respectively.\({\stackrel{\sim }{I}}_{r}^{s}\) is the vertical ionospheric delay pseudo-observation with the corresponding noise \({\varepsilon }_{{\stackrel{\sim }{I}}_{r}^{s}}\), and it is typically derived from the Global Ionosphere Map (GIM) or regional ionosphere model. For more details of Eq. (24) as well as the datum deficiency of undifferenced and uncombined model, the readers are suggested to refer to Zhao et al. (2019).

In addition, to separate \({\varvec{I}}{\varvec{F}}{\varvec{B}}\) from the receiver clock \({t}_{r}\), the following condition

$$0={{\varvec{u}}}_{2{\varvec{j}}}^{{\varvec{T}}}\bullet {\varvec{I}}{\varvec{F}}{\varvec{B}}$$
(25)

is further introduced, i.e., the sum of IFB of different satellite and frequency for each receiver \(r\) is zero. It should be noted that since the number of the processed GLONASS satellites could vary during the experimental period, a constant may be introduced to remove the additional IFB variation introduced by this datum shift.

3.3 Datum in IFB solutions

It should be noted that with PPP solution, we can generate the IFB on each frequency, which is not directly comparable with the GF IFB. And the datum effect should be taken into consideration in the transformation of GF IFB and the IFBs on each frequency. The datum difference may raise from the PPP solution with the precise GLONASS satellite clock used, as well as the constrain of Eq. (25), while the SH ionospheric delay modeling solution is free of precise satellite clock and the constrain.

As the precise clock provided by IGS is estimated with L1/L2 IF combination, the satellite clock and code bias lumped together (Lou et al. 2015) as

$${t}^{s}:={t}^{s}+{{\varvec{J}}}_{12}\bullet {\left(\begin{array}{cc}\mathrm{IFB}_{r,1}^{s}& \mathrm{IFB}_{r,2}^{s}\end{array}\right)}^{T}$$
(26)

the symbol \(:=\) here means “is replaced by”. Thus, by substituting Eq. (26) into (7), the model (21) is shifted by \({{\varvec{J}}}_{12}\bullet {\left(\begin{array}{cc}\mathrm{IFB}_{r,1}^{s}& \mathrm{IFB}_{r,2}^{s}\end{array}\right)}^{T}\) as

$$\left.\begin{array}{c}{\stackrel{\sim }{P}}_{r,f}^{s}+{{\varvec{J}}}_{12}\bullet {\left(\begin{array}{cc}\mathrm{IFB}_{r,1}^{s}& \mathrm{IFB}_{r,2}^{s}\end{array}\right)}^{T}={t}_{r}+\frac{40.3{\gamma }_{r}^{s}}{{f}^{2}}{I}_{r}^{s}+\mathrm{IFB}_{r,f}^{s}+{\varepsilon }_{P}\\ {\stackrel{\sim }{\Phi }}_{r,f}^{s}+{{\varvec{J}}}_{12}\bullet {\left(\begin{array}{cc}\mathrm{IFB}_{r,1}^{s}& \mathrm{IFB}_{r,2}^{s}\end{array}\right)}^{T}={t}_{r}-\frac{40.3{\gamma }_{r}^{s}}{{f}^{2}}{I}_{r}^{s}+{\lambda }_{f}{N}_{r,f}^{s}+{\varepsilon }_{\Phi }\end{array}\right\}$$
(27)

Since the ionospheric delay is constrained with DESIGN, \({{\varvec{J}}}_{12}\bullet {\left(\begin{array}{cc}\mathrm{IFB}_{r,1}^{s}& \mathrm{IFB}_{r,2}^{s}\end{array}\right)}^{T}\) is most likely to be absorbed by \({t}_{r}\) and \(\mathrm{IFB}_{r,f}^{s}\). Obviously, the estimated values of \({t}_{r}\) and \(\mathrm{IFB}_{r,f}^{s}\) in Eq. (27) differ from that of Eq. (21). Assuming the estimated \({t}_{r}\) and \(\mathrm{IFB}_{r,f}^{s}\) is shifted by \({x}_{t}\) and \({x}_{\mathrm{IFB}}\), respectively, then \({x}_{t}\) and \({x}_{\mathrm{IFB}}\) must satisfy the follow relations by the comparison of Eqs. (21) and (27)

$$\left.\begin{array}{c}{t}_{r}:={t}_{r}+{x}_{t}\\ \mathrm{IFB}_{r,f}^{s}:=\mathrm{IFB}_{r,f}^{s}+{x}_{\mathrm{IFB}}\\ {x}_{t}+{x}_{\mathrm{IFB}}={{\varvec{J}}}_{12}\bullet {\left(\begin{array}{cc}\mathrm{IFB}_{r,1}^{s}& \mathrm{IFB}_{r,2}^{s}\end{array}\right)}^{T}\end{array}\right\}$$
(28)

while the value of \({x}_{t}\) and \({x}_{\mathrm{IFB}}\) is subject to the constrain (25), which is introduced to separate IFB and the receiver clock.

In addition, the \(\mathrm{IFB}_{r}^{s}\) on both frequencies are shifted by the same value \({x}_{\mathrm{IFB}}\) as the identical coefficient in the design matrix, and \({x}_{\mathrm{IFB}}\) is removed in the GF combination as indicated by Eq. (11), i.e., \(\mathrm{IFB}_{r,GF}^{s}:=\left(\mathrm{IFB}_{r,1}^{s}+{x}_{\mathrm{IFB}}\right)-\left(\mathrm{IFB}_{r,2}^{s}+{x}_{\mathrm{IFB}}\right)=\mathrm{IFB}_{r,1}^{s}-\mathrm{IFB}_{r,2}^{s}\). Thus, the GF IFB derived with the IFB on individual frequency is free of the datum effect. However, special attention should be paid to this datum effect when \(\mathrm{IFB}_{r,f}^{s}\) was applied to the single-frequency or IF data processing for GLONASS.

4 Experiment

To assess the performance of GLONASS IFB estimation based on different methods, i.e., SH ionospheric delay modeling, undifferenced and uncombined PPP, we adopt both methods in the FUSING (FUSing IN Gnss) software package (Shi et al. 2018; Zhao et al. 2019; Yang et al. 2019; Gu et al. 2020). In this section, the details of the data collection, processing strategy, as well as the results of both the regional and global GLONASS IFB solution experiments will be presented.

4.1 Data and strategy

Concerning the regional experiment, observations from 236 CMONOC (the Crustal Movement Observation Network of China) stations were collected with an interval of 30 s, while 172 IGS stations were collected with an interval of 30 s. The experimental periods from March 1 to March 31, 2014, and March 1 to March 31, 2017 were selected for the high solar and low solar status, respectively. To analyze the long-term stability of IFB, the data of 172 IGS stations over 2014 and 2017 was further collected and processed with a time resolution of 10 days.

The experimental verification is organized as follows: firstly, the SH ionospheric delay modeling solution was performed with GLONASS IFB of each receiver-satellite pair treated as independent parameter, and the estimated GF IFB products were evaluated in terms of daily stability. Then, the IFB on each frequency was estimated with undifferenced and uncombined PPP, and the performance of these IFB was analyzed and compared with the GF IFB, as well as the IF IFB products of CODE analysis center. Next, we came to the discussion on the properties of the IFB estimates; finally, we discussed the calculation efficiency of two methods.

4.2 IFB performance analysis

Summarized in Table 1 is the strategy of the solutions, since there is no standard IFB products available from IGS up to now, the performance of the IFB solution is mainly evaluated by the daily repeatability, i.e., standard deviation over the experimental period. For each receiver \(r\), the standard deviation is defined as

Table 1 The strategies of IFB solution
Full size table
$$\mathrm{STD}_{r}=\frac{{\sum }_{s=1}^{j}\mathrm{STD}_{r}^{s}}{j}$$
(29)

where \(\mathrm{STD}_{r}^{s}=\sqrt[2]{\frac{{\sum }_{\mathrm{day}=1}^{\mathrm{nDay}}\left(\mathrm{IFB}_{r,\mathrm{day}}^{s}-{\stackrel{-}{\mathrm{IFB}}}_{r,}^{s}\right)}{\mathrm{nDay}-1}}\) and \({\stackrel{-}{\mathrm{IFB}}}_{r,}^{s}=\frac{{\sum }_{\mathrm{day}=1}^{\mathrm{nDay}}\mathrm{IFB}_{r,\mathrm{day}}^{s}}{\mathrm{nDay}}\) are the standard deviation and mean value of IFB for receiver \(r\) and satellite \(s\), respectively; nDay is the number of days for each experimental period, i.e., 31 in this study; \(\mathrm{IFB}_{r,\mathrm{day}}^{s}\) is the daily IFB estimate for receiver \(r\) and satellite \(s\) on day.

In addition, the IFB in undifferenced and uncombined PPP solution on each frequency is also converted to GF IFB, and compared with the results in the SH ionospheric delay modeling solution. In this case, we defined the root-mean-square error as

$$\mathrm{RMS}_{r}=\sqrt[2]{\frac{{\sum }_{s=1}^{j}{\sum }_{\mathrm{day}=1}^{\mathrm{nDay}}\left(\mathrm{IFB}_{\mathrm{GF},r,\mathrm{day}}^{s}\left(\mathrm{PPP}\right)-\mathrm{IFB}_{\mathrm{GF},r,\mathrm{day}}^{s}\right)}{j\bullet \mathrm{nDay}}}$$
(30)

where \(\mathrm{IFB}_{r,day,GF}^{s}\left(\mathrm{PPP}\right)\) is the PPP converted GF IFB; \(\mathrm{IFB}_{r,day,GF}^{s}\) is the IFB estimates in SH ionospheric delay modeling solution.

4.2.1 SH ionospheric delay modeling solution

Presented in Fig. 1 (left panel) and Fig. 2 (left panel) are the daily repeatability, i.e., STD of each CMONOC stations for March 2014 and March 2017, respectively, while Fig. 3 (left panel) and Fig. 4 (left panel) are the corresponding results for IGS stations. As we can see, the precision of IFB solution is latitude-location related. Typically, the low-latitude stations presented a larger STD which is mainly due to the higher ionospheric activity. The comparison between the results further confirms that the performance of IFB solution is rather sensitive to the ionospheric activity.

Fig. 1
figure 1

The geographical distribution of the STD for GLONASS IFB (\({\mathrm{IFB}}_{\mathrm{GF}}\)) for CMONOC stations in March 2014 based on the SH ionospheric delay modeling solution (left panel) and the undifferenced and uncombined PPP solution (right panel). The color bar represents the STD value in ns, and the averaged STD was about 0.78 ns (left panel) and 1.11 ns (right panel), respectively

Full size image
Fig. 2
figure 2

The geographical distribution of the STD for GLONASS IFB (\(\mathrm{IFB}_{\mathrm{GF}}\)) for CMONOC stations in March 2017 based on the SH ionospheric delay modeling solution (left panel) and the undifferenced and uncombined PPP solution (right panel). The color bar represents the STD value in ns, and the averaged STD was about 0.50 ns (left panel) and 0.63 ns (right panel), respectively

Full size image
Fig. 3
figure 3

The geographical distribution of the STD for GLONASS IFB (\(\mathrm{IFB}_{\mathrm{GF}}\)) for IGS stations in March 2014 based on the SH ionospheric delay modeling solution (left panel) and the undifferenced and uncombined PPP solution. The color bar represents the STD value in ns, and the averaged STD was about 0.92 ns (left panel) and 0.94 ns (right panel), respectively

Full size image
Fig. 4
figure 4

The geographical distribution of the STD for GLONASS IFB (\(\mathrm{IFB}_{\mathrm{GF}}\)) for IGS stations in March 2017 based on the SH ionospheric delay modeling solution (left panel) and the undifferenced and uncombined PPP solution. The color bar represents the STD value in ns, and the averaged STD was about 0.52 ns (left panel) and 0.59 ns (right panel), respectively

Full size image

Overall, the averaged STD of all the stations for high solar year, i.e., 2014, is 0.78 ns and 0.92 ns for CMONOC and IGS, respectively. Concerning the low solar year 2017, the precision increased by 47.2%, and the averaged STD is 0.50 ns and 0.52 ns for CMONOC and IGS, respectively.

Besides the ionospheric activity dependence of the GLONASS IFB solution, the performance of IFB for different receivers was also analyzed, and the result is presented in Table 2. As we can see, though the STD of GLONASS IFB varies for different receivers, it can be hardly determined which one performs the best among all the receiver types in term of STD, while the absolute value of the GF IFB is ranging from 2.76 ns for JPS EGGDT receivers to 20.46 ns for JAVAD TRE_G3T DELTA receivers. For more details concerning the IFB for each receiver-satellite pair, we refer to the Appendix section.

Table 2 Averaged STD for different receiver type
Full size table

4.2.2 Undifferenced and uncombined PPP solution

Similarly, Figs. 5 and 6 presented the GLONASS IFB STD of each CMONOC stations for March 2014 and March 2017, respectively, while Figs. 7 and 8 present the results of each IGS stations for March 2014 and March 2017. Different from that of GF IFB estimates based on the SH ionospheric delay modeling solution, the IFB on each frequency was derived based on the undifferenced and uncombined PPP solution.

Fig. 5
figure 5

The geographical distribution of the STD for GLONASS IFB (1: \({\mathrm{IFB}}_{1}\); 2: \({\mathrm{IFB}}_{2}\)) for CMONOC stations in March 2014 based on the undifferenced and uncombined PPP solution. The color bar represents the STD value in ns, and the averaged STD was about 1.45 ns and 2.00 ns for \({\mathrm{IFB}}_{1}\) and \({\mathrm{IFB}}_{2}\), respectively

Full size image
Fig. 6
figure 6

The geographical distribution of the STD for GLONASS IFB (1: \({\mathrm{IFB}}_{1}\); 2: \({\mathrm{IFB}}_{2}\)) for CMONOC stations in March 2017 based on the undifferenced and uncombined PPP solution. The color bar represents the STD value in ns, and the averaged STD was about 0.96 ns and 1.16 ns for \({\mathrm{IFB}}_{1}\) and \({\mathrm{IFB}}_{2}\), respectively

Full size image
Fig. 7
figure 7

The geographical distribution of the STD for GLONASS IFB (1: \({\mathrm{IFB}}_{1}\); 2: \({\mathrm{IFB}}_{2}\)) for IGS stations in March 2014 based on the undifferenced and uncombined PPP solution. The color bar represents the STD value in ns, and the averaged STD was about 1.41 ns and 1.87 ns for \({\mathrm{IFB}}_{1}\) and \({\mathrm{IFB}}_{2}\), respectively

Full size image
Fig. 8
figure 8

The geographical distribution of the STD for GLONASS IFB (1: \({\mathrm{IFB}}_{1}\); 2: \({\mathrm{IFB}}_{2}\)) for IGS stations in March 2017 based on the undifferenced and uncombined PPP solution. The color bar represents the STD value in ns, and the averaged STD was about 0.98 ns and 1.17 ns for \({\mathrm{IFB}}_{1}\) and \({\mathrm{IFB}}_{2}\), respectively

Full size image

Again, as suggested by the latitude pattern of STD distribution and the comparison between 2014 and 2017 with different solar activity, the performance of IFB with the PPP solution shows apparent ionospheric status dependence. Concerning the performance during the high solar activity year, the STD is 1.43 ns and 1.94 ns for \({\mathrm{IFB}}_{1}\) and \({\mathrm{IFB}}_{2}\), respectively, while, for the low solar activity year, the STD decreased to 0.97 ns and 1.17 ns for \({\mathrm{IFB}}_{1}\) and \({\mathrm{IFB}}_{2}\), respectively. Furthermore, with respect to the STD of \({\mathrm{IFB}}_{2}\), the STD of \({\mathrm{IFB}}_{1}\) was decreased by 22.6% averaged over the IGS and CMONOC experiments. From which, we can conclude that the signal on the first frequency performs better than the signal on the second frequency for GLONASS observation.

4.2.3 Comparison and discussion

In this section, first we derived the GF IFB from the PPP IFB on each frequency, and compared with our GF IFB based on the SH ionospheric delay modeling solution. Then, the IF IFB was derived from our PPP IFB on each frequency, and compared with the IF IFB product of CODE analysis center (ftp://cddis.gsfc.nasa.gov/pub/gps/products/mgex/). Finally, the stability of the IFB products over 2014 and 2017 with undifferenced and uncombined PPP solution of 2014 and 2017 was analyzed.

Though the STD of IFB based on the undifferenced and uncombined PPP solution was larger than that of SH ionospheric delay modeling solution, it should be noted that with PPP solution, we can generate the IFB on each frequency, and was not directly comparable with the GF IFB. Thus, we should convert these IFB to GF IFB by Eq. (11). Then the performance of PPP derived GF IFB was evaluated in terms of STD, i.e., daily stability, and the results are presented in the right panel of Figs. 1, 2, 3 and 4. Compared with the GF IFB based on SH solution shown in the left panel of Figs. 1, 2, 3 and 4, the PPP solution turned out to have a large STD be a factor of 16.8%, and the STD was 1.0 ns and 0.61 ns for 2014 and 2017, respectively. This result implied that the DESIGN ionospheric delay model (24) used in the PPP solution performs less accurate in the GLONASS IFB estimation, compared with the SH ionospheric model (20). It is most likely due to the fact that the single station ionospheric delay model DESIGN is less stable compared with the network ionospheric delay model SH.

Furthermore, Fig. 9 presents the bias of PPP derived GF IFB with respect to the SH ionospheric delay modeling solution, while plotted in black dot is the mean value of \(\delta IFB=\mathrm{IFB}_{\mathrm{GF}}\left(\mathrm{PPP}\right)-\mathrm{IFB}_{\mathrm{GF}}\) averaged over all the satellites and the corresponding experimental period of each site. As analyzed in Sect. 3.3, there should be no systematic errors between these two solutions in GF IFB estimates theoretically. However, the numerical results suggested that the GF IFB of PPP solution turned out to be larger than that of SH solution with a value of about 2 ns and 1 ns for 2014 and 2017, respectively. Obviously, these biases may be caused by the limited precision in each solution with a STD ranging from 0.50 to 1.15 ns. In addition, taking the complicated variation of the ionospheric delay in temporal and spatial into consideration, it is supposed that the divergence of the mathematic model expressed as Eqs. (20) and (24) can introduce additional systematic bias to the IFB estimates. The results of the CMONOC sites further confirmed this hypothesis. As we can see, the biases were more consistent among the CMONOC sites since, that in the regional ionospheric delay modeling, the mathematic model may diverge from the true ionospheric delay in a more consistent manner.

Fig. 9
figure 9

Difference of GF IFB (black dot) between the SH ionospheric delay modeling solution and the undifferenced and uncombined PPP solution for 2014 (upper panel) and 2017 (bottom panel), respectively, while the STD of each site is also plotted as the error bar for the SH ionospheric delay modeling solution (red) and the undifferenced and uncombined PPP solution (green), respectively

Full size image

Figure 10 further presents the residual distribution of the GF IFB between the SH ionospheric delay modeling solution and the undifferenced and uncombined PPP solution for each experiment, i.e., CMONOC in 2014, IGS in 2014, CMONOC in 2017 and IGS in 2017. Again, the GF IFB would have a positive offset once the solution changed from SH modeling to PPP.

Fig. 10
figure 10

Residual distribution of the GF IFB between the SH ionospheric delay modeling solution and the undifferenced and uncombined PPP solution for each experiment

Full size image

Besides the comparison of GF IFB derived from different solutions, we further compared our IFB product with that of CODE analysis center. Concerning our experimental period, only the IFB of IF combination was available from CODE, thus we transform the IFB on each frequency derived from PPP solution to IF IFB, i.e., \(I{FB}_{IF}={{\varvec{J}}}_{{\varvec{i}}{\varvec{j}}}\left(\begin{array}{cc}{\mathrm{IFB}}_{1}& {\mathrm{IFB}}_{2}\end{array}\right)\) first. There were 42 common stations in our IGS experiment and the product of CODE during 2014, we calculated the difference of the averaged \(I{FB}_{IF}\) of the experiment period for each receiver-satellite pair and the result is plotted in Fig. 11. Shown in the upper panel was the different of the original \(I{FB}_{IF}\) between our result and CODE. As we can see, the GLONASS IFB derived from the undifferenced and uncombined PPP solution biased due to the datum effect. And by removing the common bias across satellites and receivers, the difference was further plotted in the bottom panel, and the RMS of \(I{FB}_{IF}\) with the datum effect removed was 0.55 ns.

Fig. 11
figure 11

Difference of IF IFB between our undifferenced and uncombined PPP solution and CODE product with different station in different color (upper panel). By removing the common bias across satellites and receivers, the difference with an RMS of 0.55 ns was further plotted in the bottom panel

Full size image

Furthermore, with a resolution of 10 days, we presented the long-term stability of IFB for each IGS stations over 2014 (upper panel) and 2017 (bottom panel), respectively in Fig. 12. The STD of \({\mathrm{IFB}}_{1}\), \({\mathrm{IFB}}_{2}\), \(\mathrm{IFB}_{\mathrm{GF}}\) and \(\mathrm{IFB}_{IF}\) was denoted as triangle, square, circle and star, respectively. The results suggested that the STD was 1.48 ns, 1.87 ns, 1.17 ns and 2.34 ns for \({\mathrm{IFB}}_{1}\), \({\mathrm{IFB}}_{2}\), \({\mathrm{IFB}}_{\mathrm{GF}}\) and \(\mathrm{IFB}_{IF}\), respectively, over 2014; while the STD was 1.26 ns, 1.64 ns, 1.00 ns and 1.92 ns for \({\mathrm{IFB}}_{1}\), \({\mathrm{IFB}}_{2}\) and \({\mathrm{IFB}}_{\mathrm{GF}}\) and \(\mathrm{IFB}_{IF}\), respectively, over 2017. Again, the stability of the \({\mathrm{IFB}}_{1}\) performs better than that of \({\mathrm{IFB}}_{2}\) by a factor of about 22%. In addition, compared with \(\mathrm{IFB}_{IF}\), the stability of \({\mathrm{IFB}}_{1}\) was improved by 49% on averaged, which may due to the noise amplification of the IF transformation.

Fig. 12
figure 12

GLONASS IFB STD of each IGS stations over 2014 (upper panel) and 2017 (bottom panel), respectively. Where the triangle, square, circle and star represent \({\mathrm{IFB}}_{1}\), \({\mathrm{IFB}}_{2}\), \(\mathrm{IFB}_{\mathrm{GF}}\) and \(\mathrm{IFB}_{IF}\), respectively. The color bar represents the STD value in ns. In 2014, the averaged STD was 1.48 ns, 1.87 ns, 1.17 ns and 2.34 ns for \({\mathrm{IFB}}_{1}\), \({\mathrm{IFB}}_{2}\), \({\mathrm{IFB}}_{\mathrm{GF}}\) and \(\mathrm{IFB}_{IF}\), respectively. In 2017, the STD was 1.26 ns, 1.64 ns, 1.00 ns and 1.92 ns for \({\mathrm{IFB}}_{1}\), \({\mathrm{IFB}}_{2}\), \({\mathrm{IFB}}_{\mathrm{GF}}\) and \(\mathrm{IFB}_{IF}\), respectively

Full size image

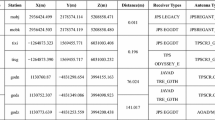
Though the stability of IFB was around 1 ns to 2 ns over the experimental period for most of the 172 IGS stations, there were jumps in the IFB series for some stations. Figure 13 presents the IFB series of stations ALIC, BRST, ONSA and NICO for satellite R3 over 2014 and 2017, and there were apparent jumps up to 10 ns for stations ALIC and ONSA as we can see. By checking the receiver types for these stations listed in Table 3, it was found that those jumps mainly due to the replacement of the receivers.

Fig. 13
figure 13

IFB series of stations ALIC (in black), BRST (in red), ONSA (in green) and NICO (in blue) for satellite R3 over 2014 and 2017. The top panel is \({\mathrm{IFB}}_{1}\) series, and the bottom panel is \({\mathrm{IFB}}_{2}\) series

Full size image
Table 3 Receiver type of stations ALIC, BRST, ONSA and NICO
Full size table

Besides the IFB precision and consistency, special attention should be given to the efficiency of the solution. And there is a long history of researchers worldwide trying to simplify the GLONASS data processing model, since that the FDMA signal will introduce a large number of parameters to be estimated. Concerning the efficiency performance of the two solutions presented in this study, Fig. 14 compared the efficiency of the SH ionospheric delay modeling solution (black) and the undifferenced and uncombined PPP solution (red) in GLONASS IFB estimation. All these experiments were carried out on a server with an Intel(R) Xeon(R) CPU E5-2630 @ 2.40 GHz CPU and 32 cores. As we can see from the upper panel of Fig. 14, the time-consuming in SH ionospheric delay modeling solution increased rapidly as the increase of the stations involved, while, for the PPP solution, the time-consuming increased linearly, since that the IFB were estimated station by station, while for the IFB solution with 250 stations, the bottom panel of Fig. 14 suggested that the averaged time-consuming per epoch was 28.4 s and 2.3 s for SH solution and PPP solution, respectively.

Fig. 14
figure 14

Efficiency comparison of the SH ionospheric delay modeling solution (black) and the undifferenced and uncombined PPP solution (red) in GLONASS IFB estimation. The upper panel presents the time-consuming per epoch against the number of stations involved, while the bottom panel presents the time-consuming series of 250 stations for 24 h with an interval of 300 s

Full size image

As a result, the SH model solution should be applied in the non-time-critical GF IFB concerned-only applications. Otherwise, the IFB solution based on the undifferenced and uncombined PPP is preferred.

5 Conclusions

Concerning the GLONASS IFBs estimation, there was no consensus on a standard solution up to now. By taking the FDMA signal property into consideration, one may naturally extend the traditional SH ionospheric delay modeling for GLONASS IFBs solution. In addition, the undifferenced and uncombined PPP presented a new potential GLONASS IFBs solution. In this paper, both these methods are analyzed and compared with experiment verification.

Based on the theoretical analysis, it is suggested that only the differential GF IFB, i.e., \(\mathrm{IFB}_{\mathrm{GF},r}^{s}=\mathrm{IFB}_{r,1}^{s}-\mathrm{IFB}_{r,2}^{s}\) can be derived in the SH ionospheric delay modeling, while the IFB on individual frequency can be derived with the undifferenced and uncombined PPP, but subject to the datum effect of the satellite clock products and the constrain \(0={{\varvec{u}}}_{2{\varvec{j}}}^{{\varvec{T}}}\bullet {\varvec{I}}{\varvec{F}}{\varvec{B}}\) to separate the IFB from the receiver clock.

Then the two solutions are assessed with 236 CMONOC stations over China, as well as 172 IGS stations globally distributed. In addition, to evaluate the IFB performance under different solar activities, both the data of March 1 to March 31, 2014, and March 1 to March 31, 2017 were collected in the experiment.

Concerning the IFB solution based on the SH ionospheric delay modeling, the averaged STD of all the stations for high solar year, i.e., 2014, is 0.78 ns and 0.92 ns for CMONOC and IGS, respectively, while the averaged STD is improved to 0.50 ns and 0.52 ns for CMONOC and IGS, respectively, for low solar year, i.e., 2017. When the undifferenced and uncombined PPP is adopted, the IFB on each individual frequency were derived. Under the high solar activity in 2014, the precision is 1.45 ns and 2.00 ns for \(\mathrm{IFB}_{1}\) and \(\mathrm{IFB}_{2}\) for CMONOC stations, and 1.41 ns and 1.87 ns for \(\mathrm{IFB}_{1}\) and \(\mathrm{IFB}_{2}\) for IGS stations, respectively, while in 2017, the averaged STD is about 0.96 ns and 1.16 ns for \(\mathrm{IFB}_{1}\) and \(\mathrm{IFB}_{2}\) for CMONOC stations, and 0.98 ns and 1.17 ns for \(\mathrm{IFB}_{1}\) and \(\mathrm{IFB}_{2}\) for IGS stations, respectively. The results suggested that the IFB performance mainly subjected to the ionospheric activity status for both solutions. In addition, the IFB performed apparently different for different frequencies in PPP solution.

Compared with the GF IFB of SH ionospheric delay modeling solutions, though the GF IFB converted from PPP solution had a slightly large STD be a factor of 16.8%, respectively. Then, the IFB on each frequency was converted to IF IFB and compared with that of CODE, and the result suggested that the averaged IF IFB has a consistency of 0.55 ns by removing the datum effect. Concerning the long-time span stability of GLONASS IFB, the STD was around 1 ns to 2 ns over one year; however, there were cases that the IFB may jump 10 ns due to the replacement of the receivers.

In summary, the undifferenced and uncombined PPP solution has its advantages for IFB estimation on each individual frequency, and more efficient in data processing, but the solution based on the SH ionospheric delay modeling has its advantage in the precision of the GF IFB estimates. Therefore the SH model should be used for non-time-critical GF IFB concerned-only applications and the undifferenced and uncombined PPP solution should be used for other things.