1 Introduction

A number of space-based laser displacement interferometers are in development including the Gravity Recovery and Climate Experiment (GRACE) Follow-On mission’s laser ranging interferometer  (Sheard et al. 2012), the Laser Interferometer Space Antenna (LISA) (Danzmann et al. 2011) and the Deci-hertz Interferometer Gravitational wave Observatory (DECIGO) (Kawamura et al. 2011). Decades of work has gone into adapting lab-based interferometry techniques to meet the robustness demanded of a space mission, driving the cost and complexity of these missions.

Here we propose a new fiber-based interferometer architecture that uses multiple spacecraft link measurements and digital signal processing to synthesize the interspacecraft displacement. Forming our combinations in post-processing, we are able to correct for errors due to misalignment of the interspacecraft links and internal pathlength fluctuations. The strict hardware integration requirements of current interferometers can therefore be relaxed, enabling a new class of missions.

In this paper, we present the concept, provide an example implementation, outline the signal processing steps required to recover the center of mass displacement and present the results of a simulated multi-link GRACE mission.

2 Measuring displacement in the presence of spacecraft rotation

Continuing the geodesy mission started by the original GRACE satellites (Tapley et al. 2004), GRACE Follow-On will measure the displacement between two satellites, mapping time and spatial variations in Earth’s gravitational field. In addition to the primary microwave ranging instrument, GRACE Follow-On will also include a laser ranging interferometer technology demonstrator.

The laser ranging interferometer must not interfere with the primary measurement. Therefore, the laser interferometer cannot be placed along the line of sight between the spacecraft centers of mass occupied by the microwave instrument. A lateral offset in the laser link from the center of mass on either spacecraft, however, will cause rotation to couple into the displacement measurement (Schütze et al. 2014).

Fig. 1
figure 1

If a laser link between spacecraft is offset from the center of mass (c.m) by d, an angular misalignment of \(\theta (t)\) in spacecraft 2 leads to a pathlength error of \(\varDelta x_\mathrm{tilt}(t) = {\textit{d}} \sin \theta (t)\).

Full size image

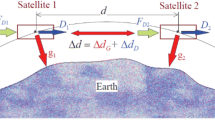
Figure 1 shows a simplified space interferometer that demonstrates this sensitivity to rotation. The laser link between spacecraft 1 and spacecraft 2 is offset a distance d from the spacecraft centers of mass. An angular misalignment of \(\theta (t)\) introduces an optical pathlength error of:

$$\begin{aligned} \varDelta x_\mathrm{tilt}(t) = d \sin \theta (t). \end{aligned}$$
(1)

Our architecture takes advantage of geometry to produce a measurement of the interspacecraft displacement while suppressing pathlength error resulting from misalignment of the laser link.

Fig. 2
figure 2

With multiple laser link measurements between the spacecraft, we are sensitive to multiple degrees of freedom that limit the spacecraft displacement measurement. Two laser links are shown, A and B, placed symmetrically either side of the spacecraft center of mass (c.m), offset by ±d. Taking an average of the displacement measured along each link, we can synthesize an estimate of the center of mass displacement shown by the dashed line that is insensitive to the angular misalignment \(\theta (t)\).

Full size image

Adding a second laser link to our simple space interferometer, as shown in Fig. 2, provides a way to disentangle the spacecraft tilt from the spacecraft displacement. The two laser links, which we denote A and B, are positioned symmetrically either side of the spacecraft center of mass. A relative tilt of spacecraft 2 by \(\theta (t)\) will result in an anti-symmetric lengthening and shortening of the two laser links.

Measuring the displacement along link A, \(x_\mathrm{A}(t)\), and link B, \(x_\mathrm{B}(t)\), we therefore have two measurements of the spacecraft displacement, \(x_{ R}(t)\), with anti-symmetric measurements of the spacecraft tilt:

$$\begin{aligned} x_\mathrm{A}(t)&= x_{ R}(t) - \varDelta x_\mathrm{tilt}(t) \end{aligned}$$
(2)
$$\begin{aligned} x_\mathrm{B}(t)&= x_{ R}(t) + \varDelta x_\mathrm{tilt}(t) \end{aligned}$$
(3)

where the pathlength error \(\varDelta x_\mathrm{tilt}(t)\) due to spacecraft rotation is calculated using Eq. 1.

Since the links are symmetric, if we average these two measurements, we are able to cancel the spacecraft tilt error and recover the spacecraft displacement:

$$\begin{aligned} x_\mathrm{c.m}(t) = \frac{1}{2}\big [x_\mathrm{A}(t) + x_\mathrm{B}(t)\big ] = x_{R}(t). \end{aligned}$$
(4)

The synthesized center of mass displacement measurement, \(x_\mathrm{c.m}(t)\), is equal to the spacecraft displacement \(x_{ R}(t)\) and has no pathlength error due to spacecraft tilt.

The GRACE Follow-On laser ranging interferometer utilizes symmetric cancellation of rotation-to-pathlength coupling using the triple mirror assembly (Sheard et al. 2012), a retroreflector that routes the laser around the GRACE microwave ranging instrument. With a virtual vertex coincident with the spacecraft’s center of mass, any rotation of the spacecraft will symmetrically lengthen and shorten the optical pathlengths of the incoming and outgoing beams, ensuring that the round-trip pathlength is unaffected.

The principal advantage of the new multi-link architecture proposed here is that we individually measure the displacement along each link and then form our linear combinations offline in post-processing. We are therefore not restricted to averaging but can individually weight the displacement measurements to form different combinations.

Unlike the triple mirror assembly, which has strict requirements on alignment and placement (Ward et al. 2014; Fleddermann et al. 2014; Schütze et al. 2014), the links in our architecture do not need to be placed symmetrically about the center of mass, but can be placed arbitrarily within the plane of the center of mass on each spacecraft. The ability to refine the weights in post-processing to suppress pathlength errors substantially relaxes the required accuracy of positioning the interferometer during spacecraft integration.

3 Multi-link laser interferometry

The multi-link laser architecture can be realized entirely in fiber. To form the multiple laser links shown in Fig. 2, we propose using a number of compact optical heads on each spacecraft. Each optical head is a fiber collimator used to transmit and receive light. The output surface of each optical head can be used as a reference, with the light coupling in from the distant spacecraft interfering with small back reflections from each optical head. A similar concept was proposed in Lay et al. (2007).

Fig. 3
figure 3

Each optical head is a transceiver. With a partially reflective output surface, the local reflections off the optical head are interfered with the frequency offset light from the distant spacecraft. The fiber length fluctuations along the return path are common and do not appear in the phase of the detected heterodyne signal

Full size image

A single optical head is shown in Fig. 3. We use heterodyne interferometry to measure the displacement along each link, interfering the local reflection from the optical head with the incoming frequency offset light from the distant spacecraft. Assuming a laser power of 1 W, if \(\sim 4\%\) is reflected off the optical head from Fresnel reflection, since the beam passes through a fibre splitter twice, we will have a 10 mW local oscillator at the detector.

The displacement along each link can be determined by measuring the phase of the heterodyne beatnote using a phasemeter (Shaddock et al. 2006), a linear phase tracker that has been experimentally verified to have a dynamic range over 9 orders of magnitude (de Vine et al. 2010).

Laser links need to be formed between all optical heads in order to sense the tilt of both spacecraft. Therefore, in addition to the two links shown in Fig. 2, in our simplified 2D example we also form links from point A on spacecraft 1 to point B on spacecraft 2 and from point B on spacecraft 1 to point A on spacecraft 2. This makes for a total of four laser links per spacecraft.

In a GRACE-like mission, more links would be required to sense rotations around all 3 spacecraft axes. To see how the roll \(\theta _\mathrm{x}\), pitch \(\theta _\mathrm{y}\), and yaw \(\theta _\mathrm{z}\) of the spacecraft couple into the displacement, we consider an arbitrary rotation of the spacecraft about its center of mass using intrinsic Tait-Bryan rotations. Assuming our optical head is offset from the center of mass by \([d_\mathrm{x},~d_\mathrm{y},~d_\mathrm{z}]\), then the displacement error due to a spacecraft rotation (yaw-pitch-roll) will be:

$$\begin{aligned} \varDelta x_\mathrm{tilt}= & {} d_\mathrm{x}\cos \theta _\mathrm{z}\cos \theta _\mathrm{y} + d_\mathrm{y} (\cos \theta _\mathrm{z}\sin \theta _\mathrm{y}\sin \theta _\mathrm{x}\nonumber \\&-\cos \theta _\mathrm{x}\sin \theta _\mathrm{z})+ d_\mathrm{z}(\sin \theta _\mathrm{z}\sin \theta _\mathrm{x}\nonumber \\&+\cos \theta _\mathrm{z}\cos \theta _\mathrm{x}\sin \theta _\mathrm{y}). \end{aligned}$$
(5)

From Eq. 5 any offsets \(d_\mathrm{x}\) in the optical head placement will lead to quadratic coupling of rotation to pathlength error. For small rotations, \(|\theta _\mathrm{x}|,|\theta _\mathrm{y}|,|\theta _\mathrm{z}|<<1\), the displacement error is:

$$\begin{aligned} \varDelta x_\mathrm{tilt} \approx d_\mathrm{x} + d_\mathrm{y} (\theta _\mathrm{y}\theta _\mathrm{x}-\theta _\mathrm{z}) + d_\mathrm{z}(\theta _\mathrm{z}\theta _\mathrm{x}+\theta _\mathrm{y}). \end{aligned}$$
(6)

Since it only adds a static error, the phasemeter will be insensitive to any offset \(d_\mathrm{x}\). Consequently, the displacement will only be sensitive to offsets \(d_\mathrm{y}\) and \(d_z\). The effect of spacecraft roll is also second order, only coupling into the length measurement when the spacecraft has also experienced a change in yaw or pitch. To first order, the displacement error is approximately:

$$\begin{aligned} \varDelta x_\mathrm{tilt} \approx -d_\mathrm{y}\theta _\mathrm{z} + d_\mathrm{z}\theta _\mathrm{y}. \end{aligned}$$
(7)

A 2D arrangement of optical heads in the plane of the center of mass would be sensitive to rotation around these two axes. Consequently, a GRACE-like mission could operate with a minimum of 3 optical heads arranged in a triangle. This would require a total of 9 laser links and therefore a minimum of 9 phasemeter channels. While this is double the number required on GRACE-FO, it is less than current LISA designs will require and well within the capabilities of a single space qualified FPGA (Shaddock et al. 2006). With the exception then of a larger FPGA and the electro-optic modulators the electronics could be the same as GRACE-FO.

Fig. 4
figure 4

The optical layout for a system with two optical heads per spacecraft. The architecture is all fiber, using Digitally Enhanced Heterodyne Interferometry (DEHI) (Shaddock 2007) to multiplex signals on the one detector. On each spacecraft, the laser is split equally between two optical heads (OHA and OHB) and a reference arm for frequency stabilization. In each arm is an Electro-Optic modulator (EOM) that is used to apply a pseudo-random phase modulation for the signal multiplexing. The interference between reflections off the output of each optical head and light from the distant spacecraft are detected on the photodetector. We assume the lasers are frequency stabilized to the reference paths with a frequency offset between the spacecraft allowing for a heterodyne detection. On the ith spacecraft, we make the following definitions: lasers have displacement equivalent frequency noise \(x_\mathrm{lasi}\), spacecraft tilt is \(\theta _{ i}\), the offsets of the optical heads from the center of mass axis are \(d_{i\mathrm{A}}\) and \(d_{i\mathrm{B}}\), and the lengths \(\varDelta x_\mathrm{ii}, \varDelta x_\mathrm{iA}, \varDelta x_\mathrm{iB}, \varDelta x_\mathrm{io}, \varDelta x_\mathrm{iref},\) are the length fluctuations in the fiber paths. Finally the interspacecraft displacement we label \(x_\mathrm{R}(t)\)

Full size image

To measure the displacement along each of the interspacecraft links, we need to be able to detect multiple heterodyne signals on each spacecraft. Instead of using a dedicated detector for each link, we use DEHI to differentiate between the links. With this signal multiplexing, it is possible to measure the phase of all links using a single detector on each spacecraft.

For our technique to work, we require the optical heads to be stable with respect to the spacecraft center of mass. This is important as any motion of the optical heads will also couple into the displacement measurement increasing the degrees of freedom. With DEHI, our architecture is able to support an arbitrary number of optical heads however. Adding additional optical heads would allow for some redundancy in the displacement measurement and allow these extra degrees of freedom to be measured and corrected for. Assuming N optical heads there would be a total of \(N^2\) interspacecraft links.

4 Implementation of a multi-link laser interferometer

Figure 4 shows an example multi-link interferometer. To simplify the discussion, we consider a system with four links per spacecraft. Each spacecraft is shown with two optical heads: A and B. The optical heads are positioned arbitrarily within the plane of the center of mass on each spacecraft. The optical heads A and B are offset from the center of mass on spacecraft 1 by \(d_\mathrm{1A}\) and \(d_\mathrm{1B}\) and on spacecraft 2 by \(d_\mathrm{2A}\) and \(d_\mathrm{2B}\), respectively. On each photodetector, we detect multiple heterodyne beatnotes between the local laser and the laser from the distant spacecraft.

The electro-optic modulators are used to perform DEHI. In contrast to traditional DEHI schemes (Shaddock 2007), instead of relying on differences in propagation times for multiplexing here we use different codes in each optical path. By phase modulating each optical head path with an orthogonal pseudo-random code, the beatnote from each link can be extracted following detection. Orthogonal codes were used to distinguish between emitter paths in  Roberts et al. (2014).

Since the local reflection and incoming beam are combined at the optical head, the fiber length fluctuations on the path to the detector will be common and therefore do not contribute to the heterodyne phase. Likewise the phase modulation in the backwards pass through the EOM is common and does not influence the phase of the beatnote. The beatnote from each link will therefore only have two phase modulations: the code on the local reflection and the code on the signal coming from the distant spacecraft.

To extract the beatnote from each link, we need to perform a double demodulation. To do this, we simply apply two code demodulations in succession. For example, to recover the beatnote along the link between optical head 1B and optical head 2A, we would demodulate with a delayed copy of the code applied in 1B and then demodulate with a delayed copy of the code applied in 2A. The delays will need to account for both optical and electronic delays in our measurements of the pseudo-random phase modulations. Double demodulations have been demonstrated before in a DEHI variant—Digitally Enhanced Homodyne Interferometry (Sutton et al. 2012).

For each link, two delays will need to be determined. Therefore in the 2 optical head example, with 8 one-way links, there will be 16 delays that need to be determined. In a GRACE-like implementation with 3 optical heads, 36 delays will need to be found. However, if the interferometer is built with equal optical head pathlengths (matched to within a chip length), the delay on the local code and delay on the distant code in each link will be the same for all links. Therefore, only 2 delays will need to be determined regardless of the number of optical heads. Initial acquisition of these delays, however, will be a challenge. This could be aided using pre-existing knowledge of the pathlengths and interspacecraft range or could potentially benefit from an auxiliary acquisition code modulation similar to those used in GPS (Akopian 2005).

As a fiber interferometer, there is no need for an ultrastable optical bench, reducing the hardware complexity and overall footprint of the interferometer. The additional fiber length, labeled \(\varDelta x_\mathrm{ref}\) in the figure, can be used as a frequency reference for laser frequency stabilization (McRae et al. 2013) removing the need for a stable cavity. Further, a fiber reference can be tuned (McRae et al. 2014). This provides a way to have frequency stabilized lasers on both spacecraft while still allowing the laser frequencies to be tuned in order to obtain heterodyne beatnotes within the detector bandwidths.

While optical fibers will ease the spacecraft integration, they will also add additional noise due to fiber length fluctuations. We show, however, in the next section that linear combinations of displacement measurements on the two spacecraft can be used to suppress this noise.

5 Recovering displacement from multi-link measurements

We now look explicitly at the signal processing required to recover the spacecraft displacement measurement from multiple laser link measurements. In the process, we will also demonstrate the suppression of pathlength error due to spacecraft tilt, fiber length fluctuations and laser frequency noise.

For a two optical head system, there are a total of 8 displacement measurements across the two spacecraft. With so many link measurements to keep track of, we now introduce notation to simplify the discussion.

We let \(x_{ i\mathrm{:}jk}\) represent the link starting at optical head j and ending at optical head k that is detected on spacecraft i. As an example, on spacecraft 2 the heterodyne beatnote between the beam from optical head A on spacecraft 1 and the local reflection from optical head B we denote \(x_{2:\mathrm{AB}}\). The displacement along the links in the opposite direction can be found by reversing the lettered subscripts. Figure 4 illustrates this notation.

To demonstrate the signal processing required to recover the spacecraft displacement from our 8 link measurements, we consider the displacement measured by optical head A on spacecraft 1. Similar combinations can be applied to the optical head B link.

In the following equations we assume that the frequency of laser 1 is higher than laser 2 and that the heterodyne beatnote between the two lasers is maintained within the bandwidth of the photodetectors using some slow feedback to the laser on spacecraft 2.

On the spacecraft 1 photodetector, we make the following displacement measurements:

$$\begin{aligned}&x_\mathrm{1:AA}(t) = x_\mathrm{las1}(t) - x_\mathrm{las2}(t-\tau ) + \varDelta x_\mathrm{1i}(t) + \varDelta x_\mathrm{1A}(t)\nonumber \\&\qquad \qquad \qquad - \varDelta x_\mathrm{2i}(t-\tau ) - \varDelta x_\mathrm{2A}(t-\tau ) - x_\mathrm{R}(t)\nonumber \\&\qquad \qquad \qquad - d_\mathrm{1A}\sin \theta _\mathrm{1}(t) + d_\mathrm{2A} \sin \theta _\mathrm{2}(t-\tau ) \end{aligned}$$
(8)
$$\begin{aligned}&x_\mathrm{1:BA}(t) = x_\mathrm{las1}(t) - x_\mathrm{las2}(t-\tau ) + \varDelta x_\mathrm{1i}(t) + \varDelta x_\mathrm{1A}(t)\nonumber \\&\qquad \qquad \qquad - \varDelta x_\mathrm{2i}(t-\tau ) - \varDelta x_\mathrm{2B}(t-\tau )\nonumber \\&\qquad \qquad \qquad - x_\mathrm{R}(t) - d_\mathrm{1A} \sin \theta _\mathrm{1}(t) - d_\mathrm{2B} \sin \theta _\mathrm{2}(t-\tau ) \end{aligned}$$
(9)

where the displacement equivalent laser frequency noise from the laser on spacecraft 1 is \(x_\mathrm{las1}\) and from the laser on spacecraft 2 is \(x_\mathrm{las2}\). The laser 2 frequency noise measurements from spacecraft 2 have been delayed by the interspacecraft delay \(\tau \). For a GRACE-like mission with spacecraft separation on the order of 200 km, this is approximately 0.67 ms.

The diagonal distance (OH2B - OH1A) is actually longer than the horizontal distance (OH2A - OH1A) by approximately \(d^2/2R\) where \(d=d_\mathrm{2A}+d_\mathrm{2B}\) is the separation between the spacecraft 2 optical heads and R is the absolute interspacecraft range. While not obvious in Fig. 4, due to the large spacecraft separation, the transmitted beam will expand significantly before it reaches the distant spacecraft. The optical heads on the distant spacecraft will effectively sample the same part of the expanded wavefront and will therefore measure similar displacements. Any differences will not appear in the displacement measurement since the phasemeter is insensitive to absolute range. We therefore assume the interspacecraft displacement measured along the links are equal.

Traveling in the opposite direction along the same links, we make the following displacement measurements on the spacecraft 2 photodetector:

$$\begin{aligned}&x_{2:AA}(t) = x_\mathrm{las1}(t-\tau ) - x_\mathrm{las2}(t) + \varDelta x_\mathrm{1i}(t-\tau ) \nonumber \\&\qquad \qquad \qquad + \varDelta x_\mathrm{1A}(t-\tau ) - \varDelta x_\mathrm{2i}(t) - \varDelta x_\mathrm{2A}(t) + x_\mathrm{R}(t) \nonumber \\&\qquad \qquad \qquad + d_\mathrm{1A} \sin \theta _\mathrm{1}(t-\tau )- d_\mathrm{2A} \sin \theta _\mathrm{2}(t) \end{aligned}$$
(10)
$$\begin{aligned}&x_\mathrm{2:AB}(t) = x_\mathrm{las1}(t-\tau ) - x_\mathrm{las2}(t)+ \varDelta x_\mathrm{1i}(t-\tau ) \nonumber \\&\qquad \qquad \qquad + \varDelta x_\mathrm{1A}(t-\tau ) - \varDelta x_\mathrm{2i}(t) - \varDelta x_\mathrm{2B}(t) + x_\mathrm{R}(t)\nonumber \\&\qquad \qquad \qquad + d_\mathrm{1A} \sin \theta _\mathrm{1}(t-\tau ) + d_\mathrm{2B} \sin \theta _\mathrm{2}(t). \end{aligned}$$
(11)

We use a time delay interferometry (Tinto and Dhurandhar 2014) combination to cancel the laser 2 frequency noise in signal processing. To do this, we form two-way spacecraft combinations where we delay the spacecraft 2 measurements by an estimate of the interspacecraft delay \(\tau \):

$$\begin{aligned} x_\mathrm{AA}(t)= & {} x_\mathrm{1:AA}(t) - x_\mathrm{2:AA}(t-\tau ) \end{aligned}$$
(12)
$$\begin{aligned} x_\mathrm{AB}(t)= & {} x_\mathrm{1:BA}(t) - x_\mathrm{2:AB}(t-\tau ). \end{aligned}$$
(13)

We use the notation \(x_\mathrm{AA}\) and \(x_\mathrm{AB}\) to indicate two-way links starting at A on spacecraft 1, traveling to A and B, respectively, on the distant spacecraft and then back to A on spacecraft 1. Substituting in Eqs. 8–11 into Eqs. 12 and 13, we get:

$$\begin{aligned}&x_\mathrm{AA}(t) = x_\mathrm{las1}(t) - x_\mathrm{las1}(t-2\tau ) - x_\mathrm{R}(t) \nonumber \\&\qquad \qquad \quad - x_\mathrm{R}(t-\tau ) - 2d_\mathrm{1A} \sin \theta _\mathrm{1}(t) + 2d_\mathrm{2A}\sin \theta _\mathrm{2}(t)\nonumber \\ \end{aligned}$$
(14)
$$\begin{aligned} x_\mathrm{AB}(t)= & {} x_\mathrm{las1}(t) - x_\mathrm{las1}(t-2\tau ) - x_\mathrm{R}(t) \nonumber \\&- x_\mathrm{R}(t-\tau ) - 2d_\mathrm{1A} \sin \theta _\mathrm{1}(t) - 2d_\mathrm{2B}\sin \theta _\mathrm{2}(t)\nonumber \\ \end{aligned}$$
(15)

these two-way combinations have suppressed pathlength fluctuations but are still sensitive to the rotation-to-pathlength coupling. Here we have ignored the delays in the fiber length fluctuations and spacecraft tilt error under the assumption that on these time scales these signals are not changing. We consider the residual noise from these sources, however, in Sect. 6.

In the next stage of signal processing, we remove the rotation-to-pathlength coupling due to spacecraft 2. Taking the two-way spacecraft combinations, we synthesize a measurement between optical head A on spacecraft 1 with the spacecraft 2 center of mass, which we denote \(x_\mathrm{A}\). To cancel the spacecraft 2 tilt error, we need to weight the two-way displacement measurements \(x_\mathrm{AA}\) and \(x_\mathrm{AB}\) with weights \(w_\mathrm{2A}\) and \(w_\mathrm{2B}\), respectively:

$$\begin{aligned} x_\mathrm{A}(t)= & {} w_\mathrm{2A} x_\mathrm{AA}(t) + w_\mathrm{2B} x_\mathrm{AB}(t) \end{aligned}$$
(16)
$$\begin{aligned} x_\mathrm{B}(t)= & {} w_\mathrm{2A} x_\mathrm{BA}(t) + w_\mathrm{2B} x_\mathrm{BB}(t). \end{aligned}$$
(17)

In the two optical head example, it is straight forward to calculate these weights, they are given by the average of the offsets \(d_\mathrm{2A}\) and \(d_\mathrm{2B}\):

$$\begin{aligned} w_\mathrm{2A}= & {} \frac{d_{2B}}{d_\mathrm{2A} + d_\mathrm{2B}} \end{aligned}$$
(18)
$$\begin{aligned} w_\mathrm{2B}= & {} \frac{d_\mathrm{2A}}{d_\mathrm{2A} + d_\mathrm{2B}}. \end{aligned}$$
(19)

Applying these weights, the displacement between optical head A on spacecraft 1 and the spacecraft 2 center of mass is given by:

$$\begin{aligned} x_\mathrm{A}(t)= & {} x_\mathrm{las1}(t) - x_\mathrm{las1}(t - 2\tau )\nonumber \\&- x_\mathrm{R}(t) - x_\mathrm{R}(t-\tau ) - 2 d_\mathrm{1A} \sin \theta _\mathrm{1}(t). \end{aligned}$$
(20)

This measurement between optical head A on spacecraft 1 and the spacecraft 2 center of mass has the pathlength error due to spacecraft 2 misalignment \(\theta _\mathrm{2}\) suppressed.

Using the same weights, we can synthesize a measurement between optical head B on spacecraft 1 and the spacecraft 2 center of mass:

$$\begin{aligned} x_\mathrm{B}(t)= & {} x_\mathrm{las1}(t) - x_\mathrm{las1}(t - 2\tau )\nonumber \\&- x_\mathrm{R}(t) - x_\mathrm{R}(t-\tau ) + 2 d_\mathrm{1B} \sin \theta _\mathrm{1}(t) \end{aligned}$$
(21)

where the two-way displacement measurements \( x_\mathrm{BB}\) and \(x_\mathrm{BA}\) have been derived from the spacecraft 1 and spacecraft 2 displacement measurements \(x_\mathrm{1:BB}\), \(x_\mathrm{1:AB}\), \(x_\mathrm{2:BB}\) and \(x_\mathrm{1:BA}\). Again we see the pathlength error due to spacecraft 2 rotation is removed.

The last step needed to recover the spacecraft displacement is to apply spacecraft 1 weights to the measurements in Eqs. 20 and 21. We can calculate spacecraft 1 weights using Eqs. 18 and 19 with the spacecraft 1 offsets \(d_\mathrm{1A}\) and \(d_\mathrm{1B}\). The center of mass displacement is then given by:

$$\begin{aligned} x_\mathrm{c.m}&= w_\mathrm{1A} x_\mathrm{A}(t) + w_\mathrm{1B} x_\mathrm{B}(t) \nonumber \\&= x_\mathrm{las1}(t) - x_\mathrm{las1}(t-2\tau )- x_\mathrm{R}(t) - x_\mathrm{R}(t-\tau ). \end{aligned}$$
(22)

The recovered center of mass displacement between spacecraft 1 and spacecraft 2 is a round-trip measurement of the interspacecraft displacement with two passes along the interferometer arm. Given the interspacecraft delay \(\tau ~<~1~\mathrm{ms}\) and the GRACE measurement band is sub-Hz this delay is negligible and the displacement measurement \(x_\mathrm{R}(t) + x_\mathrm{R}(t-\tau ) \approx 2x_\mathrm{R}(t)\). As is expected for a one-arm interferometer, the frequency noise from laser 1 is present, albeit suppressed by the round-trip. The fiber path fluctuations, laser 2 frequency noise and tilt error of both spacecraft is, however, suppressed.

6 Simulating a multi-link GRACE

Figure 5 shows simulated noise curves for a multi-link GRACE with three optical heads per spacecraft. We assume the symmetric optical head configuration shown in the figure. In the simulation, we have modeled each of the noise sources that will affect the displacement measurement and then investigated their scaling as we apply the combinations described in the previous section (Eqs. 12–22).

Fig. 5
figure 5

Simulated displacement sensitivity for a GRACE-like mission with three optical heads. The noise curves show the contributions of cyclic noise, residual rotation-to-pathlength coupling, laser 1 and 2 frequency noise, shot noise, residual fiber fluctuations and DEHI demodulation noise to the recovered center of mass displacement. We assume many of the same parameters as GRACE Follow-On in our modeling of these noise sources. For comparison, the required displacement sensitivity for the GRACE-FO laser ranging interferometer is also shown

Full size image

The noise curves are due to laser 1 and laser 2 frequency noise, the incoherent sum of optical shot noise from each link, residual demodulation noise from DEHI, residual pathlength noise from unsuppressed fiber length fluctuations, uncanceled rotation-to-pathlength coupled displacement noise and cyclic error from backscatter in the fiber. The sum of all the noise is shown as well as the required displacement sensitivity for the GRACE-FO laser ranging interferometer.

We have not included the effects of readout noise such as photodetector noise, relative intensity noise of the lasers or quantization noise in the analog-to-digital converters as we assume that like GRACE Follow-On they will be considerably smaller than the other noise sources (Sheard et al. 2012). We do, however, include the effect of shot noise as it will not only be higher given we anticipate lower received signal powers compared with GRACE-FO but also because it will be uncorrelated across the multiple links and therefore sums incoherently in our data combinations. Similarly, in a multi-link GRACE, there may be additional uncorrelated noise in each link measurement from wavefront distortion. We have, however, neglected the effect of this noise, assuming the difference between the displacement measured along each link is dominated by spacecraft pointing noise coupling.

All of the uncorrelated noise sources (shot noise, DEHI noise, fiber fluctuations, cyclic noise) will sum incoherently in the combinations used to recover the center of mass displacement. The uncorrelated noise curves shown in Fig. 5 are accordingly scaled.

Given the large interspacecraft time delays in our time delay interferometry combinations, the frequency response of the noise curves is also shaped by the following function:

$$\begin{aligned} H(f) = 2\sin (2 \pi f \tau ) \end{aligned}$$
(23)

where \(2\tau \) is the round-trip interspacecraft delay as before.

Laser 1 and laser 2 are modeled as nonlinear-planar ring oscillator (NPRO) lasers or similar, stabilized to the fiber reference paths in Fig. 4 with frequency stability of \(30\;\text {Hz}/\sqrt{\text {Hz}}\)  (McRae et al. 2013).

The laser 1 noise curve is the round-trip measurement of the laser 1 frequency noise present in Eq. 22. The frequency response is shaped by Eq. 23 assuming a double-pass of the interspacecraft delay \(2\tau \approx 1.33~\text {ms}\).

Laser 2 frequency noise is suppressed when we form the round-trip displacement measurements in Eqs. 14 and 15. However, if we allow some error \(\varDelta \tau \) in the estimate of the interspacecraft range used to delay the spacecraft 2 measurements, then there will be some residual noise. The displacement noise due to residual laser frequency noise, \(x_\mathrm{las}(f)\), is given by:

$$\begin{aligned} \varDelta x_\mathrm{residual~laser}(f) = \frac{c \varDelta \tau x_\mathrm{las}(f)}{\lambda }\;\left[ \frac{\text {m}}{\sqrt{\text {Hz}}}\right] . \end{aligned}$$
(24)

Figure 5 shows the residual laser 2 noise assuming a \(0.1~\mathrm {ms}\) error in our delay estimate. Adding a \(0.1~\mathrm {ms}\) error into Eq. 23 does not affect the laser 1 frequency noise curve since it is dominated by the \(1.33~\text {ms}\) round-trip delay.

The optical shot noise in each link, given only a small fraction of the transmitted light will reach the distant spacecraft, will be dominated by the local laser. As a result the signal to noise ratio (SNR) will be dominated by the received signal power. We model the shot noise in a single link as white noise with a root-power spectral density (Bender et al. 1998):

$$\begin{aligned} \varDelta x_\mathrm{shot}(f) = \sqrt{\frac{ \hbar c}{2\pi }\frac{\lambda }{P_\mathrm{sig}}}\;\left[ \frac{\text {m}}{\sqrt{\text {Hz}}}\right] \end{aligned}$$
(25)

where \(P_\mathrm{sig}\) is the received power from the distant spacecraft. We assume a minimum received power of \(P_\mathrm{sig} = 1\) fW in each link. Phasemeters have been used to track 30 fW optical signals with free-running laser frequency noise (Francis et al. 2014). In these experiments a cycle slip rate less than 0.01 per second was measured. With stabilized lasers, it has been predicted that a 2 kHz bandwidth could be used to track a \(1~\mathrm{fW}\) signal with a cycle slip rate less than 0.001 per second (Francis 2017). This bandwidth should be sufficient for tracking the GRACE orbital dynamics which dominate across the GRACE measurement band but quickly roll-off at higher frequencies.

Compared to the minimum trackable power required in the GRACE-FO LRI of \(3~\text {pW}\) (Wuchenich et al. 2014), if we can tolerate at worst \(1~\mathrm{fW}\) received power, this means we can use more divergent beams out of the optical heads, simplifying the spatial link acquisition between spacecraft. As an example, following launch the GRACE-FO LRI will have an initial pointing uncertainty of ±3 mrad  (Wuchenich et al. 2014). If we take this as our worst case misalignment, Fig. 6 shows the expected received power on the distant spacecraft as a function of initial beam waist out of the optical heads assuming a \(1~\mathrm{W}\) transmit power. The curve, which was calculated using an overlap integral between the transmitted and receiving fields in the plane of the receiver, shows that for beam waists less than \(1~\mathrm {mm}\) the received power will be above \(1~\mathrm {fW}\) without additional beam steering following alignment with the star cameras. For comparison, if we assume no misalignment, then a beam waist of \(1~\mathrm {mm}\) will result in 100 pW of received power.

Fig. 6
figure 6

The expected received power as a function of initial waist radius. Curves are shown for both the worst case (\(\pm 3~\mathrm {mrad}\) misalignment following launch) and the best case alignment of the optical link between spacecraft

Full size image

The shot noise curve shown in Fig. 5 is due to the incoherent sum of shot noise from the 18 link measurements, scaled by the spacecraft weights and assuming the worst case received power of \(1~\mathrm {fW}\).

In DEHI, the pseudo-random phase modulations produce spread spectrum signals. In a multi-link GRACE with 3 optical heads and a fiber reference path, there will be 36 beatnotes present at each detector. The beatnotes will have the same frequency but different pseudo-random noise code delays. When the displacement along a single link is recovered in demultiplexing, the other 35 beatnotes will remain as spread spectrum signals, adding noise to the displacement measurement. This noise will be approximately white in frequency with a root-power spectral density:

(26)

where \(f_\mathrm{chip}\) is the chip frequency of the pseudo-random noise code, \(P_\mathrm{i}\) is the power of the demodulated beatnote, and \(\sum P_\mathrm{k}\) is the sum of the other beatnotes on the detector. This equation is based off (Wuchenich et al. 2011); however, we have modified it to represent displacement noise instead of phase noise and we only sum over the 35 beatnotes that have not been demodulated. In the simulation, we assume parameters representative of the GRACE-FO laser ranging interferometer: we use wavelength \(\lambda =1064~\mathrm{nm}\) and \(f_\mathrm{chip}=38.656~\mathrm{MHz}\), equal to the GRACE-FO FPGA clock rate (PATR 2016).

Fiber path fluctuations will be mostly suppressed through the signal processing. However, since the pathlengths are sampled at different times on the two spacecraft, we again need to apply Eq. 23 to find the residual noise from each combination. The residual fiber length fluctuation curve in Fig. 5 assumes 1 / f fiber length fluctuations with a root-power spectral density of \(100\,\,\hbox {pm}/{\sqrt{\mathrm{Hz}}}\) at \(1~{\mathrm{Hz}}\) Fleddermann et al. (2009).

Rayleigh backscatter in the local fiber will interfere with incoming light from the distant spacecraft in the same way as the local oscillator. The spurious interference on the detector due to backscatter will be at the same heterodyne frequency as the link beatnotes adding cyclic error to the displacement measurements.

A DEHI scheme using a maximal-length sequence pseudo-random noise code of length L chips will suppress any spurious signals originating from outside its range gate by \(\sqrt{L}\) (Shaddock 2007). Assuming a chip rate of 38.656 MHz, the DEHI range gate in fiber is around 5 m. Therefore, with a 32767 chip (15-bit) code, DEHI will suppress any reflections that occur outside this range by 2 orders of magnitude.

Unfortunately any backscatter that occurs within 5 m of the optical head will not be suppressed by DEHI. In DEHI experiments, displacement sensitivities on the order of \(10\,\,\text {pm}/\sqrt{\text {Hz}}\), however, are routinely demonstrated in the presence of Rayleigh backscatter (Roberts et al. 2016).

To estimate an upper-bound on the contribution of cyclic noise to the overall displacement sensitivity, we consider the effect of fiber length fluctuations between the optical head reference and a scattering point within 1 chip:

$$\begin{aligned} \varDelta x_\mathrm{cyclic}(f) \approx \sqrt{\frac{P_\mathrm{scatter}}{P_\mathrm{LO}}} \varDelta x_\mathrm{path}(f) \,\,\left[ \frac{\text {m}}{\sqrt{\text {Hz}}}\right] \end{aligned}$$
(27)

where \(P_\mathrm{scatter}\) and \(P_\mathrm{LO}\) are the powers of the scattered light and optical head reference and \(\varDelta x_\mathrm{path}(f)\) are the fiber length fluctuations. Equation 27 is valid provided the fiber length fluctuations \(\varDelta x_\mathrm{path}(f)\le \lambda \). If the fibre fluctuations \(\varDelta x_\mathrm{path}(f)>\lambda \), then the cyclic error will saturate.

The Rayleigh backscatter power in optical fiber is around \(1~\mathrm{dB/km}\) at \(1064~\mathrm{nm}\) (Saleh and Teich 1991). Figure 5 shows the cyclic noise if we assume the local oscillator \(P_\mathrm{LO}\) comes from the \(4\%\) Fresnel reflection off the optical head. The low frequency shelf results from saturation of the 1 / f fiber fluctuations when they are larger than a wavelength.

The cyclic noise in Fig. 5 is a worst case estimate where we have assumed the fluctuations within 5 m of the optical head all add coherently to the cyclic error. In practice, reflections will occur at many points in the fiber and can interfere with each other. For this reason, cyclic error is difficult to model. Depending on the thermal stability of the fiber, it may be possible that the size of the fluctuations is also smaller than we have assumed. We have modeled fibre noise with a \(1\times 10^{-7}/f\,\,\text {m}/{\sqrt{\mathrm{Hz}}}\) root-power spectral density based on phasemeter measurements performed in the lab. These fluctuations could be lower, however, if passive temperature stabilization were to be implemented (McRae et al. 2013).

The impact of cyclic noise on the displacement measurement could also be limited by moving to faster chip rates, which would decrease the size of the DEHI range gate and therefore the relative fiber fluctuations, or by increasing the reflectivity of the optical head or potentially using a different fiber or wavelength. More work will need to be performed in order to determine the best method.

The last noise trace shown in Fig. 5 is due to unsuppressed rotation-to-pathlength coupling. The spacecraft weights need to be normalized to ensure that the final combination has the correct scaling for the displacement signal. There are a number of methods that could be used to determine the weights. One method would be to measure the position of the optical heads relative to the spacecraft center of mass. This then requires a precise measurement of each optical head position. An error in the knowledge of the optical head position will introduce an error into the weights, and therefore the displacement due to spacecraft rotation will not cancel completely.

Since the combinations are formed in post-processing, however, it is possible to optimize the weights in order to improve the cancellation of the spacecraft rotation error. Following launch of the spacecraft, the spacecraft orientation could be intentionally dithered, with the weights determined by finding the combination of displacement measurements that minimizes the dither signal in the recovered displacement. For this to work, the spacecraft dither would need to be at a frequency above the dominant range signal. The advantage of this approach, however, is that we are able to determine the weights following launch and therefore can accommodate shifts in the position of the optical heads during launch.

In theory, it should be possible therefore to choose weights that completely cancel the rotation. In practice, however, uncertainty in the optical head positions or errors in the calculation of the weights, may mean the noise is only partially suppressed. If we allow for some error in the weights used in Eqs. 18, 19 and 22, then the rotation noise will not completely cancel. Figure 5 shows the displacement noise due to \(1~\mathrm {mrad/\surd Hz}\) spacecraft pointing noise assuming a \(1~\mathrm{m}\) optical head separation if we are only able to suppress the rotation by 5 orders of magnitude. It should be possible to minimize this error, however, by refining the weights in post-processing.

This preliminary analysis shows that, even with imperfect cancellation of rotation-to-pathlength coupling, fiber length fluctuations and laser frequency noise, we are still below the GRACE Follow-On displacement sensitivity requirement of \(80\,\,\text {nm}/\sqrt{\text {Hz}}\).

7 Implementation specific noise

We now consider some additional sources of error that are specific to the implementation presented in this paper.

The DEHI multiplexing and suppression of backscatter can be affected by nonlinearities in the modulation and detection. Nonlinearities in the EOM phase modulation and the finite bandwidth of the detector can affect the sampling of the pseudo-random noise code adding uncorrelated high frequency noise to the beatnote. In the decoding, this noise will be suppressed by \(\sqrt{N}\), however, this adds a white noise that can potentially limit the SNR. This effect should be considered when selecting the EOM, detector and any other components that may filter the code.

In Eqs. 8–11, we assumed the interspacecraft delay \(\tau \) was the same in both directions along each link. In practice relative spacecraft motion and errors in the clock synchronization between spacecraft will mean that this is not always the case. Any error in the estimates of \(\tau \) used in the time delay interferometry combinations will limit the suppression of the laser frequency and pathlength noise.

In Francis et al. (2015) a time delay interferometry combination, similar to the round-trip combination used in this paper, was proposed for testing the technique on GRACE-FO. In order to suppress the free-running laser frequency noise below the required \(80\,\,\text {nm}/\sqrt{\text {Hz}}\) displacement sensitivity, the interspacecraft delay \(\tau \) had to be known to better than 6 ns (Francis et al. 2015). If frequency stabilized lasers are used on both spacecraft, as proposed in this paper, then a larger error in \(\tau \) can be tolerated. Figure 5, for example, shows the residual laser frequency noise from laser 2 assuming a 0.1 ms error in the \(\tau \) estimate. Further for the delays measured in both directions along a single link to be different by more than 6 ns the relative spacecraft velocities would need to be over 100 times larger than those experienced by the GRACE spacecraft (Case et al. 2002). It is therefore reasonable to assume in the analysis that the delays are equal.

More extensive simulation and analysis of the timing requirements in a GRACE time delay interferometry combination may be needed. If it is found that the proposed method is insufficient, it is possible that the multi-link interferometer could benefit from techniques developed for the GRACE microwave ranging. The GRACE dual one-way ranging (DOWR) microwave measurement is similar to the proposed link round-trip measurement (Thomas 1999). In the DOWR combination GPS data is used to interpolate one-way microwave measurements to achieve a time-tag synchronization with an error less than 100 ps  Bertiger et al. (2002). There is also an extensive body of time delay interferometry work for the LISA mission (Shaddock et al. 2003, 2004; Tinto et al. 2005), accounting for relative spacecraft motion, clock noise and other effects affecting interspacecraft delays that can be applied to the proposed multi-link interferometer.

In addition to the issues presented, there are details of the implementation that have not been discussed, that could potentially limit the sensitivity. The multi-link interferometer presented in this paper, however, is only intended as an example implementation that has been used to explain our concept. The multi-link interferometer could be implemented in a number of ways.

As an example, while the implementation discussed in this paper used time delay interferometry to suppress the laser frequency noise and DEHI to multiplex signals, the multi-link technique could also work if acousto-optic modulators were placed in each optical head path, multiplexing the signals by using different heterodyne frequencies and separate detectors in each link.

The implementation in this paper is therefore intended only as a guideline for how a multi-link interferometer could be implemented and should not be considered a final design. More testing and development needs to be performed before a multi-link interferometer can be realized.

8 Conclusion

We have presented a multi-link interferometry architecture that could be used to simplify the positioning and alignment of the optical system in a space-based laser interferometry displacement mission. Using DEHI, the all-fiber interferometer can have N optical heads on each spacecraft allowing a total of \(N^2\) interspacecraft links to be formed. The displacement along each link is measured and then combined in a weighted average to synthesize a measurement of the spacecraft center of mass displacement.

The principal advantage of the architecture comes from the ability to optimize the weights offline so that the pathlength error due to spacecraft tilt and fiber length fluctuations can be completely canceled.

To demonstrate the concept an example interferometer with 2 optical heads was analyzed. With the GRACE mission as a case study, we have shown that the multi-link architecture should be able to recover the displacement sensitivity of GRACE Follow-On while drastically relaxing the requirements placed on the hardware integration.