Ordering properties of the smallest order statistics from generalized Birnbaum–Saunders models with associated random shocks

Abstract

Let $X_{1},\ldots , X_{n}$ be lifetimes of components with independent non-negative generalized Birnbaum–Saunders random variables with shape parameters $\alpha _{i}$ and scale parameters $\beta _{i},~ i=1,\ldots ,n$, and $I_{p_{1}},\ldots , I_{p_{n}}$ be independent Bernoulli random variables, independent of $X_{i}$’s, with $E(I_{p_{i}})=p_{i},~i=1,\ldots ,n$. These are associated with random shocks on $X_{i}$’s. Then, $Y_{i}=I_{p_{i}}X_{i}, ~i=1,\ldots ,n,$ correspond to the lifetimes when the random shock does not impact the components and zero when it does. In this paper, we discuss stochastic comparisons of the smallest order statistic arising from such random variables $Y_{i},~i=1,\ldots ,n$. When the matrix of parameters $(h({\varvec{p}}), {\varvec{\beta }}^{\frac{1}{\nu }})$ or $(h({\varvec{p}}), {\varvec{\frac{1}{\alpha }}})$ changes to another matrix of parameters in a certain mathematical sense, we study the usual stochastic order of the smallest order statistic in such a setup. Finally, we apply the established results to two special cases: classical Birnbaum–Saunders and logistic Birnbaum–Saunders distributions.

1 Introduction

The generalized Birnbaum–Saunders distribution, proposed by Diáz-Garciá and Leiva-Sánchez (2005), is a lifetime model, and it has some flexible characteristics such as different degrees of kurtosis, asymmetry, and possess both unimodality and bimodality. Sanhueza et al. (2008) discussed in detail its properties, transformations and related distributions, lifetime analysis, and shape analysis. Interested readers may refer to Leiva et al. (2008a, b, c) for pertinent details. A random variable X is said to have generalized Birnbaum–Saunders distribution (“GBS” in short) if its cumulative distribution function (cdf) is given by

$$\begin{aligned} F(x; \alpha , \beta )= G\biggl [\frac{1}{\alpha }\biggl (\sqrt{\frac{x}{\beta }}-\sqrt{\frac{\beta }{x}}\biggr )\biggr ], ~~x>0, \end{aligned}$$

(1)

where $G(\cdot )$ is an elliptically contoured univariate distribution, with corresponding density and hazard rate functions $g(\cdot )$ and $r(\cdot )$, respectively. Here, $\alpha >0$ and $\beta >0$ are the shape and scale parameters, respectively. We shall use the notation $X\sim GBS(\alpha , \beta )$. We now introduce two special cases of GBS distribution which will be used later:

(i) When

$$\begin{aligned} G(x)={\varPhi }(x)=\int _{-\infty }^{x} \frac{1}{\sqrt{2\pi }}e^{-\frac{t^{2}}{2}}dt,~~x\in R, \end{aligned}$$

the distribution is known as the classical Birnbaum–Saunders distribution (“BS” in short). It was introduced by Birnbaum and Saunders (1969a, b) for modeling failure time distribution corresponding to fatigue failure. Many authors have done considerable amount of work on this model; see, for example, Chang and Tang (1993), Dupuis and Mills (1994), Ng et al. (2003, 2006), Kundu et al. (2008, 2013), Zhu and Balakrishnan (2015), Fang et al. (2016), and the references cited therein.

(ii) When

$$\begin{aligned} G(x)=\frac{1}{1+e^{-x}},~~x\in R, \end{aligned}$$

the distribution is called the logistic Birnbaum–Saunders distribution (“LBS” in short). Its properties have been discussed by Sanhueza et al. (2008).

The largest and smallest order statistics correspond to the lifetimes of parallel and series systems, respectively, in reliability theory. Stochastic comparisons of parallel and series systems with heterogeneous components have been studied by many authors. For example, one may refer to Dykstra et al. (1997), Khaledi and Kochar (2000), Khaledi et al. (2011), Balakrishnan and Zhao (2013), Zhao and Zhang (2014), Li and Li (2015), Zhao et al. (2015) and Balakrishnan et al. (2015) for details on different developments in this regard.

Here, we assume $X_{1},\ldots , X_{n}$ to be independent non-negative random variables with $X_{i}\sim GBS(\alpha _{i}, \beta _{i}),~ i=1,\ldots ,n$, and $I_{p_{1}},\ldots , I_{p_{n}}$ to be independent Bernoulli random variables, independent of $X_{i}$’s, with $E(I_{p_{i}})=p_{i},~i=1,\ldots ,n$. We then let $Y_{i}=I_{p_{i}}X_{i},~i=1,\ldots ,n$. Note that the random variables $Y_{i}$ are discrete-continuous type, which admit zero with probability $1-p_{i}$, and distributed as $X_{i}$ with probability $p_{i},~i=1,\ldots ,n$. Then, the survival function of $Y_{1:n}=\min \{Y_{1},\ldots , Y_{n}\}$ is given by

$$\begin{aligned} {\overline{F}}_{Y_{1:n}}(x; {\varvec{p}}, {\varvec{\alpha }}, {\varvec{\beta }})= \prod \limits _{i=1}^n p_{i} {\overline{G}}\biggl [\frac{1}{\alpha _{i}} \biggl (\sqrt{\frac{x}{\beta _{i}}}-\sqrt{\frac{\beta _{i}}{x}}\biggr ) \biggr ],~~ x>0. \end{aligned}$$

(2)

Hereafter, we assume that $Y_{1:n}^{*}$ denotes similarly the smallest order statistic arising from $Y_{i}^{*}=I_{p_{i}^{*}}X_{i}^{*},~i=1,\ldots ,n,$ where $X_{1}^{*},\ldots , X_{n}^{*}$ are independent non-negative random variables with $X_{i}^{*}\sim GBS(\alpha _{i}^{*}, \beta _{i}^{*}),~ i=1,\ldots ,n$, and $I_{p_{1}^{*}},\ldots , I_{p_{n}^{*}}$ are independent Bernoulli random variables, independent of $X_{i}^{*}$’s, with $E(I_{p_{i}^{*}})=p_{i}^{*},~i=1,\ldots ,n$. The survival function of $Y_{1:n}^{*}$ is then same as in (2) with $p_{i}$, $\alpha _{i}, \beta _{i}$ replaced by $p_{i}^{*}$, $\alpha _{i}^{*}, \beta _{i}^{*}$, respectively.

It is of interest to mention that this model could arise in the following reliability context. Suppose the GBS random variable $X_{i}$ represents the lifetime of the i-th component in a series (parallel) system which may receive a random shock $I_{p_{i}}$ instantaneously. When $I_{p_{i}}=1,$ this random shock may not impact the i-th component, while when $I_{p_{i}}=0,$ this random shock will impact the i-th component and result in its failure. Then, clearly, $Y_{i}=I_{p_{i}}X_{i}$ corresponds to the lifetime of the i-th component with an associated random shock that may or may not occur.

Let

$$\begin{aligned} {\mathcal {S}}_{n}=\left\{ (\mathbf {x,y})=\left( \begin{array}{c} x_{1} \ldots x_{n} \\ y_{1} \ldots y_{n} \\ \end{array} \right) : x_{i}> 0, y_{j}> 0~\text{ and }~ (x_{i}-x_{j})(y_{i}-y_{j})\ge 0, i,j = 1,\ldots ,n\right\} . \end{aligned}$$

Assume that the following conditions hold:

• (i) $0<\nu \le 2;$

• (ii) r(x) is increasing in x;

• (iii) $h: [0,1]\rightarrow (0,\infty )$ is differentiable and a strictly increasing concave function.

Under the assumptions (i)–(iii), we establish here the following results:

$(R_{1})$ (1) For $\alpha _{1}=\alpha _{2}=\alpha _{1}^{*}=\alpha _{2}^{*}=\alpha$ and $(h({\varvec{p}}), {\varvec{\beta }}^{\frac{1}{\nu }}) \in {\mathcal {S}}_{2}$, we have

$$\begin{aligned} \left( \begin{array}{c@{\quad }c} h(p_{1}) &{} h(p_{2})\\ \beta _{1}^{\frac{1}{\nu }} &{} \beta _{2}^{\frac{1}{\nu }} \\ \end{array} \right) \gg \left( \begin{array}{c@{\quad }c} h(p_{1}^{*}) &{} h(p_{2}^{*})\\ \beta _{1}^{*\frac{1}{\nu }} &{} \beta _{2}^{*\frac{1}{\nu }} \\ \end{array} \right) \Rightarrow Y_{1:2}^{*} \ge _{st} Y_{1:2}; \end{aligned}$$

(2) For $\beta _{1}=\beta _{2}=\beta _{1}^{*}=\beta _{2}^{*}=\beta$ and $(h({\varvec{p}}), {\varvec{\frac{1}{\alpha }}}) \in {\mathcal {S}}_{2}$, we have

$$\begin{aligned} \left( \begin{array}{c@{\quad }c} h(p_{1}) &{} h(p_{2})\\ \frac{1}{\alpha _{1}} &{} \frac{1}{\alpha _{2}} \\ \end{array} \right) \gg \left( \begin{array}{c@{\quad }c} h(p_{1}^{*}) &{} h(p_{2}^{*})\\ \frac{1}{\alpha _{1}^{*}} &{} \frac{1}{\alpha _{2}^{*}} \\ \end{array} \right) \Rightarrow Y_{1:2}^{*} \ge _{st} Y_{1:2}. \end{aligned}$$

We also consider some generalizations of $(R_{1})$ to the case when $n>2$ as follows:

$(R_{2})$ Suppose the T-transform matrices $T_{w_{i}}, i=1,\ldots ,k$, have the same structure. (1) For $\alpha _{1}=\cdots =\alpha _{n}=\alpha _{1}^{*}=\cdots =\alpha _{n}^{*}=\alpha$ and $(h({\varvec{p}}), {\varvec{\beta }}^{\frac{1}{\nu }}) \in {\mathcal {S}}_{n}$,

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}) &{} h(p_{2}) &{}\ldots &{} h(p_{n})\\ \beta _{1}^{\frac{1}{\nu }} &{} \beta _{2}^{\frac{1}{\nu }}&{} \ldots &{} \beta _{n}^{\frac{1}{\nu }} \\ \end{array} \right) = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}^{*}) &{} h(p_{2}^{*}) &{}\ldots &{} h(p_{n}^{*})\\ \beta _{1}^{*\frac{1}{\nu }} &{} \beta _{2}^{*\frac{1}{\nu }}&{} \ldots &{} \beta _{n}^{*\frac{1}{\nu }} \\ \end{array} \right) T_{w_{1}}\ldots T_{w_{k}} \end{aligned}$$

implies that $Y_{1:n}^{*} \ge _{st} Y_{1:n};$

(2) For $\beta _{1}=\cdots =\beta _{n}=\beta _{1}^{*}=\cdots =\beta _{n}^{*}=\beta$ and $(h({\varvec{p}}), {\varvec{\frac{1}{\alpha }}}) \in {\mathcal {S}}_{n}$,

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}) &{} h(p_{2}) &{}\ldots &{} h(p_{n})\\ \frac{1}{\alpha _{1}} &{} \frac{1}{\alpha _{2}}&{}\ldots &{} \frac{1}{\alpha _{n}} \\ \end{array} \right) = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}^{*}) &{} h(p_{2}^{*}) &{}\ldots &{} h(p_{n}^{*})\\ \frac{1}{\alpha _{1}^{*}} &{} \frac{1}{\alpha _{2}^{*}} &{}\ldots &{} \frac{1}{\alpha _{n}^{*}} \\ \end{array} \right) T_{w_{1}}\ldots T_{w_{k}} \end{aligned}$$

implies that $Y_{1:n}^{*} \ge _{st} Y_{1:n}$.

$(R_{3})$ Suppose the T-transform matrices $T_{w_{1}}, \ldots , T_{w_{k}}, k>2,$ have different structures.

(1) For $\alpha _{1}=\cdots =\alpha _{n}=\alpha _{1}^{*}=\cdots =\alpha _{n}^{*}=\alpha$, $(h({\varvec{p}}), {\varvec{\beta }}^{\frac{1}{\nu }}) \in {\mathcal {S}}_{n}$ and $(h({\varvec{p}}), {\varvec{\beta }}^{\frac{1}{\nu }})T_{w_{1}}\ldots T_{w_{i}} \in {\mathcal {S}}_{n},~i=1,\ldots , k-1,$

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}) &{} h(p_{2}) &{}\ldots &{} h(p_{n})\\ \beta _{1}^{\frac{1}{\nu }} &{} \beta _{2}^{\frac{1}{\nu }}&{} \ldots &{} \beta _{n}^{\frac{1}{\nu }} \\ \end{array} \right) = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}^{*}) &{} h(p_{2}^{*}) &{}\ldots &{} h(p_{n}^{*})\\ \beta _{1}^{*\frac{1}{\nu }} &{} \beta _{2}^{*\frac{1}{\nu }}&{} \ldots &{} \beta _{n}^{*\frac{1}{\nu }} \\ \end{array} \right) T_{w_{1}}\ldots T_{w_{k}} \end{aligned}$$

implies that $Y_{1:n}^{*} \ge _{st} Y_{1:n};$

(2) For $\beta _{1}=\cdots =\beta _{n}=\beta _{1}^{*}=\cdots =\beta _{n}^{*}=\beta$, $(h({\varvec{p}}), {\varvec{\frac{1}{\alpha }}}) \in {\mathcal {S}}_{n}$ and $(h({\varvec{p}}), {\varvec{\frac{1}{\alpha }}})T_{w_{1}} \ldots T_{w_{i}} \in {\mathcal {S}}_{n},~i=1,\ldots , k-1,$

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}) &{} h(p_{2}) &{}\ldots &{} h(p_{n})\\ \frac{1}{\alpha _{1}} &{} \frac{1}{\alpha _{2}}&{}\ldots &{} \frac{1}{\alpha _{n}} \\ \end{array} \right) = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}^{*}) &{} h(p_{2}^{*}) &{}\ldots &{} h(p_{n}^{*})\\ \frac{1}{\alpha _{1}^{*}} &{} \frac{1}{\alpha _{2}^{*}} &{}\ldots &{} \frac{1}{\alpha _{n}^{*}} \\ \end{array} \right) T_{w_{1}}\ldots T_{w_{k}} \end{aligned}$$

implies that $Y_{1:n}^{*} \ge _{st} Y_{1:n}$.

For illustrative purposes, we apply these results to two special cases, namely, the classical BS and LBS distributions with possibly different model parameters.

2 Preliminaries

In this section, we briefly review the definitions of usual stochastic order and chain majorization that are most pertinent to the discussion here. For more details on these, one may refer to Shaked and Shanthikumar (2007). Throughout this paper, we use “increasing” to mean “nondecreasing” and similarly “decreasing” to mean “nonincreasing”.

Definition 2.1

We say that Y is smaller than X in the usual stochastic order, denoted by $X\ge _{st} Y$, if ${\bar{F}}(x) \ge {\bar{G}}(x)$ for all x.

A square matrix ${\varPi }$ is said to be a permutation matrix if each row and column has a single unity and all other entries as zero. Clearly, n! such matrices are obtained by interchanging rows (or columns) of the identity matrix of size $n\times n$. The T-transform matrix has the form $T_{w}=wI_{n}+(1-w){\varPi },$ where $0 \le w \le 1$ and ${\varPi }$ is a special case of permutation matrix when only two coordinates are interchanged. Let $T_{w_{1}}=w_{1}I_{n}+(1-w_{1}){\varPi }_{1}$ and $T_{w_{2}}=w_{2}I_{n}+(1-w_{2}){\varPi }_{2}$ are two special cases of permutation matrices when only two coordinates are interchanged. When ${\varPi }_{1}={\varPi }_{2},$ we say that $T_{w_{1}}$ and $T_{w_{2}}$ have the same structure. When ${\varPi }_{1}$ and ${\varPi }_{2}$ are different, then $T_{w_{1}}$ and $T_{w_{2}}$ are said to have different structures. It is well known that a finite product of T-transform matrices with the same structure is also a T-transform matrix and has the same structure as the elements. However, this result may not hold for a finite product of T-transform matrices with different structures; see Balakrishnan et al. (2015) for more details.

We now describe a type of multivariate majorization that has been discussed in the literature.

Definition 2.2

Let $A=\{a_{ij}\}$ and $B=\{b_{ij}\}$ be $m\times n$ matrices such that $a_{1}^{R},\ldots ,a_{m}^{R}$ and $b_{1}^{R},\ldots ,b_{m}^{R}$ are the rows of A and B, respectively. Then, A is said to chain majorize B (denoted by $A \gg B$) if there exists a finite set of $n\times n$ T-transform matrices $T_{w_{1}},\ldots ,T_{w_{k}}$ such that $B = AT_{w_{1}}T_{w_{2}}\ldots T_{w_{k}}$.

The following Lemmas 2.3 and 2.4 will be useful in proving the main results in the next section; see Balakrishnan et al. (2015) for an idea about their proofs.

Lemma 2.3

A differentiable function $\phi : {\mathbb {R}}^{+^{4}}\rightarrow {\mathbb {R}}^{+}$ satisfies

$$\begin{aligned} \phi (A)\ge (\le ) \phi (B) ~~ \text{ for } \text{ all }~~ A, B~~\text{ such } \text{ that }~~ A\in {\mathcal {S}}_{2}~~ \text{ and }~~A\gg B \end{aligned}$$

(*)

if and only if

• (i)   $\phi (A)=\phi (A{\varPi })$ for all permutation matrices ${\varPi }$;

• (ii)   $\sum \limits _{i=1}^2 (a_{ik}-a_{ij})[\phi _{ik}(A)-\phi _{ij}(A)]\ge (\le )0$ for all $j,k=1,2,$ where $\phi _{ij}(A)=\partial \phi (A)/\partial a_{ij}$.

Lemma 2.4

Let the function $\psi : {\mathbb {R}}^{+^{2}}\rightarrow {\mathbb {R}}^{+}$ be differentiable, and the function $\phi _{n}: {\mathbb {R}}^{+^{2n}}\rightarrow {\mathbb {R}}^{+}$ be defined as

$$\begin{aligned} \phi _{n}(A)=\prod \limits _{i=1}^n \psi (a_{1i},a_{2i}). \end{aligned}$$

Assume that $\phi _{2}$ satisfies the inequality in $(*)$. Then, with $A\in {\mathcal {S}}_{n}$ and $B=AT_{w}$, we have $\phi _{n}(A)\ge \phi _{n}(B)$.

Lemma 2.5

(Fang and Zhang 2010) Let $h(u)=\frac{e^{-\frac{u^{2}}{2}}}{\int _{u}^{+\infty }e^{-\frac{t^{2}}{2}}dt}$, for all $u\in R$. Then, h(u) is an increasing function.

3 Main results

In this section, we establish some ordering properties for the smallest order statistics from GBS models with associated random shocks.

Theorem 3.1

Suppose $X_{1}$ and $X_{2}$ are independent non-negative random variables with $X_{i}\sim GBS(\alpha _{i}, \beta _{i}),$ and $I_{p_{1}}$ and $I_{p_{2}}$ are independent Bernoulli random variables, independent of $X_{i}$’s, with $E(I_{p_{i}})=p_{i},~i=1, 2$. Further, suppose $X_{1}^{*}$ and $X_{2}^{*}$ are independent non-negative random variables with $X_{i}^{*}\sim GBS(\alpha _{i}^{*}, \beta _{i}^{*})$, and $I_{p_{1}^{*}}$ and $I_{p_{2}^{*}}$ are independent Bernoulli random variables, independent of $X_{i}^{*}$’s, with $E(I_{p_{i}^{*}})=p_{i}^{*},~i=1, 2$. Assume that the following conditions hold:

• (i) $0<\nu \le 2;$

• (ii) r(x) is increasing in x;

• (iii) $h: [0,1]\rightarrow (0,\infty )$ is differentiable and a strictly increasing concave function.

Then:

(1) for $\alpha _{1}=\alpha _{2}=\alpha _{1}^{*}=\alpha _{2}^{*}=\alpha$ and $(h({\varvec{p}}), {\varvec{\beta }}^{\frac{1}{\nu }}) \in {\mathcal {S}}_{2}$, we have

$$\begin{aligned} \left( \begin{array}{c@{\quad }c} h(p_{1}) &{} h(p_{2})\\ \beta _{1}^{\frac{1}{\nu }} &{} \beta _{2}^{\frac{1}{\nu }} \\ \end{array} \right) \gg \left( \begin{array}{c@{\quad }c} h(p_{1}^{*}) &{} h(p_{2}^{*})\\ \beta _{1}^{*\frac{1}{\nu }} &{} \beta _{2}^{*\frac{1}{\nu }} \\ \end{array} \right) \Rightarrow Y_{1:2}^{*} \ge _{st} Y_{1:2}; \end{aligned}$$

(2) for $\beta _{1}=\beta _{2}=\beta _{1}^{*}=\beta _{2}^{*}=\beta$ and $(h({\varvec{p}}), {\varvec{\frac{1}{\alpha }}}) \in {\mathcal {S}}_{2}$, we have

$$\begin{aligned} \left( \begin{array}{c@{\quad }c} h(p_{1}) &{} h(p_{2})\\ \frac{1}{\alpha _{1}} &{} \frac{1}{\alpha _{2}} \\ \end{array} \right) \gg \left( \begin{array}{c@{\quad }c} h(p_{1}^{*}) &{} h(p_{2}^{*})\\ \frac{1}{\alpha _{1}^{*}} &{} \frac{1}{\alpha _{2}^{*}} \\ \end{array} \right) \Rightarrow Y_{1:2}^{*} \ge _{st} Y_{1:2}. \end{aligned}$$

Proof

(1) With $u_{1}=h(p_{1}),$ $u_{2}=h(p_{2})$, $\lambda _{1}=\beta _{1}^{\frac{1}{\nu }},$ and $\lambda _{2}=\beta _{2}^{\frac{1}{\nu }}$, we have $p_{1}=h^{-1}(u_{1}),$ $p_{2}=h^{-1}(u_{2})$, $\beta _{1}=\lambda _{1}^{\nu }$ and $\beta _{2}=\lambda _{2}^{\nu }$, where $h^{-1}$ denotes the inverse of the function h. From (2), the survival function of $Y_{1:2}$ is, for $x>0$,

$$\begin{aligned} {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, \alpha , {\varvec{\lambda }})= \prod \limits _{i=1}^2 h^{-1}(u_{i}) {\overline{G}}\biggl (k(x;\lambda _{i}, \alpha , \nu )\biggr ), \end{aligned}$$

where $k(x;\lambda _{i}, \alpha , \nu )=\frac{1}{\alpha }\Bigl (\frac{\sqrt{x}}{\lambda _{i}^{\nu /2}}-\frac{\lambda _{i}^{\nu /2}}{\sqrt{x}}\Bigr )$.

It is well known that the function ${\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, \alpha , {\varvec{\lambda }})$ is permutation invariant in $(u_{i},\lambda _{i})$, and so condition (i) of Lemma 2.3 is satisfied. Next, we have to show that condition (ii) of Lemma 2.3 also holds.

The assumption $({\varvec{u}},{\varvec{\lambda }})\in {\mathcal {S}}_{2}$ implies that $(u_{1}-u_{2})(\lambda _{1}-\lambda _{2})\ge 0$. This means that $u_{1}\ge u_{2}$ and $\lambda _{1}\ge \lambda _{2}$, or $u_{1}\le u_{2}$ and $\lambda _{1}\le \lambda _{2}$. We then present the proof only for the case when $u_{1}\ge u_{2}$ and $\lambda _{1}\ge \lambda _{2}$, since the proof for the other case is quite similar.

The partial derivatives of ${\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, \alpha , {\varvec{\lambda }})$ with respect to $u_{i}$ and $\lambda _{i}$ are

$$\begin{aligned} \frac{\partial {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, \alpha , {\varvec{\lambda }})}{\partial u_{i}}= & {} {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, \alpha , {\varvec{\lambda }})\frac{\frac{\partial h^{-1}(u_{i})}{\partial u_{i}}}{h^{-1}(u_{i})},\\ \frac{\partial {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, \alpha , {\varvec{\lambda }})}{\partial \lambda _{i}}= & {} \frac{\nu {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, \alpha , {\varvec{\lambda }})}{2}r\biggl (k(x;\lambda _{i}, \alpha , \nu )\biggr ) h(x;\lambda _{i}, \alpha , \nu ), \end{aligned}$$

where $h(x;\lambda _{i}, \alpha , \nu )=\frac{1}{\alpha }\Bigl (\frac{\sqrt{x}}{\lambda _{i}^{\nu /2+1}}+\frac{\lambda _{i}^{\nu /2-1}}{\sqrt{x}}\Bigr )$.

For fixed $x>0$ and $\alpha >0$, let us define the function $\varphi ({\varvec{u}}, {\varvec{\lambda }})$ as follows:

$$\begin{aligned} \varphi ({\varvec{u}}, {\varvec{\lambda }})= & {} (u_{1}-u_{2})\biggl (\frac{\partial {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, \alpha , {\varvec{\lambda }})}{\partial u_{1}}-\frac{\partial {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, \alpha , {\varvec{\lambda }})}{\partial u_{2}}\biggr )\nonumber \\&+\,(\lambda _{1}-\lambda _{2})\biggl (\frac{\partial {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, \alpha , {\varvec{\lambda }})}{\partial \lambda _{1}}-\frac{\partial {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, \alpha , {\varvec{\lambda }})}{\partial \lambda _{2}}\biggr )\nonumber \\= & {} {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, \alpha , {\varvec{\lambda }})(u_{1}-u_{2})\biggl [\frac{\frac{\partial h^{-1}(u_{1})}{\partial u_{1}}}{h^{-1}(u_{1})}-\frac{\frac{\partial h^{-1}(u_{2})}{\partial u_{2}}}{h^{-1}(u_{2})}\biggr ] \nonumber \\&+\,\frac{\nu {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, \alpha , {\varvec{\lambda }})}{2}(\lambda _{1}-\lambda _{2})\biggl [r\biggl (k(x;\lambda _{1}, \alpha , \nu )\biggr ) \nonumber \\&h(x;\lambda _{1}, \alpha , \nu )- r\biggl (k(x;\lambda _{2}, \alpha , \nu )\biggr ) h(x;\lambda _{2}, \alpha , \nu )\biggr ]. \end{aligned}$$

(3)

Note that, since h is strictly increasing and concave, $h^{-1}$ is strictly increasing and concave. Since $u_{1}\ge u_{2}$ and $\lambda _{1}\ge \lambda _{2}$, we have

$$\begin{aligned} \frac{\frac{\partial h^{-1}(u_{1})}{\partial u_{1}}}{h^{-1}(u_{1})}\le \frac{\frac{\partial h^{-1}(u_{2})}{\partial u_{2}}}{h^{-1}(u_{2})}. \end{aligned}$$

(4)

Furthermore, the functions $k(x;\lambda , \alpha , \nu )$ and $h(x;\lambda , \alpha , \nu )$ are decreasing in $\lambda$ for $0<\nu \le 2$. For the hazard rate function r that is increasing, we have

$$\begin{aligned} r\biggl (k(x;\lambda _{1}, \alpha , \nu )\biggr )\le r\biggl (k(x;\lambda _{2}, \alpha , \nu )\biggr ) \end{aligned}$$

(5)

and

$$\begin{aligned} h(x;\lambda _{1}, \alpha , \nu )\le h(x;\lambda _{2}, \alpha , \nu ). \end{aligned}$$

(6)

Upon combining the facts in (4)–(6), we see that the RHS of (3) is non-positive. Thus, $\varphi ({\varvec{u}}, {\varvec{\lambda }})\le 0$, and so condition ii) of Lemma 2.3 is satisfied, which completes the proof.

(2) With $u_{1}=h(p_{1}),$ $u_{2}=h(p_{2})$, $\lambda _{1}=\frac{1}{\alpha _{1}}$ and $\lambda _{2}=\frac{1}{\alpha _{2}}$, we have $p_{1}=h^{-1}(u_{1}),~ p_{2}=h^{-1}(u_{2})$. Then, according to (2), the survival function of $Y_{1:2}$ is, for $x>0$,

$$\begin{aligned} {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, {\varvec{\lambda }}, \beta )= \prod \limits _{i=1}^2 h^{-1}(u_{i}) {\overline{G}}\biggl (a(x; \lambda _{i}, \beta )\biggr ) \end{aligned}$$

by letting $a(x; \lambda _{i}, \beta )=\lambda _{i}\biggl (\sqrt{\frac{x}{\beta }}-\sqrt{\frac{\beta }{x}}\biggr )=\lambda _{i}l(x;\beta )$. It is easy to see that the function ${\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, {\varvec{\lambda }}, \beta )$ is permutation invariant in $(u_{i},\lambda _{i})$, and so condition i) of Lemma 2.3 is satisfied. Next, we have to show that condition ii) of Lemma 2.3 also holds.

The assumption $({\varvec{u}},{\varvec{\lambda }})\in {\mathcal {S}}_{2}$ implies that $(u_{1}-u_{2})(\lambda _{1}-\lambda _{2})\ge 0$. This means that $u_{1}\ge u_{2}$ and $\lambda _{1}\ge \lambda _{2}$, or $u_{1}\le u_{2}$ and $\lambda _{1}\le \lambda _{2}$. As before, we present the proof only for the case when $u_{1}\ge u_{2}$ and $\lambda _{1}\ge \lambda _{2}$, since the proof for the other case is quite similar.

The partial derivatives of ${\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, {\varvec{\lambda }}, \beta )$ with respect to $u_{i}$ and $\lambda _{i}$ are

$$\begin{aligned} \frac{\partial {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, {\varvec{\lambda }}, \beta )}{\partial u_{i}}= & {} {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, {\varvec{\lambda }}, \beta )\frac{\frac{\partial h^{-1}(u_{i})}{\partial u_{i}}}{h^{-1}(u_{i})},\\ \frac{\partial {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, {\varvec{\lambda }}, \beta )}{\partial \lambda _{i}}= & {} -{\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, {\varvec{\lambda }}, \beta )r\biggl (a(x; \lambda _{i}, \beta )\biggr ) l(x;\beta ). \end{aligned}$$

For fixed $x>0$ and $\alpha >0$, let us define the function $\psi ({\varvec{u}}, {\varvec{\lambda }})$ as follows:

$$\begin{aligned} \psi ({\varvec{u}}, {\varvec{\lambda }})= & {} (u_{1}-u_{2})\biggl (\frac{\partial {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, {\varvec{\lambda }}, \beta )}{\partial u_{1}}-\frac{\partial {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, {\varvec{\lambda }}, \beta )}{\partial u_{2}}\biggr )\nonumber \\&+\,(\lambda _{1}-\lambda _{2})\biggl (\frac{\partial {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, {\varvec{\lambda }}, \beta )}{\partial \lambda _{1}}-\frac{\partial {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, {\varvec{\lambda }}, \beta )}{\partial \lambda _{2}}\biggr )\nonumber \\= & {} {\overline{F}}_{Y_{1:2}}(x; {\varvec{u}}, {\varvec{\lambda }}, \beta )\biggl \{(u_{1}-u_{2})\biggl [\frac{\frac{\partial h^{-1}(u_{1})}{\partial u_{1}}}{h^{-1}(u_{1})}-\frac{\frac{\partial h^{-1}(u_{2})}{\partial u_{2}}}{h^{-1}(u_{2})}\biggr ] \nonumber \\&+\,(\lambda _{1}-\lambda _{2})l(x;\beta ) \biggl [r\biggl (a(x; \lambda _{2}, \beta )\biggr )- r\biggl (a(x; \lambda _{1}, \beta )\biggr )\biggr ]\biggr \}. \end{aligned}$$

(7)

Since $u_{1}\ge u_{2}$ and $\lambda _{1}\ge \lambda _{2}$, from (4) and the fact that the hazard rate function r is increasing, we have the RHS of (7) to be non-positive. Thus, $\psi ({\varvec{u}}, {\varvec{\lambda }})\le 0$, and so condition ii) of Lemma 2.3 is satisfied, which completes the proof. $\square$

Some generalizations of Theorem 3.1 to the case when the number of underlying random variables is arbitrary are presented below.

Theorem 3.2

Suppose $X_{1},\ldots , X_{n}$ are independent non-negative random variables with $X_{i}\sim GBS(\alpha _{i}, \beta _{i}),$ and $I_{p_{1}},\ldots , I_{p_{n}}$ are independent Bernoulli random variables, independent of $X_{i}$’s, with $E(I_{p_{i}})=p_{i}, ~i=1,\ldots ,n$. Further, suppose $X_{1}^{*},\ldots , X_{n}^{*}$ are independent non-negative random variables with $X_{i}^{*}\sim GBS(\alpha _{i}^{*}, \beta _{i}^{*})$, and $I_{p_{1}^{*}},\ldots , I_{p_{n}^{*}}$ are independent Bernoulli random variables, independent of $X_{i}^{*}$’s, with $E(I_{p_{i}^{*}})=p_{i}^{*},~i=1,\ldots ,n$. Assume that the following conditions hold:

• (i) $0<\nu \le 2;$

• (ii) r(x) is increasing in x;

• (iii) $h: [0,1]\rightarrow (0,\infty )$ is differentiable and a strictly increasing concave function.

Then:

(1) for $\alpha _{1}=\cdots =\alpha _{n}=\alpha _{1}^{*}=\cdots =\alpha _{n}^{*}=\alpha$ and $(h({\varvec{p}}), {\varvec{\beta }}^{\frac{1}{\nu }}) \in {\mathcal {S}}_{n}$, we have

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}) &{} h(p_{2}) &{}\ldots &{} h(p_{n})\\ \beta _{1}^{\frac{1}{\nu }} &{} \beta _{2}^{\frac{1}{\nu }}&{} \ldots &{} \beta _{n}^{\frac{1}{\nu }} \\ \end{array} \right) = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}^{*}) &{} h(p_{2}^{*}) &{}\ldots &{} h(p_{n}^{*})\\ \beta _{1}^{*\frac{1}{\nu }} &{} \beta _{2}^{*\frac{1}{\nu }}&{} \ldots &{} \beta _{n}^{*\frac{1}{\nu }} \\ \end{array} \right) T_{w} \Rightarrow Y_{1:n}^{*} \ge _{st} Y_{1:n}; \end{aligned}$$

(2) for $\beta _{1}=\cdots =\beta _{n}=\beta _{1}^{*}=\cdots =\beta _{n}^{*}=\beta$ and $(h({\varvec{p}}), {\varvec{\frac{1}{\alpha }}}) \in {\mathcal {S}}_{n}$, we have

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}) &{} h(p_{2}) &{}\ldots &{} h(p_{n})\\ \frac{1}{\alpha _{1}} &{} \frac{1}{\alpha _{2}}&{}\ldots &{} \frac{1}{\alpha _{n}} \\ \end{array} \right) = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}^{*}) &{} h(p_{2}^{*}) &{}\ldots &{} h(p_{n}^{*})\\ \frac{1}{\alpha _{1}^{*}} &{} \frac{1}{\alpha _{2}^{*}} &{}\ldots &{} \frac{1}{\alpha _{n}^{*}} \\ \end{array} \right) T_{w} \Rightarrow Y_{1:n}^{*} \ge _{st} Y_{1:n}. \end{aligned}$$

Proof

(1) For fixed $x>0$, let $\phi _{n}(x; {\varvec{u}}, \alpha , {\varvec{\lambda }})={\overline{F}}_{Y_{1:n}}(x; {\varvec{u}}, \alpha , {\varvec{\lambda }})$ and $\psi (x; u, \alpha , \lambda )=h^{-1}(u) {\overline{G}}\biggl [\frac{1}{\alpha }\biggl (\frac{\sqrt{x}}{\lambda ^{\nu /2}}-\frac{\lambda ^{\nu /2}}{\sqrt{x}}\biggr )\biggr ]$. Then, we have $\phi _{n}(x; {\varvec{u}}, \alpha , {\varvec{\lambda }})=\prod \limits _{i=1}^n \psi (x; u_{i}, \alpha , \lambda _{i})$. According to Part (1) of Theorem 3.1, we know that $\phi _{2}(x; {\varvec{u}}, \alpha , {\varvec{\lambda }})$ satisfies $(*)$. Now, the desired result follows from Lemma 2.4.

(2) The proof is similar to that of Part (1). $\square$

Theorem 3.3

Suppose $X_{1},\ldots , X_{n}$ are independent non-negative random variables with $X_{i}\sim GBS(\alpha _{i}, \beta _{i}),$ and $I_{p_{1}},\ldots , I_{p_{n}}$ are independent Bernoulli random variables, independent of $X_{i}$’s, with $E(I_{p_{i}})=p_{i}, ~i=1,\ldots ,n$. Further, suppose $X_{1}^{*},\ldots , X_{n}^{*}$ are independent non-negative random variables with $X_{i}^{*}\sim GBS(\alpha _{i}^{*}, \beta _{i}^{*})$, and $I_{p_{1}^{*}},\ldots , I_{p_{n}^{*}}$ are independent Bernoulli random variables, independent of $X_{i}^{*}$’s, with $E(I_{p_{i}^{*}})=p_{i}^{*},~i=1,\ldots ,n$. Assume that the following conditions hold:

• (i) $0<\nu \le 2;$

• (ii) r(x) is increasing in x;

• (iii) $h: [0,1]\rightarrow (0,\infty )$ is differentiable and a strictly increasing concave function.

If the T-transform matrices $T_{w_{1}}, \ldots , T_{w_{k}}$ have the same structure, then:

(1) for $\alpha _{1}=\cdots =\alpha _{n}=\alpha _{1}^{*}=\cdots =\alpha _{n}^{*}=\alpha$ and $(h({\varvec{p}}), {\varvec{\beta }}^{\frac{1}{\nu }}) \in {\mathcal {S}}_{n}$,

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}) &{} h(p_{2}) &{}\ldots &{} h(p_{n})\\ \beta _{1}^{\frac{1}{\nu }} &{} \beta _{2}^{\frac{1}{\nu }}&{} \ldots &{} \beta _{n}^{\frac{1}{\nu }} \\ \end{array} \right) = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}^{*}) &{} h(p_{2}^{*}) &{}\ldots &{} h(p_{n}^{*})\\ \beta _{1}^{*\frac{1}{\nu }} &{} \beta _{2}^{*\frac{1}{\nu }}&{} \ldots &{} \beta _{n}^{*\frac{1}{\nu }} \\ \end{array} \right) T_{w_{1}}\ldots T_{w_{k}} \end{aligned}$$

implies that $Y_{1:n}^{*} \ge _{st} Y_{1:n};$

(2) for $\beta _{1}=\cdots =\beta _{n}=\beta _{1}^{*}=\cdots =\beta _{n}^{*}=\beta$ and $(h({\varvec{p}}), {\varvec{\frac{1}{\alpha }}}) \in {\mathcal {S}}_{n}$,

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}) &{} h(p_{2}) &{}\ldots &{} h(p_{n})\\ \frac{1}{\alpha _{1}} &{} \frac{1}{\alpha _{2}}&{}\ldots &{} \frac{1}{\alpha _{n}} \\ \end{array} \right) = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}^{*}) &{} h(p_{2}^{*}) &{}\ldots &{} h(p_{n}^{*})\\ \frac{1}{\alpha _{1}^{*}} &{} \frac{1}{\alpha _{2}^{*}} &{}\ldots &{} \frac{1}{\alpha _{n}^{*}} \\ \end{array} \right) T_{w_{1}}\ldots T_{w_{k}} \end{aligned}$$

implies that $Y_{1:n}^{*} \ge _{st} Y_{1:n}$.

Proof

(1) As mentioned earlier, a finite product of T-transform matrices with the same structure is also a T-transform matrix. So, the desired result is readily obtained from Part (1) of Theorem 3.2.

(2) The proof is similar to that of Part (1). $\square$

Since a finite product of T-transform matrices with different structures may not be a T-transform matrix, we can present the following results.

Theorem 3.4

Suppose $X_{1},\ldots , X_{n}$ are independent non-negative random variables with $X_{i}\sim GBS(\alpha _{i}, \beta _{i}),$ and $I_{p_{1}},\ldots , I_{p_{n}}$ are independent Bernoulli random variables, independent of $X_{i}$’s, with $E(I_{p_{i}})=p_{i}, ~i=1,\ldots ,n$. Further, suppose $X_{1}^{*},\ldots , X_{n}^{*}$ are independent non-negative random variables with $X_{i}^{*}\sim GBS(\alpha _{i}^{*}, \beta _{i}^{*})$, and $I_{p_{1}^{*}},\ldots , I_{p_{n}^{*}}$ are independent Bernoulli random variables, independent of $X_{i}^{*}$’s, with $E(I_{p_{i}^{*}})=p_{i}^{*},~i=1,\ldots ,n$. Assume that the following conditions hold:

• (i) $0<\nu \le 2;$

• (ii) r(x) is increasing in x;

• (iii) $h: [0,1]\rightarrow (0,\infty )$ is differentiable and a strictly increasing concave function.

If the T-transform matrices $T_{w_{1}}, \ldots , T_{w_{k}}, k> 2,$ have different structures, then:

(1) for $\alpha _{1}=\cdots =\alpha _{n}=\alpha _{1}^{*}=\cdots =\alpha _{n}^{*}=\alpha$, $(h({\varvec{p}}), {\varvec{\beta }}^{\frac{1}{\nu }}) \in {\mathcal {S}}_{n}$ and $(h({\varvec{p}}), {\varvec{\beta }}^{\frac{1}{\nu }})T_{w_{1}}\ldots T_{w_{i}} \in {\mathcal {S}}_{n},~i=1,\ldots , k-1,$

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}) &{} h(p_{2}) &{}\ldots &{} h(p_{n})\\ \beta _{1}^{\frac{1}{\nu }} &{} \beta _{2}^{\frac{1}{\nu }}&{} \ldots &{} \beta _{n}^{\frac{1}{\nu }} \\ \end{array} \right) = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}^{*}) &{} h(p_{2}^{*}) &{}\ldots &{} h(p_{n}^{*})\\ \beta _{1}^{*\frac{1}{\nu }} &{} \beta _{2}^{*\frac{1}{\nu }}&{} \ldots &{} \beta _{n}^{*\frac{1}{\nu }} \\ \end{array} \right) T_{w_{1}}\ldots T_{w_{k}} \end{aligned}$$

implies that $Y_{1:n}^{*} \ge _{st} Y_{1:n};$

(2) for $\beta _{1}=\cdots =\beta _{n}=\beta _{1}^{*}=\cdots =\beta _{n}^{*}=\beta$, $(h({\varvec{p}}), {\varvec{\frac{1}{\alpha }}}) \in {\mathcal {S}}_{n}$ and $(h({\varvec{p}}), {\varvec{\frac{1}{\alpha }}})T_{w_{1}} \ldots T_{w_{i}} \in {\mathcal {S}}_{n},~i=1,\ldots , k-1,$

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}) &{} h(p_{2}) &{}\ldots &{} h(p_{n})\\ \frac{1}{\alpha _{1}} &{} \frac{1}{\alpha _{2}}&{}\ldots &{} \frac{1}{\alpha _{n}} \\ \end{array} \right) = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}^{*}) &{} h(p_{2}^{*}) &{}\ldots &{} h(p_{n}^{*})\\ \frac{1}{\alpha _{1}^{*}} &{} \frac{1}{\alpha _{2}^{*}} &{}\ldots &{} \frac{1}{\alpha _{n}^{*}} \\ \end{array} \right) T_{w_{1}}\ldots T_{w_{k}} \end{aligned}$$

implies that $Y_{1:n}^{*} \ge _{st} Y_{1:n}$.

Proof

(1) The required result can be obtained readily by repeating the result of Part (1) of Theorem 3.2 for $(h({\varvec{p}}), {\varvec{\beta }}^{\frac{1}{\nu }}) \in {\mathcal {S}}_{n}$ and $(h({\varvec{p}}), {\varvec{\beta }}^{\frac{1}{\nu }})T_{w_{1}}\ldots T_{w_{i}} \in {\mathcal {S}}_{n},~i=1,\ldots , k-1$.

(2) The proof is similar to that of Part (1). $\square$

Remark 3.5

Condition (ii) stating that the hazard function r(x) is increasing in x is satisfied by some well-known members of the elliptically symmetric family such as normal, logistic, etc. The results established in Theorems 3.3 and 3.4, therefore, hold for many well-known GBS distributions.

We now present two applications of the results established in the preceding subsection for the special case of classical BS and LBS distributions.

(E1) Classical Birnbaum–Saunders distribution

A random variable X is said to have the BS distribution when $G(\cdot )$ in (1.1) is the standard normal cdf ${\varPhi }(\cdot )$. We then have the corresponding hazard rate function $r(\cdot )$ to be increasing from Lemma 2.5. So, the BS distribution satisfies condition (ii) of Theorems 3.3 and 3.4. Now, let us consider the following example which illustrates the results established in Theorem 3.4 when $h(p)=\frac{p}{1+p}$.

Example 3.6

Suppose $X_{1}, X_{2}$ and $X_{3}$ are independent non-negative random variables with $X_{i}\sim BS(\alpha _{i}, \beta _{i}),$ and $I_{p_{1}}, I_{p_{2}}$ and $I_{p_{3}}$ are independent Bernoulli random variables, independent of $X_{i}$’s, with $E(I_{p_{i}})=p_{i},~i=1,2,3$. Further, suppose $X_{1}^{*}, X_{2}^{*}$ and $X_{3}^{*}$ are independent non-negative random variables with $X_{i}^{*}\sim BS(\alpha _{i}^{*}, \beta _{i}^{*})$, and $I_{p_{1}^{*}}, I_{p_{2}^{*}}$ and $I_{p_{3}^{*}}$ are independent Bernoulli random variables, independent of $X_{i}^{*}$’s, with $E(I_{p_{i}^{*}})=p_{i}^{*},~i=1,2,3$. Consider the T-transform matrices as follows:

$$\begin{aligned} T_{0.4}= & {} 0.4\left( \begin{array}{c@{\quad }c@{\quad }c} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 1\\ \end{array} \right) +0.6\left( \begin{array}{c@{\quad }c@{\quad }c} 0 &{} 0 &{} 1\\ 0 &{} 1 &{} 0\\ 1 &{} 0 &{} 0\\ \end{array} \right) ,\\ T_{0.3}= & {} 0.3\left( \begin{array}{c@{\quad }c@{\quad }c} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 1\\ \end{array} \right) +0.7\left( \begin{array}{c@{\quad }c@{\quad }c} 0 &{} 1 &{} 0\\ 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 1\\ \end{array} \right) , T_{0.1}=0.1\left( \begin{array}{c@{\quad }c@{\quad }c} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 1\\ \end{array} \right) +0.9\left( \begin{array}{c@{\quad }c@{\quad }c} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 1\\ 0 &{} 1 &{} 0\\ \end{array} \right) . \end{aligned}$$

Suppose $\nu =1$ and $h(p)=\frac{p}{1+p}$. Then:

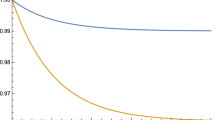
(1) for $\alpha _{1}=\alpha _{2}=\alpha _{3}=\alpha _{1}^{*}=\alpha _{2}^{*}=\alpha _{3}^{*}=2$, let $(\beta _{1}, \beta _{2}, \beta _{3})=(3,1,4)$, $(\beta _{1}^{*}, \beta _{2}^{*}, \beta _{3}^{*})=(1.78,3.342,2.878)$, $(p_{1}, p_{2}, p_{3})=(\frac{1}{4},\frac{1}{9},\frac{3}{7})$ and $(p_{1}^{*}, p_{2}^{*}, p_{3}^{*})=(0.1737,0.3110,0.2736)$. It is then easy to observe that $(\frac{{\varvec{p}}}{1+{\varvec{p}}}, {\varvec{\beta }}) \in {\mathcal {S}}_{3}$, $(\frac{{\varvec{p}}}{1+{\varvec{p}}}, {\varvec{\beta }})T_{0.4} \in {\mathcal {S}}_{3}$, $(\frac{{\varvec{p}}}{1+{\varvec{p}}}, {\varvec{\beta }})T_{0.4}T_{0.3} \in {\mathcal {S}}_{3}$ and $(\frac{{\varvec{p}}^{*}}{1+{\varvec{p}}^{*}}, {\varvec{\beta }}^{*})=(\frac{{\varvec{p}}}{1+{\varvec{p}}}, {\varvec{\beta }})T_{0.4}T_{0.3}T_{0.1}$. So, from Part (1) of Theorem 3.4, we immediately have $Y_{1:3}^{*} \ge _{st} Y_{1:3}$. Figure 1 presents the plots of survival functions of $Y_{1:3}$ and $Y_{1:3}^{*}$, which are seen to be in accordance with the above inequality.

(2) for $\beta _{1}=\beta _{2}=\beta _{3}=\beta _{1}^{*}=\beta _{2}^{*}=\beta _{3}^{*}=1.2$, let $(\alpha _{1}, \alpha _{2}, \alpha _{3})=(1,1/4,1/2)$, $(\alpha _{1}^{*}, \alpha _{2}^{*}, \alpha _{3}^{*})=(1/3.28,1/1.492,1/2.228)$, $(p_{1}, p_{2}, p_{3})=(\frac{1}{9},\frac{3}{7}, \frac{1}{4})$ and $(p_{1}^{*}, p_{2}^{*}, p_{3}^{*})=(0.3477,0.1712,0.2435)$. It is then easy to observe that $(\frac{{\varvec{p}}}{1+{\varvec{p}}}, \frac{1}{{\varvec{\alpha }}}) \in {\mathcal {S}}_{3}$, $(\frac{{\varvec{p}}}{1+{\varvec{p}}}, \frac{1}{{\varvec{\alpha }}})T_{0.4} \in {\mathcal {S}}_{3}$, $(\frac{{\varvec{p}}}{1+{\varvec{p}}}, \frac{1}{{\varvec{\alpha }}})T_{0.4}T_{0.3} \in {\mathcal {S}}_{3}$ and $(\frac{{\varvec{p}}^{*}}{1+{\varvec{p}}^{*}}, \frac{1}{{\varvec{\alpha }}^{*}})=(\frac{{\varvec{p}}}{1+{\varvec{p}}}, \frac{1}{{\varvec{\alpha }}})T_{0.4}T_{0.3}T_{0.1}$. So, from Part (2) of Theorem 3.4, we immediately have $Y_{1:3}^{*} \ge _{st} Y_{1:3}$. Figure 2 presents the plots of survival functions of $Y_{1:3}$ and $Y_{1:3}^{*}$, which are seen to be in accordance with the above inequality.

Fig. 1

Plots of survival functions of $Y_{1:3}$ and $Y_{1:3}^{*}$

Fig. 2

Plots of survival functions of $Y_{1:3}$ and $Y_{1:3}^{*}$

(E2) Logistic Birnbaum–Saunders distribution

A random variable X is said to have the LBS distribution when we choose $G(x)=\frac{1}{1+e^{-x}},~ x\in R,$ corresponding to the standard logistic distribution. In this case, it is evident that the hazard rate function $r(x)=\frac{1}{1+e^{-x}}$ is increasing in $x\in R$. So, LBS distribution satisfies condition (ii) of Theorems 3.3 and 3.4. Now, let us consider the following example which illustrates the results established in Theorem 3.4 when $h(p)=p$.

Example 3.7

Suppose $X_{1}, X_{2}$ and $X_{3}$ are independent non-negative random variables with $X_{i}\sim LBS(\alpha _{i}, \beta _{i}),$ and $I_{p_{1}}, I_{p_{2}}$ and $I_{p_{3}}$ are independent Bernoulli random variables, independent of $X_{i}$’s, with $E(I_{p_{i}})=p_{i},~i=1,2,3$. Further, suppose $X_{1}^{*}, X_{2}^{*}$ and $X_{3}^{*}$ are independent non-negative random variables with $X_{i}^{*}\sim LBS(\alpha _{i}^{*}, \beta _{i}^{*})$, and $I_{p_{1}^{*}}, I_{p_{2}^{*}}$ and $I_{p_{3}^{*}}$ are independent Bernoulli random variables, independent of $X_{i}^{*}$’s, with $E(I_{p_{i}^{*}})=p_{i}^{*},~i=1,2,3$. Consider the T-transform matrices as follows:

$$\begin{aligned} T_{0.5}=0.5\left( \begin{array}{c@{\quad }c@{\quad }c} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 1\\ \end{array} \right) +0.5\left( \begin{array}{c@{\quad }c@{\quad }c} 0 &{} 0 &{} 1\\ 0 &{} 1 &{} 0\\ 1 &{} 0 &{} 0\\ \end{array} \right) , T_{0.2}=0.2\left( \begin{array}{c@{\quad }c@{\quad }c} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 1\\ \end{array} \right) +0.8\left( \begin{array}{c@{\quad }c@{\quad }c} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 1\\ 0 &{} 1 &{} 0\\ \end{array} \right) . \end{aligned}$$

Suppose $\nu =1$ and $h(p)=p$. Then:

(1) for $\alpha _{1}=\alpha _{2}=\alpha _{3}=\alpha _{1}^{*}=\alpha _{2}^{*}=\alpha _{3}^{*}=2.2$, let $(\beta _{1}, \beta _{2}, \beta _{3})=(5,2,4)$, $(\beta _{1}^{*}, \beta _{2}^{*}, \beta _{3}^{*})=(4.5,4, 2.5)$, $(p_{1}, p_{2}, p_{3})=(0.3,0.1,0.2)$ and $(p_{1}^{*}, p_{2}^{*}, p_{3}^{*})=(0.25, 0.22, 0.13)$. It is then easy to observe that $({\varvec{p}}, {\varvec{\beta }}) \in {\mathcal {S}}_{3}$, $({\varvec{p}}, {\varvec{\beta }})T_{0.5} \in {\mathcal {S}}_{3}$ and (${\varvec{p}}^{*}, {\varvec{\beta }}^{*})=({\varvec{p}}, {\varvec{\beta }})T_{0.5}T_{0.2}$. So, from Part (1) of Theorem 3.4, we immediately have $Y_{1:3}^{*} \ge _{st} Y_{1:3}$. Figure 3 presents the plots of survival functions of $Y_{1:3}$ and $Y_{1:3}^{*}$, which are seen to be in accordance with the above inequality.

(2) for $\beta _{1}=\beta _{2}=\beta _{3}=\beta _{1}^{*}=\beta _{2}^{*}=\beta _{3}^{*}=1.5$, let $(\alpha _{1}, \alpha _{2}, \alpha _{3})=(1/7,1/4,1/5)$, $(\alpha _{1}^{*}, \alpha _{2}^{*}, \alpha _{3}^{*})=(1/6,1/5.6,1/4.4)$, $(p_{1}, p_{2}, p_{3})=(0.3,0.1,0.2)$ and $(p_{1}^{*}, p_{2}^{*}, p_{3}^{*})=(0.25, 0.22, 0.13)$. It is then easy to observe that $({\varvec{p}}, {\varvec{\beta }}) \in {\mathcal {S}}_{3}$, $({\varvec{p}}, {\varvec{\beta }})T_{0.5} \in {\mathcal {S}}_{3}$ and $({\varvec{p}}^{*}, {\varvec{\beta }}^{*})=({\varvec{p}}, {\varvec{\beta }})T_{0.5}T_{0.2}$. So, from Part (2) of Theorem 3.4, we immediately have $Y_{1:3}^{*} \ge _{st} Y_{1:3}$. Figure 4 presents the plots of the survival functions of $Y_{1:3}$ and $Y_{1:3}^{*}$, which are seen to be in accordance with the above inequality.

Fig. 3

Plots of survival functions of $Y_{1:3}$ and $Y_{1:3}^{*}$

Fig. 4

Plots of survival functions of $Y_{1:3}$ and $Y_{1:3}^{*}$

Remark 3.8

From Diáz-Garciá and Leiva-Sánchez (2005), it is known that GBS random variables are closed under reciprocation. So, it will be of interest to know whether ordering properties of the largest lifetime in the GBS models with associated random shocks will hold. Specifically, suppose $X_{1},\ldots , X_{n}$ are independent non-negative random variables with $X_{i}\sim GBS(\alpha _{i}, \beta _{i}),$ and $I_{p_{1}},\ldots , I_{p_{n}}$ are independent Bernoulli random variables, independent of $X_{i}$’s, with $E(I_{p_{i}})=p_{i},~i=1,\ldots ,n$. Further, suppose $X_{1}^{*},\ldots , X_{n}^{*}$ are independent non-negative random variables with $X_{i}^{*}\sim GBS(\alpha _{i}^{*}, \beta _{i}^{*})$, and $I_{p_{1}^{*}},\ldots , I_{p_{n}^{*}}$ are independent Bernoulli random variables, independent of $X_{i}^{*}$’s, with $E(I_{p_{i}^{*}})=p_{i}^{*},~i=1,\ldots ,n$. Assume that the following conditions hold:

• (i) $0<\nu \le 2;$

• (ii) r(x) is increasing in x;

• (iii) $h: [0,1]\rightarrow (0,\infty )$ is differentiable and a strictly increasing concave function.

If the T-transform matrices $T_{w_{1}}, \ldots , T_{w_{k}}, k>2,$ have different structures, then:

(1) for $\alpha _{1}=\cdots =\alpha _{n}=\alpha _{1}^{*}=\cdots =\alpha _{n}^{*}=\alpha$, $(h({\varvec{p}}), {\varvec{\beta }}^{-\frac{1}{\nu }}) \in {\mathcal {S}}_{n}$ and $(h({\varvec{p}}), {\varvec{\beta }}^{-\frac{1}{\nu }})T_{w_{1}}\ldots T_{w_{i}} \in {\mathcal {S}}_{n},~i=1,\ldots , k-1,$

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}) &{} h(p_{2}) &{}\ldots &{} h(p_{n})\\ \beta _{1}^{-\frac{1}{\nu }} &{} \beta _{2}^{-\frac{1}{\nu }}&{} \ldots &{} \beta _{n}^{-\frac{1}{\nu }} \\ \end{array} \right) = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}^{*}) &{} h(p_{2}^{*}) &{}\ldots &{} h(p_{n}^{*})\\ \beta _{1}^{*-\frac{1}{\nu }} &{} \beta _{2}^{*-\frac{1}{\nu }}&{} \ldots &{} \beta _{n}^{*-\frac{1}{\nu }} \\ \end{array} \right) T_{w_{1}}\ldots T_{w_{k}} \end{aligned}$$

implies that $Y_{n:n} \ge _{st} Y_{n:n}^{*};$

(2) for $\beta _{1}=\cdots =\beta _{n}=\beta _{1}^{*}=\cdots =\beta _{n}^{*}=\beta$, $(h({\varvec{p}}), {\varvec{\frac{1}{\alpha }}}) \in {\mathcal {S}}_{n}$ and $(h({\varvec{p}}), {\varvec{\frac{1}{\alpha }}})T_{w_{1}} \ldots T_{w_{i}} \in {\mathcal {S}}_{n},~i=1,\ldots , k-1,$

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}) &{} h(p_{2}) &{}\ldots &{} h(p_{n})\\ \frac{1}{\alpha _{1}} &{} \frac{1}{\alpha _{2}}&{}\ldots &{} \frac{1}{\alpha _{n}} \\ \end{array} \right) = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}^{*}) &{} h(p_{2}^{*}) &{}\ldots &{} h(p_{n}^{*})\\ \frac{1}{\alpha _{1}^{*}} &{} \frac{1}{\alpha _{2}^{*}} &{}\ldots &{} \frac{1}{\alpha _{n}^{*}} \\ \end{array} \right) T_{w_{1}}\ldots T_{w_{k}} \end{aligned}$$

implies that $Y_{n:n} \ge _{st} Y_{n:n}^{*}$. The following example presents a negative answer to this question.

Example 3.9

Consider the setting in Example 3.6, Then:

(1) for $\alpha _{1}=\alpha _{2}=\alpha _{3}=\alpha _{1}^{*}=\alpha _{2}^{*}=\alpha _{3}^{*}=2$, let $(\beta _{1}, \beta _{2}, \beta _{3})=(1/3,1,1/4)$, $(\beta _{1}^{*}, \beta _{2}^{*}, \beta _{3}^{*})=(1/1.78,1/3.342,1/2.878)$, $(p_{1}, p_{2}, p_{3})=(\frac{1}{4},\frac{1}{9},\frac{3}{7})$ and $(p_{1}^{*}, p_{2}^{*}, p_{3}^{*})=(0.148/0.852,0.2372/0.7628,0.2148/0.7852)$. It is then easy to observe that $(\frac{{\varvec{p}}}{1+{\varvec{p}}}, {\varvec{\beta }}^{-1}) \in {\mathcal {S}}_{3}$, $(\frac{{\varvec{p}}}{1+{\varvec{p}}}, {\varvec{\beta }}^{-1})T_{0.4} \in {\mathcal {S}}_{3}$, $(\frac{{\varvec{p}}}{1+{\varvec{p}}}, {\varvec{\beta }}^{-1})T_{0.4}T_{0.3} \in {\mathcal {S}}_{3}$ and $(\frac{{\varvec{p}}^{*}}{1+{\varvec{p}}^{*}}, {\varvec{\beta }}^{*-1})=(\frac{{\varvec{p}}}{1+{\varvec{p}}}, {\varvec{\beta }}^{-1})T_{0.4}T_{0.3}T_{0.1}$. Figure 5 presents the plots of distribution functions of $Y_{3:3}$ and $Y_{3:3}^{*}$ which are seen to cross, which means that $Y_{3:3} \ngeq _{st} Y_{3:3}^{*}$.

(2) for $\beta _{1}=\beta _{2}=\beta _{3}=\beta _{1}^{*}=\beta _{2}^{*}=\beta _{3}^{*}=1.2$, let $(\alpha _{1}, \alpha _{2}, \alpha _{3})=(1,1/4,1/2)$, $(\alpha _{1}^{*}, \alpha _{2}^{*}, \alpha _{3}^{*})=(1/3.28,1/1.492,1/2.228)$, $(p_{1}, p_{2}, p_{3})=(\frac{1}{9},\frac{3}{7}, \frac{1}{4})$ and $(p_{1}^{*}, p_{2}^{*}, p_{3}^{*})=(0.258/0.742,0.1462/0.8538,0.1958/0.8042)$. It is then easy to observe that $(\frac{{\varvec{p}}}{1+{\varvec{p}}}, \frac{1}{{\varvec{\alpha }}}) \in {\mathcal {S}}_{3}$, $(\frac{{\varvec{p}}}{1+{\varvec{p}}}, \frac{1}{{\varvec{\alpha }}})T_{0.4} \in {\mathcal {S}}_{3}$, $(\frac{{\varvec{p}}}{1+{\varvec{p}}}, \frac{1}{{\varvec{\alpha }}})T_{0.4}T_{0.3} \in {\mathcal {S}}_{3}$ and $(\frac{{\varvec{p}}^{*}}{1+{\varvec{p}}^{*}}, \frac{1}{{\varvec{\alpha }}^{*}})=(\frac{{\varvec{p}}}{1+{\varvec{p}}}, \frac{1}{{\varvec{\alpha }}})T_{0.4}T_{0.3}T_{0.1}$. Figure 6 presents the plots of distribution functions of $Y_{3:3}$ and $Y_{3:3}^{*}$ which are seen to cross, which means that $Y_{3:3} \ngeq _{st} Y_{3:3}^{*}$.

Fig. 5

Plots of distribution functions of $Y_{3:3}$ and $Y_{3:3}^{*}$

Fig. 6

Plots of distribution functions of $Y_{3:3}$ and $Y_{3:3}^{*}$

Now, we present the usual stochastic order for the largest order statistics from GBS models with associated random shocks when shape parameters are fixed.

Theorem 3.10

Suppose $X_{1},\ldots , X_{n}$ are independent non-negative random variables with $X_{i}\sim GBS(\alpha , \beta _{i}),$ and $I_{p_{1}},\ldots , I_{p_{n}}$ are independent Bernoulli random variables, independent of $X_{i}$’s, with $E(I_{p_{i}})=p_{i}, ~i=1,\ldots ,n$. Further, suppose $X_{1}^{*},\ldots , X_{n}^{*}$ are independent non-negative random variables with $X_{i}^{*}\sim GBS(\alpha , \beta _{i}^{*})$, and $I_{p_{1}^{*}},\ldots , I_{p_{n}^{*}}$ are independent Bernoulli random variables, independent of $X_{i}^{*}$’s, with $E(I_{p_{i}^{*}})=p_{i}^{*},~i=1,\ldots ,n$. Assume that the following conditions hold:

• (i) $0<\nu \le 2;$

• (ii) r(x) is decreasing in x;

• (iii) $h: [0,1]\rightarrow (0,\infty )$ is differentiable and a strictly decreasing convex function.

If the T-transform matrices $T_{w_{1}}, \ldots , T_{w_{k}}, k>2,$ have different structures, then for $(h({\varvec{p}}), {\varvec{\beta }}^{-\frac{1}{\nu }})T_{w_{1}}\ldots T_{w_{i}} \in {\mathcal {S}}_{n},~i=1,\ldots , k-1,$

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}) &{} h(p_{2}) &{}\ldots &{} h(p_{n})\\ \beta _{1}^{-\frac{1}{\nu }} &{} \beta _{2}^{-\frac{1}{\nu }}&{} \ldots &{} \beta _{n}^{-\frac{1}{\nu }} \\ \end{array} \right) = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h(p_{1}^{*}) &{} h(p_{2}^{*}) &{}\ldots &{} h(p_{n}^{*})\\ \beta _{1}^{*-\frac{1}{\nu }} &{} \beta _{2}^{*-\frac{1}{\nu }}&{} \ldots &{} \beta _{n}^{*-\frac{1}{\nu }} \\ \end{array} \right) T_{w_{1}}\ldots T_{w_{k}} \end{aligned}$$

implies that $Y_{n:n} \ge _{st} Y_{n:n}^{*}$.

Proof

The proof is similar to that of Part (1) of Theorem 3.4, and is therefore not presented here for the sake of conciseness. $\square$