Bankruptcy problems with reference-dependent preferences

Abstract

I study bankruptcy problems under the assumption that claimants have reference-dependent preferences. I consider different specifications for claimants’ reference points and show how perceived gains and losses impact on aggregate welfare. I can thus rank the four most prominent rules (Proportional, Constrained Equal Awards, Constrained Equal Losses, and Talmud) on the basis of the level of utilitarian and maxmin welfare that they generate. I also identify the welfare-maximizing rules and discuss their properties.

1 Introduction

In a bankruptcy problem, an arbitrator must allocate a finite and perfectly divisible resource among several claimants whose claims sum to a greater amount than what is available. Situations that match this description include the liquidation of a bankrupted firm among its creditors, the division of an estate among heirs, or the allocation of time to the completion of projects assigned by different clients.

The formal analysis of bankruptcy problems started with O’Neill (1992) and has flourished since that time (see Moulin 2002; Thomson 2003, 2015 for detailed surveys). The research question that underlies the literature is as follows: how shall the arbitrator adjudicate conflicting claims? The answer usually takes the form of an allocation rule, i.e., a procedure that processes the data of the problem (namely, the endowment of the resource and the list of individual claims) and then prescribes an allocation for the arbitrator to implement. The analysis is pursued under the assumption that claimants have monotonically increasing preferences. However, the specific functional form of these preferences is usually left unspecified. As Thomson puts it (2015, p. 57): “In the base model, preferences are not explicitly indicated, but it is implicit that each claimant prefers more of the dividend to less”.

In this paper, I study bankruptcy problems when claimants’ preferences have an explicit formulation. More precisely, I consider the case of reference-dependent preferences (RDPs), as introduced by Kőszegi and Rabin (2006). Building upon the main insights of prospect theory (Kahneman and Tversky 1979), RDPs acknowledge the fact that an agent’s perception of a given outcome is determined not only by the outcome per se but also by how this outcome compares with a certain reference point. In other words, the agent’s utility is influenced by perceived gains and losses. RDPs thus seem particularly appropriate for use in capturing the preferences of claimants in bankruptcy problems. These are, in fact, typical situations in which agents form expectations about what they will get and then inevitably compare the actual outcome with the expected one.

The idea that reference points might play a role in bankruptcy problems is not new. Chun and Thomson (1992) studied a bargaining problem with claims and interpret the disagreement point as a reference point from which agents measure their gains when evaluating a proposal. Herrero (1998) adopts a similar framework but endogenizes the reference point as a function of the agents’ claims and the set of feasible allocations. Pulido et al. (2002, 2008) study bankruptcy problems with reference points in the context of university budgeting procedures. Finally, Hougaard et al. (2012, 2013a, b) consider a more general model of rationing in which agents have claims as well as baselines, which can also be interpreted as reference points. All these papers, however, analyze the role of reference points in a context in which claimants have standard preferences.

I instead embed the analysis of reference points into the framework of RDPs and focus on the welfare implications that such a setting generates. I consider different specifications for claimants’ reference points. This reflects the role that expectations have in determining reference points (Abeler et al. 2011; Ericson and Fuster 2011) and the fact that in a bankruptcy problem there are multiple allocations that can catalyze claimants’ expectations. I thus let the vector that collects agents’ reference points to coincide with the claims vector, the zero awards vector, the minimal rights vector, and with their beliefs about the awards vector that the arbitrator will implement.

The actual feasibility of these reference points paired with some specific features of RDPs impact on how different rules perform in terms of (utilitarian and maxmin) welfare. For instance, when reference points are not feasible and claimants display diminishing marginal sensitivity to losses, the rules that achieve higher welfare are those that most asymmetrically allocate perceived losses across agents. In the opposite scenario, diminishing marginal sensitivity to gains implies that, when agents’ reference points are mutually feasible, the best rules are those that implement the most equal distributions of perceived gains.

Given any specification of agents’ reference points, I can thus rank the four most common rules (Proportional, Constrained Equal Awards, Constrained Equal Losses, and Talmud) in terms of welfare. The Constrained Equal Awards rule often outperforms other rules. It may, however, fail to select the first-best allocation. When this is the case, I define the rule that maximizes welfare and discuss its properties. The Small Claims First rule maximizes utilitarian welfare when claimants use their claims as reference points (Proposition 1) and always selects the less unequal awards vector in case of multiple solutions (Proposition 2). By relying on some new axioms, I am able to fully characterize the set of rules that lead to a welfare-maximizing solution (Proposition 3) and, in particular, the Small Claims First rule (Proposition 4). The Minimal Utility Gap rule instead maximizes maxmin welfare when reference points are given by agents’ claims (Proposition 5) or by their minimal rights (Proposition 8). The Constrained Equal Gains rule is optimal when agents use as reference points their minimal rights and the arbitrator cares about utilitarian welfare (Proposition 7). And, as said, there are scenarios in which the optimal rule is the Constrained Equal Awards rule. This is the case when claimants’ reference points coincide with the zero awards vector (Proposition 6) or are determined by their expectations about what the arbitrator will do (Proposition 9).

The analysis highlights the existence of a trade-off between the goal of welfare maximization and the equity of the resulting award vector. This is most evident when agents use their claims as reference points, as in this case at least some of the claimants must necessarily receive less than what they were expecting. The optimal rule (the Small Claims First rule) then prescribes the arbitrator to satisfy as many claimants as possible (i.e., to allocate them what they claim) while heavily disappointing the remaining ones. I show that the rule fails Equal Treatment of Equals, although it satisfies a weaker notion of equity, as embedded in a property that I label Ex-Ante Equal Treatment of Equals. Giving up Boundedness further amplifies the tension between welfare maximization and equity. Because losses loom larger than gains, welfare maximization may in fact require the arbitrator to allocate to some of the claimants more than their claims. This would, however, lead to an even more skewed distribution of the endowment. In particular, it may hinder some of the claimants from obtaining their minimal rights.

2 The model

2.1 A bankruptcy problem

Let $E\in \mathbb {R}_{+}$ denote the endowment of the resource to be allocated and $N=\left\{ 1,...,n\right\}$ be the set of claimants. Each claimant $i\in N$ has a claim $c_{i}\in \mathbb {R}_{+}$ on E. The vector $c=\left( c_{1},...,c_{n}\right)$ collects individual claims. Define $C=\sum \nolimits _{i}c_{i}$. A bankruptcy problem (or claims problem) is a pair $\left( c,E\right) \in \mathbb {R}_{+}^{N}\times \mathbb {R}_{+}$ where c is such that $C\ge E$. I denote with $\mathbb {B}^{N}$ the class of all such problems. By defining as $L=C-E$ the aggregate loss, $\left( c,L\right)$ is the dual of $\left( c,E\right)$. In other words, one can interpret a bankruptcy problem as a problem of allocating what is available (i.e., shares of E), or as a problem of allocating what is missing (i.e., shares of L).¹

A ruleR is a function that associates to any problem $\left( c,E\right) \in \mathbb {B}^{N}$ a unique awards vector $R\left( c,E\right) =\left( R_{1}\left( c,E\right) ,...,R_{n}\left( c,E\right) \right)$. The awards vector R(c, E) must satisfy $0 \le R_{i}\left( c,E\right) \le c_{i}$ for any $i\in N$ (Boundedness) and $\sum _{i}R_{i}\left( c,E\right) =E$ (Balance).

The literature has characterized a large number of rules that respond to different ethical or procedural criteria (see Thomson 2015, for a review). I first introduce the four most prominent rules (Herrero and Villar 2001; Bosmans and Lauwers 2011):

• The Proportional (P) rule allocates the endowment proportional to claims:

  $$\begin{aligned} P\left( c,E\right) =\lambda c\text { with }\lambda =E/C. \end{aligned}$$

  (1)

• The Constrained Equal Awards (CEA) rule assigns equal awards to all claimants subject to the requirement that no one receives more than his claim:

  $$\begin{aligned} CEA_{i}\left( c,E\right) =\min \left\{ c_{i},\lambda \right\} \text {for all } i\in N\text { with }\sum \nolimits _{i}\min \left\{ c_{i},\lambda \right\} =E. \end{aligned}$$

  (2)

• The Constrained Equal Losses (CEL) rule assigns an equal amount of losses to all claimants subject to the requirement that no one receives a negative amount:

  $$\begin{aligned} CEL_{i}\left( c,E\right) =\max \left\{ 0,c_{i}-\lambda \right\} \text { for all }i\in N\text { with }\sum \nolimits _{i}\max \left\{ 0,c_{i}-\lambda \right\} =E. \end{aligned}$$

  (3)

• The Talmud (T) rule, as introduced by Aumann and Maschler (1985), foresees two different solutions depending upon the relationship between the half-sum of the claims and the endowment:

  $$\begin{aligned} \begin{aligned} T(c,E)&=CEA\left( \frac{1}{2}c,E\right) \text { if } \frac{C}{2}\ge E, \\ T(c,E)&=\frac{1}{2}c+CEL\left( \frac{1}{2}c,E-\frac{C}{2}\right) \text { if } \frac{C}{2}<E. \end{aligned} \end{aligned}$$

  (4)

I then introduce four new rules whose properties I will explore in the course of the analysis. The first two rules belong to the family of sequential priority rules (Moulin 2000; Thomson 2015). Let $\preceq$ denote an order on the set of claimants, i.e., a complete and transitive binary relation on N. The strict relation $\prec$ associated with $\preceq$ is defined as usual: $i\prec j$ iff $i\preceq j$ but not $j\preceq i$. The sequential priority rule associated with $\preceq$ assigns to each agent the minimum between his claim and what remains of the endowment. The rules that I propose are based on the strict order $\prec _{c }$ that orders claimants according to their claims and starting from the lowest (ties are broken randomly).

• The Small Claims First ($SCF^{\prec _{c}}$) rule assigns to each agent the minimum amount between his claim and what remains of the endowment, starting from the first:

  $$\begin{aligned} SCF^{\prec _{c}}_{i}(c,E)=\min \left\{ c_{i},\max \left\{ E-\sum _{j\prec _{c}i}c_{j},0\right\} \right\} \quad \text { for all }i\in N. \end{aligned}$$

  (5)

• The Large Claims First ($LCF^{\prec _{c}}$) rule assigns to each agent the minimum amount between his claim and what remains of the endowment, starting from the last:

  $$\begin{aligned} LCF^{\prec _{c}}_{i}(c,E)=\min \left\{ c_{i},\max \left\{ \sum _{j\preceq _c i}c_{j} - L,0\right\} \right\} \quad \text { for all }i\in N. \end{aligned}$$

  (6)

The third rule combines the order $\prec _{c }$ with the notion of agents’ minimal rights. The minimal right of agent i ($m_{i}$) is given by what remains of the endowment (if anything) after all other agents get their claims fully honored. Formally, $m_{i}=\max \left\{ E-\sum \nolimits _{j\ne i}c_{j},0\right\}$.²

• The Constrained Equal Gains ($CEG^{\prec _{c}}$) rule assigns to each agent $i \in N$ the amount:

  $$\begin{aligned} CEG^{\prec _{c}}_{i}(c,E)=\min \left\{ c_{i},m_{i}+\frac{E- \sum _{j \succeq _c i} m_j-\sum _{j \prec _c i}CEG^{\prec _{c}}_j}{n-i+1} \right\} \quad \text { for all }i\in N. \end{aligned}$$

  (7)

The fourth rule (actually, a family of rules) relies instead on claimants’ utility functions. Let $u=(u_1(R_1(c,E)),... ,u_n(R_n(c,E)))$ denote a utility profile (I will introduce and discuss a more precise functional form for $u_i(\cdot )$ in Sect. 2.2).

• The Minimal Utility Gap ($MUG^{u}$) rule allocates the endowment such as to make agents’ utility as equal as possible:

  $$\begin{aligned} MUG^{u}(c,E)={{\mathrm{argmin}}}\{\max \{u_i(MUG^u_i(c,E))\}_{i} - \min \{u_i(MUG^u_i(c,E))\}_{i}\}. \end{aligned}$$

  (8)

Example 1 shows how the rules works in practice.

Example 1

Let $c=(30,50,80)$ and $E=100$. The rules select the following awards vectors: $P(c,E) = (18.75,31.25,50)$, $CEA(c,E) = (30,35,35)$, $CEL(c,E) = (10,30,60)$, $T(c,E) = (15,27.5,57.5)$, $SCF^{\prec _{c}}(c,E) = (30,50,20)$, $LCF^{\prec _{c}}(c,E) = (0,20,80)$, $CEG^{\prec _{c}}(c,E) = (26.67,26.67,46.66)$, and $MUG^{u}(c,E) = (54.55,27.27,18.18)$.³

Figure 1 instead illustrates the path of awards of the rules. The path of awards is the locus of allocations that a rule selects as, holding fixed the claim vector c, the endowment E grows from 0 to C.

Fig. 1

Paths of awards with $n=2$ [when $n=2$ the T(c, E) and the $CEG^{\prec _{c}}(c,E)$ solutions coincide. However, this is not generally the case (see Example 1). The $MUG^{u}(c,E)$ solution refers to the case $u=\left( R_1(c,E),3R_2(c,E) \right)$]

Next, I introduce four axioms that I will later use to describe the properties of the new rules. The first axiom is a weaker form of Equal Treatment of Equals. It says that agents with identical claims should get identical awards in expectations.

Ex-Ante Equal Treatment of Equals. For all $\left( c,E\right) \in \mathbb {B}^{N}$ and all $i,j\in N$, if $c_{i}=c_{j}$ then $\mathbb {E} \left( R_{i}\left( c,E\right) \right) =\mathbb {E} \left( R_{j}\left( c,E\right) \right)$.

The next three axioms use instead the notion of claimants i’s Cumulative Aggregate Loss, which measures the amount by which the sum of the claims of i and of all his predecessors exceeds the endowment.

Definition 1

Given the order $\prec _{c}$ defined on N, the Cumulative Aggregate Loss of claimant $i \in N$ is given by $\tilde{L}_i= \max \left\{ \sum _{j\preceq _{c}i}c_{j} - E,0 \right\}$.

The Large Losers axiom states that if the Cumulative Aggregate Loss of an agent is larger or equal than his claim, then the agent should get nothing.

Large Losers. For all $\left( c,E\right) \in \mathbb {B}^{N}$ if $\tilde{L}_i \ge c_i$ then $R_{i}\left( c,E\right) =0$.

The Unique Residual Loser axiom states that if the Cumulative Aggregate Loss of agent i is positive but smaller than his claim, then a unique agent (either agent i or one of his predecessors) must suffer that loss in full.

Unique Residual Loser. For all $\left( c,E\right) \in \mathbb {B}^{N}$, if there exists a claimant $i \in N$ such that $0< \tilde{L}_i < c_i$ then there exists a claimant $j \preceq _{c} i$ such that $R_{j}\left( c,E\right) =c_j-\tilde{L}_i$.

Finally, Unique Residual Loser Is The Last strengthens Unique Residual Loser by requiring that if the Cumulative Aggregate Loss of agent i is positive but smaller than his claim, it is actually agent i the unique agent who suffers that loss in full.

Unique Residual Loser Is The Last. For all $\left( c,E\right) \in \mathbb {B}^{N}$, if there exists a claimant $i \in N$ such that $0< \tilde{L}_i < c_i$ then $R_{i}\left( c,E\right) =c_i-\tilde{L}_i$.

2.2 Claimants’ preferences and social welfare

I deviate from the baseline model of a bankruptcy problem by assuming that claimants have reference-dependent preferences (RDPs). I adopt the specification originally proposed by Kőszegi and Rabin (2006) (see Shalev 2000, for an alternative approach).

Let $r_{i} \in [0,c_i]$ denote agent i’s reference point, whose nature I will shortly discuss. The gain-loss function $\mu ( R_{i}\left( c,E\right) -r_{i})$ then captures the (psychological) effects of perceived gains and losses when an agent who was expecting to get $r_{i}$ receives the amount $R_{i}\left( c,E\right)$. In line with the original formulation of prospect theory (Kahneman and Tversky 1979), the function $\mu (\cdot )$ is assumed to be continuous, strictly increasing and such that $\mu (0)=0$. It is is strictly convex in the domain of losses ($\mu ^{\prime \prime }(z)>0$ for any $z<0$) and strictly concave in the domain of gains ($\mu ^{\prime \prime }(z)>0$ for any $z<0$). Finally, losses loom larger than gains: $\left| \mu (-z)\right| >\mu (z)$ for any $z>0$.

Claimants’ utility function thus reads as follows:

$$\begin{aligned} u( R_{i}\left( c,E\right) \mid r_{i})= R_{i}\left( c,E\right) +\mu ( R_{i}\left( c,E\right) -r_{i}), \end{aligned}$$

(9)

The utility that the agent enjoys from the possession/consumption of $R_{i}\left( c,E\right)$ is thus linear, as it is usually assumed in the baseline model.⁴ However, his overall utility is also influenced by the $\mu (\cdot )$ function.⁵

I rely on the two most common notions of welfare (see Moulin 2003; Gravel and Moyes 2013): utilitarian welfare (10) and maxmin welfare (11).

$$\begin{aligned} W_{ut}\left( R \right)= & {} \sum \nolimits _{i}\left( R_{i}\left( c,E\right) +\mu (R_{i}\left( c,E\right) -r_{i})\right) \nonumber \\= & {} E+\sum \nolimits _{i}\mu (R_{i}\left( c,E\right) -r_{i}), \end{aligned}$$

(10)

$$\begin{aligned} W_{mm}\left( R \right)= & {} \min \left\{ R_{i}\left( c,E\right) +\mu (R_{i}\left( c,E\right) -r_{i})\right\} _{i}. \end{aligned}$$

(11)

Both notions explicitly take into account the “behavioral” part of claimants’ utility functions, namely the gain-loss function $\mu (\cdot )$. The approach is in line with the recent literature on behavioral welfare economics (see Bernheim and Rangel 2007, 2009; Fleurbaey and Schokkaert 2013, for a general discussion of the issue; see Gruber and Kőszegi 2004; O’Donoghue and Rabin 2006, for more specific applications) and fits the situations that motivate the paper. For instance, a politician who must distribute a limited amount of public funds to different associations and cares about his chances of being reelected will certainly take into account how different allocations impact on claimants’ degree of satisfaction/disappointment. Similarly, an agent who must allocate his time to the completion of different projects and cares about future collaborations with his clients must carefully consider which are the ones to please and the ones to disappoint.

Clearly, the four standard rules are welfare equivalent when all agents have identical claims ($c_{i} = c_{j}$ for all $i,j\in N$). All rules in fact select the egalitarian allocation, $R_{i}(c,E)=E / n$ for all $i \in N$. Therefore, in what follows I mainly focus on the more interesting case in which claimants are asymmetric, i.e., the vector of claims c is such that $c_{i}\ne c_{j}$ for some $i,j\in N$.

3 Reference points

Claimants’ utility function is given by Eq. (9). Here I discuss the nature of agents’ reference points $r=(r_1,..., r_n)$. I consider different specifications for r. In Sect. 3.1, I study the case in which agents’ reference points coincide with their claims, $r=c$. In Sect. 3.2, I consider the opposite case where agents set as reference points the zero awards vector, $r=\mathbf 0$. As a third possibility (Sect. 3.3), I let $r=m$ where $m=\{m_1, ..., m_n\}$ is the vector that collects agents’ minimal rights. Finally (Sect. 3.4), I study a setting in which reference points are given by claimants’ beliefs about the awards vector that the arbitrator will implement. Formally, $r=F$ where F is a probability distribution defined over the set of possible allocations.

The four specifications can be classified according to different criteria. For instance, one may focus on the relation between reference points and claims. This can be direct ($r=c$), indirect ($r=m$ and $r=F$, as claims influence agents’ minimal rights and beliefs), or non existing ($r=\mathbf 0$). Alternatively, one may describe the various reference points according to the level of optimism embedded in claimants’ expectations. The case $r=c$ is thus maximally optimistic, $r=F$ can be classified as neutral, $r=m$ is mildly pessimistic, and $r=\mathbf 0$ is maximally pessimistic.

Finally, one may consider the feasibility of the vector r and its implications on the resulting allocations and on agents’ perceived gains and losses. If $r=c$, awards vectors will inevitably generate some losses at the individual level; if instead $r=\mathbf 0$ or $r=m$, awards vectors that lead all claimants to perceive some gains are feasible; and both gains and losses are possible when $r=F$. RDPs then imply that the welfare-maximizing allocations are such that no agent receives an amount larger than $r_i$ when reference points cannot be matched (unless one is willing to give up Boundedness, see Sect. 4.2), whereas each agent receives at least $r_i$ when reference points are feasible.⁶

3.1 Claims as reference points

Let agents’ reference points be determined by their claims. Formally, let $r=c$. The use of claims as reference points can be rationalized in different ways. For instance, agents may not be fully aware that they are involved in a bankruptcy problem and that rationing must thus necessarily take place. Alternatively, they may know that the endowment is not enough to satisfy aggregate demand, yet they may think, perhaps erroneously, that they have or deserve priority with respect to others. Claims are thus interpreted as an expression of agents’ rights, needs, demands, or aspirations (Mariotti and Villar 2005).

3.1.1 Utilitarian welfare analysis

Proposition 1 ranks the Proportional rule, the Constrained Equal Awards rule, the Constrained Equal Losses rule, and the Small Claims First rule on the basis of the level of utilitarian welfare that they generate. The ranking holds because the rules differ on how they allocate the aggregate loss across claimants. Since agents display diminishing marginal sensitivity to losses, differences in the allocation of individual losses lead to differences in welfare.

Proposition 1

The ranking $W_{ut}(SCF^{\prec _{c}}) \ge W_{ut}(CEA)>W_{ut}(P)>W_{ut}(CEL)$ holds in any bankruptcy problem $(c,E)\in \mathbb {B}^{N}$ in which claimants have RDPs, $r=c$, and $c_{i}\ne c_{j}$ for some $i,j\in N$. In particular, the $SCF^{\prec _{c}}$ rule achieves maximal utilitarian welfare.

Since the Talmud rule is a combination of the CEA and the CEL rules and the latter achieves minimal welfare (see the proof of Proposition 1 in the “Appendix”), its performance in terms of utilitarian welfare falls in the middle. In particular, $W_{ut}(T)\in \left[ W_{ut}(CEL),W_{ut}(P)\right]$ when $\frac{C}{2}<E$, whereas $W_{ut}(T)\in \left[ W_{ut}(P),W_{ut}(CEA)\right]$ when $\frac{C}{2}\ge E$. The following example illustrates all these results.

Example 2

Let claimant $i \in \left\{ 1,2 \right\}$ have utility function

$$\begin{aligned} u(R_{i}\left( \cdot \right) \mid r_{i}=c_{i})=\left\{ \begin{array}{ll} R_{i}\left( \cdot \right) +\sqrt{R_{i}\left( \cdot \right) -c_{i}} &{} if~ R_{i}\left( \cdot \right) \ge c_{i} \\ R_{i}\left( \cdot \right) -3\sqrt{\left| R_{i}\left( \cdot \right) -c_{i}\right| } &{} if~ R_{i}\left( \cdot \right) <c_{i}, \end{array} \ \right. \end{aligned}$$

and consider the bankruptcy problems: (a) $c=(60,90)$, $E=100$; and (b) $c=(60,90)$, $E=70$.

• (a) Awards vectors are $P(c,E)=\left( 40,60\right)$, $CEA(c,E)=(50,50)$, $CEL(c,E)=T(c,E)=(35,65)$, and $SCF^{\prec _{c}}(c,E)=(60,40)$. Therefore, $W_{ut}(SCF^{\prec _{c}})>W_{ut}(CEA)>W_{ut}(P)>W_{ut}(CEL)=W_{ut}(T)$. See Fig. 2a.

• (b) Awards vectors are $P(c,E)=\left( 28,42\right)$, $CEA(c,E)=(35,35)$, $CEL(c,E)=(20,50)$, $T(c,E)=(30,40)$, and $SCF^{\prec _{c}}(c,E)=(60,10)$. Therefore, $W_{ut}(SCF^{\prec _{c}})>W_{ut}(CEA)>W_{ut}(T)>W_{ut}(P)>W_{ut}(CEL)$. See Fig. 2b.

Fig. 2

Utilitarian welfare when $r=c$

The $SCF^{\prec _{c}}$ rule thus dominates standard rules in terms of utilitarian welfare.⁷ Indeed, claimants’ diminishing sensitivity to losses implies that, from a purely utilitarian point of view, it is more efficient to largely disappoint a subset of agents rather than to slightly disappoint all of them. By construction, the $SCF^{\prec _{c}}$ rule does exactly that: it matches the claims of as many claimants as possible and disappoints the remaining ones as much as possible.

The awards vector $SCF^{\prec _{c}}(c,E)$ may not be the sole allocation that maximizes welfare.⁸ For instance, when there are only two claimants and $\max \left\{ c_{1},c_{2}\right\} \le E$ then there always exist two optimal allocations (see Fig. 2a). However, when multiple solutions exist, the $SCF^{\prec _{c}}$ rule selects a specific welfare-maximizing allocation.

Proposition 2

Whenever there exist multiple awards vectors that maximize utilitarian welfare, the $SCF^{\prec _{c}}$ rule selects the one with the lowest level of inequality.

The $SCF^{\prec _{c}}$ rule satisfies a number of standard axioms: Endowment Monotonicity, Scale Invariance, Path Independence, Consistency, Composition, and Order Preservation in Losses.⁹ It fails Claims Monotonicity and Order Preservation in Gains. More importantly, it fails Equal Treatment of Equals.

The analysis thus highlights a tension between the maximization of utilitarian welfare and the equity of the resulting awards vector.¹⁰ As such, the $SCF^{\prec _{c}}$ rule may not be palatable to an arbitrator who wants to be impartial and treat symmetric claimants in the same way. The $SCF^{\prec _{c}}$ rule is, however, procedurally fair (Bolton et al. 2005). In determining the priority order, ties among agents with the same claims are broken randomly so that the rule allocates the same expected award to identical claimants.¹¹ Indeed, the $SCF^{\prec _{c}}$ rule satisfies Ex-Ante Equal Treatment of Equals. Furthermore, there are situations in which an arbitrator should indeed discriminate across agents, even though their claims are symmetric. For instance, there may be differences among agents that are not captured by their claims but rather stem from individual characteristics (e.g., age, gender), exogenous rights, or merits (Moulin 2000). In these circumstances, the $SCF^{\prec _{c}}$ rule may be appropriate to guide the choice of an arbitrator who wants to minimize the aggregate level of disappointment (i.e., the negative impact that perceived losses have on welfare).

The new axioms that I introduced in Sect. 2 allow for a characterization of the set of rules that maximize utilitarian welfare (Proposition 3) and, specifically, of the $SCF^{\prec _{c}}$ rule (Proposition 4). Example 3 then illustrates the bite of the axioms.

Proposition 3

In any bankruptcy problem $(c,E)\in \mathbb {B}^{N}$ in which claimants have RDPs and $r=c$, a rule maximizes utilitarian welfare if and only if it satisfies Large Losers and Unique Residual Loser.

Proposition 4

In any bankruptcy problem $(c,E)\in \mathbb {B}^{N}$ in which claimants have RDPs and $r=c$, the $SCF^{\prec _{c}}$ rule is the only rule that satisfies Large Losers and Unique Residual Loser Is The Last.

Example 3

Consider the problem $\left( c,E\right)$ with $c=(10,20,40,50,60,80)$ and $E=100$. The vector of Cumulative Aggregate Losses is given by $\tilde{L}=(0,0,0,20,80,160)$. Large Losers thus selects all the awards vectors such that $(\cdot ,\cdot ,\cdot ,\cdot ,0,0)$. Unique Residual Loser further refines the set of awards vectors to $R(c,E)=(10,20,40,30,0,0)$, $R^{\prime }(c,E)=(10,20,20,50,0,0)$, and $R^{\prime \prime }(c,E)=(10,0,40,50,0,0)$. These are the vectors that maximize utilitarian welfare with $W_{ut}( \cdot )=100+\mu (-20)+\mu (-60)+\mu (-80)$. By substituting Unique Residual Loser with Unique Residual Loser Is The Last one gets the unique vector $R(c,E)=(10,20,40,30,0,0)$, which is the $SCF^{\prec _{c}}$ solution.

3.1.2 Maxmin welfare analysis

If the arbitrator adopts a maxmin welfare specification, the optimal allocation is the one that maximizes the utility of the worst-off individual. With no constraints on the awards vector, this allocation would then be the one that equalizes claimants’ utility. However, Boundedness may sometimes make such an allocation unfeasible, so that it is the Minimal Utility Gap rule (see (8)) the rule that maximizes maxmin welfare.¹²

Proposition 5

The $MUG^u$ rule maximizes maxmin welfare in any bankruptcy problem

$(c,E)\in \mathbb {B}^{N}$ in which claimants have RDPs and $r=c$.

The $MUG^u$ rule satisfies Equal Treatment of Equals (assuming that agents are identical also in terms of utility functions), Endowment Monotonicity, Claims Monotonicity, and Consistency. It fails Scale Invariance, Order Preservation in Gains, Order Preservation in Losses, Path Independence, and Composition.

Although the awards vector $MUG^u(c,E)$ depends on the utility profile u, it is anyway possible to infer some of its general features. Since claimants use their claims as reference points, their utility is given by

$$\begin{aligned} u(MUG^u_i(c,E))=MUG^u_i(c,E)+\mu (MUG^u_i(c,E)-c_{i}), \end{aligned}$$

so that utility depends positively on the amount of the endowment that the claimant receives, and negatively on his claim. The optimal allocation trades off these two effects across agents. With respect to the egalitarian allocation, the $MUG^u$ rule thus assigns more of the endowment to agents who have higher claims. The size of these distortions increases with the relevance that perceived losses have on claimants’ overall utility. If perceived losses have limited effects (i.e., the agent’s well-being is mainly determined by the actual amount of the endowment that he receives from the arbitrator) then the CEA rule, by allocating the endowment across agents as equally as possible, will outperform other standard rules.¹³ If instead perceived losses have a large effect on individual utilities, distortions become sizable and can modify the ranking between the CEA rule and the other rules. The following example illustrates these results.

Example 4

Let claimant $i \in \left\{ 1,2 \right\}$ have utility function

$$\begin{aligned} u(R_{i}\left( \cdot \right) \mid r_{i}=c_{i})=\left\{ \begin{array}{ll} R_{i}\left( \cdot \right) +\sqrt{R_{i}\left( \cdot \right) -c_{i}} &{} if~ R_{i}\left( \cdot \right) \ge c_{i} \\ R_{i}\left( \cdot \right) -3\sqrt{\left| R_{i}\left( \cdot \right) -c_{i}\right| } &{} if~ R_{i}\left( \cdot \right) <c_{i}, \end{array} \ \right. \end{aligned}$$

and consider the bankruptcy problems: (a) $c=(60,90)$, $E=100$ and (b) $c=(60,90)$, $E=70$.

• (a) Awards vectors are $P(c,E)=(40,60)$, $CEA(c,E)=(50,50)$, $CEL(c,E)=T(c,E)=(35,65)$, and $MUG^u(c,E) \approx (46.5,53.5)$. Thus, $W_{mm}(MUG^u)>W_{mm}(CEA)>W_{mm}(P)>W_{mm}(CEL)=W_{mm}(T)$. See Fig. 3a.

• (b) Awards vectors are $P(c,E)=(28,42)$, $CEA(c,E)=(35,35)$, $CEL(c,E)=(20,50)$, $T(c,E)=(30,40)$, and $MUG^u(c,E) \approx (32.1,37.9)$. Therefore, $W_{mm}(MUG^u)>W_{mm}(T)>W_{mm}(CEA)>W_{mm}(P)>W_{mm}(CEL)$.¹⁴ See Fig. 3b.

Fig. 3

Maxmin welfare when $r=c$

3.2 Zero awards as reference point

Let agents have null reference points ($r=\mathbf 0$). The setting is appropriate to describe all those situations in which agents do have claims on the endowment E but still consider them to be worthless, perhaps because they think that there is nothing to share (i.e., $E=0$). Examples include the case of creditors who expect the bankrupted firm not to have any asset left, or heirs who are not aware of the deceased’s net worth. Claimants are then pleasantly surprised whenever they receive an award $R_{i}(c,E) > 0$. The relevant part of the $\mu (\cdot )$ function is thus the domain of gains as each agent experiences a perceived gain of size $g_{i}=R_{i}(c,E)-0 \ge 0$.

3.2.1 Utilitarian and maxmin welfare analysis

Since agents are now perfectly symmetric (they all have the same reference point) and RDPs postulate diminishing marginal sensitivity to gains, the rules that select the most egalitarian awards vectors achieve higher levels of welfare. Proposition 6 ranks the P, CEA, and CEL rules. The CEA rule not only dominates the other rules, it actually implements the first-best solution under both welfare specifications.

Proposition 6

The ranking $W_{w}(CEA)>W_{w}(P)>W_{w}(CEL)$ with $w \in \left\{ ut,mm \right\}$ holds in any bankruptcy problem $(c,E)\in \mathbb {B}^{N}$ in which claimants have RDPs, $r=\mathbf 0$, and $c_{i}\ne c_{j}$ for some $i,j\in N$. In particular, the CEA rule achieves maximal (utilitarian and maxmin) welfare.

The performance of the Talmud rule is such that $W_{w}(T)\in \left[ W_{w}(CEL),W_{w}(CEA)\right]$ for any $w \in \left\{ ut,mm \right\}$, with $W_{w}(T) < W_{w}(P)$ if $\frac{C}{2}<E$ and $W_{w}(T) \ge W_{w}(P)$ if $\frac{C}{2}\ge E$.

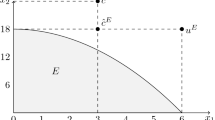
3.3 Minimal rights as reference points

Consider now the case in which agents’ reference points are determined by their minimal rights. A claimant’s minimal right is given by what remains of the endowment (if anything) after all other agents get their claims fully honored. The minimal right of agent i can thus be interpreted as the minimum amount that i can reasonably expect to get (Thomson and Yeh 2008). Formally, let $r=m$ where $m=(m_1,...,m_n)$ and $m_{i}=\max \left\{ E-\sum \nolimits _{j\ne i}c_{j},0\right\}$ for any $i \in N$. Clearly, if $m=0$ the problem is analogous to the one analyzed in Sect. 3.2 and thus Proposition 6 applies. I thus focus on the situation in which the vector m is such that $m_{i}>0$ for some $i \in N$.

3.3.1 Utilitarian welfare analysis

It is always possible for the arbitrator to implement an allocation that matches (and possibly trespasses) the minimal rights of all the claimants.¹⁵ Because of the properties of the $\mu ( \cdot )$ function (losses loom larger than gains), such an allocation will be welfare superior to any allocation in which $R_{i}(c,E) < m_i$ for some $i \in N$.

Every claimant $i \in N$ will thus experience a perceived gain of size $g_{i}=R_{i}(c,E) - m_i \ge 0$. The diminishing marginal sensitivity to gains of $\mu ( \cdot )$ then implies that the optimal utilitarian allocation is the Constrained Equal Gains rule (see (7)), since this is the rule that minimizes the variance of the vector $g=\left( R(c,E)-m \right)$. No clear ranking of the P, CEA, CEL, and T rules instead exists.

Proposition 7

The $CEG^{\prec _{c}}$ rule maximizes utilitarian welfare in any bankruptcy problem $(c,E)\in \mathbb {B}^{N}$ in which claimants have RDPs and $r=m \ge 0$.

The $CEG^{\prec _{c}}$ rule satisfies Equal Treatment of Equals, Endowment Monotonicity, Claims Monotonicity, Order Preservation in Gains, Order Preservation in Losses, Scale Invariance, and Path Independence. It fails Consistency and Composition.

3.3.2 Maxmin welfare analysis

If the arbitrator follows maxmin welfare, the Minimal Utility Gap ($MUG^u$) rule (see 8) is the optimal rule.

Proposition 8

The $MUG^u$ rule maximizes maxmin welfare in any problem $(c,E)\in \mathbb {B}^{N}$ in which claimants have RDPs and $r=m$.

With respect to the egalitarian allocation, the $MUG^u$ rule allocates more of the endowment to claimants who have higher minimal rights. The intuition is that these agents will experience lower perceived gains and must thus be compensated with a relatively higher allocation of the endowment. As it was the case in Sect. 3.1, if the relevance of perceived gains is limited then the awards vector $MUG^u(c,E)$ will be close to the egalitarian allocation. Thus, the CEA rule will outperform other standard rules. Different rankings can instead emerge when the impact of perceived gains on claimants’ total utility is sizable.¹⁶

3.4 Expected awards as reference points

As a last specification, I let claimants’ reference points be determined by their expectations about what the arbitrator will do. Say that claimants hold (common) beliefs about final outcomes, i.e., about the awards vector (analogously, the rule) that the arbitrator will select. These beliefs are described by the probability distribution F defined over the set of vectors $V=\{P(c,E),CEA(c,E),CEL(c,E),T(c,E)\}$ and with density f.

Following Kőszegi and Rabin (2007), I let claimants’ reference points coincide with their beliefs. Formally, $r=F$. A claimant’s evaluation of a given award $R_{i}\left( c,E\right) \in V$ is thus given by:

$$\begin{aligned} U( R_{i}\left( c,E\right) \mid r=F)= \int u( R_{i}\left( c,E\right) \mid v_i) \quad dF(v), \end{aligned}$$

(12)

where $v \in V$ and $u( R_{i}\left( c,E\right) \mid v_i)$ is as defined in (9). The formulation thus considers how $R_{i}\left( c,E\right)$ compares with all the possible alternatives in V.¹⁷

I first consider the case of F being a degenerate probability distribution, so that $f(v)=1$ for some $v \in V$. Claimants thus expect the arbitrator to implement a specific awards vector, perhaps because the latter publicly announced the rule that he intends to use or built a reputation for always using a certain rule. I then let F be a non-degenerate distribution, so that claimants are indeed uncertain about what the arbitrator will do.¹⁸

3.4.1 Utilitarian welfare analysis

If agents expect the arbitrator to implement the award vector R(c, E), then it is indeed R the rule that maximizes utilitarian welfare. The intuition is that if claimants have correct expectations about what the arbitrator will do they will experience no perceived gains or losses. Because of the properties of the $\mu ( \cdot )$ function, the award vector R(c, E) thus dominates any alternative allocation that does not match claimants’ expectations. It is thus welfare improving for the arbitrator to communicate (or to build a reputation for) which rule he will adopt.

If the distribution F is non-degenerate results are less clear-cut. By continuity, generic rule $R \in \{P,CEA,CEL,T\}$ remains the optimal rule when claimants are reasonably confident that the arbitrator will use it (i.e., f(R(c, E)) is high enough). When instead agents’ beliefs are more diffuse, the rule that maximizes welfare varies depending on the parameters of the problem. To see this, note that rules R and $R'$ generate utilitarian welfare:

$$\begin{aligned} W_{ut}(R)= & {} E + \sum \nolimits _{i \in N} \left( \int \mu ( R_{i}\left( c,E\right) - v) \quad dF(v) \right) , \end{aligned}$$

(14)

$$\begin{aligned} W_{ut}(R')= & {} E + \sum \nolimits _{i \in N} \left( \int \mu ( R'_{i}\left( c,E\right) - v) \quad dF(v) \right) , \end{aligned}$$

(15)

where $v \in V$ and $\mu (\cdot )=0$ for $v=R_i(c,E)$ and $v=R'_i(c,E)$ respectively. Because of the properties of the gain-loss function the last term in both equations is strictly negative. However, a clear ranking of $W_{ut}(R)$ and $W_{ut}(R')$ does not exist as it depends on the specific numerical values of the awards vectors in V and on the distribution of beliefs.

3.4.2 Maxmin welfare analysis

Contrary to the previous section, when F is such that $f(R(c,E))=1$ for some $R(c,E) \in V$, a deviation by the arbitrator from the announced policy R may increase welfare when this takes the maxmin specification and the deviation improves the well-being of the worst-off individual. As such, rule R does not necessarily maximize welfare when claimants expect the arbitrator to use it.

However, standard rules satisfy Order Preservation in Gains. The order of awards thus reflects the order of claims such that the worst-off individual is the agent with the lowest claim. By construction, the CEA rule is the most generous one towards the claimant with the lowest claim as it allocates him the award $CEA_i(c,E)=\min \{c_i, E/n \}$. Then, if agents expect the arbitrator to implement the CEA allocation, the CEA rule indeed maximizes welfare. Any deviation to a different rule decreases the utility of the worst-off individual: not only the alternative rule assigns to the agent less of the endowment, it also inflicts him a loss as the actual amount that the agent gets falls short of his expectations.

Proposition 9

The CEA rule maximizes maxmin welfare in any problem $(c,E)\in \mathbb {B}^{N}$ in which claimants have RDPs, $r=F$, and $f(CEA(c,E))=1$.

The result of Proposition 9 partly extends to the setting in which F is non-degenerate. As said, the CEA rule is the rule that allocates the largest amount to the agent who gets the least. Moreover, the actual realization of CEA(c, E) generates some additional pleasant feelings of perceived gains as the agent compares $CEA_i(c,E)$ with all other (less favorable) awards he could have got. As such, the CEA rule maximizes welfare for a wide range of parameters.

4 Extensions

In this section I discuss some additional topics of interest and extensions of the baseline model.

4.1 Duality

How do standard duality results get affected when claimants have RDPs? To answer this question I define as a Bankruptcy Problem with Reference Points a triplet (c, E, r). With respect to the notation (c, E) that I used so far, the new notation highlights the role that agents’ reference points may play in determining the awards vectors that different rules select.¹⁹ I can then immediately define the notions of dual problems and dual rules.

Definition 2

The dual of problem (c, E, r) is given by problem $(c,L,c-r)$ and two rules R and $R^*$ are said to be dual if $R(c,E,r)=c-R^*(c,L,c-r)$.

The vector $(c-r)$ thus collects agents’ Dual Reference Points. The interpretation is that if in problem (c, E, r) a claimant expects to get $r_i$ units of the endowment E, then in the dual problem $(c,L,c-r)$ the agent expects to bear $(c_i-r_i)$ units of the loss L. The definition of dual rules embeds standard duality results. Agents’ reference points in fact do not affect the awards vectors that classical rules select. Thus, the Proportional rule and the Talmud rule are still self-dual, whereas the Constrained Equal Awards rule and the Constrained Equal Losses rule remain dual of each other.

The analysis, however, showed that reference points influence the awards vectors that some other rules select. When this is the case, Definition 2 leads to novel duality results. For instance, when claimants use their claims as reference points, the dual of the Small Claims First rule is the Large Claims First rule (see 6).

Example 5

Consider the bankruptcy problem $\left( c,E,r \right) =((30,50,80), 100, (30,50,80))$. It follows that $SCF^{\prec _{c}}(c,E,r)=(30,50,20)$ and $LCF^{\prec _{c}}(c,E,r)=(0,20,80)$.

In the dual problem $\left( c,L, c-r\right) =((30,50,80), 60, (0,0,0))$ the two rules instead lead to the awards vectors $SCF^{\prec _{c}}(c,L,c-r)=(30,30,0)$ and $LCF^{\prec _{c}}(c,L,c-r)=(0,0,60)$.

Similarly to the $SCF^{\prec _{c}}$ rule, the $LCF^{\prec _{c}}$ rule fails Equal Treatment of Equals but satisfies its weaker version, Ex-Ante Equal Treatment of Equals. The $LCF^{\prec _{c}}$ rule also satisfies Endowment Monotonicity, Claims Monotonicity, Order Preservation in Gains, Scale Invariance, Path Independence, and Consistency. It fails Order Preservation in Losses and Composition. Duality, however, has no implications on how a rule performs in terms of welfare. The $SCF^{\prec _{c}}$ rule maximizes utilitarian welfare when $r=c$ (see Proposition 1). Still, it is not true that the $LCF^{\prec _{c}}$ rule achieves minimal welfare.²⁰

4.2 No boundedness

Boundedness may sometimes act as a constraint toward the goal of welfare maximization. The (utilitarian or maxmin) social welfare function may in fact achieve a global maximum outside of the domain defined by this condition. Example 6 illustrates the situation.²¹

Example 6

Let claimant $i \in \left\{ 1,2 \right\}$ have utility function

$$\begin{aligned} u(R_{i}\left( \cdot \right) \mid r_{i}=c_{i})=\left\{ \begin{array}{ll} R_{i}\left( \cdot \right) +k\sqrt{R_{i}\left( \cdot \right) -c_{i}} &{} if~ R_{i}\left( \cdot \right) \ge c_{i} \\ R_{i}\left( \cdot \right) -3\sqrt{\left| R_{i}\left( \cdot \right) -c_{i}\right| } &{} if~ R_{i}\left( \cdot \right) <c_{i}, \end{array} \ \right. \end{aligned}$$

and consider the problem $c=(60,90)$ and $E=100$ in two different settings: (a) $k=1$; and (b) $k=2$. In (a) the allocations that maximize utilitarian welfare are $R^*=(4,96)$ and $R^{**}=(66,34)$—see Fig. 4a—, whereas in (b) the unique maximizing allocation is $R^*=(100,0)$—see Fig. 4b.

Fig. 4

Utilitarian welfare when $r=c$ and Boundedness does not necessarily hold

Figure 4a shows that welfare gets maximized by two allocations that fail Boundedness, as both of them assign to one of the claimant more than his claim. Figure 4b shows that in some circumstances welfare is maximal when the arbitrator allocates the entire endowment to a single claimant, in this case claimant 1. However, all these allocations assign to some of the claimants less than their minimal rights, $m=(10,40)$. As such, it would be hard for the arbitrator to actually implement them as some agents would perceive these solutions as extremely unfair. The compliance to allocate to each claimant (at least) his minimal rights thus provides a welfare rationale for Boundedness.

4.3 Heterogeneous gain-loss functions

The utility function defined in Sect. 2.2 postulates that agents have a symmetric gain-loss function: $\mu _i(\cdot )=\mu (\cdot )$ for any $i \in N$. Here I study the implications of assuming heterogeneous gain-loss functions. I thus adopt the following utility specification:

$$\begin{aligned} u_i( R_{i}\left( c,E\right) \mid r_{i})= R_{i}\left( c,E\right) +\mu _i ( R_{i}\left( c,E\right) -r_{i}), \end{aligned}$$

(16)

where $\mu _i( \cdot )$ is now idiosyncratic to agent $i \in N$ but still obeys the general properties defined in Sect. 2.2.

How different rules perform in terms of aggregate welfare continues to be driven by agents’ diminishing sensitivity to gains and losses. However, the strength of these effects now differs across claimants and this can affect some of the results. The implications on maxmin welfare are minimal. By construction, the $MUG^u$ rule (see 8) maximizes the well-being of the worst-off individual and thus achieves maximal welfare even when claimants have different gain-loss functions. The only difference is that when claimants have a null reference point (i.e., $r=\mathbf 0$) the CEA rule (which in Sect. 3.2 coincided with the $MUG^u$ rule) does not necessarily achieve the first-best solution and is thus dominated by the $MUG^u$ rule.

The implications on utilitarian welfare are more substantial. Consider for instance the case $r=c$ so that award vectors fall in the domain of losses. Diminishing sensitivity still leads to a strictly convex social welfare function. This in turn implies that award vectors that heavily punish a subset of claimants achieve higher welfare with respect to more egalitarian vectors. Heterogeneity in claimants’ gain-loss functions may affect the identity of the agents that should bear the loss. In the main analysis this set simply consisted of those with the largest reference points. With heterogeneous gain-loss functions, it instead comprises those who have the “best” combination of reference point and gain-loss function, i.e., a combination that allows the arbitrator to attribute them large perceived losses without their disappointment impacting on aggregate welfare that much. Depending on how these two effects combine, this new channel may either reinforce or overturn the ranking of standard rules and the optimality of the $SCF^{\prec _{c}}$ rule.

The logic is similar when awards vectors fall in the domain of gains (the cases $r=\mathbf 0$ and $r=m$). The social welfare function is strictly concave and diminishing sensitivity makes egalitarian allocations achieve higher levels of welfare. The optimal awards vector, however, is no longer the vector that makes claimants’ awards (the case $r=\mathbf 0$, see Sect. 3.2) or perceived gains (the case $r=m$, see Sect. 3.3) as equal as possible, but rather the vector that makes their marginal benefits as equal as possible.

5 Conclusions

I studied bankruptcy problems when claimants have reference-dependent preferences. The setting is natural and leads to important welfare implications that I explored under different specifications of claimants’ reference points and different measures of welfare.

Within the class of standard rules that satisfy Equal Treatment of Equals, the Constrained Equal Awards rule often outperforms other rules. Focusing on utilitarian welfare, this happens when agents’ reference points coincide with their claims or with the zero awards vector. Focusing on maxmin welfare, this happens when agents’ reference points coincide with the zero awards vector or with their beliefs about the awards vector that the arbitrator will implement. It also verifies when perceived losses have second order effects and claimants use as reference points their claims or their minimal rights.

It is, however, often the case that none of the standard rules maximize welfare. I thus introduced some new rules (the Small Claims First, Minimal Utility Gap, and Constrained Equal Gains rules) that implement the first-best allocations, discussed their properties, and highlighted a tension between the goal of welfare maximization and the equity of the resulting awards vectors. The findings shed further light on the welfare implications of reference-dependent preferences that can be relevant also beyond the realm of bankruptcy problems.

Appendix

Proof of Proposition 1

Let $\left( c,E\right) \in \mathbb {B}^{N}$ and $r=c$. Generic rule R selects the awards vector R(c, E) and generates utilitarian welfare $W_{ut}(R)=E+\sum _{i}\mu (-l_{i}(R))$, where $l_{i}(R)=c_{i}-R_{i}(c,E) \ge 0$ is claimant i’s loss. Aggregate loss is $L=\sum _{i}l_{i}(R)=C-E$ and mean loss is $\bar{l}(R)=\frac{L}{n}$ for any R. Therefore, rules only differ in how they allocate individual losses, holding fixed aggregate loss and mean loss. Let R and $R^{\prime }$ be two rules, l(R) and $l( R^{\prime } )$ be the vectors of individual losses, and $\sigma ^{2}(l(R))$ and $\sigma ^{2} ( l ( R^{\prime }) )$ be the variance of the elements of l(R) and $l( R^{\prime } )$. Without loss of generality, let $\sigma ^{2}(l(R)) > \sigma ^{2} ( l ( R^{\prime }) )$. Then l(R) is a mean-preserving spread of $l ( R^{\prime } )$ given that $\sum _{i}l_{i}(R)=\sum _{i} l_{i}( R^{\prime } )=L$ and $\bar{l}(R)=\bar{l}( R^{\prime } )=\frac{L}{n}$. Because of the strict convexity of the $\mu (\cdot )$ function in the domain of losses, it follows that $\sum _{i}\mu ( -l_{i} ( R^{\prime }) )<\sum _{i}\mu ( -l_{i}(R)) <0$ and thus $W_{ut}(R)>W_{ut} ( R^{\prime } )$. It is thus sufficient to show that $\sigma ^{2}(l(R)) > \sigma ^{2} ( l ( R^{\prime }) )$ to prove that $W_{ut}(R)>W_{ut} ( R^{\prime } )$.

Consider now the P, CEA, and CEL rules. By construction, the CEL rule allocates L as equally as possible. Given that $CEL(c,E)\ne R(c,E)$ for $R\in \left\{ P,CEA\right\}$ whenever $c_{i}\ne c_{j}$ for some $i,j\in N$, it follows that $l(CEL)\ne l(R)$. It then must be the case that $\sigma ^{2}(l (R))>\sigma ^{2}(l(CEL))$ for any $R\in \left\{ P,CEA\right\}$. Therefore, $\min \left\{ W_{ut}(P),W_{ut}(CEA)\right\} >W_{ut}(CEL)$.

Now compare the CEA and the P rules. Assume first that the condition $c_{i}\ge \frac{E}{n}$ for all i holds. Then, $CEA(c,E)=( \frac{E}{n},...,\frac{E}{n})$. Therefore, l(CEA) is such that $l_{i}(CEA))=c_{i}-\frac{E}{n}$ for all i. As such, $\sigma ^{2}(l(CEA))=\sigma ^{2}(c)$. Instead, $P(c,E)=\lambda c$ with $\lambda =\frac{E}{C}$ such that $\lambda \in \left( 0,1\right)$. Therefore, $l_{i}(P)=\left( 1 - \lambda \right) c_{i}$ for all i. It follows that $\sigma ^{2}(l(P))=(1-\lambda )^{2}\sigma ^{2}(c)$ and thus $\sigma ^{2}(l(CEA))>\sigma ^{2}(l(P))$. If instead $c_{i}<\frac{E}{n}$ for some i, then l(CEA) is such that $l_{i}(CEA)=0$ for some i, whereas l(P) is such that $l_{i}(P)>0$ for all i. The relation $\sigma ^{2}(l(CEA))>\sigma ^{2}(l(P))$ thus still holds. Therefore, $W_{ut}(CEA)>W_{ut}(P)$. Since we already showed that $\min \{ W_{ut}(P),W_{ut}(CEA)\} >W_{ut}(CEL)$, we can conclude that $W_{ut}(CEA)>W_{ut}(P)>W_{ut}(CEL)$.

Now consider the problem $\max _{l}W_{ut}=E+\sum _{i}\mu (- l_i)$ where $l=(l_1,...,l_n )$. If $C=E$ then $l=\left( 0,...,0 \right)$ and the $SCF^{\prec _{c}}$ rule (as any other rule) trivially maximizes welfare. If instead $C>E$ then l is such that $l_{i}>0$ (and thus $\mu (- l_{i}) < 0$) for $\xi (l)\in \{ 1,...,n\}$ claimants. Let R and $R^{\prime }$ be two rules and denote with l(R) and $l( R^{\prime } )$ the vectors of individual losses. Given that $\sum _{i} l_i (R)= \sum _{i \in N} l_i (R^{\prime })=L$, the diminishing marginal sensitivity to losses of $\mu (\cdot )$ implies that if $\xi (l(R))<\xi (l (R^{\prime } ) )$ then $W_{ut}\left( R\right) >W_{ut}( R^{\prime })$. By construction the $SCF^{\prec _{c}}$ rule minimizes $\xi (l(R))$ and thus maximizes utilitarian welfare. It follows that $W_{ut}(SCF^{\prec _{c}}) \ge W_{ut}(CEA)>W_{ut}(P)>W_{ut}(CEL)$. $\square$

Proof of Proposition 2

With no loss of generality, let the problem $(c,E)\in \mathbb {B}^{N}$ be such that $c_i \le c_{i+1}$ for any $i \in \{1, ..., n-1\}$. The $SCF^{\prec _{c}}$ rule selects the awards vector

$$\begin{aligned} SCF^{\prec _{c}}(c,E)=\left( c_{1},c_{2},...,\overbrace{E-\sum _{j = 1}^{k-1} c_j}^{SCF^{\prec _{c}}_k(c,E) \ \text {with} \ k \in \{1,...,n\}}, 0, ..., 0 \right) , \end{aligned}$$

where claimant $k \in \{1, ..., n \}$ is such that $\sum _{j = 1} ^{k-1} c_j < E \le \sum _{j = 1} ^{k} c_j$. The awards vector can be analogously expressed as

$$\begin{aligned} SCF^{\prec _{c}}(c,E)=\left( c_{1},c_{2},...,c_{k}-\left( L-\sum _{j=k+1}^{n} l_j \right) , 0, ..., 0 \right) , \end{aligned}$$

where $l_j=c_j-SCF^{\prec _{c}}_j(c,E) \ge 0$ is claimant j’s loss. The $SCF^{\prec _{c}}$ rule thus achieves utilitarian welfare

$$\begin{aligned} W_{ut}(SCF^{\prec _{c}})=E \quad + \quad \overbrace{\mu \left( - \left( L-\sum _{j=k+1}^{n} l_j \right) \right) }^{\text {perceived loss of} \ k} \quad + \overbrace{\sum _{j=k+1}^{n} \mu \left( - c_j \right) }^{\text {perceived losses of} \ j>k}. \end{aligned}$$

By Proposition 1, this is the maximum level of utilitarian welfare that any rule can achieve. Consider now the awards vector

$$\begin{aligned} \hat{R}(c,E)=\left( c_{1},...,c_{\hat{k}}-\left( L-\sum _{j=k+1}^{n} l_j \right) , c_{\hat{k}+1}, ..., c_k, 0, ..., 0 \right) , \end{aligned}$$

with $\hat{k} \in \{1,...,k-1\}$ and $c_{\hat{k}}-(L-\sum _{j=k+1}^{n} l_j ) \ge 0$. Rule $\hat{R}$ achieves utilitarian welfare

$$\begin{aligned} W_{ut}(\hat{R})=E \quad + \quad \overbrace{\mu \left( - \left( L-\sum _{j=k+1}^{n} l_j \right) \right) }^{\text {perceived loss of} \ \hat{k} } \quad + \overbrace{\sum _{j=k+1}^{n} \mu \left( - c_j \right) .}^{\text {perceived losses of} \ j>k} \end{aligned}$$

Therefore, $W_{ut}(\hat{R})=W_{ut}(SCF^{\prec _{c}})$ and rule $\hat{R}$ also maximizes utilitarian welfare.²² To compare the two rules in terms of inequality, let $\sigma ^2 \left( R \right) = \frac{\sum _{i=1}^n\left( \left( R_i(c,E) - E/n \right) \right) ^2}{n}$ be the variance of R(c, E). Then, the condition $\sigma ^2 \left( SCF^{\prec _{c}} \right) \le \sigma ^2 ( \hat{R} )$ holds if and only if

$$\begin{aligned}&\left( c_{\hat{k}} - E/n \right) ^2 + \left( c_{k}-\left( L-\sum _{j=k+1}^{n} l_j \right) - E/n \right) ^2 \\&\qquad \le \left( c_{\hat{k}}-\left( L-\sum _{j=k+1}^{n} l_j \right) - E/n \right) ^2 + \left( c_{k} - E/n \right) ^2, \end{aligned}$$

since all other terms cancel out. This simplifies to

$$\begin{aligned} -2 \left( L-\sum _{j=k+1}^{n} l_j \right) \left( c_k-c_{\hat{k}} \right) \le 0, \end{aligned}$$

which is always true given that $(L-\sum _{j=k+1}^{n} l_j ) \ge 0$ and $c_k \ge c_{\hat{k}}$. $\square$

Proof of Proposition 3

I first show that if a rule R maximizes utilitarian welfare, then the awards vector R(c, E) satisfies Large Losers and Unique Residual Loser. By the proof of Proposition 3, we know that the rules that maximize utilitarian welfare are those that select an awards vector

$$\begin{aligned} \hat{R}(c,E)=\left( c_{1},...,c_{\hat{k}}-\left( L-\sum _{j=k+1}^{n} l_j \right) , c_{\hat{k}+1}, ..., c_k, 0, ..., 0 \right) , \end{aligned}$$

where claimant $k \in \{1, ..., n \}$ is such that $\sum _{j = 1} ^{k-1} c_j < E \le \sum _{j = 1} ^{k} c_j$, and $\hat{k} \in \{1,...,k\}$ is such that $c_{\hat{k}}-(L-\sum _{j=k+1}^{n} l_j ) \ge 0$. I now show that $\tilde{L}_i < c_i$ for all $i \in \{1,..,k\}$, whereas $\tilde{L}_i \ge c_i$ for all $i \in \{k+1,..,n\}$, where $\tilde{L}_i$ is claimant i’s Cumulative Aggregate Loss (see Definition 1 in the main text).

Consider claimant k. Then, $\tilde{L}_k = \sum _{i=1}^{k} c_i - E \ge 0$ because k is the first agent for which the condition $\sum _{i = 1} ^{k} c_i \ge E$ holds. However, $\tilde{L}_k < c_k$ since $\tilde{L}_k - c_k = \sum _{i=1}^{k-1} c_i - E < 0$. Since the condition $\tilde{L}_i < c_i$ holds for claimant k, it also holds for all $i \in \{1,..,k-1\}$. Consider now claimant $k+1$. Then, $\tilde{L}_{k+1} = \sum _{i=1}^{k+1} c_i - E > 0$ because $c_{k+1} \ge c_k > 0$. However, it is now the case that $\tilde{L}_{k+1} \ge c_{k+1}$ since $\tilde{L}_{k+1} - c_{k+1} = \sum _{i=1}^{k} c_i - E = \tilde{L}_{k} \ge 0$. Since the condition $\tilde{L}_i \ge c_i$ holds for claimant $k+1$, it also holds for all $i \in \{k+2,..,n\}$.

The awards vector $\hat{R}(c,E)$ thus satisfies Large Losers, since it assigns $\hat{R}_i(c,E)=0$ to each claimant $i \in \{k+1,...,n\}$ and these are the agents for which the condition $\tilde{L}_i \ge c_i$ holds. The vector $\hat{R}(c,E)$ also satisfies Unique Residual Loser since claimant $k \in \{1,...,n\}$ is the agent for which $0< \tilde{L}_k < c_k$ and claimant $\hat{k} \in \{1,...,k\}$ is the agent that fulfills the condition $R_{\hat{k}}\left( c,E\right) =c_{\hat{k}}-\tilde{L}_{k} \ge 0$.

I now prove that if an awards vector R(c, E) satisfies Large Losers and Unique Residual Loser, then rule R maximizes utilitarian welfare. Consider the generic awards vector:

$$\begin{aligned} R(c,E)=\left( R_{1}(c,E),...,R_{n}(c,E) \right) , \end{aligned}$$

with $R_{i}(c,E) \in [0, c_i ]$ for any $i \in N$. Large Losers implies:

$$\begin{aligned} R(c,E)=\left( R_{1}(c,E),R_{2}(c,E),...,R_{k}(c,E), 0, ..., 0 \right) , \end{aligned}$$

since claimants $j \in \{ k+1, ..., n\}$ are those for which the condition $\tilde{L}_j \ge c_j$ holds. Unique Residual Loser then implies that there exists a claimant $\hat{k} \in \{1,...,k\}$ such that:

$$\begin{aligned} R(c,E)=\left( R_{1}(c,E),...,c_{\hat{k}}- \tilde{L}_k, R_{\hat{k}+1}(c,E), ..., R_{k}(c,E), 0, ..., 0 \right) . \end{aligned}$$

By construction, $\tilde{L}_k + \sum _{j=k+1}^n \tilde{L}_j = L$. Balance implies $\sum _{i=1}^k R_i(c,E)=E$. Boundedness then necessarily leads to:

$$\begin{aligned} R(c,E)=\left( c_{1},...,c_{\hat{k}}-\left( L-\sum _{j=k+1}^{n} l_j \right) , c_{\hat{k}+1}, ..., c_k, 0, ..., 0 \right) , \end{aligned}$$

which is a vector that maximizes utilitarian welfare (see the proof of Proposition 2). $\square$

Proof of Proposition 4

It is immediate to verify that the $SCF^{\prec _{c}}$ rule satisfies Large Losers and Unique Residual Loser Is The Last. I now prove that the converse also holds true. As in the proof of Proposition 3, Large Losers implies:

$$\begin{aligned} R(c,E)=\left( R_{1}(c,E),R_{2}(c,E),...,R_{k}(c,E), 0, ..., 0 \right) , \end{aligned}$$

where $k \in \{1, ..., n \}$ is such that $0<\tilde{L}_k < c_k$. Unique Residual Loser Is The Last then implies:

$$\begin{aligned} R(c,E)=\left( R_{1}(c,E),R_{2}(c,E),..., c_{k}- \tilde{L}_k, 0, ..., 0 \right) . \end{aligned}$$

Since $\tilde{L}_k + \sum _{j=k+1}^n \tilde{L}_j = L$, Boundedness and Balance then necessarily require:

$$\begin{aligned} R(c,E)=\left( c_{1},c_2...,c_{k}-\left( L-\sum _{j=k+1}^{n} l_j \right) , 0, ..., 0 \right) , \end{aligned}$$

and given that $c_{k}-(L-\sum _{j=k+1}^{n} l_j )=E-\sum _{j =1}^{k-1} c_j$, the awards vector can be rewritten as

$$\begin{aligned} R(c,E)=\left( c_{1},c_{2},...,E-\sum _{j =1}^{k-1} c_j, 0, ..., 0 \right) , \end{aligned}$$

which is the $SCF^{\prec _{c}}$ solution. $\square$

Proof of Proposition 5

The utility function of any claimant $i \in N$ is continuous and strictly increasing in $R_i(c,E)$ and the awards vector satisfies Balance. Then, if feasible, maxmin welfare gets maximized by the vector R(c, E) such that $\min \{u(R_i(c,E)\mid r_{i}=c_i)\}_{i \in N} = \max \{u(R_i(c,E)\mid r_{i}=c_i)\}_{i \in N}$. If instead Boundedness makes such a vector unfeasible, then maxmin welfare gets maximized by any vector R(c, E) with $R_j(c,E)=c_j$ where agent $j \in N$ is the agent for which $u(c_j\mid r_{j}=c_j)= c_j=\min \{u(R_i(c,E)\mid r_{i}=c_i)\}_{i \in N}$. By construction, the $MUG^u$ rule selects these award vectors in both cases and thus it always maximizes welfare. $\square$

Proof of Proposition 6

Let $\left( c,E\right) \in \mathbb {B}^{N}$ and $r=\mathbf 0$. Generic rule R generates utilitarian welfare $W_{ut}(R)=E+\sum _{i}\mu (g_{i}(R))$, where $g_{i}(R)=R_{i}(c,E)-0=R_{i}(c,E)$ is claimant i’s perceived gain. It follows that $g_{i}(R) \ge 0$ for all $i \in N$ and $\sum _{i} g_i(R)=E$.

Because of the strict concavity of $\mu (\cdot )$ in the domain of gains, the lower is the variance of $g(R)=(R_1(c,E),...,R_n(c,E))$, the higher is the welfare that R generates. Since the CEA rule allocates E as equally as possible, the awards vector CEA(c, E) maximizes welfare and thus $W_{ut}(CEA)>\max \left\{ W_{ut}(P),W_{ut}(CEL)\right\}$ whenever $c_{i}\ne c_{j}$ for some $i,j\in N$.

Now compare the P and the CEL rules. Assume first that $c_{i}\ge \frac{L}{n}$ for all $i \in N$. Then, $g_{i}(P)=\lambda c_{i}$ (with $\lambda \in \left( 0,1\right)$) and $g_{i}(CEL)=c_{i}-\frac{L}{n}$ for all i. Thus, $\sigma ^{2}(g(P))<\sigma ^{2}(g(CEL))$ since $\sigma ^{2}(g(P))=\lambda ^{2}\sigma ^{2}(c)$ whereas $\sigma ^{2}(g(CEL))=\sigma ^{2}(c)$. If instead $c_{i}< \frac{L}{n}$ for some $i \in N$, then $g_{i}(CEL)=0$ for some $i \in N$ whereas $g_{i}(P)>0$ for all $i \in N$ such that the relation $\sigma ^{2}(g(P))<\sigma ^{2}(g(CEL))$ still holds. Therefore, $W_{ut}(CEA)>W_{ut}(P)>W_{ut}(CEL)$. $\square$

Proof of Proposition 7

Let $\left( c,E\right) \in \mathbb {B}^{N}$ and $r=m$. Then $W_{ut}(R)=E+\sum _{i}\mu (g_{i}(R))$ where $g_{i}(R)=R_{i}(c,E)-m_i \ge 0$ for all $i \in N$. The strict concavity of $\mu (\cdot )$ in the domain of gains implies that the lower is the variance of g(R), the higher is $W_{ut}(R)$. The $CEG^{\prec _{c}}$ rule implements the awards vector

$$\begin{aligned} CEG^{\prec _{c}}(c,E)=\left( c_{1},...,c_{j-1}, m_{j}+\xi ,..., m_{n}+\xi \right) , \end{aligned}$$

where $\xi =\frac{E- \sum _{i \succeq _c j} m_i-\sum _{i \prec _c j}CEG^{\prec _{c}}_i}{n-j+1}$ and claimant $j \in \{1,...,n\}$ is the first agent for which the condition $m_{j}+\xi \le c_j$ holds. Therefore, the vector of perceived gains is

$$\begin{aligned} g(CEG^{\prec _{c}})=\left( c_{1}-m_{1},...,c_{j-1}-m_{j-1},\xi ,...\xi \right) , \end{aligned}$$

such that $g_i(CEG^{\prec _{c}}) < \xi$ for all $i \in \{1,...,j-1 \}$ and the last $n-j+1$ terms are equal. Boundedness implies that there are no awards vector R(c, E) such that $g_i(R) > g_i(CEG^{\prec _{c}})$ for some $i \in \{1,...,j-1 \}$. Balance implies that if an awards vector R(c, E) is such that $g_i(R) < \xi$ for some $i \in \{j,...,n\}$ then it must be the case that $g_k(R) > \xi$ for some $k \in \{j,...,n\}$ with $k \ne i$. Therefore, $\sigma ^2(g(CEG^{\prec _{c}}))<\sigma ^2(g(R))$ for any $R \ne CEG^{\prec _{c}}$ so that the $CEG^{\prec _{c}}$ rule maximizes utilitarian welfare. $\square$

Proof of Proposition 8

The proof replicates the proof of Proposition 5 with the condition $r_i=m_i$ instead of $r_i=c_i$. $\square$

Proof of Proposition 9

Let $\left( c,E\right) \in \mathbb {B}^{N}$. Let $r=F$ and F be such that $f(CEA(c,E))=1$. Define agent 1 as an agent for which $c_1 \le c_i$ for any $i \in N$. Then, $W_{mm}(CEA)=CEA_1(c,E)$ since, for any $i \in N$, $u(CEA_i(C,E) \mid (CEA_i(c,E))=CEA_i(C,E)$ and $CEA_1(c,E) \le CEA_i(c,E)$ because the CEA rule satisfies the property of Order Preservation in Gains. Any rule $R \ne CEA$ leads instead to $W_{mm}(R)=R_1(c,E)+\mu (R_1(c,E)-CEA_1(c,E))$. Given that $R_1(c,E) \le CEA_1(c,E)$ and $\mu (R_1(c,E)-(CEA(c,E)) \le 0$, it follows that $W_{mm}(CEA) \ge W_{mm}(R)$ for any $R \ne CEA$. $\square$