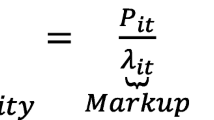Measuring market power when firms price discriminate

Abstract

We propose conduct parameter-based market power measures within a model of price discrimination, extending work by Hazledine (Econ Lett 93:413–420, 2006) and Kutlu (Econ Lett 117:540–543, 2012) to certain forms of second-degree price discrimination. We use our model to estimate the market power of US airlines in a price discrimination environment. We find that a slightly modified version of our original theoretical measure is positively related to market concentration. Moreover, on average, market power for high-end segment is greater than that of low-end segment.

1 Introduction

The relationship between price discrimination and market power has been extensively researched.¹ In a theoretical setting, Dana (1999) shows that when capacity is costly and prices are set in advance, firms facing uncertain demand will sell output at multiple prices. As the market becomes more competitive, the prices become more dispersed. Hence, the model of Dana (1999) supports a negative relationship between market power and price dispersion. On the other hand, McAfee et al. (2006) find no theoretical connection between the strength of price discrimination and market power. Dai et al. (2014) show that the relationship between the unit transportation cost (intensity of competition) and price dispersion (measured by the Gini coefficient) is non-monotonic and can be inverse U-shaped. As for the empirical literature, Borenstein and Rose (1994) and Stavins (2001) find a negative relationship between price dispersion and market power. Gerardi and Shapiro (2009) show a positive relationship, while Dai et al. (2014)² and Chakrabarty and Kutlu (2014) show a non-monotonic relationship between market power and price dispersion. These studies rely on the Herfindahl–Hirschman Index (HHI) as a proxy for market power when examining this relationship.³ It would seem, however, that for these studies a term such as price dispersion would be more appropriate than price discrimination. This is due to the need to control for the effect of costs in order to properly identify price discrimination, which these studies do not do as they utilize reduced-form regressions to estimate the degree of price discrimination instead of using a structural empirical model.⁴ Structural models exist to address such matters. In this paper, we estimate a structural model that is consistent with our theoretical model of what Pigou calls second-degree price discrimination, which approximates the first-degree price discrimination by assuming a finite number of prices based on the willingness to pay of customers.⁵

We propose market power measures that are specifically designed to capture price discrimination. Our measures are derived from a conduct parameter game where the firms price discriminate.⁶ Hence, when firms price discriminate, our measures are designed to better identify the presence of market power compared with measures ignoring price discrimination, such as HHI as a proxy for market power. By utilizing our conduct parameter game, we can show that for a variety of sensible scenarios, a positive relationship between market power, measured by the conduct, and price discrimination is supported. Conduct is a supply-related concept and is associated with the way firms play the game. By saying “conducts of high-end and low-end segments” we differentiate potentially different conducts of firms that the firms implement for different consumer segments.

In the presence of price discrimination, using a single-price index can lead to biased estimation results. The first estimation problem concerns the demand equation. In particular, the estimated price elasticity of demand would be biased and inconsistent if a single-price index is used in demand estimation when firms price discriminate due to model misspecification. As we will discuss later in Sect. 2, the source of the bias relates to different interpretations of observed quantities in single-price and price discrimination settings. The bias goes away as the market structure approaches perfect competition. Consistent estimation of the price elasticity of demand is important for deriving consistent conduct parameter estimates. A second estimation problem involves the supply equation. While the single-price version of the conduct parameter game necessitates some functional form assumptions on the marginal cost so as to identify the conduct parameter, in the price discrimination framework we do not have to make any such assumptions if conduct is invariant to price segment. The reason is that the price discrimination version of the conduct model can be written in a form that does not require knowledge of marginal costs. However, the researcher must specify the high-end and low-end prices as well as corresponding quantities. These prices and quantities can be obtained in an ad hoc way or can be determined by econometric analysis.

We consider the US airline industry in order to illustrate how our theoretical model can be applied to measure the market power of firms which price discriminate. We estimate the market power of US airlines under price discrimination settings during the period 1999 I to 2009 IV. We find that for almost all airlines in our sample the average market power either remains more or less the same over the years or it decreases. On average, market power for high-end segment is greater than that of low-end segment. We also examined the relationship between market concentration (measured by HHI) and market power. We find that there is a positive relationship between market power and concentration.

In the next section, we introduce our theoretical model and results. This is followed by the empirical model and estimations, and finally our conclusions.

2 Theoretical model

2.1 Supply side

In this section, we introduce a conduct parameter model, which enables us to measure market powers of firms in the price discrimination framework. There are N firms in the market. Each consumer buys no more than one unit of the good. The distribution of customer valuations is known to the firms, and resale of the good is not possible. The customers are segmented into bins based on their reservation prices. The price of the good for the $k\hbox {th}$ bin is given by:

$$\begin{aligned} P_{k}=P\left( \sum \limits _{i=1}^{k}Q_{i}\right) \end{aligned}$$

(1)

where $q_{i,n}$ is the quantity sold in bin i by firm n; $Q_{k}=\sum _{n=1}^{N}q_{k,n}$ is the total quantity sold in the bin $k=1,2$; and P is an inverse demand function that represents consumers’ valuations.⁷ In our empirical illustration the market is segmented into two bins ($K=2)$ and we discuss our model using the two-bin segmentation in the discussion to follow. The total quantity demanded in the market is denoted by $Q=Q_{1}+Q_{2}$. Hence, $P_{1}=P\left( Q_{1}\right)$ and $P_{2}=P\left( Q_{1}+Q_{2}\right) =P\left( Q\right)$. Following earlier studies that use this demand structure, we concentrate on the airline industry. The valuation of a buyer is a function of characteristics of the ticket including the time of the purchase. The business travelers, whose plans are often made with relatively minimal lead times and tend to be relatively inflexible, have high valuations, whereas the tourists, whose plans are generally flexible, have relatively low valuations. Hence, the airlines can optimally group the buyers based on the day they want to buy a particular airline seat and the lead time in reserving the seat.

In our conduct parameter model the consumer segmentation is optimal in the sense that the size of each bin is determined by the firm. This contrasts with price discrimination models wherein each segment is taken to be exogenous to the firms so that each segment is taken as a separate market. In a commonly used price discrimination scenario we would have two separate markets determining each segment so that the demands of consumers belonging to these segments are independent of each other. This sort of price discrimination may be reasonable where the segments fixed, say by gender or race. Segmentation by race is considered by Graddy (1995), among others, in her work on price discrimination.

However, in a market where reservation prices depend on the age of customers, firms could choose quantities indirectly by choosing a threshold age. In this setting, customers who are older than the threshold age would be assigned to bin 1 and the rest assigned to bin 2. The firm could then implicitly decrease the size of bin 1 by increasing the age threshold. In the airline context, airlines can segment customers by choosing the number of days before the flight. If the firms can adjust the segment size, then our model can capture this behavior.

2.2 Demand estimation

Demand estimation is an essential part of market power measurement, and below we examine how demand estimates are biased when price discrimination is ignored. As Nash equilibrium is a special case of the conduct parameter setting, we illustrate the problems in demand estimation using this special case. The qualitative results are the same for the conduct parameter setting. As in the earlier section, assume that the firms segment their customers based on their reservation prices. The researcher observes the average price, $\bar{P}$, rather than the demand function, P, representing the valuations of customers. While for the single-price scenario there is no distinction between $\bar{P}$ and P, for the price discrimination scenario $\bar{P}$ and P are not the same. If the researcher assumes that a single-price index, $\bar{P}$, constitutes the demand function, then this would lead to a systematic measurement error. We consider a linear inverse demand function:

$$\begin{aligned} P(Q)=\alpha +\beta Q \end{aligned}$$

(2)

where $\beta <0$. The corresponding average price is:⁸

$$\begin{aligned} \bar{P}\left( Q_{1},Q_{2}\right)&=\frac{P_{1}Q_{1}+P_{2}Q_{2}}{Q_{1}+Q_{2}}\nonumber \\&=P_{2}+\left( P_{1}-P_{2}\right) \frac{Q_{1}}{Q}\nonumber \\&=P\left( Q\right) -\beta Q_{2}\frac{Q_{1}}{Q}\nonumber \\&=\alpha +\beta \left( Q-\frac{Q_{1}Q_{2}}{Q}\right) \nonumber \\&=\alpha +\beta \left( 1-s(1-s)\right) Q \end{aligned}$$

(3)

where $s=\frac{Q_{1}}{Q}$ is the share of high-end customers. The relevant first-order conditions for the conduct parameter setting, which is more general than a Cournot competition, are given in the next section. To estimate this relationship the researcher would collect data for total revenue, $\bar{P}Q$, and total quantity, Q, in order to construct the dependent variable for the demand function. The $(\bar{P},Q)$ pair then would be viewed as constituting the demand function, and thus, it would be assumed by the researcher that $\bar{P}(Q)=\alpha +\beta Q$, which of course excludes the $-\beta \frac{Q_{1}Q_{2}}{Q}$ term, and thus, coefficient estimates for the demand function, $P\left( Q\right)$, are biased even when an instrumental variable approach is used. The reason for the bias is the measurement error in an endogenous variable, which is correlated with the instruments that are used.⁹ If the average price is calculated this way, it is unlikely that the measurement error could be attenuated since standard instruments such as quantities and prices from other similar markets and lagged values of quantities and prices would likely be correlated with the measurement error, $\frac{Q_{1}Q_{2}}{Q}$, by definition. The asymptotic bias in $\beta$ estimate is given by:

$$\begin{aligned} \hbox {plim }\hat{\beta }&=\beta +\frac{\hbox {Cov}\left( Z,u\right) }{\hbox {Cov}\left( Z,Q\right) }\nonumber \\&=\beta +\frac{\hbox {Cov}\left( Z,-\beta \frac{Q_{1}Q_{2}}{Q}\right) }{\hbox {Cov}\left( Z,Q\right) }\Rightarrow \nonumber \\ \hbox {plim}\left( \frac{\hat{\beta }-\beta }{\left| \beta \right| }\right)&=\frac{\hbox {Cov}\left( Z,\frac{Q_{1}Q_{2}}{Q}\right) }{\hbox {Cov}\left( Z,Q\right) }\nonumber \\&=\frac{\hbox {Cov}\left( Z,s(1-s)Q\right) }{\hbox {Cov}\left( Z,Q\right) } \end{aligned}$$

(4)

where $u=-\beta \frac{Q_{1}Q_{2}}{Q}>0$ is the measurement error in the endogenous variable and Z is the instrumental variable. In the (symmetric) Cournot game with price discrimination equilibrium, $s\left( 1-s\right) =\frac{N}{\left( N+1\right) ^{2}}$. If we place this number into the above formula, we have:

$$\begin{aligned} \hbox {plim}\left( \frac{\hat{\beta }-\beta }{\left| \beta \right| }\right) =\frac{N}{\left( N+1\right) ^{2}}>0. \end{aligned}$$

(5)

Based on these arguments the bias will most likely be positive, i.e., $\hat{\beta }>\beta$, and $\left| \hat{\beta }\right| <\left| \beta \right|$. For perfectly competitive markets, as expected, the bias vanishes and for monopoly the bias reaches its highest value in percentage of $\beta$, i.e., $25\%$. For a linear demand scenario, the bias falls below 5% only when the number of firms reaches 18 in this example.

We conclude that using a single-price index may seriously bias the estimates of demand equation parameters. One of the consequences of estimating the demand elasticity incorrectly may be flawed market power estimates. Without the knowledge of $\beta$ the conduct parameter approach cannot identify market conduct. Similarly, if $\beta$ is biased, then conduct parameter estimates as a market power measure may be biased as well. In the context of quantity competition, Hazledine (2006) and Kutlu (2012, 2016) note that the average price paid is independent of the extent of price discrimination. At a first look, this may suggest that price discrimination may be ignored in empirical works by using average price as a price index. However, our results suggest that while the result of Hazledine (2006) and Kutlu (2012, 2016) may be considered as a predictor of average price in a price discrimination setting, this does not necessary imply that price discrimination can be ignored as this would lead to biased demand estimates. The intuition for this puzzle is given as follows. In the price discrimination setting, the total quantity and the total revenue both increase compared to the single-price setting. Hence, the total quantity sold and thus recorded in any data set is the quantity that corresponds to the quantity sold in the price discrimination setting, which is higher than its single-setting counterpart. Hence, if a researcher assumes a single-price market and assumes that total quantity sold, Q, is the relevant quantity for the single price (i.e., the quantity weighted average price), then since the relevant quantity is lower this would lead to incorrect demand parameter estimates. Basically, interpretation of the quantity must be adjusted if a single-price model is estimated and the true model is the price discrimination one. This is in line with the finding of Hazledine (2006) and Kutlu (2012, 2016) though their result may easily be misinterpreted as if the price discrimination may be ignored when estimating market power and demand.

In the next section, we construct a market power measure in the price discrimination framework that addresses this issue.

2.3 Market power estimation

We now consider a conduct parameter model in the price discrimination framework and propose market power measures consistent with this model. Assume that firm n is choosing quantities for each bin, $(q_{1n},q_{2n})$. The optimization problem of the representative firm is given by:

$$\begin{aligned} \max _{q_{1n},q_{2n}}\pi _{n}=P_{1}q_{1n}+P_{2}q_{2n}-C_{n}(q_{1n}+q_{2n}) \end{aligned}$$

(6)

where $C_{n}$ stands for the total cost of firm n. The first-order conditions are:

$$\begin{aligned} \frac{\partial \pi _{n}}{\partial q_{1n}}= & {} P_{1}+P_{1}^{\prime }q_{1n} \frac{\partial Q_{1}}{\partial q_{1n}}+P_{2}^{\prime }q_{2n}\frac{\partial Q}{\partial q_{1n}}-c_{n}\left( q_{1n}+q_{2n}\right) \\= & {} P_{1}+P_{1}^{\prime }q_{1n}\eta +P_{2}^{\prime }q_{2n}\eta -c_{n}(q_{1n} +q_{2n})=0 \nonumber \end{aligned}$$

(7)

$$\begin{aligned} \frac{\partial \pi _{n}}{\partial q_{2n}}= & {} P_{2}+P_{2}^{\prime }q_{2n} \frac{\partial Q}{\partial q_{2n}}-c_{n}\left( q_{1n}+q_{2n}\right) \\= & {} P_{2}+P_{2}^{\prime }q_{2n}\eta -c_{n}\left( q_{1n}+q_{2n}\right) =0\nonumber \end{aligned}$$

(8)

where $c_{n}$ stands for the marginal cost of firm n.¹⁰ After summing over n and rearranging these first-order conditions, we have:

$$\begin{aligned} \frac{1}{N}\sum _{n=1}^{N}\left( \frac{\partial \pi _{n}}{\partial q_{1n}} -\frac{\partial \pi _{n}}{\partial q_{2n}}\right)&=P_{1}-P_{2}+P_{1} ^{\prime }Q_{1}\frac{\eta }{N}=0\Rightarrow \\ P_{1}-P_{2}&=-P_{1}^{\prime }Q_{1}\theta \nonumber \end{aligned}$$

(9)

where $\theta =\frac{\eta }{N}$ represents the market power. The conducts $\theta =\left\{ 0,\frac{1}{N},1\right\}$ correspond to perfect competition, price discriminating (symmetric) Cournot competition, and price discriminating monopoly (joint profit maximization), respectively. When $\theta =0$, as perfect competition suggests, there is only one price and this price is equal to the marginal cost.

We consider only the firm’s optimization problem with respect to a particular route and do not consider the complications inherent in modeling the decision to optimize with respect to all of its and its competitor’s routes. For example, the number of directional routes in our data sets is 1153. This is consistent with a large body of theoretical and empirical work on the airline industry that assumes independence of city-pair markets.

Given that the segment sizes are determined by the firms, the common conduct assumption for high-end and low-end segments seems to be a relatively sensible assumption for our homogenous product setting. Note that although the high-end and low-end segments would likely have different demand elasticities, which affects the price-marginal cost markups, this difference does not necessarily imply distinct conducts.

Equation (9) can be generalized to a setting where there are more than two prices. The generalized version of this equation is

$$\begin{aligned} P_{j}-P_{j+1}=-P_{j}^{\prime }Q_{j}\theta \end{aligned}$$

(10)

for $j=1,2,\ldots ,K-1$, where K is the number of prices and $Q_{j}$ is the total quantity for segment j. Then, for the K price scenario, the conduct can be written as:

$$\begin{aligned} \theta =\varepsilon _{j}\frac{P_{j}-P_{j+1}}{P_{j}} \end{aligned}$$

(11)

where $\epsilon _{j}=-\frac{1}{P_{j}^{\prime }}\frac{P_{j}}{Q_{j}}$ is the price elasticity of demand for segment j.¹¹ The conduct parameter game that we consider assumes a single conduct for all price segments, which is derived from a conjectural variations game. If one is willing to consider conduct as an index for market power, we even can extend our market power index to allow different values for different segments:

$$\begin{aligned} \theta _{j}=\varepsilon _{j}\frac{P_{j}-P_{j+1}}{P_{j}} \end{aligned}$$

(12)

where $\theta _{j}$ is the market power for segment j. This equation allows us to compare the market powers of firms for different price segments. In what follows, we concentrate on the case where the number of price segments is two.

Bresnahan (1989) argues that one should consider $\theta$ as a parameter that can take values consistent with existing theories. If the researcher considers $\theta$ as a parameter coming from several theories, the estimated parameter value can be used to categorize the market using statistical tests. For example, one can test whether the market outcome is consistent with symmetric Cournot competition or not by testing $\theta =\frac{1}{N}$. Another approach is considering $\theta$ as a continuous-valued parameter. An interpretation of this approach is that the conduct is described in terms of firms’ conjectural variations, which are the “expectations” about other firms’ reactions. This interpretation allows $\theta$ to take a continuum of values. The important point in this interpretation is that the “conjectures” do not refer to what firms believe will happen if they change their quantity levels. In the conjectural variations language, what is being estimated is what firms do as a result of their expectations. As Corts (1999) mentions, the conduct parameter can be estimated “as if” the firms are playing a conjectural variations game that would give the observed price–cost margins. We consider $\theta$ as a market power index that can take a continuum of values and measure the size of the elasticity-adjusted price–cost markup. For instance, we may interpret a market with $\theta$ value between 0 and $\frac{1}{N}$ as a market level that is more competitive than a symmetric Cournot competition.

We define price discrimination as:

$$\begin{aligned} \hbox {PD}=P_{1}-P_{2}. \end{aligned}$$

(13)

Hence, the conduct parameter is given by:

$$\begin{aligned} \theta&=\frac{P_{1}-P_{2}}{-P_{1}^{\prime }Q_{1}}\nonumber \\&=\epsilon _{1}\frac{\hbox {PD}}{P_{1}} \end{aligned}$$

(14)

where $\epsilon _{1}=-\frac{1}{P_{1}^{\prime }}\frac{P_{1}}{Q_{1}}$. Our price discrimination measure is reminiscent of the price-marginal cost markup for the Lerner index:

$$\begin{aligned} L=\frac{P-\hbox {MC}}{P} \end{aligned}$$

(15)

where $\hbox {MC}$ is the “marginal cost” for the market. Generally $\hbox {MC}$ is defined as a weighted average of the marginal costs of the firms in the market. For the single-price conduct parameter game, the conduct parameter is nothing more than the elasticity- adjusted Lerner index:

$$\begin{aligned} \tilde{\theta }=\epsilon L \end{aligned}$$

(16)

where $\epsilon =-\frac{1}{P^{\prime }}\frac{P}{Q}$ is the price elasticity of demand. The price–cost markup takes a central role for the Lerner index. In our case, the relevant markup is $P_{1}-P_{2}$ and the counterpart of Lerner index is $\frac{P_{1}-P_{2}}{P_{1}}$, which may be considered as an alternative for Lerner index in the context of price discrimination. An important implication of this is that marginal cost information is not required. In the single-price conduct parameter setting the firms determine the price in such a way that the equilibrium price lies above the marginal cost. Hence, the optimal price lies somewhere at or above the marginal cost. In the price discrimination setting, the firms choose quantities for low-end and high-end segments and these quantities determine the prices for these segments. In our model, if the price of the low-end segment, $P_{2}$, were a function of $Q_{1}$ so that $Q_{2}$ is fixed (i.e., $Q_{2}$ is given) and the firms choose high-end market quantities, then their optimal choice (conditional on $Q_{2}$) would be to choose $Q_{1}$ treating $P_{2}$ as if it is the marginal cost. This is because in reality $P_{2}$ is the effective opportunity cost for the high-end market pricing option. Similar to the standard single-price setting, for a given $Q_{2}$ level, the optimal $P_{1}$ value lies somewhere at or above this effective (marginal) opportunity cost, i.e., $P_{2}$.¹² The derivation of our market power measure is based on this idea that, for any given low-end quantity, the choice of high-end quantity is determined so that the low-end price represents the effective (marginal) opportunity cost.

Identification is an important issue in the conduct parameter approach, and the constant marginal cost assumption is widely used in order to overcome this difficulty.¹³ Since we do not need cost information, we need not make functional form assumptions on the cost function. However, we do require data for group-specific prices and have to assume a single conduct for all price segments. If the indices are constructed from ticket-specific price data, the researcher must either identify the group to which each individual passenger belongs or divide the sample based on some characteristics of the customers. For example, in case of movie theaters these criteria can be based on the age of customers. In case of airlines, the segmentation can be based on length of time between the flight and purchase of ticket. However, such information can be hard for the researcher to acquire. An indirect way to segment the customers might be to use information on ticket characteristics. An alternative solution is using the counterpart of Lerner index, i.e., $\frac{P_{1}-P_{2}}{P_{1}}$, for the price discrimination setting. For example, $P_{1}$ and $P_{2}$ may be chosen as specific percentiles of prices such as 80th and 20th percentile prices.

We utilize Eq. (14) to examine the relationship between price discrimination and market power. The derivative of price discrimination with respect to conduct is given by:

$$\begin{aligned} \frac{\partial \hbox {PD}}{\partial \theta }&=\left( \frac{1}{\tilde{\epsilon }_{1} }\right) ^{2}\left( \tilde{\epsilon }_{1}-\tilde{\epsilon }_{1\theta } \theta \right)>0\Leftrightarrow \\ \tilde{\epsilon }_{1}&>\tilde{\epsilon }_{1\theta }\theta \nonumber \end{aligned}$$

(17)

where $\tilde{\epsilon }_{1}=\frac{\epsilon _{1}}{P_{1}}$ and $\tilde{\epsilon }_{1\theta }=\frac{\partial \tilde{\epsilon }_{1}}{\partial \theta }$. The conduct would be changing $\tilde{\epsilon }_{1}$ through its effect on the equilibrium quantities and prices. If $\tilde{\epsilon }_{1}$ is relatively non-responsive to changes in conduct and market power is relatively low, then price discrimination is likely to increase as market power increases. An example of a positive correlation between $\hbox {PD}$ and $\theta$ is a situation in which the inverse demand function is in lin–log form as this would imply that $\tilde{\epsilon }_{1}>0$ is a constant. Two less obvious examples of a positive relationship are situations in which the inverse demand function is in lin–lin or log–lin form.¹⁴ Hence, for a variety of demand function scenarios, price discrimination and market power are positively related.

3 An empirical illustration to analyze US airline industry

In this section, we illustrate our methodology for estimating market powers of firms in the price discrimination framework. We estimate the market powers of the US airlines utilizing our conduct parameter framework and compare them with the market concentration measure. First, we introduce our data set. Then, we present our empirical model and results.

3.1 Data

Our quarterly data set covers a sample of airline tickets from reporting carriers over the period from 1999 I to 2009 IV. The US airlines faced serious financial troubles during this period. Historically, the demand for the US airline industry grew steadily. However, in our sample period there were exceptions to this pattern. The effect of these negative shocks is boosted by sticky labor prices and exogenous cost shocks such as increased taxes and jet fuel prices. The financial implications of these factors on domestic airline operations were stark—the airlines lost an order of magnitude more (in 2009 dollars) during our sample period, the decade of 1999–2009 compared to the entire previous two decades of 1979–1999.¹⁵

Our data set is compiled from a variety of data sources. Price indices are constructed from the airline origin and destination survey (DB1B) data provided by the Bureau of Transportation Statistics. The DB1B is a 10% sample of airline tickets from reporting carriers collected by the Office of Airline Information of the Bureau of Transportation Statistics. Information on the number of enplanements is obtained from the T100 database. We concentrate on direct one-way or round-trip itineraries. The round-trip fares are divided by two in order to derive corresponding one-way fares.¹⁶ Two different groups of prices and quantities are calculated. The low-end group price is taken as 20th percentile price for a given airline and quarter. The high-end group price is taken as 80th percentile price for a given airline and quarter. We use the 5th percentile of prices for a given airline and quarter as a proxy for marginal cost, $\hbox {MC}$. The price percentiles are calculated using airline-specific data so that the dispersion does not reflect inter-airline price differences, which would otherwise lead to a deceptive measure for market power. When the price dispersion, $\hbox {PD}$, is based on a limited number of ticket-specific observations or when routes had a very small number of passengers (i.e., 1000 passengers a quarter, which means 100 data points to calculate price percentiles), the observations were dropped. Top and bottom 1% of the price dispersion measure, $\hbox {PD}$, is dropped to avoid outliers. As a robustness check we also estimate the same model without dropping limited number of ticket-specific observations and top–bottom 1% of $\hbox {PD}$. Finally, outliers, such as observations based on itineraries with “incredible” fare data according to the variable “DollarCred,” are dropped as well.

When calculating prices, multi-destination tickets are excluded because it is not possible to identify the ticket’s origin and destination. Also, following Brueckner et al. (1992) we excluded any ticket that does not have the same fare class for all segments of the trip. One potential issue is that coach class tickets are not always consistently reported across carriers. For example, our ticket-level raw data set includes some small carriers that designate all their tickets as only first class and business class. We consider the quality for these tickets as coach class. This may cause a downwards bias in our price discrimination measure. However, similarly, dropping such airlines may cause some upwards bias in the price discrimination measure. In any case, the share of such airlines is small. Finally, sometimes the class information for a ticket is not available and we drop such tickets.

Our data set also includes city-specific demographic variables such as population weighted per capita income ($\hbox {PCI}$) and the average population for each city-pair ($\hbox {POP}$) based on metropolitan statistical area (MSA) data from the US Census. As the MSA data are annual, interpolations were used to generate quarterly versions of the $\hbox {PCI}$ and $\hbox {POP}$ variables. When merging the MSA data with the airline data, we lost some cities as we had Census information on just the metropolitan areas.

The final database contains 1153 directional routes. We deflated nominal prices by the $\hbox {CPI}$. The first quarter of 2005 is the base quarter. Our data set includes information about flight distance ($\hbox {DIST}$) between city-pairs and the average size ($\hbox {SIZE}$) of the fleets. The larger-sized fleets can help airlines provide more services without a proportional increase in costs. Also, larger aircraft are generally perceived as safer and thus improve service quality. On the other hand, larger aircraft carry more people, which might cause congestion, increase the possibility that luggage is mishandled, and increase waiting time for baggage claims. Therefore, the net quality effect of aircraft size is ambiguous. Flight distance is one of the more important determinants of flight cost. It also captures the indirect competition effects from other modes of transportation. Finally, the (logarithm of) quantity for the industry (QOTH), which is calculated using the quantities in other route markets, is used as an instrument. Table 1 provides a summary statistics for the primary data used in the study, i.e., data after dropping outliers. In the table, the route-specific quantity is denoted by Q.

Table 1 Descriptive statistics

3.2 Empirical model

In the theoretical section, we considered a model that shows how a market-specific conduct can be estimated. In order to estimate the demand equation and the conduct parameters, we must assign customers to segments. We divide customers into two groups: high-end and low-end (bin 1 and bin 2, respectively). We take the high-end segment price as 80th percentile of prices, $P_{1}$, for a given route, time, and airline. The low-end segment price is assumed to be 20th percentile of prices, $P_{2}$, for a given route, time, and airline. Based on this assumption we do not know the corresponding market quantities. We assume that the market quantity for high-end segment, $Q_{1}$, is a constant multiple of total market quantity, Q, so that $Q_{1}=k_{rt}Q$, where $k_{rt}$ is route- and time- specific constant. The practical implication of this assumption is that in our demand estimations the logarithm of Q can be replaced by the logarithm of $Q_{1}$ as long as we include route- and time- specific dummy variables in the demand model.¹⁷ Hence, for the demand estimation we simply replace $Q_{1}$ by Q.

We specify the inverse demand function in log–log form as follows:

$$\begin{aligned} \ln P_{1,rti}=\beta _{0}+\beta _{1}\ln Q_{1rt}+\beta _{2}\ln Q_{1rt}\ln \hbox {DIST}_{r}+\sum \limits _{j>2}\beta _{j}X_{rti}+\varepsilon _{rti} \end{aligned}$$

(18)

where $P_{1,rti}$ is the 80th percentile price for route r, time t, and airline i; $Q_{1rt}$ is the high-end segment quantity for route r and time t; $X_{rti}$ are the control variables; and $\varepsilon _{rti}$ is the error term. Based on Eq. (14), our route–time–airline-specific market power measure can be calculated by:

$$\begin{aligned} \theta =\epsilon _{1}\frac{P_{1}-P_{2}}{P_{1}}=\frac{P_{1}-P_{2}}{\left( \beta _{1}+\beta _{2}\ln \hbox {DIST}_{r}\right) P_{1}}. \end{aligned}$$

(19)

Ideally, if we knew which tickets are served as high-end and low-end in the data set, the $\theta$ values would lie in the theoretical boundaries provided in the market power estimation section. However, $\theta$ does not necessarily lie in the unit interval. The reason is that our high-end and low-end price choices do not necessarily coincide with the theoretical high-end and low-end prices. However, since $P_{1}$ and $P_{2}$ are chosen from the same percentiles (i.e., 80th and 20th) for all routes–time–airline triples, $\theta$ values may be useful to analyze “relative” market powers for airline markets.

Table 2 provides the demand estimates from 2SLS estimation.¹⁸ As a robustness check, in the third column, we weighted observations by the average number of passengers for each route–carrier pair over the sample.¹⁹ As we mentioned above, since the inverse demand function is in log–log form and the route and time dummies are included in the estimations, we can replace $Q_{1}$ by Q in the model. The instruments include the explanatory variables of the model, (logarithm) of total quantities for the industry (excluding the relevant carrier’s route quantity), and lagged values of $\ln Q_{rt}$ and $\ln Q_{rt}\ln \hbox {DIST}_{r}$. The quantity for the industry instrument is based on the quantities in other route markets. The quantity for a market and sum of all quantities for the other markets are assumed to be independent. A similar set of instruments were used in Kutlu and Sickles (2012). Under-identification and weak identification are rejected at any conventional significance levels. The F statistic of excluded instruments is given by $F(392{,}172)=32{,}081$. While Sargan’s test for over-identification fails, it is unclear whether the large number of observations is the reason for the rejection. As argued by Nevo (2001), it is well known that with a large enough sample such tests will be rejected by essentially any model. Moreover, when we only use the lagged values of endogenous variables as instruments, so that we have exact identification, the conduct estimates from this model have a correlation of 1 with the conduct estimates from the benchmark model.

Table 2 Demand estimation

The 5th, 50th, and 95th percentiles of price elasticity estimates are 1.77, 2.06, and 2.41, respectively. Moreover, the minimum, maximum, and mean values for elasticities are 1.67, 2.84, and 2.07, respectively. Hence, the elasticity and slope of demand have correct signs for all sample observations. Moreover, as expected, the median demand elasticity for short-distance flights (distance below 50th percentile) is smaller than that of long-distance flights (distance above 50th percentile), i.e., 1.93 and 2.21, respectively. Both Pearson and Spearman correlations of $\theta$ estimates from benchmark and weighted models are 0.94. Hence, the market power estimates are similar.

In their meta-study for airline price elasticities, Brons et al. (2002) find that mean and standard deviation of price elasticity estimates, based on 204 different studies, are 1.15 and 0.62. The highest price elasticity value in their meta-study is 3.20. This suggests that our price elasticity estimates are reasonable. The 5th, 50th, and 95th percentiles of $\theta$ estimates are 0.59, 0.95, and 1.46, respectively.²⁰ The mean and standard deviation for $\theta$ estimates are 0.97 and 0.26, respectively. As mentioned above, $\theta$ does not lie in the theoretical bounds as it is not constructed from the theoretical quantity and price values. However, it still provides us some useful information about the relative market powers of airlines. Figure 1 provides the carrier-specific average $\theta$ estimates over time. Since route-specific market power is heterogeneous, there are variations in the $\theta$ estimates. Hence, in order to provide more information about the distributions of $\theta$ estimates, we also provide 10th and 90th percentiles for the $\theta$ estimates. The fitted values in the figure are obtained from regressing the $\theta$ values on time. As it can be seen, in general, the market powers of airlines either remained relatively constant or decreased.

Fig. 1

Carrier-specific mean market power

One relevant question is whether our market power measure has a positive relationship between market concentrations. For this purpose, we regress our $\theta$ estimates on route–time-specific $\hbox {HHI}$ values, $\ln \hbox {POP}$, $\ln \hbox {PCI}$, $\ln \hbox {SIZE}$, time dummies, and route–airline dummies. Since $\hbox {HHI}$ may potentially be endogenous, we estimate two models. In the first one we assume that $\hbox {HHI}$ is exogenous, and in the second one, we assume that $\hbox {HHI}$ is endogenous and instrument $\hbox {HHI}$ by its lagged values. For both cases the coefficient estimates for $\hbox {HHI}$ variable are positive and significant at any conventional significance level. The estimation results are given in Table 3.

Table 3 Conduct and HHI relationship

So far, in line with our conduct parameter model, we assumed that the market powers of high-end and low-end segments are the same. It is worth to explore whether this is a sensible assumption by using our general market power index given in Eq. (12). We already calculated the market power index for the high-end segment, i.e., $\theta _{1}=\theta$. The market power index for the low-end segment is:

$$\begin{aligned} \theta _{2}=\epsilon _{2}\frac{P_{2}-\hbox {MC}}{P_{2}} \end{aligned}$$

where $\epsilon _{2}$ is the price elasticity for low-end segment as defined earlier, $P_{2}$ is the low-end segment price, and $\hbox {MC}$ is the marginal cost, which is proxied by the 5th percentile of prices. The comparison of market power estimates for high-end and low-end segments and single-price scenario is given in Table 4.

Table 4 Conduct estimates comparison

A mean equality test concludes that $\theta _{1}>\theta _{2}$ for any conventional significance level.²¹ Since our empirical version of the conduct is a relative measure, in Table 4 we show the Spearman correlations of conduct estimates with high-end and low-end estimates. Interestingly, the low-end and high-end markets have a very low (yet statistically significant) Spearman correlation. This result illustrates how differently these markets can behave. Relatively low Spearman correlation between price discrimination and single-price conduct estimates shows that using a single-price index may be deceptive.

The carrier-specific market power estimates for the low-end segment are provided in Fig. 2. Our qualitative results for the relationship between $\theta _{2}$ and $\hbox {HHI}$ are the same as what we found for $\theta =\theta _{1}$, i.e., for both exogenous and endogenous $\hbox {HHI}$ scenarios, the relationship is positive at any conventional significance levels.

Fig. 2

Carrier-specific mean market power for low-end segment

4 Conclusion

In many industries price discrimination is prevalent yet often mergers are analyzed in a single-price framework. If antitrust authorities ignore price discrimination, then they may end up blocking socially beneficial mergers or accepting socially harmful mergers. A conduct parameter measure of market power specific for the price discrimination environment can potentially prevent such suboptimal decisions. For this purpose we designed a conduct parameter model that enables estimation of market power in the presence of price discrimination. Like many other market power measures, our measure is static. In dynamic environments, this might result in inconsistent parameter estimates. This is a general criticism for concentration measures, such as HHI, the Lerner index, and in conduct parameter models.²² A possible solution would be to extend our model to a framework such as that in the single-price model of Kutlu and Sickles (2012) so that the firms play a dynamic efficient super-game. However, such an extension is beyond the scope of this paper.

An important aspect of our model is that it enables us to examine the relationship between price discrimination and market power. For this purpose we used a variety of (widely used) functional forms that lead to a closed-form solution for the equilibrium. For all of these scenarios there is a positive relationship between market power and price discrimination. Hence, while we do not have compelling theoretical evidence for such a positive relationship, it appears that for many of the sensible scenarios a positive relationship is likely to hold.

Our empirical example illustrated how our methodology for the estimating market power of firms in the price discrimination framework can be applied by estimating the market power of US airlines. Our illustrative empirical model serves as an example for how a price discrimination model can be estimated in our framework. Although our data do not allow us to precisely categorize the price groups, we partially solve this problem by using specific percentiles of prices. We overcame estimation problems for demand function by choosing the log–log demand form and including airline–route- and time-specific dummy variables. It turns out that market power for the high-end segment, on average, is greater than that of the low-end segment. Moreover, we conclude that using a single-price conduct measure may be deceptive due to low correlation between price discrimination and single-price conduct estimates. In general, the market powers of US airlines did not increase over time, i.e., they either remained relatively stable or decreased. We also showed that market concentration is directly related to the market power. Other empirical settings and other data sources may provide such precise categories, while many, such as ours, may not, and we have developed a method to analyze price discrimination in both scenarios.