Applying a microfounded-forecasting approach to predict Brazilian inflation

Abstract

We investigate whether combining forecasts from surveys of expectations is a helpful empirical strategy for forecasting inflation in Brazil. We employ the FGV–IBRE Economic Tendency Survey, which consists of monthly qualitative information from approximately 2000 consumers since 2006, and also the Focus Survey of the Central Bank of Brazil, with daily forecasts since 1999 from roughly 250 professional forecasters. Natural candidates to win a forecast competition in the literature of surveys of expectations are the (consensus) cross-sectional average forecasts (AF). We first show that these forecasts are a bias-ridden version of the conditional expectation of inflation using the no-bias tests proposed in Issler and Lima (J Econom 152(2):153–164, 2009) and Gaglianone and Issler (Microfounded forecasting, 2015). The results reveal interesting data features: Consumers systematically overestimate inflation (by 2.01 p.p., on average), whereas market agents underestimate it (by 0.68 p.p. over the same sample). Next, we employ a pseudo out-of-sample analysis to evaluate different forecasting methods: the AR(1) model, the Granger and Ramanathan (J Forecast 3:197–204, 1984) forecast combination (GR) technique, a Phillips-curve based method, the Capistrán and Timmermann (J Bus Econ Stat 27:428–440, 2009) combination method, the consensus forecast (AF), the bias-corrected average forecast (BCAF), and the extended BCAF. Results reveal that: (i) the MSE of the AR(1) model is higher compared to the GR (and usually lower compared to the AF); and (ii) the extended BCAF is more accurate than the BCAF, which, in turn, dominates the AF. This validates the view that the bias corrections are a useful device for forecasting using surveys. The Phillips-curve based method has a median performance in terms of MSE, and the Capistrán and Timmermann (2009) combination method fares slightly worse.

1 Introduction

From a theoretical and empirical point-of-view, Bates and Granger (1969) made the econometric profession aware of the benefits of forecast combination. Their empirical results were later confirmed by a variety of time-series studies—e.g., Granger and Ramanathan (1984), Palm and Zellner (1992), Stock and Watson (2002a, (2002b, (2006), Timmermann (2006), and Genre et al. (2013)—where the simple average of forecasts is shown to perform relatively well.

In a pioneering study on forecasting using panel-data techniques, Davies and Lahiri (1995) proposed testing forecast rationality using information across forecasts and forecast horizons by employing a three-way decomposition.¹ This lead to a subsequent literature on what could be labeled a panel-data approach to forecasting; see Baltagi (2013) for a broader discussion on this topic. Some of these studies focused on forecast combination and others on density-forecast estimation, e.g., Issler and Lima (2009), Gaglianone et al. (2011), Gaglianone and Lima (2012, (2014), Gaglianone and Issler (2015), and Lahiri et al. (2015).

In Issler and Lima and Gaglianone and Issler, the main idea is that the consensus forecast (the cross-sectional average of individual forecasts) is a bias-ridden version of the conditional expectation, which is the optimal forecast under a mean-squared-error (MSE) risk function. Once these potential biases are properly removed, one can construct forecasting devices that are optimal in the limit, i.e., that can approach the conditional expectation asymptotically.

In this paper, we show empirically that combining forecasts in surveys is a promising empirical strategy to increase forecast accuracy. Our focus is on Brazilian inflation, a key variable on the Inflation Targeting Regime , implemented by the Central Bank of Brazil (BCB). In Brazil, there are two main surveys of expectations regarding inflation. The first is the Focus Survey—a survey of professional forecasters—kept by the BCB. The second is the FGV–IBRE Economic Tendency Survey—a survey of individual consumers. Both include forecasts for the official index used in the Inflation Targeting Regime—the IPCA, a Broad Consumer Price Index (CPI). Using information in these surveys, we employ the techniques in Issler and Lima and in Gaglianone and Issler to construct potentially optimal forecasts under MSE risk. The method discussed in the former shows that the mean of the consensus forecast is biased. The method discussed in the latter is microfounded and shows that the optimal forecast decision faced by an individual agent is related to the conditional expectation by an affine structure. This leads to the fact that the consensus forecast has two sources of bias—an intercept bias and a slope bias. Fortunately, they can be estimated to filter out the conditional expectation from a database of survey responses.

Using bias correction for the consensus forecast is a relevant empirical issue, since there is a growing forecasting literature in macroeconomics where the consensus forecast is used with no correction and rationality tests employing it usually find a result opposite to rationality; see, e.g., Coibion and Gorodnichenko (2012). Below, we show some evidence of these phenomena and discuss some important implications regarding rationality tests.

The usefulness of survey data for forecasting has been recently shown in a variety of studies. For example, Ang et al. (2007) find that true out-of-sample survey forecasts (e.g., Michigan; Livingston) outperform a large number of out-of-sample single-equation and multivariate time-series competitors. Faust and Wright (2013) argue that subjective forecasts of inflation based on surveys seem to outperform model-based forecasts in certain dimensions, often by a wide margin. In a world where there is an increasing availability of reliable survey data provided electronically, it is interesting to examine how one could efficiently use it. This is exactly the objective of this paper, where we exploit the fact that the Focus Survey has information on more than 250 professional forecasters and that the Economic Tendency Survey keeps responses of about 1500 respondents on inflation expectations in every month.

The rest of the paper is divided as follows. Section 2 discusses the econometric techniques employed in this paper, with some focus on the work of Issler and Lima (2009) and of Gaglianone and Issler (2015), but covering the adjacent literature as well. Section 3 presents a real-time forecasting exercise with data from the FGV survey of consumer expectations on inflation and from the Focus survey of the BCB on inflation expectations of professional forecasters. It also discusses rationality tests using the consensus forecasts and its possible shortcomings. Section 4 concludes.

2 Econometric methodology

Forecast combination has proved to be a valuable tool at least since Bates and Granger (1969). Palm and Zellner (1992) and Davies and Lahiri (1995) pioneered the use of panel-data techniques in forecasting. This section discusses in some detail the forecast-combination approach put forth by Gaglianone and Issler (2015) on how to combine survey expectations to obtain optimal forecasts in a panel-data context. Some parts of the material therein can also be found in Issler and Lima (2009) and in Lahiri et al. (2015).

The techniques discussed in this section are appropriate for forecasting a weakly stationary and ergodic univariate process $\left\{ y_{t}\right\}$ using a large number of forecasts, coming from forecast surveys (expectations) on the variable in question – $y_{t}$. Some (or all) of these responses can be generated by using econometric models, but then we have no knowledge of them. We label individual forecasts of $y_{t}$, computed using information sets lagged h periods, by $f_{i,t}^{h}$, $i=1,2,\ldots ,N$, $h=1,2,\ldots ,H$, and $t=1,2,\ldots ,T$. Therefore, $f_{i,t}^{h}$ are h-step-ahead forecasts of $y_{t}$, formed at period $t-h,$ and N is the number of respondents of this opinion poll regarding $y_{t}$. Gaglianone and Issler show that, in a variety of interesting cases, optimal forecasts are related to $\mathbb {E}_{t-h}(y_{t})$—the conditional expectation of $y_{t}$, computed using information lagged h periods—by an affine function:

$$\begin{aligned} f_{i,t}^{h}=k_{i}^{h}+\beta _{i}^{h}\mathbb {E}_{t-h}(y_{t})+\varepsilon _{i,t}^{h}. \end{aligned}$$

(1)

This result is somewhat expected given the pioneering work of Granger (1969). He shows that, under a mean-squared-error (MSE) risk function and proper regularity conditions, the optimal forecast is equal to $\mathbb {E}_{t-h}(y_{t})$. Moreover, if the risk function is asymmetric and proper regularity conditions are met, then Granger showed that the optimal forecast is equal to $\mathbb {E}_{t-h}(y_{t})+k_{i}^{h}$; see also the later developments in Christoffersen and Diebold (1997), Elliott and Timmermann (2004), Patton and Timmermann (2007), and Elliott et al. (2008), for example.

Gaglianone and Issler consider a setup with two layers of decision making. In the first layer, individuals (survey respondents) form their optimal point forecasts $\left( f_{i,t}^{h}\right)$ of a random variable $y_{t}$ by using a specific loss function. They allow for the existence of asymmetry of the loss function and different assumptions about knowledge of the DGP of $y_{t}$. The optimal forecasts $f_{i,t}^{h}$ will be available as survey results, where the number of respondents is potentially large, i.e., $N\rightarrow \infty$, and these surveys can be periodically taken on a large number of different occasions, i.e., $T\rightarrow \infty$. In the second layer of decision making, an econometrician will be the final user of this large number of forecasts, operating under an MSE risk function. Her/his challenge is to uncover $\mathbb {E}_{t-h}\left( y_{t}\right)$—the optimal forecast of the second layer of decision making.

Gaglianone and Issler employ the basic assumptions in the econometric forecast literature to derive a consistent estimate of $\mathbb {E} _{t-h}\left( y_{t}\right)$, which can be obtained by using Hansen’s (1982) generalized method of moments (GMM). Start by taking a cross-sectional average of (1), after using:

$$\begin{aligned} y_{t}=\mathbb {E}_{t-h}(y_{t})-\eta _{t}^{h}, \end{aligned}$$

(2)

noting that $\eta _{t}^{h}$ is a martingale-difference sequence by construction, i.e., $\mathbb {E}_{t-h}(\eta _{t}^{h})=0$. Under suitable assumptions, they show that the following system of equations can be used to estimate the key parameters $\overline{k^{h}}$ and $\overline{\beta ^{h}}$ in:

$$\begin{aligned} \mathbb {E}\left[ \left( \overline{f_{\cdot ,t}^{h}}-\overline{k^{h}}- \overline{\beta ^{h}}y_{t}\right) \otimes z_{t-s}\right] =0,\quad h=1,2,\ldots ,H, \end{aligned}$$

(3)

where $z_{t-s}$ is a vector of instruments, dated $t-s$ or older, $s\ge h$, $\overline{f_{\cdot ,t}^{h}}=\frac{1}{N}\sum \nolimits _{i=1}^{N}f_{i,t}^{h}$, $\overline{k^{h}}=\frac{1}{N}\sum \nolimits _{i=1}^{N}k_{i}^{h}$ and $\overline{ \beta ^{h}}=\frac{1}{N}\sum \nolimits _{i=1}^{N}\beta _{i}^{h}$, for each h. Over-identification requires that $dim(z_{t-s})>2$.

Gaglianone and Issler argue that there is no need to estimate individual coefficients $k_{i}^{h}$ and $\beta _{i}^{h}$—only their means to be able to identify and estimate $\mathbb {E}_{t-h}(y_{t})$. In doing so, they avoid the curse of dimensionality given that $N\rightarrow \infty$. As long as these cross-sectional averages converge, GMM using time-series restrictions delivers consistent estimates of the respective parameter means.

Current surveys, however, usually approximate better the case where $T\rightarrow \infty$, while N is small or diverges at a smaller rate than T. Under additional conditions on the cross-sectional averages $\overline{ f_{\cdot ,t}^{h}}=\frac{1}{N}\sum \nolimits _{i=1}^{N}f_{i,t}^{h}$, $\overline{ k^{h}}=\frac{1}{N}\sum \nolimits _{i=1}^{N}k_{i}^{h}$ and $\overline{\beta ^{h} }=\frac{1}{N}\sum \nolimits _{i=1}^{N}\beta _{i}^{h}$, Gaglianone and Issler show that one can still estimate $\mathbb {E}_{t-h}(y_{t})$ consistently, when $T\rightarrow \infty$ first, and then $N\rightarrow \infty$.

One way to exploit all possible moment conditions implicit in (3) is to stack all the restrictions across h (finite) as:

$$\begin{aligned} \mathbb {E}\left[ \left( \begin{array}{c} \overline{f_{\cdot ,t}^{1}}-\overline{k^{1}}-\overline{\beta ^{1}}y_{t} \\ \overline{f_{\cdot ,t}^{2}}-\overline{k^{2}}-\overline{\beta ^{2}}y_{t} \\ \vdots \\ \overline{f_{\cdot ,t}^{H}}-\overline{k^{H}}-\overline{\beta ^{H}}y_{t} \end{array} \right) \otimes z_{t-s}\right] =0, \end{aligned}$$

(4)

where the problem collapses to one where we have $H\times dim(z_{t-s})$ restrictions and 2H parameters to estimate. As before, over-identification requires that $dim(z_{t-s})>2$. Given a choice of H, GMM estimation of (4) is efficient.² A less efficient alternative to estimate the whole stacked system (4) is to estimate separately (3) for every horizon h, which could also be attempted for computational reasons. As is usual within GMM estimation, one can perform a standard misspecification test of correlation between errors and instruments by employing the J-test proposed by Hansen (1982).

Using GMM estimates, $\widehat{\overline{k^{h}}}$ and $\widehat{\overline{ \beta ^{h}}}$, obtained when $T\rightarrow \infty$, Gaglianone and Issler show the critical result that:

$$\begin{aligned} \frac{1}{N}\sum \limits _{i=1}^{N}\frac{f_{i,t}^{h}-\widehat{\overline{k^{h}} }}{\widehat{\overline{\beta ^{h}}}}\overset{p}{\longrightarrow }\mathbb {E} _{t-h}\left( y_{t}\right) , \end{aligned}$$

(5)

in a variety of different setups: when $T\rightarrow \infty$ first, and then $N\rightarrow \infty$; when $N\rightarrow \infty$ first, and then $T\rightarrow \infty$; and when $N,T\rightarrow \infty$ in a joint limit framework, all using the method in Phillips and Moon (1999). The conditions under which (5) holds vary according to the asymptotic setup.

Equation (5) offers a way to filter the consensus forecast $\frac{1}{N}\sum \nolimits _{i=1}^{N}f_{i,t}^{h}$ extracting $\mathbb {E} _{t-h}\left( y_{t}\right)$ in the limit. Thus, it delivers an estimate of the optimal forecast in the second layer of decision making. It can be viewed immediately as a forecast-combination method.

A paper that delivers a similar result, although suggests a different estimation method, is Capistrán and Timmermann (2009). Start with Eq. (1) and take the cross-sectional average to obtain³:

$$\begin{aligned} \frac{1}{N}\sum \limits _{i=1}^{N}f_{i,t}^{h}= & {} \frac{1}{N} \sum \limits _{i=1}^{N}\left( k_{i}^{h}+\beta _{i}^{h}\mathbb {E} _{t-h}(y_{t})+\varepsilon _{i,t}^{h}\right) ,\quad \text {or, in standard notation, } \nonumber \\ \overline{f_{\cdot ,t}^{h}}= & {} \overline{k^{h}}+\overline{\beta ^{h}}\mathbb { E}_{t-h}(y_{t})+\overline{\varepsilon _{\cdot ,t}^{h}} \end{aligned}$$

(6)

Combine (6) with (2) to obtain, for large enough N:

$$\begin{aligned} y_{t}=-\frac{\overline{k^{h}}}{\overline{\beta ^{h}}}+\frac{1}{\overline{ \beta ^{h}}}\overline{f_{\cdot ,t}^{h}}-\eta _{t}^{h}. \end{aligned}$$

(7)

The approach in Capistrán and Timmermann yields a single equation where $\overline{k^{h}}$ and $\overline{\beta ^{h}}$ can be estimated to filter $\mathbb {E}_{t-h}\left( y_{t}\right)$ in a similar fashion to that in (5). As can be seen by comparing (7) and (3), these two equations identify $\overline{k^{h}}$ and $\overline{\beta ^{h}}$. A potential advantage for the method in Gaglianone and Issler using (4) is that it allows stacking moment conditions across horizons and joint estimation of the bias terms. Thus, it benefits from the efficiency gains associated with employing a multi-equation setup as opposed to the single-equation setup in Capistrán and Timmermann. In the empirical section, we shall compare directly these two methods regarding their out-of-sample mean-squared error.

In an out-of-sample forecasting exercise involving surveys, there are usually three consecutive distinct time sub-periods, where time is indexed by $t=1,2,\ldots ,T_{1},\ldots ,$ $T_{2},\ldots ,T$. The first sub-period E is labeled as the “estimation sample,” where models are usually fitted to forecast $y_{t}$ in the subsequent period, if that is the case. The number of observations in it is $E=T_{1}=\kappa _{1}\cdot T$, comprising ($t=1,2,\ldots ,T_{1}$). For the other two, we follow the standard notation in West (1996). The sub-period R (for regression) is labeled as the post-model-estimation or “training sample,” where realizations of $y_{t}$ are usually confronted with forecasts produced in the estimation sample, and weights and bias-correction terms are estimated, if that is the case. It has $R=T_{2}-T_{1}=\kappa _{2}\cdot T$ observations in it, comprising ($t=T_{1}+1,\ldots ,T_{2}$). The final sub-period is P (for prediction), where genuine out-of-sample forecast is entertained. It has $P=T-T_{2}=\kappa _{3}\cdot T$ observations in it, comprising ($t=T_{2}+1,\ldots ,T$). Notice that $0<\kappa _{1},\kappa _{2},\kappa _{3}<1$ , $\kappa _{1}+\kappa _{2}+\kappa _{3}=1$, and that the number of observations in these three sub-periods keep a fixed proportion with T—respectively, $\kappa _{1}$, $\kappa _{2}$ and $\kappa _{3}$—being all $O\left( T\right)$.

It is worth mentioning that the method proposed by Gaglianone and Issler extends the previous literature of forecasting within a panel-data framework, e.g., Palm and Zellner (1992), Davies and Lahiri (1995), Issler and Lima (2009), and Lahiri et al. (2015).

For example, their setup encompasses that of Davies and Lahiri (1995), reproduced below with our notation:

$$\begin{aligned} y_{t}-f_{i,t}^{h}=-\left( k_{i}^{h}+\eta _{t}^{h}+\varepsilon _{i,t}^{h}\right) , \end{aligned}$$

(8)

who imposed $\beta _{i}^{h}=1$ for all $i=1,\ldots ,N$ and $k_{i}^{h}=k_{i}$ for all $h=1,\ldots ,H$. Also, it generalizes the results in Issler and Lima, where slopes are restricted as $\beta _{i}^{h}=1$ for all $i=1,\ldots ,N$. Here, we have two sources of bias correction: intercept and slope. Notice that both arise from a structural affine function that links individual forecasts to the conditional expectation. In itself, this provides a general framework that can be used whenever a panel of forecasts is available.

The method proposed by Gaglianone and Issler is appropriate to cover any type of survey where potentially the number of observations T is large, encompassing the cases where the number of survey respondents and of time observations is large—big data, and also the case where the number of time observations is large but the number of respondents is fixed—standard continuous macroeconomic surveys.

The way Gaglianone and Issler identify the conditional expectation can be viewed as a combination of cross-sectional averages with standard GMM moment restrictions, where the affine structure offers natural orthogonality restrictions allowing the estimation of bias-correction terms. They circumvent the curse of dimensionality that arises from the factor structure (large N) by employing these cross-sectional averages.

3 Empirical application

3.1 Data

3.1.1 FGV’s consumer survey

The FGV–IBRE Economic Tendency Survey compiles business and consumers expectations of key economic series in Brazil. The Brazilian Institute of Economics (IBRE) is a pioneer in surveys, and this one runs since 1966. Since September, 2005, FGV–IBRE conducts a monthly consumer survey, which consists of qualitative information on household consumption, savings, financial variables, employment, etc. The survey has a country-wide coverage (seven major state capitals) with approximately 2000 consumers. Survey respondents are classified into four classes of household monthly income as follows⁴: Income Level 1—Up to R$2100; Income Level 2—Between R$ 2100.01 and R$ 4800.00; Income Level 3—Between R$4800.01 and R$ 9600.00; Income Level 4—More than R$ 9600.01. Survey information can also be broken down by different classes of education: Group 1—No education or incomplete first year; Group 2—Complete first year or incomplete primary education; Group 3—Complete primary education or incomplete secondary education; Group 4—Complete secondary education or incomplete undergraduate; Group 5—Complete undergraduate; and Group 6—Graduate studies.

The panel is unbalanced, and on average, each household is interviewed 7.81 times (months) per year. We possess microdata at the individual level for this survey, beginning in January 2006 through to May 2015 ($T=113$ months). Overall, our sample has $N\times T$ = 164,479 responses. Decomposing our sample into N and T gives the following breakdown: $T=113$ months, and an average of approximately $N=1456$ individuals per month. The key question of interest for us is the following: “In your opinion, how much will be Brazilian inflation over the next 12 months?” We excluded outliers in the data set whenever the respondent answered that inflation would be greater than 100 % in the next 12 months. In our sample, it was rare to observe 12-month inflation greater than 10 %, so we considered this type of response completely out of scope.⁵

3.1.2 Focus survey of the Central Bank of Brazil

The Focus Survey of forecasts of the Central Bank of Brazil (BCB) contains daily (working days) forecasts from roughly 250 registered institutions since 1999, the year when Brazil implemented its Inflation-Targeting Regime.⁶ About 100 of these institutions are actively feeding the database with forecasts on any given day. Institutions include professional forecasters—commercial banks, asset management firms, consulting firms, non-financial firms or institutions, academics, etc. Participants can provide forecasts for a large number of economic variables, e.g., inflation using different price indices, interest and exchange rates, GDP, industrial production, balance of payments accounts, and fiscal variables and for different forecast horizons.

Our focus here is on Brazilian inflation, measured by the Brazilian Consumer Price Index—IPCA, which is the official inflation target of the Brazilian Inflation-Targeting Regime. Our sample covers daily inflation forecasts collected from January 2nd, 2004 until May, 28th, 2015 (2861 workdays).⁷ In each day t, $t=1,\ldots ,T$, survey respondent i, $i=1,\ldots ,N$, may inform her/his expectations regarding inflation rates all the way up to the next 18 months, as well as for the next twelve months and for the next 5 years on a year-end basis. The data set regarding the twelve-month-ahead inflation forecasts forms an unbalanced panel ($N\times T$) containing an amount of 244,043 observations. Decomposing our total number of observations into N and T gives the following breakdown: T = 2861 daily observations and an average of $N=85.3$ forecasters in our sample. For more information on this data set, see Carvalho and Minella (2012) and Marques (2013).

Despite the fact that the Focus Survey has a longer time span and a higher frequency than FGV’s Consumer Survey (working day vs. monthly), our sample size is, most of the time, constrained by the span and frequency of the latter.

3.1.3 Consensus forecasts

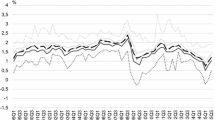
Our target variable $y_{t}$—is Brazilian inflation—as measured by the Broad Consumer Price Index (IPCA) collected at the monthly frequency. The consumer forecasts $f_{i,t}^{h}$ from the FGV survey regarding expected inflation rate over the next 12 months ($h=12$ months) are cross-sectionally averaged, forming the so-called consensus forecasts $\overline{f_{\cdot ,t}^{h}}=\frac{1}{N}\sum \nolimits _{i=1}^{N}f_{i,t}^{h}$. Besides the average over the entire data set (approximately 1500 households), labeled hereafter as “cons_all”, the individual forecasts are also averaged by selected demographic groups, according to the education level of the survey participant or to its level of income. The breakdown by education yields the following consensuses: cons_educ_1_3; cons_educ_4 and cons_educ_5_6, respectively, educational levels groups 1 through 3, level 4, and group level 5 through 6. For income, we breakdown the groups numbered from 1 to 4, respectively: cons_inc_1; cons_inc_2; cons_inc_3; cons_inc_4. Figure 1 plots these eight time series of aggregate (cross-sectional mean) forecasts.

Fig. 1

Consensus inflation forecasts $\overline{f_{\cdot ,t}^{h} }$ from the FGV consumer survey (% 12-months-ahead)

Fig. 2

Comparison of the consumer and market inflation forecasts $\overline{f_{\cdot ,t}^{h}}$ with the actual inflation rate $y_{t}$ (% 12 months)

There is considerable heterogeneity across groups, either from an education or income point of view. Low-income households usually forecast higher inflation rates vis-à-vis the forecasts of higher-income families. Obviously, inflation is not perceived equally by all families, each with its own consumption bundle. Low-income households spend more on food, while higher-income households spend a larger proportion of their budget on housing, education, and leisure. By construction, the IPCA index follows closely the cost-of-living of households with income well above the income level of our categories 1 and 2.

Figure 2 compares the consensuses of consumer forecasts (cons_all), professional (or market forecasts from the Focus Survey), and the twelve-month-ahead IPCA inflation rate. The latter is exactly what these forecasts are supposed to track. Market forecasts are collected at the 10th and 15th day of each month (focus_day10, focus_day15). This makes the focus consensus consistent with the days in which the data are collected for the FGV consumer survey. On average, the consumer consensus has a positive bias, while the consensus of professional forecasters has a negative bias. It is also worth noting that the behavior of both consensuses is very different at the end of the sample period. While the consumer consensus follows the observed increase in inflation, the consensus of professional forecasters gets it completely wrong, predicting a decrease in inflation.

3.2 Empirical results

3.2.1 Descriptive statistics

Table 1 shows the pairwise sample correlations of the consensuses forecasts. Notice that all series are highly correlated. The consensus forecasts of consumers and of market agents show a sample correlation of 0.80.

Table 1 Sample correlations

Table 2 presents the sample mean and the respective estimation of the asymptotic standard error based on the number of sample observations $T=113$. Next, we investigate whether or not the consensuses forecasts Granger Cause future inflation using Sims’ test. More than half of the consensuses forecasts for consumers Granger Cause future inflation, i.e., are leading indicators of future inflation. This is also true for the consensus including all consumers. The same is true for both the consensuses of professional forecasters. Therefore, they will be useful as tools in forecasting future inflation.

Table 2 Mean forecast, SE, and Granger Causality test

3.2.2 Bias-correction devices

In Fig. 2, we provided soft evidence that the consensuses forecasts are biased as predictors of future inflation. Next, we formally test for zero bias employing the bias-corrected average forecast (BCAF) approach of Issler and Lima (2009). There, the estimate of the out-of-sample additive forecast bias $\overline{k^{h}}$ is:

$$\begin{aligned} \widehat{\overline{k^{h}}}=\frac{1}{NR}\sum \limits _{t=T_{1}+1}^{T_{2}}\sum \limits _{i=1}^{N}\left( y_{t}-f_{i,t}^{h}\right) , \end{aligned}$$

(9)

where its robust standard error is computed taking into account possible spatial and time dependence. Here, we employ the whole sample in estimating $\overline{k^{h}}$: $t=1,2,\ldots ,T$, where the consensus data runs from January 2006 to July 2014, whereas the IPCA sample runs from December 2006 to June 2015.

Results of the zero-bias test are presented in Table 3. As expected from the plot in Fig. 2, all consumer forecasts showed a negative bias, i.e., consumers overestimated future inflation, while all professional forecasts underestimated future inflation. The formal evidence provided below calls for the use of bias-correction devices in constructing optimal forecasts.

Table 3 BCAF additive bias $\overline{k^{h}}$ test (Issler and Lima 2009)

Table 4 Extended BCAF estimation and No Bias test

A possible shortcoming of the test in Table 3 is that it is implicitly assumed that $\overline{\beta ^{h}}=1.$ However, Gaglianone and Issler (2015) showed that, in general, there is an intercept and a slope bias term for the consensus forecast, suggesting the use of the Extended BCAF setup, where the parameters $\overline{k^{h}}$ and $\overline{\beta ^{h}}$ are estimated by the generalized method of moments (GMM) based on $y_{t}$ and $f_{i,t}^{h}$.⁸

Results of GMM estimation and of the no-bias test are presented in Table 4. We use a set of instruments $z_{t-s}$ containing two lags of the consensus forecasts $\overline{f_{\cdot ,t}^{h}}$, up to four lags of the output gap⁹ and two lags of the Commodity Price Index (IC-Br), which weighting structure is designed to measure the impact of commodity prices on Brazilian consumer inflation¹⁰; see Appendix for results using an alternative set of instruments. Hansen’s Over-Identifying Restriction (OIR) test is employed in order to check the validity of GMM estimates. At the usual significance levels, we do not observe any rejection for the OIR test. The no-bias test consists of a joint test of the null hypothesis $H_{0}{:}\,[\overline{k^{h}}=0; \overline{\beta ^{h}}=1]$. We reject the null of no-bias on all occasions, showing that the consensus forecasts are a bias-ridden version of the conditional expectation $\mathbb {E}_{t-h}\left( y_{t}\right)$.

From Eq. (5), note that, under the null $H_{0}{:}\,[\overline{ k^{h}}=0;\overline{\beta ^{h}}=1]$, the aggregate forecast $\overline{ f_{\cdot ,t}^{h}}$ should converge in probability to the conditional expectation $\mathbb {E}_{t-h}\left( y_{t}\right)$, with no need for bias correction. However, if the null is rejected, we should expect a corrected version of the consensus forecast to produce superior forecasts vis- à-vis the consensus forecasts. These are exactly our findings below.

Table 5 Forecast combination (Granger and Ramanathan 1984) $\mathrm{IPCA}_{t+12}{=\alpha +\beta }_{1}{\mathrm{cons}\_\mathrm{all}}_{t} {\,+\,\beta }_{2}{\mathrm{focus}\_\mathrm{day}10}_{t}{\,+\,\varepsilon }_{t+12}$

3.2.3 Forecast combination of consumer and market expectations

Next, we apply the Granger and Ramanathan (1984) forecast combination technique for the entire sample. It consists of a standard OLS regression (including an intercept) of IPCA inflation on the two consensus forecasts—consumer and market, respectively: cons_all and focus_day10. We run those regressions in two different ways: When the two slope coefficients are unrestricted and when they are restricted to add up to unity. Also, we cover two different sample periods: the whole sample and only the last five years. Results are presented in Table 5. Notice that, for the last 5 years, the consumer consensus is not significant, which does not happen for the whole sample.

The estimated slopes can be interpreted as optimal weights under a MSE loss function. The combined (consumer-market) forecast is given by:

$$\begin{aligned} \widetilde{fcm}_{t}^{h}=\widehat{{\small \alpha }}+\widehat{\beta _{1}} \mathrm{cons}\_all_{t}+\widehat{\beta _{2}}\mathrm{focus}\_\mathrm{day}10_{t}. \end{aligned}$$

3.2.4 Out-of-sample forecasting exercise

In this section, we conduct a truly out-of-sample forecasting exercise, incorporating what we have learned from the previous sections. We compare different forecast methods by computing their out-of-sample mean-squared error (MSE) of forecasting. Our whole sample for the experiment runs from January 2006 through July 2014 for the forecasts and from February, 2006 through June 2015 for the realizations of inflation, comprising 103 and 113 observations, respectively. We leave the last 60 observations (5 years, comprising July 2010 through June 2015) for a pseudo out-of-sample evaluation of several forecasting strategies (or methods), which are estimated with a growing window. Thus, model parameters are estimated recursively as we incorporate every new time-series observation, one at a time. These forecasting methods include: a “best” model, chosen by information criteria, a Phillips-curve based forecast, the Granger and Ramanathan (1984) forecast-combination technique, the Capistrán and Timmermann (2009) consensus regression, the average forecast (or consensus forecast), the bias-corrected average forecast (BCAF), proposed by Issler and Lima (2009), and the extended BCAF, proposed by Gaglianone and Issler (2015). For the last four strategies, we also present the MSEs by category of income and education.

The best model using information criteria is the AR(1) model for the monthly inflation rate, see Cordeiro et al. (2015) and Gaglianone et al. (2016). The AR(1) model for the monthly inflation rate $y_{t}$ is as follows:

$$\begin{aligned} y_{t}=c+\beta y_{t-1}+\varepsilon _{t}. \end{aligned}$$

(10)

From a sample with $t=1,\ldots ,T$ observations, the respective estimates $\left[ \widehat{c}_{T};\widehat{\beta }_{T}\right] ^{\prime }$ are computed. The respective h-step-ahead forecast ($h>1$) is given by

$$\begin{aligned} \widehat{y_{T+h}}=\left( \widehat{\beta }_{T}\right) ^{h}y_{T}+\underset{i=1}{\overset{h}{\sum }}\widehat{c}_{T}\left( \widehat{\beta }_{T}\right) ^{i-1}, \end{aligned}$$

(11)

and the cumulative twelve-month rate ahead $y_{T+12}^{12m\_rate}$, in percentage is:

$$\begin{aligned} \widehat{y_{T+12}^{12m\_rate}}=100\left( \left( \underset{h=1}{\overset{12}{ \Pi }}\left( 1+\frac{\widehat{y_{T+h}}}{100}\right) \right) -1\right) . \end{aligned}$$

(12)

We also estimate a Phillips-curve model (PC), which has a long tradition in forecasting inflation (for a comprehensive survey, see Stock and Watson 2009). The Brazilian Central Bank (BCB) has had several years of experience fitting different versions of the Phillips curve, and we benefit from that in our forecasting exercise. Here, we consider a hybrid (New Keynesian) version of the Phillips curve, which includes backward and forward looking terms, lagged imported inflation (to consider a pass-through channel), and a lagged output gap. In the BCB experience, what works best for forecasting IPCA inflation is to disaggregate inflation into two main components: market prices (roughly 75 % of IPCA) and the so-called regulated and monitored prices (approximately 25 % of IPCA), which contains consumer items that are relatively insensitive to domestic demand and supply conditions or that are in some way regulated by a public agency. Since these two groups have completely different time dynamics, they are modeled separately. We first estimate a Phillips curve for inflation of the market prices basket, as follows:

$$\begin{aligned} \pi _{t}^\mathrm{market}=\alpha _{0}+\alpha _{1}\pi _{t-1}^\mathrm{market}+\alpha _{2}\pi _{t| t-1}^{\exp }+\alpha _{3}\pi _{t-4}^\mathrm{imp}+\alpha _{4}g_{t-1}+\varepsilon _{t}, \end{aligned}$$

(13)

where $\pi _{t}^\mathrm{market}$ is the monthly inflation of market prices, $\pi _{t| t-1}^{\exp }$ denotes the one-month ahead expected inflation (from the Focus survey), $\pi _{t}^\mathrm{imp}$ is what has been labeled as imported inflation (R$/US$ exchange rate variation plus the U.S. PPI), and $g_{t}$ is the output gap.¹¹ We also impose the coefficient restriction: $\alpha _{1}+\alpha _{2}+\alpha _{3}=1$, to guarantee a vertical long-run Phillips curve. For the so-called monitored prices, we estimate an auxiliary AR model. The usual criteria for lag order selection indicate one lag only (and the estimated autoregressive coefficient is 0.53). Then, we use each model to produce h-step ahead point forecasts ($h=1,\ldots ,12$ months) which are, then, aggregated through time to form a 12-month cumulated forecast for each component.¹² Both forecasts are then aggregated (using corresponding CPI weights) in order to generate an aggregated 12-month ahead point forecast for the whole IPCA inflation.

Table 6 presents the comparison of the out-of-sample MSE of the different forecast strategies listed above. First, the MSE of the AR(1) model is higher when compared to that of the Granger and Ramanathan combination of the consensuses of consumers and of professional forecasters, and it is lower than that of the average forecasts—exceptions are the consensus for the highly educated forecasters, higher income forecasters, and professional forecasters (Focus Survey). Second, when we compare the MSE of the average forecast, BCAF and Extended BCAF, there is a clear pecking order: The extended BCAF is more accurate than the BCAF, which, in turn, dominates the average forecast. This validates the view that the bias corrections performed either by the BCAF, or by the extended BCAF, are a useful device for forecasting using surveys. Third, when we compare the best forecasts for all consumers (Extended BCAF, cons_all) with the best forecasts for all professional forecasters (Extended BCAF, focus_day15), we observe a reduction in MSE in favor of professional forecasters of 22.5 %, which is sizable. This happens despite the fact that, for consumers, we are averaging the forecast of approximately 1500 individuals, whereas for professional forecasters, we employ about 85 individuals. This may be a sign that it matters to employ informed and well-trained professionals in forecasting inflation—a relief for the profession as a whole.

Forecasts using the Phillips curve ranked relatively well here—a median result—better than the AR(1) model, the average forecast, and the Capistrán and Timmermann method, but worse than the Granger–Ramanathan combination, the BCAF, and the extended BCAF. The Capistrán and Timmermann (2009) consensus regression did slightly worse than the Phillips curve. A direct comparison of Capistrán and Timmermann’s method with the extended BCAF is interesting here, since, in principle, both could potentially identify the intercept and slope biases present in the consensus forecast, respectively, denoted by $\overline{k^{h}}$ and $\overline{\beta ^{h}}$ in Sect. 2. Indeed, the MSEs of the Extended BCAF and that of the Capistrán and Timmermann method are very different across all levels of education and income for consumers, as well as for all days in the Focus Survey. When we consider all consumers, the MSE of the extended BCAF is 0.42 of that of Capistrán and Timmermann’s method, a sizable reduction.

In order to check whether the differences in MSE listed in Table 6 are significant, we employ the equal predictive accuracy test of Clark and West (2007) for nested models, and the equal predictive ability test of Diebold and Mariano (1995) for non-nested models. All MSE comparisons are direct between the MSE of the extended BCAF and that of any specific cell in Table 6. In most cases, the extended BCAF produces an MSE that is statistically different (and smaller) than that of the direct competitor. Details are as follows: The average forecast and the BCAF have an inferior out-of-sample MSE vis-à-vis the extended BCAF forecast. Comparisons of the extended BCAF with the AR(1) model using a Diebold–Mariano test for equal variances shows that the former is statistically superior to the latter (at the 10 % significance level) in almost all cases. The Extended BCAF for the market forecasts also statistically improves (at a 10 % level) the out-of-sample accuracy compared to the Granger and Ramanathan (1984) forecast combination approach. Also, it statistically improves on the Capistrán and Timmermann (2009) consensus-forecasting approach almost everywhere.

All in all, if we had to suggest a single forecasting strategy for Brazilian inflation one-year ahead, we would suggest the use of extended BCAF based on the Focus Survey consensus (15th working day).

Table 6 Forecast evaluation: mean-squared error (MSE) out of sample

3.2.5 Rationality tests

In testing for rationality, we employed two alternative approaches. The first is based on the well-known Mincer–Zarnowitz regression. It is only valid if one assumes that the forecaster minimizes the MSE risk function. For other functions, the test no longer applies,¹³ and one must find alternative ways of testing rationality. Here, we employed the quantile Mincer–Zarnowitz regression test proposed by Gaglianone et al. (2011).

Let $y_{t}$ be the 12-month inflation rate measured by IPCA, $f_{i,t}^{h}$ be the respective inflation forecast of survey participant i formed at period $t-h$, and $\overline{f_{\cdot ,t}^{h}}$ be the consensus forecast. The cross-sectional dimension is considered in two ways: (i) disaggregated data, with an individual OLS regression for each $i=1,\ldots ,N$ ¹⁴; and (ii) aggregated data (consensus forecast), with OLS regression. We focus on the widely employed rationality test of Mincer and Zarnowitz (1969), hereafter MZ. First, we consider disaggregate data, with an individual OLS regression for each $i=1,2,\ldots ,N$. The individual-forecasts OLS regressions are given as follows:

$$\begin{aligned} y_{t}=\alpha _{i}+\beta _{i}f_{i,t}^{h}+\varepsilon _{i,t}, \end{aligned}$$

(14)

where $y_{t}$ denotes observed inflation on period t, and $f_{i,t}^{h}$ denotes individual i forecast of $y_{t}$ using only information up to period $t-h$. The MZ test is based on a Wald test of the joint null hypothesis of rationality, $H_{0}{:}\,[\alpha _{i}=0;\beta _{i}=1]$ for each i. We then compute the proportion of agents for which we do not reject the null of rationality. Next, we consider aggregate data (consensus forecast), with OLS regression in time-series data. The consensus-forecast OLS regression is given by:

$$\begin{aligned} y_{t}=\alpha +\beta \overline{f_{\cdot ,t}^{h}}+\varepsilon _{t}, \end{aligned}$$

(15)

where the rationality test is based on a Wald test of the joint null hypothesis $H_{0}{:}\,[\alpha =0;\beta =1]$. In testing all the null hypotheses listed above, we have employed robust (HAC) standard errors. Results for consumer forecasts are summarized in Table 7.¹⁵

Table 7 Rationality (MZ) tests for consumers

When we consider tests using Mincer–Zarnowitz regressions with disaggregate data, individual OLS regressions for each i show that 35 % of the consumers indeed pass rationality tests at the 5 % significance level. Moreover, this percentage increases to 40 % and 37 % for the consensuses of higher educated consumers and for those with higher income, respectively. However, when we analyze test results using the consensus forecasts with OLS regressions, the null is always rejected at the 5 % level, which is consistent with results previously found in the literature, where rationality was rejected overwhelmingly in Mincer–Zarnowitz tests (Coibion and Gorodnichenko 2012), and the results are shown in Tables 3 and 4, in which the null of zero bias is strongly rejected.¹⁶

Next, we test for rationality by employing the quantile Mincer–Zarnowitz regression test proposed by Gaglianone et al. (2011). Similarly to the OLS-MZ regression, the idea is to estimate a quantile regression (QR), for a given quantile level $\tau$, of the form: $Q_{\tau }(y_{t}| \mathcal {F}_{i,t-h})=\theta _{0,i}(\tau )+\theta _{1,i}(\tau )f_{i,t}^{h}$, in the case of individual forecasts, and of the form: $Q_{\tau }(y_{t}| \mathcal {F}_{t-h})=$ $\theta _{0}(\tau )+\theta _{1}(\tau )\overline{f_{\cdot ,t}^{h}}$ for the consensus forecast.

The QR-MZ test is performed by using a Wald test of the joint null hypothesis $H_{0}:[\theta _{0,i}(\tau )=0;\theta _{1,i}(\tau )=1]$ at a given level $\tau \in \left( 0,1\right)$, for individual forecasts, or $H_{0}:[\theta _{0}(\tau )=0;\theta _{1}(\tau )=1]$ for the consensus forecast. The results are presented in Table 10 of the Appendix. Overall, there is an increase in the percentage of rational forecasters as long as the quantile level $\tau$ increases, suggesting that consumer’s rationality in Brazil is more likely to occur at the right tail of the inflation conditional distribution.¹⁷ This result is perfectly in line with the fact that consumers systematically overestimate inflation (which might be a sign that consumers assign more weight to positive forecast errors than to negative ones). With respect to the consensus forecast, similar to the result from the OLS-MZ test, we again strongly reject the null hypothesis of rationality (at a 1 % significance level) in the QR-MZ sense, for all considered cases.

We can summarize our results in this section as follows: We provide evidence that rationality test results based on a time series of individual forecasts are very different from those using the time series of the aggregate measure represented by the consensus forecast. When testing individuals separately, we find evidence of rationality for a subset of consumers, whereas we find the opposite for the consensus forecasts. These results are stronger when we focus on the mean forecast (standard MZ test), but are still present when we employ the quantile Mincer–Zarnowitz regression test proposed by Gaglianone et al. (2011). One possible explanation is that the group of “non-rational” consumers contaminates the result of the consensus.

4 Conclusions

In this paper, we investigate empirically whether or not combining forecasts from surveys of expectations is a helpful strategy for forecasting one-year-ahead CPI inflation for Brazil. Combining forecasts has been a promising strategy at least since the seminal paper of Bates and Granger (1969). The techniques used in this paper have their roots in the pioneering work of Davies and Lahiri (1995) on what could be labeled a panel-data approach to forecasting. In this literature, some of the studies focused on forecast combination and others on density-forecast estimation, e.g., Issler and Lima (2009), Gaglianone et al. (2011), Gaglianone and Lima (2012, (2014), Gaglianone and Issler (2015), and Lahiri et al. (2015); see Baltagi (2013) for a broader discussion on this topic.

We investigate inflation forecasts from the Brazilian Consumer Survey conducted by FGV–IBRE, which consists of monthly quantitative and qualitative information from consumers in seven major capitals of the country, with a representative sample of the population and the rate of consumption of each capital with approximately 2000 consumers. Our sample ranges from January 2006 up to May 2015, forming an unbalanced panel with NT = 164,479 responses ($T=113$ months; and an average of N = 1456 individuals per month). We also use The Focus Survey of the Central Bank of Brazil. It contains daily (working days) forecasts from roughly 250 registered institutions since 1999, the year when Brazil implemented its Inflation-Targeting Regime. About 100 of these institutions are actively feeding the database with forecasts on any given day. Institutions include professional forecasters working in commercial banks, asset management firms, consulting firms, non-financial firms or institutions, academics, etc.

Natural candidates to win a forecasting competition in the literature of surveys of expectations are the so-called consensus forecasts, i.e., the cross-sectional average among survey respondents. In an exploratory investigation, we first show that these consensus forecasts are a bias-ridden version of the conditional expectation of one-year ahead inflation. No-bias tests are conducted for the intercept and slope using the methods in Issler and Lima (2009) and Gaglianone and Issler (2015). The bias-test results reveal interesting features of the data: Consumers systematically overestimate inflation by 2.01 p.p., on average, whereas professional forecasters underestimate it by 0.68 p.p., on average, over the same sample. Furthermore, we show that these biases lead to rejection in the Mincer–Zarnowitz tests of rationality using the consensus forecasts for consumers, although from 22 to 40 % of consumers pass rationality tests at the individual level. We also apply the quantile Mincer–Zarnowitz regression test proposed by Gaglianone et al. (2011), where we found an increase in the percentage of rational forecasters as long as the quantile level $\tau$ increases, suggesting that consumer’s rationality in Brazil is more likely to occur at the right tail of the inflation conditional distribution.

In a pseudo out-of-sample analysis, we evaluate seven different forecasting methods consisting of: A “best” model chosen by information criteria, the Granger and Ramanathan (1984) forecast combination technique, the Phillips-curve based forecasts, the Capistrán and Timmermann (2009) consensus-forecast method, the consensus forecast, the bias-corrected average forecast (BCAF), and the extended BCAF; we found very interesting results. The out-of-sample MSE of the AR(1) model is higher to that of the Granger and Ramanathan combination of the consensuses of consumers and of professional forecasters. It is also lower than the out-of-sample MSE of the average forecasts—with a few exceptions. When we compare the MSE of the average forecast, BCAF, and Extended BCAF, there is a clear pecking order: The extended BCAF is more accurate than the BCAF, which, in turn, dominates the average forecast. This validates the view that the bias corrections performed either by the BCAF, or by the extended BCAF, are a useful device for forecasting using surveys. The results for the Capistrán and Timmermann (2009) consensus-forecast method are mixed. It beats the average forecast and the AR(1) model, but it is beaten by all the other combination methods and also by Phillips-curve based forecasts. The latter achieved a median result, since it was beaten by the Granger and Ramanathan combination, the BCAF, and the Extended BCAF.

Finally, when we compare the best forecasts for all consumers (Extended BCAF, cons_all) with the best forecasts for all professional forecasters (Extended BCAF, focus_day15), we observe a reduction in MSE in favor of professional forecasters of 22.5 %, which is sizable. This happens despite the fact that, for consumers, we are averaging the forecast of approximately 1500 individuals, whereas for professional forecasters, we employ a little less than 100 individuals. This may be a sign that it matters to employ informed and well-trained professionals in forecasting inflation—a relief for the profession.

All in all, if we had to suggest a single forecasting strategy for Brazilian inflation one-year ahead, we would suggest the use of extended BCAF based on the Focus Survey consensus (15th working day).

Appendix

In the Appendix, Tables 8–11, we provide complementary empirical evidence supporting some of the results presented in the text.

Table 8 Extended BCAF estimation

Table 9 Consensus forecast OLS regression of Capistrán and Timmermann (2009): $\ y_{t}=a+b\overline{f_{\cdot ,t}^{h}} +\epsilon _{t}$

Table 10 Rationality (QR-MZ) tests for consumers

Table 11 Phillips curve estimation $\pi _{t}^{market}=\alpha _{0}+\alpha _{1}\pi _{t-1}^{market}+\alpha _{2}\pi _{t| t-1}^{\exp }+\alpha _{3}\pi _{t-4}^{imp}+\alpha _{4}g_{t-1}+\varepsilon _{t}$