1 Introduction

The core components of the twin-screw compressor are a pair of conjugate male and female rotors, as shown in Fig. 1. In the compression process, the rotor contact line, the male and female rotor profiles, and the body shell form a closed space to seal the air, and the male rotor drives the contact line to translate and compress the volume of the closed space to increase the air pressure [1]. In order to ensure that there is no interference between the male and female rotor pairs in the case of the normal expansion and manufacturing errors, it is necessary to design the suitable size of the rotor pair contact line gap first. However, the size of the contact line gap affects the leakage of compressed gas and thus affects the working efficiency of the twin-screw compressor. Therefore, reducing the manufacturing error of rotor profile and increasing the allowable scale of contact line clearance are important methods to improve the efficiency of compressor [2]. Because of the high manufacturing precision, machining efficiency, the form grinding process is often used in the finishing machining process of screw rotor. However, the geometrical characteristics of the contact line between the variable lead screw rotor and the grinding wheel are strongly related to the axial position of the rotor. Therefore, the segmented grinding and ball-end milling method were used in the finish machining process of the variable screw rotor instead of form grinding.

Fig. 1
figure 1

Structure of twin-screw compressor

Full size image

The screw rotor milling process is a nonlinear chaotic process under the action of multi-physical field coupling [3]. The establishment of the contact condition of the tool edge micro-element trajectory and the workpiece surface is the prerequisite for numerical simulation of the screw rotor milling process, and is the basis for accurately simulating the mechanical characteristics of the milling process and the workpiece surface topography. For the simulation method of the cutting process, many scholars have carried out related studies, as follows:

For the cutting force modeling, the cutting force coefficient identification, undeformed chip thickness model, and cut-in angle and cut-out angle model [4] are the main parts of the sculpture surface cutting force model. Toris [5] proposed a new method to estimate the cutting force accurately based on the load cell and the accelerometers, which can help to identify the cutting force coefficients precisely. The average milling force coefficient [6] identification method is the most commonly method for solving the milling force coefficients; a transient milling force parameter identification method is proposed by Ko. J [7]. Compared with the average milling force parameter identification algorithm, this method is more convenient to analyze the influence of process parameters on milling force coefficients. Cai [8] established the undeformed chip thickness model of the five-axis milling process of face gear with end milling cutter. And the cutting force coefficients of the milling process of small diameter milling cutter were calculated based on the transient cutting force coefficient identification method. Then, the five-axis milling force and machining error of the face gear were simulated. Cao and Kim [9, 10] studied the influence of tool attitude on the shape of tool-workpiece contact area, and simulated the milling force of ball-end milling cutter. On this basis, Tuysuz and Altintas [11] studied the influence of workpiece deformation on milling force in the cutting process, and simulated the milling force for the milling of end mills and side cutters. Base on the cutting force model, Oh JY [12] established the cutting force model of the milling process using the robot machining system considering the position error of the robot. Malekian [13] calculated the geometry parameters of the critical undeformed chip thickness when the plowing action occurs in the cutting process through the average milling force data of multiple groups of milling experiments, and established the milling force model based on the contact area, extrusion coefficient, and edge coefficient considering the plowing process. J Yi [14] established the micro milling cutting force model of the difficult-to-machine materials such as titanium alloys considering the deformation of the cutter. KIM [10] used the Z-map method to study the influence of tool posture on the shape of the contact area between the ball-end milling cutter and the workpiece, established the model of the undeformed chip thickness and cut-in angle and cut-out angle when the ball-end milling cutter milled the sculpture surface, and simulated the three-axis milling force. Rao [15] proposed an iterative calculation method for the undeformed chip thickness in the process of five-axis flank milling of sculpture surfaces and then calculated the milling force in the process of flank milling of sculpture surfaces. X. Liu [16] studied the cutting force of the peripheral milling process and proposed a new model to calculate the geometry parameter of the contact area and the undeformed chip thickness.

For the simulation of surface topography in the milling process, domestic and foreign scholars generally study the modeling of dynamic characteristics of the process system and simulate the surface topography of the cutting process under the influence of vibration. Cai [8, 17] established the mathematical model of tool tip frequency response function based on rigid coupling dynamics and flexible coupling dynamics. On this basis, the simulation method of surface topography and manufacturing precision of variable pitch milling cutter and sculpture surface machining process was studied. Li [18] calculated the instantaneous vibration of the tool tip based on the measured frequency response function of the tool tip and the milling force model of the five-axis flank milling process and calculated the geometry parameters of the undeformed chip thickness in the cutting process considering the tool trajectory considering the tool vibration. The milling force under the influence of coupled tool vibration was simulated. Li [19] used the birth–death element method to study the influence of the workpiece material removal process on the dynamic model of the workpiece system and predicted the milling force considering the deformation of thin-walled parts and the machining accuracy of thin-walled parts. According to the tool posture in the process of milling thin-walled parts, Altintas [20] calculated the shape of the tool-workpiece contact area in the process of milling thin-walled parts by ball-end milling cutter, established the milling force model of ball-end milling cutter, combined with the measured modal parameters of thin-walled parts, predicted the manufacturing error of thin-wall parts, optimized the tool path, and effectively improved the manufacturing precision of thin-wall parts.

Based on the above research, it can be seen that the simulation of geometry parameters of the cutting process is the basis of studying the geometry parameters of the cutting process and the formation mechanism of surface topography. The geometry parameters model of spatial multi-axis milling process is a nonlinear complex model, which is a difficult problem to accurately simulate the cutting force and surface topography of multi-axis milling process. To solve this problem, this paper proposes a milling force model and surface topography formation mechanism method based on the iterative algorithm of normal cutting depth, and the algorithm is shown in Fig. 2. The continuous mathematical model of the screw rotor profile composed of discrete points is studied, the geometry parameters of the profile are solved, and the mathematical model of the rotor profile is established. On this basis, considering the surface parameters, a two-dimensional mesh is established to discretize the surface of the rotor surface, so as to simulate the transition surface topography and surface topography of the cutting process, and to solve the geometry parameters of discrete points on the surface. At the same time, the initial position and orientation of the cutter in the ball-end milling process are studied according to the rotor end section and its space dimension. Additionally, the mathematical model of the cutting edge trajectory in the milling process is established considering the geometry parameters of the helicoid. Based on the mathematical model of tool edge trajectory, the Taylor series expansion form of tool edge trajectory surface, and the normal direction of discrete points, an iterative algorithm is established to approximate the normal interference of surface points in the ball end milling process, and the time-varying characteristics of screw rotor surface in the ball end milling process are studied. Taking the theoretical contact point as the initial searching position, the searching method of normal cutting depth is studied, the space point range of the existing solution is constrained, and the solving time is reduced. Combined with the cutting edge element width and milling coefficient, the mechanical characteristics and the time-varying characteristics of the surface topography of screw rotor in milling process were studied. Compared with the traditional cutting force modeling method, there are three advantages of the algorithm proposed in this paper as followed: (1) The normal cutting depth iteration algorithm was proposed in this article which can calculate the real cutting depth considering the influence of the transitional surface during the cutting process. (2) The normal cutting depth parameter was applied to replace the undeformed chip thickness, the cut-in angle, and the cut-out angle of the cutting force model, and the new cutting force model proposed in this article considering the influence of the cutting parameter during the cut-in process and cut-out process which is not simulated by the traditional cutting force model. (3) Compared with the Boolean operation method, the normal cutting depth iteration algorithm is a numerical solution method. This method simplified the 3D grids into the 2D grid of curve parameter which can improve the efficiency of the simulation. And the simulation accuracy of the normal cutting depth is not dependent on the grid density which also can improve the efficiency and the accuracy of the simulation.

Fig. 2
figure 2

Framework of modeling methods for surface topography and cutting force

Full size image

2 Mathematical model of ball milling process of screw rotor

The profile of the screw rotor of a twin-screw compressor is complex, which is typically composed of arc, cycloid, and elliptical arc with different parameters. The discrete points are commonly employed to characterize it in the processing process. As is shown in Fig. 3, a coordinate system of the screw rotor was presented. The coordinate system \(O-{X}_{0}{Y}_{0}{Z}_{0}\) is attached to the rotor, rotating around the z0-axis. The mathematical model of the rotor is expressed in Eq. (1), where\(X\left(t,\theta \right)\),\(Y\left(t,\theta \right)\), and \(Z\left(t,\theta \right)\) are the rotor profile coordinates,\(x\left(t\right)\) and \(y\left(t\right)\) are the rotor end section coordinates, \(t\) is the end section parameter,\(p\) is the rotor lead, and \(\theta\) is the rotation angle of the rotor.

Fig. 3
figure 3

Coordinate system of the rotor

Full size image
$$\left\{\begin{array}{l}X\left({\text{t}},\theta \right)=x\left(t\right)cos\theta -y\left(t\right)sin\theta \\ Y\left({\text{t}},\theta \right)=x\left(t\right)sin\theta +y\left(t\right)cos\theta \\ {\text{Z}}\left({\text{t}},\theta \right)=p\theta \end{array}\right.$$
(1)

A mathematical model of the end section of the screw rotor is established in the end coordinate system\(O-{X}_{0}{Y}_{0}\). The end section of the screw rotor is interpolated using a cubic spline interpolation method by combining the coordinates \({x}_{i}\) and \({y}_{i}\) of discrete points. The coordinate \(x\) and \(y\) interpolation models are established with the cumulative chord length t as the parameter. The mathematical expression of the i-th segment interpolation model is shown in Eq. (2), where\({a}_{xi}\),\({b}_{xi}\),\({c}_{xi}\), and \({d}_{xi}\) are the coefficients of the interpolation function in the x direction,\({a}_{yi}\),\({b}_{yi}\),\({c}_{yi}\), and \({d}_{yi}\) are the coefficients of the interpolation function in the \(x\) direction, and \({t}_{i}\) is the accumulated chord length of the i-th interpolation point.

$$\left\{\begin{array}{c}{x}_{i}\left(t\right)={a}_{xi}+{b}_{xi}\left(t-{t}_{i}\right)+{c}_{xi}{\left(t-{t}_{i}\right)}^{2}+{d}_{xi}{\left(t-{t}_{i}\right)}^{3}\\ {y}_{i}\left(t\right)={a}_{yi}+{b}_{yi}\left(t-{t}_{i}\right)+{c}_{yi}{\left(t-{t}_{i}\right)}^{2}+{d}_{yi}{\left(t-{t}_{i}\right)}^{3}\end{array}\right.$$
(2)

Since the solution of the interpolation coefficient in the x direction is consistent with that in the y direction, to simplify the expression of the interpolation mathematical model,\({x}_{i}\left(t\right)\) and \({y}_{i}\left(t\right)\) in the subsequent formulas in this paper are replaced by \({g}_{i}\left(t\right)\). As is shown in Eq. (3), the profile cubic spline mathematical model is established by combining the free boundary condition, node continuity condition, first-order derivative continuity condition, and second-order derivative continuity condition, where, \({\ddot{g}}_{0}\) and \({\ddot{g}}_{n}\) is the second-order derivative at the end point of the profile, and the second-order derivative at the end point of the free boundary condition is 0.\({\dot{g}}_{i}\left(t\right)\) is the derivative of the i-th interpolation function at the \(i+1\) end point, and \({\dot{g}}_{i+1}\left(t+1\right)\) is the derivative of the \(i+1\) interpolation function at \(i+1\) end point.

$$\left\{\begin{array}{l}{\ddot{g}}_{0}={\ddot{g}}_{n}=0\\ {g}_{i}\left({t}_{i+1}\right)={g}_{i+1}\left({t}_{i+1}\right)\\ {\dot{g}}_{i}\left({t}_{i+1}\right)={\dot{g}}_{i+1}\left({t}_{i+1}\right)\\ {\ddot{g}}_{i}\left({t}_{i+1}\right)={\ddot{g}}_{i+1}\left({t}_{i+1}\right)\end{array}\right.$$
(3)

Assuming that \({m}_{i}={\ddot{g}}_{i}\), the expression forms of Eqs. (4) and (5) can be obtained by simplifying Eq. (3), where \({h}_{i}\) is the chord length. The second derivative of the node position can be obtained by using the chasing method to solve Eq. (4).

$$\left\{\begin{array}{c}\left[\begin{array}{cccccccc}1& 0& 0& 0& ...& 0& 0& 0\\ {h}_{0}& 2\left({h}_{0}+{h}_{1}\right)& {h}_{1}& 0& ...& 0& 0& 0\\ 0& {h}_{1}& 2\left({h}_{1}+{h}_{2}\right)& {h}_{2}& ...& 0& 0& 0\\ ...& ...& ...& ...& ...& ...& ...& ...\\ 0& 0& 0& 0& ...& {h}_{n-2}& 2\left({h}_{n-2}+{h}_{n-1}\right)& {h}_{n-1}\\ 0& 0& 0& 0& ...& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{m}_{0}\\ {m}_{1}\\ {m}_{2}\\ ...\\ {m}_{n-1}\\ {m}_{n}\end{array}\right]=6\left[\begin{array}{c}0\\ \left({g}_{2}-{g}_{1}\right)/{h}_{1}-\left({g}_{1}-{g}_{0}\right)/{h}_{0}\\ \left({g}_{3}-{g}_{2}\right)/{h}_{2}-\left({g}_{2}-{g}_{1}\right)/{h}_{1}\\ ...\\ \left({g}_{n}-{g}_{n-1}\right)/{h}_{n-1}-\left({g}_{n-1}-{g}_{n-2}\right)/{h}_{n-2}\\ 0\end{array}\right]\\ {h}_{i}={t}_{i+1}-{t}_{i}\end{array}\right.$$
(4)

The coefficients of each interpolation function and the first derivative can be obtained by using Eq. (5).

$$\left\{\begin{array}{l}{a}_{i}={g}_{i}\\ {c}_{i}={m}_{i}/2\\ {\dot{g}}_{i}={b}_{i}=\frac{{g}_{i+1}-{g}_{i}}{{h}_{i}}-\frac{{h}_{i}}{2}{m}_{i}-\frac{{h}_{i}}{6}\left({m}_{i+1}-{m}_{i}\right)\\ {d}_{i}=\frac{{m}_{i+1}-{m}_{i}}{6{h}_{i}}\end{array}\right.$$
(5)

Solve the derivative expression of coordinates to parameters in combination with Eq. (1), as shown in Eq. (6).

$$\left\{\begin{array}{l}\frac{\partial X}{\partial t}=\frac{\partial x}{\partial t}\text{cos}\theta -\frac{\partial y}{\partial t}\text{sin}\theta \\ \frac{\partial Y}{\partial t}=\frac{\partial x}{\partial t}\text{sin}\theta +\frac{\partial y}{\partial t}\text{cos}\theta \\ \frac{\partial Z}{\partial t}=0\end{array}\left\{\begin{array}{l}\frac{\partial X}{\partial \theta }=x\text{sin}\theta -y\text{cos}\theta \\ \frac{\partial Y}{\partial \theta }=x\text{cos}\theta -y\text{cos}\theta \\ \frac{\partial Z}{\partial \theta }=p\end{array}\right.\right.$$
(6)

According to the derivative mathematical model, the expression of the space normal at any position of the screw rotor profile can be solved, as shown in Eq. (7), where n is the normal vector of the profile point.

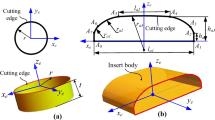
$$n=\left|\begin{array}{ccc}i& j& k\\ \frac{\partial X}{\partial t}& \frac{\partial Y}{\partial t}& \frac{\partial Z}{\partial t}\\ \frac{\partial X}{\partial \theta }& \frac{\partial Y}{\partial \theta }& \frac{\partial Z}{\partial \theta }\end{array}\right|$$
(7)

The machining path of the tool is represented in the screw rotor coordinate system \(O-{X}_{0}{Y}_{0}{Z}_{0}\), as is shown in Eq. (8), where \(\left({x}_{i},{y}_{i},{z}_{i}\right)\) and \(\left({X}_{Ti},{Y}_{Ti},{Z}_{Ti}\right)\) are the coordinate and the tool path points of the \(i\)-th end section point. A cutting edge motion model is established, as shown in Eq. (9), where \(\omega\) is the angular velocity, \(n\) is the serial number of the cutting edge, \(r\) is the radius of the cutter, \({P}_{L}\) is the lead of the rotor, \({a}_{p}\) is the height of the contact point between the tool and the workpiece,\(f\) is the feed rate, and \(T\) is the milling time.

$$\left\{\begin{array}{l}{X}_{Ti}={x}_{i}+{n}_{x}r\\ {Y}_{Ti}={y}_{i}+{n}_{y}r\\ {\text{Z}}_{Ti}={n}_{z}r\end{array}\right.$$
(8)
$$\begin{array}{l}S\left(T, {a}_{p}\right)=\left[\begin{array}{l}\text{cos}(\omega T+360\left(n-1\right)/n)\\ \text{sin}\left(\omega T+\frac{360\left(n-1\right)}{n}\right)\end{array}\begin{array}{l}-\text{sin}\left(\omega T+\frac{360\left(n-1\right)}{n}\right)\\ \text{cos}\left(\omega T+\frac{360\left(n-1\right)}{n}\right)\end{array} \begin{array}{l}0\\ 0\\ 1\end{array}\right]\\ \left[\begin{array}{l}\text{cos}{\int }_{ap}^{r}\frac{2\pi }{{P}_{L}}{d}_{L}\begin{array}{l}\begin{array}{ll} -\text{sin}{\int }_{ap}^{r}\frac{2\pi }{{P}_{L}}{d}_{L}& 0\end{array}\\ 0\end{array}\\ \begin{array}{c}\text{sin}{\int }_{ap}^{r}\frac{2\pi }{{P}_{L}}{d}_{L}\\ 0\end{array}\begin{array}{l}\begin{array}{ll}\text{ cos}{\int }_{ap}^{r}\frac{2\pi }{{P}_{L}}{d}_{L}& \begin{array}{l}0\\ \\ 1\end{array}\end{array}\\ 0\end{array}\end{array}\right]\left[\begin{array}{l}\begin{array}{l}\text{cos}\frac{2\pi f\text{T}}{p}-\begin{array}{ll}\text{sin}\frac{2\pi f\text{T}}{p}& 0\end{array}\\ \text{sin}\begin{array}{l}\frac{2\pi f\text{T}}{p}\\ 0\end{array}\text{cos}\begin{array}{ll}\begin{array}{l}\frac{2\pi f\text{T}}{p}\\ 0\end{array}& \begin{array}{l}0\\ \begin{array}{l}\\ 1\end{array}\end{array}\end{array}\end{array}\\ \\ \end{array}\right]\left[\begin{array}{l}r\\ 0\\ 0\end{array}\right]+\left[\begin{array}{l}{X}_{Ti}\\ {Y}_{Ti}\\ {Z}_{Ti}+fT\end{array}\right]\end{array}$$
(9)

3 Iterative algorithm of normal cutting quantity

The mapping relationship between the tool path and the workpiece surface is an important geometric parameter for establishing the cutting force model and simulating the workpiece surface topography. Traditional cutting force models typically characterize the cut-in angle, cut-out angle, and undeformed chip thickness. In this paper, an iterative algorithm for normal cutting rate is proposed to solve the normal cutting rate of the surface point in the cutting process, which represents the cut-in angle, cut-out angle, and undeformed chip thickness, and characterizes the mapping relationship between the cutting edge trajectory and the workpiece surface. Simultaneously, the cutting force model and the workpiece surface topography model are established. In the process of cutting force modeling, the influence of transition surface topography on undeformed chip thickness in the process of cutting edge cut-in and cut-out is considered. The iterative algorithm flow of normal cutting depth is illustrated in Fig. 4. The geometric expression of the algorithm is presented in Fig. 5. The method reduces the solving dimension of the nonlinear model to the solving problem of a linear equation, and the algorithm steps are as follows:

Fig. 4
figure 4

Iterative algorithm of normal cutting quantity

Full size image
Fig. 5
figure 5

Iteration of normal cutting quantity

Full size image

1) The coordinate \(\left({T}_{k0},{a}_{k0}\right)\) of the theoretical contact point Q0 on the tool is solved according to the normal direction of the theoretical contact position between the tool and the workpiece at the moment \({T}_{k}\), where α is the phase angle of the contact point. The cutting depth is measured by the phase angle of the contact point, as shown in Fig. 6, which is taken as the iteration initial value of the normal cutting volume iteration algorithm.

Fig. 6
figure 6

Schematic representation of the parameter α

Full size image

2) Assume that the point P is a node of rotor profile, and the normal vector \({n}_{p}\) of the point P will be solved. The mathematical model \({S}^{*}\left({T}_{k0},{\alpha }_{k0}\right)\) is derived by Taylor formula at the contact point Q0, and calculate the solution Q1* of the linear equation \({\mathbf{S}}^{\boldsymbol{*}}\left({T}_{k0},{a}_{k0}\right)={\mathbf{n}}_{p}\).

3) The parameters are mapped to the working profile of the rotor to obtain the solution Q1*.

4) The process is repeated to carry out iterative calculation until the iterative stopping condition is met, the calculation is terminated, and the normal cutting depth is output.

Modeling is performed on the mathematical model in the above algorithm steps. An iteration initial value mathematical model is established, as shown in Eq. (10), where \(\left({x}_{\mathtt{Q}0},{y}_{\mathtt{Q}0},{z}_{\mathtt{Q}0}\right)\) is the coordinate of the point Q0. The relationship between the contact angle a and \({a}_{p}\) is shown in Eq. (11).

$${S}^{*}\left({T}_{k0},{\alpha }_{k0}\right)=\left({x}_{Q0},{y}_{Q0},{z}_{Q0}\right)$$
(10)
$$\alpha =\text{arccos}\frac{\sqrt{{r}^{2}-{\left(r-{a}_{p}\right)}^{2}}}{r}$$
(11)

The coordinate of the contact point on the cutting edge trajectory can be obtained by substituting Eq. (9), which is the initial coordinate of the iterative calculation of the normal cutting depth of all profile points at \({T}_{k}\). And solve for its derivative as shown in Eq. (12), where \(\beta\) is that helix angle of the non-spherical portion of the ball end mill and \({P}_{L}\) is the lead of the helical mill.

$$\left\{\begin{array}{c}\frac{\partial x}{\partial T}=\omega \left|r\text{sin}\alpha \right|cos\left[T\omega +\text{cos}\alpha \text{tan}\beta -\frac{2\pi \left({P}_{L}/n-{P}_{L}\right)}{n}\right]cos\left(\frac{2\pi fT}{p}\right)-\frac{1}{p}2\pi fcos\left(\frac{2\pi fT}{p}\right)\left({y}_{Q0}-r\text{cos}\alpha \right)\\ \begin{array}{cc}& \end{array}-\frac{1}{p}2\pi fsin\left(\frac{2\pi fT}{p}\right)\left[{x}_{Q0}+\left|r\text{cos}\alpha \right|\frac{\text{sin}\left(\omega T+\text{cos}\alpha \text{tan}\beta -\left(2\pi \left({P}_{L}/n-{P}_{L}\right)\right)\right)}{n}\right]\\ \frac{\partial y}{\partial T}=\omega \left|r\text{sin}\alpha \right|\frac{\text{cos}\left(\omega T+\text{cos}\alpha \text{tan}\beta -\left(2\pi \left({P}_{L}/n-{P}_{L}\right)\right)\right)}{n}sin\left(\frac{2\pi fT}{p}\right)-\frac{1}{p}2\pi fsin\left(\frac{2\pi fT}{p}\right)\left({y}_{Q0}-r\text{cos}\alpha \right)\\ \begin{array}{cc}& \end{array}+\frac{1}{p}2\pi fcos\left(\frac{2\pi fT}{p}\right)\left[{x}_{Q0}+\left|r\text{cos}\alpha \right|\frac{\text{sin}\left(\omega T+\text{cos}\alpha \text{tan}\beta -\left(2\pi \left({P}_{L}/n-{P}_{L}\right)\right)\right)}{n}\right]\\ \frac{\partial z}{\partial T}=f-\omega rsin\alpha \frac{\text{sin}\left(\omega T+\text{cos}\alpha \text{tan}\beta -\left(2\pi \left({P}_{L}/n-{P}_{L}\right)\right)\right)}{n}\end{array}\right.\left\{\begin{array}{c}\frac{\partial x}{\partial \alpha }=rcos\alpha cos\left(\frac{2\pi fT}{p}\right)sin\left(\omega T+\text{cos}\alpha \text{tan}\beta -\frac{2\pi \left({P}_{L}/n-{P}_{L}\right)}{n}\right)\\ \begin{array}{cc}& \end{array}-\left|r\text{sin}\alpha \right|sin\alpha tan\beta cos\left(\omega T+\text{cos}\alpha \text{tan}\beta -\frac{2\pi \left({P}_{L}/n-{P}_{L}\right)}{n}\right)-rsin\alpha sin\left(\frac{2\pi fT}{p}\right)\\ \frac{\partial y}{\partial \alpha }=rcos\alpha sin\left(\frac{2\pi fT}{p}\right)sin\left(\omega T+\text{cos}\alpha \text{tan}\beta -\frac{2\pi \left({P}_{L}/n-{P}_{L}\right)}{n}\right)\\ \begin{array}{cc}& \end{array}-\left|r\text{sin}\alpha \right|sin\alpha tan\beta cos\left(\omega T+\text{cos}\alpha \text{tan}\beta -\frac{2\pi \left({P}_{L}/n-{P}_{L}\right)}{n}\right)+rsin\alpha cos\left(\frac{2\pi fT}{p}\right)\\ \frac{\partial z}{\partial \alpha }=rcos\alpha cos\left(\omega T+\text{cos}\alpha \text{tan}\beta -\frac{2\pi \left({P}_{L}/n-{P}_{L}\right)}{n}\right)\\ \begin{array}{cc}& \end{array}+\left|r\text{sin}\alpha \right|sin\alpha tan\beta \frac{\text{sin}\left(\omega T+\text{cos}\alpha \text{tan}\beta -\frac{2\pi \left({P}_{L}/n-{P}_{L}\right)}{n}\right)}{n}\end{array}\right.$$
(12)

The Taylor series expansion model \({\mathbf{S}}^{\boldsymbol{*}}\left({T}_{k},{a}_{k}\right)\) is shown in Eq. (13).

$${S}^{*}\left({T}_{k0},{\alpha }_{k0}\right)=S\left({T}_{k0},{\alpha }_{k0}\right)+\frac{\partial S}{\partial {T}_{k}}\Delta T+\frac{\partial S}{\partial {\alpha }_{k}}\Delta \theta$$
(13)

The solution model of Q1* is established, as shown in Eq. (14), where \(\left({x}_{p},{x}_{p},{z}_{p}\right)\) and \(\left({n}_{xp},{n}_{yp},{n}_{zp}\right)\) are the coordinate and normal vector of point P, and u is the normal parameter.

$${S}^{*}=\left[\begin{array}{ccc}{x}_{p}& {y}_{p}& {z}_{p}\end{array}\right]+u\left[\begin{array}{ccc}{n}_{xp}& {n}_{yp}& {n}_{zp}\end{array}\right]$$
(14)

Equations (12) and (13) are used to iteratively solve the normal cutting depth, and the iteration termination condition is shown in Eq. (15), where \(\varepsilon\) is the amount considered to be given.

$$\left\{\begin{array}{c}\left|{T}_{k}-{T}_{k-1}\right|<\varepsilon \\ \left|{\alpha }_{k}-{\alpha }_{k-1}\right|<\varepsilon \end{array}\right.$$
(15)

As is shown in Eq. (16), he normal allowance \({d}_{p}\) of point P cut by the tool can be obtained from Eqs. (9), (11), and (16) with \({T}_{k}\) and \({a}_{k}\) satisfying the iteration condition, where P represents the coordinate of point P.

$${d}_{p}={\Vert S\left({T}_{k},{\alpha }_{k}\right)-P\Vert }_{2}$$
(16)

The normal cutting depth \({c}_{p}\) can be obtained by substituting \({d}_{p}\) into Eq. (17), where \({A}_{p}\) is the normal allowance of the profile point.

$${c}_{p}={A}_{p}-{d}_{p}$$
(17)

4 Time-varying mapping relationship between cutting edge element trajectory and workpiece surface

To enhance the efficiency of solving workpiece surface topography and cutting force, constraint planning for the solution range and path is essential. The solution flow chart is depicted in Fig. 7, and the solving steps are as follows:

Fig. 7
figure 7

Procedure for finding the mapping relationship between tool and workpiece

Full size image

1) Take the parameter coordinates t and \(\theta\) as base vectors to establish the two-dimensional mesh of the rotor profile. Utilize the node normal allowance to characterize the rotor surface topography and the amount of time-varying material removal. The theoretical profile of the meshed rotor is illustrated in Fig. 8a, and the node coordinate matrix and normal matrix of the rotor are established as shown in Eq. (18).The position of each element represents the sequence of the grid node in the two-dimensional grid, and the value table of the element represents the \(x,y,z\) coordinates and normal components of the node.

Fig. 8
figure 8

Scanning method of tool-workpiece contact region in the milling process

Full size image
$$\begin{array}{cc}\left\{\begin{array}{c}{G}_{nx}=\left[\begin{array}{ccc}\begin{array}{c}{n}_{x11}\\ \begin{array}{c}{n}_{x21}\\ \begin{array}{c}\dots \\ {n}_{xn1}\end{array}\end{array}\end{array}& \begin{array}{c}{n}_{x12}\\ \begin{array}{c}{n}_{x22}\\ \begin{array}{c}\dots \\ {n}_{xn2}\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\dots \\ \begin{array}{c}\dots \\ \begin{array}{c}\dots \\ \dots \end{array}\end{array}\end{array}& \begin{array}{c}{n}_{x1m}\\ \begin{array}{c}{n}_{x2m}\\ \begin{array}{c}\dots \\ {n}_{xnm}\end{array}\end{array}\end{array}\end{array}\end{array}\right]\\ {G}_{ny}=\left[\begin{array}{ccc}\begin{array}{c}{n}_{y11}\\ \begin{array}{c}{n}_{y21}\\ \begin{array}{c}\dots \\ {n}_{yn1}\end{array}\end{array}\end{array}& \begin{array}{c}{n}_{y12}\\ \begin{array}{c}{n}_{y22}\\ \begin{array}{c}\dots \\ {n}_{yn2}\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\dots \\ \begin{array}{c}\dots \\ \begin{array}{c}\dots \\ \dots \end{array}\end{array}\end{array}& \begin{array}{c}{n}_{y1m}\\ \begin{array}{c}{n}_{y2m}\\ \begin{array}{c}\dots \\ {n}_{ynm}\end{array}\end{array}\end{array}\end{array}\end{array}\right]\\ {G}_{nz}=\left[\begin{array}{ccc}\begin{array}{c}{n}_{z11}\\ \begin{array}{c}{n}_{z21}\\ \begin{array}{c}\dots \\ {n}_{zn1}\end{array}\end{array}\end{array}& \begin{array}{c}{n}_{z12}\\ \begin{array}{c}{n}_{z22}\\ \begin{array}{c}\dots \\ {n}_{zn2}\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\dots \\ \begin{array}{c}\dots \\ \begin{array}{c}\dots \\ \dots \end{array}\end{array}\end{array}& \begin{array}{c}{n}_{z1m}\\ \begin{array}{c}{n}_{z2m}\\ \begin{array}{c}\dots \\ {n}_{znm}\end{array}\end{array}\end{array}\end{array}\end{array}\right]\end{array}\right.& \left\{\begin{array}{c}{G}_{x}=\left[\begin{array}{ccc}\begin{array}{c}{x}_{11}\\ \begin{array}{c}{x}_{21}\\ \begin{array}{c}\dots \\ {x}_{n1}\end{array}\end{array}\end{array}& \begin{array}{c}{x}_{12}\\ \begin{array}{c}{x}_{22}\\ \begin{array}{c}\dots \\ {x}_{n2}\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\dots \\ \begin{array}{c}\dots \\ \begin{array}{c}\dots \\ \dots \end{array}\end{array}\end{array}& \begin{array}{c}{x}_{1m}\\ \begin{array}{c}{x}_{2m}\\ \begin{array}{c}\dots \\ {x}_{nm}\end{array}\end{array}\end{array}\end{array}\end{array}\right]\\ {G}_{y}=\left[\begin{array}{ccc}\begin{array}{c}{y}_{11}\\ \begin{array}{c}{y}_{21}\\ \begin{array}{c}\dots \\ {y}_{n1}\end{array}\end{array}\end{array}& \begin{array}{c}{y}_{12}\\ \begin{array}{c}{y}_{22}\\ \begin{array}{c}\dots \\ {y}_{n2}\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\dots \\ \begin{array}{c}\dots \\ \begin{array}{c}\dots \\ \dots \end{array}\end{array}\end{array}& \begin{array}{c}{y}_{1m}\\ \begin{array}{c}{y}_{2m}\\ \begin{array}{c}\dots \\ {y}_{nm}\end{array}\end{array}\end{array}\end{array}\end{array}\right]\\ {G}_{z}=\left[\begin{array}{ccc}\begin{array}{c}{z}_{11}\\ \begin{array}{c}{z}_{21}\\ \begin{array}{c}\dots \\ {z}_{n1}\end{array}\end{array}\end{array}& \begin{array}{c}{z}_{12}\\ \begin{array}{c}{z}_{22}\\ \begin{array}{c}\dots \\ {z}_{n2}\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\dots \\ \begin{array}{c}\dots \\ \begin{array}{c}\dots \\ \dots \end{array}\end{array}\end{array}& \begin{array}{c}{z}_{1m}\\ \begin{array}{c}{z}_{2m}\\ \begin{array}{c}\dots \\ {z}_{nm}\end{array}\end{array}\end{array}\end{array}\end{array}\right]\end{array}\right.\end{array}$$
(18)

2) On this basis, the allowance for semi-finishing is determined, and the profile allowance matrix is established. The geometric model of the matrix is shown in Fig. 8b. The mathematical model is represented in Eq. (19).

$${G}_{dp0}=\left[\begin{array}{cccc}{A}_{p}& {A}_{p}& ...& {A}_{p}\\ {A}_{p}& {A}_{p}& ...& {A}_{p}\\ ...& ...& ...& ...\\ {A}_{p}& {A}_{p}& ...& {A}_{p}\end{array}\right]$$
(19)

3) According to the processing time \({T}_{k}\), the cent motion position of the cutter is determined. The parameter coordinate \({t}_{Tk}\) and \({\theta }_{Tk}\) of the theoretical contact point of the cutter and the rotor are solved.

4) Take the theoretical machining contact position as the initial point to search for the solution along the grid direction, as shown in Fig. 8c. Initially, proceed from two directions along the grid helix direction, and combine the normal cutting depth iteration algorithm to calculate the normal allowance of each node. When the normal allowance is greater than the semi-finishing allowance, it indicates that the tool at the node is not in contact with the workpiece surface, and the node is the upper or lower boundary of the helix.

5) At this time, the theoretical contact point is increased or decreased by one unit along the serial number direction of the end section shape, and the above steps are repeated until the normal allowance after the serial number is increased or decreased at a certain time is greater than the semi-finishing allowance. At this time, it means that the left and right boundaries of the end section shape are found. The simulation of the surface appearance and cutting amount at this time step is completed.

The above algorithm enables the rapid solution of the mapping relationship between the cutting edge trace and the workpiece surface in the screw rotor milling process, and simulate the surface topography and cutting force curve in the machining process.

5 Ball-end milling force model of screw rotor

To establish the milling force model of the screw rotor, the extraction of material property parameters is essential using the transient milling force coefficient identification method, and its mathematical model is shown in Eq. (20), where \({\overline{F} }_{x}\),\({\overline{F} }_{y}\),and \({\overline{F} }_{z}\) are the three-dimensional milling force,\({h}_{pi}\) is the undeformed chip thickness,s is the tool edge-workpiece contact length, n is the number of cutting force sampling points for calculation, and \({k}_{tc}\), \({k}_{rc}\), and \({k}_{ac}\) are the tangential, radial, and axial shear coefficients.\({k}_{te}\), \({k}_{re}\), and \({k}_{ae}\) are the tangential, radial, and axial cutting edge coefficients, and \({b}_{j}\) is the height of the \(j\)-th cutting edge element participating in the cutting.

$$\left\{\begin{array}{l}{\overline{F} }_{x}=\frac{1}{n}\left[\left({k}_{tc}\sum_{j=1}^{m}\sum_{i=1}^{n}{h}_{pi}{b}_{j}+{nk}_{te}s\right)\text{cos}\omega T-\left({k}_{rc}\sum_{j=1}^{m}\sum_{i=1}^{n}{h}_{pi}{b}_{j}+{nk}_{re}s\right)\text{sin}\omega T\right]\\ {\overline{F} }_{Y}=\frac{1}{n}\left[\left({k}_{tc}\sum_{j=1}^{m}\sum_{i=1}^{n}{h}_{pi}{b}_{j}+{nk}_{te}s\right)\text{sin}\omega T+\left({k}_{rc}\sum_{j=1}^{m}\sum_{i=1}^{n}{h}_{pi}{b}_{j}+{nk}_{re}s\right)\text{cos}\omega T\right]\\ {\overline{F} }_{z}=\frac{1}{n}\left({k}_{ac}\sum_{j=1}^{m}\sum_{i=1}^{n}{h}_{pi}{b}_{j}+{nk}_{ae}s\right)\end{array}\right.$$
(20)

Following the milling force experiment, the cutting force curve is initially extracted. Subsequently, the milling force coefficient is solved by the least square method in combination with Eq. (21), where \({w}_{x}\) and \({w}_{y}\) are the weight coefficient for adjusting the fitting accuracy in x and y directions, and\({\widehat{F}}_{x}\),\({\widehat{F}}_{y}\), and \({\widehat{F}}_{z}\) are the measured average milling force in x,y, and z directions.\({\overline{F} }_{x}\),\({\overline{F} }_{y}\), and \({\overline{F} }_{z}\) are the theoretical average milling force in \(x\),\(y\), and \(z\) directions. The results are presented in Table 1. Through this method, the milling force coefficients can be identified only by a group of milling force experiments.

Table 1 Three-way milling force coefficient
Full size table
$$\left\{\begin{array}{l}{l}_{r}={w}_{x}{\left({\widehat{F}}_{x}-{\overline{F} }_{X}\right)}^{2}+{w}_{y}{\left({\widehat{F}}_{y}-{\overline{F} }_{Y}\right)}^{2}\\ {l}_{z}={\left({\widehat{F}}_{z}-{\overline{F} }_{Z}\right)}^{2}\end{array}\right.$$
(21)

The mapping relationship between the profile points and the motion surface of the cutting edge can be studied through the iterative algorithm of the normal cutting depth, as shown in Fig. 9.

Fig. 9
figure 9

Calculation of cutting edge element height

Full size image

The infinitesimal length \({d}_{z}\) between two contact points is solved. The normal cutting depth parameter is projected onto the section characterized by the deformed chip thickness to obtain the mathematical model shown in Eq. (22), and the tangential, radial, and axial cutting force models shown in Eq. (23) are established, where \({n}_{xp}\) is the component of the normal vector at point P of the profile in the\(x\),\(y\), and \(z\) directions, and \({h}_{p}\) is the undeformed chip thickness.

$${h}_{p}={d}_{p}\frac{\sqrt{{n}_{xp}^{2}+{n}_{yp}^{2}}}{\sqrt{{n}_{xp}^{2}+{n}_{yp}^{2}+{n}_{zp}^{2}}}$$
(22)
$$\left\{\begin{array}{c}{F}_{tij}={k}_{tc}{h}_{pi}{b}_{j}+{k}_{te}s\\ {F}_{rij}={k}_{rc}{h}_{pi}{b}_{j}+{k}_{re}s\\ {F}_{aij}={k}_{ac}{h}_{pi}{b}_{j}+{k}_{ae}s\end{array}\right.$$
(23)

Upon transforming it into the rotor coordinate system, the cutting force model is expressed in Eq. (24). Equation (24) reveals that the new cutting force model replaces the undeformed chip thickness and the cut-in angle and the cut-out angle with the normal cutting depth. When the normal cutting depth is 0, the cutting force is 0, so it is unnecessary to solve the cut-in angle and the cut-out angle according to the macroscopic contact area to judge whether the cutting edge participates in cutting. This method simplifies the characterization method of material removal calculated by the cutting force model, and the influence of the cutting transition surface on the material in the cut-in and cut-out process is studied.

$$\left\{\begin{array}{l}{F}_{X}=\left({k}_{tc}\left(\sum_{j=1}^{m}\sum_{i=1}^{n}{h}_{pi}{b}_{j}\right)+n{k}_{te}s\right)cos\omega T\\ \begin{array}{cc}& \end{array}-\left({k}_{rc}\left(\sum_{j=1}^{m}\sum_{i=1}^{n}{h}_{pi}{b}_{j}\right)+n{k}_{re}s\right)sin\omega T\\ {F}_{Y}=\left({k}_{tc}\left(\sum_{j=1}^{m}\sum_{i=1}^{n}{h}_{pi}{b}_{j}\right)+n{k}_{te}s\right)sin\omega T\\ \begin{array}{cc}& \end{array}+\left({k}_{rc}\left(\sum_{j=1}^{m}\sum_{i=1}^{n}{h}_{pi}{b}_{j}\right)+n{k}_{re}s\right)cos\omega T\\ {F}_{Z}={k}_{ac}\left(\sum_{j=1}^{m}\sum_{i=1}^{n}{h}_{pi}{b}_{j}\right)+n{k}_{ae}s\end{array}\right.$$
(24)

6 Results and discussion of milling force and surface topography of screw rotor

In this paper, a five-axis CNC milling machine is employed to conduct the ball end milling experiment on the female rotor of a three-cube screw compressor. The milling machine is in the form of double swing table, and the rotating axes are A and C. The geometric parameters of the rotor are detailed in Table 2. The experimental platform is shown in Fig. 10. The 9270 dynamometer platform is fixed on the C-axis turntable by bolts. The rotor blank is fixed on the dynamometer. During milling, the A-axis rotates 90°, forming the horizontal milling machine processing mode. The cutting experiment is carried out by using Φ4 ball-end milling cutter. The geometry parameters of the milling cutter are shown in Table 3. The cutter location points and profile points in the processing process are shown in Fig. 11. The blue curved surface points are the tool position points in the machining process, and the red points are the screw rotor profile points.

Table 2 Geometry parameters of three cube negative rotor
Full size table
Fig. 10
figure 10

Milling process of screw rotor

Full size image
Table 3 Geometry parameters of ball end milling cutter
Full size table
Fig. 11
figure 11

Profile points and cutter locations of rotor

Full size image

The rotor milling force and workpiece surface topography are simulated according to the algorithm proposed in this paper. The convergence curve of one of the time steps while calculating the cutting force was proposed as shown in the Fig. 12. The simulation results of workpiece surface topography are depicted in Fig. 13. It can be seen that due to the large curvature radius of the long side of the rotor, when the chord length of the profile points is consistent, the cutting residue is large. When the curvature radius of the short side is smaller and the chord length of the profile point is the same, the cutting residue is smaller.

Fig. 12
figure 12

The convergence curve of the simulation

Full size image
Fig. 13
figure 13

Simulation results of surface topography in milling process

Full size image

The manufacturing error of the machined rotor is measured using a three-coordinate measuring machine. The measurement process is shown in Fig. 14.The rotor surface was segmented into nine regions for error measurement evaluation. The measurement evaluation regions are shown in Fig. 15. Measure the errors of five profile points in each area and take the average value to compare with the simulation errors. The comparison results are shown in Table 4, revealing that the measurement error is within 10%, affirming the model’s capability to predict surface topography with reliable accuracy.

Fig. 14
figure 14

Measurement process of machined rotor

Full size image
Fig. 15
figure 15

Measurement area of screw rotor surface topography

Full size image
Table 4 Comparison of simulation errors and measurement errors in different areas of screw rotor
Full size table

The curves of cutting force and experimental mechanics are displayed in Fig. 16. Simulation comparison tests are carried out on the milling force of No. 1, No. 300, No. 500, and No. 700 surface point tracks. The comparison results are as follows. It can be seen that the trend of the simulated milling force is consistent with that of the actual milling force. The maximum amplitude error does not exceed 15% of the overall milling force amplitude.

Fig. 16
figure 16

Numerical simulation results of cutting force

Full size image

Some errors persist in predicting topography and cutting force. The reasons for the errors are as follows: (1) the initial phase angle at the beginning of milling is not accurately measured, leading to a phase deviation in topography; (2) during the milling process, the vibration of the tool and the workpiece will affect the surface topography and the geometry parameters of the cutting process, resulting in some manufacturing errors and cutting force errors; (3) the tool is worn in the cutting process, and there are some errors between the geometry parameters of the cutting process and the real geometry parameters, and the influence of the damping force formed by the worn surface on the actual cutting force is not considered.

7 Conclusion

In this paper, a new method based on the iterative algorithm of the normal cutting depth is proposed to study the time-varying mapping relationship between the cutting edge trajectory and the workpiece surface. The surface topography prediction model and cutting force prediction model are established. The mathematical model and geometric characteristic parameters of the screw rotor working surface are studied. On this basis, the cutting path of the tool and the micro-unit motion path of the cutting edge are calculated. And the 2D mesh model of the screw rotor profile is established. The solving method and constraint conditions of the tool-workpiece contact region are studied. The normal cutting quantity of the profile node is solved based on the normal cutting quantity iteration algorithm. The relationship between the normal cutting depth and the undeformed chip thickness is clarified. Based on the transient milling force coefficient identification algorithm, the milling force model is established, and the surface topography and milling force in the machining process are simulated.

Compared with the traditional model, the advantages of the cutting force model and the surface topography model proposed in this paper are listed as followed:

  1. 1)

    The normal cutting depth iteration algorithm was proposed in this article which can calculate the real cutting depth considering the influence of the transitional surface during the cutting process.

  2. 2)

    The normal cutting depth parameter was applied to replace the undeformed chip thickness, the cut-in angle, and the cut-out angle of the cutting force model, and the new cutting force model proposed in this article considering the influence of the cutting parameter during the cut-in process and cut-out process which is not simulated by the traditional cutting force model.

  3. 3)

    Compared with the Boolean operation method, the normal cutting depth iteration algorithm is a numerical solution method. This method simplified the 3D grids into the 2D grid of curve parameter which can improve the efficiency of the simulation. And the simulation accuracy of the normal cutting depth is not dependent on the grid density which also can improve the efficiency and the accuracy of the simulation.