1 Introduction

In recent years, rising demands for product variety and quality have resulted in an increasingly high demand for ultra-precision machining technology. The primary processing aim is achieving high-precision shape and surface. However, several faults during the machining process will impair the part’s ultimate accuracy, such as geometric errors, kinematic errors, and thermal errors, to mention a few [1]. Thermal errors, on the other hand, account for more than 75% of all errors, and one of the primary sources of thermal errors is the feed drive system (ball screw and guideway) [2, 3]. Therefore, accurate modeling and experimental studies of the feed drive system’s heat transfer characteristics are essential to enhance the forming accuracy for ultra-precision machining technology.

Because of its high transmission efficiency, superior stiffness, and low cost, the ball screw is commonly utilized in computer numerical control feed drives. However, the traditional drive method still has issues, such as obtaining a precise and uniform feed at low speeds. Therefore, Feng et al. proposed a dual-drive feed system. It operates with the simultaneous drive of the screw shaft and nut, and the system has been shown to significantly reduce nonlinear friction [4, 5]. When it works, the screw shaft and the nut are driven at the same time. However, due to the simultaneous drive of the screw shaft and the nut in the dual-drive feed system, the system adds two moving heat sources, the nut bearing and the nut motor. Therefore, the dual-drive feed system produces more heat, and the temperature and deformation fields are more complex. This essential factor restricts the dual-drive feed system from achieving high-precision micro-feed, to understand the responsive mechanism of the thermal characteristics of the dual-drive feed system and clarify the dynamic changes in the system’s thermal behavior, establishing a high-precision simulation thermal model of the dual-drive feeding system is necessary.

Researchers have employed various means to decrease thermal errors caused by internal and external heat sources in ultra-precision machining operations. One is data-driven modeling of thermal characteristics, which utilizes high-precision sensors to detect and analyze the temperature field and thermal errors in real time, primarily through the use of linear regression, neural networks, fuzzy logic, and deep learning. Cao et al. [6] developed a thermal error prediction model for the spindle of a machine tool using a multiple linear regression method. To increase the accuracy of forecasting the thermal deformation induced by a machine tool under the action of a heat source, Li et al. [7] used particle swarm optimization to tune the parameters of the support vector machine to establish a thermal error model for a high-speed electric spindle. Abdulshahed et al. [8] created a thermal error prediction model using fuzzy c-means (FCM) clustering to establish a functional mapping relationship between real-time machine tool data provided by thermal imaging cameras and machine tool thermal errors. By combining thermal images with sensor, Wu et al. [9] used deep learning to forecast the radial and axial errors of spindles accurately. Data-driven thermal modeling makes compensation decisions by monitoring the machine tool system in real time, skipping the process of modeling, and quantifying the complex formation and evolution mechanisms of thermal errors. Therefore, it is more suitable for dynamic thermal error compensation of machine tool systems in real time, but it also increases the cost of the test system due to the large number of sensors required. Moreover, the data-driven thermal characteristic modeling is a remedial measure after the event, which makes it challenging to guide the optimal design of machine tools.

More scholars, on the other hand, have conducted model-driven thermal characteristics modeling research, as well as creating a virtual prototype of the system based on the actual physical prototype for simulation and optimization [10, 11]. Model-driven thermal characteristic modeling has apparent advantages in thermal design and precise implementation of thermal error prediction. Model-driven method discloses the generation mechanism and evolution law of the system’s thermal deformation error. Establishing accurate thermal boundary conditions (TBCs) is essential for obtaining high-precision thermal errors in thermal field simulation analysis. However, the TCR between the solid contact parts inside the machine tool was ignored in many current studies, and it was assumed that the contact parts were smooth and the heat was transferred without loss from one contact surface to another [12, 13]. Real contact between solid surfaces, on the other hand, happens only at distinct places and tiny areas, and heat flow diminishes as it passes through the contact interface, which is known as TCR. Some research looked at the effect of TCR on the thermal behavior of machine tools to accurately characterize the development and performance characteristics of thermal mistakes. Li et al. [14] established a finite element simulated model of the thermal structure of the feed system and considered the influence of TCR on the overall thermal characteristics, listed the TCR between the key interfaces. But the model did not give a specific way to obtain them, just cited references. Uhlmann et al. [15] created a simulated model of a machining center with a linear motor as a feeding component and considered a complex TCR between the bonding parts. But the TCR in the paper was assumed to be a simple series superposition of two resistances in space, which was obviously different from reality, and the assumption was not verified in the paper. Ji et al. [16] performed thermal characterization on the Z-axis of a large grinding machine tool, and used fractal theory to solve the TCR of each component of the Z-axis of the grinding machine. However, the model oversimplified the spatial physical conditions of the TCR at the gap, such as grease and air. Liu et al. [17] established the TCR between the bearing inner ring and the journal using fractal theory, which was different from the single-point TCR model used in the past. However, only the TCR model of the contact surface asperity under elastic and plastic deformation was constructed, and the influence of air or grease in the clearance on the total TCR was also overlooked.

In conclusion, certain TCRs recommended for the thermal analysis of machine tools are directly given, while others oversimplify the TCR modeling procedure. This situation results in some divergence in the final simulation results of the created thermal characteristics simulation model. As a result, under the premise of the dual-drive feed system, this paper proposes a model for calculating the full-state TCR inside a machine tool by decomposing asperities on a rough surface into multiple intermediate transition states and considering the heat transfer hindrance of grease or air. The temperature rise characteristics and the thermal deformation of the dual-drive feed system are analyzed. The influence of TCR on temperature field distribution is discussed.

2 Thermal model of the dual-drive feed system

The structure of the dual-drive feed system is shown in Fig. 1. Two servo motors, respectively, drive the screw and the nut. The worktable may obtain an exact micro-feed by the difference between the two speeds when the two motors revolve in the same direction at roughly equal speeds. Switching two motors from opposite to reverse spin can also adjust the worktable’s speed from extremely low to very high. The system becomes a traditional ball screw drive system when just the screw motor is powered.

Fig. 1
figure 1

Structure of the dual-drive feed system

Full size image

However, due to the simultaneous drive of the screw and nut of the dual-drive feed system, the bearing of the nut and the nut servo motor are added to the system as the two primary moving heat sources. According to studies, the ball screw and bearings are the most significant heat generators in the feed drive system. However, because the ball screw and bearings have many rough surfaces, heat transfer will be hampered, causing the temperature to decrease dramatically. The modeling analysis of thermal responsive characteristics and thermal error of the feed drive system will be severely harmed if the heat transfer between the rough joints is not precisely depicted. Experiments can be used to calculate the TCR between solid contact parts, but experiments take considerable time and resources. While statistical modeling tools rely significantly on instrument accuracy and other factors, resulting in random measuring findings, this article employs fractal theory to develop a TCR model for rough bonded surfaces. The analytical results of the fractal contact model are not bound by the sampling length and resolution of the measuring device, and the results are deterministic and unique when compared to statistical-based modeling techniques.

2.1 TCR between rough contact surfaces

The surface of the internal joint of the feed system is particularly rough at the micro level due to the processing level constraint, resulting in the so-called rough joint. When heat flows through a rough joint, it differs from conduction in a solid, which is hampered, and a portion of the heat is lost. As a result, the temperature will drop on both contact surfaces. The TCR between the rough joints can be expressed as:

$${R}_{t}=\frac{\Delta T{A}_{a}}{Q}$$
(1)

where \(Q\) is the heat flux flowing through the contact surface (W), \({A}_{a}\) is the nominal contact area between the rough surfaces (m2), and \(\Delta T\) is the temperature drop due to the existence of TCR (℃).

The gap at the rough connection comprises several tiny asperities, which are filled with air or grease. The static contact surface joint between the bearing inner ring and the journal, the dynamic contact joint between the rolling elements and the raceway inside the ball screw. The grease rough joint on the surface of the sliding guideway are all examples of joints found in the dual-drive feed system. The asperities’ contact status with the filled medium inside the various bonds varies. Some bonding portions contain only air, whereas others have a media that includes air and grease. Because the asperities and filled media will block heat flow, heat must pass through the substrate thermal resistance generated by the asperities, interface shrinkage thermal resistance, and interstitial air or grease thermal resistance before passing through the rough bonding part. As shown in Fig. 2, the total TCR for the rough bond where all media are present can be expressed as:

$$\frac{1}{{R}_{t}}=\frac{Q}{{A}_{a}\Delta T}=\frac{1}{{R}_{b}+{R}_{c1}}+\frac{1}{\rho +\frac{1}{{R}_{g}+{R}_{i}}+\frac{1}{\rho +\frac{1}{{R}_{b}+{R}_{c2}}+\frac{1}{\rho +\frac{1}{{R}_{g}+{R}_{i}}+\frac{1}{\rho +\cdots \, }}}}$$
(2)

where \({R}_{b}\) is the substrate thermal resistance generated by the asperities (m2·k/w), \({R}_{cL}\) is the interface shrinkage thermal resistance (m2·k/w), \({R}_{g}\) is the grease conduction thermal resistance (m2·k/w), \({R}_{i}\) is the gap air conduction thermal resistance (m2·k/w), and \(\rho\) is the thermal resistance between the rough surface asperities (m2·k/w).

Fig. 2
figure 2

TCR of the rough joint

Full size image

As seen from Eq. 1, to obtain the TCR between the rough junction, the morphological characterization of the asperities and the rough surface layout need to be accurately described. Moreover, in fractal theory, the W-M function can be used to describe such a 2D rough plane, whose surface profile can be expressed as:

$$z(x)={G}^{(D-1)}\sum_{n={n}_{1}}^{\infty }{\gamma }^{-(2-D)n}{\text{cos}}\left(2\pi {\gamma }^{n}x\right)$$
(3)

where \(G\) is the fractal roughness parameter, \(D\) is the fractal dimension, \(\gamma\) is the spatial frequency of the contour, \({n}_{1}\) is the characteristic parameter of the W-M function, and \(x\) is the geometric coordinate of the contour.

It can be seen from Eq. 3 that the fractal roughness parameter and fractal dimension need to be determined to reconstruct the rough surface of the joint using fractal theory. There are many methods for solving fractal parameters. This paper uses the power spectrum method to solve the fractal parameters of rough surfaces. The continuous power spectrum function of the rough surface profile represented by Eq. 2 is:

$$P(\omega )=\frac{{G}^{2(D-1)}}{2{\text{ln}}\gamma }\frac{1}{{\omega }^{(5-2D)}}$$
(4)

where \(\omega\) is the angular frequency of the random profile.

From Eq. 4, the contour surface power spectrum obeys a power law relationship, so taking the logarithm at both sides of Eq. 4, then:

$${\text{lg}}P(\omega )=(2D-5){\text{lg}}\omega +2(D-1){\text{lg}}G-{\text{lg}}(2{\text{ln}}\gamma )$$
(5)

From Eq. 5, the slope of the fitted curve of the structure function is affected by the fractal dimension, and the intercept is affected by both the fractal dimension and the fractal roughness parameter. Therefore, the power spectrum can be obtained by reconstructing the three-dimensional topography of the rough surface with an optical 3D profilometer to solve the fractal dimension and fractal roughness parameter of different rough surfaces. The morphology of the bearing was measured using a KC-X1010 laser microscope manufactured by KathMatic, as shown in Fig. 3a. The obtained surface roughness profile is shown in Fig. 3b, the profile height is shown in Fig. 3c, and the profile power spectrum is shown in Fig. 3d. The double logarithmic power spectrum is fitted by the least squares method, and based on the slope of the solution as well as the intercept the solution yielded D of 1.85 and G of 1.81 × 10−7 m.

Fig. 3
figure 3

Acquisition of bearing fractal parameters

Full size image

2.1.1 Analysis of the deformation state of asperities in rough junctions

Studies have shown that the contact deformation and actual contact area of the asperities in the rough joint directly affect the values of the substrate’s thermal resistance, shrinkage, and the thermal resistance of the gap [18, 19]. Therefore, the first step in creating a full-state TCR model of the feed system is to characterize the deformation state of each rough joint’s internal asperity under various operating situations. On the other hand, much previous research solely investigated TCR modeling analysis when the asperity is in elastic or plastic deformation, ignoring the asperity’s change from elastic to plastic deformation. Therefore, this paper fully considers the whole process of deformation of the asperity. According to Mo et al. [20], the elastic critical deformation of the asperity during contact can be expressed as:

$${\delta }_{ec}={\left(\frac{\pi H}{2E}\right)}^{2}\cdot \frac{{a}_{ec}^{D/2}}{{\pi }^{2}{G}^{D-1}}$$
(6)

where \(H\) is the micro-hardness of the softer material of the two objects in contact with each other (\({\text{N}}\cdot {\text{m}}^{-2}\)), \(E\) is the equivalent elastic modulus (Pa), and \({a}_{ce}\) is the critical contact area for the elastic deformation of the asperity (m2).

When the interference height of the asperities on two rough surfaces reaches 110 times the elastic critical deformation, the asperities enter the plastic deformation stage. Therefore, the plastic critical deformation \({\delta }_{pc}\) can be expressed as:

$${\delta }_{pc}=110\cdot {\delta }_{ec}=110\cdot {\left(\frac{\pi H}{2E}\right)}^{2}\cdot \frac{{a}_{ec}^{D/2}}{{\pi }^{2}{G}^{D-1}}$$
(7)

The deformation amount of the asperity \(\delta\) can be expressed by the fractal parameter and the deformation contact area \(a\) as:

$$\delta ={G}^{D-1}{a}^{(2-D)/2}$$
(8)

From Eqs. (6), (7), and (8), it can be seen that the elastic critical contact area \({a}_{ec}\) and the plastic critical contact area \({a}_{pc}\) can be solved by \(\delta ={\delta }_{ec}\) and \(\delta ={\delta }_{pc}\) calculated respectively:

$${a}_{ec}=\frac{{G}^{2}}{{(H/2E)}^{2/(D-1)}}$$
(9)
$${a}_{pc}=\frac{{G}^{2}}{{\left[110{(H/2E)}^{2}\right]}^{1/(D-1)}}$$
(10)

2.1.2 Analysis of the contact area of asperities in rough junctions

Even if the external load reaches 10 MPa, the actual contact area for the two rough surfaces in contact is only 1–2% of the nominal contact area, which is another key cause of TCR impacting the thermal properties of the system. A dimensionless contact area \({A}^{*}\) is introduced to precisely represent the contact area between the asperities and so construct a mathematical model of the thermal resistance of each part, which can be expressed as:

$${A}^{*}={A}_{c}/{A}_{a}$$
(11)

To accurately establish the mathematical model of the dimensionless contact area \({A}^{*}\) in the whole process of asperity deformation, it is necessary to accurately describe the deformation state of the asperity in the contact surface. Therefore, the max contact area \({a}_{L}\) of the asperities in the fractal domain is introduced to measure the comparative analysis. When \({a}_{pc}<{a}_{L}<{a}_{ec}\), the asperities are in an elastic and elastic–plastic transition state, then [21]:

$${A}^{*}=\frac{D{\psi }^{1-0.5D}{a}_{pc}^{*}p}{1.1H(2-D)}$$
(12)

where \(\psi\) is the domain expansion coefficient, which is only related to the fractal dimension \(D\), \(p\) is the apparent pressure of the rough junction(N), and \({a}_{pc}^{*}\) is the normalized critical micro-contact area of plastic deformation (m2), and \({a}_{pc}^{*}\) can be expressed as:

$${a}_{pc}^{*}=\frac{2{a}_{pc}}{L{u}^{2}}$$
(13)

where \(Lu\) is the max value of the sampling length (m).

When \({a}_{L}\le {a}_{pc}\), all the asperities in the fractal domain are in the plastic deformation state, namely:

$${A}^{*}=\frac{p}{1.1H}$$
(14)

When \({a}_{L}\ge {a}_{ec}\), the asperities in the elastic, elastic–plastic transition, and plastic deformation states are present, namely:

$${A}^{*}\left\{\begin{array}{l}{\left(\frac{3\sqrt{2\pi }}{4}\right)}^{\frac{2}{3-D}}{\left(\frac{Lu}{G}\right)}^{\frac{2D-2}{3-D}}{\left[{2}^\frac{D}{2}{\left(\frac{2-D}{D}\right)}^\frac{D}{2}\frac{D}{3-2D}{\psi }^{\frac{3D-2-{D}^{2}}{4}}\right]}^{\frac{2}{D-3}}{\left(\frac{D}{4-2D}\right)}^{\frac{3-2D}{3-D}}{\left(\frac{P}{E}\right)}^{\frac{2}{3-D}},D<1.5;\\ {\left({2}^\frac{D}{2}{\psi }^{\frac{4-4D+{D}^{2}}{4}}\right)}^{\frac{-2}{D}}{\left(\frac{p}{E}\right)}^\frac{2}{D}{\left\{\frac{-4}{3\sqrt{2}}{\left(\frac{G}{Lu}\right)}^{D-1}{\left(\frac{2-D}{D}\right)}^\frac{D}{2}\frac{D}{3-2D}{\left({a}_{ec}^{*}\right)}^{\frac{3-2D}{2}}+\frac{H}{E}{\left(\frac{D}{2-D}\right)}^{\frac{2-D}{2}}{\left({a}_{ec}^{*}\right)}^{\frac{2-D}{2}}\right\}}^{\frac{-2}{D}},D\ge 1.5.\end{array}\right.$$
(15)

where \({a}_{ec}^{*}\) is the normalized elastic deformation critical micro-contact area (m2).

2.1.3 Substrate thermal resistance and shrinkage thermal resistance

Because the asperities are so small compared to the contact surface, the heat flow through them will have a significant blocking effect due to the substrate’s thermal resistance. Therefore, while calculating the TCR of rough connections, the thermal resistance of the substrate should not be overlooked, and the TCR of individual asperities should be computed first, followed by the total TCR in parallel [22]. The TCRs of single asperities formed in elastic, elastic–plastic, and plastic deformations are \({R}_{be}\), \({R}_{bep}\), and \({R}_{bp}\), respectively. According to the theory related to contact mechanics, it is known that:

$${R}_{be}=\frac{\sqrt{2\pi }{k}_{1}{k}_{2}{\left[1-{\left({A}^{*}\right)}^\frac{1}{2}\right]}^\frac{3}{2}}{2\sqrt{{a}^{\prime}}\left({k}_{1}+{k}_{2}\right)}$$
(16)
$${R}_{bep}=\frac{\sqrt{2\pi }{k}_{1}{k}_{2}{\left[1-{\left({A}^{*}\right)}^\frac{1}{2}\right]}^\frac{3}{2}}{2\sqrt{{a}^{\prime}}\left({k}_{1}+{k}_{2}\right){\left(1+f\left({a}^{\prime}\right)\right)}^\frac{1}{2}}$$
(17)
$${R}_{bp}=\frac{\sqrt{\pi }{k}_{1}{k}_{2}{\left[1-{\left({A}^{*}\right)}^\frac{1}{2}\right]}^\frac{3}{2}}{2\sqrt{{a}^{\prime}}\left({k}_{1}+{k}_{2}\right)}$$
(18)

where \({a}^{\prime}\) is the micro-contact cross-sectional area (m2), \(f\left({a}^{\prime}\right)\) is a sample function that can be solved by referring to the study of Zhao et al. [23], and \({k}_{1}\) \({k}_{2}\) are the thermal conductivities of the two parts in contact, (W·m−1·℃). When the asperities undergo elastic deformation, it can be expressed as:

$${a}^{\prime}=2a$$
(19)

When the asperities undergo plastic deformation, \({a}^{\prime}\) can be expressed as:

$${a}^{\prime}=a$$
(20)

When heat flows through a rough joint, the actual contact area is lower than the nominal contact area, resulting in shrinkage thermal resistance, according to traditional contact thermal conductivity theory. As a result, to thoroughly understand the TCR of the rough connection, it is essential to precisely solve not only the substrate thermal resistance but also the shrinkage thermal resistance when flowing through the asperities. The shrinkage thermal resistance can be expressed as:

$${R}_{c}=\frac{{\left(1-{\left({A}^{*}\right)}^\frac{1}{2}\right)}^\frac{3}{2}\left({k}_{1}+{k}_{2}\right)}{2{k}_{1}{k}_{2}r}$$
(21)

where \(r\) is the contact point radius (m).

2.1.4 Grease thermal resistance and interstitial air thermal resistance

In fact, because the asperities’ contact area inside the rough bond is significantly lower than the gap’s, the gap air’s thermal resistance in the non-vacuum situation is the essential role in heat transmission between the two components. Boeschoten et al. [24] have experimentally confirmed that the interstitial air thermal resistance is not negligible in the heat transfer phase, assuming that the interstitial air inside the rough bond can be expressed in terms of the average height of the air \(Y\). Thus, referring to Fourier’s law of heat conduction, the thermal resistance of the interstitial gas can be expressed as:

$${R}_{i}=\frac{Y}{{k}_{i}}$$
(22)

where \(k_{i}\) is the thermal conductivity of the interstitial air (W·m−1·℃).

For the feed system of the machine tool, the rough junction interstitial air average height \(Y\) is divided into two cases: a gap filled with grease in the case of the average height of air \({Y}_{1}\), and a gap not filled with grease in the case of the average height of air \({Y}_{2}\). Since the clearance of the asperity is filled with grease and air under the condition of grease, it has a certain degree of fluid characteristics. Its volume will fluctuate to a certain extent under the changes in external pressure and temperature. Therefore, the average height of air under the condition of grease is affected by pressure and temperature. According to the research of Somé et al. [25], it can be expressed as:

$${Y}_{1}\approx \sigma \sqrt[6]{\frac{2}{\pi }}\sqrt[3]{\frac{2{P}_{0}}{{P}_{b}+{P}_{r}}\times \frac{{T}_{c}}{{T}_{0}}}$$
(23)

where \(\sigma\) is the standard error of the asperity height (m), \({P}_{0}\) is the initial gap gas pressure (Pa), \({P}_{b}\) is the grease carrying pressure (Pa), and \({P}_{r}\) is the capillary pressure caused by surface energy (Pa).

For the case where the gap is not filled with grease, the air height can be solved by using the fractal theory above, which can be expressed as [26]:

$${Y}_{2}=2\left[Z-{\psi }^{{(D-2)}^{2}/4}{G}^{D-1}{\left(\frac{4-2D}{D}\right)}^{(2-D)/2}{\left({A}^{*}\right)}^{(2-D)/2}L{u}^{2-D}\right]$$
(24)

where \(Z\) is the arithmetic mean of the height of the asperities (m).

It has already been demonstrated that the rough bond and its internal grease have fluid properties and hence correspond to the conventional liquid–solid micro-surface heat transfer problem. Hamasaiid et al. [27] provided a theoretical model of the thermal resistance of interstitial liquid–solid contact.

$${R}_{g}==\frac{{\left(1-\frac{<{a}_{s}>}{<{b}_{s}>}\right)}^{1.5}\left({k}_{3}+{k}_{4}\right)}{2{k}_{3}{k}_{4}{n}_{s}<{a}_{s}>}$$
(25)

where \(<{a}_{s}>\) and \(<{b}_{s}>\) are the average radius of the contact surface of grease and asperities as well as the base of asperities (m), respectively, \({n}_{s}\) is the micro-contact area density (m−2), and \({k}_{3}\) \({k}_{4}\) are the thermal conductivity of grease and asperities parts (W·m−1·℃), respectively.

As seen from Eq. 25, to establish the TCR model for the liquid–solid contact between the grease and the asperities, the surface morphology of the two contacts should be described first, and the expressions for \(<{a}_{s}>\), \(<{b}_{s}>\), and \({n}_{s}\) need to be determined. Considering the influence of surface tension of grease and other factors, the surface morphology of grease and micro-convex body after making reasonable assumptions is shown in Fig. 4. The morphology curves are above the mean plan (y = 0).Thus, the distribution function can be expressed as:

Fig. 4
figure 4

Liquid–solid contact interface morphology

Full size image
$$\phi (y)=\frac{2}{\sqrt{2\pi }\sigma }{\text{exp}}\left(\frac{-{y}^{2}}{2{\sigma }^{2}}\right)\text{}y\in [0,\infty +)$$
(26)

According to the characteristics of the liquid–solid surface morphology and the distribution function of Eq. 26, we can obtain the expressions of \(<{a}_{s}>\), \(<{b}_{s}>\), and \({n}_{s}\), respectively.

$$<{a}_{s}>={\int }_{y=Y}^{\infty }\frac{(y-Y)}{{m}_{n}}\phi (y)dy=\frac{{R}_{sm}}{2}\left({\text{exp}}\left(-\frac{{Y}^{2}}{2{\sigma }^{2}}\right)-\sqrt{\frac{\pi }{2}}\frac{Y}{\sigma }{\text{erfc}}\left(\frac{Y}{\sqrt{2}\sigma }\right)\right)$$
(27)
$$<{b}_{s}>=\frac{{R}_{sm}}{2}$$
(28)
$${n}_{s}=\frac{8}{\varepsilon {\pi }^{2}}{\left(\frac{1}{{R}_{sm}}\right)}^{2}{\text{erfc}}\left(\frac{Y}{\sqrt{2}\sigma }\right)$$
(29)

where \({R}_{sm}\) is the average spacing of asperities (m), \(\varepsilon\) is the surface morphology coefficient, which is taken as 1.5, and \({m}_{n}\) is the slope of the asperities, which can be expressed as:

$${m}_{n}=2\sqrt{\frac{2}{\pi }}\frac{\sigma }{{R}_{sm}}$$
(30)

From Eqs. 25, 27, 28, 29, and 30, the interstitial liquid–solid TCR is obtained as:

$${R}_{g}=\frac{1.5{\pi }^{2}{R}_{sm}{\left(1-\left({\text{exp}}\left(-\frac{{Y}^{2}}{2{\sigma }^{2}}\right)-\sqrt{\frac{\pi }{2}}\frac{Y}{\sigma }{\text{erfc}}\left(\frac{Y}{\sqrt{2}\sigma }\right)\right)\right)}^{1.5}\left({k}_{3}+{k}_{4}\right)}{8{k}_{3}{k}_{4}{\text{erfc}}\left(\frac{Y}{\sqrt{2}\sigma }\right)\left({\text{exp}}\left(-\frac{{Y}^{2}}{2{\sigma }^{2}}\right)-\sqrt{\frac{\pi }{2}}\frac{Y}{\sigma }{\text{erfc}}\left(\frac{Y}{\sqrt{2}\sigma }\right)\right)}$$
(31)

2.1.5 Full-state TCR between rough junctions

The above analysis has been able to determine the substrate thermal resistance \({R}_{b}\), the shrinkage thermal resistance \({R}_{c}\), the thermal resistance between the asperities of the grease \({R}_{g}\), and the gap air thermal resistance \({R}_{i}\). However, from Eq. 2, the mathematical model of the full-state TCR between rough junctions also requires an expression for the thermal resistance between asperities on rough surfaces. Referring to the study of Li et al., the thermal resistance between asperities can be expressed as [28]:

$$\rho =\frac{{G}^{(D-1)}}{{k{L}_{a}}^{D}}{\left[\frac{D}{(2-D){A}^{*}}\right]}^\frac{D}{2}$$
(32)

where \(k\) is the thermal conductivity of the material (W·m−1·℃), and \({L}_{a}\) is the surface characteristic length of asperities (m).

In summary, the TCR of each junction of the dual-drive feed system is solved using the proposed full-state TCR. To compare and analyze the accuracy as well as the superiority of the full-state TCR. The solution for the general TCR model is obtained in the existing literature [16, 17]. The main difference between the general TCR model and the full-state TCR model is that the obstruction of air or grease is not considered. The TCR of the key junctions is shown in Table 1.

Table 1 The TCRs of the dual-drive feed system at key junctions
Full size table

2.2 Heat generation and heat transfer of the dual-drive feed system

2.2.1 Analysis of heat generation

The dual-drive feed system has 4 major heat sources: (1) heat generation of guide ways, (2) heat generation of servo motors, (3) heat generation of bearings, and (4) heat generation of ball screw. The sliders move continuously on the guide ways. The friction caused by the rotating motion of the ball between the sliders and guide ways is the main reason for the heat generation of the guide way; the heat generated by the guide ways \({H}_{g}\) can be expressed as:

$${H}_{g}=\lambda {f}_{g}{F}_{g}{v}_{g}$$
(33)

where \({f}_{g}\) is the friction coefficient of the guide ways, \({F}_{g}\) is the vertical load (N) carried by the guide ways, and \({v}_{g}\) is the moving speed (m/s) of the sliders relative to the guide ways.

The dual-drive system has two servo motors, which drive the screw shaft and the nut respectively, and the motor heat generation can be calculated by [29]:

$${H}_{m}=\frac{{M}_{T}n}{9550}(1-\eta )$$
(34)

where \({M}_{T}\) is the output torque of the motor (N·mm), \(n\) is the rotation speed of the motor (rpm), and \(\eta\) is the mechanical efficiency of the motor.

Bearing as a rotating part, friction is the main source of heat. The heat generation of bearings can be calculated by:

$${H}_{b}=1.047\times {10}^{-4}{n}_{b}({M}_{l}+{M}_{v})$$
(35)

where \({n}_{b}\) is the rotation speed of the bearing (rpm), \({M}_{l}\) is the load friction torque caused by the elastic lag of the material and the local differential friction (N·mm), and \({M}_{v}\) is the viscous friction torque generated by the bearing and the lubricant (N·mm). The load friction torque can be calculated by:

$${M}_{l}={f}_{1}{p}_{1}{d}_{b}$$
(36)

where \({f}_{1}\) is the coefficient related to the type and load of the bearing, \({p}_{1}\) is the preload of the bearing (N), and \({d}_{b}\) is the mean diameter of the bearing (mm).

For front bearing and nut bearing:

$${f}_{1a}={{1}{\text{0}}}^{-3}{\left({P}_{0}/{C}_{0}\right)}^{0.33}$$
(37)
$${p}_{1a}=\text{1.4}Fa-0.1Fr$$
(38)

where \({P}_{0}\), \({C}_{0}\), \(Fa\), and \(Fr\) are the equivalent static load (N), rated static load (N), axial load (N), and radial load of the bearing (N), respectively.

For rear bearing:

$${f}_{1b}=9\times {10}^{-4}{\left({P}_{0}/{C}_{0}\right)}^{0.55}$$
(39)
$${p}_{1b}={3}Fa-0.1Fr$$
(40)

The viscous friction torque generated by the bearing and the lubricant can be calculated by:

$$\begin{array}{cc}{M}_{v}={10}^{-7}{f}_{0}{({v}_{0}{n}_{b})}^{2/3}{d}_{b}& {v}_{0}{n}_{b}\ge {2000}\end{array}$$
(41)
$$\begin{array}{cc}{M}_{v}={160}\times {10}^{-7}{{f}_{0}{d}_{b}}^{3}& {v}_{0}{n}_{b}<{2000}\end{array}$$
(42)

where \({f}_{0}\) is the coefficient related to the bearing type and lubrication, and \({v}_{0}\) is the kinematic viscosity of the lubricant inside the bearing. In this study, Eq. (9) was used for the calculation.

Friction is still an important source of heat generation for ball screws, mainly from the relative motion between the ball and groove in the process of screw and nut rotation, which can be calculated by:

$${H}_{s}=0.12\pi {f}_{s}{v}_{s}{n}_{s}{M}_{s}$$
(43)

where \({f}_{s}\) is the coefficient related to nut type and lubrication, \({v}_{s}\) is the kinematic viscosity of the lubricant inside the groove (mm2/s), \({n}_{s}\) is the relative rotation speed of the screw and nut (rpm), and \({M}_{s}\) is the total frictional torque of the nut (N·mm).

2.2.2 Analysis of heat transfer

The heat transfer process of the dual-drive feed system can be divided into two types. One is the natural convective heat transfer between the fixed surface and the surrounding air, and the other is the forced convective heat transfer due to the relative motion of the parts and the air. The convective heat transfer coefficients (CHTCs) of both can be expressed as [30]:

$$h=\frac{Nu\cdot \lambda }{{L}_{s}}$$
(44)

where \(Nu\) is the Nusselt number,\(\lambda\) is the fluid thermal conductivity (W/m·K), and \({L}_{s}\) is the component feature size (mm).

Natural convection heat transfer occurs on the surfaces of fixed components such as the bearing housing and base. The Nusselt number \(N{u}_{n}\) can be calculated by:

$$N{u}_{n}=C{(Gr\cdot Pr)}_{\tau }^{\partial }$$
(45)

where \(C\), \(\partial\) is the constant determined by the shape of the heat source and fluid conditions, \(Gr\) is the Grashof number, \(Pr\) is the Prandtl number, and \(\tau\) is the qualitative temperature. \(Gr\) can be calculated by:

$$Gr=\frac{{g\beta {L}_{s}}^{3}({T}_{s}-{T}_{a})}{{{v}_{a}}^{2}}$$
(46)

where \(g\) is the acceleration of gravity (m/s2), \(\beta\) is the volume expansion coefficient of air, \({T}_{s}\) is the surface temperature of the part (℃), \({T}_{a}\) is the ambient temperature (℃), and \({v}_{a}\) is the kinematic viscosity of the air (mm2/s).

Forced convection heat transfer occurs on the surface of the moving components, mainly including the screw shaft, worktable, nut servo motor, and other parts. The screw shaft is rotating and has a spiral groove on its surface, and its Nusselt number can be calculated as

$$N{u}_{s}=0.133R{e}^{2/3}P{r}^{1/3}$$
(47)

where \(Re\) is the Reynolds number. For the top and lateral surfaces of the remaining parts, the Nusselt constant \(N{u}_{p}\) can be calculated by:

$$N{u}_{p}=0.332R{e}^{1/2}P{r}^{1/3}$$
(48)

For the front surface perpendicular to the direction of motion, the Nusselt constant \(N{u}_{\text{v}}\) can be calculated by:

$$N{u}_{\text{v}}=0.228R{e}^{0.731}P{r}^{1/3}$$
(49)

The motion of the worktable of the dual-drive feed system is the combined motion of the screw motor and the nut motor. To analyze the thermal field characteristics of the dual-drive system at different feed speeds, the system heat generation and the key heat transfer coefficients of each part are calculated based on Eqs. (33–49) at an ambient temperature of 21 ℃, as shown in Table 2 for different speed combinations.

Table 2 The partial TBCs of the dual-drive feed system
Full size table

3 Thermal model verification of the dual-drive feed system

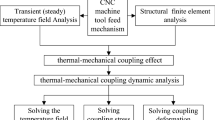
To validate the effectiveness of the proposed full-state TCR model in analyzing the thermal characteristics of the feed system, the established thermal models of full-state TCR, general TCR, and without TCR are loaded into finite element simulation analysis, and experiments are carried out to verify the comparative analysis.

3.1 Finite element simulation model of dual-drive feed system

A finite element simulation model of the dual-drive feed system is created based on the TCR, system heat generation, and heat transfer coefficient calculated above to test the correctness of the proposed full-state TCR and study the thermal characteristics of the dual-drive feed system. To increase the solving efficiency, the finite element analysis approach is used to provide useful recommendations for the optimization design of machine tools prior to manufacture. The following appropriate simplifications and assumptions are made:

  1. (1)

    The chamfers and some tiny parts inside the system are ignored.

  2. (2)

    The screw shaft ignores the grooves on its surface and treats it as a cylinder.

  3. (3)

    The parameters of heat generation and CHTCs obtained from the previous calculation do not vary with the movement and temperature rise of the components.

The hexahedral and tetrahedral meshes are used to mesh the model once it is imported into ANSYS. The heat sources, such as screws and bearings, are coarsely meshed to reduce simulation error. The mesh create 639,784 nodes and 280,220 elements. The dual-drive feed system is subjected to the same TBCs and material attributes as the preceding section. Table 3 shows the material qualities of several of the system's essential components.

Table 3 Material properties of the dual-drive feed system
Full size table

3.2 Experimental verification device and scheme

To verify the accuracy of the solution of the FEM simulated model created in the previous research, an experimental study on the temperature rise and deformation of the dual-drive feed system is necessary. The test device is shown in Fig. 5. Concerning current studies, the temperature measuring locations that have a substantial impact on the total thermal field of the feed system are chosen [31, 32]. The temperatures of the front bearing (T1), the rear bearing (T2), the nut flange (T3), the screw shaft (T4), the worktable (T5), the environment (T6), and the axial deformation of the screw shaft (\(D\)) were measured separately. The temperature data were acquired at T1–T3, T5, and T6 by five PT100 temperature sensors with a resolution of 0.1 ℃. The NI PXIe-1082 was used to acquire and process the temperature data, and the temperature at T4 was measured by a thermal infrared imager E86 from FLIR with a resolution of 0.1 ℃. Axial deformation (\(D\)) was measured by the CL-3000 laser displacement sensor made by Keyence. When the temperature rise reached 95% of the max temperature rise and the stable fluctuation of the value of the multiple temperature measuring points curve was less than 0.5 ℃, the system can be considered to have reached the thermal equilibrium state. According to the preliminary experiment, the temperature rose rapidly in the initial period. Therefore, each 120 s was taken as a measuring cycle before 600 s, and each 600 s was taken as a measuring cycle after 600 s. To minimize the influence of experimental errors on the analysis results, the temperatures of the T1–T5 temperature measuring points and the axial deformation of the screw were measured five times at a synthesis speed of 0.18 m/min, and the values of each temperature measuring point were taken as the results of this experiment when the system reached the thermal equilibrium state. The results are shown in Table 4.

Fig. 5
figure 5

Temperature rise and deformation test device

Full size image
Table 4 Statistical analysis of measured data
Full size table

As seen from Table 4, the standard error of all temperature measuring points and axial deformation is less than 0.3, indicating that the numerical range of the repeated five experimental results has little change. It is reliable to analyze the average value as the experimental result, which can effectively reduce the error caused by the randomness of the experiment.

3.3 Comparison analysis of simulation and experimental results

The reciprocating motion of the nut relative to the screw is defined in the simulation platform, and the transient thermal analysis end time is set to 10,800 s. The temperature field and the axial deformation of the screw after stabilization of the dual-drive feed system are obtained. The simulated results for three different combinations speeds are included. Due to space limitations, only the simulated results based on the full-state TCR model and the general TCR model are listed. The simulated results are shown in Figs. 6 and 7.

Fig. 6
figure 6

Temperature field and axial deformation of the screw based on the full-state TCR. a The synthesis speed is 0.18 m/min. b The synthesis speed is 0.36 m/min. c The synthesis speed is 0.54 m/min

Full size image
Fig. 7
figure 7

Temperature field and axial deformation of the screw based on the general TCR. a The synthesis speed is 0.18 m/min. b The synthesis speed is 0.36 m/min. c The synthesis speed is 0.54 m/min

Full size image

From the results in Figs. 6 and 7, it can be seen that the distributions of temperature and deformation fields based on the full-state TCR and the general TCR model are similar. The front bearing, the nut flange, and the rear bearing are the main heat distribution areas of the dual-drive feed system. The min and max temperatures of the thermal field increase with increasing speed. The lowest temperature is at the base, and the highest is at the nut flange. The reason is that the nut is affected by the heat generated by the ball screw and the nut bearing at the same time and because the nut is inside the nut housing. It does not produce convection heat dissipation with the surrounding air, resulting in heat accumulation and local high temperature. The axial elongation of the screw shaft increases with increasing rotational speed. The max elongation occurs at the connection between the screw shaft and the rear bearing, because the rear bearing is a support bearing and cannot limit the axial displacement of the screw at all.

The temperature and deformation fields are solved based on the two models, which significantly differ in value. At the same rotational speed, the max value of the temperature field in Fig. 6 is higher than that in Fig. 7. In comparison, the min temperature is lower than that in Fig. 7. This is because the highest temperature is at the heat source and the lowest temperature is at the non-heat source location. The adopted full-state TCR model considers the thermal resistance between the joints more fully than the general TCR model. Therefore, the temperature at the heat source is higher and the temperature at the non-heat source is lower. In addition, the thermal elongation of the screw in Fig. 6 is higher than that in Fig. 7 at the same rotational speed condition. The reason is that the screw is deformed under thermal stress, and heat generation from a heat source is the root cause of thermal stress. The corresponding thermal elongation produced is larger since the temperature is higher at the heat source in Fig. 6.

To deeply analyze the superiority of the proposed full-state TCR model, transient data based on full-state TCR, general TCR, and without TCR are extracted. The characteristics of temperature rise and deformation during the operation of the feed system are compared and analyzed. The results of the comparative analysis are shown in Figs. 8, 9, and 10. The errors of the results after the system reaches thermal equilibrium is shown in Table 5.

Fig. 8
figure 8

Comparative analysis results at a synthesis speed of 0.18 m/min. a Temperature comparison of T1. b Temperature comparison of T2. c Temperature comparison of T3. d Temperature comparison of T4. e Temperature comparison of T5. f Axial thermal elongation of the screw

Full size image
Fig. 9
figure 9

Comparative analysis results at a synthesis speed of 0.36 m/min. a Temperature comparison of T1. b Temperature comparison of T2. c Temperature comparison of T3. d Temperature comparison of T4. e Temperature comparison of T5. f Axial thermal elongation of the screw

Full size image
Fig. 10
figure 10

Comparative analysis results at a synthesis speed of 0.54 m/min. a Temperature comparison of T1. b Temperature comparison of T2. c Temperature comparison of T3. d Temperature comparison of T4. e Temperature comparison of T5. f Axial thermal elongation of the screw

Full size image
Table 5 Comparison of measuring and simulation results
Full size table

As seen from Figs. 8, 9, and 10, along with the increase in motor speed and synthesis speed, the temperature of each part of the system and the axial thermal elongation of the screw will increase. As the speed increases, the rate of increase of temperature and deformation will also increase, and the time needed for the system to reach thermal equilibrium will gradually become shorter. The reason is that when the speed increases, the heat generation rate of the system increases, and the heat dissipation efficiency with the surrounding environment increases significantly, so the system can reach the thermal equilibrium state faster.

As shown in Table 5, for the temperatures at the heat source, such as T1, T2, and T4, the comparison relationship between the experimental measuring and the three TCR models is measured value > full-state TCR > general TCR > without TCR. For the temperatures at the non-heat source, such as T3 and T5, the comparison relationship between the experimental measuring and the three TCR models is measured value < full-state TCR < general TCR < without TCR. The reason is that compared with the general TCR or without TCR, the full-state TCR model is used to consider the TCR between the rough joint fully. Therefore, the heat flow between the heat source and the surroundings and components is reduced. The temperature simulated results at the heat source are higher and closer to the measured values, similar to the reduction in heat gathered at the non-heat source. As a result, the simulated temperature at the non-heat source is lower and closer to the measured value. However, there is still an error between the full-state TCR model and the measured value. The reason is that with the operation of the system, many think that only the oil joint enters the air, and many think that only the air joint enters the grease. There are many uncertain factors in actual operation. Therefore, it is difficult to analyze the TCR form between the joint completely and accurately. As a result, the accuracy of the simulated model established by the full-state TCR is difficult to improve further, which is the application limitation of the full-state TCR model.

As shown in the errors in the temperature at the heat and non-heat sources, the error of the temperature at the non-heat sources is significantly higher than the error of the temperature at the heat source. The reason is that the non-heat source needs to pass through multiple rough joints to achieve heat exchange. Therefore, the process of heat transfer causes the continuous accumulation of errors, which leads to a large simulation error at the non-heat source.

It can also be seen from Table 5 that the temperature simulation error of the thermal model built with full-state TCR is not higher than 5%, and the error of the axial deformation of the screw is not higher than 7%. The min temperature simulated error of the thermal model built with general TCR is 6.68%, and the min error of the axial deformation of the screw is 11.28%. The error of the thermal model built without TCR is much larger. It is illustrated that the accurate description of TCR has an essential impact on the accuracy of the simulation model. At the same time, the effect of air or grease on TCR cannot be neglected. Since the full-state TCR model fully describes the thermal resistance between the joints, it considers the thermal resistance of the air or grease in the gap, which has been neglected in previous models. The full-state TCR model makes the temperature field and the deformation field solution results more accurate. This indicates that the accuracy of the finite element simulation model can be significantly improved by using the full-state TCR model. Moreover, the error of the axial deformation of the screw is slightly higher than the error of each temperature measuring point. Because the axial deformation of the screw is the result of the joint action of several temperature measuring points in the feed system. The error of several key temperature points does not fully represent the final axial deformation of the screw. Therefore, the key temperature points of the dual-drive feed system should be further selected and optimized, and the system’s TBCs should be optimized.

Thermal simulation can obtain much operational process data compared to experiments, thus providing insight into the thermal characteristics of the feed system. Taking the synthesis speed of 0.36 m/min as an example, based on the full-state TCR model, the temperature field of the screw shaft with time and position changes is solved.

As shown in Fig. 11, over time, all parts of the screw have different degrees of temperature rise. The temperature in the middle of the screw is the highest. At any time, the temperature along the axial direction of the screw decreases first and then increases, then decreases and then increases. The reason is that the ends of the screw are mated to the bearings and have a higher temperature rise. The exposed screws have a lower temperature rise because of the forced convection heat transfer with the air. The temperature at both ends is approximately symmetrical relative to the middle. The conventional screw axial temperature distribution is the opposite of the dual-drive sliding feed system. The axial temperature distribution of the conventional screw is low in the middle and high at both ends. The reason for this difference is that the bearing is added inside the nut, and the nut motor also affects the distribution of the temperature field during operation. Therefore, the structure of the dual-drive feed system should be further optimized to improve the temperature field distribution.

Fig. 11
figure 11

Overall temperature rise of the screw

Full size image

4 Conclusions

To accurately describe the thermal field characteristics of the dual-drive feed system and to clarify the mechanism of temperature rise and thermal deformation, this study proposes a full-state TCR calculation model considering multiple deformation states of the asperities between the rough junction and the contact gap air and grease. According to the results and analysis, the following conclusions can be drawn.

  1. (1)

    The thermal field of the dual-drive feed system is different from that of the conventional feed system. Due to the difficulty of heat dissipation, as well as the combined effect of screw and nut bearing, the front bearing, nut, and rear bearing are the primary heat distribution of the dual-drive feed system. The feed and rotational speed have an essential influence on the thermal characteristics of the dual-drive feed system. With the increase in feed and rotational speed, the heat generation and heat transfer will be higher, resulting in a faster rise in temperature and a higher thermal deformation rate of the system. The time needed to reach thermal equilibrium becomes shorter.

  2. (2)

    The TCR has an essential effect on the temperature distribution. Due to the existence of TCR, the thermal characteristics of different temperature measuring points are different. The simulated results at the heat source are lower than the experimentally measured temperature. Meanwhile, the simulated results at the non-heat source are higher than the experimentally measured temperature. The simulated error at the non-heat source is significantly higher than that at the heat source.

  3. (3)

    The accurate description of the TCR has an essential impact on the accuracy of the simulated model. The proposed full-state TCR model can effectively improve the simulated accuracy of the temperature at key temperature measuring points and the axial deformation of the screw. The error of the temperature at key temperature points is not higher than 5%, and the error of the axial deformation of the screw is not higher than 7%. It is much smaller than the error of the simulated model based on the general TCR model and without TCR.