1 Introduction

The use of industrial robots for machining processes has become increasingly popular owing to its low cost, good flexibility, high efficiency, and wide workspace [1, 2]. Compared to manual polishing, automated polishing systems increase efficiency, reduce costs [3] labor [4], and minimize manufacturing time [6]. Generally, these criteria are important considerations when polishing different surfaces such as manufacturing molds, airfoils, engine blades, and other compound or complex surfaces. Automated robotic polishing systems describe the interrelated settings and parameters required to create manufactured workpieces with smooth and shiny surfaces. These settings and parameters include robot motion control through trajectory planning and force control, material removal profile (MRP) modeling, and the selection of abrasive grain features, the rotating speed of the tool, etc. The most important factor during a polishing operation is maintaining the equality and accuracy of the material removal depth. This can be achieved by providing smooth motion and controlling the contact polishing force. However, accomplishing this can be quite challenging, especially for compound and complex surfaces [7,8,9]. Invariably, contact force errors produce an excess or insufficient material removal depth, poor surface quality, and less safety during polishing operations [10]. Maintaining a constant contact force is crucial for eliminating these problems. Advanced force control algorithms are required to control the contact force for compound and complex surfaces [7, 11]. To realize an effective automated robotic polishing system, a smooth trajectory planning method coupled with a constant polishing force should be implemented to achieve uniform material removal and high-quality polishing [12, 13].

Several studies have been conducted on automatic robotic polishing to reduce costs and enhance the polishing quality of different workpieces. To ensure uniform material removal, Tasi et al. [15] proposed a robotic polishing system based on contact force control. They achieved a contact force with a nearly uniform surface roughness. Zhang et al. [16] presented a methodology to achieve a constant force by controlling the dynamic output of the force. Li et al. [17] proposed a polishing system with a controlled contact force based on the rising bandwidth of force control. To enhance the accuracy and quality of polishing curved surfaces, Oba et al. [18] presented an approach to control the tool position and contact force while polishing curved surfaces using a series-parallel mechanism to enhance control accuracy. They stated that the rotation of the polishing tool produces robust vibrations, making it difficult to predict and control the contact force. Tian et al. [14] studied an automatic polishing platform for curved surface finishing processes, wherein continuous polishing power was maintained through active and passive control. The results revealed that their polishing method offered good practicality for polishing curved surfaces, achieving a mirror impact surface, and maintaining a perfectly uniform removal depth. Fengjie et al. [19] also investigated an automated polishing platform to enhance the quality of robotic polishing and ensure stability during the polishing process. Considering polishing precision, Xu et al. [20] designed a hybrid manipulator for achieving high-precision polishing. The results revealed that their design could achieve high-precision polishing. Mohammed et al. [21] presented a new design comprising an automated electro-mechanical tool attached to an industrial robot for automated polishing. The surface roughness, reflection precision, and appearance of the polished surface using this setup were good. To ensure the accuracy of path planning and reduce the execution time of the polishing process, Kharidege et al. [22] proposed a robotic polishing method wherein the planning approach and programming tool were described based on the data of a computer aided design system (CADs) to generate path planning. Ding et al. [23] proposed a technique for polishing concave workpieces using a robot arm based on an adaptive proportional-integral force controller method. The effectiveness of their method was established through simulations and experiments.

These studies are primarily related to the control and modeling of robotic polishing processes. The common aspect of these studies is that uniform material removal was viewed as the key to achieving an accurate and high-quality surface finish. The main factor for achieving uniform material removal is the polishing force, which must be precisely adjusted to maintain a constant value along the entire polished surface. For curved, complex, and compound surfaces, maintaining constant stress during polishing cannot be achieved through traditional force control methods. Notably, most of these studies did not discuss motion smoothness, which has a significant effect on polishing quality. Herein, we present an automatic polishing system for compound surfaces composed of sensitive materials (aluminum and resin) that can be difficult to polish accurately. This problem was encountered by the one of Chinese factory in China. Through this study, we aim to introduce an effective polishing process that can achieve high-quality polishing of compound surfaces. The study comprised the following stages: first, a smooth path was generated through non-uniform rational B-spline interpolation using the harmonic model; second, a constant polishing force was implemented based on the OSRDF impedance controller combined with the fast gravity compensation approach; third, the removal depth profiles were modeled on plane and curved surfaces based on the distance between two points formula and Pythagorean theory, respectively; finally, we conducted experiments and herein report the results of our evaluation of the proposed polishing methodology for achieving precise polishing of compound surfaces.

This paper is organized as follows: the trajectory planning method is presented in Section 2. The description of force controller strategy is provided in Section 3. A removal profiles are showed in Section 4. Then, experimental study results are explained in Section 5. Finally, the conclusions were drawn in Section 6.

2 Trajectory planning algorithm

The main target of trajectory planning in Cartesian space is maintaining the continuous and smooth motion of the end effector through multiple points [24]. A non-uniform rational cubic B-spline is used to fit these points in order to generate a smooth path for the polishing process. Then the harmonic model is used to guarantee these points’ continuity and easy interpolation. Finally, squad quaternion is performed to calculate the arc length parameter by obtaining corresponding discrete points of this algorithm.

2.1 Cubic B-spline curve

In order to achieve the tool center points (TCPs) in a coordinate system, the following formula can describe it.

$$\begin{aligned} Q(t) = \sum \limits _{i = 0}^n {{P_i}{N_{i,k}}(t)} \end{aligned}$$
(1)

where \( P_i \) (i = 0, 1,..., n) represents a control points, while k is a polynomial order of a B-spline curve. The \( N_{i,k}(t) \) represents a B-spline functions; it can be described by the order k; and \( t_i \): i = 0,..., \( n + k \) which is commonly called the knot sequence. In addition, Eq. 1 can be described as a non-uniform rational cubic basis spline curve as:

$$\begin{aligned} C(t) = \frac{{\sum \limits _{i = 0}^n {{N_{i,k}}(t){w_i}{P_i}} }}{{\sum \limits _{i = 0}^n {{N_{i,k}}(t){w_i}} }}{\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {t_k} \le t \le {t_{n + 1}} \end{aligned}$$
(2)

where \(w_i(\)i=0,1,2,...n) is rational weights of basis spline curve; where \(w_i>0\) and if \(w_i=1\) the integral piecewises of polynomial spline will connected and recovered smoothly. The functions \(N_{i,k}\) can be written as:

$$\begin{aligned} {N_{i,1}}(t) = \left\{ \begin{array}{l} 1\,\,\,if\,t \in [{t_i},\mathrm{{ }}{t_{i + 1}}],\\ 0\,\,\,\,\,\,\,\,\,otherwise. \end{array} \right. \end{aligned}$$
(3)

In a case of \( k > 1 \),

$$\begin{aligned} {N_{i,k}}(t) = \frac{{t - {t_i}}}{{{t_{i + k - 1}} - {t_i}}}{N_{i,k - 1}}(t) + \frac{{{t_{i + k + 1}} - t}}{{{t_{i + k}} - {t_{i + 1}}}}{N_{i + 1,k - 1}}(t) \end{aligned}$$
(4)

Noting that the quotient (\(\frac{0}{0}\)) is defined as zero, where \(t = ({t_0},{t_1},{t_2}.....,{t_{n + p + 1}})\) are knot vector with \({t_i} \le {t_{i + 1}},\,0 \le i \le n + p\) and it is calculated as: \({t_0} = {t_1} = {t_2} = {t_3}\), and \({t_i} = {w_{i - 2}}\) \((i=4,5,...)\). By considering \(\{ {P_i}\} _{i = 0}^n\) are control points and assuming the first and last point \( {P_0}\) and \( {P_n} \) for start and last point, respectively.

To calculate an arc length of C(t) on parameters of [a, b], we can use Simpson’s approach [25], which is described as:

$$\begin{aligned} s = \int \limits _a^b {f(x)dx} \end{aligned}$$
(5)

where s is approximation of an integral of f(x). Then an approximated result of the composite Simpson approach can be used to calculate the arc length of this curve as follows:

$$\begin{aligned} \int \limits _a^b {f(x)dx} \!= \!\int \limits _{x_0}^{x_4}{\frac{h}{{12}}({f(x_0)} \!+\! 4{(x_1)} + 2{(x_2)} + 4{(x_3)} + {(x_4)})} \end{aligned}$$
(6)

where \( {x_0} = a,{x_4} = b,h = b - a,{x_2} = {x_1} + h,{x_3} = {x_2} + h;{f_i} = f({x_i}),i = 0,1,..4 \). Then, through this Boolean formula, the arc length parameter and total arc length of the TCPs can be obtained. Figure 1 shows the Simpson rule formula.

Fig. 1
figure 1

Simpson rule principle

Full size image

2.1.1 Harmonic model

The harmonic trajectory planning provides the smoothness, continuity, and easy interpolation of segments between any two points of the curve. A harmonic motion is described by an acceleration based on the position formula, with a negative sign [26]. The mathematical expression of the harmonic formula can be formulated from Fig. 2 below.

Fig. 2
figure 2

The harmonic motion diagram

Full size image

According to Fig. 2 the harmonic motion can be described as:

$$\begin{aligned} s(\theta ) = R(1 - \cos \theta ) \end{aligned}$$
(7)

The actual position can be formulated as:

$$\begin{aligned} q(t) = \frac{Q}{2}\left( {1 - \cos \frac{{\pi (t - {t_0})}}{T}} \right) + {q_0} \end{aligned}$$
(8)

where \( Q = q_1 - q_0 \) is total displacement between any two points through curve, and \( T = t_1 - t_0 \), represents a total time, then velocity, acceleration and jerk can be written as:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{q}(t) = \frac{{\pi Q}}{{2T}}\sin \left( {\frac{{\pi (t - {t_0})}}{T}} \right) \\ \ddot{q}(t) = \frac{{\pi ^2 {Q}}}{{2{T^2}}}\cos \left( {\frac{{\pi (t - {t_0})}}{T}} \right) \\ \overset{\varvec{\cdots }}{q}(t) = - \frac{{\pi ^3 {Q}}}{{2{T^3}}}\sin \left( {\frac{{\pi (t - {t_0})}}{T}} \right) \end{array} \right. \end{aligned}$$
(9)

2.1.2 Squad interpolation approach

The spherical quadrangle interpolation (squad) here is used to achieve rotation interpolation curve; the general form of squad is:

$$\begin{aligned} \begin{array}{l} squad({q_n},{a_n},{a_{n + 1}},{q_{n + 1}};t) =\\ slerp(slerp({q_n},{q_{n + 1}},t), slerp({q_i},{q_{i + 1}},t);2t(t - 1)) \end{array} \end{aligned}$$
(10)

where

$$\begin{aligned} a_n = {q_n}\exp ( - \frac{{\log ({q_n}*{q_{n - 1}}) + \log ({q_n}*{q_{n + 1}}}}{4}) \end{aligned}$$
(11)

where in this formula \( {q_n} \) is sequences of quaternions; t is an interpolation factor which lies between [0,1]; \( {a_n} \), \( {a_{n + 1}} \) represent a middle quaternions. Using the squad quaternions will keep these parts and maintain smooth motion from one point to another.

3 Force control algorithm

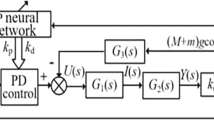
Controlling a contact force between a polishing tool and work object is essential [7], where the constant controlled force increases the polished surfaces’ accuracy and quality. In order to obtain delicate polishing, it is not only possible to rely on the motion control system to accurately determine the position and posture of a polishing tool; in addition, there should be a good force control algorithm between a tool and a work object. The position-based impedance controller is assumed as a good methodology to obtain constant force and adjusting robot end effector position and posture [27, 28] of a polishing tool. Most industrial robots have no problem with position control, but they have a vital challenge of force tracking in case of interaction. This issue causes inaccurate contact between the used polishing tool and workpieces, leading to over or under removal depth. Therefore, the accurate force control strategy solves the force tracking issue and enhances an end effector’s posture, leading to high-quality polishing. In this paper, we used our previous work, the OSRDF impedance controller [29] to solve the problem of contact polishing force.

3.1 Constant force tracking

The OSRDF variable impedance controller described in Fig. 5 gives constant force to the polishing process and can adjust the position with high accuracy. The result of this controller is treated as the required normal polishing force. The force strategy depends on two parameters: firstly, online stiffness is calculated according to desired position and force; then, merge contact force error with reverse damping force. For accurate position and contact force, the second order system (\({M_r}\), \({B_r}\), \({K_r}\)) parameters and trajectory \({X_d}\) must accurately designed. A mathematical expression of the OSRDF impedance controller can be summarized as follows: firstly, contact force based on Fig. 3 is:

$$\begin{aligned} {F_e} = {K_e}({X_e} - {X_a}) \end{aligned}$$
(12)

where \( K_e \) is the environment stiffness, \( X_e \) is the location of an environment, and \( X_a \) is the real location. According to Fig. 3, a robot motion must be analyzed as:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{M_r}(\ddot{X}_s^a) + {B_r}(\dot{X}_s^a) + {K_r}(X_s^a - X_s^b) = 0}\\ {{K_r}(X_s^a - X_s^b) = {F_d}} \end{array}} \right. \end{aligned}$$
(13)

where \( X^a_s \), \( X^b_s \) are positions before and after spring respectively and \( F_d \) is desired force, by referring to Fig. 7 suppose that \({X_t} = {X_a} = {X_d} + \delta X\). Also \({X^a_s} - X^b_s= \delta X \), and real location can be re-formulated as:

$$\begin{aligned} {X_a} = {X_d} + {X^a_s} - {X^b_s} \end{aligned}$$
(14)
Fig. 3
figure 3

Contact force model

Full size image

By rearrangement Eq. (19) and considering matching case between both desired and environment positions, \( {X_d}={X_e} \), then an error can be written as:

$$\begin{aligned} ({X_a} - {X_d}) = {X_d} - \frac{{{K_r}}}{{{K_e}}}({X_a} - {X_d}) \end{aligned}$$
(15)

The steady-state error of position must be accurately expressed by a desired position, an environment stiffness and robot mass based on Eq. 15 as:

$$\begin{aligned} e_{ss}^X = \frac{{{K_e}{X_d}}}{{{K_r} + {K_e}}} \end{aligned}$$
(16)

The estimation of a force value is calculated by merging a position error and a robot stiffness as follows:

$$\begin{aligned} {F_d^ \oplus } = \left( {\frac{{{F_d}{K_e}}}{{{K_e}{X_d} + {F_d}}}} \right) \left( {\frac{{{K_e}{X_d}}}{{{K_r} + {K_e}}}} \right) \end{aligned}$$
(17)

An online robot stiffness is calculated based on the following expression:

$$\begin{aligned} K_{_r}^ \oplus = \frac{{{F_d^ \oplus }}}{{e_{ss}^X}} = \left( {\frac{{{F_d}{K_e}}}{{{K_e}{X_d} + {F_d}}}} \right) \end{aligned}$$
(18)

The following expression represents the force error before compensation:

$$\begin{aligned} \delta F = {F_e} - {F_d} = {K_e}({X_e} - {X_a}) - {F_d} \end{aligned}$$
(19)

The reverse reference damped force can be represented by \( {{F_{X_d}} = B_r{\dot{X}_d}} \), in order to reduce force error to zero, this expression must be added to Eq. 19 yield:

$$\begin{aligned} \delta \mathrm{{F'}} = \delta \mathrm{{F + }}{F_{X_d}} = {F_d} - {K_e}({X_e} - {X_a}) + {F_{X_d}} \end{aligned}$$
(20)

A practice force control by the OSRDF controller can be concluded as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {{\ddot{X}}_t}(t) ={\ddot{X}}_d (t) + 1 \big /{M_r} ( F_d(t) - \\ {B_r}({{\dot{X}}_t}(t - 1) - 2{{\dot{X}}_d}(t))- K_r^ \oplus X_d(t)\\ {{\dot{X}}_t}(t) = {{\dot{X}}_t}(t - 1) + {{\ddot{X}}_t}(t){T_s}\\ {X_t}(t) = {X_t}(t - 1) + {{\dot{X}}_t}(t){T_s} \end{array} \right. \end{aligned}$$
(21)

3.2 Gravity compensation

A force sensor measures the force between a tool and a work object during polishing. This study utilized a 6D force and torque sensor which can measure three-dimensional forces/torques (\({F_x},{F_y},{F_z}\), \({T_x},{T_y},{T_z}\)), where Fig. 4 shows a gravity analysis. The coordinates system of gravity compensation is represented by (xyz) .

Fig. 4
figure 4

Force sensor gravity compensation analysis

Full size image

The relationship between forces and moments can be derived using the right-hand rule [30] by referring to Fig. 4 as:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{T_{{g_x}}} = {G_y} \times z - {G_z} \times y}\\ {{T_{{g_y}}} = {G_z} \times x - {G_x} \times z}\\ {{T_{{g_z}}} = {G_x} \times y - {G_y} \times x} \end{array}} \right. \end{aligned}$$
(22)

When the load has no external force, the measured values of the forces and torques by the force sensor have the following relationship:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{G_x} = {F_x} - {F_{{x_0}}}}\\ {\begin{array}{*{20}{l}} {{G_y} = {F_y} - {F_{{y_0}}}}\\ {{G_z} = {F_z} - {F_{{z_0}}}} \end{array}}\\ {{T_{{g_x}}} = {T_x} - {T_{{x_0}}}}\\ {{T_{{g_y}}} = {T_y} - {T_{{y_0}}}}\\ {{T_{{g_z}}} = {T_z} - {T_{{z_0}}}} \end{array}} \right. \end{aligned}$$
(23)

By combining Eqs. 22 into 23, then substituting gravity components, yield:

$$\begin{aligned} \left\{ \begin{array}{l} {T_x} = {F_y} \times z - {F_z} \times y + {T_{x_0}} + {F_{z_0}} \times y - {F_{y_0}} \times z\\ {T_y} = {F_z} \times x - {F_x} \times z + {T_{y_0}} + {F_{x_0}} \times y - {F_{z_0}} \times z\\ {T_z} = {F_x} \times y - {F_y} \times x + {T_{z_0}} + {F_{y_0}} \times y - {F_{x_0}} \times z \end{array} \right. \end{aligned}$$
(24)

In Eq. 24, \( {F_{x_0}},{F_{y_0}},{F_{z_0}}, {T_{x_0}},{T_{y_0}},{T_{z_0}} \) in x, y, and z are all constants, then:

$$\begin{aligned} \left\{ \begin{array}{l} {k_1} = {T_{x_0}} + {F_{z_0}} \times y - {F_{y_0}} \times z\\ {k_2} = {T_{y_0}} + {F_{x_0}} \times y - {F_{z_0}} \times x\\ {k_3} = {T_{z_0}} + {F_{y_0}} \times y - {F_{x_0}} \times y \end{array} \right. \end{aligned}$$
(25)
Fig. 5
figure 5

Schematic diagram of an OSRDF variable impedance controller with gravity compensation

Full size image

The feedback of the sensor is composed of a zero point, the force and moment components caused by a load of gravity, and the external force as follows:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{F_{e_x}} = {F_x} - {F_{x_0}} - {G_x}}\\ \begin{array}{l} {F_{e_y}} = {F_y} - {F_{y_0}} - {G_y}\\ {F_{e_z}} = {F_z} - {F_{z_0}} - {G_z} \end{array}\\ {{T_{e_x}} = {T_x} - {T_{x_0}} - {T_{g_x}}}\\ {{T_{e_y}} = {T_y} - {T_{y_0}} - {T_{g_y}}}\\ {{T_{e_z}} = {T_z} - {T_{z_0}} - {T_{g_z}}} \end{array}} \right. \end{aligned}$$
(26)

Figure 5 describes the OSRDF force controller with gravity compensation.

4 Material removal profiles

A material removal process is a manufacturing process in which the finishing product is obtained after removing material from the surface of workpiece. The fundamental theory of the successful polishing process is to distribute the normal force evenly over all parts of the workpiece to maintain an equal material removal rate. This section describes the modeling of removal depth on the plane and curved surfaces of the box workpiece. The contact models are designed as plane and curved surfaces to calculate the removal depth based on the measurement of the z-axis value for each point before and after polishing. These models consider that a contact area is a flat and arc surface, so maximum contact normal force in the case of a flat surface is equal for all tool areas while concentrated around the center of the arc for the curved surface. This workpiece’s mathematical model of a material removal depth is divided into two parts 1) material removal depth on plane and 2) material removal depth on arc surface.

4.1 Material removal depth on plane

The distance between points of \({P_0} = ({x_0},{y_0},{z_0})\) and \({P_1} = ({x_1},{y_1},{z_1})\) in xyz space is given by the following formula:

$$\begin{aligned} d_1({P_0},{P_1}) = \sqrt{{{({x_1} - {x_0})}^2} + {{({y_1} - {y_0})}^2} + {{({z_1} - {z_0})}^2}} \end{aligned}$$
(27)

Equation 27 can be rewritten as:

$$\begin{aligned} {z_1} - {z_0} = \sqrt{{d_1^2}({P_0},{P_1}) - {{({x_1} - {x_0})}^2} - {{({y_1} - {y_0})}^2}} \end{aligned}$$
(28)

Similarly, for calculating serial multi- distances to n points as \(({P_0},{P_1})\), \(({P_1},{P_2})\),...,\(({P_{n - 1}},{P_n})\), the z-distances before polishing can be represented as:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{z_1} - {z_0} = \sqrt{d_1^2({P_0},{P_1}) - {{({x_1} - {x_0})}^2} - {{({y_1} - {y_0})}^2}} }\\ {{z_2} - {z_1} = \sqrt{d_2^2({P_1},{P_2}) - {{({x_2} - {x_1})}^2} - {{({y_2} - {y_1})}^2}} }\\ \cdots \\ {{z_n}} - {z_{n - 1}} = \\ \sqrt{d_n^2({P_{n - 1}},{P_n}) - {{({x_n} - {x_{n - 1}})}^2} - {{{({y_n} - {y_{n - 1}})}^2}} } \end{array}} \right. \end{aligned}$$
(29)
Fig. 6
figure 6

Removal depth on plane surface (a) z-position before polishing (b) z-position after polishing

Full size image

After polishing a plane surface the overall distances: \(d_1^2({P_0},{P_1}),d_2^2({P_1},{P_2}) \cdots d_n^2({P_{n - 1}},{P_n})\), x-distances: \(({x_1} - {x_0}),({x_2} - {x_1}), \cdots ,({x_n} - {x_{n - 1}})\) and y-distances: \(({y_1} - {y_0}),({y_2} - {y_1}), \cdots ,({y_n} - {y_{n - 1}})\) should be taken same values, while z-distances will take different values named as \(({{z'}_1} - {{z'}_0}),({{z'}_2} - {{z'}_1}), \cdots ,({{z'}_n} - {{z'}_{n - 1}})\), then Eq. 29 can be represented after polishing as:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{{z'}_1} - {{z'}_0} = \sqrt{d_1^2({P_0},{P_1}) - {{({x_1} - {x_0})}^2} - {{({y_1} - {y_0})}^2}} }\\ {{{z'}_2} - {{z'}_1} = \sqrt{d_2^2({P_1},{P_2}) - {{({x_2} - {x_1})}^2} - {{({y_2} - {y_1})}^2}} }\\ {{\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} \vdots }\\ {{{z'}_n}} - {{z'}_{n - 1}} =\\ \sqrt{d_n^2({P_{n - 1}},{P_n}) - {{({x_n} - {x_{n - 1}})}^2} - {{{({y_n} - {y_{n - 1}})}^2}} } \end{array}} \right. \end{aligned}$$
(30)

By combining Eqs. 29 and 30 we can get:

$$\begin{aligned} \left\{ \begin{array}{l} {z_1} - {{z'}_1} = {z_0} - {{z'}_0}\\ {z_2} - {{z'}_2} = {z_1} - {{z'}_1}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, \vdots \\ {z_n} - {{z'}_n} = {z_{n - 1}} - {{z'}_{n - 1}} \end{array} \right. \end{aligned}$$
(31)

where \( ( {{z_0} - {{z'}_0}} ),( {{z_1} - {{z'}_1}} ),( {{z_2} - {{z'}_2}} ),..., ( {{z_{n - 1}} - {{z'}_{n - 1}}} ),( {{z_n} - z'} ) \) are removal depth of the points: \( {P_0} \), \( {P_1} \), \( {P_2} \),..., \( {P_{n-1}} \), \( {P_n} \) respectively. Equation 31 shows the equality condition of the material removal depth on plane surface, which mainly depends on the measurement of z-axes values for all selected points before and after polishing (as shown in Fig. 6).

4.2 Material removal depth on arc

In the same manner, the length of arc between any two points on curved xyz space is calculated by the Pythagorean theorem as:

$$\begin{aligned} S = \sqrt{{{(\Delta x)}^2} + {{\left( {\Delta y} \right) }^2} + {{\left( {\Delta z} \right) }^2}} \end{aligned}$$
(32)
Fig. 7
figure 7

Multi-points lengths on arc

Full size image

Therefore, lengths of arc for (n) points (as shown in Fig. 7) in a general form can be written according to Eq. 29 and Fig. 8 as:

$$\begin{aligned} \left\{ \begin{array}{l} \begin{array}{l} {S_1} = \sqrt{{{(\Delta {x_1})}^2} + {{\left( {\Delta {y_1}} \right) }^2} + {{\left( {\Delta {z_1}} \right) }^2}} \end{array}\\ {{S_2} = \sqrt{{{(\Delta {x_2})}^2} + {{\left( {\Delta {y_2}} \right) }^2} + {{\left( {\Delta {z_2}} \right) }^2}} }\\ {{\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} \vdots }\\ {{S_{n - 1}} = \sqrt{{{(\Delta {x_{n - 1}})}^2} + {{\left( {\Delta {y_{n - 1}}} \right) }^2} + {{\left( {\Delta {z_{n - 1}}} \right) }^2}} }\\ {{S_n} = \sqrt{{{(\Delta {x_n})}^2} + {{\left( {\Delta {y_n}} \right) }^2} + {{\left( {\Delta {z_n}} \right) }^2}} } \end{array} \right. \end{aligned}$$
(33)

Equation 33 is re-described to give positions of z before polishing as:

$$\begin{aligned} \left\{ \begin{array}{l} \Delta {z_1} = \sqrt{S_{_1}^2 - {{(\Delta {x_1})}^2} - {{\left( {\Delta {y_1}} \right) }^2}} \\ \Delta {z_2} = \sqrt{S_2^2 - {{(\Delta {x_2})}^2} - {{\left( {\Delta {y_2}} \right) }^2}} \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\vdots \\ \Delta {z_{n - 1}} = \sqrt{S_{_{n - 1}}^2 - {{(\Delta {x_{n - 1}})}^2} - {{\left( {\Delta {y_{n - 1}}} \right) }^2}} \\ \Delta {z_n} = \sqrt{S_n^2 - {{(\Delta {x_n})}^2} - {{\left( {\Delta {y_n}} \right) }^2}} \end{array} \right. \end{aligned}$$
(34)
Fig. 8
figure 8

Material removal depth on arc surface (a) z-position before polishing (b) z-position after polishing

Full size image

After the polishing process, the z-dimensions will change to various values, while x and y dimensions will remain constant (as shown in Fig. 8), so z-positions after polishing can be described as:

$$\begin{aligned} \left\{ \begin{array}{l} \Delta '{z_1} = \sqrt{S_{_1}^2 - {{(\Delta {x_1})}^2} - {{\left( {\Delta {y_1}} \right) }^2}} \\ \Delta '{z_2} = \sqrt{S_2^2 - {{(\Delta {x_2})}^2} - {{\left( {\Delta {y_2}} \right) }^2}} \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\vdots \\ \Delta '{z_{n - 1}} = \sqrt{S_{_{n - 1}}^2 - {{(\Delta {x_{n - 1}})}^2} - {{\left( {\Delta {y_{n - 1}}} \right) }^2}} \\ \Delta '{z_n} = \sqrt{S_n^2 - {{(\Delta {x_n})}^2} - {{\left( {\Delta {y_n}} \right) }^2}} \end{array} \right. \end{aligned}$$
(35)

by combining Eqs. 34 and 35 yield:

$$\begin{aligned} \left\{ \begin{array}{l} \Delta '{z_1} = \Delta {z_1}\\ \Delta '{z_2} = \Delta {z_2}\\ \,\,\,\,\,\,\,\,\,\,\vdots \\ \Delta '{z_{n - 1}} = \Delta {z_{n - 1}}\\ \Delta '{z_n} = \Delta {z_n} \end{array} \right. \end{aligned}$$
(36)

In the same manner, Eq. 36 can be described as the removal depth on arc surface for points \( (0,1,2,...,n-1,n) \).

To make the removal depth is equal to all surface points of the workpiece, the distance between tracks designed by the trajectory method is adjusted according to the dimensions of the used polishing tool. The theoretical and practical assumption of trajectory designation for polishing uniformity is that the distance between the trajectories and the polishing tool diameter must be identical to prevent the process of overlapping the varnished areas.

5 Experimental study

In this section the experiments are conducted on the compound surface in order to validate the proposed polishing methodology. The compound surface is divided into three parts: top plane, side plane and arc surface with four equal areas, so the experimental results focused on one plane surface and one arc surface. This experiment aims to calculate polishing paths, normal contact forces, and removal depth, assess surface roughness before and after polishing, and evaluate the final polishing effect. Firstly, this section describes the experimental setups used in these experiments, then showing the results and discussion.

Fig. 9
figure 9

Experimental setup

Full size image

5.1 Experimental setup

Figure 9 shows the experiment setup; which including the hardware and software of a robotic polishing system.

5.1.1 Hardware and software implementation

The hardware components of the polishing system are as follows:

  • An UR robot manipulator.

  • An industrial computer that contains the software systems.

  • An UR control system.

  • A force sensor with accuracy of 2.3%.

  • A force/torque modulator (Net F/T).

  • A polishing tool-type APT-127N with attached abrasive paper of aluminum oxide\((AL_2O_3)\) type of P240 and rectangular polisher piece has dimension of 95*65 mm.

  • The air pressure source with pressure regulator.

  • Compound box workpiece composite material of aluminum and resin with hardness of 6061-T651.

While softwares can be described as follows:

  • Windows 7 operating system.

  • Qt graphical user interface (GUI) system.

  • UR motor motion control system.

  • User diagram protocol (UDP).

Fig. 10
figure 10

Automatic polishing of compound surface (a) top plane (b) side plane, (c) arc surface

Full size image
Fig. 11
figure 11

The polishing paths (a) control points on workpiece (b) path on top plane, (c) path on side plane and (d) path on arc surface

Full size image

5.1.2 Working principle of automatic polishing system

The working principles of a system shown in Fig. 9 can be described as follow: the Qt is used to identify gravity compensation parameters in real-time, collects and saves the coordinate system of taught points on the workpiece, adjusts desired normal force and executes the actual path through taught points by the robot on a workpiece. To control the robot’s motors, trajectory planning algorithm, and force control strategy with gravity compensation method were programmed using C++ codes. The UDP connects the force sensor and industrial PC through speed reaches to 9000Hz. Then, the force control algorithm calculates the error and generates a correction of the force value. The communication between industrial computer and robot controller via (TCP/IP) protocol through Ethernet due to high-speed processing in real-time of 2 ms clock cycle. The polishing tool is attached to the force sensor and powered by air pressure. During the polishing process, the Qt environment saves the data of forces and torques in three dimensions (x, y, z), in addition to gravity compensation information and generated path of taught points. The paths generated by the C++ program can be saved and used for other similar workpieces on the condition that they are placed in the exact coordinates.

Figure 10 (a), (b), and (c) show the automatic polishing setup for top, side plane, and the arc surface, respectively.

5.2 Results and discussion

This section describes the experiments results and then discussion of it.

Table 1 The taught control points (mm) on the box work object
Full size table
Fig. 12
figure 12

Simulation of contact forces on (a) plane and (b) arc surfaces based on OSRDF impedance controller

Full size image

5.2.1 Results:

The experiments results can be described as follows:

1) Firstly, the planning trajectory is done on top plane surface with 21 control points, side plane with 10 points and arc surface with 10 points as shown in Fig. 11(a) using weight of \( w_n=1 \) for all points and a=0, b=1 for Simpson formula. While harmonic model parameters were assumed as follows: \( q_0=0, q1=5\,cm \), \(\dot{q}_0=0 \), \(\dot{q}_1=0 \), \( \dot{q}_{\max } =15\,cm/s \) and \( \ddot{q}_{\max }=20cm/s^2 \). Figure 11(b), (c), and (d) represent the actual experimental paths for top plane, side plane, and arc surfaces, respectively. Table 1 shows the coordinates system (xyz) for these surfaces before the polishing process.

2)Secondly, operating the automatic polishing system using the applied normal forces of 10N, 20N, and 30N in the Z-direction for both cases,where the Fig. 12(a) and (b) shows simulation results of an OSRDF impedance controller and experimental results shown in Fig. 13(a)and (b) for polishing overall top plane and one arc surface with 60 s and 12 s respectively. An impedance parameters used were \({M_r}\)=1 \( (N.{s^2}/m) \), \( {{{B}}_r} \) = 40(N.s/m) , \({F_d}\)= (10, 20, 30)N, constant environment stiffness \( K_e \)= 5000 N/m and \( X_t=0.15 m \); with identified gravity of 12.7606N/kg.

3) Thirdly, measuring the z-positions of all points after the polishing process by automatically moving the robot to these points and reading new values of z-axes by the Qt platform (GUI). Tables 2, 3 and 4 show the z-axis positions after polishing for top plane and arc surface using the normal forces 10N, 20N, and 30N, respectively. Where the symbol z refers to depth before polishing, while \( z' \),\( z'' \),\( z''' \) refer to the depth after polishing by 10N, 20N, nd 30N, respectively over the same points. Actually, in these experiments, the box workpiece was polished three times: the first time was polished using 10N; the second time was polishing with 20N (onto polishing of the first time); and the third time was polishing with 30N (onto the polishing of second time). Therefore, symbol z refers to depth before polishing.

3.1) The surfaces of this workpiece were polished under the effect of a normal force of 10N, and then the depth will be changed from z to \(z'\) after polishing.

3.2) The \(z'\) becomes the new depth of surface before polishing by 20N; after polishing by this force value, the new depth will become \(z''\).

3.3) The \(z''\) became the new depth before polishing by 30N, and also after polishing the surface for the third time by this value, the depth will become \(z'''\).

Then calculated the removal depths by subtracted the values of z-axes positions before polishing form values after polishing as resulted in Sections 4.1 and 4.2. Figure 14(a) and (b) show removal depths for the first five points on the plane and arc surfaces, receptively. Finally, selecting suitable normal force to polish the surface with specific times to achieve the needed requirements quality for this workpiece.

Fig. 13
figure 13

Real polishing contact forces on (a) plane and (b) arc surfaces based on OSRDF impedance controller

Full size image

4) Fourthly, the final polishing process was conducted based on the machining parameters and a force value of 20N as the normal force in the z-direction for all surfaces of a box workpiece. Then, assessing the surface roughness using 3D measuring laser microscope device type (OLS5000) to evaluate the surface. Figures 15, 16, 17, 18, 19, 20, 21, and 22 show the surface roughness description on plane and arc surfaces before and after polishing. Two points were selected for these measurements, one on the plane and other on the arc surface, and by using laser measurements technology, horizontal/vertical center-lines (X,Y) were focused on to measure the roughness of a surface in 2D and 3D, as in Figs. 15 and 19 before polishing and Figs. 17 and 21 after polishing. The results of a surface roughness on the plane show that this surface was rough before polishing with minimum–maximum of \(-\)20.934 to 33.370 \(\mu m\) and \(-\)17.539 to \(-\)5.940 \(\mu m\) for vertical and horizontal lines, respectively, as shown in Fig. 16(a) and (b). In the same manner for arc surface is rough and fluctuated between the minimum–maximum measured values were \(-\)91.468 to 90.485 \(\mu m\) and \(-\)91.468 to 90.485 \(\mu m\) for same sequences as shown in Fig. 20(a) and (b). Then, after polishing the roughness for both points were reduced around zero as shown in Fig. 17(c, d), Fig. 18(a, b), Fig. 21(c, d), and Fig. 22 (a, b) for plane and arc surfaces, receptively. Figure 23(a), (b), and (c) show a surface before polishing, after polishing, and after painting, respectively in order to show final evaluation of the polishing experiment.

Table 2 z-axes positions (mm) of top plane and arc surfaces after polished by 10N
Full size table

The main reason causing the large removing depth for some points is not at the beginning and turning of the transition point is that the contact force applied at this point has a large fluctuation, especially when the surface is polished at 30N. In addition, the removing depth is found at the middle of the smooth transition point because the measurement of these depths is made on the same points vertically along the z-axis after polishing by 10N as shown in Fig. 15 —red line; then 20N as shown in Fig. 15 —yellow line; and 30N as shown in Fig. 15 —purple line.

Table 3 z-axes positions of top plane and arc surfaces after polished by 20N
Full size table
Table 4 z-axes positions of top plane and arc surfaces after polished by 30N
Full size table
Fig. 14
figure 14

Removal depth measurement of five first points on (a) top plane and (b) arc surfaces with effect of three contact forces

Full size image

5) Fifthly, given that, the rotating speed of the polishing tool is directly affected by the value of applied air pressure, in these experiments, the air regulator with a scale of 0–10 bar is used to control air pressure. In fact, the material of this workpiece is composed of a resin which has a high sensitivity to polishing stress produced by rotating the polishing tool. Experimentally and refer to manual user of used polishing tool found that:

  1. 1.

    At 0–2.5 bar, the speed is reached to 0–2500 rpm, and this range of speeds is not enough for the required level of polishing.

  2. 2.

    At 2.7–4.75 bar, the speeds reach 2700–4750 rpm; these range of speeds are suitable for polishing and have a good result.

  3. 3.

    At 5–10 bar, the speeds reach 5000–10,000 rpm; this range of speeds led to an over-cut polishing level and poor results. For this reason, it was found that at 5000rpm and above, the result was experimentally not good according to the appearance of a workpiece surface after polishing.

Fig. 15
figure 15

Surface microstructure of plane before polishing in (a) 2D, (b) 3D, (c) surface roughness on Y-axis and (d) X-axis

Full size image
Fig. 16
figure 16

Surface roughness analysis on plane before polishing on (a) X-axis, (b) Y-axis

Full size image
Fig. 17
figure 17

Surface microstructure of plane after polishing in (a) 2D, (b) 3D, surface roughness on (c) Y-axis and (d) X-axis

Full size image
Fig. 18
figure 18

Surface roughness analysis on plane after polishing on (a) Y-axis and (b) X-axis

Full size image

6) Lastly, the effect of robotic polishing using adjustment methods compared to traditional polishing without these methods were as follows:

  • Manual polishing reduces surface roughness from around \((+40) - (-20)\) to about \((+15) - (-15)\mu \)m according to results obtained by the factory, while for robotic polishing using adjustment methods the roughness is reduced from \((+40) - (-20)\) to about \((+5) - (-5) \mu \)m.

  • In addition, the efficiency of the polishing process for this workpiece is improved in the factory because the manual work cannot be reliable and accurate for long periods, but using the adjustment methods through the robot arm can provide it.

  • Moreover, it reduces the time consumption of the polishing process. According to manual polishing, the overall time to polish this surface depends on the laborer’s experience. It takes approximately 7.5 min for manual pre-treatment polishing. However, robotic polishing completes the process in around 3.53 min.

  • Similarly, the number of laborers in this factory can be reduced by 70%, i.e., using two robots for every section minimizes the number of laborers from ten to three, leading to decreased production costs.

Fig. 19
figure 19

Surface microstructure of arc before polishing in (a) 2D, (b) 3D and surface roughness (c) Y-axis and (d) X-axis

Full size image
Fig. 20
figure 20

Surface roughness analysis for arc surface before polishing on (a) Y-axis and (b) X-axis

Full size image
Fig. 21
figure 21

Surface microstructure of arc after polishing in (a) 2D, (b) 3D and surface roughness on (c) Y-axis and (d) X-axis

Full size image
Fig. 22
figure 22

Surface roughness analysis on arc surface after polishing on (a) Y-axis and (b) X-axis

Full size image
Fig. 23
figure 23

Box work object surface (a) before polishing, (b) after polishing and (c) after painting

Full size image

5.2.2 Discussion:

According to the polishing results shown in Fig. 13(a) and (b), found that at the normal force of 10N, the polished surfaces were not good enough. While at 20 N, the polishing effect is quite suitable for needed requirements; on the other hand, using 30 N will lead to over-cutting and unequal polishing. In addition, according to the force results, we can notice that the force fluctuation is directly proportional to the applied force value because the contact force is one of machining parameters causing vibration during polishing process; while the other machining parameters such as rotating speed of tool, abrasive paper, and contact stress. So, at low value of force, the fluctuation will be low while at high value, the fluctuation will be high. Also, in the case of plane surface, the force results for three values are regular around desired value. In contrast, the arc surface has varying regularity of forces curves, shown in periods between 2–4 s and 8–10 s because of suddenly changing position polishing tool between side plane and arc surfaces. The deviations occurred during these periods because the surface of a head of the polishing tool is not as circular as the surface itself. However, the results of polishing on this surface were good enough. So, we can conclude that the suitable polishing force for this workpiece is 20N according to resulted force behavior and polishing effect. In the same manner, using different forces will affect removal depth as shown in Fig. 14(a) and (b), the removal depth has some varying at 10N and 30N while using 20N gives more equality of removal depth for the different points. This result supports the suitability of using 20N for the polishing process.

6 Conclusions

Manual polishing is characterized by low efficiency, less surface uniformity, high effort, and high costs. Therefore, we proposed a new automatic robotic polishing system for compound surfaces.

The proposed polishing approach includes theoretical models for trajectory planning, force control, and material removal, and was validated experimentally. The proposed approach can be used to polish different complex surfaces. The experiments focused on the combined surface between flat and curved parts, as shown in the box workpiece, because it represents a challenge for manual polishing processes at the one of Chinese factory in Guangzhou city.

In the proposed method, the non-uniform rational B-spline curve is interpolated with the harmonic model to generate smooth and automatic paths for the polishing process to enhance stability. The constant contact polishing force is combined with fast gravity compensation to enhance the accuracy of the polishing force control on the workpiece surface and reduce the vibration of the polishing tool. The material removal profiles are modeled on a plane and arc surface, wherein the removal depth primarily depends on the positions of the z-axes at all the selected points before and after polishing. An equal removal depth at all the selected points indicates accurate polishing.

The proposed polishing methodology was successfully implemented to automatically polish compound box parts made of a composite aluminum and resin material. The key feature of the proposed approach is executing the real-time constant polishing force, which can enhance the accuracy of achieving a uniform removal depth and reduce the surface roughness as much as possible.

Experimental tests were conducted using polishing forces of 10 N, 20 N, and 30 N. The results revealed that high-quality polishing can be achieved with a normal polishing force of 20 N as it reduces fluctuations and has a suitable polishing effect on the composite material. Normal forces of 10 N and 30 N had a lower polishing stress effect and high fluctuations, respectively, leading to a poor-quality surface finish. The results proved the efficacy and ability of the proposed approach in achieving a smooth polished surface. After painting, a high-quality surface finish was achieved on the music box, further validating the experimental results and the efficacy of the proposed approach.