1 Introduction

Inconel718 is a typical nickel-based superalloy, which has excellent thermal stability, excellent fatigue resistance, corrosion resistance, and oxidation resistance [1, 2]. It is commonly used not only in aeroengine and aircraft, but also in electric power, petroleum, the chemical industry, and other fields [3]. Inconel718 has excellent tensile and low cycle fatigue properties at about 700 ℃, as well as excellent forging and welding properties [4]. However, it is characterized by poor thermal conductivity, work hardening, and hard particles [5]. In the machining process, the cutting force fluctuates greatly, the temperature is high, and the machining efficiency is low. Inconel718 is a typical polycrystalline difficult-to-machine material [6].

For polycrystalline metal materials, the grain size generally ranges from a few microns to tens of microns. According to the Hall–Petch theory, the smaller the grain size, the greater the proportion of grain boundary and the greater the barrier of grain boundary to dislocation slip [7]. At this time, the influence of grain boundary, dislocation substructure, and deformation of a single grain on the overall mechanical response of the workpiece is more significant [8]. In high-speed cutting Inconel718, when the material is in the state of high temperature and high strain rate, the internal damage evolution, mechanical properties, and microstructure of the material become more complex.

Some scholars have studied the grain boundary effect. In the study of Kaira et al. [9] and Haque and Saif [10], it was found that during uniaxial tension and compression of polycrystalline materials, dislocations will nucleate and slip on the grain boundary, and dislocation slip within the grain will be blocked on the grain boundary and absorbed by the grain boundary. AlMotasem et al. studied the material removal of ferrite/austenitic iron bicrystals. The research results show that the local softening/hardening of the material occurred due to the interaction between dislocation and grain boundary [11]. Chang et al. conducted a TEM experiment of in situ deformation and detailed crystallography analysis. The effect of grain boundary orientation errors on the nucleation mechanism of deformation twins at grain boundary in Fe-31Mn-3Al-3Si TWIP steel was studied. The results showed that it is of practical importance to consider grain boundary characteristics to understand the mechanism of deformation twinning in addition to the well-known factors such as bedding fault energy and grain size [12].

The plastic deformation of polycrystalline materials is essentially non-uniform because of the differences in mechanical properties of the grains in polycrystalline materials. In order to ensure the compatibility of deformation, geometrically necessary dislocations (GNDs) will be gathered at the grain boundary to coordinate the plastic deformation between grains [13].

Some scholars have conducted research on the distribution patterns and reinforcement effects of GNDs. Zhao et al. studied the evolution and distribution of GNDs in TA15 titanium alloy during high-temperature stretching at 750 ℃ using EBSD, TEM, and crystal plasticity finite element models. Research results have shown that the density of GNDs increases with the increase of applied strain. The regular arrangement of GNDs near grain boundaries is caused by incompatible intergranular deformation caused by different orientations of adjacent grains [14]. Arsenlis et al. taking the Burgers vector conservation principle as the basis of the SSD evolution equation introduced the strengthening effect of GNDs according to Nye’s dislocation density tensor. The shear simulation results of thin plates show that the material strength increases significantly with thickness thinning [15]. Evers et al. incorporated the non-uniform deformation-induced evolution and distribution of GNDs into the crystal plasticity phenomenological continuum theory. It was found that the density of SSDs in the grain was the highest. When the lattice mismatch is more obvious, more GNDs are accumulated at the grain boundary. The uniaxial tensile simulation results show that the model successfully reproduces the Hall–Petch effect of flow stress [16]. In order to study the influence of the local hardening effect of GNDs on the mechanical properties of dual-phase steel, Xue et al. determined the distribution characteristics of GNDs of dual-phase steel through EBSD, constructed a dual-phase steel model of GND hardening layer, and conducted tensile simulation. The simulation results show that the overall stress–strain curve obtained is basically consistent with the experimental results [17].

Some scholars have studied the cutting process from the microscopic point of view. Wang et al. studied the grain boundary–related mechanism and bicrystal Cu nano-cutting through molecular dynamics simulation and experiment. The research results show that the blocking movement of dislocations at grain boundaries, the absorption of dislocations at grain boundaries, and the nucleation of dislocations at grain boundaries are the main deformation modes of bicrystal Cu nano-cutting [18]. Wang et al. studied the removal of polycrystalline copper material, the change of cutting force, and the mutual transformation mechanism between grain boundary and dislocation in nano-cutting. The research results show that the blocking effect of grain boundary changes the chip flow direction and forms grooves and burrs on the machined surface. The gradual accumulation of material deformation energy in front of the grain boundary and the final fracture of the grain boundary causes the fluctuation of cutting force [19].

Bai et al. proposed a finite element orthogonal cutting model based on the strain gradient constitutive equation of dislocation density, studied the characteristics of the subsurface damage layer, dislocation distribution, and microstructure changes of Ti-6Al-4 V under different cutting conditions, and clarified the correlation between microscale effect and geometrically necessary dislocation. The research results show that the machined surface microstructure can refine the grain composition, and the fine grain produces an obvious scale effect. A large number of dislocations are accumulated in grain boundaries and shear slip bands [20, 21]. Ding et al. established an orthogonal cutting finite element model based on dislocation density to study the grain refinement in the cutting process of Al 6061T6 and OFHC Cu under different cutting conditions. The research results show that the established finite element model with embedded dislocation density can capture the basic characteristics of cutting deformation and grain refinement mechanism in the cutting process [22]. Taking H13 die steel as the research object, Bla et al. established a finite element model based on dislocation density evolution and studied the influence of cutting parameters on grain size. The study showed that the dislocation density and grain size fluctuated periodically in a wavy manner when the sawtooth chip was formed [23].

From the above discussions, it can be seen that the existing research methods, except the homogeneous model, study grain boundaries through cohesive force models and cannot obtain the magnitude of stress at grain boundaries. At the same time, it cannot well reflect the hindrance effect of grain boundaries on grain slip.

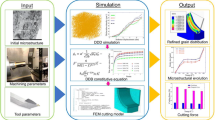
In this paper, a constitutive model containing geometrically necessary dislocations at grain boundaries and a two-dimensional polycrystalline cutting finite element model containing grain boundaries are established. The established constitutive model is used for cutting simulation through secondary development, and this method is used to compensate for the shortcomings of the cohesive force model. The results show that this method is accurate and reliable. It can truly reflect the influence of grain boundaries on cutting force, cutting temperature, and equivalent stress during the cutting process, as well as the slip of grains, the evolution of chip morphology, and crack initiation and propagation.

2 Material and experimental process

2.1 Mechanical property experiment

In order to obtain the quasi-static mechanical property parameters, a cylindrical test piece (\(\phi\) 18 \(\times\) 10 mm) was prepared by the EDM method. The CMT5205 series microcomputer controlled electronic universal test compressor shown in Fig. 1a was used to carry out compression experiment at the strain rate of 0.001 s−1 at 20 ℃.

Fig. 1
figure 1

a, b Mechanical property test equipment

Full size image

The cylindrical test piece (\(\phi\) 4 \(\times\) 2 mm) was prepared by the EDM method to obtain dynamic mechanical properties under high temperature and high strain rate. The upper and lower end faces of the test piece were polished to ensure the parallelism and roughness and then to ensure the accuracy of the experimental data results. The split-Hopkinson pressure bar (SHPB) is used for compression test (under the conditions of 500–800 ℃ and 5000–11,000 s−1 strain rate), as shown in Fig. 1b.

2.2 High-speed cutting experiment

The CA6140 lathe is used for the cutting experiment (see Fig. 2), and the workpiece size is \(\phi\) 100 \(\times\) 500 mm. PVD-TiAlN coated tool (rake angle \({\gamma }_{0}=0-9^\circ\), relief angle \({\alpha }_{0}=7^\circ\)) is used in the cutting experiment. The cutting force is collected through the Kistler 9257A three-way dynamometer, 5007 charge amplifier, and data acquisition card, as shown in the amplification at A in Fig. 2. The cutting temperature was measured by a natural thermocouple, and the thermoelectric potential was recorded by an X–Y function recorder model LM20A200.

Fig. 2
figure 2

Cutting detection device

Full size image

In order to obtain the chip root metallographic specimen, the explosive rapid tool drop method is used to freeze the changing state of materials in the cutting process, and then, the grinding, polishing, and corrosion treatment are carried out. The microscopic morphology was observed by Olympus series SC50 metallographic microscope, as shown in Fig. 3.

Fig. 3
figure 3

Cutting root acquisition

Full size image

The experimental material in this study is Inconel718 (solid solution state). Its chemical composition is shown in Table 1. Its physical and mechanical properties are shown in Table 2, and its thermal conductivity and specific heat capacity are shown in Table 3 [24].

Table 1 Chemical compositions of Inconel718 (wt.%)
Full size table
Table 2 Basic physical properties
Full size table
Table 3 Thermal conductivity and specific heat capacity characteristics [24]
Full size table

2.3 EBSD experiment

In order to ensure the accuracy of the 2D polycrystal cutting model, the microstructure of the sample was characterized by a JSM-7800F field emission scanning electron microscope equipped with an EBSD probe (Oxford Nordly Max3), as shown in Fig. 4. Raw materials are made into cylindrical specimen (Φ2 × 2 mm) through wire-electrode cutting. The 120#, 400#, 800#, 1000#, 1500#, and 2000# water sanding paper were used in sequence to sand the cylindrical specimen, and finally, the specimen was polished with a diamond polishing paste. After polishing, the sample is washed with water and washed with alcohol, subsequently blown dry, and then subjected to vibration polishing at a frequency of 50 Hz for a duration of 15 h. After the EBSD scan is completed, Channel5 software needs to be used to process the data and obtain the required microstructure information.

Fig. 4
figure 4

JSM-7800F field emission scanning electron microscope

Full size image

3 Modeling and simulation process

3.1 Establishment of a geometric model

In order to study the chip formation mechanism and microstructure change of Inconel718, a finite element model of polycrystalline metal cutting with grain boundaries was established. Some experts and scholars have proposed a variety of random methods based on lattice phases. At present, most of them use the Monte Carlo method, cellular automata method, and the Voronoi diagram [25]. Because the Voronoi diagram has the advantages of good geometric foundation and strong local boundary control ability, this paper uses the Voronoi diagram to establish a polycrystalline geometric model.

Through the grain orientation imaging diagram and grain size distribution diagram (see Fig. 5a, b) obtained by the EBSD experiment described in Section 2.3, the grain size can be determined. It can be seen that the grain size is mainly around 20–50 μm. The grain boundary size can be calculated by the formula t = 0.133d0.7[26], and the grain boundary thickness is about 1.5 μm.

Fig. 5
figure 5

Image of grain orientation and grain size distribution

Full size image

When converting from 3D cutting to 2D cutting, the spindle rotation direction is the X-direction in 2D cutting. The feed direction is the Y-direction in 2D cutting. The cutting depth can be set using the plane strain thickness option of the software. The simulation model parameters are set to \(f\) = 0.1 mm/r, \({a}_{p}=\) 1 mm, rake angle \({\gamma }_{0}=0-9^\circ\), relief angle \({\alpha }_{0}=7^\circ\). The tool is set as a rigid body with a tool radius of 0.005 mm. The workpiece model and chip are in normal hard contact, and separation after contact is not allowed. A general contact method is chosen between grains.

Python programming language, as a built-in language, can directly interact with ABAQUS data, greatly reducing the workload of pre-processing. The modeling process using the Python script program is shown in Fig. 6. Finally, the geometric model of polycrystal with grain boundaries was obtained, as shown in Fig. 7.

Fig. 6
figure 6

Polycrystalline cutting modeling process

Full size image
Fig. 7
figure 7

Geometric model of polycrystalline cutting

Full size image

3.2 Establishment of a constitutive model

Metal cutting is plastic deformation at a high temperature and a high strain rate. Johnson and Cook established the classical Johnson–Cook model, which is suitable for large deformation, high strain rate, and high temperature of the metal. The constitutive model has a simple form, so it has been widely used in the process of cutting simulation [27]. The model is expressed as

$$\sigma =\left(A+B{\varepsilon }^{n}\right)\left(1+C\left(\mathrm{ln}\frac{\dot{\varepsilon }}{\dot{{\varepsilon }_{0}}}\right)\right)\left(1-{\left(\frac{T-{T}_{r}}{{T}_{m}-{T}_{r}}\right)}^{m}\right)$$
(1)

where \(\sigma\) is the flow stress at a non-zero strain rate. A is the initial yield stress of the material. B and n are strain-hardening parameters. \(\dot{\varepsilon }\) is the equivalent plastic strain rate. \(\dot{{\varepsilon }_{0}}\) is the reference strain rate usually taken as 0.001 s−1. C is the strain rate sensitivity coefficient of the material. m is the softening coefficient of the material. T, Tr, and Tm are the dynamic temperature, room temperature, and melting temperature of the material respectively.

Through the quasi-static compression experiment and the SHPB experiment, the relevant parameters of Inconel718 in the JC model were obtained, among which parameters A, B, and n can be obtained through the true stress–strain curve shown in Fig. 8.

Fig. 8
figure 8

Quasi-static compression curve

Full size image

The real stress–strain curves at different temperatures and strain rates are obtained through the SHPB experiment, as shown in Fig. 9. The parameters C and m can be obtained through Fig. 9.

Fig. 9
figure 9

Dynamic compression curve

Full size image

By fitting the stress–strain curve, the values of various parameters in the Johnson–Cook model of Inconel718 are obtained, as shown in Table 4.

Table 4 Inconel718 JC constitutive parameters
Full size table

From the microscopic point of view, the plastic deformation of metal materials is mainly caused by the slip movement of dislocation, and dislocation will interact randomly in the process of movement. Such random dislocations are also called statistically stored dislocations (SSDs) [28]. In addition to the lack of statistical averaging of microstructure, there is also the additional reinforcement effect caused by geometrically necessary dislocations (GNDs) [29]. To calculate the shear stress of materials, the contributions of statistical storage dislocation density and geometric dislocation density must be considered. That is, Taylor’s flow stress formula is expressed as [30]

$$\uptau =\mathrm{\alpha Gb}\sqrt{{\rho }_{s}+{\rho }_{G}}$$
(2)
$$\upsigma =M\mathrm{\alpha Gb}\sqrt{{\rho }_{s}+{\rho }_{G}}$$
(3)

where \(\tau\) is the flow shear stress. \({\rho }_{s}\) is the statistical storage dislocation density. \({\rho }_{G}\) is the geometrically necessary dislocation density. \(\mathrm{\alpha }\) is the Taylor coefficient, with a value range of 0.3–0.5. G is the shear modulus, with a value of 77,200 MPa, and b is the Burgers constant, with a value of 0.304 nm. M is the Taylor factor, usually taking the value of constant 3.06.

Ashby believes that when some non-deformable hard particles are dispersed in the material matrix, dislocation movement will be hindered even though deformation of hard particles may occur, making dislocation density rise sharply with strain [31]. During the deformation process of polycrystalline materials, due to the different physical and mechanical properties of the materials, the grain orientation is different, and the grain anisotropy is large. If the grains are free to deform under stress, the slip system which is the easiest to slip in the grains will slip preferentially, resulting in incongruous deformation between the crystals, as shown in Fig. 10a. Ashby believes that such incongruity will cause holes or overlaps between crystals as shown in Fig. 10b and destroy the material. Therefore, in the process of plastic deformation, the crystal is constrained by the deformation of surrounding grains, and the deformation between crystals is coordinated by generating GNDs at the grain boundary as shown in Fig. 10c so that the deformation between grains is matched so that the material produces plastic deformation [32].

Fig. 10
figure 10

a–c GND schematic diagram

Full size image

Microscopically, the shear strain gradient of the slip system leads to the curvature of the lattice, and additional dislocations of the same sign are required to ensure the geometric continuity of the lattice. These dislocations are GNDs, which are directly related to the geometric deformation and strain gradient of the lattice. Statistical storage dislocation \({\rho }_{s}\) is independent of strain gradient and can be determined by material experiments. JC model is selected as the statistical storage dislocation constitutive relationship.

$${\upsigma }_{s}=M\mathrm{\alpha Gb}\sqrt{{\rho }_{s}}={\sigma }_{JC}$$
(4)

Polycrystalline materials are composed of grain boundary affect zone (GBAZ) and grain internal phase (GI) [33]; the calculation formula of intracrystalline volume fraction \({f}_{\mathrm{GI}}\) is

$${f}_{\mathrm{GI}}=\frac{{\left({D}_{\mathrm{GS}}-{\delta }_{\mathrm{GBAZ}}\right)}^{3}}{{{D}_{\mathrm{GS}}}^{3}}$$
(5)

where \({D}_{\mathrm{GS}}\) and \({\delta }_{\mathrm{GBAZ}}\) are grain diameter and grain boundary thickness.

Then, the flow stress contributed by the statistical storage dislocation in the crystal is [34]

$${\upsigma }_{GI}=M\mathrm{\alpha Gb}\sqrt{{\rho }_{s}{f}_{\mathrm{GI}}}$$
(6)

Under the action of external shear stress, the region affected by the grain boundary deforms first. As the dislocation absorption source and emission source, the generation of dislocations is hindered by the grain boundary, and dislocations accumulate in the region affected by the grain boundary. Due to the heterogeneity of microstructure (grain orientation), more geometrically necessary dislocations gather at the grain boundary. The expression of geometrically necessary dislocation density is

$${\rho }_{G}=\left(\frac{1}{{\lambda }_{\mathrm{PC}}}\right)\left(\frac{3\upgamma }{b}\right)$$
(7)

Then, the flow stress contributed by geometrically necessary dislocation is

$${\upsigma }_{\mathrm{GBAZ}}=M\mathrm{\alpha Gb}\sqrt{{\rho }_{G}}=M\mathrm{\alpha Gb}\sqrt{\left(\frac{1}{{\lambda }_{\mathrm{PC}}}\right)\left(\frac{3\upgamma }{b}\right)}$$
(8)

where \({\lambda }_{PC}\) is the characteristic length of polycrystalline material deformation. \(\upgamma\) is a plastic strain. b is the Burgers vector.

Therefore, the key to establish the constitutive relationship is to solve the characteristic length \({\lambda }_{\mathrm{PC}}\) of the main deformation zone, and the shear zone length can be obtained from the cutting theory:

$${\lambda }_{\mathrm{PC}}=\frac{h}{\mathrm{sin}\left(\phi \right)} \phi =\frac{r\mathrm{cos\alpha }}{1-r\mathrm{sin\alpha }} r=\frac{h}{t}$$
(9)

where \(\phi\) is the shear angle. \(h\) is the uncut thickness. α is the cutting rake angle. t is the thickness of chip formation.

Then, the constitutive model at the grain boundary is

$$\upsigma ={\sigma }_{\mathrm{JC}}\sqrt{{f}_{\mathrm{GI}}}+\mathrm{ M\alpha Gb}\sqrt{\left(\frac{1}{{\lambda }_{\mathrm{PC}}}\right)\left(\frac{3\upgamma }{b}\right)}={\sigma }_{JC}\sqrt{{f}_{\mathrm{GI}}}+\mathrm{M\alpha Gb }\sqrt{\left[{~}^{\mathrm{sin}\left(\frac{\left({~}^{h}\!\left/ \!{~}_{t}\right.\right)cos\mathrm{\alpha }}{1-\left({~}^{h}\!\left/ \!{~}_{t}\right.\right)sin\mathrm{\alpha }}\right)}\!\left/ \!{~}_{h}\right.\right]}\left(\frac{3\gamma }{b}\right)$$
(10)
$$\upsigma =\left(A+B{\varepsilon }^{n}\right)\left(1+C\left(\mathrm{ln}\frac{\dot{\varepsilon }}{\dot{{\varepsilon }_{0}}}\right)\right)\left(1-{{T}^{*}}^{m}\right)\sqrt{{f}_{\mathrm{GI}}}+\mathrm{ M\alpha Gb }\sqrt{\left[{~}^{\mathrm{sin}\left(\frac{\left({~}^{h}\!\left/ \!{~}_{t}\right.\right)cos\mathrm{\alpha }}{1-\left({~}^{h}\!\left/ \!{~}_{t}\right.\right)sin\mathrm{\alpha }}\right)}\!\left/ \!{~}_{h}\right.\right]}\left(\frac{3\gamma }{b}\right)$$
(11)

The secondary development of ABAQUS can be realized through the VUMAT subroutine flow shown in Fig. 11, and the established constitutive model can be used in cutting simulation.

Fig. 11
figure 11

VUMAT subroutine flow chart

Full size image

3.3 Cutting separation criteria

In the process of cutting, due to the extrusion of the rake face, some materials are separated from the matrix to form different kinds of chips. Therefore, appropriate chip separation criteria should be selected to simulate the chip separation process. The Johnson–Cook separation criteria are adopted in this paper. The failure evolution of materials can be measured by \(\omega\) value, as shown in Eq. (13).

$$\omega =\sum \frac{\Delta {\overline{\xi }}^{\mathrm{pl}}}{{\xi }_{0}^{\mathrm{pl}}}$$
(12)

where \(\Delta {\overline{\xi }}^{\mathrm{pl}}\) is the equivalent plastic strain increment. \({\xi }_{0}^{\mathrm{pl}}\) is the equivalent plastic strain at initial failure. \({\xi }_{0}^{\mathrm{pl}}\) can be expressed as

$${\xi }_{0}^{\mathrm{pl}}=\left[{d}_{1}+{d}_{2}\mathrm{exp}\left({d}_{3}\frac{P}{S}\right)\right]\left(1+{d}_{4}\mathrm{ln}\frac{\dot{\varepsilon }}{\dot{{\varepsilon }_{0}}}\right)[1-{d}_{5}{\left(\frac{T-{T}_{r}}{{T}_{m}-{T}_{r}}\right)}^{m}]$$
(13)

where \(\frac{P}{S}\) is the dimensionless deviatoric stress ratio (P is positive pressure, and S is Mises stress). \(\dot{\varepsilon }\) is the plastic strain rate. \(\dot{{\varepsilon }_{0}}\) is the reference strain rate. d1, d2, d3, d4, and d5 are the failure parameters of the material, which are shown in Table 5 [35].

Table 5 Failure parameters of Johnson–Cook fracture criterion for Inconel718 [35]
Full size table

3.4 Establishment of a friction model

In high-speed cutting of superalloys, a large amount of friction heat will be generated due to friction. The friction model has a great influence on the cutting temperature, effective stress, and chip deformation in the cutting simulation results, so it is very necessary to accurately use the friction model for metal cutting simulation. The friction model proposed by Zorev is adopted in this paper [36].

$$\left\{\begin{array}{c}w=\mu {\sigma }_{n},\left(\mu {\sigma }_{n}\le {\tau }_{\mathrm{max},}\right)\\ w={\tau }_{\mathrm{max},}\left(\mu {\sigma }_{n}>{\tau }_{\mathrm{max},}\right)\end{array}\right.$$
(14)

where μ is the friction coefficient, and the value is 0.3. \({\tau }_{\mathrm{max}}\) is the maximum shear flow stress \({ (\tau }_{\mathrm{max}}={\sigma }_{y}/\sqrt{3}\), and \({\sigma }_{y}\) is the positive pressure of the contact surface).

4 Results and discussions

4.1 Cutting force

In the traditional metal cutting theory, the workpiece is usually regarded as a continuous isotropic medium. However, considering the internal microstructure of polycrystals, the simulation model of single crystals is no longer applicable. Therefore, the constitutive model and finite element model established in this article are selected for cutting simulation research. In order to study the effect of grain boundary on cutting force, the comparison diagram between experimental values and simulation values under the same cutting conditions ( \({\gamma }_{0}=9^\circ\), \({\alpha }_{0}=7^\circ\), \(v\) =50 m/min) was obtained through the test, as shown in Fig. 12.

Fig. 12
figure 12

Comparison between experimental values and simulation values

Full size image

It can be seen from Fig. 12 that when the cutting process reaches a stable state, the cutting force will fluctuate regularly. However, the fluctuation of transient cutting force obtained by the JC model is relatively stable, and the change rate is small. The fluctuation ranges of the transient cutting force obtained by the GND model are large, and the magnitude and fluctuation trend of the cutting force are closer to the experimental results. First, due to the different physical characteristics of grain boundaries and grains, the cutting tool contacts with different phases alternately. Second, because the grain boundary hinders the slip of dislocations in the crystal, dislocations cannot cross the grain boundary during deformation but produce a dislocation plug near the grain boundary. The formation of a dislocation stacking group leads to the improvement of material strength. Thus, the fluctuation ranges of cutting force are large.

Figure 13 shows the variation of the average main cutting force with different cutting speeds (v = 30, 35, 40, and 45 m/min). According to Fig. 13, the average principal cutting force decreases with the increase in cutting speed. This is because that as the cutting speed increases, the cutting temperature increases. The material softens, and it is easier to remove, resulting in less cutting force. The simulation value of the GND model is larger, while the simulation value of the JC model is smaller, and the simulation value obtained by the GND model is closer to the experimental value. This also proves the accuracy of the established model.

Fig. 13
figure 13

Variation of average main cutting force with different cutting speeds

Full size image

4.2 Cutting temperature

4.2.1 Temperature distribution in the cutting area

In the cutting process, the cutting heat mainly comes from two aspects: one is the elastic and plastic deformation of the metal in the cutting layer and the other is the friction heat between the chip and the rake face and the workpiece and the flank face. Under the same cutting conditions (\({\gamma }_{0}=3^\circ\), \({\alpha }_{0}=7^\circ\), v = 90 m/min). The temperature distribution of the JC model and the GND model is shown in Fig. 14.

Fig. 14
figure 14

a–e Temperature cloud diagram and temperature contour diagram

Full size image

When serrated chips are formed, as shown in Fig. 14a, it can be clearly seen that an obvious shear slip occurs in the first deformation zone. The heat source in the first deformation zone is generated by the shear slip of the material. Compared with Fig. 14d, e and b, c, it can be seen that the temperature distribution width of the GND model in the first deformation zone is obviously higher than that of the traditional JC model, and the temperature distribution width of other slip zones is also obviously higher than that of the traditional JC model. This is because when the material is subjected to shear slip deformation, the internal slip direction of the grain is different due to the grain boundary that hinders the dislocation movement, which leads to the internal slip of the grain that is not unified and the width of the temperature distribution becomes wider.

Figure 15(a–c) further shows the cutting zone temperature diagram of the GND model and the JC model at different cutting speeds (v = 50, 60, and 70 m/min). Because the formation time of the sawtooth chip is very short, the temperature in the shear zone rises sharply, and the heat cannot be lost quickly, which can be approximately considered an adiabatic process. After \(\Delta t\) period, temperature rise in shear region can be expressed as

$$\Delta {T}_{\mathrm{pl}}={\eta }_{\mathrm{pl}}\frac{{\sigma }_{\mathrm{el}}{\overline{\varepsilon }}_{\mathrm{pl}}\Delta t}{C\rho }$$

where \({\sigma }_{\mathrm{el}}\) is the effective stress, \({\overline{\varepsilon }}_{\mathrm{pl}}\) is the effective plastic strain, \(C\) is the specific heat, and \(\rho\) is the material density.

Fig. 15
figure 15

Cutting zone temperature diagram of GND model and JC model at different cutting speeds

Full size image

In the experimental process, the temperature was measured using the thermocouple method. The temperature in the cutting zone was collected multiple times and averaged. After obtaining the temperature values in the experimental process and simulation process, the comparison diagram can be obtained, as shown in Fig. 16. It can be found that the simulation results of the GND model are closer to the experimental values.

Fig. 16
figure 16

Comparison of temperature values between simulation and experimental process

Full size image

4.2.2 Effect of cutting temperature on GNDs

Temperature is one of the important factors for the shear localization of materials. The cutting temperature and material softening have a great influence on the movement of dislocations. Therefore, the influence of temperature gradient on geometric dislocation density at grain boundary will be deeply analyzed.

When the tool begins to contact the workpiece, the material will undergo elastic–plastic deformation under the action of external force. As shown in Fig. 17(a-1), a heat source with small distribution is formed, and the internal GND density of the material must rise rapidly, as shown in Fig. 17(b-1). At the initial moment at which the shear zone is formed when the tool moves further forward, an obvious temperature gradient distribution can be seen on the shear zone, as shown in Fig. 17(a-2). According to Fig. 17(b-2), it can be seen that the GND density changes significantly along the shear zone direction, and the GND density at the center of the heat source is significantly lower than the dislocation density at the edge of the shear zone.

Fig. 17
figure 17

Temperature cloud diagram and GND density diagram

Full size image

When serrated chips are formed, as shown in Fig. 17(a-3), the GND density along both sides of the shear zone changes opposite to the temperature gradient. First, due to the softening and dynamic recrystallization of the material with the increase of temperature, the blocking effect of grain boundary on dislocation movement is reduced. Second, the increase in temperature leads to the increase of the dislocation movement energy, intensifies the movement, and slightly strengthens the dislocation proliferation. However, the dislocation cross-slip speed decreases, and the dislocation climbing movement increases significantly, resulting in a dislocation phase offset. At this moment, dislocation annihilation plays a leading role, resulting in the decrease of dislocation density [37,38,39]. As the tool moves forward to the same position of the workpiece, the chip is formed from the uncut zone to the shear slip zone. The temperature changes from low to high and then to low, as shown in Fig. 17(a-4). The GND density increases to small and then to large, as shown in Fig. 17(b-4).

On the whole, under the action of a certain external force, dislocation will proliferate and annihilate with the change of temperature, and dislocation density will fluctuate with the change of temperature. When this result is mapped to the macro, it means that the machining at a higher temperature can effectively inhibit the work hardening phenomenon.

Similar conclusions are also confirmed in the high-temperature compression experiment of Inconel718 material [40]. Dynamic recrystallization is an important softening mechanism of Inconel718. Figure 18a shows the developing substructure near the original grain boundary. It can be seen that the substructure is composed of dislocation walls, and more dislocations are absorbed and annihilated in the grains formed by dynamic recrystallization. Figure 18b shows the dislocations proliferated due to deformation and cellular dynamic recrystallized nuclei. The dynamic recrystallized grains in the growth of nuclei will absorb dislocations and contain underdeveloped dislocation substructures with very low dislocation density.

Fig. 18
figure 18

a, b TEM diagram of Inconel718 high-temperature compression deformation

Full size image

4.3 Sawtooth chip formation

4.3.1 Analysis of shear zone morphology

Adiabatic shearing is a special phenomenon of workpiece material under high-speed deformation conditions such as high-speed impact, high-speed cutting, explosion, and high-speed wear. In the material, it is specifically manifested as a bright white highly localized narrow zone shear zone formed after local region deformation [41]. In order to deeply study the formation mechanism of the sawtooth chip and the friction mechanism of the tool-chip contact area, it is very important to observe and analyze the microstructure and microstructure evolution of the adiabatic shear zone. It is generally believed that shear deformation localization is the result of plastic instability, which is closely related to strain hardening, strain rate hardening, heat conduction, and thermal softening.

In the cutting process, the chip is plastically deformed due to the extrusion of the tool. When the work hardening degree and thermal softening effect of the material reach an equilibrium state, the shear deformation of the material is highly localized. Adiabatic shear behavior occurs, and an adiabatic shear zone is formed. Figure 19a is the geometric diagram of the shear zone. In the process of sawtooth chip formation, the temperature at the adiabatic shear zone is very high. The thermal conductivity of Inconel718 is small, and the deformation heat cannot be quickly transferred to the chip due to the barrier effect of the adiabatic shear zone. This causes the heat to converge in a narrow zone as shown in Fig. 19b in the cutting deformation area.

Fig. 19
figure 19

Geometric diagram and temperature cloud diagram of the shear zone

Full size image

The shear zone produced under a high strain rate load can be divided into a deformation band and a phase-transformed band according to the morphology of the metallographic section. The microstructure of the adiabatic shear band at the cutting root (obtained at the cutting condition: f = 0.1 mm/r, \({a}_{p}\) = 1 mm, \({\gamma }_{0}=0^\circ\), \(v\) = 80 m/min) can be observed through a metallographic microscope, as shown in Fig. 20a. The metallographic image of the chip root shows a clear narrow band, that is, the deformation band. Figure 20b shows the chip deformation cloud diagram, and Fig. 20c, d shows the strain cloud diagram obtained in the simulation process when using the GND model and the JC model respectively. It can be seen that the closer to the shear band, the greater the deformation and the obvious relative displacement of the grains on both sides of the shear band due to shear. The grains are highly elongated along the shear direction. The greater the deformation, the more obvious the degree of grain elongation, resulting in the grains gradually becoming slender fibers, which is called fiber structure, and the distribution direction of fibers is the extension direction of metal plastic deformation.

Fig. 20
figure 20

a–d Micro-morphology of deformation band and cloud diagram of chip

Full size image

The deformation band is the initial stage in the process of deformation localization. When the deformation continues, a so-called “white” shear zone, namely, a phase-transformed band, will be formed on the basis of the deformation band [42]. Through the metallographic microscope, it can be observed that the structure in the shear zone presents a fine dot-like white layer structure, as shown in Fig. 21a. With the formation of serrated chips, a large amount of cutting heat is accumulated in the shear band, resulting in a sharp rise in temperature, as shown in Fig. 21b. The reason for the white layer structure may be the grain refinement caused by dynamic recrystallization as shown in Fig. 21c, or the phase transition temperature of the material is exceeded, which leads to the phase transition of the material.

Fig. 21
figure 21

a–c Micro-morphology of the phase-transformed band and cloud diagram of chip

Full size image

4.3.2 Effect of grain boundary on chip morphology

Figure 22 shows the comparison diagram of the chip shape obtained in the simulation and experimental process under the same cutting conditions (\(f\) = 0.1 mm/r, \({a}_{p}\) = 1 mm, \({\gamma }_{0}=3^\circ\), \(v\) = 90 m/min). It can be seen that compared with the JC model, chip morphology obtained by the GND model is more irregular, and chip morphology is closer to experimental results.

Fig. 22
figure 22

a–c Comparison of chip morphology between simulated and experimental results

Full size image

In the cutting process of polycrystalline, the deformation of each grain is hindered by the grain boundary and adjacent grains, which requires the deformation cooperation of other grains and cannot deform freely. When the applied shear stress acts on a single grain, a dislocation “horizontal combination” shown in Fig. 23a will be formed. Under the action of shear stress, the F-R dislocation source moves along the slip plane, the front dislocations are dense, and the rear dislocations are gradually reduced. When the slip line encounters the grain boundary as shown in Fig. 23b, the dislocation line will stop forming a dislocation plug at the grain boundary, and the slip cannot continue. The critical shear stress of dislocation source actuation is expressed as [43]

$${\tau }_{c}=\left(\tau -{\tau }_{f}\right){\left(\frac{d}{r}\right)}^\frac{1}{2}$$
(15)

where \(\tau\) is the yield shear stress of polycrystalline. \({\tau }_{f}\) is to overcome the resistance suffered by dislocations moving on the sliding surface of the grain. r is the distance between the plug head and the dislocation source in the adjacent grain. d is the grain diameter.

Fig. 23
figure 23

a, b Stacking of dislocations before obstacles [43]

Full size image

It can also be seen from Fig. 22b that dislocation stacking will cause stress concentration. Effective shear stress of dislocation stacking group \(\tau \ge {\tau }_{c}\), the dislocation source in the adjacent grains will be activated, and the adjacent grains will be forced to slip accordingly so that the deformation continues. Due to the randomness of the dislocation slip direction within each grain, the shear plane in Fig. 22b is more irregular than that in Fig. 22a. Macroscopically, the tooth spacing has a certain randomness in the formation of the sawtooth chip.

It can be also seen that the sawtooth degree obtained by the GND model is slightly larger. When the applied shear stress acts on the polycrystal, the shear stress acting on the slip system of each grain is very different since the stress on each grain is not consistent so that some grains slip first and some grains slip later. Due to the existence of grain boundaries, dislocation stacking will lead to stress concentration at grain boundaries. It is easy to produce dislocation defect sources at grain boundaries, which is more conducive to the formation of the sawtooth chip. Therefore, in the GND model, the adjacent teeth on the serrated chip were of different heights and widths, and the chip shape became irregular, which was closer to the experimental results.

From the above compression experiment, it can be seen that during deformation, dislocations in the grain develop and accumulate at the grain boundary so that local grain boundary migration has been formed, as shown in Fig. 24a [40]. Due to the blocking effect of the grain boundary on dislocation, the uneven local strain gradient formed along the grain boundary leads to grain boundary shear, which promotes the grain boundary bow-out mechanism. This results in uneven deformation of the material, as shown in Fig. 24b, and provides favorable conditions for the dynamic recrystallization softening mechanism of the material.

Fig. 24
figure 24

Grain boundary migration and grain boundary bowing under high-temperature compression deformation of Inconel718

Full size image

4.4 Stress and crack

4.4.1 Stress analysis

When the cutting parameters are \(f\) = 0.1 mm/r, \({a}_{p}\) = 1 mm, \({\gamma }_{0}=3^\circ\), and \(v\) = 90 m/min, the simulation processes were carried out using the JC model without grain boundary and the geometric dislocation model with grain boundary respectively. The stress distribution diagrams were obtained, as shown in Fig. 25.

Fig. 25
figure 25

a, b Stress cloud diagram

Full size image

It can be seen from Fig. 25 that the stress is concentrated in the first deformation zone. For the traditional JC model, the maximum stress is about 1470 MPa. For the GND model, the maximum stress inside the grain is about 1510 MPa, while the maximum stress at the grain boundary is about 1599 MPa. The stress distribution of the traditional JC model tends to be average, while the high-stress distribution of the GND model is distributed at the grain boundary. This also proves that grain boundaries hinder the shear slip of grains, leading to the phenomenon of stress concentration at grain boundaries, which plays a role in strengthening materials.

4.4.2 Crack analysis

Before cutting, the dislocation distribution in the material has no regular directionality and is in a mechanically stable state. In the process of metal cutting, on the one hand, the grain boundary hinders the dislocation slip. When the stress concentration caused by dislocation reaches a certain limit, the workpiece material will produce cracks on the free surface of the edge of the shear band because it cannot bear such a large strain. On the other hand, there are holes, impurities, and other defects in the metal. Under the action of shear stress, micro-voids are formed in the shear band, which continue to grow and aggregate, and finally form cracks.

The crack source model proposed by Wang and Fan [43] is a planar plug product containing a series of random dislocations on the barrier. The stress concentration at the top of the dislocation plug group may lead to the convergence of several dislocations at the plug head to form a crack source. When the dislocation stacking reaches a sufficient number, the dislocation at the top is forced to close to each other. When the distance between them reaches an atomic distance, a large dislocation is formed, as if several wedges with atomic plane thickness are inserted between cleavage planes. In order to relax the stress, the subsequent dislocations successively enter between the cleavage planes, and the wedge thickness increases until a crack is formed, as shown in Fig. 26a.

Fig. 26
figure 26

a–c Crack generated owing to dislocation plug

Full size image

According to the formation mechanism of machining crack. The stress concentration at the front end of the plug accumulation group leads to crystal fracture, and the shear stress along the slip plane is [43]

$$\tau =\sqrt{\frac{3\pi eG}{8\left(1-v\right)L}}$$
(16)

The number of dislocations on the slip plane is obtained by

$$n=\frac{3{\pi }^{2}e}{8\tau b}$$
(17)

According to the energy conservation, the average length of the crack and the number of dislocations can be expressed as

$$C=\frac{{n}^{2}{b}^{2}{G}^{2}}{8\left(1-v\right)e}={K}_{1}\mathrm{bn}$$
(18)

where L is the length of the sliding surface. C is the crack length. e surface energy. K1 and G are material-related constants.

The condition of dislocation stacking to form the crack is \(n\tau \ge {K}_{1}G\). \({K}_{1}G\) is the material-related constant. The larger the value of \(n\tau\), the more likely it is to crack. According to Eq. (18), under the same conditions, the higher the number (n) of dislocations per unit area, the larger the length of microcracks formed, that is, the more obvious the cracks are.

According to Fig. 27, intersecting slip bands can also cause crack nucleation, in addition to dislocation plug causing cracks. According to the viewpoint of dislocation theory. When two groups of dislocations meet, they will react to form a new dislocation and reduce the elastic energy. As shown in Fig. 27b, it can be seen that the directions of slip lines on both sides of the crack are different, so cracks are generated at the intersection of slip lines.

Fig. 27
figure 27

a–c Cracks caused by intersecting slip bands

Full size image

In addition to the above analysis, it is found that there are some cavities and a small amount of impurities, as well as cracks formed by cavity propagation and cracks formed between impurities and matrix. The propagation of holes goes through four stages: nucleation, growth, aggregation, and finally crack formation. When local shear deformation passes through grain boundaries, inclusions, and other defects, under the action of adiabatic temperature rise, the cracks formed by fracture at these defects will rapidly expand and passivate into relatively smooth elliptical holes under the action of stress concentration [44]. The holes will grow gradually, and some may continue to grow by swallowing the surrounding holes, and finally grow and aggregate with the continuous growth of the holes. As shown in Fig. 28, the shear band is gradually destroyed to form macro-cracks.

Fig. 28
figure 28

a, b Propagation of impurity and cavity crack

Full size image

The traditional JC model only considers the effect of SSDs related to plastic strain, while the GND model not only considers the effect of SSDs but also the effect of GNDs. It can coordinate the corresponding deformation of polycrystalline grains at the same time to maintain the continuity of the chip. Therefore, GND model can simulate the cutting process more accurately and better reveal the mechanism of chip formation from a microscopic perspective, which can provide a reference for the study of sawtooth chip formation and the finished surface quality.

5 Conclusions

This paper studied the deformation mechanism in cutting Inconel718 from a micro point of view. A new material constitutive model with grain boundary effect is established by introducing GNDs into the JC model. The newly established constitutive model is applied to cutting simulation through compiling the VUMAT user subroutine. The comparison of simulated and experimental results has been carried out at the condition of v = 30–90 m/min. The conclusions can be drawn as.

  1. (1)

    With the increase of cutting speed, the cutting heat softens the grain boundary, reduces the barrier of grain boundary to dislocation slip, and reduces the cutting force. In addition, compared with the traditional JC model, the cutting force of the GND model fluctuates greatly, which is more in line with the experimental values.

  2. (2)

    The temperature distribution obtained by the GND model is more consistent with the experiment. With the change in temperature, dislocations will proliferate and annihilate. The dislocation density shows a high-low jump fluctuation state with the change in temperature. The increase in temperature leads to a decrease in dislocation density.

  3. (3)

    The shear zone is composed of the deformation band in the initial stage of deformation localization and the phase transformation band that may undergo dynamic recrystallization or phase transformation. The grains are distributed as slender fibers along the shear zone. Due to the existence of grain boundaries, the dislocation slip direction of each grain has a certain randomness, resulting in a certain randomness in the state and shape of sawtooth chip formation.

  4. (4)

    The stress distribution of the traditional JC model tends to be equalization. The high-stress region of the GND model is distributed at the grain boundary, which is consistent with the stress distribution characteristics in the cutting process of polycrystalline. In addition, the grain boundary model can better simulate and explain the causes of crack initiation and propagation.