1 Introduction

Researches have been conducted for many years to reveal the physics of chatter phenomenon and to suppress it [1]. Regenerative chatter causes a poor surface quality, an excessive tool wear, and a waste of workpiece materials and energy; limits the material removal rate, etc.; and leads to various negative effects.

During the last decades, different techniques for suppression of chatter have been developed [2,3,4, 7].

There are many earlier studies which investigated the suppression of chatter in machine tools. These studies focused on the evaluation of chatter stability, and methods of stability chart analysis for self-excited vibration system with a constant spindle speed were studied, and the method for estimating the stability was already established [4,5,6,7,8].

Together with the development of servo control devices that can control automatically the speed of spindle, spindle speed variation (SSV) that changes the spindle speed continuously in process has recently attracted the interests of researchers.

A semi-discretization technique was applied to the case of turning with SSSV in order to obtain a stability chart, and some numerical results assessing the stabilization effectiveness for fast SSV were given [8, 11]. A simple method was published to analyze the stability in turning for slowly time-varying spindle speed by Jiri Falta et al. [19] where a theory for analyzing the stability of delay differential equation (DDE) with slowly time-varying delay was proposed, the stability behavior of system was analyzed, and the method for selection of SSV parameters was studied.

On the one hand, the effectiveness of different types of SSV, using the numerical methods for time response of a system in machine tools, were evaluated [3, 7, 9,10,11,12,13,14,15]. In these literatures, time responses were obtained using different SSV signals such as triangular, rectangular, sinusoidal, random multi-level, chaotic signals and their suppressing effectiveness was tested and showed that use of a special random multi-level signal or chaotic signals is more effective than use of a sine signal for suppressing chatter. Demir et al. [13] observed that sinusoidal spindle speed variation (SSSV) is more effective than triangular for suppression of chatter. A model combining Fourier expansion with Bessel function expansion was used to determine the stability chart for SSV turning, and it was validated by numerical time domain simulation and experiments by De Canniere et al. [6]. Fansen [17] showed that when SSSV and chaotic signals in turning were used together, and the effectiveness in suppression of a beat was good. Dong et al. [24] presented a method to analyze the stability in turning process with variable spindle speed using the reconstructed semi-discretization method and proved that using presented method, calculation speed was more without reducing calculation accuracy than using the well-accepted semi-discretization method.

On the other hand, various kinds of SSV signals and methods to determine their parameters optimally were studied in order to improve the effectiveness of chatter suppression. For example, a number of time-varying parameters were applied to suppress a regenerative chatter in turning [9]. Al Regib et al. [10] presented a method to select optimally SSV parameters under the same assumptions. In order to suppress a chatter in turning, Kambiz Haji Hajikolaei et al. [16] used generic algorithm (GA), with one and three sinusoidal speed modulations, respectively, in order to obtain the optimal amplitudes of modulating signal, and they finally, by comparing numerical and experimental results of responses of tools, concluded that the time span required for chatter suppression by three sinusoidal signals is shorter than by one sinusoidal.

Wang, Zhang et al. [25] used multi-harmonic spindle speed variation including the phase factor for chatter suppression and optimized parameters of the speed variation function using the genetic algorithm. And they showed that the optimized milling process had higher stability limits in the high speed range through the numerical simulation.

Al bertelli et al. pointed out that in the case of rapid SSV, there are still problems with possibility of discretization of signal in industrial implementation of SSV and with the methods to optimize the parameters in SSV [18].

In addition to the literatures mentioned above, Wang et al. [26] presented a method for chatter suppression in milling process using the adaptive vibration reshaping technique and Dang et al. [27] presented a method to analyze and mitigate the chatter in milling of the pocket-shaped thin-walled workpieces with viscous fluid. Zhu and Liu [28] summarized the recent progress of chatter prediction, detection, and suppression in milling, and Alzghoul et al. [29] reviewed and summarized the researches for chatter prediction, suppression, and avoidance in turning, but until now, we cannot discover any reference that presented a method for suppressing a chatter optimally in turning with SSV.

Through analyzing the previous works, it can be understood that the suppression of a chatter using SSV in practical machine tool industry has been applied only to the simple SSV signals whose type is already given as triangular, rectangular, and sinusoidal. In turning, the methods to determine the type of SSV signals and its parameters in an optimal way to suppress chatter more efficiently have still not been reported in the earlier works.

This paper introduced a method for determining the spindle speed variation signal type for chatter suppression in turning, considering the practical characteristics of spindle drive. The spindle speed variation is expressed in terms of multi-harmonic series and shows a method for determining the number of harmonic series, the amplitudes, and the modulation frequencies of signals optimally in the case of slowly time-varying spindle speed.

2 Determination of spindle speed variation type

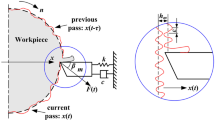
Consider a cylindrical workpiece rotates orthogonally on a lathe with straight cutting edge tool.

Considering that the cutting force is proportional to the chip area, the equation of tool’s motion in the horizontal direction normal to the cutting edge can be written as follows [15, 16]:

$$m\ddot{x}+c\dot{x}+kx={K}_{c}b\left[x\left(t-T\right)-x\left(t\right)\right]$$
(1)

where \(m\) is equivalent mass of the whole vibrational system of tool and its corresponding attachments (kg), \(x\) is coordinate of tool in the horizontal direction normal to the cutting edge (m), \(k\) and \(c\) are equivalent stiffness (N/m) and damping (Ns/m) of the system respectively, \({K}_{c}\) is cutting force coefficient (N/m2), \(b\) is the width of cut (m), \(T\) is the time that the tool passes during one revolution (\(T=\frac{60}{N}\)) (s), and \(N\) is the spindle rotational speed \((\mathrm{r}/\mathrm{min})\) (Fig. 1).

Fig. 1
figure 1

Dynamic model of the system

Full size image

The variation of chip thickness in \(x\) direction is denoted by \(x\left(t-T\right)-x\left(t\right)\), and the right-hand side of Eq. (1) means the dynamic cutting force of tool.

Equation (1) can be rewritten as follows:

$$\ddot{x}\left(t\right)+2\xi {\omega }_{n}\dot{x}\left(t\right)+{\omega }_{n}^{2}x\left(t\right)=\upgamma {\omega }_{n}^{2}\left[x\left(t-T\right)-x\left(t\right)\right]$$
(2)

where

$${\omega }_{n}=\frac{k}{m}, \xi =\frac{c}{2\sqrt{km}}, \gamma =\frac{{K}_{c}b}{k}$$
(3)

The fundamental frequency of spindle variation signal is limited by the characteristics of spindle servo-drive [18].

Because any periodical signal can be expressed in multi-harmonic series, the spindle variation speed is approximated in n harmonic series in this paper:

$$N\left(t\right)=\frac{60}{T}={N}_{m}\left[1+\sum_{i=1}^{n}{(A}_{i}\mathrm{cos}\left(i{\omega }_{s}t\right)+{B}_{i}\mathrm{sin}\left(i{\omega }_{s}t\right))\right]$$
(4)

where \({N}_{m}\) is the average spindle speed, \({A}_{i},{B}_{i}\) are the amplitude ratios of varied signal, and \({\omega }_{s}\) is its fundamental angular frequency.

3 Setting up an optimization problem to determine the amplitude and frequency of spindle speed variation

Now, let us consider a problem to determine optimally the type of spindle speed variation signal to suppress a chatter before matching actually a workpiece provided that dynamic model of turning system was established as Eq. (1).

Since one of the key factors that cause chatter in turning is dynamic cutting force, we set an objective function such that the dynamic cutting force has a minimum:

$${\mathrm F}_{\max}=\begin{array}{c}\max\\\mathrm t\end{array}\left\{{bK}_{c}\left[x\left(t-T\right)-x\left(t\right)\right]\right\}\Rightarrow\min$$
(5)

where \({F}_{\mathrm{max}}\) is the maximum magnitude of dynamic cutting force over the time range.

It should be noted that the dynamic cutting force is different from the nominal cutting force generated under nominal cutting conditions.

In general, the total cutting force is composed of the nominal cutting force and the dynamic cutting force and is as follows: \({K}_{c}\mathrm{b }[{h}_{0}+x\left(t-T\right)-x\left(t\right)]\).

The nominal cutting force is the static force and is equal to \({K}_{c}b{h}_{0}\). \({h}_{0}\) is the nominal thickness of chip. The dynamic cutting force is \({K}_{c}\mathrm{b }[x\left(t-T\right)-x\left(t\right)]\).

Chatter is dependent on the dynamic cutting force and independent on the static, nominal cutting force.

The magnitude of the dynamic cutting force is the basic cause of chatter generation, and smaller dynamic cutting force gives better performance of chatter suppression [2,3,4,5,6,7,8,9,10].

The time range should be one cycle of chatter at least.

In general, a chatter occurring in actual turning has a complex periodic function type. However, for simplicity as in some references, we assume that the vibration of the cutting tool can be represented as follows [10, 16]:

$$\left\{\begin{array}{c}x\left(t\right)={x}_{0}\mathrm{cos}\left(\omega t\right)\\ x\left(t-T\right)={x}_{0}\mathrm{cos}\left(\omega t-\omega T\right)\end{array}\right.$$
(6)

Substituting Eq. (4) into Eq. (6) and considering that \(b\) and \({K}_{c}\) are constants in Eq. (5), ignoring these factors, the objective function can be expressed as follows:

$${F}_{\mathrm{max}}=\begin{array}{c}\mathrm{max}\\ t\end{array}\left\{{x}_{0}\left[\mathrm{cos}\left(\omega t-\omega T\right)-\mathrm{cos}\left(\omega t\right)\right]\right\}$$
(7)

Considering Eq. (4), we write;

$${F}_{\mathrm{max}}=\begin{array}{c}\mathrm{max}\\ t\end{array}\left\{{x}_{0}\left[\mathrm{cos}\left(\omega t-\frac{60\upomega }{{N}_{m}\left[1+\sum_{i=1}^{n}{A}_{i}\mathrm{cos}\left(i{\omega }_{s}t\right)+{B}_{i}\mathrm{sin}\left(i{\omega }_{s}t\right)\right]}\right)-\mathrm{cos}\left(\omega t\right)\right]\right\}$$
(8)

In Eq. (8), spindle speed variation parameters that control the chatter are amplitude ratios, \({A}_{i},{B}_{i}\), and fundamental angular frequency of rotational speed variation,\({\omega }_{s}\), and therefore, we select these as optimal design variables for suppressing a chatter:

$${\varvec{X}}=\left\{{x}_{1}, {x}_{2}, \cdots ,{x}_{2n}, {x}_{2n+1}\right\}=\left\{{A}_{1}, {A}_{2}, \cdots ,{A}_{n}, {{B}_{1}, {B}_{2}, \cdots ,{B}_{n}, \omega }_{s}\right\}$$
(9)

Optimization objective function is set such that Eq. (8) characterizing a dynamic cutting force is minimized:

$$\begin{array}{c}\max\\t\end{array}\left\{x_0\left[cos\left(\omega t-\frac{60\omega}{N_m\left[1+\sum_{i=1}^nA_i\cos\left({i\omega}_st\right)+B_i\sin\left({i\omega}_st\right)\right]}\right)-\cos\left(\omega t\right)\right]\right\}\Rightarrow\min$$
(10)

Then, the constraint conditions on the design variables may be written as:

$$\left\{\begin{array}{c}{A}_{iL}<{A}_{i}<{A}_{iU},{B}_{iL}<{B}_{i}<{B}_{iU}, i=1,\dots ,n \\ {\omega }_{sL}<{\omega }_{s}<{\omega }_{sU}\end{array}\right.$$
(11)

where \({A}_{iL}, {A}_{iU}, {{B}_{iL}, {B}_{iU}, \omega }_{sL}, {\mathrm{and} \omega }_{sU}\) are the lower and upper bounds of design variables, \({A}_{i}, {B}_{i},{\mathrm{and} \omega }_{s}\), respectively.

We take the thermal load condition of spindle drive motor as an additional constraint condition on the design variables. The thermal overload ratio of motor necessary for the spindle variation can be defined as follows [18]:

$$OR=\frac{{C}_{VRMS}}{{C}_{RMS}}$$
(12)

where \({C}_{VRMS}\) is RMS (root means square) torque required to perform a turning operation with variable cutting speed and it is calculated as follows:

$${C}_{VRMS}=\sqrt{\frac{1}{{T}_{1}}\underset{0}{\overset{{T}_{1}}{\int }}{\left[{F}_{tSSV}\frac{\delta \bullet D}{2}+\frac{{J}_{TOT}}{\delta }\frac{d\Omega }{dt}\right]}^{2}\mathrm{d}t}$$
(13)

where \(\Omega \left(t\right)\) is the rotational angler speed of the spindle.

Considering.

$${\Omega \left(t\right)=\frac{\pi }{30}N\left(t\right)=\frac{\pi }{30}N}_{m}\left[1+\sum_{i=1}^{n}\left({A}_{i}\mathrm{cos}\left(i{\omega }_{s}t\right)+{B}_{i}\mathrm{sin}\left(i{\omega }_{s}t\right)\right)\right],$$

Equation (13) becomes as follows:

$${C}_{VRMS}=\sqrt{\frac{1}{{T}_{1}}\underset{0}{\overset{{T}_{1}}{\int }}{\left[{F}_{tSSV}\frac{\delta \bullet D}{2}+\frac{{J}_{TOT}}{\delta }\frac{{N}_{m}\pi {\omega }_{s}}{30}\left(\sum_{i=1}^{n}\left(-i{A}_{i}\mathrm{sin}\left(i{\omega }_{s}t\right)+{B}_{i}\mathrm{cos}\left(i{\omega }_{s}t\right)\right)\right)\right]}^{2}\mathrm{d}t}$$
(14)

where \({T}_{1}\) is the time required to calculate RMS and \({F}_{tSSV}\) is RMS tangential cutting force.

Tangential cutting force is determined as follows:

$${F}_{t}=b{K}_{tc}\left(\beta ,V\right)h$$

where \({K}_{tc}\) is cutting coefficient which is determined experimentally as a function of the rake angle \(\beta\), cutting speed \(V\), lead angle \(\chi ,\) and lubrication condition, and \(h\) is the depth of cut, i.e., the sum of nominal depth of cut and dynamic depth of it,\(x\left(t-T\right)-x\left(t\right)\); \(D\) is workpiece diameter; \({J}_{TOT}\) is the global spindle inertia (including motor, transmission and workpiece) which is reduced to the motor; and \(\delta\) is the the spindle transmission ratio. \({C}_{RMS}\) is the \(\mathrm{RMS}\) torque required to perform the equivalent turning operation without spindle variation.

Considering Eq. (14), it can be seen that Eq. (12) is of strong nonlinearity with respect to design variables \({A}_{i}, {{B}_{i},\mathrm{and }\omega }_{s}\).

On the other hand, permissible thermal loads of spindle drive motors are determined by characteristics of motor. An example of characteristic data of the motor thermal load for spindle in lathe is given in Fig. 2 [18], where A, B, C, and D are parameters for the practical cutting conditions as in Table 1.

Fig. 2
figure 2

Permissible thermal load ratio of spindle motors [18]

Full size image
Table 1 Cutting conditions in cases of A, B, C, and D [18]
Full size table

The nominal cutting speeds are selected as 70 to 500 \(\mathrm{m}/\mathrm{min}\) (i.e., \(1.166 6 \sim 8.333\mathrm{ m}/\mathrm{s}\)), which is wide enough for practice of processing steel workpiece).

Therefore, in the case of steel turning, the limitation of thermal load of motors over the range of cutting speeds of \(70\) to \(500\mathrm{ m}/\mathrm{min}\) can be represented in terms of an overload factor:

$$OR<\left[OR\right]$$
(15)

where \(OR\) is a function of design variables and \(\left[OR\right]\) is a permissible load which is a function of cutting speed as shown in Fig. 2.

In addition to Eq. (11), Eq. (15) constitutes an other constraint on the design variables.

Optimization problem, Eq. (9) ~ (11), Eq. (15) established above, has strong non-linearity in the type of transcendental function of design variables and thus may have multiple extrema.

Also, because the objective function and the constraint functions are of complicated integral type, it is difficult to solve the optimization problem analytically.

It is known that metaheuristic methods such as GA are useful to solve such non-linear optimization problem with multiple extrema.

In his investigation Yang [21] shows that firefly algorithm (FA) that has a more simple control property and better search performances than GA is used [21].

A method is proposed to find the number of multi-harmonic series,\(n\), and the amplitudes \({A}_{i},{B}_{i}\) of the \(i\) th variation signal component in order to minimize the objective function (Eq. (8)).

  1. 1)

    Select an angular frequency of variation signal,\({\omega }_{s}\), considering the characteristics of spindle drive.

  2. 2)

    Increase \(n\) gradually from \(1\) to a certain number. Then, the type of the function is changed and the number of design variables is increased with the number \(n\) of multi-harmonic series in the right side in Eq. (8).

  3. 3)

    Find optimum amplitude ratios \({A}_{i}{, B}_{i}\) for each fixed n and a response solution after substituting them into Eq. (4) and (2).

  4. 4)

    By comparing amplitudes of response for all the numbers \(n\), select a value of \(n\) having the lowest amplitude and its corresponding amplitude ratio as optimal values.

These optimal values can be verified through the time response of system.

To find a numerical solution of time response, Eq. (2) is expressed as follows:

$$\ddot{x}\left(t\right)+2\xi {\omega }_{n}\dot{x}\left(t\right)+{\omega }_{n}^{2}x\left(t\right)=\gamma {\omega }_{n}^{2}\left[x\left(t-T\right)-x\left(t\right)\right]=\frac{F\left(t\right)}{m}$$
(16)

where dynamic cutting force is;

$$F\left(t\right)=m{K}_{c}b\left[x\left(t-T\right)-x\left(t\right)\right]=m\gamma {\omega }_{n}^{2}\left[x\left(t-T\right)-x\left(t\right)\right]$$

Also, \(T\left(t\right)=\frac{60}{N\left(t\right)}\) is delay time that the tool contacts at a point on workpiece and, considering Eq. (4), it is given as:

$$T\left(t\right)=\frac{60}{{N}_{m}\left[1+\sum_{i=1}^{n}\left({A}_{i}\mathrm{cos}\left(i{\omega }_{s}t\right)+{B}_{i}\mathrm{sin}\left(i{\omega }_{s}t\right)\right)\right]}$$

We solve Eq. (16) using the solver, DDESD (delay differential equation with a variable delay time) in MATLAB.

4 Solution of optimization problem using the FA

4.1 Preliminary for the FA

FA is one of the metaheuristic algorithms, and it emulates fireflies’ properties that fireflies that fly in night sky are attracted to a brighter firefly flashing.

FA is grounded on the following three hypotheses [21].

  1. a)

    All fireflies are unisex so that their attractiveness is independent of their sex.

  2. b)

    Attractiveness is proportional to their brightness; thus, for any two flashing fireflies, the less bright firefly will move towards the brighter one.

The attractiveness decreases as their distance increases. If there is not any brighter firefly than a particular one, it moves randomly.

  1. iii)

    The brightness of a firefly is determined according to the nature of the objective function.

For a maximization problem, the brightness of a firefly can simply be proportional to the value of objective function.

When a firefly \(i\) moves towards a brighter one \(j\), the movement of the former \(i\) is expressed as follows:

$${X}_{j}={X}_{i}+{\beta }_{0}{\mathrm{e}}^{-{\gamma r}_{ij}^{2}}\left({X}_{j}-{X}_{i}\right)+\alpha {\varepsilon }_{i}$$
(17)

where \({X}_{i}\) and \({X}_{j}\) are the spatial locations of firefly \(i\) and firefly \(j\), respectively; \({r}_{ij}=\Vert {X}_{i}-{X}_{j}\Vert =\sqrt{\sum_{k=1}^{d}{\left({x}_{i,k}-{x}_{j,k}\right)}^{2}}\) is the distanc between firefly \(i\) and firefly \(j\); \({\beta }_{0}\) is the attractiveness at \(r=0\); \(\gamma\) is the light absorption coefficient; \(d\) is the dimension of space; and \({x}_{i,k}\) is the \(k\) th parameter of the spatial coordinates \({X}_{i}\) of the \(i\)-th firefly. \(\alpha\) is random parameter having a value between \(0\) and \(1\) and, according to some literatures, it is usually \(0.2\) and \({\varepsilon }_{i}\) which is a vector of random numbers drawn from Gaussian distribution or uniform distribution is distributed between \(-0.5\) and \(0.5\).

The second term in the right-hand side in Eq. (17) means the attraction towards a point, directivity, and the third term represents randomization, dispersibility. The parameter \(\gamma\) characterizes the attractiveness, and if \(\gamma\) is close to \(0\), it is almost constant and all fireflies orient easily to any extremum.

On the other hand, if \(\gamma\) is very large, the second term approaches to 0 and the attractiveness disappears; thus, fireflies move away randomly and it comes to be classic random search method.

Parameters \(\alpha\) and \(\gamma\) are control parameters that characterize the capability of global search of FA.

5 Improvement of FA.

Azad et al. [22] proposed that \(\alpha\) in the third term on the right hand in Eq. (17) was not kept as a constant as in [21] but changed it with the number of iteration:

Changing \(\alpha\) with the number of iteration improves the accuracy and rate of convergence.

$$\alpha ={\alpha }_{\mathrm{max}}-\frac{{\alpha }_{\mathrm{max}}-{\alpha }_{\mathrm{min}}}{{t}_{\mathrm{max}}}t$$
(18)

where \({\alpha }_{\mathrm{max}}=1, {\alpha }_{\mathrm{min}}=0.2\)

However, Azad et al. did not present numerical comparison between Eqs. (18) and (17)

Meanwhile, in [23], the first term in the right-hand side in Eq. (17) was modified in order to improve the convergence rate of fireflies as follows:

$${X}_{i}={X}_{j}+{\beta }_{0}{\mathrm{e}}^{-{\gamma r}_{ij}^{2}}\left({X}_{j}-{X}_{i}\right)+\alpha {\varepsilon }_{i}$$
(19)

Equation (19) shows that when firefly \(i\) moves towards firefly \(j\), it starts at proximity of the position of brighter firefly \(j\) rather than at the position of firefly \(i\) as in Eq. (17).

However, this work did not validate the effectiveness of Eq. (19), comparing with Eq. (17) and did not evaluate quantitatively the convergence of fireflies towards the poles.

The methods considered in the above works cannot evaluate quantitatively the convergence in multi-extremes value problem.

For example, the order of magnitudes of function values at the poles, the number of fireflies converged at the poles, and dispersed distance of fireflies from the poles cannot be reflected as the quantitative index.

If the number of fireflies converged at the poles becomes large and the dispersed distance of fireflies from the poles becomes short according to the order of magnitudes of function values at the poles, the optimization algorithm will be more effective, and if the quantitative index exists, it will be very useful.

In this paper, in order to evaluate the convergence considering the convergence radius of fireflies and the number of fireflies converged according to the order of magnitudes of function values at the all the poles in optimalization problem having multi-extremes, we take the following index \(W\):

$$W=\frac{1}{M}\sum_{j=1}^{M}{W}^{j}=\frac{\sum_{j=1}^{M}\sum_{i=1}^{L}{\psi }_{i}{W}_{i}^{j}}{M}$$
(20)

where \(M\) is the number of total run of FA iteration and \(L\) is the number of poles.

$${W}^{j}=\sum_{i=1}^{L}{W}_{i}^{j}$$
(21)
$${W}_{i}^{j}=\frac{{p}_{i}^{j}}{\widetilde{N}}\frac{{\overline{f}}_{i}^{j}}{{f}_{mi}}$$
(22)
$${\psi }_{i}=\frac{1}{L}\frac{{f}_{i}}{{f}_{\mathrm{max}}}$$
(23)

where \({p}_{i}^{j}\) and \({\overline{f}}_{i}^{j}\) are the number of fireflies and the average value of objective function for fireflies entering into a certain convergence radius in proximity of \(i\) th pole at \(j\) th running, \(\widetilde{N}\) is the total number of fireflies, and \({f}_{mi}\) is the function value at \(i\) th pole.\(\frac{{p}_{i}^{j}}{\widetilde{N}}\) represents the ratio of the number of fireflies converging to the \(i\) th pole to the total number of fireflies, \(\frac{{\overline{f}}_{i}^{j}}{{f}_{mi}}\) is the ratio of the function value for the \(i\) th pole to the average function value for fireflies converging to the \(i\) th pole, and this means that the closer \(\frac{{\overline{f}}_{i}^{j}}{{f}_{mi}}\) is to \(1\), the higher its convergence accuracy is.

Equation (22) represents the convergence index for individual pole over one running and \(0<{W}_{i}^{j}<1\).

It can be seen that the larger \({W}_{i}^{j}\) is, the higher its convergence accuracy to the \(i\) th pole is.

In Eq. (23), \({f}_{\mathrm{max}}\) is the global maximum and \({f}_{i}\) is the \(i\) th extremum.\({\psi }_{i}\) can be considered as a weight coefficient in view of the global maximum search:

It takes a value equal to \(1\) for the global maximum, but a value less than \(1\) for poles other than the global maximum. \(W\) represents the capability of global optima search.

\({W}^{j}\) stands for the convergence index for all the poles over \(j\) th running, while \(W\) is the averaged convergence index over the total runnings, and it takes a value between \(0\) and \(1\).

If the objective function with multiple extrema takes identical extrema or a single maximum, one can also see that a larger \(W\) calculated from Eq. (20) indicates a higher capability of multi-pole search, i.e., higher performance of global search.

6 Cas study

We compared and evaluated the performance of global search of Eq. (19) using the following exponential function having four extremes or poles:

$$f\left(x,y\right)={\mathrm{e}}^{-{\left(x-4\right)}^{2}-{\left(y-4\right)}^{2}}+{\mathrm{e}}^{-{\left(x+4\right)}^{2}-{\left(y-4\right)}^{2}}+2\left[{\mathrm{e}}^{-{x}^{2}-{y}^{2}}+{\mathrm{e}}^{-{x}^{2}-{\left(y+4\right)}^{2}}\right]$$
(24)

This function has two global maxima value of \(2\) at \((0, 0)\) and \((0, -4)\) and has two global minima value of \(1\) at \((-4, 4)\) and \((4, 4)\) (Fig. 3).

Fig. 3
figure 3

Exponential function (Eq. (20))

Full size image

First, we implement FA using Eq. (17) in MATLAB and search for the extremum, where \(\alpha\) is set to \(0.2\) and the values of \(\gamma , \beta ,p, \mathrm{and} M\) are taken according to [21], i.e., \(\gamma =1, \beta =1, p=40, M=1 500\).

The results of search are shown in Fig. 4

Fig. 4
figure 4

Results using Eq. (17) (\(\alpha =0.2, W=0.573\))

Full size image

Here in the figure, the horizontal axis and longitudinal axis represent variables \(x\) and \(y\) in Eq. (24), respectively; different colors indicate different function values; a contour line expresses a connection of the same valued points; and the striking separate dots represent the fireflies.

As can be seen, the fireflies tend to converge to all four extrema, but the degrees of convergence are different.

The convergence indices averaged over 10 iterations at the poles are:

$${\overline{W}}_{1}=0.078, {\overline{W}}_{2}=0.075, {\overline{W}}_{3}=0.22, {\overline{W}}_{4}=0.20, W=0.573$$

Then, optimum search using Eq. (18) was performed as parameters \({\alpha }_{\mathrm{max}}\) and \({\alpha }_{\mathrm{min}}\) are changed in different ways for their qualitative comparisons.

We can see that the capability of simultaneous search for all the poles is not sufficient when \({\alpha }_{\mathrm{min}}=0.2\) and \({\alpha }_{\mathrm{max}}\) ranging from \(0.2\) to \(1\) but that concentration around a single pole appears to be great (Fig. 5a, b, c).

Fig. 5
figure 5

Results when using Eq. (18): a \({\alpha }_{\mathrm{max}}=0.5, {\alpha }_{\mathrm{min}}=0.2, W=0.24;\) b \({\alpha }_{\mathrm{max}}=0.7, {\alpha }_{\mathrm{min}}=0.2, W=0.23\); c \({\alpha }_{\mathrm{max}}=1, {\alpha }_{\mathrm{min}}=0.2, W=0.22;\) d \({\alpha }_{\mathrm{max}}=0.2, {\alpha }_{\mathrm{min}}=0.02, W=0.89\); e \({\alpha }_{\mathrm{max}}=0.002, {\alpha }_{\mathrm{min}}=0.002, W=0.71\); f \({\alpha }_{\mathrm{max}}=0.2, {\alpha }_{\mathrm{min}}=0.002, W=0.91\)

Full size image

The capability of simultaneous search for all the poles is not satisfactory again, when \({\alpha }_{\mathrm{max}}=1\), \({\alpha }_{\mathrm{min}}=0.2\) as in [22].

When we decrease the values of \({\alpha }_{\mathrm{max}}\) and \({\alpha }_{\mathrm{min}}\) further, the convergence radii of fireflies become smaller and also the simultaneous concentration around each pole becomes greater.

However, there is left an inactive firefly which did not approach to the neighborhood of any poles (Fig. 5d, e, f).

When we set an identical value of both \({\alpha }_{\mathrm{max}}\) and \({\alpha }_{\mathrm{min}}\) and decrease it, there appears a tendency that a few fireflies do not converge to any poles at all (Fig. 5e).

Comparing and summarizing all these results quantitatively in terms of the convergence index, it is concluded that when \({\alpha }_{\mathrm{max}}=0.2, { \alpha }_{\mathrm{min}}=0.002\), fireflies converge to all the poles simultaneously with relatively small convergence radii and the convergence index, \(W\), becomes \(0.91\), the highest of all (Fig. 5f).

However, even in this case, a firefly does not approach to and stands far away from any poles.

Through a careful real-time observation chasing after the movement of fireflies with every iteration, the reason why this firefly does not converge is elucidated as follows:

As the initial position of this firefly was relatively far away from poles, the second term in the right-hand side in Eq. (17) is small, while the moving distance greatly depends on the third term, i.e., \(\alpha\).

In order that this firefly may approach to a pole in its neighborhood, its movement during the initial iteration had to be great enough that it could escape from the position, but it failed to do because the walk was too small.

It shows that \(\alpha\) in Eq. (18) decreases in linear proportion to the number of iteration, t, and it is not large enough for the firefly to escape from the first position during initial iteration.

Therefore, it seems rational to control in such a way that \(\alpha\) in the initial iteration process is taken a large value and we decrease it in a nonlinear way as the firefly approaches to a pole (Fig. 6a).

Fig. 6
figure 6

Non-linear change of \(\alpha ;\) a a firefly approaches to a pole b non-linear; b variation of \(\alpha\) versus iteration number \(t\)

Full size image

From Fig. 6b, it can be seen that the walk,\(\alpha\), becomes larger in the case of non-linear variation than in linear one.

Through a number of numerical tests, curve-fitting, and analysis of the relationship of the data of \(\alpha\) with the iteration number,\(t\), it was found that its suitable approximation can be of a cosine form.

Expressing the initial random walk of \(\alpha\) as \({\alpha }_{\mathrm{max}}\), and the final number of iteration and random walk as \({t}_{\mathrm{max}}\) and \({\alpha }_{\mathrm{min}}\), respectively, the walk in the \(t\) th iteration can be expressed as follows:

$${\alpha }_{t}=\left({\alpha }_{\mathrm{max}}-{\alpha }_{\mathrm{min}}\right)\mathrm{cos}\frac{\pi t}{2{t}_{\mathrm{max}}}+{\alpha }_{\mathrm{min}}$$
(25)

Some results obtained when applying Eqs. (17) and (25) are shown in Fig. 7.

Fig. 7
figure 7

Search results of poles; a \({\alpha }_{\mathrm{max}}=0.2, {\alpha }_{\mathrm{min}}=0.002, W=0.22\) when using Eqs. (17) and (25); b \({\alpha }_{\mathrm{max}}=0.2, {\alpha }_{\mathrm{min}}=0.002, W=0.93\) when using Eqs. (19) and (25)

Full size image

From the figure, we can see that when \({\alpha }_{\mathrm{max}}=0.2, { \alpha }_{\mathrm{min}}=0.002\), all the fireflies converge to all the poles and the convergence radii are also very small with the convergence index, \(W\), equal to \(0.93\) which is sufficiently larger in comparison with other cases.

The walk \(\alpha\) in initial iteration is large enough for a firefly standing far away from poles to escape from its original position, and thus, its ability to approach to poles becomes great, and this improvement of convergence validates the effectiveness of Eq. (25).

When \({\alpha }_{\mathrm{max}}=0.2, { \alpha }_{\mathrm{min}}=0.02\), similar tendency is also shown (Fig. 7b).

Comparing Fig. 5d, Fig. 5f, and Fig. 7, we can know that all the fireflies converge to poles using Eq. (25).

Then, some of search results when applying Eqs. (19) and (25) are given in Fig. 7b.

The results show that all the fireflies converge to a single optimum. The reason is that the position of each firefly has moved largely into the neighborhood of brighter one during iteration process.

Thus, the use of Eq. (19) is not suitable to the case of multi-pole search.

Combined use of Eqs. (18) and (19) yields a tendency similar to the case of applying Eq. (19), and all the fireflies converge to only one optimum again.

Some results obtained by using Eq. (19) with a constant \(\alpha\) and by using Eqs. (19) and (25) are shown in Fig. 8.

Fig. 8
figure 8

Results when using Eqs. (19) and (25)

Full size image

From Fig. 8, it can be shown that all the fireflies have a similar tendency as the case of applying Eq. (19) and all the fireflies converge to the same one pole which shows degraded performance of global search.

The reason is that the position of each firefly has moved largely into the neighborhood of brighter one during iteration process.

Such a similar tendency appears again when using other benchmark functions such as Ackley function which has a single global optimum.

Therefore, for the multi-pole search problem considered above, adoption of a convergence index as Eq. (21) provides a possibility of quantitative evaluation of the performance of optima search of FA, while non-linear change of a firefly’s walk, \(\alpha ,\) with iteration number, in the form of cosine function as in Eq. (25) greatly improves the capability of global search of FA.

Next, a method is proposed to find the number \(n\) of multi-harmonic series and the magnitude \({A}_{i}\) of the \(i\) th modulating signal component, so that Eq. (8) is minimized.

To this end, we primarily select angular frequency of modulating signal,\({\omega }_{s}\), considering the characteristics of spindle drive.

Secondly, we increase \(n\) gradually starting from \(1\), considering that the type of the function and the number of design variables are changing with increasing number \(n\) of multi-harmonic series in the right side in Eq. (8).

Next, we find an optimum amplitude ratio \({A}_{i}\) for each fixed n, and then, substituting it into Eqs. (4) and (2), calculate the response solution.

Afterwards, comparing the amplitudes of response for all the numbers \(n\), we select a value of \(n\) having the lowest amplitude and its corresponding amplitude ratio as the best results.

Finally, we get an optimum solution applying FA which is known to be efficient to solve a global optimization problem of a multi-pole function [20].

7 Numerical example

We use the following properties of a chatter system in turning as a numerical example, as in [16]:

In Eq. (1), \(m=50\mathrm{kg}, c=2 000\mathrm{ Ns}/\mathrm{m}, k=2\times {10}^{7}\mathrm{ N}/\mathrm{m}, {K}_{c}=3.5\times {10}^{8}\mathrm{ N}/{\text{m}}{2}\), \({N}_{m}= 1 410\mathrm{ r}/\mathrm{min}\), \({\omega }_{s}=2\mathrm{\pi rad}/\mathrm{s}\).

Numerical solutions for the case of constant spindle speed, obtained using the solver in MATLAB, DDE23, of delay differential equation with a constant delay time, show that the displacement of the tool in chattering has the average amplitude of about \(0.8\mathrm{ mm}\) and does not decrease but remains nearly constant (Fig. 9).

Fig. 9
figure 9

Displacement of tool in the case of constant spindle speed

Full size image

Then, in order to suppress chatter, the spindle speed is varied in the same way as proposed above.

First, taking the number of harmonic terms as three sine terms in Eq. (3) and finding the amplitude ratio using the data of [16] and FA, optimal amplitude ratios are \({A}_{1}=0.129 4, {A}_{2}=0.002 5, \mathrm{and} {A}_{3}=0.039 6\), which agree fairly well with the results of [16], i.e., \({A}_{1}=0.129 7, {A}_{2}=0.003 8, {\mathrm{and A}}_{3}=0.038 7\).

In this case, the results of response solution, numerically obtained using DDESD solver in MATLAB, are shown in Fig. 10 together with results of [16].

Fig. 10
figure 10

Comparison of results

Full size image

Figure 10a shows the result obtained in [16] where by expressing the spindle speed variation with 3 sine terms and using GA(generic algorithm), its coefficients were determined optimally.

Figure 10b shows the result obtained by expressing the spindle speed variation with 3 sine terms and using the same initial data as in [16] in order to test the accuracy of the numerical program developed by authors using FA and solution of delay differential equation with a variable delay time, but does not show the result obtained by multi-harmonic series expansion proposed in the current paper.

According to the response signal results by [16], the amplitude decreases initially, oscillates once in the range of \(0.05\) to \(0.12\mathrm{ s}\), increases monotonously after \(0.12\mathrm{s}\), reaches the maximum amplitude of \(0.0003\mathrm{ m}\) at \(0.4\mathrm{s}\), and then, it starts to decrease due to the effects of modulation and becomes completely suppressed after \(0.65\mathrm{s}\) with evaluated suppressing time of \(0.25\mathrm{ s}\) (Fig. 10a).

Meanwhile, the results of current paper show that the amplitude decreases initially, oscillates once between \(0.05\) and \(0.3\mathrm{ s}\), increases monotonously after \(0.3\mathrm{ s}\), and reaches the maximum amplitude of \(0.000 3\mathrm{ m}\) at \(0.5\mathrm{ s}\).

And then it decreases due to the effects of modulation and, after \(0.75\mathrm{ s}\), it is suppressed completely. The suppressing time is \(0.25\mathrm{ s}\) (Fig. 10b).

The maximum amplitudes and the suppressing time for chatter are in good agreement between the previous work and ours.

We compared the time response result of chatter suppression obtained by integrating Eq. (16) and the response result in [16] which was based on GA.

The maximum amplitudes and suppressing time for chatter are in good agreement, and this proves the correctness of the numerical method proposed above.

Considering the data of [16] and [18], the variation range of amplitude ratio of multi-harmonic components in Eq. (4) is selected as follows:

$$0.001<{A}_{i},{B}_{i}<0.4, \left(i=\mathrm{1,2},\cdots ,5\right)$$

In general, the frequencies of spindle speed variation are limited within a certain range by servo controller for spindle speed.

In this paper, considering the data of [17] and [18], the range of angular frequencies of modulating signal is taken as:

$$0<{\omega }_{s}\le 20\pi \text{rad/s}$$

For a fixed value of \({\omega }_{s}\) in this range, we determine the optimal amplitude ratio using FA by increasing the number of harmonics from \(1\) to 5.

After substituting the optimal amplitudes obtained for \(\mathrm{differnt }{\omega }_{s} \mathrm{and}\) \(n\), into Eq. (14), we calculated the time response of tool, by solving Eq. (11) with the help of DDESD in MATLAB.

Numerical calculation shows that different values of \({\omega }_{s}\) can yield different optimal amplitude ratios and suppressing time.

Some of example results of time response simulations when \({\omega }_{s}=2\pi \mathrm{ rad}/\mathrm{s}\) and \({\omega }_{s}=20\pi \mathrm{ rad}/\mathrm{s}\), \(n=1\),\(n=5\) are shown in Fig. 11.

Fig. 11
figure 11

Results of response

Full size image

It can be seen from Fig. 11a that in case that \(n=1\),\({\omega }_{s}=2\pi \mathrm{ rad}/\mathrm{s}\), \({A}_{1}=0.26\), \({B}_{1}=-0.14\), the amplitude decreases and oscillates with a large value. After that it becomes small and it is fully suppressed after \(0.3\mathrm{ s}\).

But in case that \(n=5\), \({\omega }_{s}=2\pi \mathrm{rad}/\mathrm{s}\), \({A}_{1}=0.25\),\({A}_{2}=0.11\),\({A}_{3}=0.40\),\({A}_{4}=0.25\), \({A}_{5}=0.003,\) \({B}_{1}=0.16\), \({B}_{2}=0.0025\), \({B}_{3}=0.013\), \({B}_{4}=0.006\), and \({B}_{5}=0.001\), the amplitude oscillates with a small value and decreases and it is fully suppressed after \(0.4\mathrm{ s}\) (Fig. 11b).

In case that \(n=1\), \({\omega }_{s}=20\pi \mathrm{rad}/\mathrm{s}\), \({A}_{1}=0.248\), and \({B}_{1}=-0.18\), the amplitude decreases without a oscillation and it is fully suppressed after \(0.2\mathrm{ s}\) (Fig. 11c).

In case that \(n=5\), \({\omega }_{s}=20\pi \mathrm{rad}/\mathrm{s}\), \({A}_{1}=0.241\),\({A}_{2}=0.071\),\({A}_{3}=0.352\),\({A}_{4}=0.0093\), \({A}_{5}=0.0032,\) \({B}_{1}=0.123\), \({B}_{2}=0.0017\), \({B}_{3}=0.015\), \({B}_{4}=0.0043\), and \({B}_{5}=0.00097\), the amplitude decreases linearly and after \(0.1\mathrm{ s}\) it becomes small suddenly and is fully suppressed (Fig. 11d).

It can be known that the higher the fundamental angular frequencies,\(\omega\), of modulating signal, the quicker the chatter is suppressed.

Now, we compare the effects of SSV-based suppressing of chatter, using the multi-harmonic series and some simple forms proposed in previous works.

In case of \({\omega }_{s}=2\pi \mathrm{rad}/\mathrm{s}\), we use triangular and sawtooth wave in return for multi-harmonic series in Eq. (4).

Fourier expansions of triangular and sawtooth wave that has a periodicity in [\(-\pi , \pi\)] are expressed as follows:

$$\left\{\begin{array}{c}F=\frac{\pi }{2}-\frac{4}{\pi }\sum_{k=1}^{\infty }\frac{\mathrm{cos}\frac{\left(2k-1\right)\pi x}{\pi }}{{\left(2k-1\right)}^{2}}\\ F=\frac{1}{2}-\frac{1}{2\pi }\sum_{k=1}^{\infty }\frac{\mathrm{sin}2k\pi x}{k}\\ \end{array}\right.$$

Substituting these equations into right hand in Eq. (4) and solving Eq. (1), the amplitude of the tool is represented as in Fig. 12.

Fig. 12
figure 12

Time response of system for various SSV forms

Full size image

Using multi-harmonic series having \(n=5\), \({\omega }_{s}=2\pi \mathrm{rad}/\mathrm{s}\), the amplitude oscillates a little, but it is fully suppressed after \(0.4\mathrm{ s}\) (Fig. 11b).

But in the case of triangular and sawtooth wave, the suppressing speed of the amplitude is slower than in the case of multi-harmonic series (Fig. 12a, b).

All these evidences show that the type of multi-harmonic series proposed in this paper is most effective for chatter suppression.

To summarize, in order to effectively suppress the chatter in the shortest time by changing the spindle speed periodically in turning, the fundamental frequency of a modulating signal, \({\omega }_{s}\), should be taken higher and the number and/or amplitudes of modulating components should be determined depending on it.

The method proposed here is verified on a numerical example, and we will test it in actual turning if a servocontroller that can vary the spindle speed as any complex periodical signal shall be developed in future.

8 Conclusion

In order to determine the rational type of spindle speed variation signal that can suppress chatter in turning effectively, whose system can be described with a SDOF equation of motion, we, expressing it in multi-harmonic series, proposed a method to optimally determine the number, the amplitude ratio, and the angular frequencies of harmonics and obtained some results through a number of numerical calculations.

Firstly, we selected the number of harmonics and the amplitude of multi-harmonic modulating signal of spindle as optimal design variables and the thermal overload condition of spindle drive as constraint function, and thus set up an optimization problem such that dynamical cutting force becomes minimal.

As the objective and constraint functions are expressed in transcendental function of design variables, this optimization comes to be a non-linear problem with multiple extrema, which was solved using FA.

Also, a convergence index equal to Eq. (21) is introduced, the use of which makes it possible to quantitatively evaluate the extremum search performance of FA.

This paper also showed that if the walk of movement of firefly, \(\alpha\), is changed in the way of non-linear cosine function of iteration number, the global search performance of FA can be improved greatly.

According to the result, it is generally reasonable to select a higher value of the fundamental angular frequency of a signal of spindle speed variation in order to suppress the chatter more rapidly.

In case that \({\omega }_{s}\) is low, the higher the value of n, the more rapidly the amplitude reduces, but in case that \({\omega }_{s}\) is high, the decrease of amplitude dose not greatly depend on the value of n.