1 Introduction

As aerospace exploration deepens, the performances of the aircraft are needed to be improved. A large number of aerospace structural parts, which were previously made as assemblies, are gradually being improved into monolithic thin-walled workpieces [1,2,3,4]. Monolithic workpieces have lower height, higher assembly quality, and higher structural efficiency. However, these workpieces are large in size, complex in structure, and often thin-walled. More than 90% of the material would be removed from the blank in the machining process, which results in their lower rigidity and larger machining deformation (MD) [5].

It is essential to understand the main causes of MD induced throughout the manufacturing process with the involvement of the cutting process system [6]. That is, all elements of the cutting process system are the incentives of MD, involving at least machine tools, workpieces, auxiliary devices, process parameters, environmental conditions and so on [7]. Shi et al. [8] investigated that the machining error induced by the thermal effect of machine tools was reduced more than 52% via an optimizing strategy with real-time error compensation. More importantly, the material [9], size [10], and shape [11] of workpieces all affect the degree and distribution of MD. Gao et al. [12] believed that the optimization of process parameters significantly reduced the MD but also induced higher roughness and lower surface compressive residual stress (CRS). Moreover, Gonzalo et al. [13] proposed a floating clamping mode to compensate for the low stiffness of the thin-walled workpiece, which corrected the geometric distortion. Generally, MD is a complex coupled effect of the cutting process system, and the finite element simulation also provides an economical and effective method for the MD prediction and control [4].

It is clear that the most important factor of MD is residual stress (RS), including initial residual stress (IRS) and machining-induced residual stress (MIRS) [14, 15]. After machining, the coupled effects of IRS redistribution and MIRS on the surface contribute jointly to the MD of the thin-walled workpiece [16]. Li et al. [17] investigated that when both IRS and MIRS were considered, the prediction accuracy of MD using the finite element simulation would be better. But, for aluminum alloys, the MIRS does not affect the depth beyond 500 μm [18], or even only 8 μm [19]. Moreover, optimized reasonable machining parameters significantly reduced the MD induced by MIRS [20]. Li et al. [21] believed that MIRS, clamping stress, and even thermal stress could be ignored in the MD analysis. Furthermore, Huang et al. [22] determined that IRS in the 7075 alloy blank induced 90% of the total MD, while machining-induced MD was only 10%.

The rolled ring is the most typical monolithic thin-walled workpiece in aerospace, and its IRS and MD are of more general interest [23,24,25]. The amplitude and distribution of IRS are directly affects the MD degree and law [26]. Rings manufactured by the ring rolling process, such as transition-rings of rocket tanks, aero-engine casings, and connecting flanges, have wide applications in aerospace fields [23]. These factors, including rolling stress, rolling rate, process temperature, and plastic deformation, make the metal flow unevenly during the ring rolling process and eventually lead to the inhomogeneous and large-amplitude IRS [26,27,28,29]. Lv et al. [30] proposed that this optimization method, which combines the response surface method and the finite element method, was suitable for selecting the rolling parameters to control the IRS, reducing by at least 25.2%. Then, Ma et al. [31] found that IRS values up to + 265 MPa for 2219 alloy rolled ring with an inhomogeneous IRS distribution, although the IRS would be partially relieved after the post-treatment process [23]. Additionally, the generation and release of IRS heavily affected the MD of rings [32, 33]. More notably, Wang et al. [34] concluded that the IRS distributed in the rolled ring was the dominant factor affecting the MD during the early stages of the turning process, and even accounted for about 90% of the total MD.

The annular end surfaces of the rings are usually the important assembly surfaces, so the radial dimensions must be machined with high accuracy. Circularity or ellipticity of rings has become a major concern for MD, and numerous studies have been reported on the causes of MD. However, the thermoplastic deformation coupled to thermomechanical behavior will easily induce inhomogeneous IRS during the ring rolling process. This IRS cannot be completely relieved and even becomes the dominant factor in the MD for thin-walled and weakly rigid rings. Thus, it is fundamental to study IRS distributions and MD laws for rolled rings. This paper, a new theoretical analytical model, is established to qualitatively analyze the MD induced by the IRS for rings; continuous simulations combined the ring rolling; and turning processes are performed to analyze the IRS distribution and the MD law; the MD and IRS results are verified by the RS measurements and turning machining experiments and eventually the MD evolution process and the final MD state of the thin-walled rolled ring are discussed in detail.

2 Equivalent analytical model

RS is self-equilibrated internal stress remaining in workpieces after almost all manufacturing process. When ring workpiece is machined, RS within the material is also relieved, which breaks the equilibrium state of IRS. So workpiece distorts in an attempt to re-establish the equilibrium of IRS. For 2219 aluminum alloy ring, the IRS, induced by ring rolling, heat treatment, and bulging process, meets the self-equilibrated state that the vector sums of equivalent resultant forces and equivalent resultant moments are zero on all cross-sections.

$$\int_S\;\sigma\left(x,y,z\right)dS=0,$$
(1)
$$\int_S\;\sigma\left(x,y,z\right)d\;dS=0,$$
(2)

where \(S\) is the area of cross-section, \(\sigma (x,y,z)\) is the IRS at coordinate position and \(d\) is the distance from the equivalent force to the rotation axis or fulcrum.

In the simplified model of ring (Fig. 1a), the radius of the outside circle is \({R}_{o}\), the radius of the inner circle is \({R}_{i}\), the axial length is \(L\), and the unilateral thickness of the ring is \(H={R}_{o}-{R}_{i}\). The radial stress is \({\sigma }_{r}\), the tangential stress is \({\sigma }_{t}\), and the axial stress is \({\sigma }_{a}\). In cutting area, the radial cutting thickness is \(h\), the axial cutting thickness is \(t\), and the tangential angle is \(\theta\). After cutting, the outer circle radius becomes \(R\), and the axial length becomes \(l\).

Fig. 1
figure 1

Theoretical analysis model: a simplified model of ring; b regular hexagon equivalent model

Full size image

When MIRS is ignored, IRS is released along with the machining process. It is assumed that the additional equivalent stress that is equal in magnitude but opposite in direction with RS is applied on the cutting area. This means that equivalent stress is equal in magnitude but opposite in direction. After cutting with a cutting thickness of \(h\), the axial equivalent force on the ring cutting cross-section is:

$${F}_{a}=\int -{\sigma }_{ai}{dS}_{ai}={\sigma }_{a}{S}_{a}=2\pi Rh{\sigma }_{a},$$
(3)

where \({\sigma }_{ai}\) and \({S}_{ai}\) are respectively the RS and the corresponding area on the arbitrary cutting cross-section, and \({\sigma }_{a}\) and \({S}_{a}\) are respectively the equivalent axial stress and the corresponding effect area. The equivalent force \({F}_{a}\) acts on the ring cutting cross-section, and its direction is consistent to \({\sigma }_{a}\).

According to mechanics of materials, the axial deformation \(\Delta l\) and the tangential deformation \(\Delta\) caused by the RS release at a tiny area are:

$$\Delta l=l\varepsilon =l\frac{\sigma }{E}=l\frac{{\sigma }_{a}}{E},$$
(4)
$$\Delta =-\mu \Delta l,$$
(5)

where \(\varepsilon\) is the strain in axial direction, \(E\) is Young’s modulus of material, and \(\mu\) is Poisson’s ratio.

The tangential RS is studied by simplifying the ring into the inscribed regular polygon with reference to its outer circle. If the edges number of the inscribed polygon is more, the simplified model will be more realistic, but also more complex. This paper sets it as an inscribed regular hexagon, and each side is numbered \(a\sim f\), as shown in Fig. 1b. The cutting process of link \(a\) can be regarded as the loading of equivalent stress \({\sigma }_{t}\). The equivalent force produced by the equivalent stress is:

$$F_{a1}=A\sigma_t=\int_S\;{-\sigma}_{ti}\left(x,y,z\right)dS,$$
(6)

where \({F}_{a1}\) is equivalent force acting on link \(a\), \(A\) is the cross-sectional area of the equivalent link, \({\sigma }_{t}\) is the equivalent tangential stress value, \(S\) is the area under tangential RS, and \({\sigma }_{ti}(x,y,z)\) having a functional relationship to the coordinate position is the tangential RS of the simplified ring.

It is assumed that the RS of the removed material is expressed as compressive stress, then, link \(a\) is subjected to the equivalent tensile force \({F}_{a1}\) and \({F}_{a2}\). At the junction with link \(a\), link \(b\) is subjected to the reaction force \({F}_{b1}\) of \({F}_{a1}\), and it is subjected to \({F}_{b2}\) at the connection with link \(c\) to maintain static balance. Thereby, the force condition of each link can be obtained, as shown in Fig. 1b. Link \(a\) and link \(d\) are respectively subjected to tension and pressure along the direction of link, and the other links are respectively subjected to the moment \(M\), which is:

$$M=A{\sigma }_{t}\times Rsin\alpha ,$$
(7)

where \(R\) is the radius of the outer circle after turning and \(\alpha\) is the acute angle between hypotenuse of regular hexagon and \(x\) coordinate axis.

To obtain the radial RS, it is assumed that the cutting process is the whole layer cutting of the ring segment with width \(t\) and thickness \(h\), so the equivalent stress is applied on the small cylindrical cutting surface to replace the release of initial radial RS. If the RS is a uniformly distributed compressive stress, then there are equivalent stress \({\sigma }_{r1}={\sigma }_{r2}=\cdot \cdot \cdot ={\sigma }_{rn}\), which are radially outward, as showing in Fig. 1a. Within a tiny range of \(d\theta\), the equivalent force is:

$$d{F}_{ri}={\sigma }_{i1}tRd\theta .$$
(8)

In the range of \(d\theta\), along the axial direction, the slice of the ring is equivalent to a cantilever beam which has a concentrated load \(d{F}_{ri}\) on the free end. As shown in Fig. 1, in the coordinate system, the moment of each cross-section is:

$$M\left(z\right)=\left[L-L(z)\right]\times d{F}_{ri}.$$
(9)

Then, the stress generated by the equivalent force \(d{F}_{ri}\) is:

$$\upsigma \left(x,y,z\right)=\frac{M(z)}{{I}_{Rx}-{I}_{{R}_{i}x}}y,$$
(10)

where \({I}_{Rx}-{I}_{{R}_{i}x}\) is the moment of inertia of sectoral ring cross-section and \({I}_{Rx}\) and \({I}_{{R}_{i}x}\) are respectively the moment of inertia of radius \(R\) sector and radius \({R}_{i}\) sector.

The moment of inertia of sector is:

$$I_x=\int_Ay^2dA=\int_0^{R\cos\frac\theta2}y^2\times2y\;\tan\frac\theta2dy+\int_{R\cos\frac\theta2}^Ry^2\times2\sqrt{R^2-y^2}dy.$$
(11)

Due to the release of the radial RS, the stress becomes:

$${\upsigma }_{i}^{^{\prime}}\left(x,y,z\right)={\sigma }_{i}\left(x,y,z\right)+\frac{M(z)}{{I}_{x}}y.$$
(12)

The radial deformation is:

$$\Delta R\left(z\right)=\frac{FL{z}^{2}}{2EI}-\frac{F{z}^{3}}{6EI}.$$
(13)

However, in the actual turning process, the equivalent stresses \({\sigma }_{r1},{\sigma }_{r2},\cdot \cdot \cdot ,{\sigma }_{rn}\) appear in sequence, and the value is fluctuating. Uneven stress distribution causes the uneven deformation of the ring part, showing an approximate circular cross-section.

Through the above analysis, the axial IRS of the ring mainly causes the change of the axial dimension during the turning process, while the tangential and radial IRS mainly cause the change of the cross-section, which is a more serious deformation problem in terms of the final machining quality of the ring. With the release of the tangential and radial IRS, the cross-sectional dimension increases, and the shape is elliptic or irregular circular.

3 Experiment and simulation

3.1 Experiment material

Aluminum alloys have a wide range of application prospects and an irreplaceable status due to their lightweight, high specific stiffness/strength, and excellent formability. 2219 aluminum alloy is widely used in the aerospace industry, such as the structural rings for rocket launcher tanks. The chemical composition of 2219 aluminum alloy is shown in Table 1. The physical properties of 2219 aluminum alloy are shown in Table 2. The material properties of 2219 aluminum alloy at different temperatures are shown in Table 3.

Table 1 Chemical composition of 2219 aluminum alloy (wt. %)
Full size table
Table 2 Physical properties of 2219 aluminum alloy
Full size table
Table 3 Material properties of 2219 aluminum alloy at different temperatures
Full size table

3.2 IRS and MD measurement experiment

3.2.1 IRS measurement of rolled ring

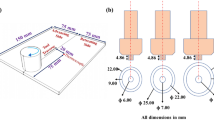
The experiment ring is rolled by a self-made ring rolling mill, and the process parameters are shown in Table 4. The IRS of the rolled ring is measured using a Prism Electronic Speckle Interference Borehole RS Gauge manufactured by Stresstech Group in Finland, as shown in Fig. 2b. The measurement parameters of the Prism system are shown in Table 5.

Table 4 Parameters of the ring rolling process [23]
Full size table
Fig. 2
figure 2

IRS measurement experiment: a rolled ring and test points; b IRS measurement

Full size image
Table 5 Measurement parameters of Prism system
Full size table

Two sets of test points are set along the axial direction, and each group is uniformly distributed with four test points in the circumferential direction, as shown in Fig. 2a. IRS measurement experiments with a depth of 2 mm are performed sequentially at selected test points, and date at 0.2-mm and 2-mm depths are discarded. Therefore, IRS in the X and Y directions are measured at 10 different depths of each point (X direction is the circumferential direction, Y direction is the axial direction, and Z direction is the radial direction).

3.2.2 MD measurement of rolled ring

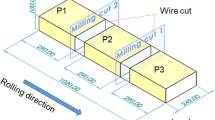
Turning experiment is performed to investigate the MD of the rolled ring. The MAZAK-860 lathe from Jinan No. 1 Machine Tool Plant is used for the turning experiment, and the process parameters are given in Table 6. MD is characterized by a change in the inner diameter of the ring, which is measured by a measuring probe of the numerical control machining center with an accuracy of 0.0001.

Table 6 Turning experiment parameters
Full size table

Firstly, the rolled ring is directly clamped by a three-jaw chuck, as shown in Fig. 3a. It is important to note that the correction of the inner and outer circles is performed using the dial test indicator before the turning experiment, as shown in Fig. 3b. Then, the inner and outer ring walls of the ring are turned smooth. The MD measurement of the ring is shown in Fig. 3c. Along the circumferential direction, the inner diameter is measured every 45 degrees so that the initial ellipticity of the inner circle is measured to be 0.0101 mm. Repeating this experiment procedure, the ring is turned with a thickness of 0.5 mm, the diameter of the inner circle is measured once, and the ring is loaded and corrected again.

Fig. 3
figure 3

Turning and MD measurement experiment: a turning experiment; b alignment of outer and inner circle; c inner diameter measurement experiment; d change of clamping position, “1 to 1” initial position and “1 to 3” changed position

Full size image

In addition, this type of repeated clamping-measurement method induces little effect on the thin-walled ring. As shown in Fig. 3d, the clamping position of the ring changes from “1 to 1” to “1 to 3” during two adjacent turning operations. According to the MD measurements, the positions of the maximum and minimum inner diameters are unchanged. Clamping force has little effect on MD. Furthermore, the clamping and measurement positions are respectively located on opposite sides of the ring, at relatively long distances from each other. As a result, by Saint–Venant’s principle, the clamping force has little influence on the measurement point.

The effects of other factors are of interest during the turning experiment, including the clamping force, the cutting heat, and the cutting force. To reduce the effect of the clamping force, a rib of width 2 mm is left on the clamping side to increase the rigidity. To reduce the effect of cutting heat, lower feed velocity and spindle speed are applied [15], and coolant is used. To reduce the effects of cutting force, the final turning ring has a sufficient thickness. Therefore, the influence of other factors on MD is controlled, while IRS is mainly considered.

3.3 IRS and MD simulation

3.3.1 IRS simulation

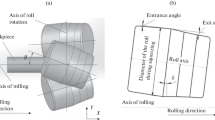
The production and evolution of RS is investigated by using the SIMUFACT 13.2 software to simulate the ring rolling process and the heat treatment process of 2219 aluminum alloy ring. A finite element model of the ring rolling process is established as shown in Fig. 4a, which includes the main roll, the mandrel, the workpiece, two axial rolls, and two guide rolls [23]. The mandrel pushes the ring towards the main roll, which is driven by an angular velocity. The friction between the ring and the main roll and between the ring and the mandrel results in a rotation of the ring and the mandrel. By decreasing the radial rolling gap, the ring grows in both tangential and axial directions. In the opposing axial rolling gap, the ring height is controlled and reduced by the axial lower roll and the axial upper roll. The degree of circularity of the ring is controlled by the left centering roll and the right centering roll.

Fig. 4
figure 4

Simulation model of the ring rolling process: a rolling process model; b IRS distribution

Full size image

The parameters of the ring rolling process and the heat treatment process are shown in Table 4. The material model of ring is set to be the elasto-plastic behavior, while all rolls are set to be rigid. The high-temperature mechanical properties of 2219 aluminum alloy are shown in Table 3. The friction between the ring and the rolls is Coulomb friction with a friction coefficient of 0.6. The mesh of the ring model is a tetrahedron with 10/4 nodes and the element type is tetrahedral 157. The minimum element length is set to 0.8 mm and the meshing mode is set to adaptive division. The heat treatment process is performed based on the stress result model of the rolled ring, thereby obtaining the IRS distribution state of the final ring, as shown in Fig. 4b.

After post-processing, the average IRS values in the X and Y directions are measured along the radial depth from 0.2 to 1.8 mm, which are used to verify the accuracy of the ring rolling simulation model. The RS values of 10 points in each layer are measured along the radial depth in the X, Y, and Z directions to describe the IRS filed of the rolled ring.

3.3.2 MD simulation

IRS that cannot be fully released is the main cause of MD and even account for 90% of the total MD [15, 22]. In this study, the MD is simulated in a layer-by-layer method after setting the IRS of the ring, while the MIRS and other factors are ignored. The method of birth and death element in ANSYS 18.0 software is applied to simulate the turning process, which not only ensures the accuracy but also improves the efficiency.

In ANSYS, the first step is to establish the rolled ring with IRS, where the loading IRS method of dividing layer-area is used. The details of the IRS loading are as follows: firstly, the three-dimensional model of the ring is divided into 9 layers along the radial direction, while the IRS is also divided into 9 layers according to “force equilibrium and moment equilibrium” conditions. Secondly, different layers of the ring model in ANSYS, defined as the unit sets separately, are loaded with the corresponding IRS which is obtained in SIMUFACT. Finally, the rolled ring model with IRS filed is established in ANSYS. The geometrical dimension of ring is set to Φ108 × Φ90 × 60 mm, and the wall thickness is 9 mm. The solid 168 element is adopted, and the rolled ring model is meshed with hexahedral element. A meshed finite element model with IRS is shown in Fig. 5a. This research adopts the method that the layer with a thickness of 1 mm is integrally removed instead of gradually turning. This death elements method can directly study MD of ring caused by IRS, as shown in Fig. 5b. The diameter and ellipticity of inner circle are measured after each “death elements.”

Fig. 5
figure 5

ANSYS finite element model of cutting process: a ring with IRS in each layer; b MD of ring after different cutting thickness

Full size image

4 Results and discussions

4.1 IRS distribution of rolled ring

The overall IRS distribution of the rolled ring is obtained from the simulation of the ring rolling process. The positive stress represents tensile residual stress (TRS), and the negative stress represents CRS. As shown in Fig. 6a, the IRS of the rolled ring is CRS in the range of 0.2 ~ 1.8 mm. The measured thickness increases, while the CRS first increases and then decreases. At a radial thickness of 0.60 mm, the IRS reaches its maximum in the X and Y directions at − 46.80 MPa and − 51.40 MPa, respectively. The measured IRS has a tendency to change from CRS to TRS in the radial direction from the outer surface inward. As shown in Fig. 6b, the IRS fields of the ring is distributed symmetrically, with good agreement in the X, Y, and Z directions. The stress changes from CRS to TRS and then turns to CRS. At a radial thickness of 5 mm, the RS in the X, Y, and Z directions reach the maximum TRS, respectively 44.80 MPa, 41.50 MPa, and 44.60 MPa.

Fig. 6
figure 6

IRS values of ring simulation model: a IRS values with 0.2–1.8-mm thickness; b IRS distribution of rolled ring

Full size image

The IRS values of the simulation results are compared with the experiment results, as shown in Fig. 7a. The maximum CRS values of the experiment results in the X and Y directions are − 79.20 MPa and − 74.00 MPa, respectively, which are larger than the simulation results. But, the trends and values of the IRS variability are consistent along the radial depth. The average IRS experiment values at thickness of 0 ~ 1 mm and 1 ~ 2 mm are compared with the corresponding simulation values, as showing in Fig. 7b. In the first layer, the relative error of the simulation results is 25.59% along the X direction compared to the experiment results, while the relative error along the Y direction is only 17.23%. In the second layer, the relative error of the simulation stress is 40.51% along the X direction, which is affected by the smaller IRS value and the density of the simulation grid. By analyzing the simulation and experiment results, the trends and values of the IRS variability along the radial depth direction are consistent, so the simulation model of the ring rolling process is accurate in terms of IRS prediction.

Fig. 7
figure 7

Simulation and experiment results of IRS distribution: a IRS on different measurement thickness; b IRS on different layer

Full size image

The inhomogeneous IRS is balanced in the rolled ring under the influence of the rolling stress, the process temperature, and the phase transition. Lv et al. [30] and Ma et al. [31] theoretically analyzed the stress evolution and the formation of RS for the ring rolling process. In detail, the IRS of the rolled ring is greater than 120 MPa [23, 31]. In order to improve the mechanical properties of 2219 aluminum alloy by solid solution and precipitation strengthening, heat treatment (quenching + thermal stress relief) is performed on the rolled ring. Due to the rapid cooling of quenching, the large granular solid solutions generate, and large RS is induced and even more than 200 MPa [25]. Then, Song et al. [35] concluded that the precipitation phase of 2219 aluminum alloy was dispersed, and dislocations were stabilized, so IRS was also released under the action of thermal stress relief. In the studies of [23] and [35], the amplitude of IRS remains around 50 MPa after the heat treatment of the rolled ring. Additionally, the novel thermal vibration stress relief process and the mechanical expansion process also achieve the similar effect of IRS homogenization. Meanwhile, the IRS distribution shows a change state of first decreasing and then increasing along the radial thickness, which is consistent with [24, 31], and [35]. This type IRS distribution is induced by both roll extrusion and temperature cooling, and it is inevitable.

4.2 MD of rolled ring

The influence of IRS on MD is analyzed by simulations and experiments. Four sets of diameter data for the ring can be obtained for each inner diameter measurement, and the variation of the inner circle diameter of the ring with cutting thickness is shown in Fig. 8a. The maximum and minimum diameter positions of the rolled ring are substantially constant and perpendicular to each other, showing an approximate ellipse. The increment of diameter \({d}_{1}\) is the largest, varying from 89.9985 to 90.4001 mm. The diameter \({d}_{3}\) first increases and then decreases, eventually reaching 89.9329 mm. The changes in diameter \({d}_{2}\) and diameter \({d}_{4}\) are consistent with smaller fluctuations. As shown in Fig. 8b, the final average diameter is up to 90.0945 mm with an ellipticity of 0.4672 mm. The average diameter gradually increases with the total cutting thickness, and the increase rate is rapid in the early stage and then slows as the IRS is gradually released. The total increase of average diameter is 0.1076 mm, from 89.9869 mm to 90.0945 mm. The ellipticity of the inner circle gradually increases, from 0.0202 to 0.4672 mm, indicating that the turning process breaks the equilibrium of the IRS and induces MD.

Fig. 8
figure 8

Deformation of turning experiment: a fluctuation of inner diameter values; b fluctuation of ellipticity and average inner diameter values

Full size image

Although the IRS is well controlled, MD is induced and specifically appears as a fluctuation of diameter \({d}_{1}\sim {d}_{4}\), as shown in Fig. 8a. It is worth noting that after the total cutting thickness reaches 4.5 mm, both the largest diameter \({d}_{1}\) and the smallest diameter \({d}_{3}\) show more significant fluctuations, which appear to increase or decrease rapidly. This MD phenomenon is consistent with [34] and is directly related to the continuous release of IRS in ring. More deeply, the IRS relief in the previous turning stage has caused the deformation tendency of the elliptical cross-section, so ring is more likely to cause MD in the next turning stage. Furthermore, thinner-walled workpieces are easier to MD under the same stress conditions due to the stiffness characteristics [9, 11]. This means that the IRS induces MD throughout the turning process, while the weaker stiffness characteristic of thin-walled ring further magnifies the elliptical deformation behavior, as shown in Fig. 8b.

Comparing the simulation results with the experiment results, \(K\) and \(Correction value\) are introduced to explain the linear proportional relationship of simulation and experiment. As shown in Fig. 9, the greater total turning thickness, the more serious MD. In Fig. 9a, the average inner diameter values of final simulation results and experiment results have similarities in the trend, and the simulation values of inner diameter are larger than the experiment values. But, the maximum \({K}_{1}\) value is only 1.0024, and the average value is 1.0013. The relative error of final simulation value is 23.92%, and the final correction value of average inner diameter is 90.1909 mm. In Fig. 9b, the ellipticity of the inner circle gradually increases as the total cutting thickness in the simulation and experiment results. The maximum \({K}_{2}\) value of ellipticity is only 1.1130, and the average value is 1.2290. The relative error of final simulation value is 11.30%, and the final correction value of ellipticity value is 0.4269 mm.

Fig. 9
figure 9

MD comparison of experiment and simulation: a fluctuation of inner diameter; b fluctuation of ellipticity

Full size image
$$\begin{array}{c}K=\frac{Simulation\;value}{Experiment\;value},\\Correction\;value=\frac{Simulaiton\;value}{Average\;value\;of\;K}.\end{array}$$

The birth and death element method is an ideal state to simulate the turning process, which does not take into account the effect of MIRS on MD. But, the average inner diameter value and the ellipticity value of simulation and experiment results are in good agreement, and the values of \({K}_{1}\) and \({K}_{2}\) are very close to 1. In more detail, the relative error values of the final results are 23.92% and 11.30%, respectively. By using the similar finite element method, the MD results of [9] show that the relative errors is greater than 25% for aluminum alloy thin-walled frame workpieces. Huang et al. [22] concluded that when only the IRS is considered, the relative error of MD is 19.7% compared to the experimental result, but the coupling IRS and MIRS leads to larger error. Li et al. [17] also demonstrate that as material is removed, the contribution of IRS to MD remains approximately 85%. In comparison, the simulation method and simulation results for the rolled ring in this study are feasible and effective. The relative error of MD may be caused by turning stress [17]. But, the conclusion is that IRS induces an elliptical cross-section of the rolled ring.

Combined with the equivalent analytical model, the MD mechanism of the rolled ring during turning process is analyzed. As the material is removed, the inhomogeneous IRS is released and the stiffness is decreased, which induces the elliptical cross-section MD of the rolled ring. When the ring is turned, the axial IRS changes the ring height and seriously deteriorates the flatness error of the end face beyond tolerance. The tangential IRS causes torsional deformation in the form of a moment. Radial IRS changes the diameter, which directly affects both the dimension error and the circularity error. Therefore, the coupling results for the MD in the three directions are more complicated due to the uneven IRS. Overall the fluctuations in the inner diameter values are dominated by the radial IRS. The uneven distribution of IRS causes the different MD at different positions, as shown in Fig. 8a. The coupling of the radial and tangential IRS aggravates the MD of the cross-section appearing elliptical, as shown in Fig. 8b.

5 Conclusions

  1. 1.

    A theoretical analysis model is newly proposed to qualitatively analytical the relationship between IRS and MD of the ring. The coupling effect of non-uniform radial IRS and tangential IRS is the main reason for the ellipticity variability of the ring.

  2. 2.

    An accurate elasto-plastic finite element model coupling multi-physics and multi-processing is established. For the entire rolled ring, the IRS amplitude fluctuates from − 60 MPa ~  + 50 MPa, and the average inner diameter increases from 90.04 to 90.31 mm after the turning process, reaching a maximum ellipticity of 0.52 mm.

  3. 3.

    The MD experiments are conducted to validate the simulation model. The measured IRS amplitude mainly fluctuates in the range of 40 ~ 80 MPa. With the increase of the total cutting thickness, the average diameter of the inner circle first increases rapidly and then slowly, eventually reaching 90.0945 mm, while the ellipticity continues to increase and eventually reaches 0.4672 mm. IRS induces an elliptical cross-section MD of the rolled ring during the turning process.

  4. 4.

    The finite element model accurately predicted the MD of the ring. The relative error of final average inner diameter value is 23.92%, and the relative error of final inner circle ellipticity is 11.30%.