1 Introduction

With the increasing demand for optical equipment performance, modern optical systems also put forward higher and higher requirements for the profile accuracy and surface quality of optical components. Fine polished optical mirrors often need to reach nanometer or even sub-nanometer level. If workpiece is large then processing usually takes long. Therefore, how to realize efficient and controllable processing of optical components has become an urgent problem to be solved in modern optical manufacturing.

Bonnet polishing was first proposed by London optical laboratory and Zeeko company at the end of the twentieth century [1]. In BP, the amount of removed material is a convolution of the tool influence function (TIF) and the dwell time. Hence, TIF is the basis of the dwell time algorithm, and it is also the key factor affecting the processing efficiency and convergence accuracy [2]. The removal characteristics of bonnet polishing have been studied by researchers through a large number of experiments with certain results [3]. In general situations, Preston equation can be used to describe the relationship between material removal rate and various processing parameters. The most accurate method to measure TIF is through experiments. Many researches of TIF show that it usually turns out to be M-shaped when adopting a large contact depth during polishing. But few studies of M-shaped TIF modeling have been done and nor the applying of it in the dwell time algorithm.

The removal amount of BP is a 2-dimension convolution of TIF and dwell time, so solution algorithm of dwell time is essentially a deconvolution process. When the TIF used is not Gaussian-like, there are chances that iterative impulse algorithm may not converge due to non-Gaussian-like TIF in the solution process [4]. Therefore, we adopted the non-negative least square method to calculate the dwell time when using a M-shaped TIF with large contact depth, and used the Gaussian-like TIF with small contact depth by iterative impulse method to further improve the converge accuracy of the surface in fine polishing stage.

In this paper, we not only analyzed the mechanism of M-shaped TIF with large contact depth, but also proposed a dual-Gaussian model to fit it. Then, we used the model in rough polishing stage combined with Gaussian-like TIF in fine polishing stage, to explore an efficient BP approach based on dual- mode contact depth TIF.

2 Dual-mode contact depth TIF in BP

The Preston equation is the very foundation of BP TIF model [5]:

$$\Delta Z=K\bullet P(x,y)\bullet V(x,y)\bullet \Delta t$$
(1)

where \(\Delta Z\) denotes the removed material amount (i.e., removal depth) from workpiece by polishing in a certain dwell time \(\Delta t\). \(K\) denotes the Preston coefficient. \(P\) and \(V\) denote the contacting pressure and relative velocity distribution on the contact area.

Therefore, \(P\) and \(V\) distribution models are needed for TIF model.

2.1 The velocity and pressure distribution analysis

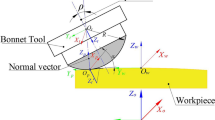
According to the precession polishing characteristics of bonnet, the polishing velocity model of bonnet is established, in which \(R\) is the radius of flexible bonnet and \(\rho\) is the precession angle, \({\omega }_{H}\) is rotation angle, and \(d\) is contact depth. The coordinate system is shown in Fig. 1: \(C\) and \(O\) represent the bonnet center and the circle center of the contact area, respectively; \(P\) is an arbitrary point in the contact area; \({V}_{P}\) is the effective polishing velocity vector at point \(P\).

Fig. 1
figure 1

Bonnet polishing TIF velocity distribution

Full size image

The velocity at point \(P\):

$${V}_{P}={\omega }_{H}\left[\begin{array}{c}{l}_{1}cos{\alpha }_{i}+{l}_{2}sin{\alpha }_{i}\\ {l}_{2}cos{\alpha }_{i}-{l}_{1}sin{\alpha }_{i}\\ 0\end{array}\right]$$
(2)

In which \({l}_{1}=y\mathrm{cos}\rho\), \({l}_{2}=\left(R-d\right)\mathrm{sin}\rho -x\mathrm{cos}\rho\).

Set the initial polishing posture \({\alpha }_{1}=0\), then \({\alpha }_{i}\):

$${\alpha }_{i}=\frac{\left(i-1\right)2\pi }{N}, i=\mathrm{1,2},3,\dots N$$
(3)

The radius of contact area:

$${r}_{i}=\sqrt{2Rd-{d}^{2}}$$
(4)

According to the analysis, we can get the velocity distribution in Fig. 2:

Fig. 2
figure 2

One posture bonnet polishing TIF velocity distribution

Full size image

The parameters for calculation are shown in Table 1. As shown in Fig. 2, the velocity at an arbitrary point during non-procession TIF is proportional to the distance between the point and zero point.

Table 1 Parameters in TIF simulation
Full size table

It is generally believed that the pressure distribution conforms to the Gaussian distribution traditionally [6]:

$$p={p}_{max}{[\mathrm{exp}(-\frac{{\lambda }^{2}}{2{\sigma }^{2}})]}^{\varphi }$$
(5)

where \({p}_{max}\) is the maximum contact pressure. \(\lambda\) is the distance from an arbitrary point to the contact area center. \(\sigma\) is the standard deviation. \(\varphi\) is the correction factor.

The pressure distribution obtained according to this model [7]:

The parameters for calculation are shown in Table 1. As shown in Fig. 3, the pressure distribution is Gaussian-like. Combining the velocity distribution and pressure distribution together, the traditional non-procession TIF model is shown in Fig. 4.

Fig. 3
figure 3

Bonnet polishing TIF Gaussian-like pressure distribution

Full size image
Fig. 4
figure 4

Gaussian-like bonnet polishing TIF \(V*P\) distribution

Full size image

From the analysis above, it is concluded that the M-shaped TIF is not obtainable if based on the traditional TIF model. Since the velocity distribution is accurate and stays the same, it can be seen that the difference must be that pressure distribution is no longer Gaussian-like with large contact depth. Thus, a new BP TIF model, especially the pressure distribution model part with large contact depth, is needed.

2.2 Mechanical model of M-shaped TIF

The M-shaped TIF has been proved by many researches; however, studies on M-shaped TIF model are few. With the increase of contact depth, the Gaussian-like TIF turns into M-shaped TIF. Thus, a new TIF model is needed.

The pressure distribution is considered to be superimposed by two main parts:

$$P={P}_{rub}+{P}_{air}$$
(6)

where \(P\) is the total pressure. \({P}_{rub}\) is the pressure caused by rubber bonnet’s elastic deformation. \({P}_{air}\) is the constant pressure from inner air.

The bonnet polishing mechanical model is shown as Fig. 5:

Fig. 5
figure 5

Bonnet polishing mechanical model

Full size image

The strain of bonnet polishing tool head is:

$$\varepsilon =E-e$$
(7)

where \(\varepsilon\) is the actual strain of bonnet. \(E(d)\) is the total strain of the bonnet (\(E(d)\) increases with \(d\)). \(e\) is the virtual strain of the bonnet. \(d\) is contact depth.

According to the compressive force-strain curve of an elastic hollow ball compression [8], there is an inflection point during elastic deformation stage which divides small contact depth part from large contact depth part.

On the left side of the inflection point, the bonnet polishing TIF presents a Gaussian pressure distribution, the same as shown in Fig. 3. On the right side of the inflection point, the bonnet polishing TIF starts to present an M-shaped pressure distribution, as shown in Fig. 6. The \(V*P\) distribution of TIF is shown in Fig. 7. The parameters for calculation are shown in Table 1.

Fig. 6
figure 6

M-shaped pressure distribution

Full size image
Fig. 7
figure 7

M-shaped Bonnet polishing TIF \(V*P\) distribution

Full size image

Therefore, the new TIF fitting model is:

$$\mathrm{f}\left(\mathrm{x}\right)=\left\{\begin{array}{c}{A}_{1}{e}^{-\left(\frac{{\left(x-\mu \right)}^{2}}{2{{\sigma }_{1}}^{2}}\right)}, d<{d}_{{\varepsilon }_{0}}\\ {A}_{2}{e}^{-\left(\frac{{\left(x-{\mu }_{1}\right)}^{2}}{2{{\sigma }_{2}}^{2}}\right)}+{A}_{2}{e}^{-\left(\frac{{\left(x+{\mu }_{2}\right)}^{2}}{2{{\sigma }_{2}}^{2}}\right)}, d\ge {d}_{{\varepsilon }_{0}}\end{array}\right.$$
(8)

where \(d\) is the contact depth. \({d}_{{\varepsilon }_{0}}\) is the inflection point of contact depth.

Clearly, the M-shaped pressure distribution leads to a M-shaped TIF. The new model explains the mechanism of M-shaped TIF with large contact depth and agrees with the TIF experimental results. In M-shaped TIF modeling part, the new model agrees with the following experimental results better.

2.3 TIF with small contact depth analysis

The BP system is shown in Fig. 8, including a six-joint robot (ABB-IRB6620) with a position repeatability of the robot less than 0.05 mm, BP tool head device, and a 3-axis force sensor. Diamond powder (size 1.5 μm) polishing slurry is selected to guarantee purely mechanical removal. The workpiece (SiC) is installed on an adjustment platform equipped with a 3-axis force sensor to monitor the polishing force. Through the adjustment of leveling nuts on the bottom fixture, the workpiece surface is kept parallel to the coordinate plane of robot (XYZ). To suppress the edge effect, the top fixture is kept at the same height as the workpiece by adjusting leveling nuts. The TIF and workpiece surface profiles followed are measured by the white-light interferometer (Zygo, NX2).

Fig. 8
figure 8

Bonnet polishing system

Full size image

With 0.15 mm contact depth, the measured TIF is shown in Fig. 9, and the profile basically conforms to a Gaussian-like form.

Fig. 9
figure 9

Measured Gaussian-like TIF profile with 0.15 mm contact depth

Full size image

As shown in Fig. 10, the model fits the TIF well. The measured removal amount of TIF is 1.218 × 10^7 μm3 and the removal amount of fit TIF is 1.281 × 10^7 μm3. The relative error is 5.3%.

Fig. 10
figure 10

Gaussian-like TIF section lines and section profiles

Full size image

Therefore, the Gaussian-like pressure distribution is still suitable when using small contact depth TIF [9].

$$p={p}_{max}{[exp(-\frac{{\lambda }^{2}}{2{\sigma }^{2}})]}^{\varphi }$$
(9)

The TIF is still Gaussian-like:

$$y=A{e}^{-\left(\frac{{\left(x-\mu \right)}^{2}}{2{\sigma }^{2}}\right)}$$
(10)

Comparing the profile of measured TIF with the one from new model in Fig. 10, the new model can be used to calculate Gaussian-like TIF with small contact depth as expected.

2.4 TIF with large contact depth analysis

With 0.50 mm contact depth, the measured TIF is shown in Fig. 11, and apparently it is M-shaped in section.

Fig. 11
figure 11

Measured M-shaped TIF profile with 0.50 mm contact depth

Full size image

With large contact depth, the cross-section of the TIF presents a clear M-shape. Therefore, the pressure distribution should not be Gaussian-like as analyzed above. We adopt a dual-Gaussian TIF pressure model:

$$p=A{e}^{-\left(\frac{{\left(x-{\mu }_{1}\right)}^{2}}{2{\sigma }^{2}}\right)}+A{e}^{-\left(\frac{{\left(x+{\mu }_{2}\right)}^{2}}{2{\sigma }^{2}}\right)}$$
(11)

The M-shaped pressure distribution calculated by the new model is shown in Fig. 6, and the \(V*P\) distribution is shown in Fig. 7. It is clear that the new model fits the measured M-shaped TIF profile better.

As shown in Fig. 12, the measured removal amount of TIF is 1.549 × 10^7 μm3 and the removal amount of fit TIF is 1.622 × 10^7 μm3. The relative error is 4.7%; In Fig. 13, with Gaussian-like TIF model, the removal amount of fit TIF is 1.696 × 10^7 μm3. The relative error is 9.5%.

Fig. 12
figure 12

M-shaped TIF section lines and section profiles using M-shaped TIF model

Full size image
Fig. 13
figure 13

M-shaped TIF section lines and section profiles using Gaussian-like TIF model

Full size image

Therefore, the new TIF model is both suitable in fitting M-shaped TIF’s profile and removal amount. And it is obvious that traditional Gaussian-like TIF model does not match with M-shaped TIF.

In the paper, since most material removal is expected to be achieved in rough polishing stage, we define the rough polishing stage as stage where at least 80% of the total material removal happens.

It can be seen that the removal amount of TIF with small contact depth is smaller than that of TIF with large contact depth, due to the small contact area caused by small contact depth. Thus, it is more effective to use TIF with large contact depth in terms of removal efficiency. Since high removal efficiency is more needed in rough polishing stage to quickly remove workpiece material as much as possible, basically we would try to adopt TIF with large contact depth in rough polishing stage.

To sum up, based on the TIF analysis above, the whole model proposed can describe both Gaussian-like TIF with small contact depth and M-shaped TIF with large contact depth, in both profile and removal amount.

3 BP approach based on dual-mode contact depth TIF

3.1 Dwell time calculation in BP

The total material removal amount of the workpiece surface is a 2-dimension spatial convolution of the removal function (i.e., TIF) and dwell time, so the BP approach is mainly about solving dwell time distribution using the TIF model proposed above.

Taking the dwell time \(D(x,y)\) of the polishing tool in any area as an independent variable when it moves on the workpiece surface, the material removal amount on the surface of the workpiece is described in the form [10]:

$$T={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }D(x,y)dxdy$$
(12)

where \(D(x,y)\) is the dwell time function. \(T\) is the total polishing time.

With the removal function moving on the surface of workpiece, if the removal amount of each point on the workpiece surface is added up, the total material removal amount of the whole surface can be calculated [11]. According to this differential idea, the removal function of the polishing tool is differentiated to \(\delta \alpha\), the dwell time function of the workpiece surface is differentiated to \(\delta \beta\), and the removal amount of the area scanned by the polishing tool is superimposed in infinite differential elements [12]:

$$\Delta h\left(x,y\right)=\underset{\alpha \to 0,\beta \to 0}{\mathrm{lim}}\sum_{\alpha }\sum_{\beta }R\left(x-\alpha ,y-\beta \right)D\left(\alpha ,\beta \right)\delta \alpha \delta \beta$$
(13)

When \(\delta \alpha ,\delta \beta \propto 0\), \(\delta \alpha ,\delta \beta\) can be infinitely reduced to area microelement \(d\alpha ,d\beta\):

$$\Delta h\left(x,y\right)=\iint [R\left(x-\alpha ,y-\beta \right)D\left(\alpha ,\beta \right)d\alpha d\beta ]$$
(14)

The total material removal amount of the workpiece surface is regarded as 2-dimension spatial convolution of the removal function \(R\left(x,y\right)\) and dwell time \(D(x,y)\) [13]:

$$H\left(x,y\right)=R\left(x,y\right)*D(x,y)$$
(15)

With certain removal function \(R\left(x,y\right)\) related to TIF and total material removal amount \(H\left(x,y\right)\), the aim of BP dwell time algorithms is to figure out dwell time distribution \(D\left(x,y\right)\) on each dwell point during processing.

3.2 Dwell time solving algorithms

Based on dual-model contact depth TIF, iterative impulse method and non-negative least square method are chosen to be used in the BP approach.

3.2.1 Iterative impulse method

The general idea of iterative impulse method is to stack one dwell time increment \(\Delta {T}_{k}\) in each iteration, and then the new removal amount \({H}_{k}\) after stacking is calculated. Comparing \({H}_{k}\) with the required total removal amount \({\Delta E}_{0}\) to get the residual error \({\Delta E}_{k+1}\). If the residual error \({\Delta E}_{k+1}\) is bigger than the required residual error \(\Delta e\), iteration continues; Otherwise, it is considered that the iteration has entered the required residual convergence range, and the calculation is over:

$$\begin{array}{c}{H}_{k+1}={H}_{k}+R*\Delta {T}_{k+1}\\ {H}_{0}={\Delta E}_{0},\Delta {T}_{0}={\Delta E}_{0}/{R}_{0} , \Delta {T}_{k+1}={\Delta E}_{k+1}/{R}_{0} , {{\Delta E}_{k+1}=\Delta E}_{0}-{H}_{k}\end{array}$$
(16)

where \({H}_{k}\) is the calculating total material removal amount until iteration \(k\). \(\Delta {T}_{k}\) is the calculating dwell time increment in iteration \(k\). \({H}_{0}\) & \(\Delta {T}_{0}\) are the initial iteration parameter s. \({\Delta E}_{0}\) is the required total removal amount of the surface. \({R}_{0}\) is a given constant. \(R\) is the removal function calculated from TIF. \(\Delta e\) is the required residual error.

If \({\Delta E}_{k+1}>\Delta e\), then iteration continues; Otherwise, the calculation stops and the total dwell time is:

$${T}_{sum}=\sum_{i=0}^{k}\Delta {T}_{i}$$
(17)

The algorithm works well with Gaussian-like TIF with small contact depth as shown in Fig. 21. However, when using M-shaped TIF with large contact depth, there is a problem here: the iterative calculation may end up non-convergence. For example, an M-shaped TIF with 0.70 mm contact depth is shown in Fig. 14, workpiece is a 50 \(*\) 50 \(*\) 10 mm3 silicon carbide block (SiC) with an initial surface (PV 3.410 μm) shown in Fig. 15. Simulation purpose is to polish an initial surface into a plane.

Fig. 14
figure 14

Measured M-shaped TIF profile with 0.70 mm contact depth

Full size image
Fig. 15
figure 15

Initial surface in 50 \(*\) 50 mm.2

Full size image

As shown in Fig. 16, the residual surface is divergent in 1000 iterations, and will not come to convergence in more iterations. The results are clearly wrong and not usable. The time consumed in calculating is less than 2 min.

Fig. 16
figure 16

Divergent residual surface and dwell time by iterative impulse method with M-shaped TIF

Full size image

From our observation and analysis, the problem lies in the dwell time increment \(\Delta {T}_{k}\) in each iteration of the algorithm:

$$\Delta {T}_{k}={\Delta E}_{k}/{R}_{0}$$
(18)

In the equation, \({R}_{0}\) is a constant because the removal function \(R\) is supposed to be an ideal impulse function with no convolution effect on nearby dwell points. \(R\) from a Gaussian-like TIF is close to it. But if the TIF is not Gaussian-like, e.g., M-shaped, then it cannot be regarded as an ideal impulse function with no convolution effect anymore, which may lead to non-convergence results.

Though the calculating results are not right, there is a clear periodicity in the solution distribution as shown in Fig. 17. The diameter of these cycle regions is about 3 mm. It is close to the distance between 2 peaks of M-shaped TIF used, which is 3–5 mm. So, it might be relevant to the profile and size of certain TIF used.

Fig. 17
figure 17

Vertical view of divergent residual surface and dwell time by iterative impulse method with M-shaped TIF

Full size image

Since the iterative impulse method does not work well with M-shaped TIF sometimes, it is necessary to apply other algorithms which can deal with M-shaped TIF.

3.2.2 Non-negative least square method

To apply the non-negative least square method, firstly the 2-dimension convolution between the removal function and dwell time should be expanded into a matrix equation. Each line is equivalent to a linear constraint, and the objective function is nonlinear:

$$\begin{array}{c}min\left(H\right)=min\left({\Vert e\Vert }^{2}\right)=min({\Vert Ax-b\Vert }^{2})\\\Delta e=Ax-b\end{array}$$
(19)

where \(A\) is constraint matrix. \(b\) is a vector. \(\Delta e\) is residual error.

The objective function is the sum of the squares of the residuals of each point, which is directly proportional to RMS. The dwell time points and calculating points are independent from each other.

The calculating PV is 0.152 μm after rough polishing with M-shaped TIF, down from 3.416 μm of the initial surface. And according to the calculation results shown in Fig. 18, the M-shaped TIF can be used in rough polishing stage by this algorithm. The TIF used is shown in Fig. 14.

Fig. 18
figure 18

Residual surface and dwell time by non-negative least square method with M-shaped TIF

Full size image

The disadvantage is that this algorithm takes longer time than iterative impulse method. With 3600 dwell points, it takes 35 min to calculate dwell time distribution, much slower than 2 min with iterative impulse method.

And there are still cycle regions in the solution distribution with non-negative least square method shown in Fig. 19; the diameter of these cycle regions is about 5 mm. It needs further research.

Fig. 19
figure 19

Vertical view of residual surface and dwell time by non-negative least square method with M-shaped TIF

Full size image

The tool path shown in Fig. 20 is calculated based on the dwell time distribution and feed movement trajectory. The tool path must be continuous.

Fig. 20
figure 20

Tool path and dwell time distribution in rough polishing stage with M-shaped TIF

Full size image

From the analysis in iterative impulse method part above, the more a TIF’s profile is close to an ideal impulse function, the less convolution effect it has on its nearby dwell time points, and thus, the more algorithm convergence accuracy it has. Though a Gaussian-like TIF with small contact depth has lower removal efficiency than an M-shaped TIF with large contact depth, the profile of a Gaussian-like TIF is clearly closer to an ideal impulse function than an M-shaped TIF, which means less convolution effect and more algorithm convergence accuracy. Actual TIF are not ideal impulse functions, so they always have convolution effect. In general, if both types of TIF are applied in the same situation with same algorithm, Gaussian-like TIF will have better convergence accuracy but longer polishing time.

Therefore, after rough polishing with large contact depth TIF, it is more suitable for Gaussian-like TIF with small contact depth to be applied in fine polishing stage to further improve the surface convergence accuracy. Results are shown in Fig. 21. The TIF used is shown in Fig. 9. The calculating PV is 0.041 μm after fine polishing with Gaussian-like TIF. Therefore, iterative impulse method can be applied in this stage.

Fig. 21
figure 21

Residual surface and dwell time by iterative impulse method with Gaussian-like TIF

Full size image

With Gaussian-like TIF, the 3–5 mm cycle regions do not appear in the solution distribution. But there is still smaller periodicity in the results as shown in Fig. 21. According to the results and analysis above, it may relate to the profile and size of TIF used.

Based on dual-mode contact depth TIF, we develop an adaptive BP approach: In rough polishing stage, in order to improve removal efficiency, non-negative least square method is adopted to calculate dwell time using M-shaped TIF with large contact depth; In fine polishing stage, iterative impulse method is adopted to calculate dwell time using Gaussian-like TIF with small contact depth, which further improves the convergence accuracy.

4 Experimental study

In order to verify the BP approach, a 50 \(*\) 50 \(*\) 10 mm3 silicon carbide block (SiC) with an initial surface (PV 3.416 μm) is chosen as the workpiece, shown in Fig. 15. Dual-mode contact depth TIF (0.15 mm and 0.70 mm) are shown in Fig. 9 and Fig. 14, with parameters shown in Table 2. Bonnet polishing system is shown in Fig. 8. It takes 347 min and 276 min in rough polishing and fine polishing stages. The experiment is to polish an initial surface into a plane.

Table 2 Polishing TIF’s parameters
Full size table

The results in Fig. 22 reveal that most material removal happen in rough polishing stage using large contact depth TIF as expected, the PV is down from 3.416 to 1.638 μm. M-shaped TIF are viable in rough polishing stage to improve removal efficiency and non-negative least square method can be applied with M-shaped TIF in rough polishing; In fine polishing stage, Gaussian-like TIF have advantages in better convergence accuracy, with PV value further down from 1.638 to 1.442 μm. Thus, the effectiveness and convergence accuracy of the adaptive BP approach are confirmed.

Fig. 22
figure 22

Experimental results of adaptive BP approach based on dual-mode contact depth TIF

Full size image

5 Conclusion

In this paper, a new compound model suitable for both Gaussian-like and M-shaped TIF was proposed, and the mechanism of dual-mode contact depth TIF was analyzed in the aspect of stress and strain properties of the elastic bonnet with inflated inner air. Then, based on the new TIF model, an adaptive BP approach was proposed to improve the removal efficiency and, meanwhile, guarantee the convergence accuracy. Experiment results showed that removal efficiency is higher in rough polishing stage with M-shaped TIF. And with Gaussian-like TIF, surface PV value was further down to 1.442 μm. Therefore, the removal efficiency and the surface convergence accuracy of the approach are verified.