1 Introduction

With the rapid development of modern industry, CNC machine tools are vital in aerospace, national defence and military, energy power, automobile and motorcycle manufacturing and other high-end industries. The main factors affecting the accuracy of machine tools include static accuracy geometric error, dynamic load and thermal error deformation, among which geometric error and thermal error are the primary source of error affecting the accuracy of machine tools, accounting for more than 60% of the overall error [1]. The geometric error of the machine tool has the characteristics of high repeatability, good systematicity, continuous operation stability and easy data detection. The technique of predicting the machining accuracy of a machine tool by measuring its geometrical errors has become an essential tool for improving design efficiency and provides a strong basis for spatial motion accuracy prediction and machine tool error compensation mechanisms.

Therefore, over the past few decades, researchers have investigated geometric error modeling and accuracy prediction techniques, and the commonly used methods include the mechanism method [2], rigid body kinematics method [3], HTM [4] and multi-body system (MBS) theory [5]. Among them MBS is the mainstream modelling method, which aims to establish a coordinate system mainly in each motion unit, conduct a high degree of abstraction and generalization for a complex motion system and clearly express the accuracy model error factors and machine tooltip offset relationship [6].

Tao [7] et al. investigated the prioritisation analysis of geometric errors of arbitrary surfaces using the random forest method. A preliminary volume error model was established to calculate the tool position error by using the multi-body system (MBS) theory. Yang [8] et al. used the MBS theory to analyse the motion process of the machine tool and considered the motion transfer relationship in the action chain to establish the kinematic model of each motion axis in the form of twisted exponential. Liu [9] et al. used the multi-body system (MBS) theory to comprehensively analyze and calibrate geometric errors of the dual main axis-symmetric structure and cross-slide layout of an ultra-precision drum lathe. In addition to MBS theory, some other theories have also been applied to the error modelling of machine tools, such as the HTM theory. Huang [10] used the HTM method for kinematic analysis of rigid bodies in the volumetric error modelling of machine tools and derived error terms for the direction of motion. Sangjin Maeng [11] proposed a method to reduce geometric errors in ultra-precision five-axis machines by using on-machine measurements to identify rotation axis and tool setting position-independent geometric errors simultaneously. Jinwei Fan [12] proposed a new method for FAMT accuracy enhancement based on quantitative interval sensitivity analysis (QISA). A volumetric error model and a geometric error model for FAMT were developed based on multi-body system theory and the chi-square transformation matrix.

The geometric error between the machined part and the tooltip can be obtained from the error model, and thus, the error distribution of the entire machine tool workspace can be obtained, providing a basis for the subsequent error compensation. In order to further improve the compensation efficiency, researchers have established error models and then carried out sensitivity analysis studies on the geometric errors so as to obtain the most critical error elements affecting the machine tool error and to compensate for them in a targeted manner. Guoqiang Fu [13] used sensitivity analysis of the different effects of different axes on the accuracy of the machine tool to model the contribution of geometric errors and sensitivity assessment of each axis of the machine tool in order to obtain the degree of influence on each axis and to identify the critical axes of the machine tool. Li [14] adopted sensitivity analysis methods to elucidate the relationship between toolpath error and feed axis error motion. A surface coordinate system is established for each tool centre point to define the tool trajectory and trajectory error based on the free curve trajectory in five-axis simultaneous machining. Wu [15] et al. utilized a reliability theory-based design method for geometric accuracy analysis and tolerance robustness of vertical machining centres. Based on the establishment of the accuracy prediction model and the critical geometric error traceability, the machining accuracy limit state equation was obtained by combining the predicted accuracy and machining performance requirements of the machine tool, and the machining accuracy reliability model relationship was derived based on the reliability theory. The approximate solution of the machining accuracy reliability is obtained by using the first- and second-order method of moments. The vital geometric errors are used as tolerance robustness design variables. The relationship with manufacturing cost and accuracy reliability is used to establish a machine tool cost-geometry tolerance robustness design model for implementing machine tool design.

The above methods can be used to obtain the critical error elements of the machine tool and optimise their accuracy and compensate for their error. However, the error value associated with the motion position changes with the motion, and the sensitivity analysis of the error elements basically does not take into account this particular nature, so that the analysis results obtained lack practical guidance significance on the error compensation. And existing methods of modelling machine tool kinematics generally require separate coordinate systems be established on all motion units. As a result, the modelling involves a large number of coordinate transformations, and the modelling process is very complex. Besides, there are a large number of variables, and it is difficult to express discreet relationships. Currently, there is not much research related to the prediction of machine accuracy through sensitivity analysis in the global range of motion of the machine tool.

When it comes to the methods of machine tool accuracy prediction and compensation, the primary purpose is to improve the compensation efficiency and machining accuracy by compensating the error of crucial motion axes. Liu [16] et al. analysed the impact of the vertical error on the error modelling accuracy and complexity of five-axis CNC machine tools and modelled angular error characteristics for multi-axis machine tools and the complexity of the angular error modelling process to get the regular characteristics of a translation error and angular error. Gu et al. [17] proposed a global offset method based on measurements of one or more identical machined parts to compensate for five-axis machine tool errors in order to improve machine tool accuracy, as well as global offset parameters for machine tool errors based on machining features of the part measured in a CMM and evaluated by a compensation processor. The method is able to compensate for the overall effect of position-dependent and position-independent systematic errors on specific workpiece accuracy. Machine accuracy-machined part accuracy was investigated by Shneor et al. [18]. In combination with a database of machines connected to a virtual machining process and a specific part as a predictive model, it was able to simulate multi-task machining accuracy by modifying the shaping function of this predictive model.

The above research methods have all achieved specific results. However, at present, there are relatively few studies on the accuracy of multi-axis CNC machine tools combined with machine tool error sensitivity and accuracy prediction [18, 19]. Therefore, this paper takes a five-axis machining centre as the research object and uses the theory of multi-body system and sensitivity analysis to solve the above problems. In this paper, we propose a new geometric error modeling method to predict the geometric accuracy deviation of a 5-axis vertical machining centre and use global sensitivity analysis to analyze the contribution of geometric errors to the machining accuracy. Firstly, the errors in six degrees of freedom in five axes of motion are accurately quantified, and the error variation pattern is explored, which is an important and central contribution of this study while previous studies on five-axis machines have focused on individual feed axes for error term modeling without considering the final tool end deviation of multi-axis machines. Next, the degree of influence of key geometric error elements on machining accuracy is analysed using global sensitivity. Finally, this method is utilized to machine an aerospace blade. The feasibility of the above method is verified by compensating the machining motion trajectory of the machine tool before and after the critical geometric error elements. This method has a wide range of application scenarios, not only for five-axis machines, but also for any other forms of machines to improve manufacturing accuracy.

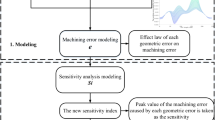
The organisation of this paper is shown in Fig. 1. In Section 1, the error modelling of the machine tool is carried out using the multi-body system theory; in Section 2, the error data of the machine tool is collected, the error model is obtained by fitting the data points, and the accuracy of the accuracy model is verified through experiments; in Section 3, the moving parts with the greatest influence on the accuracy are obtained using sensitivity analysis; in Section 4, the law before the motion position and error distribution is studied through machining experiments. The accuracy compensation scheme is also specified; in Section 5, some concluding remarks are made.

Fig. 1
figure 1

Sensitivity analysis and accuracy prediction process for machine tools

Full size image

2 Error modelling based on multi-body system theory

The structure of the 5-axis simultaneous machining centre is shown in Fig. 2, which consists of five major components, such as the XYZ-axis and the AC-axis.

Fig. 2
figure 2

Five-axis simultaneous machining centre construction

Full size image

The vertical five-axis machining centre consists of three linear axes of motion XYZ and two rotary axes of motion AC. The bed is a monolithic casting with a low front and a high rear. The front is used to mount a fixed table or a five-axis twin-axis turntable, and the rear is fitted with a precision linear guide rail, on which the beam moves backwards and forwards to achieve Y-axis movement, powered by a precision ball screw mounted in the middle of the rear of the bed. The cross slide is mounted in front of the cross beam and is driven by a precision ball screw mounted in the middle of the front of the cross beam and guided by a precision linear guide to achieve the X-axis movement. The ram is mounted on the cross slide for up and down movement in the Z-direction, and its screw and guide are mounted on the ram. The precision high-speed spindle is mounted on the lower end of the ram, and the tool mounted on the spindle is used for high-speed milling of the parts fixed on the table.

2.1 Error modelling based on multi-body system theory

As shown in Fig. 3, the kinematic system of a machine tool is composed of several axes of motion. According to the theory of multi-body systems, the mechanism consisting of individual moving parts is abstracted as a kinematic chain [20]. The bed (base), Y-axis slide, X-axis slide, Z-axis slide, spindle, tool and the bed (base), A-axis turntable, C-axis turntable and workpiece have respective corresponding symbols, and the corresponding error elements are listed.

Fig. 3
figure 3

Multi-body system kinematic chain

Full size image

During the machining process, there is an error factor between the individual moving bodies due to the transfer of motion. Each moving part, as shown in Fig. 4, contains three linear errors (two straightness errors, one linearity error) and three angular errors (pitch angle, deflection angle, roll deflection angle) [15, 21]. The parameters for the error elements of the machine are named as shown in Table 1.

Fig. 4
figure 4

Diagram of error elements

Full size image
Table 1 Table of error elements
Full size table

2.2 Modeling the accuracy of a 5-axis machining centre

As shown in Fig. 5, figure \({O}_{i}\left(i=1,...,9\right)\) represents the rigid body coordinate system of the machining centre; figure \({L}_{i}\left(i=1,...,10\right)\) represents the position-related constants of the machining centre components; all the motion quantities are \(S=\left(x,y,z,\theta a,\theta c\right)\), and they represent the coordinates of the individual moving components respectively.

Fig. 5
figure 5

Coordinate sketch of a 5-axis vertical machining centre

Full size image

For accuracy modelling, all the established coordinate systems are on the central axis of motion. The relative motion position characteristic matrix is obtained from Fig. 5 as \({T}_{s\left(i-j\right)}\) as follows:

$${T}_{S\left(1-0\right)}=\left[\begin{array}{c}\begin{array}{cccc}1& 0& 0& 0\end{array}\\ \begin{array}{cccc}0& 1& 0& 0\end{array}\\ \begin{array}{cccc}0& 0& 1& 0\end{array}\\ \begin{array}{cccc}0& 0& 0& {L}_{1}\end{array}\end{array}\right]$$
(1)
$$T_{S\left(2-1\right)}=\begin{bmatrix}1&0&0&L_2\\0&\cos\;\theta_c&-\sin\;\theta_c&0\\0&\sin\;\theta_c&\cos\;\theta_c&0\\0&0&0&1\end{bmatrix}$$
(2)
$$T_{S\left(3-2\right)}=\begin{bmatrix}\cos\;\theta_a&0&\sin\;\theta_a&0\\0&1&0&0\\-\sin\;\theta_a&0&-\cos\;\theta_a&L_3\\0&0&0&1\end{bmatrix}$$
(3)
$${T}_{S\left(4-0\right)}=\left[\begin{array}{c}\begin{array}{cccc}1& 0& 0& {x}_{0}\end{array}\\ \begin{array}{cccc}0& 1& 0& {y}_{0}\end{array}\\ \begin{array}{cccc}0& 0& 1& {z}_{0}+{L}_{4}\end{array}\\ \begin{array}{cccc}0& 0& 0& 1\end{array}\end{array}\right]$$
(4)
$${T}_{S\left(5-4\right)}=\left[\begin{array}{c}\begin{array}{cccc}1& 0& 0& 0\end{array}\\ \begin{array}{cccc}0& 1& 0& y+{L}_{5}\end{array}\\ \begin{array}{cccc}0& 0& 1& {L}_{6}\end{array}\\ \begin{array}{cccc}0& 0& 0& 1\end{array}\end{array}\right]$$
(5)
$${T}_{S\left(6-5\right)}=\left[\begin{array}{c}\begin{array}{cccc}1& 0& 0& x+{L}_{7}\end{array}\\ \begin{array}{cccc}0& 1& 0& 0\end{array}\\ \begin{array}{cccc}0& 0& 1& 0\end{array}\\ \begin{array}{cccc}0& 0& 0& 1\end{array}\end{array}\right]$$
(6)
$${T}_{S\left(7-6\right)}=\left[\begin{array}{c}\begin{array}{cccc}1& 0& 0& 0\end{array}\\ \begin{array}{cccc}0& 1& 0& {L}_{8}\end{array}\\ \begin{array}{cccc}0& 0& 1& z+{L}_{9}\end{array}\\ \begin{array}{cccc}0& 0& 0& 1\end{array}\end{array}\right]$$
(7)
$${T}_{S\left(8-7\right)}=\left[\begin{array}{c}\begin{array}{cccc}1& 0& 0& 0\end{array}\\ \begin{array}{cccc}0& 1& 0& {L}_{10}\end{array}\\ \begin{array}{cccc}0& 0& 1& {L}_{11}\end{array}\\ \begin{array}{cccc}0& 0& 0& 1\end{array}\end{array}\right]$$
(8)

The \({T}_{m\left(i-j\right)}\) relative motion error position characteristic matrix is as follows:

$${T}_{m\left(1-0\right)}=\left[\begin{array}{cccc}1& -{\varepsilon }_{{z}_{\mathrm{c}}\left({\uptheta }_{\mathrm{c}}\right)}& -{\varepsilon }_{{y}_{\mathrm{c}}\left({\uptheta }_{\mathrm{c}}\right)}& {\updelta }_{{x}_{\mathrm{c}}\left({\uptheta }_{\mathrm{c}}\right)}\\ {\varepsilon }_{{z}_{\mathrm{c}}\left({\uptheta }_{\mathrm{c}}\right)}& 1& -{\varepsilon }_{{x}_{\mathrm{c}}\left({\uptheta }_{\mathrm{c}}\right)}& {\updelta }_{{y}_{\mathrm{c}}\left({\uptheta }_{\mathrm{c}}\right)}\\ -{\varepsilon }_{{y}_{\mathrm{c}}\left({\uptheta }_{\mathrm{c}}\right)}& {\varepsilon }_{{x}_{\mathrm{c}}\left({\uptheta }_{\mathrm{c}}\right)}& 1& {\updelta }_{{z}_{\mathrm{c}}\left({\uptheta }_{\mathrm{c}}\right)}\\ 0& 0& 0& 1\end{array}\right]$$
(9)
$${T}_{m\left(3-2\right)}=\left[\begin{array}{cccc}1& -{\varepsilon }_{{z}_{a}\left({\uptheta }_{a}\right)}& {\varepsilon }_{{y}_{a}\left({\uptheta }_{a}\right)}& {\delta }_{{x}_{a}\left({\uptheta }_{a}\right)}\\ {\varepsilon }_{{z}_{a}\left({\uptheta }_{a}\right)}& 1& -{\varepsilon }_{{x}_{a}\left({\uptheta }_{a}\right)}& {\delta }_{{y}_{a}\left({\uptheta }_{a}\right)}\\ -{\varepsilon }_{{y}_{a}\left({\uptheta }_{a}\right)}& {\varepsilon }_{{x}_{a}\left({\uptheta }_{a}\right)}& 1& {\delta }_{{z}_{a}\left({\uptheta }_{a}\right)}\\ 0& 0& 0& 1\end{array}\right]$$
(10)
$${T}_{m\left(5-4\right)}=\left[\begin{array}{cccc}1& -{\varepsilon }_{{z}_{y}\left({\uptheta }_{y}\right)}& {\varepsilon }_{{y}_{y}\left({\uptheta }_{y}\right)}& {\delta }_{{x}_{y}\left({\uptheta }_{y}\right)}\\ {\varepsilon }_{{z}_{y}\left({\uptheta }_{y}\right)}& 1& -{\varepsilon }_{{x}_{y}\left({\uptheta }_{y}\right)}& {\delta }_{{y}_{y}\left({\uptheta }_{y}\right)}\\ -{\varepsilon }_{{y}_{y}\left({\uptheta }_{y}\right)}& {\varepsilon }_{{x}_{y}\left({\uptheta }_{y}\right)}& 1& {\delta }_{{z}_{y}\left({\uptheta }_{y}\right)}\\ 0& 0& 0& 1\end{array}\right]$$
(11)
$${T}_{m\left(6-5\right)}=\left[\begin{array}{cccc}1& -{\varepsilon }_{{z}_{x}\left({\uptheta }_{x}\right)}& {\varepsilon }_{{y}_{x}\left({\uptheta }_{x}\right)}& {\delta }_{{x}_{x}\left({\uptheta }_{x}\right)}\\ {\varepsilon }_{{z}_{x}\left({\uptheta }_{x}\right)}& 1& -{\varepsilon }_{{x}_{x}\left({\uptheta }_{x}\right)}& {\delta }_{{y}_{x}\left({\uptheta }_{x}\right)}\\ -{\varepsilon }_{{y}_{x}\left({\uptheta }_{x}\right)}& {\varepsilon }_{{x}_{x}\left({\uptheta }_{x}\right)}& 1& {\delta }_{{z}_{x}\left({\uptheta }_{x}\right)}\\ 0& 0& 0& 1\end{array}\right]$$
(12)
$${T}_{m\left(7-6\right)}=\left[\begin{array}{cccc}1& -{\varepsilon }_{{z}_{z}\left({\uptheta }_{z}\right)}& {\varepsilon }_{{y}_{z}\left({\uptheta }_{z}\right)}& {\delta }_{{x}_{z}\left({\uptheta }_{z}\right)}\\ {\varepsilon }_{{z}_{z}\left({\uptheta }_{z}\right)}& 1& -{\varepsilon }_{{x}_{z}\left({\uptheta }_{z}\right)}& {\delta }_{{y}_{z}\left({\uptheta }_{z}\right)}\\ -{\varepsilon }_{{y}_{z}\left({\uptheta }_{z}\right)}& {\varepsilon }_{{x}_{z}\left({\uptheta }_{z}\right)}& 1& {\delta }_{{z}_{z}\left({\uptheta }_{z}\right)}\\ 0& 0& 0& 1\end{array}\right]$$
(13)

In addition to this, the X-axis, Y-axis and Z-axis also have a vertical error degree, whose error characteristic equation is expressed as

$${P}_{xy}=\left[\begin{array}{cccc}1& -{T}_{xy}& 0& 0\\ {T}_{xy}& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$
(14)
$${P}_{xy}=\left[\begin{array}{cccc}1& -{T}_{xz}& 0& 0\\ {T}_{xz}& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$
(15)
$${P}_{xy}=\left[\begin{array}{cccc}1& -{T}_{zy}& 0& 0\\ {T}_{zy}& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$
(16)

where \(\begin{array}{ccc}{x}_{0}& {y}_{0}& {z}_{0}\end{array}\) is the vector distance between the turntable on the bed and the coordinate point of the x-axis guide.

\(\begin{array}{ccc}x& y& z\end{array}\) is the linear axis working position vector.

\({L}_{i}\left(i=1.2...11\right)\) is structural constant.

The relative motion position characteristic matrix is \({T}_{s\left(i-j\right)}\), and the relative motion error position characteristic matrix is \({T}_{m\left(i-j\right)}\). \({T}_{s\left(i-j\right)}\) is the ideal transformation coordinate of motion coordinate system \(i\) relative to motion coordinate system \(j\) \({T}_{m\left(i-j\right)}\) is the position coordinate transformation of motion coordinate system i relative to motion coordinate system j under the effect of generating the error; P_ij is the verticality error characteristic matrix of \(i\) axis equivalent to \(j\) axis; \({K}_{a}\) and \({K}_{b}\) are the coordinates of the tool at the machining point and the coordinates of the workpiece at the machining point respectively,which can be expressed as

$${K}_{\text{A}}=\left(\begin{array}{ccc}{\mathrm{x}}_{\mathrm{A}}& {\mathrm{y}}_{\mathrm{A}}& {\mathrm{z}}_{\mathrm{A}}\end{array}\right)$$
(17)
$${K}_{\text{B}}=\left(\begin{array}{ccc}{\mathrm{x}}_{\mathrm{B}}& {\mathrm{y}}_{\mathrm{B}}& {\mathrm{z}}_{\mathrm{B}}\end{array}\right)$$
(18)

The above equation gives the error model for the tool endpoint A and the workpiece kinematic chain B. The equation is expressed as follows:

$${E}_{A}={P}_{xy}{P}_{xz}{P}_{zy}{T}_{sA\left(5-4\right)}{T}_{mA\left(5-4\right)}{T}_{sA\left(6-5\right)}{T}_{mA\left(6-5\right)}{T}_{sA\left(7-6\right)}{T}_{mA\left(7-6\right)}{T}_{sA\left(8-7\right)}{K}_{A}$$
(19)
$${E}_{B}={T}_{sB\left(1-0\right)}{T}_{mB\left(1-0\right)}{T}_{sB\left(2-1\right)}{T}_{sB\left(3-2\right)}{T}_{mB\left(3-2\right)}{K}_{B}$$
(20)

The resulting error model for a five-axis machine is as follows:

$$\Delta E=\Delta {E}_{A}-\Delta {E}_{A}={T}_{sA\left(i-j\right)}{T}_{mA\left(i-j\right)}{K}_{A}-{T}_{sB\left(i-j\right)}{T}_{mB\left(i-j\right)}{K}_{B}$$
(21)

In summary, once the 33 error factors of the machine tool on the travel range have been determined, the error model is substituted, and the coordinates of the machine tool at the machining coordinates parameters are entered, i.e. the error values of the machine tool at the current coordinates are solved for, that is, \(\Delta {E}_{x}, \Delta {E}_{y},\Delta {E}_{z}\).

3 Error test data collection and analysis of machine tools

In this paper, the AVC1200/2 five-axis vertical machining centre is used as an example, with basic parameters as shown in Table 2, to verify the geometric error contribution values of the motion axes and the effectiveness of the error compensation by using the multi-body system theory and the response surface similarity polynomial method.

Table 2 Basic parameters of the AVC1200/2 product
Full size table

3.1 Error data collection

Geometric errors are measured on the AVC1200/2 machine tool for analysis. The error data are collected with a laser interferometer (Renishaw XL-80), and the specific detection principle is shown in Figs. 6 and 7 The data acquisition environment and methods are shown in Tables 3 and 4.

Fig. 6
figure 6

Field measurement error data

Full size image
Fig. 7
figure 7

Principle of detection

Full size image
Table 3 Testing environmental parameters
Full size table
Table 4 Collection methods
Full size table

After setting the current parameters, according to the machine structure, the X-axis is 550 mm of travel; the Y-axis is 610 mm of travel, and the Z-axis is 400 mm of travel. The error data is measured by using a testing device for the three linear axes. The six errors measured in the X-axis movement are \(\Delta {x}_{x}\) \(\Delta {y}_{x}\) \(\Delta {z}_{x}\) \(\Delta {\alpha }_{x}\) \(\Delta {\beta }_{x}\) \(\Delta {\gamma }_{x}\); the six errors measured in the Y-axis movement are \(\Delta {x}_{y}\) \(\Delta {y}_{y}\) \(\Delta {z}_{y}\) \(\Delta {\alpha }_{y}\) \(\Delta {\beta }_{y}\) \(\Delta {\gamma }_{y}\); the six errors measured in the Z-axis movement are \(\Delta {x}_{z}\) \(\Delta {y}_{z}\) \(\Delta {z}_{z}\) \(\Delta {\alpha }_{z}\) \(\Delta {\beta }_{z}\) \(\Delta {\gamma }_{z}\) and 12 errors in the A-axis and C-axis.

According to the standard method of measurement, the measurement is repeated four times and averaged in the case of linear motion, in which the error data of the motion axis are obtained and plotted for the X-, Y- and Z-axes, as shown in Figs. 8, 9 and 10.

Fig. 8
figure 8

Plot of X-axis error data

Full size image
Fig. 9
figure 9

Plot of Y-axis error data

Full size image
Fig. 10
figure 10

Plot of Z-axis error data

Full size image

According to the formula \(\Delta {V}_{ij}=\mathrm{arctan}\frac{{\Delta i}_{j}}{{a}_{j}}-\mathrm{arctan}\frac{{\Delta j}_{i}}{{a}_{i}}\), the perpendicularity \(\Delta {V}_{xy},\Delta {V}_{xz},\Delta {V}_{yz}\) between the X-axis, Y-axis and Z-axis is obtained. \({a}_{i}\) is the effective guide length of each axis. (\(i\) and \(j\) in the above are \(x\), \(y\) and \(z\) respectively). The results of the perpendicularity calculation are shown in Table 5.

Table 5 Vertical error degree parameters
Full size table

3.2 Solution to error model

By bringing in the above error source data and substituting the machine’s mechanical coordinate points, the machine’s \(\Delta {E}_{x}\) \(\Delta {E}_{y}\) and \(\Delta {E}_{z}\) deviation values at the current coordinates can be solved for [22]. Taking \({K}_{B}\) as an example, the workpiece endpoint coordinate error model counts in the XYZ direction as shown in the Appendix in Eqs. (31), (32) and (33).

After the calculation of each error value of the XYZ direction of the tooltip coordinate point, the value of each error element is substituted into the formula to obtain the XYZ direction error value. However, there will be different error values in different places because the distribution of error points is discrete, while the machine tool movement is a continuous motion process. According to the error data distribution point map in Figs. 8, 9 and 10, plus the law of machine tool movement, its discrete data points can be turned into a continuous error distribution curve by the polynomial fitting method, providing data for the extraction of the subsequent real-time coordinate point error values. The data fitting curves obtained from the X-, Y- and Z-axes are shown in Figs. 11, 12 and 13, by the polynomial fitting method.

Fig. 11
figure 11

X-axis data fitting

Full size image
Fig. 12
figure 12

Y-axis data fitting

Full size image
Fig. 13
figure 13

Z-axis data fitting

Full size image

The final fitted equations for each axis in each direction are shown in Eqs. (34), (35) and (36) in the Appendix.

3.3 Analysis of error data

The fitted error equation is substituted into the accuracy model, and the energy diagram of the error distribution at the overall machine travel is obtained according to \(\sqrt{\Delta {E}_{x}^{2}+\Delta {E}_{y}^{2}+\Delta {E}_{z}^{2}}\), which allows a specific observation of the magnitude of the error at the machining point within the travel range and serves as a reference for subsequent work.

As shown in Fig. 14, the integrated error of the machine gradually tends to increase with the feeding of the Y-axis, and with the feeding of the X-axis, the area with the larger integrated error is distributed in a concave shape. With the feeding of the Z-axis, the integrated error gradually becomes smaller due to the specificity of the machine structure. In summary, the impact of the integrated error on the machining accuracy is most obvious in the processing of large-size parts in a machine tool.

Fig. 14
figure 14

Spatial error distributions

Full size image

3.4 Validation of effectiveness of the error model

In order to verify the accuracy of the error model predictions, the error distribution of the tool tip at different positions is obtained by bringing the fitted equations into the error model quasi. As shown in Fig. 15, a simple machining model is selected by means of machining experiments, and the edge profile toolpath of the machined part is extracted and brought into the error model [23, 24], and the model accuracy is obtained by comparing its edge hub dimension data with a CMM.

Fig. 15
figure 15

Inspection of workpieces

Full size image

In this study, firstly, in order to verify the accuracy of the model, the accuracy of the model is verified by using a simple model for machining. The advantage of doing so is that it can facilitate data collection, as well as quickly obtain the accuracy of the model for subsequent model adjustment. As this simple part does not contain a typical surface for five-axis machining, when we are machining it, in order to verify the effect of five-axis simultaneous machining, we programme machining programming with an off-angle fixture for multi-axis simultaneous machining, and we mainly turn the AC axis through a slow rotation for 5-axis simultaneous machining, so that the accuracy of the five-axis machine tool error model can be guaranteed, as shown in Fig. 16.

Fig. 16
figure 16

Inspection of workpieces

Full size image

As shown in Fig. 17, it was first determined that the machined part was fixed to the table and its datum was determined at the centre, and the surface error data of the actual workpiece was taken through a CMM instrument with a circular trajectory as the path, segmented into 32 points, with the specific values shown in Fig. 18.

Fig. 17
figure 17

Principle of testing

Full size image
Fig. 18
figure 18

Error point value

Full size image

As shown in Fig. 19, the blue line is the error model derived from the machining toolpath contour, which is the distance between the 32 points in the selected inspection contour. The longest linear distance is 106 μm, and the shortest is 83 μm. The longer the distance from the predicted contour, the darker red colour.

Fig. 19
figure 19

Error distance between trajectory and test point

Full size image

The accuracy of the error model can be obtained by bringing the above data into the following equations:

$$Y={S}_{s}-{\text{S}}_{\text{y}}$$
(22)
$$X=\frac{{S}_{s}-{\text{S}}_{\text{y}}}{{S}_{s}}100\%$$
(23)
$$T=Y-X$$
(24)

In the equations, \({S}_{s}\) represents actual value, \({S}_{y}\) represents predicted value, \(Y\) represents prediction error, \(X\) represents relative error, and \(T\) represents model accuracy [25,26,27]. The final result is T = 98.37%, so the error model allows the geometric accuracy of any position in the machining space to be predicted.

4 Sensitivity analysis and simulation of error parameters for machine tools

According to the accuracy model of the machine tool, the displacement deviation of the tool has a specific mathematical mapping relationship with the 33 input error parameters, so the sensitivity of the error parameters can be described quantitatively, and the interaction effect of the parameters on the sensitivity of the error results can be analysed [28, 29]. However, as the machine tool involves a large number of moving parts, and the functions in the error model are too complex and involve too many error parameters to be solved with the original differential derivatives, numerical iteration of the response surface is used to simplify the error model of the machine tool by establishing an approximate model between the error parameters and the response quantities, and then further calculate the sensitivity of the error parameters.

4.1 Simplification of the error model

The error components of \(\Delta {E}_{x}\), \(\Delta {E}_{y}\) and \(\Delta {E}_{z}\) are first used to establish the arithmetic, with the function being a polynomial between \({{a}_{i}x}_{i}\) and the response quantity y as follows:

$${E}_{i}={a}_{0}+{a}_{0}{x}_{1}+...+{a}_{n+1}{x}_{1}^{2}+...+{a}_{n+1}{x}_{1}{x}_{2}+...+{b}_{0}$$
(25)

The derivatives by differentiating polynomials are as follows:

$${E}_{i}dx={a}_{1}d{x}_{1}+...+2{a}_{n+1}d{x}_{1}+...+{a}_{n+1}d{x}_{1}{x}_{2}+...+{b}_{0}$$
(26)

The final sensitivity coefficients for each error parameter are obtained as follows:

$${N}_{xi}={a}_{i}d{x}_{i}$$
(27)
$${N}_{xixj}={a}_{i}d{x}_{i}{x}_{j}$$
(28)

Due to the need to model the similarity between the error parameters and the sensitivity evaluation indicators, in this paper, a central composite experimental design (CCD) is used to do the experimental data, consisting of a full factorial design, an axial point design and a zero-level centroid repeated experiment in 3 parts, by selecting 33 error parameters as variables to provide data sample points for the response surface mathematical model, which are limited to the same error range. Crossover experiments were conducted for a total of 5072 calculated samples. The samples were finally fitted to a similar model to simplify the complex error model.

4.2 Analysis of the sensitivity of error elements

The absolute value of the derivative of the differential of the function by defining the response surface similarity model function is the error sensitivity contribution, and the equation is as follows:

$$m_i=\frac{\partial E_i}{\partial x_i}\;\;\;\;\;i=x,y,z$$
(29)

The sensitivity of the response is obtained by normalising the proportion of each error coefficient as follows:

$$M_i=\frac{m_i}{\sum_{j=1}^nm_i}100\%\;\;\;\;\;i=x,y,z$$
(30)

Ultimately, the sensitivity of each error parameter to\(\Delta {E}_{x}\),\(\Delta {E}_{y}\), and \(\Delta {E}_{z}\) is obtained, as shown in Fig. 20.

Fig. 20
figure 20

Error parameter sensitivity

Full size image

Using the sensitivity of the error component \(\Delta {E}_{x}\) of the 5-axis machining centre as a column, the critical geometric error parameters of \(\Delta {E}_{x}\) are identified as \(\Delta Vxy\), \(\Delta {X}_{{\theta }_{c}}\), \(\Delta {X}_{{\theta }_{a}}\), \(\Delta {\beta }_{x}\); in order to reduce the geometric errors on the X-component, the focus should be on compensating for the error parameters with high sensitivity and reasonably enhancing the accuracy on the remaining YZ-component.

The critical error elements for the remaining Y-components and the components of Z are all prominently identified, as shown in Fig. 19.

The following conclusions can be drawn from Table 6: two displacement errors, five angular errors and three perpendicularity errors have an impact on the positioning errors of the 5-axis machining centre, with the perpendicularity and angularity errors having the most significant impact, while the displacement errors have a minor impact compared to the other errors. These errors should be minimised during the design of the machine by a reasonable allocation of tolerances and error compensation.

Table 6 Key error sensitivities
Full size table

5 Simulation compensation and validation

In order to verify the validity of the sensitivity analysis method for the geometrical error parameters, this experiment was carried out on an AVC1200/2 vertical machining centre with a Huazhong CNC 848 system for accuracy compensation. Due to the corresponding amount of motion required, this experiment was carried out as an example of a path for machining a surface of a turbine blade for simulation compensation as well as experimental verification.

As shown in Fig. 21, the turbine blade is modelled with the machining toolpath, which is generated by the finish milling process, and the machining path code is extracted to provide data for the subsequent carry-in error model.

Fig. 21
figure 21

Models and surface machining toolpaths

Full size image

5.1 Models and surface machining toolpaths

The machining toolpath code is brought into the error model to obtain the errors in \(\Delta {E}_{x}\), \(\Delta {E}_{y}\) and \(\Delta {E}_{z}\) in the machining of the turbine blade surface, as shown in Figs. 22, 23 and 24.

Fig. 22
figure 22

Distribution of X-component error contribution values

Full size image
Fig. 23
figure 23

Distribution of Y-component error contribution values

Full size image
Fig. 24
figure 24

Distribution of Z-component error contribution values

Full size image

By analysing the distribution of error contribution values for each component, it can be seen that the Z-axis component has the most expansive error distribution area and the most significant contribution value.

5.2 Error compensation

Error compensation plays a vital role in improving the accuracy of 5-axis machining centres [30]. Based on the sensitivity analysis method, the uncertainty and coupling effect of the geometrical errors are integrated to add compensation values to the machining code in the reverse direction to correct the coordinate position of the tooltip point to achieve error compensation.

The largest error contribution of the Z-component was obtained from the analysis. As shown in Figs. 25, 26 and 27, the error distributions for the Z-directional component error element only and for the integrated error element are shown respectively. According to the machine tool geometry error model proposed in the paper, the comprehensive error distribution of the machining of the blade is analysed. Through the error contribution value comparison analysis, the Z-component of the error contribution rate obtained is the largest, so the Z-component of the error value is used to compensate, respectively, only compensate the Z-directional component of the error element and compensate the comprehensive error element of the error distribution graph. The average error without compensating for the combined error of the machine is 84.2 μm, while the average error with only compensating for the Z-directional component error is 48.3 μm, an improvement of 57.2%. The results of the analysis show that compensating only for sensitive errors has good results, thus verifying the accuracy of the sensitivity analysis and providing a theoretical basis for subsequent machine tool optimisation work.

Fig. 25
figure 25

Composite error distribution chart

Full size image
Fig. 26
figure 26

Composite error distribution of the X-component of compensation

Full size image
Fig. 27
figure 27

Integrated compensation error distribution chart

Full size image

6 Conclusion

  1. 1.

    Based on the theory of the multi-body system and the method of the chi-square transformation matrix, the structure of the machine tool is comprehensively analysed, and a model for the prediction of geometric errors of five-axis machining centres is established.

  2. 2.

    Based on the error model, a sensitivity analysis method for the error parameters of the 5-axis machining centre is proposed, and a simplified model of similar sensitivity is established by fitting the response surface.

  3. 3.

    According to the sensitivity similarity model, the geometric parameters sensitive to \(\Delta {E}_{x}\) \(\Delta {E}_{y}\) and \(\Delta {E}_{z}\) components are obtained, and finally, the critical error parameters that have the most significant impact on the machining accuracy of the machine tool are obtained, which provides a theoretical basis for the design and accuracy prediction of the machine tool.

  4. 4.

    Through the error model of the five-axis machining centre, the error parameters are compensated and simulated. The results show that after the geometric parameters of the critical components are compensated, the integrated error is reduced by 42.6%. After the integrated geometric error is compensated, the overall error is reduced by 89.6%. Through the above results, the feasibility, accuracy and effectiveness of the method of this paper are verified.