1 Introduction

Thin-walled parts, such as impellers and blades, are widely used in aviation and aerospace fields. The stiffness of this kind of part changes continuously and worsens gradually with the material removal during CNC milling. Especially in finishing, the workpiece is easily deformed by cutting force. It causes the deviation between the theoretical cutter-contact (CC) point and the actual CC point, leading to machining error and affecting machining quality. Conservative machining parameters or multiple machining are often used to guarantee machining quality. Although these methods reduce machining error, they seriously affect machining efficiency [1]. Therefore, how to reduce the machining deformation of thin-walled parts in milling is still a challenging problem.

Fixtures can reduce deformation, but fixture design is time-consuming, costly, and non-universal. Additional support to improve stiffness for weakly rigid thin-walled parts can reduce deformation directly. For example, materials such as melted low melting point alloy or paraffin wax can be poured around the blade profile to hold the blade [2]. Smith et al. [3] proposed to add sacrificial structure preforms to thin-walled parts by forging, welding, bonding, and casting to improve the stiffness of thin-walled parts during machining. However, additional support will introduce deformation of over-positioning clamping, and the stress released inside the workpiece after unloading the supporting fixture will also lead to deformation.

Deformation prediction and error compensation are widely studied in the current research. Ferry et al. [4] presented the method of cutting force prediction for the five-axis flank milling of jet engine impellers. Altintas et al. [5, 6] proposed the concept of virtual compensation and presented a mathematical model of error prediction and digital compensation process in the virtual environment before actual processing. Some scholars developed the flexible deformation prediction model to achieve a better prediction accuracy [7,8,9,10]. To solve the problem of the low computational efficiency of the flexible deformation prediction model, Wang et al. [11] proposed fast deformation prediction compensation methods, which improved the computational efficiency of the flexible deformation prediction model through fast convergence. Although many deformation prediction methods have been studied, there are still many problems in the practical application of compensation algorithms. Such as the over-cutting phenomenon caused by applying the compensation method or the increase of machining time caused by multiple compensation processes due to an inaccurate prediction model.

Some scholars considered the material removal sequence planning to reduce the machining deformation. Koike et al. [12, 13] proposed a design method of material removal sequence to minimize the cantilever workpiece displacement at cutting points generated by adding materials from the final to initial workpiece shapes. Based on this, Wang et al. [14] extended an improved cutting sequence optimization algorithm that combined the finite element method (FEM) to reduce the maximum workpiece deformation. While these works mainly focused on designing the material removal sequence to reduce deformation, some other researchers concentrated on planning the material removal amount to homogenize deformation. Ma et al. [15] presented an instantaneous cutting amount planning method for thin-walled surface parts based on position-dependent rigidity by scheduling the feed speed.

Studying the stiffness characteristics of weakly rigid thin-walled parts is necessary, some scholars use the allowance planning method to enhance the workpiece stiffness. Tian et al. [16] proposed a non-uniform allowance (NUA) method based on eigenvalue sensitivity to improve the process stiffness of thin-walled parts. Lutfi et al. [17] proposed a methodology for selecting stock shape and tool axis to improve the stability of thin-wall parts, compared the influence of constant allowance and variable allowance, and generated the corresponding machining tool path. Wu et al. [18] adopted a regional processing strategy to design NUA for blades, and the experimental results proved that NUA could improve surface accuracy compared with uniform allowance (UA). All these studies show that NUA can improve workpiece stiffness, but most focus on solving the problems of chatter and machining stability.

Shan et al. [19] carried out NUA planning for blades based on the geometric shape of the workpiece. Linear and sinusoidal function distribution are applied to the blade radial and section line direction, respectively. Specifically, the allowance thickened linearly from tip to root of the blade, and the allowance at the blade’s leading edge and trailing edge are the smallest, while the allowance at the midpoint of the convex and concave surface is the largest. However, this geometry-based NUA method did not consider the workpiece material characteristics and material removal. Chen et al. [20] introduced an allowance optimization method by genetic algorithm, which established a parameterized finite element model to consider the influence of coupling relation between different layers and the change of stiffness on deformation. Yan et al. [21] described a multi-pass semi-finishing tool path planning strategy of the variable cutting depth for thin-wall parts to shorten the machining time and control the deformation. With deformation as the constraint, the cutting depth is obtained by determining the maximum cutting force at the cutting contact. However, they obtained the workpiece stiffness characteristics depending on experimental calibration. Hou et al. [22] proposed an optimization method of variable radial depth for the thin-walled blade based on the stable-state deformation field, which determined workpiece stiffness using the FEM.

According to Hooke law, machining deformation is mainly affected by workpiece stiffness and cutting force. Considering that the allowance determines the cutting force, and the workpiece stiffness is also affected by the allowance distribution, this indicates that the deformation is closely related to the allowance. The research on the effect of NUA on deformation is mainly based on simple stiffness and deformation analysis. To the authors’ best knowledge, few existing studies on controlling deformation by NUA planning of thin-walled parts have considered stiffness variations to establish the relationship between allowance and deformation, which cannot maximize the role of stiffness optimization.

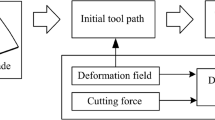
In this paper, an NUA planning method for thin-walled parts based on deformation constraints is proposed as an example of a thin cantilever plate, which does not require the experimental method for stiffness measurement and modeling. The influence of material removal on stiffness is analyzed by assembling the element stiffness matrix and adding elements in a reverse cutting sequence, and the relationship between deformation and allowance is established. First, the FEM is used to analyze the stiffness at different positions on the workpiece surface to determine the maximum cutting force that every point can bear under the allowable deformation of the workpiece. Next, the allowance can be selected as much as possible by establishing the relationship between cutting force and allowance. Then, starting from the final geometric model of the workpiece, the element to be added is determined subject to the maximum allowance, which is added in the reverse cutting sequence, and the stiffness is updated. Therefore, the stock shape of the workpiece is determined according to the added allowance. Finally, the effectiveness of the proposed method is verified by simulation and machining experiments, and the proposed method is compared with the traditional UA and geometry-based NUA methods.

Henceforth, this paper is structured as follows. Section 2 presented the cutting force threshold calculation method in detail. Section 3 provided the NUA planning method based on the cutting force model. Section 4 performed the simulation and physical cutting experiments, and the conclusions are summarized in Section 5.

2 Cutting force threshold calculation under the deformation constraint

For the machining process of thin-walled parts, the machining deformation is affected by many factors, the most important of which are cutting force and stiffness, so it can be controlled by reducing cutting force or increasing stiffness. However, the cutting force will also increase when the workpiece stiffness is enhanced by increasing the allowance. The stiffness and cutting force are not simple linear changes, so the relationship between machining allowance and deformation is complicated to calculate directly. In this paper, an NUA planning method based on deformation constraint is proposed to reserve as much allowance as possible within the allowable deformation range. The machining allowance is determined according to the maximum cutting force of the CC point on the workpiece surface under the allowable deformation, and the allowance is added to the workpiece geometric model along the reverse machining sequence to obtain the finishing stock shape. This section mainly calculates the maximum cutting force that the CC point can bear under the allowable machining deformation, that is, the cutting force threshold under the deformation constraint Fmax, which is used as the basis for adding the allowance in reverse.

2.1 Establish the global stiffness matrix K G

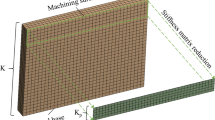
For a better description of the algorithm in this paper, a thin cantilever plate with one end fixed (see Fig. 1) is used as the sample to be machined. As for the thin plate shown in Fig. 1, its stiffness is poor and position-dependent due to its structural characteristics. Let k (x, z) represent the stiffness at a point P on the workpiece surface S. Different from the direct measurement of stiffness by the experimental method in [21], k (x, z) is obtained by the FEM in this paper, and it is represented by the node stiffness matrix Knd. Moreover, the global stiffness matrix KG needs to be established first.

Fig. 1
figure 1

The CAD model and FE model of the thin plate

Full size image

According to the FEM, the workpiece model is meshed to obtain the finite element model, as shown in Fig. 1(b), thus bringing the element stiffness matrix Ke. Since the workpiece in this paper is a simple thin plate, the hexahedron element with eight nodes is used. The global stiffness matrix KG can be obtained by assembling each element stiffness matrix by encoding the sequence of nodes:

$${K}^{G}=\sum {K}^{e}\text{=}\left(\begin{array}{ccc}{K}_{11}& \dots & {K}_{1n}\\ \vdots & \ddots & \vdots \\ {K}_{n1}& \cdots & {K}_{nn}\end{array}\right)$$
(1)

where n is the number of nodes, Kij (i,j = 1,2,…,n) is the global stiffness matrix coefficient. Then, the global stiffness equation is established as follows:

$$\left(\begin{array}{ccc}{K}_{11}& \dots & {K}_{1n}\\ \vdots & \ddots & \vdots \\ {K}_{n1}& \cdots & {K}_{nn}\end{array}\right)\left(\begin{array}{c}{\delta }_{1}\\ \vdots \\ {\delta }_{n}\end{array}\right)=\left(\begin{array}{c}{F}_{1}\\ \vdots \\ {F}_{n}\end{array}\right)$$
(2)

where \(\delta_i\) is the nodal displacement of ith node, Fi is the associated nodal force, and Kij represents the force needed to be exerted on the ith node to cause the unit displacement of the jth node when the displacement component of the other nodes is zero.

2.2 Calculate the cutting force threshold F max

For Knd plays as a precondition for the further calculation of Fmax, the calculation method of Knd is described firstly. The global flexibility matrix PG is obtained by inverting the global stiffness matrix KG as Eq. (3). It should be noted that a nodes re-sorting method based on the calculation order of the matrix blocks in LU decomposition and inverse calculation, as reported by Xi [23], is used to improve the inverse calculation efficiency of the stiffness matrix.

$${P}^{G}={({K}^{G})}^{-1}\text{=}\left(\begin{array}{ccc}{P}_{11}& \dots & {P}_{1n}\\ \vdots & \ddots & \vdots \\ {P}_{n1}& \cdots & {P}_{nn}\end{array}\right)$$
(3)

It can be obtained from Eq. (2) and Eq. (3):

$$\left(\begin{array}{ccc}{P}_{11}& \dots & {P}_{1n}\\ \vdots & \ddots & \vdots \\ {P}_{n1}& \cdots & {P}_{nn}\end{array}\right)\left(\begin{array}{c}{F}_{1}\\ \vdots \\ {F}_{n}\end{array}\right)=\left(\begin{array}{c}{\delta }_{1}\\ \vdots \\ {\delta }_{n}\end{array}\right)$$
(4)

in which, Pij (i,j = 1,2,…,n) is global flexibility matrix coefficient.

Since the workpiece is only subjected to the cutting force at the CC point at a specific moment in the milling process, it is assumed that the nodal force Fi is applied only at node i while the nodal force on all the other nodes is equal to zero, then,

$${P}_{ii}{F}_{i}={\delta }_{i}$$
(5)

Refer to Eq. (5), the following expression is obtained:

$${F}_{i}={\delta }_{i}{\left({P}_{ii}\right)}^{-1}$$
(6)

That is, given the nodal displacement δi, the associated nodal force Fi can then be calculated from Eq. (6) when the other nodal force is zero. Hence, (Pii)−1 of Eq. (6) is the node stiffness matrix Knd that must be obtained. Let Pii be denoted as the node flexibility matrix Pnd, then,

$${P}_{nd}={P}_{ii}$$
(7)

Hence, Knd is obtained by inverse Pnd:

$${K}_{nd}={P}_{nd}^{-1}$$
(8)

Since each node has three degrees of freedom in each direction, Knd can be expressed as the following form:

$${K}_{nd}=\left(\begin{array}{ccc}{k}_{xx}^{nd}& {k}_{xy}^{nd}& {k}_{xz}^{nd}\\ {k}_{yx}^{nd}& {k}_{yy}^{nd}& {k}_{yz}^{nd}\\ {k}_{zx}^{nd}& {k}_{zy}^{nd}& {k}_{zz}^{nd}\end{array}\right)$$
(9)

where the first value of the footnote of knd ij represents the direction of the force, and the second value of the footnote of knd ij represents the direction of the stiffness, i.e., knd xy represents the stiffness value in the y-direction under the action of the cutting force in the x-direction.

The allowable deformation determined in combination with the actual machining condition is δ, so the maximum deformation δmax at each node is equal to δ. Therefore, the maximum force that the node can bear Fndmax can be calculated as

$${F}_{nd\;\mathrm{max}}={K}_{nd}\;{\delta }_{\mathrm{max}}\text{=}\left(\begin{array}{ccc}{k}_{xx}^{nd}& {k}_{xy}^{nd}& {k}_{xz}^{nd}\\ {k}_{yx}^{nd}& {k}_{yy}^{nd}& {k}_{yz}^{nd}\\ {k}_{zx}^{nd}& {k}_{zy}^{nd}& {k}_{zz}^{nd}\end{array}\right)\left(\begin{array}{c}{\delta }_{x\mathrm{max}}\\ {\delta }_{y\mathrm{max}}\\ {\delta }_{z\mathrm{max}}\end{array}\right)\text{=}\left(\begin{array}{c}{F}_{x\mathrm{max}}\\ {F}_{y\mathrm{max}}\\ {F}_{z\mathrm{max}}\end{array}\right)$$
(10)

The node nearest to the CC point in the FE model is approximately regarded as the CC point in the machining process, and Fmax can be expressed by Fndmax, that is,

$${F}_{\mathrm{max}}\text{=}{F}_{nd\;\mathrm{max}}$$
(11)

3 NUA planning method of thin plate

For cantilevered thin-walled parts in milling, the machining deformation is severely due to the poor stiffness of the workpiece, which is terrible for the machining quality. In this study, the NUA planning method based on workpiece deformation constraint is presented to reduce the machining deformation, with the idea of adding materials in the reverse material removal sequence. It strives to maximize the allowance to enhance the stiffness of the in-process workpiece, that is, to control the deformation according to the allowance. The cutting force model is established, which is used to obtain the relational model of the allowance calculated by cutting force. Based on this, the maximum allowance aemax at the node is calculated according to Fmax. And the finishing stock surface is finally fitted so that the deformation at all points on the workpiece surface after finishing is under the allowable deformation. Then, the global stiffness matrix of the workpiece is updated by adding elements in a reverse cutting sequence until the allowance of all nodes is calculated. Finally, the NURBS surface is used to fit the finishing stock surface.

3.1 Calculation of maximum allowance based on cutting force model

In this paper, flank milling of the end milling cutter is used to machine the thin plate (see Fig. 2) because it is line contact and has higher processing efficiency, where ae is the radial depth, and ap is the axial depth.

Fig. 2
figure 2

The schematic diagram of flank milling

Full size image

Since much research has been done on this technique, this paper adopts the cutting force model proposed by Altintas [24] and briefly introduced here. The differential radial (dFr, j), axial (dFa, j), and tangential (dFt, j) forces acting on a differential element with height dz are expressed as follows:

$$\left\{\begin{array}{c}dF_{r,\;j}(\phi,z)=\lbrack K_{rc}h_j(\phi_j(z))+K_{re}\rbrack dz\\dF_{a,\;j}(\phi,z)=\lbrack K_{ac}h_j(\phi_j(z))+K_{ae}\rbrack dz\\dF_{t,\;j}(\phi,z)=\lbrack K_{tc}h_j(\phi_j(z))+K_{te}\rbrack dz\end{array}\right.$$
(12)

where hj (ϕ, z) is the instantaneous chip thickness, ϕ j(z)is the immersion angle for flute j at the axial depth of cut z. Kre, Kae, and Kte are the edge cutting coefficients and Krc, Kac, and Ktc are the shear force coefficients, which all depend on the material and size of the tool and workpiece and can be identified by the orthogonal cutting testing method [25].

The directions of the cutting forces are aligned with the cutter axis. The elemental forces are resolved into feed (x), normal (y), and axial (z) directions using the transformation as follows:

$$\left\{\begin{array}{l}dF_{x,\;j}(\phi,z)=-dF_{r,\;j}(\phi,z)sin\;\phi_j(z)-dF_{t,\;j}(\phi,z)cos\;\phi_j\;(z)\\dF_{y,\;j}(\phi,z)=dF_{t,\;j}(\phi,z)sin\;\phi_j(z)-dF_{r,\;j}(\phi,z)cos\;\phi_j\;(z)\\dF_{z,\;j}(\phi,z)=dF_{a,\;j}(\phi,z)\end{array}\right.$$
(13)

The differential cutting forces are integrated analytically along the in-cut portion to obtain the total cutting force produced as follows:

$$\left\{\begin{array}{c}F_x(\phi)=\sum\limits_{j=1}^N\sum\limits_{z=0}^{a_p}dF_{x,j}(\phi,\;z)\\F_y(\phi)=\sum\limits_{j=1}^N\sum\limits_{z=0}^{a_p}dF_{y,j}(\phi,\;z)\\F_z(\phi)=\sum\limits_{j=1}^N\sum\limits_{z=0}^{a_p}dF_{z,j}(\phi,\;z)\end{array}\right.$$
(14)

The cutting experiments are performed on the KMC-400SU five-axis CNC machining center to obtain the cutting force coefficients, and the cutting forces are measured using a Kistler 9129AA dynamometer. The workpiece material used in our physical cutting experiments is 7075 aluminum alloy, and the cutting tool is S-400 series aluminum end milling cutter with a diameter of 8 mm, a helix angle of 45°, and three flutes. The experimental platform and process are shown in Fig. 3. The cutting force coefficients calibrated from the cutting experiments are shown in Eq. (15), with units of N/mm2.

Fig. 3
figure 3

Cutting force identification experimental platform and experimental process

Full size image
$$\begin{array}{l}{K}_{rc}=574.565,{K}_{re}=48.802\\ {K}_{tc}=-1214.299,{K}_{te}=-36.817\\ {K}_{ac}=-337.555,{K}_{ae}=-2.009\end{array}$$
(15)

The established model is simulated with the different parameters as the cutting force coefficient identification experiment to verify the correctness of the model, and the comparison with the experimental results is shown in Fig. 4. The maximum deviation between the predicted and experimental data in the x, y, and z directions is 5.73%, 12.8%, and 11.58%, respectively. Moreover, the average deviation between the predicted and experimental data in the x, y, and z directions is 2.57%, 5.05%, and 7.2%, respectively. Therefore, the data predicted by the cutting force model and the experimental data have slight differences, which can be considered that the calculation results of this model are valid.

Fig. 4
figure 4

Comparison of predicted and experimental results

Full size image

Refer to Eq. (12) - (15), given ns, f, ap, ae, Fx, Fy, and Fz can be calculated. Since the deformation of the thin plate mainly occurs in the workpiece thickness direction (see Fig. 2y-direction), it is considered that only the force component in the y-direction Fy causes the deformation of the workpiece. And this paper mainly considers radial depth ae for allowance planning, so the relationship model between cutting force and allowance is established as follows:

$${F}_{y}\text{ = }f({a}_{e})$$
(16)

However, this paper needs to calculate ae according to Fy, so the inverse operation of Eq. (16) is required, that is, aemax = f −1(Fymax). Since the relationship between aemax and Fymax is not linear, a cubic polynomial fitting is used, and the steps are as follows:

  1. (1)

    Given the value range and interpolation interval of ae, a group of Fy can be calculated according to Eq. (16)

  2. (2)

    Construct cubic polynomials as Eq. (17), and get the values of coefficients p1, p2, p3, and p4 by using polynomial fitting

    $${a}_{e}={p}_{1}{{F}_{y}}^{3}+{p}_{2}{{F}_{y}}^{2}+{p}_{3}{{F}_{y}}^{1}+{p}_{4}$$
    (17)

Thus, given the cutting force threshold in y-direction Fymax, the corresponding maximum allowance aemax can be calculated.

3.2 NUA planning method

Based on the calculation method of aemax at a single node in Section 3.1, aemax at any node can be calculated. However, KG of the workpiece changes continuously with material removal during machining. Therefore, this paper realizes the overall allowance planning by adding elements and calculating the allowance along the reverse material removal sequence. The overall allowance planning algorithm for the thin-walled parts is summarized in Fig. 5, and the detailed steps are as follows.

  • Step 1: determine the initial workpiece blank model and divide the mesh. According to the allowable allowance, the initial blank model is determined, composed of the workpiece part and the allowance part. Thus, two types of elements are divided: base element (elebs) and candidate element (elecandidate), which is achieved in HyperMesh (see Fig. 6(a)). Afterward, the FE model is imported into ANSYS, and the element stiffness matrix Ke is obtained using the /DEBUG command in the ANSYS parametric design language (APDL).

  • Step 2: assemble the initial workpiece global stiffness matrix [KG]w according to the method in Section 2.1, where the initial workpiece is composed of all elebs. Note that the computational efficiency of assembly [KG]w can be improved by reordering the nodes, in which the nodes that comprise the initial workpiece part are numbered first. In addition, since the internal structure of the initial workpiece part does not change during the processing, [KG]w is regarded as the stiffness matrix of a big element and stored, which can be directly called in the subsequent calculation to avoid repeated calculation.

  • Step 3: determine the nodes of the workpiece surface involved in the calculation according to the material removal sequence and cutting parameters, e.g., ns, f, and ap.

  • Step 4: set initial values for m = 1 and n = 1, representing the first node in the first row of the workpiece surface involved in the calculation.

  • Step 5: calculate Knd and Fndmax according to the method in Section 2.2.

  • Step 6: calculate aemax through Eq. (17) and modify aemax according to the allowance range, as shown in Eq. (18).

    $$a_{e\;max}\;'=\left\{\begin{array}{l}a_{e,\mathrm{upper}}\;\;\;\;\;\;\;a_{e\max}\;\geq a_{e,\mathrm{upper}}\\a_{e\max}\;\;\;\;\;\;\;\;\;\;a_{e,\mathrm{upper}}\;>a_{e\max}\;\;>a_{e,\mathrm{lower}}\\a_{e,\mathrm{lower}}\;\;\;\;\;\;\;\;a_{e\max}\;\leq a_{e,\mathrm{lower}}\end{array}\right.$$
    (18)

    where ae,upper and ae,lower represent the upper and lower limits of the allowance, respectively.

  • Step 7: add candidate elements and update [KG]w. The elements to be added are selected from the candidate element according to aemax’ and added to the initial workpiece to form a new workpiece, as shown in Fig. 6(b). Considering the small amount of material removal in the finishing process, to improve the calculation efficiency, [KG]w is updated after each row of nodes is calculated. It should be noted that steps 2 to 7 above are all implemented through MATLAB programming.

  • Step 8: Construct the finishing stock model. With the allowance at all nodes obtained, the coordinates of nodes are offset according to the calculated allowance value. Where the values of x and z coordinate at the node do not change, and the values of y coordinate values are calculated as follows:

    $$y\;'=\left\{\begin{array}{l}y+a_{e\max}\;\;\;\;\;\;\;\;\;\;y=y_{up}\\y-a_{e\max}\;\;\;\;\;\;\;\;\;\;y=y_{down}\end{array}\right.$$
    (19)

    where y’ is the offset y coordinate, yup and ydown are the y coordinate value of the upper surface and the lower surface of the thin plate, respectively. And then, the stock surface of the finish machining operation is obtained by fitting the offset points with the NURBS surface. The related case is shown in Section 4.1.

Fig. 5
figure 5

Flowchart of NUA planning for thin-walled parts

Full size image
Fig. 6
figure 6

Schematic diagram of initial blank mesh division and adding elements

Full size image

4 Static deformation simulation and cutting experiment

4.1 Generation of the finishing stock based on the NUA method

The proposed NUA planning method has been verified in the finishing milling of a thin plate through both static deformation simulation and cutting experiments. The material of the experimental workpiece is 7075 aluminum alloy, the theoretical model size after finishing is 60 × 40 × 2 mm, and the finishing allowance is obtained by semi-finishing. To better fit the cantilever blade processing condition, the allowable deformation δ of the thin plate is set as 0.05 mm, and the size of the initial workpiece stock is 60 × 40 × 4 mm. The finishing machining parameters are shown in Table 1, so the relation between ae and Fy can be expressed as Eq. (20). The removal sequence of the finishing materials is shown in Fig. 7, where materials in each row are removed in the direction of the feed.

Table 1 Parameters of finish machining experiment
Full size table
Fig. 7
figure 7

Schematic diagram of thin plate and material removal sequence for experiment

Full size image
$${a}_{e}=-2.041\times {10}^{-7}{F}_{y}^{3}+7.479\times {10}^{-5}{F}_{y}^{2}+1.693\times {10}^{-3}{F}_{y}-0.01109$$
(20)

Based on the above, the allowance planning results for the thin plate by using the method proposed in this paper are shown in Fig. 8, where (a) and (b) are the allowance distribution points of side A and B, respectively, and (c) is the finishing stock model obtained by using NURBS surface to fit the allowance distribution points. Note that the NURBS surface fitting is done by secondary development of NX through C +  + language, and then the fitted surfaces are applied to model the finishing stock in NX.

Fig. 8
figure 8

NUA planning results of the experimental thin plate

Full size image

4.2 Static deformation simulation

The static deformation of the thin plate finishing stock under the concentrated force is simulated to approximate the deformation of the stock under the cutting force. Since the free-end of the thin plate has the worst stiffness and most significant deformation, the deformation of the midpoint p on the edge line of the free-end under force F = f (ae,p) is approximately regarded as its maximum deformation δmax. The simulation results for the stock in Fig. 8(c)are shown in Fig. 9(a), δmax of the stock is 0.0482 mm, which is less than δ, indicating that the method presented in this paper is effective.

Fig. 9
figure 9

Simulation results of workpiece deformation under different allowance strategies

Full size image

Ten UA schemes are selected for simulation to facilitate comparison between the presented NUA method and the traditional UA method, which are in the allowance range of 0–1 mm with an interval of 0.1 mm. The simulation result diagram of ae = 0.5 mm is compared with the NUA method in this paper, as shown in Fig. 9(b), and the values of maximum deformation obtained by ten simulation groups are listed in Table 2.

Table 2 Static deformation of different UA schemes
Full size table

The results in Table 2 show that within a given allowance range, δmax gradually increases and then decreases with the increase of ae. It shows that when the allowance is large, the influence of stiffness on deformation is more significant than that of cutting force, while when the allowance is small, the influence of cutting force on deformation is more significant. In addition, compared with the UA scheme, it is found that the deformation of the proposed NUA scheme in this paper is much smaller than that of any UA scheme.

However, as a result of adopting some assumptions and ignoring the stiffness variations caused by material removal in static simulation, the simulation results can only be used to roughly compare the deformation of the two allowance planning methods.

4.3 Cutting experiments

The machining verification experiment is conducted based on the proposed NUA method, denoted as experiment 1. A five-axis CNC machining center KMC-400SU is used in the experiments. The tool used in finishing is a carbide end milling cutter with a diameter of 8 mm, the same as the tool used in the cutting force coefficient identification experiment. Due to the deformation of the thin plate mainly occurring at the free end, only the upper part near the free end is machined. The machining deformation of the thin plate after machining is measured by wireless probe RMP30 of Renishaw, and the process of machining and measuring is shown in Fig. 10. The measuring points are selected according to the machining tool path, where 5 × 7 measuring points are selected on each side, as shown in Fig. 11.

Fig. 10
figure 10

Machining process and measurement of the experiments

Full size image
Fig. 11
figure 11

Distribution of measuring points

Full size image

The measurement results show that the machining errors of the measuring points range from 0.004 mm to 0.035 mm, which are all less than the given allowable deformation of 0.05 mm, indicating that the NUA planning method based on deformation constraints can control the machining errors within the allowable deformation.

To further illustrate the advantages of the proposed method, the geometry-based NUA planning method described in [19] and the traditional UA planning method are respectively used for the allowance planning of the thin plate. The corresponding experiments are carried out with the same initial blank, finishing tool trajectory, and cutting parameters as the first experiment, denoted as experiment 2 and experiment 3, respectively. Combined with the processing technology and static deformation simulation results, the UA of experiment 3 is selected as 0.5 mm.

Figure 12 shows the thin plates machined with three different allowance planning strategies. The machining error diagram is drawn to compare the measurement results of the three experiments, as shown in Fig. 13. The overall machining error of the workpiece in experiment 2 is 0.056–0.119 mm, and that in experiment 3 is 0.096–0.165 mm, both of which are larger than that in the first experiment. Compared with the other two allowance strategies, the NUA planning strategy in this paper has the slightest machining error, and the machining error distribution is more uniform and is not affected by the cantilever position.

Fig. 12
figure 12

The thin plates machined with three different strategies

Full size image
Fig. 13
figure 13

Comparison of machining error of three allowance planning strategies

Full size image

Several evaluation indices for the machining error are employed to compare the three strategies more directly, i.e., the average error, the error standard deviation, and the percentage reduction in error of the two NUA strategies over the UA strategy (see Table 3). The results show that, compared with experiment 3, the machining error on side A and side B of the thin plate in experiment 2 are reduced by 29.4% and 41.8%, respectively. Moreover, the machining error of side A and side B in experiment 1 is reduced by 82.6% and 82.5% compared with experiment 3. The reason for this phenomenon is that the geometry-based NUA method is only related to the geometry of the workpiece but does not consider the stiffness change caused by material removal. However, the allowance planning method proposed in this paper takes into account the stiffness changes affected by position and material removal, so it can not only reduce the machining error but also make the error distribution more uniform.

Table 3 Error evaluation of three allowance planning strategies
Full size table

5 Conclusion

The paper presents a non-uniform machining allowance planning method for thin-walled parts based on the workpiece deformation constraint to reduce machining deformation. Compared with conventional error compensation methods, the proposed method does not require accurate deformation prediction and extensive experiments but improves the workpiece stiffness during machining by retaining as much allowance as possible. First, the maximum cutting force that can be born at the contact position is determined according to the allowable deformation constraints. Then, the maximum allowance of the point is determined by the corresponding maximum cutting force. Finally, the whole allowance planning is carried out by adding elements in reverse, and the finishing stock is obtained by surface fitting. The results of static deformation simulation and machining experiments show that the overall deformation of the workpiece can be controlled within the allowable deformation using the NUA planning method. It is shown that the proposed method can reduce the machining error by about 83% compared with the traditional UA planning method. In addition, the proposed method can make the error distribution more uniform than the NUA method based on geometry. The research in this paper provides an idea for the deformation control of thin-walled blades and will be applied to the allowance planning of finishing machining of thin-walled parts with complex surfaces such as blades in future research.