A novel estimation of tearing limit in deep drawing process based on strain energy; experimental characterization and numerical validation

Abstract

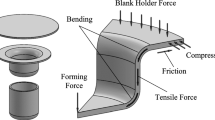
Deep drawing is a forming process widely used in aerospace, military, automotive, and various industries. One of the essential useful parameters in the quality of deep-drawn products is blank holder force (BHF). By controlling BHF during the forming process, formability can be improved and it can reduce forming energy. Tearing is one of the most common and crucial defects in this process due to high radial stress in the cup’s wall, resulting in many limitations in this field. In this process, the BHF plays an indispensable role in causing tearing. Therefore, controlling BHF during the process would be inevitable to avoid tearing or even wrinkling. This study aims to calculate the tearing limit with new criteria in analytical dominating plasticity equations based on the slab method. The St14 sheet with 1 mm thickness and 200 mm diameter is used in this study. The maximum BHF in each stage of punch stroke with new criterion based on strain energy with three different frictional coefficients is calculated, compared, and verified with FEM simulation and experimental results. Analytical results with new criterion are also compared with previous procedures. Finally, it is realized that results related to energy criteria have a lot more similarity with FEM simulation and experimental results in comparison with the previous methods.

1 Introduction

A manufacturing company’s mission today is to create high-quality products with no defects, reduce lead times, and increase production rates. Metal forming is an integral part of deformation-based manufacturing. These mechanical components can be found in automobiles [1], aerospace [2], home appliance industry [3], and food industry [4]. In addition to its strength and durability, metal manufacturing is also crucial for all sectors of the economy. It is possible to fabricate metal components in as many ways as desired, but deep drawing is the most common metal forming process used when a cup-like cylindrical component is to be made by radially drawing the metal blank into a die. With deep drawing, metals are reshaped while still solid by taking advantage of the plasticity of certain metals. In order to plastically deform a metal, more force must be applied than the yield strength. The deep drawing process, however, entails a number of problems including wrinkles, ruptures, tearing, and cracking. Several methods can be used to identify and detect the process parameters used during the forming process. Many key parameters are taken into account in deep drawing, including BHF, friction coefficient, die configuration, and material characterization. For assessing the effect of process parameters and determining the optimal process parameters in deep drawing, researchers have recently proposed online monitoring methods. Using deep drawing parameters, Dwivedi and Agnihotri [5] identified directions for future research, and the results of the present study demonstrated the production of aluminum alloy cups successfully. Numerous studies have been conducted on the experimental aspect of key process parameters and the impact they have on objective function [6,7,8,9,10].

As demonstrated by Padmanabhan et al. [11], variables such as die radius, holder force, and friction coefficient affect the deep drawing characteristics of axis-symmetric stainless steel cups more than other parameters. In addition to the BHF and the friction coefficient, the small die radius can also affect the BHF and the friction coefficient. Experimentally, Afshin and Kadkhodayan [12], shown in a deep drawing process using laminated sheets, demonstrate the ability to thin and wrinkle materials such as Al 1050/St 304 and Al 5052/St 304. As a result of the study, their results indicate that the BHF determines the forming load variation when the temperature is raised. Research by Reddy et al. [13] has investigated the effects of key process parameters (punch nose radius, die shoulder radius, and BHF). Consequently, the BHF (56.98%) was the most significant parameter, followed by punch nose radius (30.12%), and the die profile radius (12.90%) was the least significant parameter. The influence of the aluminum alloy AA5754-O on the blank holder and sheet plate during the forming process was investigated by Demirci et al. [14] by applying variable forces in a computer-controlled manner to the blank holder and sheet plate. According to their findings, the best formation occurred at a pressure of 5 MPa. In [15], numerical analysis and experimental validation of deep drawing were performed for the purpose of preventing thinning and wrinkles. Deep-drawn cups commonly tear due to a crack near the bottom of the vertical wall caused by high tensile stress that results in thinned and cracked metal. Two analytical approaches are proposed to predict the safe area in the forming operation: slab [16] and upper bound [17]. Friction is considered in the slab method (SM), also called stress local analysis method (SLA). Consequently, the results obtained by employing this method are generally better than the ones obtained by using other methods. Rubio [18] evaluated tube drawing processes by an analytical model employing the slab method (SM) and the upper bound method (UBM). The plastic deformation zone is also modeled using triangular rigid zones (TRZ). In order to understand the wrinkling limit diagram for two-layer sheets, Bagdad and Hashemi [19] used a mathematical model, a numerical method, and experimental tests. The authors conclude that material properties, blank geometry, and stack order influence optimum BHFs. During deep drawing of two-layer (aluminum-stainless steel) sheets, we developed an analytical method, performed numerical simulations, and performed experiments to investigate the effects of wrinkling [20]. Our results show that the optimum BHF is affected by the geometry of the sheet, the properties of the material, and the layup. The study by Gharib et al. [21] proposes an optimization method for linearly varying BHF that seeks to minimize the maximum punch force and avoid process limitations. In their study, they found that the slope of the linear BHF increases linearly with drawing ratio. Additionally, the intercept of the function showed a nearly linear relationship to the drawing ratio. Following is an equation that shows what force is optimal regardless of drawing ratio. Because metal parts are nonlinearly deformed, there are many different types of stress distributions. Large deformations can cause meshes to distort and generate defects [22]. For this reason, selecting the right formulation for developing an appropriate FE model for the problem is crucial. Sugiyanto et al. [23] developed a finite element model based on the finite element method (FEM) to evaluate the effect of a blank holder on the deep drawing process. The clearance variable should result in a decrease in the force required for deep drawing, according to simulations of this process without blank holders. Nevertheless, the force required for the drawing will still be greater. A 3-D finite element simulation was used to analyze the hydro-mechanical deep drawing process of anisotropic laminated bimetallic sheets with an implementation of a Fortran-based code to accurately model the distribution of non-uniform oil pressure in Bagherzadeh et al. [24]. As part of their study of force control in deep drawing, Yoshihara et al. [25] used finite element simulations to verify the LDR of magnesium alloy sheets. In FEM simulations, we confirm that the behavior resembles that observed in experiments, with *-rupture occurring during the fracture at the wall. Sheng et al. [26] developed an adaptive simulation strategy during the simulation process. By doing so, it is possible to predict a BHF profile from a single simulation, thereby reducing computation time. The proposed strategy has been successfully applied to several conical cup drawing operations. To compare the predictions, experimental results have been used, and they show that the adaptive simulation strategy may also be useful for improving drawing for non-symmetric parts. Qin et al. [27] have developed a blank holding technique that allows BHF to be independently loaded during sheet metal forming using electro-permanent magnets (EPM). The theoretical method and FEM are used to analyze and solve the coupling problem involving the magnetic field and stress field. Also, the new technique can be used to obtain the blank holding force and the BHF on the sheet. Despite the design cushion’s BHF being large enough, the selected sheet could go through a deep drawing process with the BHF applied through the design cushion.

To the best of the authors’ knowledge, there is a lack of investigation for the numerical solution, FEM simulation, and experiment of the deep drawing process for estimating tearing limit with slab method and new criteria based on strain energy. In order to prevent cracking, this study provides a suitable mathematical approach to determine the maximum BHF, tearing threshold, over the punch stroke. Furthermore, a new method based on strain energy was used to predict the tearing limit. The slab method’s methodological perspective with the assumption of a constant volume of material was used to evaluate stress and strain in different stages of deep drawing process. The impact of friction and material anisotropy were also taken into account in this study. In order to assure the accuracy of analytical results, an adequate number of experiments as well as FEM simulations were carried out, and the results of analytical method as well as FEM simulation were verified with the experimental tests. In addition, to evaluate the efficacy of the proposed method based on strain energy, previous methods estimating the tearing limit were compared with this new method, and they were eventually compared and verified with FEM and experimental tests. The following scheme diagram shows the concept of this study as a systematic investigation (Fig. 1). As can be seen from Fig. 1, firstly, FEM simulation was carried out precisely, and then they were verified with experimental ones. After assurance of the FEM simulation accuracy, FEM simulations were done with various BHFs to estimate tearing threshold along the punch stroke. To this end, firstly, it is necessary to calculate the safe area. In the deep drawing process, the region free from tearing and wrinkling is deemed as the safe area (Fig. 9). Indeed, in FEM simulations, all of the deep drawing parameters were considered the constant parameters, and just BHF was altered to obtain their corresponding drawn depth either at the tearing moment or at wrinkling. Furthermore, in the tearing area where BHFs vary from 25 to 200 kN (Fig. 9), a various numbers of h_i(s), according to their corresponding BHF, were obtained from FEM simulations. These h_i(s), then, were considered the inputs for the analytical approach such that they were imported into analytical calculations, and with the usage of these h_i(s), contrary to the previous stage, the corresponding BHFs were calculated. Accordingly, as illustrated by Fig. 1, different BHFs in tearing area (Fig. 9) were firstly used as the inputs in FEM simulation, and then for each BHF, h_i(s) were obtained, and these h_i(s) were used as the inputs in analytical approach for calculating their corresponding BHFs. Finally, the BHFs obtained from analytical approach as well as FEM simulations were compared to each other in accordance with their corresponding h_i(s) (Fig. 12). They were also compared with previous analytical methods to evaluate the practicality of the new criteria to estimate BHF during the deep drawing process (Fig. 12). This method can also be generalized to other cylindrical deep drawing molds to predict tearing threshold with various BHFs along the punch stroke. However, it is mandatory to have sheet metal properties precisely in addition to process parameters including coefficient of friction, die or punch speed, clearance, and the exact dimension of the mold’s components.

Fig. 1

Flow chart of the validation and calculation of BHF_max

This paper present a novel method intended to estimate the tearing limit in deep drawing process with new criterion in analytical dominating plasticity equations based on the slab method. The maximum BHF along the punch stroke with new criterion based on strain energy is calculated, compared, and verified with FEM simulation and experimental tests. Analytical results with new criterion are also compared with the previous ones, and the practicality of this new method is evaluated by three different frictional coefficients. This paper is organized as follows. Section 2 presents analytical method in which BHF_max is calculated with plasticity equation based on slab method in addition to FEM simulation using ABAQUS software and tensile tests based on ASTM E8 [31] to extract sheet’s mechanical properties. In this section, calculations were conducted by MATLAB software. It is followed by experimental studies in Sect. 3. This section describes the steps of deep drawing mold manufacturing and the information associated with mold’s components dimensions and properties. Results obtained using our analytical method based on strain energy, along with an evaluation of its performance using FEM simulation and experimental tests, are presented in Sect. 4. Finally, conclusion and ideas for future works on this issue is presented in Sect. 5.

2 Analytical method

2.1 Radial stress calculation in the flange

In this section, the slab method was used to anticipate the maximum BHF along the punch stroke with the following assumptions (Fig. 2):

• 1. The volume of the sheet during the process is considered constant.

• 2. The Tresca yield criterion is used to calculate the equilibrium stress.

• 3. The metal flow in the flange part is considered a plane strain.

• 4. The effects of friction and material anisotropic are also considered in the analysis.

Fig. 2

Deep drawing process

Axial and radial stresses in an element can be seen from Fig. 3. Under the condition of force equilibrium in an element of the flange and the absence of friction, the radial stress in the form of mathematical equation can be obtained as follows [32]:

$$rd{\sigma }_{r}d\theta {t}_{0}-{\sigma }_{r}{d}_{r}d\theta {t}_{0}-2{\sigma }_{\theta }\mathrm{sin}\frac{d\theta }{2}dr{t}_{0}=0$$

(1)

where r is the inside radius, ${\sigma }_{r}$ is the radial stress, $d\theta$ is a small portion angle of the flange, ${t}_{0}$ is the initial thickness of the sheet, and ${\sigma }_{\theta }$ is the tangential stress in the flange. As $d\theta$/2 is very small, it can be considered to be equal to sin($d\theta$/2). Therefore, by simplifying Eq. (1), the following relation is obtained [32]:

Fig. 3

The equilibrium force diagrams of the flange in a small element

$$d{\sigma }_{r}=({\sigma }_{r}-{\sigma }_{\theta })\frac{dr}{r}$$

(2)

Considering Tresca criterion:

$${\sigma }_{r}-{\sigma }_{\theta }={\sigma }_{f}$$

(3)

By substituting Eq. (3) into Eq. (2) and integrating Eq. (2), the radial stress is obtained at each stroke of the forming process, as follows:

$${\sigma }_{r,i}={\sigma }_{f}\mathrm{ln}\frac{{R}_{1,i}}{{r}_{i}}\;\mathrm{Or}\;{\sigma }_{r,i}={\sigma }_{f}\mathrm{ln}\frac{{d}_{1,i}}{{d}_{i}}$$

(4)

where ${\sigma }_{f}$ is the mean flow stress between points 1 and 2, flange segment, in Fig. 4, ${d}_{1,i}$ is the outer diameter of the blank in each step of the process, and ${d}_{i}$ is the average diameter of the cylindrical cup or the inner die diameter minus the sheet thickness ${(d}_{i}= {d}_{D}-{t}_{0})$.

Fig. 4

Different steps of deep drawing process a first step and b second step

2.2 The effect of sheet anisotropy on radial stress

As can be seen from Eq. (4), radial stress can be calculated, regardless of the anisotropy coefficients. In order to simplify the effect arising from sheet anisotropy on radial stress, Hill’s relation for a planar isotropy material was used in this regard; using this, the following relation is established [28]:

$${\left({\sigma }_{r}-{\sigma }_{z}\right)}^{2}+{\left({\sigma }_{z}-{\sigma }_{\theta }\right)}^{2}+{R\left({\sigma }_{\theta }-{\sigma }_{r}\right)}^{2}=\left(R+ 1\right){{\sigma }_{f}}^{2}$$

(5)

where R is anisotropy coefficient. As sheet thickness’s deviation, just in flange area because of its small deviation, can be ignored, so, in z direction, ${d\varepsilon }_{z}$ can be considered relatively equal to zero. If so;

$${d\varepsilon }_{z}=d\lambda \left[F\left({\sigma }_{z}-{\sigma }_{\theta }\right)-G\left({\sigma }_{r}-{\sigma }_{z}\right)\right]=0$$

(6)

Since, in a Planar isotropy condition, F = G, so:

$${\sigma }_{z}=\frac{{\sigma }_{r}+{\sigma }_{\theta }}{2}$$

(7)

By substituting Eq. (7) into Eq. (5), in case that the equivalent stress is equal to the flow stress, so:

$${\sigma }_{r}-{\sigma }_{\theta }=\sqrt{\frac{2(R+1)}{2R+1}}{\sigma }_{f}$$

(8)

2.3 Calculation of radial stress of the wall in 3 parts of the cup by strain relief

This section aims to estimate the radial stress in different parts of the cup along the punch stroke. As shown by Fig. 3, to calculate radial stress in different parts of the sheet, in this method, the sheet is divided into two parts. Calculating strain at different stages of the process is necessary to calculate stress in the wall during the forming process. With strain at points 1, 2, and 3 of the sheet and plastic properties of the sheet along the punch stroke, it is possible to calculate flow stress in different sheet’s parts using work hardening relations. For this purpose, it is first essential to calculate the outer diameter of the sheet at different deep drawing stages. Considering that the volume of the sheet is assumed constant before and after the process, by writing the equilibrium volume equation for a cylindrical cup with bends, as illustrated by Fig. 2, the outer diameter along punch stroke is obtained as follows: [29]

$${d}_{1,i}=\sqrt{{{d}_{0}}^{2}-4{d}_{D}[{h}_{i}-\left(0.43{r}_{p}-0.43{r}_{D}\right)]}$$

(9)

As shown by Fig. 4, ${h}_{i}$ is the height of the cup or punch displacement, ${d}_{D}$ is the internal diameter of the die,${r}_{D}$ is die edge radius, ${d}_{0}$ is the initial outer diameter of the sheet, and ${d}_{1,i}$ is the outer diameter along punch stroke at different stages of forming process. Accordingly, considering ${d}_{0}$, ${d}_{D}$, ${r}_{p}$, and ${r}_{D}$ are constant and related to die and punch diameters and with ${h}_{i}$ which can be obtained from FEM simulation, we will be able to calculate ${d}_{1,i}$ at different stages of punch stroke. With ${d}_{1,i}$ and ${d}_{0}$, it is possible to calculate the equivalent strain at point 1 at different stages of punch movement, according to Eq. (12).

In order to calculate the equivalent strain at point 2, it is necessary to calculate the length of this point (twice the distance from point 2 to the z-axis, Fig. 4) at different stages of the deep drawing process. Given that the material volume from the initial outer diameter ${d}_{0}$ to the initial stage of the sheet at point 2 (${d}_{int.i}$) is always constant by writing the equilibrium of volume in this distance and at different stages of the punch stroke, the mathematical equation of ${d}_{int,i}$ can be written as follows:

$${t}_{0}\left(\frac{\pi {{d}_{0}}^{2}}{4}-\frac{\pi {{d}_{int.i}}^{2}}{4}\right)={t}_{0}(\frac{\pi {{d}_{1,i}}^{2}}{4}-\frac{\pi {\left({d}_{D}+2{r}_{D}\right)}^{2}}{4})$$

(10)

By simplifying Eq. (10) and having ${d}_{1,i}$ at each stage of the punch stroke and as the other parameters are constant,${d}_{int.i}$ can be calculated at each step of the punch stroke as follows.

$${d}_{int,i}=\sqrt{{{d}_{0}}^{2}+{({d}_{D}+2{r}_{D})}^{2}-{{d}_{1,i}}^{2}}$$

(11)

It is important to note that both of ${d}_{1,i}$ and ${d}_{int.i}$ are functions of the height of the cup or the punch stroke (${h}_{i}$). In other words, ${d}_{1,i}$ and ${d}_{int.i}$ are dependent upon h_i, as other parameters are related to die and punch dimensions and they are constant parameters.

Therefore, by computing ${d}_{1,i}$ and ${d}_{int.i}$ and taking into account the anisotropy of the sheet in calculations. The equivalent strain at points 1 and 2 can be obtained at each stage of the punch stroke from Eqs. (12) and (13), respectively:

$${\varepsilon }_{1,i}=\sqrt{\frac{2(R+1)}{2R+1}}ln\frac{{d}_{0}}{{d}_{1,i}}$$

(12)

$${\varepsilon }_{2,i}=\sqrt{\frac{2(R+1)}{2R+1}}ln\frac{{d}_{int,i}}{{d}_{D}+2{r}_{D}}$$

(13)

After calculating the equivalent strains at points 1 and 2, the mean flow stress between points 1 and 2 can be calculated according to Eqs. (14) and (15) [32]:

$${\sigma }_{f1-2,i}=\frac{1}{2}k\left({\varepsilon }_{1,i}^{n}+{\varepsilon }_{2,i}^{n}\right)$$

(14)

$${\sigma }_{f1-2,i}=\frac{1}{2}k\left({\varepsilon }_{1,i}^{n}+{\varepsilon }_{2,i}^{n}\right)+{\sigma }_{0}$$

(15)

where k is the strength coefficient of the material and n is the strain hardening exponent of material. Depending on the type of work hardening relation, both Eqs. (14) and (15) can be used. In this research, it is worth mentioning that tensile tests were conducted, and the interpolation of stress and strain data were conducted by MATLAB software. According to the MATLAB software’s estimated function, Eq. (15) is used to estimate the work-hardening relation. Besides, taking into account the bending effects in this region, the equivalent strain at point 3 was calculated as follows [29]:

$${\varepsilon }_{3,i}={\varepsilon }_{2,i}+\sqrt{\frac{2(R+1)}{2R+1}}\mathrm{ln}(1+\frac{{t}_{0}}{2{r}_{d}+{t}_{0}})$$

(16)

According to the sheet deformation, when it flows over the die radius and under bending condition, mean flow stress can be anticipated either by Eqs. (17) or (18):

$${\sigma }_{f2-3,i}=\frac{1}{2}k\left({\varepsilon }_{2,i}^{n}+{\varepsilon }_{3,i}^{n}\right)$$

(17)

$${\sigma }_{f2-3,i}=\frac{1}{2}k\left({\varepsilon }_{2,i}^{n}+{\varepsilon }_{3,i}^{n}\right)+{\sigma }_{0}$$

(18)

As the estimated function arising from tensile test data in the plastic region, sheet behavior during the forming process had more conformity with Eq. (18), used as work-hardening relation. MATLAB software was used for regression in which k, n, and ${\sigma }_{0}$ are calculated 359.3, 0.7718, and 223.3 respectively.

2.4 Effect of friction and BHF on the radial stress

Friction between the blank holder and the flange increases the radial stress. BHF can also be considered a line force of magnitude $\frac{{F}_{BHF}}{\pi {d}_{0}}$ per unit length, as can be seen from Fig. 5. The friction force on the flange, per unit length around the edge, was calculated as follows [32]:

$${\sigma }_{r,BHF}=\frac{2\mu {F}_{BHF}}{\pi {d}_{1,i}{t}_{0}}$$

(19)

where ${t}_{0}$ is the initial thickness of the sheet, ${F}_{BHF}$ is the blank holder force, $\mu$ is the friction coefficient, and ${d}_{1,i}$ is the outer diameter along the punch stroke. Therefore, by applying the BHF and considering the effects of sheet anisotropy, the flange’s radial stress can be obtained from calculation according to Eq. (20).

Fig. 5

Effect of BHF on radial stress

$${\sigma }_{r,i}=\sqrt{\frac{2(R+1)}{2R+1}}{\sigma }_{f1-2,i}\mathrm{ln}\left(\frac{{d}_{1,i}}{{d}_{i}}\right)+\frac{2\mu {F}_{BHF}}{\pi {d}_{1,i}{t}_{0}}$$

(20)

By applying friction on all surfaces in addition to the tension in bending at the die radius, the radial stress equation can be written as follows: [29]

$${\sigma }_{r,i}={e}^{\left(\mu \frac{\pi }{2}\right)}\left[\sqrt{\frac{2\left(R+1\right)}{2R+1}}{\sigma }_{f1-2,i}\mathrm{ln}\left(\frac{{d}_{1,i}}{{d}_{i}}\right)+\frac{2\mu {F}_{BHF}}{\pi {d}_{1,i}{t}_{0}}\right]+ {\sigma }_{f2-3,i}\frac{{t}_{0}}{2{r}_{d}}$$

(21)

2.5 Calculation of tearing limit with the energy criterion

2.5.1 Crack initiation criteria

As indicated in the introduction, this study’s analytical purpose is to calculate the tearing limit with a new criterion based on the strain energy. The first criterion for estimation of the crack initiation was the maximum stress of the material (Eq. (22)) [29].

$${\sigma }_{r,1, crack}\ge c.UTS$$

(22)

Previous researchers calculated the tearing limit based on this criterion (Eq. (22)), where UTS is the ultimate tensile stress and c is the cracking factor which should be greater than unity [29]. Since the sheet material is St14 steel in this study, c was considered between 1.05 and 1.55 [29]. In this study, c is considered 1.25, according to tensile tests. This study intends to calculate the tearing limit with the first failure criterion and new criterion based on the strain energy and compare them with simulation and experimental results. The second criterion of failure based on the strain energy is written as follows:

$${\sigma }_{r,2, crack} .{\varepsilon }_{3,i}\ge c.{S}_{UTS}$$

(23)

So:

$${\sigma }_{r,2, crack}\ge \frac{c.{S}_{UTS}}{{\varepsilon }_{3,i}}$$

(24)

where S_UTS is the area under the stress–strain curve and ${\varepsilon }_{3,i}$ is the strain at point 3, where tearing happens. According to Eq. (23), when the strain energy in each element of the wall reaches critical energy, tearing would happen in sheet metal. In other words, if it becomes equal to multiple of the area under the stress–strain curve of the uniaxial tensile test, the sheet will be faced tearing. Therefore, if the wall’s radial stress (${\sigma }_{r,i}$) reaches each of these stresses (${\sigma }_{r,j,crack}$), tearing or cracking on the wall will happen. Finally, F_BHF,max is obtained using Eq. (21). In order to calculate F_BHF,max based on the first and second criteria, ${\sigma }_{r,j,crack}$ is, firstly, obtained using either Eqs. (22) or (24), thereby F_BHF,max is obtained at different stages of the punch stroke using Eq. (25).

$${F}_{BHF,max}\le \frac{\pi {d}_{1,i}{t}_{0}}{2\mu }[\frac{{\sigma }_{r,j,crack}}{{e}^{\mu \frac{\pi }{2}}}-\frac{{\sigma }_{f2-3,i}\frac{{t}_{0}}{2{r}_{D}}}{{e}^{\mu \frac{\pi }{2}}}-\sqrt{\frac{2\left(R+1\right)}{2R+1}}{\sigma }_{f1-2,i}\mathrm{ln}\left(\frac{{d}_{1,i}}{{d}_{i}}\right)]$$

(25)

Therefore, the maximal force is a function of:

$${F}_{BHF,max}=f(k,n,UTS,R,{t}_{0},{d}_{0},{d}_{D},{r}_{p},{d}_{1,i},{h}_{i}{,d}_{int,i},\mu )$$

(26)

2.5.2 Finite element method

In this simulation, a sheet of deformable and 3D element with 1 mm thickness and 200 mm diameter was considered, and other mold parts are simulated in 3D, shell, and rigid instead of the blank, which was considered a 3D and deformable part. For all mold components, the reference points were considered the center of gravity, and each of the volumes was calculated in SOLIDWORKS, and then they were applied in ABAQUS. To extract the sheet’s material properties including modulus of elasticity, stress–strain curve, and anisotropy coefficient, uniaxial tensile tests based on ASTM E8 [31] were applied, as can be seen from Fig. 6a. In order to obtain anisotropy properties of the sheet, the tensile tests were done on three samples, which had been cut in three different directions including parallel, perpendicular, and angle of 45 degrees in proportion to the rolling direction (Table 1). The sheet had a thickness of 1 mm and was tested with a strain rate of 0.001 s⁻¹.

Fig. 6

a Tensile test based on ASTM E8, before necking and b after necking

Table 1 Mechanical properties of St-14 obtained by uniaxial tensile test

In order to estimate the energy needed for ductile failure, the area under the stress–strain diagram was utilized. Then, the stress–strain data of plastic area was imported directly in ABAQUS to simulate sheet’s behavior precisely during metal forming process and to obtain fracture properties of the sheet, considering that the sheet material is of ductile type. To simulate tearing or element removal in ABAQUS using ductile damage criterion, four parameters including strain at crack initiation, stress triaxiality, strain rate, and fracture energy are required.

$$\sigma =\frac{{\sigma }_{H}}{\overline{\overline{\sigma }}}$$

(27)

According to Eq. (27), triaxial stress was calculated. For obtaining fracture properties, the test sample should be similar to standard test samples but at the same time should have a groove in the middle with a determined radius. If the model has a circular cross-section, this groove would be troughout, but if the sample has a rectangular cross-section, the groove is made on both sides of the sample. Of course, by considering the radius of the groove, one can calculate the triaxial stress index. If fracture properties are obtained from the standard sample, the related groove radius should be taken as infinity. Equation (28) is Bridgman modified formula with which the triaxial stress index will work out 0.577 for the standard tensile test sample.

$$\eta =\frac{1}{\sqrt{3}}+\frac{2}{3}\mathrm{ln}(1+\frac{a}{2})$$

(28)

For choosing a suitable element for modeling the sheet, it was referred to the ABAQUS library (Fig. 7). With choosing explicit dynamic elements, three-dimensional stress element, C3D8R element was recognized as ideal for studying the process. The continuous shell element is a 3-dimensional element for modeling high and narrow structures with similar sheet behavior. The use of this element is for thin shells, high deformation, and nonlinear behavior. This element is suitable for the thin shell, high deformation, and nonlinear behavior such as the elastoplastic behavior of material like spring back in the deep drawing process. 3D stress element is a solid element for calculating stress–strain in a 3D space, and studying the possibility of sheet tearing during forming is an appropriate option. It should be mentioned that this element has sheet properties like fracture strain and fracture energy, which can model sheet tearing but cannot directly show the changes in sheet thickness. The continuum shell element is suitable for studying thickness changes, whereas 3D strain elements can be used to study sheet-tearing possibilities and exchange for each other. It was referred to the ABAQUS library for choosing suitable elements for punch, die, and the other mold components. Since the components of mold were rigid shell elements, R3D4 was used. This element cannot describe properties for stress–strain calculation because it is used for the rigid surface without strain. It can only calculate and report force, speed, and torch.

Fig. 7

Exploded view from components of the simulated model in ABAQUS

3 Experiment

The experimental cup is an axial symmetrical cylinder with about 40 mm depth, while its initial and final diameters are 200 and 100 mm, respectively. Punch and die materials were chosen from VCN200 steel to avoid heat treatment and provide a good abrasion resistance against tensile strength tests. The internal diameter was taken 2 mm larger than a punch to avoid friction on the die surface. More looseness would cause the blank after forming would come out of the die easily without deformation. Considering that forming height is variable, the height of the die is taken 105 mm. The blank holder was a ring with a 92-mm internal diameter. The blank holder’s thickness was chosen 25 mm to have an appropriate resistance against the BHF transfer and exertion uniform force to the sheet. Both surfaces of the holder were polished with magnetic grinding to have uniform force transfer on both sides. The punch was designed based on the drawn depth and external diameter of the blank. The material for punch was also VCN200, and the contact surface with sheet and radius of punch angles were the same as the die burnished in three stages. Two rams with st52 material were designed suitable with a hydraulic press and die dimensions. Two standard guideposts for the alignment of mold components were used. In the lower ram, four holes were considered for the passage of press air pin bars. To assembly, the guideposts of mold are fastened to the lower ram with pin and screw, and then the punch is fastened to the middle of the lower ram with pin and screw. The upper ram is also located on guideposts, and after alignment, the holder is placed around the punch, and the die is placed on top of that. Then, with the use of standard holders, looseness between punch and die was adjusted. With the use of pins and screws, the die was assembled on the upper ram. Different parts of the manufactured mold are shown in Fig. 8.

Fig. 8

Different parts of the deep drawing mold (a) punch, blank holder, and guidepost (b) die

It is also crucial to note that parameters, including d₀, d_D, r_p, r_D, t₀, UTS, R, and yield stress, are needed to calculate tearing limit; these parameters related to the dimension of mold’s elements, and sheet properties are listed in Table 2. In addition, the deep drawing process was conducted without lubricant. The friction of coefficient was measured 0.2 for all surfaces, and the die speed was 33 mm/s. A sliding friction test was applied to measure the friction between surfaces in contact with each other. Testing took place by dragging a flat block of known mass across a flat table. Graphs of force, displacement, and time were used to measure both static and kinetic frictions. Defining friction coefficients requires precisely and repeatedly measuring peak forces required to initiate (static) and maintain (kinetic) movement.

Table 2 Die’s element dimensions

4 Results and discussions

This research’s main objective is to introduce and develop a new method for estimating the tearing limit by analytical approach. As a result of this, it is necessary to compare and verify the FEM results with that of the experiment to ensure the accuracy of FEM simulation. After insurance of FEM simulation accuracy, analytical results based on strain energy as well as previous criterion are compared with FEM simulation results, to evaluate the efficacy and practicality of each fracture criterion.

4.1 Comparing and verifying FEM simulation with experimental results

In order to compare and verify FEM simulation with experimental results, first of all, it is imperative to anticipate the safe area by FEM simulation and then determine the area related to tearing limit. Eventually, drawn depth at the tearing moment, which was obtained from FEM, simulation should be compared and verified with that of experimental tests with different BHFs. The safe area in the deep drawing process is referred to as the area in which it is free from tearing and wrinkling. One of the most critical parameters leading to the occurrence of these defects is the BHF. Therefore, researchers present a region as a safe area in which the maximum and minimum force is calculated at different stages of punch stroke. In order to calculate safe area by FEM simulation, all of the deep drawing parameters were considered the constant parameters, and just BHF was altered to obtain their corresponding drawn depth either at the tearing moment or at wrinkling. Tearing threshold and wrinkling threshold, as can be seen from Fig. 9, accordingly, was calculated with different BHFs along the punch stroke. FEM simulation was carried out with friction coefficient of 0.2 and the die speed of 33 mm/s, these two parameters are equal to experimental ones. It is also important to note that 1.6t₀ (sheet thickness) is considered the wrinkling criteria, meaning that when the distance between blank holder and die reach 1.6t₀, wrinkling will happen.

Fig. 9

Safe area plot with FEM simulation $\upmu =0.2,$ $v=33\frac{mm}{s}$

After simulation and conducting experimental tests with these parameters, it was determined that when the BHF become more than 200kN, the sheet cannot move on the blank holder, so drawn depth will not be changed, albeit BHF increasing. Therefore, the BHFs of over 200kN are not considered in Fig. 9. After FEM simulation and evaluating its results, the safe area was divided into three independent parts in accordance with the amount of BHFs in addition to their specific features.

Frist region: When BHF was between 25 and 200 KN. In this area, in case of BHF decreasing, the drawn depth will increase, and tearing also happened in the upper region of the cup’s wall. The location of the tearing in the first region can be seen from Fig. 9.

Second region: When the BHF is between 10 and 25kN, the drawn depth is more than other regions. Supplementary to this, drawn depth deviations, in this region, are much less than that of the first region. Drawn depth in this area does not have a specific pattern along with changes of BHFs. In other words, in this area, changes of drawn depth are not uniform, meaning that drawn depth deviations have no any linear relation with BHFs variations. In the second region, tearing of the sheet happens in the lower region of the cup that is close to the flange. The location of the tearing in the second area is shown in Fig. 9.

Third region: When the BHF is less than 10kN, the sheet will be wrinkled. Different criteria are used in determining the moment of wrinkling, in most of which, when the distance between the die and blank holder reaches a coefficient of the sheet thickness, wrinkling will happen. This coefficient can vary from 1.25 to 2, depending on the sheet’s properties and thickness [30]. In this study, the coefficient of wrinkling is considered 1.6. Figure 9 shows wrinkling in the flange region.

After reviewing these regions’ specifications, knowing that drawn depth variations have no specific pattern in the second region, sheet behavior cannot be estimated in this area by plasticity relationships. The experimental and analytical study, accordingly, was conducted merely in the first region. As detecting the drawn depth at the tearing moment is so difficult in experimental tests and needs a lot of try and errors, drawn depth was calculated by five BHFs at the tearing moment, the results of which are shown in Table 3 and Figs. 10 and 11. Considering process parameters when the BHF becomes more than 200kN, the BHF is so much that the sheet can hardly move over the blank holder. As simulation and experimental results show, drawn depth at the moment of tearing with a constant BHF of 300 and 250kN is almost equal.

Table 3 Comparison and verification of FEM simulation results and experimental results

Fig. 10

Comparison of the drawn depth at the moment of tearing with the 294kN BHF, $\upmu =0.2,$ $v=33\frac{mm}{s}$, a drawn depth in the experimental sample: 26.32 mm, b drawn depth in the FEM simulation sample: 26.38 mm

Fig. 11

Comparison of the drawn depth at the moment of tearing with the 98kN BHF,$\upmu =0.2,$ $v=33\frac{mm}{s}$, a drawn depth in the experimental sample: 32.36 mm, b drawn depth in the FEM simulation sample: 34.2 mm

4.2 Comparison of analytical and FEM simulation results

This section aims to calculate the tearing limit with the first and second approaches in an analytical method using plasticity relations and compare them with FEM and experimental ones. The tearing limit was calculated by FEM simulation, first criterion (Eq. (22)), and the second criterion (Eq. (24)), separately, and the results of them were compared with each other. The method for calculation of the effective parameters on the tearing limit is that the safe area, at first, is calculated using FEM simulation. After obtaining safe area calculated by FEM and determination of variation range of punch stroke, different values for ${h}_{i}$ in each stage will be specified according to FEM results. With having parameters ${d}_{1,i},\;{d}_{int,i},\;{\varepsilon }_{1,i},\;{\varepsilon }_{2,i},\;{\sigma }_{f,1-2,i}$ and ${\sigma }_{f,2-3,i}$, BHF_max is calculated along punch stroke with the use of Eq. (24). Parameters, including d₀, d_D, r_p, r_D, t₀, UTS, R, and yield stress, are needed to calculate mentioned items; these parameters related to mold’s element dimensions are listed in Table 2.

With the Eqs. (22), (24) and (25) and having parameters given in Tables 2 and 4, BHF_max in each stage of punch stroke was calculated with two methods based on strain energy and maximum stress of material criteria, and they were compared with FEM results according to Table 5. It is important to note that in the FEM simulation, BHF was considered the input and then, corresponding drawn depth at the tearing moment, was measured. Furthermore, h_i(s) obtained from ABAQUS were considered the outputs of FEM simulation. By contrast, in analytical calculations (the first and second approach), h_i measured by ABAQUS was considered as the input of analytical calculation, and with usages of them, BHF_max was calculated by Eq. (25) in different stages of punch stroke. This process is shown in Fig. 1 in a more detail.

Table 4 Analytic calculation of strain and mean flow stress in flange at 3 different points

Table 5 Analytical results for BHF, max; $\mu =0.2$

Using parameters given in Table 4, ${\sigma }_{r,j,crack}$ was, firstly, calculated using either Eqs. (22) or (24). Then, with the usage of ${\sigma }_{r,j,crack}$, BHF_max was calculated using two criteria based on strain energy and maximum stress of material. The related results are provided in Table 5, and tearing threshold with three methods of FEM, analytical approach based on strain energy and maximum stress of material with friction coefficient of 0.2 can be seen from Fig. 12.

Fig. 12

Comparison of maximum BHF with energy criteria, UTS criteria, and FEM simulation; $\mu =0.2$

In Table 5, ${BHF}_{1,max}$ is the maximum BHF, which was calculated using ultimate tensile stress criterion, first criterion, ${BHF}_{2,max}$ is the maximum BHF, which was calculated using the strain energy criterion, second criterion, and ${BHF}_{FEM}$ is the maximum BHF, which was calculated using FEM simulation. As shown in Fig. 12, the second approach is related to BHF_max calculated using strain energy criterion, FEM is BHF_max obtained from FEM simulation, and the first approach is associated with the BHF_max calculated from ultimate tensile stress criterion. As shown in Table 5 and Fig. 12, there is considerable consistency between the results related to the strain energy criterion and FEM. The results related to the strain energy criterion were much closer to the FEM ones in comparison with that of the ultimate tensile stress criterion. To evaluate the efficacy and practicality of the proposed model based on strain energy, BHF_max was calculated with two methods of FEM and strain energy method (second approach) with two other friction coefficients of 0.1 and 0.15, the results of which can be seen from Figs. 13 and 14, respectively.

Fig. 13

Comparison of BHFmax with energy criteria and FEM simulation; $\mu =0.1$

Fig. 14

Comparison of BHF_max with energy criteria and FEM simulation; $\mu =0.15$

5 Conclusion

A new method based on strain energy was presented for predicting BHF_max along the punch stroke for the first time (Tables 6 and 7). Supplementary to this, using dynamic explicit analysis of ABAQUS software, 3D finite element simulation of deep drawing was conducted, in which a new method based on ductile damage criterion was introduced to simulate cracking in sheet metal forming. Additionally, experimental investigations were carried out to be compared with FEM ones. Firstly, FEM results were verified with experimental ones, demonstrating that the results of these two were considerably close to each other. Then, BHF_max was calculated by two criteria based on strain energy and ultimate tensile stress, and the results of these two approaches were compared with FEM ones. The results related to the strain energy criterion were much closer to the FEM ones in comparison with that of the ultimate tensile stress criterion. Finally, the BHF_max was calculated by two new friction coefficients based on the energy strain criterion, and their results were compared to the FEM ones to ensure the new method accuracy. Compared to previous related research, the strain energy criterion would seem to be a better approach for estimation of tearing threshold in the deep drawing process.

Table 6 Analytic calculation of strain and mean flow stress in flange every punch stroke; $\mu =0.1$

Table 7 Analytic calculation of strain and mean flow stress in flange every punch stroke; $\mu =0.1$ 5