Asymmetrical Pythagorean-hodograph spline-based ${{\mathrm{C}}}^{4}$ continuous local corner smoothing method with jerk-continuous feedrate scheduling along linear toolpath

Abstract

In computer numerical control systems, linear segments generated by computer-aided manufacturing software are the most widely used toolpath format. Since the linear toolpath is discontinuous at the junction of two adjacent segments, the fluctuations on velocity, acceleration and jerk are inevitable. Local corner smoothing is widely used to address this problem. However, most existing methods use symmetrical splines to smooth the corners. When any one of the linear segments at the corner is short, the inserted spline will be micro to avoid overlap. This will increase the curvature extreme of the spline and reduce the feedrate on it. In this article, the corners are smoothed by a ${C}^{4}$ continuous asymmetric Pythagorean-hodograph (PH) spline. The curvature extreme of the proposed spline is investigated first, and $K=2.5$ is determined as the threshold to constrain the asymmetry of the spline. Then, a two-step strategy is used to generate a blended toolpath composed of asymmetric PH splines and linear segments. In the first step, the PH splines at the corners are generated under the condition that the transition lengths do not exceed half of the length of the linear segments. In the second step, the splines at the corners are re-planned to reduce the curvature extremes, if the transition error does not reach the given threshold and there are extra linear trajectories on both sides of the spline trajectory. Finally, the bilinear interpolation method is applied to determine the critical points of the smoothed toolpath, and a jerk-continuous feedrate scheduling scheme is presented to interpolate the smoothed toolpath. Simulations show that, under the condition of not affecting the machining quality, the proposed method can improve the machining efficiency by $7.27$ to $75.11\%$ compared to ${G}^{3}$ and ${G}^{4}$ methods.

1 Introduction

To machine 3D products with freeform surfaces, computer-aided design (CAD) models are designed first, Then, the cutter contact (CC) paths are converted into the cutter location (CL) paths by the computer-aided manufacturing (CAM) software. Since the linear interpolation (G01) is supported by all multi-axis computer numerical control (CNC) machining, the CL paths are usually divided into a large number of linear trajectories as the toolpath to guide the movement of machine axes [1]. However, due to the tangential discontinuities at the intersection of linear paths, there will be infinite acceleration of axes and discontinuous motion, which will excite structural vibration. If it is simply planned to stop at the corner junction, frequent acceleration and deceleration processes are inevitable, which will increase machining time significantly [2]. Therefore, to improve machining efficiency and quality, the toolpath should be processed to get higher order continuity [3]. The approaches can be divided into global smoothing [4,5,6,7,8] and local smoothing [3, 9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29] methods.

The global smoothing methods usually utilize one or several smooth spline curves, such as B-splines, polynomial splines and non-uniform rational B-spline (NURBS) curves to approximate the discrete G01 points. The high-order continuity of the proposed curves makes them guarantee smoothness along the entire toolpath [9]. However, they have shortages such as numerical instability, lack of chord error constraint and lack of assurance result [4].

The local smoothing methods usually replace the shape corners with one or a pair of micro-curves [10], among which the spline trajectory, such as B-spline and Bezier, has attracted more interests of the researchers.

B-spline and Bezier spline are the most widely used transition curves to achieve second-order geometric (${G}^{2}$) continuity or second-order parametric (${C}^{2}$) continuity. Zhao et al. [11] adopted a cubic B-spline with five control points to smooth the adjacent linear segments, which made the overall smoothed path ${C}^{2}$ continuous. Sencer and Shamoto [12] employed a quintic Bezier curve to blend the adjacent straight lines, and the curvature extreme was minimized for higher machining efficiency. In [13], a two-step strategy was proposed to generate ${G}^{2}$ continuous toolpath, where the curvature energy of the cubic Bezier curve was minimized first, then the optimal transition length was determined by minimizing the sum of two curvature extremes. Jin et al. [14] proposed a transition method for five-axes machining in workpiece coordinate system (WCS), which utilized a dual-Bezier splines as transition curves. Bi et al. [15] developed a ${G}^{2}$ continuous transition method with a cubic Bezier curve; the approximation error at the segment junction can be accurately guaranteed, and the curvature extreme can be analytically computed and optimized. These methods [11,12,13,14,15] above can only guarantee that the toolpath is ${C}^{2}$ or ${G}^{2}$ continuous; however, higher continuity is desired to obtain smooth feedrate profile. Tulsyan and Altintas [16] inserted a quintic B-spline with seven control points for tool tip at the adjacent linear segments and a septic B-spline with nine unit control vectors for the tool orientation. The optimal control points and vectors were calculated to generate ${C}^{3}$ continuous toolpath. In [17], two symmetric quartic Bezier curves were proposed to generate ${C}^{3}$ interpolative toolpath, and a jerk-continuous feedrate scheduling was given. Zhang et al. [18] proposed a symmetric quartic B-spline curve to smooth the tool tip position in WCS and an asymmetric quartic B-spline curve to smooth the tool orientation in machine coordinate system (MCS), which constrained both errors of tool tip position and tool orientation in WCS. In addition, Xie et al. [19] employed a single quintic B-spline with seven control points to achieve ${G}^{3}$ continuity and applied it to five degrees of freedom (5-DoF) machining robot. In [3], by adopting a quintic B-spline with nine control points, the toolpath was improved to ${G}^{4}$ continuous, and a corresponding jerk-smooth feedrate scheduling scheme was presented.

Although B-spline and Bezier spline can smooth the toolpath, their arc lengths have no analytical solutions respect with spline parameters, which makes it difficult to calculate the next parameter in the fine interpolation. To overcome this problem, the clothoid spline-based methods [10, 20,21,22,23,24] and Pythagorean-hodograph (PH) spline-based methods [9, 25,26,27,28,29] have been developed. Shahzadeh et al. [22] used biclothoid fillets as transition curves to smooth the corners and ensure the ${G}^{2}$ continuity of the toolpath. The main advantage of this fillet fitting method was that it was not limited to line to line transitions; it can smooth two arcs or a line and arc as well. In [23], the traditional clothoid was extended from 2 to 3 dimensions, which can achieve a higher degree of continuity, i.e. ${G}^{3}$ continuity. Huang et al. [24] proposed a novel curve ‘airthoid’ based on clothoid spline, then the biairthoid was involved to smooth the corners of the tool position in the WCS and the corners of the tool orientation in the MCS. In [10], a novel smoothing method based on a pair of clothoid splines was proposed to realize the integral planning of the geometrical curve and the feedrate profile, which can achieve the adaptive contour accuracy. Since the clothoid is defined with respect to the Fresnel integral, which cannot be calculated analytically, these methods can only be carried out offline. In [26], the sharp corners on the toolpath were interpolated with PH interpolation, which minimized the geometric and interpolator approximation errors simultaneously. Shi et al. [29] proposed a smoothing method by using a pair of quintic PH curves to round the corners of linear five-axis tool path. Hu et al. [9] applied a quintic PH spline with twelve control points to achieve ${C}^{3}$ continuity. In [30], an asymmetrical PH spline-based ${C}^{3}$ continuous corner smoothing algorithm was developed for five-axis tool paths with short segments. However, they were limited to the second-order or third-order continuity. When the fourth-order continuity is reached, the first and second curvature derivatives are both continuous along the combined toolpath; the jerk and jounce are both continuous if a smooth jerk profile is proposed in feedrate scheduling, which can reduce vibration and tracking error [3].

In this paper, the asymmetric PH spline with sixteen control points is developed and inserted among linear toolpath segments. The control points are optimized to decrease the curvature extreme of the proposed PH spline and achieve ${C}^{4}$ continuity of the combined toolpath. A corresponding jerk-continuous feedrate scheduling scheme is also presented to interpolate the toolpath. The remainder of this paper is organized as follows. In Sect. 2, the basic concepts of the proposed PH spline are introduced, and the curvature extreme is investigated. Section 3 provides a PH spline curve transition method to generate ${C}^{4}$ smooth path. In Sect. 4, a jerk-continuous feedrate scheduling scheme is given. Section 5 presents the simulations, and the results are compared with two conventional methods. Finally, Sect. 6 gives the conclusions and future works.

2 Introduction of the proposed transition curve

2.1 Introduction of planar Pythagorean-hodograph spline

A planar parameter curve $r\left(t\right)=(x\left(t\right),y(t))$ is called Pythagorean-hodograph (PH) curve, if it satisfies

$${x}^{2}\left(t\right)+{y}^{2}\left(t\right)={\sigma }^{2}(t)$$

(1)

where $\sigma \left(t\right)$ is the parametric speed of $r\left(t\right)$ and also a polynomial respect with $t$. To get a PH curve, usually let ${x^\prime}\left(t\right)={u}^{2}(t)-{v}^{2}(t)$ and ${y}^{^{\prime}}\left(t\right)=2u\left(t\right)v\left(t\right)$, where $u\left(t\right)$ and $v\left(t\right)$ are two relatively prime polynomials, so $\sigma \left(t\right)=\vert{r^\prime}(t)\vert=\sqrt{{x^\prime}^{2}\left(t\right)+{y}^\prime\left(t\right)}={u}^{2}\left(t\right)+{v}^{2}(t)$, which is a polynomial.

Let $u\left(t\right)={\sum }_{i=0}^{m}{u}_{i}{b}_{i}^{m}(t)$ and $v\left(t\right)={\sum }_{i=0}^{m}{v}_{i}{b}_{i}^{m}(t)$, where ${u}_{i}={[{ux}_{i},{uy}_{i}]}^{T}$ and ${v}_{i}={[{vx}_{i},{vy}_{i}]}^{T}$ are control points, $m$ is the degree of these two spline function. ${b}_{i}^{m}\left(t\right)=\left(\begin{array}{c}m\\ i\end{array}\right){t}^{i}{(1-t)}^{m-i}$ are the Bezier basis functions, where $\left(\begin{array}{c}m\\ i\end{array}\right)=\frac{m!}{i!(m-i)!}$. Integrating ${x}^{^{\prime}}\left(t\right)$ and ${y}^{^{\prime}}\left(t\right)$ gives the planar PH spline $r\left(t\right)={\sum }_{i=0}^{n}{B}_{i}{b}_{i}^{n}(t)$, where $n=2m+1$. ${B}_{i}={[{x}_{i},{y}_{i}]}^{T}$ are control points, which will be detailed in the next section. The parametric speed function can be written as $\sigma \left(t\right)={\sum }_{i=0}^{n-1}{\sigma }_{i}{b}_{i}^{n-1}(t)$; ${\sigma }_{i}={[{\sigma x}_{i},{\sigma y}_{i}]}^{T}$ are control points, which can be calculated by the following formula:

$$\begin{aligned}{\sigma }_{i}=&\;\sum{_{j=max(0,i-m)}^{min(m,i)}}\frac{(\begin{array}{c}m\\ j\end{array})(\begin{array}{c}m\\ i-j\end{array})}{(\begin{array}{c}n-1\\ i\end{array})}({u}_{j}{u}_{i-j}+{v}_{j}{v}_{i-j}),\\& i=\mathrm{0,1},\dots ,n-1\end{aligned}$$

(2)

The cumulative arc length function $s\left(t\right)$ of $r\left(t\right)$ can be obtained by integrating $\sigma \left(t\right)$; we arrive at

$$\left\{\begin{array}{c}s\left(t\right)={\sum }_{i=0}^{n}{s}_{i}{b}_{i}^{m}(t) \\ {s}_{0}=0, {s}_{i}=\frac{1}{n}{\sum }_{j}^{i-1}{\sigma }_{j}, i=\mathrm{1,2},\dots ,n\end{array}\right.$$

(3)

As can be seen from Eq. (3), $s\left(t\right)$ is also a polynomial respect with $t$, which makes PH spline of great application value in interpolation.

2.2 Design of the PH transition curve

In this research, a ${C}^{4}$ continuous PH spline is inserted to smoothly transition two successive linear segments. It has been proved that only when $m\ge 7$ can a ${C}^{4}$ continuous PH spline be designed [27]. For simplicity, let $m=7$; then, $u\left(t\right)={\sum }_{i=0}^{7}{u}_{i}{b}_{i}^{7}(t)$ and $v\left(t\right)={\sum }_{i=0}^{7}{v}_{i}{b}_{i}^{7}(t)$. The designed ${C}^{4}$ continuous PH spline is written as

$$r\left(t\right)=\left(x\left(t\right),y\left(t\right)\right)={\sum }_{i=0}^{15}{B}_{i}{b}_{i}^{15}\left(t\right), t\in [0, 1]$$

(4)

where ${B}_{i}(i=\mathrm{0,1},2,\dots ,15)$ are control points, which will be given later.

As shown in Fig. 1, the corner is formed by two linear segments, i.e. ${P}_{0}{P}_{1}$ and ${P}_{1}{P}_{2}$; their unit directions are ${T}_{1}=\overrightarrow{{P}_{0}{P}_{1}}/\left|\overrightarrow{{P}_{0}{P}_{1}}\right|$ and ${T}_{2}=\overrightarrow{{P}_{1}{P}_{2}}/\left|\overrightarrow{{P}_{1}{P}_{2}}\right|$. $\theta$ is the angle between these two unit directions, which can be calculated by

Fig. 1

Description of the ${C}^{4}$ transition curve

$$\theta =arccos({T}_{1}\cdot {T}_{2})$$

(5)

$\{{B}_{0}, {B}_{1}, \dots ,{B}_{15}\}$ are the sixteen control points of the proposed PH curve. From Ref. [9], the transition curve is ${C}^{4}$ continuous only when the first five control points $\{{B}_{0}, {B}_{1}, {B}_{2}, {B}_{3}, {B}_{4}\}$ lie in segment ${P}_{0}{P}_{1}$, the last five control points $\{{B}_{11}, {B}_{12}, {B}_{13}, {B}_{14}, {B}_{15}\}$ lie in segment ${P}_{1}{P}_{2}$ and they meet the following equations:

$$\overrightarrow{{B}_{0}{B}_{1}}=\overrightarrow{{B}_{1}{B}_{2}}=\overrightarrow{{B}_{2}{B}_{3}}=\overrightarrow{{B}_{3}{B}_{4}}$$

(6)

$$\overrightarrow{{B}_{11}{B}_{12}}=\overrightarrow{{B}_{12}{B}_{13}}=\overrightarrow{{B}_{13}{B}_{14}}=\overrightarrow{{B}_{14}{B}_{15}}.$$

(7)

To make the control points meet the above conditions, $\{{u}_{0}, {u}_{1}, {u}_{2}, {u}_{3}, {u}_{4}, {u}_{5}, {u}_{6}, {u}_{7}\}$ and $\{{v}_{0}, {v}_{1}, {v}_{2}, {v}_{3}, {v}_{4}, {v}_{5}, {v}_{6}, {v}_{7}\}$ should satisfy the following relationship:

$$\left\{\begin{array}{c}{u}_{0}={u}_{1}={u}_{2}={u}_{3}\\ \begin{array}{c}{u}_{4}={u}_{5}={u}_{6}={u}_{7}\\ {v}_{0}={v}_{1}={v}_{2}={v}_{3}\end{array}\\ {v}_{4}={v}_{5}={v}_{6}={v}_{7}\end{array}\right.$$

(8)

Then, the control points${B}_{i}(i=\mathrm{0,1},2,\dots ,15)$, ${u}_{i}(i=\mathrm{0,1},2,\dots ,7)$ and ${v}_{i}(i=\mathrm{0,1},2,\dots ,7)$ have the following relation:

$$\left\{\begin{array}{c}\begin{array}{c}\overrightarrow{{B}_{0}{B}_{1}}=\overrightarrow{{B}_{1}{B}_{2}}=\overrightarrow{{B}_{2}{B}_{3}}=\overrightarrow{{B}_{3}{B}_{4}}=\overrightarrow{{n}_{1}} \\ \overrightarrow{{B}_{4}{B}_{5}}=\frac{133}{143}\overrightarrow{{n}_{1}}+\frac{10}{143}\overrightarrow{m} \\ \overrightarrow{{B}_{5}{B}_{6}}=\frac{105}{143}\overrightarrow{{n}_{1}}+\frac{38}{143}\overrightarrow{m} \end{array}\\ \begin{array}{c}\overrightarrow{{B}_{6}{B}_{7}}=\frac{175}{429}\overrightarrow{{n}_{1}}+\frac{254}{429}\overrightarrow{m}\\ \overrightarrow{{B}_{7}{B}_{8}}=\overrightarrow{m} \\ \overrightarrow{{B}_{8}{B}_{9}}=\frac{175}{429}\overrightarrow{{n}_{2}}+\frac{254}{429}\overrightarrow{m}\end{array} \\ \begin{array}{c}\overrightarrow{{B}_{9}{B}_{10}}=\frac{105}{143}\overrightarrow{{n}_{2}}+\frac{38}{143}\overrightarrow{m} \\ \overrightarrow{{B}_{10}{B}_{11}}=\frac{133}{143}\overrightarrow{{n}_{2}}+\frac{10}{143}\overrightarrow{m} \\ \overrightarrow{{B}_{11}{B}_{12}}=\overrightarrow{{B}_{12}{B}_{13}}=\overrightarrow{{B}_{13}{B}_{14}}=\overrightarrow{{B}_{14}{B}_{15}}=\overrightarrow{{n}_{2}}\end{array}\end{array}\right.$$

(9)

where $\overrightarrow{{n}_{1}}={\left({\mathrm{u}}_{0}^{2}-{\mathrm{v}}_{0}^{2},2{u}_{0}{v}_{0}\right)}^{T}/15$, $\overrightarrow{{n}_{2}}={\left({\mathrm{u}}_{7}^{2}-{\mathrm{v}}_{7}^{2},2{u}_{7}{v}_{7}\right)}^{T}/15$ and $\overrightarrow{m}={\left({u}_{0}{u}_{7}-{v}_{0}{v}_{7},{u}_{0}{v}_{7}+{u}_{7}{v}_{0}\right)}^{T}/15$.

To get the relationship between the control points and the corner point ${P}_{1}$, two theorems are given as follows:

Theorem 1

Let $\overrightarrow{{n}_{1}}={l}_{1}\overrightarrow{{T}_{1}}$ and $\overrightarrow{{n}_{2}}={l}_{2}\overrightarrow{{T}_{2}}$, then $\left|\overrightarrow{{B}_{7}{B}_{8}}\right|=\left|\overrightarrow{m}\right|=\sqrt{{{l}_{1}l}_{2}}$. In addition, $\frac{\overrightarrow{{B}_{7}{B}_{8}}}{\left|\overrightarrow{{B}_{7}{B}_{8}}\right|}=\frac{\overrightarrow{{T}_{1}}+\overrightarrow{{T}_{2}}}{\left|\overrightarrow{{T}_{1}}+\overrightarrow{{T}_{2}}\right|}$ if the values of ${u}_{0}$, ${v}_{0}$, ${u}_{7}$ and ${v}_{7}$ are determined appropriately.

Theorem 2

Extend linear segment ${B}_{7}{B}_{8}$ from both ends to intersect ${P}_{0}{P}_{1}$ and ${P}_{1}{P}_{2}$ at ${Q}_{1}$ and ${Q}_{2}$ respectively, then $\left|\overrightarrow{{B}_{4}{Q}_{1}}\right|=\frac{889}{429}{l}_{1}$, $\left|\overrightarrow{{B}_{11}{Q}_{2}}\right|=\frac{889}{429}{l}_{2}$ and $\left|\overrightarrow{{Q}_{1}{P}_{1}}\right|=\left|\overrightarrow{{Q}_{2}{P}_{1}}\right|=\frac{1225\sqrt{{{l}_{1}l}_{2}}}{858\mathrm{cos}\frac{\theta }{2}}$.

The proof process of Theorems 1 and 2 can be found in Appendices 1 and 2 respectively. According to these two theorems, the relation between the control points and the corner point ${P}_{1}$ is as follows:

$$\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{B}_{0}={P}_{1}-\left(4{l}_{1}+\frac{889}{429}{l}_{1}+l\right)\overrightarrow{{T}_{1}}\\ {B}_{1}={B}_{0}+{l}_{1}\overrightarrow{{T}_{1}}\\ {B}_{2}={B}_{1}+{l}_{1}\overrightarrow{{T}_{1}}\end{array}\\ \begin{array}{c}\begin{array}{c}{B}_{3}={B}_{2}+{l}_{1}\overrightarrow{{T}_{1}}\\ {B}_{4}={B}_{3}+{l}_{1}\overrightarrow{{T}_{1}}\end{array}\\ {B}_{5}={B}_{4}+\frac{10}{143}\overrightarrow{m}+\frac{133}{143}{l}_{1}\overrightarrow{{T}_{1}} \\ {B}_{6}={B}_{5}+\frac{38}{143}\overrightarrow{m}+\frac{105}{143}{l}_{1}\overrightarrow{{T}_{1}} \end{array}\\ \begin{array}{c}{B}_{7}={B}_{6}+\frac{254}{429}\overrightarrow{m}+\frac{175}{429}{l}_{1}\overrightarrow{{T}_{1}}\\ {B}_{8}={B}_{7}+\overrightarrow{m}\end{array}\end{array}\\ \begin{array}{c}\begin{array}{c}{B}_{9}={B}_{8}+\frac{254}{429}\overrightarrow{m}+\frac{175}{429}{l}_{2}\overrightarrow{{T}_{2}}\\ {B}_{10}={B}_{9}+\frac{38}{143}\overrightarrow{m}+\frac{105}{143}{l}_{2}\overrightarrow{{T}_{2}}\\ {B}_{11}={B}_{10}+\frac{10}{143}\overrightarrow{m}+\frac{133}{143}{l}_{2}\overrightarrow{{T}_{2}}\end{array}\\ \begin{array}{c}{B}_{12}={B}_{11}+{l}_{2}\overrightarrow{{T}_{2}}\\ {B}_{13}={B}_{12}+{l}_{2}\overrightarrow{{T}_{2}}\\ {B}_{14}={B}_{13}+{l}_{2}\overrightarrow{{T}_{2}}\end{array}\\ {B}_{15}={B}_{14}+{l}_{2}\overrightarrow{{T}_{2}}\end{array}\end{array}\right.$$

(10)

where $\overrightarrow{m}=\sqrt{{l}_{1}{l}_{2}}\frac{\overrightarrow{{T}_{1}}+\overrightarrow{{T}_{2}}}{\left|\overrightarrow{{T}_{1}}+\overrightarrow{{T}_{2}}\right|}$, $l$=$\frac{1225\sqrt{{{l}_{1}l}_{2}}}{858cos\frac{\theta }{2}}$. It can be seen from Eq. (10) that for a certain corner, once ${l}_{1}$ and ${l}_{2}$ are determined, all control points are determined, which means the transition curve is determined.

To calculate the arc length of the proposed PH spline, the parametric speed function should be obtained first. Applying $m=7$, $n=15$ and Eq. (8) into Eq. (2), the control points of the parametric speed function $\upsigma \left(t\right)={\sum }_{i=0}^{14}{\sigma }_{i}{b}_{i}^{n-1}(t)$ are as follows:

$$\left\{\begin{array}{c}\begin{array}{c}{\sigma }_{0}={\sigma }_{1}={\sigma }_{2}={\sigma }_{3}={u}_{0}^{2}+{v}_{0}^{2}\\ {\sigma }_{4}=\frac{10}{143}{\times (u}_{0}{u}_{7}+{v}_{0}{v}_{7})+\frac{133}{143}\times ({u}_{0}^{2}+{v}_{0}^{2})\\ {\sigma }_{5}=\frac{38}{143}{\times (u}_{0}{u}_{7}+{v}_{0}{v}_{7})+\frac{105}{143}\times ({u}_{0}^{2}+{v}_{0}^{2})\end{array}\\ \begin{array}{c}{\sigma }_{6}=\frac{254}{429}{\times (u}_{0}{u}_{7}+{v}_{0}{v}_{7})+\frac{175}{429}\times ({u}_{0}^{2}+{v}_{0}^{2})\\ {\sigma }_{7}={u}_{0}{u}_{7}+{v}_{0}{v}_{7}\\ {\sigma }_{8}=\frac{254}{429}{\times (u}_{0}{u}_{7}+{v}_{0}{v}_{7})+\frac{175}{429}\times ({u}_{7}^{2}+{v}_{7}^{2})\end{array}\\ \begin{array}{c}{\sigma }_{9}=\frac{38}{143}{\times (u}_{0}{u}_{7}+{v}_{0}{v}_{7})+\frac{105}{143}\times ({u}_{7}^{2}+{v}_{7}^{2})\\ {\sigma }_{10}=\frac{10}{143}{\times (u}_{0}{u}_{7}+{v}_{0}{v}_{7})+\frac{133}{143}\times ({u}_{7}^{2}+{v}_{7}^{2})\\ {\sigma }_{11}={\sigma }_{12}={\sigma }_{13}={\sigma }_{14}={u}_{7}^{2}+{v}_{7}^{2}\end{array}\end{array}\right.$$

(11)

where ${u}_{0}^{2}+{v}_{0}^{2}=15{l}_{1}$ and ${u}_{7}^{2}+{v}_{7}^{2}=15{l}_{2}$; the only unknown value is ${u}_{0}{u}_{7}+{v}_{0}{v}_{7}$. From Eq. (9), $\overrightarrow{{B}_{4}{B}_{5}}=\frac{10}{143}\overrightarrow{{n}_{1}}+$ $\frac{133}{143}\overrightarrow{m}=\frac{10}{143}\times$ ${\frac{1}{15}\left({\mathrm{u}}_{0}^{2}-{\mathrm{v}}_{0}^{2},2{u}_{0}{v}_{0}\right)}^{T}$ $+\frac{133}{143}\times$ $\frac{1}{15}{\left({u}_{0}{u}_{7}-{v}_{0}{v}_{7},{u}_{0}{v}_{7}+{u}_{7}{v}_{0}\right)}^{T}$. Considering the length of vector $\overrightarrow{{B}_{4}{B}_{5}}$, then ${(143\times 15\times \left|\overrightarrow{{B}_{4}{B}_{5}}\right|)}^{2}=$ ${10}^{2}\times \left({u}_{0}^{2}+{v}_{0}^{2}\right)\times \left({u}_{7}^{2}+{v}_{7}^{2}\right)$ $+{133}^{2}\times {\left({u}_{0}^{2}+{v}_{0}^{2}\right)}^{2}+$ $2\times 10\times 133\times ({u}_{0}{u}_{7}+{v}_{0}{v}_{7})\times\;$$\left({u}_{0}^{2}+{v}_{0}^{2}\right)$ , ${u}_{0}{u}_{7}+{v}_{0}{v}_{7}$ can be calculated as

$${u}_{0}{u}_{7}+{v}_{0}{v}_{7}=\frac{{(2145\left|{B}_{4}{B}_{5}\right|)}^{2}-22500{{l}_{1}l}_{2}-{(1995{l}_{1})}^{2}}{39900{l}_{1}}.$$

(12)

As the parametric speed function is known, the cumulative arc length function $\mathrm{s}\left(t\right)={\sum }_{i=0}^{15}{s}_{i}{b}_{i}^{15}(t)$ can be obtained by substituting Eq. (11) into Eq. (3), which is omitted here.

2.3 The curvature extreme of the proposed PH spline

In feedrate scheduling, the feedrate is constrained by the curvature of the tool path, and the tool path is usually divided into several blocks according to critical points, where the points with local curvature extreme are usually regarded as critical points [31]. In this section, the curvature extreme of the proposed PH spline and the parameter of curvature extreme point are investigated.

From the previous section, the proposed PH spline is determined by two characteristic lengths ${l}_{1}$ and ${l}_{2}$, the corner point ${P}_{1}$ and two unit directions ${T}_{1}$ and ${T}_{2}$. Since the curvature is intrinsic geometries, which is not affected by the selection of coordinate system, the curvature of the proposed PH spline is determined only by two characteristic lengths ${l}_{1}$, ${l}_{2}$ and the corner angle $\theta$. Without loss of generality, let ${l}_{2}\ge {l}_{1}$. In addition, when the ratio of ${l}_{2}$ and ${l}_{1}$ and corner angle $\theta$ are fixed, the curvature of each point at the proposed PH spline is inversely proportional to ${l}_{1}$; then, the value of ${l}_{1}$ does not affect the trend of curvature on the proposed PH spline. For simplicity, we let ${l}_{1}=1\mathrm{mm}$; ${l}_{2}$ varies from $1$ to $10 \mathrm{mm}$ in steps of $0.01 \mathrm{mm}$, and $\theta$ varies from $0$ to $\pi$ in steps of $\frac{\pi }{180}$. To calculate the curvature extreme of the proposed PH spline, we take $0.001$ as the parameter step to sample the points on the proposed PH spline and calculate its curvature; the largest one is recorded as the curvature extreme, and the corresponding parameter is recorded as the parameter of the curvature extreme point. When $\theta =\pi /4$, $\theta =\pi /2$ and $\theta =3\pi /4$, the curvature extreme of the proposed PH spline with different characteristic length ${l}_{2}$ is calculated and shown as follows:

As can be seen from Fig. 2, even for different corner angles, the curvature extreme of the proposed PH spline has the same change trend: as the characteristic length ${l}_{2}$ is increased, the curvature extreme is first reduced and then increased. For a given corner angle $\theta$, the characteristic length ${l}_{2}$ is limited by the length of the linear trajectory in the corner smoothing process. In most cases, ${l}_{2}$ cannot equal to the value (the abscissa of the red points in Fig. 2) that makes the curvature extreme of the proposed PH spline minimal. As an alternative, an optimal value for ${l}_{2}$ is determined by the following steps:

• Step 1: Initialize ${l}_{2}=1 \mathrm{mm}$, Calculate the curvature extreme ${K}_{1}$.

• Step 2: If ${l}_{2}<10 \mathrm{mm}$, ${l}_{2}={l}_{2}+\Delta l$, where $\Delta l$ is a small increment and $\Delta l=0.01 \mathrm{mm}$ is chosen in the searching algorithm, go to Step 3; otherwise, go to Step 5.

• Step 3: Calculate the curvature extreme ${K}_{2}$. If $\frac{{{K}_{1}-K}_{2}}{{K}_{1}}>\delta$, where $\delta$ is a small scalar and $\delta =0.08\%$ is chosen in the searching algorithm, then ${K}_{1}={K}_{2}$, go to Step 2; otherwise, go to Step 4.

• Step 4: The optimal value equals to ${l}_{2}-\Delta l$; terminate the algorithm.

• Step 5: The optimal value equals to ${l}_{2}$; terminate the algorithm.

Fig. 2

The curvature extreme of the proposed PH spline with various characteristic length ${l}_{2}$ and the corner angle. (a) $\theta =\pi /4$. (b) $\theta =\pi /2$. (c) $\theta =3\pi /4$

Following the above algorithm, the optimal value for ${l}_{2}$ and corresponding curvature extreme for three different corner angles are obtained and shown as the blue points in Fig. 2. Similarly, the curvature extreme of the proposed PH spline with different characteristic length ${l}_{2}$ and corner angle $\theta$ is calculated and shown in Fig. 3. The blue curve represents the optimal value for ${l}_{2}$ and its corresponding curvature extreme at different angles. The red curve represents the value for ${l}_{2}$ that makes the curvature extreme of the proposed PH spline minimal and its corresponding curvature extreme at different angles. It can be observed that at different angles, the optimal value for ${l}_{2}$ is between $2 \mathrm{mm}$ and $3\mathrm{ mm}$. For simplicity, $K=2.5$ is selected as the threshold of the ratio between ${l}_{1}$ and ${l}_{2}$, which will play an important role in the process of determining the characteristic lengths in the next section. Since the curvature extreme points will be regarded as critical points in feedrate scheduling, to detect the curvature extreme point of the inserted PH spline quickly, the parameters of the curvature extreme points on the proposed PH spline with various characteristic length ${l}_{2}$ and the corner angle $\theta$ are stored in matrix $M$, where $M(i,j)$ represents the parameter of the curvature extreme point when ${l}_{1}=1\mathrm{ mm}$, ${l}_{2}=(0.99+0.01\times j)\mathrm{mm}$ and $\theta =(i-1)\times \pi /180$. The parameters of the curvature extreme points on the proposed PH spline with various characteristic length ${l}_{2}$ and the corner angle $\theta$ are shown as Fig. 4. Since $K=2.5$ is selected as the threshold to constrain the ratio between ${l}_{1}$ and ${l}_{2}$, only the parts where ${l}_{2}$ is between $1\mathrm{ mm}$ and $3\mathrm{ mm}$ are displayed.

Fig. 3

The curvature extreme of the proposed PH spline with various characteristic length ${l}_{2}$ and the corner angle $\theta$

Fig. 4

The parameters of the curvature extreme points on the proposed PH spline with various characteristic length ${l}_{2}$ and the corner angle $\theta$

3 Generation of ${{\mathrm{C}}}^{4}$ smooth path

3.1 Error constraint

As shown in Fig. 1, the proposed PH spline introduces a geometric deviation compared to the original toolpath, which should be constrained in the path-smoothing method for NC machining. Assuming the maximum geometric error allowed by the CNC systems is denoted as $\varepsilon$, then the two characteristic lengths ${l}_{1}$ and ${l}_{2}$ should be determined appropriately so that the actual geometric error is not greater than the given threshold. Before giving the constraint of ${l}_{1}$ and ${l}_{2}$, two theorems are given as follows:

Theorem 3

If ${l}_{1}={l}_{2}$, then the maximum deviation is at the middle of the PH spline curve and calculated as.

$$\begin{aligned}{e}_{max}=&\;\left|r\left(0.5\right)-{P}_{1}\right|=\frac{1}{{2}^{14}}\mathit{sin}\left(\frac{\theta }{2}\right)\\&\left[\left(\frac{397}{429}+10207\right){l}_{1}+\frac{16384\times 1225}{858cos(\frac{\theta }{2})}{l}_{1}\right].\end{aligned}$$

(13)

Theorem 4

Let $R(t)$ be the transition PH spline with equal characteristic lengths ${l}_{0}=max({l}_{1},{l}_{2})$, denote the maximal deviation between the linear trajectory ${P}_{0}{-P}_{1}-{P}_{2}$ and the transition PH spline $R(t)$ as ${e}_{R}$, and the maximal deviation between the linear trajectory ${P}_{0}{-P}_{1}-{P}_{2}$ and the transition PH spline $r\left(t\right)$ as ${e}_{r}$, then ${e}_{r}\le {e}_{R}$.

The proof process of Theorems 3 and 4 can be found in Appendices 3 and 4 respectively. From these two theorems, we get that if ${l}_{1},{l}_{2}\le {l}_{\varepsilon }$, then the maximal deviation between the linear trajectory ${P}_{0}{-P}_{1}-{P}_{2}$ and the transition PH spline $r\left(t\right)$ satisfies ${e}_{\mathrm{max}}\le \varepsilon$, where

$${l}_{\varepsilon }=\frac{{2}^{14}\varepsilon }{sin(\frac{\theta }{2})\left(\frac{4072849}{429}+714+\frac{16384\times 1225}{858cos(\frac{\theta }{2})}\right)}$$

(14)

3.2 Length constraint

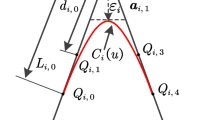
In Fig. 5, ${P}_{i}$ are $G01$ points, ${L}_{1,i}$ and ${L}_{2,i}$ are two transition lengths at point ${P}_{i}$, which can be obtained by

$$\left\{\begin{array}{c}{L}_{1,i}=\frac{2605}{429}{l}_{1,i}+\frac{1225}{858\mathrm{cos}\left(\frac{{\theta }_{i}}{2}\right)}\sqrt{{l}_{1,i}{l}_{2,i}}\\ {L}_{2,i}=\frac{2605}{429}{l}_{2,i}+\frac{1225}{858\mathrm{cos}\left(\frac{{\theta }_{i}}{2}\right)}\sqrt{{l}_{1,i}{l}_{2,i}}\end{array}\right.$$

(15)

where ${l}_{1,i}$ and ${l}_{2,i}$ are two characteristic lengths of the transition PH spline at point ${P}_{i}$, and ${\theta }_{i}$ is the corner angle. Let ${L}_{i}$ be the length of linear segment ${P}_{i}{P}_{i+1}$ and $n$ denote the maximum index of $G01$ points (i.e. the $G01$ points are presented by $\{{P}_{0}, {P}_{1}, \dots , {P}_{n}\}$). To preserve the shape of the toolpath, the sum of two adjacent transition lengths should be less than the linear segment, that is, the following inequalities should be satisfied:

Fig. 5

Length constraint of corner smoothing

$$\left\{\begin{array}{c}{L}_{\mathrm{1,1}}\le {L}_{0}\\ {L}_{2,i}+{L}_{1,i+1}\le {L}_{i} i=1,\dots ,n-2\\ {L}_{2,n-1}\le {L}_{n-1}\end{array}\right..$$

(16)

From Sect. 2.3, to make full use of the linear lengths, the following equation also needs to be satisfied:

$$\mathit{max}\left(\frac{{l}_{1,i}}{{l}_{2,i}},\frac{{l}_{2,i}}{{l}_{1,i}}\right)\le K=2.5.$$

(17)

3.3 The determination of $\mathrm{l}_{1}$ and $\mathrm{l}_{2}$ under error constraint and length constraint

In this section, the determination of characteristic lengths ${l}_{1}$ and ${l}_{2}$ for only one corner is given; then, it extends naturally to the toolpath with multiple corners, which is detailed in the next section. For simplicity, denote the corner by linear trajectory ${P}_{0}{-P}_{1}-{P}_{2}$, and the subscript $i$ in Sect. 3.2 is omitted in this section. The error constraint gives ${l}_{1},{l}_{2}\le {l}_{\varepsilon }$, where ${l}_{\varepsilon }$ is calculated by Eq. (14). The length constraint gives $\frac{2605}{429}{l}_{1}+\frac{1225}{858cos\left(\frac{\theta }{2}\right)}\sqrt{{l}_{1}{l}_{2}}\le {L}_{b}$ and $\frac{2605}{429}{l}_{2}+\frac{1225}{858cos\left(\frac{\theta }{2}\right)}\sqrt{{l}_{1}{l}_{2}}\le {L}_{f}$, where ${L}_{b}$ and ${L}_{f}$ are the upper bound of the transition lengths, and ${L}_{b}=\left|{P}_{0}{P}_{1}\right|$, ${L}_{f}=\left|{P}_{1}{P}_{2}\right|$ for this corner. Combining these inequalities with Eq. (17), the constraint model is as follows:

$$\left\{\begin{array}{c}{k}_{1}{l}_{1}+{k}_{2}\sqrt{{l}_{1}{l}_{2}}\le {L}_{b}\\ \begin{array}{c}{k}_{1}{l}_{2}+{k}_{2}\sqrt{{l}_{1}{l}_{2}}\le {L}_{f}\\ {l}_{1}\le {l}_{\varepsilon }\\ {l}_{2}\le {l}_{\varepsilon }\end{array}\\ \mathit{max}\left(\frac{{l}_{1}}{{l}_{2}},\frac{{l}_{2}}{{l}_{1}}\right)\le K=2.5\end{array}\right.$$

(18)

where ${k}_{1}=\frac{2605}{429}$ and ${k}_{2}=\frac{1225}{858\mathrm{cos}\left(\uptheta /2\right)}$.

The goal is to construct a transition spline that satisfies the above constraints and has the smallest curvature extreme. Since the expression of the curvature extreme of the transition spline is too complicated, it is not practical to construct such a transition spline. Considering that the curvature extreme is almost inversely proportional to the characteristic lengths, the goal here is simplified to make the characteristic length as big as possible, which means the first four inequalities in Eq. (18) can take as many equal signs as possible. An algorithm proposed to achieve such a goal is shown below:

• Step 1: Let the first two inequalities in Eq. (18) take equal sign; solve this two-dimensional quadratic equations to get ${l}_{1}$ and ${l}_{2}$.

• Step 2: If $\frac{{l}_{2}}{{l}_{1}}>K$, let ${l}_{2}=K{l}_{1}$ and ${l}_{1}$ takes the maximum value that satisfies the first two inequalities in Eq. (18).

• Step 3: If $\frac{{l}_{1}}{{l}_{2}}>K$, let ${l}_{1}=K{l}_{2}$ and ${l}_{2}$ takes the maximum value that satisfies the first two inequalities in Eq. (18).

• Step 4: If ${l}_{1},{l}_{2}>{l}_{\varepsilon }$, then ${l}_{1}={l}_{2}={l}_{\varepsilon }$.

• Step 5: If ${l}_{1}>{l}_{\varepsilon }\ge {l}_{2}$, then ${l}_{1}={l}_{\varepsilon }$ and ${l}_{2}$ takes the maximum value that satisfies the first four inequalities in Eq. (18).

• Step 6: If ${l}_{2}>{l}_{\varepsilon }\ge {l}_{1}$, then ${l}_{2}={l}_{\varepsilon }$ and ${l}_{1}$ takes the maximum value that satisfies the first four inequalities in Eq. (18).

The pseudocode of this algorithm is also shown as follows:

3.4 Detailed method

For the toolpath presented by $\{{P}_{0}, {P}_{1}, \dots , {P}_{n}\}$, the ${C}^{4}$ smooth path is generated once the characteristic lengths ${l}_{1,i}$ and ${l}_{2,i} (i=\mathrm{1,2},\dots ,n-1)$ are determined. From Sect. 3.3, we can see that for the corner at point ${P}_{i}$, the characteristic lengths ${l}_{1,i}$ and ${l}_{2,i}$ are determined by the corner angle ${\theta }_{i}$, error constraint ${l}_{\varepsilon ,i}$ (which is totally depended on $\upvarepsilon$ and ${\theta }_{i}$) and the upper bound of the transition lengths ${L}_{b,i}$ and ${L}_{f,i}$. Among these three variables, the first two are fixed; the only one degree of freedom left is the choice of ${L}_{b,i}$ and ${L}_{f,i}$, and they are limited by the length constraint, i.e. ${L}_{b,1}\le {L}_{0}$, ${L}_{f,i}+{L}_{b,i+1}\le {L}_{i} (i=1,\dots ,n-2)$ and ${L}_{f,n-1}\le {L}_{n-1}$.

Our method consists of two steps, where STEP I guarantees that the length constraint will not be violated, and STEP II makes full use of the length of the linear trajectory to make the curvature extreme of the transition curve as small as possible.

• STEP I

• • 1. Let the upper bound of the transition lengths equal to the half of the length of the corresponding linear trajectory, i.e. ${L}_{f,i}=\frac{1}{2}{L}_{i},{L}_{b,i}=\frac{1}{2}{L}_{i-1}(i=1,\dots ,n-1)$. Since the first and the last linear trajectory are not shared by two corners, let ${L}_{f,n-1}={L}_{n-1},{L}_{b,1}={L}_{0}$.

  • 2. Calculate ${\theta }_{i}$ and ${l}_{\varepsilon ,i}$ by Eqs. (5) and (14), and determine ${l}_{1,i}$ and ${l}_{2,i}$ by $l\_generation(\theta ,{L}_{b,i},{L}_{f,i},{l}_{\varepsilon ,i})$ for $i=1,\dots ,n-1$.

• STEP II

• • 1. Set i = 1.

  • 2. If $i<n$, calculate the transition lengths ${L}_{2,i-1}$, ${L}_{1,i}$, ${L}_{2,i}$ and ${L}_{1,i+1}$ by Eq. (15); otherwise, stop.

  • 3. Check whether there exists linear trajectory on the line segment $\overline{{P }_{i-1}{P}_{i}}$ and $\overline{{P }_{i}{P}_{i+1}}$ (see Fig. 5). If ${L}_{m,i-1},{L}_{m,i}>0$, go to (4); otherwise, go to (6).

  • 4. If ${l}_{1,i},{l}_{2,i}<{l}_{\varepsilon ,i}$, the characteristic lengths of the transition PH spline can be increased, go to (5); otherwise, go to (6).

  • 5. Let ${L}_{b,i}={L}_{i-1}-{L}_{2,i-1}$ and ${L}_{f,i}={L}_{i}-{L}_{1,i+1}$; update ${l}_{1,i}$ and ${l}_{2,i}$ by $l\_generation(\theta ,{L}_{b,i},{L}_{f,i},{l}_{\varepsilon ,i})$.

  • 6. $i=i+1$, go to (2).

The flow chart of the proposed method is illustrated in Fig. 6.

Fig. 6

The flow chart of the proposed method

3.5 A simple case

To demonstrate the advantages of our corner smoothing method, our method and other two B-spline based methods in [3] (denoted by ${G}^{4}$ method) and [18] (denoted by ${G}^{3}$ method) are applied to the same $G01$ toolpath, which is shown as Fig. 7. To show the geometric properties of the three smooth paths generated by these methods, the curves with the arc length as the abscissa value and the curvature value as the ordinate value corresponding to it are shown in Fig. 8. Compared with ${G}^{3}$ method and ${G}^{4}$ method, the curvature extreme has been decreased by $59.63\%$ and $86.14\%$, and the arc length has been decreased by $0.25\%$ and $3.33\%$. In most cases, the smaller arc length and curvature extreme will lead to shorter machining time. To further verify whether our method can reduce the machining time, a feedrate scheduling scheme is introduced in Sect. 4, and the simulation is shown in Sect. 5.

Fig. 7

A polygonal shape $G01$ toolpath and its three smooth paths

Fig. 8

Curvature as a function of arc length for these three smoothing algorithms

4 Feedrate planning of ${{\mathrm{C}}}^{4}$ smooth path

In this section, the critical points of the smooth path and their maximum allowable feedrate are determined first; then, the division of the smooth path is presented, and the jerk-continuous feedrate scheduling scheme in Ref. [32] is adopted finally.

4.1 Determination of critical points and their feedrate

When planning the feedrate along a PH spline, the chord error, centripetal acceleration and jerk limitations should be taken into account. From Ref. [31], the maximum allowable feedrate can be calculated by

$${v}_{m}=min(F,\frac{2}{{T}_{s}}\sqrt{\frac{2\delta }{k}-{\delta }^{2}},\sqrt{\frac{{A}_{n}}{k}},\sqrt[3]{\frac{{J}_{n}}{{k}^{2}}})$$

(19)

where $F$ is the command feedrate, ${T}_{s}$ is the interpolation period, $k$ is the curvature, $\delta$ is the chord error limitation, ${A}_{n}$ and ${J}_{n}$ are the acceleration and jerk limitations respectively. From Eq. (19), the local minimum feedrate occurs at the local curvature extreme points of the smooth path, which are also the curvature extreme points of all inserted PH splines. However, the parameter of the curvature extreme point of the inserted PH spline cannot be given analytically because the PH spline is asymmetric. Instead, the bilinear interpolation method is applied to estimate the parameters of the curvature extreme points.

For an inserted PH spline, assuming its characteristic lengths are ${l}_{1}$ and ${l}_{2}$, and the corresponding corner angle is $\theta$. The parameter of the curvature extreme point of this inserted PH spline is determined as follows:

• Step 1: Define the ratio of the two characteristic lengths as ${R}_{\mathrm{1,2}}=max(\frac{{l}_{1}}{{l}_{2}},\frac{{l}_{2}}{{l}_{1}})$, and let $i=\left\lfloor180\times\theta/\pi\right\rfloor$ and $j=\lfloor {R}_{\mathrm{1,2}}/0.01\rfloor$.

• Step 2: According to matrix $M$ in Sect. 2, denote four close parameters of the curvature extreme point as ${t}_{\mathrm{0,0}}=M(i+1,j-99)$, ${t}_{\mathrm{1,0}}=M(i+2,j-99)$, ${t}_{\mathrm{0,1}}=M(i+1,j-98)$ and ${t}_{\mathrm{1,1}}=M(i+2,j-98)$.

• Step 3: Apply bilinear interpolation method to estimate the parameter as ${t}_{m}=\left(1-x\right)\left(1-y\right){t}_{\mathrm{0,0}}+x\left(1-y\right){t}_{\mathrm{1,0}}+\left(1-x\right)y{t}_{\mathrm{0,1}}+xy{t}_{\mathrm{1,1}}$, where $x=\frac{180\theta }{\pi }-i$ and $y=100{R}_{\mathrm{1,2}}-j$.

• Step 4: Let ${t}_{\mathrm{max}}=\mathrm{max}\left({t}_{\mathrm{0,0}},{t}_{\mathrm{1,0}},{t}_{\mathrm{0,1}},{t}_{\mathrm{1,1}}\right)$, ${t}_{\mathrm{min}}=\mathrm{min}\left({t}_{\mathrm{0,0}},{t}_{\mathrm{1,0}},{t}_{\mathrm{0,1}},{t}_{\mathrm{1,1}}\right)$, ${n}_{1}=\lfloor 1000{t}_{\mathrm{min}}\rfloor$ and ${n}_{2}=\lceil 1000{t}_{max}\rceil$. Determine a parameter set as $\left\{{t}_{a}|{t}_{a}=\frac{a+{n}_{1}}{1000},a=\mathrm{0,1},2,\dots ,n\right\}$, where $n={n}_{2}-{n}_{1}$.

• Step 5: If ${l}_{1}>{l}_{2}$, let ${t}_{m}=1-{t}_{m}$ and ${t}_{a}=1-{t}_{a}$ for $a=\mathrm{0,1},2,\dots ,n$.

• Step 6: Calculate the curvature of the inserted PH spline at parameter ${t}_{m}$ and ${t}_{a} (a=\mathrm{0,1},2,\dots ,n)$, and denote them as ${k}_{m}$ and ${k}_{a}$. Let ${k}_{\mathrm{max}}=\mathrm{max}({k}_{m},{k}_{a})$ and ${t}_{m}$ equals to the parameter whose curvature is ${k}_{\mathrm{max}}$.

The critical point of this PH spline can be obtained by substituting ${t}_{m}$ into the parametric equation $r(t)$, and the maximum allowable feedrate can be calculated by Eq. (19).

4.2 The division of the smooth path

For the toolpath presented by $\{{P}_{0}, {P}_{1}, \dots , {P}_{n}\}$, denote the inserted PH spline at point ${P}_{i}$ as ${r}_{i}\left(t\right) (i=\mathrm{1,2},\dots ,n-1)$. The parameter of the curvature extreme point of ${r}_{i}\left(t\right)$ and its maximum allowable feedrate can be obtained by the bilinear interpolation method in Sect. 4.1, which are denoted as ${t}_{i}$ and ${v}_{i}$ respectively. Then, the smooth path is split into $n$ blocks based on the critical points ${r}_{i}\left({t}_{i}\right)$.

The first block contains the remainder of the first linear segment and part of ${r}_{1}\left(t\right)$. The start point and end point of this block are ${P}_{0}$ and ${r}_{1}\left({t}_{1}\right)$, the start velocity and end velocity of this block are $0$ and ${v}_{1}$ and the length of this block can be calculated as follows:

$${S}_{1}^{b}={l}_{1}^{r}+{s}_{1}\left({t}_{1}\right)$$

(20)

where ${l}_{1}^{r}$ is the length of the remainder of the first linear segment, ${s}_{1}\left(t\right)$ is the cumulative arc length function of ${r}_{1}\left(t\right)$, which can be obtained by Eq. (3).

The $ith (i=\mathrm{2,3},\dots ,n-1)$ block contains part of ${r}_{i-1}\left(t\right)$, the remainder of the $ith$ linear segment and part of ${r}_{i}\left(t\right)$. The start point and end point of this block are ${r}_{i-1}\left({t}_{i-1}\right)$ and ${r}_{i}\left({t}_{i}\right)$, the start velocity and end velocity of this block are ${v}_{i-1}$ and ${v}_{i}$ and the length of this block can be calculated as follows:

$${S}_{i}^{b}={({s}_{i-1}\left(1\right)-s}_{i-1}\left({t}_{1}\right))+{l}_{i}^{r}+{s}_{i}\left({t}_{i}\right)$$

(21)

where ${l}_{i}^{r}$ is the length of the remainder of the $ith$ linear segment, and ${s}_{i}\left(\mathrm{t}\right)$ is the cumulative arc length function of ${r}_{i}\left(t\right)$.

The last block contains part of ${r}_{n-1}\left(t\right)$ and the remainder of the last linear segment. The start point and end point of this block are ${r}_{n-1}\left({t}_{n-1}\right)$ and ${P}_{n}$, the start velocity and end velocity of this block are ${v}_{n-1}$ and $0$ and the length of this block can be calculated as follows:

$${S}_{n}^{b}={({s}_{n-1}\left(1\right)-s}_{n-1}\left({t}_{n-1}\right))+{l}_{n}^{r}$$

(22)

where ${l}_{n}^{r}$ is the length of the remainder of the $nth$ linear segment, and ${s}_{i}\left(\mathrm{t}\right)$ is the cumulative arc length function of ${r}_{i}\left(t\right)$.

It is worth noting that the remainder of linear segment may degenerate into a point when it is completely replaced by two adjacent inserted PH splines. At this time, ${l}_{i}^{r}$ in Eqs. (20–22) equals to $0$, which will not have an essential effect on the division of the smooth path.

4.3 The jerk-continuous feedrate scheduling scheme

Since the start and end velocity of blocks are obtained only considering the chord error limitation, the acceleration limitation and the jerk limitation, when the length is too short, the feedrate may not be able to smoothly transition from the start velocity to the end velocity. To guarantee the continuity of the feedrate at the junctions between successive blocks, the bidirectional scanning module in [32] is applied to adjust the start velocity and the end velocity if necessary. Then, the velocity scheduling module in [32] is used to plan the feedrate along every block. Combining the feedrate along every block together, a jerk-continuous feedrate profile along the ${C}^{4}$ smooth path is obtained.

5 Simulation results

In this section, the proposed corner smoothing method is validated by three different types of toolpaths. As a comparison, other two B-spline based methods in [18] (denoted by ${G}^{3}$ method) and [3] (denoted by ${G}^{4}$ method) are also applied to the same toolpaths. After the toolpaths are rounded by different smoothing methods, the feedrate scheduling scheme in Sect. 4 is proposed to interpolate the smooth paths. Then, the contour errors, feedrate, acceleration and jerk profiles are analyzed to compare the above three smoothing methods in machining quality and efficiency. The related parameters used in this section are listed in Table 1.

Table 1 The parameters used in simulation

5.1 Simulation 1

In this section, a 2D NURBS curve named butterfly-shaped curve is discretized to linear segments as a toolpath to evaluate the performance of the proposed corner smoothing method. The degrees, control points, knot vectors and weight vectors of butterfly-shaped curve are given in Appendix 5.

As shown in Fig. 9, the linear trajectories near the corners are replaced by PH splines, which makes the toolpath ${C}^{4}$ continuous. To clearly illustrate the generated corner transition curve, two regions are enlarged as shown in Fig. 9b, c. The feedrate, acceleration, jerk and chord errors profiles of the proposed method, ${G}^{4}$ method and ${G}^{3}$ method can be calculated by interpolation points, which are presented in Figs. 10, 11, 12 and 13.

Fig. 9

Butterfly-shaped toolpath with ${C}^{4}$ continuity. (a) Toolpath smoothing. (b) Detailed result of region 1. (c) Detailed result of region 2

Fig. 10

The feedrate profiles of butterfly-shaped toolpath compared with ${G}^{4}$ method and ${G}^{3}$ method

From Figs. 10 and 11, the feedrate and acceleration are all subjected to the given limitations. However, it can be noted from Fig. 12 that the jerk profile of ${G}^{3}$ method excesses the maximum allowable jerk in some interpolating points, which will lead to violent vibration of the machine tool, and the machining quality will be affected. As can be seen from Fig. 13, although the chord errors of the proposed method are larger than ${G}^{4}$ method and ${G}^{3}$ method, they are all smaller than the given threshold, so the machining quality is not significantly affected.

Fig. 11

The acceleration profiles of butterfly-shaped toolpath compared with ${G}^{4}$ method and ${G}^{3}$ method

Fig. 12

The jerk profiles of butterfly-shaped toolpath compared with ${G}^{4}$ method and ${G}^{3}$ method

Fig. 13

The chord errors profiles of butterfly-shaped toolpath compared with ${G}^{4}$ method and ${G}^{3}$ method

In machining efficiency, the machining time of these three different methods are $5.848\mathrm{s}$, $6.678\mathrm{s}$ and $6.445\mathrm{s}$ respectively. The machining time of the proposed method is $12.43\%$ shorter than ${G}^{4}$ method and $9.26\%$ shorter than ${G}^{3}$ method, which means the proposed method can improve the machining efficiency when the machining parameters are set as in Table 1. To further validate the machining efficiency of the proposed method, the machining time of these three different methods when the feedrate, tangential acceleration, centripetal acceleration, tangential jerk and centripetal jerk constraints take different values are calculated and compared. As listed in Table 2, based on the machining time of the proposed method, the machining time of ${G}^{4}$ method and ${G}^{3}$ method has increased by $7.84\%$ to $14.24\%$. In other words, the machining efficiency can be improved by the proposed method under different constraints.

Table 2 The machining times of butterfly-shaped toolpath under different constraints

5.2 Simulation 2

In this section, a 3D parametric curve named spherical helix curve is discretized to linear segments as a toolpath to evaluate the performance of the proposed corner smoothing method. The parametric equation of this curve is given as follows:

$$\left\{\begin{array}{c}x=6sin(\theta )cos(\varphi )\\ y=6sin(\theta )sin(\varphi )\\ z=6cos(\theta )\end{array}\right.$$

(23)

where $\theta =\pi t$, $\varphi =20\pi t$ and $t\in [\mathrm{0,1}]$.

From Figs. 14, 15, 16, 17 and 18, in terms of machining quality of spherical helix toolpath, we can get the same conclusion as in Simulation 1. However, in machining efficiency, the machining time of these three different methods are $4.125\mathrm{s}$, $5.022\mathrm{s}$ and $5.114\mathrm{s}$ respectively. The machining time of the proposed method is $17.86\%$ shorter than ${G}^{4}$ method and $19.34\%$ shorter than ${G}^{3}$ method. As listed in Table 3, based on the machining time of the proposed method, the machining time of ${G}^{4}$ method and ${G}^{3}$ method has increased by $15.49\%$ to $23.98\%$. It is worth noting that compared with ${G}^{4}$ method and ${G}^{3}$ method, the proposed method has a greater improvement in machining efficiency of spherical helix toolpath than butterfly-shaped toolpath. The reason is that the linear segments of spherical helix toolpath change more frequently in direction and length, so that the advantages of the asymmetry of the proposed method can be fully utilized.

Fig. 14

Spherical helix toolpath with ${C}^{4}$ continuity. (a) Toolpath smoothing. (b) Detailed result

Fig. 15

The feedrate profiles of spherical helix toolpath compared with ${G}^{4}$ method and ${G}^{3}$ method

Fig. 16

The acceleration profiles of spherical helix toolpath compared with ${G}^{4}$ method and ${G}^{3}$ method

Fig. 17

The jerk profiles of spherical helix toolpath compared with ${G}^{4}$ method and ${G}^{3}$ method

Fig. 18

The chord errors profiles of spherical helix toolpath compared with ${G}^{4}$ method and ${G}^{3}$ method

Table 3 The machining times of spherical helix toolpath under different constraints

5.3 Simulation 3

In this section, a compound freeform surface composed of two NURBS patches, which presented in Fig. 19, is tested. The toolpath of this freeform surface is generated by Su’s method [33], which is composed of 58 linear toolpaths with corner points number ranging from 32 to 224. The transition error is $0.02\mathrm{mm}$ and other related parameters are the same as in Table 1.

Fig. 19

A compound freeform surface. (a) Surface. (b) Toolpath

Fig. 20

The feedrate profiles of freeform surface toolpath compared with ${G}^{4}$ method and ${G}^{3}$ method

Fig. 21

The acceleration profiles of freeform surface toolpath compared with ${G}^{4}$ method and ${G}^{3}$ method

It can be seen from Figs. 19, 20, 21 and 22, for the toolpath of freeform surface, the proposed method can replace the sharp corners with transition curves and generate smooth velocity, acceleration, jerk profiles whose extremes do not exceed the given limitations, while the jerk extreme of ${G}^{4}$ method and ${G}^{3}$ method excesses the maximum allowable jerk in some interpolating points, which will affect the machining quality. From Fig. 23, although the chord errors of the proposed method are larger than ${G}^{3}$ method and ${G}^{4}$ method, they are all subjected to the given limitations, so the machining quality is not significantly affected.

Fig. 22

The jerk profiles of freeform surface toolpath compared with ${G}^{4}$ method and ${G}^{3}$ method

Fig. 23

The chord error profiles of freeform surface toolpath compared with ${G}^{4}$ method and ${G}^{3}$ method

In machining efficiency, the machining time of these three different methods are $79.436\mathrm{s}$, $319.090\mathrm{s}$ and $85.860\mathrm{s}$ respectively. The machining time of the proposed method is $75.11\%$ shorter than ${G}^{4}$ method and $7.48\%$ shorter than ${G}^{3}$ method. It can be noted that in the previous two simulations, the machining time of the proposed method, ${G}^{3}$ method and ${G}^{4}$ method are similar. However, in this simulation, the machining time of ${G}^{4}$ method is much higher than the other two methods. Actually, in the order of magnitude, it is closer to the machining time of point-to-point method, which is $545.177\mathrm{s}$. The reason is that the toolpath of the freeform surface consists of a large number of dense and short linear segments, while ${G}^{4}$ method requires longer transition lengths for the same transition error, which makes the curvature extreme at the corners larger, so that the maximum allowable velocity at the corners is close to zero. From the previous two simulations, it can be seen that the proposed method is more efficient than ${G}^{3}$ method and ${G}^{4}$ method; even the feedrate, tangential acceleration, centripetal acceleration, tangential jerk and centripetal jerk constraints take different values, so only the cases with the same parameters as in Table 1 are compared.

6 Conclusions and future work

This study presents a novel local corner transition method based on asymmetrical ${C}^{4}$ continuous PH spline curve and a jerk-continuous feedrate scheduling scheme. Due to the asymmetry of PH spline curve, the construction of transition curve is more flexible. Although the asymmetry leads to unanalytical curvature extreme and corresponding parameter, a matrix $M$ which stored the parameters of curvature extreme points of different PH spline curves can be pre-calculated to solve this problem.

Advantages of our method are summarized as follows:

• a. The corner transition method guarantees the curvature continuity, ${C}^{4}$ continuity and maximum transition error of the smoothed toolpath. Furthermore, the cumulative arc length is a polynomial with respect to parameter of the transition curve, which makes the calculation of interpolation points more efficient.

• b. The curvature extreme of the smoothed toolpath is greatly reduced. Compared with two existing method, it has been decreased by $59.63\%$ and $86.14\%$.

• c. The proposed method generates a smooth feedrate profile, continuous acceleration curve and continuous jerk curve. Meanwhile, the actual maximum acceleration and jerk are under the confined range strictly.

• d. Machining efficiency is greatly improved. Compared with two conventional method, the machining time have decreased by $7.27$ to $75.11\%$.

To further improve machining quality and efficiency, future work will focus on analytical one-step corner for linear toolpath. In addition, to increase the generality of the local corner transition method, the toolpath composed of lines and arcs will also be considered.

Appendices

Appendix 1. Proof process of Theorem 1

When trigonometric functions are used to express $\overrightarrow{{n}_{1}}$ and $\overrightarrow{{n}_{2}}$, $\overrightarrow{{n}_{1}}={l}_{1}\overrightarrow{{T}_{1}}={l}_{1}{\left(cos\alpha ,sin\alpha \right)}^{T}={\left({u}_{0}^{2}-{v}_{0}^{2},2{u}_{0}{v}_{0}\right)}^{T}/15$ and $\overrightarrow{{n}_{2}}={l}_{2}\overrightarrow{{T}_{2}}={l}_{2}{\left(cos\beta ,sin\beta \right)}^{T}={\left({u}_{7}^{2}-{v}_{7}^{2},2{u}_{7}{v}_{7}\right)}^{T}/15$. According to the half angle formula of trigonometric function, ${u}_{0}$, ${v}_{0}$, ${u}_{7}$ and ${v}_{7}$ can be written as ${u}_{0}=\pm \sqrt{15{l}_{1}}cos\frac{\alpha }{2}$, ${v}_{0}=\pm \sqrt{15{l}_{1}}sin\frac{\alpha }{2}$, ${u}_{7}=\pm \sqrt{15{l}_{2}}cos\frac{\beta }{2}$ and ${v}_{7}=\pm \sqrt{15{l}_{2}}sin\frac{\beta }{2}$, where ${u}_{0}$ and ${v}_{0}$, ${u}_{7}$ and ${v}_{7}$ take the same sign. Substituting the above four parameters into $\overrightarrow{m}=\frac{{\left({u}_{0}{u}_{7}-{v}_{0}{v}_{7},{u}_{0}{v}_{7}+{u}_{7}{v}_{0}\right)}^{T}}{15}$, $\overrightarrow{{B}_{7}{B}_{8}}$ can be written as $\overrightarrow{{B}_{7}{B}_{8}}=\overrightarrow{m}=\pm \sqrt{{l}_{1}{l}_{2}}{\left(cos\frac{\alpha +\beta }{2},sin\frac{\alpha +\beta }{2}\right)}^{T}$. It is obvious that the length of $\overrightarrow{{B}_{7}{B}_{8}}$ equals to $\sqrt{{l}_{1}{l}_{2}}$. In addition, according to the sum-to-product trigonometric identities, $\overrightarrow{{T}_{1}}+\overrightarrow{{T}_{2}}={\left(2cos\frac{\alpha +\beta }{2}cos\frac{\alpha -\beta }{2},2sin\frac{\alpha +\beta }{2}cos\frac{\alpha -\beta }{2}\right)}^{T}=2cos\frac{\alpha -\beta }{2}{\left(cos\frac{\alpha +\beta }{2},sin\frac{\alpha +\beta }{2}\right)}^{T}$. Since ${P}_{0}{P}_{1}$ and ${P}_{1}{P}_{2}$ are two different linear segments, and they are not on the same line, $cos\frac{\alpha -\beta }{2}\ne 0$ can be deduced. If $cos\frac{\alpha -\beta }{2}>0$, $\frac{\overrightarrow{{T}_{1}}+\overrightarrow{{T}_{2}}}{\left|\overrightarrow{{T}_{1}}+\overrightarrow{{T}_{2}}\right|}={\left(cos\frac{\alpha +\beta }{2},sin\frac{\alpha +\beta }{2}\right)}^{T}$, let ${u}_{0}$ and ${v}_{0}$ take the same sign, then $\frac{\overrightarrow{{B}_{7}{B}_{8}}}{\left|\overrightarrow{{B}_{7}{B}_{8}}\right|}{=\left(cos\frac{\alpha +\beta }{2},sin\frac{\alpha +\beta }{2}\right)}^{T}=\frac{\overrightarrow{{T}_{1}}+\overrightarrow{{T}_{2}}}{\left|\overrightarrow{{T}_{1}}+\overrightarrow{{T}_{2}}\right|}$. On the contrary, let ${u}_{0}$ and ${v}_{0}$ take different signs, then $\frac{\overrightarrow{{B}_{7}{B}_{8}}}{\left|\overrightarrow{{B}_{7}{B}_{8}}\right|}{=-\left(cos\frac{\alpha +\beta }{2},sin\frac{\alpha +\beta }{2}\right)}^{T}=\frac{\overrightarrow{{T}_{1}}+\overrightarrow{{T}_{2}}}{\left|\overrightarrow{{T}_{1}}+\overrightarrow{{T}_{2}}\right|}$.

Appendix 2. Proof process of Theorem 2

According to Eq. (9), $\overrightarrow{{B}_{4}{B}_{7}}=\overrightarrow{{B}_{4}{B}_{5}}+\overrightarrow{{B}_{5}{B}_{6}}+\overrightarrow{{B}_{6}{B}_{7}}=\frac{398}{429}\overrightarrow{m}+\frac{889}{429}\overrightarrow{{n}_{1}}$. At the same time, $\overrightarrow{{B}_{4}{B}_{7}}=\overrightarrow{{B}_{4}{Q}_{1}}+\overrightarrow{{Q}_{1}{B}_{7}}$. Since $\overrightarrow{m}$ and $\overrightarrow{{n}_{1}}$ are two different vectors, $\overrightarrow{{B}_{4}{B}_{7}}$ has only unique expression when expressed by base {$\overrightarrow{m}, \overrightarrow{{n}_{1}}\}$. Considering $\overrightarrow{{B}_{4}{Q}_{1}}$ and $\overrightarrow{{n}_{1}}$, $\overrightarrow{{Q}_{1}{B}_{7}}$ and $\overrightarrow{m}$ have the same directions, it can be deduced that $\overrightarrow{{B}_{4}{Q}_{1}}=\frac{889}{429}\overrightarrow{{n}_{1}}$ and $\overrightarrow{{Q}_{1}{B}_{7}}=\frac{398}{429}\overrightarrow{m}$, i.e. $\left|\overrightarrow{{B}_{4}{Q}_{1}}\right|=\frac{889}{429}{l}_{1}$. Similarly, $\left|\overrightarrow{{B}_{11}{Q}_{2}}\right|=\frac{889}{429}{l}_{2}$. From Theorem 1, it is known that ${B}_{7}{B}_{8}$ and the angle bisector of $\mathrm{\angle }{{P}_{0}P}_{1}{P}_{2}$ are perpendicular. As shown in Fig. 1, the angle bisector of $\mathrm{\angle }{{P}_{0}P}_{1}{P}_{2}$ and ${B}_{7}{B}_{8}$ intersect at point ${B}_{m}$; then, ${B}_{m}$ is the midpoint of ${B}_{7}{B}_{8}$. In right triangle ∆${Q}_{1}{P}_{1}{B}_{m}$, $\left|\overrightarrow{{B}_{m}{Q}_{1}}\right|=\left|\overrightarrow{{Q}_{1}{B}_{7}}\right|+\frac{\left|\overrightarrow{{B}_{7}{B}_{8}}\right|}{2}=\frac{1225}{858}\sqrt{{{l}_{1}l}_{2}}$, $\angle {{Q}_{1}P}_{1}{B}_{m}=\frac{\pi -\theta }{2}$, then $\left|\overrightarrow{{Q}_{1}{P}_{1}}\right|=\frac{1225\sqrt{{{l}_{1}l}_{2}}}{858\mathrm{cos}\frac{\theta }{2}}$. Similarly, $\left|\overrightarrow{{Q}_{2}{P}_{1}}\right|=\frac{1225\sqrt{{{l}_{1}l}_{2}}}{858cos\frac{\theta }{2}}$.

Appendix 3. Proof process of Theorem 3

When ${l}_{1}={l}_{2}$, the proposed PH spline is symmetrical about the angle bisector of $\angle {{P}_{0}P}_{1}{P}_{2}$; then, the maximum deviation error occurs between the mid-point of the proposed PH spline and corner point ${P}_{1}$, which can be expressed as

$$\begin{aligned}{e}_{max}&=\left|r\left(0.5\right)-{P}_{1}\right|=\frac{1}{{2}^{15}}|{(B}_{0}-{P}_{1})+15{(B}_{1}-{P}_{1})\\&+105{(B}_{2}-{P}_{1})+455{(B}_{3}-{P}_{1})+1365{(B}_{4}-{P}_{1})\\&+3003{(B}_{5}-{P}_{1})+5005{(B}_{6}-{P}_{1})+6435{(B}_{7}-{P}_{1})\\&+6435{(B}_{8}-{P}_{1})+5005{(B}_{9}-{P}_{1})+3003{(B}_{10}-{P}_{1})\\&+1365{(B}_{11}-{P}_{1})+455{(B}_{12}-{P}_{1})+105{(B}_{13}-{P}_{1})\\&+15{(B}_{14}-{P}_{1})+{(B}_{15}-{P}_{1})|=\frac{1}{{2}^{15}}|{(B}_{0}+{B}_{15}-{2P}_{1})\\&+15{(B}_{1}+{B}_{14}-{2P}_{1})+105{(B}_{2}+{B}_{13}-{2P}_{1})\\&+455{(B}_{3}+{B}_{12}-{2P}_{1})+1365{(B}_{4}+{B}_{11}-{2P}_{1})\\&+3003{(B}_{5}+{B}_{10}-{2P}_{1})+5005{(B}_{6}+{B}_{9}-{2P}_{1})\\&+6435{(B}_{7}+{B}_{8}-{2P}_{1})|.\end{aligned}$$

(24)

From Eq. (10), it can be deduced that

$$\left\{\begin{array}{c}\begin{array}{c}{B}_{0}+{B}_{15}-{2P}_{1}=(4{l}_{1}+\frac{889}{429}{l}_{1}+l)(\overrightarrow{{T}_{2}}-\overrightarrow{{T}_{1}})\\ {B}_{1}+{B}_{14}-{2P}_{1}=(3{l}_{1}+\frac{889}{429}{l}_{1}+l)(\overrightarrow{{T}_{2}}-\overrightarrow{{T}_{1}})\\ {B}_{2}+{B}_{13}-{2P}_{1}=(2{l}_{1}+\frac{889}{429}{l}_{1}+l)(\overrightarrow{{T}_{2}}-\overrightarrow{{T}_{1}})\end{array}\\ \begin{array}{c}{B}_{3}+{B}_{12}-{2P}_{1}=({l}_{1}+\frac{889}{429}{l}_{1}+l)(\overrightarrow{{T}_{2}}-\overrightarrow{{T}_{1}})\\ {B}_{4}+{B}_{11}-{2P}_{1}=(\frac{889}{429}{l}_{1}+l)(\overrightarrow{{T}_{2}}-\overrightarrow{{T}_{1}})\\ \begin{array}{c}{B}_{5}+{B}_{10}-{2P}_{1}=(\frac{490}{429}{l}_{1}+l)(\overrightarrow{{T}_{2}}-\overrightarrow{{T}_{1}})\\ {B}_{6}+{B}_{9}-{2P}_{1}=(\frac{175}{429}{l}_{1}+l)(\overrightarrow{{T}_{2}}-\overrightarrow{{T}_{1}})\\ {B}_{7}+{B}_{8}-{2P}_{1}=l(\overrightarrow{{T}_{2}}-\overrightarrow{{T}_{1}})\end{array}\end{array}\end{array}.\right.$$

(25)

Combining Eqs. (24) and (25), the maximum deviation error ${e}_{\mathrm{max}}$ is expressed as

$${e}_{\mathrm{max}}=\frac{1}{{2}^{15}}\left|\overrightarrow{{T}_{2}}-\overrightarrow{{T}_{1}}\right|\left(\left(\frac{397}{429}+10207\right){l}_{1}+16384l\right).$$

(26)

Considering $\left|\overrightarrow{{T}_{2}}-\overrightarrow{{T}_{1}}\right|=2\mathit{sin}\left(\frac{\theta }{2}\right)$ and $l=\frac{16384\times 1225}{858cos(\frac{\theta }{2})}\sqrt{{{l}_{1}l}_{2}}=\frac{16384\times 1225}{858cos(\frac{\theta }{2})}{l}_{1}$, Eq. (13) can be obtained and Theorem 3 is proved.

Appendix 4. Proof process of Theorem 4

If ${l}_{1}={l}_{2}$, $R(t)$ is the same as $r(t)$ and ${e}_{r}={e}_{R}$. Without loss of generality, translate, rotate and, if necessary, reflect transition PH spline such that ${P}_{1}$ is at the origin, ${P}_{0}$ is on the negative x-axis, ${P}_{2}$ is above the x-axis and ${l}_{1}>{l}_{2}$. Replace ${l}_{1}$ and ${l}_{2}$ in Eq. (10) with ${l}_{0}=\mathrm{max}\left({l}_{1},{l}_{2}\right)={l}_{1}$ to get the control points of $R(t)$, which is denoted by ${\overline{B} }_{i} (i=\mathrm{0,1},2,\dots , 15)$. Subtracting ${B}_{i}$ from ${\overline{B} }_{i}$, we arrive at

$$\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{\overline{B} }_{0}-{B}_{0}=-\frac{1225}{858cos\frac{\theta }{2}}\sqrt{{l}_{1}}(\sqrt{{l}_{1}}-\sqrt{{l}_{2}})\overrightarrow{{T}_{1}}\\ {\overline{B} }_{1}-{B}_{1}=-\frac{1225}{858cos\frac{\theta }{2}}\sqrt{{l}_{1}}(\sqrt{{l}_{1}}-\sqrt{{l}_{2}})\overrightarrow{{T}_{1}}\\ {\overline{B} }_{2}-{B}_{2}=-\frac{1225}{858cos\frac{\theta }{2}}\sqrt{{l}_{1}}(\sqrt{{l}_{1}}-\sqrt{{l}_{2}})\overrightarrow{{T}_{1}}\end{array}\\ \begin{array}{c}{\overline{B} }_{3}-{B}_{3}=-\frac{1225}{858cos\frac{\theta }{2}}\sqrt{{l}_{1}}(\sqrt{{l}_{1}}-\sqrt{{l}_{2}})\overrightarrow{{T}_{1}}\\ {\overline{B} }_{4}-{B}_{4}=-\frac{1225}{858cos\frac{\theta }{2}}\sqrt{{l}_{1}}(\sqrt{{l}_{1}}-\sqrt{{l}_{2}})\overrightarrow{{T}_{1}}\\ {\overline{B} }_{5}-{B}_{5}=-\frac{1195}{858cos\frac{\theta }{2}}\sqrt{{l}_{1}}\left(\sqrt{{l}_{1}}-\sqrt{{l}_{2}}\right)\overrightarrow{{T}_{1}}+\frac{10}{286cos\frac{\theta }{2}}\sqrt{{l}_{1}}\left(\sqrt{{l}_{1}}-\sqrt{{l}_{2}}\right)\overrightarrow{{T}_{2}}\end{array}\\ \begin{array}{c}{\overline{B} }_{6}-{B}_{6}=-\frac{1081}{858cos\frac{\theta }{2}}\sqrt{{l}_{1}}\left(\sqrt{{l}_{1}}-\sqrt{{l}_{2}}\right)\overrightarrow{{T}_{1}}+\frac{48}{286cos\frac{\theta }{2}}\sqrt{{l}_{1}}\left(\sqrt{{l}_{1}}-\sqrt{{l}_{2}}\right)\overrightarrow{{T}_{2}}\\ {\overline{B} }_{7}-{B}_{7}=-\frac{827}{858cos\frac{\theta }{2}}\sqrt{{l}_{1}}\left(\sqrt{{l}_{1}}-\sqrt{{l}_{2}}\right)\overrightarrow{{T}_{1}}+\frac{398}{858cos\frac{\theta }{2}}\sqrt{{l}_{1}}\left(\sqrt{{l}_{1}}-\sqrt{{l}_{2}}\right)\overrightarrow{{T}_{2}}\\ {\overline{B} }_{8}-{B}_{8}=-\frac{398}{858cos\frac{\theta }{2}}\sqrt{{l}_{1}}\left(\sqrt{{l}_{1}}-\sqrt{{l}_{2}}\right)\overrightarrow{{T}_{1}}+\frac{827}{286cos\frac{\theta }{2}}\sqrt{{l}_{1}}\left(\sqrt{{l}_{1}}-\sqrt{{l}_{2}}\right)\overrightarrow{{T}_{2}}\end{array}\end{array}\\ \begin{array}{c}{\overline{B} }_{9}-{B}_{9}=-\frac{48}{286cos\frac{\theta }{2}}\sqrt{{l}_{1}}\left(\sqrt{{l}_{1}}-\sqrt{{l}_{2}}\right)\overrightarrow{{T}_{1}}+\left(\frac{175}{429}\left({l}_{1}-{l}_{2}\right)+\frac{1081}{858cos\frac{\theta }{2}}\sqrt{{l}_{1}}\left(\sqrt{{l}_{1}}-\sqrt{{l}_{2}}\right)\right)\overrightarrow{{T}_{2}}\\ {\overline{B} }_{10}-{B}_{10}=-\frac{10}{286cos\frac{\theta }{2}}\sqrt{{l}_{1}}\left(\sqrt{{l}_{1}}-\sqrt{{l}_{2}}\right)\overrightarrow{{T}_{1}}+\left(\frac{490}{429}\left({l}_{1}-{l}_{2}\right)+\frac{1195}{858cos\frac{\theta }{2}}\sqrt{{l}_{1}}\left(\sqrt{{l}_{1}}-\sqrt{{l}_{2}}\right)\right)\overrightarrow{{T}_{2}}\\ {\overline{B} }_{11}-{B}_{11}=\left(\frac{889}{429}\left({l}_{1}-{l}_{2}\right)+\frac{1225}{858cos\frac{\theta }{2}}\sqrt{{l}_{1}}\left(\sqrt{{l}_{1}}-\sqrt{{l}_{2}}\right)\right)\overrightarrow{{T}_{2}}\end{array}\\ \begin{array}{c}{\overline{B} }_{12}-{B}_{12}=\left(\left(\frac{889}{429}+1\right)\left({l}_{1}-{l}_{2}\right)+\frac{1225}{858cos\frac{\theta }{2}}\sqrt{{l}_{1}}\left(\sqrt{{l}_{1}}-\sqrt{{l}_{2}}\right)\right)\overrightarrow{{T}_{2}}\\ {\overline{B} }_{13}-{B}_{13}=\left(\left(\frac{889}{429}+2\right)\left({l}_{1}-{l}_{2}\right)+\frac{1225}{858cos\frac{\theta }{2}}\sqrt{{l}_{1}}\left(\sqrt{{l}_{1}}-\sqrt{{l}_{2}}\right)\right)\overrightarrow{{T}_{2}}\\ \begin{array}{c}{\overline{B} }_{14}-{B}_{14}=\left(\left(\frac{889}{429}+3\right)\left({l}_{1}-{l}_{2}\right)+\frac{1225}{858cos\frac{\theta }{2}}\sqrt{{l}_{1}}\left(\sqrt{{l}_{1}}-\sqrt{{l}_{2}}\right)\right)\overrightarrow{{T}_{2}}\\ {\overline{B} }_{15}-{B}_{15}=\left(\left(\frac{889}{429}+4\right)\left({l}_{1}-{l}_{2}\right)+\frac{1225}{858cos\frac{\theta }{2}}\sqrt{{l}_{1}}\left(\sqrt{{l}_{1}}-\sqrt{{l}_{2}}\right)\right)\overrightarrow{{T}_{2}}\end{array}\end{array}\end{array}\right.$$

(27)

It is obvious that ${\overline{B} }_{i}-{B}_{i}={a}_{i}\overrightarrow{{T}_{1}}+{b}_{i}\overrightarrow{{T}_{2}}$, ${a}_{i}\le 0$ and ${b}_{i}\ge 0$ for $i=\mathrm{0,1},\dots ,15$. Considering $r\left(t\right)={\sum }_{i=0}^{15}{B}_{i}{b}_{i}^{15}\left(t\right)$ and $R\left(t\right)={\sum }_{i=0}^{15}{\overline{B} }_{i}{b}_{i}^{15}\left(t\right)$, we have

$$\overrightarrow{r\left(t\right)R\left(t\right)}={\sum }_{i=0}^{15}\left({\overline{B} }_{i}-{B}_{i}\right){b}_{i}^{15}\left(t\right)={f}_{1}(t)\overrightarrow{{T}_{1}}+{f}_{2}(t)\overrightarrow{{T}_{2}}$$

(28)

where ${f}_{1}(t)\le 0$ and ${f}_{2}(t)\ge 0$ for arbitrary $t\in [0, 1]$. As shown in Fig. 24, the region bounded by the transition PH spline $r(t)$ and the linear trajectory ${P}_{0}{-P}_{1}-{P}_{2}$ is denoted as $\mathrm{S}$. Then, it can be deduced from Eq. (27) that $R\left(t\right)$ is outside of $\mathrm{S}$ for arbitrary $t\in [0, 1]$. From the convex hull property of Bezier spine, the transition PH spline $R(t)$ is inside of ∆${P}_{0}{P}_{1}{P}_{2}$. Then, for arbitrary ${t}_{1}\in [0, 1]$, there is an intersection point between the line segment $\overline{{P }_{1}R({t}_{1})}$ and the transition PH spline $r(t)$; in other words, there is a ${t}_{2}\in [0, 1]$ such that $\left|\overrightarrow{{P}_{1}r({t}_{2})}\right|\le \left|\overrightarrow{{P}_{1}R({t}_{1})}\right|$, which gives ${e}_{r}\le {e}_{R}$ naturally.

Fig. 24

The schematic diagram of two transition PH spline $r(t)$ and $R(t)$

Appendix 5. Parameters of butterfly-shaped curve

The degree: p = 3.

The control point (mm): P = [(54.493, 52.139), (55.507,52.139), (56.082, 49.615), (56.780, 44.971), (69.575,51.358), (77.786, 58.573), (90.526, 67.081), (105.973,63.801), (100.400, 47.326), (94.567, 39.913), (92.369,30.485), (83.440, 33.757), (91.892, 28.509), (89.444,20.393), (83.218, 15.446), (87.621, 4.830), (80.945, 9.267),(79.834, 14.535), (76.074, 8.522), (70.183, 12.550), (64.171,16.865), (59.993, 22.122), (55.680, 36.359), (56.925, 24.995),(59.765, 19.828), (54.493, 14.940), (49.220, 19.828), (52.060,24.994), (53.305, 36.359), (48.992, 22.122), (44.814, 16.865),(38.802, 12.551), (32.911, 8.521), (29.152, 14.535), (28.040,9.267), (21.364, 4.830), (25.768, 15.447), (19.539, 20.391),(17.097, 28.512), (25.537, 33.750), (16.602, 30.496), (14.199,39.803), (8.668, 47.408), (3.000, 63.794), (18.465, 67.084),(31.197, 58.572), (39.411, 51.358), (52.204, 44.971), (52.904,49.614), (53.478, 52.139), (54.492, 52.139)].

The knot vector: U = [0, 0, 0, 0, 0.0083, 0.015, 0.0361, 0.0855, 0.1293, 0.1509, 0.1931, 0.2273, 0.2435, 0.2561, 0.2692, 0.2889, 0.3170, 0.3316, 0.3482, 0.3553, 0.3649, 0.3837, 0.4005, 0.4269, 0.4510, 0.4660, 0.4891, 0.5000, 0.5109, 0.5340, 0.5489, 0.5731, 0.5994, 0.6163, 0.6351, 0.6447, 0.6518, 0.6683, 0.6830, 0.7111, 0.7307, 0.7439, 0.7565, 0.7729, 0.8069, 0.8491, 0.8707, 0.9145, 0.9639, 0.9850, 0.9917, 1.0, 1.0, 1.0, 1.0].

The weight vector: W = [1.0, 1.0, 1.0, 1.2, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1, 2, 1.0, 1.0, 5.0, 3.0, 1.0, 1.1, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.1, 1.0, 3.0, 5.0, 1.0, 1.0, 2.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.2, 1.0, 1.0, 1.0].