1 Introduction

Polishing is a critical process for workpiece surface quality enhancement in many industries such as automobile, marine, and aerospace. Different from milling and drilling, polishing is characterized by low contact force and material removal depth, which aims to achieve consistent surface quality [1–3]. As manual polishing suffers from drawbacks such as low efficiency, inconsistent polishing quality, and hazardous work environment, robotic polishing becomes a promising solution to improve the polishing quality and efficiency.

Compliant polishing discs are widely used as polishing tools due to their flexibility for various surfaces. Typically, a small tilt angle of \(5^\circ \sim 25^\circ\) will be maintained between the compliant polishing disc and the workpiece surface during the polishing process to avoid the inconsistent polishing marks caused by zero velocity zone at the centre of polishing disc and remove the abrasive dust [1, 4]. To achieve consistent polishing quality, the tilt angle of disc and normal contact force exerted on the workpiece surface need to be controlled simultaneously.

For robotic polishing, heavy-duty industrial robots are normally employed, which have large moving mass and slow dynamic response. As such, the around-the-arm method is appropriate for force control applications, in which the industrial robot combines with a force-controlled end-effector to form a macro-mini robotic system [5, 6].

Force-controlled end-effectors with single degree of freedom rely on the industrial robots to adjust the tool orientation [7,8,9], which have limited performance in situations where hybrid orientation/force control is required, such as curved surface polishing. For such applications, a 3-DOF force-controlled end-effector with two-rotational-one-translational (2R1T) motions has been investigated [10]. The 2R motions, characterized with the azimuth and tilt angles, are utilized to adjust the tool orientation, while the 1T motion, i.e. the translational motion along the z-axis of the end-effector’s base frame, is utilized to achieve force control. Research efforts on hybrid orientation/force control of the 2R1T robotic device have been conducted. J. Cazalilla et al. [11] adopted a conventional hybrid orientation/force controller for a 2R1T 3-PRS ankle rehabilitation device. The maximum force error was about 5 N when tracking a sinusoidal force reference with an amplitude of 15 N and a frequency of 0.2 Hz. Yuta Oba and Yasuhiro Kakinuma [10] employed disturbance observer (DOB) and reaction force observer (RFOB) to achieve hybrid orientation/force control for a serial-parallel manipulator (an XY stage + a 2R1T 3-PRS parallel mechanism). The maximum force error was about 2.5 N when tracking a z-axis force ranging from 2 to 6 N. An increase in the force error was observed when tilting angle is increasing. To achieve high force control accuracy, the hybrid orientation/force control of the 2R1T robotic device needs to be further investigated.

Conventional hybrid position/force control is realized through specifying motion and force in the corresponding subspace with selective matrices [6], yet it often suffers from serious position and force oscillations during the contact transitions. To achieve a steady contact transition, a number of modified control methods have been developed. A hybrid position-force control method for a redundant 7R manipulator, in which chattering-free sliding mode control was employed in the force control due to its inherent robustness [12]. An adaptive fuzzy sliding mode control was developed to achieve hybrid position/force control for a Stewart platform with state-dependent uncertainties, in which a modified extended Kalman filter was used for estimating contact parameters [13].

Recently, the integration of hybrid position/force control and impedance/admittance control, namely hybrid impedance control [14,15,16], has drawn widespread attention due to the flexibility in choosing the desired impedance. Although neither the position nor the force reference is independently tracked in conventional impedance/admittance control [17, 18], admittance control is more suitable to achieve force tracking [13] which can be summarized as reference trajectory modification approach [19] and variable impedance modification approach [20]. However, during the polishing process of the curved surfaces with a 2R1T force-controlled end-effector, it is realized that the adjustment of the tilt angle will significantly decrease the force control accuracy due to the displacement variation of the contact point. As small displacement variation can lead to significant force fluctuations, the displacement variation of the contact point along the force control direction needs to be accurately compensated.

Despite lots of research works on hybrid position/force control and impedance/admittance control, the modeling and compensation of contact point variation issue is not well addressed in hybrid orientation/force control of the 2R1T force-controlled end-effectors.

In this paper, three major factors that result in the contact point variation, i.e. the inherent parasitic motion of the end-effector’s moving platform, the geometry of the disc, and the compliance of the disc, are identified and modeled. To accurately achieve simultaneous orientation and force control, a hybrid orientation/force control architecture with contact point (displacement) compensation along the force control direction is proposed. Specifically, the control architecture consists of the selective matrices of orientation/force subspace, a contact point compensation model, an admittance controller, and a joint space motion controller. Utilizing the proposed contact point compensation model, the contact point variation can be predicted according to the desired orientation and force, which is employed as a feed-forward reference to modify the compliant motion commands of the admittance controller. Integrated with the desired orientation, the task-space pose commands of the moving platform are generated, while the corresponding active joints commands for the closed-loop control in the joint space are determined based on the inverse kinematics. In this way, the control accuracy of contact force can be improved when the tilt angle of the end-effector’s moving platform changes.

The rest of this paper is organized as follows. In Sect. 2, the prototype of the 2R1T force-controlled end-effector and the displacement analysis are briefly introduced. In Sect. 3, the influence of tilt angle regulation on contact force accuracy is elaborated. Analyses for the three major affecting factors of the contact point variation, i.e. the inherent parasitic motion of the moving platform, the geometry of the disc, and the compliance of the disc are detailed. In Sect. 4, a hybrid orientation/force controller with contact point compensation model is investigated. In Sect. 5, the key parameters of the stress-strain model of compliant polishing disc are identified, and experimental results are compared and discussed. Finally, Sect. 6 summarizes the paper.

2 The 2R1T force-controlled end-effector

2.1 Mechanical structure

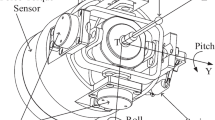
A prototype of the 3-DOF 2R1T force-controlled end-effector is developed based on a 3-PPS parallel mechanism in our previous work [21]. The prototype, as shown in Fig. 1, can independently adjust the azimuth \(\&\) tilt angles of the moving platform, as well as the translational motion of the moving platform along the normal of the base plate. It has a symmetric structure with three identical PPS legs placed \(120^\circ\) apart. There is a vertical active prismatic joint, a horizontal passive prismatic joint, and a passive spherical joint in each leg. Its three active joints are driven by voice coil motors (VCMs). Three passive prismatic joints are flexure-based joints which are designed with high off-axis stiffness ratio and frictionless in the designated motion direction. Three spherical joints are off-shelf precision spherical joints. The key structure parameters are listed in Table 1.

Table 1 Key structure parameters of the 3-DOF 2R1T force-controlled end-effector
Full size table
Fig. 1
figure 1

The proposed 2R1T force-controlled end-effector prototype

Full size image
Fig. 2
figure 2

Kinematic diagram of the proposed 2R1T force-controlled end-effector

Full size image

2.2 Displacement analysis

As detailed formulations are addressed in our previous work [21], only some key results are briefly presented in this subsection.

The kinematic diagram of the 2R1T force-controlled end-effector is shown in Fig. 2. The base frame B is attached to the centre of the base plate with its z-axis perpendicular to the base plate and x-axis parallel to \(B_2B_3\). The moving platform frame M is attached to the centre of \(\Delta P_1P_2P_3\), while its z-axis is perpendicular to \(\Delta P_1P_2P_3\) and x-axis is parallel to \(P_2P_3\).

For the zero-torsion 3-PPS parallel mechanism, our previous work [21] proposed two parameters (\(e_x\), \(e_y\)) to describe the orientation of the moving platform, in which \(e_x\) and \(e_y\) represent the x and y coordinates of the z-axis of the moving platform with respect to frame \(M_0\), respectively, as shown in Fig. 3. It is noted that frame \(M_0\) in Fig. 3 is attached to the origin of moving platform frame M with the same orientation as the base frame B. The proposed orientation description is intuitive as the orientation of the moving platform is equivalent to a rotation about a unit vector (axis) \(\varvec{k}\) parallel to the base plate. Moreover, it is equivalent to the tilt-and-torsion angles conventions, i.e. azimuth angle \(\phi\) and tilt angle \(\theta\).

Fig. 3
figure 3

Equivalent rotation about a unit axis \(\varvec{k}\) parallel to the base plate

Full size image

According to the Rodrigues’ formula and the two-parameter orientation description (\(e_x\), \(e_y\)), such a rotation can be determined as

$$\begin{aligned} {}^{B}{\varvec{R}_{M}}= \left[ \begin{array}{ccc} \dfrac{e_x^2 e_z+e_y^2}{e_x^2+e_y^2} &{} \dfrac{e_x e_y \left( e_z-1\right) }{e_x^2+e_y^2} &{} e_x \\ \dfrac{e_x e_y \left( e_z-1\right) }{e_x^2+e_y^2} &{} \dfrac{e_x^2 + e_y^2 e_z}{e_x^2+e_y^2} &{} e_y \\ -e_x &{} -e_y &{} e_z \\ \end{array} \right] \end{aligned}$$
(1)

where \(e_z = \sqrt{1-e_x^2-e_y^2}\).

For the 3-PPS force-controlled end-effector, the closed-form forward displacement solution is derived in [21] as

$$\begin{aligned} \left\{ \begin{array}{l} e_x=\dfrac{q_{a2}-q_{a3}}{\sqrt{3} r} \\ e_y=\dfrac{ -2 q_{a1}+q_{a2}+q_{a3}}{3 r} \\ m_{z}=H_{BM}+\dfrac{q_{a1}+q_{a2}+q_{a3}}{3} \end{array} \right. \end{aligned}$$
(2)

where \(m_z\) is the z-coordinate of the origin of the moving platform frame M with respect to the base frame B, r is the radius of the circumcircle passing through three centres of the sphere joints, \(q_{ai}\) is the active joint variables in the i-th leg, \(H_{BM}\) is the distance between the origins of frame B and M when all three active joints are at the minimal strokes, i.e. home positions. The values of design parameters are listed in Table 1.

The inverse displacement solution is derived readily from the closed-form forward displacement solution, i.e. Eq. 2, as follows:

$$\begin{aligned} \left\{ \begin{array}{l} q_{a1}=m_{z}-H_{BM}-r e_y \\ q_{a2}=m_{z}-H_{BM}+\dfrac{r}{2} \left( \sqrt{3} e_x+ e_y\right) \\ q_{a3}=m_{z}-H_{BM}+\dfrac{r}{2} \left( - \sqrt{3} e_x+ e_y\right) \end{array} \right. \end{aligned}$$
(3)

3 Formulation of contact point variation model

The schematic diagram of the macro-mini robotic polishing process is shown in Fig. 4. The tool frame T is fixed at the disc edge along the y axis of the frame B, where the active joints are all at half strokes. As the macro-mini robotic polishing system feeds along the curved surface, the 2R1T force-controlled end-effector regulates the tilt angle of the tool and the normal contact force simultaneously, while the macro robot operated in position control mode and performs as little attitude and orientation adjustment as possible.

During the polishing process with a 2R1T force-controlled end-effector, it is realized that the adjustment of the tilt angle will lead to displacement variations of the contact point \(P_c\) along the force control direction. Such contact point variation has a portion coinciding with the force control direction, which will significantly decrease the force control accuracy.

Fig. 4
figure 4

Contact point variation

Full size image

This contact point variation can be further illustrated with the contact on the curved surface as shown in Fig. 5. The radius of the polishing disc is \(R_t\) and the length between the frame M origin and the disc centre, i.e. the tool length, is \(L_t\). As the equivalent rotation axis \(\varvec{k}\) of the moving platform will not pass through the actual contact point, the Cartesian coordinates of the contact point with respect to the frame B change accordingly. The variation portion \(X_h\) along the surface normal \(\varvec{n}\) has the most sever influence on the contact force accuracy.

Fig. 5
figure 5

The total contact point variation due to the tilt angle regulation

Full size image

Careful inspections of the 2R1T end-effector and the compliant polishing disc indicate that the inherent parasitic motion of the end-effector’s moving platform, the geometry of the disc, and the compliance of the disc are three major factors resulting in the contact point variation. The contact point variation \(X_h\) along the surface normal \(\varvec{n}\) is up to a few millimeters, which has significant impact on the contact force accuracy and needs to be accurately compensated.

The contact point variation \(X_h\) consists of elastic deformation of the disc \(h_0\) and the projection of both the parasitic motion of the end-effector’s moving platform and the geometry of the disc onto the normal \(\varvec{n}\), i.e. \(h_1\), which is given by:

$$\begin{aligned} X_h= \left( \begin{array}{ccc} 0&\,0\,&h_1 \!-\! h_0 \end{array}\right) ^{\top } \end{aligned}$$
(4)

The following subsections present detailed analysis of the three major factors that result in the contact point variation.

3.1 Analysis of the parasitic motion

The 3-DOF 2R1T force-controlled end-effector is based on the 3-PPS parallel mechanism and three independent parameters (\(e_x\), \(e_y\), \(m_z\)) are employed to determine the pose of the moving platform. Based on the kinematic analysis, the inherent parasitic motion of the end-effector’s moving platform is the translational motions along the x- and y-axis, i.e. the \(x-\) and \(y-\) coordinates of the frame M origin with respect to the base frame B, denoted as (\(m_x\), \(m_y\)). According to displacement analysis [21], the parasitic motion of the moving platform can be determined with the rotation matrix entries.

$$\begin{aligned} m_{x}= {} \dfrac{r \left( R_{11} - R_{22} \right) }{2} \end{aligned}$$
(5)
$$\begin{aligned} m_{y}= -r R_{21} \end{aligned}$$
(6)

where the subscript (i, j) of the rotation matrix \(\varvec{R}\) denotes the entry in the i-th row and j-th column.

Combining with Eq. 1, the parasitic motion of the moving platform is further derived as

$$\begin{aligned} m_{x}= \dfrac{ r e_x e_y \left( 1-\sqrt{ 1-e_x^2-e_y^2}\right) }{e_x^2+e_y^2} \end{aligned}$$
(7)
$$\begin{aligned} m_{y}= \dfrac{r \left( e_x^2-e_y^2\right) \left( 1-\sqrt{ 1-e_x^2-e_y^2}\right) }{2 \left( e_x^2+e_y^2\right) } \end{aligned}$$
(8)

Equations 5 and 6 suggest that the parasitic motion is only related to the orientation of the moving platform.

To further illustrate the parasitic motion of the moving platform, the parasitic motion map with constant azimuth angle \(\phi\) or tilt angle \(\theta\) is shown in Fig. 6.

Fig. 6
figure 6

The parasitic motion map with constant azimuth (dotted line) or tilt (solid line) angles

Full size image

The projection distance of the parasitic motion D onto the XOY plane of the base frame B is derived as

$$\begin{aligned} D= \dfrac{r}{2} \left( 1-\sqrt{ 1-e_x^2-e_y^2} \right) \end{aligned}$$
(9)

3.2 Analysis of the geometry of the disc

Without considering the deformation of the polishing disc, its geometry can be represented by two parameters, i.e. the disc radius \(R_t\) and the tool length \(L_t\).

When the orientation of the moving platform is given, the displacement variation related to the geometry of the disc with respect to the tool frame T can be readily determined.

As no compliance is taken into account for analyses of the parasitic motion and the geometry of the disc, the displacement variation resulting from these two factors is treated as the kinematic projection onto the surface normal \(\varvec{n}\), denoted as \(h_1\), which is formulated as

$$\begin{aligned} h_1 = \left( \begin{array}{ccc} {}^{T}{P_{cx}}&{}^{T}{P_{cy}}&{}^{T}{P_{cz}} \end{array}\right) \cdot \left( \begin{array}{ccc} n_x&\,n_y\,&n_z \end{array}\right) ^{\top } \end{aligned}$$
(10)

where the entries are given by

$$\begin{aligned} {}^{T}{P_{cx}}= m_{x} + L_t R_{13} +R_t \left( 1- R_{11} \right) \end{aligned}$$
(11)
$$\begin{aligned} {}^{T}{P_{cy}}= m_{y}+ L_t R_{23} +R_t R_{21} \end{aligned}$$
(12)
$$\begin{aligned} {}^{T}{P_{cz}}= m_{z}- z_0 - L_t R_{33} + R_t R_{13} \end{aligned}$$
(13)

where \(z_0\) represents the initial distance along the normal of base plate between frame B and frame T, which is 137.5 mm in the prototype.

3.3 Analysis of the compliance of the disc

When the compliant polishing disc contacts with the workpiece surface, the bottom of the disc deforms locally, which result in a displacement variation of the contact point \(P_c\). Such an elastic deformation \(h_0\) along the surface normal \(\varvec{n}\) is determined by [2]

$$\begin{aligned} h_0 \approx \left( \dfrac{F \theta ^{1.5}}{C \hat{R}^{0.5}}\right) ^{{2}/{\left( 3+2 \beta \right) }} \end{aligned}$$
(14)

where F is the normal contact force, \(\theta\) is the tilt angle between the tool and the tangent vector along the feed direction passing through the contact point, and \(\beta\) is the power index. C given by Eq. 15 is a function of the thickness of the polishing disc, the nonlinear material modulus \(\hat{E}\) and the power index \(\beta\). \(\hat{R}\) given by Eq. 16 is the equivalent disc radius, in which b is the normal curvature perpendicular to the feed direction.

$$\begin{aligned} C= \dfrac{2\sqrt{2} \hat{E}}{\left( \beta +1\right) H ^{\beta }} \int _{0}^{1} \left( 1-t^2\right) ^{\beta +1}\,dt \end{aligned}$$
(15)
$$\begin{aligned} \hat{R}= \dfrac{1}{b/\sin {\theta }+1/R_t} \end{aligned}$$
(16)

4 Hybrid orientation/force control architecture

To achieve simultaneous orientation and force control, a hybrid orientation/force control architecture with contact point (displacement) compensation along the force control direction is proposed, as shown in Fig. 7. The control architecture consists of selective matrices for orientation/force subspace, a contact point compensation model, an outer-loop admittance controller, and a inner-loop joint space motion controller. The selective matrices divide the task space of the 2R1T end-effector into orientation and force subspaces and generate the corresponding commands \(X_R\) for the orientation subspace. The admittance controller gives the compliant motion commands \(X_c\) along the force control direction based on the contact force error. The contact point compensation model gives the prediction of the contact point variation \(X_h\) according to the desired orientation and force, which is employed as a feed-forward reference to modify the compliant motion commands of the admittance controller. The outputs of three components are integrated together to generate the task-space pose commands of the moving platform, while the corresponding active joints commands for the motion control of the joint space are determined based on the inverse kinematics. The active joint displacements are measured by linear encoders and the actual contact force is measured by a force sensor. In such way, the orientation of the tool and the normal contact force are controlled simultaneously and the negative effects of tilt angle regulation on contact force accuracy is mitigated.

Since the contact point compensation model is presented in Sect. 3, the rest parts of the hybrid orientation/force control architecture are discussed as follows.

Fig. 7
figure 7

Hybrid orientation/force control architecture with contact point compensation model

Full size image

4.1 Selective matrices for orientation/force subspace

The proposed 2R1T force-controlled end-effector has a unique orientation retention property such that as long as the relative displacements among three active joints are fixed, the tool orientation will be retained. Let the globe coordinates of the moving platform be denoted as \(\left( e_x, e_y, m_z\right)\), then the selection matrix \(\varvec{S}\) for orientation control subspace is given by

$$\begin{aligned} \varvec{S}= \left[ \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 \end{array} \right] \end{aligned}$$
(17)

The corresponding orientation commands \(X_R\) are given by

$$\begin{aligned} X_R= \left( \begin{array}{ccc} e_x&e_y&0 \end{array}\right) ^{\top } \end{aligned}$$
(18)

The orthogonal selection matrix \(\varvec{S}^\perp\) for force control subspace is given by

$$\begin{aligned} \varvec{S}^\perp = \left[ \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right] \end{aligned}$$
(19)

For orientation control subspace, based on the inverse kinematics, the well-developed computed-torque model combined with a proportional–differential (PD) controller is implemented.

4.2 Force tracking in admittance controller

To achieve desired force tracking, an admittance controller is adopted. The objective of conventional admittance control is to establish a desired dynamic relationship between motion and force [18]. Furthermore, to achieve force tracking, the target impedance is regulated through the error between desired \(n \times 1\) force \(F_r\) and actual contact force \(F_e\) exerted on the robot system by the environment.

Typically, the target impedance is modeled as a mass-damper-spring system, as shown in Fig. 8. The outer impedance loop is isolated from inner position loop by introducing the compliant motion command \(X_c\), while the corresponding second-order target impedance is formulated as

$$\begin{aligned} M_d \ddot{E}_x\left( t\right) +B_d \dot{E}_x \left( t\right) +K_d E_x\left( t\right) =E_f\left( t\right) \end{aligned}$$
(20)

where \(E_x=X_c-X_r\) denotes the position error, \(X_r\) denotes the position reference, and \(E_f=F_r-F_e\) denotes the contact force error.

Considering one element of target impedance with constant reference position, i.e. \(\ddot{x}_r=\dot{x}_r=0\), the target impedance in this specific direction becomes

$$\begin{aligned} m_d \ddot{x}_c\left( t\right) +b_d \dot{x}_c \left( t\right) +k_d e_x\left( t\right) =e_f\left( t\right) \end{aligned}$$
(21)

Using the linear-spring model of the environment, the actual position x can be described as

$$\begin{aligned} x= \frac{f_e}{k}_e +x_e = \frac{f_r-e_f}{k_e} +x_e \end{aligned}$$
(22)

As the residual position-tracking error \(\delta x=x_c-x\) is inevitable in practice, the compliant motion command \(x_c\) can be rewritten as

$$\begin{aligned} x_{c}= \frac{f_r-e_f}{k_e} +x_e+\delta x \end{aligned}$$
(23)
Fig. 8
figure 8

Simplified robot dynamics in contact with environment

Full size image

Substituting Eq. 23 in Eq. 21 yields

$$\begin{aligned} m_d \ddot{e}_f &{} +b_d \dot{e}_f +\left( k_d+k_e\right) e_f\\ &{}\quad =m_d \ddot{f}_r+b_d \dot{f}_r+k_d f_r\\ &{} +k_e \left( m_d\ddot{x}_e +b_d \dot{x}_e +k_d x_e \right) \\ &{}+ k_e\left[ m_d \ddot{\delta x} + b_d \dot{\delta x} +k_d \left( \delta x - x_r\right) \right] \end{aligned}$$
(24)

In robotic polishing, the desired force \(F_r\) is usually set to be a constant value. Thus, the steady-state force-tracking error is obtained

$$\begin{aligned} e_{fss}= \frac{k_d}{k_d+k_e} \left[ f_r + k_e \left( x_e + \delta x - x_r\right) \right] \end{aligned}$$
(25)

It is noted that residual position-tracking error \(\delta {x}\) will contribute to the steady-state force-tracking error \(e_{fss}\). Limited by the servo system performance, it is difficult to obtain an acceptable \(e_{fss}\) even with the precise knowledge of environment position \(x_e\) and stiffness \(k_e\). To achieve desired force-tracking performance, Eq. 25 suggests that a zero stiffness gain \(k_d\) can realize the zero steady-state error without precise environment parameters.

Thus the contact phase impedance law yields

$$\begin{aligned} m_d \ddot{x}_c\left( t\right) +b_d \dot{x}_c \left( t\right) =e_f\left( t\right) \end{aligned}$$
(26)

It can be proved that the impedance law is asymptotically stable even with unknown environment. The corresponding compliant motion commands \(X_c\) are given by

$$\begin{aligned} X_c= \left( \begin{array}{ccc} 0&0&x_c \end{array}\right) ^{\top } \end{aligned}$$
(27)

5 Experiments and results

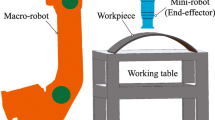
To verify the effectiveness of the proposed hybrid orientation/force control method, several experiments were conducted on a macro-mini robotic polishing system. The test bench is shown in Fig. 9. The macro robot was a 6-DOF industrial robot operating in position control mode, while the mini robot was the proposed 2R1T force-controlled end-effector. An F/T sensor was installed between the moving platform and the pneumatic polishing tool to measure the contact force. A wheel hub was chosen as the workpiece to be polished.

Fig. 9
figure 9

The proposed macro-mini robotic polishing system integrated with 2R1T force-controlled end-effector prototype

Full size image

5.1 Contact point variation model identification

The normal force-elastic deformation relationship of the compliant polishing disc was derived from Eq. 14 as follows:

$$\begin{aligned} F \approx C \hat{R}^{0.5} \theta ^{-1.5} h_0^{{3}/{\left( 2+ \beta \right) }} \end{aligned}$$
(28)

The actual values of the coefficients in Eq. 28 were determined through experiments. As the polishing disc moving towards the workpiece along the surface normal at a low speed of 0.05 mm/s, the polishing disc gradually deformed. The deformation along the normal was measured by the encoder with a resolution of 0.5 \(\mathrm {\mu }\)m, and the normal force was measured by the F/T sensor with a resolution of 0.125 N. During the five groups of pressure tests, the tilt angle of the polishing disc was fixed as \(3^\circ\), \(5^\circ\), \(7^\circ\), \(9^\circ\) and \(11^\circ\), respectively. As the deformation was typically less than 3 mm for polishing discs, the test range of \(h_0\) was also set within this range. The experimental data and the fitting results are shown in Fig. 10 with coloured markers and dotted lines, respectively. The fitting results were in the form of power functions given by Eq. 29, in which \(h_0\) was the independent variable and F was the dependent variable. The values of the coefficients \(C_1\) and \(C_2\) were given in Fig. 10.

$$\begin{aligned} F = C_1 h_0^{C_2} \end{aligned}$$
(29)
Fig. 10
figure 10

The normal force-elastic deformation \(h_0\) relationships in steady state

Full size image

According to the experimental data, the nonlinear material modulus \(\hat{E}\) and the power index \(\beta\) can be calculated through power-law contact force formula Eqs. 14, 15, 16 and 28.

The average values within the confidence interval were taken as the identification results: the nonlinear material modulus \(\hat{E}=0.11656\) MPa, and the power index \(\beta =0.2915\).

$$\begin{aligned} h_0 \approx \left( \dfrac{F \theta ^{1.5}}{0.438557}\right) ^{0.558191} \end{aligned}$$
(30)

The tool length \(L_t\) is 152.6 mm, the radius of the polishing disc \(R_t\) is 37.5 mm, and the thickness H of the polishing disc is 15 mm. When the surface normal is coincided with z-axis of the tool frame T and the tilt angle \(\theta\) changes from \(0^\circ\) to \(15^\circ\), the kinematic projection \(h_1\) considering both parasitic motion and the geometry of the disc can be calculated from Eq. 10, as shown in Fig. 11.

Fig. 11
figure 11

The kinematic projection \(h_1\) changes with tilt angle

Full size image

5.2 Force-tracking performance with contact point compensation

In order to verify the force-tracking performance combined with contact point compensation model, experiments with three different kinds of tilt angle references were carried out. As this paper mainly focused on the improvement of force control accuracy when tilt angle changed, all the experiments were conducted during the continuous contact period. The parameters of the admittance controller were set as follows: \(m_d\) =0.1 kg, \(b_d\) =2 Ns/m and \(k_d\)=0 N/m. The control loop period was set to 1 ms, the sampling frequency of force sensor was 4 kHz. The force reference \(F_r\) was plotted with green dashed line, the contact force \(F_e\) was plotted with blue solid line and tilt angle \(\theta\) was plotted with red dash-dotted line.

The first kind of tilt angle reference implemented in the experiments was a step signal. The desired tilt angle of the moving platform changed from \(3^\circ\) to \(10^\circ\) in steps of \(1^\circ\). The desired force was set to 10 N.

Before the contact point compensation model was introduced, the maximum force during orientation adjusting was 6.91 N, and the mean force error was 1.99 N, as shown in Fig. 12. The experimental results also indicated that as the tilt angle increased, the magnitude of force fluctuation decreased. The reason behind was that although both the elastic deformation \(h_0\) and the kinematic projection \(h_1\) were increased when the tilt angle increased, as shown in Figs. 10 and 11, the increasing rates of \(h_1\) were lower than that of \(h_0\) so that the difference between \(h_1\) and \(h_0\) decreased. Consequently, the magnitude of force fluctuation decreased as the tilt angle of the polishing disc increased.

After the contact point compensation model was introduced, the maximum force during orientation adjusting was 1.09 N, and the mean force error was 0.42 N, as shown in Fig. 13. The mean force error was reduced from 1.99 N to 0.42 N, achieving 78.9% reduction on the mean force error.

Fig. 12
figure 12

Control performance of a \(1^\circ\) step reference from set point 10 N without contact point compensation

Full size image
Fig. 13
figure 13

Control performance of a 1\(^\circ\) step reference from set point 10 N with contact point compensation

Full size image

The second kind of tilt angle reference implemented in the experiments was a ramp signal. The desired tilt angle of the moving platform changed between \(3^\circ\) and \(10^\circ\) continuously and the angular velocity of tilt angles was set to 5\(^\circ\)/s. The desired force was set to 10 N.

The hybrid orientation/force control performance without and with contact point compensation was shown in Figs. 14 and 15, respectively. \(F_{e-noC}\) and \(F_{e-C}\) of the symbol \(F_e\) represented the contact force without and with contact point compensation, respectively. With contact point compensation, the maximum force error was reduced from 3.58 N to 1.05 N, while the mean force error was reduced from 1.9 N to 0.36 N, achieving \(81.1\%\) reduction on the mean force error.

Fig. 14
figure 14

Control performance of a \(5^\circ /s\) ramp reference without contact point compensation

Full size image
Fig. 15
figure 15

Control performance of a \(5^\circ /s\) ramp reference with contact point compensation

Full size image

The third kind of tilt angle reference implemented in the experiments was a sinusoidal signal. The desired tilt angle of the moving platform changed continuously with a sinusoidal signal with an amplitude of \(4^\circ\) and a frequency of 0.2 Hz. The desired force was set to 10 N.

As shown in Figs. 16 and 17, with contact point compensation, the maximum force error was reduced from 2.62 N to 1.17 N, while the mean force error was reduced from 1.41 N to 0.39 N, achieving \(72.3\%\) reduction on the mean force error.

Fig. 16
figure 16

Control performance of a 0.2 Hz sinusoidal reference without contact point compensation

Full size image
Fig. 17
figure 17

Control performance of a 0.2 Hz sinusoidal reference with contact point compensation

Full size image

These experimental results indicated that the orientation control was accurate and the force-tracking performance under different tilt angle references was significantly improved with the contact point compensation. Small force fluctuations still existed, which were mainly due to the identification errors of the contact point compensation model. Nevertheless, after the proposed hybrid orientation/force control was implemented, the mean force errors with these three different kinds of tilt angle references were reduced by 78.9\(\%\), 81.1\(\%\) and 72.3\(\%\), respectively, which validated the effectiveness of the proposed control method.

6 Conclusion

In order to achieve consistent surface quality in robotic polishing, a 2R1T force-controlled end-effector is developed. It is realized that the changes of the tilt angle of the end-effector’s moving platform will result in displacement variations of the contact point along the force control direction, thereby decrease the accuracy of force control. Three major factors resulting in the contact point variation, i.e. the inherent parasitic motion of the moving platform, the geometry of the disc, and the compliance of the disc, are identified, and a contact point compensation model is developed to predict the contact point variation. A new hybrid orientation/force control architecture with contact point compensation model is proposed to simultaneously control the tool orientation and the contact force. The experimental results indicate that the orientation control is accurate and the force-tracking performance under three different tilt angle references is significantly improved with the contact point compensation, achieving 78.9\(\%\), 81.1\(\%\) and 72.3\(\%\) reduction on the mean force error, respectively, which validate the effectiveness of the proposed control architecture.