1 Introduction

Cutter runout, as an interference factor in the milling process, has become one of the main obstacles to inhibit the further improvement of machining efficiency and quality [1,2,3]. Cutter runout is very common in the actual machining. The main reasons for its appearance are due to the non-ideal installation of the spindle-holder-cutter joints, the geometric error of the spindle system, the manufacturing error of the cutter, the tool wear in cutting process, the flexible vibration of the spindle shaft during operation and so on. At present, with the increasing requirement for machining quality and efficiency, the cutter runout and its influence on milling process have attracted extensive attention.

Due to the existence of cutter runout, the actual tooth cutting radius will be changed, and the cutter-workpiece engagement process will be destroyed when compared with the no runout condition, resulting in the deterioration of the milling mechanics and dynamics characteristics.

Firstly, the cutter runout will directly affect the excitation characteristics of milling force. The reason is that it changes the instantaneous uncut chip thickness (IUCT) for each tooth during cutter-workpiece engaging. In the milling case without cutter runout, the IUCT can be characterized by the arc approximation model [4]. Nevertheless, Sutherland and DeVor [5], Wang and Liang [6], and Wan et al. [7] proposed a correction term on the IUCT model for considering the influence of cutter runout when it appears. In order to obtain better prediction accuracy for milling force, some early studies had taken the cutter runout into account [8,9,10]. In the follow-up in-depth analysis, Desai et al. [11] found that the cutter runout can seriously change the tooth start/end cutting angles. Rivière-Lorphèvre and Filippi [12] utilized two simple and complex models of the radial runout for a milling tool, and its impact on the accuracy of IUCT was discussed. Yang et al. [13] presented a cutting force modeling method in peripheral milling, the mathematical model was emphasized to derive the detail IUCT and entry/exit angles in occurrence of cutter runout. Zhang et al. [14] investigated a linear iterative algorithm to accurately calculate the IUCT. The results showed that a better prediction accuracy for milling force can be obtained when considering the cutter runout. Matsumura and Tamura [15] demonstrated a milling force model with the orthogonal cutting used for the simulation, where the variation in the milling force was induced by the cutter runout. In the micro-milling process, Guo et al. [16] adopted an IUCT model with consideration of cutter runout, variable pitch, and helix angles. In five-axis machining, Sun and Guo [17] put forward a new method to predict the instantaneous milling forces based on the tool motion analysis, where the IUCT model took runout effect into account. Li et al. [18] studied a novel approach to accurately predict the cutting forces. In the model, the arc-surface intersection method was presented to determine the CWE boundaries considering the cutter runout effect. Zhu et al. [19] built up a cutting edge element moving method to calculate the IUCT to simulate cutting force in five-axis machining considering runout for general end mills.

Secondly, cutter runout will cause the current tooth to cut the machined surface left by the previous several tooth. At this time, the time delays of all teeth will no longer be the same. This kind of multiple time delay effect would have an impact on the milling dynamics. Insperger et al. [20] investigated the chatter for the case of cutter runout based on frequency spectra and vibration signals. Wan et al. [21] proposed an improved version of the semi-discrete method, which considered the influence of multiple time delays caused by cutter runout on milling stability. Zhang et al. [22] found that the runout can change the tooth cutting state, especially when the feed rate per tooth or radial depth of cut is small, which further gives rise to the change of the stability topology. Niu et al. [23] employed a periodic-coefficient delay differential equation for the dynamic system with variable pith variable helix tools, the joint influences of runout and pitch/helix angles on milling dynamics are discussed. Totis et al. [24] deeply studied the symmetry breaking mechanism with taking into account the influence of forced vibrations on the tool-workpiece engagement conditions, and pointed out that the cutter runout is one of the main factors for inducing the nonlinear increasing of cutting state.

Thirdly, cutter runout will also affect the roughness of the machined surface during stable milling. Altintas and Lee [25, 26] analyzed the effects of cutter runout and dynamic response on surface morphology. In face milling, Franco et al. [27] proposed a numerical model for predicting the surface profile and roughness. Here, the round insert tools had been focused on with the influence of tool errors such as radial and axial runouts. Schmitz et al. [2] used the surface location error to describe the machining quality, and analyzed the influence of cutter runout on the surface roughness and surface location error. Arizmendi et al. [28] presented a model for the band geometry and the roughness prediction in the topography of machined surfaces during peripheral milling. In which the cutter runout, including its setting error and cutter grinding error was analyzed. A geometric model in Ref. [29] was used for obtaining surface topography in peripheral milling with cylindrical cutter, and the influence of feed, runout and helix angle on surface roughness was investigated. David et al. [30] pointed out that evaluation of the machined surface morphology in end-milling process provides useful information about the effect of the vibration phenomena caused by cutter runout. Wang et al. [31] carried out a theoretical study for aiming to reveal the influence of the axial, radial runout and tool corner radius on surface roughness in the slot micro-milling process.

Because of the negative effects of cutter runout in the above aspects, its accurate calibration becomes particularly important. In the engineering field, enterprises mainly have two methods to consider the cutter runout. The first one is to measure the cutter radius with a tool gauge. This method can only ensure the consistency of multiple tooth radiuses when the tool is off the machine. The second one is to use a dial indicator to measure the deviation of cutting radius after installing the tool on the spindle of machine tool, but it is difficult to determine the runout angle.

In terms of academic research, some scholars have proposed to calibrate the cutter runout by the experimental testing data, among which there have three typical methods. The first one is to identify the runout parameters by combining the morphology of machined surface. Arizmendi et al. [32] clarified a method for obtaining the tool parallel axis offset based on the analysis of transition bands created in the topography of machined surfaces during peripheral milling. The second one is to identify the runout parameters based on the relationship between the cutter runout and the frequency domain characteristics of milling force. Zheng and Liang [33] proposed an angle domain convolution approach to estimate the tilt magnitude and orientation of cutter by giving the dynamic cutting force components along with the cutter/workpiece geometry and cutting parameters. Liang and Wang [34, 35] identified the cutter offset by using the frequency domain information of experimental milling force data. The advantage of this method is that there is no need to know the specific cutting force coefficients in advance. The third one is to identify the parameters by combining the time-domain data of milling force. On the basis of a priori cutting force coefficients, Wan et al. [36] used the perturbation of the instantaneous cutting force per tooth relative to the average one in time domain to identify the offset parameters. Ko and Cho [37] and Wan et al. [38] proposed a numerical ergodic optimization method for the identification of offset parameters. Later, Wan et al. [7] further identified two parameters including cutter offset and inclination. Krüger and Denkena [39] demonstrated a runout identification approach based on the average cutting energy distribution of cutter. Yao et al. [40] applied a milling condition with low cutting depth and varying lead angle with a cylindrical surface to identify the cutter runout. Guo et al. [41] projected a new algorithm to compute the cutter runout parameters for a flat-end mill by utilizing the cutting forces and geometry parameters based on the true trajectory of the cutting edge. In [42], the method for measuring a runout of tool holder-spindle by laser displacement sensor in micro end milling was developed. Zhang et al. [43, 44] proposed an efficient calibration method for cutter runout. The main advantage of the method is that it is unnecessary to have a prior knowledge of cutting force coefficients and simple for studying the effect of spindle speed. Recently, Nakatani et al. [45] applied a visual measurement with a camera to calibrate the cutter runout, in which a tool holder with adjustment mechanism was used and the uneven tool wear under cutter runout was discussed.

The above literature reviews show that the cutter runout is an important and complex subject. However, the vast majority of existing studies only consider the cutter offset, and always ignore the other two cases of rotation axis and bottom edge eccentricity. Besides, the inclination in geometric axis eccentricity is also less considered. That makes the analysis of the causes for cutter runout very lacking. Therefore, this paper proposes an effective method to systematically identify cutter runout parameters through the on-machine non-contact measurement, which can make up for the defects of the existing methods.

The rest contents of this paper are arranged as follows: in Sect. 2, the geometric model of the milling cutter runout is parametrically defined. In Sect. 3, a non-contact calibration method for cutter runout is proposed. In Sect. 4, the experimental verification is carried out. The last part is the conclusion of this paper.

2 The geometric model of the milling cutter runout

2.1 General parametric definition of cutter geometric parameters

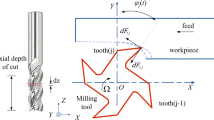
Figure 1a, b are the two typical kinds of milling cutters: integral milling cutter and inserted milling cutter. The feature of the integral milling cutter is that the tooth and body of the cutter are a whole during manufacturing. While the blade and body of the inserted milling cutter are two components that can be separated. The blades are usually fastened to the cutter body by means of screws or welding. The main purpose of the parametric definition is to use a set of general mathematical model to describe the geometric dimensions for both the integral and inserted milling cutters, such as their contour outline, helix line of tooth, position of cutting point, lag angle, spacing angle, and rotation angle, etc.

Fig. 1
figure 1

General parametric definition of tool geometric parameters. a Typical types of integral milling cutter. b Typical types of inserted milling cutter. c Outline of cutter geometry. d Helix line of tooth. e Position of cutting point Q. f Lag angle. g Helix angle and spacing angle. h Rotation angle

Full size image

2.1.1 The helix line of tooth

As shown in Fig. 1c, the available programming tool system of CAM is usually to construct the general geometric profile of an integral milling cutter by seven independent parameters, such as D, Rz, Rr, Rc, αc, βc, and Hc. In fact, this kind of parametric method can be extended to characterize the equivalent outline shape of the inserted milling cutter.

As shown in Fig. 1d, in order to further parametrically describe the tooth shape of cutter, it is necessary to determine the coordinate of an arbitrary cutting point P on the tooth helix. XcYcZc is defined as the cutter geometric coordinate system, and the position of point P can be decided by the axial height \(z\), radial distance \(r{(}z{)}\) and lag angle \(\psi_{p} (z)\). Here, the radial distance is equal to the distance between the point P and the cutter geometric axis, and the lag angle is defined as the projection angle on the XcOcYc plane between the segment \(\overline{{PO_{c} }}\) and the tangent of helix line at z = 0.

At this time, the helix line under the cutter geometric coordinate system XcYcZc can be expressed as

$$P{ = }\left[ \begin{array}{c} x_{p} \\ y_{p} \\ z_{p} \\ \end{array} \right]{ = }\left( \begin{array}{c} r{(}z{\mathrm{)cos(}}\chi_{1,i}^{0} + \psi_{p} (z) + {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}{)} \\ r{(}z{\mathrm{)sin(}}\chi_{1,i}^{0} + \psi_{p} (z) + {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}{)} \\ z \end{array} \right)$$
(1)

where \(z\) is the axial height. \(r{(}z{)}\) is the radial distance. \(\psi_{p} (z)\) is the lag angle of helix line. The detail expression of radial distance and lag angle can be seen in [46]. \(\chi_{1,i}^{0}\) is the nominal spacing angle between the ith and 1st tooth.

2.1.2 The position of cutting point

In Fig. 1d, one establishes the local coordinate system XpYpZp on the helix line of tooth at point P, in which the Yp axis coincides with the radial direction of point P, and the Zp axis points to the direction of Zc. In Fig. 1e, for the inserted milling cutter, the bottom center point of the lth blade on the ith tooth (the number of blades on each tooth is Nl, if it is an integral milling cutter, let Nl = 1) is set at point P. On this basis, one further establishes the blade local coordinate system XiYiZi, where the XiOiYi plane coincides with the bottom surface of the blade, and the Zi axis points to the upper surface of the blade. As we know, the installation attitude angle of the blade on the tool body is also determined in the design stage of the inserted milling cutter. That is to say the rotation relationship between the coordinate system XpYpZp and the coordinate system XiYiZi has been fixed in advance, which is represented by the rotation matrix Rotip.

Then, the conversion relationship between the coordinate system XpYpZp and the geometric coordinate system XcYcZc is:

$$\left[ \begin{array}{c} {\mathrm{X}}_{c} \\ {\mathrm{Y}}_{c} \\ {\mathrm{Z}}_{c} \\ \end{array} \right]{ = }P{ + }{\mathbf{Rot}}_{{p{\mathrm{c}}}} \left[ \begin{array}{c} {\mathrm{X}}_{p} \\ {\mathrm{Y}}_{p} \\ {\mathrm{Z}}_{p} \end{array} \right]$$
(2)

where \({\mathbf{Rot}}_{{p{\mathrm{c}}}}\) is the rotation matrix of the tooth attitude.

After that, the position of cutting point \(Q_{i}\) on the blade edge in the geometric coordinate system XcYcZc can be derived by:

$$Q_{c,i,l} { = }\left[ \begin{array}{c} x_{qc,i,l} \\ y_{qc,i,l} \\ z_{qc,i,l} \end{array} \right] = P{ + }{\mathbf{R}}_{{p{\mathrm{c}}}} {\mathbf{R}}_{ip} Q_{i}$$
(3)

where Rotip is the rotation matrix between the coordinate system XpYpZp and XiYiZi.\(Q_{i}\) is the position of the cutting point on the blade edge in the coordinate system XiYiZi.

Accordingly, the actual cutting radius of cutting point \(Q_{c,i,l}\) is

$$r_{qc,i,l} {(}z{) = }\sqrt {x_{qc,i,l}^{2} { + }y_{qc,i,l}^{2} }$$
(4)

Combining Fig. 1d with Fig. 1e, for the integral milling cutter, let Qi = 0 in Eq. (3), and the position of cutting point \(Q_{c,i,l}\) would degenerate into point P, which can be expressed as follows.

$$Q_{c,i,l} { = }P$$
(5)

2.1.3 The lag angle

As shown in Fig. 1f, the lag angle of cutting point \(Q_{c,i,l}\) is equal to the lag angle of point P subtracting the angle \(\theta_{pq} (z)\), which is the projection angle between \(\overline{{O_{c} P}}\) and \(\overline{{O_{c} Q}}\) on the XcOcYc plane. Here, the projection angle \(\theta_{pq} (z)\) can be calculated by:

$$\begin{aligned} \theta_{pq,i,l} (z) & = arc\cos \frac{{\overrightarrow {{P_{0} P}} \overrightarrow {{Q_{0} Q}} }}{{\left| {\overrightarrow {{P_{0} P}} } \right|\left| {\overrightarrow {{Q_{0} Q}} } \right|}}\\ & = arc\cos \frac{{x_{p} x_{qc,i,l} + y_{p} y_{qc,i,l} }}{{\sqrt {x_{p}^{2} + y_{p}^{2} } \sqrt {x_{qc,i,l}^{2} + y_{qc,i,l}^{2} } }} \end{aligned}$$
(6)

Then, the lag angle of cutting point \(Q_{c,i,l}\) is obtained as follows.

$$\begin{aligned} \psi_{i,l} (z) & = \psi_{p} (z) - \theta_{pq,i,l} (z) \\ & = \psi_{p} (z) - arc\cos \frac{{x_{p} x_{qc,i,l} + y_{p} y_{qc,i,l} }}{{\sqrt {x_{p}^{2} + y_{p}^{2} } \sqrt {x_{qc,i,l}^{2} + y_{qc,i,l}^{2} } }} \end{aligned}$$
(7)

2.1.4 The spacing angle

As shown in Fig. 1g, the helix angle of the ith tooth is defined as \(\alpha_{i}\), and the nominal spacing angle at an axial height of zero between the ith tooth and (i + 1)th tooth is \(\chi_{i,i + 1}^{0}\). Then, the spacing angle of cutting point \(Q_{c,i,l}\) can be obtained by:

$$\chi_{i,i + 1,l} (z){ = }\chi_{i,i + 1}^{0} + \psi_{i + 1,l} (z) - \psi_{i,l} (z)$$
(8)

2.1.5 The rotation angle

As shown in Fig. 1h, it is the rotation state of cutter running at a speed of n. When time t = 0, one lets the tangent of the 1st tooth at z = 0 coincides with the Yc axis. At an arbitrary time t, the rotation angle of the cutting point \(Q_{c,i,l}\) will become:

$$\phi_{i,l} (z,t) = \frac{\pi nt}{{30}} - \chi_{1,i,l}^{{}} (z) - \psi_{1,l} (z)$$
(9)

where \(\chi_{1,i,l}^{{}} (z)\) is the spacing angle between the 1st tooth and ith tooth at an axial height of z, in which \(\left\{ \begin{gathered} \chi_{1,i,l}^{{}} = 0\;\;(i = 1) \hfill \\ \chi_{1,i,l}^{{}} = \sum\limits_{i} {\chi_{{i{ - }1,i,l}}^{{}} (z)} \;\;(1 < i \le N_{t} ) \hfill \\ \end{gathered} \right.\). n is the spindle speed.

2.2 Parametric definition of cutter runout

Figure 2a is the installation diagram of the cuter-holder-spindle-box system. In the actual cutting process, the cutter runout is an inevitable phenomenon, which is caused by many factors, such as the geometric error of machine tool, manufacturing error of cutter, installation error of cuter-holder-spindle joints, tool wear caused by cutting process, and vibration of spindle shaft under running status, etc. Its existence will make the cutter geometric axis deviate from its ideal position, resulting in the change of the position of the tooth cutting edge, which will further cause the actual cutting radius of the side edge to be different, and the axial height of the bottom edge to vary from its nominal value, thus eventually affect the dynamic engaging between the cutter and workpiece.

Fig. 2
figure 2

Parametric definition of cutter runout. a Spindle-holder-cutter assembly system. b Cutter geometric axis eccentricity. c Cutter geometric and rotation axis eccentricity. d Cutter bottom edge eccentricity

Full size image

To the best of the author’s knowledge, the cutter runout can be divided into three main types: (1) the cutter geometric axis eccentricity, (2) the cutter rotation axis eccentricity, and (3) the cutter bottom edge eccentricity. Among them, the cutter geometric axis eccentricity mainly refers to the deviation between the geometric axis and the rotation axis of the cutter after the tool is installed on the spindle. The cutter rotation axis eccentricity mainly means the non-parallel relationship between the rotation axis of cutter and the Z axis of the machine tool. The cutter bottom edge eccentricity is that the height inconsistency of the tip point of tooth in the axial direction.

As shown in Fig. 2b, if the deflection of the rotation axis of the spindle system relative to the Zm axis of the machine tool is not considered, that is, the cutter rotation coordinate system XrYrZr is always parallel to the machine tool coordinate system XmYmZm, but only the deflection of the cutter geometric axis relative to the rotation axis is considered, the runout at this time includes two cases named the offset and inclination. The offset can be described by its value \(\rho\) and angle \(\lambda\), and in this situation the cutter geometric axis will always keep parallel to its rotation axis. The inclination can be described by its value \(\gamma\) and angle \(\eta\), while in this situation, the cutter geometric axis will be no longer parallel to the cutter rotation axis.

As shown in Fig. 2c, if the deflection of the rotation axis of the whole spindle system relative to the Zm axis of the machine tool coordinate system is considered, the cutter rotation axis will also be skewed. Under this condition, the cutter rotation axis eccentricity status can be represented by two parameters: inclination value \(\delta\) and angle \(\beta\).

As shown in Fig. 2d, due to the manufacturing error of the cutter, the axial height of the bottom edge will also change, and the heights between teeth are inconsistent. Here, the axial height difference of the adjacent teeth \(\Delta z\) is used to characterize the eccentricity parameter of the bottom edge.

To sum up, the cutter runout can be parametrically described by the three kinds of status and seven independent parameters. They are the cutter rotation axis eccentricity (inclination value \(\delta\), inclination angle \(\beta\)), the cutter geometric axis eccentricity (offset value \(\rho\), offset angle \(\lambda\); inclination value \(\gamma\), inclination value \(\eta\)), and bottom edge eccentricity (value \(\Delta z\)), respectively.

2.3 Tool geometric parameters under the influence of cutter runout

In order to describe the influence of cutter runout on the actual cutting radius for different teeth and heights, the cutting edge of tooth has been discretized into several cutting units with small thickness along the axial direction of cutter. At this time, in the cutter geometric coordinate system, the position of cutting point \(Q_{c,i,l}\) can be expressed as:

$$\left[ {\begin{array}{*{20}c} {x_{c,i,l,j} } \\ {y_{c,i,l,j} } \\ {z_{c,i,l,j} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - r_{qc,i,l,j} \sin (\chi_{1,i,l,j} { + }\psi_{1,l,j} )} \\ {r_{qc,i,l,j} \cos (\chi_{1,i,l,j} { + }\psi_{1,l,j} )} \\ {z_{qc,i,l,j} } \\ \end{array} } \right]$$
(10)

where the subscript j is obtained by discretizing the height z with small cutting units.

As shown in Fig. 2b, when there is a cutter geometric axis eccentricity, the position of the cutting point \(Q_{c,i,l}\) in the cutter geometric coordinate system can be shown as:

$$\left[ {\begin{array}{*{20}c} {x_{r0,i,l,j} } \\ {y_{r0,i,l,j} } \\ {z_{r0,i,l,j} } \\ \end{array} } \right] = {\mathbf{Rot}}(\gamma ,\eta )\left( {\left[ \begin{gathered} x_{c,i,l,j} \hfill \\ y_{c,i,l,j} \hfill \\ z_{c,i,l,j} \hfill \\ \end{gathered} \right]{ + }\left[ \begin{gathered} \rho \sin \lambda \hfill \\ \rho \cos \lambda \hfill \\ - L_{oh} \hfill \\ \end{gathered} \right]} \right) + \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {L_{oh} } \\ \end{array} } \right]$$
(11)

where \(L_{oh}\) is the tool overhang length.

\({\mathbf{Rot}}(\gamma ,\eta ) = \left[ {\begin{array}{*{20}c} {\cos^{2} \eta (1 - \cos \gamma ) + \cos \gamma } & { - \sin \eta \cos \eta (1 - \cos \gamma )} & { - \sin \eta \sin \gamma } \\ { - \sin \eta \cos \eta (1 - \cos \gamma )} & {\sin^{2} \eta (1 - \cos \gamma ) + \cos \gamma } & { - \cos \eta \sin \gamma } \\ {\sin \eta \sin \gamma } & {\cos \eta \sin \gamma } & {\cos \gamma } \\ \end{array} } \right]\) is the geometric axis inclination matrix.

When the spindle rotates, the position of the cutting point \(Q_{c,i,l}\) in the cutter rotation coordinate system at time t can be derived as follows.

$$\left[ {\begin{array}{*{20}c} {x_{r,i,l,j} (t)} \\ {y_{r,i,l,j} (t)} \\ {z_{r,i,l,j} (t)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {x_{r0,i,l,j} \sin (\phi_{i,l,j} (t))} \\ {y_{r0,i,l,j} \cos (\phi_{i,l,j} (t))} \\ {z_{r0,i,l,j} } \\ \end{array} } \right]$$
(12)

As shown in Fig. 2c, when the cutter has both geometric axis eccentricity and rotation axis eccentricity, the position of cutting point \(Q_{c,i,l}\) under the machine tool coordinate system can be further derived as:

$$\left[ {\begin{array}{*{20}c} {x_{m,i,l,j} (t)} \\ {y_{m,i,l,j} (t)} \\ {z_{m,i,l,j} (t)} \\ \end{array} } \right] = {\mathbf{Rot}}(\delta ,\beta )\left[ {\begin{array}{*{20}c} {x_{r,i,l,j} (t)} \\ {y_{r,i,l,j} (t)} \\ {z_{r,i,l,j} (t) - L_{z} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {L_{z} } \\ \end{array} } \right]$$
(13)

where \(L_{z}\) is the axis deflection length, which refers to the distance from the cutter tip to the average height of the upper and lower support bearings of the spindle.

\({\mathbf{Rot}}(\delta ,\beta ) = \left[ {\begin{array}{*{20}c} {\cos^{2} \beta (1 - \cos \delta ) + \cos \delta } & { - \sin \beta \cos \beta (1 - \cos \delta )} & { - \sin \beta \sin \delta } \\ { - \sin \beta \cos \beta (1 - \cos \delta )} & {\sin^{2} \beta (1 - \cos \delta ) + \cos \delta } & { - \cos \beta \sin \delta } \\ {\sin \beta \sin \delta } & {\cos \beta \sin \delta } & {\cos \delta } \\ \end{array} } \right]\) is the rotation axis inclination matrix.

Right now, it can be obtained the actual cutting radius of the cutting point \(Q_{c,i,l}\) under the influence of cutter runout as:

$$R_{i,l,j} (t) = \sqrt {x_{m,i,l,j} (t)^{2} + y_{m,i,l,j} (t)^{2} }$$
(14)

In addition, the height deviation of the tip point on the adjacent bottom edges in the machine tool coordinate system is:

$$\Delta he_{i} (t){ = }\Delta z_{i} { + }z_{m,i,1,1} (t) - z_{{m,i{ + }1,1,1}} (t{ + }\frac{{\chi_{i,i + 1,1,1} }}{2\pi }T)$$
(15)

where \(T\) is the rotation period of spindle.

3 Non-contact calibration of the cutter runout parameters

3.1 Non-contact measurement principle

According to the above analysis, the cutter geometric and rotation axis eccentricity will cause the actual tooth cutting radius to deviate from its nominal value. However, the actual cutting radius is difficult to be measured directly. Only the influence of cutter runout on the actual cutting radius variation of the adjacent cutter teeth is measurable. Therefore, the paper proposes to calibrate the cutter runout parameters by measuring the change value of the actual cutting radius between adjacent teeth.

As shown in Fig. 3a, when the spindle running, the eddy current sensor is employed to measure the distance between the cutting edge of the tooth and the end face of the sensor. Here, the measured distance is defined as the target length, which is used to indirectly reflect the variation of actual tooth cutting radius. According to the working principle of the sensor, when the measured object has electrical conductivity and the distance between the sensor and the measured surface is close enough, the sensor can output voltage through the electromagnetic induction. The closer the sensor is to the measured surface, the lower the output voltage is. When the sensor distance is fully coincident with the measured surface, the output voltage will be zero. When the target length exceeds the measurement range, the voltage will remain at its maximum. Based on the output voltage value V, the target length can be calculated by Kx/VV, where Kx/V is the sensitivity of the sensor.

Fig. 3
figure 3

Non-contact measurement of target length by eddy current sensor. a Location of the eddy current sensor. b Measurement process of the jth unit on the lth insert. c Measurement moment of the target length. d Measurement results of the target length

Full size image

Here, two eddy current sensors are used in the measurement as described in Fig. 3a. The 1st sensor is placed at different axial heights to measure the target length of cutting points with different blades. In addition, in order to ensure the synchronization of multi-channel signals output by the 1st sensor. That is, the measurement data at different heights can ensure the time axis alignment, one pastes a thin iron wire (diameter ≤ 0.05 mm, length ≈ 5 mm) at the cutter or holder bar, and use the 2nd sensor to measure the signal generated by the thin iron wire as the marker for data synchronization.

As illustrated in Fig. 3b, it is the measurement process of the target length when the cutter rotates at a speed of n. The measurement moment of the ith tooth is shown in Fig. 3c. When the tooth edge rotates to the center of the sensor, the sensor will generate the voltage signal. Figure 3d is the schematic diagram of the measurement results of the target length of different teeth, blades, and cutting units. Here, the 2nd sensor generates a pulse signal as a marker in one rotation period of spindle. The 1st sensor can output multiple target distances at different positions, in which each tooth will generate a pulse, and the peak value of each pulse corresponds to the time when the tooth passing. Finally, the target length of the jth cutting unit of the lth blade on the ith tooth can be obtained as \(L_{i,l,j}^{M}\), in which the superscript \(^{M}\) represents the measured value.

3.2 The influence of cutter runout on the target length

In order to clarify the above measurement principle more clearly, this section analyzes the variation of target length under different cutter runout parameters through numerical simulation. The cutter adopted here is an integral milling cutter with its detail parameters in Sect. 4.1. The total length L in Fig. 3c for the side edge is 10 mm, and 2 mm for the bottom edge.

The simulation results of the influence of cutter runout on the target length is plotted in Fig. 4. As shown in Fig. 4a, when there has no cutter geometric and rotation axis eccentricity, the target length is constant at 2 mm, no matter how the axial height changes. Under the condition with cutter geometric eccentricity, the target length will gradually decrease with the increase of rotation axis eccentricity, and the changes under multiple axial height positions are different. In order to describe the variation more clearly, one sets the target length at axial height z = 0 as the reference and calculates the relative target lengths of other axial heights, which is described in Fig. 4b. We can clearly see that when there is only geometric axial eccentricity, the relative target lengths of the 1st tooth at position \({\mathrm{Y}}_{m}^{ + }\) and \({\mathrm{X}}_{m}^{ + }\) are exactly the same. But, when there is rotation axis eccentricity, the relative target lengths at position \({\mathrm{Y}}_{m}^{ + }\) and \({\mathrm{X}}_{m}^{ + }\) are not the same. This indicates that only the rotation axis eccentricity would cause the different relative target lengths at position \({\mathrm{Y}}_{m}^{ + }\) and \({\mathrm{X}}_{m}^{ + }\), while the geometric axis eccentricity would not. The above analysis provides us with the idea to distinguish the runout induced by rotation and geometric axis eccentricities, which will be described in detail in the Sect. 3.3.

Fig. 4
figure 4

Simulation results of the influence of cutter runout on the target length. a The influence of geometric and rotation axis eccentricity on the target length. b The influence of geometric and rotation axis eccentricity on the relative target length. c The influence of bottom edge eccentricity on the relative target length

Full size image

Similarly, one can further find that the cutter bottom edge eccentricity will cause the change of the tooth axial height, as shown in Fig. 4c. Here, it is particularly important that not only the change of tooth axial height caused by the bottom edge eccentricity will be reflected in the target distance, but also the geometric and rotation axis eccentricity will.

3.3 Calibration of the rotation axis eccentricity parameters

From the above analysis, compared with the geometric axis eccentricity, the particularity of the rotation axis eccentricity is that it will affect the target lengths at different rotation angles. As shown in Fig. 5a, b, the 1st sensor is placed at the four different positions on the Ym axis (\({\mathrm{Y}}_{m}^{ + }\) and \({\mathrm{Y}}_{m}^{ - }\)) and Xm axis (\({\mathrm{X}}_{m}^{ + }\) and \({\mathrm{X}}_{m}^{ - }\)) in the machine tool coordinate system to measure the target length. Here, the superscript \(^{ + }\) and \(^{ - }\) denote the positive and negative directions of the coordinate axes, respectively. During the measurement process, the position of the 1st sensor is fixed by a bracket, and the target distances at different heights are measured by moving the spindle system up and down. The final target length measurement results are shown in Fig. 5c.

Fig. 5
figure 5

Calibration for the rotation axis eccentricity parameters. a Measurement positions of sensor. b Measurement process. c Measured target length without rotation axis eccentricity. d Measured target length with rotation axis eccentricity

Full size image

At this time, by taking the value at the height \(z_{1,1}\) as the reference point, the variation and slope of other heights relative to the reference point under above four different positions are the same. That is:

$$\begin{aligned} k_{i,l,j}^{{}} & { = }\frac{{L_{i,l,j}^{{}} ({\mathrm{Y}}_{m}^{ + } ) - L_{i,1,1}^{{}} ({\mathrm{Y}}_{m}^{ + } )}}{{z_{l,j} - z_{1,1} }} \\ & { = }\frac{{L_{i,l,j}^{{}} ({\mathrm{X}}_{m}^{ + } ) - L_{i,1,1}^{{}} ({\mathrm{X}}_{m}^{ + } )}}{{z_{l,j} - z_{1,1} }} \\ & { = }\frac{{L_{i,l,j}^{{}} ({\mathrm{Y}}_{m}^{ - } ) - L_{i,1,1}^{{}} ({\mathrm{Y}}_{m}^{ - } )}}{{z_{l,j} - z_{1,1} }} \\ & { = }\frac{{L_{i,l,j}^{{}} ({\mathrm{X}}_{m}^{ - } ) - L_{i,1,1}^{{}} ({\mathrm{X}}_{m}^{ - } )}}{{z_{l,j} - z_{1,1} }} \end{aligned}$$
(16)

When the cutter rotation axis is skewed, the variation and slope of the measured values at the above four different positions relative to the reference point are different, as shown in Fig. 5d. Therefore, the variation of the slope can be used to identify the rotation axis eccentricity. Setting the tool geometric axis eccentricity parameters to zero in Eq. (14), one can theoretically calculate the slope variation of \({\mathrm{Y}}_{m}^{ + }\) relative to \({\mathrm{Y}}_{m}^{ - }\), and \({\mathrm{X}}_{m}^{ + }\) relative to \({\mathrm{X}}_{m}^{ - }\) by the following formulas.

$$\begin{aligned}\triangle k_{i,l,j}\left(Y_m^+\right)&=\frac{L_{i,l,j}\left(Y_m^+\right)-L_{i,1,1}\left(Y_m^+\right)}{z_{l,j}-z_{1,1}}-\frac{L_{i,l,j}\left(Y_m^-\right)-L_{i,1,1}\left(Y_m^-\right)}{z_{l,j}-z_{1,1}}\\&=\frac{L-R_{i,l,j}\left(Y_m^+\right)-\left(L-R_{i,1,1}\left(Y_m^+\right)\right)}{z_{l,j}-z_{1,1}}-\frac{L-R_{i,l,j}\left(Y_m^-\right)-\left(L-R_{i,1,1}\left(Y_m^-\right)\right)}{z_{l,j}-z_{1,1}}\\&=\frac{-R_{i,l,j}\left(Y_m^+\right)+R_{i,1,1}\left(Y_m^+\right)}{z_{l,j}-z_{1,1}}-\frac{-R_{i,l,j}\left(Y_m^-\right)+R_{i,1,1}\left(Y_m^-\right)}{z_{l,j}-z_{1,1}}\end{aligned}$$
(17)
$$\begin{aligned}\triangle k_{i,l,j}\left(X_m^+\right)&=\frac{L_{i,l,j}\left(X_m^+\right)-L_{i,1,1}\left(X_m^+\right)}{z_{l,j}-z_{1,1}}-\frac{L_{i,l,j}\left(X_m^-\right)-L_{i,1,1}\left(X_m^-\right)}{z_{l,j}-z_{1,1}}\\&=\frac{L-R_{i,l,j}\left(X_m^+\right)-\left(L-R_{i,1,1}\left(X_m^+\right)\right)}{z_{l,j}-z_{1,1}}-\frac{L-R_{i,l,j}\left(X_m^-\right)-\left(L-R_{i,1,1}\left(X_m^-\right)\right)}{z_{l,j}-z_{1,1}}\\&=\frac{-R_{i,l,j}\left(X_m^+\right)+R_{i,1,1}\left(X_m^+\right)}{z_{l,j}-z_{1,1}}-\frac{-R_{i,l,j}\left(X_m^-\right)+R_{i,1,1}\left(X_m^-\right)}{z_{l,j}-z_{1,1}}\end{aligned}$$

Accordingly, their experimental measured value are:

$$\begin{array}{l} \Delta k_{i,l,j}^{M} ({\mathrm{Y}}_{m}^{ + } ){ = }\frac{{L_{i,l,j}^{M} ({\mathrm{Y}}_{m}^{ + } ) - L_{i,1,1}^{M} ({\mathrm{Y}}_{m}^{ + } )}}{{z_{l,j} - z_{1,1} }} - \frac{{L_{i,l,j}^{M} ({\mathrm{Y}}_{m}^{ - } ) - L_{i,1,1}^{M} ({\mathrm{Y}}_{m}^{ - } )}}{{z_{l,j} - z_{1,1} }} \\ \Delta k_{i,l,j}^{M} ({\mathrm{X}}_{m}^{ + } ){ = }\frac{{L_{i,l,j}^{M} ({\mathrm{X}}_{m}^{ + } ) - L_{i,1,1}^{M} ({\mathrm{X}}_{m}^{ + } )}}{{z_{l,j} - z_{1,1} }} - \frac{{L_{i,l,j}^{M} ({\mathrm{X}}_{m}^{ - } ) - L_{i,1,1}^{M} ({\mathrm{X}}_{m}^{ - } )}}{{z_{l,j} - z_{1,1} }} \end{array}$$
(18)

Then, when calibrating the cutter rotation axis eccentricity parameters, one sets the cutter geometric axis eccentricity and bottom edge eccentricity parameters as zeros, and the objective function as the deviation between the theoretical and experimental values of the slope variation, as shown in the following formula.

$$\min \left\{ {\Delta {\mathbf{k}}_{i,l,j}^{{}} ({\mathbf{X}})|(\Delta k_{i,l,j}^{{}} - \Delta k_{i,l,j}^{M} )^{2} } \right\}\;\;({\mathrm{Y}}_{m}^{ + } ,{\mathrm{X}}_{m}^{ + } )$$
(19)

where \({\mathbf{X}} = \left[ {\delta ,\beta } \right]^{T}\) is the optimization variable.

Furthermore, the Levenberg–Marquardt numerical optimization algorithm is used to calibrate the cutter rotation axis eccentricity parameters. The optimization flow is as follows:

Step (1): Let \(k = 1\), initialize the optimization variable by:

$${\mathbf{X}}^{(1)} = {\mathbf{X}}_{0}$$
(20)

In this paper, the initial value \({\mathbf{X}}_{0}\) is set as a minimum greater than zero, its value is \([1,1]^{T} \times 10^{ - 6}\)

Step (2): Let \(k = k + 1\), calculate the Jacobian matrix by using the following formula.

$${\mathbf{J}}^{(k)} = \left[ {\begin{array}{*{20}c} {\frac{{\partial \Delta {\mathbf{k}}_{1,1,1}^{{}} ({\mathbf{X}}^{(k)} )}}{\partial \delta }} & {\frac{{\partial \Delta {\mathbf{k}}_{1,1,1}^{{}} ({\mathbf{X}}^{(k)} )}}{\partial \beta }} \\ \vdots & \vdots \\ {\frac{{\partial \Delta {\mathbf{F}}_{i,l,j}^{{}} ({\mathbf{X}}^{(k)} )}}{\partial \delta }} & {\frac{{\partial \Delta {\mathbf{F}}_{i,l,j}^{{}} ({\mathbf{X}}^{(k)} )}}{\partial \beta }} \\ \vdots & \vdots \\ {\frac{{\partial \Delta {\mathbf{F}}_{{N_{t} ,N_{l} ,N_{j} }} ({\mathbf{X}}^{(k)} )}}{\partial \delta }} & {\frac{{\partial \Delta {\mathbf{F}}_{{N_{t} ,N_{l} ,N_{j} }} ({\mathbf{X}}^{(k)} )}}{\partial \beta }} \\ \end{array} } \right]$$
(21)

Step (3): Calculate the optimization variable \({\mathbf{X}}^{(k + 1)}\) by the following equation.

$${\mathbf{X}}^{(k + 1)} = {\mathbf{X}}^{(k)} - (({\mathbf{J}}^{(k)} )^{T} {\mathbf{J}}^{(k)} + \xi {\mathbf{I}})^{ - 1} ({\mathbf{J}}^{(k)} )^{T} \Delta {\mathbf{k}}_{i,l,j}^{(k)} ({\mathbf{X}})$$
(22)

where \(\xi\) is the iteration step coefficient, which is assigned as 0.01 in the paper.

Then, if \(||{\mathbf{X}}^{(k + 1)} - {\mathbf{X}}^{(k)} || < \varepsilon\) is satisfied, where \(\varepsilon\) is the convergence accuracy, go to finish the iteration. Otherwise, return to step (2) and continue the iteration until the convergence condition is met.

Step (4): Finally, the cutter rotation axis eccentricity parameters can be identified as:

$${\mathbf{X}}^{*} = \left[ {\delta^{*} ,\beta^{*} } \right]^{T} = {\mathbf{X}}^{(k + 1)}$$
(23)

What should be pointed out is that the inclination value of the cutter rotation axis should be greater than or equal to zero based on the physical meaning. Hence, if its value is less than zero, the following transformation is required.

$$\left\{ \begin{array}{ll} {\mathrm{if}} & \delta^{*} < 0 \\ & \delta^{*} { = } - \delta^{*} \\ & \beta^{*} { = }\beta^{*} { + }\pi \hfill \\ \end{array} \right.$$
(24)

3.4 Calibration of the geometric axis eccentricity parameters

After the above calibration, substituting the obtained cutter rotation axis eccentricity parameters into Eq. (14), then only the cutter geometric axis eccentricity parameters has not been determined in the actual cutting radius expression, which can be simplified as:

$$R_{i,l,j} (t) = R_{i,l,j} (t,\rho ,\lambda ,\gamma ,\eta ,\delta^{*} ,\beta^{*} )$$
(25)

As shown in Fig. 6a, one assigns the 1st sensor at the 1st position (\({\mathrm{Y}}_{m}^{ + }\)) and 2nd position (\({\mathrm{X}}_{m}^{ + }\)) to measure the target lengths of different teeth. The measured results are plotted in the Fig. 6b. Then, the measured relative change of the cutting radius of the adjacent teeth can be achieved by:

$$\begin{aligned} \Delta R_{i,l,j}^{M} (t)&{ = }R_{i,l,j}^{M} (t) - R_{{i{ + }1,l,j}}^{M} (t) \\ & = (L - L_{i,l,j}^{M} (t)) - (L - L_{{i{ + }1,l,j}}^{M} (t)) \\ & = - L_{i,l,j}^{M} (t) + L_{{i{ + }1,l,j}}^{M} (t) \end{aligned}$$
(26)
Fig. 6
figure 6

Calibration for the geometric axis eccentricity parameters. a Measurement positions. b Measured target length with geometric axis eccentricity

Full size image

Meanwhile, its theoretical value can be calculated as follows.

$$\Delta R_{i,l,j} (t){ = }R_{i,l,j} (t) - R_{{i{ + }1,l,j}} (t)$$
(27)

Then, when calibrating the cutter geometric axis eccentricity parameters, one sets the objective function as the difference between the theoretical and measured value of the cutting radius variation, as shown in the following formula.

$$\min \left\{ {\Delta {\mathbf{R}}_{i,l,j}^{{}} ({\mathbf{X}})|(\Delta R_{i,l,j}^{{}} (t) - \Delta R_{i,l,j}^{M} (t))^{2} } \right\}\;\;({\mathrm{X}}_{m}^{ + } ,{\mathrm{Y}}_{m}^{ + } )$$
(28)

where \({\mathbf{X}} = \left[ {\rho ,\lambda ,\gamma ,\eta } \right]^{T}\) is the optimization variable.

Being similar to the Sect. 3.3, the Levenberg–Marquardt algorithm is also applied here to solve the numerical optimization problem. But the difference is that the Jacobian matrix at the kth iteration step should be calculated by:

$${\mathbf{J}}^{(k)} = \left[ {\begin{array}{*{20}c} {\frac{{\partial \Delta {\mathbf{R}}{}_{1,1,1}({\mathbf{X}}^{(k)} )}}{\partial \rho }} & {\frac{{\partial \Delta {\mathbf{R}}{}_{1,1,1}({\mathbf{X}}^{(k)} )}}{\partial \lambda }} & {\frac{{\partial \Delta {\mathbf{R}}{}_{1,1,1}({\mathbf{X}}^{(k)} )}}{\partial \gamma }} & {\frac{{\partial \Delta {\mathbf{R}}{}_{1,1,1}({\mathbf{X}}^{(k)} )}}{\partial \eta }} \\ \vdots & \vdots & \vdots & \vdots \\ {\frac{{\partial \Delta {\mathbf{R}}_{i,l,j} ({\mathbf{X}}^{(k)} )}}{\partial \rho }} & {\frac{{\partial \Delta {\mathbf{R}}_{i,l,j} ({\mathbf{X}}^{(k)} )}}{\partial \lambda }} & {\frac{{\partial \Delta {\mathbf{R}}_{i,l,j} ({\mathbf{X}}^{(k)} )}}{\partial \gamma }} & {\frac{{\partial \Delta {\mathbf{R}}_{i,l,j} ({\mathbf{X}}^{(k)} )}}{\partial \eta }} \\ \vdots & \vdots & \vdots & \vdots \\ {\frac{{\partial \Delta {\mathbf{R}}_{{N_{t} ,N_{l} ,N_{j} }} ({\mathbf{X}}^{(k)} )}}{\partial \rho }} & {\frac{{\partial \Delta {\mathbf{R}}_{{N_{t} ,N_{l} ,N_{j} }} ({\mathbf{X}}^{(k)} )}}{\partial \lambda }} & {\frac{{\partial \Delta {\mathbf{R}}_{{N_{t} ,N_{l} ,N_{j} }} ({\mathbf{X}}^{(k)} )}}{\partial \gamma }} & {\frac{{\partial \Delta {\mathbf{R}}_{{N_{t} ,N_{l} ,N_{j} }} ({\mathbf{X}}^{(k)} )}}{\partial \eta }} \\ \end{array} } \right]$$
(29)

Besides, the initial value \({\mathbf{X}}_{0}\) here is set as \([1,1,1,1]^{T} \times 10^{ - 6}\). Through the numerical optimization, the cutter geometric axis eccentricity parameters can be identified as:

$${\mathbf{X}}^{*} = \left[ {\rho^{*} ,\lambda^{*} ,\gamma^{*} ,\eta^{*} } \right]^{T} = {\mathbf{X}}^{(k + 1)}$$
(30)

Lastly, if the offset or the inclination value of the cutter geometric axis is less than zero, the following transformation should also be required.

$$\left\{ \begin{array}{ll} {\mathrm{if}}&\rho^{*} < 0 \\ & \rho^{*} { = } - \rho^{*} \\ & \lambda^{*} { = }\lambda^{*} { + }\pi \\ {\mathrm{if}}&\gamma^{*} < 0 \\ & \gamma^{*} { = } - \gamma^{*} \\ & \eta^{*} { = }\eta^{*} { + }\pi \end{array} \right.$$
(31)

3.5 Calibration of the bottom edge eccentricity parameters

The axial height of the tip point of bottom edge will be inconsistent due to the bottom edge eccentricity. As shown in Fig. 7a, one places the 1st sensor at the 5th position along the Zm axis direction of the machine tool, and lets it faces the tip point of the bottom edge to measure the target lengths of different teeth. The measured data is shown in Fig. 7b. Here, the measured value of the height difference between the adjacent teeth can be obtained as:

$$\Delta he_{i} { = }L_{i,l,j}^{M} ({\mathrm{Z}}_{m}^{ - } ) - L_{i + 1,l,j}^{M} ({\mathrm{Z}}_{m}^{ - } )$$
(32)
Fig. 7
figure 7

Calibration for the bottom edge eccentricity parameters. a Measurement positions. b Measured target length of bottom edge

Full size image

Combining with Eq. (15), the eccentricity parameter of the bottom edge can be calibrated by:

$$\begin{aligned} \Delta z_{i} & { = }\Delta he_{i} - z_{m,i,1,1} ({\mathrm{Z}}_{m}^{ - } ,\rho^{*} ,\lambda^{*} ,\gamma^{*} ,\eta^{*} ,\delta^{*} ,\beta^{*} ) \\ & { + }z_{{m,i{ + }1,1,1}} ({\mathrm{Z}}_{m}^{ - } ,\rho^{*} ,\lambda^{*} ,\gamma^{*} ,\eta^{*} ,\delta^{*} ,\beta^{*} ) \end{aligned}$$
(33)

3.6 Comparison with the conventional methods

Here, the calibration method proposed in this paper has been compared with the traditional ones, and the comparison results are shown in Table 1. In summary, the advantages of this method are mainly in the following aspects:

Table 1 Comparison between the proposed calibration method and conventional methods
Full size table
  1. 1.

    This paper can realize the systematic identification of non-ideal cutter installation status, such as cutter geometric axis eccentricity, rotation axis eccentricity, and bottom edge eccentricity. Compared with the traditional method, it well expands the research scope of cutter runout.

  2. 2.

    By analyzing the influence of cutter runout on the actual cutting radius variation, the above three kinds of eccentricities are separated for identifying, which can improve the convergence of the numerical optimization algorithm.

  3. 3.

    The cutter is installed on the spindle for calibration measurement. This kind of on-machine direct measurement method can accurately reflect the real status of the cutter under running conditions, and the spindle rotates under non-cutting situation during measurement, which can eliminate the influence of cutting vibration.

  4. 4.

    Through the non-contact measurement by the eddy current sensor, the calibration of cutter runout under different spindle speeds can be easily realized.

4 Verification

4.1 Experimental device

In order to verify the validity of the proposed method, a series of experiments were carried out on the DMG DMU50 high-speed machine tool. Figure 8a shows the experimental test process. As seen in Fig. 8a, b, two kinds of integral and inserted milling cutters made by cemented carbide were used in the experiment with its geometric parameters listed in Table 2. Two eddy current sensors were employed in the experiment. The 1st sensor (type: με-DT3010; measurement range: 0–0.5 mm; resolution: 0.025 μm; sensitivity: Kx/V = 33.24 μm/V) was placed to measure the target length, the 2nd one was utilized to generate the synchronization signal. The data acquisition system is shown in Fig. 8c with a sampling frequency of 5.0 kHz. Furthermore, several groups of milling experiments were carried out in the verification, including side milling and face milling with its machining parameters shown in Table 3. In order to minimize the influence of milling force on the cutter-workpiece engagement and restrain the tool deformation and vibration, the radial depth of cut in side milling and the axial depth of cut in end milling were only 0.02 mm. In order to analyze the influence of cutter runout on the morphology and contour error of machined surface, a three-coordinate measuring machine (type: global classic SR 575; resolution: 1.8 μm) was adopted to measure the machined surface contour. A contacting aspheric surface contour measurer (type: Taylor Hobson PGI3D; resolution: 0.125 μm; measurement speed: 1 mm/s) was applied to measure the micro profile of the machined surface. The morphology of the machined surface was also observed by an optical microscope (type: Smart series rzsp-200c), as shown in Fig. 8f.

Fig. 8
figure 8

Experimental device. a Non-contact measurement for the integral cutter under five different positions. b Non-contact measurement for the inserted cutter. c Data acquisition. d Dial gauge test. e Machined surfaces. f Micro-profile measurement for the machined surfaces

Full size image
Table 2 Cutter geometric parameters
Full size table
Table 3 Machining parameters in milling experiment
Full size table

4.2 Verification results

The eddy current sensor is used for the non-contact measurement of target length on the integral milling cutter. The spindle speed is 4000 rpm. The actual measured data are shown in Fig. 9, including the output voltage curves generated by the 1st sensor at five different positions, and three different side edge heights (z = 0, 20, 40 mm). The synchronization mark signal recorded by the 2nd sensor is also plotted in the figure. Obviously, it can be seen that the pulse troughs of different cutter teeth and different cutting points on the same tooth will no longer be consistent, which is exactly caused by the cutter runout.

Fig. 9
figure 9

The measured voltage of the integral milling cutter by the eddy current sensor

Full size image

Using the cutter runout calibration algorithm proposed in Sect. 3, firstly the cutter rotation and geometric axis eccentricity parameters can be solved. Their iterative convergence curves are shown in Fig. 10a, c, d, respectively. To reflect the performance of the optimization algorithm, the convergence curve of the objective function for rotation and axis eccentricity calibration process are both given in Fig. 10b, e, respectively. Based on the above results, the bottom eccentricity parameters of the end cutting edge are also calculated. Finally, the specific parameters of the three types of eccentricity status for the two kinds of cutters are obtained, as shown in Table 4.

Fig. 10
figure 10

Numerical optimization iteration process of cutter runout parameters. a Convergence curves for the rotation axis inclination parameters. b Convergence curve for the objective function of rotation axis eccentricity calibration. c Convergence curves for the geometric axis offset parameters. d Convergence curves for the geometric axis inclination parameters. e Convergence curve for the objective function of geometric axis eccentricity calibration

Full size image
Table 4 Calibrated results of cutter runout parameters
Full size table

In order to verify the accuracy of the calibration results, a comparison method is proposed to verify the results indirectly. As shown in Fig. 8d, the change of cutting radius of adjacent teeth was measured with a dial indicator, and the average of multiple measurements is taken and compared with the calculated value calibrated by the proposed method. The comparison results are shown in Table 5. Besides, the 95% confidence interval of measured value by dial indicator is also listed in the table. It is known that the relative error between the two methods is large, this is because the spindle is stationary when the dial indicator is measuring, while the spindle is rotating when using the eddy current sensor. Considering the measurement error by the dial indicator, the comparison shows that the calibration results in this paper are effective.

Table 5 Comparison of the cutting radius variation
Full size table

Figure 11 detailly analyzes the topography and contour error of the machined surface by the integral milling cutter with cutter runout. The side milling and face milling are completed on the 1st and 5th surface, respectively, as shown in Fig. 8e. Among them, with the aid of the cutter runout parameters identified in the experiment, we simulate the cutter tooth trajectory surface during the feed movement, as shown in Fig. 11a.

Fig. 11
figure 11

Topography and contour error of the machined surface by the integral milling cutter with cutter runout. a Tooth trajectory surface. b Topography of the machined surface in side milling. c Simulated scallop height of the side machined surface. d Comparison of the scallop height on the side machined surface. e Topography of the machined surface in face milling. f Simulated scallop height of the bottom machined surface. g Comparison of the scallop height on the bottom machined surface. h Comparison of the relative contour error on the side machined surface

Full size image

For the side milling, Fig. 11b takes a picture of the machined surface morphology through a microscope. Due to the limited shooting range of the microscope, we take multiple photos and splice them at the marked points to finally obtain the overall morphology picture. Based on the trajectory surface, the morphology of the machined surface of side milling is further extracted, as shown in Fig. 11c. One can further deduce that although the four teeth of the cutter participate in cutting, the adjacent cutter teeth over cut each other in the end cutting stage due to the cutter runout. The most significant phenomenon is that the ridge lines on the scallop height of the cutter teeth become crossed with each other, and the change period of the scallop height along the feed direction is equal to the feed per revolution of the cutter, not the feed per tooth. Figure 11d further compares the measured and simulated values of the scallop height at an axial height of 13 mm and 28 mm in side milling. The comparison results demonstrate that the proposed method can well reflect the real changes of machined surface profile even under the influence of cutter runout.

Similarly, for the face milling, Fig. 11e shows the morphology of the machined surface, and Fig. 11f shows the simulation results of the scallop height extracted from Fig. 11a. It can also be seen that the cutter runout significantly changes the state of adjacent cutter teeth participating in cutting, thus the scallop height formed by the adjacent teeth becomes no longer consistent, and more complex than that without runout. Figure 11g compares the measured and simulated values of the scallop height at the tool center point in face milling, which also shows that the proposed model can accurately reflect the cutter runout status.

Figure 11h further compares the measured and simulated value of the contour error of the machined surface in side milling. The comparison index here adopts the relative contour error and takes the axial height of 3 mm as the reference point. The measured value adopts the average of multiple measurement data. The comparison results show that the variation trend of the simulation curve is consistent with the measured one. Just as shown in the figure, the theoretical analysis can accurately predict the influence of cutter runout on the contour error, and also confirms the identification accuracy of cutter runout parameters. In addition, the above analysis also indicate that the cutter runout will not only worsen the roughness of the machined surface but also increase the contour error, especially the axis inclination.

For the inserted milling cutter, the topography and contour error of the machined surface under the influence of cutter runout are also studied in detail, as shown in Fig. 12a–h. Here, the side milling is completed on the 3rd surface, and the face milling is completed on the 6th surface in Fig. 8e.

Fig. 12
figure 12

Topography and contour error of the machined surface by the inserted milling cutter with cutter runout. a Tooth trajectory surface. b Topography of the machined surface in side milling. c Simulated scallop height of the side machined surface. d Comparison of the scallop height on the side machined surface. e Topography of the machined surface in face milling. f Simulated scallop height of the bottom machined surface. g Comparison of the scallop height on the bottom machined surface. h Comparison of the relative contour error on the side machined surface

Full size image

What should be emphasized here is that since the height of each blade of the inserted milling cutter is 8 mm, under the given experimental conditions, there are actually five blades on each tooth to participate in cutting. Through the comprehensive comparison in Fig. 12a–d, it can be seen that the cutting state of the blade in the second layer is significantly different from that of other layers. In detail, both the two blades in the second layer participate in cutting, while only one blade in other layers participates in cutting. This is the significantly different from the integral milling cutter. As seen from Fig. 12e–g, during face milling, the bottom eccentricity also significantly affects the engagement between the cutter and workpiece, resulting in only one of the two blades on the first layer participating in the effective cutting.

4.3 Discussion

4.3.1 The influence of spindle speed on cutter runout status

As we know, the shaft-holder-cutter assembly in the spindle system is actually a flexible structure. When the spindle rotates at a high speed, it will produce the gyroscopic force and centrifugal force, which will further cause its vibration form, and eventually affect the runout status of the cutter. In addition, according to the working principle of the high-speed motorized spindle, it often works in the constant torque state at low speed and in the constant power state at high speed, that is to say, with the increase of speed, there is still a change of working mode of the spindle.

Since this paper is based on the non-contact measurement by the eddy current sensor, it is very easily to analyze the cutter runout under different spindle speeds. Figure 13a shows the output voltage signal measured by the 1st sensor at the \({\mathrm{X}}_{m}^{ + }\) position with the spindle rotating at different speeds. The running time at each speed is about 3 s. From this figure, we can see that there is a remarkable increase in the signal amplitude at 2500 rpm when the spindle speed gradually increases from low to high speed. This is because the 2500 rpm is exactly the switching speed of the working mode of the motorized spindle. Based on the test data, the cutter runout parameters at different spindle speeds are further calibrated. The detailed results are shown in Fig. 13b–d. We can conclude that at different speeds, the cutter runout status is not constant, but being fluctuate. We also think that the explanation for the speed-dependent characteristics of cutter runout must be combined with the vibration mode of the flexible slender rotor system. Moreover, under two different working modes, the runout in the high spindle speed area is significantly less than that in the low speed area, which shows that the high-speed motorized spindle can just play its excellent dynamic rotation performance, especially the self-centering characteristics, in the high speed running operation.

Fig. 13
figure 13

The influence of spindle speed on cutter runout. a Output voltage of the 1st eddy current sensor at \({\mathrm{X}}_{m}^{ + }\) position under different spindle speeds. b Rotation axis inclination parameters under different spindle speeds. c Geometric axis offset parameters under different spindle speeds. d Geometric axis inclination parameters under different spindle speeds

Full size image

4.3.2 The feed direction-dependent characteristics of rotation axis inclination

In the traditional studies of cutter runout, the factor of rotation axis inclination is often ignored. However, due to the manufacturing and assembly limitations of the spindle, Z axis moving and fixing parts of machine tool, the cutter rotation axis inclination is very common in actual machining. As shown in Fig. 14, the relative contour error of the integral milling cutter is analyzed on the 2nd and 4th machined surfaces in Fig. 8e. It is found that although the design positions of the two surfaces are spatially parallel, and the milling parameters are the same, the contour error of them are significantly different, as shown by the red line and blue line in the below figure. However, if the rotation axis inclination is not considered and only the geometric axis inclination and offset are considered, the relative contour error obtained by simulation is shown by the black line in the figure, which will be very different from the actual measured data.

Fig. 14
figure 14

The influence of rotation axis inclination on the relative contour error

Full size image

For further analysis, although the geometric axis eccentricity will change the cutting radius of cutter teeth, the cutting radius will not change with the cutter rotation angle. Nevertheless, the rotation axis inclination will change the cutting radius of cutter teeth with different rotation angles. Therefore, with the cutter moving along different feed directions, the rotation angle corresponding to the tooth start/end cutting stage will also change, which thus makes the actual cutting radius for generating the machined surface different. This result shows that the influence of rotation axis inclination on the contour error has a significant feed direction-dependent characteristics, which has always been ignored by the existing research.

5 Conclusions

The paper presents a general on-machine non-contact calibration method for the cutter runout parameters in milling process. Through the theoretical modeling and experimental analysis, the causes, types and identification method for the cutter runout are systematically clarified. The main conclusions are as follows:

  1. 1.

    A general geometric mathematical model for the integral and inserted milling cutters is established. Three kinds of runout status, including the cutter rotation axis eccentricity, geometric axis eccentricity (offset and inclination) and bottom edge eccentricity, are quantitatively described by the seven independent parameters.

  2. 2.

    Based on the influence relationship of the cutter runout on the actual tooth cutting radius, a separated identification strategy is proposed, which firstly identifies the rotation axis eccentricity, then the geometric axis eccentricity, and finally the bottom edge eccentricity. This strategy can reduce the interference between the multiple factors and improve the convergence of the numerical optimization algorithm.

  3. 3.

    Using the eddy current sensor for the non-contact measurement of the target length can not only ensure high measurement accuracy, but also facilitate the study of the effect of different spindle speeds on the cutter runout. In addition, as the cutter is installed on the spindle, this on-machine direct measurement can accurately reflect the status of the cutter under non-cut running conditions, and also can eliminate the influence of cutting vibration.

  4. 4.

    Based on the analysis of the topography and contour error of the machined surface, the experimental cases well verify the validity of the proposed method. Besides, the results show that the spindle speed can affects the cutter runout status, especially during the switching of the working mode of the motorized spindle. It is also found that the contour error of machined surface in side milling process is feed direction-dependent as a result of cutter rotation axis inclination.