1 Introduction

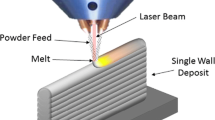
The coaxial powder flow directed energy deposition (DED) additive manufacturing technique has been studied extensively in literatures. The most studied material in the DED technique is metal, while laser beam is dominantly used as the energy source [1]. Major control parameters for laser-based DED include laser power, laser beam size, scanning speed, powder feed rate, and material properties [2]. A typical DED process involves complex energy and material transport phenomena such as conduction of heat into the powder and substrate, convection of liquid due to Marangoni effect and surface tension, and direct mass and heat deposition due to injection of powder into melted clad (melt-pool). The complex interactions among these phenomena are the big challenges for understanding the DED process and ultimately the effect of the control parameters on the overall process.

Experimental studies of DED processes have been carried out. Corbin et al. [3] conducted a series of experiments to study the effects of laser power, travel speed, working distance, and initial substrate temperature on the shape of the deposited material. Based on experiment data, empirical models were built for prediction of clad geometries. Shah et al. [4] experimentally investigated the effects of powder flow and laser beam modes on the melt-pool disturbance and surface roughness of the deposited part. Mazzucato et al. [5] studied the effect of the laser power and scanning strategy on the shape and the mechanical properties of the final printed part. Most of the studied quantities are geometrical dimensions and mechanical properties which can only be measured after the DED process has finished. Other time-dependent or instantaneous quantities, such as thermal history and melting pool circulation, are much more difficult or impossible to measure due to the extremely height temperature of deposited materials and very small spatial–temporal scales. Using cameras, Boddu et al. [6] and Miedzinski [7] were able to capture instantaneous top and side view of a melt-pool and adjacent region during the process. However, internal structures and characteristics of the melt-pool were not able to be observed clearly.

The limitations of experimental studies can be complemented by numerical simulations. In order to achieve that, the numerical models should account as many real DED processes as possible, such as to consider the transient and complex mass and energy transport phenomena in melt-pools, melting-solidification of materials, and formation of microstructures. These models will provide important information about geometries, mechanical properties, and defects in the printed parts. Given the significant benefits of numerical studies, there have been many efforts focussing on building numerical models for DED in literature. Models for melt-pool with powder stream mass and temperature have been the main focus in most of these numerical studies. These include the works in [8,9,10,11,12,13]. Some works focused on more details of transient heat transfer, temperature distribution, cooling rate, and flow distribution in the melt-pool such as [14, 15]. Several attempts to build comprehensive numerical models for multi-track, multi-layer deposition have also been reported [16, 17]. These numerical models were based on conservation equations of mass, momentum, and energy which were solved by continuum methods such as finite element and finite volume methods (FEM, FVM) combined with surface tracking methods such as volume of fluid (VOF) and level set (LS). Powder flow simulations were conducted using powder nozzle and inert gas model in [18,19,20,21,22,23]. The powder depositions on the substrate and melt-pool were modelled by analytical or empirical formulas where bulk mass, momentum, and energy were added into the melt-pool. These methods were very cost-effective as it did not require explicit discretization of powder particles as well as the dynamics of powder impingement; hence, it did not require refined mesh and time step. These simplifications could, however, lead to wrong dynamics of the melt-pool being captured [24, 25].

Pinkerton [25] and Guan and Zhao [26] highlighted several physical aspects that are essential and need to be carefully treated in the simulation of a DED process. These includes the physical properties of used material as well as their relationships with physical variables such as temperature, the powder stream, and its interaction with laser beam and impact on the melt-pool. The attenuation of laser beam due to powder stream and powder catchment should be considered. Wessels et al. [27] employed an efficient ray tracing algorithm to model a laser beam. The method significantly improved the accuracy of absorption and vaporization as compared with volumetric heat source approach. The method could still be expensive for large scale DED simulations. The melt-pool is particularly important in all DED simulations. Many numerical models considered the addition of mass and energy from the captured powder particles, i.e., those fall into the melt-pool, liquid flow dynamics, Marangoni effect, heat transfer, and phase transformation. However, because of high computational cost involved, fully coupled numerical approaches have not been extensively applied. Furthermore, very few models considered every individual powder particle and the full effects of powder impingement into the melt-pool. Han et al. [24] was one of those, although the model was still two-dimensional. The model was based on continuum approach, and falling particles were treated as droplets. Numerical results showed strong effects of powder injection on the melt-pool geometry, temperature, and fluid flow. Anedaf et al. [28] used meshless finite pointset method (FPM) to simulate the fluid flow from the powder stream into the melt-pool explicitly. However, results were of low resolution and did not pick up the details of the melt-pool. The major challenge remained at tracking each of powder particles [26]. Other meshfree methods, such as the optimal transportation meshfree (OTM) and smoothed particle hydrodynamics (SPH), have been successfully used in simulations of selective laser melting (SLM) processes before [29,30,31,32,33,34].

In the previous studies [29,30,31], SPH models have shown their capabilities to track and simulate every single powder particle interacting with the laser beam, the melt-pool, and interactions with other powders in the powder stream. Major and important underlying physical processes are considered in the model. These include the transient powder-laser interaction, heat transfer, formation and dynamics of the melt-pool, powder-melt-pool interaction, and the phase change. In [29], the SPH model was validated for individual processes as well as against a real SLM process. It was also demonstrated the feasibility of modelling a DED process. In this paper, the SPH model will be enhanced and coupled with a powder generator model for simulations of DED processes. The coupled model is further studied and validated before being applied to real DED processes. Model results will then be used to analyse melt-pool characteristics which otherwise not available in experiment measurements.

The main content of the paper is organized as follows. Section 2 proposes a modelling workflow for a coaxial powder-blown DED process which includes the power generator, the SPH model, and the coupling of the two models. In Sect. 3, various evaluations on the performance of the SPH model will be presented including a sensitivity study for the particle size. Simulations of two real DED processes at relatively different scales, validations against experiment data, detailed analyses of the results, and discussions are also presented in this section. Section 4 follows with a conclusion.

2 Modeling workflow

The coaxial powder-blown directed energy deposition (DED) (or direct metal deposition (DMD)) printing involves multi-physics (powder flow, laser heating, solid–liquid phase change, air–liquid interface, etc.) and multi-scale (powder, melt-pool, part scales) processes. A workflow for the simulation of a powder-blown AM process is proposed in Fig. 1. Two major components of the workflow are the powder generator and the laser-powder interaction model. The powder generator can be considered as a prepossessing module to prepare data for the actual numerical simulation in the laser-powder interaction model.

Fig. 1
figure 1

A workflow for simulation of a powder blown DED process and definition of process parameters

Full size image

2.1 Random power generator

The proposed DED modelling workflow in Fig. 1 starts with a random power generator. In the random generator, the powders are assumed spherical and having the same size. The total number of powders,\({N}_{p}\), is first calculated from the feed rate \(\dot{m}\) (mass/time), the simulation time \({T}_{s}\), and the powder properties of density \(\rho\) and radius \(R\), as

$${N}_{p}=\frac{\dot{m}{T}_{s}}{4/3\pi {R}^{3}\rho }$$
(1)

All \({N}_{p}\) powders are randomly distributed on a plane following a Gaussian (normal) distribution along the radial axis, \({r}_{D}\sim \mathcal{N}({\mu }_{D},{\sigma }_{D})\) with a standard deviation of \({\sigma }_{D}={R}_{S}/3\) and a mean of \({\mu }_{D}=0\) and a uniform distribution over \([0, 2\pi ]\) in the tangential direction, \({\varphi }_{D}\sim \mathcal{U}(0, 2\uppi )\). The planar coordinates of the powders, \({x}_{p}\) and \({y}_{p}\), are then calculated as

$$\begin{array}{c}{x}_{p}={r}_{D}\mathrm{cos}({\varphi }_{D})\\ {y}_{p}={r}_{D}\mathrm{sin}({\varphi }_{D})\end{array}$$
(2)

Figure 2 shows examples of distributions and histograms of all powder particles generated from the random Gaussian distributions for 3,000, 30,000 and 300,000 powders in a powder jet area.

Fig. 2
figure 2

Planar distributions (a–c) and histograms (d–f) of all powder particles generated from random distributions for 3,000 (a, d), 30,000 (b, e), and 300,000 (c, f) powders. The dash circles demarcate the input powder jet area

Full size image

And finally, the planar distributed powders are randomly distributed along the direction of injection (usually vertical) to form a powder column

$${z}_{p}\sim \mathcal{U}(0, {L}_{Z})$$
(3)

where \({L}_{Z}={v}_{Z}{T}_{s}\) is the height of the powder column, which can be computed from the injection velocity of the powders, \({v}_{Z}\), and the simulation time, \({T}_{s}\). The powder column starts from a predefined position which usually is the laser source location (as shown in Fig. 1). Figure 3 shows portions of powder column calculated based on a Gaussian distribution for different feeding rates. In these examples, the same injection velocity is used; hence, denser powder columns can be seen for larger feeding rates.

Fig. 3
figure 3

A portion of vertical distributions of powder column calculated based on a horizontal distribution and feeding rates. Feeding rates of a 2.9, b 4.3, c 5.8, d 7.3 g/min. Axis unit is mm

Full size image

The powders in the powder column will not be simulated by the SPH model. Their positions in time are updated in the model by their injection velocity at every model time step \(\Delta t\) and are adjusted horizontally according to the movement of the laser source:

$$\begin{array}{c}{z}_{p}\leftarrow {z}_{p}-{v}_{z}\Delta t\\ {x}_{p}\leftarrow {x}_{p}+{U}_{Sx}\Delta t\\ {y}_{p}\leftarrow {y}_{p}+{U}_{Sy}\Delta t\end{array}$$
(4)

Here, \({U}_{Sx}\) and \({U}_{Sy}\) are the projection of the laser scanning speed on the two horizontal axes. Once a powder falls below the laser source, it is discretized by SPH particles and will be included in the SPH simulation. Figure 4 shows examples of a spherical powder being discretised into 4, 19, and 81 SPH particles. Each SPH particle is initialized with the same properties, i.e., density, temperature, etc., as of the powders. The powder-powder interaction will be modelled automatically in the SPH simulation when they come near to each other as defined by the kernel length of the SPH method. The proposed powder column strategy will help to save the computational cost as only powders that fall below the laser source are considered in the SPH approximation.

Fig. 4
figure 4

A spherical powder being discretised into a 4, b 19, and c 81 SPH particles. Axis unit is mm

Full size image

2.2 The laser-powder interaction model

The laser-powder interaction is modelled by the smoothed particle hydrodynamics (SPH) methods. The in-house code was developed in [29] and was validated for SLM processes. In the SPH method, each powder is resolved by many SPH particles that carry the same initial properties of the powder (temperature, velocity, material properties). A laser source at the standoff plane comprises of laser power, shape, angle, and scan speed. The SPH model accounts for the absorption of thermal energy from the laser and loss of thermal energy through interface with air, heat transfer and melting of powder particles, powder-powder interaction, melting/solidification and dynamics of the melt-pool, and impingement of powder particles into the melt-pool.

2.2.1 Smoothed particle hydrodynamics

The fundamental of the SPH method is an interpolation which allows a function to be evaluated by the contribution of its values at all points \(\mathbf{x}=\left(x, y,z\right)\) in a three-dimensional (3D) space. In a discrete problem, the SPH approximation at a discrete point \({\mathbf{x}}_{a}\) is a summation over all surrounding points \({\mathbf{x}}_{b}\) including \({\mathbf{x}}_{a}\) weighted by kernel functions \({W}_{ab}=W({\mathbf{x}}_{b}-{\mathbf{x}}_{a},{h}_{w})\) as

$${f}_{a}=f({\mathbf{x}}_{a})={\sum }_{b}\frac{{m}_{b}}{{\rho }_{b}}f({\mathbf{x}}_{b}){W}_{ab}$$
(5)

Each discrete point \({\mathbf{x}}_{a}\) is represented by an SPH particle \(a\) having properties of mass \({m}_{a}\), density \({\rho }_{a}\), velocity \({\mathbf{u}}_{a}\), temperature \({T}_{a}\), and other material properties. Here, the subscript \({}_{a}\) or \({}_{b}\) next to a variable/parameter/function indicates the quantity belong to particle \(a\) or \(b\). The kernel function is chosen so that its value drops rapidly to zero for \(\left|{\mathbf{x}}_{b}-{\mathbf{x}}_{a}\right|>{kh}_{w}\). The sphere at \({\mathbf{x}}_{a}\) having an ambient radius of \({kh}_{w}\) is called support domain of particle \(a\); and \({h}_{w}\) is the supporting (or smoothing) length of the kernel function. In this application, the following 3D quintic Wendland kernel is used:

$$W\left({\mathbf{x}}_{b}-{\mathbf{x}}_{a},{h}_{w}\right)=W\left(q\right)=\left\{\begin{array}{cc}{\alpha }_{d}\left(2q+1\right){\left(1-0.5q\right)}^{4},& 0\le q\le 2\\ 0,& q>2\end{array}\right.$$
(6)

where \(q=\left|{\mathbf{x}}_{b}-{\mathbf{x}}_{a}\right|/{h}_{w}\) and \({\alpha }_{d}=(21/16\pi {)h}_{w}^{3}\). The kernel length is chosen as 1.5 times the particle size, \({h}_{w}=1.5R\). The operator \({\sum }_{b}\) indicates a summation over all particles within the support domain. The gradient of the function at the particle location, \({\nabla }_{a}f\), is approximated as

$${\nabla }_{a}f={\sum }_{b}\frac{{m}_{b}}{{\rho }_{b}}{f}_{b}{\nabla }_{a}{W}_{ab}$$
(7)

2.2.2 SPH formulation for laser-aided additive manufacturing

There are two definitions of “particle” involved in the following text. The first definition is the “powder particle” which is a physical particle that is laid on the substrate or blown-in during SLM and DED, respectively. The second definition is the “SPH particle” which is a fictitious particle used in the SPH computation to represent a control volume of fluid. In the following text, the SPH particle will be sometimes simply referred to as “particle,” while the powder particle will always be explicitly mentioned as “powder particle.”

2.2.3 Model for thermal dynamics

The partial differential equation governing the thermal dynamics process is expressed as

$$c\frac{dT}{dt}=\frac{1}{\rho }\nabla \left(k\nabla T\right)+\Phi$$
(8)

where \(T\) is the temperature; \(k\) and \(c\) are the thermal conductivity and specific heat capacity; and \(\Phi\) is the thermal source and sink representing laser heating and heat loss at the interface with air. In the SPH formulation, the thermal dynamics equation is approximated as

$${c}_{a}\frac{{dT}_{a}}{dt}={\sum }_{b}\frac{4{m}_{b}}{{\rho }_{a}{\rho }_{b}}\frac{{k}_{a}{k}_{b}}{{k}_{a}+{k}_{b}}\ {T}_{ab}\frac{{\mathbf{r}}_{ab}\cdot {\nabla }_{a}{W}_{ab}}{{\mathbf{r}}_{ab}^{2}+0.01{h}_{w}^{2}}+{\Phi }_{a}$$
(9)

where \({T}_{ab}={T}_{b}-{T}_{a}\). The heat source or sink at particle \(a\) locating at the interface with air (surface particle) is computed as

$${\Phi }_{a}=\frac{{\alpha }_{\theta a}{\widehat{q}}_{Sa}+{k}_{A}\left({T}_{a}-{T}_{A}\right)+{\varepsilon }_{A}{\sigma }_{A}({T}_{a}^{4}-{T}_{\infty }^{4})}{6\left(1-{C}_{a}\right){({m}_{a}/{\rho }_{a})}^{1/3}{\rho }_{a}}$$
(10)

where \({k}_{A}\), \({\varepsilon }_{A}\), and \({\sigma }_{A}\) are the thermal conductivity, emissivity, and Stephan-Boltzmann coefficients for air; \({T}_{A}\) and \({T}_{\infty }\) are the ambient and far field temperatures; \({\alpha }_{\theta }\) is the absorption coefficient; \({\widehat{q}}_{S}\) is the intensity of the laser beam at the surface of the particle; and \(C\) is a “colour” function measuring the completeness of the SPH summation. The colour function and its gradient are evaluated as

$${C}_{a}={\sum }_{b}\frac{{m}_{b}}{{\rho }_{b}}{W}_{ab}\ {\text{and}}\ \nabla {C}_{a}={\sum }_{b}\frac{{m}_{b}}{{\rho }_{b}}{\nabla }_{a}{W}_{ab}$$
(11)

The heat source or sink \(\Phi\) is applied only at surface particles which are identified by a variable \(R\). A particle is “near” the air interface (surface particle) if \(R=1\) or further inside the material body (inner particle) if \(R=0\). The value of \(R\) at particle \(a\) is set to one if the completeness of the SPH summation, \({C}_{a}\), is close to one and its gradient, \(\nabla {C}_{a}\), is larger than zero. In actual simulations, the criteria are often set as \({C}_{a}\ge 0.95\) and \(\nabla {C}_{a}\ge 0.01{h}_{w}\).

2.2.4 Model for laser energy absorption and shading effect

Energy from a laser beam is absorbed through the free surface of the powder and the substrate. The intensity of the laser beam from the source to a surface particle is attenuated due to the absorption and reflection (shading) on other surface particles along the beam before it reaches the particle. In a small portion of the laser beam having area of \({\delta A}_{S}\), the laser energy is absorbed by particles scattering from the laser source to the particle of interest. The remaining laser intensity that reaches the particle is

$${\widehat{q}}_{Sa}={q}_{S}-{\sum }_{b\in {\delta A}_{S}}\frac{{m}_{b}{\alpha }_{\theta b}{\widehat{q}}_{Sb}}{6\left(1-{C}_{b}\right){({m}_{b}/{\rho }_{b})}^{1/3}{\rho }_{b}}$$
(12)

where \({q}_{S}\) is the intensity of the laser without attenuation and summation is the laser energy absorbed by all particles \(b\) scattering from the laser source to particle \(a\). For a typical laser beam of Gaussian distribution, \({q}_{S}\) at an SPH particle is computed as

$${q}_{Sa}=\frac{{a}_{G}{Q}_{S}}{\pi {R}_{S}^{2}}{\mathrm{e}}^{-{b}_{G}{r}_{a}^{2}/{R}_{s}^{2}}$$
(13)

where \({Q}_{S}\) is the laser source power; \({R}_{S}\) is the radius of the laser source area; and \({r}_{a}\) is the radial distance from particle \(a\) to the centre of the laser source. The coefficients \({a}_{G}\), \({b}_{G}\) define the distribution shape. Note that with \({b}_{G}=0\), the Gaussian distribution becomes a uniform distribution. The absorption of laser energy by the surface particle is dependent on the absorptivity of the material \(\alpha\) and the angle \(\theta\) between the laser beam direction and the surface normal vector at the particle position

$${\alpha }_{\theta }=\alpha \mathrm{max}(-\mathrm{cos}\theta ,0)$$
(14)

2.2.5 Model for phase change

The phase change (melting and solidification) of an SPH particle is modelled as

$$\left\{\begin{array}{c}T\le {T}_{S}\\ {T}_{S}\le T<{T}_{L}\\ T\ge {T}_{L}\end{array}\right. \to \begin{array}{c}\text{solid phase}\\ \text{phase change}\\ \text{liquid phase}\end{array} \to \begin{array}{c}k={k}_{S}; c={c}_{S}\\ k={k}_{M}; c={c}_{M}\\ k={k}_{L}; c={c}_{L}\end{array}$$
(15)

where \({T}_{S}\) and \({T}_{L}\) are the critical temperatures for solidification and melting and \({k}_{S}\), \({c}_{S}\) and \({k}_{L}\), \({c}_{L}\) are the thermal conductivity and specific heat capacity at the solid and liquid phases, respectively. At the phase change, the thermal conductivity is \({k}_{M},\) and the specific heat capacity is \({c}_{M}={H}_{M}/({T}_{L}-{T}_{S})\) where \({H}_{M}\) is the latent heat. If an SPH particle having temperature below \({T}_{L}\), it is labelled and modelled as solid with special treatments on its acceleration and velocity; otherwise, it is treated as liquid (fluid) and is governed by fluid dynamics.

2.2.6 Model for fluid dynamics

The fluid dynamics is governed by the Navier–Stokes equations for incompressible fluids. In a in a Lagrangian frame, the equations have a form of

$$\frac{d\rho }{dt}=-\rho \cdot \nabla \mathbf{u};\ \frac{d\mathbf{u}}{dt}=\mathbf{g}-\frac{1}{\rho }\nabla p+\nabla \left(\nu \nabla \mathbf{u}\right)+{\mathbf{F}}_{S};\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\ \frac{d\mathbf{x}}{dt}=\mathbf{u}$$
(16)

where \(\rho\) is the density, \(p\) is the pressure, \(\nu\) is the effective kinematic viscosity, \(\mathbf{u}\) is the velocity, \(\mathbf{x}\) is the Lagrangian displacement, and \(\mathbf{g}\) is gravitational acceleration. The forcing term \({\mathbf{F}}_{S}\) comprise of surface tension, Marangoni force followed the continuum surface force model as

$${\mathbf{F}}_{Sa}=-\sigma \kappa \mathbf{n}+{d}_{T}\sigma \left[\nabla T-\left(\nabla T\cdot \mathbf{n}\right)\mathbf{n}\right]$$
(17)

where \(\sigma\) and \({d}_{T}\sigma\) are the surface tension and thermo-capillary coefficients and \(\kappa\) is the surface curvature. The dynamics of an SPH particle \(a\) at liquid phase under influences of particles \(b\) in the support domain are approximated as

$$\begin{aligned}\frac{{d\rho }_{a}}{dt}=&-{\rho }_{a}{\sum }_{b}\frac{{m}_{b}}{{\rho }_{b}}{\mathbf{u}}_{ab}\cdot {\nabla }_{a}{W}_{ab};\\ \frac{{d\mathbf{u}}_{a}}{dt}=&{\mathbf{g}}_{a}-{\sum }_{b}\frac{{m}_{b}}{{\rho }_{a}{\rho }_{b}}\left({p}_{a}+{p}_{b}\right){\nabla }_{a}{W}_{ab}\\&+{\nu }_{a}{\sum }_{b}4{m}_{b}\left(\frac{1}{{\rho }_{a}}+\frac{1}{{\rho }_{b}}\right)\frac{{\mathbf{r}}_{ab}\cdot {\mathbf{u}}_{ab}}{{\mathbf{r}}_{ab}^{2}+0.01{h}_{w}^{2}}\\&\cdot {\nabla }_{a}{W}_{ab}+{\mathbf{F}}_{Sa}\boldsymbol{ };\ \frac{d{\mathbf{x}}_{a}}{dt}={\mathbf{u}}_{a}\end{aligned}$$
(18)

where \({\mathbf{r}}_{ab}={\mathbf{r}}_{b}-{\mathbf{r}}_{a}\) and \({\mathbf{u}}_{ab}={\mathbf{u}}_{b}-{\mathbf{u}}_{a}\). The pressure is computed from the density via an equation of state as

$${p}_{a}={u}_{s}^{2}\left({\rho }_{a}-{\widehat{\rho }}_{r}\right)$$
(19)

Here, \({u}_{s}\) is the sound speed and \({\widehat{\rho }}_{r}\) is the reference density of the material at the temperature \(T\) and is modelled as a function of a reference density \({\rho }_{r}\) at a temperature \({T}_{r}\) and the thermal expansion constant \({\alpha }_{T}\) as

$${\widehat{\rho }}_{r}={\rho }_{r}\left[1+{\alpha }_{T}\left(1-\frac{T}{{T}_{r}}\right)\right]$$
(20)

The forcing term \({\mathbf{F}}_{S}\) is computed at surface particles as

$${\mathbf{F}}_{Sa}=-{\sigma }_{a}{\kappa }_{a}{\mathbf{n}}_{a}+{{d}_{T}\sigma }_{a}\left[\nabla {T}_{a}-\left(\nabla {T}_{a}\cdot {\mathbf{n}}_{a}\right){\mathbf{n}}_{a}\right]$$
(21)

where the curvature \(\kappa\), thermal gradient \(\nabla T\), and normal vector \(\mathbf{n}\) at particle \(a\) are computed as

$$\begin{aligned}{\kappa }_{a}&=\frac{1}{{\kappa }_{Sa}}{\sum }_{b}\frac{{m}_{b}}{{\rho }_{b}}({\mathbf{n}}_{b}-{\mathbf{n}}_{a})\cdot {\nabla }_{a}{W}_{ab};\\ {\kappa }_{Sa}&={\sum }_{b\ne a}\frac{{m}_{b}}{{\rho }_{b}}\mathrm{min}({R}_{b},{R}_{a}){W}_{ab}\\ \nabla {T}_{a}&=-\frac{1}{{C}_{a}}{\sum }_{b}\frac{{m}_{b}}{{\rho }_{b}}{T}_{a}{\nabla }_{a}{W}_{ab};\\ {\mathbf{n}}_{a}&=\left\{\begin{array}{c}\frac{\nabla {C}_{a}}{\left|\nabla {C}_{a}\right|}\\ 0\end{array} \begin{array}{c}\frac{\nabla {C}_{a}}{{h}_{w}}>0.1\\ {\text{otherwise}}\end{array}\right.\end{aligned}$$
(22)

2.2.7 Model for solid particles

An SPH particle at its solid phase, including re-solidified, is modelled flowing the motion of the solid object comprising of all solid particles that are interconnected. A pair of SPH particles is identified to have interconnection if \(\left|{\mathbf{r}}_{ab}\right|\le {h}_{w}\). There are two scenarios for the motion of a solid object: (1) the solid object has inter-connections with boundary particles, and the motion of the solid object is set as the motion of the boundary; and (2) the solid object has no interconnection with any boundary particle, and the solid object is modelled as a rigid body \({\mathbb{B}}\) with total translational and rotational acceleration as

$$\begin{aligned}&\frac{{d\mathbf{U}}_{\mathbb{B}}}{dt}=\left({\sum }_{b\in {\mathbb{B}}}{m}_{b}\frac{{d\mathbf{u}}_{b}}{dt}\right)/{\sum }_{b}{m}_{b} ;\\& \frac{{d{\varvec{\Omega}}}_{\mathbb{B}}}{dt}=\left({\sum }_{b\in {\mathbb{B}}}{\mathbf{r}}_{b{\mathbb{B}}}\times \frac{{d\mathbf{u}}_{b}}{dt}\right)/{\sum }_{b}{\mathbf{r}}_{b}^{2}\end{aligned}$$
(23)

Here, \({\mathbf{r}}_{b{\mathbb{B}}}={\mathbf{x}}_{b}-{\mathbf{x}}_{\mathbb{B}}\) where \({\mathbf{x}}_{\mathbb{B}}\) is rigid body’s centre of mass. Velocity of each individual particle is then re-computed as

$${\mathbf{u}}_{b}={\mathbf{U}}_{\mathbb{B}}+{\mathbf{r}}_{b{\mathbb{B}}}\times {{\varvec{\Omega}}}_{\mathbb{B}}$$
(24)

2.2.8 Boundary condition

At the boundaries, several layers of stationary SPH particles are introduced. The bottom boundary is generally more important, especially for the very first powders that are directly depositing on it. The powders impacting on the bottom boundary layer are often at high velocity and could penetrate. To prevent it, a density of 2–3 times of the powder density is used for the boundary particles to artificially generate stronger upward force on the impacting powder particles. Other properties of the boundary particles are generally the same as those of the powder particles. If a particular material of the base plate is provided, properties of the bottom boundary particles are set to those of the base plate accordingly. Furthermore, the temperature of the boundary particles is set at a constant value, \({T}_{B}\). At the lateral boundaries, boundaries particles are often not necessary unless the domain is too narrow that the melt-pool could extend to the boundaries. Depositing powders are allowed fly out or spill out of the lateral boundaries. Particles leaving the lateral boundaries will be removed from the SPH simulation.

2.2.9 Time integration scheme

The second-order predictor–corrector scheme is used for time integration. With the energy, continuity, momentum and position equations rewritten in compact forms as

$$\frac{{dT}_{a}}{dt}={H}_{a}; \frac{{d\rho }_{a}}{dt}={D}_{a}; \frac{{d\mathbf{u}}_{a}}{dt}={\mathbf{F}}_{a};\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\frac{d{\mathbf{x}}_{a}}{dt}={\mathbf{u}}_{a};\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }{p}_{a}=f\left({\rho }_{a}\right)$$
(25)

and the current time-step is denoted by the superscript \(n\); the temperature, density, velocity, position, and pressure of an SPH particle are calculated at the half step in the predictor as

$$\begin{aligned}{T}_{a}^{n+\frac{1}{2}}&={T}_{a}^{n}+\frac{\Delta t}{2}{H}_{a}^{n}; \\{\rho }_{a}^{n+\frac{1}{2}}&={\rho }_{a}^{n}+\frac{\Delta t}{2}{D}_{a}^{n}; {\mathbf{u}}_{a}^{n+\frac{1}{2}}={\mathbf{u}}_{a}^{n}+\frac{\Delta t}{2}{\mathbf{F}}_{a}^{n};\\ \boldsymbol{ }\boldsymbol{ }{\mathbf{x}}_{a}^{n+\frac{1}{2}}&={\mathbf{x}}_{a}^{n}+\frac{\Delta t}{2}{\mathbf{u}}_{a}^{n} ; {p}_{a}^{n+\frac{1}{2}}=f\left({\rho }_{a}^{n+\frac{1}{2}}\right)\end{aligned}$$
(26)

The right-hand side terms in (25) are updated using the values of temperature, density, velocity, and position at the predictor step which are, in turn, updated in the corrector as

$$\begin{aligned}{T}_{a}^{n+\frac{1}{2}}&={T}_{a}^{n}+\frac{\Delta t}{2}{H}_{a}^{n+\frac{1}{2}}; {\rho }_{a}^{n+\frac{1}{2}}={\rho }_{a}^{n}+\frac{\Delta t}{2}{D}_{a}^{n+\frac{1}{2}};\\ {\mathbf{u}}_{a}^{n+\frac{1}{2}}&={\mathbf{u}}_{a}^{n}+\frac{\Delta t}{2}{\mathbf{F}}_{a}^{n+\frac{1}{2}};\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }{\mathbf{x}}_{a}^{n+\frac{1}{2}}={\mathbf{x}}_{a}^{n}+\frac{\Delta t}{2}{\mathbf{u}}_{a}^{n+\frac{1}{2}}\end{aligned}$$
(27)

Finally, the temperature, density, velocity, position, and pressure of an SPH particle at the new time step are calculated as

$$\begin{aligned}{T}_{a}^{n+1}&=2{T}_{a}^{n+\frac{1}{2}}-{T}_{a}^{n}; {\rho }_{a}^{n+1}=2{\rho }_{a}^{n+\frac{1}{2}}-{\rho }_{a}^{n};\\ {\mathbf{u}}_{a}^{n+1}&=2{\mathbf{u}}_{a}^{n+\frac{1}{2}}-{\mathbf{u}}_{a}^{n};\boldsymbol{ }{\mathbf{x}}_{a}^{n+1}=2{\mathbf{x}}_{a}^{n+\frac{1}{2}}-{\mathbf{x}}_{a}^{n};\\ {p}_{a}^{n+1}&=f\left({\rho }_{a}^{n+1}\right)\end{aligned}$$
(28)

The time step is controlled by a modified Courant-Friedrichs-Levy condition based on the forcing, viscous diffusion, and thermal diffusion terms:

$$\begin{array}{c}\Delta t=CFL\times \mathrm{min}({\Delta t}_{f},{\Delta t}_{\nu },{\Delta t}_{T})\\ {\Delta t}_{f}={\mathrm{min}}_{a}\sqrt{\frac{{h}_{w}}{\left|{\mathbf{F}}_{a}\right|}}; {\Delta t}_{\nu }={\mathrm{min}}_{a}\frac{{h}_{w}}{{u}_{s}+{\mathrm{max}}_{b}\left|\frac{{h}_{w}{\mathbf{r}}_{ab}\bullet {\mathbf{u}}_{ab}}{{\mathbf{r}}_{ab}^{2}}\right|}; {\Delta t}_{T}={\mathrm{min}}_{a}\frac{{\rho }_{a}{c}_{a}{h}_{w}^{2}}{{k}_{a}}\end{array}$$
(29)

Here, \(CFL\) is a scalar having value from 0.1 to 0.5.

3 Simulation results and discussions

3.1 Laser-powder interaction

The cloud of powders falling below the laser source will interact with the laser beam. The shading model is able to model the shading effect of the powder cloud on individual SPH particles constituting the powders. In these simulations, streams of Inconel 718 powders are injected into a 1100-μm radius laser beam with power ranging from 640 to 1040 W. The powder radius is \(R=15 \mathrm{\mu m}\). The laser source and the powder injection plane are stationary at 6 mm above the substrate. Other parameters for the SPH model and material obtained from [35] are given in Table 1.

Table 1 Model parameters for simulation of laser-powder interaction
Full size table

Figure 5a shows the powder streams and deposited layer. Here, half of the powder stream is presented to show the shading of the SPH particles inside the deposited clad. Simulation results of temperatures of 3,000 powder particles falling into the melt-pool under different laser power and feeding rate are shown in Fig. 5b–f. Due to the randomness of the powder initialization, the resulted temperature distribution also inhibits the randomness. The shading model also applies to the SPH particles discretizing the substrate and melt-pool.

Fig. 5
figure 5

Shading of powders exposed to laser beam (0, no shade; 1, fully shaded) and planar profiles of temperature of all 3,000 powder particles falling into the melt-pool under different laser power Qs (W) and feeding rate ṁ (g/min). Axis unit is mm; temperature unit is Kelvin

Full size image

3.2 Resolution study for DED simulations

In this section, the convergence and running time of the SPH model for a DED process will be evaluated at different particle sizes. In [29], it was concluded that a resolution of 3 SPH particles over a powder radius is relatively coarse, while the ratio of 5 is acceptable. It must be emphasized that those resolution ratios were evaluated for the selected laser melting (SLM) processes, where the sizes of the powders are relatively in the same order compared to the sizes of the laser beams and the melt-pools. For examples, in the SLM experiment [36], the averaged powder diameter is 27 µm, the laser beam diameter is 54 µm, and the width and depth of the melt-pool are approximately 75 µm and 30 µm. In the DED experiments [24], the diameter ratio of the powder and the laser beam is 60 µm:750 µm; the width and depth of the melt-pool are approximately 1500 µm and 100 µm. In the DED experiment [35], the powder and the laser beam ratio is 30 µm:2200 µm, and the width and depth of the melt-pool are 2200 µm and 1000 µm, respectively. One can estimate that if the resolution ratio of 5 is used for a DED simulation, the number of SPH particles needed to discretize the computational domain (with the width and depth sufficiently larger than the width and depth of the melt-pool) will be very large and hence will significantly impact the efficiency of the model.

In this convergence study, a short DED process of 20 ms is simulated with 3 different SPH particle sizes as shown in Table 2. The powder discretization can be seen in Fig. 4. The diameters of the powder and the laser beam remain the same at 30 µm and 1000 µm, respectively. The feed rate is 2.9 g/min. The substrate dimension is 1500 × 1500 × 300 µm in length, width, and depth. Other parameters for the Inconel 718 can be found in Table 1. One can see, with the resolution ratio increasing from 1 to 3, the total number of SPH particle and CPU hour triple or quadruple each time.

Table 2 Cases for SPH resolution study: SPH particle size dx, number of SPH particles, and CPU computation time taken for simulations of 20 ms
Full size table

Simulation results of melt-pool geometries and temperature distributions at different time instances for cases A, B, and C are presented in Fig. 6. In columns A, B, and C, only a haft of the melt-pools with the cut-plane being at the centre of the melt-pool to show its internal temperature. In column D, all side-view profiles of the melt-pools are plotted together. In Fig. 7, the temperature–time histories at selected locations in the melt-pool are plotted. One can see that Case A result shows much more splash as compared to the other two cases. The melt-pool shapes and temperature distributions of Cases B and C agree well with each other. The temperature–time histories also show a convergence of Case B result towards case C. Considering the total runtimes between Case B and Case C, and the sizes of the experiment cases to be simulated in the subsequent sections, the resolution of Case B is chosen.

Fig. 6
figure 6

Melt-pool geometries and temperature distributions at different time instances (I, 5 ms; II, 10 ms; III, 20 ms). Columns A–C: 3D views of a haft of the melt-pool (with the cut-plane at the centre of the melt-pool) for Cases A, B, and C, respectively. In column D, all melt-pool side-view profiles are plotted together. Axis unit is mm; temperature unit is Kelvin

Full size image
Fig. 7
figure 7

Temperature–time histories at selected locations in the melt-pool

Full size image

3.3 Simulations of experimental cases

In this section, the SPH model is used to simulate two real DED processes that were conducted in the experiments of Han et al. [24] and Song et al. [35]. In these simulations, the resolution of Case B, i.e., 2 SPH particles per powder radius or 19 SPH particles to discretize a powder, is chosen.

3.3.1 Experiment 1

In Experiment 1, a 3 g/min stream of stainless steel 304 powder of 50 μm radius is injected into a laser beam of 350 μm radius. The laser power levels are 300, 500, 750, and 1000 W. The laser source is at 10 mm above the substrate. The scan speed of the laser source is 12.7 mm/s in one direction. The model and material parameters are given in Table 3.

Table 3 Model parameters for DED simulations of Experiment 1
Full size table

The SPH particle size corresponding to the resolution of Case B is 30 μm. The dimension (L × W × D) of the initial substrate is 8 × 3 × 1.5 mm. The duration of the simulation is 0.5 s. With this length and time scales of the problem, the total SPH particles required is 1.6 millions. The runtime for each simulation is approximately 230 h in a 24-core parallel computation node (Intel Xeon E5-2690v3 2.60 GHz, 128 GB DDR4 RAM). Simulation results are presented in Figs. 8–12. Results of the 750 W laser power case (Case E) will be analysed.

Fig. 8
figure 8

Results of clad from the simulation of 750 W laser power (Case E) and comparison with numerical simulation and experiment in [24]. a 3D view, b side view. Colour code in panel (a) is the height of the clad measured from the surface of the substrate

Full size image

Figure 8 shows the deposited clad produced by the numerical simulation for the 750 W laser scan. The snapshot is taken when the laser position is at X = 8 mm. The top panel presents a 3D view of the clad and the substrate with colour code being the height of the clad measured from the surface of the substrate. The bottom panel shows a side view of the solidified clad on a vertical plan at the centre of the domain. The substrate is grey, while the solidified clad is green. As one can observe, the top surface of the clad are quite rough. The clad heights along the centre line range from below 0.4 mm to close to 0.6 mm. This is the result of the randomness in the powder injection and the powder impact on the melt-pool. The clad height along the laser scan line is in good agreement with the experiment data.

The lengths and peak temperatures of the melt-pool obtained from the SPH simulations for different laser power levels are plotted in Fig. 9 together with the experiment data and a 2D numerical simulation extracted from [24]. The SPH results are seen agreeing well with experiment data and the other numerical simulation, except for the pool length at laser power of 300 W.

Fig. 9
figure 9

Comparisons of melt-pool characteristics with numerical and experiment results in Han et al. [24]

Full size image

An instantaneous melt-pool geometry and its internal distributions of temperature are presented in Fig. 10, respectively. For the convenience of presenting the interiors, the melt-pool is cut by two vertical planes through its centre: plane (A) is parallel to the scan direction, and plane (B) is perpendicular to the scan direction. Contradicting to many mass-added continuum-based simulations, the melt-pool obtained from the SPH shows a bowl shape with uneven surface at the inside and at the top. The temperature of the metal liquid is generally high at a thin layer near the surface directly under the laser beam. There are spots of higher temperature at the surface, which are seen corresponding to the impingement of melted powder on the melt-pool.

Fig. 10
figure 10

Temperature distributions in the melt-pool from the simulation of Case E. Each plot presents one half of the melt-pool cut by the centre cross planes A and B to show the internal temperature. Temperature unit is Kelvin

Full size image

Figure 11 presents the velocity magnitudes and directions on the two vertical planes. One can observe that, although the solidified clad is of 0.4 mm from the substrate, the surface of the melt-pool at the centre is only 0.1 to 0.2 mm high. The melt-pool is also shallow and thin. Velocity is pointing downwards from the surface and diverges to the front and the back parts of the melt-pool in plane (A) and to the two sides in plane (B). In each of these parts, the velocity arrows generally point outwards and upwards. The velocity magnitude is generally low in the melt-pool, except at a small area at the centre, high downwards magnitude occurs. Noting that in the simulation of a stainless steel 304 block under laser beam in [29], where the flow is driven by the Marangoni force, the circulations are in opposite direction, i.e., the velocity direction at the centre of the melt-pool points upwards. This trend of velocity was also captured by the simulation without powder injection in [24].

Fig. 11
figure 11

Velocity of metal liquid in the melt-pool on the two cross planes. Result from the simulation of Case E. Background colour code demarcates velocity magnitude (m/s), and arrows indicate velocity direction

Full size image

Figure 12 presents the temperature–time histories at 4 vertical points at the centre of the melt-pool (and in the solidified clad). At location P1, the temperature curve is smooth. At P2, although this location is entirely in the un-melted region of the substrate, the temperature curve at the peak slightly oscillates. Locations P3 and P4 are inside the melt-pool, and their temperature at the peak significantly oscillate. P4 is above the substrate; hence, it only records temperature when the clad has been built up.

Fig. 12
figure 12

Temperature–time histories recorded from the SPH simulation of Case E at 4 locations on a cross section at X = 2 mm

Full size image

3.3.2 Experiment 2

In Experiment 2, a 4.3 g/min stream of Inconel 718 powder of 15 μm radius is injected into a 1100-μm radius laser beam. The laser power level is 840 W. The scan speed of the laser source is 10 mm/s in one direction. The laser source is at 6 mm above the substrate. This setup (Case H) corresponds to the experiment case #2 in [35]. In this sub-section, other two scan speeds of 15 mm/s (Case G) and 20 mm/s (Case F) will also be simulated. Other model and material parameters remain the same. The model and material parameters are given in Table 4.

Table 4 Model parameters for DED simulations of Experiment 2
Full size table

The SPH particle size corresponding to the resolution of Case B is 9 μm. The dimension (L × W × D) of the initial substrate is 5 × 4 × 1.3 mm. The initial duration of the simulation is 0.2 s. The initial domain is initiated at a reasonable size to save the computational resources. Extensions of the substrate and more powder can be straightforwardly added into the computational domain if necessary. Although the length and time scales of this problem are smaller than that of Experiment 1, the total SPH particles required is enormous due to the small size of the SPH particle: approximately 38 millions SPH particles are required. The runtime for each simulation is more than 60 days in 10 × 24-core parallel computation nodes (Intel Xeon E5-2690v3 2.60 GHz, 128 GB DDR4 RAM). At 0.2 s, the simulated DED processes have reached their quasi-steady states as the melt-pool’s characteristics are generally unchanged. Simulation results are presented in Figs. 13–19.

Fig. 13
figure 13

Dimensions of solidified clad and melt-pool and comparison of current SPH simulation of Case H with COMSOL’s FEM simulation and experiment of Case 2 in [35]. Solid circles in the side and front view plots indicate locations for records of temperature time series. Dimension and axis units are mm

Full size image

In Fig. 13, the dimensions of solidified clad and melt-pool are compared against those measured in the experiment and numerical simulation using finite element method and mass-added in [35]. The clad height Hc and melt-pool depth Dm agree well with the experiment and the FEM simulation. The clad width from the SPH simulation is significantly larger than that reported in the experiment and the FEM simulation which is close to the diameter of the laser beam. The width of melted substrate, Wm, is closer to the reported clad width. The melt-pool shape obtained from the SPH simulation is very well shaped and much smoother than that from the simulation of Experiment 1. This is because the melt-pool is much better resolved by the SPH particles as compared to the previous case. Based on this melt-pool shape, other dimensions are also defined for subsequent analysis. These include the pool length Lm, pool height Hm, pool front length Lf, and back length Lb measured from the centre of the laser beam. Several locations for extracting temperature and velocity–time histories are also presented.

Figure 14 shows three-dimensional views of the melt-pools obtained from the SPH for three different scan speeds. It is clearer that the melt-pools are in the form of elongated bowls with high temperature at the inner surface. The melt-pool surfaces are much smoother as compared to the Experiment 1. The tiny dots above the inner surface of the melt-pools are the injecting powders. Internal distributions of temperature and flow structures are presented in Figs. 15, 16. The melt-pools are cut along the two vertical planes (A) and (B), and the velocity field are plotted on the planes, similarly to those shown in Figs. 10, 11. In these plots, the axis (X-axis) in the scan direction is adjusted so that laser centre is always at X = 0 for the convenience of comparison.

Fig. 14
figure 14

Three-dimensional view of melt-pools with temperature from SPH simulations for three scan speeds: (F) 20 mm/s, (G) 15 mm/s, (H) 10 mm/s. Axis unit is mm, temperature unit is Kelvin

Full size image
Fig. 15
figure 15

Front Side view of the melt-pools with colour codes of velocity magnitude (left) and temperature (right) of Cases F, G, and H. Axis unit is mm, velocity unit is m/s, temperature unit is Kelvin, and arrows indicate velocity direction

Full size image
Fig.  16
figure 16

Front view of the melt-pools with colour codes of velocity magnitude (left) and temperature (right) of Cases F, G, and H. Axis unit is mm, velocity unit is m/s, temperature unit is Kelvin, and arrows indicate velocity direction

Full size image

The side views of the melt-pool on the plane parallel to the scan direction in Fig. 15 clearly show the front and the back parts of melt-pool. As the scan speed increases, the melt-pool is more elongated, and the back part is thicker and longer than the front part. In each of the front and back parts, a well define circulation of metal liquid could be seen. The velocity points downwards at the centre and turns upwards near the bottom of the melt-pool. The velocity magnitude is highest at the centre and reduces quickly towards both sides of the melt-pool. The temperature varies drastically across the thin liquid layer of the melt-pool. On the inner surface of the pool, uneven temperature could be seen with some spots having almost 100–200 K higher than the surrounding areas.

The front views of the melt-pool on the plane perpendicular to the scan direction are shown in Fig. 16. Two opposite circulations of liquid can be seen at both sides of the centre of the melt-pool. The shapes of the pool and the circulation are quite symmetric about the centre line. The melt-pool dimensions are generally larger as the scan speed is slower. Detail comparisons of melt-pool dimensions among the three simulations are shown in Fig. 17.

Fig. 17
figure 17

Clad dimensions for Cases F, G, and H from SPH simulations. Dimension unit is mm

Full size image

The inner surfaces of the melt-pool shown in Figs. 15, 16 resemble upside down cone shapes. It is clearly a result of the powder impingement on the melt-pool surface. Figure 18 shows that, as soon as the powder stream has stopped, the inner surface bounces up with metal liquid from the sides and front and back flowing towards the centre and turning upwards. Without the shade of the powder cloud, the melt-pool absorbs more energy and its temperature quickly increases.

Fig. 18
figure 18

Side and front view of the melt-pools with colour codes of velocity magnitude and temperature of Case F after powder flow has stopped. Axis unit is mm, velocity unit is m/s, temperature unit is Kelvin, and arrows indicate velocity direction

Full size image

Figure 19 presents the temperature–time histories at 4 vertical points at the centre of the melt-pool obtained from the simulation of Case F. Location P1 is entirely inside the un-melted region of the substrate. Location P2 is either in the melt-pool or the un-melted substrate. P3 locates almost on the inner surface of the melt-pool, while P4 is above the melt-pool surface for a certain period. The curves show similar trends to the those of Experiment 1 (shown Fig. 12). Temperature at P2 slightly oscillates at the peak. Temperatures at P3 and P4 widely fluctuate when the laser beam and the powder stream are passing by. Outside that period, the temperature–time history curves at P2, P3, and P4 remain stable with maximum temperature of around 1800 K. The durations that the temperature curves stay above the melting temperature of the material (1609 K) are indeed equal to the length of the melt-pool at those levels over the scan speed.

Fig. 19
figure 19

Temperature–time histories at selected locations at the centre melt-pool and in the substrate extracted from the simulation of Case F

Full size image

4 Discussions

In the proposed workflow, a random powder generator is used with an assumption of pre-defined planar distribution and powder flow rate being given instead of a high-fidelity nozzle and powder-gas flow model. This assumption is reasonable for a quasi-steady-state powder flow. That means the powder column could be decomposed into sub-columns; each corresponds to a planar distribution and powder flow rate. Furthermore, as there is no restriction on the powder sizes and properties, the current powder generator model could take into account the powder size and property distributions as an input. And finally, as the powder generator model is a pre-possessing module independent from the SPH simulation, it could be replaced by a high-fidelity nozzle and powder-gas flow model without affecting the main simulation module.

The shading and laser power absorption algorithm in the SPH model seems to work well although it is nearly impossible to verify the shading index and temperature of each powder particles in the powder stream. The results of melt-pool’s surface temperature, which is strongly influenced by the laser power received at its surface and the temperature of powders falling into it, being in good agreement to experiment data is an indicator of the performance of the algorithm. This also indicates that the chosen resolution is adequate although the SPH resolution to resolve a powder particle chosen from the mesh convergence study in this paper is lower than that concluded in the previous SLM study. It could be attributed to several reasons. Firstly, in the SLM process, there is significant heat conduction from the upper surface of the powder through the powder itself and into the substrate. Whereas in the DED, the powder is almost at uniform temperature and quickly absorped into the melt-pool as it falls into. However, a certain resolution of the powder must be considered in order to avoid over-predicting the impact of the powders on the melt-pool which could generate strong splashing on the melt-pool surface as one can see in Fig. 6. Secondly, the size of the melt-pool and the laser beam relative to the size of the powder in the DED simulation are much larger than that in the SLM simulation. As a result, the melt-pool in the DED simulation will still be well resolved by the SPH particles, allowing the heat transfer and fluid dynamics to be captured well. This, however, might not be true for a general DED process as these size ratios could vary.

The SPH simulations of two different real DED setups generally agree well with experiment data in terms of geometrical dimensions of deposited clad and melt-pool surface temperature. The analysis of the 3D results reveals other characteristics of the melt-pool which otherwise impossible to measure in experiments. The melt-pool generally has a bowl shape and is elongated in the scan direction. Unlike the bell shapes observed in many continuum-based simulations with empirical mass deposition, the surface of the melt-pool is concave. The concave melt-pool shape is shown quickly disappearing when the powder stream has stopped. Hence, this concave shape could be attributed to the impingement of the powder stream on the liquid surface of the melt-pool. Also due to this impingement, the liquid at the centre of the melt-pool flows downwards and bifurcates to the sides near the bottom. The downward flow in the simulation of stainless steel 304 is seen overwhelming the Marangoni effect which otherwise pulls the liquid upwards in the melt-pool. The bifurcation could generate flow circulation in the side, front, and back parts of the melt-pool. Furthermore, this flow dynamics seems to push the liquid outwards from the centre of the melt-pool and redistribute the deposited powder mass making the clad wider than the size of powder stream. The impingement of the powders into the melt-pool surface also affects the temperature distribution, both at the surface and inside the melt-pool. On the surface of the pool, uneven spatial temperature distributions could be seen with some spots having almost 100–200 K higher than the surrounding areas. The temporal variations of temperature inside the liquid also fluctuate significantly when the powder stream passing by.

The present SPH model could provide important insights into the heat transfer and flow dynamics in the melt-pool. A major drawback of current code is the enormous computational resource and time required to run which prevents it from large-scale simulations. One may need 10 to more than 60 days with 24 to 240 parallel CPU cores to complete a very short simulation of a DED process. The code has however not been optimized yet. The modelling strategies that are current being used to speed up the simulation are to consider powder particles only when they fall below the laser source level and to solve the fluid dynamic equations only for liquid and moving solid particles. There are rooms for further optimize the code to boost its efficiency, such as CPU-GPU hybrid or multi-resolution approaches which have been adopted elsewhere for other applications.

5 Conclusions

This paper presents an application of a developed three-dimensional smoothed particle hydrodynamics model to simulate directed energy deposition additive manufacturing processes. A new workflow that comprises a random powder generator with the SPH core simulation module was proposed. A study to select adequate SPH particle resolution and simulations of two different DED setups for model validation was performed. The simulation results were shown in good agreement with experimental data in terms of geometrical dimensions of deposited material and melt-pool surface temperature. Detail analyses on the results revealed internal characteristics of the melt-pool. The SPH model is not very efficient for a large-scale simulation at the current stage without further optimization. However, it could be useful for deep insight of AM processes or providing inputs to other numerical models. There are also several options to improve its efficiency which could be explored in the future.