1 Introduction

In modern manufacturing systems, modern automated machining equipment uses higher cutting speeds in order to achieve high efficiency and low-cost machining [1]. Grinding wheel wear will cause a series of grinding defects such as grinding burns, surface vibration pattern, and crack, and affect the tool spiral groove (rake angle, core diameter, blade width) [2]. Therefore, the detection of grinding wheel wear has always been an important research content in grinding processing.

Through investigating the literature, it is found that some scholars used error separation technology, image method, and mathematical method to measure grinding wheel wear. Mu and Zhang [3] aimed at the problem that it is difficult to measure the wear profile of the grinding wheel in real time during grinding, a grinding wheel profile measurement method based on error separation technology is proposed, and the accuracy of the method is proved by experiments. Hu et al. [4] proposed an integrated method of grinding and in situ detection of sand contour for contour curve grinding, designed an in situ visual inspection system of sand contour. The results show that this method can effectively improve the shape and dimensional accuracy of the machining contour of the part. Fan et al. [5] established a constant helix angle cutting edge curve model of a rotating parabolic milling cutter and numerically simulated the established cutting edge curve model, which provided a theoretical basis for solving the grinding wheel’s shape. Lachance et al. [6] used a scanning electron microscope to capture the grinding wheel’s digital image to obtain the wear area of the grinding wheel, but this method is not suitable for multiple repeated measurements. Xiao et al. [7] studied the rail grinding process and grinding wheel wear detection and proposed a self-referenced three-point method for indirect measurement of rail grinding wheel wear. The simulation measurement of the two sinusoids on the front and back surfaces of the rail is carried out, and the simulation results show that detecting the grinding wheel’s wear is feasible. Tohoku University and Hunan University in Japan have developed an in-machine sand profile detection device [8, 9]. They clamped the high-precision displacement sensor probe on a precision rotary platform and realized the sand profile through the rotary table rotation—scan of cross-section. Zhang [10] used differential pressure technology and error separation technology to establish an online detection of the grinding wheel’s wear and passivation by detecting the change in the liquid pressure between the end face of the grinding coolant nozzle and the working surface of the grinding wheel. Furutani et al. [11] proposed a wet grinding measurement method. Use a pressure sensor to measure the fluid dynamic pressure to detect the wear of the grinding wheel of the cylindrical grinding machine.

Some scholars used acoustic emission technology and wavelet packet technology to detect grinding wheel wear. Mokbel and Maksoud and Hwang et al. [12, 13] applied acoustic emission (AE) to grinding wheel wear detection, and obtained a series of relationship between AE signal and grinding wheel wear. Wu et al. [14] proposed a grinding wheel wear measurement and machining error compensation system based on acoustic emission detection technology. The system can feedback the grinding wheel wear to the CNC system to realize automatic compensation. Furthermore, the effectiveness of the proposed method is verified through experiments. Shi and Ding [15] use the wavelet packet decomposition coefficient statistical method to study the corresponding relationship between the normal grinding force and the grinding wheel wear, establishes a neural network-based grinding wheel wear status recognition model, and proves the feasibility with experiments.

This paper uses image processing technology to detect the edge section profile of the spiral groove of the solid end mill grinded by the worn grinding wheel, extract the edge, and fit the edge point of the spiral groove end section into an equation, based on the principle of the contact line, in the grinding wheel position. Under the premise that the profile and spiral groove shape are known, the worn sand profile is solved, which provides a theoretical basis for analyzing the influence of grinding wheel wear on the spiral groove parameters (rake angle, core diameter, blade width).

2 Reverse algorithm for contour of wearing sand

2.1 Principle of contact line

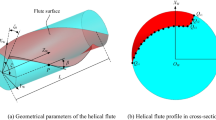
The spatial position movement relationship between the spiral groove and the grinding wheel can be shown in Fig. 1 [16]. The formation of the spiral groove is completed by the rotation of the workpiece around the axis and the grinding wheel’s movement along the axis. The following coordinate system can clearly describe the movement relationship between the two. The grinding wheel coordinate system \(\left[ {O_{G} ,X_{G} ,Y_{G} ,Z_{G} } \right]\) is fixed on the grinding wheel. This coordinate system’s origin coincides with the center point of the working surface of the grinding wheel. It is used to define the grinding wheel’s size and geometric shape and does not change the direction and position with the movement of the grinding wheel. The workpiece coordinate system \(\left[ {O_{W} ,X_{W} ,Y_{W} ,Z_{W} } \right]\) is fixed on the workpiece, the origin coincides with the center of the workpiece, and the coordinate axis coincides with the axis of the workpiece which is used to describe the geometry of the tool spiral groove.

Fig. 1
figure 1

Relationship between spiral groove and grinding wheel spatial position

Full size image

The coordinates of the center point of the grinding wheel refer to the center of the front face of the grinding wheel in the workpiece coordinate system. It is indicated by ax, ay, az in the figure, and the grinding wheel has a certain swing angle during grinding, which is indicated by λ in the figure. Assuming that the workpiece’s movement is spiral and the radius of the workpiece is R, it rotates around the axis at an angular velocity ω, and the grinding wheel moves along the coordinate axis ZW at a linear velocity v. The constant k can be described by the geometric parameters of the tool and the spiral groove. As shown in Eq. (1),

$$k = \frac{R}{{\tan (\delta_{0} )}}$$
(1)

where R is the tool radius and δ0 is the spiral groove spiral angle.

The expression of the profile curve of the spiral groove end in the XWYW plane is shown in Eq. (2), and m represents the curvilinear coordinates of the surface:

$$r_{w}^{W} (m) = \left[ {f_{1} (m),\;f_{2} (m),\;0} \right]^{\prime }$$
(2)

The profile curve equation of the spiral groove end section can be obtained by sweeping. Assuming that the spiral direction is to the right, the cross-sectional profile of the spiral groove end rotates an angle vw around the tool’s axis while moving along the axis by a distance kvw, and the spiral groove surface can be obtained. The spiral groove surface equation is shown in Eq. (3):

$$R_{w}^{W} (m,v_{w} ) = \left[ {\begin{array}{*{20}c} {x_{w}^{W} } \\ {y_{w}^{W} } \\ {z_{w}^{W} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {f_{1} (m)\cos v_{W} - f_{2} (m)\sin v_{W} } \\ {f_{1} (m)\sin v_{W} - f_{2} (m)\cos v_{W} } \\ {kv_{W} } \\ \end{array} } \right]$$
(3)

The vector relationship between the grinding wheel and the spiral groove’s surface is shown in Fig. 2, where point P is any contact point on the contact line.

Fig. 2
figure 2

Contact line between grinding wheel surface and spiral groove surface

Full size image

In the workpiece coordinate system, the position vector of any contact point P on the spiral groove’s surface can be represented by \(m_{w}^{W} = \left[ {x_{w}^{W} ,y_{w}^{W} ,z_{w}^{W} } \right]^{\prime }\). The position vector of the grinding wheel is known and can be represented by \(m_{D}^{W} = \left[ {a_{x} ,a_{y} ,a_{z} } \right]^{\prime }\). The contact relationship between the grinding wheel’s surface and the spiral groove’s surface shows that the grinding wheel and the spiral groove the standard normal \(\overrightarrow{n}\) at any contact point P intersects the axis of the grinding wheel at point Q. Also, the surface of the grinding wheel is obtained by rotating the cross-section of the grinding wheel. During the grinding process, the common normal\(\overrightarrow{n}\), the grinding wheel axis ZG, and the vector \(m_{w} - m_{D}\) are on the same plane, so the three vectors’ product is zero. Therefore, the relationship between the three can be expressed by Eq. (4):

$$(m_{w}^{W} - m_{D}^{W} ) \bullet (\overrightarrow {{Z_{G} }} \times \vec{n}) = 0$$
(4)

where · and × represent the inner vector product and outer vector product of two vectors, respectively.

The available vector \(\overrightarrow {{Z_{G} }} = \left[ {0,\sin \lambda ,\cos \lambda } \right]\) represents the axial vector of the grinding wheel, where λ is the deflection angle of the grinding wheel and \(\overrightarrow {n} = \left[ {n_{x} ,n_{y} ,n_{z} } \right]\) is the standard average vector of any contact point on the surface of the spiral groove. In order to obtain the component of the standard average vector \(\overrightarrow{n}\) at any contact point P of the spiral groove surface, the average vector at the contact point P can be expressed by Eq. (5):

$$\left\{ {\begin{array}{*{20}c} {\overrightarrow {n} = (R_{w}^{W} )_{{v_{m} }} \times (R_{w}^{W} )_{{v_{w} }} } \\ {(R_{w}^{W} )_{{v_{m} }} = \frac{{\partial R_{w}^{W} }}{{\partial v_{m} }}} \\ {(R_{w}^{W} )_{{v_{w} }} = \frac{{\partial R_{w}^{W} }}{{\partial v_{w} }}} \\ \end{array} } \right.$$
(5)

where \({R}_{w}^{W}\) is spiral groove surface contact line, and Vm and Vw are two different angles at which the profile of the spiral groove end rotates around the tool axis.

In order to express this relationship clearly, the subscript in Eq. (3) is omitted, and the standard average vector at any contact point P on the surface of the spiral groove is shown in Eq. (6):

$$\overrightarrow {n} = \left[ {\begin{array}{*{20}c} {k\left[ {f^{\prime}_{1} (m)\sin v + f^{\prime}_{2} (m)\cos v} \right]} \\ { - k\left[ {f^{\prime}_{1} (m)\sin v + f^{\prime}_{2} (m)\cos v} \right]} \\ {f_{1} (m)f^{\prime}_{1} (m) + f_{2} (m)f^{\prime}_{2} (m)} \\ \end{array} } \right]$$
(6)

The four vectors in Eq. (4) are all calculated, and they are all known vectors.

Substituting the four obtained vectors into Eq. (4), the contact relationship between the surface of the grinding wheel and the surface of the spiral groove can be expressed by Eq. (7):

$$\left\{ {\begin{array}{*{20}c} {\left[ {A_{d} (m)\sin v + B_{d} (m)\cos v + C_{d} (m)} \right] + \left[ {D_{d} (m)\sin v + E_{d} (m)\cos v} \right]v = 0} \\ {A_{d} (m) = \left[ {F(m)f_{2} (m) - ka_{z} f^{\prime}_{1} (m)} \right]\sin \lambda - k\left[ {a_{y} f^{\prime}_{1} (m) - a_{x} f^{\prime}_{2} (m)} \right]\cos \lambda } \\ {B_{d} (m) = - \left[ {F(m)f_{1} (m) - ka_{z} f^{\prime}_{2} (m)} \right]\sin \lambda - k\left[ {a_{x} f^{\prime}_{1} (m) - a_{y} f^{\prime}_{2} (m)} \right]\cos \lambda } \\ {C_{d} (m) = F(m)(a_{x} \sin \lambda + k\cos \lambda )} \\ {D_{d} (m) = k^{2} f^{\prime}_{1} (m)\sin \lambda } \\ {E_{d} (m) = k^{2} f^{\prime}_{2} (m)\sin } \\ {F(m) = f_{1} (m)f^{\prime}_{1} (m) + f_{2} (m)f^{\prime}_{2} (m)} \\ \end{array} } \right.$$
(7)

This contacting relationship is only a prerequisite for solving the worn sand’s contour, and it is also necessary to determine the final contour of the worn grinding wheel through this relationship. The contact relationship expressed by Eq. (7) represents the contact line between the grinding wheel and the spiral groove processed in a physical sense, and m and v represent the curved surface coordinates. However, to obtain the profile of the worn grinding wheel, the value obtained through this contact relationship must be converted to the grinding wheel coordinate system to obtain the contact line in the grinding wheel coordinate system. Therefore, Eq. (8) can be used to express the contact curve \({R}_{tm}^{G}\) in the grinding wheel coordinate system, as the same time calculate and expand the matrix to get

$$\begin{aligned}&R_{tm}^{G} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & {\cos \lambda } & {\sin \lambda } & 0 \\ 0 & { - \sin \lambda } & {\cos \lambda } & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & { - a_{x} } \\ 0 & 0 & 0 & { - a_{y} } \\ 0 & 0 & 0 & { - a_{z} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]\\&R_{w}^{W} = \left[ {\begin{array}{*{20}c} {x_{tm}^{G} } \\ {y_{tm}^{G} } \\ {z_{tm}^{G} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {x_{w}^{W} - a_{x} } \\ {(y_{w}^{W} - a_{y} )\cos \lambda + (z_{w}^{W} - a_{z} )\sin \lambda } \\ { - (y_{w}^{W} - a_{y} )\sin \lambda + (z_{w}^{W} - a_{z} )\cos \lambda } \\ \end{array} } \right]\end{aligned}$$
(8)

Equation (8) represents the contact curve equation in the machine tool coordinate system, so it uniquely defines the profile of the worn grinding wheel required to generate the spiral groove section. Since the contact point trajectory in the grinding wheel coordinate system is the envelope of the grinding wheel, Eq. (2) can also be expressed as the contact trajectory of the grinding wheel and the spiral groove surface. Therefore, the relationship between the surface of the grinding wheel and the contact trajectory can be equivalent to Eq. (9):

$$\left[ {\begin{array}{*{20}c} {g_{1} (u_{g} )\cos v_{g} } \\ {g_{1} (u_{g} )\sin v_{g} } \\ {g_{2} (u_{g} )} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {x_{tm}^{G} } \\ {y_{tm}^{G} } \\ {z_{tm}^{G} } \\ \end{array} } \right]$$
(9)

However, in order to obtain the final wear wheel profile, it is necessary to solve the two unknown quantities \(g_{1} (u_{g} )\) and \(g_{2} (u_{g} )\) in Eq. (9). The grinding wheel is a rotating body, and the contour expression of the worn grinding wheel can be obtained by the rotating generatrix equation, as shown in Eq. (10):

$$\left[ {\begin{array}{*{20}c} {g_{1} (u_{g} )} \\ 0 \\ {g_{2} (u_{g} )} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \sqrt {(x_{tm}^{G} )^{2} + (y_{tm}^{G} )^{2} } } \\ 0 \\ {z_{tm}^{G} } \\ \end{array} } \right]$$
(10)

The above study is to reverse the worn grinding wheel’s profile by describing the meshing conditions between the grinding wheel and the spiral groove it grinds. In this relationship, the cross-sectional profile curve of the spiral groove end is represented by an equation, and the process of the reverse calculation is based on the principle that the common normal of any contact point on the contact line of the grinding wheel and the spiral groove surface must intersect the axis of the grinding wheel, which is the principle of contact line [17]. The image processing technology is used to fit the coordinates of the contour points of the spiral groove end surface extracted into a curve equation, combined with the contact line’s principle between the grinding wheel and the spiral groove and finally obtain the desired contour wear grinding wheel.

2.2 Numerical solution of rotation angle vp

The contact equation between the grinding wheel and the spiral groove surface mentioned in Sect. 2.1 is a nonlinear transcendental equation, and the solution of this equation cannot be obtained by the calculation method of the conventional equation. Therefore, a numerical calculation method can be used to cyclically distribute the rotation angle of each point on the contour line of the spiral groove end of the wear disc, and calculate the distribution value and compare to obtain the contour curve. The purpose of solving the rotation angle of each point. According to the characteristics of the spiral groove curve formed by the worn grinding wheel, the range of the rotation angle of any contact point P on the spiral groove is \(\left[ {v_{p\min } ,v_{p\max } } \right]\), and any rotation angle is specified in this range, and the value is\({\text{v}}_{\text{p}}\). If the assignment is correct rotation angle\({\text{v}}_{\text{pR}}\), then Eq. (7) is satisfied; if the assignment is \({\text{v}}_{\text{p}}\) not equal to\({\text{v}}_{\text{pR}}\), the following relationships are satisfied respectively:

$$\left[ {A_{d} (u)\sin v + B_{d} (u)\cos v + C_{d} (u)} \right] + \left[ {D_{d} (u)\sin v + E_{d} (u)\cos v} \right]v > 0$$
(11)

or

$$\left[ {A_{d} (u)\sin v + B_{d} (u)\cos v + C_{d} (u)} \right] + \left[ {D_{d} (u)\sin v + E_{d} (u)\cos v} \right]v < 0$$
(12)

combine the following content to explain the above two formulas, assign a value to the rotation angle of any point P on the profile curve of the spiral groove end, expressed as \({\text{v}}_{\text{p}}\), then \({\text{v}}_{\text{p}}\) can be expressed by Eq. (13):

$$v_{p} = v_{pR} + Lv$$
(13)

then point P can be expressed by formula (14) after a series of coordinate transformations:

$$R_{w}^{W} (m,v) = \left[ {\begin{array}{*{20}c} {x_{w}^{W} } \\ {y_{w}^{W} } \\ {z_{w}^{W} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {f_{1} (m)\cos (v_{pR} + Lv) - f_{2} (m)\sin (v_{pR} + Lv)} \\ {f_{1} (m)\sin (v_{pR} + Lv) + f_{2} (m)\cos (v_{pR} + Lv)} \\ {k(v_{pR} + Lv)} \\ \end{array} } \right]$$
(14)

and the normal vector \(\overrightarrow{\text{n}}\) of the contact line corresponding to point P is:

$$\overrightarrow {n} = \left[ {\begin{array}{*{20}c} {k\left[ {f^{\prime}_{1} (m)\sin (v_{pR} + Lv) + f^{\prime}_{2} (m)\cos (v_{pR} + Lv)} \right]} \\ { - k\left[ {f^{\prime}_{1} (m)\sin (v_{pR} + Lv) + f^{\prime}_{2} (m)\cos (v_{pR} + Lv)} \right]} \\ {f_{1} (m)f^{\prime}_{1} (m) + f_{2} (m)f^{\prime}_{2} (m)} \\ \end{array} } \right]$$
(15)

If \(Lv=0\), then \({v}_{P}={v}_{PR}\), in line with the principle of the contact line between the spiral groove surface and the grinding wheel surface, the average vector of any contact point P on the contact line perpendicularly intersects the axial vector of the grinding wheel, which meets the requirements of Eq. (4). If \(L\nu \ne 0\), it does not satisfy the principle of the contact line; it is impossible to use Eq. (4) to prove that the average vector of the contact point P on the contact line perpendicularly intersects the axial vector of the grinding wheel. Equations (11) and (12) cannot be obtained directly according to the conventional equation solution method, so they can be solved by the numerical solution method. The law of the equation solution is shown in Fig. 3, where H is the discriminant:

$$H = \left[ {A_{d} (u)\sin v + B_{d} (u)\cos v + C_{d} (u)} \right] + \left[ {D_{d} (u)\sin v + E_{d} (u)\cos v} \right]v$$
(16)
Fig. 3
figure 3

The variation of discriminant H

Full size image

To verify this rule, NUMROTO grinding simulation software was used to grind a spiral groove with a diameter of 10 mm on a bar of 10 mm using a 1A1 grinding wheel with a radius of 75 mm. Any three contact points A, B, and C on the spiral groove are selected; when the rotation angles corresponding to the three points take different values, the change rule of the discriminant H value is shown in Fig. 3.

From the change rule of the three contact points A, B, and C on the figure, we can see that as the rotation angle increases, the value of the discriminant H gradually rises, proving the regularity of Eqs. (11) and (12). This method can be used to obtain the contact point with the surface. Grinding wheels and spiral grooves. rotation angle.

2.3 The algorithm flow to solve the wear profile of the grinding wheel

According to the above description of the research on the reverse calculation of the grinding wheel wear curve, the grinding wheel wear curve calculation process is briefly introduced in conjunction with Fig. 4. The flowchart is shown in Fig. 4.

Fig. 4
figure 4

Calculation process

Full size image

After the worn grinding wheel grinds the spiral groove, the tool is removed from the machine tool, and an ultra-depth microscope is used to collect images of the end cross-sectional profile, and use a series of image processing techniques to preprocess the collected images. According to the center of gravity algorithm, the origin of the coordinates of the specific part of the image knife is determined, and the coordinates of the profile points of the spiral end groove section are extracted accordingly, and the cftool function in MATLAB is used to make it suitable for the determined equation. Input the workpiece parameters, the unworn grinding wheel parameters, and the grinding wheel attitude parameters into MATLAB software in turn, and calculate the contour points of the spiral groove end section profile curve of the unworn grinding wheel through simulation. The rotation angle corresponding to the unworn contour point can be obtained according to the grinding wheel’s position and parameters, and the value range of the rotation angle \({\text{v}}_{\text{p}}\) of the contact point of the spiral groove end profile curve of the worn grinding wheel can be determined accordingly. After obtaining the unworn contour points and the worn contour points, compare and analyze the two sets of coordinate data, and divide the worn contour points into two parts: the spiral groove curve of the worn part of the worn wheel and the curve of the unworn part of the spiral groove worn wheel. The unworn contour points have been calculated, so only the contour curve of the worn part of the worn wheel needs to be solved, which greatly reduces the amount of calculation. The number of wear contour points is denoted by N, and each contour point is numbered. The value range of wear profile point P is calculated, and then the value is assigned to the rotation angle \({\text{v}}_{\text{p}}\) to calculate the value of the criterion H (Eq. 16). In addition, because the discriminant H is a nonlinear transcendental equation, its zero point cannot be solved by conventional analytical methods, so it is solved by numerical calculation method. It is necessary to analyze the accuracy of the absolute value of the discriminant H, and set the accuracy to ε for comparison. If the set accuracy requirements are met, the principle of the contact line is considered to be satisfied, and the rotation angle \({\text{v}}_{\text{p}}\) is considered the correct rotation angle \({\text{v}}_{\text{pR}}\). If the set accuracy requirements are not met, the rotation is calculated according to the numerical calculation method described in Sect. 1.2, reallocate and calculate the angle \({\text{v}}_{\text{p}}\) until it meets the set accuracy requirements and solves the required rotation angle\({\text{v}}_{\text{pR}}\). When the correct rotation angle \({\text{v}}_{\text{pR}}\) is solved, substitute the solved \({\text{v}}_{\text{pR}}\) value into Eq. (7) to obtain the coordinate position of point P on the contact line. Since the above calculation is done in the workpiece coordinate system, it needs to be calculated according to Eq. (8). The result is converted to the grinding wheel coordinate system, and the axial position and radius of the grinding wheel at the grinding point P can be obtained. According to the above process, each point on the wear contour is calculated one by one until all the edge points are calculated and expressed in the grinding wheel coordinate system. The calculated coordinate points are sorted, and the grinding wheel wear contour curve in Fig. 10 is obtained.

3 Extraction and fitting of the contour point coordinates of the spiral groove end section

3.1 Image edge detection

In this paper, we use the KEYENCE VHX-1000 super depth of field microscope to sample the hardened end milling cutter’s helical groove end section profile. The collected cross-section profile image of the spiral groove end is shown in Fig. 5. Before the edge detection, binarization processing [18] is needed to distinguish the image’s target and background with the appropriate threshold value.

Fig. 5
figure 5

Spiral groove end section profile image

Full size image

The equation of the spiral groove curve can be obtained by edge point fitting, and the contour of the worn grinding wheel can be obtained through this equation. Edge detection is the last and key step of image preprocessing. The accuracy of the detection will directly affect the contour of the worn sand. The accuracy of the reversed form. According to the characteristics of the image, this paper uses mathematical morphology to locate the edge coarsely [19], and the Harris algorithm to accurately determine the edge realizes the edge detection of the profile of the spiral groove end. The principle of Harris corner detection is to use the concept of the gray difference of adjacent pixels to calculate the gray change value in the image with a moving window to determine whether it is a corner, edge, or smooth area. This paper needs to detect the profile of the spiral groove end, after the image is binarized, which is very suitable for Harris algorithm detection. Because the end section of the spiral groove’s profile image is uniform and symmetrical, only need to perform edge detection on one of the grooves. Figure 6 is an enlarged view of one of the groove edge detection results, and the intersection of “ + ” in the figure is the edge point of the detected groove.

Fig. 6
figure 6

Spiral groove image edge detection

Full size image

3.2 Extraction and fitting of the contour point coordinates of the spiral groove end section

After the edge point detection on the image, the next step is to extract the image’s edge point coordinates and perform fitting according to the extracted edge point coordinates. This needs to calibrate the center point of the image tool part as the origin of the spiral groove image coordinates.

Because the section image of the spiral groove is regular and symmetrical, the center gravity of the image is obtained by using the image matrix, and the center position of the image is calibrated by obtaining the center of the binarized image gravity. As shown in Eq. (17), the zero-order moment M00 of the image represents the formula:

$$M_{00} = \sum\limits_{I} {\sum\limits_{J} {V(i,j)} }$$
(17)

The gray value of the single-channel image at the \(\left(\text{i , j}\right)\) point can be represented by\({\text{V}}\left(\text{i , j}\right)\), after the image is binarized, the image appears in black and white, and the sum of the white parts on the image is represented by\({M}_{00}\). Therefore, after the sum of the white parts is determined, the binary image area can be expressed by the zero-order moment of the image. The first-order moment expression of the image \({M}_{00}\) is shown in Eq. (18):

$$\begin{cases} M_{10} = \sum\limits_{I} {\sum\limits_{J} {i \bullet V(i,j)} } \hfill \\ M_{01} = \sum\limits_{I} {\sum\limits_{J} {j \bullet V(i,j)} } \hfill \\ \end{cases}$$
(18)

After the image is binarized,\({\text{V}}\left(\text{i , j}\right)\) only has two values of 0 (black) and 1 (white). \({\text{M}}_{10}\) can be expressed by the cumulative value of the X coordinate values of all white areas on the image. Similarly, \({\text{M}}_{01}\) can be expressed by the cumulative value of the Y coordinate values of all black areas on the image. Therefore, the center of gravity of the binary image of the cross section of the spiral groove is also the center of the binary image\(\left({\text{x}}_{\text{c}}\text{,}{\text{ y}}_{\text{c}}\right)\), as shown in Eq. (19):

$$x_{c} = \frac{{M_{10} }}{{M_{00} }},\;y_{c} = \frac{{M_{01} }}{{M_{00} }}$$
(19)

After the image center point is calculated, it is converted to the origin coordinate by the coordinate translation matrix \({M}_{\tau }\), and the calibration of the image center point origin coordinate is completed.

After using the edge detection technology to complete the calibration of the image center origin, the coordinates of the edge point need to be extracted. Without changing the hardware system, the algorithm is used to improve the system’s detection accuracy, that is, the sub-pixel edge detection method [20]. The pixel values of the horizontal gradient \(\overrightarrow{\text{X}}\) and the vertical gradient \(\overrightarrow{\text{Y}}\) of this pixel can be obtained by calculation. According to the gradient values of these two directions, the normal vector gradient of this point is calculated as \(\overrightarrow{\text{N}}\), and its size \(\left|\left.\overrightarrow{\text{N}}\right|\right.\) and direction τ are as Eq. (20) shows:

$$\begin{cases} \left| {\overrightarrow {N} } \right| = \sqrt {\overrightarrow {X}^{2} + \overrightarrow {Y}^{2} } \hfill \\ \tau = \arctan \frac{{\left| {\overrightarrow {X} } \right|}}{{\left| {\overrightarrow {Y} } \right|}} \hfill \\ \end{cases}$$
(20)

After extracting the sub-pixel edge point coordinates, translate it to the center point coordinate system (multiply by the translation matrix Mτ) to obtain the sub-pixel edge point coordinates in the tool center point coordinate system, and then by calculating the actual length between the two pixels, the actual profile point coordinates of the spiral groove end section are calculated.

After extracting the coordinates of the spiral groove’s profile point, it needs to be fitted. The curve fitting function of cftool in MATLAB software is used. The specific appropriate steps are shown in Fig. 7.

Fig. 7
figure 7

Based on MATLAB curve fitting steps

Full size image

4 Experimental verification

Based on the research on the model and process of the reverse calculation of the grinding wheel wear profile, the experimental method is used to verify the algorithm’s accuracy and practicability.

The experimental material is a cemented carbide rod. Cemented carbide materials have high hardness and are powder metallurgical products made by sintering micron powders of refractory metal compounds (mainly WC and TIC) with metals such as cobalt and nickel as a binder. The hardness of WC and TIC solid cemented carbide is much higher than that of high-speed steel, reaching HRA89-93. Within a certain temperature range, some solid cemented carbides have the same hardness as high-speed steel at room temperature, so their heat resistance is better. The grinding wheel used in the experiment is a 1A1 flat grinding wheel with a radius of 75 mm and a thickness of 5 mm. The initial installation position X and Y coordinates of the center point of the grinding wheel and the swing angle B of the grinding wheel are respectively (− 10.005, 73.223) and 35.313°, and the grinding diameter is 10 mm. Four-edged solid end mill spiral groove with a blade length of 20 mm and a helix angle of 30° and use an ultra-depth-of-field microscope to collect the end cross-sectional profile of the solid end mill ground by a worn grinding wheel, as shown in Fig. 5. The image processing method described in Sect. 3 is used to preprocess the profile image of the spiral groove end of the solid end mill and perform edge detection, as shown in Fig. 8.

Fig. 8
figure 8

Spiral groove end section profile edge detection

Full size image

Use MATLAB to fit the extracted spiral groove edge points into an equation. The equation is as shown in Eq. (21). Substituting this equation into the contact equation between the grinding wheel and the spiral groove, the spiral groove ground by the worn grinding wheel can be calculated contact line.

$$\left\{ {\begin{array}{*{20}c} {f(x_{1} ) = x} \\ {f(x_{2} ) = 13.04x^{3} - 10.88x^{2} + 22.82x + 362.5} \\ \end{array} } \right.$$
(21)

The point on the spiral groove contour curve corresponding to any contact point on the contact line of the spiral groove grinding by the unworn grinding wheel, and the rotation angle of this point can be obtained. According to the previous research on the rotation angle’s numerical solution, the rotation angle required for the spiral groove ground by the unworn grinding wheel provides a value range for the rotation angle required by the worn grinding wheel to grind the spiral groove. The contact line of the spiral groove ground by the worn grinding wheel obtained by calculation is shown in Fig. 9.

Fig. 9
figure 9

Diagram of contact curve

Full size image

Convert the contact line obtained by calculation to the grinding wheel coordinate system, and the sand profile after wear is shown in Fig. 10. Table 1 shows the coordinates of the contour points of part of the spiral groove section.

Fig. 10
figure 10

Grinding wheel wear profile

Full size image
Table 1 Coordinates of some points in the profile of spiral groove end
Full size table

The wear sand profile is transferred to the graphite sheet for comparison. The experimental process is shown in Fig. 11. The wear sand profile calculated by the algorithm is compared with the sand profile obtained by the replica method [21] to verify the algorithm’s accuracy.

Fig. 11
figure 11

The experimental procedure of reworking

Full size image

The contour of the worn sand obtained by the reconstruction method was sampled, and its contour points were extracted. The results are shown in Fig. 12. Through processing, it was verified that a circular arc notch appeared on the edge of the worn grinding wheel, and the radius of the circular arc notch was 0.2 mm.

Fig. 12
figure 12

The grinding wheel profile is worn by copying

Full size image

The installation position and posture of the grinding wheel and the workpiece are shown in Fig. 13a, where the center point coordinates of the grinding wheel \(\left({\text{a}_\text{x}}, \text{a}_\text{y}, \text{a}_{\text{z}}\right)\) and the swing angle λ of the grinding wheel jointly control the position and posture of the grinding wheel. The B-B section in the figure represents the unworn sand profile model. The worn sand profile obtained by the re-engraving method and the worn sand profile calculated by the algorithm are integrated into the \({\text{X}}_{\text{w}}{{\text{Y}}}_{\text{w}}\) plane for comparison and analysis. The results are shown in Fig. 13b.

Fig. 13
figure 13

Sand profile. a Unworn grinding wheel model. b Grinding wheel profile contrast diagram

Full size image

It can be seen from Fig. 13b that the sand profile obtained by the re-engraving experiment is consistent with the sand profile calculated by the algorithm, which means that the accuracy of the inverse algorithm for the grinding wheel wear profile can be guaranteed. Form comparison can also obtain the amount of wear of the grinding wheel, so the algorithm can also meet actual production needs requirements. However, the contour of the worn sand calculated by the algorithm cannot wholly coincide with the worn sand’s contour obtained by the re-engraving method at the grinding wheel’s front surface. When the radius of the grinding wheel reaches 74.80 mm, the arc-shaped gap begins to appear. Because the front face of the worn grinding wheel does not participate in the grinding of the spiral groove, this is why the contour of the worn sand is missing at the corresponding position through calculation.

When the grinding wheel reaches a certain degree of wear, it can no longer be used. Use the detection method shown in Fig. 14 to determine the wear state of the grinding wheel. There are three different-colored lines in the figure. The blue represents the theoretical contour of the workpiece, and the error range between the green line and the red line is the error range ε; when the contour of the workpiece falls within ε, the workpiece size is considered qualified, and the grinding wheel has no error or small error acceptable and can continue to be used; when the contour of the workpiece is higher than the red line, the workpiece is considered unqualified, and the grinding wheel is severely worn, and the grinding wheel should be replaced or compensated immediately; when the contour of the workpiece is below the green line, it indicates that the initial installation position of the grinding wheel is wrong, and it is necessary adjustment.

Fig. 14
figure 14

Test method for grinding wheel wear state

Full size image

5 Conclusions

To meet the actual demand for solving the contour of the worn sand, this paper researches the inverse calculation of the grinding wheel’s wear profile, the extraction and fitting of the point coordinates of the spiral groove end section profile, and the experimental verification. The conclusions obtained are as follows:

  1. 1.

    Based on the contact line principle, the contact equation between the surface of the grinding wheel and the surface of the spiral groove is established. According to this contact equation’s characteristics, a numerical solution to the unknown parameter of the equation, the rotation angle vp is proposed, and the calculation process of the algorithm is described.

  2. 2.

    Using image processing technology, complete the collection and edge detection of the spiral groove end section’s profile image and fit the edge points of the spiral groove end section into an equation.

  3. 3.

    The traditional re-engraving method is used to verify the grinding wheel wear profile reverse algorithm. The experiment shows that the sand profile obtained by the re-engraving experiment is consistent with the algorithm’s sand profile, which means that the grinding wheel wears. The accuracy of the reverse contour algorithm is guaranteed, and the detection method of the grinding wheel wear state is determined.

In this paper, the limitations of the method of grinding wheel wear are mainly reflected in two points:

  1. 1.

    This algorithm is only suitable for the detection of the wear of flat grinding wheels and disc-shaped grinding wheels.

  2. 2.

    Using the algorithm in this paper to solve the wear of the grinding wheel can achieve in situ detection, that is, without disassembling the grinding wheel, but it still cannot be detected on the machine, and it takes some process to calculate the specific grinding wheel wear.