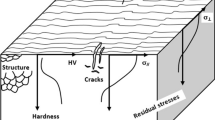
Abstract
Fatigue is one of the main reasons for the failure of structural components. In practical engineering, machined surface integrity, including geometrical parameters, mechanical parameters, and metallurgical parameters significantly influence the fatigue life of structural parts. However, due to the unclear correlations of these parameters, there is no fatigue life prediction model that takes all three kinds of surface integrity parameters into account. In this paper, a framework for fatigue life prediction model is proposed in which the effect mechanisms of geometrical, mechanical, and metallurgical parameters to fatigue life were distinguished. Then, the practical model based on the proposed framework was established using specified integrity parameters: stress concentration factor (SCF), surface residual stress, and work hardening effect related metallurgical parameter. The prediction accuracy of the proposed model is compared to those of other models with 5 experimental data sets; the results show that better average prediction accuracy is achieved by the proposed model.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Fatigue is one of the main reasons for the failure of structural components. In practical engineering, the fatigue performance of structural parts is affected by the surface integrity of the machined parts, which can cause the fatigue lives of different parts to vary by even an order of magnitude [1]. The surface integrity of machined parts can be significantly modified by the machining process [2], which can be described by 3 groups of parameters: geometrical parameters (surface morphology), mechanical parameters (residual stresses), and metallurgical parameters (the microstructure and microhardness) [3].
Many researchers have investigated the surface integrity of machined parts and its effect on fatigue life. Researchers found that the arithmetic average roughness Ra has a remarkable effect on fatigue life [4,5,6]. The effect of roughness on fatigue life decreases with decreasing roughness. When the roughness is less than a certain value, the experimental results show that roughness has no effect on fatigue life [7]. Researchers also found that Ra is not the best parameter with which to describe the roughness effect on fatigue life. The parameter that describes the maximum height or the average slope of the profile more significantly influences the fatigue life of machined parts [2]. However, the fatigue life of machined surfaces with identical roughness may be different [8]. The influence of residual stress on fatigue life has been studied for many years and continues to attract researchers’ attention [3, 9, 10]. Generally, compressive residual stress is beneficial to the fatigue life of parts, while tensile residual stress is harmful. As the surface roughness decreases, the influence of residual stress becomes dominant [11]. Some studies have also focused on the influence of metallurgical aspects on fatigue life. The cold work hardening effect can retard crack nucleation [12] and prevent dislocation lines or microcracks from extending to the surface [13]. It was found that a higher hardness will reduce the fatigue life under the strain-life regime and increase the fatigue life under the stress-life regime [14, 15]. Many researchers have also measured all three kinds of surface integrity parameters and conducted fatigue tests on these specimens [16,17,18].
The experimental studies show the influence of surface integrity parameters on fatigue performance and make corresponding conjectures on its influence mechanism. Based on these observations and corresponding conjectures, some mathematical relationships between machined surface integrity and fatigue life were established. The first category of parameters that researchers adopted to model the fatigue life was geometrical parameters. First, scholars used roughness parameters to model the fatigue performance of parts [7, 19]. However, it was found that establishing a mechanical relation between surface roughness parameters and fatigue behavior is challenging. Then, Murakami proposed a method that correlates the machined surface geometry to the fatigue strength using a parameter called the defect area [20]. He modeled the relationship by correlating the defect area with the stress intensity factor (SIF). Researchers also use SIF of the internal and surface defects to investigate the different fatigue initiation sites in the fatigue test of additive manufactured 316L stainless steel [21]. Later, Arola and Williams [22, 23] presented research on the stress concentration factor (SCF) of machined surfaces. It was noted that the relationship between surface topography and fatigue life could be reflected by SCF [24, 25]. The two methods mentioned above have linked the surface geometry to the local stress state; however, there are still some empirical parameters used in these methods. Some researchers have used the finite element method to investigate the geometric influence on the local stress state [26,27,28]. However, due to the complexity of the surface geometry, very small geometric features were distributed on the surface to reflect the measured surface morphology. These features resulted in difficulties in the FEM analysis of the machined surface. Therefore, researchers have ignored the small features measured on the surface [26, 27, 29] according to the finding that defects smaller than a typical size did not affect the fatigue behavior of parts [20]. Some analytical methods have also been proposed to calculate the stress field of a rough surface geometry [30]. In the modeling of fatigue life, residual stress is normally seen as uniformly distributed on the machined surface and is thought to be a part of the real stress in the fatigue test [31, 32]. For HCFs, the residual stress relaxation was slow [1]; thus, it was seen as influencing the fatigue behavior by the mean stress effect [33, 34]. Some researchers have also investigated the residual stress influence on the crack growth stage [35]. Hardness was the most commonly used parameter to predict the fatigue life of metals. The ultimate tensile stress and fatigue limit were found to have an approximately linear relation to hardness. Based on these findings, some fatigue life prediction models were proposed [14], and Murakami extended his model to include the effect of hardness [20]. The influence of residual stress and microhardness on the fatigue limit of specimens with small surface defects was also proved by Fernández-Pariente et al. [36].
Although several models have been proposed to characterize the influence of surface integrity on fatigue life, there are still some questions on the reliability of these models. One of the most important issues is that none of the proposed models considered all of the above-mentioned integrity parameters. The reason for these issues may result from the limited data in their studies, giving the impression that the fatigue life is mainly influenced by only one of these kinds of parameters. Another reason may be that the influences of these parameters were difficult to distinguish. For example, shot-peening is often used to enhance the fatigue performance of parts. However, it is difficult to distinguish between the contributions of shot-peening-induced residual compressive stress and work hardening.
In this paper, a method to predict fatigue life is proposed based on the effects of geometrical, mechanical, and metallurgical parameters. This paper is organized as follows. In the next section, three kinds of previous fatigue life prediction models based on surface integrity parameters are introduced, and a new model is proposed. Then, the method to calculate SCF in this paper is introduced in the 3rd section. Comparisons between the proposed fatigue life prediction model and previously proposed models are described in the Sect. 4. Finally, the closing remarks are given in the final section.
2 Fatigue life prediction models based on surface integrity parameters
The stress-based approach was the earliest proposed approach for fatigue life prediction and is still the most frequently used. In this approach, the fatigue life (number of cycles \({N_f}\)) is related to the applied stress range or the stress amplitude. As mentioned above, the surface integrity, including the geometrical, mechanical, and metallurgical parameters, has been shown to have a significant effect on fatigue behavior. To predict the fatigue life based on surface integrity parameters, a general form can be expressed by Eq. (1) according to the Basquin-type power law [37]:
where \(\sigma_{eqv}\) denotes the equivalent stress; \(\sigma_l\) denotes the crack initiation threshold or fatigue limit; \({\mathbf{p}}\) denotes the surface integrity parameters; \(k\) denotes the exponent of stresses in the formula of S-N curve; and \(\sigma_f\) and \(c\) are material constants called the fatigue strength coefficient and fatigue strength exponent, respectively. Equation (1) shows that the fatigue life tends to be infinite when \(\sigma_{eqv} - \sigma_l \leq 0\). This is because no cyclic local plastic strain is induced at the machined surface, even in isolated grains beneath the machined surface, and consequently, a crack is not initiated at the machined surface.
In this paper, all the models are based on the stress-based approach. Sects. 2.1–2.2 shows the approaches to consider machined surface properties according to the previous and proposed models. Sect. 2.3 shows the relations and differences of these 4 models. Moreover, the complete form of fatigue life prediction models was not given in Sects. 2.1 to ensure the conciseness of the article. Instead, the complete form of these models can be derived from Table 1 and Eq. (1).
2.1 Previous model
2.1.1 Murakami model
Murakami studied the influence of surface integrity on the fatigue limit \(\sigma_l\). Two basic quantities, Vickers hardness and defect area \(area\), were used to predict the fatigue limit. Considering single defect cases, \(area\) was defined as the area obtained by projecting a small defect or crack onto a plane perpendicular to the maximum principal stress. The relation between these two quantities to the fatigue limit is shown in Eq. (2) [20]:
where H denotes the metallurgical parameter, which is directly related to the work hardening effect, for example, hardness and chord width [3], and \(\alpha\) and \(\beta\) denote material constants.
However, the influences caused by a single defect and periodical defects are different due to the interference effect between successive notches on the stress field. Therefore, Murakami proposed a method that integrated the groove depth \(a\) and pitch \(2b\) into one parameter \(are{a_R}\), which was then used to replace the parameter of defect area in Eq. (2). For periodic shallow grooves, \(are{a_R}\) is given by the following equation [20]:
where \(F\left( {{a \mathord{\left/ {\vphantom {a {2b}}} \right. \kern-\nulldelimiterspace} {2b}}} \right)\) is a geometric correction factor. The graphic illustration of groove depth \(a\) and pitch \(2b\) are shown in Fig. 1 with the value of this geometric correction factor.
a Illustration of surface defects with a succession of grooves, b function value of F [20]
2.1.2 SCF-based model
SCF is often used to determine the effect of macroscopic geometric discontinuities (notches) on the strength of engineering components. Machined surface morphology, which includes a series of peaks and valleys, was treated as continuously distributed notches. Thus, the influence of surface morphology was investigated by the SCF of these continuously distributed notches [22,23,24,25,26,27,28,29,30]. In these studies, the machined surface morphology measured in the direction parallel to the maximum principal stress was often used to calculate the SCF. Researchers who modeled fatigue life via SCF believe that the real equivalent stress \(\sigma_{eqv}\) equals the product of SCF and the nominal equivalent stress [25,26,27]. Using the model proposed by Xiong, the real equivalent stress derived from SCF is as follows [25]:
where \({K_t}\) denotes the SCF of the machined part, \({\sigma_{max,nom}}\) denotes the maximum nominal stress during the fatigue test, and \(R\) denotes the stress ratio during a fatigue test and is equal to \({\sigma_{min,nom}}\) divided by \({\sigma_{max,nom}}\). Zheng’s model of fatigue life prediction [38] was adopted in this SCF-based model. The exponent coefficients \(k\) and \(c\) were derived as \({2 \mathord{\left/ {\vphantom {2 {\left( {1 + n} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 + n} \right)}}\) and \(- 0.5\), respectively. The coefficient \(n\) denotes the strain hardening exponent in the original paper [38] and is obtained by the regression analysis of the fatigue life test data in this SCF-based model [25].
2.1.3 Residual-stress-based model
Some researchers have focused on the influence of residual stress. Residual-stress-based models have been proposed to predict fatigue life [3, 31]. The residual stress was uniformly distributed on the machined surface and was superimposed onto the nominal stress to obtain the real stresses. Moussaoui et al. [3] used maximum stress to predict fatigue life:
2.2 Proposed framework and model
The previous subsections introduced three kinds of prediction models based on surface integrity parameters. However, although these three kinds of surface integrity parameters have a significant influence on fatigue life, there was no prediction model that took all three kinds of integrity parameters (i.e., the geometrical, mechanical, and metallurgical parameters) into consideration. The reason for this problem may result from the limited amount of experimental data considered in their studies, giving the impression that the fatigue life is mainly influenced by only one of these kinds of parameters. Another reason may be that the influences of these parameters were difficult to distinguish. For example, shot-peening is often used to enhance the fatigue performance of parts; however, it is difficult to distinguish between the contributions of residual compressive stress and work hardening.
In this study, to avoid the problems mentioned above, a total of 5 data sets collected with different materials or different machining methods are used to ensure the reliability of the proposed model. As shown in Eq. (1), the fatigue life is determined by the equivalent stress and fatigue stress. The surface morphology leads to the stress concentration effect. The surface mechanical parameters determine the initial stress field of the machining-influenced layer. In addition, metallurgical parameters such as hardness, grain size, and dislocation density do not affect the elastic modulus of metal materials. Thus, the equivalent stress is only determined by the geometric and mechanical parameters. Additionally, the surface geometrical parameters and mechanical parameters only affect the stress field of the machining-influenced layer, which means that these parameters have no effect on the fatigue limit. The metallurgical parameters affect the flow stress. No plastic deformation can be accumulated to form a crack if the actual stress is lower than the flow stress. Thus, metallurgical parameters can affect the fatigue limit. Accordingly, a framework for the fatigue life prediction model is derived:
where \({{\mathbf{p}}_{{\mathbf{geom}}}}\), \({{\mathbf{p}}_{{\mathbf{mech}}}}\), and \({{\mathbf{p}}_{{\mathbf{meta}}}}\) are the geometric, mechanical, and metallurgical parameters, respectively.
Then, a practical model that carefully chooses the SCF, surface residual stress, and the parameter that is directly related to the work hardening effect is established to specify the fatigue life prediction model. The reasons chosen these parameters are as follows: The maximum local stress during cyclic loading occurs on the volume of material within the depth of penetration of the X-rays [3]. Due to the limitation of residual stress measurement techniques, the residual stress fields within the volume of material within the depth of penetration of the X-rays are not capable to obtain. Thus, for the practicality of the proposed model, the residual stress on the machined surface and within the depth of penetration of the X-rays is assumed to be uniform. In addition, as the stress concentration effect could occur near the valleys of machined surface morphology, the maximum local stress during cyclic loading occurs near the valleys of machined surface morphology (grooves). In the proposed model, an element near a valley of the surface morphology is investigated as shown in Fig. 2. According to the hypothesis that the residual stress on the machined surface and within the depth of penetration of the X-rays is uniform, the value of residual stress near the grooves is seen equal to the measured value of surface residual stress. Moreover, the stress concentration effect is depicted by SCF. Thus, the stress state of the element can be derived by SCF and surface residual stress. And, the fatigue limit of metal material can be estimated by work-hardening corresponded parameters [20]. Then, a fatigue life prediction model is derived as follows:
where \({\sigma_{ar}}\) denotes an equivalent fully reversed stress amplitude that leads to the same fatigue life under the combination of SCF and residual stress; \({\sigma_{lr}}\) denotes the fatigue limit under fully reversed stress conditions; and \(H\) denotes the metallurgical parameter, which corresponds to the work hardening tendency (specifically, the hardness, or chord width used in [3]).
The ratio of the local stress and loading stress induced by the external load is defined as SCF. Therefore, the local stress state at the valley of the surface morphology is derived as follows:
where \({\sigma_{min}}\) is the minimum local stress at the surface valley, \({\sigma_{max}}\) is the maximum local stress at the surface valley, \({\sigma_{min,nom}}\) is the minimum nominal stress, and \({\sigma_{max,nom}}\) is the maximum nominal stress.
Equation (8) shows the consideration of geometrical parameters and mechanical parameters. In other words, these two kinds of parameters are modeled to influence the maximum stress and minimum stress at a valley of the surface morphology. Then, a correction step is conducted to consider the mean stress effect. Notably, there are many correction methods to model the mean stress effect on the equivalent fully reversed stress amplitude [33]. Smith’s method is chosen in this study, as follows:
where \({\sigma_m}\) is the local mean stress and \({\sigma_a}\) is the local stress amplitude. These two values can be derived from Eq. (10):
As shown in Eq. (10), we can see that the local stress amplitude was affected by only the geometrical parameters. Therefore, the effect of residual stress on fatigue life is determined by the mean stress effect.
The microscopic effect of work hardening on the fatigue limit is difficult to determine. The widely used parameters to define the work hardening degree are microhardness and chord width [3]. Meanwhile, the work hardening degree is also related to the tensile properties and fatigue strength [20] of metal parts and is approximately linearly dependent over a wide range. Thus, the relation between the work hardening parameters and fully reversed fatigue limit can be approximated as follows:
Substituting Eq. (11) into Eq. (7), the following relation between the surface integrity parameters and fatigue life can be derived:
2.3 Relations and differences of these 4 models
These three fatigue life prediction models were all defined by Eq. (1). The definition of each term is listed in Table 1. As shown in Table 1, all these 4 models are based on the stress-based approach. The proposed model is able to consider all of these three properties which were seen as crucial to the fatigue behavior of machined parts, while previous models are not. The consideration of machined surface morphology is different as well. Murakami considers the effect of machined surface morphology by correcting the fatigue limit, while the SCF-based and the proposed model corrected the loading stress.
3 Calculation of SCF (Kt)
In the proposed model, the mechanical parameter (residual stress) and metallurgical parameter (microhardness or chord width) are directly obtained by standard tests. However, the method to determine the geometrical parameter SCF is still controversial.
Arola’s method is the most commonly used method to calculate SCF [22, 23]. However, the determination principle for its critical parameter \(\bar \rho\) was unclear. The measurement of radius at the bottom of the defect \(\bar \rho\) at local or global scales leads to a remarkable difference in SCF values [27]. Defects whose depths were below a certain value were observed to have no influence on the fatigue behavior of machined parts. Therefore, the very local grooves can be ignored in the calculation of SCF. Thus, the smoothed profile was used to calculate the SCF values of the machined surface [26,27,28,29, 39].
A parameter called the lower limit of defect depth \(c_{min}\) was proposed to determine the critical groove size under which the groove size would have no influence on the fatigue behavior of machined parts [29, 40].
In this article, steel materials, nickel-based alloys, and titanium alloys were investigated. Because the hardness of these materials ranged from 200 to 400 Hv, the lower limit of the defect depth \(c_{min}\) ranged from 2.7 to 0.78 μm. Because the surface roughness caused by the fine grinding process was within 0.7 μm [19], the influence of surface morphology caused by the fine grinding process on fatigue life was negligible if no other surface defects existed. In other words, the SCF of a finely ground surface equals 1 in the proposed model. Similarly, the SCF of turned or milled surfaces can be calculated according to the smoothed roughness profile, which can be estimated as the theoretical roughness profile. The theoretical roughness profiles of the turned surface and milled surface along the loading direction are shown in Fig. 3. It is worth mentioning that the predicted profiles of the machined surface are related to the geometry of the machining tools and processing parameters.
The theoretical roughness profile used to calculate SCF (a turning/end milling [41]; b peripheral milling)
Although many SCF calculation methods based on the arithmetical operation of measured profile data have been used to calculate the SCF, the FEM method has always been used to validate its accuracy. In other words, FEM methods can be used to perform a more accurate calculation than possible with arithmetic methods. In this study, we do not focus on the quick calculation method to determine the SCF values. Thus, the FEM method is used to determine the SCF values.
In this 2D FEM model, the material behavior is set to be linear elastic and follows the plane strain hypothesis. Quadrilateral elements with linear interpolation are adopted. The mesh size is refined according to the curvature of the machined profile, as shown in Fig. 4a. The meshes in all FEM calculation pass the convergence analysis, as shown in Fig. 4b. A fixed support and uniform load are set as boundary conditions on the two sides of this FEM model. The maximum von Mises equivalent stress is derived from the calculation of this model. The SCF is derived by dividing the maximal von Mises equivalent stress by the nominal von Mises equivalent stress, as shown in Fig. 5.
4 Model validation and comparison
In this section, the proposed model is assessed with experimental data sets from Javidi et al. [42], Sasahara [9], Yang [16], Moussaoui et al. [32], and Li et al. [18]. These articles recorded residual stresses, work hardening parameters, and fatigue life of machined specimens. Also, machining process parameters and necessary tool geometry parameters were recorded, by which the theoretical roughness profile can be derived. Then, the SCF is calculated through FEM according to the method described in Sect. 3. In addition, particular attention is focused on the coverage and completeness of data sets selected for model verification, which ranges from 103 to 107 cycles of fatigue life and contains both turned, milled, and grounded surfaces.
To avoid numeric overflow in the regression process, Eq. (13) is transformed to a logarithmic form as Eq. (14). The regression results of the proposed model coefficients for the 5 data sets are listed in Table 2.
The predicted fatigue life and tested fatigue life are compared in Figs. 6 and 7. To quantify the difference between the predicted and experimental fatigue life, a parameter called the model prediction error, PE, is used. The value of PE is calculated by Eq. (15). In Figs. 6 and 7, the dashed lines indicate that the PE equals ± 0.3 or ± 0.5.
Fatigue life predicted by the proposed model versus tested lives of data sets (LiTI represents the fatigue life data of Ti6Al4V [18])
where \({N_{predict}}\) denotes the fatigue life predicted by the proposed model and \({N_{test}}\) denotes the experimental fatigue life. The fatigue life is underestimated when PE is negative and overestimated when PE is positive. To quantitatively distinguish the prediction ability of these four models, a probability analysis of model PE is carried out. A Shapiro-Wilk test is conducted on the PE values to distinguish the prediction capabilities of these prediction models. The null hypothesis of this test is that the PE values followed a normal distribution. The test results are shown in Table 3. The p value shows the reliability of the hypothesis. Therefore, a model with a higher p value means that the PE of the model was more likely to be the random error produced by the limitation of the testing technology. Meanwhile, lower mean and standard deviation (SD) values correspond to higher prediction accuracy.
For the proposed model, as seen from Fig. 6, all the PE values are within ± 0.3 when the experimental fatigue life is fewer than 105.5 cycles and within ± 0.5 when the experimental fatigue life is more than 105.5 cycles. Setting the significance level as 0.05, the hypothesis is retained for all cases, which means that all PEs can be regarded as random errors [43]. More specifically, as seen in Fig. 8, the proposed model provides comparable or better accuracy in almost all cases compared with the SCF-based model and residual-stress-based model. With the Javidi and Yang data sets, the prediction accuracy of the proposed model is lower than that of Murakami’s model. However, the averaged prediction accuracy of the proposed model in these 5 data sets was better than that of Murakami’s model. In addition, according to Table 3, the hypothesis of normality of the PE of Murakami’s model is rejected. It means that the model may have deficiencies in principle, which leads to the PE not obeying the normal distribution. Figure 6 and Table 3 highlight that the proposed model can be applied to predicting fatigue life under the complex state of the machined surface. Considering the overall performance of each model mentioned above, the proposed model predictions are better than others, suggesting that the proposed model provides a good choice for fatigue life prediction under the consideration of surface integrity parameters. The main reasons behind the improvement in accuracy with the proposed method were as follows: All of the other models ignored the effect of at least one kind of integrity parameter. However, all kinds of parameters are influential to the fatigue life of machined parts. Thus, by taking into account all of these three kinds of integrity parameters, the applicability and accuracy of the proposed model are improved compared with other models.
For the Murakami model, as seen from Figs. 7a and 8, most PEs are within 0.5, while the PEs of some data points in the Hiroyuki and Moussaoui data sets exceeded an absolute value of 0.5. More specifically, the Murakami model provides better or similar accuracy in all cases compared with the SCF-based model. This phenomenon shows that considering the work hardening effect in fatigue life, modeling was beneficial to prediction accuracy.
5 Conclusions
The main conclusions of this work can be presented as follows:
-
1.
A prediction model based on surface integrity parameters is proposed. In this model, fatigue life is predicted based on a surface geometrical parameter (SCF), a surface mechanical parameter (residual stress), and a surface metallurgical parameter (hardness or chord width). Four independent coefficients are used in this model. The proposed model prediction accuracy is verified with 5 experimental data sets.
-
2.
The comparison between the proposed model and previous models in the literature indicates that more accurate predictions can be achieved by the proposed model. Meanwhile, the highest p value of the proposed model indicates that the PE of this model is more likely to be the random error produced by the limitation of the testing technology.
-
3.
It is worth mentioning that this model can only be used to predict the fatigue life of specimens after the material removal process (such as turning, milling, grinding) if the model does not undergo any modification. For example, specimens that undergo the surface strengthening process may have a maximum compressive residual stress happened in the sub-surface layers. Significant compressive stresses in the sub-surface layer may delay crack propagation and thus increase fatigue life. A possible way to apply the proposed model to predict the fatigue life of the specimens that undergo the surface strengthening process is to replace the surface residual stress term with the average of surface residual stress and maximum compressive residual stress.
The prospect of this work:
-
1.
In order to predict the reliability of critical parts such as turbine disks, this method requires further development to a probabilistic form [44] to accurately reflect the influence of the size effect.
-
2.
As there was no other prediction model of fatigue life that totally considered the effect of surface morphology, residual stress, and work hardening, which are the main parameters of machining integrity, this model can provide a reference for the research of anti-fatigue mechanical processing technology.
Abbreviations
- \(area\) :
-
Area obtained by projecting a small defect or crack onto a plane perpendicular to the maximum principal stress
- \({area}_{R}\) :
-
Equivalent \(area\) in the case of successive notches
- a, b :
-
Depth and half pitch of successive notches
- \({c}_{min}\) :
-
Lower limit of defect depth
- \({c}^{'},\;{\sigma }_{f},\;{\sigma }_{f}^{'}\) :
-
Material constants described the relation of equivalent stress to fatigue life
- H :
-
Metallurgical parameter that directly relates to the work hardening effect
- Hv :
-
Vickers hardness
- k :
-
Exponent of stresses in the formula of S-N curve;
- K t :
-
Stress concentration factor
- n :
-
Strain hardening exponent
- \({N}_{predict},\;{N}_{test}\) :
-
Predicted and tested fatigue life
- P :
-
Surface integrity parameters
- \({\mathbf{P}}_{\mathbf{g}\mathbf{e}\mathbf{o}\mathbf{m}},\;{\mathbf{P}}_{\mathbf{m}\mathbf{e}\mathbf{c}\mathbf{h}},\;{\mathbf{P}}_{\mathbf{m}\mathbf{e}\mathbf{t}\mathbf{a}}\) :
-
Geometric, mechanical, and metallurgical parameters
- PE :
-
Prediction error of logarithmic fatigue life
- R :
-
Stress ratio
- a, β :
-
Material constants showed the influence of work hardening to fatigue limit
- \({\sigma }_{a}\) :
-
Local stress amplitude
- \({\sigma }_{ar}\) :
-
Equivalent fully reversed stress amplitude
- \({\sigma }_{m}\) :
-
Local mean stress
- \({\sigma }_{max}, \;{\sigma }_{min}, \;{\sigma }_{eqv}\) :
-
Local maximum, minimum, and equivalent stress
- \({\sigma }_{*,nom}\) :
-
Maximum, minimum, and equivalent nominal stress
- \({\sigma }_{l}\) :
-
Fatigue limit
- \({\sigma }_{lr}\) :
-
Fatigue limit under fully reversed stress conditions
- \({\sigma }_{rs}\) :
-
Residual stress
References
Withers P (2007) Residual stress and its role in failure. Rep Prog Phys 70(12):2211. https://doi.org/10.1088/0034-4885/70/12/R04
Davim J (2010) Surface integrity in machining. Springer, London
Moussaoui K, Mousseigne M, Senatore J, Chieragatti R (2015) The effect of roughness and residual stresses on fatigue life time of an alloy of titanium. Int J Adv Manuf Tech 78(1–4):557–563. https://doi.org/10.1007/s00170-014-6596-7
Yao C, Ma L, Du Y, Ren J, Zhang D (2017) Surface integrity and fatigue behavior in shot-peening for high-speed milled 7055 aluminum alloy. Proc Inst Mech Eng B J Eng 231(2):243–256. https://doi.org/10.1177/0954405415573704
Wang J, Zhang Y, Sun Q, Liu S, Shi B, Lu H (2017) Giga-fatigue life prediction of FV520B-I with surface roughness. Mater Design 89:1028–1034. https://doi.org/10.1016/j.matdes.2015.10.104
Li C, Dai W, Duan F, Zhang Y, He D (2017) Fatigue life estimation of medium-carbon steel with different surface roughness. Appl Sci-Basel 7(4):338. https://doi.org/10.3390/app7040338
Novovic D, Dewes R, Aspinwall D, Voice W, Bowen P (2004) The effect of machined topography and integrity on fatigue life. Int J Mach Tool Manu 44(2–3):125–134. https://doi.org/10.1016/j.ijmachtools.2003.10.018
Warren A, Guo Y (2010) The impact of surface integrity by hard turning versus grinding on rolling contact fatigue-Part I: Comparison of fatigue life and acoustic emission signals. Fatigue Fract Eng M 30(8):698–711. https://doi.org/10.1111/j.1460-2695.2007.01144.x
Sasahara H (2005) The effect on fatigue life of residual stress and surface hardness resulting from different cutting conditions of 0.45% C steel. Int J Mach Tool Manu 45.2:131–136. https://doi.org/10.1016/j.ijmachtools.2004.08.002
Yao C, Tan L, Ren J, Lin Q, Liang Y (2014) Surface integrity and fatigue behavior for high-speed milling Ti–10V–2Fe–3Al titanium alloy. J Fail Anal Prevent 14.1:102–112. https://doi.org/10.1007/s11668-013-9772-4
Koster W (1991) Effect of residual stress on fatigue of structural alloys. Proc 3rd Int Conf ASM Int 1–9
Burlat M, Julien D, Levesque M, Bui-Quoc T, Bernard M (2008) Effect of local cold working on the fatigue life of 7475–T7351 aluminium alloy hole specimens. Eng Fract Mech 75(8):2042–2061. https://doi.org/10.1016/j.engfracmech.2007.10.011
Josefson B, Stigh U, Hjelm H (1995) A nonlinear kinematic hardening model for elastoplastic deformations in grey cast iron. J Eng Mater-T ASME 117(2):145–150. https://doi.org/10.1115/1.2804521
Shamsaei N, Fatemi A (2009) Effect of hardness on multiaxial fatigue behaviour and some simple approximations for steels. Fatigue Fract Eng M 32(8):631–646. https://doi.org/10.1111/j.1460-2695.2009.01369.x
Roessle M, Fatemi A (2000) Strain-controlled fatigue properties of steels and some simple approximations. Int J Fatigue 22(6):495–511. https://doi.org/10.1016/S0142-1123(00)00026-8
Yang D (2017) Milling induced surface integrity and its effects on fatigue life of the titanium alloy TI6AL4V. Dissertation, Shandong University
Li X, Zhao P, Niu Y, Guan C (2017) Influence of finish milling parameters on machined surface integrity and fatigue behavior of Ti1023 workpiece. Int J Adv Manuf Tech 91(1–4):1297–1307. https://doi.org/10.1007/s00170-016-9818-3
Li X, Wang Y, Xu R, Yang S, Guan C, Zhou Y (2019) Influence of surface integrity on fatigue behavior of Inconel 718 and Ti6Al4V workpieces with CBN electroplated wheel.Int J Adv Manuf Tech 102(5–8):2345–2356. https://doi.org/10.1007/s00170-019-03345-6
Xiao W, Chen H, Yin Y (2013) Effects of surface roughness on the fatigue life of alloy steel. Key Eng Mater 525:417–420. https://doi.org/10.4028/www.scientific.net/KEM.525-526.417
Murakami Y (2019) Metal fatigue: effects of small defects and nonmetallic inclusions. Academic Press, London
Solberg K, Guan S, Razavi S, Welo T, Chan K, Berto F (2019) Fatigue of additively manufactured 316L stainless steel: the influence of porosity and surface roughness. Fatigue Fract Eng M 42(9):2043–2052. https://doi.org/10.1111/ffe.13077
Arola D, Williams C (2002) Estimating the fatigue stress concentration factor of machined surfaces. Int J Fatigue 24(9):923–930. https://doi.org/10.1016/S0142-1123(02)00012-9
Arola D, Ramulu M (1999) An examination of the effects from surface texture on the strength of fiber reinforced plastics. J Compos Mater 33(2):102–123. https://doi.org/10.1177/002199839903300201
Yao C, Wu D, Jin Q, Huang X, Ren J, Zhang D (2013) Influence of high-speed milling parameter on 3D surface topography and fatigue behavior of TB6 titanium alloy. Trans Nonferr Metal Soc 3:650–660. https://doi.org/10.1016/S1003-6326(13)62512-1
Xiong Y, Wang W, Shi Y, Jiang R, Lin K, Liu X (2020) Fatigue behavior of in-situ TiB2/7050Al metal matrix composites: Fracture mechanisms and fatigue life modeling after milling. Int J Fatigue 138:105698. https://doi.org/10.1016/j.ijfatigue.2020.105698
Suraratchai M, Limido J, Mabru C, Chieragatti R (2008) Modelling the influence of machined surface roughness on the fatigue life of aluminium alloy. Int J Fatigue 30(12):2119–2126. https://doi.org/10.1016/j.ijfatigue.2008.06.003
Abroug F, Pessard E, Germain G, Morel F (2018) A probabilistic approach to study the effect of machined surface states on HCF behavior of a AA7050 alloy. Int J Fatigue 116:473–489. https://doi.org/10.1016/j.ijfatigue.2018.06.048
Li G, Tang J, Zhou W, Li L (2018) Fatigue life prediction of workpiece with 3D rough surface topography based on surface reconstruction technology. J Cent South Univ 25(9):2069–2075. https://doi.org/10.1007/s11771-018-3896-3
Cheng Z, Liao R (2015) Effect of surface topography on stress concentration factor. Chin J Mech Eng 28(6):1141–1148. https://doi.org/10.3901/CJME.2015.0424.047
Cheng Z, Liao R, Lu W, Wang D (2017) Fatigue notch factors prediction of rough specimen by the theory of critical distance. Int J Fatigue 104:195–205. https://doi.org/10.1016/j.ijfatigue.2017.07.004
Hua Y, Liu Z (2019) Effects of machining induced residual shear and normal stresses on fatigue life and stress intensity factor of Inconel 718. Appl Sci Basel 9(22):4750. https://doi.org/10.3390/app9224750
Moussaoui K, Mousseigne M, Senatore J, Chieragatti R (2015) Influence of milling on the fatigue lifetime of a Ti6Al4V titanium alloy. Metals Basel 5(3):1148–1162. https://doi.org/10.3390/met5031148
Zhu S, Lei Q, Huang H, Yang Y, Peng W (2016) Mean stress effect correction in strain energy-based fatigue life prediction of metals. Int J Damage Mech 26(8):1219–1241. https://doi.org/10.1177/1056789516651920
Bagherifard S, Guagliano M (2014) Application of different fatigue strength criteria on shot peened notched parts. Part 2: nominal and local stress approaches. Appl Surf Sci 289:173–179. https://doi.org/10.1016/j.apsusc.2013.10.130
Van DV, Lee C, Chang K (2015) High cycle fatigue analysis in presence of residual stresses by using a continuum damage mechanics model. Int J Fatigue 70:51–62. https://doi.org/10.1016/j.ijfatigue.2014.08.013
Fernández-Pariente I, Bagherifard S, Guagliano M, Ghelichi R (2013) Fatigue behavior of nitrided and shot peened steel with artificial small surface defects. Eng Fract Mech 103:2–9. https://doi.org/10.1016/j.engfracmech.2012.09.014
Cui W (2002) A state-of-the-art review on fatigue life prediction methods for metal structures. J Mar Sci Tech-Japan 7(1):43–56. https://doi.org/10.1007/s007730200012
Zheng X (1986) A further study on fatigue crack initiation life—mechanical model for fatigue crack initiation. Int J Fatigue 8(1):17–21
As S, Skallerud B, Tveiten B (2008) Surface roughness characterization for fatigue life predictions using finite element analysis. Int J Fatigue 30(12):2200–2209. https://doi.org/10.1016/j.ijfatigue.2008.05.020
Miyazaki T, Aono Y, Noguchi H (2007) A practical stress analysis for predicting fatigue limit of metal with axisymmetric complex surface. Int J Fracture 143(4):355–367. https://doi.org/10.1007/s10704-007-9068-3
Baek D, Ko T, Kim H (2001) Optimization of feedrate in a face milling operation using a surface roughness model. Int J Mach Tool Manuf 41(3):451–462. https://doi.org/10.1016/S0890-6955(00)00039-0
Javidi A, Rieger U, Eichlseder W (2008) The effect of machining on the surface integrity and fatigue life. Int J fatigue 30(10–11):2050–2055. https://doi.org/10.1016/j.ijfatigue.2008.01.005
Hyndman R, Athanasopoulos G (2014) Forecasting: principles and practice. OTexts, London
Zhu S, Liu Q, Lei Q, Wang Q (2018) Probabilistic fatigue life prediction and reliability assessment of a high pressure turbine disc considering load variations. Int J Damage Mech 27(10):1569–1588. https://doi.org/10.1177/1056789517737132
Funding
This research was supported by Sichuan Science and Technology Program (Nos. 2019ZDZX0021 and 2020ZDZX0014) and special project of basic scientific research of Sichuan University and Deyang (20826041D4254).
Author information
Authors and Affiliations
Contributions
Yanxuan Song: Conceptualization, Data curation, Methodology, Validation, Writing-original draft. Ming Yin: Conceptualization, Funding acquisition, Methodology, Writing-review and editing. Pengyan Lei: Formal analysis, Validation. Shuo Huang: Visualization, Software. Guofu Yin: Funding acquisition, Validation. Yang Du: Visualization.
Corresponding author
Ethics declarations
Ethics approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Song, Y., Yin, M., Lei, P. et al. Predicting the fatigue life of machined specimen based on its surface integrity parameters. Int J Adv Manuf Technol 119, 8159–8171 (2022). https://doi.org/10.1007/s00170-021-08429-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00170-021-08429-w