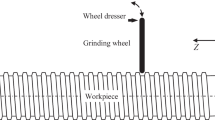
Abstract
Based on the topology analysis of a screw grinder mapping the dressing error of the grinding wheel (DEGW) to the geometric errors of the virtual axis, an improved accuracy model of the screw grinder with 36 geometric errors is established, and an error model of ball screw profile parameters is established according to the forming principle. Then, the Sobol method is performed to analyze the error sensitivity and obtain the crucial geometric errors affecting the profile parameters by considering the individual and intercoupling effect. It is worth mentioning that the overall change of the global sensitivity sum of the crucial geometric errors for lead error (EL) and pitch diameter error (EPD) is 22.9% and 30.2%, respectively, which indicates that the model considering the DEGW has a stronger ability to identify the geometric errors. Lastly, the grinding experiments of ball screw under the adjustment of four grinder geometric errors are conducted. The results show that the crucial geometric error corresponding to the EL and EPD is consistent with the calculation results of the Sobol method, which verifies the effectiveness of the proposed method, and provides a way to trace the machining errors.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The parameters of ball screw raceway profile directly determine the load distribution in ball screws, and therefore affect the contact rigidity, friction characteristics, and service life [1]. The grinding surface of the ball screw raceway is Archimedes spiral, which has a relatively complex process compared with cylindrical grinding and surface machining. The machining accuracy of the raceway is affected by multi-source errors, such as geometric error, grinding wheel error, thermal error, deformation error, and servo control error. Considering that the geometric error accounts for about 40% of all the errors and its advantage in repeatability, stability, and systematisms, it could be measured and compensated [2]. Therefore, the crucial geometric errors of screw grinder should be analyzed, which can provide an efficient way to improve the machining quality of raceways [3].
Existing researches on machine tool manufacturing errors mainly used the homogeneous transformation matrix method of the multi-body system theory [4]. Based on the multi-body theory, Han et al. developed a geometric error model of a three-axis CNC machine tool and studied the distribution and evolution of the comprehensive error in the workspace, which indicated that the positioning error of an axis constitutes a high proportion in the axial component of the comprehensive error [5]. Wu et al. used the homogeneous transformation matrix to establish the relative motion constraint equation of the five-axis machine tool for iterative compensation of geometric errors [6]. Wang et al. established a geometric error model of a five-axis CNC machine tool based on multi-body system theory, of which effectiveness was verified through cutting experiments [7]. Chen et al. proposed a model including the geometric errors of the translation axes and rotary axis for a large-scale grinding machine tools with six axes [8], and Khan et al. presented a systematic geometric model for calibration of a newly designed 5-axis turbine blade grinding machine [9]. Summarily, the mentioned machine tool error models mainly focused on the traditional workpiece-tool error transmission chain composed of five axes and lacked the research of dressing error under the error transmission chain.
With regard to the generation of geometric errors in the forming process of complex surfaces, existing researches mainly involved the importance of cutting tool displacements and dynamic deflections in terms of the surface finish and the error modeling and analysis by point contact and line contact machining [10, 11]. Pimenov et al. determined the torsional angle of a machine tool-device-spindle unit and developed a flatness deviation model considering milling and tool wear [12]. Wojciechowski et al. analyzed of relations between the instantaneous tool displacements and surface roughness formed during ball end milling of surface with inclination towards the tool’s axis, demonstrating that the value of tool’s overhang significantly affects the mechanisms of surface roughness generation [13]. Pimenov et al. studied the influence of the relative position of the face mill towards the workpiece and milling kinematics on the components of the cutting forces, the acceleration of the machine spindle, and the surface roughness [14]. For point contact machining, Lin and Shen established a tool pose error model to characterize the machining error [15]. Fan et al. studied the error source of the CNC machine tool and proposed an error space model of side milling for the S-shaped specimen [16]. For the workpiece processed based on the line contact meshing principle such as gear and worm, Li et al. studied the gear transmission by the fourth-order polynomial function and established a modified tooth surface error model to describe the local deviation [17]. Dudás et al. analyzed the pitch fluctuation of conical thread surface caused by the geometric error of machine tool spindle and designed the pin which can eliminate the pitch error [18]. Wei and Zhang carried out the error simulation by mapping the relative pose error of the grinding wheel and screw rotor into the center distance, grinding wheel deflection angle, and wear error [19]. The forming mechanism of the ball screw raceway is similar to that of the screw rotor and the worm, and the effect of the error on the surface can be analyzed by the forming process of the spiral surface. Considering that the performance of the ball screw is essentially affected by the error accumulation in the effective travel, the geometric error of the screw grinder acts on the relative position of the grinding wheel and workpiece will generate the error and affect the performance. Summarily, the existing researches mainly concentrated on the machining accuracy of conventional revolving surface, while few scholars have studied the influence of geometric errors on the profile parameters reflecting the product performance for the ball screw.
Considering the various geometric errors and the complex coupling relationship in machine tools, it is of significance to identify the crucial geometric errors. Based on the error model, the parameter sensitivity can quantify the influence of parameters in the whole, including local sensitivity and global sensitivity [20, 21]. Li et al. analyzed the error sensitivity of the precision model of machining center based on the matrix differential method [22]. Based on the theory of exponential product and the relation of differential axis in a coordinate system, Fu et al. proposed a contribution model of geometric error for the motion axis of a five-axis CNC machine tool [23, 24]. Cheng et al. used the Sobol method and Morris method and Liu et al. used the reliability theory to analyze the error sensitivity [21]. Sobol method, which has both characteristics of local sensitivity and global sensitivity, possesses advantages of fast convergence speed and simple operation and has good applicability for quantifying the influence of machine tool geometric errors [25,26,27].
Therefore, to analyze the crucial geometric errors that affect the profile parameters in the processing of ball screw with screw grinder, this paper proposes a novel accuracy model based on the topology analysis mapping the DEGW to the geometric errors of the virtual V-axis and introducing the geometric error into the transmission chain of tool-workpiece. To study the relationship between revolving surface and profile parameters, an error model of ball screw profile parameters referring to the forming principle is established. The rest of this paper is organized as follows. In “Section 2,” the accuracy model of the screw grinder considering DEGW is established. In “Section 3,” the error model of profile parameters based on forming error is established. In “Section 4,” the sensitivity analysis of crucial geometric parameters is carried out based on the Sobol method. In “Section 5,” the sensitivity results are analyzed and verified by designed experiments. Finally, “Section 6” is the conclusion of the paper.
2 Accuracy model of screw grinder considering the DEGW
2.1 Structure of screw grinder
According to the forming mechanism of the ball screw raceway, during the raceway forming process, the workpiece rotates around its own axis, while the grinding wheel rotates around its own axis at a high speed and moves along the workpiece axis at a constant speed. Under the circumstance, every time the workpiece rotates for one circle, the grinding wheel moves forward a lead travel. The schematic diagram of the main shafting for external and internal screw grinder is shown in Fig. 1.
The forming process of raceway with equidistant helicoids is mainly the linkage between the rotation of C-axis and the translation of Z-axis, of which motion relationship satisfies the specific functions. The grinding wheel frame is set on the translational shaft (X-axis) to realize the reciprocating movement of the grinding wheel from the workpiece to the diamond roller, which is used in the dressing if the grinding wheel is worn. To meet the requirements of the specific helical angle of the ball screw, A-axis is used to adjust the angle between the axis of the grinding wheel and the workpiece.
The topological structure of grinding machine suitable for both external screw and internal screw grinder can be established based on the theory of multi-body system, which is shown in Fig. 2. 1-2-3-S is the error transmission branch chain from bed to workpiece, and 1-4-5-6-W is the error transmission branch chain from bed to grinding wheel. In the grinding process of the screw grinder, carriage 2 moves along Z-axis to realize the axial feed of workpiece and grinding wheel. The cross slide 4 slides along the X-axis to realize the grinding wheel dressing during grinding. The slipway 5 is fixed on the moving pair of y-direction, so there is no relative movement in the grinding process, but its pose error affects the grinding. The pendulum shaft 6 can rotate along A-axis to adjust the deflection angle of the grinding wheel.
2.2 Traditional accuracy model
The geometric errors of the grinder include position-independent geometric errors (EPIGs) and position-dependent geometric errors (EPDGs). The EPIG is caused by the assembly error of shafting, which has nothing to do with the position of the motion axis. The EPDG is caused by the manufacturing defects of the shafting, which is related to the position of the moving shaft. In the traditional multi-axis CNC machine tools, X-axis, Y-axis, and Z-axis are the main translational axes, which constitute the basic orthogonal axis system of CNC machine tools. In the rigid analysis of the screw grinder, the model is simplified to describe the grinding completely. Considering that there is no translational motion in Y-axis, the geometric error caused by Y-axis is not considered, and the geometric error of other axes along y-direction is retained.
In the multi-body theory, the machine tool is regarded as a multi-body system, and low order volume array is used to describe the relationship among the bodies in the topology. Establishing the generalized coordinate system for the multi-body system, the reference coordinate system O − xyz is set on Z-axis. Analyzing the EPIGs between adjacent bodies, the error relations can be obtained. There are some perpendicular errors between spindle C and x-direction and y-direction of machine tool coordinate system. There are some perpendicular errors between X-axis and Z-axis. There are some perpendicular errors between slipway 5 (y-direction degrees of freedom) and x-direction and z-direction of the machine tool coordinate system. There are some perpendicular errors between A-axis and y-direction and z-direction in the machine tool coordinate system. Accordingly, the grinder contains 7 EPIGs. Fig. 3 is a schematic diagram of geometric error transmission between bodies which is independent of position based on the topological structure of the screw grinder. SZX is the perpendicular error between X-axis and z-direction; SXy is the perpendicular error between X-axis and y-direction; εXC is the angular misalignment error of C-axis around X-axis; εyC is the angular misalignment error of C-axis around y-direction; and other error terms have a similar referential relationship.
Due to the inevitable manufacturing defects, each axis will produce 6 geometric errors, including 3 translational errors and 3 rotational errors, which generate the errors between the actual motion and the ideal motion. The grinder contains 24 EPDGs, and Fig. 4 shows the schematic diagram of geometric error transmission which is dependent on the position based on the topological structures. δx(Z) is the radial runout of Z-axis along x-direction; δz(Z) is the positioning error of Z-axis; εx(Z) is the swing angle error of Z-axis around x-direction; εz(Z) is the roll angle error of Z-axis around z-direction; δx(C) is the radial runout of C-axis along x-direction; δz(C) is the axial runout of C-axis; εx(C) is the angular error of C-axis around x-direction; and εz(C) is the angular positioning error of C-axis around z-direction.
2.3 DEGW
In the grinding process, a small amount of surface damage on the grinding wheel is inevitable, and the wear caused by long-term operation needs to be trimmed to ensure the normal profile and machining accuracy. In the dressing process, the geometric error will cause the deviation of the position and pose of the grinding wheel and produce the raceway profile error by influencing the revolving surface of the grinding wheel.
Based on the action mode of each error and the multi-body system theory, the traditional accuracy model is improved, that is, introducing the virtual V-axis into the model and representing the grinding wheel dressing error by the geometric errors of V-axis. The DEGW is inserted into the error transmission branch chain of the bed-grinding wheel and is regarded as the typical high order body of A-axis and the typical low order body of grinding wheel. The error transmission branch of the bed-grinding wheel is changed to 1-4-5-6-V-W, and the geometric error transmission diagram of the screw grinder considering the DEGW is established, as shown in Fig. 5.
The effect of DEGW on raceway profile error is equivalent to that of the geometric error of virtual V-axis, which is suitable for both internal and external screw grinding methods. The coordinate system in the grinding wheel dressing process is constructed in Fig. 6.
Fig. 7a shows the EPIGs in the mapping process of the DEGW to the geometric error of virtual V-axis. Among them, εAV represents the Abbe error caused by the assembly of the wheel axis and the diamond roller shaft. This can be obtained by the perpendicular error between A-axis and the virtual V-axis.
Fig. 7b shows the EPDGs in the mapping process of the DEGW to the geometric error of virtual V-axis. Among them, εa(V) represents the wheel deflection angle error, which can be equivalent to the swing angle error of virtual V-axis around A-axis. δx(V) is the positioning error of the grinding wheel carriage moving along the x-direction guideway. The error affects the actual center distance between the grinding wheel shaft and the diamond roller shaft, which can be equivalent to the positioning error of the virtual V-axis along x-direction. The straightness errors of the X-axis in the y and z-directions δy(V) and δz(V) affect the relative position of the grinding wheel and the diamond roller, which can be equivalent to the straightness error of the virtual V-axis in the y and z-directions. Therefore, the virtual V-axis contains 1 EPIG and 4 EPDGs.
2.4 Improved model
After adding the DEGW into the model, the screw grinder can be regarded as a special five-axis machine tool with 36 geometric errors. The geometric errors of the screw grinder are shown in Table 1, including 8 EPIGs and 28 EPDGs.
According to the structure of the screw grinder, 1-2-3-S is the error transmission chain from bed to workpiece, and 1-4-5-6-V-W is the error transmission chain from bed to grinding wheel. The ideal position matrix between adjacent bodies can be expressed as a fourth-order unit matrix I4 × 4, and the position error matrix can be expressed by EPIGs. The homogeneous characteristic matrix is represented by T, and T12 is the characteristic matrix of geometric error transfering from rigid body 1 to body 2. Table 2 shows all the position characteristic matrices between adjacent rigid bodies in the screw grinder.
The motion axis includes two translation axes (Z-axis and X-axis) and two rotation axes (C-axis and A-axis). The position parameters are regarded as variables, and the ideal motion matrix between adjacent bodies can be obtained. The motion error matrix can be obtained by expressing the EPDG with the homogeneous characteristic matrix. The ideal motion matrix of virtual V-axis contains no variable, while the motion error matrix contains 4 EPDGs. Table 3 shows all motion characteristic matrices of adjacent rigid bodies of the screw grinder.
According to the structure of the screw grinder, 1-2-3-S is the error transmission chain from bed to workpiece, and 1-4-5-6-V-W is the error transmission chain from bed to grinding wheel. Therefore, the complete transmission chain of geometric error from grinding wheel to workpiece is W-V-6-5-1-2-3-S. The accuracy model of the screw grinder considering the DEGW can be obtained. The ideal homogeneous characteristic transformation matrix \( {T}_{ws}^i \) from the grinding wheel coordinate system to the workpiece coordinate system is as follows:
The actual homogeneous characteristic transformation matrix \( {T}_{ws}^a \) from the grinding wheel coordinate system to the workpiece coordinate system is as follows:
The accuracy model of screw grinder considering DEGW can be expressed by the position error δw and the pose error εw of grinding wheel:
where \( {T}_{ws}^i \) denotes the actual characteristic matrix considering the DEGW; \( {T}_{ws}^a \) denotes the ideal characteristic matrix; the coordinate vector of any point on the revolving surface in the grinding wheel coordinate system is Rw = [Rx, Ry, Rz, 1]T; and the normal vector of any point is nw = [nx, ny, nz, 0]T. The forming process of the workpiece spiral surface is discretized, and the position and pose error of the grinding wheel in the whole machining path can be calculated by the simulation program.
3 Error model of profile parameters based on forming surface
According to the spiral surface forming theory of the grinding wheel, the radius vector r is constructed from the origin O of the workpiece coordinate system to the point on the revolving surface of the grinding wheel. If the linear velocity vector \( \overrightarrow{\boldsymbol{v}} \) of this point during the spiral motion around the workpiece axis is perpendicular to the normal vector \( \overrightarrow{\boldsymbol{n}} \) of the revolving surface at this point, the point is defined as the contact point on the revolving surface, and the contact line is connected by many contact points. Assuming that i, j, k represent the unit vectors in the x, y, z-directions of the workpiece coordinate system. The ideal contact line on the formed spiral surface can be obtained from the revolving surface of the grinding wheel, which can be expressed as:
where p = Ph/2π; Ph is the lead. In the finish grinding process of workpiece, the geometric error of grinding synthetically affects the final position and pose of the grinding wheel, which causes the relative spatial position error between the grinding wheel and workpiece. In that case, the actual contact line deviates from the ideal contact line, and the final spiral surface has a certain degree of deviation to generate the profile errors.
Assuming that the unit vectors of the grinding wheel coordinate system are i′,j′,k′, and (ZW, RW) is the array of the two-dimensional profile of the grinding wheel. If Rw is a variable, the two-dimensional profile of the grinding wheel can be expressed as (f(RW), RW). The coordinate vector of any point on the revolving surface of the grinding wheel can be expressed as:
The vector diameter r can be expressed as r = Rw + ai, where constant a is the vertical distance between the workpiece axis and the grinding wheel axis. The normal vector of grinding wheel revolving surface can be expressed as:
The derivative of RW to ZW is calculated by the difference method. If λ is the helical angle of the workpiece, the relationship between the unit vector of the grinding wheel coordinate system and the workpiece coordinate system is as follows:
The new position of the grinding wheel is obtained from the grinding wheel-workpiece geometric error transmission chain. In the geometric error model of screw grinder, the characteristic transformation matrix from grinding wheel to workpiece affects the position and pose of grinding wheel, and the actual modified contact line equation considering the geometric error of screw grinder is obtained. The equations of the ideal contact line and the actual contact line are as follows:
The influence of characteristic transformation matrix TWs should precede the transmission of the unit vector between grinding wheel and workpiece coordinate system. By solving the above two contact line equations, the grinding wheel parameter array with geometric error \( \left[{R}_W,{Z}_W,{\varphi}_W^a\right] \) and parameter array without geometric error \( \left[{R}_W,{Z}_W,{\varphi}_W^i\right] \) can be obtained. Then the ideal contact line lsi and the actual contact line lsa in the workpiece coordinate system are expressed as:
where Msw is the homogeneous transformation matrix from the grinding wheel coordinate system to the workpiece coordinate system, given by:
Considering that the contact line belongs to a space curve, the vector equation of the workpiece spiral surface is expressed as:
where θ is the phase angle of the space curve turning around the workpiece axis.
Fig. 8 shows the ideal contact line and the actual contact line considering the geometric errors in the forming process. The actual raceway can be obtained by spiral transformation of the actual contact line. Considering that the ball screw raceway is formed by spiral motion based on its normal profile, the normal profile can be obtained by projecting the workpiece spiral surface to any normal section. Essentially, the ideal normal profile vector rspi and the actual normal profile vector rspa are composed of numerous discrete points.
where fp is the projection function of the spiral raceway to the normal section. After calculating the ideal normal profile vector and the actual normal profile vector, four raceway profile errors can be obtained, namely, EL, EPD, contact angle error, and raceway arc radius error [28, 29]. Fig. 9 is the schematic diagram of the four profile errors, where rGa is the actual arc radius of the raceway; α0a is the actual contact angle of the raceway; ∆rG is the error of arc radius; ∆α0 is the error of contact angle; ∆DP is the error of pitch diameter; and ∆Ph is the lead error. Accordingly, the error model of raceway profile parameters can be established:
where ffit is the fitting function of the normal discrete points with respect to four parameters.
4 Analysis of crucial geometric errors of raceway profile parameters
4.1 Global sensitivity analysis based on Sobol method
The profile parameter model established in “Section 3” is a typical multi-input and multi-output system, that is, 36 geometric errors inputs corresponding to 4 errors outputs of raceway profile parameter, which can be simplified to:
where G = [x1, x2, …, xm]T refers to the vector group of geometric errors, and ΔF refers to the vector group of raceway profile errors. To identify the crucial geometric errors of the grinder affecting four raceway profile parameters, the Sobol method based on variance is used to calculate the error sensitivity by estimating the error contribution to the output variance of the model. The sensitivity calculation method based on variance is to decompose the function ΔF = f(G) into 2n increasing terms:
where f0 is a constant, fi(xi) is a univariate function with respect to xi, and fij(xi, xj) is a function with respect to xi and xj, and so on. The variance of the function f(G) is decomposed into multiple sub-items, given by:
where V is the total of the model output variance; Vi is the output variance caused by xi; Vij is the output variance caused by the coupling of xi and xj; and other high-level sub-items have similar definitions.
To characterize the contribution of individual variables to the total variance of the model output, the first-order sensitivity index Si can be calculated by:
Similarly, to characterize the comprehensive contribution of variables to the total output variance of the model, the global sensitivity index STi is introduced. It can be obtained by comprehensively calculating the influence of the individual variable and the mutual coupling with any other input items.
The traditional sensitivity calculation obtains the expectation and variance of the model by calculating the corresponding integral value, which results in a surge of computation. Considering the statistical significance of the geometric error, it is inappropriate to set it as a specific value for analysis. The Sobol method based on variance uses the quasi-Monte Carlo method to estimate the integral value, which significantly reduces the computation. It converts sensitivity calculation into mutual calculations between two sampling matrices, which ensures any calculation of the sampling matrix can be input at a time.
Fig. 10 is the sensitivity analysis flow of grinder crucial geometric errors which affects the profile error. Generally, the raceway calculation can be solved by substituting the raceway parameters and wheel profile data into the contact line equation, which is based on the grinding wheel model and the raceway model. The ideal raceway equation can be obtained by the ideal contact line after substituting the discrete processing tracepoints into the ideal characteristic matrix of grinder geometric error transmission. The actual raceway can be obtained by the actual contact line equation after substituting the Sobol sampling results and the discrete processing tracepoints into the actual characteristic matrix of grinder geometric error transmission.
For the screw grinder, 12 EPDGs and 3 EPIGs of the two linear axes are measured by the Renishaw XL-80 laser interferometer, and 12 EPDGs of the two rotational axes are measured by the Renishaw XR-20W laser interferometer. According to the measuring results, the position error and the pose error are distributed in [0,20] μm and [0,30] mdeg, respectively, and the sampling range of the perpendicular error is [0,30] mdeg. For the model proposed in this paper, the number of sampling is N and the matrix dimension m is 36, and the total number of sampling calculation is N(m + 2). The statistics in the case of N = 100 is shown in Table 4.
Finally, the sensitivity index of a single variable can be obtained by:
Fig. 11 shows the calculation flow of the Sobol method. Firstly, generating two sampling matrices (A and B) with the dimension of N × 36 according to the Sobol sequence and the probability distribution of geometric errors. Secondly, replacing the ith column of B with the ith column of A, and the other columns remain the same as B to obtain the matrix \( {\boldsymbol{A}}_{\boldsymbol{B}}^i \). Thirdly, taking any row of A, B, and \( {\boldsymbol{A}}_{\boldsymbol{B}}^i \) as a set of inputs, and the output results f(A), f(B), and\( f\left({\boldsymbol{A}}_{\boldsymbol{B}}^i\right) \) can be obtained by the model. The calculated methods are implemented by programming.
4.2 Sensitivity analysis of crucial parameters for raceway profile
The Sobol method takes enough samples to calculate the influence of a single variable on the output result. Therefore, it is necessary to study the influence of the increase of sample capacity on the stability of the results. Fig. 12 is the influence of sampling times on the sensitivity index of EL. When the number of samples is greater than 1500, there is no large fluctuation in the result. When the sampling times are 3000, 4000, and 5000, the sensitivity result is gradually stable. As the number of samples increases, the variables can be easily divided into two groups according to the obvious difference of sensitivity index. Therefore, 5000 is selected as the final sampling time.
A moving coordinate system CS1 = {x1, y1, z1}, with its origin on the nominal ball center pathway, is established such that its x1-axis has a helical angle with the screw axis, and y1-axis is along the radial direction of the screw. The normal section of the ideal raceway is in a two-dimensional x1-y1 plane. The EL (ΔPh) is the offset of the actual ball center along the x1-direction in the plane. The result of the sensitivity indices of the EL is shown in Fig. 13. Similarly, the EPD (ΔDp) is the offset of the ball center along the y1-direction in the plane. The result of the sensitivity indices of the EPD is shown in Fig. 14.
When the raceway profile changes, it can be indicated by the contact angle error of the left and right raceways. The contact angle error Δα0 is expressed as:
where \( {\alpha}_0^a \) is the actual contact angle; \( {\alpha}_0^i \) is the ideal contact angle. The actual contact angle can be obtained by fitting the points on the raceway arc. Fig. 15 shows the calculation results of the sensitivity indices of 36 geometric errors to the contact angle error.
The error of the raceway arc radius ΔrG is expressed as:
where rGa is the actual radius of the raceway; rGi is the design radius of the raceway. Fig. 16 is the result of the sensitivity indices of the raceway radius error.
5 Discussion and validation
5.1 Results analysis based on Sobol method
From the sensitivity result in “Section 4.2,” it can be seen that the relative trends of the sensitivity index Si and STi are the same in most cases, and the individual effect of each variable on the output result is basically consistent with its coupling ability, which indirectly verifies the reliability of the result. Whether a single variable has a strong individual effect or a strong coupling ability, it is the performance of a variable with high sensitivity. It has to be mentioned that the sensitivity index and performance of a variable are inconsistent in some cases, such as No. 22 and No. 28 variables in Fig. 13. They have a significantly lower sensitivity index Si than most other variables. Although their sensitivity index STi are less than that of the five highest variables, they are significantly higher than the other nearly 30 variables. This indicates that these two variables have little individual contribution to the output, but they have a strong coupling ability with other variables. As such, the index STi and Si should be considered comprehensively.
Table 5 is the crucial geometric errors affecting the sensitivity of profile parameters. According to the results, the EL is mainly caused by linear geometric errors, and the contact angle error is mainly caused by angular geometric errors. The crucial errors with respect to the raceway radius and pitch diameter include linear and angular geometric errors. According to the machining experience, the EPD is greatly affected by the linear geometric error related to x-direction, and the EL is greatly affected by the linear geometric error related to z-direction, which are consistent with the experimental results.
To analyze the influence of the improved accuracy model on the sensitivity index of crucial errors, the total of the global sensitivity STi of the crucial geometric errors in the proposed model and the traditional model is compared respectively. For the traditional accuracy model, the global sensitivity sum of the crucial geometric errors for the EL is 0.61, and that for the EPD is 0.52. For the improved model, the global sensitivity sum of crucial geometric errors for the EL is 0.75, and that for the EPD is 0.68. The overall change of the global sensitivity sum of the crucial geometric errors for EL and EPD is 22.9% and 30.2%, respectively, which indicates that the model considering the DEGW has a stronger ability to identify the geometric error.
5.2 Experiment verification
To verify the effectiveness of the established model and the sensitivity analysis results, it is persuasive to process the raceways after changing the geometric errors of the grinder. For the screw grinder, only part of the positioning parameters can be adjusted manually within a certain range, and the rest parameters are regarded as fixed values after the factory calibration. By analyzing the influence of several controllable geometric errors on profile parameters, the sensitivity of geometric errors can be verified.
The angle between the axis of the grinding wheel and the workpiece can be adjusted along A-axis by the rotary gear located at the rear of the bed. The angle between the axis of the grinding wheel and the diamond roller can be adjusted along V-axis, which can be monitored by an electronic angle measuring instrument. The displacement fine-tuning along the X-axis and Z-axis of the grinder is often used for positioning error compensation of the feed system. Therefore, the geometric errors that can be changed include εx(A), εx(V), δx(X), and δz(Z). According to Fig. 13 and Fig. 14, δz(Z) (the positioning error of Z-axis) is sensitive to the EL; δx(X) (the positioning error of the X-axis) is sensitive to the EPD; and both εx(A) and εx(V) are insensitive to the EL and EPD. The errors Δεx(A) and Δεx(V) in the same direction and action mode are applied to the angular positioning errors εx(A) and εx(V) through angle adjustment. The errors Δδx(X) and Δδz(Z) in the same direction and action mode are applied to the linear positioning errors δx(X) and δz(Z) by modifying the numerical control program.
In the experiments, the grinder was adjusted to a good condition according to the requirements, and the semi-finished ball screw before the fine grinding was selected to process in the constant temperature workshop. To obtain an obvious contrast effect, three groups of tests under the gradient errors corresponding to a geometric error were set. The gradient was 0.030° for the angular positioning error, and 0.015 mm for the linear positioning error. Considering the difference between the angular positioning error and the linear positioning error of the grinder shaft, two ball screws were used to complete the tests respectively. Since the measurement of EPD and EL needs more than two raceways, three raceways were processed respectively under each error condition. According to the specified processing technology, after finishing three raceways each time, a different error was applied on the grinder for the next group of raceways. Additionally, the travel of three raceways was added as an ideal reference group test under the condition of no error input. Therefore, the final machining ball screw was determined as R25-10, and the effective length should be more than 21 raceways.
During the machining, the ball screw was installed by the headstock and tailstock, and a chuck was used in the headstock rotating device to connect one end of the ball screw. A fixed shaft support unit was placed under the ball screw to reduce the deflection caused by the weight. The ball screw processing corresponding to four geometry errors on the screw grinder is shown in Fig. 17. As shown in Fig. 18, the axial profile of the ball screw raceways corresponding to different parts of two ball screws was measured using an Opticom roughness profilometer, at a speed of 12 mm min−1. And the probe was adjusted by the XOY mobile platform to get the axial section along the generatrix. By the arc range selection and axial-normal transformation, the normal section can be obtained according to the helical angle. After calculating the contact angle and arc radius of each normal section by arc fitting, the EL can be analyzed by the axial fluctuation of fitted ball center of two adjacent raceways, and the EPD can be analyzed by the radial runout of the ball center relative to the axis, which are shown in Fig. 19.
The measuring results of machined raceways are shown in Table 6. In terms of the consistency of raceway processing, the maximum STDEV of the EPD and EL is 15.31e−3 μm and 12.34e−3 μm for the raceway corresponding to the error condition of δx(A). For the raceway corresponding to the error condition of δx(V), the maximum STDEV of the EPD and EL is 18.77e−3 μm and 11.68e−3 μm, respectively. For the raceway corresponding to the error condition of δx(X), the maximum STDEV of the EPD and EL is 9.84e−3 μm and 11.13e−3 μm, respectively. For the raceway corresponding to the error condition of δz(Z), the maximum STDEV of the EPD and EL is 20.55e−3 μm and 25.23e−3 μm, respectively. The fluctuation of the index proves that the machined raceways under the same conditions are relatively uniform and can meet the experimental requirements.
The difference represents the change of the measured value relative to that of the control group. For the influence of the EPD, when the angular error Δεx(A) and Δεx(V) increase from 0.030 to 0.090°, the difference corresponding to the EPD is 0.463% and 0.961%, respectively. When Δδz(Z) increases by 0.045 mm, the difference is only 0.214%. However, when the linear error Δδx(X) increases by 0.015 mm, a more obvious difference corresponding to the EPD is 10.377%. Therefore, the geometric error δx(X) is sensitive to the EPD compared to the other three geometric errors.
For the influence of the EL, when the angular error Δεx(A) and Δεx(V) increase to 0.030°, the corresponding EL is 2.225% and 2.295%, respectively. When the linear error Δδx(X) increases by 0.045 mm, the error difference is only 0.278%, which indicates that δx(X) has little effect on the EL. When Δδz(Z) increases by 0.015 mm, the corresponding EL increases by 800%, which shows that the geometric error δz(Z) is very sensitive to the EL. Similarly, the result shows that the angular error has a small influence on the profile parameter, while the linear error has an extreme influence on the parameter. That is, the influence of the sensitive linear error is very large, while the influence of the non-sensitive linear error is so small that it can be ignored. These results can verify the feasibility and effectiveness obtained by the Sobol method in Table 5.
6 Conclusion
In this paper, by converting the DEGW into the geometric error of virtual V-axis, the accuracy model of screw grinder with 36 geometric errors is established, unifying the raceway forming process of internal and external screw grinder. Furthermore, according to the forming principle, the error model of raceway profile parameters is established, constructing the relationship between geometric error and profile error. Based on the proposed model, the sensitivity of crucial geometric error to profile parameters is calculated by the Sobol method. Experiments are designed to verify the influence of crucial geometric parameters on profile parameters. The main contributions and conclusions are summarized as follows.
-
(1)
For the grinder with a grinding wheel dressing device, the dressing error is mapped to the geometric error of the virtual axis on the tool error transmission chain, and the dressing error is introduced to study the influence of the crucial geometric errors on the profile parameters. Analysis shows that the effect of DEGW to EL, EPD, and arc radius error of ball screw cannot be ignored, which is an important error source in raceway forming.
-
(2)
The global sensitivity method is used to calculate the contribution of 36 geometric errors of the screw grinder to the profile parameters. The results show that the contact angle error is mainly affected by the angular geometric error, and the EL is mainly affected by the linear geometric error. The sensitive geometric errors of raceway radius and EPD include both linear and angular geometric errors, which provide guidance for the traceability of profile parameter errors. Considering the DEGW, the overall change of the global sensitivity sum of the crucial geometric errors for EL and EPD is 22.9% and 30.2%, respectively, which indicates that the improved model has a higher identification ability.
-
(3)
The experiment results show that δx(X) is sensitive to the EPD compared to εx(A), Δεx(V), and δz(Z), and the change of δz(Z) is very sensitive to the EL, which verified the validity of the established model and the accuracy of the Sobol method. Additionally, the angular geometric error has little effect on the EPD and EL, and the influence of the linear geometric error has an extreme phenomenon, which provides a theoretical basis for error control in the machining process.
-
(4)
The accuracy model and analysis method established in this paper have universal applicability. The research theory can be extended to the study of the forming error of the spiral surface machined by the general grinder.
In future work, the analysis of the causes for the DEGW and how to improve the machining quality of ball screw in an economic way is still a valuable research issue.
Data Availability
Data transparency.
Abbreviations
- EPIGs:
-
the position-independent geometric errors
- EPDGs:
-
the position-dependent geometric errors
- S ZX :
-
the perpendicular error between X-axis and z-direction
- S Xy :
-
the perpendicular error between X-axis and y-direction
- ε XC :
-
the angular misalignment error of C-axis around X-axis
- ε yC :
-
the angular misalignment error of C-axis around y-direction
- δ x(Z):
-
the radial runout of Z-axis along x-direction
- δ z(Z):
-
the positioning error of Z-axis
- ε x(Z):
-
the swing angle error of Z-axis around x-direction
- ε z(Z):
-
the roll angle error of Z-axis around z-direction
- δ x(C):
-
the radial runout of C-axis along x-direction
- δ z(C):
-
the axial runout of C-axis
- ε x(C):
-
the angular error of C-axis around x-direction
- ε z(C):
-
the angular positioning error of C-axis around z-direction
- DEGW:
-
the dressing error of the grinding wheel
- ε AV :
-
the Abbe error caused by the assembly of the wheel axis and the diamond roller shaft
- ε a(V):
-
the swing angle error of virtual V-axis around A-axis
- δ x(V):
-
the positioning error of the grinding wheel carriage moving along the x-direction guideway
- I 4 × 4 :
-
the fourth-order unit matrix
- T :
-
the homogeneous characteristic matrix
- T 12 :
-
the characteristic matrix of geometric error transferring from rigid body 1 to body 2
- α 0 a :
-
the actual contact angle of the raceway
- \( {T}_{ws}^a \) :
-
the actual homogeneous characteristic transformation matrix
- δ w :
-
the position error
- ε w :
-
the pose error
- R w :
-
the coordinate vector of any point on the revolving surface in the grinding wheel coordinate system
- S Ti :
-
the global sensitivity index
- r :
-
the radius vector
- \( \overrightarrow{\boldsymbol{v}} \) :
-
the linear velocity vector
- \( \overrightarrow{\boldsymbol{n}} \) :
-
the normal vector
- i, j, k :
-
the unit vectors in the x, y, z-directions of the workpiece coordinate system
- P h :
-
the lead of ball screw
- i ′ ,j ′ ,k ′ :
-
the unit vectors of the grinding wheel coordinate system
- (Z W, R W):
-
the array of the two-dimensional profile of the grinding wheel
- a :
-
the vertical distance between the workpiece axis and the grinding wheel axis
- λ :
-
the helical angle of the workpiece
- l si :
-
the ideal contact line
- l sa :
-
the actual contact line
- M sw :
-
the homogeneous transformation matrix from the grinding wheel coordinate system to the workpiece coordinate system
- θ :
-
the phase angle of the space curve turning around the workpiece axis
- r spi :
-
the ideal normal profile vector
- r spa :
-
the actual normal profile vector
- f p :
-
the projection function of the spiral raceway to the normal section
- EL (ΔP h):
-
the offset of the actual ball center along the x1-direction in the plane
- EPD (ΔD p):
-
the offset of the ball center along the y1-direction in the plane
- r G a :
-
the actual arc radius of the raceway
- \( {T}_{ws}^i \) :
-
the ideal homogeneous characteristic transformation matrix
- f fit :
-
the fitting function of the normal discrete points with respect to four parameters
- G :
-
the vector group of geometric errors
- Δ F :
-
the vector group of raceway profile errors
- S i :
-
the first-order sensitivity index
- \( {\alpha}_0^a \) :
-
the actual contact angle
- CS1 :
-
a moving coordinate system
- Δα 0 :
-
the contact angle error
- n w :
-
the normal vector of any point on the revolving surface in the grinding wheel coordinate system
- \( {\alpha}_0^i \) :
-
the ideal contact angle
- Δr G :
-
the error of the raceway arc radius
- r G a :
-
the actual radius of the raceway
References
Zhou C, Feng H, Chen Z, Ou Y (2016) Correlation between preload and no-load drag torque of ball screws. Int J Mach Tools Manuf 102:35–40. https://doi.org/10.1016/j.ijmachtools.2015.11.010
Min X, Jiang S (2011) A thermal model of a ball screw feed drive system for a machine tool. Proc Inst Mech Eng C J Mech Eng Sci 225(1):186–193. https://doi.org/10.1177/09544062JMES2148
Wang J, Guo J (2013) Algorithm for detecting volumetric geometric accuracy of NC machine tool by laser tracker. Chinese J Mech Eng 26(1):166–175. https://doi.org/10.3901/CJME.2013.01.166
Tang H, Zhang Z, Li C, Ko T (2019) A geometric error modeling method and trajectory optimization applied in laser welding system. Int J Precis Eng Manuf 20(8):1423–1433. https://doi.org/10.1007/s12541-019-00151-8
Han F, Zhao J, Zhang L, Zhao G, Ji S (2012) Synthetical analysis and experimental study of the geometric accuracy of CNC machine tools[J]. Jixie Gongcheng Xuebao(Chinese Journal of Mechanical Engineering) 48(21):141–147. https://doi.org/10.3901/JME.2012.21.141
Wu C, Fan J, Wang Q, Chen D (2018) Machining accuracy improvement of non-orthogonal five-axis machine tools by a new iterative compensation methodology based on the relative motion constraint equation. Int J Mach Tools Manuf 124:80–98. https://doi.org/10.1016/j.ijmachtools.2017.07.008
Wang S, Yun J, Zhang Z, Liu Y, Zhang Q (2003) Modeling and compensation technique for the geometric errors of five-axis CNC machine tools. Chinese J Mech Engineering (Eng Ed) 16(2):197–201
Chen G, Mei X, Li H (2013) Geometric error modeling and compensation for large-scale grinding machine tools with multi-axes. Int J Adv Manuf Technol 69(9-12):2583–2592. https://doi.org/10.1007/s00170-013-5203-7
Khan A, Wuyi C (2010) Systematic geometric error modeling for workspace volumetric calibration of a 5-axis turbine blade grinding machine. Chin J Aeronaut 23(5):604–615. https://doi.org/10.1016/S1000-9361(09)60261-2
Tao L, Wang Y, He Y, Feng H, Ou Y, Wang X (2016) A numerical method for evaluating effects of installation errors of grinding wheel on rotor profile in screw rotor grinding. Proc Inst Mech Eng B J Eng Manuf 230(8):1381–1398. https://doi.org/10.1177/0954405416654418
Liu Z, Tang Q, Liu N, Song J (2019) A profile error compensation method in precision grinding of screw rotors. Int J Adv Manuf Technol 100(9):2557–2567. https://doi.org/10.1007/s00170-018-2841-9
Pimenov D, Guzeev V, Krolczyk G, Mia M, Wojciechowski S (2018) Modeling flatness deviation in face milling considering angular movement of the machine tool system components and tool flank wear. Precis Eng 54:327–337. https://doi.org/10.1016/j.precisioneng.2018.07.001
Wojciechowski S, Wiackiewicz M, Krolczyk G (2018) Study on metrological relations between instant tool displacements and surface roughness during precise ball end milling. Measurement 129:686–694. https://doi.org/10.1016/j.measurement.2018.07.058
Pimenov D, Hassui A, Wojciechowski S, Mia M, Magri A, Suyama D, Bustillo A, Krolczyk G, Gupta M (2019) Effect of the relative position of the face milling tool towards the workpiece on machined surface roughness and milling dynamics. Appl Sci 9(5):842. https://doi.org/10.3390/app9050842
Lin Y, Shen Y (2003) Modelling of five-axis machine tool metrology models using the matrix summation approach. Int J Adv Manuf Technol 21(4):243–248. https://doi.org/10.1007/s001700300028
Fan J, Tang Y, Chen D, Wu C (2017) A geometric error tracing method based on the Monte Carlo theory of the five-axis gantry machining center. Advances in Mech Eng 9(7):1687814017707648. https://doi.org/10.1177/1687814017707648
Li G, Wang Z, Zhu W, Kubo A (2017) A function-oriented active form-grinding method for cylindrical gears based on error sensitivity. International Journal of Advanced Manufacturing Technology, 92. 92:3019–3031. https://doi.org/10.1007/s00170-017-0363-5
Dudás I, Bodzás S, Mándy Z (2013) Solving the pitch fluctuation problem during the manufacturing process of conical thread surfaces with lathe center displacement. Int J Adv Manuf Technol 69(5-8):1025–1031. https://doi.org/10.1007/s00170-013-5010-1
Wei J, Zhang G (2011, August) Error analysis of precision grinding for screw rotors. In 2011 IEEE international conference on mechatronics and automation (pp. 1939-1944). IEEE. https://doi.org/10.1109/ICMA.2011.5986277
Chen H, Ju Z, Qu C, Cai X, Zhang Y, Liu J (2013) Error-sensitivity analysis of hourglass worm gearing with spherical meshing elements. Mech Mach Theory 70:91–105. https://doi.org/10.1016/j.mechmachtheory.2013.07.010
Cheng Q, Zhao H, Zhang G, Gu P, Cai L (2014) An analytical approach for crucial geometric errors identification of multi-axis machine tool based on global sensitivity analysis. Int J Adv Manuf Technol 75(1-4):107–121. https://doi.org/10.1007/s00170-014-6133-8
Li J, Xie F, Liu X (2016) Geometric error modeling and sensitivity analysis of a five-axis machine tool. Int J Adv Manuf Technol 82(9-12):2037–2051. https://doi.org/10.1007/s00170-015-7492-5
Fu G, Fu J, Xu Y, Chen Z (2014) Product of exponential model for geometric error integration of multi-axis machine tools. Int J Adv Manuf Technol 71(9-12):1653–1667. https://doi.org/10.1007/s00170-013-5586-5
Fu G, Fu J, Xu Y, Chen Z, Lai J (2015) Accuracy enhancement of five-axis machine tool based on differential motion matrix: geometric error modeling, identification and compensation. Int J Mach Tools Manuf 89:170–181. https://doi.org/10.1016/j.ijmachtools.2014.11.005
Cheng Q, Feng Q, Liu Z, Gu P, Zhang G (2016) Sensitivity analysis of machining accuracy of multi-axis machine tool based on POE screw theory and Morris method. Int J Adv Manuf Technol 84(9):2301–2318. https://doi.org/10.1007/s00170-015-7791-x
Zhang Z, Liu Z, Cai L, Cheng Q, Yin Q (2017) An accuracy design approach for a multi-axis NC machine tool based on reliability theory. Int J Adv Manuf Technol 91(5-8):1547–1566. https://doi.org/10.1007/s00170-016-9824-5
Saltelli A., Ratto M., Andres T., et al. Chapter 4. Variance-based methods[M]// global sensitivity analysis. The primer. John Wiley & Sons, Ltd, 2008.
Li SY (2008) Precision and ultra-precision machine tool accuracy modeling technology[M]. National University of Defense Technology Press
Wang K, Feng H, Zhou C, Ou Y (2020) Optimization measurement for the ballscrew raceway profile based on optical measuring system. Meas Sci Technol 32(3):035010. https://doi.org/10.1088/1361-6501/abc3de
Code availability
Custom code.
Funding
This project is supported by the National Science and Technology Major Projects of China (No. 2018ZX04039001), National Natural Science Foundation of China (Grant No. 51705252, 51905274), and the Postgraduate Research & Practice Innovation Program of Jiangsu Province (No. KYCX19_0263).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Ou, Y., Xing, YS., Wang, K. et al. Investigation of crucial geometric errors of screw grinder for ball screw profile parameters. Int J Adv Manuf Technol 118, 533–550 (2022). https://doi.org/10.1007/s00170-021-07917-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00170-021-07917-3